Abstract
We prove that the maximal number of pairwise disjoint 4-blocks in a MOL(6) is 3. We recall various proofs for the non-existence of a MOL(6) and show: with the theorem the proofs can be simplified considerably.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For the notions of latin squares and orthogonal squares see [9] and [8]. Latin squares of order 6 are studied in [11] and [4]. A MOL(6), i.e., a pair of orthogonal latin squares of order 6, is a linear space on 24 points with 4 blocks of length 6 and 36 blocks of length 4. Each 4-block is a quadruple \(\{(r,c,d,t), r,c,d,t \in \{1,2,3,4,5,6\}\}\) consisting of a row r, a column c, a digit d and a transversal t. Two 4-blocks are called disjoint, if they differ in rows, columns, digits and transversals. We prove that the maximal number of pairwise disjoint 4-blocks in a MOL(6) is 3 (Theorem 1). This simplifies the proofs in [3, 5, 7, 12] for the non-existence of two orthogonal latin squares of order 6 (the problem of Euler [10] and Tarry [13]).
2 Disjoint Quadruples
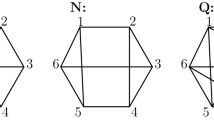
In order to show that the maximal number of pairwise disjoint 4-blocks in a MOL(6) is 3, we start—by contradiction—with a quadruple of pairwise disjoint 4-blocks. This means that the MOL(6) has up to isomorphism a substructure:
Therefore the MOL(6) can be generated by the following point tactical decomposition scheme:
Proposition 1
The point tactical decomposition scheme (2) refines uniquely to the following tactical decomposition scheme:
Proof
Refining the decomposition (2) (computer program TDO-method, [1, 2]) we get one (point and block)-tactical decomposition (3). \(\square \)
Remark
The refining step (done by the computer program automatically) can also be carried out by hand: one has to establish and to solve some system of linear equations, see the “Appendix”.
Proposition 2
The substructure (1) extends (up to isomorphism) uniquely to the following partial MOL(6):
Proof
We extend the subscheme of (3):
This extended tactical decomposition generates exactly one geometry:
This is the MOL(4), (pair of orthogonal latin squares of order 4). On the main diagonal there is the quadruple we started with, and on the secondary diagonal there is the quadruple (in brackets) we added. We now delete this added quadruple and get the proposition.
Proposition 3
The partial MOL(6) (4) extends uniquely (up to isomorphism) to
Proof
In order to complete the upper half of the decomposition (3), we have to add the 24 vertical pairs which are not yet joined. These come from the quadruple of elements of the MOL(4) which we have deleted. For instance the element (1,4,3,2) gives the 6 pairs (1,4,.,.),(1,.,3,.), (1,.,.,2), (.,4,3,.),(.,4,.,2),(.,.,3,2). Similarly for the elements (2,3,4,1), (3,2,1,4) and (4,1,2,3). These are the 24 4-blocks of the MOL(6) and we get the unique incidence structure of the first 16 variables:
In order to extend this structure to the lower part (8 variables) of (3), we have to replace the points in the 24 4-blocks by numbers 5 or 6. In particular the four empty positions in (4) have to be filled by the four elements (5, 5), (5, 6), (6, 5), (6, 6). For the following proposition each permutation of these elements can be taken. \(\square \)
Remark
The automorphism group of MOL(4) has a subgroup which acts as symmetry group \(S_4\) on the secondary diagonal. Therefore we can reach the permutation as given in the proposition.
Proposition 4
The partial MOL(6) (5) cannot be extended to a MOL(6).
Proof
Let the position (1, 4) be occupied by, say, (5, 5). Then in the first row the two digits 3 and 6 are missing and also the two transversals 2 and 6. Since 66 is already used, we have only the combination 36 and 62. The same happens in the fourth column and there are the pairs 36 and 62 missing and must be inserted. But then the pair \((d,t)=(3,6)\) (and also (6, 2)) occurs twice, a contradiction.

\(\square \)
So we have proved:
Theorem 1
The maximal number of pairwise disjoint 4-blocks in a MOL(6) is 3.
3 Latin Squares of Shape C
In [3] there were derived 3 different shapes A), B) and C) for latin squares of order 6. It was proved that squares of shape A) and B) have no or at most 4 transversals, therefore they cannot have an orthogonal square. So only squares of shape C have to be considered for the problem of Euler and Tarry. Let \(d\in \{1,2,3\}\) and \(D\in \{4,5,6\}\) then we give in the following figure the shape C) and a special example:

There are the following conditions for the transversals in Case C), see [3, Lemma p. 425]:
Proposition 5
(a) The three elements with low digits in the \((3 \times 3)\)-subsquare left down have three different transversals. (b) In each of the two \((2 \times 3)\)-rectangles in the first two rows there are six different transversals.
Now we can show
Theorem 2
For each latin square of shape C there does not exist an orthogonal square.
Proof
Start with the three different transversals of the three low digits left down. Take a fourth transversal. This transversal occurs in the \((2 \times 3)\)-rectangle right above. Since in this rectangle there are only high digits, we get 4 pairwise disjoint blocks in contradiction to Theorem 1. \(\square \)
4 Stinson’s Proof for the Non-existence of a MOL(6)
In [12] Stinson gave a proof for the non-existence of a MOL(6) using coding theory. He derived one situation where a MOL(6) might occur and then excluded this by geometric reasoning. This single situation can be described by the following tactical decomposition scheme:

Columns 5 and 10 of the scheme lead to the geometry at the right side, and here we have indicated four pairwise disjoint 4-blocks, a contradiction to Theorem 1.
5 The Two Tactical Decompositions in [5]
In [5] we reduced the problem of the existence of a MOL(6) to the two tactical decompositions TDO I and TDO II and then proved that these cannot generate a geometry. By TDO we mean a tactical decomposition by ordering, a notion which was introduced in [6].
In TDO I columns 6 and 13 define 6 pairwise disjoint 4-blocks. And in TDO II the three disjoint 4-blocks of column 6 together with one 4-block from column 13 define 4 pairwise disjoint 4-blocks, a contradiction to Theorem 1.
References
Betten, A., Betten, D.: Proper linear spaces on 18 points. In: Betten, A., et al. (Eds.) Proceedings of the European Conference on Algorithm and Combined Applications. Gössweinstein, Sept. 12–19 (1999), pp. 40–54. Springer, Berlin (2001)
Betten, A., Betten, D.: There is no Drake/Larson linear space on 30 points. J. of Comb. Designs 18, 48–70 (2010)
Betten, D.: Zum Satz von Euler–Tarry. Der mathematische und naturwissenschaftliche Unterricht 36, 449–453 (1983)
Betten, D.: Die 12 lateinischen Quadrate der Ordnung 6. Mitteilungen Math. Sem. Giessen 136, 181–188 (1984)
Betten, D.: The Reye configuration in a MOL(6). Mitteilungen Math. Ges. Hamburg 39, 1–18 (2019)
Betten, D., Braun, M.: A tactical decomposition for incidence structures. Ann. Discrete Math. 52, 37–43 (1992)
Beth, Th., Jungnickel, D., Lenz, H.: Design Theory. Bibl. Inst. Mannheim, Wien, Zürich (1985)
Colbourne, C.J., Dinitz, J.H.: The CRC Handbook of Combinatorial Designs. CRC Press, Boca Raton (1996)
Denes, J., Keedwell, A.D.: Latin Squares and Their Applications. English University Press, London (1974)
Euler, L.: Recherches sur une nouvelle espece des quarres magiques. Leonardi Euleri opera, ser. I 7, 291–392 (1782). Leipzig, Berlin: Teubner 1923
Fisher, R.A., Yates, F.: The \(6\times 6\) latin squares. Proc. Camb. Philos. Soc. 30, 492–507 (1934)
Stinson, D.R.: A short proof of the nonexistence of a pair of orthogonal latin squares of order six. J. Comb. Theory A 36, 373–376 (1984)
Tarry, M.G.: Le probleme des 36 officiers. Comptes rendus Ass. Franc. Sci. nat. 1(1900), 170–203 (1901). 2
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to the memory of Heinrich Wefelscheid
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof 2 of Proposition 1: We give a proof by hand avoiding the use of a computer:
The 32 blocks of length 4 distribute to the 16- and 8-part in the following way:
We count the flags and the pairs of points in the upper part (the 16 point region) and get the following system of linear equations:
This system has the following solutions, the distribution of block types:
Next we determine the point types of the first 16 points, which means the distribution of the 5 flags to the blocks \(b_4,b_3, b_2, b_1\). Let a, b, c, d be the corresponding numbers (\(a+b+c+d = 5\)). Since the given point has to be joined to 9 other points of the upper part and to 6 points of the lower part, we get the linear equations:
This system has the following solutions (the point types):
The distribution of the point types follows then from the system of linear equations:
There is only one solution for the block type distribution \(b_4=8, b_2=24\) giving \(a=2, c=3\). This leads to the tactical decomposition (3).\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Betten, D. Disjoint Blocks in a MOL(6). Results Math 76, 9 (2021). https://doi.org/10.1007/s00025-020-01311-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-020-01311-3