Additivity Coefficients for all Classes in the Algebra of Darboux-Like Maps on $\mathbb {R}$

Abstract

The class $\mathbb D$ of generalized continuous functions on $\mathbb {R}$ known under the common name of Darboux-like functions is usually described as consisting of eight families of maps: Darboux, connectivity, almost continuous, extendable, peripherally continuous, those having perfect road, and having either the Cantor Intermediate Value Property or the Strong Cantor Intermediate Value Property. The algebra $\mathcal {A}(\mathbb D)$ of classes of functions generated by these families contains 17 atoms. In this work we will calculate the values of the additivity coefficient ${{\,\mathrm{A}\,}}(\mathcal {F})$ for all atoms $\mathcal {F}$ in the algebra $\mathcal {A}(\mathbb D)$. We also determine the values ${{\,\mathrm{A}\,}}(\mathcal {F})$ for a lot of other families $\mathcal {F}\in \mathcal {A}(\mathbb D)$. Open questions and new directions of research shall also be provided.

1 Introduction and Preliminary Results

There are eight classical Darboux-like families of elements in $\mathbb {R}^\mathbb {R}$: Darboux, connectivity, almost continuous, extendable, peripherally continuous, functions having perfect road, and having either the Cantor Intermediate Value Property (CIVP) or the Strong Cantor Intermediate Value Property (SCIVP). The algebra $\mathcal {A}(\mathbb D)$ of classes of functions generated by these families contains 17 atoms (and, of course, $2^{17}$ elements). The aim of this work is to provide (among other results) the value of the additivity coefficient ${{\,\mathrm{A}\,}}(\mathcal {F})$ for all atoms in this algebra.

This paper’s arrangement is, briefly, as follows. This first introductory section focuses on presenting definitions, notations, and preliminary results that shall be needed throughout the article. This section shall also provides a summary of all results contained in this work. The remaining ten sections will each consider the values of ${{\,\mathrm{A}\,}}$ for different elements of the algebra. Throughout these sections we shall build the tools that will eventually allow us to find the values of ${{\,\mathrm{A}\,}}$ coefficient for all atoms of $\mathcal {A}(\mathbb D)$. In the process, we will also determine the values ${{\,\mathrm{A}\,}}(\mathcal {F})$ for many other families in the algebra. Open questions and new directions of research shall also be provided.

Let us begin with providing the definitions of eight classes of Darboux-like functions mentioned above.

Fig. 1

Jean-Gaston Darboux (1842–1917), the Ph.D. supervisor of E. Borel, examined the intermediate value property of discontinuous functions in his 1875 paper [21], which first page is displayed on the right hand side

1.1 Definitions of Darboux-like Functions

Consider the following classes of maps from $\mathbb {R}$ to $\mathbb {R}$ associated with different properties of continuous functions, usually referred to as Darboux-like functions.

${{\,\mathrm{\mathscr {D}}\,}}$:

of all Darboux functions $f\in \mathbb {R}^\mathbb {R}$, that is, such that f[C] is connected (i.e., an interval) for every connected $C\subset \mathbb {R}$ (or, equivalently, that f has the intermediate value property). This class was first systematically investigated by Jean-Gaston Darboux (1842–1917) in his 1875 paper [21], see Fig. 1.

${{\,\mathrm{PC}\,}}$:

of all peripherally continuous functions $f\in \mathbb {R}^\mathbb {R}$, that is, such that for every number $x\in \mathbb {R}$ there exist two sequences $s_n\nearrow x$ and $t_n\searrow x$ with $\lim _{n\rightarrow \infty }f(s_n)=f(x)=\lim _{n\rightarrow \infty }f(t_n)$. This class was introduced in a 1907 paper [51] of John Wesley Young (1879–1932). The name comes from the papers [30, 31, 50].

${{\,\mathrm{PR}\,}}$:

of all functions $f\in \mathbb {R}^\mathbb {R}$ with perfect road, that is, such that for every $x\in \mathbb {R}$ there exists a perfect $P\subset \mathbb {R}$ having x as a bilateral limit point (i.e., with x being a limit point of $(-\infty ,x)\cap P$ and of $(x,\infty )\cap P$) such that $f\upharpoonright P$ is continuous at x. This class was introduced in a 1936 paper [40] of Isaie Maximoff, where he proved that ${{\,\mathrm{\mathscr {D}}\,}}\cap \mathcal B_1={{\,\mathrm{PR}\,}}\cap \mathcal B_1$, where $\mathcal B_1$ is the class of Baire class 1 functions.

${{\,\mathrm{Conn}\,}}$:

of all connectivity functions $f\in \mathbb {R}^\mathbb {R}$, that is, such that the graph of f restricted to any connected $C\subset \mathbb {R}$ is a connected subset of $\mathbb {R}^2$. This notion can be traced to a 1956 problem [41] stated by John Forbes Nash (1928–2015). We also refer to [31, 49]. Connectivity maps on $\mathbb {R}^2$ are defined in a similar fashion.

${{\,\mathrm{AC}\,}}$:

of all almost continuous functions $f\in \mathbb {R}^\mathbb {R}$ (in the sense of Stallings), that is, such that every open subset of $\mathbb {R}^2$ containing the graph of f contains also the graph of a continuous function from $\mathbb {R}$ to $\mathbb {R}$. This class was first seriously studied in a 1959 paper [49] of John Robert Stallings (1935–2008); however, it appeared already in a 1957 paper [31] by Olan H. Hamilton (1899–1976).

${{\,\mathrm{Ext}\,}}$:

of all extendable functions $f\in \mathbb {R}^\mathbb {R}$, that is, such that there exists a connectivity function $g:\mathbb {R}\times \left[ 0,1\right] \rightarrow \mathbb {R}$ with $f(x)=g(x,0)$ for all $x\in \mathbb {R}$. The notion of extendable functions (without the name) first appeared in a 1959 paper [49] of J. Stallings, where he asks a question whether every connectivity function defined on [0, 1] is extendable.

${{\,\mathrm{CIVP}\,}}$:

of all functions $f\in \mathbb {R}^\mathbb {R}$ with Cantor Intermediate Value Property, that is, such that for all distinct $p,q\in \mathbb {R}$ with $f(p)\ne f(q)$ and for every perfect set K between f(p) and f(q), there exists a perfect set C between p and q such that $f[C]\subset K$. This class was first introduced in a 1982 paper [27] of Richard G. Gibson and Fred William Roush.

${{\,\mathrm{SCIVP}\,}}$:

of all functions $f\in \mathbb {R}^\mathbb {R}$ with Strong Cantor Intermediate Value Property, that is, such that for all $p,q\in \mathbb {R}$ with $p\not =q$ and $f(p)\not =f(q)$ and for every perfect set K between f(p) and f(q), there exists a perfect set C between p and q such that $f[C]\subset K$ and $f\upharpoonright C$ is continuous. This notion was introduced in a 1992 paper [48] of Harvey Rosen, R. Gibson, and F. Roush to help distinguish extendable and connectivity functions on $\mathbb {R}$.

Fig. 2

All inclusions, indicated by arrows, among the Darboux-like classes $\mathbb D$. The only inclusions among the intersections of these classes are those that follow trivially from this schema (see [12, 26])

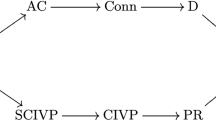
In what follows we will denote the collection of these classes of functions by the symbol $\mathbb D$, that is, $\mathbb D\!:=\!\{{{\,\mathrm{Ext}\,}},{{\,\mathrm{AC}\,}},{{\,\mathrm{Conn}\,}},{{\,\mathrm{\mathscr {D}}\,}},{{\,\mathrm{SCIVP}\,}},{{\,\mathrm{CIVP}\,}},{{\,\mathrm{PR}\,}},{{\,\mathrm{PC}\,}}\}$. The diagram in Fig. 2 shows the relations between the classes in $\mathbb D$. The arrows denote strict inclusions.

The inclusions ${{\,\mathrm{Conn}\,}}\subset {{\,\mathrm{\mathscr {D}}\,}}\subset {{\,\mathrm{PC}\,}}$, ${{\,\mathrm{PR}\,}}\subset {{\,\mathrm{PC}\,}}$, and ${{\,\mathrm{SCIVP}\,}}\subset {{\,\mathrm{CIVP}\,}}$ are obvious from the previous definitions. On the other hand, the remaining inclusions are less obvious. Among them the inclusions ${{\,\mathrm{Ext}\,}}\subset {{\,\mathrm{AC}\,}}\subset {{\,\mathrm{Conn}\,}}$ were proved by Stallings [49], while ${{\,\mathrm{CIVP}\,}}\subset {{\,\mathrm{PR}\,}}$ was stated without proof in [28] (although its proof can be found in [26, Theorem 3.8]). The inclusion ${{\,\mathrm{Ext}\,}}\subset {{\,\mathrm{SCIVP}\,}}$ comes from [48].

The inclusions indicated in Fig. 2 are the only inclusions among these classes even when we add to the considerations the intersections of the classes from the top and bottom rows of Fig. 2. This is well described in the expository papers [10, 12, 26]. Specifically, ${{\,\mathrm{AC}\,}}\setminus {{\,\mathrm{CIVP}\,}}\ne \emptyset$ and ${{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{AC}\,}}\ne \emptyset$ was shown in a 1982 paper [27]. The fact that ${{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}}\ne \emptyset$ is the trickiest to prove and is related to late 1960’s papers: [47] of John Henderson Roberts, [20] of James L. Cornette, [32] of F. Burton Jones and Edward S. Thomas Jr., and [6] of J. Brown. The result ${{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}}\not =\emptyset$ can be traced to the 1965 paper [7] of Andrew M. Bruckner and Jack Gary Ceder (see also [6]), while examples for ${{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}}\ne \emptyset$, ${{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{CIVP}\,}}\ne \emptyset$, and ${{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}}\ne \emptyset$ to the 2000 paper [12] of K. C. Ciesielski and Jan Jastrzȩbski.

The inclusions indicated in Fig. 2 suggest a natural split of $\mathbb D$ into two subclasses: $\mathbb U:=\{{{\,\mathrm{Ext}\,}},{{\,\mathrm{AC}\,}},{{\,\mathrm{Conn}\,}},{{\,\mathrm{\mathscr {D}}\,}},{{\,\mathrm{PC}\,}}\}$ and $\mathbb L:=\{{{\,\mathrm{Ext}\,}},{{\,\mathrm{SCIVP}\,}},{{\,\mathrm{CIVP}\,}},{{\,\mathrm{PR}\,}},{{\,\mathrm{PC}\,}}\}$, each consisting of the families that are mutually comparable by inclusion. In particular, the algebra $\mathcal {A}(\mathbb U)$ of subsets of ${{\,\mathrm{PC}\,}}$ generated by the classes in $\mathbb U$ has 5 atoms:

$$\begin{aligned} \left\{ {{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}}, {{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}}, {{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}}, {{\,\mathrm{AC}\,}}\setminus {{\,\mathrm{Ext}\,}}, {{\,\mathrm{Ext}\,}}\right\} . \end{aligned}$$

Similarly, $\mathcal {A}(\mathbb L)$ generated by the classes in $\mathbb L$ has also 5 atoms:

$$\begin{aligned} \left\{ {{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}}, {{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{CIVP}\,}}, {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}}, {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}}, {{\,\mathrm{Ext}\,}}\right\} . \end{aligned}$$

This means that the algebra $\mathcal {A}(\mathbb D)$ has theoretically 25 atoms, the intersections $L\cap U$, where $L\in \mathcal {A}(\mathbb L)$ and $U\in \mathcal {A}(\mathbb U)$. However, if ${{\,\mathrm{Ext}\,}}\in \{U,L\}$, then $L\cap U=\emptyset$ unless $L=U={{\,\mathrm{Ext}\,}}$. Thus, $\mathcal {A}(\mathbb D)=\mathcal {A}(\mathbb U\cup \mathbb L)$ has actually 17 atoms: ${{\,\mathrm{Ext}\,}}$ and the 16 atoms presented in Table 1, where for $\mathcal {F}\subset \mathbb {R}^\mathbb {R}$ we use the symbol $\lnot \mathcal {F}$ to denote the complement of $\mathcal {F}$ with respect to $\mathbb {R}^\mathbb {R}$, that is, $\lnot \mathcal {F}:=\mathbb {R}^\mathbb {R}\setminus \mathcal {F}$.

Next, and still within this preliminary section of the paper, let us provide a full account on the notion of additivity coefficient.

Table 1 All atoms of $\mathcal {A}(\mathbb D)$ with exception of ${{\,\mathrm{Ext}\,}}$

1.2 Additivity Coefficient: Definition and Background

The important recent developments in modern analysis concern the cardinal functions that are defined for different classes of functions in terms of algebraic operations on functions. Probably the most important of them is the additivity coefficient of $\mathcal {F}$. Its definition was motivated by the following property of Darboux functions due to Henry Fast [23]: for every family $\mathcal {F}\subset \mathbb {R}^\mathbb {R}$ of size $\le \mathfrak c$ there exists a $g\in \mathbb {R}^\mathbb {R}$ such that $g+\mathcal {F}\subset {{\,\mathrm{\mathscr {D}}\,}}$, where $g+\mathcal {F}:=\{g+f:f\in \mathcal {F}\}$. Of course $\mathfrak c$ stands for $|\mathbb {R}|$, that is, the cardinality of $\mathbb {R}$.

In 1974 Kellum [37] proved the similar result for the class ${{\,\mathrm{AC}\,}}$, and in 1991 Natkaniec [43] defined the following cardinal number for every $\mathcal {F}\subset \mathbb {R}^\mathbb {R}$.

Definition 1.1

For $\mathcal {F}\subset \mathbb {R}^\mathbb {R}$, we define the additivity coefficient of $\mathcal {F}$ by

$$\begin{aligned} {{\,\mathrm{A}\,}}(\mathcal {F})=\min \left( \left\{ |F|:F\subset \mathbb {R}^\mathbb {R},\ \forall g\in \mathbb {R}^\mathbb {R},\ g+F\not \subset \mathcal {F}\right\} \cup \left\{ \left( 2^\mathfrak c\right) ^+\right\} \right) . \end{aligned}$$

This notion was thoroughly studied in a 1996 paper [35] of Francis Edmund Jordan. (See also his Ph.D. Dissertation [34], written under the supervision of K. C. Ciesielski.) The values of the additivity coefficient for Darboux-like classes were investigated by Natkaniec [43], Ciesielski and Miller [14], Ciesielski and Recław [17]. They are listed in [26, Table 1]. Jordan [35] studied the values of ${{\,\mathrm{A}\,}}(\mathcal {F})$ for the complements of Darboux-like functions (see, also, [1, 4, 24] for some recently discovered links of additivity to other algebraic notions). A summary of these previously mentioned investigations is presented in Proposition 1.2 (see, e.g., [17, 35]).

Proposition 1.2

Let $\mathcal G,\mathcal {F}\subset {\mathbb R}^{{\mathbb R}}$. Then,

• (i) ${{\,\mathrm{A}\,}}(\mathcal {F})\ge 2 \text { if, and only if, } \mathcal {F}\ne \emptyset$;

• (ii) ${{\,\mathrm{A}\,}}(\mathcal {F})\le 2^{\mathfrak c} \text { if, and only if, } \mathcal {F}\ne {\mathbb R}^{{\mathbb R}}$;

• (iii) if $\mathcal {F}\subset \mathcal G$ then ${{\,\mathrm{A}\,}}(\mathcal {F})\le {{\,\mathrm{A}\,}}(\mathcal G)$;

• (iv) if $\mathcal {F}\ne \emptyset$ then ${{\,\mathrm{A}\,}}(\mathcal {F})=2 \text { if, and only if, } \mathcal {F}- \mathcal {F}\ne {\mathbb R}^{{\mathbb R}}$;

Proof

All of these properties are straight consequences of the definition of the operator ${{\,\mathrm{A}\,}}$. Parts (i)-(iii) come from [17] while (iv) from [35]. $\square$

Let $\kappa$ be a cardinal number $>0$ and X a set of cardinality $\ge \kappa$. We define $[X]^\kappa =\{Y\subset X:|Y|=\kappa \}$, $[X]^{<\kappa }=\{Y\subset X:|Y|<\kappa \}$, and $[X]^{\le \kappa }=\{Y\subset X:|Y|\le \kappa \}$.

Let $e_\mathfrak c$ denote the following cardinal number

$$\begin{aligned} e_\mathfrak c=\min \left\{ |F|:F\subset \mathbb {R}^\mathbb {R},\forall g\in \mathbb {R}^\mathbb {R},\exists f\in F\text { such that }|f\cap g|<\mathfrak c\right\} , \end{aligned}$$

see [14], and let ${{\,\mathrm{PES}\,}}$ stand for the family of all perfectly everywhere surjective maps $f\in \mathbb {R}^\mathbb {R}$, that is, such that $f[P]=\mathbb {R}$ for every perfect set $P\subset \mathbb {R}$. Also, following [35], we define

$$\begin{aligned} d_\mathfrak c=\min \{|F|:F\subset \mathbb {R}^\mathbb {R},\forall g\in \mathbb {R}^\mathbb {R},\exists f\in F\text { such that }|f\cap g|=\mathfrak c\}, \end{aligned}$$

and

$$\begin{aligned} d_\mathfrak c^* =\min \{|F|:F\subset \mathbb {R}^\mathbb {R},\forall G\in [\mathbb {R}^\mathbb {R}]^\mathfrak c,\exists f\in F\text { such that }\forall g\in G,\ |f\cap g|=\mathfrak c\}. \end{aligned}$$

Proposition 1.3

We have the following results.

• (a) $\mathfrak c^+\le {{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{PES}\,}})=e_\mathfrak c\le 2^\mathfrak c$ and this is all that can be proved in ZFC, see [14, 24] or [13, Proposition 1.8].

• (b) ${{\,\mathrm{A}\,}}({{\,\mathrm{Ext}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}})=\mathfrak c^+$, see [17].

• (c) ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}})=2^\mathfrak c$, see [17].

• (d) ${{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{PC}\,}})=\omega _1$ (Ciesielski, see [35, Theorem 7]).

• (e) ${{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{Ext}\,}})={{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{PR}\,}})=2^\mathfrak c$, see [35].

• (f) $d_\mathfrak c\le {{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{\mathscr {D}}\,}})\le {{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{Conn}\,}})\le {{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{AC}\,}})\le d_\mathfrak c^*$, see [35, Theorem 8].

  If $|[\mathfrak c]^{<\mathfrak c}|=\mathfrak c$, then ${{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{\mathscr {D}}\,}})={{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{Conn}\,}})={{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{AC}\,}})=d_\mathfrak c=d_\mathfrak c^*$, see [35, Corollary 12].

  If $|[\mathfrak c]^{<\mathfrak c}|=\mathfrak c$ and $\mathfrak c=\lambda ^+$, then $d_\mathfrak c\le e_\mathfrak c$, see [35, Theorem 11].

  Moreover, in [15], it was proven that $\mathfrak c^+\le d_\mathfrak c\le 2^\mathfrak c$ and

  ($f_1$):

  For every cardinals $\lambda \ge \kappa \ge \omega _{2}$ such that $cof(\lambda )>\omega _{1}$ and $\kappa$ is regular, it is relatively consistent with ZFC+CH that $2^\mathfrak c=\lambda$ and $d_\mathfrak c=e_\mathfrak c=\kappa$. In particular, $\mathfrak c^+<d_\mathfrak c={{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{\mathscr {D}}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}})=e_\mathfrak c<2^\mathfrak c$ is consistent with ZFC+CH.

  ($f_2$):

  For every cardinal $\lambda >\omega _{2}$ such that $cof(\lambda )>\omega _{1}$, it is relatively consistent with ZFC+CH that $\mathfrak c^+=\omega _2={{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{\mathscr {D}}\,}})=d_\mathfrak c<e_\mathfrak c= {{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}})=2^\mathfrak c=\lambda$.

1.3 Summary of the Results

The following Table 2, summarizing the main results of this work, shows the values of ${{\,\mathrm{A}\,}}(\mathcal {F})$ for the atoms of $A(\mathbb D)$ presented in Table 1. The value of ${{\,\mathrm{A}\,}}$ for the remaining atom ${{\,\mathrm{Ext}\,}}$ is ${{\,\mathrm{A}\,}}({{\,\mathrm{Ext}\,}})=\mathfrak c^+$, as shown in [17]. We define

$$\begin{aligned} \mathfrak c_-:={\left\{ \begin{array}{ll} \kappa &{} \text{ when } \mathfrak c=\kappa ^+,\\ \mathfrak c&{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

Table 2 The values ${{\,\mathrm{A}\,}}(\mathcal {F})$ for $\mathcal {F}$ from Table 1 and the references to these results, where $\#$ denotes the additivity of the family $\mathcal {F}$ in the respective cell of Table 1

Furthermore, the results of this work also show the additivities of some families $\mathcal {F}\in {{\,\mathrm{A}\,}}(\mathbb D)$ that are not necessarily the atoms of $\mathcal {A}(\mathbb D)$. This is shown in Table 3, in which the cells of Table 1 have been combined in order to show the union of the atoms of $\mathcal {A}(\mathbb D)$ using either two (second and fifth rows of Table 3) or three (second row and fifth column).

Table 3 The values of ${{\,\mathrm{A}\,}}(\mathcal {F})$ for some $\mathcal {F}\in A(\mathbb D)$ as indicated and the references to these results, where $\#$ denotes the additivity of the family $\mathcal {F}$ in the respective cell of Table 1

We will finish this section with the notations and definitions that will be useful in the remainder of this work. We will use the symbol ${{\,\mathrm{\mathscr {B}}\,}}(X)$ to denote the class of Borel functions from a topological space X into $\mathbb {R}$. We will also write ${{\,\mathrm{\mathscr {B}}\,}}$ for ${{\,\mathrm{\mathscr {B}}\,}}(\mathbb {R})$.

The families of all perfect subsets of $\mathbb {R}$, of nonempty open intervals, and of nonempty open intervals with rational endpoints in $\mathbb {R}$ will be denoted by ${{\,\mathrm{Perf}\,}}$, $\mathcal J$, and $\mathcal B$, respectively. It is well known that $|{{\,\mathrm{Perf}\,}}|=|\mathcal J|=\mathfrak c$ and $|\mathcal B|=\omega$.

The symbol ${{\,\mathrm{SZ}\,}}$ will denote the class of all Sierpiński-Zygmund maps $f:\mathbb {R}\rightarrow \mathbb {R}$, that is, such that $f\upharpoonright X$ is discontinuous for every $X\subset \mathbb {R}$ of cardinality $\mathfrak c$. Recall (see, e.g., [45]) that if $|f\cap g|<\mathfrak c$ for every $g\in {{\,\mathrm{\mathscr {B}}\,}}$, then $f\in {{\,\mathrm{SZ}\,}}$. We will also consider the following notation:

• The symbol ${{\,\mathrm{ES}\,}}$ denotes the family of everywhere surjective functions $f\in \mathbb {R}^\mathbb {R}$, that is, such that $f[(a,b)]=\mathbb {R}$ for all $a<b$.

• The symbol ${{\,\mathrm{SES}\,}}$ denotes the family of strongly everywhere surjective functions $f\in \mathbb {R}^\mathbb {R}$, that is, $f^{-1}(y)\cap J$ has cardinality $\mathfrak c$ for every $y\in \mathbb {R}$ and every nonempty open interval $J\subset \mathbb {R}$. Clearly ${{\,\mathrm{PES}\,}}\subset {{\,\mathrm{SES}\,}}\subset {{\,\mathrm{ES}\,}}\subset {{\,\mathrm{\mathscr {D}}\,}}$, where ${{\,\mathrm{PES}\,}}$ was already defined on page 5.

Let $\mathcal {F}\subset \mathbb {R}^\mathbb {R}$ be nonempty, $f\in \mathbb {R}^\mathbb {R}$, and $X\subset \mathbb {R}$. We say that the property “$f\in \mathcal {F}$” is decided on X provided every $g\in \mathbb {R}^\mathbb {R}$ with $g\upharpoonright X=f\upharpoonright X$ has the same property, that is, $g\in \mathcal {F}$.

2 ${{\,\mathrm{A}\,}}(\mathcal {F})=2$ for $\mathcal {F}\in \mathcal {A}(\mathbb D)$ with $\emptyset \ne \mathcal {F}\subset {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{AC}\,}}$

First, we will prove the inequality ${{\,\mathrm{A}\,}}({{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{AC}\,}})\le 2$. To do so, we will use the fact that a function $f:\mathbb {R}\rightarrow \mathbb {R}$ is almost continuous if, and only if, it intersects every blocking set, that is, a closed set $K\subset \mathbb {R}^2$ which meets the graph of every continuous map from $\mathbb {R}$ into $\mathbb {R}$ and which is disjoint with a graph of at least one function from $\mathbb {R}$ into $\mathbb {R}$. We can assume that the first coordinate projection $dom(K)$ of every blocking set K contains a non-degenerate interval, see [37] or [43, Remark 1.1]. In particular, every blocking set K contains a graph of a Borel function h from a non-degenerate interval $I\subset \mathbb {R}$ into $\mathbb {R}$, see [16, p. 117].¹ This immediately implies

Fact 2.1

If $f:\mathbb {R}\rightarrow \mathbb {R}$ is such that $f\cap h\ne \emptyset$ for every Borel map h from an $J\in \mathcal J$ into $\mathbb {R}$, then $f\in {{\,\mathrm{AC}\,}}$.

Lemma 2.2

${{\,\mathrm{A}\,}}({{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{AC}\,}})\le 2$.

Proof

Let $f\in \mathbb {R}^\mathbb {R}$ be such that $f\cap \psi \ne \emptyset$ for every Borel function $\psi$ from a perfect set into $\mathbb {R}$. If $\{B_h:h\in {{\,\mathrm{\mathscr {B}}\,}}\}$ is a partition of $\mathbb {R}$ into Bernstein sets (see, e.g., [9, Theorem 7.3.4]), then $f:=\bigcup _{h\in {{\,\mathrm{\mathscr {B}}\,}}} h\upharpoonright B_h$ is as needed.

Let $\Theta$ be the constant zero function and put $F=\{f,\Theta \}$. It is enough to show that $g+F\not \subset {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{AC}\,}}$ for every $g\in \mathbb {R}^\mathbb {R}$.

Indeed, let $g\in \mathbb {R}^\mathbb {R}$ be such that $g=g+\Theta \in {{\,\mathrm{SCIVP}\,}}$. It is enough to show that $g+f\in {{\,\mathrm{AC}\,}}$. We will prove this by using Fact 2.1. So, fix a Borel map h from an $J\in \mathcal J$ into $\mathbb {R}$. We need to show that $(g+f)\cap h\ne \emptyset$.

To see this, notice that $g=g+\Theta \in {{\,\mathrm{SCIVP}\,}}$ implies the existence of a perfect $C\subset J$ such that $g\upharpoonright C$ is continuous. (This is obvious when $g\upharpoonright J$ is constant and, otherwise, follows directly from the definition of ${{\,\mathrm{SCIVP}\,}}$.) Then $\psi :=(h-g)\upharpoonright C$ is Borel. So, by the choice of f, there is an $x\in C$ with $f(x)=\psi (x)=h(x)-g(x)$. Hence, $(f+g)(x)=h(x)$ and we have the desired $(g+f)\cap h\ne \emptyset$. $\square$

Theorem 2.3

${{\,\mathrm{A}\,}}(\mathcal {F})=2$ for every nonempty $\mathcal {F}\in A(\mathbb D)$ with $\mathcal {F}\subseteq {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{AC}\,}}$.

Proof

The atoms of $A(\mathbb D)$ contained in ${{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{AC}\,}}$ consists of the sets ${{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}}$, ${{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Conn}\,}}$, and ${{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{AC}\,}}$. By Proposition 1.2 (iii), the additivity for each of them is $\le {{\,\mathrm{A}\,}}({{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{AC}\,}})\le 2$. To see that they all are also $\ge 2$, by Proposition 1.2 (i) it is enough to show each of these classes is nonempty. This is the case, since any Darboux Borel function is SCIVP and there are Baire class 2 examples that distinguish between the classes ${{\,\mathrm{\mathscr {D}}\,}}$, ${{\,\mathrm{Conn}\,}}$, and ${{\,\mathrm{AC}\,}}$, see e.g. [12, Theorem 1.2]. More specifically, a map in ${{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}}$ is given in [12, Example 3.5], while the other two examples come from [5]. $\square$

3 ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\setminus {{\,\mathrm{PR}\,}})=e_\mathfrak c$

Theorem 3.1

${{\,\mathrm{A}\,}}(\mathcal {F})=e_\mathfrak c$ for every $\mathcal {F}\in \mathcal {A}(\mathbb D)$ with ${{\,\mathrm{AC}\,}}\setminus {{\,\mathrm{PR}\,}}\subset \mathcal {F}\subset {{\,\mathrm{AC}\,}}$.

Proof

As ${{\,\mathrm{AC}\,}}\setminus {{\,\mathrm{PR}\,}}\subset \mathcal {F}\subset {{\,\mathrm{AC}\,}}$, Proposition 1.2 (iii) implies that ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\setminus {{\,\mathrm{PR}\,}})\le {{\,\mathrm{A}\,}}(\mathcal {F})\le {{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}})=e_\mathfrak c$. Therefore, to finish the proof it is enough to show that ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\setminus {{\,\mathrm{PR}\,}})\ge e_\mathfrak c$.

So, let $F\subset \mathbb {R}^\mathbb {R}$ be a family of cardinality $<e_\mathfrak c$. We need to find a $g\in \mathbb {R}^\mathbb {R}$ so that $g+F\subset {{\,\mathrm{AC}\,}}\setminus {{\,\mathrm{PR}\,}}$. The family $F-{{\,\mathrm{\mathscr {B}}\,}}\supset F$ still has cardinality $<e_\mathfrak c$ and, by Proposition 1.3 (a), there exists a $g\in \mathbb {R}^\mathbb {R}$ so that $g+(F-{{\,\mathrm{\mathscr {B}}\,}})\subset {{\,\mathrm{PES}\,}}$. We claim, that this g is as needed.

To see this, fix an $f\in F$. To prove that $g+f\in {{\,\mathrm{AC}\,}}$ we will use Fact 2.1. So, fix a Borel map h from an $J\in \mathcal J$ into $\mathbb {R}$ and let $\bar{h}\in {{\,\mathrm{\mathscr {B}}\,}}$ be its extension. We need to show that $(g+f)\cap h\ne \emptyset$. But $g+f-\bar{h}\in {{\,\mathrm{PES}\,}}$, so there exists an $x\in J$ so that $(g+f-\bar{h})(x)=0$. Hence, $(g+f)(x)=\bar{h}(x)=h(x)$ and indeed $(g+f)\cap h\ne \emptyset$.

To see that $g+f\notin {{\,\mathrm{PR}\,}}$ it is enough to prove that $g+f$ is unbounded on any $P\in {{\,\mathrm{Perf}\,}}$. But this is clear since, for $h\equiv 0$, $(g+f)[P]=(g+f-h)[P]=\mathbb {R}$.

$\square$

4 On ${{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})$

We will start with investigating the upper bound. Of course, the obvious upper bound here is

$$\begin{aligned} {{\,\mathrm{A}\,}}\left( {{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}}\right) \le {{\,\mathrm{A}\,}}\left( {{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{AC}\,}}\right) \le \min \left\{ {{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}),{{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{AC}\,}})\right\} =\min \left\{ e_\mathfrak c,d_\mathfrak c^*\right\} , \end{aligned}$$

where the last equality is justified by parts (a) and (f) of Proposition 1.3. Nevertheless, this upper bound is suboptimal, as shown by the following two lemmas.

4.1 The Upper Bounds

Lemma 4.1

${{\,\mathrm{A}\,}}\left( {{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{AC}\,}}\right) \le {{\,\mathrm{A}\,}}\left( {{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{AC}\,}}\right) \le \mathfrak c$.

Proof

To see this, let $F:={{\,\mathrm{\mathscr {B}}\,}}$. Then $|F|=\mathfrak c$. Fix a $g:\mathbb {R}\rightarrow \mathbb {R}$. It is enough to show that $g+F\not \subset {{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{AC}\,}}$.

Indeed, take any $f\in F$ and assume that $g+f\notin {{\,\mathrm{AC}\,}}$. Then, by Fact 2.1, there is an $h\in {{\,\mathrm{\mathscr {B}}\,}}=F$ and a nonempty $J:=(a,b)$ such that $g+f$ is disjoint with $h\upharpoonright J$. But this means that $g+(f-h)\in g+F$ takes no value 0 on J. Modifying f at the points a and b, if necessary, we can also assume that $(g+f-h)(a)<0$ and $(g+f-h)(b)>0$. But this means that $g+F\not \subset {{\,\mathrm{\mathscr {D}}\,}}$. $\square$

The next lemma shows that even the upper bound $\mathfrak c$ for ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{AC}\,}})$ can be, consistently with ZFC, even lower than $\mathfrak c$.

Lemma 4.2

If $2^{\mathfrak c_-}=\mathfrak c$ and $cof(\mathfrak c_-)>\omega$, then ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{AC}\,}})\le \mathfrak c_-$.

Proof

By Lemma 4.1 and the definition of $\mathfrak c_-$ we can assume that $\mathfrak c=\kappa ^+$ with $cof(\kappa )>\omega$. We need to prove that ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{AC}\,}})\le \kappa$.

For this, we will define the sequence $\langle f_\zeta \in \mathbb {R}^\mathbb {R}:\zeta <\kappa \rangle$ so that for the family $F:= \{f_\zeta \in \mathbb {R}^\mathbb {R}:\zeta <\kappa \}$ there is no $g\in \mathbb {R}^\mathbb {R}$ with $g+F\subset {{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{AC}\,}}$.

If for some $g\in \mathbb {R}^\mathbb {R}$, we have $g+F\subset \lnot {{\,\mathrm{AC}\,}}$, then, by Fact 2.1, for every $\zeta <\kappa$ there is a pair $\langle h_\zeta ,J_\zeta \rangle \in {{\,\mathrm{\mathscr {B}}\,}}\times \mathcal B$ such that $(g+f_\zeta )\cap (h_\zeta \upharpoonright J_\zeta )=\emptyset$. If we knew in advance, that it is a sequence $\langle \langle h_\zeta ,J_\zeta \rangle \in {{\,\mathrm{\mathscr {B}}\,}}\times \mathcal B:\zeta <\kappa \rangle$ that justifies $g+F\subset \lnot {{\,\mathrm{AC}\,}}$, then an argument as in Lemma 4.1 shows that for F being the collection of all differences $f_\zeta -h_\zeta$, we would have $g+F\not \subset {{\,\mathrm{ES}\,}}$ for every $g\in \mathbb {R}^\mathbb {R}$.

To formalize the above inside, enumerate $\{\langle \langle h_\zeta ^\xi , J_\zeta ^\xi \rangle :\zeta<\kappa \rangle :\xi <\mathfrak c\}$ all $\kappa$-length sequences in ${{\,\mathrm{\mathscr {B}}\,}}\times \mathcal B$. This is possible, since $|({{\,\mathrm{\mathscr {B}}\,}}\times \mathcal B)^{\kappa }|=2^\kappa =2^{\mathfrak c_-}=\mathfrak c$. Also, fix a one-to-one enumeration $\{r_\xi :\xi <\mathfrak c\}$ of $\mathbb {R}$. For each $\xi <\mathfrak c$ we will choose the values $\langle f_\zeta (r_\xi ):\zeta <\kappa \rangle$ so that it will restrict the possibility for each sequence among $\{\langle \langle h_\zeta ^\eta , J_\zeta ^\eta \rangle :\zeta<\kappa \rangle :\eta <\xi \}$ to justify $g+F\subset \lnot {{\,\mathrm{AC}\,}}$ and, at the same time, to allow $g+F\subset {{\,\mathrm{ES}\,}}$. The choice of values of $\langle f_\zeta (r_\xi ):\zeta <\kappa \rangle$ for each $\xi$ is independent of these values for any other $\xi$. So, there is no induction on $\xi <\mathfrak c$.

For every $\eta <\mathfrak c$ choose a $J^\eta \in \mathcal B$ such that $K_\eta :=\{\zeta <\kappa :J_\zeta ^\eta = J^\eta \}$ has cardinality $\kappa$. This can be done, since $cof(\kappa )>\omega$. Let $\alpha _\eta :=\min K_\eta$.

Fix a $\xi <\mathfrak c$ and let $\langle \langle \eta _\nu ,\delta _\nu \rangle :\nu <\kappa \rangle$ list all elements of $(\xi +1)\times (\xi +1)$, each pair $\langle \eta ,\delta \rangle \in (\xi +1)\times (\xi +1)$ appearing $\kappa$-many times. By induction on $\nu <\kappa$ define

$$\begin{aligned} \zeta _\nu = \min (K_{\eta _\nu }\setminus \{\zeta _\mu :\mu <\nu \}) \end{aligned}$$

(what ensures that $J^{\eta _\nu }_{\zeta _\nu }=J^{\eta _\nu }$) and, if $\zeta _\nu \ne \min K_{\eta _\nu }=\alpha _{\eta _\nu }$, put

$$\begin{aligned} f_{\zeta _\nu }\left( r_\xi \right) :=h^{\eta _\nu }_{\zeta _\nu }\left( r_\xi \right) +f_{\alpha _{\eta _\nu }}\left( r_\xi \right) -r_{\delta _\nu }. \end{aligned}$$

(4.1)

For all $\zeta <\kappa$ for which (4.1) does not apply, the value of $f_\zeta (r_\xi )$ is chosen arbitrarily. This finishes the construction of the family F.

To see that F is as needed, choose a $g\in \mathbb {R}^\mathbb {R}$ so that $g+F\subset \lnot {{\,\mathrm{AC}\,}}$. We need to show that there is an $f\in F$ so that $g+f\notin {{\,\mathrm{ES}\,}}$.

For every $\zeta <\kappa$ choose $\langle h_\zeta , J_\zeta \rangle \in {{\,\mathrm{\mathscr {B}}\,}}\times \mathcal B$ so that $(h_\zeta \upharpoonright J_\zeta )\cap (g+f_\zeta )=\emptyset$. Fix a $\eta <\mathfrak c$ such that $\langle \langle h_\zeta ^\eta , J_\zeta ^\eta \rangle :\zeta<\kappa \rangle =\langle \langle h_\zeta , J_\zeta \rangle :\zeta <\kappa \rangle$. We will show that $g+f_{\alpha _\eta }\notin {{\,\mathrm{ES}\,}}$ by arguing that $(g+f_{\alpha _\eta })[J^\eta ]=\mathbb {R}$ leads to a contradiction.

To see this, first notice that

$$\begin{aligned} (g+f_{\alpha _\eta })(r_\xi )\ne r_\delta \text{ for } \text{ every } \xi \ge \eta \text{ with } r_\xi \in J^\eta \text{ and } \text{ every } \delta \le \xi \end{aligned}$$

(4.2)

Indeed, otherwise $g(r_\xi )=r_\delta -f_{\alpha _\eta }(r_\xi )$. Also, a pair $\langle \eta ,\delta \rangle$ equals to $\langle \eta _\nu ,\delta _\nu \rangle$ for $\kappa$-many $\nu <\kappa$. So, there is such $\nu <\kappa$ with $\zeta _\nu \ne \alpha _{\eta }=\alpha _{\eta _\nu }$ in which case, by (4.1), $f_{\zeta _\nu }(r_\xi ) =h^{\eta _\nu }_{\zeta _\nu }(r_\xi )+f_{\alpha _{\eta _\nu }}(r_\xi )-r_{\delta _\nu } =h^{\eta _\nu }_{\zeta _\nu }(r_\xi )+f_{\alpha _{\eta }}(r_\xi )-r_{\delta }$. Combining this with $g(r_\xi )=r_\delta -f_{\alpha _\eta }(r_\xi )$ gives $(g+f_{\zeta _\nu })(r_\xi )=h^{\eta _\nu }_{\zeta _\nu }(r_\xi )$, contradicting the fact that $h_{\zeta _\nu }=h^{\eta }_{\zeta _\nu }=h^{\eta _\nu }_{\zeta _\nu }$ has no common values with $g+f_{\zeta _\nu }$ on the interval $J^\eta =J^{\eta _\nu }=J^{\eta _\nu }_{\zeta _\nu }$. So, (4.2) indeed holds.

Now, if $(g+f_{\alpha _\eta })[J^\eta ]=\mathbb {R}$, then, for every $\delta \ge \eta$, there is a $\xi _\delta <\mathfrak c$ so that $r_{\xi _\delta }\in J^\eta$ and $(g+f_{\alpha _\eta })(r_{\xi _\delta })= r_\delta$. But, by (4.2), we must have ${\xi _\delta }<\delta$. Therefore, the mapping $\mathfrak c\setminus \eta \ni \delta \mapsto \xi _\delta \in \mathfrak c$ is regressive. Thus, by the pressing-down lemma (see [38, page 80]), it is a constant on a stationary subset S of $\mathfrak c$. This means, in particular, that there exist distinct $\delta ,\delta '<\mathfrak c$ such that $\xi _\delta =\xi _{\delta '}$.

Therefore $(g+f_{\alpha _\eta })(r_{\xi _\delta })=(g+f_{\alpha _\eta })(r_{\xi _{\delta '}})$ has two distinct values, $r_\delta$ and $r_{\delta '}$, which is certainly impossible.

Thus, we must have $(g+f_{\alpha _\eta })[J^\eta ]\ne \mathbb {R}$, so that $g+f_{\alpha _\eta }\notin {{\,\mathrm{ES}\,}}$. $\square$

4.2 The Lower Bound and the Value of ${{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})$

Lemma 4.3

Let $S\subset \mathbb {R}$ be $\mathfrak c$-dense, that is, such that $|S\cap (p,q)|=\mathfrak c$ for every $p<q$. Also, let $F\subset \Phi \subset \mathbb {R}^\mathbb {R}$ be such that $|F|<\mathfrak c_-$ and $|\Phi |<\mathfrak c$. Then there exist a $g\in \mathbb {R}^\mathbb {R}$ and a linear map $\ell _a$ of the form $\ell _a(x):=ax$ such that

• (i) $(g+f)\cap \ell _a=\emptyset$ for every $f\in F$;

• (ii) for every $f\in \Phi$ we have $g+f\in {{\,\mathrm{ES}\,}}$ and this is decided on S.

Proof

For every $\varphi \in \Phi$ and $J\in \mathcal B$ consider the following set

$$\begin{aligned} A_{\varphi ,J}:=\left\{ a\in \mathbb {R}:\left( \exists y_a\in \mathbb {R}\right) \left| \left\{ x\in S\cap J:\left( \forall f\in F\right) \ \ell _a(x)-y_a\ne f(x)-\varphi (x) \right\} \right| <\mathfrak c\right\} . \end{aligned}$$

Let $\lambda :=|F|^2$ when $\mathfrak c$ is a regular cardinal and $\lambda :=\max \{|F|^2,cof(\mathfrak c)\}$, when $\mathfrak c$ is a singular cardinal. Notice that $\lambda ^+<\mathfrak c$. We will show that, for every $\varphi \in \Phi$ and $J\in \mathcal B$,

$$\begin{aligned} |A_{\varphi ,J}|\le \lambda . \end{aligned}$$

(4.3)

To see (4.3) assume, by way of contradiction, that this is not the case, that is, that $|A_{\varphi ,J}|\ge \lambda ^+$. Let $T_a:=\left\{ x\in S\cap J:(\forall f\in F) \ \ell _a(x)-y_a\ne f(x)-\varphi (x) \right\}$ and notice that $|T_a|<\mathfrak c$ for every $a \in A_{\varphi ,J}$. We claim that

$$\begin{aligned} \left| \bigcup _{a\in A}T_a\right| <\mathfrak c\ \ \text{ for } \text{ some } A\subset A_{\varphi ,J} \text{ of } \text{ cardinality } \left( |F|^2\right) ^+. \end{aligned}$$

(4.4)

Indeed, if $\mathfrak c$ is a regular cardinal, then any $A\subset A_{\varphi ,J}$ of cardinality $(|F|^2)^+$ satisfies (4.4). So, assume that $\mathfrak c$ is a singular cardinal. Then $|A_{\varphi ,J}|\ge \lambda ^+\ge cof(\mathfrak c)^+$, and there is a cardinal $\mu <\mathfrak c$ and an $A_0\subset A_{\varphi ,J}$ of cardinality $\lambda ^+$ such that $|T_a|\le \mu$ for every $a \in A_0$. So, any $A\subset A_0$ of cardinality $(|F|^2)^+$ satisfies (4.4).

By (4.4) the set $Z:=(S\cap J)\setminus \bigcup _{a\in A}T_a$ has cardinality $\mathfrak c$. For any $x\in Z$ the set $\{\ell _a(x)-y_a:a\in A\}$ is contained in the set $W_x:=\{f(x)-\varphi (x):f\in F\}$ of cardinality $\le |F|$. Since $|A|>|F|^2$, by the pigeon hole principle, there is an $A_0\subset A$ of cardinality $>|F|$ such that $\ell _a(x)-y_a=\ell _{a'}(x)-y_{a'}$ for every $a,a'\in A_0$. Next, choose $x'\in Z$ with $x'\ne x$. Then, as before, $\{\ell _a(x')-y_a:a\in A_0\}$ is contained in the set $W_{x'}$ of cardinality $\le |F|$. So, there are distinct $a,a'\in A_0\subset A$ such that $\ell _a(x')-y_a=\ell _{a'}(x')-y_{a'}$. But we have also $\ell _a(x)-y_a=\ell _{a'}(x)-y_{a'}$. This means, that two linear functions, $\ell _a-y_a$ and $\ell _{a'}-y_{a'}$, with different slopes, have the same values at two different points, a contradiction. This finishes the argument for (4.3).

Now, we can define g. By (4.3), we can pick an $a\in (0,\infty )\setminus \bigcup _{\varphi \in \Phi ,J\in \mathcal B}A_{\varphi ,J}$. For this, use (4.3) to fix an $a\in (0,\infty )\setminus \bigcup _{\varphi \in \Phi ,J\in \mathcal B}A_{\varphi ,J}$. Let $\langle \langle J_\xi ,\varphi _\xi ,y_\xi \rangle :\xi <\mathfrak c\rangle$ be an enumeration of $\mathcal B\times \Phi \times \mathbb {R}$. By induction on $\xi <\mathfrak c$ we will choose a one-to-one sequence $\langle x_\xi \in J_\xi \cap S:\xi <\mathfrak c\rangle$ and define the value of $g(x_\xi )$ such that the following properties hold:

• (a) $g(x_\xi )+\varphi _\xi (x_\xi )=y_\xi$;

• (b) $g(x_\xi )+f(x_\xi )\ne a x_\xi$ for every $f\in F$.

Of course, for any fixed $x_\xi$ the property (a) forces us to define $g(x_\xi ):=y_\xi -\varphi _\xi (x_\xi )$. On the other hand, to have (b) we need to ensure that $g(x_\xi )\ne a x_\xi -f(x_\xi )$ for every $f\in F$. Thus, to ensure (a) and (b), we need to choose an $x_\xi \in S\cap J_\xi \setminus \{x_\zeta :\zeta <\xi \}$ so that $y_\xi -\varphi _\xi (x_\xi )\ne a x_\xi -f(x_\xi )$ or, equivalently, that $\ell _a(x_\xi )-y_\xi \ne f(x_\xi )-\varphi _\xi (x_\xi )$. But the existence of such $x_\xi$ is ensured by our choice of a, by which $a\notin A_{\varphi _\xi ,J_\xi }$, that is, the set $\left\{ x\in S\cap J_\xi :(\forall f\in F) \ \ell _a(x)-y_\xi \ne f(x)-\varphi _\xi (x) \right\}$ has cardinality $\mathfrak c$.

We extend g, so far defined only on the set $B=\{x_\zeta :\xi <\mathfrak c\}$, by defining g(x), for every $x\in \mathbb {R}\setminus B$, so that $g(x)+f(x)\ne a x$ for every $f\in F$ (i.e., by picking $g(x)\in \mathbb {R}\setminus \{ax-f(x):f\in F\}$).

Notice that this choice, together with (b), ensures that (i) is as satisfied. Now, to see (ii), fix a $\bar{g}\in \mathbb {R}^\mathbb {R}$ such that $\bar{g}\upharpoonright S=g\upharpoonright S$. We need to show that $\bar{g}+\Phi \subset {{\,\mathrm{ES}\,}}$. So, choose a $J\in \mathcal B$ and an $\varphi \in \Phi$. We need to show that $(\bar{g}+\varphi )[J]=\mathbb {R}$. Thus, fix a $y\in \mathbb {R}$. We will find an $x\in J\cap S$ for which $(\bar{g}+\varphi )(x)=(g+\varphi )(x)=y$. But, $\langle J,\varphi ,y\rangle \in \mathcal B\times \Phi \times \mathbb {R}$. So, there is a $\xi <\mathfrak c$ such that $\langle J,\varphi ,y\rangle = \langle J_\xi ,\varphi _\xi ,y_\xi \rangle$. Hence, $x_\xi \in J_\xi \cap S=J\cap S$ and, by (a), $(\bar{g}+\varphi )(x_\xi )=g(x_\xi )+\varphi _\xi (x_\xi )=y_\xi =y$, as needed. $\square$

Lemma 4.4

Let $S\subset \mathbb {R}$ be $\mathfrak c$-dense. Also, let $\Phi \subset \mathbb {R}^\mathbb {R}$ be such that $|\Phi |<\mathfrak c$ when $cof(\mathfrak c_-)=\omega$ and $|\Phi |<\mathfrak c_-$ otherwise. Then there exist a $g\in \mathbb {R}^\mathbb {R}$ and a countable family $\Lambda \subset \mathbb {R}^\mathbb {R}$ of continuous functions such that

• (I) for every $f\in \Phi$ there is $\langle \lambda _f,I_f\rangle \in \Lambda \times \mathcal J$ such that $(g+f)(x)\ne \lambda _f(x)$ for every $x\in I_f$;

• (II) for every $f\in \Phi$ we have $g+f\in {{\,\mathrm{ES}\,}}$ and this is decided on S.

In particular, $g+ \Phi \subset {{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}}$ so that ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})\ge \mathfrak c_-$ and, when $cof(\mathfrak c_-)=\omega$, also ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})\ge \mathfrak c$.

Proof

First notice that (I) and (II) indeed imply that $g+ \Phi \subset {{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}}$. So, fix an $f\in \Phi$. Then clearly $g+f\in {{\,\mathrm{ES}\,}}$. Also, if $\langle \lambda _f,I_f\rangle \in \Lambda \times \mathcal J$ are as in (I), then there exist $p<q$ in $I_f$ such that $(g+f)(p)>\lambda _f(p)$ and $(g+f)(q)<\lambda _f(q)$. Let $L_1:=\{p\}\times (-\infty ,\lambda _f(p)]$, $L_2:=\lambda _f\upharpoonright [p,q]$ and $L_3:=\{q\}\times [\lambda _f(q),\infty )$ and notice that the curve $L_1\cup L_2\cup L_3$ separates $g+f$. Thus, $g+\Phi \subset \lnot {{\,\mathrm{Conn}\,}}$, as needed.

To prove (I) and (II) first assume that $cof(\mathfrak c_-)>\omega$. Then, by Lemma 4.3 applied to $F=\Phi$, there exist a $g\in \mathbb {R}^\mathbb {R}$ and an $a>0$ such that

• (i) $(g+f)\cap \ell _a=\emptyset$ for every $f\in F=\Phi$;

• (ii) for every $f\in \Phi$ we have $g+f\in {{\,\mathrm{ES}\,}}$ and this is decided on S.

Therefore, g and $\Lambda =\{\ell _a \}$ satisfy (I) and (II).

Finally, assume that $cof(\mathfrak c_-)=\omega$. Then $|\Phi |<\mathfrak c$ and $\mathfrak c_-<\mathfrak c$, since $\mathfrak c$ has uncountable cofinality. Furthermore, since $cof(\mathfrak c_-)=\omega$, we have that $\Phi =\bigcup _{n<\omega } F_n$ for some families $F_n$ of cardinality $<\mathfrak c_-$. By Lemma 4.3, for every $n<\omega$ we can find a $g_n\in \mathbb {R}^\mathbb {R}$ and a linear map $\ell _{a_n}$ satisfying (i) and (ii) of Lemma 4.3 for $F=F_n$. Let $\{J_n:n<\omega \}$ be a partition of $\mathbb {R}$ into non-trivial intervals. Then $g:=\bigcup _{n<\omega } g_n\upharpoonright J_n$ and $\Lambda :=\{\ell _{a_n}:n<\omega \}$ satisfy (I) and (II). $\square$

Theorem 4.5

$\mathfrak c_-\le {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})\le \mathfrak c$ and the first inequality is strict when $cof(\mathfrak c_-)=\omega$. Moreover

• (i) It is consistent with ZFC, follows from the arithmetic $2^\omega =2^{\omega _1}=\omega _2$, that $\mathfrak c_-={{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})<\mathfrak c$.

• (ii) It is consistent with ZFC, follows from CH or the arithmetic $2^\omega =(\omega _\omega )^+$, that $\mathfrak c_-<{{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})=\mathfrak c$.

• (iii) It is consistent with ZFC, follows from a possible arithmetic $2^\omega =\omega _{\omega _1}$, that $\mathfrak c_-={{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})=\mathfrak c$.

Proof

Notice that Lemma 4.4, the inclusions ${{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}}\subset {{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}}\subset {{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{AC}\,}}$ together with Proposition 1.2 (iii), and Lemma 4.1 imply that

$$\begin{aligned} \mathfrak c_-\le {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{AC}\,}})\le \mathfrak c. \end{aligned}$$

Thus, to finish the proof of the main part of the theorem it is enough to show that ${{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})$. To see this, choose an $F\subset \mathbb {R}^\mathbb {R}$ such that $|F|<{{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})$. We need to show that $|F|<{{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})$, that is, that there exists a $g\in \mathbb {R}^\mathbb {R}$ such that $g+F\subset {{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}}$.

To argue for this, let $\hat{F}:=\{f+q{\chi }_{\{p\}}:f\in F\ \& \ p,q\in \mathbb {Q}\}$ and notice that $|\hat{F}|<{{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}})$, since, by Lemma 4.4, ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus {{\,\mathrm{Conn}\,}})>\omega$.

So, there is a $g\in \mathbb {R}^\mathbb {R}$ such that $g+\hat{F}\subset {{\,\mathrm{\mathscr {D}}\,}}\setminus {{\,\mathrm{Conn}\,}}$. Since $F\subset \hat{F}$, this clearly gives $g+F\subset \lnot {{\,\mathrm{Conn}\,}}$. It remains to show that $g+F\subset {{\,\mathrm{ES}\,}}$. But, since $g+F\subset g+\hat{F}\subset {{\,\mathrm{\mathscr {D}}\,}}$, it is enough to show that, for every $f\in F$, $g+f$ has a dense graph in $\mathbb {R}^2$. Indeed, assume that there exist nonempty open sets $U,V\subset \mathbb {R}$ such that $(g+f)\cap (U\times V)=\emptyset$. Choose $p\in U\cap \mathbb {Q}$ and $q\in \mathbb {Q}$ such that $g(p)+f(p)+q\in V$. Then $\hat{f}:=f+q{\chi }_{\{p\}}$ is in $\hat{F}$ and $(g+\hat{f})\cap (U\times V)$ is a singleton showing that $g+\hat{f}\notin {{\,\mathrm{\mathscr {D}}\,}}$, a contradiction. This finishes the proof of the main part of the theorem.

Now, the additional parts (i)–(iii) follow immediately from the main part and the inequalities given by Lemmas 4.2 and 4.4. $\square$

5 The Value of ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}})$

The upper bounds for ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}})$ will come from the previous section. So, we concentrate here on the lower bound. Let

$$\begin{aligned} \mathbb {K}:=\{K\subset \mathbb {R}^2:K \text { is compact connected and } dom(K)=[a,b] \text { for some } a<b \}. \end{aligned}$$

The following fact will be of major importance for the results presented in this section. It is commonly cited in the literature related to the class of connectivity functions as well known or folklore. (See e.g. [12, p. 208] or [19, p. 188].) However, our recent intensive search for its explicit proof in literature brought no results.² Therefore, we include below its easy proof, which nevertheless relies on a deep topological result $\bullet$ (related to the fact that the 2-cell $[0,1]^2$ is unicoherent) stated below.

Lemma 5.1

If $f:\mathbb {R}\rightarrow \mathbb {R}$ intersects every $K\in \mathbb {K}$, then $f\in {{\,\mathrm{Conn}\,}}$.

Proof

In the argument we will use [44, thm 14.3, p. 123)]:

• Let $X=[a,b]\times [c,d]$. If there are two points in X separated by a closed $F\subset X$, then they are separated by a connected component of F.³

To prove Lemma 5.1, fix an $f\in \lnot {{\,\mathrm{Conn}\,}}$. It is enough to show that $f\cap K=\emptyset$ for some $K\in \mathbb {K}$.

As $f\in \lnot {{\,\mathrm{Conn}\,}}$, there are $a<b$ in $\mathbb {R}$ such that the points $p=\langle a, f(a)\rangle$ and $q=\langle b, f(b)\rangle$ are separated by some closed $F\subset \mathbb {R}^2$ disjoint with f. Thus, for every large enough $n\in \mathbb {N}$ the points p and q belong to $X_n:=[a,b]\times [-n,n]$ and, furthemore, the points p and q are separated by the closed set $F\cap X_n$. So, by $\bullet$, they are separated by a connected component $K_n$ of $F\cap X_n$. Such compact connected $K_n$ is our desired $K\in \mathbb {K}$, unless $dom(K_n)$ is a single point $x_n\in (a,b)$ and $K_n=\{x_n\}\times [-n,n]$. However, if $K_n$ is of this format for infinitely many n, then the closed set $F\cap ([a,b]\times \mathbb {R})$ contains a vertical line, contradicting the fact that F is disjoint with f. So, there is an $n\in \mathbb {N}$ for which $K:=K_n$ is as needed. $\square$

On the other hand, J.H. Roberts constructed in [47] a subset $Z\subset [0,1]^2$ homeomorphic to the Cantor set $\mathfrak {C}$ such that $Z\cap g\ne \emptyset$ for every continuous function $g:[0,1]\rightarrow [0,1]$. Thus, Z is a blocking set for maps from [0, 1] to [0, 1]. This construction was slightly modified by Ciesielski and Rosłanowski in [19, Lemma 2.1] to obtain a blocking set $\bar{Z}$ for functions from $\mathbb {R}$ to $\mathbb {R}$ that have the following additional properties.

Proposition 5.2

Let Q be a countable dense subset of $(-1,1)$ and $G:=(-1,1)\setminus Q$. Then there exists an embedding $F=\langle F_0,F_1\rangle :\mathbb {R}\rightarrow (-1,1)\times \mathbb {R}$ such that $F_0$ is non-decreasing,

• (a) $B:=F[\mathbb {R}]$ is a blocking set;

• (b) zero-dimensional $\bar{Z}:=F[\mathbb {Z}+\mathfrak {C}]\subset B$ is also a blocking set;

• (c) $\gamma :=\bar{Z}\cap (G\times \mathbb {R})=B\cap (G\times \mathbb {R})$ is a continuous function on G; and

• (d) for every $x\in Q$ the vertical section $B\cap (\{x\}\times \mathbb {R})$ of B is a non-trivial closed interval and $\bar{Z}\cap (\{x\}\times \mathbb {R})$ consists of the two endpoints of that interval.

Notice that $\bar{Z}$ is also a 0-dimensional and for every $x\in Q$ the right hand side limit of $\gamma (x)$ exists. Using Robert’s set Z it is relatively easy to construct a connectivity function $f:[0,1]\rightarrow [0,1]$ which is not almost continuous. Below, we will use set $\bar{Z}$ to obtain a lower bound of the additivity of ${{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}}$.

In what follows, for $\alpha >0$ and $k\in \mathbb {Z}$ we define

$$\begin{aligned} \alpha \bar{Z}_k:=\{\langle x+2k,\alpha y\rangle :\langle x,y\rangle \in \bar{Z}\}. \end{aligned}$$

Clearly, each set $\alpha \bar{Z}_k$ is a blocking set. Also let

$$\begin{aligned} \mathbb {K}_k:=\{K\in \mathbb {K}:dom(K)\cap (2k-1,2k+1)\ne \emptyset \}. \end{aligned}$$

Theorem 5.3

Assume that $S\subset (-1,1)$ is such that $|S\cap (p,q)|=\mathfrak c$ whenever $-1\le p<q\le 1$. Also, let $\Phi \subset \mathbb {R}^\mathbb {R}$ be countable. Then for every $f\in \Phi$ there exist a $g\in \mathbb {R}^\mathbb {R}$, an $\alpha >0$, and a countable $T\subset (-1,1)$ such that

• (i) $(g+f)\cap (\alpha \bar{Z}_0)=\emptyset$;

• (ii) $dom(K\cap (g+\varphi ))\cap (S\cup T) \ne \emptyset$ for every $\varphi \in \Phi$ and $K\in \mathbb {K}_0$.

Proof

Let $\mathcal B_0$ be a countable basis for $(-1,1)$. We actually will prove a seemingly stronger version of (ii) that the set $dom(K\cap (g+\varphi ))\cap (S\cup T)$ in its statement is dense in $dom(K)\cap (-1,1)$. For this, we will first show that for an appropriately chosen $\alpha$ and T we can inductively choose for every tripple $\langle K,\varphi ,J\rangle \in \mathbb {K}_0\times \Phi \times \mathcal B_0$ with nonempty $dom(K)\cap S\cap J$ a distinct $x\in dom(K)\cap (S\cup T)\cap J$ and define g(x) so that $\langle x, (g+\varphi )(x)\rangle \in K$ while $\langle x, (g+f)(x)\rangle \notin \alpha \bar{Z}_0$. Such defined partial function g ensures (ii) while preserving (i). Then any extension of g to $\mathbb {R}$ that preserves (i) will satisfy both (i) and (ii).

To carry this plan, consider the family $\mathcal {E}$ of all $\langle K,\varphi ,J,\alpha \rangle \in \mathbb {K}_0\times \Phi \times \mathcal B_0\times (0,\infty )$ which can give us difficulty, that is, such that $J\subset dom(K)\cap (-1,1)$ and for which the set $C_{\langle K,\varphi ,J,\alpha \rangle }:=dom\left( K\setminus \bigl ( (\varphi - f)\upharpoonright G+\alpha \ \gamma \bigr ) \right) \cap J\cap S$ has cardinality less than $\mathfrak c$.

For any quadruple $\langle K,\varphi ,J,\alpha \rangle \in \mathcal {E}$ let $D_{\langle K,\varphi ,J,\alpha \rangle }:=J\cap S\setminus (C_{\langle K,\varphi ,J,\alpha \rangle }\cup Q)$ and $\psi _{\langle K,\varphi ,J,\alpha \rangle }:=K\cap (D_{\langle K,\varphi ,J,\alpha \rangle }\times \mathbb {R})$. We will need the following fact:

Claim Assume that $\langle K,\varphi ,J,\alpha \rangle ,\langle K',\varphi ,J,\alpha '\rangle \in \mathcal {E}$.

• (A) $(\varphi - f)\upharpoonright D_{\langle K,\varphi ,J,\alpha \rangle }$ and $\psi _{\langle K,\varphi ,J,\alpha \rangle }$ are continuous maps from $D_{\langle K,\varphi ,J,\alpha \rangle }$ to $\mathbb {R}$.

• (B) If $\psi _{\langle K,\varphi ,J,\alpha \rangle }$ and $\psi _{\langle K',\varphi ,J,\alpha '\rangle }$ can be both extended to a continuous functions on J, then $\alpha '=\alpha$.

• (C) If $\alpha '=\alpha$, then $\psi _{\langle K,\varphi ,J,\alpha \rangle }=\psi _{\langle K',\varphi ,J,\alpha '\rangle }$ on $D_{\langle K,\varphi ,J,\alpha \rangle }\cap D_{\langle K',\varphi ,J,\alpha '\rangle }$.

To see (A) notice that $\psi _{\langle K,\varphi ,J,\alpha \rangle }$ is a function since it is contained in the map $(\varphi - f)\upharpoonright G+\alpha \ \gamma$. It is continuous, since its graph $K\cap (D_{\langle K,\varphi ,J,\alpha \rangle }\times \mathbb {R})$ is bounded and closed in $D_{\langle K,\varphi ,J,\alpha \rangle }\times \mathbb {R}$. Finally, $(\varphi - f)\upharpoonright D_{\langle K,\varphi ,J,\alpha \rangle }$ is continuous since it is equal to the continuous function $\psi _{\langle K,\varphi ,J,\alpha \rangle } - \alpha \ \gamma \upharpoonright D_{\langle K,\varphi ,J,\alpha \rangle }$.

To see (B) notice that $D:=D_{\langle K,\varphi ,J,\alpha \rangle }\cap D_{\langle K',\varphi ,J,\alpha '\rangle }$ is dense in J and that both $\psi _{\langle K,\varphi ,J,\alpha \rangle }\upharpoonright D=(\varphi - f)\upharpoonright D+\alpha \ \gamma \upharpoonright D$ and $\psi _{\langle K',\varphi ,J,\alpha '\rangle }\upharpoonright D=(\varphi - f)\upharpoonright D+\alpha '\ \gamma \upharpoonright D$ can be extended to the continuous maps on J. Therefore, also their difference $(\alpha -\alpha ')\ \gamma \upharpoonright D$ can be extended to a continuous map on J. But this is impossible, unless $\alpha =\alpha '$.

The property (C) holds, since under its assumptions both $\psi _{\langle K,\varphi ,J,\alpha \rangle }\upharpoonright D$ and $\psi _{\langle K',\varphi ,J,\alpha '\rangle }\upharpoonright D$ are equal to $(\varphi - f)\upharpoonright D+\alpha \ \gamma \upharpoonright D$. This completes the proof of Claim.

Now let $\mathcal {E}_0$ be the family of all $\langle K,\varphi ,J,\alpha \rangle \in \mathcal {E}$ for which $\psi _{\langle K,\varphi ,J,\alpha \rangle }$ can be extended to a continuous function on J and notice that by part (B) of Claim the set $A:=\{\alpha :\langle K,\varphi ,J,\alpha \rangle \in \mathcal {E}_0\}$ is at most countable.

From this point on we fix an $\alpha \in (0,\infty )\setminus A$. We will show that this $\alpha$ satisfies the statement of the theorem. To see this, notice that

• (D) If $\langle K,\varphi ,J,\alpha \rangle \in \mathcal {E}$, then there is a $T^{\langle \varphi ,J\rangle }\subset \mathbb {R}^2$ such that $dom(T^{\langle \varphi ,J\rangle })$ is dense in J, the x-vertical section $T_x^{\langle \varphi ,J\rangle }:=\{y:\langle x,y\rangle \in T^{\langle \varphi ,J\rangle }\}$ of $T^{\langle \varphi ,J\rangle }$ is a non-trivial interval for every $x\in dom(T^{\langle \varphi ,J\rangle })$ , and $T^{\langle \varphi ,J\rangle }\subset K'$ for every $\langle K',\varphi ,J,\alpha \rangle \in \mathcal {E}$.

To argue for (D), assume that $\langle K,\varphi ,J,\alpha \rangle \in \mathcal {E}$ and choose an $I\in \mathcal B_0$ contained in J. Notice that the choice of $\alpha$ implies that $\langle K,\varphi ,I,\alpha \rangle \notin \mathcal {E}_0$. In particular, there is an $x_I\in I$ such that the numbers

$$b_I:=\limsup _{{x\rightarrow x_I}, x\in D_{\langle K,\varphi ,J,\alpha \rangle }} \psi _{\langle K,\varphi ,J,\alpha \rangle }(x)$$

and

$$a_I:=\liminf _{{x\rightarrow x_I}, x\in D_{\langle K,\varphi ,J,\alpha \rangle }} \psi _{\langle K,\varphi ,J,\alpha \rangle }(x)$$

are distinct. It is enough to show that the segment $\{x_I\}\times [a_I,b_I]$ is contained in $K'$ for every $\langle K',\varphi ,J,\alpha \rangle \in \mathcal {E}$, as then $T^{\langle \varphi ,J\rangle }:=\bigcup _{I\in \mathcal B_0,\, I\subset J} \{x_I\}\times [a_I,b_I]$ is as needed.

To see that $\{x_I\}\times [a_I,b_I]\subset K'$ notice that by the property (C) we have $\psi _{\langle K,\varphi ,J,\alpha \rangle }=\psi _{\langle K',\varphi ,J,\alpha \rangle }$ on $D:=D_{\langle K,\varphi ,J,\alpha \rangle }\cap D_{\langle K',\varphi ,J,\alpha \rangle }$ and that D is dense in $D_{\langle K,\varphi ,J,\alpha \rangle }$.⁴ Since, by (A), $\psi _{\langle K,\varphi ,J,\alpha \rangle }:D_{\langle K,\varphi ,J,\alpha \rangle }\rightarrow \mathbb {R}$ is continuous, there are the sequences $\langle p_n\in D:n<\omega \rangle$ and $\langle q_n\in D:n<\omega \rangle$ both converging to $x_I$ and such that $a_I=\lim _{n\rightarrow \infty } \psi _{\langle K',\varphi ,J,\alpha \rangle }(p_n)$ and $b_I=\lim _{n\rightarrow \infty } \psi _{\langle K',\varphi ,J,\alpha \rangle }(q_n)$. Thus, $\langle x_I,a_I\rangle ,\langle x_I,b_I\rangle \in K'$. To see that $\{x_I\}\times [a_I,b_I]\subset K'$ fix an $r\in (a_I,b_I)$. We need to show that $\langle x_I,r\rangle \in K'$.

So, by way of contradiction, assume that $\langle x_I,r\rangle \notin K'$. Since $K'$ is compact, there exists an ${\varepsilon }>0$ such that the segment $[x_I-{\varepsilon },x_I+{\varepsilon }]\times \{r\}$ is disjoint with $K'$. Choose an $n<\omega$ such that $\psi _{\langle K',\varphi ,J,\alpha \rangle }(p_n)<r$, $\psi _{\langle K',\varphi ,J,\alpha \rangle }(q_n)>r$, and $p_n,q_n\in [x_I-{\varepsilon },x_I+{\varepsilon }]$. Assume that $p_n<q_n$, the other case being similar. Then the closed three-segments set

$$N:=(\{p_n\}\times [r,\infty ))\cup ([p_n,q_n]\times \{r\})\cup (\{q_n\}\times (-\infty ,r])$$

separates $K'$, what contradicts connectedness of $K'\in \mathbb {K}$. This completes the proof of (D).

Now, we are ready to construct our function g. For this, first notice that, by (D), the family $\mathcal {T}:=\{T^{\langle \varphi ,J\rangle }:\langle K,\varphi ,J,\alpha \rangle \in \mathcal {E}\}$ is at most countable, so we can enumerate it as $\{T_n:n<\omega \}$. By induction choose a sequence $\langle p_n:n<\omega \rangle$ so that $p_n\in dom(T_n)\setminus \{p_i:i<n\}$ and define g on the set $T:=\{p_n:n<\omega \}$ so that if $T_n=T^{\langle \varphi ,J\rangle }$, then $\langle p_n, (g+\varphi )(p_n)\rangle \in T_n$ while $\langle p_n, (g+f)(p_n)\rangle \notin \alpha \bar{Z}_0$. This is insured by choosing $g(p_n)$ in the interval $-\varphi (p_n)+\{y:\langle p_n,y\rangle \in T_n\}$ while not in the at most two element set $-f(p_n)+\{y:\langle p_n,y\rangle \in \alpha \bar{Z}_0\}$. This establishes the definition of g on T. Notice g defined so far satisfies (i) and that, by (D), $dom(K\cap (g+\varphi ))\cap T\cap J \ne \emptyset$ provided $\langle K,\varphi ,J,\alpha \rangle \in \mathcal {E}$.

To finish the construction of g let $\{\langle K_\xi ,\varphi _\xi ,J_\xi \rangle :\xi <\mathfrak c\}$ be an enumeration of the family $\{\langle K,\varphi ,J\rangle \in \mathbb {K}_0\times \Phi \times \mathcal B_0:\langle K,\varphi ,J,\alpha \rangle \notin \mathcal {E}\}$. By induction on $\xi <\mathfrak c$ choose

$$\begin{aligned} x_\xi \in dom\left( K_\xi \setminus \left( \left( \varphi _\xi - f\right) \upharpoonright G+\alpha \ \gamma \right) \right) \cap J_\xi \cap S\setminus \left( Q\cup T\cup \left\{ x_\zeta :\zeta <\xi \right\} \right) . \end{aligned}$$

The choice is possible since $\left| dom\left( K_\xi \setminus \bigl ( (\varphi _\xi - f)\upharpoonright G+\alpha \ \gamma \bigr ) \right) \cap J_\xi \cap S\right| =\mathfrak c$ as $\langle K_\xi ,\varphi _\xi ,J_\xi ,\alpha \rangle \notin \mathcal {E}$. This allows us to choose $g(x_\xi )$ so that

$$\begin{aligned} \langle x_\xi ,\left( \varphi _\xi +g\right) \left( x_\xi \right) \rangle \in K_\xi \setminus \left( \left( \varphi _\xi - f\right) \upharpoonright G+\alpha \ \gamma \right) . \end{aligned}$$

This ensures that (ii) is satisfied as $x_\xi \in dom(K_\xi \cap (g+\varphi _\xi ))\cap S$, while (i) is satisfied by g defined so far, as $(\varphi _\xi +g)(x_\xi )\ne (\varphi _\xi - f+\alpha \ \gamma )(x_\xi )$ so that $\langle x_\xi ,(f+g)(x_\xi )\rangle$ does not belong to $\alpha \bar{Z}_0$.

To finish the constriction of g it is enough to extend it to the entire $\mathbb {R}$ so that the property (i) is preserved. $\square$

Corollary 5.4

Assume that $S\subset \mathbb {R}$ is $\mathfrak c$-dense and let $\Phi =\{f_k\in \mathbb {R}^\mathbb {R}:k\in \mathbb {Z}\}$. Then there exist a $g\in \mathbb {R}^\mathbb {R}$ and a countable $T\subset \mathbb {R}$ such that

• (i) for every $k\in \mathbb {Z}$ there is an $\alpha _k>0$ for which $(g+f_k)\cap (\alpha _k\bar{Z}_k)=\emptyset$;

• (ii) for every $\varphi \in \Phi$ we have $g+\varphi \in {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}$ and this is decided on $S\cup T$.

In particular, $g+ \Phi \subset {{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}}$ and so $\omega _1\le {{\,\mathrm{A}\,}}( {{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}})\le \mathfrak c$.

Proof

First notice that for every $k\in \mathbb {Z}$ there exist a $g_k\in \mathbb {R}^\mathbb {R}$, an $\alpha _k>0$, and a countable $T_k\subset (2k-1,2k+1)$ such that

• (I) $(g_k+f_k)\cap (\alpha _k\bar{Z}_k)=\emptyset$;

• (II) $dom(K\cap (g_k+\varphi ))\cap (S\cup T_k)\cap (2k-1,2k+1) \ne \emptyset$ for every $\varphi \in \Phi$ and $K\in \mathbb {K}_k$.

This follows from Theorem 5.3 applied, for every $k\in \mathbb {Z}$, to the 2k-translated versions of $f=f_k$, $\Phi$, and S.

We will show that $T:=\bigcup _{k\in \mathbb {Z}} T_k$ and $g:=\bigcup _{k\in \mathbb {Z}} g_k\upharpoonright [2k-1,2k+1)$ are as needed. Indeed, the property (i) follows from (I) since $dom(\alpha _k\bar{Z}_k)\subset [2k-1,2k+1)$ so that $(g+f_k)\cap (\alpha _k\bar{Z}_k)=(g+f_k)\upharpoonright [2k-1,2k+1)\cap (\alpha _k\bar{Z}_k)=(g_k+f_k)\cap (\alpha _k\bar{Z}_k)=\emptyset$.

To see (ii), fix $\varphi \in \Phi$ and $K\in \mathbb {K}$. It is enough to show that there exists an $x\in S\cup T$ such that $\langle x,(g+\varphi )(x)\rangle \in K$. But clearly there exists a $k\in \mathbb {Z}$ for which $dom(K)\cap (2k-1,2k+1)\ne \emptyset$ so that $K\in \mathbb {K}_k$. Then, by (II), there is an $x\in (S\cup T)\cap (2k-1,2k+1)$ for which $\langle x,(g_k+\varphi )(x)\rangle \in K$. But $g(x)=g_k(x)$ for such x. So, indeed $\langle x,(g+\varphi )(x)\rangle \in K$ and (ii) is proved.

To see the additional part, notice that by (i) for every $f_k\in \Phi$ the sum $g+f_k$ does not intersect a blocking set $\alpha _k\bar{Z}_k$, so $g+f_k\notin {{\,\mathrm{AC}\,}}$. So, $g+ \Phi \subset \lnot {{\,\mathrm{AC}\,}}$. Since clearly (ii) implies that $g+ \Phi \subset {{\,\mathrm{Conn}\,}}$, this proves the main part and the lower bound of ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}})$.

The upper bound for ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus {{\,\mathrm{AC}\,}})$ follows from Proposition 1.2 and Lemma 4.1. $\square$

6 Additivity of ${{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}}$ and Its Refinements

Theorem 6.1

${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}})=2^\mathfrak c$.

Proof

In [17], to prove that ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}})=2^\mathfrak c$ the authors show that for every $F\subset \mathbb {R}^\mathbb {R}$ with $|F|<2^\mathfrak c$ there exists a $g:\mathbb {R}\rightarrow \mathbb {R}$ such that for every $f\in F$ the graph of $g+f$ is dense in $\mathbb {R}^2$, so that $g+f\in {{\,\mathrm{PC}\,}}$. The same argument shows also a bit stronger result:

• (PC) Let X be a second countable space with every nonempty open set having cardinality $\mathfrak c$. Then for every $F\subset \mathbb {R}^X$ with $|F|<2^\mathfrak c$ there exists a $g:X\rightarrow \mathbb {R}$ such that for every $f\in F$ the graph of $g+f$ is dense in $X\times \mathbb {R}$.

Since ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}})=2^\mathfrak c$, we need to show only that ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}})\ge 2^\mathfrak c$. To see this, fix a family $F\subset \mathbb {R}^\mathbb {R}$ of size less than $2^\mathfrak c$. We will find a $g\in \mathbb {R}^\mathbb {R}$ such that $g+F\subset {{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}}$.

Let $\{B_P:P\in {{\,\mathrm{Perf}\,}}\}$ be a family of pairwise disjoint Bernstein sets indexed by ${{\,\mathrm{Perf}\,}}$. For every $P\!\in \! {{\,\mathrm{Perf}\,}}$ let $X_P\!:=\!P\cap B_P$ and $F_P\!:=\!\{f\upharpoonright X_P:f\!\in \! F\}$. By property (PC), we can find a $g_P:X_P\rightarrow \mathbb {R}$ such that for every $f\in F$ the graph of $g_P+f\upharpoonright X_P$ is dense in $X_P\times \mathbb {R}$.

Let $g:\mathbb {R}\rightarrow \mathbb {R}$ be any extension of $\bigcup _{P\in \mathcal {P}}g_P$. Then g is as needed. Indeed, for every $f\in F$ and $P\in {{\,\mathrm{Perf}\,}}$ the restriction of $g+f$ to P has a dense graph in $P\times \mathbb {R}$, so $g+f\in {{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}}$, as needed. $\square$

To decide the additivity of the refinements of the class ${{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}}$ we will need also the following lemma.

Lemma 6.2

For every countable $\Lambda \subset \mathbb {R}^\mathbb {R}$, Bernstein set $B\subset \mathbb {R}$, and $F\subset \mathbb {R}^\mathbb {R}$ with $|F|<\mathfrak c$ there exists a $g\in \mathbb {R}^\mathbb {R}$ such that

• (i) $(g+f)\cap \lambda =\emptyset$ for every $f\in F$ and $\lambda \in \Lambda$;

• (ii) $(g+f)\upharpoonright P\cap B$ is unbounded for every $f\in F$ and $P\in {{\,\mathrm{Perf}\,}}$.

Proof

Let $\Lambda$, B, and F be as in the assumptions. Let $\langle \langle P_\xi ,n_\xi ,f_\xi \rangle :\xi <\mathfrak c\rangle$ be an enumeration of ${{\,\mathrm{Perf}\,}}\times \mathbb {N}\times F$ and, by induction on $\xi <\mathfrak c$, define a sequence $\langle \langle x_\xi ,y_\xi \rangle :\xi <\mathfrak c\rangle$ such that

• (a) $x_\xi \in B\cap P_\xi \setminus \{x_\zeta :\zeta <\xi \}$, and

• (b) $y_\xi \in (n_\xi -f_\xi (x_\xi ),\infty )\setminus \{\lambda (x_\xi )-f(x_\xi ):f\in F\ \& \ \lambda \in \Lambda \}$.

Then $g_0:=\{\langle x_\xi ,y_\xi \rangle :\xi <\mathfrak c\}$ is a function on $D:=\{x_\xi :\xi <\mathfrak c\}$. Extend it to a $g\in \mathbb {R}^\mathbb {R}$ so that for every $x\in \mathbb {R}\setminus D$ we have

$$ \begin{aligned} g(x)\in \mathbb {R}\setminus \{\lambda (x)-f(x):f\in F\ \& \ \lambda \in \Lambda \}. \end{aligned}$$

(6.1)

Then g is as needed.

Indeed, to see (i), fix $f\in F$ and $x\in \mathbb {R}$. We need to show that for every $\lambda \in \Lambda$ we have $(g+f)(x)\ne \lambda (x)$, that is, that $g(x)\ne \lambda (x) -f(x)$. But this is ensured by (b) and (6.1).

To see (ii), fix $f\in F$, $P\in {{\,\mathrm{Perf}\,}}$, and $n\in \mathbb {N}$. Then, there exists a $\xi <\mathfrak c$ such that $\langle P,n,f\rangle =\langle P_\xi ,n_\xi ,f_\xi \rangle$. Then, by (a), we have $x_\xi \in B\cap P_\xi =B\cap P$, while, by (b),

$$\begin{aligned} (g+f)(x_\xi )=g(x_\xi )+f_\xi (x_\xi )=y_\xi +f_\xi (x_\xi )>n_\xi =n. \end{aligned}$$

Therefore, $g+f$ takes arbitrary large values on $P\cap B$, that is, $(g+f)\upharpoonright B\cap P$ is indeed unbounded. $\square$

Theorem 6.3

We have $\mathfrak c_-\le {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))\le {{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))\le \mathfrak c$ and $\omega _1\le {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{AC}\,}}))\le {{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{AC}\,}}))\le \mathfrak c$. Furthermore, ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))= \mathfrak c$ when $cof(\mathfrak c_-)=\omega$. Moreover

• (i) It is consistent with ZFC, follows from the arithmetic $2^\omega =2^{\omega _1}=\omega _2$, that $\mathfrak c_-={{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))<\mathfrak c$.

• (ii) It is consistent with ZFC, follows from CH or the arithmetic $2^\omega =(\omega _\omega )^+$, that $\mathfrak c_-<{{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))=\mathfrak c$.

• (iii) It is consistent with ZFC, follows from a possible arithmetic $2^\omega =\omega _{\omega _1}$, that $\mathfrak c_-={{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))=\mathfrak c$.

• (iv) It is consistent with ZFC, follows from CH, that ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{AC}\,}}))=\mathfrak c$.

Proof

The upper bounds follow from Lemma 4.1.

To argue for the lower bounds choose a Bernstein set $B\subset \mathbb {R}$, put $S:=\mathbb {R}\setminus B$, and let $\kappa =\mathfrak c$ when $cof(\mathfrak c_-)=\omega$ and $\kappa =\mathfrak c_-$ otherwise.

To see that ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}}))\ge \kappa$ choose $\Phi \in [\mathbb {R}^\mathbb {R}]^{<\kappa }$ We need to find a $g\in \mathbb {R}^\mathbb {R}$ such that $g+\Phi \subset {{\,\mathrm{ES}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{Conn}\,}})$. By Lemma 4.4 there exist an $h\in \mathbb {R}^\mathbb {R}$ and a countable family $\Lambda \subset \mathbb {R}^\mathbb {R}$ of continuous functions such that

• (a) for every $f\in \Phi$ there is $\langle \lambda _f,I_f\rangle \in \Lambda \times \mathcal J$ such that $(h+f)(x)\ne \lambda _f(x)$ for every $x\in I_f$;

• (b) for every $f\in \Phi$ we have $h+f\in {{\,\mathrm{ES}\,}}$ and this is decided on S.

Also, by Lemma 6.2, there exists an $h'\in \mathbb {R}^\mathbb {R}$ such that

• (c) $(h'+f)\cap \lambda =\emptyset$ for every $f\in \Phi$ and $\lambda \in \Lambda$;

• (d) $(h'+f)\upharpoonright P\cap B$ is unbounded for every $f\in \Phi$ and $P\in {{\,\mathrm{Perf}\,}}$.

Then $g:=(h\upharpoonright S)\cup (h'\upharpoonright B)$ is as needed. Indeed, (b) and (d) imply, respectively, that $g+\Phi \subset {{\,\mathrm{ES}\,}}$ and $g+\Phi \subset \lnot {{\,\mathrm{PR}\,}}$. Moreover, by (a) and (c), for every $f\in \Phi$ there is $\langle \lambda _f,I_f\rangle \in \Lambda \times \mathcal J$ such that $(h+f)(x)\ne \lambda _f(x)$ for every $x\in I_f$. This, together with $g+\Phi \subset {{\,\mathrm{ES}\,}}$, implies that $g+f\in \lnot {{\,\mathrm{Conn}\,}}$.

To show that ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{AC}\,}}))\ge \omega _1$ assume that $\Phi$ is countable and let $\{f_k:k\in \mathbb {Z}\}$ be an enumeration of $\Phi$. Then, by Corollary 5.4, there exist an $h\in \mathbb {R}^\mathbb {R}$ and a countable $T\subset \mathbb {R}$ such that

• (A) for every $k\in \mathbb {Z}$ there is an $\alpha _k>0$ for which $(h+f_k)\cap (\alpha _k\bar{Z}_k)=\emptyset$;

• (B) for every $\varphi \in \Phi$ we have $h+\varphi \in {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}$ and this is decided on $S\cup T$.

Now, let $\Lambda$ be such that $\bigcup \Lambda$ covers $\bigcup _{k\in \mathbb {Z}}\alpha _k\bar{Z}_k$. We can also replace B with $B\setminus T$, and notice that this new set B is still a Bernstein set. Thus, we can apply Lemma 6.2 to these B, $\Lambda$, and $\Phi$, to find an $h'\in \mathbb {R}^\mathbb {R}$ satisfying (c) and (d) in this setting.

As before define $g:=(h\upharpoonright \mathbb {R}\setminus B)\cup (h'\upharpoonright B)$. We need to show that $g+\Phi \subset {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{AC}\,}})$. Indeed, (B) and (d) imply, respectively, that $g+\Phi \subset {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}$ and $g+\Phi \subset \lnot {{\,\mathrm{PR}\,}}$. Moreover, by (A) and (c), we have $(g+f_k)\cap (\alpha _k\bar{Z}_k)=\emptyset$ for every $f_k\in \Phi$. Since $\alpha _k\bar{Z}_k$ is a blocking set, we conclude that $g+f_k\in \lnot {{\,\mathrm{AC}\,}}$.

The statement (i) is a direct consequence of Theorem 4.5 (i). $\square$

Problem 6.4

Is it possible to prove in ZFC that ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{AC}\,}}))=\omega _1$ or ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{AC}\,}}))=\mathfrak c$? If not, is it possible to improve the lower or upper bounds of ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{AC}\,}}))$ in $\hbox {ZFC}+\lnot \hbox {CH}$?

7 Additivity of ${{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{CIVP}\,}}$ and Its Refinements

We say that $M\subset \mathbb {R}$ is perfect-dense provided for every $J\in \mathcal J$ there is a nonempty perfect set contained in $M\cap J$.

Lemma 7.1

For every countable $\Lambda \subset \mathbb {R}^\mathbb {R}$, perfect-dense $M\subset \mathbb {R}$, $\Phi \in [\mathbb {R}^\mathbb {R}]^{\le \mathfrak c}$, and $F\in [\mathbb {R}^\mathbb {R}]^{<\mathfrak c}$ there exists a $g\in \mathbb {R}^\mathbb {R}$ such that

• (i) $(g+f)\cap \lambda =\emptyset$ for every $f\in F$ and $\lambda \in \Lambda$;

• (ii) $g+\Phi \subset \lnot {{\,\mathrm{CIVP}\,}}$;

• (iii) for every $f\in \Phi$ we have $g+f\in {{\,\mathrm{PR}\,}}$ and this is decided on M.

In particular, ${{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{CIVP}\,}})=\mathfrak c^+$.

Proof

First notice (see [2, Lemma 2] and, for better understanding, [22]) that there exists a sequence $\langle \langle H_\alpha ,x_\alpha \rangle :\alpha <\mathfrak c\rangle$ such that

• (a) $H_\alpha \cup \{x_\alpha \}\subset \mathbb {R}$ is compact perfect, $x_\alpha \notin H_\alpha$, and $x_\alpha$ is a bilaterally limit point of $H_\alpha$;

• (b) $H_\alpha \cap H_\beta =\emptyset$ for any $\alpha<\beta <\mathfrak c$;

• (c) for every $x\in \mathbb {R}$, there exist $\mathfrak c$-many $\gamma <\mathfrak c$ such that $x=x_\gamma$;

• (d) $H_\alpha \subset M$ for any $\alpha <\mathfrak c$.

To see this, let $\{x_\alpha :\alpha <\mathfrak c\}$ be an enumeration of $\mathbb {R}$ such that for every $x\in \mathbb {R}$, there exist $\mathfrak c$-many $\gamma <\mathfrak c$ with $x=x_\gamma$. Choose a family of pairwise disjoint perfect sets $\{C_I\subset I\cap M:I\in \mathcal B\}$ and for every $I\in \mathcal B$ let $\{C_I^\alpha \in {{\,\mathrm{Perf}\,}}:\alpha <\mathfrak c\}$ be a partition of $C_I$. For every $\alpha <\mathfrak c$ and $n<\omega$ choose $I_{\alpha ,n},J_{\alpha ,n}\in \mathcal B$ with $I_{\alpha ,n}\subset (x_\alpha -2^{-n},x_\alpha )$ and $J_{\alpha ,n}\subset (x_\alpha ,x_\alpha +2^{-n})$. Then sets $H_\alpha :=\bigcup _{n<\omega } (C_{I_{\alpha ,n}}^\alpha \cup C_{J_{\alpha ,n}}^\alpha )$ are as needed.

Next, list $\Phi =\{\varphi _\alpha :\alpha <\mathfrak c\}$, $\mathbb {R}=\{r_\beta :\beta <\mathfrak c\}$, and let $\{\langle x_\xi , y_\xi ,f_\xi \rangle :\xi <\mathfrak c\}$ be an enumeration of $\mathbb {R}\times \mathbb {R}\times \Phi$. By induction on $\xi <\mathfrak c$, choose a sequence $\langle P_\xi :\xi <\mathfrak c\rangle$ of distinct sets from $\{H_\zeta :\zeta <\mathfrak c\}$ such that, for every $\xi <\mathfrak c$, the set $P_\xi \cup \{x_\xi \}$ satisfies (a). Also, fix a perfect set $K\subset \mathbb {R}$ such that

$$\begin{aligned} int(S+ K)=\emptyset \text { for every } S\in [\mathbb {R}]^{<\mathfrak c}. \end{aligned}$$

(7.1)

Notice that this holds for any $K\subset \mathbb {R}$ for which the linear space $LIN_\mathbb {Q}(K)$ spanned by K over $\mathbb {Q}$ has co-dimension $\mathfrak c$, as then, for $S\in [\mathbb {R}]^{<\mathfrak c}$, $LIN_\mathbb {Q}(S+K)$ has the same co-dimension. In particular, any non-trivial portion K of a linearly independent perfect set H (see [38, Theorem 2, Chapter XI, Sect. 7] for the existence of H) will have such property.

We define g by choosing, for every $r=r_\alpha \in \mathbb {R}$, the value g(r) so that it satisfies

$$\begin{aligned} (g+f)(r)\notin K\cup \{\lambda (r):\lambda \in \Lambda \}\text { for every } f\in F_{\alpha }:=F\cup \{\varphi _\beta :\beta <\alpha \} \end{aligned}$$

(7.2)

and

$$\begin{aligned} |\left( g+f_\xi \right) (r)-y_\xi |<|r-x_\xi |\text { whenever } r\in P_\xi . \end{aligned}$$

(7.3)

This is ensured by choosing

$$\begin{aligned} g(r)\in U_r\setminus \bigcup _{f\in F_\alpha } \left( -f(r)+\left( K\cup \left\{ \lambda (r):\lambda \in \Lambda \right\} \right) \right) , \end{aligned}$$

where $U_r:=y_\xi -f_\xi (r)+(-|r-x_\xi |,|r-x_\xi |)$ whenever $r\in P_\xi$ for some $\xi <\mathfrak c$ and $U_r:=\mathbb {R}$, otherwise. The possibility of such choice is ensured by (7.1).

To finish the proof, we need to show that such defined g satisfies the properties (i), (ii), and (iii). Indeed (i) is ensured by the choice as in (7.2).

To see (ii), first notice that for every $f=\varphi _\alpha \in \Phi$ the graph of $g+f$ is dense in $\mathbb {R}^2$. For every $\langle x,y\rangle \in \mathbb {R}^2$ and ${\varepsilon }>0$ there exist a $\xi <\mathfrak c$ and an $r\in P_\xi$ so that $\langle x_\xi , y_\xi ,f_\xi \rangle =\langle x, y,f\rangle$ and $|r-x_\xi |<{\varepsilon }$. Therefore, by (7.3), we have

$$\begin{aligned} \Vert \langle r,(g+f)(r)\rangle -\langle x,y\rangle \Vert = \Vert \langle r-x_\xi ,(g+f_\xi )(r)-y_\xi \rangle \Vert <2{\varepsilon }, \end{aligned}$$

where the inequality follows from (7.3) and the fact that $|r-x_\xi |<{\varepsilon }$. So, indeed the graph of $g+f$ is dense in $\mathbb {R}^2$. But there is no perfect set C with $(g+f)[C]\subset K$, since, by (7.2), $|(g+f)^{-1}[K]|<\mathfrak c$. So, (ii) is proved.

To see (iii), choose a $\bar{g}\in \mathbb {R}^\mathbb {R}$ such that $\bar{g}\upharpoonright M=g\upharpoonright M$, an $f\in \Phi$, and an $x\in \mathbb {R}$. We need to find a perfect $P\subset \mathbb {R}$ having x as a bilateral limit point such that $(\bar{g}+f)\upharpoonright P$ is continuous at x. For this, let $\xi <\mathfrak c$ be such that $\langle x_\xi , y_\xi ,f_\xi \rangle =\langle x, (\bar{g}+f)(x),f\rangle$ and let $P:=P_\xi \cup \{x\}$. Then x is a bilateral limit point of P and, by (7.3), for every $r\in P_\xi =P\setminus \{x\}$ we have

$$\begin{aligned} |\left( \bar{g}+f\right) (r)-\left( \bar{g}+f\right) (x)|=|\left( g+f_\xi \right) (r)-y_\xi |<|r-x_\xi |=|r-x|. \end{aligned}$$

This clearly implies that $(\bar{g}+f)\upharpoonright P$ is continuous at x, as needed. $\square$

Theorem 7.2

We have the inequalities $\omega _1\le {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}}))$

$\le {{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}}))\le \mathfrak c$ and $\mathfrak c_-\le {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))$

$\le {{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))\le \mathfrak c$. Also ${{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))= \mathfrak c$ when $cof(\mathfrak c_-)=\omega$. Moreover

• (i) It is consistent with ZFC, follows from the arithmetic $2^\omega =2^{\omega _1}=\omega _2$, that $\mathfrak c_-={{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))<\mathfrak c$.

• (ii) It is consistent with ZFC, follows from CH or the arithmetic $2^\omega =(\omega _\omega )^+$, that $\mathfrak c_-<{{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))=\mathfrak c$.

• (iii) It is consistent with ZFC, follows from a possible arithmetic $2^\omega =\omega _{\omega _1}$, that $\mathfrak c_-={{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))=\mathfrak c$.

• (iv) It is consistent, follows from CH, that ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}}))=\mathfrak c$.

Proof

The proof is similar to that for Theorem 6.3.

Once again, the upper bounds follow from Lemma 4.1. To argue for the lower bounds choose a Bernstein set $B\subset \mathbb {R}$, a perfect-dense meager $M\subset \mathbb {R}$, and $\Phi \subset \mathbb {R}^\mathbb {R}$ such that $|\Phi |<\mathfrak c$ when $cof(\mathfrak c_-)=\omega$ and $|\Phi |<\mathfrak c_-$ otherwise. We need to show that $\Phi$ can be shifted into ${{\,\mathrm{ES}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}})$ and, in case when $|\Phi |\le \omega$, also into ${{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}})$.

Let $S=\mathbb {R}\setminus (B\cup M)$. By Lemma 4.4, we can find a countable family $\Lambda$ of continuous functions and $h\in \mathbb {R}^\mathbb {R}$ such that

• (a) for every $f\in \Phi$ there is $\langle \lambda _f,I_f\rangle \in \Lambda \times \mathcal J$ such that $(g+f)(x)\ne \lambda _f(x)$ for every $x\in I_f$;

• (b) for every $f\in \Phi$ we have $h+f\in {{\,\mathrm{ES}\,}}$ and this is decided on S.

Also, by Lemma 6.2, there exists an $h'\in \mathbb {R}^\mathbb {R}$ such that

• (c) $(h'+f)\cap \lambda =\emptyset$ for every $f\in \Phi$ and $\lambda \in \Lambda$;

• (d) $(h'+f)\upharpoonright P\cap B$ is unbounded for every $f\in \Phi$ and $P\in {{\,\mathrm{Perf}\,}}$.

Finally, since $|\Phi |<\mathfrak c$, by Lemma 7.1 used with $F=\Phi$, there exists an $h''\in \mathbb {R}^\mathbb {R}$ such that

• (e) $(h''+f)\cap \lambda =\emptyset$ for every $f\in \Phi$ and $\lambda \in \Lambda$;

• (f) $h''+\Phi \subset \lnot {{\,\mathrm{CIVP}\,}}$;

• (g) for every $f\in \Phi$ we have $h''+f\in {{\,\mathrm{PR}\,}}$ and this is decided on M.

Define $g:=(h\upharpoonright S)\cup (h'\upharpoonright B\setminus M)\cup (h''\upharpoonright M)$ and notice that it is as needed, that is, that $g+\Phi \subset {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{Conn}\,}})$. Indeed, (b) and (g) imply, respectively, that $g+\Phi \subset {{\,\mathrm{ES}\,}}$ and $g+\Phi \subset {{\,\mathrm{PR}\,}}$. We have $g+\Phi \subset \lnot {{\,\mathrm{Conn}\,}}$ since $g+\Phi \subset {{\,\mathrm{ES}\,}}$ and, by (a), (c), and (e), for every $f\in \Phi$ there is $\langle \lambda _f,I_f\rangle \in \Lambda \times \mathcal J$ such that $(g+f)\cap \lambda _f\upharpoonright I_f=\emptyset$.

Finally, to see that $g+\Phi \subset \lnot {{\,\mathrm{CIVP}\,}}$ fix an $f\in \Phi$. Since $h''+\Phi \subset \lnot {{\,\mathrm{CIVP}\,}}$, there are $p<q$ and a $K\in {{\,\mathrm{Perf}\,}}$ between $(h''+f)(p)$ and $(h''+f)(q)$ such that $(h''+f)[C]\not \subset K$ for any $C\in {{\,\mathrm{Perf}\,}}$ contained in (p, q). Since $g+f\in {{\,\mathrm{ES}\,}}$, there are $p'<q'$ in (p, q) such that $K\subset ((g+f)(p'),(g+f)(q'))$. To prove that $g+f\in \lnot {{\,\mathrm{CIVP}\,}}$ it is enough to show that $(g+f)[C]\not \subset K$ for any $C\in {{\,\mathrm{Perf}\,}}$ contained in $(p',q')$. So, fix a $C\in {{\,\mathrm{Perf}\,}}$ contained in $(p',q')$. If $C\setminus M$ is uncountable, then there is a $C'\in {{\,\mathrm{Perf}\,}}$ contained in $C\setminus M\subset (p,q)$. Then, by (d), $(g+f)[C'\cap B]=(h'+f)[C'\cap B]$ is unbounded, so $(g+f)[C]\supset (g+f)[C'\cap B]$ cannot be a subset of any bounded K. So, assume that $C\setminus M$ is countable. Then there is a $C'\in {{\,\mathrm{Perf}\,}}$ contained in $C\cap M$ and we cannot have $(g+f)[C]\subset K$, since this would imply $(h''+f)[C']=(g+f)[C']\subset (g+f)[C]\subset K$, contradicting our choice of set K.

To show that ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}}))\ge \omega _1$ assume that $\Phi$ is countable, and let $\{f_k:k\in \mathbb {Z}\}$ be an enumeration of $\Phi$ (we can extend $\Phi$ if necessary). Then, by Corollary 5.4, there exist an $h\in \mathbb {R}^\mathbb {R}$ and a countable $T\subset \mathbb {R}$ such that

• (A) for every $k\in \mathbb {Z}$ there is an $\alpha _k>0$ for which $(h+f_k)\cap (\alpha _k\bar{Z}_k)=\emptyset$;

• (B) for every $\varphi \in \Phi$ we have $h+\varphi \in {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}$ and this is decided on $S\cup T$.

Now, let $\Lambda \subset \mathbb {R}^\mathbb {R}$ be such that $\bigcup \Lambda$ covers $\bigcup _{k\in \mathbb {Z}}\alpha _k\bar{Z}_k$. We can assume that B is disjoint with T and that $h'$ as above was obtained for such B and $\Lambda$. Notice also that $M\setminus T$ is still perfect-dense and that $|\Phi |=\omega$. So, by Lemma 7.1, there exists an $h''\in \mathbb {R}^\mathbb {R}$ such that

• (E) $(h''+f)\cap \lambda =\emptyset$ for every $f\in \Phi$ and $\lambda \in \Lambda$;

• (F) $h''+\Phi \subset \lnot {{\,\mathrm{CIVP}\,}}$;

• (G) for every $f\in \Phi$ we have $h''+f\in {{\,\mathrm{PR}\,}}$ and this is decided on $M\setminus T$.

Define $g:=(h\upharpoonright S\cup T)\cup (h'\upharpoonright B\setminus M)\cup (h''\upharpoonright M\setminus T)$. A similar argument as above shows that $g+\Phi \subset {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}})$. $\square$

Problem 7.3

Is it possible to prove in ZFC that ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}}))=\omega _1$ or ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}}))=\mathfrak c$? If not, is it possible to improve the lower or upper bounds of ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{AC}\,}}))$ in $\hbox {ZFC}+\lnot \hbox {CH}?$

8 Additivity of ${{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}}$ and Its Refinements

Lemma 8.1

For every countable $\Lambda \subset \mathbb {R}^\mathbb {R}$, perfect-dense $M\subset \mathbb {R}$, $\Phi \in [\mathbb {R}^\mathbb {R}]^{\le \mathfrak c}$, and $F\in [\mathbb {R}^\mathbb {R}]^{<\mathfrak c}$ there exists a $g\in \mathbb {R}^\mathbb {R}$ such that

• (i) $(g+f)\cap \lambda =\emptyset$ for every $f\in F$ and $\lambda \in \Lambda$;

• (ii) $g+\Phi \subset {{\,\mathrm{SZ}\,}}\subset \lnot {{\,\mathrm{SCIVP}\,}}$;

• (iii) for every $\varphi \in \Phi$ we have $g+\varphi \in {{\,\mathrm{CIVP}\,}}$ and this is decided on M.

In particular, ${{\,\mathrm{A}\,}}({{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}})=\mathfrak c^+$.

Proof

Let $\mathcal {P}$ be a family of pairwise disjoint sets in ${{\,\mathrm{Perf}\,}}$ contained in M such that every $J\in \mathcal J$ contains $\mathfrak c$-many $P\in \mathcal {P}$, and extend $\Phi$, if necessary, so that $|\Phi |=\mathfrak c$. Choose a one-to-one mapping ${{\,\mathrm{Perf}\,}}\times \mathcal J\times \Phi \ni \langle K,J,\varphi \rangle \mapsto P_{\langle K,J,\varphi \rangle }\in \mathcal {P}$ such that $P_{\langle K,J,\varphi \rangle }\subset J$. Let $\{r_\xi :\xi <\mathfrak c\}$ be an enumeration, with no repetitions, of $\mathbb {R}$ and put ${{\,\mathrm{\mathscr {B}}\,}}=\{h_\xi :\xi <\mathfrak c\}$ and $\Phi =\{\varphi _\xi :\xi <\mathfrak c\}$. By induction on $\xi <\mathfrak c$ choose $g(r_\xi )$ such that

• (a) $g(r_\xi )\!\in \! -\varphi (r_\xi )+K$ provided $r_\xi \!\in \! P_{\langle K,J,\varphi \rangle }$ for some $\langle K,J,\varphi \rangle \!\in \!{{\,\mathrm{Perf}\,}}\times \mathcal J\times \Phi$;

• (b) $g(r_\xi )\notin \{(\lambda -f)(r_\xi ):f\in F\ \& \ \lambda \in \Lambda \}\cup \{(h_\zeta -\varphi _\eta )(r_\xi ) :\zeta ,\eta <\xi \}$.

Then g is as needed.

Indeed, (i) and (ii) are ensured by (b). To see (iii) fix $\varphi \in \Phi$, $J\in \mathcal J$, and $K\in {{\,\mathrm{Perf}\,}}$. Then, by (a), the perfect set $P_{\langle K,J,\varphi \rangle }$ contained in $M\cap J$ is mapped into K, as needed. Hence, ${{\,\mathrm{A}\,}}({{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}})>\mathfrak c$. On the other hand, by Proposition 1.2, ${{\,\mathrm{A}\,}}({{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}})=\mathfrak c^+$, so we have ${{\,\mathrm{A}\,}}({{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}})=\mathfrak c^+$. $\square$

Theorem 8.2

We have

$$\begin{aligned} \omega _1\le & {} {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}}))\\\le & {} {{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}}))\le \mathfrak c\end{aligned}$$

and

$$\begin{aligned} \mathfrak c_-\le & {} {{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))\\\le & {} {{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))\le \mathfrak c. \end{aligned}$$

Also ${{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))= \mathfrak c$ when $cof(\mathfrak c_-)=\omega$. Moreover

• (i) It is consistent with ZFC, follows from the arithmetic $2^\omega =2^{\omega _1}=\omega _2$, that $\mathfrak c_-\!=\!{{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\!\cap \!{{\,\mathrm{CIVP}\,}}\!\setminus ({{\,\mathrm{SCIVP}\,}}\!\cup \!{{\,\mathrm{Conn}\,}}))\!=\!{{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{CIVP}\,}}\!\setminus ({{\,\mathrm{SCIVP}\,}}\!\cup \!{{\,\mathrm{Conn}\,}}))\!<\!\mathfrak c$.

• (ii) It is consistent with ZFC, follows from CH or the arithmetic

  $$2^\omega =(\omega _\omega )^+,$$

  that

  $$\mathfrak c_-\!<{{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))=\mathfrak c.$$

• (iii) It is consistent with ZFC, follows from a possible arithmetic $2^\omega =\omega _{\omega _1}$, that

  $$\mathfrak c_-\!={{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))={{\,\mathrm{A}\,}}({{\,\mathrm{\mathscr {D}}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{Conn}\,}}))=\mathfrak c.$$

• (iv) It is consistent, follows from CH, that

  $${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}}))=\mathfrak c.$$

Proof

The proof is similar to that for Theorem 7.2, where we replace the use of Lemma 7.1 with Lemma 8.1.

The upper bounds follow from Lemma 4.1. For the lower bounds it is enough to prove the following. For any $\Phi \subset \mathbb {R}^\mathbb {R}$ such that $|\Phi |<\mathfrak c$ when $cof(\mathfrak c_-)=\omega$ and $|\Phi |<\mathfrak c_-$ otherwise, the set $\Phi$ can be shifted to

$$\begin{aligned} {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{Conn}\,}}). \end{aligned}$$

Furthemore, if $\Phi$ is countable, then the same can be said for ${{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}})$.

Let B and M be a Bernstein set and a perfect-dense meager set of $\mathbb {R}$, respectively. Put $S:=\mathbb {R}\setminus (B\cup M)$. By Lemma 4.4, there exist a countable family $\Lambda \subset \mathbb {R}^\mathbb {R}$ of continuous functions and an $h\in \mathbb {R}^\mathbb {R}$ such that

• (a) for every $f\in \Phi$, there is $\langle \lambda _f,I_f\rangle \in \Lambda \times \mathcal J$ such that $(h+f)\cap \lambda _f\upharpoonright I_f=\emptyset$;

• (b) for every $f\in \Phi$, we have $h+f\in {{\,\mathrm{ES}\,}}$ and this is decided on S.

By Lemma 6.2, there exists an $h'\in \mathbb {R}^\mathbb {R}$ such that

• (c) $(h'+f)\cap \lambda =\emptyset$ for every $f\in \Phi$ and $\lambda \in \Lambda$;

• (d) $(h'+f)\upharpoonright P\cap B$ is unbounded for every $f\in \Phi$ and $P\in {{\,\mathrm{Perf}\,}}$.

Finally, by Lemma 8.1, since $|\Phi |<\mathfrak c$, there exists an $h''\in \mathbb {R}^\mathbb {R}$ such that

• (e) $(h''+f)\cap \lambda =\emptyset$ for every $f\in \Phi$ and $\lambda \in \Lambda$;

• (f) $h''+\Phi \subset \lnot {{\,\mathrm{SCIVP}\,}}$;

• (g) for every $f\in \Phi$, we have $h''+f\in {{\,\mathrm{CIVP}\,}}$ and this is decided on M.

Define $g:=(h\upharpoonright S)\cup (h'\upharpoonright B\setminus M)\cup (h''\upharpoonright M)$. Then g is as needed. Indeed, (b) and (g) imply that $g+\Phi \subset {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{CIVP}\,}}$. Also, $g+\Phi \subset \lnot {{\,\mathrm{Conn}\,}}$ since $g+\Phi \subset {{\,\mathrm{ES}\,}}$ and, by (a), (c) and (e), for every $f\in \Phi$, there is $\langle \lambda _f,I_f\rangle \in \Lambda \times \mathcal J$ such that $(g+f)\cap \lambda _f\upharpoonright I_f=\emptyset$.

It remains to show that $g+\Phi \subset \lnot {{\,\mathrm{SCIVP}\,}}$. To see this, fix an $f\in \Phi$ and notice that $g+f\subset \lnot {{\,\mathrm{SCIVP}\,}}$. Indeed, (f) implies that $h''+f\subset \lnot {{\,\mathrm{SCIVP}\,}}$. So, there are $p<q$ and a $K\in {{\,\mathrm{Perf}\,}}$ between $(h''+f)(p)$ and $(h''+f)(q)$ such that

• (i) for any $P\in {{\,\mathrm{Perf}\,}}$ contained in (p, q), if $(h''+f)\upharpoonright P$ is continuous, then $(h''+f)[P]\not \subset K$.

Since $g\!+\!f\!\in \!{{\,\mathrm{ES}\,}}$, there are $p'<q'$ in (p, q) such that $K\!\subset \! ((g\!+\!f)(p'),(g\!+\!f)(q'))$. To prove that $g+f\in \lnot {{\,\mathrm{SCIVP}\,}}$, it is enough to show that for any $C\in {{\,\mathrm{Perf}\,}}$ contained in $(p',q')$, it is impossible that

• (ii) $(g+f)\upharpoonright C$ is continuous and $(g+f)[C]\subset K$.

Indeed, if $C\cap M$ is uncountable, then it contains a $P\in {{\,\mathrm{Perf}\,}}$ for which we have $(g+f)\upharpoonright P=(h''+f)\upharpoonright P$. Thus, in this case, (ii) contradicts (i).

So, assume that $|C\cap M|\le \omega$. Then $C\setminus M$ contains a $P\in {{\,\mathrm{Perf}\,}}$ for which we have $(g+f)\upharpoonright P\cap B=(h'+f)\upharpoonright P\cap B$. Hence $(h'+f)[P\cap B]\subset (g+f)[C]$ and, by (d), the set $(h'+f)[P\cap B]$ is unbounded. So, $(g+f)[C]$ cannot be contained in bounded K, that is, once again (ii) is impossible.

The argument for ${{\,\mathrm{A}\,}}({{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}}))\ge \omega _1$ is similar to that above, except that (similarly as in the proof of Theorem 7.2) we replace in it Lemma 4.4 with Corollary 5.4, by which there exists an $h\in \mathbb {R}^\mathbb {R}$ and a countable $T\subset \mathbb {R}$ such that

• (A) for every $k\in \mathbb {Z}$, there is an $\alpha _k>0$ for which $(h+f_k)\cap (\alpha _k\bar{Z}_k)=\emptyset$;

• (B) for every $\varphi \in \Phi$, we have $h+\varphi \in {{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}$ and this is decided on $S\cup T$.

The properties (A), (B), and (c)–(g) imply that

$$\begin{aligned} g:=\left( h\upharpoonright S\cup T\right) \cup \left( h'\upharpoonright B\setminus M\right) \cup \left( h''\upharpoonright M\setminus T\right) \end{aligned}$$

shifts $\Phi$ to ${{\,\mathrm{ES}\,}}\cap {{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}})$, as needed. $\square$

Problem 8.3

Is it provable in ZFC that ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}}))=\omega _1$ or ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}}))=\mathfrak c$? If not, is it possible to improve the lower or upper bounds of ${{\,\mathrm{A}\,}}({{\,\mathrm{Conn}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{AC}\,}}))$ in $\hbox {ZFC}+\lnot \hbox {CH}?$

9 ${{\,\mathrm{A}\,}}(\mathcal {F})=\mathfrak c^+$ for $\mathcal {F}\in \mathcal {A}(\mathbb D)$ with $\mathcal {F}\subset {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})$ or $\mathcal {F}\subset {{\,\mathrm{AC}\,}}\cap {{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{SCIVP}\,}}$

According to the author of [36], the equality ${{\,\mathrm{A}\,}}({{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}})=\mathfrak c^+$, which was stated in [10, Theorem 4.18], was already proven in a preliminary version of [36]. However, until now, a proof of this result has not been published anywhere. Thus, we will include it below.

Theorem 9.1

We have ${{\,\mathrm{A}\,}}({{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))=\mathfrak c^+$ and ${{\,\mathrm{A}\,}}({{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})){\,=\,}{{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})) {=}{{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))$ $=\mathfrak c^+$. In particular, ${{\,\mathrm{A}\,}}(\mathcal {F})=\mathfrak c^+$ for any nonempty $\mathcal {F}\in A(\mathbb D)$ with $\mathcal {F}\subset {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{\mathscr {D}}\,}}\cup {{\,\mathrm{SCIVP}\,}})$.

Proof

Since ${{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})\subset {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}) \subset {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})\subset {{\,\mathrm{PR}\,}}$, and ${{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}}\subset {{\,\mathrm{CIVP}\,}}\setminus ({{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})\subset {{\,\mathrm{PR}\,}}$, by Propositions 1.2 and 1.3 (b) we have that

$$\begin{aligned} {{\,\mathrm{A}\,}}\left( {{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{PR}\,}}\setminus \left( {{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}\right) \right)\le & {} {{\,\mathrm{A}\,}}\left( {{\,\mathrm{PR}\,}}\setminus \left( {{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}\right) \right) \\\le & {} {{\,\mathrm{A}\,}}\left( {{\,\mathrm{PR}\,}}\setminus \left( {{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}\right) \right) \le {{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}})= \mathfrak c^+ \end{aligned}$$

and

$$\begin{aligned} {{\,\mathrm{A}\,}}\left( {{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}}\right) \le {{\,\mathrm{A}\,}}\left( {{\,\mathrm{CIVP}\,}}\setminus \left( {{\,\mathrm{SCIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}\right) \right) \le {{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}})= \mathfrak c^+. \end{aligned}$$

So, to finish the proof it is enough to show that

$$\begin{aligned} {{\,\mathrm{A}\,}}\left( {{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{PR}\,}}\setminus \left( {{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}\right) \right) \ge \mathfrak c^+ \end{aligned}$$

(9.1)

and

$$\begin{aligned} {{\,\mathrm{A}\,}}\left( {{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}}\right) \ge \mathfrak c^+. \end{aligned}$$

(9.2)

Proof of the inequality (9.1)

To see this, fix an $F \subset \mathbb {R}^\mathbb {R}$ with $|F|\le \mathfrak c$. We need to find a $g\in \mathbb {R}^\mathbb {R}$ so that $g+F\subset {{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})$. First let

$$ \begin{aligned} \hat{F}:=\left\{ f+b{\chi }_{\{a\}}:f\in F\ \& \ a,b\in \mathbb {R}\right\} . \end{aligned}$$

(9.3)

Notice that $F\subset \hat{F}$ and $|\hat{F}|=\mathfrak c$. Thus, it is enough to find a $g\in \mathbb {R}^\mathbb {R}$ so that $g+\hat{F}\subset {{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{PR}\,}}\setminus ({{\,\mathrm{CIVP}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})$. We use $\hat{F}$ in place of F to ensure the following property:

$$\begin{aligned} \text{ If } g+\hat{F}\subset {{\,\mathrm{PR}\,}}, \text{ then } g+f \text{ has } \text{ a } \text{ dense } \text{ graph } \text{ in } \mathbb {R}^2 \text{ for } \text{ every } f\in \hat{F}. \end{aligned}$$

(9.4)

First of all, notice that if $g+f$ has a dense graph for every $f\in F$, then also $g+f$ has a dense graph for every $f\in \hat{F}$. Thus, to prove (9.4), fix an $f\in F$ and, by way of contradiction, assume that $g+f$ does not have a dense graph in $\mathbb {R}^2$. Then, there exist nonempty open sets $U,V\subset \mathbb {R}$ such that $(g+f)\cap (U\times V)=\emptyset$. Choose $a\in U$ and $b\in \mathbb {R}$ such that $g(a)+f(a)+b\in V$. Then $\hat{f}:=f+b{\chi }_{\{a\}}$ is in $\hat{F}$ and $(g+\hat{f})\cap (U\times V)$ is a singleton, which contradicts the assumption that $g+\hat{f}\in {{\,\mathrm{PR}\,}}$.

Let $\{r_\beta :\beta <\mathfrak c\}$ be an enumeration, without repetition, of $\mathbb {R}$. We define the values $\{g(r_\beta ) :\beta <\mathfrak c\}$ by induction on $\beta <\mathfrak c$. The choice of each value $g(r_\beta )$ will be guided by three kind of conditions which will ensure, respectively, that $g+\hat{F}\subset {{\,\mathrm{PR}\,}}$, $g+\hat{F}\subset \lnot {{\,\mathrm{CIVP}\,}}$, and $g+\hat{F}\subset \lnot {{\,\mathrm{\mathscr {D}}\,}}$. We start with the first of these requirements.

We know that there exists a sequence $\langle \langle H_\alpha ,p_\alpha \rangle :\alpha <\mathfrak c\rangle$ (see the proof of Lemma 7.1) such that

• (a) $H_\alpha \cup \{p_\alpha \}\subset \mathbb {R}$ is compact perfect, $p_\alpha \notin H_\alpha$, and $p_\alpha$ is a bilaterally limit point of $H_\alpha \cup \{p_\alpha \}$;

• (b) $H_\alpha \cap H_\beta =\emptyset$ for all $\beta<\alpha <\mathfrak c$;

• (c) for every $r\in \mathbb {R}$, there exist $\mathfrak c$-many $\gamma <\mathfrak c$ such that $r=p_\gamma$.

Let $\{\langle \beta _\alpha ,f_\alpha \rangle :\alpha <\mathfrak c\}$ be an enumeration of $\mathfrak c\times \hat{F}$ such that $\beta _\alpha \le \alpha$ for every $\alpha <\mathfrak c$. By induction on $\alpha <\mathfrak c$, choose a sequence $\langle P_\alpha :\alpha <\mathfrak c\rangle$ of pairwise disjoint sets from $\{H_\zeta :\zeta <\mathfrak c\}$ such that $P_\alpha \cup \{r_{\beta _\alpha }\}$ satisfies the property (a) and

$$\begin{aligned} P_\alpha \cap \{r_\beta :\beta \le \alpha \}=\emptyset . \end{aligned}$$

(9.5)

To have $g+\hat{F}\subset {{\,\mathrm{PR}\,}}$, we will choose the values of g so that for every $\alpha <\mathfrak c$

$$\begin{aligned} |\left( g+f_\alpha \right) \left( r_\beta \right) -\left( g+f_\alpha \right) \left( r_{\beta _\alpha }\right) |<|r_\beta -r_{\beta _\alpha }|\ \text{ for } \text{ every } r_\beta \in P_\alpha . \end{aligned}$$

(9.6)

This will ensure $g+\hat{F}\subset {{\,\mathrm{PR}\,}}$, since for every $f\in \hat{F}$ and $r\in \mathbb {R}$ there exists an $\alpha <\mathfrak c$ such that $\langle r_{\beta _\alpha },f_\alpha \rangle =\langle r, f\rangle$ while (9.6) implies that $g+f=g+f_\alpha$ is continuous at $r=r_{\beta _\alpha }$ on the perfect set $P_\alpha \cup \{r_{\beta _\alpha }\}$.

To enforce (9.6) notice that if $r_\beta$ belongs to some $P_\alpha$, then, by (9.5), $\beta _\alpha \le \alpha <\beta$. So, $g(r_{\beta _\alpha })$ is already defined and we can put

$$\begin{aligned} J_\beta :=\left( \left( g+f_\alpha \right) \left( r_{\beta _\alpha }\right) -{\varepsilon },\left( g+f_\alpha \right) \left( r_{\beta _\alpha }\right) +{\varepsilon }\right) \ \text{ where } {\varepsilon }:=|r_\beta -r_{\beta _\alpha }|. \end{aligned}$$

(9.7)

Define nonempty open set $U_\beta$ as

$$\begin{aligned} U_\beta := {\left\{ \begin{array}{ll} - f_\alpha (r_\beta )+J_\beta &{} \text{ when } r_\beta \text{ belongs } \text{ to } \text{ a } P_\alpha ,\\ \mathbb {R}&{} \text{ when } r_\beta \text{ belongs } \text{ to } \text{ no } P_\xi \end{array}\right. } \end{aligned}$$

and notice that the choice

$$\begin{aligned} g\left( r_\beta \right) \in U_\beta \end{aligned}$$

(9.8)

ensures (9.6).

Next, we turn our attention to the requirement $g+\hat{F}\subset \lnot {{\,\mathrm{CIVP}\,}}$. For this, choose an arbitrary perfect nowhere dense compact $K\subset \mathbb {R}$ and let $f\in \hat{F}$. Since, by the above construction, $g+f$ will have a dense graph, we will need only to ensure that $(g+f)[C]\not \subset K$ for every $C\in {{\,\mathrm{Perf}\,}}$. For this, let $\{B_\xi :\xi <\mathfrak c\}$ be a partition of $\mathbb {R}$ into Bernstein sets and let $\{\varphi _\xi :\xi <\mathfrak c\}$ be an enumeration, without repetitions, of $\hat{F}$. When choosing $g(r_\beta )$ we will require that

$$\begin{aligned} g\left( r_\beta \right) \notin -\varphi _\xi \left( r_\beta \right) +K, \ \text{ where } \xi <\mathfrak c\hbox { is unique with } r_\beta \in B_\xi . \end{aligned}$$

(9.9)

Then, for every $f\in \hat{F}$ and $C\in {{\,\mathrm{Perf}\,}}$ there is a unique $\xi <\mathfrak c$ with $f=\varphi _\xi$ and $r_\beta \in C\cap B_\xi$, for which $(g+f)(r_\beta )=(g+\varphi _\xi )(r_\beta )\notin K$, as needed. Therefore, the properties (9.8) and (9.9) indeed imply that $g+\hat{F}\subset \lnot {{\,\mathrm{CIVP}\,}}$.

Now, to ensure that $g+\hat{F}\subset \lnot {{\,\mathrm{\mathscr {D}}\,}}$ holds, for every $\beta <\mathfrak c$ we choose a number $y_\beta \in \mathbb {R}\setminus (g+\varphi _\beta )[\{r_\zeta :\zeta <\beta \}]$ and then add a requirement

$$\begin{aligned} g\left( r_\beta \right) \notin \left\{ y_\zeta -\varphi _\zeta \left( r_\beta \right) :\zeta \le \beta \right\} . \end{aligned}$$

(9.10)

This ensures that, for every $\zeta <\mathfrak c$, $y_\zeta \notin (g+\varphi _\zeta )[\mathbb {R}]$ and, taking under consideration that $g+\varphi _\zeta$ has a dense graph, also $g+\varphi _\zeta \in \lnot {{\,\mathrm{\mathscr {D}}\,}}$.

Finally, we just need the requirement for $g+\hat{F}\subset {{\,\mathrm{SZ}\,}}$. Let $\{h_\xi :\xi <\mathfrak c\}$ be an enumeration of ${{\,\mathrm{\mathscr {B}}\,}}$. For any $\beta <\mathfrak c$, when choosing $g(r_\beta )$ we just need to guarantee that

$$\begin{aligned} g\left( r_\beta \right) \notin \left\{ \left( h_\eta -\varphi _\zeta \right) \left( r_\beta \right) :\zeta ,\eta \le \beta \right\} . \end{aligned}$$

(9.11)

Clearly (9.11) guarantees that $g+\hat{F}\subset {{\,\mathrm{SZ}\,}}$.

In summary, for every $\beta <\mathfrak c$ we choose $g(r_\beta )$ satisfying (9.8), (9.9), (9.10), and (9.11), that is,

$$\begin{aligned}&g\left( r_\beta \right) \in \left( U_\beta \setminus \left( -\varphi _\xi \left( r_\beta \right) +K\right) \right) \setminus \left( \left\{ y_\zeta -\varphi _\zeta \left( r_\beta \right) :\zeta \le \beta \right\} \right. \\&\quad \left. \cup \left\{ -\varphi _\zeta \left( r_\beta \right) +h_\eta \left( r_\beta \right) :\zeta ,\eta \le \beta \right\} \right) . \end{aligned}$$

The choice is possible, since the set $\bigl (U_\beta \setminus ( -\varphi _\xi (r_\beta )+K)\bigr )$ has cardinality $\mathfrak c$, as being residual in $U_\beta$, while

$$\left| \{y_\zeta -\varphi _\zeta (r_\beta ):\zeta \le \beta \} \cup \{-\varphi _\zeta (r_\beta )+h_\eta (r_\beta ):\zeta ,\eta \le \beta \}\right| <\mathfrak c.$$

Proof of the inequality (9.2)

To see ${{\,\mathrm{A}\,}}({{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}})\ge \mathfrak c^+$, choose a family $F\subset \mathbb {R}^\mathbb {R}$ of cardinality $\mathfrak c$. We need to find a $g\in \mathbb {R}^\mathbb {R}$ such that $g+F\subset {{\,\mathrm{SZ}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{\mathscr {D}}\,}}$.

Let $\mathcal {P}$ be a family of pairwise disjoint sets in ${{\,\mathrm{Perf}\,}}$ such that every $J\in \mathcal J$ contains $\mathfrak c$-many $P\in \mathcal {P}$. Let $\{r_\xi :\xi <\mathfrak c\}$ be an enumeration, with no repetitions, of $\mathbb {R}$, and let $\{f_\xi :\xi <\mathfrak c\}$, $\{\langle K_\xi ,J_\xi ,\varphi _\xi \rangle :\xi <\mathfrak c\}$, and $\{h_\xi \in \mathbb {R}^\mathbb {R}:\xi <\mathfrak c\}$ be the enumerations of F, ${{\,\mathrm{Perf}\,}}\times \mathcal J\times F$, and ${{\,\mathrm{\mathscr {B}}\,}}$, respectively. By induction on $\xi <\mathfrak c$ define the sequence $\langle \langle g(r_\xi ),y_\xi ,P_\xi \rangle \in \mathbb {R}\times \mathbb {R}\times \mathcal {P}:\xi <\mathfrak c\rangle$ so that

• (i) $g(r_\xi )\notin \bigcup _{\zeta ,\eta <\xi }\{(h_\zeta -f_\eta )(r_\xi ),y_\eta -f_\eta (r_\xi )\}$;

• (ii) $g(r_\xi )\in -\varphi _\zeta (r_\xi )+K_\zeta$ when there exists a $\zeta <\xi$ so that $r_\xi \in P_\zeta$;

• (iii) $P_\xi \subset J_\xi$ is distinct from all $P_\zeta$, ${\zeta <\xi }$, and $y_\xi \notin \{g(r_\zeta )+f_\eta (r_\zeta ):\zeta ,\eta \le \xi \}$.

Then g is as needed.

To see this, fix an $f\in F$. Then $g+f\in {{\,\mathrm{CIVP}\,}}$ is ensured by (ii) since for every $\langle K,J\rangle \in {{\,\mathrm{Perf}\,}}\times \mathcal J$ there is a $\zeta <\mathfrak c$ with $\langle K,J,f\rangle =\langle K_\zeta ,J_\zeta ,\varphi _\zeta \rangle$, and $g+f=g+\varphi _\zeta$ maps $P_\zeta \subset J_\zeta =J$ into $K_\zeta =K$. Also $g+f\in \lnot {{\,\mathrm{\mathscr {D}}\,}}$ since, by the above (ii), $g+f$ has a dense graph, while for $\eta <\mathfrak c$ with $f=f_\eta$ we have $y_\eta \notin (g+f)[\mathbb {R}]$ from (i) and (iii). Finally, $g+f\in {{\,\mathrm{SZ}\,}}$ since for every Borel function $h_\zeta$ and for $\xi >\eta ,\zeta$ we have $\{x\in \mathbb {R}:(g+f)(x)=h_\zeta (x)\}\subset \{r_\alpha :\alpha \le \xi \}$ , that is, $|(g+f)\cap h_\zeta |<\mathfrak c$. $\square$

Lemma 9.2

Let $F\subset \mathbb {R}^\mathbb {R}$ be of cardinality $\mathfrak c$ and $G\subset \mathbb {R}$ be a dense $G_\delta$ set of measure 0.

• (i) There exists a $\gamma _0\in \mathbb {R}^{G}$ such that for every $g\in \mathbb {R}^\mathbb {R}$ extending $\gamma _0$ and $f\in F$:

  • $g+f\in {{\,\mathrm{AC}\,}}$,

  • for every perfect $P\subset G$, the restriction $(g+f)\upharpoonright P$ is discontinuous and $\mathbb {Q}\cap (g+f)[P]\ne \emptyset$.

• (ii) There exists a $\gamma _1\in \mathbb {R}^{\mathbb {R}\setminus G}$ such that for every $g\in \mathbb {R}^\mathbb {R}$ extending $\gamma _1$ and $f\in F$:

  • for every nonempty open $I,J\subset \mathbb {R}$ there is a perfect $P\subset I\setminus G$ such that $(g+f)[P]\subset J$,

  • for every perfect $P\subset \mathbb {R}\setminus G$, we have $\mathbb {Q}\cap (g+f)[P]\ne \emptyset$.

• (iii) There exists a $\gamma _2\in \mathbb {R}^{\mathbb {R}\setminus G}$ such that for every $g\in \mathbb {R}^\mathbb {R}$ extending $\gamma _2$, and $f\in F$:

  • for every $p<q$ and $K\in {{\,\mathrm{Perf}\,}}$ there exists a perfect $P\subset (p,q)\setminus G$ with $(g+f)[P]\subset K$,

  • for every perfect $P\subset \mathbb {R}\setminus G$, the restriction $(g+f)\upharpoonright P$ is discontinuous.

Proof

(i) Let $\{B_f^i:f\in F\ \& \ i<3\}$ be a partition of $\mathbb {R}$ into Bernstein sets. For every $f\in F$ let $g_f:B_f^0\cap G\rightarrow \mathbb {R}$ intersect every blocking set. Also, let $h\in \mathbb {R}^\mathbb {R}$ be such that $h+F\subset {{\,\mathrm{SZ}\,}}$, which exists, since ${{\,\mathrm{A}\,}}({{\,\mathrm{SZ}\,}})>\mathfrak c$. For every $f\in F$ define

$$\begin{aligned} \gamma _0\upharpoonright (B_f^i\cap G):=\left\{ \begin{array}{rl} g_f- (f\upharpoonright B_f^0\cap G) &{} \text { when }i=0,\\ - (f\upharpoonright B_f^1\cap G) &{} \text { when }i=1,\\ h\upharpoonright B_f^2\cap G &{} \text { when }i=2. \end{array}\right. \end{aligned}$$

Then $\gamma _0$ is as needed. Indeed, for every $f\in F$, $g+f\in {{\,\mathrm{AC}\,}}$, since it extends $\gamma _0\upharpoonright (B_f^0\cap G)+f\upharpoonright (B_f^0\cap G)=g_f$, which intersects every blocking set. Also, for every perfect $P\subset G$, the map $(g+f)\upharpoonright P$ is discontinuous, since so is

$$\begin{aligned} (g+f)\upharpoonright B_f^2\cap P=\gamma _0\upharpoonright (B_f^2\cap P)+f\upharpoonright (B_f^2\cap P)=(h+f)\upharpoonright B_f^2\cap P \end{aligned}$$

as $|B_f^2\cap P|=\mathfrak c$. Also, there is an $x\in P\cap B_f^1$ for which $(g+f)(x)=0\in \mathbb {Q}$.

To see (ii) and (iii), let $\mathcal B_0$ be a countable basis of $\mathbb {R}$ with $\emptyset \notin \mathcal B_0$, fix a family $\{P_I\subset I\setminus G:I\in \mathcal B_0\}$ of pairwise disjoint perfect sets. Let $\{B_{f'}:f'\in F \}$ be a partition of $\mathbb {R}$ into Bernstein sets.

To construct $\gamma _1$, for every $I\in \mathcal B_0$ let $\{P^I_{f,J}:f\in F\ \& \ J\in \mathcal B_0\}$ be a partition of $P_I$ into perfect sets. For every $x\in \mathbb {R}\setminus G$ choose $\gamma _1(x)$ so that

• $\gamma _1(x)\in -f'(x)+\mathbb {Q}$, where $f'\in F$ is unique such that $x\in B_{f'}$ and

• $\gamma _1(x)\in -f(x)+J$, provided $x\in P^I_{f,J}$ for some $f\in F$ and $I,J\in \mathcal B_0$.

Such choice is clearly possible, since $-f(x)+J$ is an open nonempty set and $-f'(x)+\mathbb {Q}$ is dense in $\mathbb {R}$. We extend $\gamma _1$ to $\mathbb {R}\setminus G$ arbitrarily. Then $\gamma _1$ is as needed.

Finally, to construct $\gamma _2$, let $\{x_\xi :\xi <\mathfrak c\}$ be an enumeration, with no repetitions, of $\mathbb {R}\setminus G$. For every $J\in \mathcal B_0$ let $\{P^J_{f,K}:f\in F\ \& \ K\in {{\,\mathrm{Perf}\,}}\}$ be a partition of $P_J$ into perfect sets and let ${{\,\mathrm{\mathscr {B}}\,}}\times F=\{\langle h_\xi ,f_\xi \rangle :\xi <\mathfrak c\}$. For every $\xi <\mathfrak c$ let $P_\xi :=-f(x_\xi )+K$ provided $x_\xi \in P^J_{f,K}$ and $P_\xi :=\mathbb {R}$ provided $x_\xi \notin \bigcup _{J\in \mathcal J} P_J$. For $\xi <\mathfrak c$ choose

$$\begin{aligned} \gamma _2\left( x_\xi \right) \in P_\xi \setminus \left\{ \left( h_\eta -f_\eta \right) \left( x_\xi \right) :\eta <\xi \right\} . \end{aligned}$$

Then $\gamma _2$ is as needed. Indeed, let g be an extension of $\gamma _2$. For every $p<q$, $f\in F$, perfect $K\subset \mathbb {R}$ there exists a $J\in \mathcal B_0$ with $J\subset (p,q)$. Then $P^J_{f,K}\subset P_J\subset (p,q)$ and for every $x_\xi \in P^J_{f,K}$ we have $(g+f)(x_\xi )\in f(x_\xi )+P_\xi =K$, that is, $(g+f)[P^J_{f,K}]\subset K$. Also, if $P\subset \mathbb {R}\setminus G$ is perfect, then $(g+f)\upharpoonright P$ cannot be continuous, since otherwise there is an $\eta <\mathfrak c$ so that $f_\eta = f$ and $h_\eta \upharpoonright P=(g+f)\upharpoonright P$. But then, for every $\xi \ge \eta$ with $x_\xi \in P$ we have $(g+f)(x_\xi )=\gamma _2(x_\xi )+f_\eta (x_\xi )\ne h_\eta (x_\xi )=(g+f)(x_\xi )$, a contradiction. $\square$

Theorem 9.3

${{\,\mathrm{A}\,}}(\mathcal {F})=\mathfrak c^+$ for any $\mathcal {F}\in A(\mathbb D)\setminus \{\emptyset \}$ with $\mathcal {F}\subset {{\,\mathrm{AC}\,}}\cap {{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{SCIVP}\,}}$. In particular, ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{CIVP}\,}})={{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}})=\mathfrak c^+$.

Proof

We have ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{CIVP}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{SCIVP}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}})=\mathfrak c^+$ and ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{PR}\,}})=\mathfrak c^+$. Thus, it is enough to show that

$$\begin{aligned} {{\,\mathrm{A}\,}}\left( {{\,\mathrm{AC}\,}}\cap {{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{CIVP}\,}}\right)>\mathfrak c\ \text{ and } \ {{\,\mathrm{A}\,}}\left( {{\,\mathrm{AC}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus {{\,\mathrm{SCIVP}\,}}\right) >\mathfrak c. \end{aligned}$$

To see this, fix a family $F=\{f_\alpha :\alpha <\mathfrak c\}\subset \mathbb {R}^\mathbb {R}$. It is enough to find functions $g_1,g_2\in \mathbb {R}^\mathbb {R}$ such that $g_1+F\subset {{\,\mathrm{AC}\,}}\cap {{\,\mathrm{PR}\,}}\setminus {{\,\mathrm{CIVP}\,}}$ and $g_2+F\subset {{\,\mathrm{AC}\,}}\cap {{\,\mathrm{CIVP}\,}}\setminus$ ${{\,\mathrm{SCIVP}\,}}$. For this, let $\gamma _0$, $\gamma _1$, and $\gamma _2$ be as in Lemma 9.2. We claim that $g_1:=\gamma _0\cup \gamma _1$ and $g_2:=\gamma _0\cup \gamma _2$ are as needed.

Indeed, $g_1+F\subset {{\,\mathrm{AC}\,}}$ and $g_2+F\subset {{\,\mathrm{AC}\,}}$ by the choice of $\gamma _0$. The fact that $g_1+F\subset {{\,\mathrm{PR}\,}}$ easily follows from the choice of $\gamma _1$.

To see that $g_1+F\subset \lnot {{\,\mathrm{CIVP}\,}}$ choose an $f\in F$ and a perfect set $K\subset (0,1)\setminus \mathbb {Q}$. By the choice of $\gamma _1$, there exist $a,b\in \mathbb {R}$ with $(g_1+f)(a)<0<1<(g_1+f)(b)$. Thus, it is enough to show that $(g_1+f)[C]\subset K$ for no perfect set C. Since G is Borel, we can decrease C, if necessary, so that either $C\subset G$ or $C\subset \mathbb {R}\setminus G$. But if $C\subset G$, the choice of $\gamma _0$ ensures that $\mathbb {Q}\cap (g_1+f)[C]\ne \emptyset$, that is, $(g_1+f)[C]\not \subset K$. Similarly, if $C\subset \mathbb {R}\setminus G$, the choice of $\gamma _1$ ensures that $\mathbb {Q}\cap (g_1+f)[C]\ne \emptyset$, so again $(g_1+f)[C]\not \subset K$. Thus, indeed, $g_1+F\subset \lnot {{\,\mathrm{CIVP}\,}}$.

The fact that $g_2+F\subset {{\,\mathrm{CIVP}\,}}$ is immediately ensured by the choice of $\gamma _2$. To see that $g_2+F\subset \lnot {{\,\mathrm{SCIVP}\,}}$ choose an $f\in F$ and a perfect set P. We need to show that $(g_2+f)\upharpoonright P$ is discontinuous. Indeed, as before, we can assume that either $P\subset G$ or $P\subset \mathbb {R}\setminus G$. But then, the discontinuity of $(g_2+f)\upharpoonright P$ is ensured by the choice of $\gamma _0$ for $P\subset G$ and the choice of $\gamma _2$ for $P\subset \mathbb {R}\setminus G$. $\square$

10 On ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))$

The goal of this section is to prove the following result.

Theorem 10.1

$d_\mathfrak c\le {{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))\le d_\mathfrak c^*$. In particular, if $|[\mathfrak c]^{<\mathfrak c}|=\mathfrak c$, then ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))={{\,\mathrm{A}\,}}(\lnot {{\,\mathrm{\mathscr {D}}\,}})= d_\mathfrak c=d_\mathfrak c^*$.

Proof

It is enough to prove that ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))\ge d_\mathfrak c$, as the rest of the theorem follows from Proposition 1.3 (f).

To see this inequality, fix an $F\in [\mathbb {R}^\mathbb {R}]^{<d_\mathfrak c}$. We need to find a $g\in \mathbb {R}^\mathbb {R}$ such that $g+F\subset {{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})$. Since this is obvious for $F=\emptyset$, we can assume that $F\ne \emptyset$.

Let $\{B_{\langle P,J\rangle }:\langle P,J\rangle \in {{\,\mathrm{Perf}\,}}\times \mathcal B\}$ be a partition of $\mathbb {R}$ into Bernstein sets. For $\langle P,J,f\rangle \in {{\,\mathrm{Perf}\,}}\times \mathcal B\times F$ define $f_{\langle P,J,f\rangle }:B_{\langle P,J\rangle }\rightarrow \mathcal B$ so that $f_{\langle P,J,f\rangle }(x)\subset -f(x)+J$ for every $x\in B_{\langle P,J\rangle }$. Since the family $\{f_{\langle P,J,f\rangle }:f\in F \}$ has cardinality $<2^\mathfrak c$, $|B_{\langle P,J\rangle }|=\mathfrak c$, and $|\mathcal B|=\omega$, by [17, Lemma 2.2] (compare also [17, Theorem 2.2]) there exists a mapping $B_{\langle P,J\rangle }\ni x\mapsto J_x\in \mathcal B$ such that for every $f\in F$ there is an $x\in B_{\langle P,J\rangle }$ with $J_x=f_{\langle P,J,f\rangle }(x)$. Now, if $\mathbb {R}\ni x\mapsto J_x\in \mathcal B$ is the union of all such mappings, then

• (i) for every $\langle P,J,f\rangle \in {{\,\mathrm{Perf}\,}}\times \mathcal B\times F$ there is an $x\in P$ with $J_x\subset -f(x)+J$.

Next, fix an additive $\Phi \in {{\,\mathrm{ES}\,}}$, see e.g. [9, Corollary 7.3.5]. Since $\hat{F}:=\{\Phi \circ f:f\in F\}$ has cardinality $<d_\mathfrak c$, there exists a $\bar{g}\in \mathbb {R}^\mathbb {R}$ so that for every $f\in F$ the set $\bar{g}\cap (\Phi \circ f)$ has cardinality $<\mathfrak c$.

Choose a $g\in \prod _{x\in \mathbb {R}} J_x$ such that $\Phi \circ g=-\bar{g}$. This can be done since $\Phi \in {{\,\mathrm{ES}\,}}$. We claim that g is as needed, that is, such that $g+F\subset {{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})$.

To see this, fix an $f\in F$. Then, by (i), for every $P\in {{\,\mathrm{Perf}\,}}$ the map $(g+f)\upharpoonright P$ is dense in $P\times \mathbb {R}$. In particular, $g+f\in {{\,\mathrm{PC}\,}}\setminus {{\,\mathrm{PR}\,}}$.

To see that $g+f\in \lnot {{\,\mathrm{\mathscr {D}}\,}}$, by density of the graph of $g+f$ in $\mathbb {R}^2$, it is enough to show that $(g+f)[\mathbb {R}]\ne \mathbb {R}$. Indeed, otherwise $\Phi \circ (g+f)(x)=0$ for $\mathfrak c$-many $x\in \mathbb {R}$. Since $\Phi$ is additive, for any such x we have

$$\begin{aligned} \left( -\bar{g}+\Phi \circ f\right) (x)=\left( \Phi \circ g+\Phi \circ f\right) (x)=\Phi \circ (g+f)(x)=0, \end{aligned}$$

that is, $|\bar{g}\cap (\Phi \circ f)|=\mathfrak c$, contradicting the choice of $\bar{g}$. $\square$

Remark 10.2

Let us denote by ${{\,\mathrm{\mathscr {D}}\,}}^*$ the family of Darboux functions $f\in \mathbb {R}^\mathbb {R}$ that are nowhere constant, that is, $f\upharpoonright J$ is not constant for every $J\in \mathcal J$. Notice that ${{\,\mathrm{\mathscr {D}}\,}}^*\subset {{\,\mathrm{\mathscr {D}}\,}}$. Then, by Proposition 1.2, we have that ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))\le {{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}^*))$. Furthemore, by using similar arguments to those in the proof of [35, Lemma 25], it is easy to show that ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}^*))\le {{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))$. Thus, ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}^*))={{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}}))$.

Remark 10.3

Notice that we have ${{\,\mathrm{A}\,}}({{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{SES}\,}}))\ge d_\mathfrak c$. This is a straightforward consequence of Theorem 10.1, since ${{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{\mathscr {D}}\,}})\subset {{\,\mathrm{PC}\,}}\setminus ({{\,\mathrm{PR}\,}}\cup {{\,\mathrm{SES}\,}})$.

11 On ${{\,\mathrm{AC}\,}}\cap {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}}$

Theorem 11.1

$2\le {{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}})\le {{\,\mathrm{A}\,}}({{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}})\le \mathfrak c$.

Proof

Ciesielski and Rosłanowski proved in [19] that ${{\,\mathrm{AC}\,}}\cap {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}}\ne \emptyset$. So, by Proposition 1.2 (i), we have ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}})\ge 2$.

To see the other inequality we will use the following key fact:

• for every perfect-dense meager set $M\subset \mathbb {R}$ there exists an $h\in {{\,\mathrm{Ext}\,}}$ such that $h\upharpoonright M$ is Borel and “$h\in {{\,\mathrm{Ext}\,}}$” is decided on M.

This easily follows from the results presented in [17]. Specifically, the authors constructed there, in [17, Theorem 3.3], a connectivity function $f:\mathbb {R}^2\rightarrow \mathbb {R}$ such that for some dense $G_\delta$-subset G of $\mathbb {R}^2$ any map $\tilde{f}:\mathbb {R}^2\rightarrow \mathbb {R}$ which agrees with f on $\mathbb {R}^2\setminus G$ is connectivity. We need to notice that this f constructed in [17, Theorem 3.3] is (can be) Borel. (See property ($*$) in the proof of [17, Theorem 3.3].) Now, this implies, see [17, Corollary 3.4], that there exists a dense $G_\delta$-subset $\tilde{G}$ of $\mathbb {R}$ and a section $\hat{h}(\cdot )=f(\cdot ,y)$ of f such that any extension $\bar{h}\in \mathbb {R}^\mathbb {R}$ of $\hat{h}\upharpoonright \mathbb {R}\setminus \tilde{G}$ is in ${{\,\mathrm{Ext}\,}}$. Decreasing $\tilde{G}$, if necessary, we can assume that $\tilde{M}:=\mathbb {R}\setminus \tilde{G}$ is a perfect-dense meager set. Recall also, that there exists a homeomorphism $\varphi \in \mathbb {R}^\mathbb {R}$ with $\varphi [M]=\tilde{M}$ (see [29, Lemma 4]). Then $h:=\hat{h}\circ \varphi \upharpoonright M$ is as needed.

To see that ${{\,\mathrm{A}\,}}({{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}})\le \mathfrak c$, let $F:={{\,\mathrm{\mathscr {B}}\,}}$. Then $|F|=\mathfrak c$. Fix a $g\in \mathbb {R}^\mathbb {R}$. It is enough to show that $g+F\not \subset {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}}$.

Indeed, since the constant zero function is Borel, we have $g\in g+F$. We can assume that $g\in {{\,\mathrm{SCIVP}\,}}$. It is enough to find an $f\in F$ with $g+f\in {{\,\mathrm{Ext}\,}}$. But $g\in {{\,\mathrm{SCIVP}\,}}$ implies that there is a perfect-dense meager set M such that $g\upharpoonright M$ is Borel. Thus, by $\bullet$, there is an $h\in {{\,\mathrm{Ext}\,}}$ such that $h\upharpoonright M$ is Borel, and there is an $f\in F$ such that $(g+f)\upharpoonright M=h\upharpoonright M$. But then, by $\bullet$, $g+f\in {{\,\mathrm{Ext}\,}}$, as needed. $\square$

Problem 11.2

Is it possible to find in ZFC the exact value of ${{\,\mathrm{A}\,}}({{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}})$ or of ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}})$? If not, what better lower and upper bounds do we have for ${{\,\mathrm{A}\,}}({{\,\mathrm{AC}\,}}\cap {{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}})$ and ${{\,\mathrm{A}\,}}({{\,\mathrm{SCIVP}\,}}\setminus {{\,\mathrm{Ext}\,}})$?