Steiner Loops of Affine Type

Abstract

Steiner loops of affine type are associated to arbitrary Steiner triple systems. They behave to elementary abelian 3-groups as arbitrary Steiner Triple Systems behave to affine geometries over ${\mathrm {GF}}(3)$. We investigate algebraic and geometric properties of these loops often in connection to configurations. Steiner loops of affine type, as extensions of normal subloops by factor loops, are studied. We prove that the multiplication group of every Steiner loop of affine type with n elements is contained in the alternating group $A_n$ and we give conditions for those loops having $A_n$ as their multiplication groups (and hence for the loops being simple).

In this paper we want to describe Steiner triple systems by means of a standard tool in algebra, that is, the reduction to simple objects via a composition series, the corresponding extension theory, and the (possible) classification of these simple objects. Although the literature on Steiner triple systems is huge and authoritative, and the idea of associating a loop to a Steiner triple system can often be found there, this approach has not yet been examined in depth. We succeeded in the first two aims. As for a possible classification of simple Steiner triple systems, the situation is more delicate, first of all because the multiplication group of a simple loop is, in general, only a primitive group, secondly because our conjectured question, whether a simple Steiner loop of affine type with n elements is a section of the alternating group on n letters over the stabilizer of one letter, remains open, even in the case where its multiplication group is simple. However, to the best of our knowledge, this has always been the case.

The paper is organized as follows. We give the definition of a Steiner loop of affine type and we prove the basic results in Sects. 1 and 2. In order to make the paper self-contained for a broader audience, in the Introduction we give also the basic definitions of Steiner triple systems and of loops, and the role played by the group of left (or right) multiplications. Before switching over to the reduction to simple Steiner loops of affine type, we investigate in Sect. 3, which turns therefore to be more technical, the connection between the most common configurations in Steiner triple systems and loop properties, such as the inverse property, additionally we study Veblen points and Hall points (which are defined in the present paper). In Sect. 4 extensions of Steiner loops by normal subloops are investigated, and in Sect. 5 those Steiner loops of affine type are considered, which have the alternating group as multiplication group. These loops are simple.

1 Introduction

A quasigroup is a set ${{\mathscr {L}}}$ of elements endowed with a binary operation $(\circ )$ which does not need to be associative, and which is such that the equations $a\circ x =b$ and $y\circ a = b$ determine unique solutions $x=a\backslash b$ and $y=b / a$, thus its multiplication table is a latin square, and a loop is a quasigroup which has a neutral element $\varOmega$ (see [28] and [11] for a general reference).

As pointed out first by R. Baer in [5], Th. 1.1., Corollary 1.2, loops can be described as homogeneous spaces of their multiplication group $G_{{\mathscr {L}}}$, generated by the left (resp. right) translations $\lambda _a: x\mapsto a\circ x$ (resp. $\rho _a:y\mapsto y\circ a$): if $\pi : G_{{\mathscr {L}}}\longrightarrow {{\mathscr {L}}}$, $g\mapsto g\varOmega$ is the orbit map, then the stabilizer H of $\varOmega$ in $G_{{\mathscr {L}}}$ is a subgroup containing no non-trivial normal subgroup of $G_{{\mathscr {L}}}$.

The section $\sigma : {{\mathscr {L}}} \rightarrow G_{{\mathscr {L}}}$, $x \mapsto \lambda _x$, of $\pi$ is such that: (i) $\sigma ({{\mathscr {L}}})$ is a transversal of H in $G_{{\mathscr {L}}}$, (ii) $\sigma (\varOmega )=\mathrm {id} \in G_{{\mathscr {L}}}$, (iii) $\sigma ({{\mathscr {L}}})$ generates $G_{{\mathscr {L}}}$, and iv) for every $x,y \in {{\mathscr {L}}}$ there exists precisely one $\lambda _z \in \sigma ({{\mathscr {L}}})$ such that $\lambda _z (x)=y$ (cf. also [25], Sect. 1.2).

The operation $xH*yH=\sigma \big (xy(\varOmega )\big )H$ makes the quotient $G_{{\mathscr {L}}}/H$ a loop, isomorphic to ${{\mathscr {L}}}$ via the mapping ${{\mathscr {L}}}\longrightarrow G_{{\mathscr {L}}}/H$, $g \mapsto \lambda _gH$, because

$$\begin{aligned} g \circ h\mapsto \lambda _{g \circ h} H=\sigma \big (g\circ h)H=\sigma \big (gh(\varOmega )\big )H=\sigma \big (\lambda _g\lambda _h(\varOmega )\big )H=\lambda _g H *\lambda _h H \end{aligned}$$

(cf. [25], Proposition 1.5, [32] Proposition 1).

If ${{\mathscr {L}}}_1(\circ )$ and ${{\mathscr {L}}}_2(*)$ are loops, a triple of bijections $(\alpha ,\beta ,\gamma ):{\mathscr {L}}_1\longrightarrow {{\mathscr {L}}}_2$ such that $\alpha (x)*\beta (y)=\gamma (x\circ y)$ is called an isotopism. As the only basic property for a loop is that its left and right multiplications $\lambda _a:x\mapsto a\circ x$ and $\rho _a:x\mapsto x\circ a$ are bijections, loop theory is often developed up to isotopisms, instead of isomorphisms (which, in particular, turn out to be isotopisms where $\alpha =\beta =\gamma$).

Kernels N of homomorphisms turn out to be defined by the relations

$$\begin{aligned} x\circ N=N\circ x,\quad x\circ (N\circ y)=(x\circ N)\circ y,\quad x\circ (y\circ N)=(x\circ y)\circ N \end{aligned}$$

for any $x,y\in {{\mathscr {L}}}$, which define normal subloops, and which, in the case of a commutative loop ${{\mathscr {L}}}(+)$ reduce to the only

$$\begin{aligned} x+ (y+ N)=(x+ y)+ N \end{aligned}$$

(1)

(cf. [29], p. 1189). A normal subloop N determines a partition of the loop ${{\mathscr {L}}}$ in cosets (notice that this is not necessary for arbitrary subloops), thus $|{{\mathscr {L}}}|=|N|\cdot |{{\mathscr {L}}}/N|$. If a loop L has only its trivial normal subloops $\{\varOmega \}$ and L, then it is called simple. In the case where L is a simple loop, the multiplication group of L turns out to be primitive (see [1], Th. 8, p. 516).

A Steiner triple system is a pair $({\mathscr {S}},{\mathscr {T}})$, where ${\mathscr {T}}$ is a family of triples of elements of ${\mathscr {S}}$ such that any two elements of ${\mathscr {S}}$ are contained exactly in one triple of the family ${\mathscr {T}}$. Steiner triple systems exist if and only if n is equivalent to 1 or 3 modulo 6. We will use the abbreviation ${\mathrm {STS}}$ or ${\mathrm {STS}}(n)$ for a Steiner triple system, or for a Steiner triple system on n elements, respectively. Since the mid-twentieth century, a large literature has been devoted to Steiner triple systems (a fundamental monograph on the subject is [12]). Basic examples of ${\mathrm {STS}}$’s include the point-line geometry of any projective space over $\mathrm {GF}(2)$ or the one of any affine space over $\mathrm {GF}(3)$, which for $n=7$ and $n=9$ are the only ${\mathrm {STS}}(n)$ (for our convenience, we take the occasion to recall that the unique $\mathrm {STS}(7)$ is usually called the Fano plane). If any two distinct intersecting triples are such that the minimal Steiner triple subsystem containing them is the ${\mathrm {STS}}(9)$, then the ${\mathrm {STS}}$ is called a Hall triple system (${\mathrm {HTS}}$). An isomorphism $f:{\mathscr {S}}_1\longrightarrow {\mathscr {S}}_2$ of Steiner triple systems $({\mathscr {S}}_1,{\mathscr {T}}_1)$ and $({\mathscr {S}}_2,{\mathscr {T}}_2)$ is a bijective map which moves the triples of ${\mathscr {T}}_1$ onto triples of ${\mathscr {T}}_2$.

In the present paper, we study a family of commutative loops of exponent 3 associated to STS’s, which are defined by the following operation:

Definition 1

Let ${\mathscr {S}}$ be a Steiner triple system, and let $\varOmega \in {\mathscr {S}}$ be fixed. For each $x\in {\mathscr {S}}$, define its opposite $-x$ as the third point $\mu (x)$ in the triple $\{x,\varOmega ,\mu (x)\}$ through x and $\varOmega$, define the addition $x+\varOmega =x$, $x+x=-x$, and, for any $y\ne x\in {\mathscr {S}}\setminus \{\varOmega \}$,

$$\begin{aligned} x+y=-z, \end{aligned}$$

where z is the third point in the triple through x, y.

With the above defined operation, the Steiner triple system ${\mathscr {S}}$ turns into a loop ${\mathscr {L}}_S$, that we will call Steiner loop of affine type with identity $\varOmega$, where the triples $\{x,y,z\}$ of $({\mathscr {S}},{\mathscr {T}})$ are characterized by the property that

$$\begin{aligned} x+y+z=\varOmega . \end{aligned}$$

We stress the fact that for any triple in ${\mathscr {T}}$ the associative property holds. The Steiner loop of affine type associated to a ${\mathrm {STS}}$ is a group exactly in the case where the ${\mathrm {STS}}$ is an affine geometry $\mathrm {AG}(d,3)$ of the affine lines over the Galois field $\mathrm {GF}(3)$.

Remark 1

Note that, if ${\mathscr {L}}_1$ and ${\mathscr {L}}_2$ are the commutative Steiner loops of affine type associated to the same ${\mathrm {STS}}$ by fixing two different elements $\varOmega _1$ and $\varOmega _2$, and if we denote the opposite maps by $\mu _1$ and $\mu _2$, according to the triples $\{x,\varOmega _1,\mu _1(x)\}$ and $\{x,\varOmega _2,\mu _2(x)\}$ in ${\mathscr {T}}$, then the map $\gamma :{{\mathscr {L}}}_1\longrightarrow {\mathscr {L}}_2$, $\gamma (x)=\mu _2(\mu _1(x))$ induces an isotopism $(\mathrm {id},\mathrm {id},\gamma ):{{\mathscr {L}}}_1\longrightarrow {\mathscr {L}}_2$.

If ${\mathscr {S}}$ is a HTS, then any two Steiner loops of affine type associated to ${\mathscr {S}}$ by fixing two different identities $\varOmega _1$ and $\varOmega _2$, are even isomorphic (see Remark 2), but if ${\mathscr {S}}$ is not a HTS, then this is in general not true: the two Steiner loops of affine type with identity 1 and 2, defined by the following addition tables

$$\begin{aligned} \begin{array}{c|ccccccc} +&{}1&{}2&{}3&{}4&{}5&{}6&{}7\\ \hline 1&{}1&{}2&{}3&{}4&{}5&{}6&{}7\\ 2&{}2&{}3&{}1&{}5&{}4&{}7&{}6\\ 3&{}3&{}1&{}2&{}6&{}7&{}4&{}5\\ 4&{}4&{}5&{}6&{}7&{}2&{}3&{}1\\ 5&{}5&{}4&{}7&{}2&{}6&{}1&{}3\\ 6&{}6&{}7&{}4&{}3&{}1&{}5&{}2\\ 7&{}7&{}6&{}5&{}1&{}3&{}2&{}4 \end{array}\quad \quad \quad \quad \begin{array}{c|ccccccc} +&{}1&{}2&{}3&{}4&{}5&{}6&{}7\\ \hline 1&{}3&{}1&{}2&{}5&{}4&{}7&{}6\\ 2&{}1&{}2&{}3&{}4&{}5&{}6&{}7\\ 3&{}2&{}3&{}1&{}7&{}6&{}5&{}4\\ 4&{}5&{}4&{}7&{}6&{}1&{}2&{}3\\ 5&{}4&{}5&{}6&{}1&{}7&{}3&{}2\\ 6&{}7&{}6&{}5&{}2&{}3&{}4&{}1\\ 7&{}6&{}7&{}4&{}3&{}2&{}1&{}5 \end{array} \end{aligned}$$

can be shown, after tedious computations, to be non-isomorphic, still isotopic and defining the same $\mathrm {STS}(7)$.

Remark 2

(i) In Definition 1 we denoted with $-b$ the third element in the triple containing b and $\varOmega$, so that $-b+b=\varOmega$. Since, usually, $a-b$ denotes in Loop theory the solution of the equation $x+b=a$, and since this turns to be identically equal to $a+(-b)$ (if and) only if the Steiner loop of affine type has the inverse property (cf. Theorem 5) we have to stress that, to avoid ambiguity, we will always write $-b+a$ or, when this is not possible, we will write $a+(-b)$. We thank the referee for suggesting this more exact notation.

(ii) The addition $+$ given above in Definition 1 is the same as the second addition $\circ$ given by Chein in [11], II.9.9 Example, p. 86. In this paper, Chein gives two different additions, which turn to coincide precisely in the case where the STS is a Hall triple system, as we remark here. For Hall triple systems, however, this other addition $*$ was already given in the 1960’s by M. Hall and R. H. Bruck, who put, in fact, $x*y=z$, where z is the third point in the triple through the two elements lying, respectively, in the triple through $\varOmega$ and x and in the triple through $\varOmega$ and y, that is, in our notation (see Proposition 3),

$$\begin{aligned} x*y=-\big ((-x)+(-y)\big ). \end{aligned}$$

For a Hall triple system ${\mathscr {S}}$, the Steiner loop of affine type ${{{\mathscr {L}}}_S}$ turns out to be a commutative Moufang loop of exponent 3 [20] (see also [16]), i.e. the sequence of incidence systems $\mathrm {AG}(n,3)$’s, $\mathrm {HTS}$’s, $\mathrm {STS}$’s corresponds to the sequence of loops: elementary abelian 3-groups, commutative Moufang loops of exponent 3, Steiner loops of affine type.

Since isotopic commutative Moufang loops are isomorphic [7], any two Steiner loops of affine type associated to a HTS by fixing two different identities $\varOmega _1$ and $\varOmega _2$, are isomorphic.

Whereas the loops of affine type associated to Hall triple systems fulfill Moufang’s identity

$$\begin{aligned} x+\big (x+(y+z)\big )=(x+y)+(x+z), \end{aligned}$$

general Steiner loops of affine type only fulfill

$$\begin{aligned} y+y=x+\big ((x+y)+(x+y)\big ), \end{aligned}$$

which is obtained by the former when one takes $z=y$ (cf. [3]).

Remark 3

To any ${\mathrm {STS}}$ one can associate another commutative loop. In fact, already in 1958, Bruck remarked that a commutative totally symmetric loop, that is, such that $x\circ (x\circ y)=y$ is essentially an algebraic version of a Steiner triple system, where the triples are exactly the sets $\{x,y,x\circ y\}$, and the identity $\varOmega$ is an extra point, not in the STS [7]. These other loops have been studied, among the others, in [29] and in [30]. Also in such totally symmetric loop, the triples $\{x,y,z\}$ of $({\mathscr {S}},{\mathscr {T}})$ are characterized by the property that, however we associate the product, the equality

$$\begin{aligned} x\circ y\circ z=\varOmega \end{aligned}$$

holds (and in fact we came to the present paper after a series [9, 10, 14, 15], concerned with this characterization of blocks in a design). Such Steiner loop associated to a ${\mathrm {STS}}$ is a group exactly in the case where the triples of the ${\mathrm {STS}}$ are the projective lines of a projective geometry $\mathrm {PG}(d,2)$ over the Galois field $\mathrm {GF}(2)$.

For any $a,b\in {\mathscr {S}}$ the solution $x \in {\mathscr {S}}$ of the equation $a+x=b$ is $x=-(-b+a)$. As stressed in Remark 2 (i), we will see in Sect. 3 that $-(-b+a)=-a+b$ if and only if a,  $-b$ and $\varOmega$ form a mitre centered in $\varOmega$.

As remarked already in II.9.9 Example in [11], p. 86, our definition yields a commutative loop ${{{\mathscr {L}}}_S}$ of exponent 3 fulfilling the weak inverse property (introduced in [27]), that is, such that for any 3-sets $\{x,y,z\}$ of $\mathscr {L_S}$ with $x+y+z=\varOmega$ the associative property holds. Conversely, it is easy to see that, if $\mathscr {L_S}$ is a commutative loop fulfilling the weak inverse property such that $3x=\varOmega$, then $\mathscr {L_S}$ gives the structure of a Steiner triple system $\mathscr {S_L}$. Obviously, ${\mathscr {S}}=\mathscr {S_{L_S}}$ and ${\mathscr {L}}=\mathscr {L_{S_L}}$.

Since the left translation map from $\mathscr {L_S}$ to $\mathscr {L_S}$, $\lambda _a:x\mapsto a+x$, coincides, for all $a \in \mathscr {L_S}$, with the right translation map $\rho _a:x\mapsto x+a$, the group generated by all left translations of $\mathscr {L_S}$ coincides with the group generated by all right translations of $\mathscr {L_S}$ and we denote it by ${\mathrm {Mult}}(\mathscr {L_S})$.

Finally, for a Steiner loop $\mathscr {L_S}$ of affine type, and for any $z\in \mathscr {L_S}$, we will use the following map

$$\begin{aligned} \iota _z=\rho _{-z}\circ \rho _z=\lambda _{-z}\circ \lambda _z. \end{aligned}$$

(2)

2 General Facts

In this section we settle the basic correspondences between Steiner triple systems and their associated Steiner loops of affine type.

Theorem 1

Let ${\mathscr {S}}$ be a Steiner triple system and $\mathscr {L_S}$ the corresponding Steiner loop of affine type with identity $\varOmega \in {\mathscr {S}}$.

• (i) $\mathscr {L_R}$ is a subloop of $\mathscr {L_S}$ if and only if ${\mathscr {R}}$ is a Steiner triple subsystem of ${\mathscr {S}}$ containing $\varOmega$.

• (ii) If $\mathscr {L_R}$ is a normal subloop of $\mathscr {L_S}$, then each coset $x+\mathscr {L_R}$ corresponds to a Steiner triple subsystem of ${\mathscr {S}}$.

• (iii) If $\mathscr {L_R}$ is a normal subloop of $\mathscr {L_S},$ then the quotient loop Q yields a Steiner triple system $\mathscr {S_Q}$.

Proof

• (i) ${\mathscr {R}}$ is a subsystem of ${\mathscr {S}}$ containing $\varOmega$ if and only if $\mathscr {L_R}$ is closed under the operation of $\mathscr {L_S}$, hence the assertion follows.

• (ii) If $\mathscr {L_R}$ is a normal subloop of $\mathscr {L_S}$, then $\mathscr {L_S}/\mathscr {L_R}$ is such that, for any $x\in \mathscr {L_S}$,

  $$\begin{aligned} (x+\mathscr {L_R})+(x+\mathscr {L_R})+(x+\mathscr {L_R})=\mathscr {L_R}, \end{aligned}$$

  hence, for any $\omega _1,\omega _2\in \mathscr {L_R}$ the third element in the triple through $x+\omega _1$ and $x+\omega _2$ belongs to $x+\mathscr {L_R}$, that is, $x+\mathscr {L_R}$ is a Steiner triple subsystem of ${\mathscr {S}}$.

• (iii) This follows from the fact that Q is a commutative loop of exponent 3 with the weak inverse property.$\square$

Remark 4

It must be noticed that, in the case where $\mathscr {L_R}$ is a normal subloop of $\mathscr {L_S}$, the corresponding cosets are not necessarily isomorphic Steiner triple subsystems. This will be manifest in the case 4.3 described in Sect. 4, where $\mathscr {L_R}$ is an affine hyperplane.

Theorem 2

Let $({\mathscr {S}},{\mathscr {T}})$ be a Steiner triple system and $\mathscr {L_S}$ be the corresponding Steiner loop of affine type with identity $\varOmega$. The automorphisms of ${\mathscr {S}}$ fixing $\varOmega$ are exactly the automorphisms of $\mathscr {L_S}$.

Proof

Let $\{x,y,z\}$ be a triple of ${\mathscr {T}}$. If $f\in \mathrm {Aut}(\mathscr {L_S})$, then clearly $f(\varOmega )=\varOmega$ and from

$$\begin{aligned}f\big (-(x+y)\big )=-\big (f(x)+f(y)\big )\end{aligned}$$

it follows that f maps $\{x,y,z\}$ onto $\{f(x),f(y),f(z)\}$, that is, $f\in \mathrm {Aut}({\mathscr {S}})$. Conversely, if $f\in \mathrm {Aut}({\mathscr {S}})$ is such that $f(\varOmega )=\varOmega$, then the element $f(x+y)=f(-z)$ is in the triple through f(z) and $f(\varOmega )=\varOmega$, hence it is $-f(z)=f(x)+f(y)$.$\square$

Theorem 3

Let ${\mathscr {S}}$ be a Steiner triple system with n points, and let ${\mathscr {L}}_{\mathscr {S}}$ be the associated Steiner loop of affine type with identity $\varOmega \in {\mathscr {S}}$. Then each translation of ${\mathscr {L}}_{\mathscr {S}}$ is even and has the form

$$\begin{aligned} \lambda _x=(\varOmega ,x,-x)\tau _1\ldots \tau _r \end{aligned}$$

where each $\tau _i$ is an even permutation of the form

$$\begin{aligned} \tau _i=(v_{1}, v_{2}, \dots ,v_{t_i})(-v_{t_i}, \dots , -v_{2},-v_{1}). \end{aligned}$$

Proof

Each $\lambda _x$ can be written as

$$\begin{aligned} \lambda _x = (\varOmega , x, -x) \sigma _x, \end{aligned}$$

where $\sigma _x$ is a permutation without any fixed point on the set $\mathscr {L_S}\setminus \{\varOmega ,x,-x\}$ for each $x\in \mathscr {L_S}\setminus \{\varOmega \}.$ As $\sigma _x$ has no fixed point it does not contain any 1-cycle. If $\sigma _x$ contains the j-cycle $(v_1, v_2, v_3, ...,v_j)$, then the ${\mathrm {STS}}$ has the following blocks: $\{x,v_1,-v_2\}$, $\{-v_2,\varOmega ,v_2\}$, $\{x,v_2,-v_3\}$, $\{-v_3,\varOmega , v_3\}$, ..., $\{x,v_j,-v_1\}$, $\{-v_1,\varOmega ,v_1\}$, since $x+v_1=v_2$, $x+v_2=v_3$, ..., $x+v_j=v_1$. Using these blocks the permutation $\sigma _x$ has also the j-cycle $(-v_2,-v_1,-v_{j},-v_{j-1}, \dots ,-v_3)$. So each j-cycle $(v_1, v_2, v_3, ...,v_j)$ of $\sigma _x$ appears in $\sigma _x$ together with j-cycle $(-v_j,..., -v_3, -v_2,-v_1)$. Since in $\sigma _x$ every j-cycle appears with such a disjoint j-cycle, it is an even permutation. Then also every $\lambda _x= (\varOmega , x, -x) \sigma _x$ is an even permutation.$\square$

Remark 5

For our convenience, we remark that ${\mathrm {Mult}}(\mathscr {L_S})$ is contained in $A_n,$ and the stabilizer ${\mathrm {Stab}}_{{\mathrm {Mult}}(\mathscr {L_S})}(\varOmega )$ is contained in $A_{n-1}.$

3 Computing within a Steiner Loop of Affine Type

Steiner triple systems are often studied through their configurations, which are given subsets of triples. Starting from two triples $\{z,a_1,a_2\}$ and $\{z,b_1,b_2\}$ through one point z, two cases are possible: either the third point $c_1$ in the triple through $a_1$ and $b_1$ coincides with the third point $c_2$ in the triple through $a_2$ and $b_2$ (Pasch configuration $C_{16}$), or not (configuration $C_{14}$). In the latter case, one can distinguish further the case where the triple containing the two points $c_1$ and $c_2$ contains also z (the mitre configuration centered in z) and the case where it does not (configuration $C_A$).

The Pasch configuration (that is, the 4-triples configuration on the left-hand side in Fig. 1) and the mitre centered at the point $\varOmega$ (that is, the 5-triples configuration on the right-hand side in Fig. 1), which are those appearing in the projective geometry $\mathrm {PG}(d,2)$ and in the affine geometry $\mathrm {AG}(d,3)$, respectively, are the two most commonly studied configurations.

Fig. 1

On the left-hand side there is a Pasch configuration. On the right-hand side there is a mitre centered in $\varOmega$

According to the well-known axioms by Veblen and Young [31] (see [12], p. 147), a point x is called a Veblen point, if any two triples through x determine a Pasch configuration (hence a Fano plane). Similarly, in 3.2 we call a point z a Hall point, if any two triples through z determine a mitre centered at z.

A celebrated result states that any point in a Steiner triple system ${{\mathscr {S}}}$ is a Veblen point if, and only if, ${{\mathscr {S}}}$ is a projective geometry $\mathrm {PG}{(d,2)}$ (see [12], Th. 8.15, p. 147). More recently, it was proved in [22] that any point in ${{\mathscr {S}}}$ is a Hall point if, and only if, ${{\mathscr {S}}}$ is a HTS.

In fact, as we show in the present section, the following intermediate properties hold:

• (1.i) $\varOmega$, x and y define a Pasch configuration if, and only if, $x+y=(-x)+(-y)$. Moreover, in this case $\iota _x\ne {\mathrm {id}}$,

• (1.ii) $\varOmega$ is a Veblen point if, and only if, for all $y\ne x$ it holds $x+y=(-x)+(-y)$ and $\iota _x(\pm y)=\mp y$.

• (2.i) $\{-x,\varOmega ,x\}$ and $\{-y,\varOmega ,y\}$ define a mitre centered at $\varOmega$ if, and only if, $-(x+y)=(-x)+(-y)$ and $\iota _x(y)=y$,

• (2.ii) $\varOmega$ is a Hall point if, and only if ${\mathscr {L}}_{{\mathscr {S}}}$ has the inverse property (equivalently, $-(x+y)=(-x)+(-y)$, or $\iota _x(y)=y$ for all x and y in ${\mathscr {S}}$).

Thus the map $\iota _x$, defined in (2), plays a role in distinguishing the case where $\varOmega$ is contained in a Pasch configuration (see Proposition 1) from the case where $\varOmega$ is a Hall point (see Proposition 5).

3.1 Veblen Points in Steiner Loops of Affine Type

We begin by pointing out the role played by the map $\iota _x$ when $\varOmega$ is contained in a Pasch configuration:

Proposition 1

A Steiner triple system contains the Pasch configuration $\{x,\varOmega ,-x\}$, $\{y,\varOmega ,-y\}$, $\{x,y,-(x+y)\}$, $\{-x,-y,-(x+y)\}$ if and only if $x+y=(-x)+(-y)$. Moreover, $\iota _x(-(x+y))=x+y$.

Proof

The first assertion is just an algebraic description of Fig. 1. As for the second one, it is sufficient to note that, with the notations in Fig. 1, $\iota _x(-(x+y))=x+y$. $\square$

Proposition 2

Let $\mathscr {L_S}$ be a Steiner loop of affine type with identity element $\varOmega$. The Pasch configuration $\{x,y,-(x+y)\}$, $\{-x,-y,-(x+y)\}$, $\{x,\varOmega ,-x\}$, $\{y,\varOmega ,-y\}$ is contained in a Fano plane if and only if $\lambda _x^2(y)=y$ and $\iota _x(y)=-y.$

Proof

We use the notations of Fig. 1 in order to make the proof descriptive. Let w be the third point in the triple determined by $x, -y$.

If the Pasch configuration is contained in a Fano plane, then, together with $\{x,-y,w\}$, also $\{-x,y,w\}$ is a triple, and $\{-w,-x,-y\}$ and $\{x,y,-w\}$ are triples, as well. Thus

$$\begin{aligned}\lambda _x^2(y)=x+(x+y)=x+w=y\end{aligned}$$

and

$$\begin{aligned}\iota _x(y)=-x+(y+x)=-x +w=-y.\end{aligned}$$

For the other direction, under the assumption that $\lambda _x^2(y)=y$ and $\iota _x(y)=-y$, we have to show that $\{x+y,x,-y\}$ and $\{x+y,-x,y\}$ are blocks. We have

$$\begin{aligned}\varOmega =-y+y=\iota _x(y)+y=\big (-x+(y+x)\big )+y\end{aligned}$$

and

$$\begin{aligned} \varOmega =-y +y=-y+\lambda _x^2(y)=-y+\big (x+(x+y)\big ), \end{aligned}$$

and the assertion follows. $\square$

As mentioned above, for Steiner triple systems, the concept of Veblen point reduces to the following (see [12], p. 147):

Definition 2

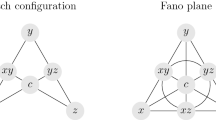
Let x be a point in a Steiner triple system ${\mathscr {S}}$. If for any $y,p_1,p_2,p_3,p_4 \in {\mathscr {S}}$ such that $y\ne x$ and together with $\{x, p_1, p_3\}$, $\{x,p_2,p_4\}$, $\{y,p_1,p_2\}$, also $\{y,p_3,p_4\}$ is a triple of ${\mathscr {S}}$, then x is called a Veblen point. Alternatively, the point x is called a Veblen point, if any two triples through x determine a Fano plane (Fig. 2).

Fig. 2

The Veblen point x

The following theorem will be used in Theorem 12 to prove that the multiplication group of a simple Steiner loop of affine type, corresponding to a STS(n) containing a Veblen point, is the alternating group on n letters.

Theorem 4

Let ${\mathscr {S}}$ be a ${\mathrm {STS}}(n)$ containing a Veblen point v. Then $n\equiv 3\; (\text{ mod } 4)$ and it holds

• (i) v is the identity element $\varOmega$ of $\mathscr {L_S}$ if and only if, for any $x\ne \varOmega$,

  $$\begin{aligned} \lambda _x=(\varOmega ,x,-x)(p_1, q_1)(-q_1, -p_1)\cdots \left( p_{\frac{n-3}{4}},q_{\frac{n-3}{4}}\right) \left( -q_{\frac{n-3}{4}},-p_{\frac{n-3}{4}}\right) . \end{aligned}$$

  Moreover, $\lambda _{-x}=(\varOmega ,-x,x)(p_1, -q_1)(q_1, -p_1)\cdots (p_{\frac{n-3}{4}},-q_{\frac{n-3}{4}})(q_{\frac{n-3}{4}},-p_{\frac{n-3}{4}})$, whereas $\lambda _{p_i}$ interchanges x with $q_i$, and $-x$ with $-q_i$.

• (ii) If $v\ne \varOmega$, then

  $$\begin{aligned} \left\{ \begin{array}{l} \lambda _v=(\varOmega ,v,-v)(p_1, q_1)(-q_1, -p_1)\cdots \left( p_{\frac{n-3}{4}},q_{\frac{n-3}{4}}\right) \left( -q_{\frac{n-3}{4}},-p_{\frac{n-3}{4}}\right) \\ \lambda _{-v}=(\varOmega ,-v,v)(p_1, -q_1)(q_1, -p_1)\cdots \left( p_{\frac{n-3}{4}},-q_{\frac{n-3}{4}}\right) \left( q_{\frac{n-3}{4}},-p_{\frac{n-3}{4}}\right) . \end{array}\right. \end{aligned}$$

Proof

(i) If $\varOmega$ is a Veblen point, then any two triples through $\varOmega$ generate a Fano plane and this yields the assertions in (i). Conversely, if $\lambda _{x}$ and $\lambda _{-x}$ have the form as in (i), then $q_i=x +p_i=(-x)+(-p_i)$, that is, the triples $\{-q_i,x,p_i\}$ and $\{-q_i,-x,-p_i\}$ form a Pasch configuration.

(ii) If $v\ne \varOmega$ is a Veblen point, then the assertions about $\lambda _v$ and $\lambda _{-v}$ are a reformulation of Fig. 2 with $y=\varOmega$, because the assumption is equivalent to saying that, if the block through v and $p_i$ contains $-q_i$, then the block through v and $-p_i$ contains $q_i$. $\square$

Remark 6

In the case where

$$\begin{aligned} \lambda _x=(\varOmega ,x,-x)(p_1, q_1)(-q_1, -p_1)\cdots \left( p_{\frac{n-3}{4}},q_{\frac{n-3}{4}}\right) \left( -q_{\frac{n-3}{4}},-p_{\frac{n-3}{4}}\right) , \end{aligned}$$

the assumption that

$$\begin{aligned} \lambda _{-x}=(\varOmega ,-x,x)(p_1, -q_1)(q_1, -p_1)\cdots \left( p_{\frac{n-3}{4}},-q_{\frac{n-3}{4}}\right) \left( q_{\frac{n-3}{4}},-p_{\frac{n-3}{4}}\right) \end{aligned}$$

is equivalent to the assumption that $\iota _x$ fixes the points x, $-x$, and $\varOmega$, and interchanges y and $-y$, for any $y\ne x$.

3.2 Hall Points in Steiner Loops of Affine Type

In this section we consider the mitre configuration within the frame of Steiner loops of affine type. The following straightforward proposition has already been mentioned in the above Remark 2, where we wrote that for HTS’s the two definitions given by Chein coincide with the one given by Hall and Bruck.

Proposition 3

Let $\mathscr {L_S}$ be a Steiner loop of affine type with identity $\varOmega$. The points x, y and $\varOmega$ form a mitre centered in $\varOmega$ if and only if $-(x+y)=(-x)+(-y)$. Moreover, $\iota _x(y)=y$.

Proof

This is again an algebraic description of Fig. 1. $\square$

Now we want to give the following definition, that runs parallel to that of Veblen point.

Definition 3

Let z be a point in a Steiner triple system ${\mathscr {S}}$. If for any point $u, w, p_1$, $p_2$, $p_3$, $p_4 \in {\mathscr {S}}$ such that $u\ne z$ together with the triples $\{z, p_1, p_3\}$, $\{z,p_2,p_4\}$, $\{u,p_1,p_2\}$ and $\{w,p_3,p_4\}$, also $\{u,w,z\}$ is a triple of ${\mathscr {S}}$, then z is called a Hall point. Alternatively, the point z is called a Hall point, if any two triples through z determine a mitre centered at z (Fig. 3).

Fig. 3

The Hall point z

Recall that a loop $({{\mathscr {L}}},*)$ fulfills the inverse property if there exists a bijective map ${\cdot }^{-1}: {\mathscr {L}} \longrightarrow {{\mathscr {L}}}$ such that $a^{-1} * (a * b) = (b * a) * a^{-1} = b$, for all $a,b \in {{\mathscr {L}}}$. The following theorem demonstrates a connection between IP loops and mitre configurations.

Theorem 5

Let $\mathscr {L_S}$ be a Steiner loop of affine type with identity $\varOmega$. The following are equivalent:

• (i) $\iota _x=\mathrm {id}$ for any $x\in {\mathscr {S}}$,

• (ii) $\mathscr {L_S}$ has the inverse property,

• (iii) $\varOmega$ is a Hall point.

Proof

If $\iota _x=\mathrm {id}$ for any $x\in {\mathscr {S}}$, then $y=\iota _x(y)=-x+(x+y)$, which is precisely the right inverse property of $\mathscr {L_S}$.

If $\mathscr {L_S}$ has the inverse property, that is, $y=-x+(x+y)$ for all $x\ne y$ in ${\mathscr {S}}$, but this means that the third point in the triple through $-x$ and $x+y$ is $-y$, which proves the assertion.

Finally, if $\varOmega$ is a Hall point, then $\iota _x=\mathrm {id}$ for any $x\in {\mathscr {S}}$ by Proposition 3.

$\square$

Corollary 1

If ${\mathscr {S}}$ is a Hall triple system, then $x\mapsto -x$ is an automorphism of $\mathscr {L_S}$, hence $\mathscr {L_S}$ has the inverse property.

Proof

The assertion follows from the fact that, in a HTS, every point is a Hall point (cf. [22]), and we can apply Proposition 3 and Theorem 5. $\square$

Theorem 6

If ${\mathscr {S}}$ is a Hall triple system and ${{\mathscr {L}}}_{{\mathscr {R}}}$ is the associated Steiner loop of affine type with identity $\varOmega$, then, for any $x\ne \varOmega$, it holds

$$\begin{aligned} \lambda _x=(\varOmega ,x,-x)(a_1, b_1, c_1)(-c_1,-b_1, -a_1)\cdots (a_t, b_t, c_t)(-c_t,-b_t, -a_t). \end{aligned}$$

Proof

If ${\mathscr {R}}\le {\mathscr {S}}$ is a Steiner triple subsystem of order 9 containing the triple $T_0=\{-x,\varOmega ,x\}$, then ${{\mathscr {L}}}_{{\mathscr {R}}}$ is the elementary abelian group of cardinality 9 and the triples are exactly the 3-subsets of elements summing up to zero. In particular, the two parallel triples to $T_0=\{-x,\varOmega ,x\}$ are $\lambda _y(T_0)$ and $\lambda _{-y}(T_0)$, for a chosen $y\in {\mathscr {R}}\setminus T_0$. Thus the restriction of $\lambda _x$ to ${{\mathscr {R}}}$ is simply $\lambda _x=(\varOmega ,x,-x)(y,y+x,-x+y)(-y,-y+x,(-y)+(-x))$. The claim follows inductively. $\square$

Remark 7

Note that, by Theorem 3, the condition on $\lambda _{x}$ in Theorem 6 is equivalent to saying that $\lambda _x$ has order three.

Remark 8

By a well known theorem, proved first by B. Fisher, thereafter by many others (see [18], cf. also Theorem 8 in the present paper), the order of any Hall triple system is $n=3^k$, hence the number $2t+1$ of 3-cycles in Theorem 6 is obtained for $t=\frac{3^{k-1}-1}{2}$.

Theorem 7

Let ${\mathscr {S}}$ be a STS and let $\mathscr {L_S}$ be the corresponding Steiner loop of affine type with identity element $\varOmega$. Each left translation $\lambda _x$ is an automorphism of ${\mathscr {S}}$ if and only if ${\mathscr {S}}$ is a Hall triple system.

Proof

Let ${\mathscr {S}}$ be a ${\mathrm {HTS}}$, let $x\ne \varOmega$ be in ${\mathscr {S}}$, and let $\{a,b,c\}$ be a triple. If $x\notin \{a,b,c\}$, then the translation $\lambda _x$ maps the triple $\{a,b,c\}$ onto the triple parallel to it and not containing x in the plane through x and $\{a,b,c\}$. If $x\in \{a,b,c\}$ and $\varOmega \notin \{a,b,c\}$, then the translation $\lambda _x$ maps the triple $\{a,b,c\}$ onto the triple parallel to it and not containing $\varOmega$ in the plane through $\varOmega$ and $\{a,b,c\}$. Finally, if $\{a,b,c\}=\{-x,\varOmega ,x\}$, then the translation $\lambda _x$ maps the triple $\{a,b,c\}$ onto itself.

Conversely, assume that each left translation $\lambda _x$ is an automorphism of the STS ${\mathscr {S}}$. Let $\{a,b,c\}$ be a triple and x an element not contained in it. We have to prove that $\{a,b,c\}$ and x generate a ${\mathrm {STS}}(9)$.

First, we note that, together with each triple $\{y_1,y_2,y_3\}$, also $\{-y_1,-y_2,-y_3\}$ is a triple, because when we apply $\lambda _{-y_1}$ to the triple $\{-y_2,\varOmega ,y_2\}$, we obtain that $\{(-y_1)+(-y_2),-y_1,-y_1 +y_2\}$ is a triple, that is,

$$\begin{aligned} -y_1+\big ((-y_1)+(-y_2)\big )=-(-y_1 +y_2). \end{aligned}$$

On the other hand, we have that

$$\begin{aligned} -(-y_1 +y_2)=-y_1 +y_3, \end{aligned}$$

because if we apply $\lambda _{-y_1}$ to $\{y_1,y_2,y_3\}$, we get the triple $\{\varOmega ,-y_1 +y_2,-y_1 +y_3\}$, thus

$$\begin{aligned} -y_1+\big ((-y_1)+(-y_2)\big )=-y_1 +y_3, \end{aligned}$$

which means that $(-y_1)+(-y_2)=y_3$, that is $\{-y_1,-y_2,-y_3\}$ is a triple.

Second, together with $\{a,b,c\}$ and $\{a+x,b+x,c+x\}$, also $\{-(a+x),-(b+x),-(c+x)\}$ is a triple.

Finally, let $T_1=\{-(a+x),c,m\}$ and $T_2=\{-(c+x),a,n\}$ be triples, and apply $\lambda _x$ to $T_2$ to produce the triple $T_3=\{a+x,n+x,-(x+c)+x\}$. From the triple $T_4=\{c,x,-(c+x)\}$ we derive that $-(c+x)+x=-c$, thus $T_3=\{a+x,n+x,-c\}$. Comparing now the triples $T_3=\{a+x,n+x,-c\}$ and $T_1=\{-(a+x),c,m\}$, we find that $n+x=-m$, because of the argument that the opposite of a triple is also a triple. This proves that $\{a,b,c\}$ and x are contained in a $\mathrm {STS}(9)$. $\square$

Corollary 2

Let ${\mathscr {S}}$ be a Hall triple system and $\mathscr {L_S}$ the corresponding Steiner loop of affine type with identity element $\varOmega$. The map f is an automorphism of ${\mathscr {S}}$ if and only if $f(z)=f_0(z)+f(\varOmega )$, with an automorphism $f_0$ of $\mathscr {L_S}$.

Proof

Let f be an automorphism of ${\mathscr {S}}$ and let $f_0(z)=-f(\varOmega )+f(z)$, that is, $\{f(z),-f(\varOmega ),$ $-f_0(z)\}$ is a triple. Note that, since ${\mathscr {S}}$ is a HTS, this can be written also as $f(z)=f_0(z)+f(\varOmega )$.

The assertion that $f_0$ is an automorphism of $\mathscr {L_S}$ follows because the map $f_0=\lambda _{-f(\varOmega )}\circ f$ is (again) an automorphism of ${\mathscr {S}}$, such that $f_0(\varOmega )=\varOmega$ and we can apply Theorem 2.

Conversely, for any automorphism $f_0$ of $\mathscr {L_S}$, and for any given $\omega \in {\mathscr {S}}$, the map $f(z)=f_0(z)+\omega$ is an automorphism of ${\mathscr {S}}$ simply because $f=\lambda _\omega \circ f_0$, and we apply Theorems 2 and 7. $\square$

Remark 9

According to the original paper [19] of M. Hall, HTS’s can also be defined as STS’s such that to any point $z_0$ one can associate an involutory automorphism f which leaves $z_0$ fixed, that is, the map $f(x)=y$, where $\{x,z_0,y\}$ is a triple (hence, in the loop ${\mathscr {L}}_S$, $f(x)=(-x)+(-z_0)$). The automorphism $f_0$ of ${\mathscr {L}}_{\mathscr {S}}$ associated to the involution f is therefore equal to $f_0(x)=-f(\varOmega )+\big ((-x)+(-z_0)\big )$.

4 Extensions of Steiner Loops of Affine Type

In this section we reduce the structure of Steiner loops of affine type to consecutive extensions of simple ones. As one can expect, by considering that the number of STS’s with n elements increases as $\big (n/{e^2}+o(n)\big )^{n^2/6}$ (see [21]), this construction is very flexible, compared with the corresponding extension theory for commutative groups.

Theorem 8

Any Steiner loop $\mathscr {L_S}$ of affine type has a subnormal series

$$\begin{aligned} \varOmega \unlhd {\mathscr {L}}_{{{\mathscr {S}}}_1}\unlhd \cdots \unlhd {\mathscr {L}}_{{{\mathscr {S}}}_t}=\mathscr {L_S}, \end{aligned}$$

where the factors ${\mathscr {L}}_{{{\mathscr {S}}}_{i+1}}/{\mathscr {L}}_{{{\mathscr {S}}}_i}$ are simple Steiner loops of affine type. If $\mathscr {L_S}$ corresponds to a ${\mathrm {HTS}}$, then there exists such a series where the factors have order 3.

Proof

The first result is standard. The second one follows from the fact that the commutative Moufang loop of exponent 3 corresponding to a ${\mathrm {HTS}}$ always contains a proper normal subloop, namely the associative center $Z({{\mathscr {L}}_{{{\mathscr {S}}}}}) = \{z : \forall x, y \in {\mathscr {L}}_{{{\mathscr {S}}}}, (x + y) + z =x + (y + z)\}$ (see [6]), thus we can make a recursive argument on $Z({{\mathscr {L}}_{{{\mathscr {S}}}}})$ and ${{\mathscr {L}}_{{{\mathscr {S}}}}}/Z({{\mathscr {L}}_{{{\mathscr {S}}}}})$. $\square$

Extensions of normal (sub-)loops N by (quotient) loops Q are much more relaxed than in the case of groups (cf. [2] and [8, 24]), simply because for Steiner loops of affine type the associativity holds only for elements x, y and z such that $x+y+z=\varOmega$ (where possibly $x=y=z$). We illustrate this in Example 4.1, after giving the following definition, where we brief these conditions for a Steiner loop of affine type to be such an extension (for our convenience, here we will denote the identity elements by 0).

Definition 4

Let N and Q be Steiner loops of affine type of order n and m, and identity elements $0'$ and ${\bar{0}}$, respectively, and let ${\mathscr {Q}}(N)$ be the set of $n\times n$ latin squares with coefficients in the set N.

An operator $\varPhi :Q\times Q\longrightarrow {\mathscr {Q}}(N)$, which maps the pair $({{\bar{x}}},{{\bar{y}}})$ to a latin square $\varPhi _{{{\bar{x}}},\bar{y}}:N\times N\longrightarrow N$, is called a Steiner operator if it fulfills the following conditions:

• (i) the latin square $\varPhi _{{{\bar{0}}},{{\bar{0}}}}$ is the (symmetric) table of addition of N;

• (ii) $\varPhi _{{{\bar{y}}},{{\bar{x}}}}(y',x')=\varPhi _{{{\bar{x}}},\bar{y}}(x',y')$, that is, $\varPhi _{{{\bar{y}}},{{\bar{x}}}}$ is the transpose of $\varPhi _{{{\bar{x}}},{{\bar{y}}}}$;

• (iii) $\varPhi _{{{\bar{x}}},{{\bar{0}}}}(x',0')=x'$

• (iv) $\varPhi _{{{\bar{x}}},{{\bar{x}}}}(x',x')=-x'$;

• (v) $\varPhi _{{{\bar{x}}},-{{\bar{x}}}}(x',-x')=0'$;

• (vi) $\varPhi _{{{\bar{y}}},{{\bar{z}}}}(y',z')=-x'\iff \varPhi _{{{\bar{x}}},\bar{z}}(x',z')=-y'$ (hence also $\iff \varPhi _{{{\bar{x}}},{{\bar{y}}}}(x',y')=-z'$),

for all $({{\bar{x}}},x'),({{\bar{y}}},y')\in Q\times N$, for all $z'\in N$, and for ${{\bar{x}}}+{{\bar{y}}}+{{\bar{z}}}={{\bar{0}}}$.

Remark 10

We want to stress the fact that the conditions in the above definition are weak.

• This is manifest for conditions (i) and (ii).

• For ${{\bar{x}}} = {{\bar{0}}}$, conditions (iii), (iv) and (v) hold, simply because $\varPhi _{{{\bar{0}}},{{\bar{0}}}}$ is the table of addition of a commutative loop of exponent 3.

• For ${{\bar{x}}} \ne {{\bar{0}}}$, once arbitrary latin squares $\varPhi _{{{\bar{x}}},{{\bar{x}}}}$ and $\varPhi _{-{{\bar{x}}},-{{\bar{x}}}}$ are rearranged in such a way to fulfill condition iv), which will determine the same main diagonal of these latin squares, condition v) determines only the places of the element $0'$ in each row of the otherwise arbitrary latin square $\varPhi _{{{\bar{x}}},-{{\bar{x}}}}$. On the contrary, once the latin squares $\varPhi _{{{\bar{x}}},{{\bar{x}}}}$, $\varPhi _{-{{\bar{x}}},-{{\bar{x}}}}$, and $\varPhi _{{{\bar{x}}},-{{\bar{x}}}}$ are chosen, conditions iv) and v) determine now the whole latin squares $\varPhi _{{{\bar{x}}},{{{\bar{0}}}}}$ and $\varPhi _{{{{\bar{0}}}},-{{\bar{x}}}}$, as we show in Example 4.1, working on the table

$$\begin{aligned} \begin{array}{c|c|c} \varPhi _{{{\bar{x}}},{{\bar{x}}}} &{} \varPhi _{{{\bar{x}}},{{{\bar{0}}}}} &{}\varPhi _{{{\bar{x}}},-\bar{x}}\\ \hline \varPhi _{{{{\bar{0}}}},{{\bar{x}}}} &{} \varPhi _{{{{\bar{0}}}},{\bar{0}}}&{}\varPhi _{{{{\bar{0}}}},-{{\bar{x}}}}\\ \hline \varPhi _{-{{\bar{x}}},{{\bar{x}}}} &{}\varPhi _{-{{\bar{x}}},{{{\bar{0}}}}}&{} \varPhi _{-{{\bar{x}}},-{{\bar{x}}}} \end{array}. \end{aligned}$$

(3)

• Finally, we note that condition (vi) simply means that, as soon as ${{\bar{z}}}$ is such that ${{{\bar{x}}}}+{{{\bar{y}}}}+{{{\bar{z}}}}={{{\bar{0}}}}$, the latin squares $\varPhi _{{{\bar{x}}},{{\bar{z}}}}$ and $\varPhi _{{{\bar{y}}},{{\bar{z}}}}$ are thoroughly determined by the arbitrarily chosen latin square $\varPhi _{{{\bar{x}}},{{\bar{y}}}}$, as shown again in Example 4.1, by working on the table

$$\begin{aligned} \begin{array}{c|c} \varPhi _{{{\bar{x}}},{{\bar{y}}}} &{} \varPhi _{{{\bar{x}}},{{\bar{z}}}} \\ \hline &{} \varPhi _{\bar{y},{{\bar{z}}}} \end{array}. \end{aligned}$$

Theorem 9

Let N, resp. Q, be a Steiner loop of affine type with identity $0'$, resp. ${{\bar{0}}}$, of order n, resp. m, and let $\varPhi :Q\times Q\longrightarrow {\mathscr {Q}}(N)$ be a Steiner operator.

If we define on ${{\mathscr {L}}}=Q\times N$ the addition

$$\begin{aligned} ({{\bar{x}}}, x')+({{\bar{y}}},y')=({{{\bar{x}}}}+{{{\bar{y}}}}, x'\oplus y'), \end{aligned}$$

where we denote, with abuse of notation, $x'\oplus y'=\varPhi _{\bar{x},{{\bar{y}}}}(x',y')$, then ${{\mathscr {L}}}$ is a Steiner loop of affine type of order $v=nm$, with identity $({{\bar{0}}},0')$, such that the opposite of the element $({{\bar{x}}}, x')\in {{\mathscr {L}}}$ is $-({{\bar{x}}}, x')=(-{{\bar{x}}}, -x')$. The subloop ${\hat{N}}$ containing all the elements $({{\bar{0}}}, x')$, $x'\in N$, is a normal subloop, isomorphic to N, and such that ${{\mathscr {L}}}/{\hat{N}}$ is isomorphic to Q.

Conversely, any Steiner loop ${{\mathscr {L}}}$ of affine type, having a normal subloop N and a quotient loop $Q={{\mathscr {L}}}/N$, is isomorphic, for some given Steiner operator $\varPhi$, to the above one.

Proof

Let ${{\mathscr {L}}}$ be defined as above. By Definition 4, condition (ii), the addition is commutative; by condition (iii), the element $({{\bar{0}}},0')$ is the identity, and, by condition v), $-({{\bar{x}}}, x')=(-{{\bar{x}}}, -x')$. Conditions iv) and v) yield $3({{\bar{x}}}, x')=({{\bar{0}}}, 0')$. The weak inverse property

$$\begin{aligned} ({{\bar{x}}}, x')+\big (({{\bar{y}}},y')+({{\bar{z}}}, z')\big )=({{\bar{0}}}, 0') \ \hbox {whenever} \ \big (({{\bar{x}}}, x')+({{\bar{y}}},y')\big )+({{\bar{z}}}, z')=({{\bar{0}}}, 0') \end{aligned}$$

is equivalent to saying that, for ${{\bar{x}}}+{{\bar{y}}}+{{\bar{z}}}={{\bar{0}}}$,

$$\begin{aligned} \varPhi _{{{\bar{x}}},-{{\bar{x}}}}(x',\varPhi _{{{\bar{y}}},{{\bar{z}}}}(y',z'))=0'\iff \varPhi _{-{{\bar{z}}},{{\bar{z}}}}(\varPhi _{{{\bar{x}}},{{\bar{y}}}}(x',y'),z')=0', \end{aligned}$$

which, together with condition v), yields condition (vi).

If $({{\bar{a}}}, a')$ and $({{\bar{b}}}, b')$ are two given elements in ${{\mathscr {L}}}$, then the equation

$$\begin{aligned} ({{\bar{a}}}, a')+({{\bar{x}}}, x')=({{\bar{b}}}, b') \end{aligned}$$

has a unique solution $({{\bar{x}}}, x')$, where ${{\bar{x}}}=-(-{{\bar{b}}}+\bar{a})\in Q$ and $x'$ is the unique element in N such that $\varPhi _{\bar{a},-(-{{\bar{b}}}+{{\bar{a}}})}(a',x')=b'$. Thus ${{\mathscr {L}}}$ is a commutative loop of exponent 3 with the weak inverse property, that is, a Steiner loop of affine type with identity $\varOmega =(\bar{0}, 0')$. The subloop

$$\begin{aligned} {\hat{N}}=\{({{\bar{0}}}, x'):x'\in N\} \end{aligned}$$

is isomorphic to N and is normal, because both $\big ((\bar{a},a')+({{\bar{b}}},b')\big )+{\hat{N}}$ and $({{\bar{a}}},a')+\big ((\bar{b},b')+{\hat{N}}\big )$ coincide with

$$\begin{aligned} \{({{\bar{a}}}+{{\bar{b}}}, x'):x'\in N\}. \end{aligned}$$

Conversely, for any Steiner loop ${{\mathscr {L}}}$ of affine type, having a normal subloop N and a quotient loop $Q={{\mathscr {L}}}/N$, let $\sigma :Q\longrightarrow {{\mathscr {L}}}$ be a section such that $\sigma (N)=0$ and $\sigma (-x+N)=-\sigma (x+N)$, and let $\cdot ':{{\mathscr {L}}}\longrightarrow N$ be such that $x=\sigma (x+N)+x'$. If x and y are in ${{\mathscr {L}}}$, then

$$\begin{aligned} \varPhi _{x+N, y+N}(x',y')=(x+y)' \end{aligned}$$

defines a latin square on N, and the map $\varPhi :(x+N,y+N)\mapsto \varPhi _{x+N, y+N}$ is a Steiner operator: indeed, condition (i) holds, because $\sigma (N)=0$; condition (ii) holds because ${{\mathscr {L}}}$ is commutative; condition (iii) holds, again because $\sigma (N)=0$; condition iv) holds, because $\sigma (-x+N)=-\sigma (x+N)$; condition (v) holds because ${\mathscr {L}}$ has exponent 3; and condition (vi) holds because ${\mathscr {L}}$ has the weak inverse property. $\square$

Remark 11

The same table (3) that we considered in Remark 10, shows that the set

$$\begin{aligned} M=\Big \{(\bar{a},b'): {{\bar{a}}}\in \{{{\bar{x}}},{{\bar{0}}}, -{{\bar{x}}}\}, b'\in N\Big \} \end{aligned}$$

is closed under the loop operation, thus, by Theorem 1 (i), ${{\mathscr {S}}}_M$ gives us in turn a $\mathrm {STS}$ subsystem of ${{\mathscr {S}}}_{{\mathscr {L}}}$ with $|M|=3\cdot |N|$, a fact which will also be stated in Corollary 3. An example is given in table (4) in the following Example 4.1.

Finally, we want to give an example and to examine some special extensions.

4.1 Example

We sketch the construction of the addition table of a Steiner loop ${{\mathscr {L}}}$ of affine type with 21 elements as an extension of a normal subloop N with 3 elements with a Steiner quotient loop Q of affine type with 7 elements, for which we fix the following addition tables:

$$\begin{aligned} N:\;\begin{array}{c|ccc} + &{} -1 &{} 0 &{} 1 \\ \hline -1 &{} 1 &{} -1 &{} 0 \\ 0 &{} -1 &{} 0 &{} 1 \\ 1 &{} 0 &{} 1 &{} -1 \end{array}\quad \quad \quad Q:\;\begin{array}{c|ccccccc} + &{} {{\bar{z}}} &{} {{\bar{y}}} &{} {{\bar{x}}} &{} \varOmega &{} -{{\bar{x}}} &{} -{{\bar{y}}} &{} -{{\bar{z}}} \\ \hline {{\bar{z}}} &{} -{{\bar{z}}} &{} {{\bar{x}}} &{} {{\bar{y}}} &{} {{\bar{z}}} &{} -{{\bar{y}}} &{} -{{\bar{x}}} &{} \varOmega \\ {{\bar{y}}} &{} {{\bar{x}}} &{} -{{\bar{y}}} &{} {{\bar{z}}} &{} {{\bar{y}}} &{} -{{\bar{z}}} &{} \varOmega &{} -{{\bar{x}}} \\ {{\bar{x}}} &{} {{\bar{y}}} &{} {{\bar{z}}} &{} -{{\bar{x}}} &{} {{\bar{x}}} &{} \varOmega &{} -{{\bar{z}}} &{} -{{\bar{y}}} \\ \varOmega &{} {{\bar{z}}} &{} {{\bar{y}}} &{} {{\bar{x}}} &{} \varOmega &{} -{{\bar{x}}} &{} -{{\bar{y}}} &{} -{{\bar{z}}} \\ -{{\bar{x}}} &{} -{{\bar{y}}} &{} -{{\bar{z}}} &{} \varOmega &{} -{{\bar{x}}} &{} {{\bar{x}}} &{} {{\bar{z}}} &{} {{\bar{y}}} \\ -{{\bar{y}}} &{} -{{\bar{x}}} &{} \varOmega &{} -{{\bar{z}}} &{} -{{\bar{y}}} &{} {{\bar{z}}} &{} {{\bar{y}}} &{} {{\bar{x}}} \\ -{{\bar{z}}} &{} \varOmega &{} -{{\bar{x}}} &{} -{{\bar{y}}} &{} -{{\bar{z}}} &{} {{\bar{y}}} &{} {{\bar{x}}} &{} {{\bar{z}}} \end{array}\;. \end{aligned}$$

The elements of ${{\mathscr {L}}}$ will be represented by pairs $(\bar{x}, x')$ in $Q\times N$ and the addition table of ${{\mathscr {L}}}$ will be given in $3\times 3$ block matrices $\varPhi _{{{\bar{i}}},{{\bar{j}}}}$

$$\begin{aligned} {{\mathscr {L}}}:\;\begin{array}{lllllll} \varPhi _{{{\bar{z}}},{{\bar{z}}}} &{} \varPhi _{{{\bar{z}}},{{\bar{y}}}} &{} \varPhi _{{{\bar{z}}},{{\bar{x}}}} &{} \varPhi _{{{\bar{z}}},\varOmega } &{} \varPhi _{{{\bar{z}}},-{{\bar{x}}}} &{} \varPhi _{{{\bar{z}}},-{{\bar{y}}}} &{} \varPhi _{{{\bar{z}}},-{{\bar{z}}}} \\ \varPhi _{{{\bar{y}}},{{\bar{z}}}} &{} \varPhi _{{{\bar{y}}},{{\bar{y}}}} &{} \varPhi _{{{\bar{y}}},{{\bar{x}}}} &{} \varPhi _{{{\bar{y}}},\varOmega } &{} \varPhi _{{{\bar{y}}},-{{\bar{x}}}} &{} \varPhi _{{{\bar{y}}},-{{\bar{y}}}} &{} \varPhi _{{{\bar{y}}},-{{\bar{z}}}} \\ \varPhi _{{{\bar{x}}},{{\bar{z}}}} &{} \varPhi _{{{\bar{x}}},{{\bar{y}}}} &{} \varPhi _{{{\bar{x}}},{{\bar{x}}}} &{} \varPhi _{{{\bar{x}}},\varOmega } &{} \varPhi _{{{\bar{x}}},-{{\bar{x}}}} &{} \varPhi _{{{\bar{x}}},-{{\bar{y}}}} &{} \varPhi _{{{\bar{x}}},-{{\bar{z}}}} \\ \varPhi _{\varOmega ,{{\bar{z}}}} &{} \varPhi _{\varOmega ,{{\bar{y}}}} &{} \varPhi _{\varOmega ,{{\bar{x}}}} &{} \varPhi _{\varOmega ,\varOmega } &{} \varPhi _{\varOmega ,-{{\bar{x}}}} &{} \varPhi _{\varOmega ,-{{\bar{y}}}} &{} \varPhi _{\varOmega ,-{{\bar{z}}}} \\ \varPhi _{-{{\bar{x}}},{{\bar{z}}}} &{} \varPhi _{-{{\bar{x}}},{{\bar{y}}}} &{} \varPhi _{-{{\bar{x}}},\bar{x}} &{} \varPhi _{-{{\bar{x}}},\varOmega } &{} \varPhi _{-{{\bar{x}}},-{{\bar{x}}}} &{} \varPhi _{-{{\bar{x}}},-{{\bar{y}}}} &{} \varPhi _{-{{\bar{x}}},-{{\bar{z}}}} \\ \varPhi _{-{{\bar{y}}},{{\bar{z}}}} &{} \varPhi _{-{{\bar{y}}},{{\bar{y}}}} &{} \varPhi _{-{{\bar{y}}},\bar{x}} &{} \varPhi _{-{{\bar{y}}},\varOmega } &{} \varPhi _{-{{\bar{y}}},-{{\bar{x}}}} &{} \varPhi _{-{{\bar{y}}},-{{\bar{y}}}} &{} \varPhi _{-{{\bar{y}}},-{{\bar{z}}}} \\ \varPhi _{-{{\bar{z}}},{{\bar{z}}}} &{} \varPhi _{-{{\bar{z}}},{{\bar{y}}}} &{} \varPhi _{-{{\bar{z}}},\bar{x}} &{} \varPhi _{-{{\bar{z}}},\varOmega } &{} \varPhi _{-{{\bar{z}}},-{{\bar{x}}}} &{} \varPhi _{-\bar{z},-{{\bar{y}}}} &{} \varPhi _{-{{\bar{z}}},-{{\bar{z}}}} \end{array} \end{aligned}$$

according to the addition table of Q, starting from the central block $\varPhi _{\varOmega ,\varOmega }$ which, by Definition 4 (i), is the addition table of N, represented here as the set $\{(\varOmega , x'):x'\in N\}$:

$$\begin{aligned} \varPhi _{\varOmega ,\varOmega }:\;\begin{array}{c|ccc} +&{}(\varOmega ,-1) &{} (\varOmega ,0) &{} (\varOmega ,1)\\ \hline (\varOmega ,-1) &{} (\varOmega ,1) &{} (\varOmega ,-1) &{} (\varOmega ,0) \\ (\varOmega ,0) &{} (\varOmega ,-1) &{} (\varOmega ,0) &{} (\varOmega ,1) \\ (\varOmega ,1) &{} (\varOmega ,0) &{} (\varOmega ,1) &{} (\varOmega ,-1) \end{array}\;. \end{aligned}$$

This latin square corresponds to the single triple $\{(\varOmega ,-1) , (\varOmega ,0) , (\varOmega ,1)\}$ of the Steiner triple system ${\mathscr {S}}_{{\mathscr {L}}}$ with 21 elements and 70 triples.

By condition iv), which is equivalent to saying that the opposite of the element $({{\bar{z}}}, z')\in {{\mathscr {L}}}$ is $-({{\bar{z}}}, z')=(-\bar{z}, -z')$, the main diagonals for $\varPhi _{{{\bar{z}}},{{\bar{z}}}}$, $\varPhi _{\bar{y},{{\bar{y}}}}$ and $\varPhi _{{{\bar{x}}},{{\bar{x}}}}$ are uniquely determined. In this small case, where N contains only three elements, this determines in fact the whole latin square, which will be the same for $\varPhi _{{{\bar{z}}},{{\bar{z}}}}$, $\varPhi _{{{\bar{y}}},{{\bar{y}}}}$ and $\varPhi _{\bar{x},{{\bar{x}}}}$. Moreover, this determines, as well, the places of the element $(\varOmega ,0)$ in each row of the tables $\varPhi _{{{\bar{z}}},-\bar{z}}$, $\varPhi _{{{\bar{x}}},-{{\bar{x}}}}$ and $\varPhi _{{{\bar{y}}},-{{\bar{y}}}}$, and this leaves us with only two choices for $\varPhi _{{{\bar{z}}},-{{\bar{z}}}}$, which differ to the extent that we can switch 1 and $-1$. For $\varPhi _{{{\bar{z}}},-{{\bar{z}}}}$, we choose, for instance, the following:

$$\begin{aligned} \begin{array}{c|c} \varPhi _{{{\bar{z}}},{{\bar{z}}}} &{} \varPhi _{{{\bar{z}}},-{{\bar{z}}}} \\ \hline \varPhi _{-\bar{z},{{\bar{z}}}} &{} \varPhi _{-{{\bar{z}}},-{{\bar{z}}}} \end{array}:\;\begin{array}{c|ccc|ccc} + &{} ({{\bar{z}}},-1)&{} ({{\bar{z}}},0)&{} ({{\bar{z}}},1) &{} (-{{\bar{z}}},-1)&{} (-\bar{z},0)&{} (-{{\bar{z}}},1)\\ \hline ({{\bar{z}}},-1)&{} (-{{\bar{z}}} ,1) &{} (-{{\bar{z}}} ,-1) &{} (-{{\bar{z}}} ,0) &{} (\varOmega ,1) &{} (\varOmega ,-1) &{} (\varOmega ,0)\\ ({{\bar{z}}},0)&{} (-{{\bar{z}}} ,-1) &{} (-{{\bar{z}}} ,0) &{} (-{{\bar{z}}} ,1) &{}(\varOmega ,-1) &{} (\varOmega ,0) &{} (\varOmega ,1)\\ ({{\bar{z}}},1)&{} (-{{\bar{z}}} ,0) &{} (-{{\bar{z}}} ,1) &{} (-{{\bar{z}}} ,-1) &{}(\varOmega ,0) &{} (\varOmega ,1) &{} (\varOmega ,-1)\\ \hline (-{{\bar{z}}},-1)&{} (\varOmega ,1) &{} (\varOmega ,-1) &{} (\varOmega ,0) &{}({{\bar{z}}} ,1) &{} ({{\bar{z}}} ,-1) &{} ({{\bar{z}}} ,0)\\ (-{{\bar{z}}},0)&{} (\varOmega ,-1) &{} (\varOmega ,0) &{} (\varOmega ,1) &{}({{\bar{z}}} ,-1) &{} ({{\bar{z}}} ,0) &{} ({{\bar{z}}} ,1)\\ (-{{\bar{z}}},1)&{} (\varOmega ,0) &{} (\varOmega ,1) &{} (\varOmega ,-1) &{}({{\bar{z}}} ,0) &{} ({{\bar{z}}} ,1) &{} ({{\bar{z}}} ,-1) \end{array}\;. \end{aligned}$$

The previous table corresponds to 11 triples of ${{\mathscr {S}}}_{{\mathscr {L}}}$, namely, one corresponding to $\varPhi _{{{\bar{z}}},{{\bar{z}}}}$, one to $\varPhi _{-{{\bar{z}}},-{{\bar{z}}}}$ and 9 to $\varPhi _{{{\bar{z}}},-{{\bar{z}}}}$ (one triple for each entry, for instance,

$\{({{\bar{z}}},-1),(-{{\bar{z}}},-1), (\varOmega ,-1)\}$ is a triple).

This determines uniquely the latin squares $\varPhi _{{{\bar{z}}},\varOmega }$ and $\varPhi _{-{{\bar{z}}},\varOmega }$, according to the table

$$\begin{aligned} \begin{array}{c|c|c} \varPhi _{{{\bar{z}}},{{\bar{z}}}} &{} \varPhi _{{{\bar{z}}},\varOmega } &{}\varPhi _{{{\bar{z}}},-{{\bar{z}}}}\\ \hline \varPhi _{\varOmega ,{{\bar{z}}}} &{} \varPhi _{\varOmega ,\varOmega }&{}\varPhi _{\varOmega ,-{{\bar{z}}}}\\ \hline \varPhi _{-\bar{z},{{\bar{z}}}} &{}\varPhi _{-{{\bar{z}}},\varOmega }&{} \varPhi _{-{{\bar{z}}},-{{\bar{z}}}} \end{array}, \end{aligned}$$

which in particular is the following:

$$\begin{aligned} \begin{array}{c|ccc|ccc|ccc} + &{} ({{\bar{z}}},-1)&{} ({{\bar{z}}},0)&{} ({{\bar{z}}},1) &{} (\varOmega ,-1)&{} (\varOmega ,0)&{} (\varOmega ,1) &{} (-{{\bar{z}}},-1)&{} (-{{\bar{z}}},0)&{} (-{{\bar{z}}},1)\\ \hline ({{\bar{z}}},-1)&{} (-{{\bar{z}}} ,1) &{} (-{{\bar{z}}} ,-1) &{} (-{{\bar{z}}} ,0) &{} (\bar{z},1) &{} ({{\bar{z}}},-1) &{} ({{\bar{z}}},0)&{} (\varOmega ,1) &{} (\varOmega ,-1) &{} (\varOmega ,0)\\ ({{\bar{z}}},0)&{} (-{{\bar{z}}} ,-1) &{} (-{{\bar{z}}} ,0) &{} (-{{\bar{z}}} ,1) &{} (\bar{z},-1)&{} ({{\bar{z}}},0)&{} ({{\bar{z}}},1)&{}(\varOmega ,-1) &{} (\varOmega ,0) &{} (\varOmega ,1)\\ ({{\bar{z}}},1)&{} (-{{\bar{z}}} ,0) &{} (-{{\bar{z}}} ,1) &{} (-{{\bar{z}}} ,-1) &{} ({{\bar{z}}} ,0)&{} ({{\bar{z}}} ,1)&{} ({{\bar{z}}} ,-1)&{}(\varOmega ,0) &{} (\varOmega ,1) &{} (\varOmega ,-1)\\ \hline (\varOmega ,-1)&{} ({{\bar{z}}} ,1) &{} ({{\bar{z}}} ,-1) &{} ({{\bar{z}}} ,0) &{} (\varOmega ,1)&{} (\varOmega ,-1)&{} (\varOmega ,0)&{}(-{{\bar{z}}} ,1) &{} (-{{\bar{z}}} ,-1) &{} (-{{\bar{z}}} ,0)\\ (\varOmega ,0)&{} ({{\bar{z}}} ,-1) &{} ({{\bar{z}}} ,0) &{} ({{\bar{z}}} ,1) &{} (\varOmega ,-1)&{} (\varOmega ,0)&{} (\varOmega ,1)&{}(-{{\bar{z}}} ,-1) &{} (-{{\bar{z}}} ,0) &{} (-{{\bar{z}}} ,1)\\ (\varOmega ,1)&{} ({{\bar{z}}} ,0) &{} ({{\bar{z}}} ,1) &{} ({{\bar{z}}} ,-1) &{} (\varOmega ,0)&{} (\varOmega ,1)&{} (\varOmega ,-1)&{}(-{{\bar{z}}} ,0) &{} (-{{\bar{z}}} ,1) &{} (-{{\bar{z}}} ,-1)\\ \hline (-{{\bar{z}}},-1)&{} (\varOmega ,1) &{} (\varOmega ,-1) &{} (\varOmega ,0) &{} (-{{\bar{z}}} ,1)&{} (-{{\bar{z}}} ,-1)&{} (-{{\bar{z}}} ,0)&{}({{\bar{z}}} ,1) &{} ({{\bar{z}}} ,-1) &{} (\bar{z} ,0)\\ (-{{\bar{z}}},0)&{} (\varOmega ,-1) &{} (\varOmega ,0) &{} (\varOmega ,1) &{} (-{{\bar{z}}} ,-1)&{} (-{{\bar{z}}} ,0)&{} (-{{\bar{z}}} ,1)&{}({{\bar{z}}} ,-1) &{} ({{\bar{z}}} ,0) &{} (\bar{z} ,1)\\ (-{{\bar{z}}},1)&{} (\varOmega ,0) &{} (\varOmega ,1) &{} (\varOmega ,-1) &{} (-{{\bar{z}}} ,0)&{} (-{{\bar{z}}} ,1)&{} (-{{\bar{z}}} ,-1)&{}({{\bar{z}}} ,0) &{} ({{\bar{z}}} ,1) &{} ({{\bar{z}}} ,-1) \end{array}\;. \end{aligned}$$

(4)

In the previous table, the reader can find an example to what we stated in Remark 11: since the set

$$\begin{aligned}M_{{{\bar{z}}}}=\{(-\bar{z},-1), (-{{\bar{z}}},0), (-{{\bar{z}}},1), (\varOmega ,0), (\varOmega ,1), (\varOmega ,-1), ({{\bar{z}}},-1), ({{\bar{z}}},0), ({{\bar{z}}},1)\}\end{aligned}$$

is closed under the loop operation, by Theorem 1 (i) ${{\mathscr {S}}}_{M_{{{\bar{z}}}}}$ will give us in turn a $\mathrm {STS}$ subsystem of ${{\mathscr {S}}}_{{\mathscr {L}}}$ with 9 elements. Note that $M_{{{\bar{z}}}}$ cannot be normal, because Q is simple.

The reader can produce in the same way the addition tables corresponding to the cosets ${{\bar{y}}} +N$ and $-{{\bar{y}}}+N$, and to the cosets ${{\bar{x}}}+N$ and $-{{\bar{x}}}+N$, which give in turn analogous subloops $M_{{{\bar{y}}}}$ and $M_{{{\bar{x}}}}$, as well. For instance, the switch $-1\leftrightarrow 1$ in both the addition tables $\varPhi _{\bar{x},{{\bar{x}}}}$ and $\varPhi _{-{{\bar{x}}},-{{\bar{x}}}}$, respectively $\varPhi _{\bar{y},{{\bar{y}}}}$ and $\varPhi _{-{{\bar{y}}},-{{\bar{y}}}}$ yields the following:

$$\begin{aligned} \begin{array}{c|c} \varPhi _{{{\bar{x}}},{{\bar{x}}}} &{} \varPhi _{\bar{x},-{{\bar{x}}}} \\ \hline \varPhi _{-{{\bar{x}}},{{\bar{x}}}} &{} \varPhi _{-{{\bar{x}}},-{{\bar{x}}}} \end{array}:\;\begin{array}{c|ccc|ccc} + &{} ({{\bar{x}}},-1)&{} ({{\bar{x}}},0)&{} ({{\bar{x}}},1) &{} (-{{\bar{x}}},-1)&{} (-\bar{x},0)&{} (-{{\bar{x}}},1)\\ \hline ({{\bar{x}}},-1)&{} (-{{\bar{x}}} ,1) &{} (-{{\bar{x}}} ,-1) &{} (-{{\bar{x}}} ,0) &{}(\varOmega ,-1) &{} (\varOmega ,1) &{} (\varOmega ,0) \\ ({{\bar{x}}},0)&{} (-{{\bar{x}}} ,-1) &{} (-{{\bar{x}}} ,0) &{} (-{{\bar{x}}} ,1) &{}(\varOmega ,1) &{} (\varOmega ,0) &{} (\varOmega ,-1)\\ ({{\bar{x}}},1)&{} (-{{\bar{x}}} ,0) &{} (-{{\bar{x}}} ,1) &{} (-{{\bar{x}}} ,-1) &{}(\varOmega ,0) &{} (\varOmega ,-1) &{} (\varOmega ,1)\\ \hline (-{{\bar{x}}},-1)&{} (\varOmega ,-1) &{} (\varOmega ,1) &{} (\varOmega ,0) &{}({{\bar{x}}} ,1) &{} ({{\bar{x}}} ,-1) &{} ({{\bar{x}}} ,0)\\ (-{{\bar{x}}},0)&{} (\varOmega ,1) &{} (\varOmega ,0) &{} (\varOmega ,-1) &{}({{\bar{x}}} ,-1) &{} ({{\bar{x}}} ,0) &{} ({{\bar{x}}} ,1)\\ (-{{\bar{x}}},1)&{} (\varOmega ,0) &{} (\varOmega ,-1) &{} (\varOmega ,1) &{}({{\bar{x}}} ,0) &{} ({{\bar{x}}} ,1) &{} ({{\bar{x}}} ,-1) \end{array}\;, \end{aligned}$$

respectively

$$\begin{aligned} \begin{array}{c|c} \varPhi _{{{\bar{y}}},{{\bar{y}}}} &{} \varPhi _{\bar{y},-{{\bar{y}}}} \\ \hline \varPhi _{-{{\bar{y}}},{{\bar{y}}}} &{} \varPhi _{-{{\bar{y}}},-{{\bar{y}}}} \end{array}:\;\begin{array}{c|ccc|ccc} + &{} ({{\bar{y}}},-1)&{} ({{\bar{y}}},0)&{} ({{\bar{y}}},1) &{} (-{{\bar{y}}},-1)&{} (-\bar{y},0)&{} (-{{\bar{y}}},1)\\ \hline ({{\bar{y}}},-1)&{} (-{{\bar{y}}} ,1) &{} (-{{\bar{y}}} ,-1) &{} (-{{\bar{y}}} ,0) &{}(\varOmega ,-1) &{} (\varOmega ,1) &{} (\varOmega ,0) \\ ({{\bar{y}}},0)&{} (-{{\bar{y}}} ,-1) &{} (-{{\bar{y}}} ,0) &{} (-{{\bar{y}}} ,1) &{}(\varOmega ,1) &{} (\varOmega ,0) &{} (\varOmega ,-1)\\ ({{\bar{y}}},1)&{} (-{{\bar{y}}} ,0) &{} (-{{\bar{y}}},1) &{} (-{{\bar{y}}} ,-1) &{}(\varOmega ,0) &{} (\varOmega ,-1) &{} (\varOmega ,1)\\ \hline (-{{\bar{y}}},-1)&{} (\varOmega ,-1) &{} (\varOmega ,1) &{} (\varOmega ,0) &{}({{\bar{y}}} ,1) &{} ({{\bar{y}}} ,-1) &{} ({{\bar{y}}} ,0)\\ (-{{\bar{y}}},0)&{} (\varOmega ,1) &{} (\varOmega ,0) &{} (\varOmega ,-1) &{}({{\bar{y}}},-1) &{} ({{\bar{y}}} ,0) &{} ({{\bar{y}}} ,1)\\ (-{{\bar{y}}},1)&{} (\varOmega ,0) &{} (\varOmega ,-1) &{} (\varOmega ,1) &{}({{\bar{y}}} ,0) &{} ({{\bar{y}}} ,1) &{} ({{\bar{y}}} ,-1) \end{array}\;. \end{aligned}$$

Note that, up to now, we have determined 34 triples of $\mathscr {S}_{{\mathscr {L}}}$.

Now we can freely choose a latin square on $N=\{-1,0,1\}$ for $\varPhi _{{{\bar{z}}},{{\bar{y}}}}$, for instance:

$$\begin{aligned} \varPhi _{{{\bar{z}}},{{\bar{y}}}}:\;\begin{array}{c|ccc} +&{}({{\bar{y}}},-1) &{} (\bar{y},0) &{} ({{\bar{y}}},1)\\ \hline ({{\bar{z}}},-1) &{} ({{\bar{x}}} ,1) &{} ({{\bar{x}}} ,-1) &{} ({{\bar{x}}} ,0) \\ ({{\bar{z}}},0) &{} ({{\bar{x}}} ,0) &{} ({{\bar{x}}} ,1) &{} ({{\bar{x}}} ,-1) \\ ({{\bar{z}}},1) &{} ({{\bar{x}}} ,-1) &{} ({{\bar{x}}} ,0) &{} ({{\bar{x}}} ,1) \end{array}\;, \end{aligned}$$

(5)

(note that the latin square chosen here does not correspond to a group, nor a loop, because it is not symmetric). Again, each of the 9 entries of this latin square will correspond to a triple of ${\mathscr {S}}_{{\mathscr {L}}}$, for instance $\{({{\bar{z}}},-1),(\bar{y},-1),(-{{\bar{x}}},-1)\}$. Thus, this choice of $\varPhi _{{{\bar{z}}},{{\bar{y}}}}$ determines uniquely the corresponding latin squares $\varPhi _{\bar{z},-{{\bar{x}}}}$ and $\varPhi _{{{\bar{y}}},-{{\bar{x}}}}$, according to Definition 4 (vi), that is, we have simply to re-write the 9 triples given in (5), in the following two latin squares:

$$\begin{aligned}&\varPhi _{{{\bar{z}}},-{{\bar{x}}}}:\;\begin{array}{c|ccc} +&{}(-{{\bar{x}}},-1) &{} (-{{\bar{x}}},0) &{} (-{{\bar{x}}},1)\\ \hline ({{\bar{z}}},-1) &{} (-{{\bar{y}}} ,1) &{} (-{{\bar{y}}} ,-1) &{} (-{{\bar{y}}} ,0) \\ ({{\bar{z}}},0) &{} (-{{\bar{y}}} ,0) &{} (-{{\bar{y}}} ,1) &{} (-{{\bar{y}}} ,-1) \\ ({{\bar{z}}},1) &{} (-{{\bar{y}}} ,-1) &{} (-{{\bar{y}}} ,0) &{} (-{{\bar{y}}} ,1) \end{array}\;,\\&\varPhi _{{{\bar{y}}},-{{\bar{x}}}}:\;\begin{array}{c|ccc} +&{}(-{{\bar{x}}},-1) &{} (-{{\bar{x}}},0) &{} (-{{\bar{x}}},1)\\ \hline ({{\bar{y}}},-1) &{} (-{{\bar{z}}} ,1) &{} (-{{\bar{z}}} ,0) &{} (-{{\bar{z}}} ,-1) \\ ({{\bar{y}}},0) &{} (-{{\bar{z}}} ,0) &{} (-{{\bar{z}}} ,-1) &{} (-{{\bar{z}}} ,1) \\ ({{\bar{y}}},1) &{} (-{{\bar{z}}} ,-1) &{} (-{{\bar{z}}} ,1) &{} (-{{\bar{z}}} ,0) \end{array}\;. \end{aligned}$$

Similarly, the reader can freely choose a latin square on $N=\{-1,0,1\}$ for $\varPhi _{{{\bar{z}}},-{{\bar{y}}}}$, $\varPhi _{{{\bar{y}}},- \bar{z}}$, $\varPhi _{-{{\bar{y}}},-{{\bar{z}}}}$ and, using Definition 4 (vi), re-write the latin squares $\varPhi _{-\bar{y},{{\bar{x}}}}$, $\varPhi _{{{\bar{z}}},{{\bar{x}}}}$, $\varPhi _{-{{\bar{z}}}, {{\bar{x}}}}$, $\varPhi _{{{\bar{y}}},{{\bar{x}}}}$, $\varPhi _{-{{\bar{z}}},-{{\bar{x}}}}$, $\varPhi _{-\bar{y},-{{\bar{x}}}}$. Note that, once we have chosen the four latin squares $\varPhi _{{{\bar{z}}},{{\bar{y}}}}$, $\varPhi _{{{\bar{z}}},-{{\bar{y}}}}$, $\varPhi _{{{\bar{y}}},-\bar{z}}$, $\varPhi _{-{{\bar{y}}},-{{\bar{z}}}}$, we obtain the remaining 36 of the 70 triples ${\mathrm {STS}}(21).$ The remaining latin squares $\varPhi$-s are already determined by Definition 4 (ii), that is, by the fact that the addition table of the loop ${{\mathscr {L}}}$ is symmetric.

4.2 Schreier Extensions

A particular class of loop extensions is introduced in [26], and called Schreier extension of the normal subgroup N by the loop K, by taking a group N, a loop K, and a map $T: K \rightarrow \hbox {Aut(N)}$ from K into the automorphism group of N with $T(1)=\hbox {Id}$, and a function $f:K \times K \rightarrow N$ with the property that $f(1,\tau )=f(\tau , 1)=1$. The multiplication is defined on $K \times N$ by

$$\begin{aligned} (\tau ,t) \circ (\sigma ,s)=(\tau \sigma , f(\tau , \sigma ) t^{T(\sigma )} s). \end{aligned}$$

According to Proposition 3.2. (iii) in [26], if N is central, then T is trivial.

Let now ${\mathscr {S}}$ be a Steiner triple system and let $\mathscr {L_S}$ be the corresponding Steiner loop of affine type and assume that $\mathscr {L_S}$ is the Schreier extension of the normal subgroup ${\mathscr {N}}$ by a Steiner loop $\mathscr {L_K}$ of affine type corresponding to a ${\mathrm {STS}}$ ${\mathscr {K}}$. Since a Steiner loop ${\mathscr {N}}$ of affine type is a group precisely if the corresponding ${\mathrm {STS}}$ is $\mathrm {AG}(n,3)$, the subloop ${\mathscr {N}}$ is the elementary abelian 3-group of order $3^n$.

Since the Steiner loop of affine type $\mathscr {L_S}$ is abelian, the normal subgroup ${\mathscr {N}}$ is central (hence the map T is trivial), $\mathscr {L_S}$ is realized on $\mathscr {L_K} \times {\mathscr {N}}$ by the multiplication

$$\begin{aligned} (\kappa _1,n_1) \circ (\kappa _2,n_2)=\big (\kappa _1 + \kappa _2, n_1 + n_2 + f(\kappa _1,\kappa _2)\big ), \end{aligned}$$

(6)

where $f: \mathscr {L_K} \times \mathscr {L_K} \rightarrow {\mathscr {N}}$ is a function with the property $f(\kappa _1, \kappa _2)=f(\kappa _2, \kappa _1)$ for all $\kappa _1, \kappa _2 \in \mathscr {L_K}$ satisfying $f(\varOmega ,\kappa _2)=f(\kappa _1,\varOmega )=0$. Note that here $\varPhi _{\kappa _1,\kappa _2}(n_1,n_2)=n_1 + n_2 + f(\kappa _1,\kappa _2)$. Note that the smallest proper HTS has to be the Schreier extension of $\mathrm {AG}(2,3)$ by $\mathrm {AG}(2,3)$.

4.3 Affine Hyperplanes

Now we show that the opposite case to that of the Example 4.1, that is, the case where the quotient loop Q is a group of order 3, occurs when the normal subloop N is an affine hyperplane, as defined in [13], p. 253:

An affine hyperplane of ${\mathscr {S}}$ is a subsystem ${\mathscr {S}}_0$, such that for any $x\notin {\mathscr {S}}_0$ the set ${\mathscr {S}}_1$ of triples through x which do not intersect ${\mathscr {S}}_0$ turns out to be a second subsystem. If this is the case, the set ${\mathscr {S}}_{-1}={\mathscr {S}} \setminus \{ {\mathscr {S}}_0 \cup {\mathscr {S}}_1\}$ is a third subsystem. In other words, ${\mathscr {S}}_0$ is an affine hyperplane of ${\mathscr {S}}$ if, and only if, ${\mathscr {S}}$ is the union of three pairwise disjoint subsystems

$$\begin{aligned}{\mathscr {S}}= {\mathscr {S}}_{-1} \cup {\mathscr {S}}_0 \cup {\mathscr {S}}_1,\end{aligned}$$

of the same cardinality $w=\frac{n}{3}$, hence it is necessary that $n\equiv 3 \ (\mathrm {mod}\ 6)$ and $w\equiv 1,3 \ (\mathrm {mod}\ 6)$.

Theorem 10

${\mathscr {S}}_0$ is an affine hyperplane of ${\mathscr {S}}$ containing $\varOmega$, if and only if ${\mathscr {L}}_{{\mathscr {S}}_0}$ is a normal subloop of index 3 in $\mathscr {L_S}$.

Proof

If ${\mathscr {S}}_0$ is an affine hyperplane, then ${\mathscr {S}}$ is the union ${\mathscr {S}}={\mathscr {S}}_{-1} \cup {\mathscr {S}}_0 \cup {\mathscr {S}}_1$ of three pairwise disjoint subsystems of the same cardinality. Since $\mathscr {L_S}$ is a commutative loop, in order to prove that ${\mathscr {S}}_0$ is normal, it is sufficient to show that $(a+b)+{{\mathscr {S}}_0}=a+(b+{{\mathscr {S}}_0})$ for any $a,b\in {\mathscr {S}}$.

1) If $x\in {{\mathscr {S}}_0}$, then $-x\in {{\mathscr {S}}_{0}}$, as well, because ${{\mathscr {S}}_0}$ is a subsystem containing $\varOmega$. If $x\in {{\mathscr {S}}_i}$, then $-x\in {{\mathscr {S}}_{-i}}$, for $i\ne 0$. This follows from the definition of affine hyperplane, because $\{x,\varOmega ,-x\}$ is a triple.

2) Let both x and y belong to ${{\mathscr {S}}_i}$, thus $x+y=-z$ where $\{x,y,z\}\subset {{\mathscr {S}}_{i}}$ is a triple. Hence $x+y$ belongs to ${{\mathscr {S}}_{-i}}$, that is $x+{{\mathscr {S}}_{i}}={{\mathscr {S}}_{-i}}$.

3) If $x\in {{\mathscr {S}}_i}$ and $y\in {{\mathscr {S}}_j}$ with $i\ne j$, then the third element z in the triple $\{x,y,z\}$ belongs to the subsystem ${{\mathscr {S}}_k}$ with $i\ne k\ne j$, that is, $x+{{\mathscr {S}}_{j}}={{\mathscr {S}}_{-k}}$.

It follows that $(a+b)+{{\mathscr {S}}_0}=a+(b+{{\mathscr {S}}_0})$ for any $a,b\in {\mathscr {S}}$, that is, ${\mathscr {L}}_{{\mathscr {S}}_0}$ is normal.

Conversely, if ${\mathscr {N}}$ is a normal subloop of index 3 in $\mathscr {L_S}$, then $\mathscr {L_S}$ consists of three left cosets ${\mathscr {N}}$, $x+{\mathscr {N}}$, $-x+{\mathscr {N}}$, where $x \in \mathscr {L_S} \setminus {\mathscr {N}}$, and ${\mathscr {S}}_{\mathscr {N}}$ is a subsystem of ${\mathscr {S}}$ containing $\varOmega$. The Steiner triple system $\mathscr {S_L}$ consists of the following points:

• (i) the points of ${\mathscr {S}}_{\mathscr {N}}$, which form the trivial coset ${\mathscr {N}}$

• (ii) the third points of the triples through x and the points $a \in {\mathscr {S}}_{\mathscr {N}}$, which form the coset $-x + {\mathscr {N}}$,

• (iii) the third points of the triples through $-x$ and the points $a \in {\mathscr {S}}_{\mathscr {N}}$, which form the coset $x + {\mathscr {N}}$.

This proves that ${\mathscr {S}}_{\mathscr {N}}$ is an affine hyperplane of ${\mathscr {S}}$ containing $\varOmega$, because the cosets of a normal subloop are subsystems according to Theorem 1 (ii). $\square$

Corollary 3

If $\mathscr {L_S}$ is simple, then ${\mathscr {S}}$ does not contain an affine hyperplane.

If $\mathscr {L_S}$ is not simple, and N is a proper normal subloop of $\mathscr {L_S}$, then N is an affine hyperplane of the subloop M generated by N and x, for any $x\in {\mathscr {L}}\setminus N$.

Proof

The first assertion is trivial, and the second follows from the fact that M turns out to be the union of N, $x+N$ and $-x+N$. $\square$

4.4 Quasidirect Sums

Given two ${\mathrm {STS}}$’s ${\mathscr {R}}$ and ${\mathscr {T}}$, we can build in a standard way an ${\mathrm {STS}}$ ${\mathscr {S}}$, that we call the quasidirect sum of ${\mathscr {R}}$ by ${\mathscr {T}}$, in the following way: let ${\mathscr {R}}\longrightarrow {\text {Top}}({\mathscr {T}})$, $\bar{x}\mapsto \psi _{{{\bar{x}}}}$, be a map from ${\mathscr {R}}$ to the group of isotopisms of ${\mathscr {T}}$

$$\begin{aligned}&\{({{\bar{x}}}, x'),({{\bar{y}}}, y'),({{\bar{z}}}, z')\} \text{ is } \text{ a } \text{ triple, } \text{ if } \text{ and } \text{ only } \text{ if, } \{{{\bar{x}}}, {{\bar{y}}}, {{\bar{z}}}\} \hbox { is a triple of }{\mathscr {R}}, \hbox { and}\\&\Big \{\psi _{{{\bar{x}}}}(x'),\psi _{{{\bar{y}}}}(y'),\psi _{\bar{z}}(z')\Big \}\hbox { is a triple of } {\mathscr {T}}. \end{aligned}$$

Here $\varPhi _{{{\bar{x}}},{{\bar{y}}}}(x',y')=-\psi _{-({{\bar{x}}}+\bar{y})}^{-1}\Big (-\big (\psi _{{{\bar{x}}}}(x')+\psi _{{{\bar{y}}}}(y')\big )\Big )$. In the case where $\psi _{{{\bar{x}}}}=\mathrm {id}$ for all ${{\bar{x}}}\in {\mathscr {R}}$, we obtain the direct sum of ${\mathscr {R}}$ and ${\mathscr {T}}$.

By Theorem 9, our investigation is confined to simple Steiner loops of affine type.

5 Simple Steiner Loops of Affine Type

In this final part of the paper we describe the situation in the case when ${\mathscr {S}}$ is a simple STS, that is, the case where ${\mathscr {L}}_{\mathscr {S}}$ is a simple loop. We recall that in this case, the group ${\mathrm {Mult}}(\mathscr {L_S})$ is primitive. Moreover, we recall that this group plays a fundamental role, since that the orbit-map ${\mathrm {Mult}}({\mathscr {L}}_{\mathscr {S}})\longrightarrow {\mathscr {L}}_{\mathscr {S}}$ defined by

$$\begin{aligned} \lambda _x\mapsto x=\varOmega ^{\lambda _x} \end{aligned}$$

is a loop homomorphism whose kernel is the stabilizer of $\varOmega$.

Write $\sigma _x=\lambda _x(\varOmega ,x,-x)^{-1}$ and denote by $\varSigma$ the group generated by the set $\{\sigma _x: x\in {\mathscr {L}}_{\mathscr {S}} \}$ of permutations, thus each $\sigma _x$ fixes exactly the three elements $\varOmega$, x and $-x$, hence $\varSigma$ is contained in the stabilizer of $\varOmega$. By Theorem 3, the group ${\mathrm {Mult}}(\mathscr {L_S})$ is contained in the alternating group $A_n$, thus $\varSigma$ is contained in a subgroup isomorphic to the alternating group $A_{n-1}$.

In [30] it is proved that if the order of any product of two different translations of an ${\mathrm {STS}}$ of size $n >3$ is odd, then the multiplication group ${\mathrm {Mult}}({{\mathscr {L}}})$ of the corresponding totally symmetric Steiner loop ${{\mathscr {L}}}$ given in Remark 3 of order $n+1$ contains the alternating group of order $n+1$. For a simple Steiner loop of affine type of order n to obtain that the multiplication group ${\mathrm {Mult}}(\mathscr {L_S})$ contains the group $A_n$ it is enough to prove that the group ${\mathrm {Mult}}(\mathscr {L_S})$ contains one of the permutations $\sigma _x$, with $x\in {\mathscr {L}}_{\mathscr {S}}$.

Theorem 11

Let ${\mathscr {S}}$ be a simple Steiner triple system with $n>3$ points and $\mathscr {L_S}$ the corresponding Steiner loop of affine type.

• (i) The group ${\mathrm {Mult}}(\mathscr {L_S})$ of $\mathscr {L_S}$ is isomorphic to $A_n,$ if and only if ${\mathrm {Mult}}(\mathscr {L_S})$ contains one of the permutations $\sigma _x$.

• (ii) If the order of one of the permutations $\sigma _x$ is not divisible by 3, then the group ${\mathrm {Mult}}(\mathscr {L_S})$ of $\mathscr {L_S}$ is $A_n$.

Proof

If one has $\sigma _x\in {\mathrm {Mult}}(\mathscr {L_S})$, then the permutation $\sigma _x^{-1} \lambda _x=(\varOmega ,x,-x)$ is a 3-cycle in the primitive subgroup ${\mathrm {Mult}}(\mathscr {L_S})$ of $A_n$. By Jordan’s theorem on permutations (see also Exercise 5.6.2 in [4]), ${\mathrm {Mult}}(\mathscr {L_S})=A_n$. This proves assertion (i).

(ii) If the order of the permutation $\sigma _x$ is $3 k+2$ for some $x \in \mathscr {L_S}$, then one has $\sigma _x=\lambda _x^{3k+3}$. If the order of the permutation $\sigma _x$ is $3 k+1$ for some $x \in \mathscr {L_S}$, then one has $\sigma _x=\lambda _x^{3(2k+1)}$. Hence $\sigma _x\in {\mathrm {Mult}}(\mathscr {L_S})$ and we are done by part (i). $\square$

Remark 12

If $n=9,$ then the group ${\mathrm {Mult}}(\mathscr {L_S})$ is the elementary abelian 3-group with two generators, and $\sigma _x$ is the product of two 3-cycles (see Theorem 6). In this case, a direct computation shows that the group $\varSigma$ is the alternating group $A_8$.

Consider now the Steiner loop $\mathscr {L_S}$ of affine type corresponding to the Steiner triple system on 13 points $S_2$ defined in 2.2 in [23], p. 153, with $\varOmega =13$. With the left translations

$$\begin{aligned} \lambda _5=(\varOmega ,5,7)(3,6,10)(9,11,12)(1,8)(2,4) \end{aligned}$$

and

$$\begin{aligned}\lambda _{-5}=(\varOmega ,7,5)(2,10,11)(6,9,8)(1,3)(4,12) \end{aligned}$$

one has

$$\begin{aligned} \sigma _5=(3,6,10)(9,11,12)(1,8)(2,4)=\lambda _{-5} \lambda _5^{-2} \lambda _{-5}^{-1} \lambda _5^{-1} (\lambda _5^{-1} \lambda _{-5})^2 \lambda _{-5} \lambda _5 \lambda _{-5}^2 \end{aligned}$$

and therefore $\sigma _5 \in \langle \lambda _5, \lambda _{-5} \rangle \cong C_3 \times A_{10}.$

It remains an open problem whether any permutation $\sigma _x$ of a simple Steiner loop of affine type can be written as a product of the only permutations $\lambda _x$ and $\lambda _{-x}$.

Theorem 12

If ${\mathscr {S}}$ is a simple Steiner triple system of order n containing a Veblen point, then $\mathrm {Mult}(\mathscr {\mathscr {L_S}})=A_n$, and $\mathscr {\mathscr {L_S}}=A_n/A_{n-1}$.

Proof

The claim follows from Jordan’s theorem on the symmetric group $S_n$, because, by Theorem 4, $\lambda _x^2$ is a 3-cycle in the primitive group $\mathrm {Mult}(\mathscr {\mathscr {L_S}})$. $\square$

Corollary 4

If ${\mathscr {R}}\le {\mathscr {S}}$ is a Steiner triple subsystem of order 7, then the subloop $\mathscr {\mathscr {L_R}}$ of $\mathscr {\mathscr {L_S}}$ has the alternating group $A_7$ as its multiplication group.

Proposition 4

Let ${\mathscr {S}}$ be a Steiner triple system of order $n=13$. Then the group ${\mathrm {Mult}}(\mathscr {L_S})$ is the alternating group $A_{13}$.

Proof

We denote by $S_1$ and $S_2$ the two non-isomorphic ${\mathrm {STS}}(13)$ as they are defined in [23], p. 152-153. Taking the left translation $\lambda _1=(0,1,4)(2,7,3,10,6)(5,8,11,9,12) \in S_1$ and the left translation $\lambda _2=(0,1,4)(2,12,5,10,6)(3,8,11,9,7) \in S_2$, in both cases, the fifth power of such an element is a 3-cycle. Since ${\mathrm {Mult}}(\mathscr {L_S})$ is a primitive subgroup of $A_{13}$, then ${\mathrm {Mult}}(\mathscr {L_S})=A_{13}$ by Jordan’s theorem. $\square$

Proposition 5

Let ${\mathscr {S}}$ be a Steiner triple system of prime power cardinality $n\ne {\frac{q^a-1}{q-1}}$, for any prime power q. If ${\mathrm {Mult}}(\mathscr {L_S})$ is simple, then the group ${\mathrm {Mult}}(\mathscr {L_S})$ is the alternating group $A_{n}$.

Proof

This follows from a celebrated theorem by Guralnik ([17], Thm. 1). $\square$

Remark 13

The condition on n in Proposition 5 is fulfilled for instance, if

$$\begin{aligned}n\in \{19,25,37,43,49,61,67,73\}.\end{aligned}$$