Abstract
A new non-linear variant of a quantitative extension of the uniform boundedness principle is used to show sharpness of error bounds for univariate approximation by sums of sigmoid and ReLU functions. Single hidden layer feedforward neural networks with one input node perform such operations. Errors of best approximation can be expressed using moduli of smoothness of the function to be approximated (i.e., to be learned). In this context, the quantitative extension of the uniform boundedness principle indeed allows to construct counterexamples that show approximation rates to be best possible. Approximation errors do not belong to the little-o class of given bounds. By choosing piecewise linear activation functions, the discussed problem becomes free knot spline approximation. Results of the present paper also hold for non-polynomial (and not piecewise defined) activation functions like inverse tangent. Based on Vapnik–Chervonenkis dimension, first results are shown for the logistic function.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
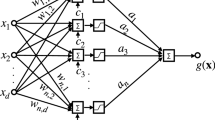
A feedforward neural network with an activation function \(\sigma \), one input, one output node, and one hidden layer of n neurons as shown in Fig. 1 implements an univariate real function g of type
with weights \(a_k, b_k, c_k\in \mathbb {R}\).
The given paper does not deal with multivariate approximation. But some results can be extended to multiple input nodes, see Sect. 5. Often, activation functions are sigmoid. A sigmoid function \(\sigma : \mathbb {R}\rightarrow \mathbb {R}\) is a measurable function with
Sometimes also monotonicity, boundedness, continuity, or even differentiability may be prescribed. Deviant definitions are based on convexity and concavity. In case of differentiability, functions have a bell-shaped first derivative. Throughout this paper, approximation properties of following sigmoid functions are discussed:
Although not a sigmoid function, the ReLU function (Rectified Linear Unit)
is often used as activation function for deep neural networks due to its computational simplicity. The Exponential Linear Unit (ELU) activation function
with parameter \(\alpha \ne 0\) is a smoother variant of ReLU for \(\alpha =1\).
Qualitative approximation properties of neural networks have been studied extensively. For example, it is possible to choose an infinitely often differentiable, almost monotonous, sigmoid activation function \(\sigma \) such that for each continuous function f, each compact interval and each bound \(\varepsilon >0\) weights \(a_0, a_1, b_1, c_1\in \mathbb {R}\) exist such that f can be approximated uniformly by \(a_0+ a_1 \sigma (b_1 x+c_1)\) on the interval within bound \(\varepsilon \), see [27] and literature cited there. In this sense, a neural network with only one hidden neuron is capable of approximating every continuous function. However, activation functions typically are chosen fixed when applying neural networks to solve application problems. They do not depend on the unknown function to be approximated. In the late 1980s it was already known that, by increasing the number of neurons, all continuous functions can be approximated arbitrarily well in the sup-norm on a compact set with each non-constant bounded monotonically increasing and continuous activation function (universal approximation or density property, see proof of Funahashi in [22]). For each continuous sigmoid activation function (that does not have to be monotone), the universal approximation property was proved by Cybenko in [14] on the unit cube. The result was extended to bounded sigmoid activation functions by Jones [31] without requiring continuity or monotonicity. For monotone sigmoid (and not necessarily continuous) activation functions, Hornik, Stinchcombe and White [29] extended the universal approximation property to the approximation of measurable functions. Hornik [28] proved density in \(L^p\)-spaces for any non-constant bounded and continuous activation functions. A rather general theorem is proved in [35]. Leshno et al. showed for any continuous activation function \(\sigma \) that the universal approximation property is equivalent to the fact that \(\sigma \) is not an algebraic polynomial.
There are many other density results, e.g., cf. [7, 12]. Literature overviews can be found in [42] and [44].
To approximate or interpolate a given but unknown function f, constants \(a_k\), \(b_k\), and \(c_k\) typically are obtained by learning based on sampled function values of f. The underlying optimization algorithm (like gradient descent with back propagation) might get stuck in a local but not in a global minimum. Thus, it might not find optimal constants to approximate f best possible. This paper does not focus on learning but on general approximation properties of function spaces
Thus, we discuss functions on the interval [0, 1]. Without loss of generality, it is used instead of an arbitrary compact interval [a, b]. In some papers, an additional constant function \(a_0\) is allowed as summand in the definition of \(\varPhi _{n,\sigma }\). Please note that \(a_k \sigma (0\cdot x + b_k)\) already is a constant and that the definitions do not differ significantly.
For \(f\in B[0, 1]\), the set of bounded real-valued functions on the interval [0, 1], let \(\Vert f\Vert _{B[0, 1]} := \sup \{ |f(x)| : x\in [0, 1]\}\). By C[0, 1] we denote the Banach space of continuous functions on [0, 1] equipped with norm \(\Vert f\Vert _{C[0, 1]}:= \Vert f\Vert _{B[0, 1]}\). For Banach spaces \(L^p[0, 1]\), \(1\le p<\infty \), of measurable functions we denote the norm by \(\Vert f\Vert _{L^p[0, 1]}:=(\int _0^1 |f(x)|^p\, dx)^{1/p}\). To avoid case differentiation, we set \(X^\infty [0, 1]:=C[0, 1]\) with \(\Vert \cdot \Vert _{X^\infty [0, 1]}:=\Vert \cdot \Vert _{B[0, 1]}\), and \(X^p[0, 1]:=L^p[0, 1]\) with \(\Vert f\Vert _{X^p[0, 1]}:=\Vert f\Vert _{L^p[0, 1]}\), \(1\le p<\infty \).
The error of best approximation \(E(\varPhi _{n,\sigma }, f)_p\), \(1\le p\le \infty \), is defined via
We use the abbreviation \(E(\varPhi _{n,\sigma }, f):=E(\varPhi _{n,\sigma }, f)_\infty \) for \(p=\infty \).
A trained network cannot approximate a function better than the error of best approximation. Therefore, it is an important measure of what can and what cannot be done with such a network.
The error of best approximation depends on the smoothness of f that is measured in terms of moduli of smoothness (or moduli of continuity). In contrast to using derivatives, first and higher differences of f obviously always exist. By applying a norm to such differences, moduli of smoothness measure a “degree of continuity” of f.
For a natural number \(r \in \mathbb {N}=\{1, 2,\dots \}\), the \(r\hbox {th}\) difference of \(f\in B[0, 1]\) at point \(x\in [0, 1-rh]\) with step size \(h>0\) is defined as
The \(r\hbox {th}\) uniform modulus of smoothness is the smallest upper bound of the absolute values of rth differences:
With respect to \(L^p\) spaces, \(1\le p<\infty \), let
Obviously, \( \omega _r (f, \delta )_p \le 2^r \Vert f\Vert _{X^p[0,1]}\), and for r-times continuously differentiable functions f, there holds (cf. [16, p. 46])
Barron applied Fourier methods in [4], cf. [36], to establish rates of convergence in an \(L^2\)-norm, i.e., he estimated the error \(E(\varPhi _{n,\sigma }, f)_2\) with respect to n for \(n\rightarrow \infty \). Makovoz [40] analyzed rates for uniform convergence. With respect to moduli of smoothness, Debao [15] proved a direct estimate that is here presented in a version of the textbook [9, p. 172ff]. This estimate is independent of the choice of a bounded, sigmoid function \(\sigma \). Doctoral thesis [10], cf. [11], provides an overview of such direct estimates in Section 1.3.
According to Debao,
holds for each \(f\in C[0, 1]\). This is the prototype estimate for which sharpness is discussed in this paper. In fact, the result of Debao for \(E(\varPhi _{n,\sigma }, f)\) allows to additionally restrict weights such that \(b_k\in \mathbb {N}\) and \(c_k\in \mathbb {Z}\). The estimate has to hold true even for \(\sigma \) being a discontinuous Heaviside function. That is the reason why one can only expect an estimate in terms of a first order modulus of smoothness. If the order of approximation of a continuous function f by such piecewise constant functions is o(1/n) then f itself is a constant, see [16, p. 366]. In fact, the idea behind Debao’s proof is that sigmoid functions can be asymptotically seen as Heaviside functions. One gets arbitrary step functions to approximate f by superposition of Heaviside functions. For quasi-interpolation operators based on the logistic activation function \(\sigma _l\), Chen and Zhao proved similar estimates in [8] (cf. [2, 3] for hyperbolic tangent). However, they only reach a convergence order of \(O\left( 1/n^\alpha \right) \) for \(\alpha <1\). With respect to the error of best approximation, they prove
by estimating with a polynomial of best approximation. Due to the different technique, constants are larger than in error bound (2).
If one takes additional properties of \(\sigma \) into account, higher convergence rates are possible. Continuous sigmoid cut function \(\sigma _c\) and ReLU function \(\sigma _r\) lead to spaces \(\varPhi _{n,\sigma _{c,r}}\) of continuous, piecewise linear functions. They consist of free knot spline functions of polynomial degree at most one with at most 2n or n knots, cf. [16, Section 12.8]. Spaces \(\varPhi _{n,\sigma _{c,r}}\) include all continuous spline functions g on [0, 1] with polynomial degree at most one that have at most \(n-1\) simple knots. We show \(g\in \varPhi _{n,\sigma _c}\) for such a spline g with equidistant knots \(x_k=\frac{k}{n-1}\), \(0\le k \le n-1\), to obtain an error bound for \(n\ge 2\):
One can also represent g by ReLU functions, i.e., \(g\in \varPhi _{n,\sigma _r}\): With (\(1\le k\le n-1\))
we get
Thus, we can apply the larger error bound [16, p. 225, Theorem 7.3 for \(\delta =(n-1)^{-1}\)] for fixed simple knot spline approximation with functions g in terms of a second modulus to improve convergence rates up to \(O\left( 1/n^2\right) \): For \(f\in X^p[0, 1]\), \(1\le p\le \infty \), and \(n\ge 2\)
Section 2 deals with even higher order direct estimates. Similarly to (3), not only sup-norm bound (2) but also an \(L^p\)-bound, \(1\le p< \infty \), for approximation with Heaviside function \(\sigma _h\) can be obtained from the corresponding larger bound of fixed simple knot spline approximation. Each \(L^p[0, 1]\)-function that is constant between knots \(x_k=\frac{k}{n}\), \(0\le k\le n\), can be written as a linear combination of n translated Heaviside functions. Thus, [16, p. 225, Theorem 7.3 for \(\delta =1/n\)]) yields for \(n\in \mathbb {N}\)
Lower error bounds are much harder to obtain than upper bounds, cf. [42] for some results with regard to multilayer feedforward perceptron networks. Often, lower bounds are given using a (non-linear) Kolmogorov n-width \(W_n\) (cf. [41, 45]),
for a suitable function space X (of functions with certain smoothness) and norm \(\Vert \cdot \Vert \). Thus, parameters \(b_k\) and \(c_k\) cannot be chosen individually for each function \(f\in X\). Higher rates of convergence might occur, if that becomes possible.
There are three somewhat different types of sharpness results that might be able to show that left sides of Eqs. (2), (3), (4) or (9) and (16) in Sect. 2 do not converge faster to zero than the right sides.
The most far reaching results would provide lower estimates of errors of best approximation in which the lower bound is a modulus of smoothness. In connection with direct upper bounds in terms of the same moduli, this would establish theorems similar to the equivalence between moduli of smoothness and K-functionals (cf. [16, theorem of Johnen, p. 177], [30]) in which the error of best approximation replaces the K-functional. Let \(\sigma \) be r-times continuously differentiable like \(\sigma _a\) or \(\sigma _l\). Then for \(f\in C[0, 1]\), a standard estimate based on (1) is
It is unlikely that one can somehow bound \(\Vert g^{(r)}\Vert _{B[0, 1]}\) by \(C\Vert f\Vert _{B[0, 1]}\) to get
However, there are different attempts to prove such theorems in [51, Remark 1, p. 620], [52, p. 101] and [53, p. 451]. But the proofs contain difficulties and results are wrong, see [24]. In fact, we prove with Lemma 1 in Sect. 2 that (5) is not valid even if constant C is allowed to depend on f.
A second class of sharpness results consists of inverse and equivalence theorems. Inverse theorems provide upper bounds for moduli of smoothness in terms of weighted sums of approximation errors. For pseudo-interpolation operators based on piecewise linear activation functions and B-splines (but not for errors of best approximation), [37] deals with an inverse estimate based on Bernstein polynomials.
An idea that does not work is to adapt the inverse theorem for best trigonometric approximation [16, p. 208]. Without considering effects related to interval endpoints in algebraic approximation one gets a (wrong) candidate inequality
By choosing \(f\equiv \sigma \) for a non-polynomial, rth times continuously differentiable activation function \(\sigma \), the modulus on the left side of the estimate behaves like \(n^{-r}\). But the errors of best approximation on the right side are zero. At least this can be cured by the additional expression \(\frac{C_r}{n^r} \Vert f\Vert _{B[0,1]}\).
Typically, the proof of an inverse theorem is based on a Bernstein-type inequality that is difficult to formulate for function spaces discussed here. The Bernstein inequality provides a bound for derivatives. If \(p_n\) is a trigonometric polynomial of degree at most n then \(\Vert p_n'\Vert _{B[0,2\pi ]}\le n \Vert p_n\Vert _{B[0,2\pi ]}\), cf. [16, p. 97]. The problem here is that differentiating \(a\sigma (bx+c)\) leads to a factor b that cannot be bounded easily. Indeed, we show for a large class of activation functions that (6) can’t hold, see (14). As noticed in [24], the inverse estimates of type (6) proposed in [51] and [53] are wrong.
Similar to inverse theorems, equivalence theorems (like (7) below) describe equivalent behavior of expressions of moduli of smoothness and expressions of approximation errors. Both inverse and equivalence theorems allow to determine smoothness properties, typically membership to Lipschitz classes or Besov spaces, from convergence rates. Such a property is proved in [13] for max-product neural network operators activated by sigmoidal functions. The relationship between order of convergence of best approximation and Besov spaces is well understood for approximation with free knot spline functions and rational functions, see [16, Section 12.8], cf. [34]. The Heaviside activation function leads to free knot splines of polynomial degree 0, i.e., less than \(r=1\), cut and ReLU function correspond with polynomial degree less than \(r=2\). For \(\sigma \) being one of these functions, and for \(0<\alpha <r\), \(f\in L^p[0, 1]\), \(1\le p<\infty \) (\(p=\infty \) is excluded), \(k:=1\) if \(\alpha <1\) and \(k:=2\) otherwise, \(q:=\frac{1}{\alpha +1/p}\), there holds the equivalence (see [17])
However, such equivalence theorems might not be suited to obtain little-o results: Assume that \(E(\varPhi _{n,\sigma }, f)_p = \frac{1}{n^\beta (\ln (n+1))^{1/q}} =o\left( \frac{1}{n^\beta }\right) \), then the right side of (7) converges exactly for the same smoothness parameters \(0< \alpha < \beta \) than if \(E(\varPhi _{n,\sigma }, f)_p = \frac{1}{n^\beta } \ne o\left( \frac{1}{n^\beta }\right) \).
The third type of sharpness results is based on counterexamples. The present paper follows this approach to deal with little-o effects. Without further restrictions, counterexamples show that convergence orders can not be faster than stated in terms of moduli of smoothness in (2), (3), (4) and the estimates in following Sect. 2 for some activation functions. To obtain such counterexamples, a general theorem is introduced in Sect. 3. It is applied to neural network approximation in Sect. 4.
Unlike the counterexamples in this paper, counterexamples that do not focus on moduli of smoothness were recently introduced in Almira et al. [1] for continuous piecewise polynomial activation functions \(\sigma \) with finitely many pieces (cf. Corollary 1 below) as well as for rational activation functions (that we also briefly discuss in Sect. 4): Given an arbitrary sequence of positive real numbers \((\varepsilon _n)_{n=1}^\infty \) with \(\lim _{n\rightarrow \infty } \varepsilon _n=0\), a continuous counterexample f is constructed such that \(E(\varPhi _{n,\sigma }, f) \ge \varepsilon _n\) for all \(n\in \mathbb {N}\).
2 Higher Order Estimates
In this section, two upper bounds in terms of higher order moduli of smoothness are derived from known results. Proofs are given for the sake of completeness. If, e.g., \(\sigma \) is arbitrarily often differentiable on some open interval such that \(\sigma \) is no polynomial on that interval then it is known that \(E(\varPhi _{n,\sigma }, p_{n-1})=0\) for all polynomials \(p_{n-1}\) of degree at most \(n-1\), i.e., \( p_{n-1}\in \varPi ^{n}:=\{ d_{n-1} x^{n-1}+d_{n-2}x^{n-2}+\dots +d_0: d_0,\dots ,d_{n-1}\in \mathbb {R}\}, \) see [42, p. 157] and (15) below. Thus, upper bounds for polynomial approximation can be used as upper bounds for neural network approximation in connection with certain activation functions. Due to a corollary of the classical theorem of Jackson, the best approximation to \(f\in X^p[0, 1]\), \(1\le p\le \infty \), by algebraic polynomials is bounded by the \(r\hbox {th}\) modulus of smoothness. For \(n\ge r\), we use Theorem 6.3 in [16, p. 220] that is stated for the interval \([-1, 1]\). However, by applying an affine transformation of [0, 1] to \([-1, 1]\), we see that there exists a constant C independently of f and n such that
Ritter proved an estimate in terms of a first order modulus of smoothness for approximation with nearly exponential activation functions in [43]. Due to (8), Ritter’s proof can be extended in a straightforward manner to higher order moduli. The special case of estimating by a second order modulus is discussed in [51].
According to [43], a function \(\sigma :\mathbb {R}\rightarrow \mathbb {R}\) is called “nearly exponential” iff for each \(\varepsilon >0\) there exist real numbers a, b, c, and d such that for all \(x\in (-\infty , 0]\)
The logistic function fulfills this condition with \(a=1/\sigma _l(c)\), \(b=1\), \(d=0\), and \(c<\ln (\varepsilon )\) such that for \(x\le 0\) there is \(0<e^x\le 1\) and
Theorem 1
Let \(\sigma :\mathbb {R}\rightarrow \mathbb {R}\) be a nearly exponential function, \(f\in X^p[0,1]\), \(1\le p\le \infty \), and \(r\in \mathbb {N}\). Then, independently of \(n\ge \max \{r, 2\}\) (or \(n>r\)) and f, a constant \(C_r\) exists such that
Proof
Let \(\varepsilon >0\). Due to (8), there exists a polynomial \(p_n\in \varPi ^{n+1}\) of degree at most n such that
The Jackson estimate can be used to extend the proof given for \(r=1\) in [43]: Auxiliary functions (\(\alpha >0\))
converge to x pointwise for \(\alpha \rightarrow \infty \) due to the theorem of L’Hospital. Since \(\frac{d}{dx}(h_\alpha (x)-x)=0 \Longleftrightarrow e^{-x/\alpha }=1 \Longleftrightarrow x=0\), the maximum of \(|h_\alpha (x)-x|\) on [0, 1] is obtained at the endpoints 0 or 1, and convergence of \(h_\alpha (x)\) to x is uniform on [0, 1] for \(\alpha \rightarrow \infty \). Thus \(\lim _{\alpha \rightarrow \infty } p_n( h_\alpha (x)) = p_n(x)\) uniformly on [0, 1], and for the given \(\varepsilon \) we can choose \(\alpha \) large enough to get
Therefore, function f is approximated by an exponential sum of type
within the bound \(C \omega _r\left( f,n^{-1}\right) + 2\varepsilon \). It remains to approximate the exponential sum by utilizing that \(\sigma \) is nearly exponential. For \(1\le k\le n\), \(\gamma _k\ne 0\), there exist parameters \(a_k, b_k, c_k, d_k\) such that
for all \(x\in [0, 1]\). Also because \(\sigma \) is nearly exponential, there exists \(c\in \mathbb {R}\) with \(\sigma (c)\ne 0\). Thus, a constant \(\gamma \) can be expressed via \(\frac{\gamma }{\sigma (c)} \sigma (0x+c)\). Therefore, there exists a function \(g_{n,\varepsilon }\in \varPhi _{n+1, \sigma }\),
such that
By combining (10), (11) and (12), we get
Since \(\varepsilon \) can be chosen arbitrarily, we obtain for \(n\ge 2\)
\(\square \)
By choosing \(a=1/\alpha \), \(b=1\), \(c=0\), and \(d=1\), the ELU activation function \(\sigma _e(x)\) obviously fulfills the condition to be nearly exponential. But its definition for \(x\ge 0\) plays no role.
Given a nearly exponential activation function, a lower bound (5) or an inverse estimate (6) with a constant \(C_r\), independent of f, is not valid, see [24] for \(r=2\). Such inverse estimates were proposed in [51] and [53]. Functions \(f_n(x):=\exp (-nx)\) fulfill \(\Vert f_n\Vert _{B[0,1]}=1\) and
For \(x\le 0\), one can uniformly approximate \(e^x\) arbitrarily well by assigning values to a, b, c and d in \(a\sigma (bx+c)+d\). Thus, each function \(f_n(x)\) can be approximated uniformly by \(a \sigma (-nb x+c)+d\) on [0, 1] such that \(E(\varPhi _{k,\sigma }, f_n)=0\), \(k>1\). Using \(f_n\) with formula (6) implies
which is obviously wrong for \(n\rightarrow \infty \). The same problem occurs with (5).
The “nearly exponential” property only fits with certain activation functions but it does not require continuity. For example, let h(x) be the Dirichlet function that is one for rational and zero for irrational numbers x. Activation function \(\exp (x)(1+\exp (x)h(x))\) is nowhere continuous but nearly exponential: For \(\varepsilon >0\) let \(c=\ln (\varepsilon )\) and \(a=\exp (-c)\), \(b=1\), then for \(x\le 0\)
But a bound can also be obtained from arbitrarily often differentiability. Let \(\sigma \) be arbitrarily often differentiable on some open interval such that \(\sigma \) is no polynomial on that interval. Then one can easily obtain an estimate in terms of the \(r\hbox {th}\) modulus from the Jackson estimate (8) by considering that polynomials of degree at most \(n-1\) can be approximated arbitrarily well by functions in \(\varPhi _{n,\sigma }\), see [42, Corollary 3.6, p. 157], cf. [33, Theorem 3.1]. The idea is to approximate monomials by differential quotients of \(\sigma \). This is possible since derivative
at \(b=0\) equals \(\sigma ^{(k)}(c) x^k\). Constants \(\sigma ^{(k)}(c)\ne 0\) can be chosen because polynomials are excluded. The following estimate extends [42, Theorem 6.8, p. 176] in the univariate case to moduli of smoothness.
Theorem 2
Let \(\sigma :\mathbb {R}\rightarrow \mathbb {R}\) be arbitrarily often differentiable on some open interval in \(\mathbb {R}\) and let \(\sigma \) be no polynomial on that interval, \(f\in X^p[0, 1]\), \(1\le p\le \infty \), and \(r\in \mathbb {N}\). Then, independently of \(n\ge \max \{r, 2\}\) (or \(n>r\)) and f, a constant \(C_r\) exists such that
This theorem can be applied to \(\sigma _l\) but also to \(\sigma _a\) and \(\sigma _e\). The preliminaries are also fulfilled for \(\sigma (x):=\sin (x)\), a function that is obviously not nearly exponential.
Proof
Let \(\varepsilon >0\). As in the previous proof, there exists a polynomial \(p_n\) of degree at most n such that (10) holds. Due to [42, p. 157] there exists a function \(g_{n,\varepsilon }\in \varPhi _{n+1,\sigma }\) such that \(\Vert g_{n,\varepsilon } - p_n\Vert _{B[0,1]}<\varepsilon \). This gives
Since \(\varepsilon \) can be chosen arbitrarily, we get (16) via Eq. (13). \(\square \)
Polynomials in the closure of approximation spaces can be utilized to show that a direct lower bound in terms of a (uniform) modulus of smoothness is not possible.
Lemma 1
(Impossible inverse estimate). Let activation function \(\varphi \) be given as in the preceding Theorem 2, \(r\in \mathbb {N}\). For each positive, monotonically decreasing sequence \((\alpha _n)_{n=1}^\infty \), \(\alpha _n>0\), and each \(0<\beta <1\) a counterexample \(f_\beta \in C[0, 1]\) exists such that (for \(n\rightarrow \infty \))
Even if the constant \(C=C_f>0\) may depend on f (but not on n), estimate (5), as proposed in a similar context in [51] for \(r=2\), does not apply.
Proof
For best trigonometric approximation, comparable counter examples are constructed in [21, Corollary 3.1] based on a general resonance theorem [21, Theorem 2.1]. We apply this theorem to show a similar result for best algebraic polynomial approximation, i.e., there exists \(f_\beta \in C[0, 1]\) such that (17) and
We choose parameters of [21, Theorem 2.1] as follows: \(X=C[0, 1]\), \(\varLambda =\{r\}\), \(T_n(f) = S_{n,r}(f):= \omega _r\left( f,\frac{1}{n}\right) \) such that \(C_2=C_{5,n}=2^r\), \(\omega (\delta )=\delta ^\beta \). Different to [21, Corollary 3.1] we use resonance functions \(h_j(x):=x^j\), \(j\in \mathbb {N}\), such that \(C_1=1\). We further set \(\varphi _n=\tau _n=\psi _n=1/n^r\) such that with (1)
We compute an r-th difference of \(x^n\) at the interval endpoint 1 to get the resonance condition
Further, let \(R_n(f):= E(\varPi ^{n+1}, f)\) such that \(R_n(h_j)=0\) for \(j\le n\), i.e., \(0=R_n(h_j)\le C_4\frac{\rho _n}{\psi _n}\) for \(\rho _n:=\alpha _{n+1}\psi _n\). Then, due to [21, Theorem 2.1], \(f_\beta \in C[0, 1]\) exists such that (17) and (19) are fulfilled.
Since polynomials of \(\varPi ^{n+1}\) are in the closure of \(\varPhi _{n+1,\sigma }\) according to [42, p. 157], i.e., \(E(\varPhi _{n+1,\sigma }, f_\beta ) \le E(\varPi ^{n+1}, f_\beta )\), we obtain (18) from (19):
\(\square \)
3 A Uniform Boundedness Principle with Rates
In this paper, sharpness results are proved with a quantitative extension of the classical uniform boundedness principle of Functional Analysis. Dickmeis, Nessel and van Wickern developed several versions of such theorems. We already used one of them in the proof of Lemma 1. An overview of applications in Numerical Analysis can be found in [23, Section 6]. The given paper is based on [20, p. 108]. This and most other versions require error functionals to be sub-additive. Let X be a normed space. A functional T on X, i.e., T maps X into \(\mathbb {R}\), is said to be (non-negative-valued) sub-linear and bounded, iff for all \(f,g\in X,\, c\in \mathbb {R}\)
The set of non-negative-valued sub-linear bounded functionals T on X is denoted by \(X^\sim \). Typically, errors of best approximation are (non-negative-valued) sub-linear bounded functionals. Let \(U\subset X\) be a linear subspace. The best approximation of \(f\in X\) by elements \(u\in U\ne \emptyset \) is defined as \(E(f):=\inf \{ \Vert f-u\Vert _X : u\in U\}\). Then E is sub-linear: \(E(f+g)\le E(f)+E(g)\), \(E(cf) = |c|E(f)\) for all \(c\in \mathbb {R}\). Also, E is bounded: \(E(f)\le \Vert f-0\Vert _X=\Vert f\Vert _X\).
Unfortunately, function sets \(\varPhi _{n,\sigma }\) are not linear spaces, cf. [42, p. 151]. In general, from \(f,g\in \varPhi _{n,\sigma }\) one can only conclude \(f+g\in \varPhi _{2n,\sigma }\) whereas \(cf\in \varPhi _{n,\sigma }\), \(c\in \mathbb {R}\). Functionals of best approximation fulfill \(E(\varPhi _{n,\sigma }, f)_p \le \Vert f-0\Vert _{X^p[0, 1]}=\Vert f\Vert _{X^p[0, 1]}\). Absolute homogeneity \(E(\varPhi _{n,\sigma }, cf)_p =|c|E(\varPhi _{n,\sigma }, f)_p\) is obvious for \(c=0\). If \(c\ne 0\),
But there is no sub-additivity. However, it is easy to prove a similar condition: For each \(\varepsilon >0\) there exists elements \(u_{f,\varepsilon },u_{g,\varepsilon }\in \varPhi _{n,\sigma }\) that fulfill
and \(u_{f,\varepsilon }+u_{g,\varepsilon }\in \varPhi _{2n,\sigma }\) such that
i.e.,
Obviously, also \(E(\varPhi _{n,\sigma }, f)_p \ge E(\varPhi _{n+1,\sigma }, f)_p\) holds true.
In what follows, a quantitative extension of the uniform boundedness principle based on these conditions is presented. The conditions replace sub-additivity. Another extension of the uniform boundedness principle to non-sub-linear functionals is proved in [19]. But this version of the theorem is stated for a family of error functionals with two parameters that has to fulfill a condition of quasi lower semi-continuity. Functionals \(S_\delta \) measuring smoothness also do not need to be sub-additive but have to fulfill a condition \(S_\delta (f+g)\le B(S_\delta (f)+S_\delta (g))\) for a constant \(B\ge 1\). This theorem does not consider replacement (20) for sub-additivity.
Both rate of convergence and size of moduli of smoothness can be expressed by abstract moduli of smoothness, see [49, p. 96ff]. Such an abstract modulus of smoothness is defined as a continuous, increasing function \(\omega \) on \([0,\infty )\) that fulfills
for all \(\delta _1,\delta _2>0\). It has similar properties as \(\omega _r (f, \cdot )\), and it directly follows for \(\lambda >0\) that
Due to continuity, \(\lim _{\delta \rightarrow 0+} \omega (\delta )=0\) holds. For all \(0<\delta _1\le \delta _2\), Eq. (22) also implies
Functions \(\omega (\delta ):=\delta ^\alpha \), \(0 < \alpha \le 1\), are examples for abstract moduli of smoothness. They are used to define Lipschitz classes.
The aim is to discuss a sequence of remainders (that will be errors of best approximation) \((E_{n})_{n=1}^\infty \), \(E_n : X\rightarrow [0,\infty )\). These functionals do not have to be sub-linear but instead have to fulfill
for all \(m\in \mathbb {N}\), \(f, f_1, f_2,\dots , f_m\in X\), and constants \(c\in \mathbb {R}\). In the boundedness condition (26), \(D_n\) is a constant only depending on \(E_n\) but not on f.
Theorem 3
(Adapted uniform boundedness principle). Let X be a (real) Banach space with norm \(\Vert \cdot \Vert _X\). Also, a sequence \((E_{n})_{n=1}^\infty \), \(E_n : X\rightarrow [0,\infty )\) is given that fulfills conditions (24)–(27). To measure smoothness, sub-linear bounded functionals \(S_\delta \in X^\sim \) are used for all \(\delta >0\).
Let \(\mu (\delta ): (0,\infty )\rightarrow (0,\infty )\) be a positive function, and let \(\varphi : [1,\infty )\rightarrow (0,\infty )\) be a strictly decreasing function with \(\lim _{x\rightarrow \infty } \varphi (x)=0\). An additional requirement is that for each \(0<\lambda <1\) a point \(X_0=X_0(\lambda )\ge \lambda ^{-1}\) and constant \(C_\lambda >0\) exist such that
for all \(x>X_0\).
If there exist test elements \(h_n\in X\) such that for all \(n\in \mathbb {N}\) with \(n\ge n_0\in \mathbb {N}\) and \(\delta >0\)
then for each abstract modulus of smoothness \(\omega \) satisfying
there exists a counterexample \(f_\omega \in X\) such that \((\delta \rightarrow 0+,\, n\rightarrow \infty )\)
For example, (28) is fulfilled for a standard choice \(\varphi (x)=1/x^\alpha \).
The prerequisites of the theorem differ from the Theorems of Dickmeis, Nessel, and van Wickern in conditions (24)–(27) that replace \(E_n\in X^\sim \). It also requires additional constraint (28). For convenience, resonance condition (31) replaces \(E_{n}(h_n) \ge c_{3}\). Without much effort, (31) can be weakened to \(\limsup _{n\rightarrow \infty } E_{4n}(h_n) > 0\).
The proof is based on a gliding hump and follows the ideas of [20, Section 2.2] (cf. [18]) for sub-linear functionals and the literature cited there. For the sake of completeness, the whole proof is presented although changes were required only for estimates that are effected by missing sub-additivity.
Proof
The first part of the proof is not concerned with sub-additivity or its replacement. If a test element \(h_j\), \(j\ge n_0\), exists that already fulfills
then \(f_\omega :=h_j\) fulfills (34). To show that this \(f_\omega \) also fulfills (33), one needs inequality
for all \(\delta >0\). This inequality follows from (23): If \(0<\delta <1\) then \(\omega (1)/1 \le 2 \omega (\delta )/\delta , \) such that \(\delta \le 2\omega (\delta )/\omega (1)\). If \(\delta >1\) then \(\omega (1)\le \omega (\delta )\), i.e., \(1 \le \omega (\delta )/\omega (1)\). Thus, one can choose \(A=2/\omega (1)\).
Smoothness (33) of test elements \(h_j\) now follows from (36):
Under condition (35) function \(f_\omega :=h_j\) indeed is a counter example. Thus, for the remaining proof one can assume that for all \(j\in \mathbb {N}\), \(j\ge n_0\):
The arguments of Dickmeis, Nessel and van Wickern have to be adjusted to missing sub-additivity in the next part of the proof. It has to be shown that for each fixed \(m\in \mathbb {N}\) a finite sum inherits limit (37). Let \((a_l)_{l=1}^m\subset \mathbb {R}\) and \(j_1,\dots ,j_m \ge n_0\) different indices. To prove
one can apply (27), (24), and (25) for \(n\ge 2m\):
Since \(\varphi (x)\) is decreasing and \(\omega (\delta )\) is increasing, \(\omega (\varphi (x))\) is decreasing. Thus, (28) for \(\lambda :=(2m)^{-1}\) and \(n>\max \{2m, X_0(\lambda )\}\) implies
With this inequality, estimate (39) becomes
According to (37), this gives (38).
Now one can select a sequence \((n_k)_{k=1}^\infty \subset \mathbb {N}\), \(n_0 \le n_k<n_{k+1}\) for all \(k\in \mathbb {N}\), to construct a suitable counterexample
Let \(n_1:=n_0\). If \(n_1,\dots ,n_k\) have already be chosen then select \(n_{k+1}\) with \(n_{k+1}\ge 2k\) and \(n_{k+1}> n_k\) large enough to fulfill following conditions:
Only condition (42) is adjusted to missing sub-additivity. The next part of the proof does not consider properties of \(E_n\), see [20].
Function \(f_\omega \) in (40) is well-defined: For \(j\ge k\), iterative application of (41) leads to
This implies
With this estimate (and because of \(\lim _{k\rightarrow \infty }\omega (\varphi (n_k))=0\)), it is easy to see that \((g_m)_{m=1}^\infty \), \(g_m:=\sum _{j=1}^m \omega (\varphi (n_i)) h_{n_i}\), is a Cauchy sequence that converges to \(f_\omega \) in Banach space X: For a given \(\varepsilon >0\), there exists a number \(N_0(\varepsilon )>n_0\) such that \(\omega (\varphi (n_k))<\varepsilon /(2C_1)\) for all \(k>N_0\). Then, due to (29) and (45), for all \(k>i >N_0\):
Thus, the Banach condition is fulfilled and counterexample \(f_\omega \in X\) is well defined.
Smoothness condition (30) is proved in two cases. The first case covers numbers \(\delta >0\) for which \(\mu (\delta )\le \varphi (n_1)\). Since \(\lim _{x\rightarrow \infty } \varphi (x)=0\), there exists \(k\in \mathbb {N}\) such that in this case
Using this index k in connection with the two bounds in (30), one obtains for sub-linear functional \(S_\delta \)
The last estimate holds true because \(\varphi (n_{k+1}) \le \mu (\delta )\) in (46). The first expression in (48) can be estimated by \(4C_2 \omega (\mu (\delta ))\) with (46): Because \(\mu (\delta )\le \varphi (n_k)\), one can apply (23) to obtain
Thus, \(S_\delta (f_\omega ) \le 6C_2 \omega (\mu (\delta ))\).
The second case is \(\mu (\delta ) > \varphi (n_1)\). In this situation, let \(k:=0\). Then only the second sum in (47) has to be considered: \(S_\delta (f_\omega ) \le 2C_2 \omega (\varphi (n_1)) \le 2C_2 \omega (\mu (\delta ))\).
The little-o condition remains to be proven without sub-additivity. From (24) one obtains \(E_{2n}(f) = E_{2n}(f+g-g) \le E_{n}(f+g)+E_{n}(-g)\), i.e.,
The estimate can be used to show the desired lower bound based on resonance condition (31) with the gliding hump method. Functional \(E_{n_k}\) is in resonance with summand \(\omega (\varphi (n_k)) h_{n_k}\). This part of the sum forms the hump.
Thus \(E_{n}(f_\omega ) \ne o(\omega (\varphi (n)))\). \(\square \)
4 Sharpness
Free knot spline function approximations by Heaviside, cut and ReLU functions are first examples for application of Theorem 3.
Let \(S_n^r\) be the space of functions f for which \(n+1\) intervals \(]x_k, x_{k+1}[\), \(0=x_0< x_1< \dots < x_{n+1}=1\), exist such that f equals (potentially different) polynomials p of degree less than r on each of these intervals, i.e. \(p\in {\varPi }^r\). No additional smoothness conditions are required at knots.
Corollary 1
(Free knot spline approximation). For \(r, \tilde{r}\in \mathbb {N}\), \(1\le p\le \infty \), and for each abstract modulus of smoothness \(\omega \) satisfying (32), there exists a counterexample \(f_{\omega }\in X^p[0,1]\) such that
Note that r and \(\tilde{r}\) can be chosen independently. This corresponds with Marchaud inequality for moduli of smoothness.
The following lemma helps in the proof of this and the next corollary. It is used to show the resonance condition of Theorem 3.
Lemma 2
Let \(g:[0, 1] \rightarrow \mathbb {R}\), and \(0=x_0< x_1< \dots < x_{N+1}=1\). Assume that for each interval \(I_k:=(x_k, x_{k+1})\), \(0\le k\le N\), either \(g(x)\ge 0\) for all \(x\in I_k\) or \(g(x)\le 0\) for all \(x\in I_k\) holds. Then g can change its sign only at points \(x_k\). Let \(h(x):=\sin (2N\cdot 2\pi \cdot x)\). Then there exists a constant \(c>0\) that is independent of g and N such that
The prerequisites on g are fulfilled if g is continuous with at most N zeroes.
Proof
We discuss 2N intervals \(A_k:=(k (2N)^{-1}, (k+1) (2N)^{-1})\), \(0\le k<2N\). Function g can change its sign at most in N of these intervals. Let \(J\subset \{0,1,\dots ,2N-1\}\) the set of indices k of the at least N intervals \(A_k\) on which g is non-negative or non-positive. On each of these intervals, h maps to both its maximum 1 and its minimum \(-1\). Thus \(\Vert h-g\Vert _{B[0,1]}\ge 1\). This shows the Lemma for \(p=\infty \). Functions h and g have different sign on (a, b) where \((a, b)=(k (2N)^{-1}, (k+1/2) (2N)^{-1})\) or \((a, b)=((k+1/2) (2N)^{-1}, (k+1) (2N)^{-1})\), \(k\in J\). For all \(x\in (a, b)\) we see that \(|h(x)-g(x)|\ge |h(x)| = \sin (2N\cdot 2\pi \cdot (x-a))\). Thus, for \(1\le p<\infty \),
\(\square \)
Proof of Corollary 1
Theorem 3 can be applied with following parameters. Let Banach-space \(X=X^p[0, 1]\).
Whereas \(S_\delta \) is a sub-linear, bounded functional, errors of best approximation \(E_n\) fulfill conditions (24), (25), (26), and (27), cf. (20), with \(D_n=1\). Let \(\mu (\delta ):=\delta ^r\) and \(\varphi (x)=1/x^r\) such that condition (28) holds: \(\varphi (\lambda x)=\varphi (x)/\lambda ^r\). Let \(N=N(n):= (4n+1)\tilde{r}\). Resonance elements
obviously satisfy condition (29): \(\Vert h_n(x)\Vert _{X^p[0, 1]}\le 1=:C_1\). One obtains (30) because of
Let \(g\in S_{4n}^{\tilde{r}}\), then g is composed from at most \(4n+1\) polynomials on \(4n+1\) intervals. On each of these intervals, \(g\equiv 0\) or g at most has \(\tilde{r}-1\) zeroes. Thus g can change sign at 4n interval borders and at zeroes of polynomials, and g fulfills the prerequisites of Lemma 2 with \(N=(4n+1)\cdot \tilde{r} > 4n+(4n+1)\cdot (\tilde{r}-1)\). Due to the lemma, \(\Vert h_n-g\Vert _{X^p[0, 1]}\ge c>0\) independent of n and g. Since this holds true for all g, (31) is shown for \(c_3=c\). All preliminaries of Theorem 3 are fulfilled such that counterexamples exist as stated. \(\square \)
Corollary 1 can be applied with respect to all activation functions \(\sigma \) belonging to the class of splines with fixed polynomial degree less than r and a finite number of knots k because \(\varPhi _{n,\sigma }\subset S_{nk}^{r}\).
Since \(\varPhi _{n,\sigma _h} \subset S_n^1\), Corollary 1 directly shows sharpness of (2) and (4) for the Heaviside activation function if one chooses \(r=\tilde{r}=1\). Sharpness of (3) for cut and ReLU function follows for \(r=\tilde{r}=2\) because \(\varPhi _{n,\sigma _c}\subset S_{2n}^2\), \(\varPhi _{n,\sigma _r}\subset S_{n}^2\). However, the case \(\omega (\delta )=\delta \) of maximum non-saturated convergence order is excluded by condition (32). We discuss this case for \(r=\tilde{r}\). Then a simple counterexample is \(f_\omega (x):=x^r\). For each sequence of coefficients \(d_0,\dots ,d_{r-1}\in \mathbb {R}\) we can apply the fundamental theorem of algebra to find complex zeroes \(a_0,\dots ,a_{r-1}\in \mathbb {C}\) such that
There exists an interval \(I:=(j (r+1)^{-1}, (j+1) (r+1)^{-1})\subset [0, 1]\) such that real parts of complex numbers \(a_k\) are not in I for all \(0\le k<r\). Let \(I_0:=((j+1/4) (r+1)^{-1}, (j+3/4) (r+1)^{-1})\subset I\). Then for all \(x\in I_0\)
This lower bound is independent of coefficients \(d_k\) such that
We also see that
Each function \(g\in S_n^r\) is a polynomial of degree less than r on at least n intervals \((j (2n)^{-1}, (j+1) (2n)^{-1} )\), \(j\in J\subset \{0,1,\dots ,2n-1\}\). For \(j\in J\):
Thus, \(E(S_n^r,x^r) \ne o\left( \frac{1}{n^r}\right) \). In case of \(L^p\)-spaces, we similarly obtain with substitution \(u=2n x-j\)
Sharpness is demonstrated by combining lower estimates of all n subintervals:
Although our counterexample is arbitrarily often differentiable, the convergence order is limited to \(n^{-r}\). Reason is the definition of the activation function by piecewise polynomials. There is no such limitation for activation functions that are arbitrarily often differentiable on an interval without being a polynomial, see Theorem 2. Thus, neural networks based on smooth non-polynomial activation functions might approximate better if smooth functions have to be learned.
Theorem 3 in [15] states for the Heaviside function that for each \(n\in \mathbb {N}\) a function \(f_n\in C[0, 1]\) exits such that the error of best uniform approximation exactly equals \(\omega _1\left( f_n, \frac{1}{2(n+1)}\right) \). This is used to show optimality of the constant. Functions \(f_n\) might be different for different n. One does not get the condensed sharpness result of Corollary 1.
Another relevant example of a spline of fixed polynomial degree with a finite number of knots is the square non-linearity (SQNL) activation function \(\sigma (x):= {\text {sign}}(x)\) for \(|x|>2\) and \(\sigma (x):= x-{\text {sign}}(x)\cdot x^2/4\) for \(|x|\le 2\). Because \(\sigma \), restricted to each of the four sub-intervals of piecewise definition, is a polynomial of degree two, we can choose \(\tilde{r}=3\).
The proof of Corollary 1 is based on Lemma 2. This argument can be also used to deal with rational activation functions \(\sigma (x)=q_1(x)/q_2(x)\) where \(q_1,q_2\not \equiv 0\) are polynomials of degree at most \(\rho \). Then non-zero functions \(g\in \varPhi _{n,\sigma }\) do have at most \(\rho n\) zeroes and \(\rho n\) poles such that there is no change of sign on \(N+1\) intervals, \(N=2\rho n\). Thus, Corollary 1 can be extended to neural network approximation with rational activation functions in a straight forward manner.
Whereas the direct estimate (3) for cut and ReLU functions is based on linear best approximation, the counterexamples hold for non-linear best approximation. Thus, error bounds in terms of moduli of smoothness may not be able to express the advantages of non-linear free knot spline approximation in contrast to fixed knot spline approximation (cf. [45]). For an error measured in an \(L^p\) norm with an order like \(n^{-\alpha }\), smoothness only is required in \(L^q\), \(q:=1/(\alpha +1/p)\), see (7) and [16, p. 368].
Corollary 2
(Inverse tangent). Let \(\sigma =\sigma _a\) be the sigmoid function based on the inverse tangent function, \(r\in \mathbb {N}\), and \(1\le p\le \infty \). For each abstract modulus of smoothness \(\omega \) satisfying (32), there exists a counterexample \(f_{\omega }\in X^p[0,1]\) such that
The corollary shows sharpness of the error bound in Theorem 2 applied to the arbitrarily often differentiable function \(\sigma _a\).
Proof
Similarly to the proof of Corollary 1, we apply Theorem 3 with parameters \(X=X^p[0, 1]\), \(E_n(f):= E(\varPhi _{n,\sigma _a}, f)_p\), \(S_\delta (f) := \omega _r(f, \delta )_p\), \(\mu (\delta ):=\delta ^r\), \(\varphi (x)=1/x^r\), and
with \(N=N(n):=8n\), such that condition (29) is obvious and (30) can be shown by estimating the modulus in terms of the \(r\hbox {th}\) derivative of \(h_n\) with (1). Let \(g\in \varPhi _{4n,\sigma _a}\),
Then
where s(x) is a polynomial of degree \(2(4n-1)\), and q(x) is a polynomial of degree 8n. If g is not constant then \(g'\) at most has \(8n-2\) zeroes and f at most has \(8n-1\) zeroes due to the mean value theorem (Rolle’s theorem). In both cases, the requirements of Lemma 2 are fulfilled with \(N(n)=8n>8n-1\) such that \(\Vert h_n-g\Vert _{X^p[0, 1]}\ge c>0\) independent of n and g. Since g can be chosen arbitrarily, (31) is shown with \(E_{4n} h_n \ge c>0\). \(\square \)
Whereas lower estimates for sums of n inverse tangent functions are easily obtained by considering O(n) zeroes of their derivatives, sums of n logistic functions (or hyperbolic tangent functions) might have an exponential number of zeroes. To illustrate the problem in the context of Theorem 3, let
Using a common denominator, the numerator is a sum of type \(\sum _{k=1}^{m} \alpha _k \kappa _k^x\) for some \(\kappa _k>0\) and \(m<2^{4n}\). According to [50], such a function has at most \(m-1<16^n-1\) zeroes, or it equals the zero function. Therefore, an interval \([k (16)^{-n}, (k+1) (16)^{-n}]\) exists on which g does not change its sign. By using a resonance sequence \(h_n(x) := \sin \left( 16^n\cdot 2\pi x\right) \), one gets \(E(\varPhi _{4n,\sigma _l}, h_n) \ge 1\). But factor \(16^n\) is by far too large. One has to choose \(\phi (x):=1/16^x\) and \(\mu (\delta ):=\delta \) to obtain a “counterexample” \(f_\omega \) with
The gap between rates is obvious. The same difficulties do not only occur for the logistic function but also for other activation functions based on \(\exp (x)\) like the softmax function \(\sigma _m(x):=\log (\exp (x) + 1)\). Similar to (15),
Thus, sums of n logistic functions can be approximated uniformly and arbitrarily well by sums of differential quotients that can be written by 2n softmax functions. A lower bound for approximation with \(\sigma _m\) would also imply a similar bound for \(\sigma _l\) and upper bounds for approximation with \(\sigma _l\) imply upper bounds for \(\sigma _m\).
With respect to the logistic function, a better estimate than (51) is possible. It can be condensed from a sequence of counterexamples that is derived in [39]. However, we show that the Vapnik–Chervonenkis dimension (VC dimension) of related function spaces can also be used to prove sharpness. This is a rather general approach since many VC dimension estimates are known.
Let X be a set and \({\mathcal {A}}\) a family of subsets of X. Throughout this paper, X can be assumed to be finite. One says that \({\mathcal {A}}\) shatters a set \(S\subset X\) if and only if each subset \(B\subset S\) can be written as \(B=S\cap A\) for a set \(A\in {\mathcal {A}}\). The VC dimension of \({\mathcal {A}}\) is defined via
This general definition can be adapted to (non-linear) function spaces V that consist of functions \(g:X\rightarrow \mathbb {R}\) on a (finite) set \(X\subset \mathbb {R}\). By applying Heaviside-function \(\sigma _h\), let
Then the VC dimension of function space V is defined as \({\text {VC-dim}}(V):={\text {VC-dim}}({\mathcal {A}})\). This is the largest number \(m\in \mathbb {N}\) for which m points \(x_1\), ..., \(x_m \in X\) exist such that for each sign sequence \(s_1,\dots , s_m\in \{-1, 1\}\) a function \(g\in V\) can be found that fulfills
cf. [6]. The VC dimension is an indicator for the number of degrees of freedom in the construction of V. Condition (52) is equivalent to
Corollary 3
(Sharpness due to VC dimension). Let \((V_n)_{n=1}^\infty \) be a sequence of (non-linear) function spaces \(V_n\subset B[0, 1]\) such that
fulfills conditions (24)–(27) on Banach space C[0, 1]. Let \(\tau :\mathbb {N} \rightarrow \mathbb {N}\) and
be an equidistant grid on the interval [0, 1]. We restrict functions in \(V_n\) to this grid:
Let function \(\varphi (x)\) be defined as in Theorem 3 such that (28) holds true. If, for a constant \(C>0\), function \(\tau \) fulfills
for all \(n\ge n_0\in \mathbb {N}\) then for \(r\in \mathbb {N}\) and each abstract modulus of smoothness \(\omega \) satisfying (32), a counterexample \(f_{\omega }\in C[0,1]\) exists such that
Proof
Let \(n\ge n_0/4\). Due to (53), a sign sequence \(s_{0},\dots ,s_{\tau (4n)}\in \{-1, 1\}\) exists such that for each function \(g\in V_{4n}\) there is a point \(x_0=\frac{i}{\tau (4n)} \in G_{4n}\) such that \(\sigma _h(g(x_0)) \ne \sigma _h(s_{i})\).
We utilize this sign sequence to construct resonance elements. It is well known, that auxiliary function
is arbitrarily often differentiable on the real axis, \(h(0)=1\), \(\Vert h\Vert _{B(\mathbb {R})}=1\). This function becomes the building block for the resonance elements:
The interior of the support of summands is non-overlapping, i.e., \(\Vert h_n\Vert _{B[0,1]}\le 1\), and because of (54) norm \(\Vert h_n^{(r)}\Vert _{B[0,1]}\) of the \(r\hbox {th}\) derivative is in \(O([\varphi (n)]^{-r})\).
We apply Theorem 3 with
\(E_n(f)\) as defined in the theorem, and resonance elements \(h_n(x)\) that represent the existing sign sequence. Function \([\varphi (x)]^r\) fulfills the requirements of function \(\varphi (x)\) in Theorem 3.
Then conditions (29) and (30) are fulfilled due to the norms of \(h_n\) and its derivatives, cf. (1). Due to the initial argument of the proof, for each \(g\in V_{4n}\) at least one point \(x_0=i \tau (4n)^{-1}\), \(0\le i\le \tau (4n)\), exists such that we observe \(\sigma _h(g(x_0))\ne \sigma _h(h_n(x_0))\). Since \(|h_n(x_0)|=1\), we get \(\Vert h_n-g\Vert _{B[0,1]} \ge |h_n(x_0)-g(x_0)| \ge 1\), and (31) because \(E_{4n} h_n \ge 1\). \(\square \)
Corollary 4
(Logistic function). Let \(\sigma =\sigma _l\) be the logistic function and \(r\in \mathbb {N}\). For each abstract modulus of smoothness \(\omega \) satisfying (32), a counterexample \(f_{\omega }\in C[0,1]\) exists such that
The corollary extends the Theorem of Maiorov and Meir for worst case approximation with sigmoid functions in the case \(p=\infty \) to Lipschitz classes and one condensed counterexample (instead of a sequence), see [39, p. 99]. The sharpness estimate also holds in \(L^p[0, 1]\), \(1\le p<\infty \). For all these spaces, one can apply Theorem 3 directly with the sequence of counterexamples constructed in [39, Lemma 7, p. 99]. Even more generally, Theorem 1 in [38] utilizes pseudo-dimension, a generalization of VC dimension, to provide bounded sequences of counterexamples in Sobolev spaces.
Proof
We apply Corollary 3 in connection with a result concerning the VC dimension of function space (\(D\in \mathbb {N}\))
see paper [6] that is based on [26], cf. [32]. Functions are defined on a discrete set with \(2D+1\) elements, and in contrast to the definition of \(\varPhi _{n,\sigma }\), a constant function with coefficient \(a_0\) is added.
According to Theorem 2 in [6], the VC dimension of \(\varPhi _{n,\sigma _l}^D\) is upper bounded by (n large enough)
i.e., there exists \(n_0\in \mathbb {N}\), \(n_0\ge 2\), and a constant \(C>0\) such that for all \(n\ge n_0\)
Since \(\lim _{E\rightarrow \infty } \frac{1+\log _2(E)}{E}=0\), we can choose a constant \(E>1\) such that
With this constant, we define \(D=D(n):= \lfloor E n(1+\log _2(n))\rfloor \) such that the VC dimension of \(\varPhi _{n,\sigma _l}^D\) is less than D for \(n\ge n_0\):
By applying an affine transform that maps interval \([-D, D]\) to [0, 1] and by omitting constant function \(a_0\), we immediately see that for \(V_n:=\varPhi _{n,\sigma _l}\) and \(\tau (n):=2D(n)\)
such that (53) is fulfilled.
We define strictly decreasing
Obviously, \(\lim _{x\rightarrow \infty } \varphi (x) = 0\). Condition (28) holds: Let \(x>X_0(\lambda ):=\lambda ^{-2}\). Then \(\log _2(\lambda ) > -\log _2(x)/2\) and
Also, (54) is fulfilled:
Thus, all prerequisites of Corollary 3 are shown. \(\square \)
The corollary improves (51): There exists a counterexample \(f_{\omega }\in C[0,1]\) such that (see (9), (16))
The proof is based on the \(O(n\log _2(n))\) estimate of VC dimension in [6]. This requires functions to be defined on a finite grid. Without this prerequisite, the VC dimension is in \(\varOmega (n^2)\), see [48, p. 235]. The referenced book also deals with the case that all weights are restricted to floating point numbers with a fixed number of bits. Then the VC dimension becomes bounded by O(n) without the need for the \(\log \)-factor. However, direct upper error bounds (9) and (16) are proved for real-valued weights only.
The preceding corollary is a prototype for proving sharpness based on known VC dimensions. Also at the price of a log-factor, the VC dimension estimate for radial basis functions in [6] or [46] can be used similarly in connection with Corollary 3 to construct counterexamples. The sharpness results for Heaviside, cut, ReLU and inverse tangent activation functions shown above for \(p=\infty \) can also be obtained with Corollary 3 by proving that VC dimensions of corresponding function spaces \(\varPhi _{n,\sigma }\) are in O(n) (whereas the result of [5] only provides an \(O(n\log (n))\) bound). This in turn can be shown by estimating the maximum number of zeroes like in the proof of the next corollary and in the same manner as in the proofs of Corollaries 1 and 2.
The problem of different rates in upper and lower bounds arises because different scaling coefficients \(b_k\) are allowed. In the case of uniform scaling, i.e. all coefficients \(b_k\) in (50) have the same value \(b_k=B=B(n)\), the number of zeroes is bounded by \(4n-1\) instead of \(16^n-2\). Let
be the non-linear function space generated by uniform scaling. Because the quasi-interpolation operators used in the proof of Debao’s direct estimate (2), see [15], are defined using such uniform scaling, see [9, p. 172], the error bound
holds. This bound is sharp:
Corollary 5
(Logistic function with restriction). Let \(\sigma =\sigma _l\) be the logistic function and \(r\in \mathbb {N}\). For each abstract modulus of smoothness \(\omega \) satisfying (32), there exists a counterexample \(f_{\omega }\in C[0,1]\) such that
To prove the corollary, we apply following lemma.
Lemma 3
\(V_n\subset C[0, 1]\), \(2\le \tau (n)\in \mathbb {N}\), \(G_n:=\left\{ \frac{j}{\tau (n)} : j\in \{0,1,\dots ,\tau (n)\}\right\} \), and \(V_{n,\tau (n)} := \{ h:G_n\rightarrow \mathbb {R} : h(x)=g(x) \text { for a function } g\in V_n\}\) are given as in Corollary 3. If \({\text {VC-dim}}(V_{n,\tau (n)}) \ge \tau (n)\) then there exists a function \(g\in V_n\), \(g\not \equiv 0\), with a set of at least \(\lfloor \tau (n)/2\rfloor \) zero points in [0, 1] such that g has non-zero function values between each two consecutive points of this set.
Proof
Because of the VC dimension, a subset \(J\subset \{0,1,\dots ,\tau (n)\}\) with \(\tau (n)\) elements \(j_1< j_2< \dots < j_{\tau (n)}\) and a function \(g\in V_n\) exist such that
Then we find a zero on each interval \([j_{2k-1} \tau (n)^{-1}, j_{2k} \tau (n)^{-1})\), \(1\le k\le \lfloor \tau (n)/2\rfloor \): If \(g(j_{2k-1} \tau (n)^{-1})\ne 0\) then continuous g has a zero on the interval \((j_{2k-1} \tau (n)^{-1}, j_{2k} \tau (n)^{-1})\). Thus, g has \(\lfloor \tau (n)/2\rfloor \) zeroes on different sub-intervals. Between zeroes are non-zero, negative function values \(g(j_k \tau (n)^{-1})\) for even k because \(\sigma _h(g(j_k \tau (n)^{-1})) = 0\). \(\square \)
Proof of Corollary 5
We apply Corollary 3 with \(V_n=\tilde{\varPhi }_{n,\sigma _l}\) and \(E_n(f) = E(\tilde{\varPhi }_{n,\sigma _l}, f)\) such that conditions (24)–(27) are fulfilled. Let \(\tau (n):=2n\) and \(\varphi (n)=1/n\) such that (54) holds true: \(\tau (4n) =8n =8/\varphi (n)\). Assume that \({\text {VC-dim}}(V_{n,\tau (n)}) \ge \tau (n)\), then according to Lemma 3 there exists a function \(f\in \tilde{\varPhi }_{n,\sigma _l}\) such that \(f\not \equiv 0\) has \(\lfloor \tau (n)/2\rfloor = n\) zeroes. However, we can write f as
Using a common denominator q(x), the numerator is a sum of type \(s(x)=\sum _{k=0}^{n-1} \alpha _k (e^{-kB})^x\) which has at most \(n-1\) zeroes, see [50]. Because of this contradiction to n zeroes, (53) is fulfilled. \(\square \)
By applying Lemma 2 for \(N(n)=n-1\) in connection with Theorem 3, one can also show Corollary 5 for \(L^p\)-spaces, \(1\le p<\infty \).
Linear VC dimension bounds were proved in [47] for radial basis function networks with uniform width (scaling) or uniform centers. Such bounds can be used with Corollary 3 to prove results that are similar to Corollary 5. Also, such a corollary can be shown for the ELU function \(\sigma _e\). However, without the restriction \(b_k=B(n)\), piecewise superposition of exponential functions leads to \(O(n^2)\) zeroes of sums of ELU functions. Then in combination with direct estimates Theorems 1 and 2, i.e., \(E(\varPhi _{n,\sigma _e}, f_{\omega }) \le C_r \omega _r\left( f_{\omega }, \frac{1}{n}\right) \), we directly obtain following (improvable) result in a straightforward manner.
Corollary 6
(Coarse estimate for ELU activation). Let \(\sigma =\sigma _e\) be the ELU function and \(r\in \mathbb {N}\), \(n\ge \max \{2, r\}\) (see Theorem 1). For each abstract modulus of smoothness \(\omega \) satisfying (32), there exists a counterexample \(f_\omega \in C[0,1]\) that fulfills
Proof
To prove the existence of a function \(f_\omega \) with \(\omega _r\left( f_{\omega }, \delta \right) \in {O}\left( \omega \left( \delta ^{r}\right) \right) \) and (56), we apply Corollary 3 with \(V_n=\varPhi _{n,\sigma _e}\) and \(E_n(f) = E(\varPhi _{n,\sigma _e}, f)\) such that conditions (24)–(27) are fulfilled. For each function \(g\in V_n\) the interval [0, 1] can be divided into at most \(n+1\) subintervals such that on the lth interval g equals a function \(g_l\) of type
Derivative
has at most n zeroes or equals the zero function according to [50]. Thus, due to the mean value theorem (or Rolle’s theorem), \(g_l\) has at most \(n+1\) zeroes or is the zero function. By concatenating functions \(g_l\) to g, one observes that g has at most \((n+1)^2\) different zeroes such that g does not vanish between such consecutive zero points.
Let \(\tau (n):=8 n^2\) and \(\varphi (n)=1/n^2\) such that (54) holds true: \(\tau (4n) = 128 n^2 =128/\varphi (n)\). If \({\text {VC-dim}}(V_{n,\tau (n)}) \ge \tau (n)\) then due to Lemma 3 and because \(n\ge 2\) there exists a function in \(\varPhi _{n,\sigma _e}\) with at least \(\lfloor \tau (n)/2\rfloor =(2n)^2>(n+1)^2\) zeroes such that between consecutive zeroes, the function is not the zero function. This contradicts the previously determined number of zeroes and (53) is fulfilled. \(\square \)
Sums of n softsign functions \(\varphi (x)=x/(1+|x|)\) can be expressed piecewise by \(n+1\) rational functions that each have at most n zeroes. Thus, one also has to deal with \(O(n^2)\) zeroes.
5 Conclusions
Corollaries 1 and 2 can be seen in the context of Lipschitz classes. Let \(r:=1\) for the Heaviside, \(r:=2\) for cut and ReLU functions and \(r\in \mathbb {N}\) for the inverse tangent activation function \(\sigma =\sigma _a\). By choosing \(\omega (\delta ):=\delta ^\alpha \), a counterexample \(f_\alpha \in X^p[0, 1]\) exists for each \(\alpha \in (0,r)\) such that
With respect to Corollary 4 for the logistic function, in general no higher convergence order \(\frac{1}{n^\beta }\), \(\beta >\alpha \) can be expected for functions in the Lipschitz class that is defined via \({\text {Lip}}^r(\alpha , C[0, 1]):=\{f \in C[0,1] : \omega _r(f, \delta ) = O\left( \delta ^\alpha \right) \}\).
In terms of (non-linear) Kolmogogrov n-width, let \(X:={\text {Lip}}^r(\alpha , C[0, 1])\). Then, for example, condensed counterexamples \(f_\alpha \) for piecewise linear or inverse tangent activation functions and \(p=\infty \) imply
The restriction to the univariate case of a single input node was chosen because of compatibility with most cited error bounds. However, the error of multivariate approximation with certain activation functions can be bounded by the error of best multivariate polynomial approximation, see proof of Theorem 6.8 in [42, p. 176]. Thus, one can obtain estimates in terms of multivariate radial moduli of smoothness similar to Theorem 2 via [30, Corollary 4, p. 139]. Also, Theorem 3 can be applied in a multivariate context in connection with VC dimension bounds. First results are shown in report [25].
Without additional restrictions, a lower estimate for approximation with logistic function \(\sigma _l\) could only be obtained with a log-factor in (55). Thus, either direct bounds (2) and (9) or sharpness result (55) can be improved slightly.
References
Almira, J.M., de Teruel, P.E.L., Romero-Lopez, D.J., Voigtlaender, F.: Negative results for approximation using single layer and multilayer feedforward neural networks. arXiv arXiv:1810.10032 (2018)
Anastassiou, G.A.: Multivariate hyperbolic tangent neural network approximation. Comput. Math. Appl. 61(4), 809–821 (2011)
Anastassiou, G.A. (ed.): Univariate hyperbolic tangent neural network quantitative approximation. In: Intelligent Systems: Approximation by Artificial Neural Networks, vol. 19, pp. 33–65. Springer, Berlin (2011)
Barron, A.R.: Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inf. Theory 39(3), 930–945 (1993)
Bartlett, P.L., Maiorov, V., Meir, R.: Almost linear VC-dimension bounds for piecewise polynomial networks. Neural Comput. 10(8), 2159–2173 (1998)
Bartlett, P.L., Williamson, R.C.: The VC dimension and pseudodimension of two-layer neural networks with discrete inputs. Neural Comput. 8(3), 625–628 (1996)
Chen, T., Chen, H., Liu, R.: A constructive proof and an extension of Cybenko’s approximation theorem. In: Page, C., LePage, R. (eds.) Computing Science and Statistics, pp. 163–168. Springer, New York (1992)
Chen, Z., Cao, F.: The properties of logistic function and applications to neural network approximation. J. Comput. Anal. Appl. 15(6), 1046–1056 (2013)
Cheney, E.W., Light, W.A.: A Course in Approximation Theory. AMS, Providence (2000)
Costarelli, D.: Sigmoidal functions approximation and applications. Doctoral thesis, Roma Tre University, Rome (2014)
Costarelli, D., Spigler, R.: Approximation results for neural network operators activated by sigmoidal functions. Neural Netw. 44, 101–106 (2013)
Costarelli, D., Spigler, R.: Constructive approximation by superposition of sigmoidal functions. Anal. Theory Appl. 29, 169–196 (2013)
Costarelli, D., Vinti, G.: Saturation classes for max-product neural network operators activated by sigmoidal functions. RM 72, 1555–1569 (2017)
Cybenko, G.: Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 2(4), 303–314 (1989)
Debao, C.: Degree of approximation by superpositions of a sigmoidal function. Approx. Theory Appl. 9(3), 17–28 (1993)
DeVore, R.A., Lorentz, G.G.: Constructive Approximation. Springer, Berlin (1993)
DeVore, R.A., Popov, V.A.: Interpolation spaces and non-linear approximation. In: Cwikel, M., Peetre, J., Sagher, Y., Wallin, H. (eds.) Function Spaces and Applications, pp. 191–205. Springer, Berlin (1988)
Dickmeis, W., Nessel, R.J., van Wickeren, E.: A general approach to counterexamples in numerical analysis. Numer. Math. 43(2), 249–263 (1984)
Dickmeis, W., Nessel, R.J., van Wickeren, E.: On nonlinear condensation principles with rates. Manuscr. Math. 52(1), 1–20 (1985)
Dickmeis, W., Nessel, R.J., van Wickeren, E.: Quantitative extensions of the uniform boundedness principle. Jahresber. Deutsch. Math.-Verein. 89, 105–134 (1987)
Dickmeis, W., Nessel, R.J., van Wickern, E.: On the sharpness of estimates in terms of averages. Math. Nachr. 117, 263–272 (1984)
Funahashi, K.I.: On the approximate realization of continuous mappings by neural networks. Neural Netw. 2, 183–192 (1989)
Goebbels, S.: A sharp error estimate for numerical Fourier transform of band-limited functions based on windowed samples. Z. Anal. Anwendungen 32, 371–387 (2013)
Goebbels, S.: A counterexample regarding “New study on neural networks: the essential order of approximation”. Neural Netw. 123, 234–235 (2020)
Goebbels, S.: On sharpness of error bounds for multivariate neural network approximation. arXiv arXiv:2004.02203 (2020)
Goldberg, P.W., Jerrum, M.R.: Bounding the Vapnik–Chervonenkis dimension of concept classes parameterized by real numbers. Mach. Learn. 18(2), 131–148 (1995)
Guliyev, N.J., Ismailov, V.E.: A single hidden layer feedforward network with only one neuron in the hidden layer can approximate any univariate function. Neural Netw. 28(7), 1289–1304 (2016)
Hornik, K.: Approximation capabilities of multilayer feedforward networks. Neural Netw. 4, 251–257 (1991)
Hornik, K., Stinchcombe, M., White, H.: Multilayer feedforward networks are universal approximators. Neural Netw. 2(5), 359–366 (1989)
Johnen, H., Scherer, K.: On the equivalence of the K-functional and moduli of continuity and some applications. In: Schempp, W., Zeller, K. (eds.) Constructive Theory of Functions of Several Variables. Proc. Conf. Oberwolfach, pp. 119–140 (1976)
Jones, L.K.: Constructive approximations for neural networks by sigmoidal functions. Proc. IEEE 78(10), 1586–1589, Correction and addition in Proc. IEEE 79 (1991), 243 (1990)
Karpinski, M., Macintyre, A.: Polynomial bounds for VC dimension of sigmoidal and general pfaffian neural networks. J. Comput. Syst. Sci. 54(1), 169–176 (1997)
Kůrková, V.: Rates of approximation of multivariable functions by one-hidden-layer neural networks. In: Marinaro, M., Tagliaferri, R. (eds.) Neural Nets WIRN VIETRI-97, Perspectives in Neural Computing, pp. 147–152. Springer, London (1998)
Lei, Y., Ding, L.: Approximation and estimation bounds for free knot splines. Comput. Math. Appl. 65(7), 1006–1024 (2013)
Leshno, M., Lin, V.Y., Pinkus, A., Schocken, S.: Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 6(6), 861–867 (1993)
Lewicki, G., Marino, G.: Approximation of functions of finite variation by superpositions of a sigmoidal function. Appl. Math. Lett. 17(10), 1147–1152 (2004)
Li, F.J.: Constructive function approximation by neural networks with optimized activation functions and fixed weights. Neural Comput. Appl. 31(9), 4613–4628 (2019)
Maiorov, V., Ratsaby, J.: On the degree of approximation by manifolds of finite pseudo-dimension. Constr. Approx. 15, 291–300 (1999)
Maiorov, V.E., Meir, R.: On the near optimality of the stochastic approximation of smooth functions by neural networks. Adv. Comput. Math. 13, 79–103 (2000)
Makovoz, Y.: Uniform approximation by neural networks. J. Approx. Theory 95(2), 215–228 (1998)
Pinkus, A.: n-Width in Approximation Theory. Springer, Berlin (1985)
Pinkus, A.: Approximation theory of the MLP model in neural networks. Acta Numer. 8, 143–195 (1999)
Ritter, G.: Efficient estimation of neural weights by polynomial approximation. IEEE Trans. Inf. Theory 45(5), 1541–1550 (1999)
Sanguineti, M.: Universal approximation by ridge computational models and neural networks: a survey. Open Appl. Math. J. 2, 31–58 (2008)
Sanguineti, M., Hlaváčková-Schindler, K.: Some comparisons between linear approximation and approximation by neural networks. In: Artificial Neural Nets and Genetic Algorithms, pp. 172–177. Springer, Vienna (1999)
Schmitt, M.: Radial basis function neural networks have superlinear VC dimension. In: Proceedings of the 14th Annual Conference on Computational Learning Theory COLT 2001 and 5th European Conference on Computational Learning Theory EuroCOLT 2001, Volume 2111 of Lecture Notes in Artificial Intelligence, pp. 14–30. Springer, Berlin (2001)
Schmitt, M.: RBF neural networks and Descartes’ rule of signs. In: Cesa-Bianchi, N. and Numao, M. and Reischuk, R (eds.) Algorithmic Learning, Theory ALT 2002, Lecture Notes in Computer Science, vol. 2533. Springer, Heidelberg (2002)
Shalev-Shwartz, S., Ben-David, S.: Understanding Machine Learning—from Theory to Algorithms. Cambridge University Press, New York (2014)
Timan, A.: Theory of Approximation of Functions of a Real Variable. Pergamon Press, New York (1963)
Tossavainen, T.: The lost cousin of the fundamental theorem of algebra. Math. Mag. 80(4), 290–294 (2007)
Wang, J., Xu, Z.: New study on neural networks: the essential order of approximation. Neural Netw. 23(5), 618–624 (2010)
Xu, Z., Cao, F.: The essential order of approximation for neural networks. Sci. China Ser. F Inf. Sci. 47(1), 97–112 (2004)
Xu, Z., Wang, J.J.: The essential order of approximation for neural networks. Sci. China Ser. F Inf. Sci. 49(4), 446–460 (2006)
Acknowledgements
Open Access funding provided by Projekt DEAL. I would like to thank an anonymous reviewer, Michael Gref, Christian Neumann, Peer Ueberholz, and Lorens Imhof for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Goebbels, S. On Sharpness of Error Bounds for Univariate Approximation by Single Hidden Layer Feedforward Neural Networks. Results Math 75, 109 (2020). https://doi.org/10.1007/s00025-020-01239-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-020-01239-8
Keywords
- Neural networks
- sharpness of error bounds
- counterexamples
- rates of convergence
- uniform boundedness principle