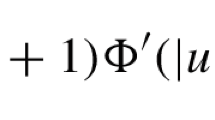Abstract
We consider the Emden–Fowler nonlinear differential equation
and discuss the problem of oscillation and nonoscillation of solutions of (1.1). The results in this paper are described by means of the function
In the case that \(B(t) \ge 0\) for \(t \ge t_{0}\), a necessary and sufficient condition for oscillation of all solutions of (1.1) can be established.
Similar content being viewed by others
References
Bhatia, N.P.: Some oscillation theorems for second order differential equations. J. Math. Anal. Appl. 15, 442–446 (1966)
Butler, G.J.: On the oscillatory behaviour of a second order nonlinear differential equation. Ann. Mat. Pura Appl. 4(105), 73–92 (1975)
Butler, G.J.: Integral averages and the oscillation of second order ordinary differential equations. SIAM J. Math. Anal. 11, 190–200 (1980)
Butler, G.J.: An integral criterion for the oscillation of a second order sublinear ordinary differential equation. Indian J. Math. 24, 1–7 (1982)
Coles, W.J.: Oscillation criteria for nonlinear second order equations. Ann. Mat. Pura Appl. 82, 123–133 (1969)
Hartman, P.: On nonoscillatory linear differential equations of second order. Am. J. Math. 74, 389–400 (1952)
Naito, M.: Nonoscillatory solutions of second order differential equations with integrable coefficients. Proc. Am. Math. Soc. 109, 769–774 (1990)
Naito, M.: Integral averages and the asymptotic behavior of solutions of second order ordinary differential equations. J. Math. Anal. Appl. 164, 370–380 (1992)
Naito, M.: Integral averaging techniques for the oscillation and nonoscillation of solutions of second order ordinary differential equations. Hiroshima Math. J. 24, 657–670 (1994)
Wintner, A.: A criterion of oscillatory stability. Q. Appl. Math. 7, 115–117 (1949)
Wong, J.S.W.: On two theorems of Waltman. SIAM J. Appl. Math. 14, 724–728 (1966)
Wong, J.S.W.: Oscillation criteria for second order nonlinear differential equations with integrable coefficients. Proc. Am. Math. Soc. 115, 389–395 (1992)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Naito, M. Oscillation and Nonoscillation of Solutions of a Second-Order Nonlinear Ordinary Differential Equation. Results Math 74, 178 (2019). https://doi.org/10.1007/s00025-019-1103-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-019-1103-y