Linking Seismic Measurements to the International System of Units

Abstract

The current state of the art in the calibration of seismometers is given by internal calibration procedures which give only incomplete information about a seismometer’s response and are based on transfer functions supplied by manufacturers. Calibrations traceable to the International System of Units (SI) provide an independent and comprehensible characterization of seismometers. These calibrations take part in a laboratory using an electrodynamic shaker or shake table. To overcome the issue that seismometers placed in seismic stations are not supposed to be moved to a calibration laboratory, novel on-site calibration methods incorporating a reference seismometer were developed. Such a reference is placed near the sensor to be calibrated, and the transfer function of the seismometer under test can be derived based on the output of both sensors.

1 Motivation: Why We Need Traceability for Seismometers

Thousands of seismometers all over the world are currently operated without proper traceability to the International System of Units (Système international d’unités, SI). The current state of the art in the calibration of seismometers is provided by internal calibration procedures which are compared to response functions given by the manufacturers with (at most) limited information on how they were derived.

1.1 Seismic Networks—Comparability of Different Sensors, after Replacing Sensors

Operating sensor networks with traceable calibration has great advantages. If the properties of a seismometer can be determined during a calibration and this calibration is traceable to the SI, sensors in seismic stations can be replaced without any data analysis issues. With the known properties, all data can be corrected for changes in the transfer function of a sensor.

The traceability to the SI ensures the international comparability of a calibration and no dependency on “golden standards” (i.e., reference sensors which cannot replaced).

There are many seismic networks in the world. One network spanning the whole globe is the International Monitoring System (IMS) of the Preparatory Commission for the Comprehensive Nuclear-Test-Ban Treaty Organization (CTBTO). The CTBTO is an international organization which monitors the compliance with the Comprehensive Nuclear-Test-Ban Treaty (CTBT). This is carried out by means of the IMS, which consists of 170 seismic, 11 hydroacoustic, 60 infrasound, and 80 radionuclide stations (CTBTO, 2023). These stations are operated by different national operators; the data analysis takes place centrally at the headquarters of the CTBTO in Vienna, Austria. The CTBTO specifies a tolerance or uncertainty of ± 5% for the reported calibration amplitude and ± 5° for the phase response values of seismometers. Additionally, the CTBTO requires all station the be recalibrated on an annual basis. Other networks such as the Global Seismographic Network (GSN) aim at publishing response data to an accuracy of 1° in phase and 1% in amplitude (Davis et al. 2005).

To overcome the current lack of traceable calibration in the field of seismic, infrasound, and underwater acoustics, the European research project titled InfraAUV within the EMPIR programme has joined together the expertise of several European institutes in the field of geoscience and measurement science, also called metrology (Ceranna et al. 2021). Results from the work focused on seismic measurements will be presented in the following sections.

1.2 Traceability: the SI and its Application to Seismic Sensors

Traceability is the most important concept in metrology. The International Vocabulary of Metrology (Vocabulaire international de métrologie, VIM) defines traceability in the following way (BIPM et al., 2012, Sect. 2.41). It is the:

“property of a measurement result whereby the result can be related to a reference through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty”.

The principle is to ensure an uninterrupted measurement chain from the highest metrology standard of the SI to the on-site instrument. This system is also called the calibration pyramid. A primary calibration uses different quantities to the one used by the sensor under test (SUT) for the determination of its properties (BIPM et al., 2012, Sect. 5.4), and often such measurements are traceable directly to the SI using national references. Unlike this, a secondary calibration compares the SUT with a reference of the same kind (BIPM et al., 2012, Sect. 5.5), which might be calibrated by primary means. In the case of this paper, the challenge is to ensure the traceability of seismometer measurements used at IMS stations to the SI metre and second standards, using the calibration pyramid. The metrological traceability chain can be represented as a pyramid of successive calibrations, where the final user calibration certificate can be traced back to the national reference and the SI unit, as shown in Fig. 1.

Figure. 1

The calibration pyramid applied to InfraAUV

National metrology institutes (NMIs), such as the Physikalisch-Technische Bundesanstalt (PTB) in Germany, the Danish Primary Laboratory for Acoustics (HBK-DPLA), and the French laboratoire national de métrologie et d’essais (LNE), are able to perform primary calibrations using primary references. They are in the highest level of the calibration pyramid and compare their results with each other in intercomparisons to ensure correct measurements.

In the case of vibration (which includes seismometers), these primary references are connected to both the metre and the second, and they are used to calibrate secondary references. To ensure the validity of these results, the mentioned inter-laboratory comparisons must occur periodically at all levels of the traceability chain.

Traceability to the SI from a primary calibration at a metrology institute to the many in-field stations is only feasible if a suitable number of secondary calibration facilities are set up. Most often it is not seen as an option for metrology institutes to provide the high number of transfer standard reference measurements to cover large scale metrology systems with perhaps hundreds or even thousands of sensors to be calibrated. This may especially be the case with global observation networks like the IMS if the station uptime and the transfer standard stability during general transport are critical. Furthermore, metrology system measurements are time-consuming and thereby lead to a significant expense. In addition, expertise on the type of units that are already part of the overall metrology system is necessary for the set-up and in-field personnel. In a similar way to large commercial global production facilities, the IMS metrology system could be divided into regions, with each region being responsible for providing the number of station references needed to perform the in-field station calibrations.

1.3 Why in-Laboratory Calibrations Don’t Work

Calibration of seismometers, whether traceable or not, is a relatively recent field of interest. In the past, calibrations were not performed frequently and the seismometers' data sheets from the manufactures were trusted or the seismometers were sent back to the manufacturers for recalibration. Further, calibration meant either co-locating with an uncalibrated reference or performing other means of testing such as weight-lift tests or electrical calibration. The calibration of existing seismometer stations or arrays, including traceability to the SI, requires each of these stations’ instruments to be dismantled and transported to a metrological laboratory for comparison to a primary reference standard. In-laboratory calibration methods are applied there too.

Apart from the large effort of dismantling all the seismometers of a station (successively or in parallel) and transporting them back and forth, ensuring their calibration during the transportation process and in different environment conditions is also an issue. During this process, the laboratory values of ambient pressure, temperature, and humidity have to adapt to the on-site station conditions. Furthermore, the instruments are removed from the stations for a large amount of time (in terms of days or weeks, at least), which is necessary for transportation to a calibration laboratory and the time-consuming calibration procedures. Remote locations and those that are difficult to reach often pose significant problems, which would further complicate the process of performing regular laboratory calibrations.

In the context of seismic stations being part of, for example, the IMS for monitoring compliance with the CTBT or being essential as backbone stations for earthquake monitoring services, it is not possible to remove those instruments from operations for elongated in-laboratory calibrations. Monitoring obligations and technical requirements of timely, continuous, and uninterrupted data availability clearly go against this procedure and are a reason why, in this context, traditional in-laboratory calibrations do not work.

Therefore, a novel approach has been developed. This is based on laboratory calibrations that are traceable to the SI by primary calibration methods. Transferring the process to a mobile reference seismometer with secondary calibration methods is also included as is performing on-site calibrations on the station instruments, which relies on instrumental comparisons during uninterrupted measurements.

1.4 Internal Electrical Calibration Methods and Their Limitations

A method widely used to check seismometers is the all electric excitation with a coil. In this case, an electric signal is fed into the seismometer and the response is measured. This method has several limitations:

1.4.1 Extent of Components Taken Into Account

By principle, this method can only take into account some of the components of the seismometer. As it only incorporates the actual sensing element only a few mechanical components in close proximity to the actual sensing element can be taken into consideration. Influences of components like housing and feet as well as the ground coupling and ground stiffness will be invisible for this method. Figure 9 in Sect. 4 shows calibration results from a multiaxis sensor, which shows a distinctive deviation at the higher frequencies due to this effect.

1.4.2 Different Conditions

The excitation with a coil can differ from a real excitation. As Wielandt and Zumberge (2013) pointed out, the mechanical behaviour of a coil-only excitation may differ from a real seismic excitation. The structural loads on the components of seismometers can be significantly different in case of real seismic events. Moreover, some force feedback seismometers use the same coil for the excitation and for the force compensation. In this case, only very small mechanical excitations will occur, because the excitation will be compensated quickly by the force feedback control.

1.4.3 Relative Method

Albeit it would be possible to calculate all required quantities for an electrical calibration to be directly applicable, in practice this method is primarily a relative method and not used to determine an absolute sensitivity of a seismometer but rather to estimate changes in the transfer function. For an absolute calibration, correction factors may be provided by the manufacturer, however, these are often incomplete and cover only a limited frequency band. These also could be determined by the user in the same way the manufacturers derive them: by a mechanical excitation using a shaker. Only little is known, how the manufacturers derive these corrections precisely (excitation level, frequency, duration of the measurement, measurement uncertainties, etc.).

1.4.4 Interruption of Recordings

During the electrical excitation no ground movements can be registered as they will be masked by the generated signal. This may violate station or network requirements.

1.4.5 No Traceability

With such an aforementioned calibration on a shaker, a traceable calibration is possible, as described in the following section of this contribution. Without a traceable reference measurement of the shaker movement, no absolute measurement is possible.

Due to these limitations, the electrical excitation method seems to the authors as a useful tool to check a seismometer regularly on-site rather than a calibration method. It can be easily implemented as many digitizers support the coil excitation and checks of seismometers can be carried out remotely with limited downtime of the seismometer for measurements. The results can provide helpful information about changes due to ageing or mechanical and electrical defects.

1.5 Previous Work on Calibration Procedures

Approaches for the calibration of seismometers beyond the electrical calibration or as an extension of the electrical calibrations have been developed in the past. Two different approaches were followed:

Determination of a base sensitivity of a seismometer using microseisms, large seismic events or tidal excitation at one frequency and a determination of the frequency response using internal electrical excitation coils relative to this fixed base sensitivity (Davis & Berger, 2012). This procedure uses simulations from earth models to predict the excitation of the seismometer and compares the expected outcome with the readout from the seismometers.

Calibration of a reference using an exciter and using the calibrated reference for on-site calibration (Davis & Berger, 2012; Xu et al., 2018).

The first approach is based heavily on earth simulations, which either have to be assumed to be correct in order apply the corrections or need independent verification, which the cited authors applied by using the exciter in the second approach. This latter approach has similar components like the methods proposed in this contribution but lacks traceability. The authors mention a reference laser vibrometer (Davis & Berger, 2012), but without details on its operation principle or calibration, or they mention a conversion factor of the voltage fed to the power amplifier, which was validated before by using interferometry (Xu et al., 2018). The on-site calibrations were carried out at certain, chosen frequencies.

The work proposed here goes beyond the previous work by establishing a reliable base for the in-laboratory calibration using the SI and by extending the excitation frequencies to both higher and lower frequencies and also by determining frequency response functions in-situ at the stations without using internal calibration procedures.

2 Calibration in a Laboratory

A calibration in a laboratory enables the determination of a sensor’s properties under well-known conditions and with estimated measurement uncertainties.

The basic principle of calibration is the same for all motion sensors: An excitation of the wanted quantity is generated and the output of the sensor is then compared to a well-known reference. In the case of the dynamic calibration of rectilinear accelerometers, velocity sensors—which also include seismometers—or of displacement sensors, the exciter is often an electrodynamic shaker, also known as a shake table, generating sinusoidal excitations. In the following sections, we will only use the general term exciter to describe these devices.

2.1 Primary Calibration Using Laser Interferometry as the Reference (ISO 16063–11)

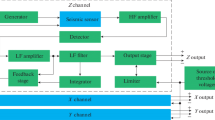
The reference for a primary calibration of motion sensors is, in most cases, a laser interferometer. The output of such a laser interferometer can be traced back to the wavelength of the laser used in the interferometer (base unit: metre) and the time (base unit: second). Based on the type of interferometer and the demodulation used, either a velocity-dependent or a displacement-dependent output signal can be found. In the case of sinusoidal excitation, both quantities do not have to be integrated/differentiated in order to be transferred into each other; they can be calculated directly in the frequency domain. A schematic of a primary calibration set-up is depicted in Fig. 2.

Figure. 2

Schematic of a primary calibration set-up with vertical excitation (Klaus et al., 2023)

The normative document applicable to primary seismometer calibrations is ISO standard 16,063–11:1999 (ISO/TC 108, 1999), which describes the calibration of accelerometers in a (recommended) frequency range from 1 Hz to 10 kHz. The recommended frequency range is based on the calibration frequencies for accelerometers at the time the standard was developed and has no technical reasons. Accelerometer calibrations based on this standard are practised down to 0.1 Hz already. While the frequencies of seismometer calibrations may be even lower, the procedures can still be applied. The standard describes a calibration using sinusoidal excitation with a reference based on a laser interferometer. The output of the reference (laser interferometer) and the seismometer (sensor under test, SUT) are acquired simultaneously. Data analysis is carried out by applying a sine approximation on both signals with which the complex transfer function of the SUT can be derived. The results are typically given as the magnitude response and phase response of the SUT.

Seismometers have to be handled differently to accelerometers. They are not supposed to be turned and therefore an excitation in the horizontal and vertical direction has to be provided to cover all measuring axes. The high sensitivity of seismometers requires exciters which will be in a sufficiently isolated environment and can generate the small excitations required. Also, seismometers can have a significant weight of up to 10 kg and more, which the exciters must be able to bear. In particular for horizontal displacement, the design of exciters is based on a long rod on which the sensor table is moved. Depending on the load of the sensor and the position of the table, this guiding device can be deformed and bent introducing a tilt of the sensor as described in the following.

In recent years, several set-ups for the calibration of seismometers have been built. The first experiences with calibrating seismometers were gained at PTB using an existing multi-component exciter (Klaus & Kobusch, 2018). Later on, dedicated set-ups in France at CEA and at the SPEKTRA company were commissioned. A comparison (Larsonnier et al., 2019) showed room for improvement. Meanwhile, set-ups in Italy (Schiavi et al., 2021), in Japan (Shimoda et al., 2022; Shimoda et al., 2023), and in the United States (Bloomquist et al., 2023) were developed.

Figures 3 and 4 show measuring set-ups at PTB, CEA and DPLA, respectively. The set-ups of PTB consist of a horizontal long-stroke exciter and a multi-axis exciter which is mainly used for vertical excitation. CEA operates dedicated vertical and horizontal exciters from SPEKTRA, and DPLA has a calibration facility for horizontal excitation.

Figure. 3

Primary calibration set-ups for the calibration of seismometers in three degrees of freedom at the multi-component exciter at PTB (left) and for horizontal calibrations at the long-stroke exciter at PTB (right)

Figure. 4

Primary calibration set-ups for the horizontal calibration of seismometers at DPLA (left) and for horizontal and vertical excitation at CEA (right)

All the devices shown apply sinusoidal excitation. PTB developed multi-sine excitation methods (Yan et al., 2022) to shorten the duration of the calibration. Especially at low frequencies, the measuring time can be significant. At 10 mHz one sine period has a duration of 100 s, and for a robust measurement, several periods are required. Superimposing several frequencies shortens the time span of a calibration significantly, but the crest factor and the signal-to-noise ratio will get worse, resulting in increased measurement uncertainties.

There are currently no written rules, standards or guidelines on the handling and mounting of seismometers during calibration, and the same thing applies to the placement of reference lasers. Accelerometers get screwed or glued onto the armature of an exciter, while seismometers are supposed to stand upright. In order to avoid unwanted movement, the sensors are typically fixed in some way (e.g., by being strapped) to the surface of the shaker armature. The fixing should be as soft as possible; it should not influence the properties of the sensor or generate internal and external mechanical stress. A rigid fixture may influence the dynamics of the coupling of a seismometer to the ground.

As the response of the seismometer under test to a ground excitation should be the basis for the calibration, the laser beam of the reference should be adjusted to be as near as possible to the feet of the sensor under test. Measuring with the reference laser on the surface of the housing should be absolutely avoided. Influences due to the coupling to the ground would not be detected, but instead local resonances on the housing, which may not affect the measurement, could be measured. For large seismometers, especially at vertical excitation, multiple measurements with the laser beam placed near to each foot of the seismometer under test might be necessary.

2.2 Secondary Calibration

The excitation methods in an in-laboratory secondary calibration are very similar to those of a primary calibration, as depicted in Fig. 5 and described in ISO 16063–21 (ISO/TC 108, 2016). An electrodynamic exciter generates sinusoidal excitations. Differently to the primary calibration, the reference here is also a seismometer. This reference could be calibrated using a primary calibration for smaller measurement uncertainties. Secondary calibrations have to have larger measurement uncertainties than primary calibrations, as the reference needs to be calibrated prior to the calibration, and all uncertainty contributions added during the secondary calibration add to the uncertainty of the reference’s output.

Figure. 5

Schematic of a secondary calibration set-up with vertical excitation

The data analysis for determining the transfer function could, in this case, be a sine approximation as given in the standard. Recently, however, other novel methods like the coherent power method (COPA) have been proposed as alternatives (Ingerslev et al., 2020; Winther, 2021). The COPA method calculates the cross-spectral density $G_{{\text{SutRe}}f}$ from the output of the seismometer under test and the reference. The signal amplitude, $S_{\text{a}}$, can be derived by doing a square root operation on $G_{{\text{SutRe}}f} { }$. To ensure real valued signal amplitudes, the absolute value of the coherent power is evaluated before the square root operation yielding the final expression for the signal amplitude

$$S_a = \sqrt {{\left| {\hat{G} _{{\text{SutRef}}} } \right|}}$$

(1)

with $\hat{G}_{{\text{SutRef}}}$ being the averaged cross-spectral density.

A set-up for secondary calibrations may be easier to realize. While exciters are still needed, the costly primary reference can be replaced by a less pricey reference seismometer.

When performing secondary low-frequency calibrations, two methods can normally be applied: calibration by direct comparison and by substitution (Licht et. al. 1987).

A direct comparison is performed by comparing the sensitivities of two transducers: a calibrated transfer reference and the sensor under test. The ratio of their outputs is measured, and then normalised using the calibration data of the transfer reference standard.

Calibration by substitution may in some areas and set-ups have the advantage of simply avoiding downtime during the calibration of the transfer standard. The calibration by means of the substitution technique involves taking two measurements. The reference measurement, in which a permanently fixed so-called working standard transducer is calibrated against the transfer standard reference transducer, which is stored when not used. The seismometer under test can then be calibrated against the working standard, producing a frequency response function measurement that is compared to the stored measurement. The working standard shall always remain fixed to the exciter head in order for the working standard spectrum to be valid.

In principle and considering the relevant frequency range of, for instance, 10 mHz to 20 Hz, there is no apparent reason not to have additional moving armatures providing the possibility to calibrate several units simultaneously in one axis. This would then take place against the same transfer standard or working standard.

2.3 Issues when Calibrating in a Laboratory

Calibrations in a laboratory should determine the properties of the seismometer under test. During the research on calibration procedures for the in-laboratory calibration of seismometers, issues occurred which are specific to the calibration of seismometers. These issues need to be taken into consideration when designing calibration set-ups, as well as when estimating measurement uncertainties for such calibrations.

2.4 Tilt

An ideal exciter would generate a precisely rectilinear excitation. However, in reality the trajectory of the excitation may tilt during the displacement. This small change in the direction of travel of the SUT may cause significant deviations in the output signal of a seismometer. The issue of tilting during calibration was first found at low-frequency calibrations of accelerometers, as described by Bruns and Gazioch (2016). The change in the direction also causes a small change in the local gravitational acceleration $g_{{\text{loc}}} ,$ which affects the output of the sensor.

The deviations due to this effect will increase with increased displacements during the excitation, i.e., at lower frequencies. In the case of seismometer calibrations, this effect becomes especially pronounced, due to small excitation levels at very low frequencies.

The superimposed measured acceleration $a_{{\text{imp}}}$ in a horizontal measuring axis with a displacement x and a tilt angle $\alpha$ equals

$$a_{{\text{imp}}} = g_{{\text{loc}}} \sin \alpha \left( x \right)$$

(2)

For calibrations, this means that at a low frequency of 10 mHz and an excitation level of 1 mm/s (which leads to output voltages in the 1 V to 2 V range for typical broadband seismometers), a very small tilting of 1 µrad over the whole displacement used for the excitation leads to a measurement error of 16%. This will not be measured by the reference interferometer.

Therefore, the tilting of exciters used for seismometer calibration needs to be assessed prior to excitation, and the measurement results need to be corrected accordingly as described in Bruns and Gazioch (2016).

2.5 Electromagnetic Influences

Seismometers can be susceptible to changes in the magnetic field, giving outputs without a real seismic signal (Tape et al., 2020). For some types of sensors, the sensitivity to the magnetic field is higher than for others depending on their design, the technology used to measure the internal displacement of the inertial mass, and the materials used in the suspension springs of the inertial mass to minimize the effect of temperature variation (Díaz et al., 2020; Forbriger et al., 2010). This impacts their low-frequency operation and results in an increase of up to 10% in their sensitivity below 0.1 Hz. It is therefore necessary to take this parameter into account with regard to the electromagnetic environment in the vicinity of the sensor during calibration. Limiting the electromagnetic field present should be considered whenever it has an impact on calibration.

Due to the design of its actuation system, the SE-13 used at CEA generates magnetic stray fields distributed all around the exciter and also on its upper part where the seismometer is installed. Simulations confirmed by measurements of the magnetic field showed that the values decreased as the distance increased. The magnetic field is about 2 mT on the table and 0.7 mT, 30 cm away. A technical solution was developed by SPEKTRA and implemented successfully on the CEA’s SE-13 to eliminate the magnetic field close to the seismometer. It consists of a compensation coil, materialized by a ring powered by an adjustable DC voltage, located horizontally around the exciter. This feature generates an adjustable magnetic field depending on the supply voltage to compensate the induced one. The residual magnetic field on the top of the exciter can be adjusted and reduced so that it no longer disturbs the seismometer.

2.6 Temperature Sensitivity

Seismic sensors, and in particular broadband sensors, are designed and manufactured to minimize the effect of temperature variation. On-site, however, environmental conditions may require the use of passive thermal insulation to stabilize the sensor temperature and improve its performances (Widmer-Schnidrig & Kurrle, 2006). Even so, significant effects of temperature sensitivity can be found (Ackerley & Gias, 2023). In the calibration laboratory, the local thermal insulation of the sensor on the exciter is not possible. Then the effect of the thermal sensitivity of a seismic sensor may occur when the amplitude and time constant of ambient temperature variations are such that they impact the sensor. The quality of the temperature regulation in air-conditioned calibration laboratories is a factor to be considered, particularly if regulation cycles occur over durations comparable to the low-frequency calibration time.

2.7 Excitation Levels and Environmental Noise

By principle, a laboratory equipped with a lot of technical equipment like electrodynamic exciters, amplifiers, heating, ventilation, and air conditioning in a busy building with other laboratories will exhibit higher environmental noise level like a remote monitoring station. Additionally, due to technical reasons (minimal displacement of exciters, feedback control requirements, resolution of the digitizers and the references) excitation levels during the calibration are significantly higher than at normal operation conditions in a vault. Up to now, there is no indication that this is problematic. It would be, if the sensors under test would exhibit significant non-linear behaviour, i. e. show different sensitivities at different excitation levels. The measurement principle of force compensated seismometers is well known for its linear behaviour, and components with reduced stiffness / significant compliance would exhibit similar relative effects at different excitation levels. Non-linearities would be found due to generated higher harmonic components, which would be apparent in the seismometer’s output, but not in in the reference signals.

3 Transfer to the Field

As mentioned in Sect. 1.3, the in-laboratory calibration for sensors in the field is not feasible. Other solutions were therefore needed to carry out traceable calibrations.

3.1 How to get the SI to a Station

Instead of taking the sensors to a laboratory, an alternative might be to take reference sensors to a station and then to carry out a secondary calibration on-site. With the constraints described in Sect. 1.3, it becomes clear that for these calibrations the SUTs need to stay in their place and remain operable.

A possible calibration could only be carried out using natural or man-made seismic signals and then using these signals to calibrate the SUT. Procedures like this have already been applied in infrasound (Gabrielson, 2011), but not for seismic sensors.

The calibration chosen is schematically depicted in Fig. 6. The reference seismometer, which is traceably calibrated with the methods described in the former sections, is placed on-site and connected to a very similar data acquisition system to the SUT. This is necessary to have a similar time delay of all analysed data.

Figure. 6

Schematic of an on-site calibration set-up using vertical excitation

For the calibration itself, both sensors are operated over a sufficiently long time period in parallel. This time period will be significantly longer than the duration of a calibration in the laboratory, as the signal levels are very small and often not sufficient for the requirements of the calibration. For example, sometimes there is only noise, or too much noise is present in the signals on many occasions.

3.2 Requirements for Reference Seismometers

Seismometers used for the calibration of other seismometers in an on-site calibration should have distinct features. Generally speaking, the reference should be as good as possible. Important features for a reference are:

3.2.1 Long-Term Stability

References should be as stable as possible so that changes of their properties between two in-laboratory calibration cycles or changes within the measurement uncertainties are unlikely.

3.2.2 Temperature Stability

References will be calibrated in a warm laboratory and also operated in colder environments on-site. Therefore, a well-known temperature sensitivity, or better still, a temperature sensitivity that is so low that it does not influence the calibration results, is favourable.

3.2.3 Bandwidth

The reference should have a broader or the same bandwidth as the SUT and should be calibrated over the whole bandwidth. Only under these circumstances can a SUT be calculated in its whole frequency band. Alternatively, if only a certain bandwidth is required, this bandwidth should be safely covered by the reference.

3.2.4 Transportability

As the reference needs to be transported between the calibration laboratory and the site, it must be sufficiently robust against influences due to shipping, like temperature changes, humidity changes, and shocks.

3.2.5 Orientation

The axes of the reference need to be exactly aligned with those of the SUT; therefore, a mean for orientation/alignment, such as scribe marks, orientation rods, and a bubble level, are required.

This list is not exhaustive. Depending on the application, other features may also be important for a reference seismometer.

3.3 Data Analysis: Gabrielson’s Method

The calibration of seismometers at a station has been of great interest for decades and has been widely addressed by many studies. What most of these studies have in common is that they are based on a sensor comparison for closely located seismometers recording coherent signals. Examples of such a relative on-site seismometer comparison can be found, among others, in Berger et al. (1979), Gomberg et al. (1988), Pavlis and Vernon (1994), and Xu et al. (2018). Often, the excitation signals used in these methods are continuous recordings of ground noise (Pavlis & Vernon, 1994) and microseisms (Anthony et al. 2018; Xu et al., 2018). Other authors suggest using the Earth’s tides (Davis & Berger, 2007). However, these methods solely characterize “errors” in the transfer function and sensor behaviour by considering a gain ratio, and traceability to the SI is commonly not given.

The goal is to obtain the full frequency response, that is both magnitude and phase, of a fully operational seismic sensor in its natural environment without any interruption. As proposed by Pavlis and Vernon (1994), two sensors are co-located, assuming that both sensors record the same ground motion. This procedure is a variant of the so-called cluster or huddle test. Furthermore, one of the sensors, hereafter referred to as the reference seismometer, must have a known absolute and traceable calibration to ensure that the SI is transferred to the station seismometer.

The basic idea behind this approach is that the convolution model is valid for recorded seismograms. For the spectrum S(ω) of the measured seismogram s_i(t), the following statement holds:

$$S_i \left( \omega \right) = I_i \left( \omega \right)A_i \left( \omega \right)E\left( \omega \right) ,$$

(3)

where I_i describes the response function of seismometer i, A_i is the response function of the complete recording system, and E represents the true spectrum of the ground motion e_i(t).

Supposing two seismometers are located sufficiently close to each other, it can be assumed that both record the same ground motion e(t). Thus, a transfer or gain function Z(ω) between these two seismometers is given as:

$$Z\left( \omega \right) = \frac{I_1 \left( \omega \right)}{{I_2 \left( \omega \right)}} = \frac{S_1 \left( \omega \right)A_2 \left( \omega \right)}{{S_2 \left( \omega \right)A_1 \left( \omega \right)}} .$$

(4)

Equation (4) indicates that the transfer function $Z\left( \omega \right)$ connecting the output of both sensors is directly related to the spectral ratio of the signals recorded by them. Hence, in order to bring the SI to the stations, one of the seismometers must have a known calibration, i.e., $I_2 \left( \omega \right)$ is known and traceable to the SI. It follows accordingly that:

$$\hat{I}_1 \left( \omega \right) = Z \left( \omega \right)I_2 \left( \omega \right).$$

(5)

The estimated response function $\hat{I}_1$(ω) is independent of the ground motion e(t) and is generally valid. However, the determination of the transfer function Z(ω) or its estimation $\hat{Z}$(ω) between the sensors remains critical, and the overall outcome depends on the accuracy of the transfer function. Pavlis and Vernon (1994) determine spectral ratios in overlapping time windows and calculate a weighted average of all determined ratios as an estimate of the transfer function Z(ω). Here, an adapted version of the Gabrielson approach (Gabrielson, 2011), which was originally developed for the field calibration of infrasound stations, is utilized with modifications from Charbit et al. (2015) and Green et al. (2021).

According to Gabrielson (2011), reducing the bias and scatter caused by noisy signals necessitates the use of averaged auto spectral ($\hat{G}_{{\text{SutSut}}}$) and cross-spectral ($\hat{G}_{{\text{SutRef}}}$) densities. As a result, incoherent signals are nullified.

$$I_{{\text{SUT}}} = \frac{{\hat{G}_{{\text{SutSut}}} }}{{\hat{G}_{{\text{SutRef}}}^* }} I_{{\text{REF}}} ,$$

(6)

where the * denotes the complex conjugate. For this approach, the following conditions apply:

• i. The reference sensor/transfer standard has a known and traceable frequency response function (this ensures traceability for the field sensor calibration).

• ii. The SUT and the reference sensor measure the same, coherent signal.

• iii. The effects of incoherent signals are assumed to be negligible.

While assumption i is necessary to bring the SI to the station, assumptions ii and iii are vital for this method. Both sensors pick up incoherent signal components. As a result, it is essential to take steps to ensure that the response is determined for signals observed by both seismometers with high coherence and similarity. Gabrielson (2011) proposes the use of magnitude squared coherence (MSC) γ² as a similarity measure:

$$\gamma^2 = \frac{{\hat{G}_{{\text{SutRef}}} \hat{G}_{{\text{SutRef}}}^* }}{{\hat{G}_{{\text{SutSut}}} \hat{G}_{{\text{RefRef}}} }} .$$

(7)

By considering only frequencies and time intervals where γ² is greater than a certain threshold, intervals with low coherence are excluded from the analysis. To obtain reliable results, a threshold of 0.98 has been found to be a good choice (Charbit et al., 2015), as it satisfies assumption ii. However, depending on the type and distribution of incoherent signals, a threshold greater than 0.8 may still achieve good results.

An additional similarity measure is introduced for seismometers, utilizing Pearson cross-correlation coefficients between the recorded signals of the test and reference sensor. This second measure is necessary because the MSC alone does not provide satisfactory results. A low MSC threshold value (e.g., < 0.8) results in significant variations in the gain ratio. Conversely, an MSC threshold value of 0.98 leads to insufficient coherent data, particularly at low frequencies (< 0.7 Hz). The cross-correlation r_xy between two time series x and y, with a time-lag of τ, is given by

$$r_{xy} \left( \tau \right) = \mathop \sum \limits_{t = t_0 }^{t_1 } f_{x,t} f_{y,t + \tau }$$

(8)

A common threshold for this measure is 0.8. Furthermore, computing the cross-correlation yields the added benefit of determining the time delay between the two timeseries, which may be advantageous for verifying any possible timing errors between the acquisition units.

If the reference and test sensors are positioned at a distance from each other, or if more than one sensor is to be calibrated with a single reference, a complementary measure of similarity is required. The proposed measure, based on the multichannel measure of coherence ρ_max, was originally presented by Green et al. (2021) for the calibration of infrasound stations. Although this method of using multiple channels is effective, it involves high computational costs due to the typically higher sampling rate and possibly larger number of seismometers in a regional array compared to infrasound stations. In accordance with Green et al. (2021), the first step is to calculate R^max (Eq. 9), which is the maximum value of the cross-correlation between each sensor pair ij for M sensors.

$$R^{{\text{max}}} = \left[ {\begin{array}{*{20}c} {\max \left( {r_{11} } \right)} & \cdots & {\max \left( {r_{1M} } \right)} \\ \vdots & \ddots & \vdots \\ {\max \left( {r_{M1} } \right)} & \cdots & {\max \left( {r_{MM} } \right)} \\ \end{array} } \right]$$

(9)

with r_ij being the cross-correlation between sensors i and j. The multichannel measure of coherence is given by

$$\rho_{{\text{max}}} = \frac{{\sum_{i = 1}^M \sum_{j = 1}^M R_{ij}^{{\text{max}}} }}{{M\sum_{i = 1}^M R_{ii}^{{\text{max}}} }}$$

(10)

The stationarity property is an additional requirement for the spectral approach. Charbit et al. (2015) extended Gabrielson’s (2011) approach by dividing the signal into a number of passbands and using varying data segment lengths in which the power spectral densities are calculated. This increases the probability of detecting low noise windows and permits the averaging of more spectral estimates for the response calculation. We have applied the eight passbands listed in Table 1.

Table 1 Passbands applied for the on-site calibration

For the on-site calibration of seismometers, the method is implemented as presented below.

The raw data time series from both sensors are filtered within the passbands using a Butterworth bandpass filter. The resulting filtered data is then segmented into differently sized segments based on the passband (Table 1). Within each segment, the cross- and auto-spectral densities are calculated using Welch’s method (Welch, 1967), which divides each segment into nine windows with a 50% overlap (using a Hanning window). Within each segment, the corresponding similarity measures are calculated. If the similarity measures exceed previously specified thresholds, the gain ratio or complex transfer function between the SUT and the reference seismometer is determined by

$$\begin{array}{*{20}c} {\hat{Z} = \frac{{\hat{G}_{{\text{SutSut}}} }}{{\hat{G}_{{\text{SutRef}}}^* }} } \\ \end{array}$$

(11)

This process is repeated for each segment within each passband. Lastly, a weighted mean is used to calculate a single gain estimate $\hat{Z}$(ω) for each frequency, based on all the gain ratios that have been determined:

$$\begin{array}{*{20}c} {\overline{{g_{\gamma^2 } }} = \frac{{\sum_{n = 1}^N w_n \left( {\hat {Z_n} } \right) }}{{\sum_{n = 1}^N w_n }} = I_{{\text{cal}}} } \\ \end{array}$$

(12)

with N being the number of gain measurements and $\hat{Z_{n}}$ the gain measurements. The weight w is given as

$$\begin{array}{*{20}c} {w = \left( {\frac{1}{{2\left( {2P + 1} \right)}}\frac{{\left( {\hat {G}_{{\text{SutSut}}} } \right) }}{{\left({ \hat{G}_{{\text{RefRef}}} } \right) }}\left( {\frac{1 - \gamma^2 }{{\left( {\gamma^2 } \right)^2 }}} \right)} \right)^{ - 1} } \\ \end{array}$$

(13)

where 2P + 1 = 9 is the number of periodograms/windows averaged to provide the spectral density estimates. Note that for high MSC thresholds, the weighted average has only little effect on the overall results. The usage of the weight is of greater importance when smaller thresholds are used. By taking the known frequency response of the reference, the response of the SUT can be determined as

$$\begin{array}{*{20}c} {I_{{\text{SUT}}} = I_{{\text{REF}}} I_{{\text{cal}}} } \\ \end{array}$$

(14)

Note that up to this point, only the complex frequency response has been considered, which can also be expressed in terms of amplitude and phase:

$$\begin{array}{*{20}c} {I_i = A_i e^{{\text{j}}\varphi_i } } \\ \end{array}$$

(15)

$$\begin{array}{*{20}c} {A_i = \left| {I_i } \right| } \\ \end{array}$$

(16)

$$\begin{array}{*{20}c} {\varphi_i = \arg I_i } \\ \end{array}$$

(17)

The amplitude A and phase φ of the test sensor’s response are estimated by the following equations:

$$\begin{array}{*{20}c} {A_{{\text{SUT}}} = A_{{\text{cal}}} A_{{\text{REF}}} } \\ \end{array}$$

(18)

$$\begin{array}{*{20}c} {\varphi_{{\text{SUT}}} = \varphi_{{\text{cal}}} - \varphi_{{\text{REF}} } } \\ \end{array}$$

(19)

Uncertainties can be assigned to the amplitude and phase estimates by using the weighted standard deviation of the gain in amplitude and phase:

$$\begin{array}{*{20}c} {\sigma_{A_{cal} } = \sqrt {{\frac{{\sum_{n = 1}^N w_n \left( {\left| {\hat{Z}_n } \right| - \left| {\overline{{g_{\gamma^2 } }}} \right|} \right)^2 }}{{\sum_{n = 1}^N w_n }}}} } \\ \end{array}$$

(20)

$$\begin{array}{*{20}c} {\sigma_{\varphi_{cal} } = \sqrt {{\frac{{\sum_{n = 1}^N w_n \left( {\arg \left( {\hat{Z}_n } \right) - \arg (\overline{{g_{\gamma^2 } )}}} \right)^2 }}{{\sum_{n = 1}^N w_n }}}} } \\ \end{array}$$

(21)

The field calibration’s measurement uncertainty results from the entire calibration process, from the laboratory to the field. The response I_REF of the reference is known from the laboratory calibration including uncertainties for both the amplitude ($u_{A_{REF} }$) and phase ($u_{\varphi_{REF} }$). The final uncertainties for the results of the test sensor can be determined under the assumption that the responses are considered to be Gaussian distributions:

$$\begin{array}{*{20}c} {u_{A_{{\text{SUT}}} } = \sqrt {{A_{{\text{SUT}}}^2 \left( {\left( {\frac{{\sigma_{A_{{\text{cal}}} } }}{{A_{{\text{cal}}} }}} \right)^2 + \left( {\frac{{u_{A_{{\text{REF}}} } }}{{A_{{\text{REF}}} }}} \right)^2 } \right)}} } \\ \end{array}$$

(22)

$$\begin{array}{*{20}c} {u_{\varphi_{{\text{SUT}}} } = \sqrt {{\varphi_{{\text{SUT}}}^2 \left( {\left( {\frac{{\sigma_{\varphi_{{\text{cal}}} } }}{{\varphi_{{\text{cal}}} }}} \right)^2 + \left( {\frac{{u_{\varphi_{{\text{REF}}} } }}{{\varphi_{{\text{REF}}} }}} \right)^2 } \right)}} } \\ \end{array}$$

(23)

4 Practical Examples from On-Site Calibrations

On-site calibration tests were conducted at the GERman Experimental Seismic System (GERES)/primary station (PS)19 seismic monitoring station (see Fig. 7) in the Bavarian Forest, Germany. The station is part of the CTBTO’s IMS and is one of the 50 primary seismic stations. BGR operates the array station, which is composed of 25 elements. It was chosen for its accessibility and outstanding infrastructure, providing the opportunity to install numerous seismometers in a single vault as well as in adjacent ones.

Figure. 7

Location of the GERES/PS19 seismic station (a, b). The positions of the individual stations within the array are given in c Reference seismometers were installed at stations C2 and C7, which are marked with a yellow circle

The field tests were performed over a 260-day period between 24 August 2022 (DOY 236) and 10 May 2023 (DOY 130) at three vaults of the station (Fig. 7). Vaults C2a and C7 are each equipped with a broadband three-component seismometer (Guralp CMG-3 T), which each represent an SUT in this study. Moreover, a vertical short-period seismometer (Geotech GS13) is installed in both vaults, serving as a reference. Vault C2b (Fig. 8), located adjacent to C2a, also comprises a three-component broadband seismometer (Streckeisen STS2.5), which serves as a reference seismometer. Both the GS13 and the STS2.5 were calibrated at PTB. The GS13 seismometers are part of PS19 and were removed for a short period of time for the laboratory calibration. PS19 is equipped with in total 25 vertical and 8 horizontal GS13 sensors, representing a commonly used IMS sensor [more than half of the IMS stations are equipped with passive sensors such as GS13, S13, or GS21 (e.g. PS46, PS47, AS82, AS111)]. Please refer to Table 2 for detailed information on the sensors and equipment.

Figure. 8

View of station element GEC2 a with co-located vaults C2a (left) and C2b (right). The installed seismometers are shown in b and c. Photographs were taken by the authors

Table 2 Information about the seismometers installed and accompanying equipment

The STS2.5 reference sensor was calibrated in the laboratory at PTB with expanded measurement uncertainties (coverage factor 95%, expansion factor k = 2) of 0.5% to 1.0% in amplitude and 0.5°in phase for frequencies greater than 0.1 Hz (Fig. 9). Frequencies lower than 0.1 Hz show increased uncertainties up to 6% in amplitude and 5° in phase, respectively. This is caused by tilt influences on the axis that—albeit compensated – still increase the measurement uncertainties. Vertical and horizontal calibrations were carried out on different calibration devices, which might explain the differing sensitivities at the lowest frequencies (which are still consistent within their respective measurement uncertainties). Note the deviation in magnitude sensitivity at higher frequencies between the vertical and horizontal axes as a result of the differing stiffness of the ground coupling and feet in the corresponding directions. Uncertainty values for single frequencies may be higher or lower. The reference seismometers were installed by experienced station operators and oriented by marks on the walls and orientation rods. The marks originate from precise measurements with a gyroscope. In this way, orientation and alignment errors are less than 2°.

Figure. 9

Results of the laboratory calibration of the Streckeisen STS2.5 seismometer serving as reference in the field study. The obtained values for magnitude (top) and phase (bottom) are shown for each axis with the respective expanded measurement uncertainties (coverage factor 95%, expansion factor k = 2) as error bars

Figure. 10

Observed frequency ranges for different sources of seismic waves. Dashed-bordered boxes illustrate anthropogenic sources, solid-bordered boxes illustrate natural sources. More saturated colours indicate commonly observed and dominant frequency ranges. The frequency ranges to be calibrated (0.01–20 Hz for seismic waves) are highlighted in grey. Note that only the most important and not all sources are included in the figure, and sources, which are well outside the frequency range under consideration, have not been included for reasons of clarity. The figure is adapted from Schwardt et al. (2022)

4.1 Excitation Methods

An important criterion for the implemented in-situ calibration method is the availability of adequate coherent excitation signals, which exceed the self-noise levels of the reference and test seismometers in the required frequency range. Previous studies employing in-situ calibration procedures suggest the use of natural sources, such as ambient noise recordings (Pavlis and Vernon 1994), microseisms (Anthony et al., 2018; Ringler et al., 2017), the Earth’s free oscillations (Davis et al., 2005), or the Earth’s tides (Davis & Berger, 2007) as excitation signals. A literature review was conducted by Schwardt et al. (2022) to identify suitable sources of seismic waves for in-situ calibrations. The sources examined included both anthropogenic and natural sources and were evaluated for their frequency bandwidth, signal characteristics and cost-effectiveness. The findings provide valuable insights into selecting optimal excitation sources for seismic calibration (Fig. 10). Cultural noise and man-made controlled sources, such as drop weights, hammer blows, and vibration sources, meet most of the requirements in addition to the natural seismic sources mentioned above.

In practice, various sources may be appropriate, yet multiple aspects affect their utility, such as signal length, frequency content, and signal strength. Additionally, relying solely on one form of excitation signal is not practical, given, for example, the repetition rates of earthquakes of specific magnitudes or the restricted frequency ranges of individual sources, such as microseismicity. It is therefore recommended to use all the data recorded by the seismometers and to exclude signals that do not meet the predefined similarity criteria during processing. Thus, all frequencies within the relevant range are covered to a certain extent, enabling the determination of the response for all relevant ground motions.

Additionally to the usage of all recorded natural and anthropogenic signals, a calibration test with controlled sources was performed using an electrodynamic vibration source and a simple sledgehammer (Pilger & Schwardt, 2023). The benefit of using such controlled sources is their ability to generate signals with high repeatability, high energy, and within a specific frequency range, the latter depending on their design. Portable in nature, these sources can be used in areas that are difficult to access. They are furthermore beneficial in detecting any misalignment between the sensors or directional influences (Fig. 11).

Figure. 11

Examples of waveforms recorded at the sensor under test (CMG-3 T, left) and the reference sensor (STS2.5, right) for a controlled source experiment conducted at the station. For all three channels the raw data without corrections for the digitizers bit weight and seismometer response are shown (top: vertical/Z-component; middle: north component; bottom: east component)

Figures 11 and 12 show examples of recorded waveforms with different amplitudes to illustrate that both the test and reference sensors record ground motions with high signal to noise. Both figures display the raw data without any corrections for the digitizers bit weight and seismometer response as this is how the data is further analysed during the on-site calibration algorithm. The first example shows the waveforms recorded for a controlled source experiment conducted at the station (Fig. 11). On that day, a lot of non-seismic background noise was recorded due to maintenance work at the station. The second example (Fig. 12) shows the waveform for an M5.6 earthquake in the Fiji Island Region (distance to station 150.2°). The signal to noise ratio over the whole experiment period is variable depending on the source of ground movement (magnitude, distance, radiation pattern).

Figure. 12

Examples of waveforms recorded at the sensor under test (CMG-3 T, left) and the reference sensor (STS2.5, right) for an M5.6 earthquake in the Fiji Island Region (distance to station 150.2°). For all three channels the raw data without corrections for the digitizers bit weight and seismometer response are shown (top: vertical/Z-component; middle: north component; bottom: east component)

In Fig. 13, the probabilistic power spectral densities (PPSD) for both sensors over the whole experiment period of 260 days are shown. The PPSDs of the two sensors are comparable for all components over the entire frequency range. While the horizontal components are very similar, the vertical components differ from each other for frequencies below 0.03 Hz. This indicates that one sensor records elevated noise levels at lower frequencies. These as well as the higher noise levels for the horizontal components in the lower frequency range may be caused by air-pressure induced tilt (e.g., Alejandro et al., 2020; Rohde et al., 2017).

Figure. 13

Probabilistic power spectral densities (PPSD) for the 3-component test sensor (top) and reference sensor (bottom) over the whole experiment period of 260 days. In general, the PPSDs of the two sensors are comparable for all components over the entire frequency range. While the horizontal components (middle, right) are very similar (mean and mode are identical for both sensors for N and E components), the vertical components (left) differ from each other for frequencies below 0.03 Hz. The grey lines show the New High/Low Noise Models, respectively (Peterson, 1993)

4.2 Results of On-Site Measurements

In the course of the study, we applied the methodology described above to various sensor pairs in order to test the possibilities of traceable on-site calibration and frequency response determination. As several primary calibrated sensors were placed on-site, we were also able to perform a “cross-check”. This meant applying the methodology to two sensors for which the frequency response function is exactly known from the laboratory in order to test whether the methodology is able to obtain these values and to see where the limits lie with real world data. Here, we compared the following pairs with each other:

• A. Cross-check: broadband vs. short period seismometer, vertical axes only

  Reference: STS2.5

  SUT: GS13

• B. Two broadband seismometers, all three components/axes

  Reference: STS2.5

  SUT: CMG-3 T

Other combinations, such as for sensor pairs installed at a greater distance from each other, were not part of this study. For each combination, we calculated the complex gain ratio (Eqs. 11, 12) from which the respective gain ratios for amplitude (Eq. 16) and phase (Eq. 17) are obtained. Following the described approach (Eqs. 14, 18, 19), the values determined in the laboratory are used to estimate the final frequency response function of the respective SUT. Note that the digitizers and possible pre-amplifiers were included with the nominal values, as no calibration values were available yet. Figure 14 shows the results of the cross-check (experiment A) performed to validate the chosen on-site calibration approach. The broadband sensor serves as a reference, while the short period sensor is the sensor to be calibrated. The obtained gain ratios and subsequent frequency response functions cover a frequency range from 0.1 Hz to 20 Hz. Values for lower frequencies were not obtained in the laboratory calibration of the short period sensor.

Figure. 14

Results of experiment A. The amplitude (top) and phase (bottom) responses are shown as black asterisks for the laboratory calibration and as blue asterisks for the on-site calibration together with the nominal values (red) for a vertical GS13 seismometer

The expected nominal values provided by the manufacturer together with the ± 5% and ± 5° deviations for amplitude and phase are shown as solid and dotted red lines, respectively. Blue asterisks show the on-site calibration values and black asterisks the laboratory calibration values. The on-site measurements are in good agreement with the laboratory data, although they differ significantly from the nominal values, especially in amplitude (Fig. 15). This indicates the importance of performing both laboratory and on-site calibrations, rather than relying solely on nominal values. Notably, the discrepancy between the on-site, the laboratory, and the nominal readings is particularly intriguing for frequencies above approximately 4 Hz to 5 Hz.

Figure. 15

Differences between nominal (red) and laboratory (blue) and on-site (black) calibration values, respectively, for amplitude (left, in percent) and phase (right, in degree) for a vertical GS13 (experiment A). For frequencies below 5 Hz, the laboratory and on-site calibration values fit well, but show significant deviation from the nominal value, especially for the phase, for larger frequencies

The results of experiment B are shown in Fig. 16. Again, the determined ratios are shown as black, blue, and green asterisks with the respective uncertainties (coverage factor 95%, expansion factor k = 2) for each component. In comparison, the red curves show the nominal gain ratios based on the manufacturer’s specifications or on data based on the Incorporated Research Institutions for Seismology (IRIS) database. In addition, deviations of ± 5% (amplitude) and ± 5° (phase) are shown in order to be able to better classify the results. The gain ratios for both amplitude and phase deviate from the nominal values for frequencies larger than approximately 8 Hz (amplitude) and 2 Hz (phase), respectively. For lower frequencies, the obtained values meet the expectations. The propagated uncertainties are larger for the lower (< 0.08 Hz) and higher (> 8 Hz) frequencies. Between these frequencies, the ratios are characterized by small uncertainties, with fall inside the ± 5% (amplitude) and ± 5° (phase) limits. This also applies to the determined responses for the CMG-3 T sensor. Similar to experiment A, a large deviation from the expected value for frequencies greater than 8 Hz is seen.

Figure. 16

Results of experiment B (SUT: CMG-3 T; REF: STS2.5). Top left: amplitude gain ratio for vertical (black), north (blue), and east (green) component. Bottom left: phase gain ratio for north (blue) and east (green) component. The ratios are shown with the measurement uncertainty (coverage factor 95%, expansion factor k = 2) as error bars. Right panels show calculated amplitude (top) and phase (bottom) responses for the CMG-3 T, including the propagated uncertainty as error bars. In all panels, red lines show the nominal gain ratios and responses

The outcomes of experiment A’s cross-check and experiment B’s calibration of the broadband station sensor (CMG-3 T) demonstrate that the suggested on-site calibration method generates reliable and robust outcomes. Nonetheless, further examination is necessary for some observed points. This includes the variability in the uncertainties as well as the large observed deviations for the higher frequencies. Possible explanations are outlined in the following sections.

4.3 Real World Data

Challenges often arise with real world data that must be taken into account during an analysis. For on-site calibrations, this includes in particular the condition that the reference and test sensors should record the same coherent signal. Even when using the specified similarity measures, it is difficult to find sufficient time periods in which the conditions are met. In Fig. 17, the MSC between two co-located broadband seismometers (REF: STS2.5; SUT: CMG-3 T) is shown for all three components between 0.01 Hz and 20 Hz for a period of 260 days. While the MSC value is high for all three components for frequencies greater than 0.7 Hz, for the whole considered time period, the coherence decreases significantly around the end of November 2022 for lower frequencies. Moreover, a clear difference can be seen between the vertical (Z) and the two horizontal axes (N, E). During winter and spring, there are several periods when the MSC is high for the vertical, but low for both the horizontal components. Another notable feature is the reduced coherence for the vertical component for frequencies around 10 Hz to 11 Hz. This is also reflected in the percentage of data used in relation to all available data (Fig. 18). In the autumn months of 2022 (September—November) in particular, 50% and more of the available data was used for the analysis; in the winter and spring months (December—April), this was significantly less (< 20%).

Figure. 17

The coherency for frequencies between 0.01 Hz and 20 Hz is shown for two co-located three-channel broadband seismometers for time series of a day’s length for a total of 260 days. It is apparent that the time series are highly coherent for frequencies greater than 0.7 Hz for all three axes. Like the cross-correlation coefficients, the coherency changes to lower values for frequencies below 0.7 Hz between November and December 2022, especially for the horizontal axes. This demonstrates that not all times of the year at a particular station are suitable for the on-site calibration approach. Note that here the values are shown for an unfiltered time series of a whole day, whereas in the method, these were calculated within each window for the filtered data

Figure. 18

The percentage of used segments per considered frequency is shown for each month. As the values of the applied similarity measures drop below the threshold (see other figures), less data is used. For frequencies between 0.06 Hz and 5 Hz, between approximately 45% and 65% of available data segments could be used for the analysis, whereas this drops below 20% for the other months

This shows that periods in which a calibration can be carried out using the methodology explained above are not readily identifiable and may require a prior analysis of the signals registered at the station. Figure 18 also provides an explanation of the variations in the uncertainties between high, medium, and low frequencies. Small uncertainties have been observed especially for frequency ranges where many segments fulfil the similarity criteria. However, for the lower and upper ends, fewer segments are available, and the uncertainties become more pronounced. Additionally, large scattering in the determined values can be seen in these frequency ranges (Fig. 19). This indicates that as the number of segments utilized increases, the outcomes tend to become more stable.

Figure. 19

Scattering of calculated ratios for a time series of one day (left) and 15 days (right) for both amplitude (top) and phase (bottom). The nominal value for the SUT is shown as red curves, the weighted mean as orange asterisks /curves. Orange error bars represent the uncertainties in amplitude and phase gain, respectively (eqs. 18 and 19). Grey shaded areas show the distribution of all values that are included in the averaging. The darker the shaded area, the more values lie within these limits

There are several factors concerned with the installation and operation of the reference sensor that need to be considered when undertaking in-situ seismometer calibration.

Both the test and reference sensor should be based on the same operating principle and have a similar bandwidth (flat to velocity part of the response). However, as shown, it is also possible to compare different sensor types to a certain extent (experiment A). Following the choice of the reference, the co-location of the sensors is of great importance to ensure coherent signals are recorded. We are aware that co-location is not always possible for all stations, perhaps due to available space. Co-location in this context refers to placing the sensors as closely together as possible but can also include placing the sensors 5–10 m apart, such as in adjacent vaults. However, one needs to be aware that seismometers being apart limits both the time windows with usable coherence and frequency passband because small distances relative to the signal wavelength lead to differences in the relative frequency response between them. The possibility of calibrating sensors that are further apart (e.g., array-wide calibration) still requires further investigation and will be carried out in the future. When installing (temporary) reference sensors, one must consider several factors like those involved in the installation of (permanent) field sensors. These include the orientation and levelling of the sensor and the alignment of the reference sensor in relation to the test sensor. A possible misalignment between the reference and the test/field sensor can be checked later on the basis of the measured data and the application of controlled sources.

Ideally, both sensors should be installed in the same vault/on the same pier as close to each other as possible. Different vaults/piers can behave differently for the same ground movement as a result of not being identical in their construction and local effects. Moreover, the influence of air pressure is also a possible factor to consider, particularly at low frequencies (< 0.03 Hz). It is well known that seismic instruments respond to local atmospheric pressure changes with elevated noise levels especially on the horizontal components as an effect of tilting in response to changes in pressure (e.g., Alejandro et al., 2020; Rohde et al., 2017). Even in a single vault, tilt by pressure variations may introduce incoherent signals on the seismometers. As a result, there may not be enough time windows that fulfil the similarity conditions for the analysis.

Ideally, both sensors should sample the signal at the same rate. The sample times should be adjusted for one signal to lead to an accurate analysis. This adjustment can be achieved by re-sampling the data (e.g., experiment A). However, re-sampling the data can lead to a reduction in resolution and the loss of higher frequencies that could be significant. Additionally, the use of integrated anti-alias filters during re-sampling can affect the calibration outcomes. Therefore, it is crucial that the samples are collected at precisely the same time to ensure accurate results.

To fully ensure traceability, the recording unit (pre-amplifier, digitizer), which converts the analogue signal to a digital one with precise timestamping, needs to be traceably calibrated as well. As this was not the case in this study, nominal values were used. This could be one reason for possible small overall shifts of the results in comparison with the expected value as seen in the amplitude response for experiment A. Wherever possible, both the test and reference sensor should be connected to the same digitizer to eliminate any potential influence of the digitizer on calibration results, as well as non-synchronization effects. If the same digitizer is used for both the reference and the field/test seismometer, its transfer function will be excluded from the analysis. If two separate digitizers must be used, time synchronization must be considered. The CTBTO requires the recording units within the IMS to have a timing accuracy of better than 10 ms with a timing accuracy of less than 1 ms between inter-array elements. However, this is not given for every station or network worldwide. If the sensors or sensor systems are not precisely synchronized in time, this can result in inaccurate phase determination during analysis, particularly in higher frequency ranges. A timing error will result in a linear deviation of the phase with increasing frequency (linear frequency axis; Fig. 20 a). A preliminary check for such behaviour entails computing the time lag between both time series. This is done within each frequency band and for the unfiltered time series, for example, by applying cross-correlation. Assuming both sensors record the same coherent signal and are situated nearby, there ought to be no time discrepancy between the signals.

Figure. 20

Visualization of a possible time delay between two sensors/acquisition units. The time delay results in a linear phase drift, which becomes evident in a linear frequency axis scaling (a). Applying Eqs. 22 and 23, the phase shift and a corrected value can be calculated. The corrected phase values are shown in b as black asterisks, while the original shifted phase values are shown in blue

The shift of the phase caused by timing errors is given by

$$\begin{array}{*{20}c} {\varphi_{{\text{shift}}} = t_{{\text{delay}}} {\rm{ \cdot }}360{\rm{ \cdot }}f} \\ \end{array}$$

(24)

with the time difference $t_{{\text{delay}}}$ (lag) between the signals given in seconds and the frequency f in Hz. Knowing the time delay between the signals and the resulting phase shift, the phase can be corrected:

$$\begin{array}{*{20}c} {\varphi_{{\text{corr}}} = \varphi_{{\text{obs}}} - \varphi_{{\text{shift}}} } \\ \end{array}$$

(25)

Figure 20 shows how such a timing error appears in the phase response. The corrected phase response values are shown as black asterisks in Fig. 20 b. The values now fit well with the previous course of the values and the expected behaviour.

An error in timing of just 0.1 samples (equivalent to 0.001 s with a sampling frequency of 100 Hz) leads to a phase shift of 0.0036° at a frequency of 0.01 Hz, and phase shifts of 0.036°, 0.36°, and 3.6° at frequencies of 0.1 Hz, 1 Hz, and 10 Hz, respectively. However, tests have indicated that a delay of at least 0.005 s (0.5 samples) is anticipated. This suggests that the time bases may be synchronized, but the exact sampling times remain uncertain. In this scenario, each channel would experience a random delay of 0 samples to 1 sample between the designated starting time and the first sampling instance. The period of delay would depend on the exact time the digitizer initiated the sampling process. On average, there would be a delay of half a sample when comparing two traces from distinct digitizers. Additionally, it is worth noting that a small distance between co-located seismometers can also cause time delays, as seismic waves may reach one sensor before the other.

The deviation between the calculated and nominal amplitude response curves for frequencies higher than 8 Hz for all three components of the CMG-3 T seismometer may represent the actual behaviour of the seismometer to ground motion. As this effect is observed for both experiments where the STS2.5 has been used as the reference sensor, it might be caused by its laboratory determined response, which shows some deviations from the expected values that need further investigation.

Lastly, it is recommended that the on-site calibration experiment lasts for at least 15 days. The duration of the experiment is dependent on the considered frequencies and on the signals recorded at the station. The lower the frequencies to be calibrated, the longer the duration of the experiment. There might be periods when there are fewer coherent signals than at other times (Fig. 17), as some signals might be seasonal. Furthermore, longer periods of time provide a larger sample size for averaging (Fig. 18), more stable results (Fig. 19), and allow for the investigation of seasonal fluctuations in the station’s behaviour, such as temperature differences or variations in dominant signals (Fig. 21).

Figure. 21

Temperature measured within the vault of the reference sensor from September 2022 to May, 2023. Temperature values are available every five minutes. The peaks around the 10th October 2022 are related to maintenance work at the vault and repeated opening of the lid

It is advisable to calibrate the reference sensor under similar conditions to those found at the seismic station or to know its behaviour under different environmental conditions. This is particularly relevant when using different sensors as reference and test sensors, as their behaviour may differ under varying conditions. Over the duration of the experiment, the temperature within the vault (measured in a height of ca. 2 m above the seismometers) varied in total about 8.2 °C (T_max = 12.8 °C; T_min = 4.6 °C, Fig. 21). Seasonal changes as observed here, should not interfere with the seismic signals (Wielandt, 2012). Doody et al. (2018) mention that the velocity output of the STS2.5, which serves here as a reference sensor, is the least sensitive to temperature of the seismometers they compared in their study. The air pressure within the vault varied between 859 and 906 hPa. If tilt is induced by varying air pressure, and the seismometers behave differently due to that, these times are likely to be excluded from the analysis as the coherency between them is below the predetermined threshold. Humidity can modify the response of a seismometer and may cause corrosion inside the sensor and/or lower than normal sensitivities if leaking into the sensor (e.g. Forbriger et al., 2010; Hutt & Ringler, 2011). This may show up as spikes in the record. We do not observe this behaviour; therefore, humidity does not seem to be an issue. The vaults are further equipped with air dehumidifiers.

If the sensor and the reference sensor respond similarly to environmental fluctuations like temperature, pressure, or humidity, an in-situ technique is unlikely to detect such changes.

5 Summary and Outlook

The traceable calibration of seismometers has many benefits. For station operators, it is possible to compensate for the transfer function of the whole seismometer including the coupling to the ground. This makes the replacement of seismometers with different (more modern or better types) possible while retaining the comparability of old and new data. Moreover, this goes beyond the state of the art, which is an electrical calibration of the internal measurement mechanics, which—by principle—cannot detect the transfer function between the seismometer and the ground.

Although requiring some effort the proposed on-site calibration procedure enables further possibilities beyond calibration: By permanently operating reference seismometers at stations, compliance with certain requirements such as the CTBTO specification of a tolerance of ± 5% for amplitude and ± 5° for phase will be constantly monitored. This increases the confidence in the operation of the monitoring system/network and validity of the data and subsequently the data analysis. Seasonal fluctuations and environmental influences on the seismometers can also be better analysed and considered. In this way, possible changes to the response function can be quickly incorporated into the metadata or defects can be recognized and corrected. The specification of uncertainties in the measured amplitude and phase values, which can be transferred by means of uncertainty propagation to the parameters determined from the recorded ground movements (origin time or location for earthquakes), is an additional benefit providing more reliable results.

Basing these calibrations on the SI instead of on special sensors, for instance, allows international comparability and a calibration which can be traced back to the base units of the SI.

This paper shows how a traceable calibration can be realized on-site using reference sensors that have been calibrated in a laboratory and are then used for calibrations on-site. Examples based on real data from a station show the data analysis and results of such a calibration. The results of the cross-check experiment with two sensors with known response functions as well as the first conducted traceable on-site calibration provide reliable results, showing that the proposed on-site calibration method can be applied to real world data. However, the reference seismometer does need occasional recalibration as it is a secondary standard. The total combined uncertainty estimate for the operational field seismometer depends on the uncertainty of the reference, which increases the more calibration steps are included between the laboratory and the field sensor, as well as on environmental factors which still have a largely unknown contribution to the uncertainty budget. The signals and time periods used are a source of uncertainty, particularly with regard to the similarity condition of the proposed approach and possible timing inaccuracies resulting from different digitizers. Nevertheless, with a prior analysis of data from existing stations and the knowledge of possible issues, this might just be a minor challenge. Future work is still required to incorporate the full operational acquisition unit into the calibration chain. Additionally, to reach the operational requirement of the IMS of ± 5%/ ± 5° over the whole frequency bandwidth, the primary calibration, especially for the lower end of the frequency range, has to improve in the future.

In the future, a thorough assessment of the measuring uncertainties from the laboratory to the site will be necessary. For such an assessment, more information about the sensitivity to environment influences and the stability of the travelling references is still needed.