1 Introduction

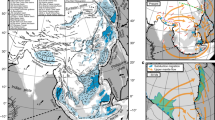
The free-air gravity anomaly in the plate subduction zones exhibits a single set of negative and positive trench-parallel belts in the overriding plate and a single positive belt in the descending plate. Generally, these gravitational belts correspond to the topography of the trench, island arc and outer rise. In certain regions along the Aleutian, Sunda and Middle American trenches, doubled negative–positive trench-parallel belts appear in the overriding plates. In the case of the Aleutian subduction zone, only the eastern region exhibits the gravitational double-arc characteristics (Fig. 1). The eastern Aleutian subduction zone exhibits a similar doubled topography comprising the inner (landward) volcanic chain of the Alaska Peninsula and its northeastward extension and the outer (seaward) nonvolcanic chain of the Kenai Peninsula, the Kodiak group of islands (Kodiak Islands), and the other islands in the fore-arc region (Fig. 1). The eastern inner–western topographic arc (i.e. the volcanic arc of the Alaska Peninsula and the Aleutian Islands) coincides with the eastern inner–western positive gravitational belt, whereas the eastern outer topographic arc (i.e. the Kenai–Kodiak nonvolcanic arc) does not coincide with the eastern outer positive gravitational belt. The remarkable outer-arc characteristics have been considered relevant to underplating (i.e. a deep accretion process of the descending materials to the base of the overriding plate) (Clendenen et al., 1992; Moore et al., 1991; Ye et al., 1997), large-scale terrane subduction (von Huene et al., 1985), low dip-angle subduction (Jadamec et al., 2013; Pavlis & Bruhn, 1983) and plate interface frictional properties (Bassett & Watts, 2015; Song & Simons, 2003). Recently, Menant et al. (2020) demonstrated that the sequential occurrence of the underplating and their spatial scale can prescribe topographic transitions and trench-parallel variations. However, owing to such diverse interpretations, the essence of the topographic and gravitational double-arc formations as well as their relation remains unconfirmed.

Figure 1
figure 1

Topography and free-air gravity anomaly in the Aleutian subduction zone. a Topography is based on ETOPO1 (Amante & Eakins, 2009). The dotted circles indicate oceanic basins (von Huene et al., 1980). Abbreviations CI, SS, St, Al, Tu, Sh and Sa denote the Cook Inlet, the Shelikof Strait and the Steavenson, Albatross, Tugidak, Shumagin and Sanak basins, respectively, and NA and PA denote the North American and Pacific plates, respectively. Red triangles indicate the location of the Holocene volcanoes listed by Global Volcanism Program (2013). b Free-air gravity anomaly is based on the WGM2012 global model (Bonvalot et al., 2012)

Full size image

The free-air gravity anomaly primarily reflects the mass excess and deficit on the Earth’s surface. The gravitating topographic system must undergo mass redistribution and isostatic adjustments. Therefore, a supporting mechanism against the gravitation is required to maintain the mass excess and deficit over a long period. This mechanism in the subduction zones typically involves long-term tectonic uplift and subsidence that are the direct consequences of the plate-to-plate interaction. Multiple models have been proposed to reproduce the topographic and gravitational characteristics of the island-arc–trench system, such as the flexure of the elastic lithosphere (Davies, 1981) and viscous flow subduction (Zhong & Gumis, 1992). The dislocation-based modelling proposed by Matsu’ura and Sato (1989) is one of the most well-defined mechanical approaches for solving these problems. In their model, the mechanical interaction is represented by the steadily increasing tangential displacement discontinuity across the curved plate interface.

In this study, we focus on two problems related to the formation of the double-arc system in the eastern Aleutian subduction zone and the deviations in the location between the topographic and gravitational outer arcs. By developing a Matsu’ura–Sato type model, we demonstrated the mechanical essence of the former problem. Subsequently, to interpret the current tectonic state, we compared the computed vertical crustal motion with the topography and free-air gravity anomaly.

2 Two-Dimensional Subduction Modelling

According to a systematic description by Backus and Mulcahy (1976a, 1976b), the displacement discontinuity across the internal surface in a continuum is expressed as the mathematically equivalent force in the continuum. In this context, the tangential displacement discontinuity along the curved plate interface can be a definite description of the plate-to-plate interaction that causes displacement and deformation in the plate interior (Matsu’ura and Sato, 1989). Herein, we considered a plate interface in a two-dimensional (2D) cross section of the subduction zone. If the 2D plate interface geometry is a perfectly circular arc with a constant curvature, a symmetric configuration of its uniform slip represents the vertical rotation of the plates with respect to a single horizontal axis, i.e. the centre of curvature. On the basis of this consideration, Fukahata and Matsu’ura (2016) demonstrated that the mechanical essence of the single island-arc–trench system formation is a combination of the following two effects: (1) vertical rotation of the descending and overriding plates in the opposite directions along the circular curve, which generates a concave bend corresponding to the trench low and elevates both the trench sides and (2) gravitational depression on both sides at distances from the trench, which generates convex bends corresponding to the island-arc and outer-rise highs. A combination of a circular-arc-like curve in the shallow part and a straight line in the deep part also reproduced such a basic single-arc pattern, as demonstrated in a series of studies by Matsu’ura and his co-workers (Fukahata & Matsu’ura, 2006, 2016; Hashimoto et al., 2004, 2008; Matsu’ura & Sato, 1989; Sato & Matsu’ura, 1988, 1992, 1993).

Considering the stress continuity condition on the plate interface, we expressed this basic plate interface curve as a twice continuously differentiable function \(z\left(y\right)\) with continuous first and second derivatives \({z}^{\prime}\) and \({z}^{{\prime}{\prime}}\), where \(z\) and y denote the depth and the horizontal distance from the trench, respectively. Subsequently, we proposed a method to express the more complicated geometry of the plate interface. The concrete procedure is illustrated in Fig. 2 and elaborated in the Methods section. Note that \({z}^{{\prime}{\prime}}\) indicates the curvature \(1/R={z}^{{\prime}{\prime}}/{\left(1+{z}^{\prime}\right)}^{3/2}\) in the case of \({z}^{\prime}\ll 1\), i.e. low-angle subduction.

Figure 2
figure 2

Schematic diagrams of the definition of the elemental functions and their superposition. a The second derivative \({z}^{{\prime}{\prime}}\) of the elemental function is defined as a continuous piecewise linear function with three knot points \({y}_{0}\), \({y}_{1}\) and \({y}_{2}\). The second derivative has a single peak at \({y=y}_{1}\) and becomes zero on both sides (\(y\le {y}_{0}, {y}_{2}\le y\)). b The first derivative \({z}^{\prime}\) is obtained by integrating the second derivative under the condition of continuity at each knot point and the conditions of \({z}^{\prime}=0\), \(\tan \theta\) at \(y={y}_{0}, {y}_{2}\). \(\theta\) represents a constant dip angle and determines the peak of \({z}^{{\prime}{\prime}}\). c The original elemental function \(z\left(y\right)\) is obtained by integrating the first derivative under the condition of continuity at each knot point and the condition of \(z=0\) at \(y={y}_{0}\). d The second derivative \({z}^{{\prime}{\prime}}\) of a composite function with \(N+2\) knots \({y}_{i}\) \(\left(i=0, 1, 2, \cdots , N+1\right)\) is defined as a continuous piecewise linear function obtained through the superposition of the second derivatives of \(N\) elemental functions. The i-th \(\left(i=1, 2, \cdots , N\right)\) elemental function is defined by one constant \({\theta }_{i}\) and three knots \({y}_{i-1}\), \({y}_{i}\) and \({y}_{i+1}\). Three-element superposition with five knots is demonstrated. e The first derivative \({z}^{\prime}\) of the composite function is obtained through the superposition of the first derivatives of \(N\) elemental functions. f The original composite function \(z\left(y\right)\) is obtained through the superposition of \(N\) elemental functions

Full size image

3 Methods

3.1 Basic Plate Interface Geometry

The basic plate interface geometry was modelled in a 2D cross section by combining an arc-like curve in the shallow part and a straight line with a dip angle \(\theta\) in the deep part. The arc-like curve was connected to a horizontal line (Earth’s flat surface) at the trench axis. To express such a monotonically increasing function (elemental function) that is twice continuously differentiable, we first defined the second derivative \({z}^{{\prime}{\prime}}\) as a continuous piecewise linear function with three knot points \({y}_{0}\), \({y}_{1}\) and \({y}_{2}\) as follows:

$$\frac{d^2 z}{{dy^2 }} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\left( { y < y_0 } \right)} \hfill \\ {\frac{{2 \tan \theta }}{{\left( { y_1 - y_0 } \right)\left( { y_2 - y_0 } \right)}}\left( { y - y_0 } \right)} \hfill & {\left( { y_0 \le y < y_1 } \right)} \hfill \\ { - \frac{{2 \tan \theta }}{{\left( { y_2 - y_1 } \right)\left( { y_2 - y_0 } \right)}}\left( { y - y_2 } \right)} \hfill & { \left( { y_1 \le y < y_2 } \right)} \hfill \\ 0 \hfill & {\left( { y_2 \le y } \right)} \hfill \\ \end{array} } \right.,$$
(1)

where \(y\) denotes the horizontal distance from the trench axis, and \({y}_{0}\), \({y}_{1}\) and \({y}_{2}\) correspond to the trench axis, the location of the peak of the second derivative and the shallower end of the deep-part straight line, respectively (Fig. 2a). Next, by integrating this second derivative twice under the condition of continuity at each knot point, we obtained the first derivative \(z^{\prime}\) (Fig. 2b) and original elemental function \(z\) (Fig. 2c) as follows:

$$\frac{dz}{{dy}} = \left\{ {\begin{array}{*{20}l} 0 \hfill & { \left( { y < y_0 } \right)} \hfill \\ {\frac{\tan \theta }{{\left( { y_1 - y_0 } \right)\left( { y_2 - y_0 } \right)}}\left( { y - y_0 } \right)^2 } \hfill & {\left( { y_0 \le y < y_1 } \right)} \hfill \\ { - \frac{\tan \theta }{{\left( { y_2 - y_1 } \right)\left( { y_2 - y_0 } \right)}}\left( { y - y_2 } \right)^2 + \tan \theta } \hfill & {\left( { y_1 \le y < y_2 } \right)} \hfill \\ {\tan \theta } \hfill & { \left( { y_2 \le y } \right)} \hfill \\ \end{array} } \right.$$
(2)

and

$$z = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\left( { y < y_0 } \right)} \hfill \\ {\frac{\tan \theta }{3}\frac{1}{{\left( { y_1 - y_0 } \right)\left( { y_2 - y_0 } \right)}}\left( { y - y_0 } \right)^3 } \hfill & {\left( { y_0 \le y < y_1 } \right)} \hfill \\ \begin{gathered} - \frac{\tan \theta }{3}\frac{1}{{\left( { y_2 - y_1 } \right)\left( { y_2 - y_0 } \right)}}\left( { y - y_2 } \right)^3 \hfill \\ + \tan \theta \, y - \frac{\tan \theta }{3}\left( { y_2 + y_1 + y_0 } \right) \hfill \\ \end{gathered} \hfill & {\left( { y_1 \le y < y_2 } \right)} \hfill \\ {\tan \theta \, y - \frac{\tan \theta }{3}\left( { y_2 + y_1 + y_0 } \right)} \hfill & {\left( { y_2 \le y } \right)} \hfill \\ \end{array} } \right..$$
(3)

3.2 Complicated Plate Interface Geometry

To represent a more complicated plate interface geometry, we superposed N elemental functions by shifting their knot points. We defined the \(N+2\) knot points \({y}_{i}\) \(\left(i=0, 1, 2, \cdots , N+1\right)\) for a single curve and assigned the first three knots \({y}_{0}\), \({y}_{1}\) and \({y}_{2}\) to the first elemental function with the constant \({\theta }_{1}\) and the three subsequent knots \({y}_{1}\), \({y}_{2}\) and \({y}_{3}\) to the second elemental function with the constant \({\theta }_{2}\). This procedure was iterated until the last three knots \({y}_{N-1}\), \({y}_{N}\) and \({y}_{N+1}\) were assigned to the \(N\)-th elemental function with the constant \({\theta }_{N}\). By such superposition, the second derivative \({z}^{{\prime}{\prime}}\) was expressed as a continuous piecewise linear function, and its integrated functions \({z}^{\prime}\) and \(z\) were expressed as continuous piecewise quadratic and cubic functions, respectively (Fig. 2d, e and f). When the elemental function with the knots \({y}_{0}\), \({y}_{1}\) and \({y}_{2}\) and the dip angle \(\theta\) is explicitly represented by \({z}^{elem}\left({y; {y}_{0}, {y}_{1}, y}_{2}; \theta \right)\), the three-element composite function with the five knots (\({y}_{0}, {y}_{1}, {y}_{2}, {y}_{3}\) and \({y}_{4}\)) and the three constants (\({\theta }_{1}, {\theta }_{2}\) and \({\theta }_{3}\)) (Fig. 2f) is expressed as \(z\left(y\right)={z}^{elem}\left({y; {y}_{0}, {y}_{1}, y}_{2}; {\theta }_{1}\right)+{z}^{elem}\left({y; {y}_{1}, {y}_{2}, y}_{3}; {\theta }_{2}\right)+{z}^{elem}\left({y; {y}_{2}, {y}_{3}, y}_{4}; {\theta }_{3}\right)\).

4 Application to the Aleutian Subduction Zone

We modelled the plate interface geometry of the western and eastern Aleutian subduction zones (i.e. the regions of the Aleutian Islands and Alaska Peninsula) in 2D cross sections along Lines 1 and 2 (Fig. 1), respectively, on the basis of hypocentre data (Reviewed ISC Bulletin) (Bondár & Storchak, 2011; International Seismological Centre, 2022), centroid moment tensor (CMT) mechanism data (Global CMT Catalog) (Dziewonski et al., 1981; Ekström et a., 2012) and topography data (ETOPO1) (Amante & Eakins, 2009). The basic conditions for constructing the models are stated as follows: the plate interface curve (1) passes through the hypocentres of large magnitude or moment magnitude (M, Mw \(\ge\) 6) low-angle reverse-fault-type earthquakes, (2) traces the topmost components of the deep hypocentre distribution and (3) is continuously connected to the Earth’s flat surface at the trench axis. We permitted a certain violation of condition 1 near the trench because of condition 3, which may not essentially affect the results in this study.

The cross sections of the Aleutian and Alaska plate interface models determined for Lines 1 and 2, respectively, are displayed in Fig. 3. We assigned five knots for three-element superposition (Fig. 2). In the case of the Line-1 model, the knot points \({y}_{0}, {y}_{1}, {y}_{2}, {y}_{3}\) and \({y}_{4}\) were determined as 0, 30, 115, 250 and 300 km, respectively, and the constants \({\theta }_{1}, {\theta }_{2}\) and \({\theta }_{3}\) of the three elemental functions were determined as 20°, 25° and 40°, respectively. The second derivative and corresponding curvature of the Line-1 model curve exhibited single-modal distribution within the interval of 0 \(<y<\) 300 [km] with a slight concavity at \(y=\) 115 [km]. The plate interface attained a depth corresponding to the lithosphere–asthenosphere boundary (\(z=\) 50 [km]) at a horizontal distance of 148 km. This indicates that only the shallower half section of the curvature distribution exists within the thickness of the elastic lithosphere.

Figure 3
figure 3

Hypocentre distribution and 2D plate interface models. Hypocentres within the 150-km-wide zones along Lines 1 and 2 are projected on the cross sections. Black and green circles represent the hypocentres of M \(\ge\) 4.5 and M \(\ge\) 6 events, respectively, obtained from the Reviewed ISC Bulletin during 01/01/1964–01/06/2020 (Bondár & Storchak, 2011; International Seismological Centre, 2022). Red solid and open circles represent the hypocentres of Mw \(\ge\) 6 low-angle reverse-fault type and other type events, respectively, obtained from the Global (Harvard) CMT Catalog during 01/01/1976–01/01/2021 (Dziewonski et al., 1981; Ekström et a., 2012). Connected pair of the green and red hypocentres represents the identical event from the two catalogues. Blue lines represent the plate interface geometry and the corresponding second derivative along Line 1 (top) and Line 2 (bottom); their knot points are represented by \({y}_{0}, {y}_{1}, {y}_{2}, {y}_{3}\) and \({y}_{4}\). Grey line represents the surface topography (ETOPO1) (Amante & Eakins, 2009). Cyan lines represent the modified plate interface under the non-flat surface condition and its second derivative along Line 1 (top) and Line 2 (bottom). Magenta curve indicates the Slab2 model (Hayes et al., 2018). Black inverted triangle indicates the location of the trench axis

Full size image

In the case of the Line-2 model, the five knot points (\({y}_{0}, {y}_{1}, {y}_{2}, {y}_{3}\) and \({y}_{4}\)) were 0, 30, 100, 400 and 480 km, respectively, and the three constants (\({\theta }_{1}, {\theta }_{2}\) and \({\theta }_{3}\)) were 8°, 0° and 50°, respectively. The dip angle of the Line-2 model curve was significantly lower than that of the Line-1 model curve at shallow depths (Fig. 3). The second derivative and corresponding curvature of the Line-2 model curve exhibited a bimodal distribution. Their two intervals of 0 \(<y<\) 100 [km] and 100 \(<y<\) 480 [km] corresponded to the depth ranges of 0 \(<z<\) 8 [km] and 8 \(<z<\) 244 [km], respectively. This indicates that a substantial portion of the deeper section as well as the shallower section exists within the thickness of the lithosphere (50 km). The Line-1 and -2 model curves were consistent with another plate interface model such as Slab2 (Hayes et al., 2018) in the lithosphere, except for an extremely shallow part connected to the flat surface at the trench (Fig. 3). The deviation between the Line-1 and Slab2 model curves in the asthenosphere may reflect the interpretation of the hypocentre distribution.

Furthermore, we computed the vertical surface velocity (uplift rate) induced by the steady slip along the Line-1 (Aleutian) and -2 (Alaska) model plate interfaces using a Matsu’ura–Sato type model that is based on the elastic–viscoelastic dislocation theory (Matsu’ura & Sato, 1989). The foundational mathematical expressions for the 2D framework computation are elaborated in studies by Sato and Matsu’ura (1993) and Fukahata and Matsu’ura (2005, 2006). The lithosphere–asthenosphere system was modelled as an elastic layer with a flat surface under gravity and an underlying Maxwellian viscoelastic half-space. The thickness of the lithosphere was assumed to be 50 km (and 40 km for reference) in the cases of the Line-1 (Aleutian) and Line-2 (Alaska) models. We employed typical values of the structural parameters as follows: the densities of the lithosphere and asthenosphere were 3000 and 3400 kg/m3, respectively; the Lamé elastic constants \(\lambda\) and \(\mu\) were 40 and 40 GPa, respectively, for the lithosphere, and 90 and 60 GPa, respectively, for the asthenosphere; the viscosity of the asthenosphere was 5 \(\times\) 1018 Pa s (Hashimoto & Matsu’ura, 2004, 2008). Note that the value of the viscosity does not affect the computational results because the steady slip on the plate interface in the asthenosphere cannot contribute to the formation of the long-term surface displacement field (Fukahata & Matsu’ura, 2006; Matsu’ura & Sato, 1989). The trench-perpendicular component of the relative velocity between the Pacific (PA) and North American (NA) plates calculated from MORVEL (DeMets et al., 2010) was imposed as the steady slip rate on the 2D plate interface. The calculated components in the cases of Line 1 and Line 2 were 6.6 and 6.1 cm/year, respectively.

5 Results

The computed surface uplift rates for the Line-1 and Line-2 models are displayed in Fig. 4. The computed surface pattern of the Line-1 model (Aleutian) exhibited uplift (\(\sim -300<y<-90\) [km]), subsidence (\(-90<y<63\) [km]) and uplift (\(63<y<380\) [km]), corresponding to the typical characteristics of a single-arc system (Fig. 4a). The maximum rates of the subsidence and uplift were 8.2 mm/year near the trench and 2.4 mm/year at \(y\approx 115\) [km], respectively. The topography (ETOPO1) (Amante & Eakins, 2009) and free-air gravity anomaly (WGM2012 global model) (Bonvalot et al., 2012) along Line 1 are displayed in Fig. 4a, exhibiting single-arc patterns similar to the computed uplift rate of the Line-1 model. The computed uplift rate adequately reproduced the ranges of the trench low and island-arc high of the single-arc system in the western Aleutian subduction zone.

Figure 4
figure 4

Comparison of the computed surface uplift rate with the topography and free-air gravity anomaly. Three solid black lines in both the panels a and b represent the topographic (ETOPO1) (Amante & Eakins, 2009) profile, gravitational (WGM2012 global model) (Bonvalot et al., 2012) profile and uplift rate computed for the 50-km-thick lithosphere. The uplift rates for the 40-km-thick lithosphere are represented by black dotted lines for reference. Red shaded areas indicate the uplift zones of the computed uplift rate profiles. Blue lines in the bottoms of the panels a and b represent the depths of the plate interfaces. The steady plate subduction is represented by the steady slip (steadily increasing tangential displacement discontinuity) uniformly imposed on the plate interface. a The computed uplift rate of the Line-1 model (Aleutian) is compared with the topographic and gravitational profiles along Line 1. b The computed uplift rate of the Line-2 model (Alaska) is compared with the topographic and gravitational profiles along Line 2. The green lines represent the topographic and gravitational profiles of Line \({2}^{\prime}\) that crosses the oceanic (Tugidak) basin located in the southwest offshore area of the Kodiak group of islands (Fig. 1). Four-times enlarged computed profiles are indicated by blue solid and dotted lines

Full size image

The computed surface pattern of the Line-2 model (Alaska) exhibited uplift (\(\sim -300<y<-95\) [km]), subsidence (\(-95<y<37.5\) [km]), uplift (\(37.5<y<125\) [km]), subsidence (\(125<y<270\) [km]) and uplift (\(270<y<600\) [km]), corresponding to the typical characteristics of a double-arc system (Fig. 4b). The peak values of the outer and inner uplifts were 1.9 mm/year at \(y\approx 75\) [km] and 0.3 mm/year at \(y\approx 355\) [km], respectively. The peak values of the trench subsidence and subsidence between the outer and inner uplift zones were 2.3 and 0.8 mm/year, respectively. The topography and free-air gravity anomaly along Line 2 (and Line \({2}^{\prime}\) illustrated in Fig. 1 for reference) are displayed in Fig. 4b. The computed uplift rate adequately reproduced the lows and highs of the double-arc system observed in the gravitational profile in the eastern Aleutian subduction zone. However, the computed and gravitational outer-arc highs did not coincide with the topographic outer-arc high of the Kodiak Islands. In contrast, the computed and gravitational outer-arc highs coincided with the seaward edge of the continental shelf, wherein the basement high was detected from the sedimentary structures of the oceanic basins (Moore et al., 1991; von Huene et al., 1980).

6 Discussion

As mentioned in the model description, the steady slip along the curved plate interface within the elastic lithosphere can serve as the mechanical source of the intraplate deformation fields. In the case of the Line-1 model (Aleutian), the nearly single-modal curvature distribution in the elastic lithosphere formed a single set of trench low and island-arc high in the overriding plate. In the case of the Line-2 model (Alaska), the shallower and deeper high-curvature sections located in the lithosphere formed the doubled trench-parallel subsidence–uplift belts in the overriding plate. This finding implies that the bimodal distribution of the curvature provides two distinct horizontal axes for the vertical rotation of the overriding plate and causes doubled concave–convex bending (i.e. doubled subsidence–uplift).

To examine the mechanical origin of the double-arc characteristics, we decomposed the original bimodal function of the Alaska model plate interface into two elemental functions that correspond to the shallower and deeper high-curvature sections of the original function (Fig. 5). The steady slip along each single-section model plate interface induced the surface uplift rate exhibiting a single set of trench low and island-arc high (Fig. 5). The profiles were characterised by shorter-wavelength rapid subsidence–uplift for the shallower-section model and by longer-wavelength gentle subsidence–uplift for the deeper-section model. The outer-arc high of the original double-arc profile almost coincided with the island-arc high of the single shallower-section model. The original inner-arc high almost coincided with the 100-km-shifted island-arc high of the single deeper-section model. This shift of 100 km represents the horizontal distance from the trench axis (\({y}_{0}\)) to the shallower end point of the deeper section (\({y}_{2}\)) of the original plate interface (Fig. 5). Consequently, the double-arc characteristics were approximately reproduced by the superposition of the two single-section models. This indicates that a low dip angle and a bimodal curvature distribution within the lithosphere form the mechanical essence of the double-arc formation.

Figure 5
figure 5

Decomposition of the Line-2 (Alaska) model plate interface geometry. a The black line indicates the uplift rate computed from the original Alaska model. The green and red lines indicate the uplift rates computed from the subduction models for the decomposed shallower- and deeper-section elemental plate interfaces, respectively. The red dotted line represents the 100-km-shifted uplift rate profile of the deeper-section elemental model. Red shaded areas indicate the uplift zones of the original Alaska model. b The black, green and red lines represent the plate interfaces of the original Alaska model, decomposed shallower-section elemental model and decomposed deeper-section elemental model, respectively. c The black, green and red lines represent the second derivatives of the original bimodal Alaska model, decomposed shallower-section single-modal model and decomposed deeper-section single-modal model, respectively. The shallower end point of the deeper section (knot point \({y}_{2}=\) 100 [km]) of the original bimodal model corresponds to the trench axis of the single deeper-section elemental model

Full size image

By shifting the plate interface model downwards (i.e. adding the trench depth \({z}_{0}\) to the original composite function) and decreasing the dip angle of the first elemental function (i.e. constant \({\theta }_{1}\)), we obtained the modified plate interface that can explain the shallow hypocentres (Fig. 3). The downward shift \({z}_{0}\) and modified constant \({\theta }_{1}\) were determined as 7.2 km and 18°, respectively, for the Line-1 model and 5.4 km and 7.2°, respectively, for the Line-2 model. These modifications did not significantly affect the second derivatives (Fig. 3), implying that the mechanical essences of the single-arc and double-arc formations were maintained under the flat surface condition of the original models as well as the realistic non-flat surface condition.

The Kenai Peninsula and the Kodiak Islands are surrounded by the Cook Inlet, Shelikof Strait and other multiple basins (Fig. 1). The long-term trend of the vertical motion in this area was interpreted as submergence from the coastal geomorphology, radiocarbon dates of the costal site materials and cirque floor levels in an early exhaustive report after the occurrence of the Alaska earthquake in 1964 (Mw = 9.2) (Plafker, 1969). In this context, Plafker (1969) regarded the topographic high of the Kenai and Kodiak Mountains as ‘anomalous’. However, later observation data partially indicated an upward trend and provided complicated details. The sedimentary core samples over multiple earthquake generation cycles (Bartsch-Winkler et al., 1983; Hamilton & Shennan, 2005; Shennan et al., 2014) agreed with the expected submergence during the past several thousand years for the coastal areas on the landward (lowland) side of the Kenai Peninsula. In contrast, apatite (U–Th)/He dating (low-temperature thermochronometry) revealed small exhumation rates on the trench-ward (mountain) side of the Kenai Peninsula (Buscher et al., 2008; Valentino, et al., 2016), implying a gradual upward motion. Similarly, the marine terrace elevation in the Kodiak Islands indicates insignificantly small emergence rates during the past 130 kilo years, except for the moderate emergence rates observed in the trench-ward-side coastal area (Carver et al., 2008).

In addition, an uplift axis along the trench in the eastern Aleutian subduction zone can be expected from the alignment of multiple basins bounded on their margins by the continental shelf edge (Fig. 1). The recent (< ~ 5 Ma) formation of the shelf edge high is crucial for preventing the flow of sediments towards the trench (Fisher & von Heune, 1980; von Huene et al., 1980). Clendenen et al. (1992) considered the two current active uplift axes in the fore-arc region, i.e. the shelf edge and Kenai–Kodiak axes, as the surface expressions of the ongoing frontal (scraping-off) and basal (underplating) accretion, respectively, beneath their locations. The active uplift of the Kenai–Kodiak axis was originally attributed to the accretionary wedge growth between roughly 50 and 30 Ma (million years ago), which was based on the interpretations of the seismic reflection survey data (Moore et al., 1991). In contrast to this interpretation of the past event, the current topographic activity along the Kenai–Kodiak axis appears to be undulated and forms localised mountain highs and basin lows (von Huene et al., 1985). The current undulated activity implies that the relative rise observed within the Kenai Peninsula and the Kodiak Islands is primarily caused by local disturbing factors, such as intraplate faulting and postglacial isostatic adjustment (Carver et al., 2008), or at least not driven by the along-trench-scale uniform tectonic factors.

The coincidence between the double-arc characteristics computationally reproduced by the Alaska model and the gravitational double-arc characteristics (Fig. 4a) indicates that the current surface mass excess and deficit primarily result from the material transport by the vertical crustal motion due to the steady plate subduction. Although the free-air gravity anomaly in the Kenai Peninsula and the Kodiak Islands exhibits local highs (Figs. 1 and 4), they are located in the computationally reproduced subsidence zone between the inner- and outer-arc highs. Therefore, these local gravitational highs may not be currently supported by the direct effect of the steady plate subduction. This interpretation is consistent with the current trends in long-term vertical motion: the computationally reproduced outer-arc highs corresponded to the active uplift along the continental shelf edge instead of the undulated vertical motion along the Kenai–Kodiak axis. Accordingly, the topographic highs of the Kenai–Kodiak Mountains appeared as vertical protrusions maintained in a broad and low topographic belt parallel to the trench. The existing (Kenai–Kodiak) and progressive (continental shelf edge) outer-arc belts in different states may provide implicit information on the formation history of the eastern Aleutian subduction zone; tectonic events in the past caused the seaward shift of the topographic activity and the subsequent topographic readjustment under the current tectonic state.

7 Conclusions

In this study, we developed a Matsu’ura–Sato type dislocation-based 2D plate subduction model to examine the mechanical origin of the double-arc system in the eastern Aleutian subduction zone. An elastic layer with a flat surface under gravity and an underlying Maxwellian viscoelastic half-space represents the lithosphere–asthenosphere system, and a steady increase in the tangential displacement discontinuity along the curved plate interface represents the steady plate subduction. We determined the across-trench profiles of the plate interface geometry for the western and eastern Aleutian subduction zones on the basis of the hypocentre distribution. The surface uplift rates computed from the 2D plate subduction model for the Aleutian plate interface profiles adequately reproduced the western single-arc and eastern double-arc characteristics. The essential factors of the double-arc formation are a low subduction dip angle and a bimodal plate interface curvature distribution within the elastic lithosphere.

To examine the deviations in the location between the topographic and gravitational outer arcs (i.e. the Kenai–Kodiak nonvolcanic arc and the eastern outer positive gravitational belt), we compared the computed vertical crustal motion with the topography and free-air gravity anomaly. The double-arc highs of the computed uplift rates more closely coincided with the gravitational highs than the current topographic highs. Accordingly, the topographic highs of the Kenai–Kodiak Mountains appeared as vertical protrusions maintained in a broad and low topographic belt parallel to the trench. This implies that tectonic events in the past caused the topographic activity shift towards the continental shelf edge and the subsequent topographic readjustment under the current tectonic state.