1 Introduction

Climate change and the current energy crisis related to the war in Ukraine urged the need to reduce the consumption of fossil fuels and increase renewable energy sources (IPCC, 2022). In this context, deep geothermal energy plays a key role as its base-load capability can effectively compensate for weather-dependent fluctuations of other renewable energy forms. The overall largest geothermal resources are found in the crystalline basement (Paschen et al., 2003; Tester et al., 2006; Frey et al., 2023), accessible by deep drillings in many regions worldwide. This study focuses on the Upper Rhine Graben (URG), where the geothermal resources have already been exploited for power and heat supply as well as for balenological purposes in the past (Frey et al., 2022a).

As the natural permeability of the crystalline basement is usually very low (< 10–16 m2), so-called Enhanced Geothermal Systems (EGS) need to be developed in order to make the geothermal resources usable (Huenges, 2010). They represent artificial reservoirs created by hydraulic, thermal or chemical stimulation. Depending on the applied technology and the subsurface conditions, existing fractures or new fractures are opened, resulting in a permeability increase of several orders of magnitude. Successful development of EGS is based on a comprehensive understanding of the natural fracture and fault network as well as fluid-rock interactions. However, first-order questions remain regarding the hydro-thermo-mechanical-thermal processes during stimulation and operation of the power plant. To make EGS feasible on a broad scale, these issues will be addressed in the upcoming GeoLaB (Geothermal Laboratory in the Mine) project (KIT, 2022). GeoLaB will consist of a newly constructed subsurface laboratory at the eastern margin of the URG, where high-flowrate experiments on faults will be conducted. The selection of a suitable site is based on the criteria catalog of Schill et al. (2016). Accordingly, the location should be geologically homogeneous, have controllable hydraulic boundary conditions (preferably no mining history), exhibit undisturbed stress conditions (several hundred meters overburden above the laboratory), and contain sufficient fractures that may potentially be reactivated in the recent stress field. Two sites have already been preselected that meet these requirements: the southern Black Forest and the Tromm Granite in the Odenwald. This article concentrates on the latter.

For the planning of the approximately 1.5 km long GeoLaB tunnel, potentially permeable faults have to be identified beforehand on which the above-described experiments can be carried out. Initial characterization of the fault and fracture network in the Tromm Granite has already been carried out by Frey et al., (2022b), locally using LIDAR surveys in outcrops and regionally by analyzing morphological lineaments in high resolution digital elevation models (DEMs). However, fault zones of hundreds of meters to several kilometers length are always buried under a meter thick sedimentary cover, preventing any direct assessment of structural and hydraulic properties. In addition, uncertainties remain as to whether the DEM lineaments indeed reflect faults in the subsurface. The characterization of the fault and fracture network therefore relies mainly on indirect geophysical measurements. Gravity data, also acquired by Frey et al., (2022b), show several hundred meters wide anomalies indicative of broad zones in which the fracture porosity may be as high as 6%. This study presents an improved mapping of potentially porous and permeable faults based on a newly acquired aeromagnetic dataset.

Aeromagnetic surveying is a widely used geophysical method that allows more efficient mapping of the crustal magnetic field than ground-based methods (Isles & Rankin, 2013). These measurements are particularly useful in rugged and remote areas like the Tromm Granite, where other datasets, such as seismic or borehole data, are sparse or unavailable. Aeromagnetic datasets are further advantageous when field mapping is not possible due to a sedimentary cover of the target structures. Applications are diverse and include geological and tectonic mapping as well as mineral and hydrocarbon prospection. Depending on the target size, the corresponding surveys are carried out at a wide range of scales, from a few hectares to several thousand km2. Until a few years ago, the surveys were mostly conducted with airplanes or helicopters, but the use of UAVs (Unmanned Aerial Vehicles) has recently increased (Cherkasov & Kapshtan, 2017; Kim, 2020; Walter et al., 2020). UAVs enable small to medium-sized surveys to be carried out generally at a lower cost and with less environmental impact.

2 Geological Setting

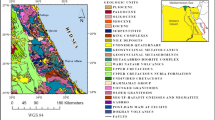
The aeromagnetic survey covers the central part of the Tromm Granite, an approximately 60 km2 large intrusion in the southern Odenwald (Fig. 1) (Amstutz et al., 1975; Krohe & Willner, 1995; Stein, 2001). The study area is located at the northeastern URG margin, which is part of the Mid-German Crystalline High (MGCH), consisting of mafic to felsic plutonic rocks intruded into Paleozoic metamorphic units. The crystalline basement of this region was primarily shaped during the Variscan orogeny (Kossmat, 1927), that reached its peak continental collision phase during the Carboniferous. In this context, the MGCH is commonly regarded as the exposed former active continental margin of the Armorican Terrane Assemblage (Altherr et al., 1999; Krohe, 1991; Okrusch et al., 1995).

Fig. 1
figure 1

Overview of the study area: (A) geological map of the Odenwald (modified after HLUG, 2007), (B) geological map of the Tromm Granite in the southern Odenwald (Klemm, 1900, 1928, 1929, 1933), including in-lines and tie-lines of the aeromagnetic survey. HG Heidelberg Granite, OZ Otzberg Shear Zone, SA Schollenagglomerat, SH Sprendlinger Horst, TG Tromm Granite, WP Weschnitz Pluton

Full size image

The Tromm Granite consists of medium- to coarse-grained, orthoclase-rich, biotite-bearing, and often reddish granitoids characterized by large potassium feldspar inclusions (Maggetti, 1975; Nickel, 1953). The southern part additionally features a fine-grained variety of this granite with similar mineralogical composition but at a younger age. The granite is often intruded by aplitic or pegmatitic dykes and veins (Klemm, 1933). To the east, the Tromm Granite is bounded by the 1–2 km wide Otzberg Zone (Schälicke, 1975), a first-order crustal shear zone that has been repeatedly reactivated since the Paleozoic. In the south, the granite gradually merges into the lithologically heterogeneous “Schollenagglomerate” (Nickel, 1975), which comprises gneiss, schists, amphibolites, and various magmatic rocks. In the northwest, the Tromm Granite adjoins the granodiorites of the Weschnitz Pluton. Clark (2020) reported that the Koenigsberger ratio of felsic igneous rocks is usually well below 0.5 (typically around 0.2). Accordingly, magnetization in the Tromm Granite is expected to be mainly influenced by induction, while remanent magnetization may be of minor importance.

The structural inventory of the Tromm Granite is characterized by its multiphase evolution, during which the regional stress field was repeatedly reoriented (Behrmann et al., 2003; Bossennec et al., 2021; Buchner, 1981; Dèzes et al., 2004; Schumacher, 2002). On the one hand, the pluton was structurally overprinted directly after its emplacement, i.e. during the final phase of the Variscan continental collision and the subsequent collapse of the orogen. At this time, deformation was especially concentrated along the Otzberg Zone, which is documented by the extensive cataclasis and mylonitization. On the other hand, opening or reactivation of fractures and faults in the Tromm Granite occurred with the formation of the adjacent URG. The main crustal extension took place between the late Eocene and early Miocene, with the orientation of the largest horizontal stress σHmax between NW–SE and NNE–SSW. This was followed by the still ongoing transtensive reactivation of the graben faults, with an orientation of σHmax around NW–SE. Frey et al. (2022b) demonstrated that the orientation of fractures in the study area is largely consistent with measurements from the URG, e.g., at Soultz-sous-Forêts. This indicates that the majority of fractures are associated with the rifting. Nevertheless, the poor outcrop situation makes it difficult to draw reliable conclusions on the exact timing of fault activity in the Tromm Granite.

Direct stress measurements are not available for the southern Odenwald due to the lack of deep boreholes. Instead, stress information is derived from wells and seismic events some tens of kilometers to the west in the URG (Reiter et al., 2016). Ahlers et al. (2021) combined all available stress data into a Germany-wide stress model, and suggest that σHmax strikes ~ 165° in the study area.

3 Material and Methods

3.1 Aeromagnetic Survey and Basic Data Processing

The acquisition and basic processing of the aeromagnetic dataset from the Tromm area were carried out by French company TERREMYS with their self-developed magnetic mono-sensor quadcopter. A Bartington MC03 fluxgate magnetometer was used for the magnetic measurements, which is attached to a 1 m long rigid pole and records data at 25 Hz. The survey was conducted in March 2022, covering an area of 13.3 km2 during 6 days of measurements (Fig. 1). A total of 252 linear km was recorded with in-line and tie-line spacings of 70 and 210 m, respectively. The flight altitude was 70 m above ground, using a barometer for vertical navigation. A 1 m precision GNSS was used for the horizontal positioning. Due to legal restrictions, buildings, gardens, and streets were excluded and the survey area was divided into seven sectors with separate take-off locations. An overlap of 60 m was chosen at the respective boundaries to ensure a good connection between the sectors.

The magnetic sensor was calibrated twice a day or when the take-off point was changed. This calibration enabled measurement sensitivity of about 1 nT. Additional measurements by an independent mobile base station were used to correct for diurnal variations. However, technical problems occurred after two days, which is why the corrections were based on data from the observatories Manhay (MAB) in Belgium and Fürstenfeldbruck (FUR) in Germany. The reference field IGRF-13 was subtracted from the measured field to calculate the total magnetic intensity anomalies (TMI). Subsequently, leveling correction was performed, which minimizes the anomaly differences at the crossing points of in- and tie-lines (the standard deviation is 0.1 nT after correction). A minimum curvature algorithm was applied to calculate a grid of the TMI anomalies with a cell size of 25 m, corresponding to about one third of the in-line spacing. Finally, a reduction to the magnetic north pole (RTP) was performed at 70 m above ground using the direction given by the IGRF-13 model. The RTP calculation facilitates the geologic interpretation of the data since it places the magnetic anomaly above the causative magnetic volume.

3.2 Anomaly Enhancement Filters

The RTP anomalies is often dominated by regional trends typically with wavelengths of several kilometers. Therefore, various filter techniques have been developed to enhance fine details and detect edges of near-surface source bodies. For this study, eight well-established algorithms were selected and compared against each other. Their mathematical principles are summarized below.

The vertical derivative (VDR) is a high-pass filters commonly calculated when interpreting magnetic anomalies. This method concentrates the anomalies above their sources in the subsurface. Expressed in a cartesian coordinates system (x,y,z) with z being the vertical coordinate, VDR of the magnetic field component (F) is:

$$VDR= \frac{\partial F}{\partial \mathrm{z}}$$

The total horizontal gradient (THG) of the field places extreme values above the edges of the source body (Cordell, 1979):

$$THG= \sqrt{{\left(\frac{\partial F}{\partial \mathrm{x}}\right)}^{2}+{\left(\frac{\partial F}{\partial \mathrm{y}}\right)}^{2}}$$

Ma and Li (2012) proposed the normalized total horizontal gradient (NTHG), which equalizes the amplitudes of THG within a moving window of pre-defined size:

$$NTH{G}_{i,j}= \frac{TH{G}_{i,j}}{max({THG}_{i-\frac{m}{2}:i+\frac{m}{2}, j-\frac{n}{2}:j+\frac{n}{2} })}$$

where m and n are the width and length of the window. The analytical signal amplitude (ASA) (Roest et al., 1992) combines the gradients of the magnetic field from all three dimensions and can be used to detect the sources edges:

$$ASA= \sqrt{{\left(\frac{\partial F}{\partial \mathrm{x}}\right)}^{2}+{\left(\frac{\partial F}{\partial \mathrm{y}}\right)}^{2}+{\left(\frac{\partial F}{\partial \mathrm{z}}\right)}^{2}}$$

The tilt derivative (TDR), proposed by Miller and Singh (1994), normalizes VDR using THG. This filter enhances the short-wavelength content of the magnetic field while preserving the polarity of the anomalies. The zero crossing marks the edges. Maxima and minimal are centered above the source bodies:

$$TDR={\mathrm{tan}}^{-1}\left(\frac{VDR}{THG}\right)$$

The theta map θ, normalizes THG using ASA (Wijns et al., 2005) and marks the sources edges by the signal’s minima:

$$\theta ={\mathrm{cos}}^{-1}\left(\frac{THG}{ASA}\right)$$

A modified version of the tilt derivative was introduced by Cooper and Cowan (2006), which normalizes THG with the absolute value of VDR. The normalized horizontal tilt derivative (TDX) marks the sources edges by the signal maxima, thus yields similar results as the theta map:

$$TDX={\mathit{tan}}^{-1}\left(\frac{THG}{|VDR|}\right)$$

Finally, Oksum et al. (2021) recently proposed an edge detection method based on a modified fast sigmoid function (FSED), which incorporates the vertical and horizontal gradients of THG. The filter provides a sharp image of the source edges:

$$FSED=\frac{R-1}{\left|R\right|+1}$$

with

$$R=\frac{\frac{\partial THG}{\partial \mathrm{z}}}{\sqrt{{\left(\frac{\partial THG}{\partial \mathrm{x}}\right)}^{2}+{\left(\frac{\partial THG}{\partial \mathrm{y}}\right)}^{2}}}$$

3.3 Synthetic Model

Before being applied to the field data, the described filters were first tested on a synthetic model (Fig. 2) that reflects the expected subsurface structure of the Tromm Granite in a simplified way. The model was created with the software IGMAS + (Interactive Geophysical Modelling ASistant) (Götze & Lahmeyer, 1988; Schmidt et al., 2020), spanning 500 m horizontally and 200 m vertically. Three 25 m thick faults were modeled, one vertical and two dipping with 70°. An overburden of 50 m was further specified for one of the dipping faults. Different magnetic susceptibilities were assigned to generate contrasts compared to the reference background. In addition, artificial noise was added to the synthetic field.

Fig. 2
figure 2

(A) 3D model comprising three fault zones, each with a thickness of 25 m. The dip angle of the red fault is 90°, while that of the blue and green faults is 70°. The top of the green line is 50 m below the surface to represent a buried structure. The magnetic properties of the faults and surrounding rock mass are given in the table below. (B) Synthetic magnetic field calculated for this model, including the fault traces. Note that the anomalies are reduced to the magnetic north pole

Full size image

For an objective selection of the most appropriate filtering method, the following criteria were defined that the filtered anomalies should satisfy:

  • Amplification of the short-wavelength content of the magnetic anomalies.

  • Correct positioning of the modelled structures without filter artifacts.

  • Amplification of the anomalies from buried sources.

  • Preservation of the polarity of the anomaly to enable the best geological interpretation.

  • Robustness to noise in the data (detection of magnetic sources should not be obstructed by the noise).

3.4 Assessing Reactivation Potential

After applying the selected filter to the aeromagnetic dataset from the Tromm Granite, linear features in the filtered magnetic field with a minimum length of 250 m were digitized and could be compared with the DEM lineament analysis performed by Frey et al. (2022b). The clustering of lineaments in specific azimuth intervals was interpreted for the recent stress conditions in the survey area based on the geomechanical modelling of Ahlers et al. (2021). For this purpose, the two parameters slip and dilation tendency were used (Ferrill & Morris, 2003; Morris et al., 1996), which are measures of the reactivation potential of a fault zone. The slip tendency Ts is defined as:

$${T}_{s}=\frac{\tau }{{\sigma }_{n}}$$

where τ is the shear stress and σn the normal stress acting on the fault plane. The dilation tendency Td can be written as:

$${T}_{d}=\frac{{\sigma }_{1}-{\sigma }_{n}}{{\sigma }_{1}- {\sigma }_{3}}$$

where σ1 and σ3 are the largest and the smallest principal stresses, respectively.

4 Results

4.1 Comparison of Different Filter Methods

A comparison of the eight filter methods described above is presented for the synthetic magnetic dataset in Fig. 3 (without noise) and Fig. 4 (with noise). The visual evaluation of the filters is based on the criteria defined in the subchapter “Synthetic model”. All filter methods amplify the short wavelength components of the field, concentrating the anomalies over the source volumes or their edges. VDR, ASA, TDR, theta map, and TDX render the location of the modelled faults with a maximum horizontal deviation of 20 m and without producing filter artefacts. The THG filter result, in contrast, does not allow an unambiguous interpretation of the fault locations. NTHG and FSED produce significant artefacts. All filter methods can detect the buried fault zone (50 m overburden), with the best gain achieved by TDR, theta map, and TDX. VDR and TDR are the only filters that preserve the original polarity of the anomalies, which is essential for the subsequent geological interpretation. Finally, the eight filters show varying sensitivity to noise in the dataset. VDR, TDR, theta map, and TDX still allow detecting all modelled faults.

Fig. 3
figure 3

Comparison of eight different enhancement filters for the magnetic data: (a) forward modeled magnetic field for the synthetic model shown in Fig. 2, (b) vertical derivative, (c) total horizontal gradient, (d) normalized total horizontal gradient, (e) analytical signal amplitude, (f) tilt derivative, (g) theta map, (h) normalized horizontal tilt derivative, and (i) fast sigmoid function. The dashed lines represent the fault traces in the synthetic model

Full size image
Fig. 4
figure 4

Comparison of eight different enhancement filters for noisy magnetic data: (a) forward modeled magnetic field for the synthetic model shown in Fig. 2, (b) vertical derivative, (c) total horizontal gradient, (d) normalized total horizontal gradient, (e) analytical signal amplitude, (f) tilt derivative, (g) theta map, (h) normalized horizontal tilt derivative, and (i) fast sigmoid function. The dashed lines represent the fault traces in the synthetic model

Full size image

In summary, only VDR and TDR meet all the predefined criteria. Since TDR amplifies the signal of the buried fault more effectively, this method was selected for filtering the aeromagnetic dataset from the Tromm Granite.

4.2 Magnetic Anomalies of the Tromm Granite

Figure 5a illustrates the magnetic anomalies recorded in the Tromm area. The RTP anomalies range from − 22.5 to 67.5 nT. Positive values of RTP are predominant at the boundary with the Schollenagglomerate in the south, which roughly coincide with mapped amphibolite bodies (Fig. 1). From the petrophysical investigations of rock samples from Odenwald by Frey et al. (2020) it is known that amphibolites (χ = 0.003 ± 0.008 [SI]) exhibit on average almost one order of magnitude higher magnetic susceptibility than the Tromm Granite (χ = 0.0007 ± 0.001 [SI]). This observation thus explains the concentration of positive anomalies over the amphibolite bodies. Further north, where no macroscopic changes in lithology are evident from geological mapping (Fig. 1), the magnetic anomalies indicate a concentric zonation of the Tromm Granite, with the magnetic maximum in the center and minima at the edges of the pluton.

Fig. 5
figure 5

Results of the aeromagnetic survey from the Tromm Granite: (A) magnetic anomalies after reduction to the pole (RTP) at 70 m above ground and with a lateral resolution 25 m, (B) Tilt derivative (TDR) of the anomalies, and (C) TDR of the anomalies with morphological and magnetic lineaments

Full size image

The TDR filter amplifies the short wavelengths of the RTP anomalies, revealing a connected network of linear magnetic minima (Fig. 5b). Magnetic lineaments with a minimum length of 250 m are interpreted as potential fault zones. In total 118 lineaments, with a maximum length of 1.3 km, were extracted from the filtered anomaly map. A comparison of the magnetic with the morphological lineaments obtained by Frey et al. (2022b) from the high-resolution DEM of the Tromm Granite is shown in Fig. 5c. Along the prominent structures in the northern part of the aeromagnetic survey, a high level of agreement between these two independent data sets is evident. In contrast, the correlation is low in the remaining parts of the Tromm Granite.

4.3 Reactivation Potential of Lineaments

Slip and dilation tendency in the current stress field were calculated for the Tromm Granite at various fault orientations (Fig. 6a). The dilation tendency exhibits a sinusoidal pattern with the maximum parallel to σHmax (~ 165°) and the minimum parallel to σhmin. In contrast, the slip tendency is more complex, with two maxima at about 005° and 140°. For comparison, the cumulative lengths of lineaments at discrete strike intervals are given in Fig. 6b. Lineaments based on the DEM do not display a preferred direction, except for the cluster between 070° and 110°. No correlation with slip or dilation tendency can be detected. The magnetic lineaments are distributed more heterogeneously. Between 040° and 180°, there is a high degree of correlation with the slip tendency. The maximum cumulative length is found between 110° and 150°, coinciding with the slip tendency peak. Likewise, few magnetic lineaments were detected in the directions of minimum slip tendency. However, only a few lineaments are present between 000° and 040°, even though another maximum of the slip tendency is reached here. A correlation with the dilation tendency is not observed.

Fig. 6
figure 6

(A) Slip and dilation tendency for the Tromm Granite at various fault plane orientations, (B) normalized cumulative length of lineaments from the high-resolution digital elevation model and the enhanced aeromagnetic anomaly map

Full size image

5 Discussion

A high-resolution aeromagnetic survey was performed for the Tromm Granite at the northwestern URG margin. The calculated RTP anomalies indicate a concentric magnetic zonation of the pluton. Similar observations have been made for other granitoid intrusions worldwide (Antolín-Tomás et al., 2009; Aydin et al., 2007; Benn et al., 1998; Gleizes et al., 1993). This possibly reflects the geochemical differentiation in the magma chamber during cooling and crystallization, resulting in a heterogeneous distribution of ferrimagnetic minerals (mainly magnetite) within the pluton. In addition, hydrothermal alteration and metamorphic overprinting may cause magnetic zonation.

Applying the TDR filter to the RTP anomalies reveals a network of magnetic lineaments characteristic of crystalline settings and usually interpreted as faults or fracture zones (Henkel & Guzmán, 1977). The transformation of magnetite into paramagnetic minerals is considered to be the main reason for the locally reduced magnetic susceptibility. This process is accelerated in active fault zones, on the one hand, through alteration processes caused by fluid-rock interaction and, on the other hand, through the crushing of larger mineral grains as a result of tectonic deformation (Isles & Rankin, 2013). In some cases, the fault core may also exhibit in increase in magnetic susceptibility compared to the surrounding undisturbed rock (Hirono et al., 2006; Tanikawa et al., 2008). Possible reasons for this include mineralogical changes caused by hydrothermal or thermo-mechanical processes in the fault zone. However, due to the lack of suitable outcrops in the Tromm Granite, this cannot be reliably assessed.

A comparison of the magnetic lineaments with lineaments from the high-resolution digital elevation model of the Tromm Granite shows that these two independent datasets are only partially correlated. Good agreement is generally found for prominent lineaments with a minimum length of 1 km. The discrepancies for the shorter lineaments might indicate that they do not necessarily represent fault zones. Alternatively, lithological variations in the pluton or magmatic veins could be responsible for the observed magnetic signal. However, the interpretation of the magnetic lineaments as fault zones is supported by the high correlation with the slip tendency under the current stress conditions. A possible explanation for this could be the repeated reactivation of favorably oriented fault planes in the Tromm Granite. The reduction of the magnetic susceptibility could be result of crushing and alteration of magnetite in these zones (Isles & Rankin, 2013).

Interestingly, significantly more magnetic lineaments occur between 110° and 150° than between 000° and 040°, although a maximum of slip tendency is reached here in each case (Fig. 6). One possible reason could be the multiphase evolution of the crystalline basement along the URG. As described in the chapter 'Geological Setting', the regional stress field has been repeatedly reoriented since the intrusion of the Tromm Granite (Behrmann et al., 2003; Bossennec et al., 2021; Buchner, 1981; Dèzes et al., 2004; Schumacher, 2002). Accordingly, the seemingly abundant NW–SE striking faults may have been reactivated most frequently during the past 330 Ma, as indicated by the magnetic signal. However, a reliable reconstruction of the reactivation potential over the entire geologic history is not possible because of the large uncertainties concerning paleo-stress conditions. Alternatively, the NW–SE faults could already have been established during the Variscan orogeny. Schumacher (2002) and Edel et al. (2007), for example, reported that large-scale pre-existing Variscan structures, such as the Otzberg Zone on the eastern margin of the Tromm Granite, had a major influence on the location and geometry of the URG. Unfortunately, however, dependable statements about the timing of the formation and activation of local faults in the study area cannot be made because no suitable outcrops of such faults exist.

Bertrand et al. (2020) analyze a comparable aeromagnetic dataset consisting of two separate surveys from the western URG shoulder. Their data were acquired over a significantly larger area (~ 1500 km2) than the one presented here, with a greater linespacing of 400 and 500 m, respectively (Gavazzi et al., 2020). They calculated the horizontal derivative of the RTP, which allows a delineation of the Variscan basement blocks, separated by ENE–WNW striking first-order fault zones. Furthermore, a compartmentalization of the N–S striking rift related faults is evident (Bertrand et al., 2020). However, internal structural features within homogeneous basement units are poorly resolved, most likely due to the lower resolution of the magnetic data compared to the Tromm survey.

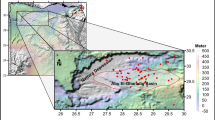
The aeromagnetic survey presented here is a cornerstone of the preliminary geological-geophysical exploration for GeoLaB. A roughly 13 km2 area of the Tromm Granite, for which little structural geological data were previously available, was surveyed at high resolution. The magnetic lineaments in the TDR map (Fig. 5) indicate potential fault zones that serve as target structures of GeoLaB. However, in addition to permeable faults, stress conditions unaffected by topography are required, suggesting that the overburden of the approximately 1.5 km long GeoLaB tunnel should be in the range of several hundred meters. Figure 7 compares this overburden with the location of magnetic lineaments. The highest overburden of up to 350 m is reached at the eastern boundary of the survey. Several magnetic lineaments are observed in this area, at least five of which have a high reactivation potential (Ts > 0.8). The TDR anomalies should now serve as a basis for more specific geophysical investigations, for example with terrestrial gravimetry and magnetics, geoelectrics, and reflection seismics. This could provide evidence of the actual existence of faults associated with the magnetic lineaments. The final proof will be ultimately provided by exploratory drilling or the tunnel itself. Once GeoLaB is constructed, detailed susceptibility measurements across fault zones in the tunnel would be useful to verify the interpretation of the aeromagnetic anomalies.

Fig. 7
figure 7

Comparison of the maximum overburden over a 1.5 km long horizontal tunnel with the magnetic lineament extracted from the TDR filtered RTP anomalies in the Tromm Granite. The relative slip tendency of the lineaments under the current stress conditions is indicated. Futhermore, the local road infrastructure is plotted on the map

Full size image

6 Conclusions

A high-resolution aeromagnetic dataset of the Tromm Granite (Odenwald, SW Germany) was acquired by drone to map and characterize the natural fault network. The following conclusions can be drawn from the investigations:

  • Aeromagnetic surveys allow efficient investigations of large surface areas in rugged and remote regions, such as the Tromm Granite.

  • Different filters for enhancing the shortwave magnetic signals have been reviewed and compared using a synthetic model. For the mapping of fault zones, the tilt derivative (TDR), applied after RTP, was shown to be the most reliable method.

  • The unfiltered RTP anomalies from the Tromm Granite indicate a concentric zonation of the pluton, which might be associated with the differentiation of the magma chamber during its emplacement.

  • The filtered RTP anomalies exhibit more than 100 magnetic lineaments that may be interpreted as potentially permeable fault and fracture zones. The clustering of these lineaments at the maximum slip tendency indicates preferential reactivation of favorably oriented fault planes.

  • The TDR anomaly map provides a significant decision-making basis for the site selection process of GeoLaB.

  • Further exploration using geophysical methods or drilling is required to validate the results presented here.