1 Introduction

High-resolution velocity structures provide important clues for studying the tectonic evolution of active blocks and geodynamic simulations (Bao et al., 2015; Fang et al., 2010; Huang et al., 2018; Shapiro et al., 2005; Yang et al., 2007). The velocity structure is an important factor in the propagation of earthquake ruptures (Ampuero & Vilotte, 2002; Huang & Ampuero, 2011; Huang et al., 2014; Jiang et al., 2021; Weng et al., 2016). Obtaining high-resolution velocity structures in fault zones plays an important role in determining the deep geometry, evolution processes and movement pattern of a fault. Accordingly, researchers have performed many dense portable array observations and studies to obtain the fine-scale velocity structure of fault zones, such as the San Jacinto fault (Lewis et al., 2005), Newport-Inglewood fault (Zhang & Langston, 2020), Tanlu fault (Luo et al., 2021), Chenghai fault (Jiang et al., 2021; Yang et al., 2020), etc.

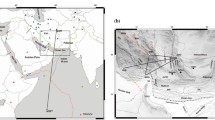
The AZXFZ is located in the southeastern margin of the Tibetan Plateau (Fig. 1a, b), and it forms the eastern boundary of the Sichuan-Yunnan Block, one of the most seismically active large strike-slip fault systems in Southwest China (Xu et al., 2005; Zhang et al., 2013). This area has experienced a series of strong earthquakes with magnitude > 7.0 (Fig. 1b; Wen et al., 2000, 2008b; Yi et al., 2008), such as the 1480 Yuexi M7.5 earthquake, 1536 Xichang M7.5 earthquake and 1850 Xichang M7.5 earthquake. Previous studies found seismic gaps and locking features along the AZXFZ, based on studies of seismic activity and geodesy, indicating a high seismic hazard in the region (Jiang et al., 2015; Wen et al., 2008a; Yi et al., 2004, 2005; Zhao et al., 2015). The frequent strong seismic activity of the fault zone is inextricably linked to its deep structure, especially the relative motion of the blocks caused by the eastward escape of material from the Tibetan Plateau (Bao et al., 2015; Wang et al., 2017). As one of the channels for material flow within the Tibetan Plateau, in-depth studies of the fine 3D velocity structure of the crust in this region are of great significance for understanding the evolution processes of the Tibetan Plateau.

Fig. 1
figure 1

a Main geological blocks of the study region (red box). b Main faults and historical earthquakes with M ≥ 5.0 since 1970. c Seismic stations used for tomography. TP Tibetan Plateau; IB Indian Plate; SCB South China Block; SP-GZB Songpan-Gangzi Block; SB, Sichuan Basin; YB Yangtze Block; S-YB Sichuan-Yunnan Block; LM-JPOB Longmenshan-Jinpingshan Orogenic Belt; XSHF Xianshuihe Fault; ANHF Anninghe Fault; ZMHF, Zemuhe Fault; DLSF, Daliangshan Fault; LJ-XJHF Lijiang-Xiaojinhe Fault; LZJF Lvzhijiang Fault; XJF Xiaojiang Fault; CXA Chuanxi Array; HMLYA Himalayan Array; XCA Xichang Array; AZXA Anninghe-Zemuhe-Xiaojiang Array

Full size image

The uplift and deformation of the Tibetan Plateau are closely related to its deep tectonics (England & Housema, 1986; Houseman & England, 1993; Willett et al., 1993). Accordingly, researchers have used a variety of methods to study the deep structure of the AZXFZ and its surrounding areas, which have resulted in a series of important insights. The crust of the southeastern margin of the Tibetan Plateau has a high geothermal heat flow of 80 mW/m2 (Hu et al., 2000; Shi & Wang, 2017; Wang et al., 2014) and a high Poisson's ratio of > 0.28 (Wang et al., 2017). Many body wave, surface wave, receiver function and magnetotelluric inversion studies have further revealed the existence of low-velocity zones (Bao et al., 2015; Huang et al., 2018; Tan et al., 2018; Yao et al., 2008; Zhang et al., 2020; Zheng et al., 2016), complex anisotropy (Huang et al., 2010, 2018; Lu et al., 2014; Xie et al., 2013; Yao et al., 2010), high attenuation (Zhao et al., 2013) and high conductivity layers (Bai et al., 2010) in the middle and lower crust of the southeastern margin of the Tibetan Plateau. However, previous studies have different interpretations of the continuity and genesis of these low-velocity zones. Some tomography results show that the low-velocity zones are continuous along the eastern margin of the Tibetan Plateau and the Xianshuihe-Xiaojiang fault zone (Li et al., 2009; Ma et al., 2008; Wei et al., 2010). Meanwhile, other results show high-velocity anomalies around Panzhihua and Shimian-Xichang (Bao et al., 2015; Fan et al., 2015; Pan et al., 2015; Yao et al., 2008; Zhang et al., 2020). Some studies have suggested that crustal flow exists in the low-velocity zones (Bai et al., 2010; Clark & Royden., 2000; Liu et al., 2014; Royden et al., 1997) and propose that the crustal flow is not continuous within the southeastern margin of the Tibetan Plateau (Bao et al., 2015; Chen et al., 2014; Huang et al., 2018; Yao et al., 2008; Zhang et al., 2020). However, these low-velocity zones have also been suggested to be associated with shear heating of the faults or the upwelling of mantle material along the faults (Li et al. 2019b; Wu et al., 2013; Yang et al., 2020; Yu et al., 2022; Zhang et al., 2020). The high-resolution velocity structure is the key to revealing the continuity of the two low-velocity zones and its genesis because it directly affects whether the genesis of the eastern low-velocity zone is related to the eastward escape of material from the Tibetan Plateau. In addition, the Gongga Shan, located in the Longmenshan-Jinpingshan Orogenic Belt (Lai et al., 2006; Xu et al., 2007), shows significant differences from the Longmenshan in terms of both elevation and uplift rate. Researchers also have different views about the uplift mechanism of the Gongga Shan, such as the 'dynamic topography' model (Clark et al., 2005) and the 'transpression' model (Chen et al., 2008; He et al., 2008; Tan et al., 2010).

Due to sparse distribution of seismic stations, short observation time and different tomography methods, there are few high-resolution velocity models near the AZXFZ. Although previous studies have imaged two low-velocity zones, but the connectivity of the two low-velocity zones is not well resolved because of low resolution (Li et al., 2009; Ma et al., 2008; Wei et al., 2010). Some studies suggest that the genesis of the two low-velocity zones is related to crustal flow (Bao et al., 2015; Huang et al., 2018; Yao et al., 2008). In addition, the uplift mechanism of the Gongga Shan is also unclear. In this article, we processed seismic data recorded by four arrays deployed in the AZXFZ with ambient noise tomography. The high-resolution 3D S-wave velocity structure of the AZXFZ and its surrounding area was determined. In addition, we explore the relationship between the velocity structures and tectonic evolution processes, providing a new velocity model (AZX-CVM1.0, Anninghe-Zemuhe-Xiaojiang Community Velocity Model 1.0) for geodynamic studies of the southeastern Tibetan Plateau.

2 Data

We collect continuous waveform data recorded by 378 stations from four arrays: CXA, HMLYA, XCA and AZXA. The distribution of stations is shown in Fig. 1c, and array information is shown in Table 1.

Table 1 Summary of seismic array information used in this study
Full size table

The data processing method in this study are similar to those of Bensen et al. (2007) and mainly include (1) single station pre-processing, (2) cross-correlation calculation and stacking, (3) dispersion curve measurement and (4) dispersion curve quality control. First, we cut the raw data into 1-day length. Then, the raw data were pre-processed with resampling to 1 Hz, band-pass filtering (4–40 s), time-domain normalization and spectral whitening. Due to the different operation periods of the arrays, the data were subjected to cross-correlation calculation and linear stacking, respectively. The dispersion measurements were then performed using an image-based analysis technique method (Yao et al., 2004, 2005, 2006). To obtain reliable dispersion curves, we performed quality control with SNR > 3.0 and station spacing > 1.5 λ (Yao et al., 2011), where SNR is the signal-noise ratio and λ is the wavelength. Then, we selected dispersions with cluster analysis (Fang et al., 2010). A total of 13,746 Rayleigh wave phase velocity dispersions were finally obtained.

The noise cross-correlation functions for R3XC01 and other stations are shown in Fig. 2. Clear surface wave signals can be seen in the positive and negative segments. Figure 3 shows an example of a Rayleigh wave phase velocity dispersion curve for the R3XC01-R5DXY09 station pair. Figure 4 shows all dispersion curves and ray path numbers for 4–30-s periods. The average inter-station distance is 99 km, and most station pairs are within 200 km. Therefore, this study only used 4-25-s dispersion data for inversion. Figure 5 shows the distribution of ray paths for different periods. The ray paths of each period intersect with each other, with dense ray paths in the central part and low density of ray coverage at the periphery of the study region.

Fig. 2
figure 2

Noise cross-correlation functions for R3XC01 and other stations

Full size image
Fig. 3
figure 3

Rayleigh surface wave phase velocity dispersion curve measurement. a SNR curve for R3XC01-R5DXY09 (red asterisk indicates the period above the SNR threshold). b Cross-correlation function (black curve) and its signal window (blue curve) and noise window (red curve). c Phase velocity dispersion curve measurement (red dots)

Full size image
Fig. 4
figure 4

Rayleigh wave phase velocity dispersion statistics. a Phase velocity dispersion measurement. b Statistics of rays at different periods

Full size image
Fig. 5
figure 5

Distribution of ray paths at different periods

Full size image

3 Methods

In this article, the one-step inversion method developed by Fang et al. (2015) is used to directly invert the S-wave velocity structure. The method considers the effect of the propagation effect of non-great circle paths of surface waves at different periods, which can effectively improve the inversion accuracy of short-period dispersion data. In recent years, this method has been well applied in the Taipei Basin, Tanlu fault and southeastern margin of the Tibetan Plateau to obtain high-resolution S-wave velocity structures (Fang et al., 2015; Li et al., 2016b; Luo et al., 2021; Zhang et al., 2018).

Compared with the traditional surface wave inversion method, the advantages of the direct inversion method are: (1) no intermediate step like constructing a two-dimensional group/phase velocity map is required, and the three-dimensional S-wave velocity structure can be obtained directly from a large amount of dispersion data, making the inversion more efficient. (2) The three-dimensional initial velocity model can be directly used. (3) The lateral variation of the structure can be better controlled. The basic principle of the method is as follows:

For points A and B, assume that the phase velocity between them is \(C_{AB} (\omega )\). Then, the traveltime \({\text{t}}_{AB} (\omega )\) from point A to point B is

$${\text{t}}_{AB} (\omega ) = \frac{{L_{AB} }}{{C_{AB} (\omega )}}{ = }\int_{{l_{AB} }} {S(l,\omega )dl = \sum\limits_{m = 1}^{M} {S_{m} (\omega )\Delta l_{m} } }$$
(1)

where \({\text{L}}_{AB}\) is the length of the great circle path between A and B, \(S(l,\omega )\) is the slowness along \(l_{AB}\), and \({\text{S}}_{{\text{m}}} (\omega )\) is the high-frequency summation approximates.

The study area is divided into J grids, and each grid point can be represented by a one-dimensional model \(\Theta_{j}\), followed by a two-dimensional slowness distribution \({\hat{\text{S}}}_{{\text{m}}} (\omega )\) calculated with frequencies \(\omega\). The slowness of each grid point along the path \(l_{AB}\) can be obtained by bilinear interpolation, i.e., \(S_{m} (\omega ) = \sum\nolimits_{j = 1}^{J} {\upsilon_{mj} \hat{S}_{j} (\omega )}\), where \(\upsilon_{mj}\) is the bilinear interpolation coefficient, and the following \(v_{ij}\) is the same.

Then, the ith surface wave traveltime is

$$t_{i} (\omega ) = \sum\limits_{j = 1}^{J} {v_{ij} \hat{S}_{j} (\omega )}$$
(2)

For the inverse problem, the objective is to minimize the differences between the observed time \(t_{i}^{obs} (\omega )\) and model prediction \(t_{i} (\omega )\), where the traveltime difference is

$$\delta t_{i} (\omega ) = t_{i}^{obs} (\omega ) - t_{i} (\omega ) = \sum\limits_{j = 1}^{J} {v_{ij} \delta \hat{S}_{j} (\omega ) \approx - \sum\limits_{j = 1}^{J} {v_{ij} \frac{{\delta C_{j} (\omega )}}{{C_{j}^{2} (\omega )}}} }$$
(3)

where \(C_{{\text{j}}}\) and \(\delta {C}_{j}(\omega )\) are the phase velocity and the perturbation at the jth grid point, respectively. \(\delta C_{{\text{j}}} \left( \omega \right)\) with the three variables of P-wave velocity, S-wave velocity and density related to the variation with depth z, respectively, rewrite Eq. (3) as

$$\begin{gathered} \delta t_{i} (\omega ) = \sum\limits_{j = 1}^{J} {( - \frac{{v_{ij} }}{{C_{j}^{2} }})} \left. {\sum\limits_{k = 1}^{K} {\left[ {R_{\alpha }^{^{\prime}} (z_{k} )\frac{{\partial C_{j} }}{{\partial \alpha_{j} (z_{k} )}} + R_{\rho }^{^{\prime}} (z_{k} )\frac{{\partial C_{j} }}{{\partial \rho_{j} (z_{k} )}} + \frac{{\partial C_{j} }}{{\partial \beta_{j} (z_{k} )}}} \right]} } \right|_{{\Theta_{j} }} \delta \beta_{j} (z_{k} ) \hfill \\ \, = \sum\limits_{n = 1}^{N} {G_{in} m_{n} } \hfill \\ \end{gathered}$$
(4)

where \(\alpha_{j} (z)\),\(\beta_{j} (z)\), and \(\rho_{j} (z)\) are the P- and S-wave velocity and density, respectively, K is the number of grids at depth, and N = J×K is the total number of grids. Write Eq. (4) as a matrix form of the inversion problem

$$d = Gm$$
(5)

where d is the traveltime residual vector of the full frequencies and paths of the surface wave, G is the sensitivity matrix, and m is the model vector, whose expression is

$$m = \left[ {\delta \beta_{1} (z_{1} ) \ldots \delta \beta_{1} (z_{K} ) \, \delta \beta_{2} (z_{1} ) \ldots \delta \beta_{2} (z_{K} ) \ldots \delta \beta_{J} (z_{K} )} \right]^{T}$$
(6)

Its solution can be obtained by solving for the minimum of the following equation

$$\Phi (m) = \left\| {d - Gm} \right\|_{2}^{2} + \lambda \left\| {Lm} \right\|_{2}^{2}$$
(7)

where the first term on the right-hand side of the equation is the \(L_{2}\)-norm of the data misfit, the second term is the \(L_{2}\)-norm of the model regularization, L is the model smoothing operator, and \(\lambda\) is the Lagrange operator.

In this study, the initial model is created by interpolating the 3D velocity model of Shen et al. (2016) with 0.15° × 0.15° grid size. As to depth, the maximum inversion depth can be set to 2–2.5 times the maximum period (Fang et al., 2015). As the vertical resolution decreases with increasing depth, the interval of the depth should gradually increase. The maximum period of the data in this study is 25 s. After checkerboard tests, our final inversion depth grid is set to be 1-km interval at 0–5 km depth, 2-km interval at 6–30 km depth and 5-km interval at 35–50 km depth. The final velocity structure is obtained by L-curve testing with a smoothing factor chosen to be 80 (Fig. 6a) and a total of 10 iterations. The standard deviation of traveltime residual is reduced from 1.25 s to 0.81 s (Fig. 6b). The mean value of the residual is also reduced to 0.014 s.

Fig. 6
figure 6

a L-curve tests. b Histogram of traveltime residual

Full size image

4 Results

4.1 Analysis of the Reliability of the Results

To analyze the resolution of the tomography results, the study area was divided into 0.3° × 0.3° grids with 2% (Fig. 7a–d) and 3% (Fig. 7e–h) random noise. The velocity perturbation was ± 5%, and the one-dimensional model was used for the checkerboard tests. The remaining parameters were the same as those in the inversion.

Fig. 7
figure 7

Checkerboard tests. a–d Recovered model with 0.3° × 0.3° velocity anomaly with 2% noise. e–h Recovered model with 0.3° × 0.3° velocity anomaly with 3% noise

Full size image

The checkerboard tests in Fig. 7 show good recovery at 5–35-km depth. The lateral resolution in this study is about 0.3° × 0.3°. Overall, the model recovery is correlated with the density of the ray paths. Because the ray paths are denser in the central part of the study area, the velocity anomaly is recovered better than at the periphery. Figure 7a–d and Fig. 7e–h show that the effect of recovery model with 3% noise is slightly worse than that with 2%, especially at the periphery. However, the checkerboard pattern can still be recovered well in the central of the study area.

To evaluate the reliability of the tomography results in this study, we compared the S-wave velocity with Zhang et al. (2020) for the same area and depth (Fig. 8). Zhang et al. (2020) used ambient noise data recorded at 132 permanent broadband stations with a lateral resolution of 1° × 1° at 0–70 km. Figure 8 shows that the general characteristics of the two models are similar, but the lateral resolution of our new model is significantly improved. At 10-km depth, both show high-velocity anomalies near Jiulong and Panzhihua and low-velocity anomalies in the Yanyuan Basin and Xichang Basin. However, the shape and velocity are slightly different. Our study shows a clear low-velocity anomaly near the Gongga Shan and a high-velocity zone along the Anninghe fault, corresponding to the location of mafic and ultramafic magma proposed by Zhang (1988). Figure 8c–d shows the low-velocity zones on the east and west sides of the study area, separated by the high-velocity zone near Emeishan-Panzhihua, with no connectivity between the two low-velocity zones in the study area. However, our result reveals clear velocity differences between the two sides of the Anninghe-Zemuhe fault zone. This shows that the model obtained in this study has a higher resolution and can reveal small-scale velocity anomalies than that of Zhang et al. (2020).

Fig. 8
figure 8

Comparison with previous results in the same area. a and c S-wave velocities at 10 km and 24 km obtained from the inversion of this study. b and d Results of Zhang et al. (2020) for similar depths

Full size image

4.2 S-wave Velocity Structure

Figure 9 shows the S-wave velocity structure at different depths. At 5–8-km depth (Fig. 9a–b), a low-velocity anomaly appears near the Gongga Shan, similar to the low-velocity structure within 5–10-km depth obtained by Wang (2016). The areas around the Xichang Basin and Yanyuan Basin show significantly low-velocity anomalies, primarily influenced by the surface sediments. The Sichuan Basin, located in the northeastern corner of the study area, also exhibits a low-velocity anomaly in the shallow crust due to thick sediments (Bao et al., 2015; Yao et al., 2008; Zhang et al., 2020).

Fig. 9
figure 9

S-wave velocity slices at different depths. The white dotted line outlines the range of the low-velocity zones in the west (LV1) and east (LV2)

Full size image

In mid-crust (12–24 km depth, Fig. 9c–e), the entire study area begins to show two low-velocity zones on the east and west sides (hereafter referred to as LV1 and LV2, respectively) of the high-velocity body in the middle. With increasing depth, the low-velocity anomaly in the Gongga Shan area is connected to LV1 and separated from the high-velocity zone on its eastern side by the southern section of the Xianshuihe fault and the Lijiang-Xiaojinhe fault. To the east of the study area, the middle and southern sections of the Daliangshan fault and the Xiaojiang fault are located in LV2. Several main faults in the northern part of the study area, such as the Lijiang-Xiaojinhe fault, the southern section of the Anninghe fault and the Zemuhe fault, have obvious east–west velocity contrasts, and the high- and low-velocity anomaly boundaries correspond more consistently with the fault boundaries. The overall characteristic of the Anninghe fault is high velocity, and the Shimian-Mianning section shows a more obvious high velocity compared with the Mianning-Xichang section. The Sichuan Basin overall presents a high-velocity anomaly. The area around Panzhihua shows high velocity, and this area gradually decreases with depth.

At 35 km (Fig. 9f), the lateral resolution decreases because of the small number of ray paths available. However, the high-velocity anomaly of the Sichuan Basin can still be observed as well as the low-velocity LV1 and LV2 separated by the high-velocity zone along the Emeishan-Panzhihua area.

Figure 10 shows the S-wave velocity profiles along 29.5°N, 28.6°N and 26.5°N (the locations of the profiles are marked in Fig. 9e). All three profiles show two low-velocity zones in the middle crust. Figure 10a indicates that there is a low-velocity anomaly beneath the Gongga Shan connected to LV1 in the middle crust, with a westward-dipping high-velocity structure in the east side. Figure 10b shows an arch-shaped high-velocity zone beneath the Lijiang-Xiaojinhe fault and the Daliangshan fault. Figure 10c indicates that there is a high-velocity anomaly with large area in Panzhihua, which may be related to magmatic activity in the Emeishan Large Igneous Province.

Fig. 10
figure 10

S-wave velocity profiles at 29.5°N, 28.6°N and 26.5°N. See Fig. 9e for profile locations. The white dashed line is the boundary of the high and low velocity anomaly zone. GGS Gonga Shan; PZH Panzhihua; others as in Fig. 1

Full size image

5 Discussion

5.1 The Genesis of LV1 and LV2

The new tomography results show two very significant low-velocity anomalies (LV1 and LV2) in the study area at 18–35-km depth (Figs. 9 and 10). The LV1 is confined by the Longmenshan fault and Lijiang-Xiaojinhe fault and is distributed in the western part of the study area. The LV2 is primarily distributed along the Daliangshan fault and Xiaojiang fault and their eastern sides. The two low-velocity zones extend to at least 35-km depth and are separated by a high-velocity anomaly around Shimian-Mianning-Xichang-Panzhihua area.

Previous tomography results using sparse seismic stations show that LV1 and LV2 are contiguous. Therefore, large-scale crustal flow is speculated to exist in the middle and lower crust of the southeastern margin of the Tibetan Plateau (Li et al., 2009; Ma et al., 2008; Wei et al., 2010). In recent years, with the deployment of portable seismic stations and new imaging algorithms, such as ambient noise tomography, the resolution of the velocity structure in the southeastern margin of the Tibetan Plateau has been greatly improved. Many studies have consistently revealed that there are two low-velocity zones or high-conductivity layers in the middle and lower crust (Bai et al., 2010; Bao et al., 2015; Chen et al., 2014; Fu et al., 2017; Huang et al., 2010, 2018; Li et al., 2016a, 2019b; Qiao et al., 2018; Wang et al., 2017; Xia et al., 2021; Yao et al., 2008; Yu et al., 2022; Zhang et al., 2020). The western low-velocity zone (LV1) extends northeastward along the Longmenshan fault, widely distributed in the Songpan-Ganzi Block, and extends southwestward to the Yunnan-Myanmar-Thailand Block. The other low-velocity zone (LV2) cuts off from the southwest side of the Sichuan Basin through the Daliangshan fault and Xiaojiang fault to the Red River fault.

Owing to the complex deformation processes on the southeastern margin of the Tibetan Plateau, controversies still exist concerning the genesis of LV1 and LV2. Some studies suggest that both LV1 and LV2 are caused by crustal flow (Huang et al., 2018; Yao et al., 2008; Zhao et al., 2013). The imaging results from Bai et al. (2010) and Bao et al. (2015) show that the boundary of the high-conductivity layers and low-velocity zones overlaps with the faults and suggest that the distribution of the two low-velocity channels may be related to the shearing of the faults. Other studies suggest that the genesis of LV2 is different from that of LV1 and may be related to shear heating of the faults (Li et al., 2019b; Yang et al., 2020; Zhang et al., 2020) and upwelling of mantle material (Wu et al., 2013; Li et al., 2019b; Yu et al., 2022).

GPS studies have obtained a clockwise-rotating velocity field around the Eastern Himalayan tectonics (Gan et al., 2007; Wang et al., 2001a; Zhang et al., 2004a). In addition, several surface wave azimuthal anisotropy studies have obtained a similar fast wave direction around LV1 (Lu et al., 2014; Wang et al., 2015; Yao et al., 2010; Yi et al., 2010), indicating the southeastward flow from the Tibetan Plateau. Leloup et al. (1999) showed that shear heating of faults can promote the melting of crustal material. In the crustal flow model, it is difficult for plateau material to sustain long distance flow via gravity alone (Bai et al., 2010). Shear heating of the faults can help reduce the strength of the crust and make it easier for crustal material to flow over long distances (Bao et al., 2015; Li et al., 2019b; Liu et al., 2014; Yang et al., 2020; Zhang et al., 2020). We speculate that left-lateral strike-slip faults such as the Xianshuihe fault and the Lijiang-Xiaojinhe fault in the LV1 region have a mutually reinforcing effect with the crustal flow.

The connectivity of the two low-velocity zones, LV1 and LV2, is a key factor that affects their genesis. If LV1 and LV2 are connected, their genesis may be similar, and both are influenced by crustal flow. However, if LV1 and LV2 are unconnected, the origin of LV2 cannot be interpreted with crustal flow exclusively. The new model (Figs. 9 and 10) clearly shows that LV1 and LV2 are unconnected and demonstrates that the low-velocity zones in the middle and lower crust are separated by the Anninghe-Zemuhe fault zone and the Panzhihua high-velocity zone, which are located in the middle and inner zones of the Emeishan Large Igneous Province. Because of the presence of a series of mafic and ultramafic magma from upper mantle (Zhang, 1988; Zhou et al., 2005), this high-velocity zone is strong enough to obstruct the continuous eastward flow of crustal material from LV1, making it impossible for plateau material to cross, resulting in LV1 and LV2 not being connected. This is inconsistent with the crustal flow model beneath the Anninghe-Zemuhe fault zone proposed by Zhu et al. (2017) and Yu et al. (2022). If LV1 and LV2 are connected, the low-velocity material possibly flows from the lower crust or upper mantle of Panzhihua or bypasses the Panzhihua high-velocity zone to the Xiaojiang fault via the Red River fault. Figs. 9 and 10c show that there is a high-velocity anomaly near Panzhihua from the surface to 35 km depth. Many tomography results indicate that this high-velocity anomaly extends from the crust to the upper mantle (Bao et al., 2015; Fan et al., 2015; Fang et al., 2022; Liu et al., 2021; Pan et al., 2015; Wu et al., 2013; Yang et al., 2014; Yao et al., 2008; Zhang et al., 2020). Therefore, it is unlikely that crustal material can flow from the bottom of the Panzhihua high-velocity anomaly to LV2.

Several surface wave azimuthal anisotropy results show that the fast wave directions in the middle and lower crust are consistent with the strike of the Red River fault and the Xiaojiang fault, respectively (Gao et al., 2020; Han et al., 2020). Positive radial anisotropy has also been found near these two faults (Huang et al., 2010; Yang et al., 2020). The Red River fault appears to possibly serve as a channel for material flow between the two low-velocity zones. However, the body wave tomography results show that the low-velocity anomalies are primarily concentrated in the northern and middle sections of the Red River fault, the northern section of the Xiaojiang fault and the southern section of the Xiaojiang fault, and there is a high-velocity zone at the intersection of the Xiaojiang fault and Red River fault (Deng et al., 2020; Wu et al., 2013; Xu et al., 2013). Ambient noise tomography results also show that the two low-velocity zones are not connected in the middle and lower crust through the Red River fault (Yao et al., 2008; Zhang et al., 2020). Li et al. (2016b) processed digital elevation model data and found that the middle and southern sections of the Red River fault uplift several hundreds of meters compared with its northern section, suggesting that the thickening of the crust is influenced by the flow of material from the middle crust. We believe that the plateau material from LV1 bypasses Panzhihua, passes through the Red River fault, but is then obstructed by the high-velocity zone in its southern section and does not flow to the Xiaojiang fault.

An increase in temperature generally leads to the reduction of S-wave velocity. According to Goes et al. (2000), when the temperature increases by 100 °C, the S-wave velocity reduces by 0.7–4.5%. According to the theoretical model of fault shear heating proposed by Leloup et al. (1999), the shear heating of fault occurs mainly along the fault, and the shear heating of the fault can affect 80 km on both sides of the fault. The slip rate of the fault is a key parameter that affects the temperature. For a slip rate of 10 mm/a, the temperature can increase by approximately 50 °C/a at a depth of 20 km. So, we infer that the shear heating contributes to the genesis of LV2. Compared with the average geothermal heat flow of 65 mW/m2 in Southwest Sichuan (Wang et al., 2001b; Xu et al., 2011), the surface heat flow increased by 10 mW/m2 and 20 mW/m2 on the eastern side of the Daliangshan fault and the northern section of Xiaojiang fault, respectively (Hu et al., 2000; Huang et al., 2018; Shi & Wang, 2017). The average amounts of slip of the Daliangshan fault and the northern section of the Xiaojiang fault are 3–4 mm/a (Wei et al., 2012) and 8–10 mm/a (Wen et al., 2011), respectively. The surface heat flows generated by the shearing movement of these faults are calculated theoretically to be approximately 6 mW/m2 and 15 mW/m2 (Leloup et al., 1999), respectively. Therefore, other factors need to be considered in addition to the increased surface heat flow resulting from the shearing movement of the fault. Because low velocity/high conductivity is found in the middle and lower crust near the Daliangshan fault and the northern section of the Xiaojiang fault and extends down to the upper mantle, many studies have proposed that the low-velocity structure in this region results from the upwelling of mantle material (Cheng et al., 2017; Lei et al., 2019; Li et al., 2019a; Wang et al., 2014; Wei et al., 2013; Yu et al., 2022). In addition, the negative radial anisotropy of the Daliangshan fault and the northern section of the Xiaojiang fault in the crust (Xie et al., 2017; Yang et al., 2020) reflect the possibility of mantle material upwelling in LV2. In summary, the shearing movements of the Daliangshan fault and Xiaojiang fault themselves can make the materials on both sides of the faults frictionally heat up and reduce the material strength of the middle crust. As with the upwelling of mantle material, this can result in the formation of a low-velocity zone with high heat flow.

5.2 The Uplift Mechanism of the Gongga Shan

Located between Kangding and Shimian, the Gongga Shan is adjacent to the Xianshuihe fault and Lijiang-Xiaojinhe fault. It has a height of approximately 7556 m, making it the highest peak on the eastern edge of the Tibetan Plateau. The Gongga Shan is currently ascending at a rate of 1–3 mm/a (Jiang et al., 2022; Liang et al., 2013; Pan & Shen., 2017). Different uplift mechanisms are proposed for the Gongga Shan. The 'dynamic topography' model and 'transpression' model are two possible end-members. The 'dynamic topography' model suggests that crustal flow existed in the middle and lower crust along the southeastern margin of the Tibetan Plateau. The flow of mechanically weak material through the Gongga Shan was blocked by the subduction of the Yangtze Block beneath it, which hindered the continuous eastward flow of plateau material and caused the uplift of the Gongga Shan (Clark et al., 2005). The 'transpression' model is based on the fact that in the Gongga Shan area, the fault direction of the Xianshuihe-Anninghe fault zone has changed to form an angle deviation with the moving direction of the Sichuan-Yunnan Block. The movement of the Sichuan-Yunnan Block can be decomposed into two components. One component corresponds to the slip motion of the faults; the other component causes compression on the Gongga Shan, which shortens the crust of the Gongga Shan area and results in vertical uplift (Chen et al., 2008).

As shown in Fig. 9d–f, at a depth of 18–35 km, the Gongga Shan exhibits a low-velocity anomaly located in the LV1. Figures 9 and 10a show that a high-velocity anomaly exists on the east of the Gongga Shan at 10–35-km depth. P-wave traveltime tomography and magnetotelluric imaging have identified a west-dipping high-velocity zone and high-conductivity layer in the middle and lower crust to the eastern side of the Gongga Shan (Jiang et al., 2022; Wang et al., 2021). Many studies indicate that the Yangtze Block subducted to the Songpan-Ganzi Block during the Oligocene (30–25 Ma; Cai et al., 1996; Guo et al., 2013; Xu et al., 2007). Xu et al. (2007), after mica 40Ar-39Ar dating from detachment faults, concluded that the shortening and deformation along the Longmenshan-Jinpingshan Orogenic Belt are related to the westward subduction of the Yangtze Block and the flow of the middle and lower crust (Royden et al., 1997; Xu et al., 1999). Therefore, the high-velocity zone within the middle crust on the eastern side of the Gongga Shan is likely a remnant of the westward subduction of the Yangtze Block, and this high-strength material is able to block eastward flow of the crustal material.

The Gongga Shan has many hot springs and high heat flow (Hochstein & Regenauer-Lieb., 1998; Shen et al., 2007). Isotope dating of zircon samples suggests that due to the east–west compressional movement of blocks (Mattauer et al., 1992) and the shearing movement of the fault (Liu et al., 2006; Wang et al., 1997), the southeastern section of the Xianshuihe fault underwent high-temperature metamorphism during the Miocene (18–12 Ma). The Gongga Shan granite beneath the sediments was the product of partial melting of crust formed under high-temperature conditions during this phase (Li et al., 1983; Li & Zhang., 2013). Many petrological and geochemical studies indicate that cooling of the molten material in the Gongga Shan occurred at 11–2 Ma (Lai et al., 2006, 2007; Li & Zhang, 2013; Roger et al., 1995; Xu & Kamp, 2000). Ar–Ar thermochromological study shows that the time of cooling to 300–400 °C in the southeastern section of the Xianshuihe fault is 3.6 Ma (Chen et al., 2006). Lai et al. (2007) simulated the thermal evolution history of apatite samples and concluded that the cooling rate of the Gongga granite in the early stage was extremely low. It started to cool rapidly at 55–70 °C/Ma until approximately 2 Ma years ago. At present, the Gongga Shan is still in the cooling period (Tan et al., 2010), and the rock strength is very low. That is why the Gongga Shan is imaged as a low-velocity anomaly at 0–12 km depth compared with the surrounding areas (Fig. 9a-c, 10a). Our tomography results (Fig. 9) show that the boundaries of high- and low-velocity zones coincide with large strike-slip faults, especially in the southeastern section of the Xianshuihe fault. Many studies have shown that the Xianshuihe fault underwent strong left lateral strike-slip shearing at 12–10 Ma (Chen et al., 2006; Roger et al., 1995; Zhang et al., 2004b). Then, influenced by the eastward flow of the crustal material, the fault strikes of the southeastern section of the Xianshuihe fault and the northern section of the Anninghe fault changed by approximately 20° from NW–SE to N-S. The movement direction of the Sichuan-Yunnan Block was consistent with the strike of the Xianshuihe fault, but inconsistent with the Anninghe fault. The change in the fault strike was able to resolve into an extrusion force on the Gongga Shan (Chen et al., 2008; Jiang et al., 2022; Tan et al., 2010). We conjecture that the weak upper crust of the Gongga Shan is prone to shorten in horizontal direction and to uplift vertically (Wen & Bai., 1985).

In summary, we considered the uplift mechanism of the Gongga Shan is as follows. Due to the eastward flow of the middle and lower crust of the Tibetan Plateau and obstruction of the strong Yangtze Block, the low-velocity and high-temperature materials beneath the Gongga Shan continued to accumulate and the crust further thickened, forming the gentle western side and steep eastern side of the Gongga Shan. Both 'dynamic topography' model and 'transpression' model contribute to the uplift of the Gongga Shan.

6 Conclusions

In this study, we obtain a new high-resolution 3D S-wave velocity model (AZX-CVM1.0) of the upper and middle crust in the Anninghe-Zemuhe-Xiaojiang fault zone with new observation data and direct surface wave inversion method. The lateral resolution of the tomography result near the fault zone is significantly improved. The main conclusions are as follows.

  1. 1.

    Two distinct low-velocity zones are observed in the middle crust of the study area, separated by the Anninghe-Zemuhe fault zone and the Panzhihua high-velocity zone in the central area. This high-velocity anomaly strip may be related to the intrusion of high-density mafic and ultramafic magma at different depths in the lithosphere during the uplift of the mantle plume.

  2. 2.

    The two low-velocity zones (LV1 and LV2) are not connected and have different genesis. The western low-velocity zone (LV1) is formed by the flow of material from the Tibetan Plateau, which is driven by gravity and shearing movement of the faults. The formation of the low-velocity anomaly (LV2) near the Daliangshan fault and Xiaojiang fault is a combination of shear heating by the faults and upwelling of mantle material.

  3. 3.

    The Gongga Shan exhibits a low-velocity anomaly at 0–35-km depth. A high-velocity zone is imaged in the middle and lower crust on the east side of the Gongga Shan. It is speculated that the rapid uplift of the Gongga Shan is the superimposition effect of the accumulation of the plateau material and the bending and compression of the left-lateral strike slip faults in the block boundary.