1 Introduction

Global search methods are well-known problem solvers for the optimization of geophysical data. They are based on stochastic inverse modeling and are divided into two big families: Monte Carlo and metaheuristic methods (Sen & Stoffa, 2013). The main advantage of stochastic inverse modeling is that it theoretically ensures the final solution to be found as (or very close to) the global solution of the problem, thus overcoming the trap of the local minima and the so-called “local minimum syndrome” (Sen & Stoffa, 2013). Another striking advantage of the global search is that the optimization process is randomly initialized, so that the final solution is not biased by the choice of the starting model, which can significantly influence the result of the inverse problem (Miensopust, 2017). The key difference between the Monte Carlo and metaheuristic methods is that the former is based on the random sampling of the solution space and a probabilistic approach (Sambridge & Mosegaard, 2002), while the latter is based on the strategical sampling and adaptive approach inspired by the complex systems of natural phenomena (Engelbrecht, 2007).

Nature-inspired metaheuristics are Computational Intelligence algorithms based on biological systems. They are divided into two main families: Evolutionary Computation (EC), that models the genetic evolution in a population, and Swarm Intelligence (SI), that models the social dynamics of organisms living in groups. The most successful examples of EC are the genetic algorithm (GA) and the differential evolution (DE), while the main SI paradigms are particle swarm optimization (PSO), grey wolf optimizer (GWO), ant colony optimization (ACO) and the bat algorithm (BA). There is also a third group of metaheuristics that are not population-based but instead physics-based, such as the simulated annealing (SA) algorithm, which has been applied to geophysics (Biswas, 2016; Biswas & Rao, 2021; Dosso & Oldenburg, 1991).

The population-based methods have increasingly been applied to solve the inverse problem of various geophysical data (Everett, 2013; Sen & Stoffa, 2013). There are continuous developments and applications of GA (Sen & Mallick, 2018; Villa Acuna & Sun, 2020) and PSO (Essa et al., 2021; Pace et al., 2021; Pallero et al., 2021). Both can be considered the benchmark metaheuristic algorithms since they have been introduced in the 90’s (Goldberg, 1989; Kennedy & Eberhart, 1995). DE, ACO and BA have been barely adopted in the geophysical literature (Balkaya, 2013; Bouchaoui et al., 2022; Essa & Diab, 2022; Yuan et al., 2009), while GWO has recently been introduced (Agarwal et al., 2018; Vashisth et al., 2022). EC and SI methods have the advantage of strategical sampling of the model space and theoretical convergence toward (or, at least, very close to) the global minimum (Sen & Stoffa, 2013). They have shown to be extremely efficient in solving the inverse problem in geophysics, which is underdetermined, ill-posed and nonlinear.

The GA mimics the inheritance rules in nature, where the individuals with the best chromosomes survive (and the weakest individuals have to die) (Goldberg, 1989). As only the selected chromosomes are inherited by the new generations, the individual survived after some generations (i.e., iterations) thanks to the best genetic features represents the final solution of the geophysical problem. The application of GA in geophysics is wide (Everett, 2013; Sen & Mallick, 2018) as it was one of the first metaheuristic algorithms applied to the inverse problem (Sen & Stoffa, 1992). Some representative examples are the inversion of seismic waveform (Sambridge & Drijkoningen, 1992), magnetotelluric data (Everett & Schultz, 1993), elastic waves (Aleardi & Mazzotti, 2017), and direct current resistivity data (Balkaya et al., 2012; Schwarzbach et al., 2005).

The PSO algorithm is inspired by the social dynamics observed in group of animals adopting a collective behavior, such as birds, schools of fish, bees, etc.… (Engelbrecht, 2007; Kennedy & Eberhart, 1995; Kennedy et al., 2001). PSO has successfully been applied to different geophysical data, such as electromagnetic (Amato et al., 2021; Godio & Santilano, 2018; Pace et al., 2017; Shaw & Srivastava, 2007), electric (Fernández Martínez et al., 2010; Pace et al., 2018), magnetic (Essa & Elhussein, 2020) and seismic data (Aleardi, 2019; Song et al., 2012). A review of recent advances in PSO geophysical applications is given by Pace et al. (2021).

The GWO algorithm is based on the social dynamics adopted by a group of wolves attacking a prey while searching for food (Mirjalili et al., 2014). Despite the recent promising outcomes, GWO has been applied to geophysical data in few occasions (Agarwal et al., 2018; Chandra et al., 2017; Song et al., 2015).

The three methods GA, PSO and GWO have their own advantages and weaknesses, but have been indistinctly applied to the optimization of geophysical data because the quality of their outcome is similar, that is, the global solution of the geophysical problem. However, there are few geophysical studies that have carefully investigated the performances of GA, PSO, GWO and compared their outcomes. PSO and GA were compared for gravity data and self-potential inversion (Göktürkler & Balkaya, 2012; Yuan et al., 2009), while PSO and GWO were tested for the inversion of magnetic, gravity and self-potential anomalies (Agarwal et al., 2018) and of apparent resistivity and apparent chargeability data (Chandra et al., 2017). Furthermore, the optimization of EM data has been less explored than other data (e.g., Alkan & Balkaya, 2018).

The objective of this work is to compare the performances of the GA, PSO and GWO algorithms through stochastic inverse modeling of time domain electromagnetic (TDEM) data. The ensuing sections explain the essential theory of GA, PSO and GWO, and how they are applied to solve the TDEM inverse problem (Sect. 2). Section 3 presents the test of the three methods on a synthetic example of TDEM noise-corrupted data. Then, the three approaches are applied to two different TDEM surveys in Italy (Sect. 4). The first case study is a TDEM sounding acquired for groundwater prospection over a known stratigraphy (Pace et al., 2019a). The second case study is located in the Travale geothermal area (central Italy), where TDEM soundings were acquired for the characterization of the uppermost part of the geothermal reservoir (Pace et al., 2022). The final results are quantitatively compared to finally show a thorough overview of the algorithms’ performances.

2 The Metaheuristic Methods

2.1 The Genetic Algorithm

The optimization procedure of GA is the computer implementation of the evolutionary phenomenon of "survival of the fittest", that is, only the selected chromosomes are inherited by the new generations (Everett, 2013). This tenet is conveyed in an algorithm where, over the iterations, the solutions with the best value of the fitness or objective function are kept, while the other solutions sampled are discarded (Sen & Mallick, 2018).

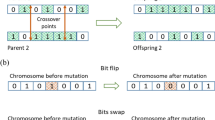
The starting group of sampled solutions is randomly chosen and represent a population of individuals with a certain sequence of chromosomes. Each candidate solution is coded as a binary bit sequence that is iteratively modified following some steps that replicate biological processes such as reproduction, gene crossing and gene mutation (Goldberg, 1989; Sen & Stoffa, 2013). After that, a new generation of candidate solutions is created and then evaluated by the objective function. As the algorithm iterates, the fittest models tend to be preserved in the subsequent generations, while the less-fit models die off. The iteration of standard GA consists of three steps (Gallagher et al., 1991). The first step is the reproduction stage, in which a new generation of models m is chosen from the previous generation based on a probability distribution PR(m). In our code, the parents were chosen according to the “roulette wheel” method, which is a random selection based on the fitness value. The fittest models are likely to be included in the new generation, whereas the least-fitting models are unlikely to be selected for reproduction. The second step is the crossover step that mixes the existing genetic information in the population. The models are randomly paired off to form couples. The members of the pair exchange a randomly chosen contiguous bit substring, according to the crossover probability PC. We adopted the “uniform” crossover, which is based on continuous uniform random numbers for the selection of the contiguous bits of the two parents. The result is the creation of two new models with slightly different genetic sequences than the original two parents. The mutation step is the third step and contributes to new genetic information for the current generation of models. Mutation rarely occurs in nature, so it is applied to GA following a certain probability, the mutation probability PM, which is usually low. Mutation is a fundamental step that ensures genetic diversity and hence a broader space for the solutions. Therefore, mutation prevents to fall in a local minimum solution. However, PM is usually a low value in order to drive the search towards the most favorable region of the model space where the current generation is evolving.

The input parameters of the GA are the population size N and the reproduction (PR(m)), crossover (PC) and mutation (PM) probabilities. The population size is problem dependent, while the other settings are suggested from the literature (Sen & Stoffa, 2013; Villa Acuna & Sun, 2020). A high value of PC means a rapid introduction of new solutions which are similar to the parents so that the algorithm rapidly converges towards the best individual (with possibly a premature end). By contrast, a low value of PC may cause a stagnation due to low exploration. The PM controls the solution diversity and search space exploration. A high value of PM in fact decreases the chance to get trapped in a local minimum solution but increases the number of iterations for convergence. A low PM speeds up the convergence (Sen & Stoffa, 2013). Typical values of PC are between 0.65 and 0.95 (Sen & Stoffa, 2013), while for PM between 0.02 and 0.05. To tune PC and PM for our geophysical application we performed a sensitivity analysis on different values. We explored the GA performance by setting PC equal to 0.6, 0.7 and 0.8, and PM equal to 0.01, 0.02, 0.03, 0.04 and 0.05. After an accurate sensitivity analysis, the values of PC and PM adopted in this work were 0.7 and 0.03, respectively. The complete result of sensitivity analysis is provided in the Supplementary material. The GA code used in this work was adapted from the original code, which is available for free in the website of the Yarpiz Project (Heris, 2020).

2.2 Particle Swarm Optimization

The PSO algorithm is based on the interactions of agents sharing knowledge to pursue the common objective of the group, such as escaping from a predator or searching for food. The particles forming the swarm represent the possible solutions of the geophysical problem and are arrays composed of as many components as the problem unknowns. The behavior of the particles is ruled by a memory component that is both cognitive, i.e., based on the individual experience, and social, i.e., driven by the group leader. The behavior of the particles is hence extremely adaptive as it can change depending on the external environment. These behavioral dynamics are the theoretical tenets of the PSO applied to geophysical data (Essa & Munschy, 2019; Essa et al., 2022; Godio & Santilano, 2018; Pace et al., 2017, 2019a, 2019b, 2021; Roy et al., 2022) and to many other scientific fields dealing with nonlinear problems (Adhan & Bansal, 2017; Poli, 2008).

The particle changes its position x in the search space of the solutions by means of the velocity vector v, defined as:

$${{\varvec{v}}}_{i}^{k+1}={\omega }^{k}{{\varvec{v}}}_{i}^{k}+{\alpha }_{1}^{k}{\gamma }_{1}\left({{\varvec{P}}}_{i}-{{\varvec{x}}}_{i}^{k}\right)+{\alpha }_{2}^{k}{\gamma }_{2}\left({\varvec{G}}-{{\varvec{x}}}_{i}^{k}\right)$$
(1)
$${{\varvec{x}}}_{i}^{k+1}={{\varvec{x}}}_{i}^{k}+{{\varvec{v}}}_{i}^{k+1}$$
(2)

where: x is the position of the particle in the search space; v is the velocity vector; i = [1, …, N]; N is the number of particles; k is the iteration number; ωk is the inertia that weights the velocity remembered from the previous iteration; α1k is the cognitive acceleration to the best individual position P (or the local minimum); α2k is the social acceleration to the best global position G (or the global minimum), and γ1 and γ2 ∈ [0,1] are uniformly distributed random values for stochastic perturbation of the solution. The particles are randomly initialized with null velocity. Then, the particle position \({{\varvec{x}}}_{i}^{k}\) is updated according to the influence of the three terms of Eq. 1 (ωk, α1k and α2k). The inertia ωk linearly decreases from 0.9 (first iteration) to 0.4 (last iteration) (Shi and Eberhart, 1998). The values of ωk, α1k and α2k influence the convergence of the problem and the balance between the global and local search, namely, the exploration of the search space and the exploitation of the best region found, respectively. To ensure the optimal balance we adopt the hierarchical PSO with time-varying acceleration coefficients (HPSO-TVAC). As the optimization starts, it enables the exploration by setting α1k larger than α2k and then the exploitation of the best regions and final convergence towards the global minimum by setting α2k larger than α1k (Ratnaweera et al., 2004). Some sensitivity analyses have been performed to assess the influence of the accelerations on the PSO final solution (Pace et al., 2019b; Ratnaweera et al., 2004). The optimal values ensuring the solution convergence have been determined for PSO of electromagnetic data and are α1k=1 = α2k=max(k) = 2 and α1k=max(k) = α2k=1 = 0.5 (Amato et al., 2021; Pace et al., 2019a, 2019b). This means that α1k linearly decreases from 2 (first iteration) to 0.5 (last iteration) and vice versa for α2k. The acceleration values must obey the stability solution conditions described in Perez and Behdinan (2007).

The particles of the swarm change their position in order to minimize the objective function and thus find the best solution of the problem, that is, the theoretical global minimum G. The link between Eqs. 2 and 1 is that at the k-iteration the particle with the minimum value of objective function is awarded as the global best G and attracts the neighboring particles depending on α2k (swarming behavior). In the end, the particle that most minimizes the objective function is selected as the final solution.

The main differences between PSO and GA are that the unknown parameters of the problem are represented by the particles of the swarm in PSO and by the individuals of the population in GA. The steps of the algorithm are called iterations in PSO and generations in GA. The sampling of the model search space is ruled by social and cognitive behavior in PSO and by natural selection (mutation and reproduction) in GA.

The PSO code used in this work has been adapted from the previously published works of the authors (Amato et al., 2021; Pace et al., 2018, 2019a).

2.3 Grey Wolf Optimizer

The GWO algorithm is an SI method that mimics the leadership hierarchy and hunting mechanism of grey wolf (canis lupus) packs in nature (Mirjalili et al., 2014). Grey wolves are considered apex predators, which means they are at the top of the food chain. In the algorithm, the leadership hierarchy is simulated by means of four types of grey wolves, that are referred to as the alpha (α), beta (β), delta (δ), and omega (ω) wolf. The optimization reproduces the three main steps of hunting, namely, tracking, encircling and attacking the prey. The tracking process represents the exploration of the search space to sample the possible solutions and find the region of the possible global solution (global search). The encircling and attacking processes represent the exploitation of the best regions found in the search space in order to converge and select the best solution (local search).

The alpha wolf, often known as the dominating wolf, should be followed by the pack. The beta wolf is the second rank of the grey wolf hierarchy. The grey wolf with the lowest ranking is the omega wolf. If a wolf is not an alpha, beta, or omega, it is referred to as the delta or subordinate wolf. The leader of the social structure, the α wolf, represents the best solution of the problem because it best minimizes the objective function. The second and third best solutions are represented by the β and δ wolves, respectively. The remaining possible solutions are all called ω solutions. The optimization process is led by the α, β and δ solutions and mimics the hunting action. The α (best candidate solution), β and δ wolves have better knowledge of the potential location of the prey. Therefore, these solutions are saved and the other wolves (ω) are forced to follow them.

The grey wolves encircle the prey during the hunt. This action is mathematically modeled by means of the following equations (Mirjalili et al., 2014):

$$\overrightarrow{{\varvec{D}}}= \left|\overrightarrow{C}\cdot {\overrightarrow{{\varvec{X}}}}_{{\varvec{p}}}\left(t\right)-\overrightarrow{{\varvec{X}}}(t)\right|$$
(3)
$$\overrightarrow{{\varvec{X}}}\left(t+1\right)= {\overrightarrow{{\varvec{X}}}}_{{\varvec{p}}}\left(t\right)-\overrightarrow{A}\cdot\overrightarrow{{\varvec{D}}}$$
(4)

where D is the distance between the solution found and the α, β and δ solutions, t denotes the current iteration, \(\overrightarrow{A}\) and \(\overrightarrow{C}\) denote the coefficients, \({\overrightarrow{{\varvec{X}}}}_{{\varvec{p}}}\left(t\right)\) denotes the vector of the prey position, and \(\overrightarrow{{\varvec{X}}}(t)\) is the vector of a grey wolf position. The coefficients \(\overrightarrow{A}\) and \(\overrightarrow{C}\) control the smooth transition from exploration to exploitation and are calculated as follows:

$$\overrightarrow{A}=2\overrightarrow{a}\cdot\overrightarrow{{r}_{1} }- \overrightarrow{a}$$
(5)
$$\overrightarrow{C}=2\cdot\overrightarrow{{r}_{2} }$$
(6)

where r1 and r2 are random vectors in [0,1] and \(\overrightarrow{a}\) linearly decreases from 2 to 0 over the iterations.

The optimization begins with the creation of a random population of grey wolves (possible solutions). The objective function is computed for each candidate solution of the problem. Then, the α, β and δ wolves are elected and estimate the optimal location of the prey (the global solution) at each iteration. Each candidate solution updates its position in relation to the estimated position of the prey. If |\(\overrightarrow{A}\)|> 1, the candidate solutions tend to diverge from the prey location (exploration of the search space), while if |\(\overrightarrow{A}\)|< 1 they tend to converge towards it (exploitation of the search space). Thanks to the adaptive value of |\(\overrightarrow{A}\)|, GWO ensures high local optima avoidance (Mirjalili et al., 2014). Finally, the grey wolves end the hunt by attacking the prey, which stops moving. To mathematically model the attack and balancing the global and local approaches, the value of \(\overrightarrow{a}\) is reduced. The GWO algorithm stops when of an ending criterion is satisfied, e.g., when the maximum number of iterations is reached.

The main scientific applications of GWO deal with economic dispatch problems (Wong et al., 2015), feature selection for text classification (Chantar et al., 2020), inversion and joint inversion of geophysical data. In detail, GWO has been applied to electromagnetic and gravity data (Agarwal et al., 2018; Chandra et al., 2017), surface wave data (Song et al., 2015; Vashisth et al., 2022) and machine learning for seismology (Sharma et al., 2021).

The GWO code used in this work has been adapted for geophysical data from the source code available at MATLAB Central File Exchange (Mirjalili, 2022).

2.4 Common Features of the Algorithms

The candidate solutions found by the metaheuristic methods are evaluated with the objective function, whose value has to be minimized to find the global solution. The solution that most minimizes the objective function is the last generation in GA, the swarm leader (G) in PSO and the α wolf in GWO.

For the optimization of TDEM data, the objective function to be minimized could be defined as:

$$F({\varvec{m}})=\frac{1}{\sqrt{M}}\Vert \frac{{{\varvec{\phi}}}_{o}-{{\varvec{\phi}}}_{c}}{{{\varvec{\sigma}}}_{\phi }}\Vert +\lambda \parallel \partial {\varvec{m}}\parallel$$
(7)

where: ϕo is the array of the observed/synthetic data; ϕc is the calculated response; the difference inside the L2-norm \(\Vert \cdot\Vert\) is normalized by the corresponding data errors (σϕ); M is the number of evaluated data; λ is the Lagrange-multiplier acting as a smoothing parameter on the first derivative of the model m. The first term of the right-hand side of Eq. 7 measures the normalized difference between the observed/synthetic data and the calculated responses. The second term acts on the roughness of the model by means of λ, which is usually identified according to the L-curve criterion (Farquharson & Oldenburg, 2004). The λ multiplier is chosen as a tradeoff between a minimum data misfit on a rough model (low λ) and a smooth model with high misfit (high λ). The λ multiplier is problem dependent and was defined by means of a sensitivity analysis for each example of the following sections.

The input parameters that are specific of the three algorithms drive the global- vs. local-search balance and have strong influence on the outcome as well as on the speed of convergence. The advantage of GA, PSO and GWO is that they do perform both local and global search, but these opposite approaches need to be balanced. To avoid the optimization being compromised towards either a pure global search or a plain local search, the algorithm input parameters need to be tuned, as described in the previous sections. The optimal values were identified after an accurate sensitivity analysis that was performed in this work for GA (see Supplementary Material), while it has already been performed for PSO (Pace et al., 2019b) and GWO (Mirjalili et al., 2014).

While each algorithm had specific values for the input arguments, other input parameters were kept identical for GA, PSO and GWO in order to quantitatively compare the three algorithms. These common settings are:

  1. 1.

    The stopping criterion. The number of iterations to be executed should be enough to ensure an effective minimization of the objective function, that is, a flat trend of it at the last iterations, meaning convergence. Since the iterations needed are problem dependent, it is recommended to consider more than one stopping criterion (Engelbrecht, 2007; Pace et al., 2021), for example, the maximum number of consecutive iterations without further decrease of the objective function (or a preselected threshold reached by the objective function) (Pace et al., 2019a). However, for this comparative study, the three algorithms GA, PSO and GWO were executed for the same number of iterations in order to quantitatively assess their performance for a given case study.

  2. 2.

    The number of candidate solutions sampled. The candidate solutions are called individuals in GA, particles in PSO and wolves in GWO. This number is problem dependent because if it is too low the search space is not completely sampled and the global minimum potentially missed, while if it is too high the computational cost increases. Some studies on PSO have demonstrated that the swarm size should be proportional to the number of the problem unknowns, namely, between 8 and 12 times (Fernández Martínez et al., 2010; Pace et al., 2019b). In the following examples, the number of candidate solutions was set equal to 9 times the unknowns.

  3. 3.

    Initialization. The strategic sampling of metaheuristic methods starts as default with a uniformly random distribution of the initial solutions. Then, the search of the global minimum is carried out by evolutionary rules for GA and swarming behavior for PSO and GWO. This standard initialization ensures the global search and hinders the ambiguity of the solution because the search space is initially sampled in an effective way. Even though it is theoretically possible to initially constrain the optimization by means of an a priori starting model, the great advantage of metaheuristic methods is that they do not need for a priori initialization because the strategic sampling is able to adjust the random initialization of the solution (Pace et al., 2019b). It has been demonstrated for PSO that if part of the swarm is initialized with a priori information, the result is independent of it, that is, highly comparable to that obtained with random initialization (Pace et al., 2019b). Therefore, PSO does not require an a priori starting model and can be successfully used for the interpretation of data from areas where a priori knowledge is unavailable or unreliable. Differently from what happens for the deterministic inversion methods, introducing a priori information in metaheuristic methods does not solve the ambiguity of the solution, but instead introduces a strong bias in the optimization process, which can prematurely be trapped in a local minimum.

  4. 4.

    Boundaries of the search space. Dealing with the optimization of TDEM data, the problem unknown is the array of the electrical resistivity of the layered 1D model, because the thickness of the layers is defined in advance with the Occam’s inversion approach (deGroot‐Hedlin and Constable, 1990). The boundary conditions of the problem are the minimum and maximum values of electrical resistivity that the solution can assume. They act as bound constraints when the solution violates the search space limits during the optimization. These values were the same for all the layers of the 1D model and did not change during the optimization. The boundaries were chosen according to the data of each case study and were kept the same for the different runs of the algorithm.

  5. 5.

    Solution assessment. Each run (or group of iterations) of the algorithm was repeated several times, or “trials”, with the same settings, because it has been demonstrated that the results of different random initializations are similar but not identical (Amato et al., 2021; Pace et al., 2019b). The inverse problem suffers from the non-uniqueness of the solution and hence the outcome of the three algorithms is represented by equivalent solutions. In the following examples, the three algorithms were executed for 10 different trials in order to show the set of equivalent final solutions and highlight the solution with the minimum nRMSE (normalized root mean square error) that can solve the solution ambiguity. In fact, being GA, PSO and GWO global search methods, it is recommended to perform a-posteriori assessment of the uncertainty of the final model (Pace et al., 2021; Pallero et al., 2018). It is also important to inspect the different outcomes from the 10 trials of the same algorithm in order to assess the similarity/dissimilarity of the solutions and hence infer about the algorithm convergence.

Our codes were parallelized in Matlab environment to run on the high-performance-computing (HPC) cluster for academic research at Politecnico di Torino. Ten cores were used from a node belonging to a cluster with a sustained global performance of 20.13 TFLOPS. The forward operator for the modeling of TDEM data was adapted from the CR1Dmod algorithm (Ingeman-Nielsen & Baumgartner, 2006).

3 GA, PSO and GWO Applied to Synthetic TDEM Data

The TDEM method is based on the propagation of an induced electromagnetic field. The acquisition is performed by forcing a steady current to flow through a loop of wire for some milliseconds in order to allow a turn-on transient to be dissipated in the ground. The induced eddy currents generate a secondary magnetic field, which is proportional to their decay. The receivers that acquire the response are composed of one or more coils. The decay of the secondary magnetic field is a function of the electrical resistivity of the subsurface; the electrical resistivity distribution with depth is hence estimated by analyzing the transient decay of the secondary field with time (McNeill, 1990). The inversion of TDEM data results in a 1-D resistivity profile under the receiver position. The method is sensitive mainly to conductive formations.

We tested the three algorithms on synthetic TDEM data. The synthetic model is composed of five layers with contrasting resistivity and different thicknesses (red-dashed line in Fig. 1b). The resistivity of the five layers is 70, 150, 30, 100, 50 Ωm. The bottom depth of each layer is 10, 30, 100, 140 and 345 m. The TDEM signal corrupted with 10% Gaussian noise is shown in Fig. 1a with red dots and error bars. The signal was computed using the forward solver mentioned before and adopted for the optimizations. This synthetic model has been adopted in Pace et al., (2019a) for another study on multi-objective optimization.

Fig. 1
figure 1

The result of GA applied to the synthetic example: a TDEM theoretical signal (the red dots with error bars) and predicted response (blue line); b the true model (the red-dashed line), the final resistivity models after 10 trials (the green lines) and the best solution highlighted in blue

Full size image

The solution to be found is a 1D model discretized into 19 layers, whose thickness was parametrized coherently with the concept of electromagnetic diffusion depth. The number of iterations was 300 for GA, PSO and GWO. However, after some tests, it was evident that GA needed more iterations than PSO and GWO to converge. Therefore, we had to increase the computations of GA up to 800 to find a result comparable with those of PSO and GWO. The population size was 170, because, as explained before, it is set around 9 times the unknowns. The runs were repeated 10 times or trials for the solution assessment. The Lagrangian multiplier for the synthetic data was estimated using the L-curve criterion and was 0.001 for all the algorithms since it depends on the data. The minimum and maximum boundary conditions of the search space of solutions were 1 and 300 Ωm, respectively.

The GA result is shown in Fig. 1. The observed data (red dots) and model response (blue line) are plotted in Fig. 1a. The 10 models of the 10 trials are plotted in green in Fig. 1b, while the best model (with the minimum nRMSE) is marked in blue. The true model corresponds to the red dashed line. The best model gave a final nRMSE on the data normalized by the errors equal to 0.0972, while the RMSE with respect the true model was 0.6667 (see Table 1). The final models obtained by GA are fairly dissimilar at both shallow and deep layers. The resistivity of the best model is overestimated with respect to that of the true model below 50 m of depth.

Table 1 Settings and performance of GA, PSO and GWO for the TDEM synthetic example
Full size table

The PSO outcome is shown in Fig. 2. The comparison between observed data (red dots) and model response (blue line) is shown in Fig. 2a. The results after 10 trials are plotted in green in Fig. 2b, together with the best model that is marked in blue. The minimum nRMSE on the data was 0.0391, while the model RMSE was 0.4276 (see Table 1). All the models present the same resistivity distribution of the best model, thus showing good convergence of the solutions and coherence with respect the global solution found. The resistivity of the best model is underestimated with respect to that of the true model in the high-resistivity layers (the upper 150 Ωm and the lower 100 Ωm layers), while the other layers are in good agreement with the true model.

Fig. 2
figure 2

The result of PSO applied to the synthetic example: a TDEM theoretical signal (the red dots with error bars) and predicted response (blue line); b the true model (the red-dashed line), the final resistivity models after 10 trials (the green lines) and the best solution highlighted in blue

Full size image

The GWO result is provided in Fig. 3a for the data fitting and in Fig. 3b for the resistivity models. The best solution (in blue) is highly comparable with the conductive layers of the true model, but the 150 Ωm and the 100 Ωm layers are underestimated, as in PSO (Fig. 2b). The final nRMSE on the data was 0.0502, while the RMSE on the model was 0.4120 (see Table 1).

Fig. 3
figure 3

The result of GWO applied to the synthetic example: a TDEM theoretical signal (the red dots with error bars) and predicted response (blue line); b the true model (the red-dashed line), the final resistivity models after 10 trials (the green lines) and the best solution highlighted in blue

Full size image

Uncertainty analysis was performed to assess the reliability of the solutions. Table 1 provides the resistivity values (mean and standard deviation) at two representative depths (19 and 50 m) at the last iteration of the 10 trials. The layer at 19 m of depth lies in a resistive region (150 Ωm), while the layer at 50 m in a conductive region (30 Ωm). This analysis highlights the values of a possible mean model with respect to the true value.

The fewest nRMSE for the data was accomplished by the PSO algorithm, while the lowest model misfit by the GWO. The three algorithms can also be compared through the curve of the objective function F(m) in Fig. 4. In fact, the inspection of this curve reveals the effectiveness of the minimization along the iterations. Figure 4 shows the decrease of the objective function over the iterations for GA (black dots), PSO (blue dots) and GWO (pink dots). The trend of the PSO curve is gradual from the highest to the lowest value, meaning good balance between exploration and exploitation of the search space. GA and GWO show a stepped trend that decreases rapidly and becomes flat earlier than PSO, meaning a possible premature exploitation phase.

Fig. 4
figure 4

The curves of the objective function evolution with the iterations for the GWO (pink), PSO (blue) and GA (black) algorithms for the synthetic example

Full size image

4 Field Data Optimization

This section presents two case studies for the optimization of TDEM field data. The first case study deals with a single TDEM sounding acquired in Stupinigi, northwest Italy, for groundwater prospection over a known stratigraphy. The second case study is more challenging than the first because it is composed of a set of TDEM soundings acquired for the characterization of a geothermal reservoir in Travale (central Italy), which is a geologically complex area.

4.1 Case study 1: Stupinigi Site

The Stupinigi TDEM sounding represent an ideal case study for the assessment of GA, PSO and GWO because geological information is available thanks to a borehole located very close to the investigated site. Moreover, the area of Stupinigi has largely been investigated for groundwater exploration and hence the stratigraphic sequence is well-known. The site is characterized by a flat morphology and by sand and gravel deposits of an alluvial plain. The shallow subsurface is composed recent coarse gravel deposits, while at depth there is an alternation of gravel and (well consolidated and cemented) sand, that host two different aquifers separated by clayey layers (Pace et al., 2019a; Piatti et al., 2010).

The TDEM acquisition was a coincident-loop configuration adopting a wire of 50 m length. The injected current was 3 A and the turn-off time was 4 μs. Time range of acquisition was between 10−5 and 10−3 s.

The resistivity model to be found was discretized into 19 layers, whose thickness logarithmically increased with depth. The number of iterations was 500 for PSO and GWO (a bit larger than in the synthetic case to ensure convergence), while it was increased up to 800 for GA (like in the synthetic case). The population size was 170. The runs were repeated for 10 trials for each algorithm. The Lagrangian multiplier was 0.001. The boundary conditions were 1 and 500 Ωm.

The outcomes of GA, PSO and GWO are plotted in Figs. 5, 6 and 7 respectively. The final data misfit (nRMSE) and runtime are supplied in Table 2. The lowest runtime and nRMSE were achieved by PSO, while GA had the worst performance. Generally, the data fitting is satisfactory for the three methods (see Figs. 5a, 6a and 7a).

Fig. 5
figure 5

The result of GA applied to Stupinigi site: a TDEM observed signal (the red dots with error bars) and GA predicted response (blue line); b the final resistivity models after 10 trials (the green lines) and the best GA solution highlighted in blue

Full size image
Fig. 6
figure 6

The result of PSO applied to Stupinigi site: a TDEM observed signal (the red dots with error bars) and PSO predicted response (blue line); b the final resistivity models after 10 trials (the green lines) and the best PSO solution highlighted in blue

Full size image
Fig. 7
figure 7

The result of GWO applied to Stupinigi site: a TDEM observed signal (the red dots with error bars) and GWO predicted response (blue line); b the final resistivity models after 10 trials (the green lines) and the best GWO solution highlighted in blue

Full size image
Table 2 Settings and performance of GA, PSO and GWO for the Stupinigi case study
Full size table

As for the synthetic example, there is similarity among the solutions of the PSO and GWO trials, while they significantly differ for GA. Particularly, we noted that in the depth range between 20 to 40 m of depth, the resistivity models identify a conductive region (< 40 Ωm), whose thickness is minimum (around 5 m) for GA and larger for PSO and GWO (around 20 m). This evidence can be appreciated in Fig. 8, where the data are depicted together with the stratigraphy available from a borehole close to the TDEM sounding. The minimum resistivity was imaged in correspondence to the clay layer and is coherent with its expected resistivity. It is straightforward that the TDEM methods is biased toward conductors, so it is not surprising that the calculated resistivity of the superficial gravel layers can be underestimated.

Fig. 8
figure 8

Comparison between the best models of the Stupinigi data set obtained from GWO (pink), PSO (blue) and GA (black). On the right, the stratigraphy from the borehole located close to the TDEM sounding

Full size image

4.2 Case study 2: Travale Sites

The Travale geothermal area is placed in central Italy (Tuscany) and belongs to the Larderello-Travale geothermal system. This is the place where geothermal exploration is said to be born in 1913 (Arias et al., 2010) and one of the most productive geothermal areas of the world (Bertani et al., 2005; Manzella et al., 2019). The Travale area has been investigated by numerous geophysical surveys over the last decades, but the electromagnetic methods have been of pivotal importance to detect the resistivity distribution of the deep features of the geothermal system (Manzella, 2004; Manzella et al., 2010; Muñoz, 2014; Pace, 2020; Pace et al., 2022; Santilano, 2017).

The TDEM soundings were acquired in Travale to be jointly interpreted along with magnetotelluric soundings and hence to improve the characterization of the geothermal field (Pace, 2020; Pace et al., 2022). The eight TDEM sites (a1, b2, b6, e1, g1, k1, k4, and k5) were located on different geological settings and are shown in Fig. 9. The instrument adopted was the TEM-FAST 48 system (AEMR company). The configuration of the wires was a coincident loop of 100 × 100 m or 75 × 75 m, depending on the site accessibility. The injected current was 3 A, the turn-off time was 7–8 μs and the samples were acquired in the range 4–4000 μs.

Fig. 9
figure 9

Location of the TDEM soundings (in blue) acquired in the Travale geothermal area (Italy)

Full size image

These TDEM soundings represent a challenge to be tested by GA, PSO and GWO due to the complex geology of the Travale area and also the lack of direct information on the subsurface resistivity. In fact, this area is highly exploited by industrial companies and hence borehole data are not publicly available. For this work, we selected four out of eight TDEM soundings belonging to different geological settings (Arias et al., 2010): k1, k5, b2 and g1. Sites k1 lies on the Tuscan Nappe basal evaporites (Late Triassic), which are characterized by high resistivity (up to 1000 Ωm) (Manzella et al., 2010; Pace et al., 2022). Site k5 belongs to the geological unit of Ligurian and sub-Ligurian flysch complex (Jurassic-Eocene). Site b2 belongs to the Quaternary deposits, that are electrically conductive (10–20 Ωm) (Manzella, 2004). Site g1 belongs to the Tuscan Nappe sediments (Late Triassic-Early Miocene) that have been associated to moderate resistivity in the literature (Manzella, 2004).

The resistivity model was discretized into 19 layers with increasing thickness. The maximum depth of each model was calculated depending on the maximum acquisition time of the sounding in order to obey the concept of skin depth. The population size was 170 individuals/particles/wolves. The boundary conditions were 1 and 300 Ωm. The Lagrange multiplier was 10–4. The input arguments of the three algorithms were specified in Sect. 3. The number of iterations was 150 for PSO and GWO. After few tests, we realized that GA needed more iterations than the PSO and GWO, that is, 800, because the GA objective function did not minimize enough after only 150 iterations. The decrease of the objective function with the iterations is reported in Fig. 10 for GA (black), PSO (blue) and GWO (pink) applied to a representative site (k1). While the objective function of PSO and GWO rapidly decreased to 0.106, that of GA flattened at 0.127 after 150 iterations and reached 0.126 after 800 iterations. The PSO and GWO runtimes for 150 iterations was around 0.8 h, while the GA runtime was 3 h for 800 iterations.

Fig. 10
figure 10

The curves of the objective function evolution with the iterations for the GWO (pink), PSO (blue) and GA (black) algorithms applied to site k1

Full size image

The results of the optimization of site k1 are shown in Figs. 11, 12 and 13 after the application of GA, PSO and GWO, respectively. The final nRMSEs are listed in Table 3 and are 2.1223 for GA, 1.8684 for PSO and 1.9080 for GWO. PSO yielded the lowest nRMSE, as well as the best minimization of the objective function (Fig. 10). The resistivity models from GA, PSO and GWO imaged a resistive region (120 Ωm) in the shallow subsurface, a conductive layer at about 50 m of depth and then an increasing resistivity trend up to 230 Ωm. The shallow resistive region is in agreement with the expected resistivity of the outcropping rocks of the Tuscan Nappe evaporites. It is peculiar that while the PSO and GWO best solutions (blue models in Figs. 12b and 13b) are similar and in agreement with the solutions from the other trials (green models in Figs. 12b and 13b), the GA best solution is a bit different from the solutions at higher nRMSE (models in Fig. 11b).

Fig. 11
figure 11

The result of GA applied to the k1 Travale site: a TDEM observed signal (the red dots with error bars) and GA predicted response (blue line); b the final resistivity models after 10 trials (the green lines) and the best GA solution highlighted in blue

Full size image
Fig. 12
figure 12

The result of PSO applied to the k1 Travale site: a TDEM observed signal (the red dots with error bars) and PSO predicted response (blue line); b the final resistivity models after 10 trials (the green lines) and the best PSO solution highlighted in blue

Full size image
Fig. 13
figure 13

The result of GWO applied to the k1 Travale site: a TDEM observed signal (the red dots with error bars) and GWO predicted response (blue line); b the final resistivity models after 10 trials (the green lines) and the best GWO solution highlighted in blue

Full size image
Table 3 Performance of GA, PSO and GWO for the TDEM sites at Travale
Full size table

The results for sites k5, b2 and g1 are depicted in Figs. 14, 15 and 16, respectively. For an effective comparison among the outcomes of GA, PSO and GWO, the best model of each algorithm was selected and plotted, while the other trials were not displayed since they had higher nRMSE.

Fig. 14
figure 14

Comparison between the three best models of the k5 site: a observed signal (red dots with error bars) and predicted responses (continuous line); b resistivity models from GA (black), PSO (blue) and GWO (pink)

Full size image
Fig. 15
figure 15

Comparison between the three best models of the b2 site: a observed signal (red dots with error bars) and predicted responses (continuous line); b resistivity models from GA (black), PSO (blue) and GWO (pink)

Full size image
Fig. 16
figure 16

Comparison between the three best models of the g1 site: a observed signal (red dots with error bars) and predicted responses (continuous line); b resistivity models from GA (black), PSO (blue) and GWO (pink)

Full size image

The data fitting of the best GA, PSO and GWO solutions for site k5 was satisfactory (Fig. 14a) and the final nRMSEs were between 0.0770 (GWO) and 0.0902 (GA) (Table 3). The final best models are reported in Fig. 14b and present some dissimilarities even though the predicted responses overlap. It could only be said that there is a conductive region above 50 m of depth and a resistive region (100–150 Ωm) below 50 m. Unfortunately, the GA and PSO solutions are fairly dissimilar, while the PSO solution compares well with that of GWO. The resistivity distribution of the upper layers is in line with mild resistivity expected for the outcropping flysch complex.

The final GA, PSO and GWO models for site b2 are shown in Fig. 15b. GA gave the worst nRMSE (Table 3) even though it ran for more iterations than PSO and GWO. All the predicted responses are acceptable if compared with the observed data. The GA model is largely different from—and more resistive than—the PSO and GWO models (Fig. 15b). These are substantially low resistivity models (< 50 Ωm), except for a 100-Ωm shallow layer (at 15 m of depth). This result is not perfectly aligned with the expected resistivity 10–20 Ωm at surface of, maybe due to the poor data fitting at early times (Fig. 15a).

For site g1, the data fitting was appropriate (Fig. 16a), except for the GA predicted response that explains the highest nRMSE (0.2451). The nRMSEs of PSO and GWO are 0.0503 and 0.0431, respectively (Table 3). The resistivity models are plotted in Fig. 16b. The GA model is poorly interpretable due to its high contrasts, while the PSO and GWO models present a smooth distribution and moderate resistivity values, in agreement with the geology.

5 Discussion

The preliminary analysis of the performance of GA, PSO and GWO applied to synthetic data demonstrated the effectiveness of the methods to converge toward the best global solution. The three algorithms GA, PSO and GWO can be evaluated by means of both the evolution of the objective function and the outcome of the resistivity models.

The minimization of the objective function can be inspected from Figs. 4 and 10, that are related to the synthetic and field case studies, respectively. In both cases, the curves of GA and GWO steeply decreased at early iterations and then flattened to a minimum value that substantially did not decrease further. The PSO objective function instead decreased gradually over the whole iterations and reached a value lower than GA and GWO at the last iteration. This could be related to the different convergence process and shows that a slow and gradual convergence ensures an effective exploration of the solution space. PSO is known for its speed of convergence and robust minimization and has proved to outperform GA in other geophysical applications (Fernández Martínez et al., 2010; Pace et al., 2019a; Song et al., 2012; Yuan et al., 2009). In the synthetic and Travale case studies, we demonstrated that GA was not able to pair the performances of PSO and GWO even with more than two times the number of iterations (Figs. 4 and 10). This was unexpected because we performed a targeted sensitivity analysis on the parameters of GA applied to TDEM data. After the optimal GA input parameters were identified (see Sect. 2.1 and Supplementary material), the GA did not converge and needed more iterations than PSO and GWO to find a solution that could be comparable to those of PSO and GWO in terms of data misfit (and model misfit for the synthetic data). This may represent a valid argument to prefer other algorithms than GA.

The GA usually found resistivity models that were quite different from those found by PSO and GWO (see Figs. 1, 8, 15 and 16). Given that the sensitivity analysis allowed the best parameters to be adopted for the GA optimization, it can be concluded that the difference in the three models relies on the different principles of the strategic sampling, that is, on EC for GA and on SI for PSO and GWO. The resistivity models obtained with GA were characterized by a certain level of contrast between consecutive layers. This cannot be owed to the smoothing parameter λ because PSO and GWO gave smooth models with the same λ value used in GA. It is possible that the GA parameters yielded the objective function to minimize more the data misfit than the model roughness. For the synthetic example, the GA model had the worst misfit for both the data and model fitting (Table 1). The GA model of the Stupinigi site (Fig. 5) gave the highest nRMSE on the data and was different from the PSO and GWO models (Fig. 8). However, the high resistivity values of the shallow subsurface (around 250 Ωm) were in line with the expected values of the gravel layer known from the stratigraphy and were underestimated by the PSO and GWO models (Fig. 8).

The similar performances of PSO and GWO have been recognized before (Chandra et al., 2017), but were here demonstrated in both the synthetic and field case studies. For the synthetic example, the PSO and GWO resistivity models were largely comparable (Figs. 2 and 3) and the GWO nRMSE was slightly higher than that of PSO (Table 1). For the Stupinigi case study, the PSO nRMSE was practically the same as that of GWO (Table 2) and the resistivity models were not only almost identical but also in good agreement with the known stratigraphy (see Fig. 8). For the four TDEM soundings in Travale (Figs. 11, 12, 13, 14, 15, 16), the PSO and GWO outcomes gave similar results for sites k1 and b2 (Figs. 12b, 13b and 15b), while the best PSO and GWO models of sites k5 and g1 (Figs. 14b and 16b) were a bit different. The nRMSE was the lowest for GWO except for site k1 (Table 3). The interpretation of the Travale models is not the focus of this paper and can be found in other works (Pace et al., 2022). Generally, the resistivity distributions of the four models were in line with the expected resistivity of the outcropping rocks of the geological formations they belonged to, except for site b2 (Manzella, 2004).

In terms of clustering of the solutions obtained after the ten trials, the GA solutions were often dissimilar to the “best solution”, while PSO and GWO succeeded in clustering around the “best” solution. The GA always gave a set of final solutions (the best plus the other trials) that were not in total agreement, especially in the shallow layers (see Figs. 1, 5 and 11). A possible reason is that each trial had a random initialization of the solutions and then a different evolution of the exploration and exploitation mechanisms, that led to different final models. Moreover, even though the convergence of GA is proved by the flatness of the objective function at final iterations (Figs. 4 and 10), this convergence came earlier than PSO and GWO, thus causing a possible collapse in a local minimum, from which GA was unlikely to get out. This also explains the different resistivity models found by the ten GA trials in Figs. 1, 5 and 11.

It could be possible that the convergence and clustering issues of GA can be solved by adopting some modified versions of the classic GA, such as a hybrid GA that incorporates the concepts borrowed from the SA algorithm (Sen & Stoffa, 2013), or from the Gibbs sampler approach (Aleardi & Mazzotti, 2017) or other variants specifically designed to improve the efficiency of GA (Villa Acuna & Sun, 2020).

The comparison of the runtimes (Tables 1–2) suggests that GA was more efficient than PSO and GWO, but this is not a core factor because the runtime is strongly affected by the forward modeling code and not by the specific optimization procedure. A possible drawback of the adoption of metaheuristic methods on a high number of soundings is the large runtime required. However, the time-consuming nature of these algorithms can be easily overcome by means of code parallelization (on clusters or workstations) or cloud computing, that nowadays are increasingly within everyone’s reach.

6 Conclusions

The main purpose of this work was to test the performance of three metaheuristic algorithms that have increasingly been applied to geophysical data, namely, the Genetic Algorithm (GA), the Particle Swarm Optimization (PSO) and the Grey Wolf Optimizer (GWO). To the best of the authors’ knowledge, this is the first work that directly and quantitatively compares GA, PSO and GWO applied to geophysical data, which have previously only been compared in pairs (i.e., GA-PSO or GWO-PSO).

The three methods were firstly validated on a synthetic model of TDEM data and then applied to two field data sets from Italy. The first data set was acquired from an area with known stratigraphy and the second set from a geothermal area with complex geology. In general, the performance of GA was significantly worse than that of PSO and GWO, as demonstrated by the ineffective minimization of the objective function and by the highest data misfits in all the case studies. PSO and GWO led to similar outcomes in terms of both resistivity distribution and data misfits, possibly because they are based on the same computational principle known as Swarm Intelligence.

This study reveals that the emerging algorithm GWO is a valid tool for geophysical applications, even though it has received scant attention so far, while GA and PSO have extensively been adopted. We demonstrate that GWO has the same performances as PSO and hence deserves consideration in future applications of metaheuristics to geophysical data. Moreover, we point out that modern Swarm Intelligence methods considerably outperform GA, that appears to be less competitive than PSO and GWO.

Dealing with global search methods is known to be time-consuming. A main disadvantage is the need for large computational resources to run the optimization modeling. However, the current advances in computer performance and the availability of computational resources are expected to mitigate the impact of time-consuming computations.

The findings of this work are encouraging and strongly support the validity of GWO for future geophysical studies, where it could usefully be applied to further geophysical data. A worthwhile direction for future research could be to improve the cost-effectiveness of existing metaheuristic methods and to investigate innovative metaheuristics that are more efficient in solving the inverse problem.