Compressive Sensing Acquisition with Application to Marchenko Imaging

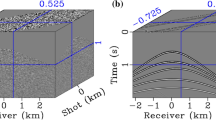
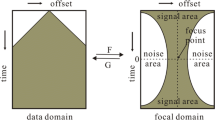
Abstract

Marchenko-based method is a novel multiple-free imaging approach for a target subsurface area. High-density acquisition can help obtain an accurate Marchenko imaging, but will significantly increase the acquisition cost. Obtaining accurate Marchenko imaging while maintaining low acquisition cost is therefore an important practical hurdle to overcome. I develop a compressive sensing-based low-cost acquisition design relying on a sparse and random irregular survey to meet the needs of the Marchenko imaging. I examine the influence of noise on Marchenko imaging, and demonstrate that reconstructing seismic data from noisy observations by using compressive sensing has a natural de-noising effect, and yield comparable Green’s functions and resultant high-quality angle gathers and Marchenko imaging. Numerical tests using a 2D model show that as few as 30% of receivers are needed when compressive-sensing reconstruction is combined with Marchenko method.

Appendices

Appendix A: Total Variation (TV)

Given a 2D image represented by x with the size of $n*n$, let $x_{ij}$ denote the value in ith row and jth column of the x. Let us define the operators

$$\begin{aligned} D_{h;ij}x=\left\{ \begin{matrix} x_{i+1,j}-x_{ij}\;\;\;i<n\\ 0 \quad i=n \end{matrix}\right. \quad D_{v;ij}x=\left\{ \begin{matrix} x_{i,j+1}-x_{ij}\;\;\;j<n\\ 0 \quad j=n \end{matrix}\right. \end{aligned}$$

(6)

and

$$\begin{aligned} D_{ij}x=\left( {\begin{array}{c}D_{h; \, ij}x\\ D_{v; \, ij}x\end{array}}\right) \end{aligned}$$

(7)

where $D_{ij}x$ can be interpreted as discrete gradient vector of x.

The total variation (Rudin and Osher, 1992) of x is simply the sum of the magnitudes of this discrete gradient at every location i, j of x:

$$\begin{aligned} TV(x)=\sum _{ij}\sqrt{(D_{h; \, ij}x)^2+(D_{v; \,ij}x)^2}=\sum _{ij}\left\| D_{ij}x \right\| _2 \end{aligned}$$

(8)

Appendix B: Fast Iterative Shrinkage-Thresholding Algorithm (FISTA)

I applied FISTA with backtracking proposed by (Beck and Teboulle, 2009) in my paper,

Step 0. Take $L_{0} > 0$, some $\eta > 1$, and $x_{0} \in {\mathbb {R}}^{n}$. Set $y_{1} = x_{0}$, $t_{1}=1$.

Step k. ($k \geqslant 1$) Find the smallest nonnegative integers $i_{k}$ such that with ${\bar{L}} = \eta ^{i_{k}}L_{k-1}$

$$\begin{aligned} F(p_{{\bar{L}}}(y_{k}) \le Q_{{\bar{L}}}(p_{{\bar{L}}}(y_{k}),y_{k}). \end{aligned}$$

(9)

Set $L_{k} = \eta ^{i_{k}}L_{k-1}$ and compute

$$\begin{aligned} \begin{aligned} x_{k}&= p_{L_{k}}(y_{k})\\ t_{k+1}&= \frac{1+\sqrt{1+4t^{2}_{k}}}{2}\\ y_{k+1}&= x_{k} + \left(\frac{t_{k} - 1}{t_{k+1}})(x_{k} - x_{k-1}\right) \end{aligned} \end{aligned}$$

(10)

For more details on ISTA and FISTA, I refer readers to these original publications (Beck & Teboulle, 2009; Daubechies et al., 2004).