Changes in Crack Shape and Saturation in Laboratory-Induced Seismicity by Water Infiltration in the Transversely Isotropic Case with Vertical Cracks

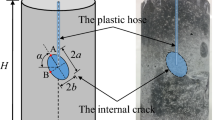
Abstract

Open cracks and cavities play important roles in fluid transport. Underground water penetration induces microcrack activity, which can lead to rock failure and earthquakes. Fluids in cracks can affect earthquake generation mechanisms through physical and physicochemical effects. Methods for characterizing the crack shape and water saturation of underground rock are needed for many scientific and industrial applications. The ability to estimate the status of cracks by using readily observable data such as elastic-wave velocities would be beneficial. We have demonstrated a laboratory method for estimating the crack status inside a cylindrical rock sample based on a vertically cracked transversely isotropic solid model by using measured P- and S-wave velocities and porosity derived from strain data. During injection of water to induce failure of a stressed rock sample, the crack aspect ratio changed from 1/400 to 1/160 and the degree of water saturation increased from 0 to 0.6. This laboratory-derived method can be applied to well-planned observations in field experiments. The in situ monitoring of cracks in rock is useful for industrial and scientific applications such as the sequestration of carbon dioxide and other waste, induced seismicity, and measuring the regional stress field.

Appendices

Appendix: Elastic Constants of Rock Material for the Case of Transversely Isotropic Symmetry along the x-3 Axis (z-Axis) with Randomly Distributed Vertical Cracks

Here we describe the method of calculation of elastic constants for the case in which plane normals of cracks are randomly distributed in directions perpendicular to the x-3 axis (z-axis). We also show that the ratio of the elastic constant of rock material that includes cracks to that of the matrix or the square of velocity ratio is expressed as (V/V₀)² = 1 − p_i ε, where V and V₀ are the elastic-wave velocities with and without cracks, respectively, and ε is the crack density parameter defined by

$$\varepsilon =\frac{3 \phi }{4 \pi \alpha } ,$$

(6)

where $\phi$ is the porosity and α = c/a is the aspect ratio of the crack ($a=b\gg c$). In addition, we derive the coefficients p_i.

The focus of this study is on a transversely isotropic medium with the x-3 axis (z-axis) as the axis of symmetry and with a vertical crack distribution in which the plane normals of the cracks are randomly distributed in horizontal directions (directions parallel to the x-1,2 plane, x–y plane). The right-handed rectangular coordinate system is used in this study (Fig. 

Fig. 13

The basic assumptions in this study: a the coordinate system, b vertical cross section of transversely isotropic rock with vertical cracks, and c side view of the direction of wave propagation and crack distribution

13a).

First, based on the method of Hudson (1981), we calculated ${C}_{ij}$ for a material that includes vertical cracks that are plane normal along the x-1 axis (x-axis) (Fig. 13b). Next, we took the rotational average of ${C}_{ij}$ around the x-3 axis (z-axis), resulting in ${\widehat{C}}_{ij}$, which were shown to be transversely isotropic with the x-3 axis (z-axis) by using a method similar to that of Nishizawa and Masuda (1991).

${{\varvec{C}}}_{{\varvec{i}}{\varvec{j}}}^{0}$ Elastic Constants of the Isotropic Rock Matrix (Fig. 14a)

Fig. 14

Procedure for calculating the elastic constants in the transversely isotropic rock with vertical cracks: a ${C}_{ij}^{0}$ elastic constants of the rock matrix; b ${C}_{ij}$ elastic constants for the rock material with vertical cracks for which the plane-normal direction is along the x-1 axis (x-axis); c $C^{\prime}_{ij} (\varphi )$ elastic constants for rock material with vertical cracks for which the angle between the plane-normal direction and the x-1 axis (x-axis) is $\mathrm{\varphi }$; and d ${\widehat{C}}_{ij}$ elastic constants for rock material with transversely isotropic symmetry along the x-3 axis (z-axis) with vertical cracks with random values of $\mathrm{\varphi }$

In this study, we use abbreviated 2-index Voigt notation to express elastic constants such as C_ij instead of 4-index notation for the fourth-rank tensor c_ijkl. We assume that the matrix of rock without cracks or inclusions is isotropic with two independent constants:

$${C}_{ij}^{0}= \left(\begin{array}{cccccc}{C}_{11}^{0}& {C}_{12}^{0}& {C}_{12}^{0}& 0& 0& 0\\ {C}_{12}^{0}& {C}_{11}^{0}& {C}_{12}^{0}& 0& 0& 0\\ {C}_{12}^{0}& {C}_{12}^{0}& {C}_{11}^{0}& 0& 0& 0\\ 0& 0& 0& {C}_{44}^{0}& 0& 0\\ 0& 0& 0& 0& {C}_{44}^{0}& 0\\ 0& 0& 0& 0& 0& {C}_{44}^{0}\end{array}\right)=\left(\begin{array}{cccccc}\lambda +2\mu & \lambda & \lambda & 0& 0& 0\\ \lambda & \lambda +2\mu & \lambda & 0& 0& 0\\ \lambda & \lambda & \lambda +2\mu & 0& 0& 0\\ 0& 0& 0& \mu & 0& 0\\ 0& 0& 0& 0& \mu & 0\\ 0& 0& 0& 0& 0& \mu \end{array}\right)$$

(7)

$${C}_{12}^{0}={C}_{11}^{0}-2{C}_{44}^{0}.$$

(8)

The relationships between the elements ${C}_{ij}^{0}$ and Lame’s parameters λ and μ of isotropic linear elasticity are.

$${C}_{11}^{0}= \lambda + 2\mu , {C}_{12}^{0}=\lambda , {C}_{44}^{0}=\mu .$$

(9)

${{\varvec{C}}}_{{\varvec{i}}{\varvec{j}}}$ Elastic Constants for Rock Material with Cracks that are Plane Normal Along the x-1 Axis (x-Axis) (Fig. 14b)

Hudson (1981) modeled fractured rock as an elastic solid with thin, penny-shaped ellipsoidal cracks or inclusions. The effective moduli ${C}_{ij}$ are given as.

$${C}_{ij}= {C}_{ij}^{0}+ {C}_{ij}^{1},$$

(10)

where C⁰_ij are the isotropic background moduli and C¹_ij are the first-order corrections. For the case in which the vertical cracks have crack normals along the x-1 axis (x-axis), the axis of symmetry of the material lies along the x-1 axis (x-axis), which has hexagonal symmetry with five independent constants as.

$${C}_{ij}^{1}= \left(\begin{array}{cccccc}{C}_{11}^{1}& {C}_{12}^{1}& {C}_{12}^{1}& 0& 0& 0\\ {C}_{12}^{1}& {C}_{22}^{1}& {C}_{23}^{1}& 0& 0& 0\\ {C}_{12}^{1}& {C}_{23}^{1}& {C}_{22}^{1}& 0& 0& 0\\ 0& 0& 0& {C}_{44}^{1}& 0& 0\\ 0& 0& 0& 0& {C}_{55}^{1}& 0\\ 0& 0& 0& 0& 0& {C}_{55}^{1}\end{array}\right) , {C}_{44}^{1}= \frac{1}{2} \left({C}_{22}^{1}- {C}_{23}^{1}\right).$$

(11)

The following correction terms are given by Schön (2011, Table 6.15) for the case in which the crack normals are aligned along the x-1 axis (x-axis), including the vertical cracks:

$${C}_{11}^{1}= -\frac{{\left(\lambda + 2\mu \right)}^{2}}{\mu } \varepsilon {U}_{3}$$

(12)

$${C}_{13}^{1}= -\frac{{\lambda \left(\lambda + 2\mu \right)}^{2}}{\mu } \varepsilon {U}_{3}$$

(13)

$${C}_{33}^{1}= -\frac{{\lambda }^{2}}{\mu } \varepsilon {U}_{3}$$

(14)

$${C}_{44}^{1}= 0$$

(15)

$${C}_{66}^{1}= -\mu \varepsilon {U}_{1},$$

(16)

in which the correction terms ${C}_{ij}^{1}$ are negative; thus, the elastic properties decrease with fracturing. U₁ and U₃ depend on the crack conditions (Mavko et al., 2009; Schön, 2011).

For dry cracks,

$${U}_{1}= \frac{16\left(\lambda + 2\mu \right)}{3\left(3\lambda + 4\mu \right)}; {U}_{3}= \frac{4\left(\lambda + 2\mu \right)}{3\left(\lambda + \mu \right)}.$$

(17)

For wet cracks, Hudson’s expressions for infinitely thin fluid-filled cracks are.

$${U}_{1}= \frac{16\left(\lambda + 2\mu \right)}{3\left(3\lambda + 4\mu \right)}; { U}_{3}= 0.$$

(18)

Therefore, for the dry case, ${C}_{ij}$ are.

$${C}_{11}= {C}_{11}^{0}+ {C}_{11}^{1}= \left(\lambda +2\mu \right)(1-6 \varepsilon )$$

(19)

$${C}_{13}= {C}_{13}^{0}+ {C}_{13}^{1}= \lambda (1-6 \varepsilon )$$

(20)

$${C}_{33}= {C}_{33}^{0}+ {C}_{33}^{1}= \left(\lambda +2\mu \right)(1-\frac{2}{3} \varepsilon )$$

(21)

$${C}_{44}= {C}_{44}^{0}+ {C}_{44}^{1}= \mu$$

(22)

$${C}_{66}= {C}_{66}^{0}+ {C}_{66}^{1} = \mu \left(1-\frac{16}{7} \varepsilon \right).$$

(23)

For the wet case,

$${C}_{11}= {C}_{11}^{0}+ {C}_{11}^{1} = \lambda +2\mu$$

(24)

$${C}_{13}= {C}_{13}^{0}+ {C}_{13}^{1} = \lambda$$

(25)

$${C}_{33}= {C}_{33}^{0}+ {C}_{33}^{1}= \lambda +2\mu$$

(26)

$${C}_{44}= {C}_{44}^{0}+ {C}_{44}^{1}= \mu$$

(27)

$${C}_{66}= {C}_{66}^{0}+ {C}_{66}^{1}= \mu \left(1-\frac{16}{7} \varepsilon \right).$$

(28)

${C}_{ij}$ has hexagonal symmetry with the x-1 axis (x-axis) expressed with five independent moduli.

$C^{\prime}_{ij} (\varphi )$ Elastic Constants for Rock Material with Vertical Cracks that have an Angle $\mathrm{\varphi }$ Between the Plane-Normal Direction and the x-1 Axis (x-Axis) (Fig. 14c)

When we rotate ${C}_{ij}$ around the x-3 axis (z-axis) by an angle of φ from the x-1 axis (x axis), ${C}_{ij}$ is a function of φ, as expressed by $C^{\prime}_{ij} (\varphi )$.

Regarding coordinate transformations, the elastic compliances c_ijkl are, in general, fourth-rank tensors and hence transform according to.

$${c}_{ijkl}^{\mathrm{^{\prime}}}= {\beta }_{ip}{\beta }_{jq}{\beta }_{kr}{\beta }_{ls}{c}_{pqrs},$$

(29)

where ${c}_{ijkl}^{^{\prime}}$ and ${c}_{pqrs}$ are the elastic compliances after and before the coordinate transformation, respectively. For rotation around the x-3 axis (z-axis), ${\beta }_{ij}$ is the following matrix element:

$$\left(\begin{array}{ccc}cos\mathrm{\varphi }& sin\mathrm{\varphi }& 0\\ -sin\mathrm{\varphi }& cos\mathrm{\varphi }& 0\\ 0& 0& 1\end{array}\right).$$

(30)

In this study, we use the abbreviated 2-index Voigt notation ${C}_{ij}$ instead of ${c}_{ijkl}^{^{\prime}}$ and ${c}_{ijkl}$. Although an elastic constant looks like a second-rank tensor (${C}_{ij}$) with this notation, it is indeed a fourth-rank tensor; when one performs a coordinate transformation, one must go back to the full notation and follow the transformation rules for a fourth-rank tensor. The usual tensor transformation law is no longer valid. However, the change of coordinates for ${C}_{ij}$ is more efficiently performed with the 6 × 6 Bond Transformation Matrices, M (Mavko et al., 2009). The advantage of the Bond method for transforming compliances is that it can be applied directly to the elastic constants given in 2-index notation, expressed as:

$$\left[{C}^{^{\prime}}\right]=\left[M\right]\left[C\right]{\left[M\right]}^{T}$$

(31)

$$\mathbf{M}=\left[\begin{array}{cccccc}{\beta }_{11}^{2}& {\beta }_{12}^{2}& {\beta }_{13}^{2}& 2{\beta }_{12}{\beta }_{13}& 2{\beta }_{13}{\beta }_{11}& 2{\beta }_{11}{\beta }_{12}\\ {\beta }_{21}^{2}& {\beta }_{22}^{2}& {\beta }_{23}^{2}& 2{\beta }_{22}{\beta }_{23}& 2{\beta }_{23}{\beta }_{21}& 2{\beta }_{21}{\beta }_{22}\\ {\beta }_{31}^{2}& {\beta }_{32}^{2}& {\beta }_{33}^{2}& 2{\beta }_{32}{\beta }_{33}& 2{\beta }_{33}{\beta }_{31}& 2{\beta }_{31}{\beta }_{32}\\ {\beta }_{21}{\beta }_{31}& {\beta }_{22}{\beta }_{32}& {\beta }_{23}{\beta }_{33}& {\beta }_{22}{\beta }_{33}+{\beta }_{23}{\beta }_{32}& {\beta }_{21}{\beta }_{33}+{\beta }_{23}{\beta }_{31}& {\beta }_{22}{\beta }_{31}+{\beta }_{21}{\beta }_{32}\\ {\beta }_{31}{\beta }_{11}& {\beta }_{32}{\beta }_{12}& {\beta }_{33}{\beta }_{13}& {\beta }_{12}{\beta }_{33}+{\beta }_{13}{\beta }_{32}& {\beta }_{11}{\beta }_{33}+{\beta }_{13}{\beta }_{31}& {\beta }_{11}{\beta }_{32}+{\beta }_{12}{\beta }_{31}\\ {\beta }_{11}{\beta }_{21}& {\beta }_{12}{\beta }_{22}& {\beta }_{13}{\beta }_{23}& {\beta }_{22}{\beta }_{13}+{\beta }_{12}{\beta }_{23}& {\beta }_{11}{\beta }_{23}+{\beta }_{13}{\beta }_{21}& {\beta }_{22}{\beta }_{11}+{\beta }_{12}{\beta }_{21}\end{array}\right].$$

(32)

Then, we obtain $C^{\prime}_{ij} (\varphi )$ as.

$${C}_{11}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right)= {cos}^{4}\mathrm{\varphi }{C}_{11}+2{sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi }{C}_{12}+{sin}^{4}\mathrm{\varphi }{C}_{22}+4{sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi }{C}_{55}$$

(33)

$${C}_{22}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right)= {sin}^{4}\mathrm{\varphi }{C}_{11}+2{sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi }{C}_{12}+{cos}^{4}\mathrm{\varphi }{C}_{22}+4{sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi }{C}_{55}$$

(34)

$${C}_{12}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right)={C}_{21}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right)= {sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi }{C}_{11}+\left({sin}^{4}\mathrm{\varphi }+{cos}^{4}\mathrm{\varphi }\right) {C}_{12}+{sin}^{2}\mathrm{\varphi }{ cos}^{2}\mathrm{\varphi }{C}_{22}-4{sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi }{C}_{55}$$

(35)

$${C}_{13}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right)={C}_{31}^{\mathrm{^{\prime}}}(\mathrm{\varphi })= {cos}^{2}\mathrm{\varphi }{C}_{12}+{sin}^{2}\mathrm{\varphi }{C}_{23}$$

(36)

$${C}_{23}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right)={C}_{32}^{\mathrm{^{\prime}}}(\mathrm{\varphi })= {sin}^{2}\mathrm{\varphi }{C}_{12}+{cos}^{2}\mathrm{\varphi }{C}_{23}$$

(37)

$${C}_{33}^{\mathrm{^{\prime}}}(\mathrm{\varphi })= {C}_{22}$$

(38)

$${C}_{44}^{\mathrm{^{\prime}}}(\mathrm{\varphi })= {cos}^{2}\mathrm{\varphi }{C}_{44}+{sin}^{2}\mathrm{\varphi }{C}_{55}$$

(39)

$${C}_{55}^{\mathrm{^{\prime}}}(\mathrm{\varphi })= {sin}^{2}\mathrm{\varphi }{C}_{44}+{cos}^{2}\mathrm{\varphi }{C}_{55}$$

(40)

$${C}_{66}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right)= {{sin}^{2}\mathrm{\varphi }cos}^{2}\mathrm{\varphi }{C}_{11}-2{sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi }{C}_{12}+{sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi }{C}_{22}+{\left({cos}^{2}\mathrm{\varphi }-{sin}^{2}\mathrm{\varphi }\right)}^{2} {C}_{55}.$$

(41)

The following non-zero elements are zero in the next step, taking the rotational average:

$${C}_{16}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right), {C}_{61}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right), {C}_{26}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right), {C}_{62}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right), {C}_{36}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right), {C}_{63}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right), {C}_{45}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right), {C}_{54}^{\mathrm{^{\prime}}}\left(\mathrm{\varphi }\right).$$

${\widehat{{\varvec{C}}}}_{{\varvec{i}}{\varvec{j}}}$ Elastic Constants for Rock Material with Transversely Isotropic Symmetry Along the x-3 Axis (z-Axis) and a Vertical Crack Distribution (Fig. 14d)

We took the rotational average of ${C}_{ij}$ around the x-3 axis (z-axis) to obtain ${\widehat{C}}_{ij}$ that showed transversely isotropic symmetry along the x-3 axis (z-axis) in the case of a random vertical crack distribution as follows:

$${\widehat{C}}_{ij}= \frac{1}{2\pi } {\int }_{0}^{2\pi }{{C}^{\mathrm{^{\prime}}}}_{ij}\left(\mathrm{\varphi }\right) d\mathrm{\varphi },$$

(42)

which uses

$$\frac{1}{2\pi } {\int }_{0}^{2\pi }{sin}^{4}\mathrm{\varphi d\varphi }= \frac{3}{8} , \frac{1}{2\pi } {\int }_{0}^{2\pi }{cos}^{4}\mathrm{\varphi d\varphi }= \frac{3}{8} , \frac{1}{2\pi } {\int }_{0}^{2\pi }{sin}^{2}\mathrm{\varphi }{cos}^{2}\mathrm{\varphi d\varphi }= \frac{1}{8} ,$$

(43)

$$\frac{1}{2\pi } {\int }_{0}^{2\pi }{sin}^{2}\mathrm{\varphi d\varphi }= \frac{1}{2} , \frac{1}{2\pi } {\int }_{0}^{2\pi }{cos}^{2}\mathrm{\varphi d\varphi }= \frac{1}{2} .$$

(44)

${\widehat{C}}_{ij}$ shows hexagonal symmetry or transversely isotropic symmetry with the x-3 axis (z-axis) in which there are five independent constants:

$${\widehat{C}}_{11}= \frac{1}{2\pi } {\int }_{0}^{2\pi }{{C}^{\mathrm{^{\prime}}}}_{11}\left(\mathrm{\varphi }\right) d\mathrm{\varphi }= \frac{3}{8} {C}_{11}+ \frac{1}{4} {C}_{12}+ \frac{3}{8} {C}_{22}+ \frac{1}{2} {C}_{55}$$

(45)

$${\widehat{C}}_{12}= \frac{1}{2\pi } {\int }_{0}^{2\pi }{{C}^{\mathrm{^{\prime}}}}_{12}\left(\mathrm{\varphi }\right) d\mathrm{\varphi }= \frac{1}{8} {C}_{11}+ \frac{3}{4} {C}_{12}+ \frac{1}{8} {C}_{22}- \frac{1}{2} {C}_{55}$$

(46)

$${\widehat{C}}_{13}= \frac{1}{2\pi } {\int }_{0}^{2\pi }{{C}^{\mathrm{^{\prime}}}}_{13}\left(\mathrm{\varphi }\right) d\mathrm{\varphi }= \frac{1}{2} {C}_{12}+ \frac{1}{2} {C}_{23}$$

(47)

$${\widehat{C}}_{33}= {C}_{22}$$

(48)

$${\widehat{C}}_{44}= \frac{1}{2\pi } {\int }_{0}^{2\pi }{{C}^{\mathrm{^{\prime}}}}_{44}\left(\mathrm{\varphi }\right) d\mathrm{\varphi }= \frac{1}{2} {C}_{44}+ \frac{1}{2} {C}_{55}$$

(49)

$${\widehat{C}}_{66}= \frac{1}{2\pi } {\int }_{0}^{2\pi }{{C}^{\mathrm{^{\prime}}}}_{66}\left(\mathrm{\varphi }\right) d\mathrm{\varphi }= \frac{1}{8} {C}_{11}- \frac{1}{4} {C}_{12}+ \frac{1}{8} {C}_{22}+ \frac{1}{2} {C}_{55}= \frac{1}{2} \left({\widehat{C}}_{11}- {\widehat{C}}_{12}\right).$$

(50)

Wave Velocities that Propagate in the Horizontal Directions

In material with transversely isotropic symmetry, there are three modes of wave propagation, and their velocities are dependent on the angle θ between the axis of symmetry (in this case, the x-3 axis or z-axis) and the direction of the wave vector:

$${V}_{P}= \sqrt{\frac{{\widehat{C}}_{11} {sin}^{2}\theta +{\widehat{C}}_{33} {cos}^{2}\theta +{\widehat{C}}_{44}+A}{2\rho }}$$

(51)

$${V}_{SV}= \sqrt{\frac{{\widehat{C}}_{11} {sin}^{2}\theta +{\widehat{C}}_{33} {cos}^{2}\theta +{\widehat{C}}_{44}-A}{2\rho }}$$

(52)

$${V}_{SH}= \sqrt{\frac{{\widehat{C}}_{66} {sin}^{2}\theta +{\widehat{C}}_{44} {cos}^{2}\theta }{2\rho } ,}$$

(53)

$$\mathrm{where \,}A = \sqrt{{\left[\left({\widehat{C}}_{11}- {\widehat{C}}_{44}\right){sin}^{2}\theta +\left({\widehat{C}}_{33}- {\widehat{C}}_{44}\right){cos}^{2}\theta \right]}^{2}+{ {\left({\widehat{C}}_{13}+{\widehat{C}}_{44}\right)}^{2}sin}^{2}2\theta }.$$

(54)

For θ = 90°, the relationship simplifies to ${A= \widehat{C}}_{33}- {\widehat{C}}_{44}$ and the wave velocity vectors that propagate perpendicular to the x-3 axis in horizontal directions (Fig. 13c) are

$${V}_{P}= \sqrt{\frac{{\widehat{C}}_{11}}{\rho }} , {V}_{SV}= \sqrt{\frac{{\widehat{C}}_{44}}{\rho }} , {V}_{SH}= \sqrt{\frac{{\widehat{C}}_{66}}{\rho }} ,$$

(55)

where V_P, V_SV, and V_SH are the longitudinal-wave velocity, shear-wave velocity with vertical polarization, and shear-wave velocity with horizontal polarization, respectively.

We consider low-porosity aggregate and flat cracks, and have ignored the effect of porosity on the density of the composite (Anderson et al., 1974).

For the dry case, the matrix is assumed to be isotropic with λ = μ, which is appropriate for crack-free granite (Anderson et al., 1974):

$${V}_{P}^{2}= \frac{{\widehat{C}}_{11}}{\rho }= \frac{\lambda +2\mu }{\rho } \left(1-\frac{71}{21}\varepsilon \right)= {V}_{P0}^{2}\left(1-\frac{71}{21}\varepsilon \right)$$

(56)

$${V}_{SV}^{2}= \frac{{\widehat{C}}_{44}}{\rho }= \frac{\mu }{\rho } \left(1-\frac{8}{7}\varepsilon \right)= {V}_{SV0}^{2}\left(1-\frac{8}{7}\varepsilon \right)$$

(57)

$${V}_{SH}^{2}= \frac{{\widehat{C}}_{66}}{\rho }= \frac{\mu }{\rho } \left(1-\frac{15}{7}\varepsilon \right)= {V}_{SH0}^{2}\left(1-\frac{15}{7}\varepsilon \right) ,$$

(58)

where V with a subscript 0 are the velocities without cracks.

For the wet case,

$${V}_{P}^{2}= \frac{{\widehat{C}}_{11}}{\rho }= \frac{\lambda +2\mu }{\rho } \left(1-\frac{8}{21}\varepsilon \right)= {V}_{P0}^{2}\left(1-\frac{8}{21}\varepsilon \right)$$

(59)

$${V}_{SV}^{2}= \frac{{\widehat{C}}_{44}}{\rho }= \frac{\mu }{\rho } \left(1-\frac{8}{7}\varepsilon \right)= {V}_{SV0}^{2}\left(1-\frac{8}{7}\varepsilon \right)$$

(60)

$${V}_{SH}^{2}= \frac{{\widehat{C}}_{66}}{\rho }= \frac{\mu }{\rho } \left(1-\frac{8}{7}\varepsilon \right)= {V}_{SH0}^{2}\left(1-\frac{8}{7}\varepsilon \right).$$

(61)

The effect of cracks on velocity, in terms of the ratio of velocities with and without cracks, is proportional to the crack density parameter ε at small values of ε:

$${\left(\frac{V}{{V}_{0}}\right)}^{2}=1- {p}_{i} \varepsilon .$$

(62)