1 Introduction

A reliable seismic velocity model of subsurface structures is needed for depth imaging of complex geological features. Conventional methods such as migration velocity analysis (Chauris et al., 2002a, 2002b; Fei & McMechan, 2006; Liu & Bleistein, 1995) or traveltime tomography (Bishop et al., 1985; Farra & Madariaga, 1988; Williamson, 1990) have been used to develop velocity models for prestack depth migration of seismic data in the past. Despite the considerable workload and long turnaround times, the resulting velocity models from these methods are influenced by personal interpretation/picking skills and suffer from low resolution. Full-waveform inversion (FWI) relaxes the user-dependency of the velocity model building task and directly extracts the velocity information from the seismic data via an automated scheme. FWI automatically updates a smooth initial velocity model via iterative local optimization algorithms, which minimize the misfit error between observed data acquired from the field and synthetic data calculated from the wave equation solution. The fundamentals of FWI were introduced decades ago (Gauthier et al., 1986; Lailly, 1983; Mora, 1987; Tarantola, 1984), but the limited computational resources could not apply FWI to the field datasets. Since FWI uses a shot-based wave equation solution algorithm to calculate the synthetic waveforms for data fitting, the computational burden dramatically increases with the number of shots. In the active-source seismic datasets, the number of shots could simply reach several thousand, and the computing resources directly control the applicability of the FWI on the field datasets. Nowadays, high-performance computing servers allow for the industrial-scale application of FWI on 2D/3D seismic data (Brown et al., 2019; Dickinson et al., 2017; Landolsi et al., 2016; Lin et al., 2018; Tiwari & Mao, 2018).

However, even with the affordable computational costs, the successful application of FWI on real data requires a dedicated workflow to address several issues. While the observed data, as the input to FWI, are expected to have a minimum level of preprocessing, the quality of the final model is influenced by many factors, including signal-to-noise ratio, surface-related multiple reflections, and seismic source instabilities. In addition, due to the nonlinearity of the FWI problem and band-limited nature of the seismic data, having a good initial velocity model which allows kinematic matching of the observed traveltimes with an error of less than half a period is a critical prerequisite for the convergence of the classical FWI problem. Otherwise, the so-called cycle skipping issue will occur, which leads the optimization algorithm towards a local rather than global minimum of the misfit functional (Beydoun & Tarantola, 1988; Jamali Hondori et al., 2015; Wang et al., 2016; Wu & Alkhalifah, 2018; Yao et al., 2019). Recent reformulations of FWI (Sun & Alkhalifah, 2019a, b; Warner & Guasch, 2016) implement matching filters in the misfit functional to overcome cycle skipping when neither a good initial model nor low frequency data are available. Alternative methods for tackling the cycle skipping issue may implement optimal transport distance as a tool to measure the discrepancy between observed and simulated seismic data (Engquist et al., 2016; Métivier et al., 2018) or extend the search space of FWI to efficiently mitigate cycle skipping by matching the data with inaccurate subsurface models via relaxation of the wave equation (Aghamiry et al., 2021; van Leeuwen & Herrmann, 2013). Because of the nonlinear nature of the FWI problem, an infinite number of mathematical solutions may equally fit the problem, within a similar range of error, among which the only one can correctly represent the subsurface structures. Therefore, regularization constraints are necessary to guarantee that FWI achieves a geologically plausible model in the presence of sharp velocity contrasts. Box constraints (Esser et al., 2016a, b) ensure that the velocity at each grid point of the inverted velocity model remains within a defined interval that may vary for each grid point. Total variation (Anagaw & Sacchi, 2012; Esser et al., 2016b; Loris & Verhoeven, 2012; Rudin et al., 1992) is another regularization method that preserves sharp edges without oversmoothing the reconstructed model. A combination of different regularization techniques for the FWI problem has been reported in the literature (Guitton, 2012; Kalita et al., 2019; Kazei et al., 2017; Lin & Huang, 2015). Several examples of FWI application to marine streamer data have been studied in the literature. Qin and Singh (2017) used a 12-km-long offset seismic reflection data and applied FWI to obtain detailed information on the incoming oceanic sediments and the trench-fill sediments near the 2004 Sumatra earthquake rupture zone. Gras et al. (2019) used short-offset and band-limited seismic data acquired with a 6-km-long streamer and re-datumed the recorded seismograms to the seafloor, applied joint refraction and reflection traveltime tomography combining the original and the re-datumed shot gathers, and then conducted FWI of the original shot gathers using the model obtained by traveltime tomography as the initial model. Cho et al. (2015) extrapolated the observed wavefield with a downward continuation approach to the seafloor and performed refraction tomography, followed by Laplace–Fourier domain FWI using the refraction tomography results as a starting model.

We present the results of the 2D acoustic FWI application on limited-offset seismic data acquired in the Japan Trench subduction zone. The maximum offset of 5.8 km does not allow for the recording of refracted energy in the seismic dataset, and the initial model must provide the long-wavelength component of the velocity model to immune the FWI against the cycle skipping. We develop a workflow to build the initial velocity model using MVA conducted via a layer-stripping scheme. A few preprocessing steps are applied to the seismic data, and the waveform inversion is applied in the frequency domain (Pratt et al., 1998). We remove the surface-related multiple reflections from the observed data to reduce the nonlinearity of the FWI problem. A frequency domain matching filter is used to match the amplitude spectrum of the shot gathers in the observed and calculated data before misfit evaluation. This filter can balance the shot by shot amplitude variations of the observed data caused by a non-uniform operation of the airgun array during the survey. We assess the quality of the FWI velocity models by evaluating the ray path illumination, sensitivity kernel illustration, and KPSDM common image gather flatness. RTM images (Baysal et al., 1983; McMechan, 1983) are also produced using initial and final velocity models to confirm that the depth images could explain the subsurface complex geology of the study area. The final KPSDM depth section illustrates details of the faulted structure reaching up to the seafloor, where we propose that a young sedimentary basin is forming. In the following sections, we first describe the historical background of the study area. The FWI fundamentals are briefly reviewed, seismic data acquisition and preconditioning details are presented, and finally, the resulting velocity models and depth images are discussed in terms of the reproduction reliability of possible geological structure below the seafloor.

2 Study Area in the Japan Trench

The 2011 Tohoku earthquake (M 9.0) with a coseismic slip of more than 50 m (Fujii et al., 2011; Ide et al., 2011; Kodaira et al., 2017; Satake et al., 2013; Simons et al., 2011) occurred in the Japan Trench subduction zone, where the Pacific Plate is subducting westward beneath the Okhotsk Plate with a subduction rate of around 10 cm/year (Isozaki et al., 2010; Ludwig et al., 1966; Taira, 2001). Figure 1 illustrates the study area with contours of large coseismic slip of the 2011 Tohoku earthquake, calculated by Satake et al. (2013) using Tsunami waveform inversion, overlaid on the seafloor bathymetry map. The yellow star marks the location of the epicenter, the black line shows the 2D seismic line D13, and the red line between points P and Q shows the selected area for FWI application. The subsurface structure and tectonic behavior of the Japan Trench have been investigated in the past by using various geological and geophysical datasets (Kirkpatrick et al., 2015; Kodaira et al., 2017; Miura et al., 2005; Nakamura et al., 2013; Tsuru et al., 2000; von Huene et al., 1994). The forearc slope of the Japan Trench, an active deformation feature residing between the island arc and the trench axis, consists of three regions. An upper slope which has a relatively flat seafloor inclined at less than 3°, a middle slope with a relatively steep slope that starts at approximately 3 km seafloor depth, and a lower slope which includes a small accretionary frontal prism (Arai et al., 2014; Boston et al., 2017). Noda (2016) suggested various models of forearc basins, among which the Japan Trench is believed to have an extensional nonaccretionary type forearc basin. Basal erosion has a direct impact on the forearc basin development alongside a system of normal faults resulting from extensional stress (Kimura et al., 2012; Noda, 2016; von Huene et al., 1994). Wang et al. (2011) suggested that basal erosion occurs during large interplate earthquakes, and extension of the forearc slope occurs during periods of interseismic wedge-stress relaxation. Seismic images and ocean drilling results showed that Pliocene–Pleistocene and Miocene sediments overlie the Cretaceous continental framework in the forearc slope, with an erosional unconformity between the Cretaceous continental framework and Miocene sediments. This unconformity is observed as a high amplitude seismic reflection, which makes it a prominent marker horizon. The Cretaceous unconformity loses continuity and shows a variable relief in the landside of the upper slope, where overlying strata are severely faulted and deformed, as Fig. 2 shows. Arai et al. (2014) used high-resolution seismic profiles and bathymetric data to investigate the forearc upper slope and basins along the Japan Trench. They found a number of isolated basins which are formed due to the subsidence occurring in the forearc slope. Boston et al. (2017) used regional residual separation of the local bathymetry to constrain fault scarp extents and isolated forearc basins. We aim to investigate the severely faulted area, as marked with the red rectangle between points P and Q on Fig. 2, in the shallow part of the upper slope by developing an accurate velocity model using FWI for depth imaging. The yellow vertical dashed lines labeled with capital letters A–I are used throughout the paper for several quality control procedures of FWI and imaging results. The major reflections from Cretaceous unconformity, backstop interface, top of the oceanic crust, oceanic Moho, and arc Moho are also marked with the arrowed labels on Fig. 2.

Fig. 1
figure 1

Location of the Japan Trench with the seismic survey line D13 shown on the map using the black line. The coseismic slip of the 2011 Tohoku earthquake calculated by Tsunami waveform inversion is displayed by the contour lines of 4-m intervals and colored surface (see Satake et al., 2013). The epicenter is marked using the yellow star sign. This 2D seismic line was processed as part of the study on crustal structure imaging, and the KPSDM section of the whole line is shown in Fig. 2. Here we focus on the area over the forearc upper slope marked with the red line between P and Q points, with a length of around 55 km, to apply FWI on the seismic data. The small box on the top-left corner of the map illustrates the relative location of the Japan Trench and Japan island arc

Full size image
Fig. 2
figure 2

KPSDM section of line D13 acquired in the Japan Trench subduction zone. The forearc slope consists of three regions: an upper slope with slightly inclined and relatively flat seafloor, a middle slope with a relatively steep seafloor, and a lower slope with rugged seafloor, which includes the small accretionary frontal prism. Reflections from the top of the oceanic crust, backstop interface, Cretaceous unconformity, Moho discontinuity, and arc Moho are labeled by text arrows and indicated by cyan dashed lines. A Cretaceous unconformity is a high amplitude reflection and marker horizon in the middle and upper slope with a varying relief and fading reflectivity in the landside of the upper slope. The red rectangle shows the selected area between points P and Q from Fig. 1, and we will apply FWI on this zone to improve the velocity model and depth images. The two black rectangles and the yellow vertical dashed lines indicate the locations used through the subsequent figures for quality control of the FWI results

Full size image

3 Method

3.1 Review of FWI

The large-scale nonlinear FWI problem is solved using iterative local optimization algorithms, in which the misfit error between observed data from the field and simulated data from the wave equation solution is minimized. The classical formulation uses a nonlinear least squares misfit functional as in Eq. (1).

$$e\left(p\right)= \frac{1}{2}\sum_{j=1}^{{N}_{s}}{\Delta \mathrm{d}}_{j}^{t}{\Delta \mathrm{d}}_{j}^{*},$$
(1)

where Δd is the residual waveform and superscripts t and * denote transpose and complex conjugate, respectively. The summation is over all seismic sources, and p denotes the model parameters. The gradient of the misfit function is calculated using the so-called adjoint-state method (Plessix, 2006; Virieux & Operto, 2009), and the model parameter is updated as in Eq. (2).

$${p}_{k+1}= {p}_{k}+ \alpha {(\mathbf{H}+ \varepsilon \mathbf{I})}^{-1}{\mathrm{g}}_{p,k},$$
(2)

where k is the iteration number, H is the diagonal pseudo Hessian matrix (Shin et al., 2001), I is the identity matrix, g is the gradient of the misfit functional, ε is a damping factor to avoid division by zero, and α is a step length calculated using parabola fitting line search methods (Vigh & Starr, 2008). The highly nonlinear and ill-posed FWI problem requires imposing some prior information of the model in the form of regularization terms for the misfit evaluation. Otherwise, the local optimization algorithm will become trapped in a local minimum instead of converging towards the global minimum of the misfit function. Box constraint (Esser et al., 2016a, 2016b) is a simple regularization method which can ensure that the velocity at each grid point of the inverted model remains within a predefined interval. In other words, the model parameter is updated with a constraint according to Eq. (3).

$$\left\{\begin{array}{c}{p}_{k+1}= {p}_{k}+ \Delta p,\\ \\ {p}_{k+1}\in \left[l,u\right],\end{array}\right.$$
(3)

where Δp is the second term in the right-hand side of Eq. (2), l and u are the lower and upper bounds for the acceptable model parameter p. More sophisticated regularization methods, e.g., total variation, could be found in the literature (Anagaw & Sacchi, 2012; Esser et al., 2016b; Loris & Verhoeven, 2012; Rudin et al., 1992). Here, we use the box constraint for this case study, as we could develop an initial velocity model that is accurate enough to let the FWI converge towards the global solution of the inverse problem.

For facilitating waveform fitting, we apply a matching filter before misfit evaluation in the frequency domain to match the amplitude spectrum of each shot gather in the observed data with the amplitude spectrum of the same shot gather in the calculated data. The filter operator could be obtained in the frequency domain by using Eq. (4).

$$W= \mathrm{sqrt}\left( \frac{{D}_{\mathrm{cal}}{D}_{\mathrm{cal}}^{*}}{{D}_{\mathrm{obs}}{D}_{\mathrm{obs}}^{*}+\gamma } \right),$$
(4)

where Dobs and Dcal are the Fourier transforms of the observed and calculated data, respectively. γ is a small positive value to avoid division by zero, and * denotes complex conjugate operation. At each iteration, the matching filter operator is designed for each shot gather independently and is applied to the same shot gather of the observed data to help the amplitude spectrum of the observed and calculated waveforms match. This operation is particularly effective in overcoming the instability of the seismic source energy from one shot to another. In the current dataset, the large-volume airgun array did not perform quite uniformly, and the source energy changes from shot to shot in several points. In order to compensate for the variations of the source energy, we implemented this matching filter. We used a spike as the source wavelet, i.e., a zero-phase and constant-amplitude signal in the frequency domain. When we apply this matching filter to the observed data, the phase characteristics of the data are not influenced, but the amplitude spectrum is scaled so that the observed data and simulated waveform amplitudes reside in a close range, which facilitates the data fitting. A somewhat similar approach is used in the phase-only waveform inversion methods, which concentrate only on the phase behavior of the observed and modeled data by replacing the amplitude spectrum of the modeled data with that of the field data in small sliding windows for each seismic trace (Jones, 2019; Maharramov et al., 2017). However, here we do not entirely ignore the amplitude behavior of the data but balance them on a shot-by-shot basis to use them in the data fitting. It should be noted that this matching filter works in a different way from the modern reformulations of the waveform inversion in which the misfit function is directly formed using the matching filter (Sun & Alkhalifah, 2019a, 2019b; Warner & Guasch, 2016). Although we use a classical least squares misfit function, the initial model here is accurate enough to relax the cycle skipping issue, and this matching filter helps to fit the waveforms in a traditional framework correctly.

3.2 Data Acquisition

Several seismic surveys were conducted after the 2011 Tohoku earthquake (M 9.0) to characterize the detailed crustal structure of the Japan Trench subduction zone. The 2D seismic reflection data of the current study were acquired along line D13 (Fig. 1) by research vessel Kairei in May 2011. For deep-penetration seismic imaging, a large volume (~ 130 litters) tuned airgun array with an air pressure of 2000 psi was used as the controlled sound source with a 50 m shot interval and 10 m towing depth. A 444-channel streamer with 12.5 m group spacing (~ 5.8 km maximum offset) was towed at a depth of 21 m to avoid collision with the floating obstacles brought to the ocean by the tsunami. The seismic data were recorded with a sampling interval of 2 ms for a total length of 18 s. This seismic data had been used by Boston et al. (2017), together with other datasets, for identifying isolated basins in the forearc upper and middle slope. However, they mainly focused on the transition area from the upper to the middle slope and excluded the shallow part of the upper slope from their analysis. Here we use the seismic data covering the landside portion of the forearc slope between points P and Q in Fig. 1 to apply FWI on the area marked with the red rectangle in Fig. 2. This area has severely faulted strata overlying the Cretaceous unconformity, and the reflection from unconformity is not continuous, so we aim to improve the velocity model by FWI for depth imaging.

3.3 Data Preconditioning and Initial Model Building

Because of the relatively large towing depth of the receivers, a strong ghost reflection was recorded in the seismic data. Bubble oscillations also contaminated the data, which could degrade the quality of the seismic images. Moreover, multiple reflections from the sea surface overlapped with the target primary reflections in the shallowest part of the study area. In order to prepare the data for waveform inversion and depth imaging, we applied a series of preprocessing to the seismic data, including debubble filtering, deghosting, swell noise suppression, and surface-related multiple elimination (SRME). It should be noted that although multiple reflections from the sea surface could be used in FWI, we removed these reflections from data by SRME and applied a Perfectly Matched Layer (PML) boundary condition (Berenger, 1994) on top of the model to reduce the nonlinearity of the FWI problem. Kazei et al. (2015) showed that multiple reflections could bring useful information in FWI only if they are modeled in the time domain or by using a dense frequency sampling in the frequency domain. Otherwise, multiple reflections adversely affect the convergence of the FWI and impose additional nonlinearity to the FWI problem. Because here we apply FWI in the frequency domain with a few frequency components, we removed the multiples from observed data using SRME. Accordingly, we applied PML on top of the model to exclude the multiples from simulated seismic waveforms for data fitting.

We developed an initial velocity model using the layer-stripping approach and iterations of KPSDM (Branham et al., 1998), a migration-based velocity analysis (MVA) method. In this method, the model is assumed to consist of a number of blocky layers, with each layer having a fixed velocity at the top of the block, which linearly increases with depth at a particular rate. After KPSDM confirms the depth of the horizon between the current and the next layer, the layers are added to the model one by one from top to bottom. A horizon-based semblance analysis is conducted to check the validity of the velocity of the current layer to produce an acceptable depth image. If needed, the velocity at the top of the current layer or its increase rate is modified before adding the next layer. Once the semblance measure shows minor velocity errors, the next layer is added. The layer stripping is continued until all the desired horizons are used for the model building. The MVA tool which we used here inherently applies a minor smoothing at the layer interfaces before applying KPSDM. A simple flowchart of MVA followed by FWI is shown in Fig. 3. Tsuru et al. (2002) extracted a velocity model from several ocean bottom seismograph (OBS) datasets in the Japan Trench. We used this OBS-derived model as prior information for fast and accurate layer-stripping model building. We developed the MVA velocity model for the whole line D13 as a part of another study to characterize the deep structures of the Japan Trench subduction zone using the KPSDM section shown in Fig. 2. The area marked with a red line between points P and Q in Fig. 1 is selected for the FWI application. Figure 2 illustrates that the shallow strata above the Cretaceous unconformity in the selected area (red rectangle) is severely deformed, and even the reflection from the unconformity is not continuous. The lack of continuity indicates that the velocity model resulting from MVA alone may not be accurate enough to image the subsurface correctly, and FWI is needed. We applied a horizontally strong smoothing filter, with a vertical operator length of 75 m and horizontal operator length of 1250 m, on the velocity model developed using the MVA method and then used it as the initial model for FWI application in the shallow part of the forearc upper slope. The MVA velocity model and the smoothed initial velocity model are shown in Fig. 4. We did not intend to destruct the useful velocity information from the MVA model, and at the same time, we wanted to challenge it and see how far FWI can further improve the subsurface images. Therefore, we applied the horizontal smoothing operator, which locally affects the KPSDM image as shown in Fig. 5, and the quality of the migrated image using the smoothed initial model becomes lower than the migrated image obtained by the MVA model. However, the long wavelength background velocity model, which is needed to overcome the cycle skipping, is still preserved for FWI and we will be able to compare the potential improvements by FWI.

Fig. 3
figure 3

Simple flowchart for developing an initial velocity model using layer stripping and KPSDM imaging, followed by FWI to update the model. The velocity model is built from top to bottom by adding blocky layers and migration-based velocity analysis (MVA) in the upper loop. Once the desired initial velocity model is obtained, the FWI is applied to iteratively update the model through the second loop in the lower part of the flowchart. The horizon-based semblance analysis in the MVA helps develop a reliable low-wavenumber background velocity model required by FWI to avoid cycle skipping

Full size image
Fig. 4
figure 4

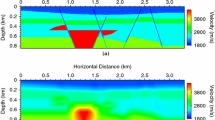
a P-wave velocity model obtained by MVA through the layer-stripping method. Although this model can be directly used as the initial model for FWI, we applied a horizontally-strong smoothing operator with operator length of 75 m and 1250 m in the vertical and horizontal directions, respectively, to see how far FWI updates the smoothed initial model and compare the results against the MVA model. The smoothed initial velocity model is shown in (b). The origin of the 0 km horizontal distance in this figure and all of the subsequent figures is at point P, i.e., the left margin of the red rectangle in Fig. 2

Full size image
Fig. 5
figure 5

Depth sections obtained by KPSDM imaging of a MVA model, and b smoothed initial model from Fig. 4. The quality of the depth section produced by the smoothed model is lower than the image generated by the MVA model, especially in the vicinity of the high velocity basement. The common image gathers at locations marked with the dashed yellow lines are displayed in Fig. 7 for the detailed comparison of the models within the two black rectangles in the western and eastern parts of the model. The amplitude scale bar refers to the relative amplitude of seismic traces in the depth sections, and is fixed for a better comparison between different panels of Figs. 5 and 6b

Full size image

4 Results

We selected five frequency components between 4 and 7 Hz from the seismic data, according to the method suggested by Sirgue and Pratt (2004), and arranged them in two groups with an overlapping band, i.e. (4.00, 4.58, 5.26 Hz) and (5.26, 6.03, 6.92 Hz). The selected frequencies for the FWI application are close enough to ensure that no wrap-around occurs (Mulder & Plessix, 2004). The RTM images shown in the following figures are generated using seismic data with a frequency bandwidth of 4–40 Hz, and the KPSDM images are produced using data with a bandwidth of 4–125 Hz. FWI is started from the lower frequencies to allow a multi-scale scheme for updating the velocity model through 50 iterations per group. The resulting FWI velocity model and the corresponding KPSDM depth section generated using this model are shown in Fig. 6. The resulting KPSDM section is profoundly improved compared to the initial KPSDM section in Fig. 5b. However, it seems that there are just slight differences between the KPSDM sections of the MVA and FWI model, and a detailed comparison between common image gathers with further quality control measures are needed. Two areas marked with black rectangles on the western and eastern sides of the model are selected to be discussed in detail. Several locations indicated by vertical dashed yellow lines and labeled with capital letters A–I are used to compare the effect of velocity model updates on the depth imaging results. Figure 7 shows the KPSDM common image gathers using MVA, initial, and FWI velocity models. The MVA image gathers are slightly better than image gathers of the initial model, but in both cases, the reflections in the far offsets and at the depths larger than 2.5 km deviate from the ideal flat line, implying an imperfect velocity model was used for imaging. On the other hand, the common image gathers resulting from KPSDM using the FWI velocity model are nearly flat even at a depth of 3.5 km at H and I locations.

Fig. 6
figure 6

a Updated P-wave velocity model by applying FWI on the smooth initial velocity model shown in Fig. 4b and by using two frequency groups of (4.00 Hz, 4.58 Hz, 5.26 Hz) and (5.26 Hz, 6.03 Hz, 6.92 Hz), with 50 iterations per group. b The KPSDM depth section obtained using the FWI velocity model. The quality of the depth section seems to be similar to the MVA depth section in Fig. 5a. However, a detailed comparison of the common image gathers in Fig. 7, and further quality control measures in the subsequent figures will illustrate the additional information provided by FWI

Full size image
Fig. 7
figure 7

KPSDM common image gathers at the locations marked with the vertical dashed yellow lines and labeled with capital letters A–I in the western and eastern part of the model in Figs. 5 and 6. The image gathers are produced using (a, d) MVA velocity model, (b, e) smoothed initial model, and (c, f) FWI velocity model. All three models obtain relatively flat reflections down to a depth of 2.5 km. However, at a depth below 2.5 km, both the MVA and initial velocity models fail to generate flat reflections in the common image gathers. FWI velocity model successfully produces flat reflections even down to a depth of 3.5 km at the H and I locations

Full size image

5 Discussion

5.1 Assessment of FWI Models

The limited offset of the seismic data used here is one of the restrictions directly affecting the FWI results. The refracted and diving waves transmitted through the model are normally expected to play a key role in updating the long to intermediate spatial wavelengths of the velocity model. The maximum offset of 5.8 km is not enough to observe the refraction and diving waves from the shallow sedimentary unit, as illustrated by the common shot gathers S1 and S2 of Fig. 8, whose spatial locations are marked with the magenta star signs and labeled in Fig. 9. However, an important event observed at the far offsets of these data is the post-critical reflection from the deeper reflectors and the basement, as marked with the labels in Fig. 8. The significant velocity contrast between the sediments and the Cretaceous continental basement generates the post-critical reflection as the dominant feature recorded at the far offsets. We performed ray tracing using the initial velocity model and FWI velocity model to understand how the updated model contributes to the generation of these post-critical reflections. We used seven shots located at the points marked with the star sign and only plotted the ray paths observed by a maximum offset of 5.8 km. Figure 9a shows the ray paths traveled in the initial model, and Fig. 9b shows the ray paths traveled in the FWI resulting model. The RTM section corresponding to each velocity model is displayed in the background. Obviously, the smooth initial model cannot generate most of the post-critical reflection energy from the basement, and only two shots located between horizontal distances of 10–20 km generate the ray paths (Fig. 9a). On the other hand, as the FWI updates the velocity model and the sharp velocity boundary at the basement is constructed, the ray paths from all the seven shots appear (Fig. 9b). The RTM image also supports the fact that the sharp boundary at the basement generates strong reflections.

Fig. 8
figure 8

Two shot gathers of the observed data located at horizontal distances of a 10.5 km for S1, and b 33 km for S2, from the left margin of the model at point P. The source locations of these shots are marked with magenta stars in Fig. 9. The limited offset of the observed data (5.8 km) does not allow us to record the refraction or diving waves, which play a key role in updating the long wavelength component of the velocity model. However, because of the sharp velocity contrast between the sedimentary unit and the Cretaceous basement, strong post-critical reflections are generated and observed in the far offsets indicated by the yellow arrows. These post-critical reflections will act in a tomographic way to update the long to the intermediate wavelength of the velocity model at the deep basement, even though the diving waves from the shallower sediments are absent. The seafloor multiple reflections which partially overlap with the primary reflections are also marked

Full size image
Fig. 9
figure 9

Ray path illumination by applying ray tracing to the a smooth initial model and b FWI updated P-wave velocity model. The seven shots at the locations marked with the stars are used to simulate the ray paths, which could be observed by a streamer with a maximum offset of 5.8 km. Since the initial velocity model is smooth and the velocity boundary at the basement is not sharp enough, only two out of seven shots can generate the ray paths recordable within the limited offset. However, the updated FWI velocity has a sharp basement, generating the ray paths reflecting from the Cretaceous basement. The two magenta signs illustrate the location of the shot gathers S1 and S2 shown in Figs. 8 and 12. The RTM images shown in the background of each velocity model clearly illustrate how the improved reflecting boundaries by FWI contribute to the generation of the ray paths, which are also in agreement with the post-critical reflections observed on the shot gathers shown in Fig. 8

Full size image

The two areas marked with the black rectangles are enlarged and displayed for a more detailed investigation. On the selected area in the western side of the model, the sedimentary strata overlying the Cretaceous unconformity is partially deformed by a number of normal faults. The smooth initial velocity model could not image the reflections from the unconformity, but the FWI velocity model could successfully image the sediments and the Cretaceous unconformity (Fig. 10). On the other hand, the eastern part of the model is severely faulted from different angles, and the reflection from the basement is not clear. The FWI velocity model improved the depth image of the faulted sediments and the unconformity boundary. The sharp velocity contrast between sedimentary strata and basement matches with the subsurface structures (Fig. 11).The sensitivity kernel of FWI using the final updated velocity model and the shot gathers S1 and S2 of Fig. 8 are shown in Fig. 12, with the sources located at the magenta star and a single receiver representing only the far channel located at the black triangle. The shot locations in Figs.12a and b are at approximate horizontal distances of 10.5 km and 33 km, respectively, from the left margin of the study area at point P. As shown in Fig. 9b, the rays from these two shots pass through the A and E locations, respectively. Jones (2019) provides a detailed explanation of the different components of the FWI sensitivity kernel. The direct transmission path between the source and receiver is the FWI “banana” which updates the low wavenumber part of the velocity model in the shallow depths using the transmitted waveforms and is marked with circle number 1 in Fig. 12. At the places above the point at which the critical angle is reached for either the downgoing or upcoming wavefields, the low frequency “rabbit ears” component of the sensitivity kernel updates the low wavenumber part of the velocity model using the information provided by the reflections. This “rabbit ears” pattern, representing the transmission path of the reflected energy from the basement by connecting the reflecting boundary to the source and receiver, is marked with circle number 2 in Fig. 12. The third component of the FWI sensitivity kernel is the FWI “migration arc” which updates the high wavenumber part of the model and is shown by circle number 3 in Fig. 12. Reflection waveform inversion (RWI) reformulates the FWI problem to separate these three components and effectively update the velocity model in a more advanced way (Brossier et al., 2015; Ren et al., 2019; Xu et al., 2012; Zhou et al., 2018). In the results presented here, the “rabbit ears” transmission paths through the reflecting boundaries suggest that FWI could successfully exploit the reflecting energy in a tomographic way to update the long to intermediate wavelengths in the deeper part of the velocity model. The migration-like component of the sensitivity kernel also contributes to further improve the velocity model in the deep parts, and this explains the relatively large updates seen near the basement on the models in Figs. 10c and 11c. Moreover, the common image gathers in Fig. 7 show nearly flat events using all three MVA, initial, and FWI models above a depth of 2.5 km. The initial velocity model is fairly accurate for imaging the shallow sediments and further updates in the shallow depths using the low frequencies and limited offsets used here by FWI are not possible. We did not push the FWI to higher frequencies because the migration-like behavior of the FWI becomes dominant at higher frequencies and for a maximum offset of 5.8 km the deeper parts of the model are adversely affected by the FWI “migration arc”. Figure 13 shows velocity profiles extracted from MVA, initial, and FWI models at the A-I locations. The sharp velocity updates at the basement are observed at depths between 2.5 and 3 km for the A-D locations and depths between 3 and 3.5 km for E-I locations, respectively. Although the resolution of the FWI model is restricted by the frequencies we used, the step-like increase in FWI velocity matches with the imaged reflection from the Cretaceous unconformity basement. The matching filter, which we used for balancing the relative amplitude spectrum of the observed and calculated data, helps to exploit the reflection amplitudes for updating the velocity model below the basement. However, the higher density of the basement may also contribute to the reflection amplitudes of the observed data. Since we apply an acoustic FWI without considering the density variations, there is a chance that density leaks into the FWI model updates and causes an increase of the velocity below the basement. Despite this possibility, the velocity profiles of Fig. 13 are in good agreement with the velocity model extracted from several OBS surveys by Tsuru et al. (2002). Close-up views of the KPSDM sections using (a) MVA, (b) initial, and (c) FWI velocity models for three different regions with noticeable improvements achieved by FWI are shown in Fig. 14. The relative location of these panels could be addressed to the other figures by the yellow dashed lines, horizontal distance, and depth values. In all these panels, the FWI velocity model provided enhanced images compared to the MVA and initial velocity models. In the first column of Fig. 14, the reflection from the basement has a higher resolution and stronger amplitude for the image produced by the FWI velocity model. In the second column, the reflection from the basement marked with the red arrow is responsible for generating the ray paths shown in Fig. 9b at the corresponding location, which is also perceived in the sensitivity kernel of Fig. 12b as the “rabbit ears” pattern. The FWI model well images the strongly faulted sediments in the third column as indicated by the red arrows.

Fig. 10
figure 10

Selected western area from Fig. 9 for a larger display of a smooth initial P-wave velocity model, b FWI resulting velocity model, and c velocity updates obtained by FWI. The RTM images are displayed in the background. The boundary of the Cretaceous unconformity is clearly imaged with the FWI velocity model. Dashed yellow lines indicate the locations for KPSDM common image gather comparison in Fig. 7. Note that the B and C locations are in the vicinity of the faulted sediments, which could not be imaged by the initial model but are correctly resolved by the FWI velocity model

Full size image
Fig. 11
figure 11

Selected eastern area from Fig. 9 for a larger display of a smooth initial P-wave velocity model, b FWI resulting velocity model, and c velocity updates obtained by FWI. The RTM images are displayed in the background. The boundary of the Cretaceous unconformity is clearly imaged with the FWI velocity model. Dashed yellow lines indicate the locations for KPSDM common image gather comparison in Fig. 7. Note that the reflection from the boundary of Cretaceous unconformity is significantly improved at locations E, F, and I. The G and H locations are also in the vicinity of the severely faulted sediments, which could not be perfectly imaged by the initial model but are correctly resolved by the FWI velocity model

Full size image
Fig. 12
figure 12

Sensitivity kernel calculated using FWI final updated velocity model and the seismic data of the second frequency group (5.26 Hz, 6.03 Hz, 6.92 Hz) for the two shot gathers in Fig. 8 at horizontal distances of a 10.5 km for S1, and b 33 km for S2, from the left margin of the model at point P. The source and the receiver are located at the positions marked with a magenta star and a black triangle with an offset of 5.8 km. The three components of the sensitivity kernel include: ① The FWI “banana” which can update the low wavenumber part of the model from the transmitted waveforms. ② The FWI “rabbit ears” which connect the source and receiver through the transmission path of the reflection energy from the basement and play a key role in updating the low wavenumber part of the velocity model in a tomographic regime. ③ The FWI “migration arc” which performs a least-squares migration-like job to update the high wavenumber part of the velocity model in the deeper zones

Full size image
Fig. 13
figure 13

MVA, initial, and FWI P-wave velocity profiles extracted at the locations marked with the dashed yellow lines and labeled with capital letters A–I in Figs. 4 and 6. The MVA velocity (green line) and initial velocity (dashed blue line) profiles are nearly the same and show only a slight difference. FWI model (red line) shows a sharp velocity increase of the basement at depths between 2.5 and 3 km for the A–D locations and depths between 3 and 3.5 km for the E–I locations, respectively

Full size image
Fig. 14
figure 14

Zoomed panels of the KPSDM sections generated by using a MVA model, b initial model, and c FWI model. Vertical dashed lines allow direct comparison of the common image gathers of Fig. 7 and their influence on the quality of the depth sections shown here. The first column is on the western side of the study area, where the higher resolution and improved reflectivity of the Cretaceous basement using the FWI velocity model are apparent. The middle column shows the images near the location marked with the capital letter E. The red arrow shows the reflection from the basement, which is improved by the FWI velocity model. The “rabbit ears” pattern seen in Fig. 12b is generated by the sharp velocity contrast at this location. The last column shows the images on the eastern side of the study area. The red arrows show the reflections from the faulted sediments above the basement, which are improved by the FWI velocity model. The normal faults reach up to the seafloor, as shown in Fig. 16, and possibly influence the evolution of the isolated basins of the forearc slope

Full size image

A comparison between preprocessed observed data and simulated data for shot gather S1 is shown in Fig. 15. The frequency domain modeling is conducted using the same forward modeling engine used for the FWI and all the frequency components are generated with Nyquist sampling criteria, followed by an inverse Fourier transform to obtain the time domain shot gathers. A source wavelet is estimated from the direct arrival, following the method in Schuster (2017). Figure 15a shows the observed data versus the modeled data using the smooth initial velocity model, and Fig. 15b shows the observed data versus the modeled data using the FWI final velocity model. All panels display the data within a range of 4–7 Hz, to be consistent with the FWI frequency range. As the red ellipse shows, the reflections in the observed data and simulated data using the FWI velocity match consistently without any cycle skipping. The red arrows indicate that the strong reflection from the basement is well generated using the FWI velocity model. The seismic amplitudes are normalized and scaled in a trace-by-trace fashion for a better illustration of the post-critical reflection. The simulated seafloor reflection appears a little dimmed in the far offsets just because the post-critical reflection, which controls the display normalization factor, becomes strong. It should be noted that the resolution of the FWI velocity model is limited by the low frequencies which we used, and also, a constant density model is applied here. Therefore, some of the visible reflections in the observed shot gather are missed in the simulated shot gather. However, the major event contributing to the FWI velocity updates, i.e., the post-critical reflection, is appropriately simulated.

Fig. 15
figure 15

a Preprocessed observed shot gather (left) versus simulated shot gather using smooth initial velocity model (right), and b preprocessed observed shot gather (left) versus simulated shot gather using FWI final velocity model (right) for the source located at point S1 indicated in Fig. 9 within a frequency range of 4–7 Hz. The red ellipse shows that the reflections in the observed data and simulated data using the FWI velocity match consistently without any cycle skipping. The red arrows indicate that the strong reflection from the basement is well generated using the FWI velocity model. A trace-by-trace amplitude normalization has been applied for better visualization of the post-critical reflection. This makes the seafloor reflection to appear a little dimmed in contrast to the strong post-critical reflection in the far offsets of the simulated data

Full size image

5.2 Geological Aspects

The tectonic activity and subduction erosion of the upper plate in the Japan Trench directly affects the development of the forearc isolated basins. Extensional stresses within the upper plate result in the deformation and normal faulting of the basement and the sedimentary units, which cause episodic subsidence. The subsidence of the strata, and eventually seafloor, provides accommodation space for the deposition of the younger sediments. Chang et al. (2020) used multibeam (MB) and subbottom profiler (SBP) data to investigate structural-morphological and sedimentary features along the Japan Trench forearc slope. They imaged dip-oriented slope gullies and a nearly dip-perpendicular slope trough bounded by a fault scarp. They also imaged normal faults with opposite dips, unconformity, sliding surfaces, underfilled (forearc trough), and filled structures that may reflect the most recent forearc subsidence and basin filling. Using these features, they proposed a model of forearc basin development starting from slope gully and transferring to slope trough, isolated basins, and finally forearc basin by active structures. On the eastern side of our study area, the normal faults seen on the KPSDM section reach up to the seafloor, as shown in Fig. 16. Although the resolution of the current seismic data is limited, yet it is visible that these faults offset the seafloor and are likely active. There is clear evidence of seafloor and shallow sediments subsidence right above these faulted structures, which implies a suitable environment for developing a newly isolated basin in this area.

Fig. 16
figure 16

a KPSDM section created using the FWI velocity model with the black rectangle marking the area with shallow sediments and seafloor subsidence, as shown in (b). The reflection from Cretaceous unconformity is marked with the cyan dashed line. The normal faults intersecting the seafloor are likely active and play a key role in the subsidence of the sedimentary strata, as the red arrows show. The gradual subsidence of the shallow sediments and seafloor provides a suitable environment for younger sediment depositions, leading to the formation of an isolated young basin. Although the KPSDM imaging of the shallow sediment is not critically affected by the accuracy of the velocity model, it is important to understand the geometry of these faults at the deeper parts of the model, which explains how the FWI updated velocity model and improved depth sections can help to understand the role of the faulted structures above the Cretaceous unconformity in forearc slope evolutions

Full size image

6 Conclusions

We designed a workflow to apply data preconditioning, initial velocity model building, and frequency domain FWI on a 2D seismic dataset acquired by a limited-offset streamer cable in the Japan Trench subduction zone. The MVA method with a layer-stripping scheme was able to build the long-wavelength background velocity model, which protected the FWI against cycle skipping. Post-critical reflections from a sharp velocity boundary at the Cretaceous basement allowed the use of reflecting energy in updating the velocity model. The quality of the FWI resulting velocity model was assessed using RTM and KPSDM depth images. The sensitivity kernel of the FWI also showed that the “rabbit ears” wave path connected the basement reflection to the source and receivers and effectively contributed to the velocity model updates by using the reflection energy in a tomographic manner. RTM and KPSDM depth sections showed improved images of the subsurface structures, including the severely faulted strata overlying the Cretaceous unconformity in the forearc upper slope. We observed evidence of subsidence in the shallow sediments, which were caused by the normal faulting and extension behavior of the forearc slope due to the basal erosion.

7 Availability of Data and Material

The 2D seismic data used in this research can be downloaded from the JAMSTEC database repository (https://www.jamstec.go.jp/obsmcs_db/e/survey/data_year.html?cruise=KR11-E03). The coseismic slip data is provided by Satake et al. (2013). The bathymetry data is obtained from GEBCO Compilation Group (2020), GEBCO 2020 Grid (https://doi.org/10.5285/a29c5465-b138-234d-e053-6c86abc040b9) https://www.gebco.net/data_and_products/gridded_bathymetry_data/.