Abstract
We use machine learning algorithms (artificial neural networks, ANNs) to estimate petrophysical models at seismic scale combining well-log information, seismic data and seismic attributes. The resulting petrophysical images are the prior inputs in the process of full-waveform inversion (FWI). We calculate seismic attributes from a stacked reflected 2-D seismic section and then train ANNs to approximate the following petrophysical parameters: P-wave velocity (\(V_\mathrm{{p}}\)), density (\(\rho \)) and volume of clay (\(V_\mathrm{{clay}}\)). We extend the use of the \(V_\mathrm{{clay}}\) by constraining it with the well lithology and we establish two classes: sands and shales. Consequently, machine learning allows us to build an initial estimate of the earth property model (\(V_\mathrm{{p}}\)), which is iteratively refined to produce a synthetic seismogram that matches the observed seismic data. We apply the 1-D Kennett method as a forward modeling tool to create synthetic data with the images of \(V_\mathrm{{p}}\), \(\rho \) and the thickness of layers (sands or shales) obtained with the ANNs. A nonlinear least-squares inversion algorithm minimizes the residual (or misfit) between observed and synthetic full-waveform data, which improves the \(V_\mathrm{{p}}\) resolution. In order to show the advantage of using the ANN velocity model as the initial velocity model for the inversion, we compare the results obtained with the ANNs and two other initial velocity models. One of these alternative initial velocity models is computed via P-wave impedance, and the other is achieved by velocity semblance analysis: root-mean-square velocity (RMS). The results are in good agreement when we use \(\rho \) and \(V_\mathrm{{p}}\) obtained by ANNs. However, the results are poor and the synthetic data do not match the real acquired data when using the semblance velocity model and the \(\rho \) from the well log (constant for the entire 2-D section). Nevertheless, the results improve when including \(\rho \), the layered structure driven by the \(V_\mathrm{{clay}}\) (both obtained with ANNs) and the semblance velocity model. When doing inversion starting with the initial \(V_\mathrm{{p}}\) model estimated using the P-wave impedance, there is some gain of the final \(V_\mathrm{{p}}\) with respect to the RMS initial \(V_\mathrm{{p}}\). To assess the quality of the inversion of \(V_\mathrm{{p}}\), we use the information for two available wells and compare the final \(V_\mathrm{{p}}\) obtained with ANNs and the final \(V_\mathrm{{p}}\) computed with the P-wave impedance. This shows the benefit of employing ANNs estimations as prior models during the inversion process to obtain a final \(V_\mathrm{{p}}\) that is in agreement with the geology and with the seismic and well-log data. To illustrate the computation of the final velocity model via FWI, we provide an algorithm with the detailed steps and its corresponding GitHub code.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Velocity model building is an inversion process that is an essential step in seismic exploration, since it is used during the acquisition and processing of seismic data. Its objective is to build an image from the recorded seismic data by repositioning the recorded data to its most probable geological position in the subsurface. All these methods require an initial velocity model. The methods for velocity model building can be categorized into ray-based, wave equation and synthetic methods in terms of their theoretical basis (see Wenqing et al. 2017). Full-waveform inversion (FWI) lies within the wave equation method category. FWI is a procedure based on the minimization of a misfit (or cost) function which is the difference between synthetic waveforms and real seismic traces, used to derive high-resolution velocity models. The minimization of this cost function consists of an iterative adjustment of the velocity model and/or some other physical parameters of the Earth’s subsurface. From a mathematical perspective, FWI is a nonlinear inverse process that can be interpreted as an optimization problem (Tarantola 1984, 2005). Even though the theory for FWI was developed in the 1980s, it is only in recent decades that the growth of high-performance computing power has enabled widespread adoption of FWI for field data sets (Virieux and Operto 2006). The success of velocity model building relies on the construction of a proper initial velocity model. A skilled seismic interpreter must invest a great deal of time to build an initial velocity model which will be the starting point of the iterative process of FWI (or any other velocity model building method), to minimize the residual.
Seismic reservoir characterization aims to provide an optimal understanding of the reservoir’s internal architecture by mapping its properties such as volume of clay, sand and shale, thickness, density, porosity, permeability, velocity, water saturation and pore fluid. Machine learning algorithms, in particular artificial neural networks, are currently used in seismic reservoir characterization to produce images of the Earth’s subsurface properties at different scales.
Deep neural networks have recently been applied to estimate the velocity model directly from seismic data (Li et al. 2019). In Araya-Polo et al. (2018), the authors applied deep-learning tomography to directly produce an accurate gridding or layered velocity model from shot gathers. In Yang and Ma (2019), deep-learning neural networks are trained to establish a nonlinear projection from multi-shot seismic data to the corresponding velocity models. As a result, during the prediction stage, the trained network can estimate the velocity models from new unseen seismic data. Convolutional neural networks (CNN), Bayesian-based support vector machine (BSVM) and the joint methods of CNN and BSVM are three methods used by Liu (2019) for direct seismic one-step inversion. In view of his results, these methods allow the user to incorporate a wider range of seismic data, well logs, geological data and experience to infer the reservoir rock properties. Convolutional neural networks have also been applied to elastic pre-stack seismic inversion in stratified media (Zheng 2019).
In order to obtain a high-resolution velocity model through the application of FWI, we need an initial velocity model. Here we use artificial neural networks (ANNs) to predict P-wave velocity (\(V_\mathrm{{p}}\)), density (\(\rho \)) and volume of clay (\(V_\mathrm{{clay}}\)) from well-log information to distributions at seismic scale. The seismic data (with their seismic attributes) come from a 2-D seismic section in the Tenerife field located in the Middle Magdalena Valley. The well logs come from a well near this survey line. There are two available wells; one will be used for training ANNs and the other will be used for testing the ANNs’ estimations and the final inverted \(V_\mathrm{{p}}\). The result is that these well-log properties are extrapolated to the seismic scale. The predicted \(V_\mathrm{{p}}\) at seismic scale will serve as prior input (or initial model) for the full-waveform inversion (FWI), and the other petrophysical estimations at seismic scale (\(\rho \) and the layered structure that comes from the \(V_\mathrm{{clay}}\)) will be employed in the forward part of the FWI. We trained different ANNs to estimate each of the desired petrophysical properties (\(V_\mathrm{{p}}\), \(\rho \) and \(V_\mathrm{{clay}}\)). Every trained ANN will produce a particular initial velocity model. This gives us the advantage of choosing the starting models that produce the highest initial correlations between synthetic and real traces.
There are other alternatives for constructing an initial velocity model, such as computing the P-wave impedance (\(I_\mathrm{{p}}\)) from seismic data, and from there the \(V_\mathrm{{p}}\). The \(I_\mathrm{{p}}\) is the product of the density and the velocity. Once the impedance is computed, one can obtain the P-wave velocity (\(V_\mathrm{{p}}\)) as follows: \(I_\mathrm{{P}}=\rho *V_\mathrm{{p}} \;\Rightarrow \; V_\mathrm{{p}}=\frac{I_\mathrm{{P}}}{\rho }\), where \(\rho \) is the density. Deriving impedance values from seismic data can be done using the band-limited impedance inversion method (BLIMP) described in Ferguson and Margrave (1996) and Maulana et al. (2016). This method was also successfully applied in Parra et al. (2017). One disadvantage of the method is that it requires the information of density in the interval of the impedance inversion. This becomes crucial when doing FWI for pre-stack data and there is no well-log information for \(\rho \) in the shallow part of the well; consequently, BLIMP cannot be applied in this case. Even so, we do not have that problem since we are not doing pre-stack inversion, and we compare the final \(V_\mathrm{{p}}\) after inversion starting from the \(V_\mathrm{{p}}\) obtained with the P-wave impedance.
Another possible procedure for building an initial velocity model is given in Iturrarán-Viveros et al. (2018b). In that work, the authors convert the volume of clay into a velocity model using the knowledge of the distribution of two facies (sands and shales) and constructing two third-degree polynomials, fitting sands or shales according to their depth and using the well-log information for \(V_\mathrm{{p}}\). The described route also applies ANN to estimate the volume of clay, and from this estimation a classification between sands and shales can be made. In the present article, we choose the path of directly using ANN to estimate the petrophysical properties needed as the starting point to conduct the iterative process of the inversion of the velocity \(V_\mathrm{{p}}\).
A standard procedure for estimating an initial velocity model is that, after the seismic processing and data velocity semblance analysis, the root-mean-square (RMS) velocity is obtained. This is a model that will also be used as prior initial velocity model for the inversion. The final results for these three different initial velocity models will be compared.
In this paper, we start by establishing a workflow for the construction of petrophysical parameters to the inversion of the velocity \(V_\mathrm{{p}}\). We continue with a review of the relevant characteristics, the interpretation, the description of the seismic and well-log data in the field, and a brief explanation of the data processing procedure. Next we introduce our strategy to combine the well-log information with the seismic data. We then report how to use the Gamma test to select the best seismic attributes for the ANNs, and we recount the architecture and training algorithms used to train ANNs to estimate the petrophysical parameters. We follow with an explanation of the 1-D Kennett solution to generate 1-D synthetic seismograms which will be compared to real acquired seismic data to perform the velocity inversion. We then give a brief account of the nonlinear squared inversion method for the problem under consideration. Lastly, we discuss numerical results and provide our concluding remarks.
2 Flow Chart
In order to build 2-D sections or estimations of \(V_\mathrm{{p}}\), \(\rho \) and \(V_\mathrm{{clay}}\) (at seismic scale) using ANNs and applying the results to the FWI iterative process to estimate a high-resolution velocity model, we implement a full procedure as shown in Fig. 1 and described in the following steps:
- Seismic survey and well-log data.:
-
We use the seismic line EXP-TENE-2D-3C (shown in Fig. 3) and the well-log data that correspond to the well Tenerife-2, which is the closest to this line. The well-log information from the well Tenerife-1 is used to validate the results. The location of these two wells is shown in Fig. 2. The reservoir characterization is defined based on the seismic and geological interpretations and petrophysical and reservoir engineering data.
- Seismic attributes.:
-
From the seismic line, we take the seismic trace closest to the well Tenerife-2 and we compute a set of seismic attributes. From these sets of seismic attributes we will choose a subset to train the ANNs to estimate each of the desired petrophysical parameters: \(V_\mathrm{{p}}\), \(\rho \) and \(V_\mathrm{{clay}}\). The same set of seismic attributes will be computed for the well Tenerife-1 to validate the results.
- Analyze the data by means of the Gamma test and train ANNs.:
-
We select the combination of seismic attributes that produced the smallest Gamma statistic \(\Vert \Gamma \Vert \). When \(\Vert \Gamma \Vert \) is small, then there is a strong predictive relationship between the input variables and the output. On the contrary, if \(\Vert \Gamma \Vert \) is large, there is no smooth predictive relationship between inputs and output, and a trained ANN to estimate \(V_\mathrm{{p}}\) for the set of given available attributes will not provide good estimations or generalizations. The same procedure is accomplished to estimate \(\rho \) and \(V_\mathrm{{clay}}\). This test is based on the assumption that if the two points x and \(x'\) are close together in the input space, their outputs y and \(y'\) will be close in the output space. If this does not happen, then there is not enough information to distinguish one from the other. This is an effective alternative for selecting the best combination of inputs (prior to training) given a desired output or target parameter. However, there are other alternatives such as that described by Guyon et al. (2006).
- Computing \(V_\mathrm{{p}}\), \(\rho \) and \(V_\mathrm{{clay}}\) at seismic scale via ANN.:
-
Combining the well-log information (from the well Tenerife-2) for \(V_\mathrm{{p}}\), \(\rho \) and \(V_\mathrm{{clay}}\), we train ANNs to extrapolate the values that are at well-log scale to the seismic scale to have these petrophysical parameters for the entire seismic section. We use the best three trained ANNs to finally estimate the \(V_\mathrm{{clay}}\), \(\rho \) and \(V_\mathrm{{clay}}\) at seismic scale using the inputs drawn by the Gamma test, given in Table 1. From the continuous volume of clay we obtain two facies, sands and shales, for the entire 2-D seismic section. This classification will be used in the 1-D Kennett forward model to establish the thicknesses of layers (of sands or shales).
- Testing the trained neural networks and applying them to obtain predictions.:
-
We test the ANN via cross-validation. This involves systematic removal of some data and re-estimating their values based on the model selected. In our case, the data set was divided into two halves: one for training and the other for testing. The well-log information from the well Tenerife-2 is used to train, and the well-log information for well Tenerife-1 is used to test the training. If the trained ANNs are capable of generalization, the results on unseen data will be reasonable with respect to the true values.
- Forward modeling.:
-
We apply the 1-D analytic method by Kennett (1983) as a forward model to compute synthetic traces, using for each trace in the seismic section its \(V_\mathrm{{p}}\), \(\rho \) and layered structure (that comes from \(V_\mathrm{{clay}}\)), all from the ANN estimations.
- Inversion of \(V_\mathrm{{p}}\).:
-
Each seismic trace within the 2-D seismic section has properties that vary only with the vertical axis (i.e. a layered medium), and this 1-D medium has a profile determined by \(\rho \), \(V_\mathrm{{p}}\) and the thickness of each layer. The thickness of the layer depends on or may vary according to the time-depth (T–Z) curve. Using the ANN-estimated \(\rho \) and \(V_\mathrm{{p}}\) seismic sections, we input these parameters in a 1-D analytic method by Kennett (1983) which allows us to build synthetic seismograms, and these results are compared to the real acquired seismic traces. The inversion process corrects the \(V_\mathrm{{p}}\) initial model to force each of the synthetic traces in the seismic section to match the real seismic data. This is done using a nonlinear least-squares optimization method.
- Validation of results.:
-
The final \(V_\mathrm{{p}}\) obtained after the inversion is compared to the real \(V_\mathrm{{p}}\) that comes from the two wells (scaled to the seismic scale).
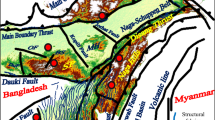
On the left-hand side, the northwestern corner of South America with the location of the Middle Magdalena Valley Basin (MMVB). The small blue square represents the Tenerife field and the red dot denotes the location of the La Cira Infantas field. On the right-hand side a zoom of the MMVB with the 2-D seismic exploration line and its location with respect to the seismic cube that was acquired after the 2-D exploration line was acquired. The red dots indicate the position of three well logs. In this paper, we have worked on well logs from Tenerife-2 (T2) and Tenerife-1 (T1) as we have information available from these wells only
Seismic line considered in this study, this corresponds to the 2-D line with three components: EXP-TENE-2D-3C. We include the structural and stratigraphic interpretation showing the intercalation of sands and shales in the Mugrosa formation. We have the location of the well Tenerife-2 (T2) in green, the white dots correspond to the formational tops identified by the well-log information and core data. MT denotes the Mugrosa top formation. The faults that cross T2 are also depicted. The distance between two adjacent traces is 5 m
This procedure is similar to that given in Iturrarán-Viveros et al. (2018b), but here we extended it by including the inversion process as in Iturrarán-Viveros et al. (2018a). In addition, we compare the ANN results after the inversion with the results after the inversion of two different alternative initial velocity models.
3 Available Data and Velocity Analysis
The Middle Magdalena Valley Basin (MMVB) is located in between the central and the eastern ranges (within the Northern Andes mountain range), in Central Colombia.
The Tenerife field (Fig. 2) is located in the central MMVB, about 20 km southwest of the La Cira-Infantas Field. Here we use the seismic data from the P-wave reflected stacked seismic section, the line EXP-TENE-2D-3C (Fig. 3). This seismic line was an experimental line and was the first acquired in the field, with an extension of 9 km with 300 sources and 903 receivers. The line EXP-TENE-2D-3C crosses the borehole Tenerife-2, which has the following well-log information: sonic log of P-wave, resistivity, spontaneous potential (SP) and induction (ILD). Some of these logs are more recent, such as the Gamma ray (GR), dipolar sonic logs, check shots and offset vertical seismic profile (OVSP). The formation unit Mugrosa C is divided into Mugrosa C-Sands and Mugrosa C-Shales. The first is the main reservoir of the basin (see Fig. 4), since it has more oil sands. It is a sandstone filled with oil, with porosity between 20 and 25%, water saturation \(S_w\) between 40 and 50%, oil saturation between 30 and 40% and gas saturation between 10 and 30%; the approximate permeability is 40.5 cp. With respect to the well Tenerife-2, the zone of Mugrosa C-Sands is located between depths 6857–7255 feet. At the top of this formation there are thin layers with depths no greater than 10 feet, with high clay content greater than 80%, and 10% sandy clay, pyrite and other minerals. The time window of the seismic section of 574–1438 ms considers the formation units from the top of Colorado to the base of Mugrosa C-Shale. The structural and stratigraphical interpretation has been carried out in the seismic section (see Fig. 3) based on the well-log information, core data and formation markers, by picking the amplitudes along the offset. The core data show that an inverse fault crosses the well Tenerife-2 at a depth of approximately 4710 feet on top of the Mugrosa formation. We compute pseudo-logs for the volume of clay (\(V_\mathrm{{clay}}\)) using spontaneous potential (SP) and the Gamma ray (GR) well logs. This technique is based on Mavko et al. (2009) and Tiab and Donaldson (2015). ANN’s estimations for both the density \(\rho \) and the layered structure obtained from the \(V_\mathrm{{clay}}\) (\(V_\mathrm{{clay}}\) < 0.5 are sands, otherwise shales) are shown in Figs. 5 and 6, respectively.
Petrophysical interpretation showing integration of core data and well logs. On the left we have the well-log information within an interval of 6800–7200 feet, the two facies: sands and shales are in yellow and brown respectively. The last track on the right-hand side shows the main productive zone Mugrosa C-Arenas with its 11 pay zones in green
Facies (sands and shales) obtained from the continuous estimation of \(V_\mathrm{{clay}}\) using a Broyden–Fletcher–Goldfarb–Shanno neural network. The classification into two facies is done by considering as sands those points that satisfy \(V_\mathrm{{clay}}<0.5\) (in yellow) and the rest are shales (in brown)
3.1 Velocity Analysis
The aim of the velocity analysis is to find the velocity that flattens a reflection so that it returns the best result when stacking is applied. Here we performed an interactive semblance velocity analysis on selected common mid-point (CMP) gathers. The seismic processing steps include sorting the data by common depth point (CDP) and offset. In order to improve the contrast of events, the data are windowed, moved out, filtered and gained following a standard procedure (Scales 1995; Gan et al. 1996; Yilmaz 2001; Yangkang et al. 2015). After processing, the resulting velocity model is called the root-mean-square (RMS) velocity and corresponds to that of a wave through subsurface layers of different interval velocity along a specific ray-path, and is typically several percent higher than the average velocity. This velocity is shown in Fig. 7, and it is used as an initial velocity model to start the inversion process. During the inversion, in addition to the initial \(V_\mathrm{{p}}\), we have used the \(\rho \) obtained from the well log, constant for the entire 2-D section, with poor results. Therefore, we opt for using the \(\rho \) obtained after training the ANNs (shown in Fig. 5), which has spatial variations (i.e. it depends on each point of the 2-D section). Note that the \(\rho \) does not change during the inversion, only the \(V_\mathrm{{p}}\). The final velocity \(V_\mathrm{{p}}\) obtained after inversion with the initial velocity in Fig. 7 is shown in Fig. 8. Figure 9 shows the initial \(V_\mathrm{{p}}\) obtained from BLIMP and after the inversion, the final result is shown in Fig. 10.
4 Neural Network Design and Training
We perform depth-to-time conversion of well logs and upscaling logs to seismic wavelengths by applying Backus averaging (Backus 1962; Lindsay and Koughnet 2001; Tiwary et al. 2009). The procedure uses a low-pass filter and subsampling of the results to match the seismic sampling. In order to estimate the time-depth (T–Z) curve, we have used available vertical seismic profile (VSP) information. The available well-log data (upscaled at seismic scale) has 450 samples for the well Tenerife-2 which will be used for training.
Deep neural networks have a large number of both hidden layers and neurons/units/nodes per layer. This involves a large number of weights (neural network parameters) to be determined during the learning phase. When we have a small data regime (i.e. a small data set), in Raissi et al. (2019) it is stated that the vast majority of state-of-the-art machine learning techniques (e.g., deep/convolutional/recurrent neural networks) are lacking robustness and fail to provide any guarantee of convergence.
The fact that we have 450 data points in our data set constrains us to use simple multilayered ANNs with two hidden layers and a small number of nodes in these hidden layers.
Our goal is to establish an initial velocity model \(V_\mathrm{{p}}\), to be used during the iterative process of FWI. Furthermore, we need two other petrophysical parameters that are acquired by the well logs: \(\rho \) and \(V_\mathrm{{clay}}\). For the inversion, these three parameters are needed at seismic scale. Since we have these three petrophysical parameters measured only for two wells, we require an extrapolation of this information to extend over the 9 km that covers the EXP-TENE-2D-3C seismic line. To do so, we combine through the use of ANNs, well-log information and seismic attributes to obtain petrophysical parameters at seismic scale. We follow the approach given in Iturrarán-Viveros (2012), Iturrarán-Viveros and Parra (2014), Parra et al. (2015) and Iturrarán-Viveros et al. (2018b). In order to combine seismic attributes to estimate petrophysical parameters, we need to ensure that the independent variables used (i.e. seismic attributes) are appropriate. One cannot discard the possibility that some regression model structures, including nonlinear ones, for example polynomial and sigmoidal models, adjust better to the data than the estimations obtained via ANNs. We have to check that our possible inputs are not redundant, since the lack of performance in multivariable regression can be due to collinearity between input variables. Hence, to select the best combination of inputs to train an ANN for each petrophysical parameter, we conduct a Gamma test analysis (Stefánsson et al. 1997; Jones 2004). A formal proof and a comprehensive description of this algorithm can be found in Evans and Jones (2002). Using this method, we obtain the best combination of attributes to train the ANNs for each of the three given petrophysical parameters. This is a problem that requires dimensionality reduction techniques such as principal component analysis or other techniques that can be also applied. For example, in Qi et al. (2020), to acquire seismic facies classification (i.e. a categorical classification), the authors use high-dimensional Gaussian mixture model (GMM) classification, and by maximizing the distances between pairs of GMM facies they determine the ideal number of attributes to use.
To predict the petrophysical parameters \(V_\mathrm{{p}}\), \(\rho \) and \(V_\mathrm{{clay}}\) at seismic scale, combining well logs and seismic attributes, we take the depth interval [2615–7414] feet, which is a region of interest since the pay zones lie there. We have well-log information from the borehole Tenerife-2 as the training data set. We use the information of the well Tenerife-1 as testing data set, to assess the performance of trained ANNs. We take the definitions of seismic attributes given in Taner et al. (1994), Taner (1997, 2001), Chopra and Marfurt (2007), Barnes (2015) and Azevedo-Guerra (2009). Then we start with a collection of 19 seismic attributes: time, seismic trace, variance, attenuation, sweetness, RMS amplitude, instantaneous bandwidth, local structural azimuth, local flatness, iso-frequency, dip illumination, dip deviation, chaos, amplitude, edge detection, envelope, edge evidence, AVO and first derivative.
Multilayer perceptron networks with back-propagation learning can solve a wide range of classification and regression problems. When the performance of this network is unsatisfactory, because of either speed or accuracy, we have also considered using conjugate gradient networks (CG), which is a variation and improvement on two-layer vanilla back-propagation; it is generally more effective (faster convergence) but requires more memory (Towsey et al. 1995; Charalambous 2003). The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is a quasi-Newtonian method and has better convergence than back-propagation. Here the best results were obtained with both CG and BFGS training algorithms. The activation function used by the neural networks is:
where \(w_{ij}\) is the weight of the connection from unit j to unit i, and \(x_j\) is the output of unit j. The sigmoidal function used by each neural node as an output function (that depends on the activation) is given by:
where k=1.5 is a scale factor and \(T=0.8333\) is called the temperature.
Using the most suitable combination of attributes drawn by the Gamma test for each petrophysical parameter (see Table 1), we train an ANN to estimate each petrophysical parameter. Table 2 shows the specific architecture of the best ANNs to estimate \(V_\mathrm{{p}}\), \(\rho \) and \(V_\mathrm{{clay}}\). In Fig. 5 we show the final best results obtained for \(\rho \) with a CG ANN with eight inputs, two hidden layers of 10 neurons each, and one output. This configuration/architecture is denoted as (8-10-10-1). For \(V_\mathrm{{clay}}\) we use a CG ANN with an architecture given by (10-9-9-1). From the continuous estimations of \(V_\mathrm{{clay}}\), we distinguish two facies: sands for \(V_\mathrm{{clay}}<\) 0.5 and shales when \(V_\mathrm{{clay}}\, \ge \) 0.5. From this classification we obtain the results depicted on Fig. 6. In order to estimate \(V_\mathrm{{p}}\) we used a BFGS ANN with an architecture given by (10-8-8-1), and the results are given in Fig. 11. Figure 12 shows the final \(V_\mathrm{{p}}\) obtained after the inversion starting with the ANN initial velocity model in Fig. 11. On Fig. 13 we have a comparison between the initial and final velocities obtained after the inversion from the initial \(V_\mathrm{{p}}\) obtained from BLIMP and the initial \(V_\mathrm{{p}}\) obtained with ANN. The number of training epochs varies depending on the data set (i.e. to estimate each of the different petrophysical properties), on average 50,000 epochs for 10 h. The running time is measured using a 2.7 GHz 12-Core Intel Xeon E5 processor.
Since the initial set of weights for training are random, it is important to mention that every time that one trains an ANN with the same set of inputs, outputs and architecture, one obtains different sets of weights that produce the best fit between the desired output and the ANN output. This does not imply that each trained ANN has to produce the same estimation for the entire seismic section. Two different trained ANNs have to produce similar outputs from the trained data set (since the target is the same) but not for the rest of the unseen data. Therefore, we can produce as many estimations as we have trained ANNs for every parameter (\(V_\mathrm{{p}}\), \(\rho \) and \(V_\mathrm{{clay}}\)), which provide a deck of possibilities for the inversion process. From these we choose the combination of \(V_\mathrm{{p}}\) and \(\rho \) that gives the highest initial correlation between synthetic and real traces. The training-testing of the ANNs is a process where we leave the information of the well Tenerife-1 out of the training data set, and once the root-mean-square error (RMSE) reaches a small value, we test the trained ANN with the unseen data and assess its performance. For the three petrophysical parameters, we kept the trained ANNs that produce between 0.89 and 0.91 correlation on average between the produced parameter and the desired one. To estimate this correlation, we use the Matlab Person correlation, and to measure the error (i.e. difference between target output and produced ANN output) during training the ANNs, we use the root-mean-square error (RMSE). The initial velocity model obtained applying the trained ANN to the well Tenerife-1 is shown in Fig. 14b. The correlation between the actual \(V_\mathrm{{p}}\), and this obtained for this unseen (during training) well Tenerife-1 is not as good as the one obtained with the trained data (i.e. the well Tenerife-2). This is somewhat expected. Nevertheless, it is good enough to show some generalization of the ANN and to be used as a \(V_\mathrm{{p}}\) initial velocity model during the FWI as shown in Fig. 14d. We have included a histogram of the relative error:
where \(V_\mathrm{{p}}\) is the target velocity and \(V_{p_{\text {model}}}\) is the initial velocity obtained either with BLIMP or with ANNs. The top part of Fig. 15 shows the histogram distributions for the initial and final velocities (using BLIMP and ANNs), and at the bottom we plot the relative error. This figure shows the results obtained for the Tenerife-1 well; we do not show this for Tenerife-2 because this is the well that was used for training.
Initial and final velocities obtained for the well Tenerife-2. a Initial velocity \(V_\mathrm{{p}}\) obtained from the P-wave impedance. b Initial velocity \(V_\mathrm{{p}}\) obtained from the trained ANN. c Final velocity \(V_\mathrm{{p}}\) model obtained after the inversion when starting from a P-wave impedance \(V_\mathrm{{p}}\). d Final velocity \(V_\mathrm{{p}}\) model obtained after the inversion when starting from an ANN \(V_\mathrm{{p}}\). This is the well that was used to train the ANNs. Correlations of these results are given in Table 3
Initial and final velocities obtained for the well Tenerife-1. a Initial velocity \(V_\mathrm{{p}}\) obtained from the P-wave impedance. b Initial velocity \(V_\mathrm{{p}}\) obtained from the trained ANN. c Final velocity \(V_\mathrm{{p}}\) model obtained after the inversion when starting from a P-wave impedance \(V_\mathrm{{p}}\). d Final velocity \(V_\mathrm{{p}}\) model obtained after the inversion when starting from an ANN \(V_\mathrm{{p}}\). This is the well that was used to train the ANNs
5 Forward Modeling
Many techniques have been used to compute the elastodynamic response of a stack of plane layers to a plane spectral wave. These variations on the original propagator matrix method, commonly called the Haskell matrix method (Haskell 1953, 1960, 1962), aim to improve the efficiency and numerical stability of the algorithm (Claerbout 1968; Kennett and Kerry 1979; Aki and Richards 1980; Chapman 2003). The displacements at the top and bottom of the stack of layers are related by a product of propagator matrices, one for each layer. The response of the model includes the effects of all multiples. The advantage of this method is that, since it is an analytic solution, the computation is very fast, and when one considers the full-waveform inversion, it could be an alternative instrument to speed up the computation. In order to compute the exact plane wave reflection response (i.e. synthetic seismograms) as a function of horizontal slowness, we use an exact algorithm called the Kennett invariant method. The Matlab implementation of this analytic tool is given in Mavko et al. (2009), and we use it together with the \(V_\mathrm{{p}}\), \(\rho \) and thickness of each layer (determined by the facies obtained with the \(V_\mathrm{{clay}}\) estimation). It is worth mentioning that all these parameters were obtained using ANNs.
We have applied commercial software to extract a wavelet from seismic data. A method called statistical wavelet extraction is part of the commercial software. This method considers all input seismic traces within the analysis region. Then, the frequency spectra of the autocorrelation of all input traces are stacked to produce the wavelet. The source wavelet extracted from the seismic data is approximated by the following expression:
where \(b=\left[ \frac{(t-t_0)f_c \pi }{2}\right] \), with \(f_c=\) dominant frequency and \(t_0\) = time delay. The expression in Eq. (4) is the integral of the Ricker wavelet which is the second derivative of a Gaussian function. The Ricker wavelet has been widely used in the analysis of seismic data, since its asymmetrical amplitude spectrum can represent the attenuation feature of seismic wave propagation through viscoelastic homogeneous media (Wang 2015). The integral of the Ricker wavelet r(t) is used to produce the synthetic full waveforms. When analyzing the frequency spectrum of the seismic trace closest to the well log, we observe that the peak frequency (the one with maximum energy) is at \(f_c=\) 25 Hz; therefore we use this peak frequency in the definition of the Ricker wavelet Eq. (4).
The images of \(V_\mathrm{{p}}\), \(\rho \) and the layers’ (of sands or shales) thicknesses obtained with the ANNs are the input parameters for the 1-D Kennett method used to compute synthetic seismograms. A nonlinear least-squares inversion algorithm minimizes the residual (or misfit) between observed and synthetic full-waveform data and improves the P-wave velocity resolution. Applying the Kennett method to each trace of the seismic section, we obtain synthetic seismograms that we compare to real seismic traces.
6 Inversion
Geophysical inversion involves the estimation of the parameters of a hypothesized earth model from a finite set of observations. Since the associated model responses can be nonlinear functions of the model parameters, nonlinear least-squares techniques prove useful for performing the inversion (Lineas and Treitel 1984; Santosa and Symes 1989). The Levenberg–Marquardt damped least-squares method is a powerful tool for the iterative solution of nonlinear problems, see for example More (1977) and Pujol (2007). This algorithm allows us to automatically change the initial velocity model to yield a refined model that better represents the subsurface. We consider the 1-D layered acoustic medium (confined to the half-space) obeying the acoustic wave equation whose model parameters are the layer velocities \(V_\mathrm{{p}}\), densities \(\rho \) and layer thicknesses, and a striking plane wave that propagates from the free surface towards the inner earth. The classical formulation of the full-waveform inversion problem is posed as the minimization of the objective (or misfit) function:
where \({\mathbf {v}} \in \mathbb {R}^m\) is the vector of velocities for each trace, and the residual or misfit function is given by:
where m is the number of time samples, \({\mathbf {H}} \in \mathbb {R}^m\) is the vector of thicknesses of layers for each trace and \(\mathbf {\rho } \in \mathbb {R}^m\) is the vector of densities for each trace. Given an earth property model \(({\mathbf {v}}, \mathbf {\rho }, {\mathbf {H}})\)= (velocity, density and thickness of layers), the 1-D Kennett wave equation operator simulates synthetic seismic data. We denote an observed seismic trace measured in the field as the vector \({\mathbf {d}}\). Each trace \({\mathbf {d}}\) has m components, and \(d_i\) in Eq. (6) represents one of these components. We perform the inversion, trace by trace, starting with either RMS velocity (Fig. 7) or ANN velocity (Fig. 11) as the initial velocity models. This strategy does not favor lateral continuity. Nevertheless, to enhance the lateral continuity one needs to use more traces (such as in the pre-stack inversion) and improve the forward modeling approach, e.g. finite difference method, to produce a 2-D wavefield. We use the density model in Fig. 5, but we do not change the density model during the inversion. To improve the initial velocity model, we performed nonlinear least-squares curve fitting between the synthetic and observed seismograms. This approach is similar to that given in Parra et al. (2017, 2019). Waveform inversion via nonlinear least-squares minimization is effective when the starting model is accurate (Tarantola and Valette 1982).
In order to assess the role of the ANNs’ initial models, we compare the results obtained using ANNs and two other models: a model obtained by velocity semblance analysis and an initial \(V_\mathrm{{p}}\) model obtained with the P-wave impedance, as prior models. When we use the \(\rho \) and \(V_\mathrm{{p}}\) obtained by ANNs the results are very good, according to Figs. 11, 13 and 14. However, when using the semblance velocity model and the density from the well log (constant for the entire 2-D section), the results deteriorate. Nevertheless, by including the density obtained with ANNs and the semblance velocity model, the results are enhanced. When using the initial \(V_\mathrm{{p}}\) obtained from the P-wave impedance (in Fig. 9), the layered structure in the final results (shown in Fig. 10) is not as good as that in the seismic section. This proves the value of the use of ANN estimations (\(\rho \), \(V_\mathrm{{p}}\) and \(V_\mathrm{{clay}}\)) during the inversion process to obtain a final \(V_\mathrm{{p}}\) that is in good agreement with the seismic data.
Note that the algorithm is implemented in the time domain. The Kennett algorithm is computed in the frequency domain and then it is transformed into the time domain via the fast Fourier transform. As a result, we could have chosen to perform the inversion in the frequency domain. However, the results we obtained in the frequency domain were not as good (i.e. neither the synthetic seismograms nor the final velocities resembled the real traces or real velocities, respectively, from the well logs) as those in the time domain. Furthermore, there is a subtle issue regarding the normalization of synthetic and real traces. Because synthetic and real traces come from different sources, they do not necessarily have the same orders of magnitude. Consequently, some normalization is needed when one defines the misfit function. Otherwise, the algorithm might not converge. We did not explicitly include this normalization in the algorithm because it is a data-dependent trial-and-error process. In the Appendix we describe the algorithm used to invert the seismic traces.
7 Results
In order to show the advantage of using ANN petrophysical parameters as initial starting models for the inversion process, we conduct four experiments. Firstly, we use the RMS velocity shown in Fig. 7, the \(\rho \) obtained from the well log (the same for all the traces) and a layered structure obtained by the facies classification shown in Fig. 6 as initial model parameters for the iterative inversion process. This produces synthetic traces that cannot match the real observed seismic data. Since the obtained correlation after inversion is very poor (0.009 on average), we do not show any results for this case. Secondly, we introduce the density given in Fig. 5 instead of a constant \(\rho \) for the 2-D section. This greatly improves the correlation between synthetic and observed seismic traces to 0.81 on average. The final velocity model obtained with this strategy is shown in Fig. 8. Although the correlation between synthetic and real traces improves, the final velocity does not have the layered structure shown in the figures for the initial parameters obtained with the ANNs or in the original seismic section (Fig. 3). In addition, it does not have a lateral continuity and it shows some strips with higher velocities parallel to the well log. This effect does not seem physically feasible. Thirdly, we use as initial velocity model for inversion the \(V_\mathrm{{p}}\) obtained from the P-wave impedance shown in Fig. 9. After the inversion, we obtain the final velocity model shown in Fig. 10, which is better than the previous experiment. Nevertheless, even though the starting initial velocity model in Fig. 9 shows a better layer structure similar to the seismic section in Fig. 3, the final inversion results show the same strips and not very clear lateral continuity. Finally, we use the \(\rho \), facies (with its corresponding layer structure) and \(V_\mathrm{{p}}\) computed from the \(V_\mathrm{{clay}}\), all obtained with the trained ANNs (Figs. 5, 6, 11, respectively) as the initial models for the inversion. This enhances the results after the inversion and produces a correlation between synthetic and real data of 0.98 on average. Moreover, one can still track the geobodies of sands and shales, and these are in agreement with the seismic amplitudes. The same can be said when looking at the estimations of \(\rho \), given in Fig. 5. We compare the \(V_\mathrm{{p}}\) initial models obtained with the P-wave impedance and those obtained with the ANNs and the \(V_\mathrm{{p}}\) final inversion results for the two wells Tenerife-2, the training data well (shown in Fig. 13) and Tenerife-1 the testing well, shown in Fig. 14. From these results we can see a better performance when using the ANNs \(V_\mathrm{{p}}\) initial velocity model with respect to the P-wave impedance \(V_\mathrm{{p}}\) initial velocity. The correlations obtained for each case are given in Table 3.
There is a good relationship between the ANNs’ estimations of \(V_\mathrm{{p}}\) and \(\rho \) in the reservoir area, and outside this, one can follow the lateral continuity of geobodies. There is also an interesting inverse relationship between \(\rho \) and \(V_\mathrm{{p}}\), taking into account that \(V_\mathrm{{p}}/\rho \) can be written as \(V_\mathrm{{p}}=(K/\rho )^{1/2}\), where K is the elastic modulus, in this case a P-stack seismic line. Using the initial velocities RMS velocity and ANN velocity, we have computed synthetic seismograms and show the results for three traces (one on the left-hand side of the 2-D section, one in the middle and a third one on the right-hand side) in Fig. 16. The black trace is the observed seismic trace, the red one corresponds to the RMS velocity and the blue one is the ANN velocity. To compute synthetics we use the \(\rho \) in Fig. 5. We follow the same procedure but we use the final velocities obtained after the inversion (RMS and ANN final velocities), shown in Figs. 8 and 12. The synthetic traces and their correlations are shown in Fig. 17. The histogram distributions of the relative error between synthetic and the real trace No. 1 before the inversion is shown in Fig. 18a. The same is shown in Fig. 18b but for the synthetic and real trace after the inversion using BLIMP and ANNs. The relative error is similar to that in Eq. (7) and is given by:
where \({\text {Synt}}_{\text {model}}\) is the synthetic trace generated with a given velocity model, and could be the initial velocity or the final velocity obtained after the inversion.
When analyzing the final velocity model obtained after the inversion, the interpreter can thus delineate the intercalation of sands (saturated with hydrocarbons) and shales that are undetected using current techniques. Since there is no ground truth available for the final velocity (or other petrophysical properties), we need the help of an interpreter.
Synthetic traces obtained from initial RMS velocity model \(V_\mathrm{{p}}\) (red). Synthetic traces obtained from the initial velocity model obtained with P-wave impedance using the BLIMP algorithm (green). Synthetic traces obtained from the initial velocity model obtained with the ANN (blue). The observed seismic traces are in black. We show three different stations (1, 386, 837) and the correlations between synthetic and observed real traces
Synthetic traces obtained after the inversion using the RMS-velocity model \(V_\mathrm{{p}}\) as initial model (red). Synthetic traces obtained from the initial velocity model obtained with P-wave impedance using the BLIMP algorithm (green). Synthetic traces obtained after the inversion using the ANN initial velocity model (blue). The observed seismic traces are in black. We show three different stations (1, 386, 837) and the correlations between synthetic and observed real traces
Histogram distributions of the relative error between synthetic and the real trace No. 1. a Using the initial velocities obtained with BLIMP and ANN we generate a synthetic and compute their relative errors. From these we plot the histogram distribution of these relative errors. This corresponds to the relative error of the synthetic trace No. 1 shown in Fig. 16. b The same as in (a), but instead of using the initial velocities, we use the final BLIMP and ANN velocities. This corresponds to the relative error of the synthetic trace No. 1 shown in Fig. 17 and ANN velocities obtained after the inversion
8 Conclusions
In the conducted experiments we have demonstrated that ANN estimations for \(\rho \), \(V_\mathrm{{p}}\) and \(V_\mathrm{{clay}}\) serve as a good starting model for the inversion process and help to produce a final velocity model that agrees with the interpretation of this area. The first-guess velocity given in Fig. 11 obtained with an ANN shows in some regions random heterogeneities with few structural features. However, the final velocity image after the inversion in Fig. 12 clearly captures the sequence of alternating sand and shale very well. We are directly comparing the petrophysical data with the high-resolution inversion data. In fact, the inversion improves the image resolution, enabling the detection of thin features that are undetectable by standard impedance inversion. Given the reasonable agreement range, we conclude that the proposed method, with the support of the petrophysical images (generated via ANNs), truly gives us the structural features (i.e. sequence of thin sand and shale) of the reservoir. When using the RMS velocity and the ANN density as starting models for the inversion, we obtained good fitting between the synthetic and observed traces. However, the final image shown in Fig. 8 does not capture the layered structure. This is because, as is well known, the inversion process is an ill-posed problem due to the lack of data. Contrary to, say, a medical tomography scan of the human body, where we have full 360\(^{\circ }\) illumination, in the seismic exploration world we can only illuminate at most 180\(^\mathrm {o}\). Consequently, there is not a unique solution when we do an inversion of seismic data. Accordingly, we need a skilled interpreter for further scrutiny of the results. The waveform inversion can provide velocity images with a high degree of resolution that can delineate important geological features in hydrocarbon reservoirs. We hope that the article makes the geophysical community aware of the potential that ANNs bring to build realistic initial velocity and density models for inversion algorithms. Future work will include the use of multi-scaling techniques taking advantage of the fact that the analytic solution is in the frequency domain. We could use the multi-scaling approach, where we start the inversion using low frequencies and continue the inversion process gradually increasing the frequency ranges. Moreover, the information from the three productive wells Tenerife-1, Tenerife-2 and Tenerife-3, will be included, plus a more complex 2-D/3-D modeling tool and perhaps, if it is available, the 3-D seismic data.
References
Aki, K., & Richards, P. G. (1980). Quantitative seismology, theory and methods. San Francisco: W. H Freeman.
Araya-Polo, M., Jennings, J., Adler, A., & Dahlke, T. (2018). Deep-learning tomography. The Leading Edge, 37, 58–66.
Azevedo-Guerra, L. (2009). Seismic attributes in hydrocarbon reservoir characterization. Master Thesis, Universidade de Aveiro, Department of Geosciences.
Backus, George E. (1962). Long-wave elastic anisotropy produced by horizontal layering. Journal of Geophysical Research, 67(11), 4427–4440.
Barnes, A. E. (2015). Hanbook of post-stack seismic attributes. Tulsa: SEG.
Chapman, C. H. (2003). Yet another elastic plane-wave, layer-matrix algorithm. Geophysical Journal International, 154, 212–223.
Charalambous, C. (1992). Conjugate gradient algorithm for efficient training of artificial neural networks IEE Proceedings G Circuits. Devices and Systems, 139, 301–310. https://doi.org/10.1049/ip-g-2.1992.0050.
Chopra, S., & Marfurt, K. (2007). Seismic attributes for prospect identification and reservoir characterization. Tulsa: Geophysical development Series Society of Exploration Geophysicists.
Claerbout, J. (1968). Synthesis of a layered medium from its acoustic transmission response. Geophysics, 33, 264–269.
Evans, D., & Jones, A. J. (2002). A proof of the Gamma test. Proceedings of the Royal Society of London A, 458, 2759–2799.
Ferguson, R. J., & Margrave, G. F. (1996). A simple algorithm for band-limited impedance inversion. Technical Report: CREWS, Research Report. Denver Colorado, USA.
Gan, S., Wang, S., Chen, Y., Qu, S., & Zu, S. (1996). Velocity analysis of simultaneous-source data using high-resolution semblance-coping with the strong noise. Geophysical Journal International, 204, 768–779.
Guyon, Isabelle, Gunn, Steve, Nikravesh, Masoud, & Zadeh, Lotfi A. (2006). Feature extraction: Foundations and applications (1st ed.). Springer: Springer.
Haskell, N. A. (1962). Crustal reflection of plane P and SV waves. Geophysical Journal International, 67, 4751–4767.
Haskell, N. A. (1960). Crustal reflection of plane SH waves. Journal of Geophysical Research, 65, 4147–4150.
Haskell, N. A. (1953). The dispersion of surface waves on multilayered media. Bulletin of the Seismological Society of America, 43, 17–34.
Iturrarán-Viveros, U., Muñoz-García, Andrés M., & Parra, J. O. (2018). Petrophysical seismic images obtained with Artificial Neural Networks as prior models for full-waveform inversion: A case study from Colombia. In Society of Exploration Geophysicists, 88th Annual International Meeting, SEG Expanded Abstracts, pp. 2236–2240.
Iturrarán-Viveros, U., Muñoz-García, A. M., Parra, J. O., & Tago, J. (2018b). Validated artificial neural networks in determining petrophysical properties: A case study from Colombia. Interpretation, 6, 1–14.
Iturrarán-Viveros, U., & Parra, J. O. (2014). Artificial neural networks applied to estimate permeability, porosity and intrinsic attenuation using seismic attributes and well-log data. Journal of Applied Geophysics, 107, 45–54.
Iturrarán-Viveros, U. (2012). Smooth regression to estimate effective porosity using seismic attributes. Journal of Applied Geophysics, 76, 1–12.
Jones, A. J. (2004). New tools in non-linear modelling and prediction. Computational Management Science, 1, 109–149.
Kennett, B. (1983). Seismic wave propagation in stratified media. Cambridge: Cambridge University Press.
Kennett, B., & Kerry, N. (1979). Seismic waves in a stratifed half-space. Geophysical Journal of the Royal Astronomical Society, 20, 557–583.
Li, S., Liu, B., Ren, Y., Chen, Y., Yang, S., Wang, Y., et al. (2019). Deep learning inversion of seismic data. IEEE Ttransactions on Image Processing In Press, 20, 1–12.
Lindsay, R., & Koughnet, R. V. (2001). Sequential Backus averaging: Upscaling well logs to seismic wavelengths. The Leading Edge, 20(2), 188–191.
Lineas, L., & Treitel, S. (1984). Tutorial: A review of least-squares inversion and its application to geophysical problems. Geophysical Prospecting, 32, 159–186.
Liu, Y. (2019). A comparison of machine learning methods for seismic inversion to estimate velocity and density, Canada, Calgary. Geoconvention, 20, 13–17.
Maulana, Z.L., Sapurto, O., & Latief, F. (2016). New modified band limited iimpedance (BLIMP) inversion method using envelope attribute. IOP conference series: Earth environ. 29.
Mavko, G., Mukerji, T., & Dvorkin, J. (2009). The rock physics handbook: Tools for seismic analysts of porous media (2nd ed.). Cambridge: Cambridge University Press.
More, J. (1977). The Levenberg–Marquardt Algorithm. Lecture Notes in Mathematics (pp. 105–116). Berlin: Springer.
Parra, J. O., Parra, J. S., & Necsoiu, M. (2019). Nonlinear inversion of subsidence signatures induced by tunnels detected with surface and remote sensing measurements. The Leading Edge, 38, 550–553.
Parra, J. O., Parra, J. S., & Iturrarán-Viveros, U. (2017). Waveform inversion of poststacked reflection seismic data with well log constrained using nonlinear optimization methods. The Leading Edge, 36, 306–309.
Parra, J. O., Iturrarán-Viveros, U., Parra, J. S., & Xu, P. C. (2015). Attenuation and velocity estimation using rock physics and neural network methods for calibrating reflection seismograms. Interpretation, 3, SA121–SA133.
Pujol, J. (2007). The solution of nonlinear inverse problems and the Levenberg–Marquardt method. Geophysics, 72, W1–W16.
Qi, Jie, Zhang, Bo, Lyu, Bin, & Marfurt, Kurt. (2020). Seismic attribute selection for machine-learning-based facies analysis. Geophysics, 85(2), O17–O35.
Raissi, M. P., & Perdikaris, G. E. Karniadakis. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686–707.
Santosa, F., & Symes, W. W. (1989). An analysts of least-squares velocity inversion. Society of Exploration Geophysicists Geophysical Monograph Series, 4, 154.
Scales, J. A. (1995). Theory of seismic imaging (1st ed.). New York: Springer.
Stefánsson, A., Končar, N., & Jones, A. J. (1997). A note on the Gamma test. Neural Computing and Applications, 5, 131–133.
Taner, M. (2001). Attributes revisited. Houston: Technical Report. Rock Solid Images.
Taner, M. (1997). Seismic trace attributes and their projected use in prediction of rocks properties and seismic facies. Houston: Technical Report. Rock Solid Images.
Taner, M.T., Schuelke, J., ODoherty, R., Baysal, B. (1994). Seismic attributes: Revisited. In SEG expanded abstracts, Tulsa Oklahoma USA, pp 1104–1106. https://doi.org/10.1190/1.1822709.
Tarantola, A. (2005). Inverse problem theory and methods for model parameter estimation (1st ed.). Philadelphia: SIAM.
Tarantola, A. (1984). Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49, 1259–1266.
Tarantola, A., & Valette, B. (1982). Generalized nonlinear inverse problems using least squares criterion. Reviews of Geophysics, 20, 219–232.
Tiab, D., & Donaldson, E. C. (2015). Petrophysics (4th ed.). Houston: Gulf Professional Publishing.
Tiwary, D. K., Bayuk, I. O., Vikhorev, A. A., & Chesnokov, E. M. (2009). Comparison of seismic upscaling methods: From sonic to seismic. Geophysics, 74(2), WA3–WA14.
Towsey, M., Alpsan, D. & Sztriha, L. (1995). Training a neural network with conjugate gradient methods. In IEEE international conference on neural networks, pp. 373–378.
Virieux, J., & Operto, S. (2006). An overview of full-waveform inversion in exploration geophysics. Geophysics, 76, WCC1.
Wang, Y. (2015). The Ricker wavelet and the Lambert W function. Geophysical Journal International, 200(1), 111–115.
Wenqing, L., Xiwen, W., & Bin, L. (2017). Study and application of velocity model building method for the areas with complicated structures. Relative fidelity processing of seismic data: Methods and applications (p. 357). New Jersey: Wiley.
Yang, F., & Ma, J. (2019). Deep-learning inversion: A next generation seismic velocity-model building method. Geophysics, 84, R583–R599.
Yangkang, C., Tingting, L., & Xiaohong, C. (2015). Velocity analysis using similarity-weighted semblance. Geophysics, 80, A75–A82.
Yilmaz, Ö. (2001). Seismic data analysis: Processing, inversion, and interpretation of seismic data. Houston: Society of Exploration Geophysicists.
Zheng, Y. (2019). Elastic pre-stack seismic inversion in stratified media using machine learning. EAGE (pp. 287–337). London: Elsevier Publishing Co.
Acknowledgements
We are grateful for the kind comments and suggestions from two anonymous reviewers. We thank Ecopetrol S.A. within the research program 0266-2013 Colciencias Ecopetrol, for providing the well and seismic data used in this research. We would like to thank J.O. Parra for fruitful discussion regarding the inversion using nonlinear least-squares. This work was partially supported by CONACYT México under Ciencia de Frontera project number 6655, PROINNOVA projects 251910, 241763; DGAPA-UNAM project number IN107720; funding from the European Union’s Horizon 2020 Programme under the ENERXICO Project (www.enerxico-project.eu), Grant agreement no. 828947; CONACYT-SENER-Hidrocarburos Grant agreement B-S-69926. This project has also received funding from the European Union’s Horizon 2020 programme under the Marie Sklodowska-Curie Grant agreement no. 777778. Part of this work was done while one of the authors (U.I-V.) was on a sabbatical leave from the National University of México at the Barcelona Super Computing Center in Barcelona Spain as a visiting researcher with support from DGAPA-UNAM. Furthermore, O.C.-R. has been 65% cofinanced by the European Regional Development Fund (ERDF) through the Interreg V-A Spain-France-Andorra program (POCTEFA2014-2020). POCTEFA aims to reinforce the economic and social integration of the French-Spanish-Andorran border. Its support is focused on developing economic, social and environmental cross-border activities through joint strategies favoring sustainable territorial development.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Here we show the algorithm that was used to generate the 1-D synthetic seismograms applying the Kennett algorithm with the implementation by Mavko et al. (2009) and the Matlab routine lsqnonlin for the 1-D inversion. We use either the initial RMS-velocity model obtained via a velocity analysis (see Fig. 7) or the initial velocity model obtained with the artificial neural networks (ANNs) (see Fig. 11). The inversion will modify only the velocity model to reduce the difference between the synthetic traces and the real acquired seismic data. For the density we use either the measured \(\rho \) from the well-log constant along the entire 2-D section or the \(\rho \) obtained with the ANNs. In addition, we include the layered structure determined by the volume of clay which provides two classes of facies, sands or shales, each layer with different thickness that varies according to its position in the seismic line.

Code availability: The Matlab code is freely available at the GitHub repository (https://github.com/Ursula-Iturraran) or by requesting the author (http://ursula@ciencias.unam.mx). Since the data shown in this paper are proprietary information, the data provided in the repository represent only an example that is not related to this information but is suitable to illustrate how to use this code. To train the ANN and apply the Gamma test, we have used an updated C version from the original WinGamma software that was published at: http://users.cs.cf.ac.uk/O.F.Rana/Antonia.J.Jones/. We used the BLIMP routine from the CREWES Matlab Toolbox to compute the initial \(V_\mathrm{{p}}\) model obtained via the P-wave impedance. This software is available at: https://www.crewes.org/ResearchLinks/FreeSoftware/.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iturrarán-Viveros, U., Muñoz-García, A.M., Castillo-Reyes, O. et al. Machine Learning as a Seismic Prior Velocity Model Building Method for Full-Waveform Inversion: A Case Study from Colombia. Pure Appl. Geophys. 178, 423–448 (2021). https://doi.org/10.1007/s00024-021-02655-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00024-021-02655-9
Keywords
- Artificial neural networks
- full-waveform inversion
- nonlinear least squares
- velocity-model building
- seismic attributes