Analytic Acoustic–Elastic Coupled Equations and Their Application in Vector-Wave-Based Imaging of Ocean Bottom 4C Data

Abstract

In conventional vector-wave-based elastic reverse-time migration, there are two types of artifacts: low-frequency artifacts and nonphysical artifacts. Vector-decomposition-based acoustic–elastic coupled equations are effective in suppressing nonphysical artifacts by using ocean bottom four component (4C) seismic data for receiver-side tensorial extrapolation. We introduce up/down-going wave separation into the vector-decomposition-based acoustic–elastic coupled equations, and deduce novel analytic acoustic–elastic coupled equations. With these novel equations, we can obtain the source-side and receiver-side up-going and down-going P/S-wave vectors in wavefield propagation, and effectively suppress both of the artifacts in vector-wave-based elastic reverse-time migration by combining receiver-side tensorial extrapolation and the decomposed vector-wave-based imaging conditions. Examples using synthetic data and field data are presented to illustrate the validity and effectiveness of our method.

1 Introduction

Vector-wave-based, elastic reverse time migration (ERTM) can avoid polarity reversal in Pressure-Shear (PS) images (Wang et al. 2016a, b; Du et al. 2017), and has a significant advantage in imaging arbitrarily complex structures without dip limitations or shadow zones (Baysal et al. 1983; McMechan 1983), imaging in the presence of gas clouds (Thomsen et al. 1997; Knapp et al. 2001), detecting fractures (Li 1998), and improving the ability to characterize lithology (Shahraeeni et al. 2012). Despite these developments, some artifacts inevitably exist in the migrated images.

Low-frequency noise is a commonly observed artifact in reverse-time migration (RTM) with cross-correlation imaging. Yoon and Marfurt (2006), and Fletcher et al. (2006) pointed out that the low-frequency noise is caused by the cross-correlation of the waves with large opening angles, and proposed a method for limiting the propagation directions to suppress the low-frequency noise before applying the imaging condition. Low-frequency noise can also be suppressed by applying a low-frequency-cutting Laplacian filter to the stacked image after employing the imaging condition (Youn and Zhou 2001; Zhang and Sun 2009). Liu et al. (2011) decomposed the source-side and receiver-side wavefields into up-going and down-going waves, respectively, and then cross-correlated the source-side and receiver-side wavefields with opposite propagation directions to attenuate the low-frequency noise. However, some artifacts are generated by the back-scattering of incident and reflected waves in the up-down image (the up-going source-side wavefield cross-correlated with the down-going receiver-side wavefield), so only the down-up image (the down-going source-side wavefield cross-correlated with the up-going receiver wavefield) is used as the final imaging results (Fei et al. 2014; Hu and Wang 2015).

Next, some additional nonphysical artifacts exist in vector-wave-based ERTM. Ocean bottom four component (4C) seismic data can sufficiently suppress these nonphysical artifacts using receiver-side tensorial extrapolation based on vector-decomposition-based acoustic–elastic coupled equations (VD-AECEs) (Yu and Geng 2018).

Zhang et al. (2007) first proposed the use of complex traces for one-way acoustic wave equation propagation, which was used by Hu and Wang (2015) in an acoustic RTM to generate a down-up image. Wang et al. (2016a, b) extended this technique to elastic wavefield up/down-going wave separation, and thus applied it to the ERTM.

In this paper, to suppress the two types of artifacts in vector-wave-based ERTM using ocean bottom 4C data, we introduce complex traces into the VD-AECEs, and deduce novel analytic acoustic–elastic coupled equations (AAECEs). With the novel AAECEs, we can effectively realize complex 4C wavefield extrapolation and fulfill the up/down-going wave separation, in both the source-side and receiver-side extrapolations. Combining the decomposed cross-correlation imaging condition and receiver-side tensorial extrapolation using ocean bottom 4C data, both types of artifacts are effectively attenuated in vector-wave-based ERTM.

2 Method

2.1 Analytic Acoustic–Elastic Coupled Equations for Up/Down-Going Wave Separation

The VD-AECEs in three dimensional (3D) isotropic media for vector-wave-based ERTM using ocean bottom 4C seismic data are as follows (Appendix):

$$\rho \frac{\partial }{\partial t}{\mathbf{v}}^{p} = {\mathbf{L}}^{p} {\varvec{\uppsi}}\text{ ,}$$

(1)

$$\rho \frac{\partial }{\partial t}{\mathbf{v}}^{s} = {\mathbf{L}}^{s} {\varvec{\uppsi}}\text{ ,}$$

(2)

$$\frac{\partial }{\partial t}{\varvec{\uppsi}} = {\mathbf{CL}}^{T} {\mathbf{v}} + {\mathbf{f}}.$$

(3)

With the VD-AECEs, some nonphysical artifacts can be effectively suppressed in vector-wave-based ERTM by using ocean bottom 4C data for receiver-side tensorial extrapolation.

After the Hilbert transform of the original signal ${\mathbf{d}}$, a new signal $H\left[ {\mathbf{d}} \right]{\kern 1pt}$ can be obtained. Then a complex analytic trace ${\tilde{\mathbf{d}}}$ can be written as (Zhang et al. 2007):

$${\tilde{\mathbf{d}}} = {\mathbf{d}} + iH\left[ {\mathbf{d}} \right].$$

(4)

Similarly, we can construct the complex analytic source ${\tilde{\mathbf{f}}}$ and complex analytic wavefields ${\tilde{\mathbf{v}}}^{p} ,{\tilde{\mathbf{v}}}^{s} ,{\tilde{\mathbf{\psi }}}$ as:

$${\tilde{\mathbf{f}}} = {\mathbf{f}} + iH\left[ {\mathbf{f}} \right],$$

(5)

$${\tilde{\mathbf{v}}}^{p} = {\mathbf{v}}^{p} + iH\left[ {{\mathbf{v}}^{p} } \right],$$

(6)

$${\tilde{\mathbf{v}}}^{s} = {\mathbf{v}}^{s} + iH\left[ {{\mathbf{v}}^{s} } \right],$$

(7)

$${\tilde{\mathbf{\psi }}} = {\varvec{\uppsi}} + iH\left[ {\varvec{\uppsi}} \right].$$

(8)

In these equations, $H\left[ {\mathbf{f}} \right]$ is the Hilbert transform of ${\mathbf{f}}$, $H\left[ {{\mathbf{v}}^{p} } \right]$ is the Hilbert transform of ${\mathbf{v}}^{p}$, $H\left[ {{\mathbf{v}}^{s} } \right]$ is the Hilbert transform of ${\mathbf{v}}^{s}$, $H\left[ {\varvec{\uppsi}} \right]$ is the Hilbert transform of ${\varvec{\uppsi}}$, ${\tilde{\mathbf{v}}}^{p}$ is the complex analytic particle velocity P-wave vector, ${\tilde{\mathbf{v}}}^{s}$ is the complex analytic particle velocity S-wave vector, and ${\tilde{\mathbf{\psi }}}$ is the complex analytic stress vector.

Due to the linear characteristic of the wavefield propagators, we can obtain novel AAECEs:

$$\rho \frac{\partial }{\partial t}{\tilde{\mathbf{v}}}^{p} = {\mathbf{L}}^{p} {\tilde{\mathbf{\psi }}}\text{ ,}$$

(9)

$$\rho \frac{\partial }{\partial t}{\tilde{\mathbf{v}}}^{s} = {\mathbf{L}}^{s} {\tilde{\mathbf{\psi }}}\text{ ,}$$

(10)

$${\tilde{\mathbf{v}}} = {\tilde{\mathbf{v}}}^{p} + {\tilde{\mathbf{v}}}^{s} ,$$

(11)

$$\frac{\partial }{\partial t}{\tilde{\mathbf{\psi }}} = {\mathbf{CL}}^{T} {\tilde{\mathbf{v}}} + {\tilde{\mathbf{f}}}.$$

(12)

Taking the up/down-going wave separation of a particle velocity P-wave vector as example, we can obtain the up-going particle velocity P-wave vector ${\mathbf{v}}_{u}^{p}$ and the down-going particle velocity P-wave vector ${\mathbf{v}}_{d}^{p}$ as follows:

$${\mathbf{v}}_{u}^{p} \left( {x,y,z,t} \right) = \text{Re} \left\{ {F^{ - 1} \left( {{\tilde{\mathbf{V}}}^{ + } \left( {x,y,k_{z} ,t} \right)} \right)} \right\},$$

(13)

$${\tilde{\mathbf{V}}}^{ + } \left( {x,y,k_{z} ,t} \right) = \left\{ {\begin{array}{*{20}c} {{\tilde{\mathbf{V}}}\left( {x,y,k_{z} ,t} \right),{\kern 1pt} } & {{\text{if}}{\kern 1pt} {\kern 1pt} k_{z} \ge 0} \\ {0,} & {{\text{if}}{\kern 1pt} {\kern 1pt} k_{z} < 0} \\ \end{array} } \right.,$$

(14)

$${\mathbf{v}}_{d}^{p} \left( {x,y,z,t} \right) = \text{Re} \left\{ {F^{ - 1} \left( {{\tilde{\mathbf{V}}}^{ - } \left( {x,y,k_{z} ,t} \right)} \right)} \right\},$$

(15)

$${\tilde{\mathbf{V}}}^{ - } \left( {x,y,k_{z} ,t} \right) = \left\{ {\begin{array}{*{20}c} {0,} & {{\kern 1pt} {\text{if}}{\kern 1pt} {\kern 1pt} k_{z} \ge 0} \\ {{\tilde{\mathbf{V}}}\left( {x,y,k_{z} ,t} \right),} & {{\text{if}}{\kern 1pt} {\kern 1pt} k_{z} < 0} \\ \end{array} } \right. .$$

(16)

In this expression, $k_{z}$ is the apparent vertical wavenumber, $F^{ - 1}$ is the inverse Fourier operator, $\text{Re} {\kern 1pt} \{ \}$ represents the real part of the complex wavefields, and ${\tilde{\mathbf{V}}}\left( {x,y,k_{z} ,t} \right)$ is the Fourier transform of ${\tilde{\mathbf{v}}}\left( {x,y,z,t} \right)$ in the $z$ direction.

After the P/S wave decomposition and up/down-going wave separation, on both source and receiver sides, we can obtain the source-side down-going P-wave vector and receiver-side up-going P- and S-wave vectors, which can be used for vector-wave-based ERTM with the corresponding imaging conditions. Thus, we can avoid low-frequency imaging noise in the migrated sections.

2.2 Decomposed Cross-Correlation Imaging Conditions

Yu and Geng (2018) gave the vector-wave-based PP- and PS-waves cross-correlation imaging conditions:

$$I^{\text{pp}} \left( {\mathbf{x}} \right) = \int_{0}^{{t_{\hbox{max} } }} {{\mathbf{v}}_{s}^{p} \left( {{\mathbf{x}},t} \right) \cdot {\mathbf{v}}_{r}^{p} \left( {{\mathbf{x}},t} \right){\text{d}}t} ,$$

(17)

$$I^{\text{ps}} \left( {\mathbf{x}} \right) = \int_{0}^{{t_{\hbox{max} } }} {{\mathbf{v}}_{s}^{p} \left( {{\mathbf{x}},t} \right) \cdot {\mathbf{v}}_{r}^{s} \left( {{\mathbf{x}},t} \right){\text{d}}t} {\kern 1pt} {\kern 1pt} ,$$

(18)

where $I^{\text{pp}} ,I^{\text{ps}}$ are the vector-wave-based PP and PS images, respectively, and ${\mathbf{v}}_{s}^{p} \left( {{\mathbf{x}},t} \right),{\mathbf{v}}_{r}^{p} \left( {{\mathbf{x}},t} \right),{\mathbf{v}}_{r}^{s} \left( {{\mathbf{x}},t} \right)$ represent the forward-extrapolated P-wave particle velocity vector on the source sides, the back-extrapolated P-wave particle velocity vector and S-wave particle velocity vector on the receiver sides, respectively.

During the vector-wave-based ERTM, the source-side and receiver-side P- and S-wave vectors are decomposed into up-going and down-going components:

$${\mathbf{v}}_{s}^{p} \left( {{\mathbf{x}},t} \right) = {\mathbf{v}}_{sd}^{p} \left( {{\mathbf{x}},t} \right) + {\mathbf{v}}_{su}^{p} \left( {{\mathbf{x}},t} \right){\kern 1pt} {\kern 1pt} ,$$

(19)

$${\mathbf{v}}_{s}^{s} \left( {{\mathbf{x}},t} \right) = {\mathbf{v}}_{sd}^{s} \left( {{\mathbf{x}},t} \right) + {\mathbf{v}}_{su}^{s} \left( {{\mathbf{x}},t} \right){\kern 1pt} {\kern 1pt} ,$$

(20)

$${\mathbf{v}}_{r}^{p} \left( {{\mathbf{x}},t} \right) = {\mathbf{v}}_{rd}^{p} \left( {{\mathbf{x}},t} \right) + {\mathbf{v}}_{ru}^{p} \left( {{\mathbf{x}},t} \right){\kern 1pt} {\kern 1pt} ,$$

(21)

$${\mathbf{v}}_{r}^{s} \left( {{\mathbf{x}},t} \right) = {\mathbf{v}}_{rd}^{s} \left( {{\mathbf{x}},t} \right) + {\mathbf{v}}_{ru}^{s} \left( {{\mathbf{x}},t} \right){\kern 1pt} {\kern 1pt} ,$$

(22)

where, ${\mathbf{v}}_{s}^{p} \left( {{\mathbf{x}},t} \right){\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\mathbf{v}}_{s}^{s} \left( {{\mathbf{x}},t} \right)$ are the source-side particle velocity P- and S-wave vectors, ${\mathbf{v}}_{r}^{p} \left( {{\mathbf{x}},t} \right){\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\mathbf{v}}_{r}^{s} \left( {{\mathbf{x}},t} \right)$ are the receiver-side particle velocity P- and S-wave vectors, ${\mathbf{v}}_{sd}^{p} \left( {{\mathbf{x}},t} \right),{\mathbf{v}}_{su}^{p} \left( {{\mathbf{x}},t} \right)$ are the source-side down-going and up-going P-wave vectors,${\mathbf{v}}_{sd}^{s} \left( {{\mathbf{x}},t} \right),{\mathbf{v}}_{su}^{s} \left( {{\mathbf{x}},t} \right)$ are the source-side down-going and up-going S-wave vectors, ${\mathbf{v}}_{rd}^{p} \left( {{\mathbf{x}},t} \right),{\mathbf{v}}_{ru}^{p} \left( {{\mathbf{x}},t} \right)$ are the receiver-side down-going and up-going P-wave vectors,${\mathbf{v}}_{rd}^{s} \left( {{\mathbf{x}},t} \right),{\mathbf{v}}_{ru}^{s} \left( {{\mathbf{x}},t} \right)$ are the receiver-side down-going and up-going S-wave vectors.

Here, we use a new decomposed cross-correlation imaging conditions with the source-side down-going wavefields and receiver-side up-going wavefields as:

$$I_{du}^{pp} \left( {\mathbf{x}} \right) = \int_{0}^{{t_{\hbox{max} } }} {\left( {v_{z} \left( {{\mathbf{x}},t} \right)} \right)_{sd}^{p} \left( {v_{z} \left( {{\mathbf{x}},t} \right)} \right)_{ru}^{p} {\text{d}}t} ,$$

(23)

$$I_{du}^{ps} \left( {\mathbf{x}} \right) = \int_{0}^{{t_{\hbox{max} } }} {\left( {v_{x} \left( {{\mathbf{x}},t} \right)} \right)_{sd}^{p} \left( {v_{x} \left( {{\mathbf{x}},t} \right)} \right)_{ru}^{s} {\text{d}}t} ,$$

(24)

where $I_{du}^{pp} ,{\kern 1pt} {\kern 1pt} I_{du}^{ps}$ are the vector-wave-based PP and PS images using up/down-going separated wavefields, respectively; $\left( {v_{x} \left( {{\mathbf{x}},t} \right)} \right)_{sd}^{p} ,{\kern 1pt} {\kern 1pt} \left( {v_{z} \left( {{\mathbf{x}},t} \right)} \right)_{sd}^{p}$ are the horizontal and vertical components of source-side down-going P-wave velocity vector, respectively; $\left( {v_{x} \left( {{\mathbf{x}},t} \right)} \right)_{ru}^{s} ,{\kern 1pt} {\kern 1pt} \left( {v_{z} \left( {{\mathbf{x}},t} \right)} \right)_{ru}^{p}$ are the horizontal component of receiver-side up-going S-wave velocity vector and the vertical component of receiver-side up-going P-wave velocity vector, respectively.

For conventional vector-wave-based ERTM, the source-side wavefields $\left( {v_{x} \left( {{\mathbf{x}},t} \right)} \right)_{sd}^{p} ,{\kern 1pt} {\kern 1pt} \left( {v_{z} \left( {{\mathbf{x}},t} \right)} \right)_{sd}^{p}$ can be obtained by forward propagation with a given model and external force, while the receiver-side wavefields $\left( {v_{x} \left( {{\mathbf{x}},t} \right)} \right)_{ru}^{s} ,{\kern 1pt} {\kern 1pt} \left( {v_{z} \left( {{\mathbf{x}},t} \right)} \right)_{ru}^{p}$ are equal to the back-extrapolated wavefields with the three components of the receiver-side particle velocity records as the boundary conditions:

$${\mathbf{v}}\left( {{\mathbf{x}}_{r} ,t} \right) = \left[ {v_{x} \left( {{\mathbf{x}}_{r} ,t} \right),v_{y} \left( {{\mathbf{x}}_{r} ,t} \right),v_{z} \left( {{\mathbf{x}}_{r} ,t} \right)} \right]^{T} ,$$

(25)

where $v_{i} \left( {{\mathbf{x}}_{r} ,t} \right)$ is the receiver-side velocity at ${\mathbf{x}}_{r}$. Subscripts $i = x,{\kern 1pt} y,{\kern 1pt} {\kern 1pt} z$ identify the component of the $i_{\text{th}}$ velocity recordings. Ocean bottom 4C seismic data includes the fluid pressure $p\left( {{\mathbf{x}}_{r} ,t} \right)$ and the solid particle velocity vector ${\mathbf{v}}\left( {{\mathbf{x}}_{r} ,t} \right)$ at the seabed (Fig. 1). Yu et al. (2016, 2018) proposed to apply 4C data to the receiver-side tensorial extrapolation with the AECEs, which can effectively suppress artifacts in migrated profiles.

Fig. 1

Workflow of vector-wave-based PP and PS images using ocean bottom 4C data

Using the ocean bottom 4C records, we can construct the complex analytic 4C records $\tilde{v}_{x} \left( {{\mathbf{x}}_{r} ,t} \right),{\kern 1pt} {\kern 1pt} \tilde{v}_{y} \left( {{\mathbf{x}}_{r} ,t} \right),\tilde{v}_{z} \left( {{\mathbf{x}}_{r} ,t} \right),\tilde{p}\left( {{\mathbf{x}}_{r} ,t} \right)$:

$$\tilde{v}_{x} \left( {{\mathbf{x}}_{r} ,t} \right) = v_{x} \left( {{\mathbf{x}}_{r} ,t} \right) + iH\left[ {v_{x} \left( {{\mathbf{x}}_{r} ,t} \right)} \right]{\kern 1pt} {\kern 1pt} ,$$

(26)

$$\tilde{v}_{y} \left( {{\mathbf{x}}_{r} ,t} \right) = v_{y} \left( {{\mathbf{x}}_{r} ,t} \right) + iH\left[ {v_{y} \left( {{\mathbf{x}}_{r} ,t} \right)} \right]{\kern 1pt} {\kern 1pt} ,$$

(27)

$$\tilde{v}_{z} \left( {{\mathbf{x}}_{r} ,t} \right) = v_{z} \left( {{\mathbf{x}}_{r} ,t} \right) + iH\left[ {v_{z} \left( {{\mathbf{x}}_{r} ,t} \right)} \right]{\kern 1pt} {\kern 1pt} ,$$

(28)

$$\tilde{p}\left( {{\mathbf{x}}_{r} ,t} \right) = p\left( {{\mathbf{x}}_{r} ,t} \right) + iH\left[ {p\left( {{\mathbf{x}}_{r} ,t} \right)} \right]{\kern 1pt} {\kern 1pt} .$$

(29)

At the seabed, we have the boundary conditions:

$${\mathbf{\tilde{v}}}\left( {{\mathbf{x}}_{r} ,t} \right) = \left( {\begin{array}{*{20}l} {\tilde{v}_{x} \left( {{\mathbf{x}}_{r} ,t} \right)} \\ {\tilde{v}_{y} \left( {{\mathbf{x}}_{r} ,t} \right)} \\ {\tilde{v}_{z} \left( {{\mathbf{x}}_{r} ,t} \right)} \\ \end{array} } \right),{\mathbf{\tilde{\psi }}}\left( {{\mathbf{x}}_{r} ,t} \right) = \left( {\begin{array}{*{20}l} {\tilde{p}\left( {{\mathbf{x}}_{r} ,t} \right)} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right)$$

(30)

where ${\tilde{\mathbf{v}}}\left( {{\mathbf{x}}_{r} ,t} \right),{\tilde{\mathbf{\psi }}}\left( {{\mathbf{x}}_{r} ,t} \right)$, respectively, represent the complex analytic velocity vector and stress vector at the receiver-side position ${\mathbf{x}}_{r}$.

With the receiver-side complex analytic 4C wavefields tensorial extrapolation, nonphysical artifacts can be suppressed, and we can obtain high-quality elastic images.

Figure 1 shows the workflow of our method in vector-wave-based ERTM using ocean bottom 4C data. With the AAECEs, there are two key techniques in the process, including vectorial P/S decomposition and up/down-going wave separation.

3 Numerical Examples

We designed three synthetic examples and a field data example to test the feasibility of our method. The first is a homogenous isotropic elastic model which shows that we can realize vectorial P/S decomposition and up/down-going wave separation with the AAECEs. The second two-layer model illustrates that we can suppress artifacts in the vector-wave-based ERTM (PP and PS images) using the ocean bottom 4C data with our method, and we can thus obtain better imaging results compared to conventional methods. The third modified Marmousi2 model shows the effectiveness of our method in vector-wave-based ERTM of this complex model. Last, we use a field Ocean Bottom Seismometer (OBS) 4C data in East China Sea to verify the robustness of our method.

3.1 Numerical Test for a Homogenous Isotropic Elastic Model

We designed a 301 × 301 homogeneous isotropic elastic model to simulate the elastic wavefields using the AAECE with a grid increment of $h = 5{\text{m}}$ and a time increment of ${\text{d}}t = 0.5\;{\text{ms}}$. Snapshots of the simulated elastic wavefields are shown in Fig. 2. With the AAECEs, we can directly obtain eight components, including the horizontal up-going P-wave (Fig. 2c), horizontal down-going P-wave (Fig. 2e), horizontal up-going S-wave (Fig. 2g), horizontal down-going S-wave (Fig. 2i), vertical up-going P-wave (Fig. 2d), vertical down-going P-wave (Fig. 2f), vertical up-going S-wave (Fig. 2h), and the vertical down-going S-wave (Fig. 2j).

Fig. 2

Horizontal (a) and vertical (b) particle velocity components of the 2D elastic wave propagation in a homogeneous isotropic elastic medium; the up-going P-wave of horizontal (c) and vertical (d) particle velocity; the down-going P-wave of horizontal (e) and vertical (f) particle velocity; the up-going S-wave of horizontal (g) and vertical (h) particle velocity; the down-going S-wave of horizontal (i) and vertical (j) particle velocity

3.2 Numerical Test for a Two-layer Model

Two P- and S-wave velocity models with a constant density of $\rho = 1800{\kern 1pt} {\kern 1pt} {{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}$ are shown in Fig. 3. We simulated one-shot data for the vector-wave-based ERTM with a pure P-wave source located at $x = 1250{\kern 1pt} {\kern 1pt} {\text{m}}$ and $z = 0{\kern 1pt} {\kern 1pt} {\text{m}}$ (indicated by a black star), with a series of receivers located at $z = 200{\kern 1pt} {\kern 1pt} {\text{m}}$ (indicated by inverted triangles).

Fig. 3

The a P- and b S-wave velocity models. The star indicates the location of a physical pure P-wave source, where receivers were placed along the seabed to record the elastic wavefields, as indicated by the triangles

Figure 4a, b display the receiver-side vectorial and tensorial extrapolated vertical component of the P-wave velocity vector at different time steps, and Fig. 4c, d are the corresponding down-going components of Fig. 4a, b at the same time steps. Snapshots in Fig. 4a show that using only particle velocity measurements in conventional receiver-side vectorial extrapolation caused three types of nonphysical events (nonphysical events 1, 2, and 3 indicated by black arrows), which have been introduced in detail by Yu et al. (2016). Receiver-side tensorial extrapolation can help to suppress some nonphysical events (events 1 and 2) in Fig. 4b. Meanwhile, decomposed up-going wavefileds can also suppress some nonphysical events (events 1 and 3) in Fig. 4c. If we use both the receiver-side tensorial extrapolation and up/down-going wavefields decomposition for receiver-side 4C data back-extrapolation, three types of nonphysical events vanish in Fig. 4d.

Fig. 4

Series of snapshots of the a vectorial, b tensorial back-extrapolated receiver-side vertical component of P-wave velocity vector; c vectorial, d tensorial back-extrapolated receiver-side up-going vertical component of P-wave velocity vector. White lines represent the position of receiver sides, and the black arrows indicate three types of nonphysical events

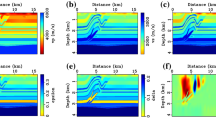
We can use the above four approaches to obtain the receiver-side back-extrapolated P-wave fields. Correspondingly, four vector-wave-based PP images can be obtained with the cross-correlation imaging conditions (Eqs. 17 and 23) in Fig. 5. Figure 5a shows the PP image obtained from the vector-wave-based ERTM using receiver-side vectorial extrapolation and the cross-correlation imaging condition (Eq. 17). Two types of artifacts (a1 and a2) are present in Fig. 5a (indicated by a white arrow). If we use the ocean bottom 4C data for receiver-side tensorial extrapolation, artifact a2 was strongly attenuated in the final result in Fig. 5b. If we decompose the source-side and receiver-side wavefields, and choose the source-side down-going P-wave vector and the receiver-side up-going P-wave vector for imaging, artifact a1 is suppressed in the final result shown in Fig. 5c. If we adopt the receiver-side tensorial extrapolation and decomposed cross-correlation imaging condition (Eq. 23) at the same time, both types of artifacts are strongly attenuated in the final result (Fig. 5d), which creates much clearer images and allows for a more accurate interpretation of subsurface structures.

Fig. 5

Single-shot PP images from the vector-wave-based ERTM a using the conventional method, b using only receiver-side tensorial extrapolation, c using only decomposed imaging condition (Eq. 23), and d using receiver-side tensorial extrapolation and decomposed imaging condition (Eq. 23) for the example in Fig. 3 with a pure P-wave source. Although the four methods can image the correct reflectors, artifacts a1 and a2 are clearly visible when using the conventional method

Nonphysical events 1, 2 and 3 (Fig. 6a) in S-wave extrapolation are similar to those of the corresponding nonphysical events in the P-wave extrapolation. Nonphysical events 1 and 2 are not present in the tensorial extrapolation (Fig. 6b), while nonphysical events 1 and 3 vanish in the up-going S-wave fields. Similarly, all three types of nonphysical events disappear in the back-extrapolated up-going S-wave with receiver-side tensorial extrapolation. Artifact a2 vanishes if we use ocean bottom 4C data for the receiver-side tensorial extrapolation with the AAECEs (Fig. 7b, d). Because we cut the direct-wave in the records for receiver-side extrapolation, artifact a1 is not observed in the PS images with the vector-wave-based cross-correlation imaging condition (Eq. 18) in Fig. 7a, c. We can obtain clearer PS images with our method using ocean bottom 4C data.

Fig. 6

Series of snapshots of the a vectorial, b tensorial back-extrapolated receiver-side horizontal component of S-wave velocity vector; c vectorial, d tensorial back-extrapolated receiver-side up-going horizontal component of S-wave velocity vector. White lines represent the position of receiver sides, and the black arrows indicate three types of nonphysical events

Fig. 7

Single-shot PS images produced by the vector-wave-based ERTM a using the conventional method, b using only receiver-side tensorial extrapolation, c using only decomposed imaging condition (Eq. 24), and d using receiver-side tensorial extrapolation and decomposed imaging condition (Eq. 24) for the example in Fig. 3 with a pure P-wave source. Because direct waves are suppressed before the receiver-side records extrapolation, artifact a1 is not observed in the PS image with the conventional method, and only artifact a2 is observed in the PS images with receiver-side vectorial extrapolation (a, c)

3.3 Numerical Test for the Truncated Marmousi2 Model

Another test was performed using synthetic elastic data from the truncated Marmousi2 model (Fig. 8) with a grid increment of $h = 2{\text{m}}$ and a time increment of ${\text{d}}t = 0.2\;{\text{ms}}$. Figure 8 depicts the P- and S-wave velocities, and the density models, which are composed of a water layer and a series of dipping layers. A pure P-wave source was fired at the sea surface (black stars in Fig. 8), and the wavefields were recorded by a horizontal array of receivers placed on the seabed (black inverted triangles). The data were simulated without free-surface-related multiples with a CPML boundary condition (Roden and Gedney 2000) at the top of the water layer.

Fig. 8

A truncated Marmousi2 model. a Density, b P-wave velocity, and c S-wave velocity. The star indicates the location of a physical pure P-wave source at the sea-surface, and the receivers are marked by triangles on the seabed

For comparison, we show PP and PS images produced by the receiver-side vectorial, tensorial extrapolation and conventional, decomposed cross-correlation imaging conditions. Figure 9a shows a PP image with receiver-side vectorial extrapolation and conventional vector-wave-based imaging condition (Eq. 17). Two types of artifacts were generated in the imaging result, which seriously degraded the image quality in Fig. 9a. Figure 9b shows a PP image with receiver-side tensorial extrapolation and conventional vector-wave-based imaging condition. Although some nonphysical artifacts (artifact a2) are suppressed in the final result, some low-frequency imaging noise still destroyed the image (indicated by black ellipses). Figure 9c shows a PP image with receiver-side vectorial extrapolation and decomposed vector-wave-based imaging condition. The low-frequency imaging noise disappeared, but some nonphysical artifacts were left in the image (indicated by white arrows). Most of the artifacts were suppressed in the PP image with receiver-side tensorial extrapolation and decomposed vector-wave-based imaging condition (Fig. 9d). Significant improvements with our new method are visible throughout the model, and both types of artifacts were almost completely suppressed.

Fig. 9

Single-shot PP images from the vector-wave-based ERTM a using the conventional method, b using only receiver-side tensorial extrapolation, c using only decomposed imaging condition (Eq. 23), and d using receiver-side tensorial extrapolation and decomposed imaging condition (Eq. 23)

The situation for the PS images is a little bit different. Only nonphysical artifacts were generated in the PS image from the receiver-side vectorial extrapolation (indicated by the white arrows in Fig. 10a, c), which are strongly attenuated in the PS images in Fig. 10b, d, providing a more accurate interpretation of subsurface structures.

Fig. 10

Single-shot PS images from the vector-wave-based ERTM a using the conventional method, b using only receiver-side tensorial extrapolation, c using only decomposed imaging condition (Eq. 24), and d using receiver-side tensorial extrapolation and decomposed imaging condition (Eq. 24)

In order to test our method’s susceptibility to noise, we added Gaussian random noise into the 4C records of the truncated Marmousi2 model with signal-to-noise ratios (SNR) of 5.0 and 2.0, respectively (Fig. 11), then used the 4C records with noise to obtain the PP and PS images from vector-wave-based ERTM with the decomposed cross-correlation imaging conditions (Fig. 12). Comparing the migrated results without noise (Figs. 9d and 10d) and the migrated results with noise (Fig. 12), we can see that our method is robust against the noise.

Fig. 11

The shot records of pressure component a without noise, b with SNR of 5.0, c with SNR of 2.0

Fig. 12

Single-shot images from the vector-wave-based ERTM using receiver-side tensorial extrapolation and the decomposed imaging conditions: a PP image containing Gaussian noise with SNR of 5.0, b PP image containing Gaussian noise with SNR of 2.0, c PS image containing Gaussian noise with SNR of 5.0, d PS image containing Gaussian noise with SNR of 2.0

3.4 Field Data Example

In 2017, we performed a 3D narrow azimuth field trial in the East China Sea, located approximately 425 km away from Shanghai. We choose to collect data from one OBS in this study, and the survey consisted of 284 shots, 37.5 m apart. The water depth of this region varies from 80 to 90 m, and the OBS located at (5.5, 0.08) km. We used the inverted P-wave velocity (Fig. 13) by Liu and Huang (2019) for ERTM. To build an elastic velocity model, we generated an S-wave velocity with the relationship $v_{s0} = {{v_{p0} } \mathord{\left/ {\vphantom {{v_{p0} } {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}$ based on a P-wave velocity model and a constant-density $\rho { = 1800}{\kern 1pt} {\kern 1pt} {{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }}$.

Fig. 13

Inverted P-wave velocity of the East China Sea the rectangle indicates the image zone in this study

Figure 14 shows the single-shot migrated results of PP from vector-wave-based ERTM using 3C of velocity records (Fig. 14a), using the pressure component (Fig. 14b), and using 4C data (Fig. 14c, d). The underground structures cannot be imaged when using only 3C of velocity records, because the S-wave energy is strong in the original 3C of velocity records. The strong S-wave energy destroyed the image quality of the PP wave in Fig. 14a. Comparing to the image in Fig. 14a, most of the structures can be correctly imaged in the other three cases (Fig. 14b–d). However, some layers were destroyed due to the artifacts in Fig. 14b, c (indicated by white arrows). In Fig. 14d, with the receiver-side tensorial extrapolation using 4C data and the decomposed imaging condition, some artifacts were suppressed, and we can obtain the clearer image in Fig. 14d, which allows a more accurate interpretation of subsurface structures.

Fig. 14

Single-shot PP images from vector-wave-based ERTM a using only 3C of velocity, b using only the pressure component, c using 4C records for receiver-side tensorial extrapolation, and d using 4C records for receiver-side tensorial extrapolation and decomposed imaging condition (Eq. 23)

Figure 15 shows the single-shot migrated results of PS from vector-wave-based ERTM using 3C of velocity records (Fig. 15a), using the pressure component (Fig. 15b), and using 4C data (Fig. 15c, d), respectively. We obtain good PS images using 3C records (Fig. 15a) and 4C records (Fig. 15c, d). In Fig. 15b, because the pressure component does not contain an S-wave, the PS image with scalar extrapolation using the pressure component is not as clear as the others. Although most of the structures can be well imaged in Fig. 15a, c, significant improvements with receiver-side tensorial extrapolation using 4C records and decomposed imaging condition are visible in Fig. 15d, especially in the zones indicated by the arrows.

Fig. 15

Single-shot PS images from vector-wave-based ERTM a using only 3C records, b using only the pressure component, c using 4C records for receiver-side tensorial extrapolation, and d using 4C records for receiver-side tensorial extrapolation and decomposed imaging condition (Eq. 24)

4 Discussion and Conclusions

In the field data example from the East China Sea, the results show that the influence of low-frequency noise is relatively small in the migrated results with the conventional method, and the improvement is not apparent with the up-/down-going wave separation at the source- and receiver-side. The damage of nonphysical noise on the migrated results is obvious. We used OBS 4C data for receiver-side tensorial extrapolation, and some nonphysical noise was suppressed. Combining the decomposed cross-correlation imaging conditions, we can provide significant improvements to the images. However, we provided only single-shot imaging results, and would expect improvements in multi-shot stacked imaging results if dense OBS data become available.

A novel method is proposed to suppress artifacts in vector-wave-based ERTM using ocean bottom 4C data. Novel AAECEs were constructed by introducing vectorial P/S decomposition and up/down-going wave separation. With the AAECEs, ocean bottom 4C data can be used for receiver-side tensorial extrapolation, and when combined with the decomposed cross-correlation imaging condition, both low-frequency and nonphysical artifacts are effectively suppressed in the vector-wave-based ERTM. We also would like to point out that our method is not only robust to random noise, but also works in field data.

Appendix: Acoustic–Elastic Coupled Equations for Vectorial P/S Wave Decomposition

Yu et al. (2016) deduced the AECE in 3D isotropic media, and the equations of motion:

$$\rho \frac{\partial }{\partial t}{\mathbf{v}} = {\mathbf{L\psi }}\text{ },$$

(31)

and the equations of stress–strain:

$$\frac{\partial }{\partial t}{\varvec{\uppsi}} = {\mathbf{CL}}^{T} {\mathbf{v}} + {\mathbf{f}}\text{ },$$

(32)

where ${\mathbf{v}} = \left( {v_{x} ,v_{y} ,v_{z} } \right)^{T}$ is the particle velocity vector, ${\varvec{\uppsi}} = \left( {p,\tau_{xx}^{s} ,\tau_{yy}^{s} ,\tau_{zz}^{s} ,\tau_{xy}^{s} ,\tau_{xz}^{s} ,\tau_{yz}^{s} } \right)^{T}$ is a vector composed of the components of the isotropic stress and the deviatoric stress, $\rho$ is the density, $t$ is the time, ${\mathbf{L}}$ is the partial differential operator matrix, and ${\mathbf{C}}$ is the stiffness of a 3D isotropic medium presented in terms of bulk $K$ and shear modulus $\mu$. In Eqs. 31 and 32:

$${\mathbf{L}} = \left( {\begin{array}{*{20}c} { - \frac{\partial }{\partial x}} & {\frac{\partial }{\partial x}} & 0 & 0 & {\frac{\partial }{\partial y}} & {\frac{\partial }{\partial z}} & 0 \\ { - \frac{\partial }{\partial y}} & 0 & {\frac{\partial }{\partial y}} & 0 & {\frac{\partial }{\partial x}} & 0 & {\frac{\partial }{\partial z}} \\ { - \frac{\partial }{\partial z}} & 0 & 0 & {\frac{\partial }{\partial z}} & 0 & {\frac{\partial }{\partial x}} & {\frac{\partial }{\partial y}} \\ \end{array} } \right)\text{ },$$

(33)

and

$${\mathbf{C}} = \left( {\begin{array}{*{20}c} K & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{4\mu }{3}} & { - \frac{2\mu }{3}} & { - \frac{2\mu }{3}} & 0 & 0 & 0 \\ 0 & { - \frac{2\mu }{3}} & {\frac{4\mu }{3}} & { - \frac{2\mu }{3}} & 0 & 0 & 0 \\ 0 & { - \frac{2\mu }{3}} & { - \frac{2\mu }{3}} & {\frac{4\mu }{3}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \mu & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \mu & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \mu \\ \end{array} } \right)\text{ }.$$

(34)

The particle velocity of a full-wave vector ${\mathbf{v}} = \left( {v_{x} ,v_{y} ,v_{z} } \right)$ can be decomposed into the particle velocity vectors of P- and S-waves, as follows:

$${\mathbf{v}} = {\mathbf{v}}^{p} + {\mathbf{v}}^{s} {\kern 1pt} .$$

(35)

In these expressions, the particle velocity vector of a P-wave is ${\mathbf{v}}^{p} = \left( {v_{x}^{p} ,v_{y}^{p} ,v_{z}^{p} } \right)$, while that of an S-wave is ${\mathbf{v}}^{s} = \left( {v_{x}^{s} ,v_{y}^{s} ,v_{z}^{s} } \right)$. Thus, Eq. 31 can also be decomposed into the P- and S-waves vector equations of motion (Yu and Geng 2018), as follows:

$$\rho \frac{\partial }{\partial t}{\mathbf{v}}^{p} = {\mathbf{L}}^{p} {\varvec{\uppsi}}\text{ },$$

(36)

$$\rho \frac{\partial }{\partial t}{\mathbf{v}}^{s} = {\mathbf{L}}^{s} {\varvec{\uppsi}}\text{ }\text{.}$$

(37)

In Eqs. 36 and 37, ${\mathbf{L}}^{p} ,{\kern 1pt} {\kern 1pt} {\mathbf{L}}^{s}$ are the partial differential operator matrices of the vectorial P- and S-waves, respectively. Thus, in Eqs. 36 and 37:

$${\mathbf{L}}^{p} = \left[ {\begin{array}{*{20}c} { - \frac{3K + 4\mu }{3K}\frac{\partial }{\partial x}} & 0 & 0 & 0 & 0 & 0 & 0 \\ { - \frac{3K + 4\mu }{3K}\frac{\partial }{\partial y}} & 0 & 0 & 0 & 0 & 0 & 0 \\ { - \frac{3K + 4\mu }{3K}\frac{\partial }{\partial z}} & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} ,$$

(38)

and

$${\mathbf{L}}^{s} = \left[ {\begin{array}{*{20}c} {\frac{4\mu }{3K}\frac{\partial }{\partial x}} & {\frac{\partial }{\partial x}} & 0 & 0 & {\frac{\partial }{\partial y}} & {\frac{\partial }{\partial z}} & 0 \\ {\frac{4\mu }{3K}\frac{\partial }{\partial y}} & 0 & {\frac{\partial }{\partial y}} & 0 & {\frac{\partial }{\partial x}} & 0 & {\frac{\partial }{\partial z}} \\ {\frac{4\mu }{3K}\frac{\partial }{\partial z}} & 0 & 0 & {\frac{\partial }{\partial z}} & 0 & {\frac{\partial }{\partial x}} & {\frac{\partial }{\partial y}} \\ \end{array} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} .$$

(39)

Using Eqs. 36 and 37 instead of Eq. 31, we can realize vectorial P- and S-wave propagation.