1 Introduction

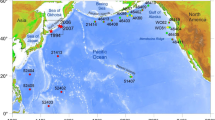
A large earthquake (Mw 6.9) occurred at the outer rise of the Middle America trench off El Salvador and Nicaragua on November 24, 2016 (Fig. 1). The Global CMT solution shows that the mechanism of the earthquake was a normal fault type (strike = 127°, dip = 50°, rake = − 89°) with a centroid depth of 12 km and the seismic moment of 3.16 × 1019 Nm (Mw 6.9). A tsunami warning was issued along the coast of Nicaragua by the Nicaraguan Institute of Territorial Studies (INETER). A small tsunami was generated by the earthquake and was detected by only one ocean bottom pressure sensor, DART 32411 in Fig. 1. No damage was reported along the coast.

Fig. 1
figure 1

A map of the tsunami computational area with the epicenters (stars) and mechanisms of the 2012 and 2016 El Salvador–Nicaragua earthquakes. A diamond shows the location of the ocean bottom pressure sensor, DART 32411

Full size image

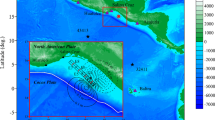
A large underthrust earthquake (Mw 7.3) occurred on August 27, 2012 near the 2016 earthquake (Fig. 2). The slip distribution of the 2012 earthquake was estimated using teleseismic body waves by Ye et al. (2013) and determined that a large slip occurred at the plate interface near the trench. Ye et al. (2013) also estimated a low radiated seismic energy ratio to the seismic moment (Er/M0) of 1.85 × 10−6 and suggested that this earthquake was a tsunami earthquake. Borrero et al. (2014) also concluded that the earthquake was a tsunami earthquake by analyzing the tsunami heights along the coast. Because the mechanism of the 2016 earthquake occurred in the outer-rise was a normal fault type, the 2016 event could be triggered by the 2012 earthquake which released the stress at the plate interface (Fig. 2).

Fig. 2
figure 2

A large slip area (a green rectangular) of the 2012 underthrust earthquake estimated by Ye et al. (2013) and the fault model (a red rectangular) of the 2016 outer-rise earthquake estimated in this study

Full size image

Previously, Christensen and Ruff (1988) suggested that in the coupled subduction zone, including Central America, tensional outer-rise earthquakes occurred after large underthrust earthquakes at the plate interface. The most recent significant sequence is the occurrence of the 2007 outer-rise Kurile earthquake (Mw 8.0) after the 2006 underthrust Kurile earthquake (Mw 8.3) (Fujii and Satake 2008; Tanioka et al. 2008). Because the outer-rise event occurred at shallow depth with a high angle fault, the tsunami contains much higher frequency component than those tsunamis caused by typical underthrust earthquakes. Toh et al. (2011) shows that the far-field observed tsunami generated by the 2007 Kurile outer-rise earthquake had a dispersive character, but the that generated by the 2006 Kurile underthrust earthquake did not.

A dispersive character of tsunamis caused by intraplate earthquakes was studied using three-dimensional tsunami simulation method by Saito and Furumura (2009). They concluded that the observed dispersive tsunami generated by the 2004 off Kii peninsula earthquake (Mw 7.4), intraplate earthquake occurred near the Nankai trough, was well modeled by the three-dimensional Navier–Stokes simulation and equally well modeled by the two-dimensional linear Boussinesq simulation but not by the linear long wave simulation. This indicates that intraplate earthquakes, including outer-rise events occurred near a trench, easily generate a short-wavelength deformation in a deep ocean and dispersive tsunamis.

The tsunami generated by the 2016 El Salvador–Nicaragua outer-rise earthquake had a dispersive character (Fig. 3). In this paper, the dispersive tsunami is modeled using appropriate tsunami numerical simulation methods. The source parameters of the earthquake are extracted from a dispersive character of the observed tsunami waveform.

Fig. 3
figure 3

A tsunami waveform at the ocean bottom pressure sensor, DART 32411 in Fig. 1. In this waveform, the tidal components have been eliminated from the original waveforms

Full size image

2 Data and Fault Model

A tsunami waveform in Fig. 3 is obtained from the original observed waveform at an ocean bottom pressure sensor, DART 32411 shown in Fig. 1, by eliminating the tide estimated using the polynomial fitting technique. The sampling rate of the waveform is 15 s. A dispersive tsunami is clearly shown in Fig. 3 at about 60 min after the origin time of the earthquake.

To calculate the initial condition of the tsunami simulation, the Global CMT mechanism of the earthquake, strike = 127°, dip = 50°, and rake = − 89°, and a centroid depth of 12 km are used as the fault parameters of the earthquake. Because the mechanism is the pure normal fault type with a dip angle of about 45°, the calculated initial conditions are almost the same for two fault planes of the CMT solution (Fig. 2). Therefore, we arbitrary chose one of those fault planes. The fault length, L, and width, W, are calculated from scaling relationships for normal fault earthquakes described by Blaser et al. (2010). The corresponding relationships are \(\log_{10} L = - \,1.61 + 0.46\,M_{\text{w}}\) for the fault length and \(\log_{10} W = - \,1.08 + 0.34\,M{\text{w}}\) for the fault width. The fault length and width is calculated to be 36.6 and 18.4 km, respectively, for the moment magnitude of 6.9. The vertical ocean bottom deformation due to the earthquake is computed from the above fault model using the equations of Okada (1985). This vertical deformation is used as the tsunami initial surface deformation.

3 Tsunami Numerical Simulation Methods

To compute a dispersive tsunami numerically, the linear Boussinesq equations are needed to be solved with an implicit scheme (e.g., Saito and Furumura 2009; Tanioka 2000). However, Imamura et al. (1990) developed a simple technique to use a numerical dispersion error caused by a finite difference scheme as a dispersion term in the Boussinesq equations. Using that technique, a dispersive tsunami is computed by solving the linear long wave equations instead of the linear Boussinesq equations. The numerical dispersion for the finite difference scheme is related to a grid spacing (\(\Delta x\)) and a time step \((\Delta t)\). Then, the condition to describe a dispersion term with a numerical dispersion is called Imamura number, Im,

$${\text{Im}} = \frac{\Delta x}{2d}\sqrt {1 - c_{0}^{2} \left( {\frac{\Delta t}{\Delta x}} \right)^{2} } \approx 1,$$
(1)

where d is the ocean depth and \(c_{0} = \sqrt {gd}\) is the phase velocity. In this study, the average ocean depth is about 3 km, and a time step \((\Delta t)\) is 2 s. By choosing a grid spacing (\(\Delta x\)) of 3 arc-minutes, Imamura number, Im, becomes 0.93. Therefore, first, we solve the linear long wave equations using a finite difference scheme with a staggered grid system of 3 arc-minutes grid spacing to model a dispersive tsunami. The 3 arc-minutes grid bathymetry data are made from the General Bathymetry Chart of the Oceans (GEBCO) dataset of 30 arc-seconds grid spacing.

Next, for more accurate simulation of a dispersive tsunami, the linear Boussinesq equations are numerically solved using a finite difference scheme with a staggered grid system (shown in Yamanaka et al. 2017). The governing equations are as follows (Goto 1991):

$$\frac{\partial \eta }{\partial t} + \frac{1}{R\cos \lambda }\left[ {\frac{\partial }{\partial \lambda }M\cos \lambda + \frac{\partial N}{\partial \theta }} \right] = 0,$$
(2)
$$\frac{\partial M}{\partial t} + \frac{gh}{R}\frac{\partial \eta }{\partial \lambda } = - fN + \frac{1}{R}\left[ {\frac{\partial }{\partial \lambda }\left\{ {\frac{{h^{3} }}{3}F_{1} + \frac{{h^{2} }}{2}F_{2} } \right\} - \frac{\partial h}{\partial \lambda }\left\{ {\frac{{h^{2} }}{2}F_{1} + hF_{2} } \right\}} \right],$$
(3)
$$\frac{\partial N}{\partial t} + \frac{gh}{R\cos \lambda }\frac{\partial \eta }{\partial \theta } = fM + \frac{1}{R\cos \lambda }\left[ {\frac{\partial }{\partial \theta }\left\{ {\frac{{h^{3} }}{3}F_{1} + \frac{{h^{2} }}{2}F_{2} } \right\} - \frac{\partial h}{\partial \theta }\left\{ {\frac{{h^{2} }}{2}F_{1} + hF_{2} } \right\}} \right],$$
(4)
$$F_{1} = \frac{1}{R\cos \lambda }\left\{ {\frac{{\partial^{2} }}{\partial t\partial \lambda }(u\cos \lambda ) + \frac{{\partial^{2} v}}{\partial t\partial \theta }} \right\},$$
(5)
$$F_{2} = \frac{1}{R\cos \lambda }\left\{ {\frac{\partial }{\partial t}\left( {u\cos \lambda \frac{\partial h}{\partial \lambda }} \right) + \frac{\partial }{\partial t}\left( {v\frac{\partial h}{\partial \theta }} \right)} \right\},$$
(6)

where η is the water surface elevation, M (= uh) and N (= vh) are the fluxes in the λ and θ directions, u and v are the velocities in the λ and θ directions, h is the still ocean depth, g is the acceleration due to gravity, R is the radius of the Earth, f is the Coriolis parameter, λ is the latitude, θ is the longitude, and t is the time. The linear long wave equations are obtained using the above equations with an assumption that F1 and F2 are zero. The linear long wave and the Boussinesq equations were discretized based on the concepts of Goto et al. (1997) and Saito et al. (2014). The General Bathymetry Chart of the Oceans (GEBCO) dataset of 30 arc-seconds grid spacing was used for this tsunami numerical simulation.

4 Results

The dispersive tsunami is numerically computed using the simple method developed by Imamura et al. (1990) with the 3 arc-minutes grid spacing, and using the Boussinesq equations with the 30 arc-seconds grid spacing. For comparison, the tsunami is computed using the linear long wave equations with the 30 arc-seconds grid spacing. First, a slip amount of 1 m is assumed in those simulations to compare dispersive characters of tsunami waveforms. In Fig. 4, the tsunami waveform observed at DART 32411 in Fig. 1 is compared with three computed tsunami waveforms. The tsunami computed using the linear long wave equations does not explain the dispersive character of the observed tsunami waveform, and arrives at the station faster than the observed one. The tsunami computed using the simple method with Imamura number (Imamura et al. 1990) explains the dispersive tsunami, and arrives at the station at the same time as the observed one. The tsunami computed using the Boussinesq equations well explains the dispersive tsunami, and arrives at the station at the same time as the observed one.

Fig. 4
figure 4

Comparisons of the observed and computed tsunamis, a computed tsunami using the linear long wave equations, b computed tsunami using Imamura number (Imamura et al. 1990), c computed tsunami using the linear Boussinesq equations, and d computed tsunami using the linear Boussinesq equations with the estimated slip amount of 0.74 m

Full size image

Next, the slip amount of 0.74 m is calculated by comparing the amplitudes of the first negative and next large positive observed waves with the computed ones using the Boussinesq equation (Fig. 4d). The observed dispersive tsunami waveform is well explained by the computed one. The seismic moment is calculated to be 3.37 × 1019 Nm (Mw 6.9) by assuming a rigidity of 6.7 × 1010 N/m2 which is a typical amount for outer-rise earthquakes (White et al. 1992; Shaw 1994). This seismic moment is similar to 3.16 × 1019 Nm (Mw 6.9) estimated in the Global CMT catalog.

Finally, we try to find the effect of the fault size on the dispersive character of tsunami and the seismic moment (or the slip amount). Previously, the fault length of 36.6 km and the fault width of 18.4 km are calculated using the scaling relationship for normal fault earthquakes described by Blaser et al. (2010). In this analysis, we keep the ratio of the fault length (L) and width (W) to be L:W = 2:1. Then, the fault size (L and W) is varied (L:W = 20 km:10 km, 30 km:15 km, 40 km:20 km, 50 km:25 km, and 60 km:30 km). The other fault parameters (strike, dip angle, rake, and the central location) are the same as those of the previous simulation. Tsunamis are again numerically computed using the linear Boussinesq equations. Figure 5 shows the comparisons of the observed tsunami waveform with the computed ones from the above five different fault sizes. The slip amount of each fault model is estimated by comparing the amplitudes of the first large positive and the next negative observed waves with the computed ones. Root-mean-square (RMS) residuals for observed and computed waveforms between 60 and 100 min after the origin time of the earthquake are calculated for five fault models and shown in Fig. 5. The computed tsunami from the fault model with a fault length of 20 km has more dispersive character than the observed tsunami as shown in Fig. 5a. The computed tsunamis from the fault models with fault lengths of 50 and 60 km have less dispersive character than the observed one (Fig. 5d, e). Finally, the computed tsunami from the fault model with a fault length of 30 km well explains the dispersive character of the observed tsunami (Fig. 5b). The RMS residual of 0.00178 m is the smallest for the computed tsunami from the fault model with a fault length of 30 km. Figure 6 shows a relationship of the seismic moment calculated from the slip amount of each fault model to the fault length (L). The calculated seismic moment of 3.16 × 1019 Nm for the best fault model with a fault length of 30 km is the same as the estimation in the Global CMT catalog. Figure 7 shows two snapshots of tsunami propagations using both the linear Boussinesq equations and the linear long wave equations at 30 min after the origin time of the earthquake. The dispersive character of tsunami in all direction in the deep ocean is clearly seen in the snapshot for the liner Boussinesq simulation, but that is not seen in the snapshot for the linear long wave simulation.

Fig. 5
figure 5

Comparisons of the observed and computed tsunamis using the linear Boussinesq equations, a for the fault length of 20 km and width of 10 km, b for the fault length of 30 km and width of 15 km, c for the fault length of 40 km and width of 20 km, d for the fault length of 50 km and width of 25 km, and e for the fault length of 60 km and width of 30 km. The RMS residual of observed and computed waveforms between 60 and 100 min for each fault model is also shown

Full size image
Fig. 6
figure 6

A relationship of the seismic moment calculated from the slip amount of each fault model to the fault length (L)

Full size image
Fig. 7
figure 7

Two snapshots of tsunami propagations using both the linear Boussinesq equations (left) and the linear long wave equations (right) at 30 min after the origin time of the earthquake. Contours show the ocean depth. The contour interval is 1000 m. Red rectangles are the estimated fault model of the 2016 outer-rise earthquake

Full size image

5 Conclusions

The dispersive tsunami observed at the ocean bottom pressure sensor, DART 32411 in Fig. 1 was well simulated using the linear Boussinesq equations. The technique developed by Imamura et al. (1990) to use a numerical dispersion error caused by a finite different scheme for a dispersion term in the Boussinesq equations was also worked. From the dispersive character of tsunami waveform, the fault length and width was estimated to be 30 and 15 km, respectively (shown in Fig. 2). The seismic moment was calculated to be 3.16 × 1019 Nm which is the same as the estimation in the Global CMT catalog. The dispersive tsunami observed in the deep ocean caused by the 2016 outer-rise El Salvador–Nicaragua earthquake constrained the fault size and the slip amount or the seismic moment of the event.