Abstract
On September 8, 2017 (UTC), a normal-fault earthquake occurred 87 km off the southeast coast of Mexico. This earthquake generated a tsunami that was recorded at coastal tide gauge and offshore buoy stations. First, we conducted a numerical tsunami simulation using a single-fault model to understand the tsunami characteristics near the rupture area, focusing on the nearby tide gauge stations. Second, the tsunami source of this event was estimated from inversion of tsunami waveforms recorded at six coastal stations and three buoys located in the deep ocean. Using the aftershock distribution within 1 day following the main shock, the fault plane orientation had a northeast dip direction (strike \(= 320^{\circ }\), dip \(= 77^{\circ }\), and rake \(=-92^{\circ }\)). The results of the tsunami waveform inversion revealed that the fault area was 240 km × 90 km in size with most of the largest slip occurring on the middle and deepest segments of the fault. The maximum slip was 6.03 m from a 30 × 30 km2 segment that was 64.82 km deep at the center of the fault area. The estimated slip distribution showed that the main asperity was at the center of the fault area. The second asperity with an average slip of 5.5 m was found on the northwest-most segments. The estimated slip distribution yielded a seismic moment of \(2.9 \times 10^{21}\) Nm (Mw = 8.24), which was calculated assuming an average rigidity of \(7\times 10^{10}\) N/m2.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
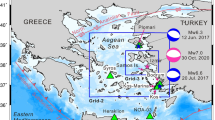
On September 8, 2017, at 04:49:18 UTC (September 7, 23:49:18 local time), a magnitude 8.2 earthquake occurred 87 km off the southeast coast of Mexico according to the National Seismological Service (SSN) of Mexico located at the Universidad Autónoma de Mexico (UNAM). The epicenter of this earthquake was located at 14.85°N 94.11°W with a focal depth of 58 km (SSN). This event was located near the Tehuantepec seismic gap, an area that has been significantly quiet in terms of large earthquakes for over 100 years and where no significant earthquake has occurred since the 1993 Mw7.2 shock (Singh et al. 1981, 2008) (Fig. 1). This earthquake struck the Gulf of Tehuantepec in Mexico. The earthquake is known as the Chiapas earthquake or the Pijijiapan earthquake of 2017, and it was felt from the Oaxaca and Chiapas regions in the south to the center of Mexico in the capital. This event is the most powerful earthquake in Mexico since the 1985 Michoacan earthquake in Mexico City (Mendoza 1993) and the 1932 Jalisco earthquake (Farreras and Sanchez 1991; Ramírez-Herrera et al. 2014). Along the Pacific coast of Mexico, there are two distinctly defined seismic gaps: the Tehuantepec and Guerrero gaps. The latter gap has been studied in detail by previous researchers (e.g., Kostoglodov et al. 2001; Cavalié et al. 2013; Bekaert et al. 2015). The main reason for such studies is because this gap represents a high hazard to nearby Mexico City (Mori et al. 2017). The tectonic setting around the epicenter is defined by the subduction of the oceanic Cocos plate beneath the North American plate (Fig. 1) with a rate of ∼ 4.8 cm/year (Bravo et al. 2004). Another essential characteristic of this region is the Tehuantepec ridge that transversely intersects the Mexican trench (Manea et al. 2017). The mechanism was an intraplate normal-fault earthquake. Its epicenter was located outside of the Tehuantepec gap; the recorded aftershocks, however, occurred mainly within the gap (Fig. 1). Furthermore, although this earthquake occurred near the subduction zone, it is of particular interest that it was along a high-angle, northeast dip direction and normal fault within the Cocos Plate rather than a regular megathrust earthquake along the Middle Americas. Thus, tsunami forecasting was a particular challenge, since forecasting methods are generally developed for interplate thrust earthquakes in subduction zones.
Rupture area of the main historical earthquakes along the Pacific coast of Mexico (light red polygons). The dark red circles indicate the aftershock distribution within 1 day following the September 8, Mw8.2 earthquake (the red star shows the epicenter). The epicenter of the Mw7.1 earthquake that occurred on September 17 (UTC) is shown by the green star. The dashed lines bound the two seismic gaps (Guerrero and Tehuantepec) on this region
The earthquake triggered a tsunami that was reported by the Pacific Tsunami Warning Center (PTWC) with a maximum peak amplitude of 1.68 m at Puerto Chiapas in Mexico. The aftermath of this event, the ground shaking, left at least 98 people dead in Oaxaca, Chiapas and Tabasco. Previous studies have focused on the tsunami hazard risk on the Tehuantepec gap, and some of these researchs (Manea et al. 2017) have previously suggested that a magnitude Mw8.0 type earthquake could potentially occur in this area (Nishenko and Singh 1987). The rupture area of this event was located over the edge between the continental shelf and the continental slope, generating a complex bathymetry region for tsunami propagation.
2 Data
2.1 Tsunami Waveform Data
In this study, we utilize six coastal tide stations located in Mexico, four northwest of the source area and two southeast of the source area, and three nearby Deep-ocean Assessment and Reporting of Tsunamis (DART) pressure gauge stations located south of the tsunami source area (Fig. 2 and Table 1). The coastal tide data were downloaded from the Sea Level Station Monitoring Facility (IOC) website, and the DART data were downloaded from the National Data Buoy Center (NDBC) website. These data originally included the tsunami and the astronomical tide signals; the latter signal was removed through fitting a robust polynomial function. A three-point moving average filter is then applied to eliminate high-frequency noise from the tsunami signals. The original sampling of the waveform data was 1 and 5 min for coastal tide gauge and offshore buoy stations, respectively. For the inversion analysis, the DART data are resampled to a 1-min sampling interval. The tsunami amplitudes recorded at the DART stations are approximately 10–20 times smaller than those recorded at coastal gauges; thus, in the source inversion analysis, the DART data are weighted by 20 times (Fujii and Satake 2013).
Computational area. The green triangles show the locations of the coastal tide stations. The blue squares show the locations of the DART stations. The dashed lines plotted in 10-min intervals indicate the tsunami travel time propagation. The red star shows the epicenter of the 2017 Mw8.2 Mexico earthquake that occurred on September 8
2.2 Bathymetry Data
In the computational domain, the employed bathymetry data are resampled from the 30 arcsec grid resolution of GEBCO 2014 DEM (Weatherall et al. 2015). Figure 2 shows the computational domain for the tsunami simulation. For the DART stations, which are located in a deep open ocean, the bathymetry resolution is set to 30 arcsec. At coastal tide stations, where the tsunami signals strongly depend on the interaction of the incoming tsunami waves with the surrounding coastline, we construct a nested grid system of 6 and 12 arcsec for the tsunami numerical simulation. The finest bathymetry resolution (6 arcsec) is for the coastal stations around the source area (Puerto Angel, Huatulco, Salina Cruz, and Chiapas). A 12 arcsec resolution is used for the Lazaro and Acajutla stations. Furthermore, the coastline around all coastal stations was manually digitized from the latest optical satellite image available from the Google Earth platform.
3 Methods
In this study, we first investigate the tsunami propagation features, focusing on the tsunami signals recorded at nearby tide gauge stations. For this purpose, we use a single-fault model to perform a nonlinear tsunami simulation. The fault geometry and location are set using the aftershock distribution within 1 day following the main shock and the backward propagation of tsunami travel computed from stations. Moreover, we also use the aftershock distribution to set the appropriate fault plane orientation from the earthquake’s focal mechanism. Second, we estimate the fault slip distribution through the tsunami waveform inversion of six coastal tide gauge stations and three deep-ocean-bottom pressure gauges (Fig. 2).
3.1 Tsunami Simulation Model
For the tsunami numerical simulation, we solve the shallow water equation using a finite difference method. A spherical coordinate system is used for wide tsunami propagation, and the planar UTM (Universal Transverse Mercator) system is used for local tsunami simulation. The core finite difference scheme is based on the TUNAMI (Tohoku University’s numerical analysis model for the investigation) code (Imamura 1996). The time step for the time domain in the nested bathymetry system is set to 0.6 s to satisfy the numerical stability condition. Details regarding the settings of the tsunami simulation based on nested bathymetry are available in (Adriano et al. 2016a). Using earthquake source parameters (strike, dip, rake, depth, slip, fault origin, and fault dimension), the initial condition for the tsunami simulation is calculated based on a rectangular fault model (Okada 1985). The time-dependent rupture is not considered. In addition, the vertical displacement due to the horizontal fault motions is added to the initial sea surface displacement (Tanioka and Satake 1996). The nonlinear tsunami simulation assumes a constant coefficient (0.025) for the bottom friction (Adriano et al. 2016a). The combination of dispersion and wave nonlinearity generates that the wave front of a tsunami propagating on a shallow bathymetry becomes steep (Baba et al. 2015). These nonlinear effects are not included in our simulation.
3.2 Early Tsunami Simulation
A tsunami response system implemented at the International Research Institute of Disaster Science, Tohoku University (initially developed in Peru (Adriano et al. 2011), for tsunami simulation is activated when a major tsunamigenic earthquake occurs. This system is based on linear tsunami modeling and a single rectangular fault model. The system is activated when a notification email from the US Geological Survey (USGS) is received after a tsunamigenic earthquake (\(Mw>7.0\)) occurs. This email contains the epicenter location, depth, and a preliminary earthquake magnitude. For calculating the initial sea surface displacement, the earthquake parameters strike, dip, and rake are searched in the Global Centroid Moment Tensor and W-phase solutions (GCMT) database. Our system chooses the closest GCMT solution to the epicenter. The fault dimension and slip amount are calculated using the magnitude and a scaling relation with respect to seismic moment (Papazachos et al. 2004). The preliminary tsunami response corresponds to the worst-case scenario from the results of simulating the two nodal planes of the chosen GCMT moment tensor solution. The initial report of the tsunami simulation of the earthquake that occurred on September 8 is available at http://www.regid.irides.tohoku.ac.jp/response/20170908_mexico_eq-en.html.
Based on the system mentioned above, we conduct a forward tsunami modeling using a single-fault model based on the latest GCMT moment tensor solution available for the 2017 Mw8.2 Mexico earthquake. The purpose of this simulation is to evaluate the characteristics of tsunami propagation around the rupture area, focusing on the nearby coastal tide gauge stations. The seismic moment of the GCMT solution is \(2.6\times 10^{21}\) Nm (associated with a Mw = 8.2 of moment magnitude) with a focal depth of 50.2 km. The parameters of the nodal planes are strike \(=148^{\circ }\), dip \(=13^{\circ }\), and slip \(=-83^{\circ }\) for the first plane, and strike \(=320^{\circ }\), dip \(=77^{\circ }\), and slip \(=-92^{\circ }\) for the second plane. Due to the two associated nodal planes, this solution provides two possible geometries for the fault area: southwest dip direction (strike \(=13^{\circ }\)) and northeast dip direction (strike \(=320^{\circ }\)) for the first and second nodal planes, respectively. To determine the appropriate fault dip direction, we utilize the aftershock distribution within 1 day following the main shock on September 8. We downloaded the aftershock data from the SSN. The aftershock distribution reveals that the rupture started near the epicenter and propagated northwest toward the Salina Cruz station (Fig. 1a). In addition to the aftershock distribution, we also confine the rupture area using the back-propagation of tsunami travel calculated from the tide stations (Heidarzadeh and Satake 2014b; Heidarzadeh et al. 2016). Figure 3a shows the tsunami source region. The travel time arcs bound the northeast (Huatulco and Salina Cruz) and southeast (Chiapas) edges of the source area acceptably well. Figure 3b shows the cross section of the source area (black rectangle in Fig. 3a). The aftershock mainly occurred between 10 and 80 km in depth. The aftershock pattern reveals that unlike the first GCMT nodal plane, the second plane (northeast dip direction) better describes the aftershock distribution.
a The rupture area of the Mw8.2 earthquake. The circles (color coded by depth) show the aftershock distribution within 1 day following the main shock on September 8, 2017. The aftershock data are from the SSN, UNAM. The blue beach ball symbol shows the focal mechanisms from the GCMT catalog. The dashed lines illustrate the back-propagation of tsunami travel time. b The cross section of the area is shown by the black rectangle in the top panel. The blue diamond and blue star show the location of the focal mechanism centroid and the epicenter, respectively. The dashed lines represent the two nodal plane dip directions. The circles (color code by depth) show the aftershock distribution
In our forward tsunami simulation, we assume the second GCMT nodal plane to construct the single-fault geometry. According to the estimated moment magnitude of the GCMT solution (Mw \(=8.2\)), the single-fault dimensions are 150 km × 40 km with a slip amount equal to 9.5 m (Papazachos et al. 2004). Considering that the centroid depth (50.2 km) and the hypocenter depth (58.0 km) are relatively close to each other, we use the centroid depth and the dip to set the top depth (30.7 km). After determining the earthquake parameters, we conduct a nonlinear tsunami simulation and analyze the tsunami propagation characteristics around the source region.
3.3 Inversion Methodology
The methodology for estimating the fault slip distribution of tsunami sources based on the inversion of tsunami waveform data was initially proposed by Satake (1987). Since then, this method has been revised and applied to primary interplate tsunamigenic earthquakes that have occurred in subduction zone regions around the world (e.g., Fujii and Satake 2007; Fujii et al. 2011; Gusman et al. 2015; Heidarzadeh and Satake 2015; Adriano et al. 2016b; Yoshimoto et al. 2016, 2017; Williamson et al. 2017). This method has also proven to be useful for solving intraplate earthquakes with complex focal mechanisms (Gusman et al. 2017a, b). In this study, we adopted the tsunami waveform inversion method described in Fujii and Satake (2013). First, the tsunami source area is divided into several segments (subfaults). Synthetic tsunami signals at each tide station are then generated by a forward tsunami simulation from each subfault using unit slip amount. We include three deepwater DART stations, where the nonlinear terms of the shallow water equations have minimal effects on modeling tsunami propagation. Thus, it is possible to more accurately simulate tsunami waveforms at these locations. However, the computation of tsunami waveforms at coastal stations becomes more difficult, because the tsunami waves highly interact with shallow bathymetry and coastline morphology in these cases, leading to nonlinear outcomes. We therefore use a linear tsunami propagation model, which is acceptable for a linear inversion analysis, to compute the tsunami waveforms at all stations. Furthermore, to address the issue regarding the coastal station records, we utilize only the first wave cycle of the calculated and recorded tsunami waveforms. Considering that the observed tsunami signal can be resolved as the linear superposition of the synthetic tsunami waveforms, it is possible to calculate the slip amount in each segment. We use the non-negative least squares method (Lawson and Hanson 1974) and the delete-half jackknife (Tichelaar and Ruff 1989) algorithm to solve the inversion problem of Green’s function and recorded tsunami waveforms (Eq. 1) and to estimate the errors, respectively.
In Eq. 1, A\(_{ij}\)(t) is the Green’s function at the i-th station from the j-th subfault, x\(_j\) is the unknown slip on the j-th subfault, and b\(_i\)(t) is the tide gauge record at the i-th station (Satake 1987). Theoretically, each subfault patch behaves independently of the neighboring segments, providing a best fit to the Green’s function (Williamson et al. 2017). Thus, our inversion model does not include any smoothing factor for the slip calculation. In this study, there are nine stations used in the inversion analysis (\(i=9\)).
4 Results and Discussion
4.1 Tsunami Simulation from Single-Fault Model
The tsunami source area mainly concentrates at the boundary of the continental shelf and the continental slope; this fact is illustrated by the aftershock distribution (Fig. 3a). Furthermore, the associated coseismic deformation is primarily confined to a concave region formed by the headland from the Puerto Angel to Acajutla stations (Gulf of Tehuantepec) and the Mexican trench (between the longitudes 91°W and 97°W). This unique configuration generates singular characteristics on the tsunami propagation (Yamazaki and Cheung 2011) that directly influence the tsunami waveforms recorded at the surrounding tide gauge stations.
Figure 4a shows four snapshots at the elapsed times of 0, 10, 30, and 60 min of the tsunami propagation. In Fig. 4a, the yellow rectangle shows the location of the single fault used to compute the initial sea surface displacement, which corresponds to the elapsed time of 0 min. The normal fault mechanism generates an uplift field of the sea surface directly above the continental slope and a subsidence field over the continental shelf, facing the coastline. The maximum subsidence and uplift values are 1.91 and 1.3 m, respectively. In our calculation, the Salina Cruz station starts registering an initial tsunami wave of \(-15\) cm. This first wave with negative polarity is not seen in the tsunami signal observed from this location (Fig. 4b), which indicates the low resolution of a single-fault model. The first negative deformation begins propagating over the continental shelf toward the coastline. A secondary positive wave appears around the epicenter after 10 min of propagation (top right in Fig. 4a). This secondary positive wave together with the first negative wave becomes trapped within the shelf, creating a series of wave systems along the coastline (Bellotti et al. 2012). This phenomenon can only be observed in the waveform recorded at the Salina Cruz station, where a larger wave (80 min) follows the relatively small early wave (30 min) (Fig. 4b).
a Snapshots of 0, 10, 30, and 60 min of tsunami propagation calculated from a single-fault model. The black rectangle in the top left panel indicates the fault area estimated using the northeast dip direction of the GCMT moment tensor solution for the September 8 earthquake. The top left panel also shows the initial seafloor deformation for the tsunami propagation. b Comparison of computed (blue lines) and observed (black lines) tsunami waveforms at coastal stations
Another consequence of the bathymetry configuration of the tsunami source region is the observed arrival time at the Salina Cruz and Huatulco stations. Although the distance between the epicenter and the Salina station (∼ 190 km) is much smaller than the distance between the epicenter and the Puerto Angel station (∼ 270 km), the tsunami arrives early at the latter station. The tsunami signals recorded at these locations also illustrate this arrival time difference (Fig. 4b). This fact is due to bathymetry along the path from the epicenter to the stations; while the shallow bathymetry reduced the tsunami speed toward the Salina Cruz station, the speed of the tsunami wave propagating toward Huatulco and Puerto Angel is less affected in the deep continental slope. This arrival time difference cannot be observed at the stations south of the fault area (Chiapas and Acajutla). After the tsunami wave passes Puerto Angel, it propagates over the Mexican trench, following an almost northwest path. The deep bathymetry along the trench reduces and disperses the tsunami wave amplitude, creating a more extended wave period that was recorded at the Lazaro station. In our simulation, the tsunami waveform at the Lazaro station is not fully well resolved, showing a phase difference between the observed and the modeled waveforms. The location of the earthquake fault and the associated coseismic deformation may be the reason for this difference. Figure 4b shows the comparison of the computed and observed tsunami waveforms. In general, the single-fault model reproduced the observed tsunami waveforms reasonably well, particularly at stations near the source area. Conversely, the simulated waveform at the Acajutla station is slightly higher than the observed one.
4.2 Fault Slip Distribution
4.2.1 Fault Geometry
Following the previous analysis based on a single-fault model, we use the second nodal plane, northeast dip direction, of the GCMT moment tensor solution (strike \(= 320^{\circ }\), dip \(= 77^{\circ }\), and rake \(=-\,92^{\circ }\)) to construct the fault area in our tsunami waveform inversion analysis. The fault area is 210 km × 90 km, covering the aftershock area. We divide the fault area into 21 subfaults that are 30 km × 30 km in size, seven subfaults along the strike direction and three subfaults along the dip direction (Fig. 5a). In our preliminary calculations, we also tested subfaults with size of 20 km × 20 km and 40 km × 40 km. The inversion solution of the selected subfault size (30 km × 30 km), however, showed a better resolution with a satisfactory balance between the slip amount and the moment magnitude. Given the dip angle and focal depth, the top depth of the shallowest (1–7), middle (8–14), and most profound (15–21) subfaults are 6.35, 35.58, and 64.82 km (Fig. 5 and Table 2), respectively. The configuration of the fault area in the vertical direction also covers the aftershock distribution, as illustrated in Fig. 5b.
a Geometry of assumed subfaults for the earthquake that occurred on September 8, 2017 (black rectangles). Aftershock distribution color coded by depth. GCMT moment tensor solution. b Cross section of the area under the dashed box shown in (a). The black line indicates the total width of the assumed fault area. The white squares indicate the top depth of the shallowest, middle, and deepest segments. c Fault slip distribution for the 2017 Mw8.2 Mexico earthquake estimated by inversion of tsunami waveforms. d Coseismic displacement computed from the estimated fault slip distribution. The contour lines indicate the displacement at 20 cm intervals
4.2.2 Slip Distribution
Figure 5c shows the slip distribution estimated by inverting tsunami waveform records. Our inversion result shows a similar slip pattern as that published by the USGS (https://earthquake.usgs.gov/earthquakes/eventpage/us2000ahv0#finite-fault), which was calculated using teleseismic data based on the algorithm proposed by Ji et al. (2002). A particular difference among these source models is the maximum slip deformation which differs by about 4 m, with the USGS model having the largest slip on a shallower depth than our model. This suggests that the seismic inversion model generates larger seabed deformation than that shown by our tsunami waveform inversion results on sea surface deformation. The particularities on energy transfer from seabed to sea surface are of interest for future studies. To solve Eq. 1, we select 160 points from the recorded waveform data to build the vector \(b_i(t)\). From the estimated slip distribution, the associated seismic moment, assuming an average rigidity of \(7\times 10^{10}\) N/m2, is \(2.9\times 10^{21}\) Nm, which is equivalent to a moment magnitude of \({\text{Mw}}=8.24\). Our result is slightly larger than the one estimated by GCMT (\(2.65\times 10^{21}\) Nm, Mw = 8.2). This small difference can be attributed to the slips of approximately 5 m that are determined near the coastline. In our calculations, these deepest subfaults show significant slip amounts to reproduce the tsunami waveform observed at Salina Cruz. Table 2 shows the standard error of the computed slip distribution. In general, for subfaults with the largest slip (> 5 m), the corresponding error is approximately ± 0.25 m, which is almost 5% of the slip amount.
The estimated slip distribution has the most significant slips around the center of the fault area (30 km northwest of the epicenter) with a maximum value of 6.03 m along the deepest subfaults (Fig. 5c, d). The inversion result also shows substantial slips in front of the Salina Cruz station. Two considerable slips of 5.01 m and 4.63 are located at the center of the fault area within the middle segments. The slip on the shallowest subfaults is approximately 2 m, also at the center of the fault plane. The resulting slip configuration indicates a large patch, which is mainly concentrated around the GCMT’s centroid and extends toward the Salina Cruz station. Figure 5d shows the computed seafloor deformation using the estimated fault slip distribution. Because of the normal faulting, similar to the single-fault model, the associated subsidence deformation faces the coastline and is contained mainly over the continental shelf. The absolute maximum displacements are 1.43 and 0.96 m at the lowest and highest points, respectively (Fig. 5d). Note that the uplift region is affected by the vertical deformation due to the horizontal motion of the fault mechanism, as shown by the red contour lines. This effect is not observed in the subsidence region because of the low slope of the ocean bottom (Tanioka and Satake 1996).
Figure 6 shows the comparison of the recorded tsunami waveforms and those computed using the estimated slip distribution. In general, the synthetic data agree well with the observed signals, particularly on the DART stations where nonlinear terms influence the tsunami propagation less. Meanwhile, the waveform fitting at coastal locations is mainly well developed within the first wave cycle. The reason for this result is, as mentioned earlier, the limitation of our linear tsunami model in accurately modeling tsunami waves on coastal locations with shallow bathymetry. This effect can be observed at the Salina Cruz station, where the initial wave cycle is roughly solved and the latest phases of the tsunami signal are poorly reconstructed. Finer bathymetry data are required to improve the reproducibility at the coastal stations (Satake 1995). We calculate the normalized root-mean-square (NRMS) misfit (Heidarzadeh et al. 2016) using only data from the coastal stations, within the inversion time range (Fig. 6), from the single-fault (1.52) and the inversion results (0.55). The NRMS misfit coefficient gives a perfect agreement between observations and simulations when it is equal to 0 (Heidarzadeh et al. 2016). It can be observed that the estimated slip distribution shows excellent improvement against the single-fault model to reproduce the recorded tsunami signals.
4.2.3 Maximum Estimated Tsunami Height
Using the estimated fault slip distribution, we conducted a second simulation to evaluate the maximum tsunami height along the coastline near the source area (Fig. 7). Here, we describe the maximum tsunami height distribution obtained 3 h after propagations, as shown in the bottom panel of Fig. 7. As expected, the highest values are founded near the fault area between the Huatulco and Chiapas stations. Then maximum tsunami height is 4.1 m, approximately 100 km east of Salina Cruz station. The distribution of the maximum tsunami height also reveals that the tsunami energy did not significantly propagate to the open ocean. The tsunami energy is directly proportional to the tsunami wave height (Titov 2005; Heidarzadeh and Satake 2014a). Despite the relatively big magnitude of this event, the tsunami amplitude primarily concentrates within to the source region unlike other events with same or smaller magnitude (Heidarzadeh and Satake 2017). This energy pattern is because of the location of the initial seafloor displacement. We compare our results against reported tsunami amplitude at seven tide gauge stations from the IOC (http://www.ioc-sealevelmonitoring.org) near the source region. Our results show good agreement with the observed tsunami north of the fault area, between Lazaro and Puerto Angel stations. The computed tsunami height, however, overestimated the reported near Salina Cruz station. Conversely, our simulation underestimates the observed data around Chiapas station. The differences can be attributed to the low spatial resolution of the bathymetry data, which is needed to appropriately simulate tsunami propagation in the shallow water.
5 Conclusions
The tsunami generated by a normal-fault Mw8.2 earthquake on September 8, 2017, was investigated using tsunami signals that were recorded at several coastal and deep ocean stations. A simple fault based on the GCMT solution (dimensions of 150 km × 40 km, slip \(= 9.5\) m, strike \(= 320^{\circ }\), dip \(= 77^{\circ }\), and rake \(=-92^{\circ }\)) satisfactorily explained the tsunami signal observed at the coastal tide stations near the tsunami source region. The single-fault model also showed that due to the location of the rupture area, the tsunami arrived approximately 10 min earlier at areas much farther from the epicenter, such as near the Puerto Angel station. Furthermore, the tsunami waves propagated toward the coastline over the continental shelf, delaying the arrival time at the Salina Cruz station, which is much closer to the epicenter. A cross-sectional analysis of the aftershock distribution supported the assumption of the northeast dip direction plane. This plane orientation was also adopted by the USGS model. The aftershock also revealed that the rupture extended northwest from the epicenter.
For our inversion analysis, a total of six tide gauge stations and three DART stations were used to compute the fault slip distribution. The estimated fault area was 240 km × 90 km in size (divided into 24 subfaults of 30 km × 30 km size). The maximum slip was 6.03 m from a 64.82 km deep segment, at the center of the fault area. The estimated slip distribution showed the main asperity at the centermost of the fault area, with maximum slips of 2.83 m and 2.93 m in the shallowest and middle segments, respectively. The second asperity with an average slip of 5.5 m was also found on the northwest-most subfaults, near the Salina Cruz station. The estimated slip distribution yielded a seismic moment of \(2.9\times 10^{21}\) Nm (assuming an average rigidity of \(7\times 10^{10}\) N/m2), which was associated with a moment magnitude of Mw \(=8.24\). This result was slightly larger than the one published by GCMT (\(2.65 \times 10^{21}\) Nm). Our result, however, represents a reasonable estimation considering that only tsunami data were employed. The coseismic deformation associated with our slip distribution produced a seafloor subsidence, in the lowest point, of 1.43 m and a maximum uplift of 0.96 m. Using the estimated seafloor displacement, we calculated the maximum tsunami height along the coastline. We ran 3 h of nonlinear tsunami propagation. We found that a significant portion of the tsunami energy was kept between the source area and the headlands. This phenomenon generated tsunami amplitudes up to 4 m in areas approximately 100 km east of the Salina Cruz station. The propagation nature was mainly due to the bathymetry configuration of the rupture area.
References
Adriano, B., Koshimura, S., & Fujii, Y. (2011). Validation of tsunami inundation modeling for the June 23, 2001 Peru Earthquake. In 8th International Conference on Urban Earthquake Engineering, pp. 1800–1804.
Adriano, B., Hayashi, S., Gokon, H., Mas, E., & Koshimura, S. (2016a). Understanding the extreme tsunami inundation in Onagawa town by the 2011 Tohoku earthquake, its effects in urban structures and coastal facilities. Coastal Engineering Journal, 58(4), 1640013.
Adriano, B., Mas, E., Koshimura, S., Fujii, Y., Yanagisawa, H., & Estrada, M. (2016b). Revisiting the 2001 Peruvian earthquake and tsunami impact along Camana beach and the coastline using numerical modeling and satellite imaging. In Santiago-Fandiño, V., Tanaka, H., Spiske, M., (Eds.), Tsunamis and Earthquakes in Coastal Environments, volume 14 of Coastal Research Library, pp. 1–16. Springer, New York.
Baba, T., Takahashi, N., Kaneda, Y., Ando, K., Matsuoka, D., & Kato, T. (2015). Parallel implementation of dispersive tsunami wave modeling with a nesting algorithm for the 2011 Tohoku tsunami. Pure and Applied Geophysics, 172(12), 3455–3472.
Bekaert, D. P. S., Hooper, A., & Wright, T. J. (2015). Reassessing the 2006 Guerrero slow-slip event, Mexico: Implications for large earthquakes in the Guerrero Gap. Journal of Geophysical Research: Solid Earth, 120(2), 1357–1375.
Bellotti, G., Briganti, R., & Beltrami, G. M. (2012). The combined role of bay and shelf modes in tsunami amplification along the coast. Journal of Geophysical Research: Oceans, 117(8), 1–13.
Bravo, H., Rebollar, C. J., Uribe, A., & Jimenez, O. (2004). Geometry and state of stress of the Wadati-benioff zone in the Gulf of Tehuantepec, Mexico. Journal of Geophysical Research B: Solid Earth, 109(4), 1–14.
Cavalié, O., Pathier, E., Radiguet, M., Vergnolle, M., Cotte, N., Walpersdorf, A., et al. (2013). Slow slip event in the Mexican subduction zone: Evidence of shallower slip in the Guerrero seismic gap for the 2006 event revealed by the joint inversion of InSAR and GPS data. Earth and Planetary Science Letters, 367, 52–60.
Farreras, S. F., & Sanchez, A. J. (1991). The tsunami threat on the Mexican west coast: A historical analysis and recommendations for hazard mitigation. Natural Hazards, 4(2–3), 301–316.
Fujii, Y., & Satake, K. (2007). Tsunami source of the 2004 Sumatra–Andaman earthquake inferred from tide gauge and satellite data. Bulletin of the Seismological Society of America, 97(1A), S192–S207.
Fujii, Y., & Satake, K. (2013). Slip distribution and seismic moment of the 2010 and 1960 Chilean Earthquakes inferred from tsunami waveforms and coastal geodetic data. Pure and Applied Geophysics, 170(9–10), 1493–1509.
Fujii, Y., Satake, K., Sakai, S., Shinohara, M., & Kanazawa, T. (2011). Tsunami source of the 2011 off the Pacific coast of Tohoku earthquake. Earth, Planets and Space, 63(7), 815–820.
Gusman, A. R., Murotani, S., Satake, K., Heidarzadeh, M., Gunawan, E., Watada, S., et al. (2015). Fault slip distribution of the 2014 Iquique, Chile, earthquake estimated from ocean-wide tsunami waveforms and GPS data. Geophysical Research Letters, 42(4), 1053–1060.
Gusman, A. R., Satake, K., & Harada, T. (2017a). Rupture process of the 2016 Wharton Basin strike-slip faulting earthquake estimated from joint inversion of teleseismic and tsunami waveforms. Geophysical Research Letters, 44(9), 4082–4089.
Gusman, A. R., Satake, K., Shinohara, M., Sakai, S., & Tanioka, Y. (2017b). Fault slip distribution of the 2016 Fukushima earthquake estimated from tsunami waveforms. Pure and Applied Geophysics, 174(8), 2925–2943.
Heidarzadeh, M., Murotani, S., Satake, K., Ishibe, T., & Gusman, A. R. (2016). Source model of the 16 September 2015 Illapel, Chile, Mw 8.4 earthquake based on teleseismic and tsunami data. Geophysical Research Letters, 43(2), 643–650.
Heidarzadeh, M., & Satake, K. (2014a). Excitation of basin-wide modes of the pacific ocean following the March 2011 Tohoku tsunami. Pure and Applied Geophysics, 171(12), 3405–3419.
Heidarzadeh, M., & Satake, K. (2014b). Possible sources of the tsunami observed in the northwestern Indian ocean following the 2013 September 24 Mw 7.7 Pakistan inland earthquake. Geophysical Journal International, 199(2), 752–766.
Heidarzadeh, M., & Satake, K. (2015). New insights into the source of the Makran Tsunami of 27 November 1945 from tsunami waveforms and coastal deformation data. Pure and Applied Geophysics, 172(3–4), 621–640.
Heidarzadeh, M., & Satake, K. (2017). Possible dual earthquake landslide source of the 13 November 2016 Kaikoura, New Zealand tsunami. Pure and Applied Geophysics, 174(10), 3737–3749.
Imamura, F. (1996). Review of the tsunami simulation with a finite difference method. In H. Yeh, P. Liu, & C. Synolakis (Eds.), Long wave run-up models (pp. 25–42). Singapore: World Scientific.
Ji, C., Wald, D. J., & Helmberger, D. V. (2002). Source description of the 1999 Hector Mine, California, earthquake, part I: Wavelet domain inversion theory and resolution analysis. Bulletin of the Seismological Society of America, 92(4), 1192–1207.
Kostoglodov, V., Valenzuela, R. W., Gorbatov, A., Mimiaga, J., Franco, S. I., Alvarado, J. A., et al. (2001). Deformation in the Guerrero seismic gap, Mexico, from leveling observations. Journal of Geodesy, 75(1), 19–32.
Lawson, C. L. & Hanson, R. J. (1974). Solving least squares problems (p. 340). Prentice-Hall, Inc., Englewood Cliffs.
Manea, V. C., Manea, M., Ferrari, L., Orozco, T., Valenzuela, R. W., Husker, A., et al. (2017). A review of the geodynamic evolution of flat slab subduction in Mexico, Peru, and Chile. Tectonophysics, 695, 27–52.
Mendoza, C. (1993). Coseismic slip of two large Mexican earthquakes from teleseismic body waveforms: Implications for asperity interaction in the Michoacan Plate Boundary Segment. Journal of Geophysical Research, 98(93), 8197.
Mori, N., Muhammad, A., Goda, K., Yasuda, T., & Ruiz-Angulo, A. (2017). Probabilistic tsunami hazard analysis of the pacific coast of Mexico: Case study based on the 1995 Colima earthquake tsunami. Frontiers in Built Environment, 3(34), 1–16.
Nishenko, S. P., & Singh, S. K. (1987). Conditional probabilities for the recurrence of large and great interplate earthquakes along the Mexican subduction zone. Bulletin of the Seismological Society of America, 77(6), 2095–2114.
Okada, Y. (1985). Surface deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America, 75(4), 1135–1154.
Papazachos, B. C., Scordilis, E. M., Panagiotopoulos, D. G., & Karakaisis, G. F. (2004). Global relations between seismic fault parameters and moment magnitude of earthquakes. In The 10th International Congress, Thessaloniki, pp. 1482–1489.
Ramírez-Herrera, M. T., Corona, N., Lagos, M., Černý, J., Goguitchaichvili, A., Goff, J., et al. (2014). Unearthing earthquakes and their tsunamis using multiple proxies: The 22 June 1932 event and a probable fourteenth-century predecessor on the Pacific coast of Mexico. International Geology Review, 56(13), 1584–1601.
Satake, K. (1987). Inversion of tsunami waveforms for the estimation of a fault heterogeneity: Method and numerical experiments. Journal of Physics of the Earth, 35, 241–254.
Satake, K. (1995). Linear and nonlinear computations of the 1992 Nicaragua earthquake tsunami. Pure and Applied Geophysics PAGEOPH, 144(3–4), 455–470.
Singh, S. K., Astiz, L., & Havskov, J. (1981). Seismic gaps and recurrence periods of large earthquakes along the Mexican subduction zone: A reexamination. Bulletin of the Seismological Society of America, 71(3), 827–843.
Singh, S. K., Pérez-Campos, X., Iglesias, A., & Pacheco, J. F. (2008). An exploratory study for rapid estimation of critical source parameters of great subduction-zone earthquakes in Mexico. Geofísica International, 47(4), 355–369.
Tanioka, Y., & Satake, K. (1996). Tsunami generation by horizontal displacement of ocean bottom. Geophysical Research Letters, 23(8), 861.
Tichelaar, B. W., & Ruff, L. J. (1989). How good are our best models? Jackknifing, bootstrapping, and earthquake depth. Eos, Transactions American Geophysical Union, 70(20), 593.
Titov, V. (2005). The global reach of the 26 December 2004 Sumatra tsunami. Science, 309(5743), 2045–2048.
Weatherall, P., Marks, K. M., Jakobsson, M., Schmitt, T., Tani, S., Arndt, J. E., et al. (2015). A new digital bathymetric model of the world’s oceans. Earth and Space Science, 2(8), 331–345.
Wessel, P., Smith, W. H. F., Scharroo, R., Luis, J., & Wobbe, F. (2013). Generic mapping tools: Improved version released. Eos, Transactions American Geophysical Union, 94(45), 409–410.
Williamson, A., Newman, A., & Cummins, P. (2017). Reconstruction of coseismic slip from the 2015 Illapel earthquake using combined geodetic and tsunami waveform data. Journal of Geophysical Research: Solid Earth, 122(3), 2119–2130.
Yamazaki, Y., & Cheung, K. F. (2011). Shelf resonance and impact of near-field tsunami generated by the 2010 Chile earthquake. Geophysical Research Letters, 38(12), L12605.
Yoshimoto, M., Kumagai, H., Acero, W., Ponce, G., Vásconez, F., Arrais, S., Ruiz, M., Alvarado, A., Pedraza García, P., Dionicio, V., Chamorro, O., Maeda, Y., & Nakano, M. (2017). Depth-dependent rupture mode along the Ecuador–Colombia subduction zone. Geophysical Research Letters, 44(5), 2203–2210.
Yoshimoto, M., Watada, S., Fujii, Y., & Satake, K. (2016). Source estimate and tsunami forecast from far-field deep-ocean tsunami waveforms-the 27 February 2010 Mw 8.8 Maule earthquake. Geophysical Research Letters, 43(2), 659–665.
Acknowledgements
The tide gauge and DART data were downloaded from the Sea Level Station Monitoring Facility website and the NOAA Center for Tsunami Research website, respectively. The pre-processing of the waveform data and construction of all figures in this paper were performed using the Generic Mapping Tools (Wessel et al. 2013). This research was supported by the Japan Society for the Promotion of Science (JSPS) under the project: Fusion of Real-time Simulation and Remote Sensing for Tsunami Damage Estimation to Latin America (JSPS-Grant: P16055) and the JST/JICA, SATREPS (Science and Technology Research Partnership for Sustainable Development) Mexico Project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Adriano, B., Fujii, Y., Koshimura, S. et al. Tsunami Source Inversion Using Tide Gauge and DART Tsunami Waveforms of the 2017 Mw8.2 Mexico Earthquake. Pure Appl. Geophys. 175, 35–48 (2018). https://doi.org/10.1007/s00024-017-1760-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00024-017-1760-2