1 Introduction

Earthquakes represent a complicated geographical phenomenon, which is shown to be self-similar in a wide range of scales (Bak et al. 2002). The universal Gutenberg–Richter scaling relation (Gutenberg and Richter 1944) states that earthquake magnitudes m are distributed according to the exponential law

$$\lambda_{0} \left( m \right) = a10^{{ - {\text{bm}}}}$$
(1)

where λ 0 is the number of expected earthquakes, a the earthquake productivity and b the magnitude scaling parameter. Assuming self-similarity in space, Eq. (1) becomes

$$\lambda_{0} \left( {m,L} \right) = a10^{{ - {\text{bm}}}} L^{D}$$
(2)

with L the size of the spatial cell and D the spatial scaling parameter or fractal dimension of earthquake epicenters (Kosobokov and Mazhkenov 1994; Molchan and Kronrod 2005). Equations (1) and (2) hold only for m ≥ m c with m c the completeness magnitude. It has been shown that this parameter is ambiguous with the \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m}_{\text{c}}\) estimate depending at a same location on the computation method and on the spatial scale considered (Mignan and Chouliaras 2014). The behavior of seismicity at m < m c is also ambiguous due to the fact that the intrinsic spatial scale of the detected seismicity phenomenon has not been considered so far. In other words, there is an implicit assumption that the detection process is also self-similar, which has recently been shown to be incorrect (i.e., the frequency-magnitude distribution does not display the same statistical properties or same shape at different scales; see Fig. 16 in Mignan 2012).

In this article, we investigate the shape of the earthquake frequency-magnitude distribution over the range m ∈ (−∞, +∞) to determine the fundamental spatial unit of the geographical phenomenon that is detected seismicity (Sect. 2; Pereira 2001). Knowing the scale of the detected seismicity phenomenon (Sect. 3) allows us (i) to study the behavior of the scaling parameters b and D on a wider magnitude range by including smaller events, and (ii) to gain more insight into the earthquake detection process (Sect. 4).

For this analysis, we use the earthquake catalog of Taiwan relocated by Wu et al. (2008). We consider the period 1994–2005 and volume 119°E ≤ x ≤ 123°E, 21°N ≤ y ≤ 26°N and z ≤ 35 km. Year 2005 corresponds to the last year analyzed in Wu et al. (2008).

2 Definition of the Spatial Scale of Detected Seismicity

We show in this section that the spatial scale of detected seismicity can be inferred from the analysis of the shape of the earthquake frequency-magnitude distribution (FMD). This was first suggested by Mignan (2012) who observed that the FMD shape differs between local and regional datasets. This is conceptualized below and verified in an earthquake catalog in the next section.

The FMD is described over the range m ∈ (−∞, +∞) by

$$\lambda \left( m \right) = \lambda_{0} \left( m \right)q(m)$$
(3)

where q(m) = Pr(Detected | m) is the earthquake detection function. Mignan (2012) coined the term elemental FMD to describe the fundamental FMD, whose shape does not depend on m c variations. This elemental FMD takes the form

$$\lambda \left( {m |k,b,m_{\text{c}} } \right) = \left\{ \begin{array}{ll} a10^{{(k - b)(m - m_{\text{c}} )}} , \quad m < m_{\text{c}} \hfill \\ a10^{{ - b(m - m_{\text{c}} )}} ,\quad m \ge m_{\text{c}} \hfill \\ \end{array} \right.$$
(4)

with k > b a detection parameter. The elemental FMD has an angular shape with q (m < m c) an exponential law and q (m ≥ m c) = 1. Since m c = f(x,y), the elemental FMD only holds in an elemental spatial cell of width L e. The FMD observed in larger cells is the sum of elemental FMDs, leading to a rounded shape of that composite FMD (Mignan 2012). This shape can be approximated by defining q (m) by the cumulative normal distribution ϕ (Ringdal 1975; Ogata and Katsura 1993; 2006; Mignan 2012). Figure 1 shows an FMD at the regional scale (L = 5°, full catalog) and an FMD at a local scale (L = 0.1°, x = 120.95°, y = 23.15°). They are rounded and angular, respectively, indicating that the regional FMD is a composite FMD (trivial) and that the local FMD is an elemental FMD, which means L ≤ L e at (x, y).

Fig. 1
figure 1

Shape of the earthquake frequency-magnitude distribution (FMD) at different observational scales over the range m ∈ (−∞, +∞): a Regional FMD in a 5° cell (full catalogue), rounded and best fitted by λ 0 (m) Φ (m) with b = 0.9, μ = 2.0 and σ = 0.4 (i.e. composite FMD); b local FMD located in a 0.1° cell centered at (x = 120.95°, y = 23.15°), angular and best fitted by Eq. (4) with b = 0.7, k = 1.8 and m c = 1.7 (i.e. elemental FMD)

Full size image

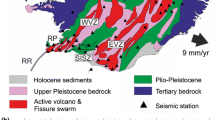
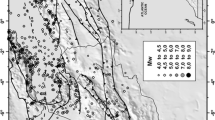
The concept of elemental cell brings us to the scale of the process. Scale is defined by two components: the grain (~grid cell) and the extent (~entire grid). Those components can be artifacts of observation or attributes of phenomena (Pereira 2001). While this distinction is common practice in ecological studies, it is not the case in seismology where all processes are assumed scale invariant (Bak et al. 2002; Ogata and Katsura 1993). Figure 2 represents maps with a same observational extent (the Taiwanese region). Figure 2a shows the spatial distribution of seismicity and seismic stations used in this study. Figure 2b, c shows maps of the estimator \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m}_{c} = m({ \hbox{max} }(\lambda ))\) using a same display resolution (0.1° pixel) but a different observational resolution with a constant coarse grain in Fig. 2b (with radius r = L/2 = 50 km) and a variable grain in Fig. 2c (with r = L/2 = f(d n ), d n being the distance to the nth seismic station). Using a variable grain function of the seismic network geometry was proposed by Mignan et al. (2011) to minimize spatial heterogeneities in m c, m c varying faster in the denser parts of a seismic network. We develop upon this idea by defining the fundamental spatial unit (or intrinsic grain) of the detected seismicity by the area within which the elemental FMD is observed. Visually, the elemental FMD represents the highest possible resolution (sharp angular shape, Fig. 1b) while the composite FMD represents a lower resolution (blurred rounded shape, Fig. 1a). Note that the intrinsic extent of the earthquake detection process corresponds to the area comprising all the seismicity declared from a given seismic network (here the same as the observational extent, Fig. 2a).

Fig. 2
figure 2

Observational spatial scale: a Spatial distribution of seismicity for magnitudes m ≥ 4.0 (gray dots), spatial distribution of seismic stations (red triangles) and example of Voronoi tessellation with n V = 100 (black polygons); b \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m}_{c} = m({ \hbox{max} }(\lambda ))\) estimated for a constant coarse grain of radius r = L/2 = 50 km (black circles); c \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m}_{c} = m({ \hbox{max} }(\lambda ))\) for a variable grain of radius r = L/2 = f(d 5), d 5 being the distance to the 5th nearest seismic station (Mignan et al. 2011). The same observational spatial extent is used in (a–c) and the same display resolution (0.1° pixel) is used in (b–c) (gray squares)

Full size image

3 Spatial Resolution Analysis

We investigate the shape of FMDs located in a partitioned space using Voronoi tessellation (Voronoi 1908). We test N V = 1,000 realizations with the number of generators n V randomly drawn from the log10 space in the range [10, 103]. Each generator, or point, is defined from random geographical coordinates (x V, y V) located in the region of interest. For each point, there is a corresponding region, or Voronoi cell, consisting of all points closer to that point than to any other. We choose this type of tessellation to objectively produce areas of various shapes and sizes (e.g., Fig. 2a) with no a priori knowledge on the spatial scale of the detected seismicity phenomenon (see also Kamer and Hiemer 2015). Each Voronoi cell is characterized by an area A, a distance \(d_{n} = \sqrt {(x_{\text{V}} - x_{n} )^{2} + (y_{\text{V}} - y_{n} )^{2} }\) between the generator and the nth nearest seismic station of coordinates (x n , y n ), and an FMD defined from all earthquakes located in the cell. Let us note that the distance d n represents a proxy to the spatial density of seismic stations—and therefore to the degree of m c variations—and that the choice of n (commonly between 3 and 5) is not critical (Mignan et al. 2011, 2013; Kraft et al. 2013; Vorobieva et al. 2013; Mignan and Chouliaras 2014; Tormann et al. 2014).

Two FMD models are tested and compared using the Bayesian Information Criterion \({\text{BIC}} = - 2 {\text{ log}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} + K{ \log }N\) with \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} \;\) the maximized value of the likelihood function f of the model, K the number of free parameters and N the number of data points (Schwarz 1978). The elemental FMD model (Fig. 1b) is described by the following likelihood function

$$f\left( {m |\kappa ,\beta ,m_{\text{c}} } \right) = \frac{1}{{\frac{1}{\kappa - \beta } + \frac{1}{\beta }}}\left\{ \begin{array}{ll} \exp \left( {\left( {\kappa - \beta } \right)\left( {m - m_{\text{c}} } \right)} \right), \quad m < m_{\text{c}} \hfill \\ \exp \left( { - \beta \left( {m - m_{\text{c}} } \right)} \right), \quad m \ge m_{\text{c}} \hfill \\ \end{array} \right.$$
(5)

where \(\kappa = k{ \log }\left( {10} \right)\) and \(\beta = b{ \log }\left( {10} \right)\) (Mignan 2012). In practice, we use a faster method introduced by Kamer (2014), which takes advantage of the piecewise structure of Eq. (4), uses the Aki maximum likelihood method (Aki 1965) and shows that K = 2 instead of 3 (i.e., b/(k − b) = N i /N c with N c and N i the number of events in the complete and incomplete parts of the FMD, respectively). The composite FMD model (Fig. 1a) is described by

$$f\left( {m |\beta ,\mu ,\sigma } \right) = \beta { \exp }\left( { - \beta \left( {m - \mu } \right) - \beta^{2} \frac{{\sigma^{2} }}{2}} \right)\varPhi (m|\mu ,\sigma )$$
(6)

where Φ(m | μ, σ) is the cumulative normal distribution and K = 3 (Ogata and Katsura 1993; 2006). The two models represent homogeneous data (elemental area with constant m c) and heterogeneous data (composite area with variable m c), respectively, which allows us to differentiate intrinsic grains and extrinsic grains relative to the spatial scale of detected seismicity.

For each Voronoi cell of all N V realizations (yielding a total of ~60,000 cells), we calculate the distance d 5 to the fifth nearest seismic station, the width of the cell \(L = 2\sqrt {A/\pi }\) and the FMD model choice C

$$\left\{ {\begin{array}{*{20}c} {C = 1,} & {{\text{if BIC }}({\text{elemental FMD}}) \le {\text{BIC }}({\text{composite FMD}})} \\ {C = 0,} & {\text{otherwise}} \\ \end{array} } \right.$$
(7)

Event location in the Taiwanese national catalog requires at least three stations and at least five phases P or S and it is therefore equally reasonable to use n = 3, 4 or 5 in d n . Mignan et al. (2011) showed that the models m c = f(d n ) with n = {3, 4, 5} give similar results in Taiwan. We then compute the ratio ∑C b/nb with n b the number of choices C b, which are all the choices C located in Δd 5 × ΔL bins defined in the (d 5, L) space. We fix Δd 5 = ΔL = 10 km ~0.1° (Fig. 3). This ratio links the observational spatial resolution (or grain) L to the intrinsic spatial resolution L e. Figure 3 shows that a constant observational spatial grain L (i.e., any horizontal line) is a poor estimator of the detected seismicity phenomenon since it includes heterogeneities in the FMD shape potentially leading to artifacts of observation at m ≤ m c. Considering 10 km < L < 150 km only (removal of earthquake location errors and of boundary effects linked to the spatial extent of the region), we find

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L} \; = { 1}. 5 6d_{ 5}-{67}. 8$$
(8)

the boundary (black line) between observational grains L which contain heterogeneities (in purple, \(L > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{e}\)) and which are homogeneous (in red, \(L \le \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{e} \;\)). This relationship verifies that m c varies faster in the denser parts of a seismic network, as independently observed by Mignan et al. (2011), and describes the intrinsic spatial scale of the detected seismicity phenomenon. This phenomenon is thus shown to be scale-variant for m ∈ (−∞, +∞) with its spatial grain a function of the configuration of the seismic network (i.e., \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{e} \; = f\left( {d_{n} } \right))\), which is opposed to the scale invariance of seismicity known for m ∈ [m c, +∞) for which the Gutenberg–Richter law holds and the network configuration is irrelevant.

Fig. 3
figure 3

Spatial scale of detected seismicity as a function of distance to the fifth nearest seismic station d 5 and of cell size L. The ratio ∑C b /nb with n b the number of choices C b in Δd 5 × ΔL bins (Eq. 7) links the observational spatial resolution (or grain) L to the intrinsic spatial resolution L e (black line, Eq. 8)

Full size image

4 Discussion

Does a better understanding of the spatial scale of the detected seismicity phenomenon allow in turn a better understanding of the behavior of seismicity below completeness and of the process of earthquake detection itself? In the aim of initiating a debate on such challenging issues, we develop upon these two important aspects with some basic illustrations.

4.1 Implications for the Universal Scaling Parameters b and D

We investigate if our results may help extending the analysis of the Gutenberg–Richter law and of the fractal dimension to lower magnitudes m < m c. We first test Eq. (2) in Taiwan by measuring the number of events

$$N\left( {m,L} \right) = \frac{{\mathop \sum \nolimits_{i} N_{i} (m,L)^{2} }}{{N(m,L_{0} )}}$$
(9)

with N i the number of events of magnitude m in cell i of size L = L 0/2h, L 0 = 4° and h = {0, …, 5} the level of hierarchy (Kosobokov and Mazhkenov 1994). Figure 4a shows that a data collapse is obtained on the Gutenberg–Richter law of slope b = 0.9 (solid line) when normalizing to N (m, L)/L D with D = 1.2, which is in agreement with results in other regions for earthquake epicenters (Bak et al. 2002). For illustration purposes, we here assume that Eq. (2) is verified if N (m, L)/L D is within a factor 2 of the theoretical curve (dotted lines). The law is verified in the range 2.1 ≤ m ≤ 5.0 for h ∈ [0, 5] while the data deviate from the law at m < 2.1 for all levels of hierarchy h (i.e. m c = 2.1).

Fig. 4
figure 4

Data collapse for universal scaling parameters b = 0.9 and D = 1.2 in Taiwan with N (m, L) the number of events, m the magnitude and L the cell size: a original data incomplete below magnitude m = 2.1; b data corrected for incompleteness, extending universality to lower magnitudes

Full size image

We then consider the corrected case N ic(m) = N i (m)/q i (m) with q i the detection function (see Eq. 3). Since this approach assumes that the Gutenberg–Richter law holds over the unbounded magnitude range, any deviation from the law observed after correction for incompleteness would suggest that a different physical process is in play at low magnitudes. Using a fixed L in Eq. (9) means that the q model depends on cell i (Fig. 3; Eq. 8). We use the cumulative normal distribution model for \(L > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{e}\) (heterogeneous composite model; Fig. 1a) and the exponential model for \(L \le \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{L}_{e}\) (homogeneous elemental model; Fig. 1b). Results are shown in Fig. 4b and indicate that the data collapse continues in the range 0.4 ≤ m < 2.1 for at least some h when the seismicity data are corrected for incompleteness. Scattering remains high and relates to under-sampling of the original data at low m values, similarly to the under-sampling observed at high m values. The scattering at low magnitudes is, however, lower here than in the case where only one detection model q would be used. These results suggest that the behavior of events at m < m c might be informative about b and D once the scale variance of the detected seismicity phenomenon is considered. This has yet to be confirmed by robust sensitivity analyses in various applications (e.g., in b-value mapping; Tormann et al. 2014; Kamer and Hiemer 2015).

4.2 Implications for the Earthquake Detection Process

The Gaussian detection model q (m) = Φ(m | μ, σ) was proposed long ago based on the assumptions that both the true magnitude m A and the threshold magnitude m T are normal variables—an event being detected if m A > m T (Ringdal 1975). This would reflect a lognormal distribution of the seismic noise amplitude (Richter 1935). Noise amplitude, defined as

$$A_{\text{norm}} = \left| {\frac{{A(t) - \overline{A(t)} }}{{\sqrt {\overline{{A(t)^{2} }} - \overline{A(t)}^{2} } }}} \right|$$
(10)

with A (t) the raw amplitude time series, has been approximated as lognormal in studies of station detection capability (Freedman 1967; Zheng et al. 2012).

An exponential detection model of magnitudes (Eq. 4) means a linear detection model of amplitudes and therefore suggests a triangular distribution of the noise amplitude A (t). This is illustrated in Fig. 5a where 100 s of waveform data from the WSF station (east–west direction) of the Taiwanese seismic network is shown for comparison (use of other stations, directions and time periods does not significantly change the results). The model q(A) = Pr(Detected | A) ∝ A for A < A c, with A c the completeness amplitude, is sketched in gray. Figure 5b shows the same empirical distribution in terms of A norm, which shows some skewness in the log10 space. Here, we simulate 1000 A (t) samples from the triangular distribution shown in Fig. 5a and compute the A norm distribution (0.05 and 0.95 quantiles as dotted gray curves in Fig. 5b). While a systematic analysis of waveform data would be needed to prove or disprove a triangular distribution of the seismic noise, our aim is not here to validate the empirical model of Mignan (2012) but to very briefly consider the earthquake detection process in a novel way, by looking at the possible relationship between noise amplitude distribution and FMD shape (Fig. 5). Such a link has never been made, to the best of our knowledge.

Fig. 5
figure 5

Seismic noise amplitude distribution, empirical (histograms) and inferred from the elemental FMD model (gray curves): a Raw amplitude A. The inset shows an example of 100 s of waveform data from the WSF station (east–west direction). Its distribution in amplitude may be approximated by a triangular distribution, which would explain Eq. (4) or in amplitude space q (A) = Pr(Detected | A) ∝ A for A < A c, with A c the completeness amplitude; b Normalized amplitude A norm (Eq. 10). The gray curves (solid and dotted) represent, respectively, the 0.50, 0.05 and 0.95 quantiles obtained for 1000 A(t) simulations sampled from the triangular distribution shown in (a)

Full size image

Our results, however, emphasize the fallacy of conclusions on the earthquake detection process inferred from regional FMD analyses. Use of the cumulative normal distribution Φ(m | μ, σ) is often justified based on the curved shape of regional FMDs (Ringdal 1975; Ogata and Katsura 1993) although its extrapolation to higher resolutions has already been shown to be incorrect (Mignan 2012). Therefore, the parameters μ and σ of Φ have no physical meaning and only represent an artifact of observation due to the difference between observational scale and the intrinsic scale of the detected seismicity phenomenon previously described. In this view, the physical origin of parameter k of Eq. (4) has yet to be understood and interpreted in terms of amplitude measurement uncertainty.

5 Conclusions

Earthquake detectability issues have always hampered the study of seismicity at the lower magnitudes. From rule of thumb, using only m ≥ m c means that up to about half of all the data are systematically discarded. In this article, we have identified the intrinsic spatial scale of the detected seismicity over m ∈ (−∞, +∞) (Fig. 3; Eq. 8), which allows us to better understand changes in the shape of the FMD, and therefore to reduce ambiguity on m c and to correct for data incompleteness.

As noted by Pereira (2001), not considering the intrinsic scale of the process leads to artifacts of observation, which may explain why data below m c had previously been considered unstable (Kagan 2002). While the usefulness of the data below m c has yet to be confirmed in future studies, there would be a clear advantage in being able to exploit this information. Statistical analyses would gain using larger datasets, for instance in the investigation of the prognostic value of earthquake precursors (see meta-analysis by Mignan 2014), which remains one of the main challenges in the field of statistical seismology.