Abstract
A suitable knowledge of the orientation and motion of the Earth in space is a common need in various fields. That knowledge has been ever necessary to carry out astronomical observations, but with the advent of the space age, it became essential for making observations of satellites and predicting and determining their orbits, and for observing the Earth from space as well. Given the relevant role it plays in Space Geodesy, Earth rotation is considered as one of the three pillars of Geodesy, the other two being geometry and gravity. Besides, research on Earth rotation has fostered advances in many fields, such as Mathematics, Astronomy and Geophysics, for centuries. One remarkable feature of the problem is in the extreme requirements of accuracy that must be fulfilled in the near future, about a millimetre on the tangent plane to the planet surface, roughly speaking. That challenges all of the theories that have been devised and used to-date; the paper makes a short review of some of the most relevant methods, which can be envisaged as milestones in Earth rotation research, emphasizing the Hamiltonian approach developed by the authors. Some contemporary problems are presented, as well as the main lines of future research prospected by the International Astronomical Union/International Association of Geodesy Joint Working Group on Theory of Earth Rotation, created in 2013.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Relevance and Features of the Earth Rotation Problem
The accurate determination and prediction of the orientation and the motion of the Earth in the space is needed in various fields, especially since the advent of the space age. Direct examples in which that knowledge is essential are: carrying out astronomical observations from an observatory located on the Earth's surface, making observations of spacecrafts from ground-located tracking stations, observing the Earth from the space, determination and prediction of satellite orbits, etc.
A good knowledge of the Earth's orientation is necessary for any applications related to pinpointing of points or objects with respect to the Earth at a global scale. There is a very broad set of such applications, ranging from popular handy simple navigation devices to the most sophisticated investigations of Space Geodesy that address the quantification of the physical effects of climate change. The most popular issue is the determination of sea level variation, whose magnitude is typically of a few millimetres per year. Besides, there is a variety of geodetic research aimed at finding the fingerprints of different geophysical processes: mass movements in oceans, ice sheets, terrestrial water storages, displacement fields associated with earthquakes, etc. (Plag et al. 2009a, 2010) All of those geodetic studies have very demanding requirements of accuracy. The GGOS (Global Geodetic Observing System) initiative developed by the International Association of Geodesy (IAG) targeted the requirements of accuracy on the level of 1 mm in position and 1 mm/year in stability (Plag et al. 2009b).
The IAG considers Earth rotation as one of the three pillars of Geodesy, because of the relevant role it plays in Space Geodesy, the other two being Earth geometry and gravity. Those “three pillars” provide the basis for the realization of the reference systems required to assign time-dependent coordinates to points and objects, and to describe the Earth’s motion in space. This is not at all new: a quick look to the table of contents of some classic treatises like Tisserand (1891) would suffice to appreciate how the interaction of those pillars have fostered theoretical advances in many fields, such as Mathematics, Physics, Astronomy, Geodesy or Geophysics.
The solution to the Earth rotation problem consists mainly in the determination of the rotation matrix linking the celestial and the terrestrial reference frames. Nowadays, one of its most remarkable features is the extreme requirements of accuracy that must be fulfilled in the near future, at the level of a millimetre on the tangent plane to the planet surface, which corresponds to an angle about 30 \(\upmu\) as from the Earth centre, roughly speaking. Due to its relevance and the broad range of its applications, there is an international service in charge of monitoring and predicting the Earth rotation, the International Earth Rotation and Reference Systems Service (IERS). It was established in 1987 by the International Astronomical Union (IAU) and the International Union of Geodesy and Geophysics (IUGG). IERS is also responsible of the realization and maintenance of the celestial and terrestrial reference frames associated with Earth rotation, namely the International Celestial Reference Frame (ICRF) (Fey et al. 2004) and the International Terrestrial Reference Frame (ITRF) (Altamimi et al. 2011). More information appears in the Annual Reports yearly published by IERS (Dick 2011). This service provides the international community with combined solutions for the EOP (Earth Orientation Parameters) (Bizouard and Gambis 2009) and also publishes the IERS Conventions, which are widely used not only in the field of Earth rotation, but in satellite orbit determination and many other geodetic or geophysical applications (Petit and Luzum 2010).
The Earth rotation is affected by many factors that must be accounted for to obtain solutions suitable to meet the present needs. Apart from the mathematical methods used to derive solutions, the main physical influences come from:
-
Lunisolar gravitational attraction and planetary attraction.
-
Earth figure and tensor of inertia (really not constant but time-varying).
-
Earth internal structure: fluid outer core (FOC), solid inner core (SIC), etc.
-
Effects at the boundaries of the inner layers, with dissipations and topography.
-
Deformations (which produce geometric and dynamical effects).
-
Tides: solid earth tides, ocean tides.
-
Many other geophysical influences: redistribution of ice–water-vapor masses, currents, winds, hydrology, magnetism, post-glacial rebound, earthquakes, etc.
2 The Rigid-Earth Model: A First Step Towards the Solution
Assuming the Earth is a rigid body is a logic first step, which has fulfilled the practical needs of accuracy for centuries. The solutions for nutations are close enough to the actual non-rigid Earth nutations, since the maximum differences between them (for each frequency) are below 30 mas (milliarcseconds), about 1 m on the Earth surface, and therefore irrelevant in ancient observations. The accuracy was thus satisfactory for applications until the development of highly accurate space geodetic techniques. Besides, the rigid model allows a great simplification for several reasons:
-
In this case, perturbations only arise from the gravitational attraction of celestial bodies on an Earth with a constant tensor of inertia.
-
The theoretical definition of the terrestrial frame is trivial, since there are no intricacies associated to deformations.
-
Rigid body rotations have been widely studied for centuries, and there are lots of well-known topics easily found in the literature: Euler equations for rigid body rotation, systems of variables, integrability issues, etc.
-
There are several well-established approaches at hand: Newtonian, Eulerian, Lagrangian, Hamiltonian.
-
The unperturbed motion is essentially the Euler-Poinsot problem; therefore, it is integrable (in the Liouville sense) and convenient to derive asymptotic solutions by means of perturbation methods.
Eulerian formulation The formulation using Euler equations (1749) is the most extended and well-known in rotational dynamics. In the Newtonian framework, we consider an inertial reference system \(\mathcal {F}\) centered at the barycenter \(O\) of the body and a system \(\mathcal {B}\) attached to the body, moving with angular velocity \(\varvec{\omega }\). The velocity of a body particle \(P\) with respect to both frames holds \(\varvec{v} _{\mathcal {F}}=\varvec{v} _{\mathcal {B}}+\varvec{\omega }\times \varvec{r}=\varvec{\omega }\times \varvec{r}\), since \(P\) is in rest in \(\mathcal {B}\). Therefore, the absolute angular momentum \(\varvec{M}\) can be expressed in the body frame as \(\varvec{M}=\Pi \varvec{\omega }\), \(\Pi\) being the matrix of inertia, constant in this case. If \(\varvec{L}\) stands for the external torque, the basic Newtonian equation in the inertial frame, \({\rm d}\varvec{M}_{\mathcal {F}}/{\rm d}t=\varvec{L}_{\mathcal {F}}\), writes in the body frame as
It is usual to choose the body axes of \(\mathcal {B}\) aligned with the principal axes of inertia of the body, and then Euler equation (1) reduces to the most familiar form
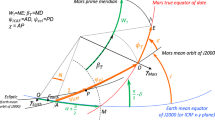
Let us notice that those equations provide the derivatives of the angular velocities, but not the angles specifying the orientation of the body system \(\mathcal {B}\) relative to the inertial one \(\mathcal {F}\). This information is necessary to determine the rotational motion, since usually the torque \(\varvec{L}\) depend on the attitude of the body. Therefore, Eq. (1) must be complemented with other equations. One choice in Astronomy is to describe the attitude by means of the Euler angles \(\psi\), \(\theta\), \(\varphi\), by performing a sequence of three consecutive rotations with respect to the 3, 1, and 3 axes, respectively (Fig. 1, left). The time derivatives of the Euler angles are related to the components of the angular velocity vector \(\omega\) by the kinematical equations (Woolard 1953a; Leimanis 1965)
Variational formulations Eulerian formulations are seldom used nowadays in Earth rotation studies. An exception is the solution by Roosbeek and Dehant (1998), that followed the Eulerian method, with direct computation of torques. Woolard (1953a) used a Lagrangian approach to derive the most accurate solution of his epoch, which was adopted by the IAU for a period. Bretagnon et al. (1988) later computed a highly accurate solution with that formalism. Nevertheless, the most successful variational approach has been the Hamiltonian one. It allowed systematic derivations of accurate solutions with the concourse of perturbation methods based on the Lie series. Kinoshita (1977) established such an approach to rigid Earth rotation that became a model to follow. His solution was the best of its class and was the base of the non-rigid solution by Wahr, adopted by the IAU in 1980. Accuracy was improved later by Kinoshita and Souchay (1990) and Souchay and Kinoshita (1996, 1997). The fundamentals of this method are presented in the next section.
3 The Hamiltonian Treatment of Rigid Earth Rotation
Variables. A key of the success of the Hamiltonian method application to rotation problems is the use of Andoyer variables, also named after Serret (Tisserand 1891; Deprit and Elipe 1993). The fixed frame \(\mathcal {F}\) of coordinates (OXYZ) is transformed into the moving frame \(\mathcal {F}\) (Oxyz) by means of five rotations, since the plane orthogonal to the angular momentum vector (often called Andoyer plane) is used as an intermediate step to go from the equinoctial plane OXY to the equator Oxy. The scheme of rotations is 3–1–3–1–3, and the corresponding angles are \(\left( \lambda ,I,\mu ,\sigma ,\nu \right)\). They are shown in Fig. 1, to the right.
Three of those five angles \(\left( \lambda ,\mu ,\nu \right)\) are canonical coordinates and the other two \(\left( I,\sigma \right)\) are auxiliary angles related to the conjugate momenta through \(\cos I=\varLambda /M\), \(\cos \sigma =N /M\). The canonical momenta are denoted as \(\Lambda\), \(M\), \(N\), and they have a clear dynamical meaning: \(M\) is the modulus of the angular momentum vector \(\varvec{M}\), \(N\) its component along the polar or figure axis Oz of the body, and \(\varLambda\) its component along the OZ axis of the fixed frame. Let us point that the notation \(\left( \lambda ,\mu ,\nu ;\varLambda ,M,N\right)\) corresponds to \(\left( h,g,l;H,G,L\right)\) used by Kinoshita; the auxiliary angle \(I\) (obliquity of the Andoyer plane) has the same notation and \(\sigma\) stands for Kinoshita’s J, the angle between \(\varvec{M}\) and the body figure axis. Further analyses of the Andoyer set appear in Efroimsky and Escapa (2009).
The components of \(\varvec{M}\) in the body system have the expressions
Unperturbed problem In Andoyer variables, the kinetic energy is
It is especially simple in the case of axial symmetry, since all the coordinates are cyclic:
The free motion of a symmetric body is easily described in Andoyer variables. As the potential \(V=0\), the Hamiltonian \(\mathcal {H}=T+V=T\). Therefore, the moments \(M\), \(N\), \(\varLambda\), are constant and angles \(I\), \(\sigma\) are as well. Coordinate \(\lambda\) (representing an ecliptic longitude) is also constant. The remaining two angles, \(\mu , \nu\), are linear functions of time. The sum \(\mu + \nu\) corresponds to the diurnal rotation with angular velocity \(\Omega _{E}\) and \(\nu\) provides the rotation of the angular momentum around the figure (or polar) axis. Its frequency is proportional to the dynamical ellipticity \(H=(C-A)/A\). That is the simplest case of the free polar motion, known as Euler free oscillation.
Let us remark that the solution to the angular variables is computed directly and no previous solution to the angular velocity is needed, unlike in the approaches based on Euler–Liouville equations. The longitude and obliquity of the Earth equator, \(\lambda _f, I_f\) can be computed from the approximate relationships
which hold up to first order in \(\sigma\), of the order of \(10^{-6}\) rad. Those differences are known as Oppolzer terms. The classic precession-nutation angles used in Astronomy are \(\psi =-\lambda _f\) and \(\epsilon =-I_f\), since they are reckoned in the opposite direction.
Perturbing potential The free rotation of a rigid earth is perturbed by the gravitational attraction of the Sun, Moon and planets. The gravitational potential due to a body of mass \(m^*\) and coordinates \((r^*,\alpha ,\delta )\) in the fixed frame has a known expansion as a series of spherical harmonics (SH) multiplied by the corresponding Stokes coefficients. In the case of the Earth, the zonal term due to the Earth oblateness (associated to \(P_{20}\) and also named MacCullagh’s term) is at least 1,000 times larger than the others, and thus provides a good approximation to the potential
It must be expressed in terms of the canonical variables and the coordinates of the disturbing body, assumed to be known functions of time provided by some ephemeris, usually referred either to an inertial (or quasi-inertial) system or to a non-inertial system with known motion (e.g., ecliptic of date). Nutation theories have relied on analytical or semi-analytical ephemeris since a long time ago (Newcombe 1898; Woolard 1953b, etc.), and they still use such ephemeris, instead of numerical ones as in the JPL series (e.g., DE432, Folkner et al. 1994, 2014). The main reason is that nutation theories intend to derive semi-analytical solutions in which the constituent frequencies are explicit, and resorting to numerical ephemeris would introduce additional complications. The ephemeris commonly used are ephemeris VSOP87 (Bretagnon 1982) and ELP2000 (Chapront-Touzé 1980), respectively. The transformation of the standard expansion in SH is a difficult task, since it requires performing five rotations. Kinoshita successively applied Wigner’s theorem of transformation of SH under rotation and calculated the second degree SH of Moon and Sun to obtain up to the order of \(\sigma\)
where subindex \(p\) stands for the perturbing body (S = Sun, M = Moon), the parameter \(k_{p}^{\prime }=3Gm_{p}(C-A)/a_{p}^{3}\) factorises the main terms of the potential generated by body \(p\) and the coefficients \(B_{i}\), \(C_{i,\tau }\), depending on the variable \(I\), are
As for arguments \(\Theta _{i}\), we have that \(\Theta _{i}=m_{1i}l_{M}+m_{2i}l_{S}+m_{3i}F+m_{4i}D+m_{5i}\Omega\), where \(l_{M}\), \(l_{S}\), \(F\), \(D\), and \(\Omega\) are the Delaunay arguments of the Moon and the Sun. Within our level of approximation, we can assume that \({\rm d}\Theta _{i} / {\rm d}t=n_{i}\), the mean motion \(n_{i}\) being constant. Let us stress that the canonical variable \(\lambda\) is implicitly contained in \(\Omega\) through \(\Omega =\Omega _{0}-\lambda\), where \(\Omega _{0}\) is the mean longitude of the Moon referred to the origin of longitude on the ecliptic of date. The numerical values of coefficients \(A_{i}^{j)}\), \(\Theta _{i}\) and \(n_{i}\), as well as of the list of the five integer numbers \(( m_{1i},\, m_{2i},\, m_{3i},m_{4i},m_{5i})\) associated to each value of the index \(i\), depend on the orbital theories of the Moon and the Sun. They were first computed by Kinoshita (1977) and updated by Kinoshita and Souchay (1990) and Navarro (2002).
3.1 Note on the Efficient Expansion of the Potential
A main difficulty of the Hamiltonian theory in the rigid case is the handling of terms of the gravitational potential due to lunisolar attraction. The expansion of the potential contains spherical harmonics (SH) of the perturbing bodies (Sun, Moon and Planets) beyond McCullagh’s approximation. Their spherical coordinates are given by numerical or semi-analytical ephemeris, which provide them as multiple Fourier series whose arguments are linear combinations of the orbital variables of the relevant body. The semi-analytical expansion of those SH is a difficult task because of the large number of terms (thousands), and the help of computer algebra is essential.
The best option is designing and using special purpose symbolic manipulators to handle the so-called Poisson series. More advanced processors exist, capable of manipulating the full expansions of the potential, including canonical variables (Kinoshita series) and performing transformations of SH, even rotations applying Wigner’s Theorem (Navarro and Ferrándiz 2002).
Since the early 1960s, investigators have used computers to generate analytical expressions. The first symbolic processors were developed to work with Poisson series, that is, multivariate Fourier series whose coefficients are multivariate Laurent series,
where \(C_{i_1,\ldots ,i_n}^{j_1,\ldots ,j_m}\in \mathbb {R}\), \(i_1,\ldots ,i_n,j_1,\ldots ,j_m\in \mathbb {Z}\), and \(x_1,\ldots ,x_n\) and \(\phi _1,\ldots ,\phi _m\) are called polynomial and angular variables, respectively. These processors were applied to problems in non-linear mechanics or non-linear differential equations in the field of celestial mechanics. One of their first applications was concerned with the orbital motion of the Moon. Delaunay devised his perturbation method to treat the lunar problem and spent 20 years doing algebraic calculations by hand to solve it. Deprit et al. (1971) extended the solution of Delaunay’s work with the help of a special purpose symbolic processor, and Henrard (1979) pushed it to order \(25\). This solution was improved by iteration by Chapront-Touzé (1980), and planetary perturbations were also introduced by Chapront-Touzé (1980). Later, analytical theories for the rotation of the Earth (Kinoshita 1977) were treated with the help of symbolic computation packages. Nowadays, there are many open problems that require massive symbolic computation. To cite one example, we will refer to the analytical theory of the resonant motion of Mercury. Motivated by the projects of space missions like BepiColombo and MESSENGER, D’Hoedt and Lemaitre (2004) developed a spin–orbit model for the rotation of Mercury. The computation of the spherical harmonics of Mercury are performed with the use of the planetary theory “Variations Séculaires des Orbites Plantaires” (VSOP) (Bretagnon 1988). The VSOP87 analytical solution of the motion of Mercury contains trigonometric series that represent the coordinates of the body (elliptic, rectangular or spherical coordinates according to the version). For instance, the solution for the distance Sun–Mercury (\(r\)) is given as a Poisson series containing 2,371 terms, and so, the calculus of \(1/r\) through a Taylor expansion requires high accuracy symbolic computation with Poisson series containing hundreds of thousands of terms.
Many Poisson series processors have been developed until now, as PSP (Broucke 1970), mechanised algebraic operations (MAO) (Rom 1969), Trigonometric Manipulator (TRIGMAN) (Jefferys 1970), MSNam (Henrard 1986), PARSEC (Richardson 1989), and others.
3.2 Analytical Solutions up to the Second Order
The Hamiltonian method allows the derivation of highly accurate asymptotic solutions, depending analytically on the canonical variables and the arguments of lunisolar and planetary orbits, considered as known functions of time. Accurate solutions need to derive perturbations up to the second order, using, e.g., Hori’s perturbation method (1966). The Hamiltonian can be cast in the form
\(\mathcal {H}_{i}\) being of order \(O(\varepsilon ^{i})\), where \(i\) is a nonnegative integer and \(\varepsilon\) is a small parameter measuring the perturbation. We will sketch this procedure at the second order in \(\varepsilon\) following a similar method to that of Kinoshita (1977).
The algorithm consists in performing a canonical transformation from the actual canonical set \((p,q)\) to a new one \((p^{*},q^{*})\). This transformation is given at the second order by the generating function \(\mathcal {W}=\mathcal {W}_{1}+\mathcal {W}_{2}\), with \(\mathcal {W}_{i}=O(\varepsilon ^{i})\), which depends on the transformed set \((p^{*},q^{*})\) of canonical variables. The transformed Hamiltonian at the second order has a similar form
with \(\mathcal {H}_{i}^{*}(p^{*},q^{*})=O(\varepsilon ^{i})\). In addition, some extra conditions are imposed on \(\mathcal {H}_{i}^{*}\) in order to ensure that \(\mathcal {H}^{*}\) is easier to integrate than \(\mathcal {H}\). In particular, we force \(\mathcal {H}^{*}\) to be free from periodic terms, that is to say, we combine the Lie transformation with an averaging method. By so doing, the transformed Hamiltonian \(\mathcal {H}^{*}\) and the generating function \(\mathcal {W}\) are determined by the so–called equations of the method (Hori 1966), which can be written up to the second order as
where the subscripts per and sec denote the periodic or secular part of the corresponding function, and the Poisson brackets are computed in the \((p^{*},q^{*})\) canonical set. The integrals are evaluated along the solutions to the unperturbed problem generated by the Hamiltonian \(\mathcal {H}_{0}^{*}\), obtained by literal substitution of the variables \((p,q)\) by the variables \((p^{*},q^{*})\) in \(\mathcal {H}_{0}\). The time evolution of the transformed canonical variables \((p^{*},q^{*})\) is determined by solving the Hamiltonian equations
The variation of a function \(f\left( p,q\right)\) of the canonical variables can be computed at the second order by the expression \(f(p,q)=f^{*}(p^{*},q^{*})+\Delta f(p^{*},q^{*})\), with
The determination of the transformed Hamiltonian \(\mathcal {H} ^{*}\) and the generating function \(\mathcal {W}\) allows to describe the time evolution of any variable of the Earth rotation up to the second order in the perturbation parameter \(\varepsilon\). For the sake of brevity, only a few expressions corresponding to a first order integration are displayed, following Getino and Ferrándiz (1995). The first order generating function \(\mathcal {W}_{1}\) is
with
\(n_\mu , n_i\) being the mean motions of \(\mu\) and \(\tau _i\), i.e., \(\left( \frac{{\rm d}\mu }{{\rm d}t},\frac{{\rm d}\Theta _i}{{\rm d}t}\right)\) respectively.
The perturbations of all the canonical variables can be obtained in a straight forward manner by taking derivates before being simplified doing \(\sigma =0\), in short as
The first order nutations of the angular momentum axis (or Andoyer plane), are
with \(K_0=K^{\prime }_0/M\). The nutations of the figure axis are obtained by adding the Oppolzer terms
No other approach but the Hamiltonian succeeded in computing the nutations up to the second order. Solutions provide the longitude of the equinox and the obliquity of the equator as Poisson series of the arguments \(\Theta _i\), with coefficients depending analytically of Andoyer variables and of numbers \(A_{i}^{j)}\). Final series result after numerical evaluation. Solutions can be computed for any of the three axes of interest: axis of figure, angular momentum and angular velocity. The number of accounted terms is very high:
-
REN 2000 solution (Souchay et al. 1999) contains several 1,000 terms of lunisolar and planetary origin; the truncation level is approximately 0.1 \(\upmu\)as.
-
FGN 2000 solution (Ferrándiz, Navarro and Getino) fully derived by computer algebra has a similar number of terms. A detailed second order solution showing the origin of the various terms was published by Getino et al. (2010).
Solutions only include the perturbations due to the external potential (“forced nutations” and precession). The secular part of the solution, arising from Eq. (13) provides the precession. The non-rigidity effects on precession are so small (Williams 1994) that is not difficult to read that the precession is independent of the considered Earth model, which is not really true (Ferrándiz et al. 2004, 2007).
4 Effect of the Liquid Core
Poincaré equations In (1891), Chandler detected variations of latitude in astrometric observations that pointed to a pole wobble, with a period of about 430 days, far from the Euler period for a rigid earth of about 305 days. The discovery of the so-called Chandler wobble (CW) stimulated the research on the effects of elasticity and the potential existence of a liquid core on Earth rotation. Poincaré (1901, 1910) developed the first satisfactory model for an Earth model consisting of a rigid mantle and a liquid core undergoing certain simple motion, often denoted as Poincaré model. He used two differentiated approaches to derive a set of equations quite similar to those of Euler,
Here, \(\varvec{M}\) and \(\varvec{L}\) are the total angular momentum and torque acting on the whole earth, \(\varvec{\omega }\) the angular velocity of the frame linked to the mantle and \(\delta {\varvec{\omega }}\) the relative angular velocity of the fluid core with respect to the mantle. \(\varvec{M}_{c}\) is the total angular momentum of the core, given by \(\varvec{M}_{c}=\Pi _c \left( \varvec{\omega }+\delta {\varvec{\omega }}\right) ,\) \(\Pi _c\) being the tensor of inertia of the core in the mantle frame. Assuming axial symmetry and after neglecting the second and higher order terms in \(\omega _1,\omega _2,\tilde{\omega }_3=\omega _3-\Omega _{E}\) and \(\delta \varvec{\omega }\), the equations for \(\tilde{\omega }_3\) and \(\delta \varvec{\omega }\) happen to be uncoupled and the problem reduces to four linear equations. In this approximation, the complex variables \(u=\omega _1+i\omega _2\), and \(v=\delta \omega _1+i\delta \omega _2\) oscillate with two free frequencies
whilst the solution of the free polar motion (PM) is a linear combination of \({\rm e}^{i\sigma _1 t}\), \({\rm e}^{i\sigma _2 t}\). The frequency \(\sigma _1\) corresponds to CW, which replaces the Euler free oscillation of the rigid case. As \(A_m < A\), frequency \(\sigma _1\) is larger for a Poincaré Earth than for a rigid Earth, so that the period of the polar oscillation is shortened by the fluid core. The lengthening of the period is mainly due to the elastic yielding of the earth, as already explained by Newcombe (1892)—see also Getino and Ferrándiz (1995) who performed more detailed calculations.
Besides, a second new free frequency \(\sigma _2\) emerges due to the presence of the liquid core, that is known as NDFW (nearly diurnal free wobble) or RFCN (retrograde free core nutation), because it does not contribute solely to PM, but also gives rise to an observable nutation, named free core nutation (FCN). It was predicted by theory in early times (Vicente and Jeffreys 1964), but its observation remained elusive for a long period and only could be evidenced after some years of very long baseline interferometry (VLBI) observations.
Poincaré (1910) also found the ratio of the amplitudes of the nutations of a rigid planet with and without a liquid core (in the linear approximation). That established the basis of the transfer function approach, which has been followed in most of the research on non-rigid earth nutations. Besides, he included in that paper a section treating a body with a fluid core contained in an elastic shell.
Hamiltonian approach to Poincaré’s earth model Nevertheless, Poincaré did not perform any numerical evaluation of his solution to obtain values of the main nutations. Accurate solutions for a Poincaré model were computed much later by Getino (1995) and Getino and Ferrándiz (1997), but using their Hamiltonian method. Let the tensors of inertia be \(\mathbf {\Pi }_{{\it m}}\) for the mantle, \(\mathbf {\Pi }_{{\it c}}\) for the core and \(\mathbf {\Pi =\Pi }_{{\it m}}+ \mathbf {\Pi }_{{\it c}}\) for the whole Earth, which are assumed constant in a frame attached to the (rigid) mantle. If \(\mathbf {M}\), \(\mathbf {M}_{{\it m}}\) and \(\mathbf {M}_{{\it c}}\) are, respectively, the angular momenta of the total Earth, the mantle and the core, they satisfy:
Notice that setting \(\mathbf {M}_{{\it c}}= \mathbf {\Pi }_{{\it c}}\left( \varvec{\omega }+\delta \varvec{\omega }\right)\) means that an appropriate definition of the core rotation (Moritz 1982) has been made, so that it is referred to a Tisserand frame (Moritz 1982), as detailed in Getino (1995). The kinetic energy is thus
This expression is canonically formulated by means of a set of canonical variables, \(\lambda\), \(\mu\), \(\nu\), \(\Lambda\), \(M\), \(N\) for the whole Earth, and \(\lambda _{{\it c}}\), \(\mu _{{\it c}}\), \(\nu _{{\it c}}\), \(\Lambda _{c}\), \(M_{c}\), \(N_{c}\) for the core, with the help of the auxiliary angles \(\sigma\), \(I\), \(\sigma _{c}\), \(I_{c}\) described by Getino (1995). The angular momenta \(\mathbf {M}\) and \(\mathbf {M}_{{\it c}}\) are given by
where \(K=M\,\sin \sigma ,\;\;\;K_{c}=M_{c}\,\sin \sigma _{c}.\) Note that \(\sigma\) and \(\sigma _{c}\) are small quantities, of the order of \(10^{-6}\) rad. The kinetic energy can be written as
\(A=A_{m}+A_{c}\), \(C=C_{m}+C_{c}\), being the principal moments of the total Earth. Let us remark that these hypotheses pose no problem related to the terrestrial frame, since the mantle is rigid and its principal axes are well defined. However, the number of canonical variables has been doubled, which increases the difficulty of the treatments. But there is an additional, essential difference with respect to the rigid case: resonance phenomena occur, which amplify the amplitudes of some Oppolzer terms, hence of nutations. That fact helps to constrain the values of certain geophysical parameters. Besides, the unperturbed problem is not integrable any more, irrespective of the axial symmetry of the body. The integrability issues in this model were studied by Ferrándiz and Barkin (2001).
5 Theories of Non-Rigid Earth Nutations
5.1 Two-Layer Earth Models
As we pointed out above, explaining the observed CW period requires taking into account elasticity besides the liquid core. A number of solutions were developed between about 1950 and 1990 by considering Earth models composed of an elastic mantle and a liquid core, the standard two-layer model. They made use of the theory of elasticity, developed by Cauchy, Green, Poisson, Stokes, Lord Kelvin, etc. These approaches are very different, but they share some features:
-
Kelvin solutions of the Laplace equations in terms of SH are used, as well as generalizations, including the assumption of variability for some parameters, such as density or Lamé parameters.
-
Some simplifying hypotheses are usually made, as radial dependence of parameters or certain equilibrium conditions.
-
In general, this procedure allows the reduction of the original continuous problem of elasticity to a discrete one, with the relevant parameters determined by quadratures assuming certain rheological models.
Jeffreys and Vicente (1957) proposed a variational formulation of Lagrangian type; therefore, the computation of the internal dissipative moments is avoided. In Molodenski’s model (1961), the elastic equations for the mantle are approximated by spherical functions, and the fluid core is treated using hydrodynamical equations. SOS equations (Sasao et al. 1980) had deep impact on later research. They are a simple generalization of Poincaré’s, including elasticity and dissipations at the core–mantle boundary (CMB) due to friction and electromagnetic coupling. The original derivation was carried out by direct methods (Euler–Liouville). Using variational methods allowed a drastic simplification (Moritz).
The IAU 1980 nutation theory Wahr’s solution Wahr (1981) was obtained by applying a certain transfer function to the rigid earth solution by Kinoshita (1977). An IAU Working Group proposed its adoption (Seidelmann 1982) and the theory was endorsed by IAU as its first non-rigid Earth nutation theory in 1981. This solution follows the method of Smith and Whar: The partial differential equations of the elastic problem are transformed into an infinite system of ordinary differential equations through a series expansion of spheroidal and toroidal harmonics. A drastic truncation produces a finite system. The resulting equations are integrated numerically over the Earth volume, assuming a certain rheological model. This solution gives the nutations of an oceanless, elastic solid Earth with a fluid core. In the framework of IAU 1980, other effects not addressed in the official theory (oceanic, atmospheric, anelastic, etc.) are treated in the moving (terrestrial) reference frame, mainly using some versions of the Euler–Liouville equations, and are usually classified as “polar motion” terms (see Sect. 6).
Earth elasticity in the Hamiltonian method The Hamiltonian method contributed with a series of papers by Getino and Ferrándiz who introduced the Hamiltonian formalism to study an elastic Earth (1990, 1991, 1995). Let us notice that the definition of the body frame has no special difficulties under the assumption of linear elasticity, since the deformations have known expressions depending on constant Love numbers, and the variations of the principal axes and moments of inertia can be derived analytically (Barkin and Ferrándiz 2000). More properties of the rotation of weakly deformable bodies are given by Barkin (1998, 2000a, b).
Getino and Ferrándiz (2000, 2001) also combined their previous results to derive an accurate Hamiltonian solution for a two-layered earth made of a liquid core and an inelastic mantle, and accounted for dissipation at CMB. That way of proceeding guarantees consistency of the new considered effects with the former pieces of theory. For instance, the main change when elasticity is put into the Poincaré model is the addition of a new term \(T_{t}\) to the Hamiltonian, which represents the increment of the kinetic energy due to the tidal deformation and is given by
where \(D_{m,c}^{t}\) are constants related to the Love number \(k_{2}\) and functions \(t_{i,j}\) have expansions similar to the components of the potential.
5.2 Three-Layer Earth Models
The improvements of the space geodetic observation techniques since the late 1980s revealed that IAU1980 was not accurate enough. Besides, the launch and operation of new geodetic satellites improved the observational possibilities and contributed to obtaining more insight into matters such as bodily tides and other geophysical properties of the Earth. New investigations aimed at explaining the new results, among them Dehant et al. (1999). Mathews et al. (1991a, b) introduced a solid inner core in the basic Earth structure. An empirical nutation model was adopted in the IERS Conventions 1996 (McCarthy 1996). In this context, an IAU Working Group on non-rigid Earth nutation theory started in 1994 and recommended that theories be based on geophysical models closer to the actual Earth (Dehant et al. 1999).
Most of the theories developed in that epoch assumed a three-layered Earth made of elastic mantle, fluid outer core (FOC) and solid inner core (SIC). They had to rely upon a pre-existent rigid Earth solution, since they used a transfer function approach. Depending on theories, elasticity might be extended to deal with in-elastic or an-elastic assumptions, include dissipations in the inner layers boundaries or consider oceanic and atmospheric effects to some extent. Among those theories, we can cite first DD97 (Defraigne and Dehant 1998), Sch97 (Schastok 1997), Hg2000 (Huang et al. 2001) among the main differentiated approaches.
In March 2000, three theories were selected as candidates to become the IAU 2000 nutation model (Dehant 2002). They were:
-
MHB2000 (Mathews et al. 2002): a transfer function derived from a generalization of Poincaré–SOS equations was applied to REN2000. It was complemented with the Kinoshita–Souchay–Folgueira (1999) planetary perturbations for the rigid Earth.
-
SF2000 (Shirai and Fukushima 2000): applied a numerical convolution in the time domain to adjust parameters of Herrings transfer function.
-
GF2000 (Getino and Ferrándiz 2000): Hamiltonian, analytical theory for the Earth rotation, extending Kinoshita and Souchay’s rigid Earth theory. It was complemented with the planetary non–rigid perturbations by Ferrándiz–Navarro–Getino and Huang et al. oceanic corrections, the final series being named FGHN.
All of them fit a low number of basic Earth parameters to observations and got similar accuracy, about 150 \(\upmu\)as in terms of wrms (weighted root mean squared) observations-model differences (if an empirical model for FCN is used). The accuracy of IAU 1980 was thus improved in more than one order of magnitude. MHB2000 was preferred and selected as IAU2000, and it is in force since 2003. In that year Fukushima (2003) published a new precession theory. The IAU1976 model of the precession (Lieske et al. 1977) was changed 6 years later and the P03 model by Capitaine et al. (2003) was adopted as the IAU2006 precession model (Hilton et al. 2006).
5.3 The Hamiltonian Method
Main features The Hamiltonian or global approach is the only one that allows the direct derivation of a non-rigid solution up to the second order of perturbation, in a fully consistent manner, since it is independent of any previous rigid Earth solution. That is because transfer function approaches are intrinsically linear. The rigid solution can be recovered when some parameters vanish. The calculation of some poorly known internal torques is avoided, since the approach is variational. The effect of geophysical Earth models is concentrated in a reduced set of parameters. Analytical solutions are convenient for several reasons, like fitting parameters, allowing the identification of resonances and providing more insight into the Earths interior and geophysical properties. Besides numerical methods have failed to provide good solutions in the non-rigid case so far: the attempts which have been successful within a fitting time interval (Krasinsky 2006) showed a quick degradation when extrapolated beyond that interval (Capitaine et al. 2009).
Free motion of a three layers Earth in the Hamiltonian approach The definition of the Andoyer variables for FOC and SIC takes into account the relations among a frame fixed to the mantle, \(Ox_my_mz_m\), the Andoyer planes defined by the angular momentums of FOC and SIC, and frames “attached” to the FOC or SIC, \(Ox_fy_fz_f\) or \(Ox_sy_sz_s\). It originates a set of 18 canonical variables, \(\lambda\), \(\mu\), \(\nu\), \(\Lambda\), \(M\), \(N\) for the total Earth, \(\lambda _{f}\), \(\mu _{f}\), \(\nu _{f}\), \(\Lambda _{f}\), \(M_{f}\), \(N_{f}\) for the fluid outer core, and \(\lambda _{s}\), \(\mu _{s}\), \(\nu _{s}\), \(\Lambda _{s}\), \(M_{s}\), \(N_{s}\) for the solid inner core, with auxiliary angles \(\sigma\), \(I\), \(\sigma _{f}\), \(I_{f}\), \(\sigma _{s}\) and \(I_{s}\). Their geometrical meaning is displayed in Fig. 2. Denoting by \(\mathbf {M}\), \(\mathbf {M_f}\) and \(\mathbf {M_s}\) the absolute angular momenta of the whole earth, FOC and SIC, respectively; the canonical moments satisfy
The three layers Earth kinetic energy \(T\) is written as
\(\mathbf {\Pi }\), \(\mathbf {\Pi _f}\) and \(\mathbf {\Pi _s}\) being the respective inertia matrices. The angular momenta hold
with \(K=M\,\sin \sigma ,K_{f}=M_{f}\,\sin \sigma _{f} ,K_{s}=M_{s}\,\sin \sigma _{s}\).
The explicit expression of the Hamiltonian is involved even for the unperturbed motion, especially if no restrictive hypothesis on the SIC attitude is made. Escapa et al. (2001) derived a solution to the linearised equations, which gives the frequencies of the four normal modes or free harmonic oscillations of the rotation pole in terms of the ellipticities and an additional small parameter \(\delta\):
Recent progress in the Hamiltonian theory of non-rigid Earth Since the year 2000, many effects have been investigated by different authors and under various approaches. Several effects have been found to contribute to the nutations with direct or indirect terms reaching the magnitude of some tens of \(\upmu\)as. Most of them are not included in the current IAU or IERS models. Those terms are often referred to as of second order, although they can be cast in at least two distinct groups. The first group is made of second order terms in the sense of perturbation theory (crossing of the ordinary first order precession–nutation terms with themselves). They are part of a solution that is non-linear with respect to the dynamical ellipticity \(H\). The other group gathers small terms of various physical origins but sharing some properties: arising from unaccounted terms of the potential, like high frequency nutations (Escapa et al. 2002) and indirect effect of sectorial and tesseral third order harmonics (Ferrándiz et al. 2003), effect of fluid core on the precession (Ferrándiz et al. 2004, 2007), direct effects of the actual rotation of the inner core (Escapa et al. 2012), effects on nutations (Ferrándiz et al. 2011) of the observed \(J_2\) variation (Cheng and Tapley 2004; Cheng et al. 2011; Cox and Chao 2002), and other time variations of the geopotential as unaccounted effects of tidal models (Ferrándiz et al. 2011), etc. The Hamiltonian method provided a systematic, consistent procedure to approach all of them in the non-steady, non-rigid case.
6 The Solution for Polar Motion
Theories of earth rotation usually devote a part to calculate the frequencies of the unperturbed or free polar motion (PM), corresponding to the oscillations or wobbles of the axis of angular velocity or angular momentum around the figure axis or vice versa. Let us note that the differences between free periods in the rigid and non-rigid cases are more marked than those in the corresponding forced motions (nutation amplitudes), whose main components are the so-called Poisson terms, practically independent of the Earth model. Conversely, the amplitudes and phases of the polar wobbles are highly dependent on the Earth physics. Woolard already mentioned the relevance of geophysical effects on nutations and what he called diurnal nutations, although his terminology differs from the currently used.
The main components of nutations have long periods in the “inertial” frame. However, the main components of PM have long periods in the terrestrial or body-fixed frame, therefore they are in the diurnal band when seen from the inertial frame. However, the terrestrial frame is more convenient for their study as well as their determination since the advent of radio-interferometric techniques like VLBI.
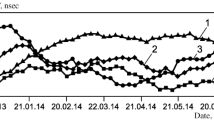
In fact, the actual motion of the Earths pole, displayed in Fig. 3, has not been fully explained by any theory yet. It includes noticeable changes of amplitudes and phases of its main components (the Chandler wobble with an amplitude usually ranging from 100 to 200 \(\upmu\)as and the annual term with an amplitude nearby 100 \(\upmu\)as) as well as a long-term drift (Barkin 2000a, b; Schuh et al. 2001). A thorough review can be found in, e.g., Gross (2007).
Whilst nutations arise from a mainly astronomical forcing, the free wobbles of the pole are excited mainly by geophysical processes, and are difficult to predict (Chao and Gross 1987; Dickey et al. 2002, Gross et al. 2005). For that reason, the solution for the forced PM is not derived analytically along with the nutations, but is computed from different equations using empirical time series providing the relevant excitation functions (Gross 1992; Brzeziński 1992).
That behaviour was essential for the definition of the set of Earth orientation parameters (EOP) currently in use. In 1982, an IAU Working Group on Nutation (Seidelmann 1982) recommended the adoption of five EOP, namely: the precession/nutation angles \(\epsilon\), \(\psi\), referred to the equinox and equator; UT1 (universal time 1), corresponding to the sidereal diurnal revolution and GMST or GAST (Greenwich Mean Sidereal Time or Greenwich Apparent Sidereal Time); the polar motion angles \(x\), and \(y\).
This set provides the transformation of coordinates from the celestial to the terrestrial frame (or vice-versa) by performing five rotations. The transformation is mathematically redundant, since the relative orientation of two reference systems can be specified by only three independent parameters. Nevertheless, that redundancy was convenient for the analysis of the VLBI observations of Earth rotation, which started in the early 1980s. It proceeded by fitting one set of five EOP to each observation session spanning a whole day.
7 Present State of the Earth Rotation Modelling and Outlook
Since the IERS establishment, EOP solutions are provided by IERS along with several Analysis Centres. Besides VLBI, other techniques contribute to determine a subset of EOP (UT1 and PM), namely satellite laser ranging (SLR) and GNSS (Global Navigation Satellite Systems). Time series of daily EOP values are produced by IERS (Bizouard and Gambis 2009), by a combination of individual solutions computed by various associated Analysis Centres for each technique. Nowadays, IERS releases two sets of EOP related by a known transformation, since the nutation offsets \(dX, dY\) and the Earth rotation angle (ERA) were recommended to replace the former three equinox-based EOP after a new paradigm was adopted by IAU in 2000, based in the use of the celestial intermediate origin and pole (CIO and CIP, respectively). Precise definitions of the main and auxiliary parameters and frames can be found in, e.g., the IERS Conventions 2010, Supplement to the Nautical Almanac (Urban and Seidelmann 2013) or standards of fundamental astronomy (SOFA) documentation (Hohenkerk 2010).
Current accuracy of EOP series is difficult to assess. Comparisons between combined solutions and individual solutions corresponding to different techniques and analysis centres provide some insight into their accuracy or uncertainty. Following the IERS Annual Report 2011 (Dick 2011), the uncertainty of VLBI solutions may be near 90 \(\upmu\)as for nutations in average and in about 170 \(\upmu\)as for PM. The accuracy of precession/nutation models, when used to make forward predictions, is stabilised at around 150 \(\upmu\)as, in terms of wrms of the observation-model differences, and the figures are larger for PM prediction. The remarkable efforts made in the last years provided a better insight into the problem and unveiled new potential sources of error, but have not been compensated yet by a significant reduction of the residuals. Let us recall that the IAG’s Global Geodetic Observing System (GGOS) initiative demands an accuracy of 1 mm to the systems of reference, besides a stability in time of 0.1 mm/year. That corresponds roughly to a value of 30 \(\mu\)as for angular EOP (2 \(\mu\)s for time).
From the observational side, the accuracy and performance of the major techniques is increasing. Therefore, series of more accurate EOP will be available in a few years. Besides, higher time resolution is expected. There are still many difficult open problems, such as magnetic effects (Huang et al. 2011), motions of inner layers (Barkin and Vilke 2004), relativistic effects (Klioner et al. 2009), consistent and comprehensive treatment of a more realistic time-varying earth model, etc. Clearer separation of nutations and polar motion is also sought as we approach the EOP determination at a sub-diurnal rate (Nilsson et al. 2010) and non-predictable constituents are accounted in the nutation angles like the free core nutation (FCN) (Lambert 2007; Krasna et al. 2013), whereas some short periodic predictable astronomical effects are included into PM (Getino et al. 2001; Escapa et al. 2002, Brzezinski 2001).
In this context, the International Association of Geodesy (IAG) and the International Astronomical Union (IAU) set up a new Joint Working Group on Theory of Earth Rotation (or JWG ThER) in April 2013. The purpose of the new JWG is: “To promote the development of theories of Earth rotation that are fully consistent and that agree with observations and provide predictions of the Earth rotation parameters (ERP) with the accuracy required to meet the needs of the near future as recommended by, e.g., GGOS, the Global Geodetic Observing System of the IAG. Its structure is more complex than usual and adapts to the characteristics of the current EOP, as well as the specialised fields of research. The people in charge are:
-
Chair: José M. Ferrándiz (IAU)
-
Vice-Chair: Richard S. Gross (IAG)
The JWG is composed of three Sub-Working Groups (SWG):
-
1.
Precession/Nutation (Chair: Juan Getino)
-
2.
Polar Motion and UT1 (Chair: Aleksander Brzezinski)
-
3.
Numerical Solutions and Validation (Chair: Robert Heinkelmann)
These SWG should work independently but in parallel for the sake of efficiency, and they must be linked together as closely as the needs of consistency demand. More information is available in Ferrándiz and Gross (2014) and on the JWG website: http://web.ua.es/en/wgther/.
7.1 Future Prospects of the Hamiltonian Method
Meeting the stringent GGOS accuracy and stability goals is a challenging task, whose fulfilment requires a joint cooperative effort of the scientific community involved in the determination, modelling and prediction of Earth rotation. In the authors’ opinion, the Hamiltonian approach can provide a valuable contribution to the theoretical modelling because of some of its features. First, the treatment addresses the Earth rotation globally, as a whole problem, and its previous results, described in former sections, show that the theory can incorporate any kind of geophysical models or effects that have been considered up to date, like the Earth division in solid and fluid layers, the various assumptions on its elastic behaviour, the dissipations at the layers boundaries, the time variation of the geopotential, etc. It also allows the incorporation of small corrections obtained independently by other theories. The inclusion of all the components in a sole Hamiltonian function (or more precisely formalism, to distinguish the generalised forces) helps to assess the magnitude of any neglected effect and ensures the self-consistency of the developments, so that there is no need to introduce corrections aimed at restoring consistency when some background models are updated. But the essential characteristic of the method is its capability to derive solutions with a prescribed level of accuracy in a systematic way, by calculating the approximate solution up to the suitable order of perturbation (usually first or second, depending on the magnitude of each group of terms), as well as to identify the contributions of the different effects included in the chosen geophysical model. This last property is not shared by any solution derived by numerical integration that also can reach high accuracy, but cannot separate the free motion component of the solution to the Earth attitude from the forced one, which is a difficulty according to the current conventions and EOP definitions.
References
Altamimi, Z., Collilieux, X. and Metivier, L. (2011), ITRF2008, an improved solution of the International Terrestrial Reference Frame, J. Geod. 85(8), 457–473.
Barkin, T. V. (1998), Unperturbed chandler motion and perturbation theory of the rotation motion of deformable celestial bodies, Astron. Astrophys. Trans. 17(3), 179–219.
Barkin, Y. V. (2000a), Towards on explanation of the secular motion of the earth’s rotation axis pole, Astron. Astrophys. Trans. 19(1), 13–18.
Barkin, Y. V. (2000b), Perturbated rotational motion of weakly deformable celestial bodies, Astron. Astrophys. Trans. 19(1), 19–65.
Barkin, Y. V. and Ferrándiz, J. M. (2000), The motion of the Earth’s principal axes of inertia caused by tidal and rotational deformations, Astron. Astrophys. Trans. 18, 605–620.
Barkin, Y. V. and Vilke, V. G. (2004), Celestial mechanics of planet shells, Astron. Astrophys. Trans. 23(6), 533–553.
Bizouard, C. and Gambis, D. (2009), The Combined Solution C04 for Earth Orientation Parameters consistent with International Terrestrial Reference Frame 2005, IAG Symp 134, 265–270.
Bretagnon, P. (1982), Theory for the motion of all the planets—The VSOP82 solution, Astron. Astrophys. 114, 278.
Bretagnon, P. (1988), Planetary theories in rectangular and spherical variables. VSOP 87 solution, Astron. Astrophys. 202, 304–315.
Bretagnon, P., Rocher, P., and Simon, J.-L. (1997), Theory of the rotation of the rigid Earth, Astron. Astrophys. 319, 305–317.
Broucke, R. (1970), How to assemble a Keplerian processor, Celest. Mech. 2, 9–20.
Brzeziński, A. (1992), Polar motion excitation by variations of the effective angular momentum function: considerations concerning deconvolution problem. Manuscr. Geod. 17, 3–20.
Brzeziński, A. (2001), Diurnal and sub-diurnal terms of nutation: a simple theoretical model for a nonrigid Earth, In N. Capitaine (ed.), Proc. of the Journées 2000—Systèmes de Référence Spatio-temporels, Observatoire de Paris, pp. 243–251.
Capitaine, N., Wallace, P. T. and Chapront, J. (2003), Expressions for IAU 2000 precession quantities, Astron. Astrophys. 412, 567–586.
Capitaine, N., Mathews, P. M., Dehant, V., Wallace, P. T. and Lambert, S. B. (2009), On the IAU 2000/2006 precession nutation and comparison with other models and VLBI observations, Celest. Mech. Dyn. Astron. 103, 179–190.
Chao, B. F. and R. S. Gross (1987), Changes in the Earths rotation and low-degree gravitational field induced by earthquakes, Geophys. J. Roy. Astr. Soc. 91, 569–596.
Chandler, S.C. (1891) On the variation of latitude. Astron. J. 11, 59–61.
Chapront-Touzé, M. (1980), La solution ELP du problème central de la Lune, Astron. Astrophys. 83–86.
Chapront-Touzé, M. (1982), Progress in the analytical theories for the orbital motion of the Moon, Celest. Mech. 26, 53–62.
Cheng, M. and Tapley, B. D. (2004), Variations in the Earth’s oblateness during the past 28 years, J. Geophys. Res. 109, B09402.
Cheng, M. K., Ries, J. C. and Tapley, B. D. (2011), Variations of the Earth’s Figure Axis from Satellite Laser Ranging and GRACE, J. Geophys. Res. 116, B01409.
Cox, C. M. and Chao, B. F. (2002), Detection of a large-scale mass redistribution in the terrestrial system since 1998, Science 297, 831–833.
Defraigne, P. and Dehant, V. (1998), New theoretical model for nutations and comparison with VLBI observations. In: Capitaine, N. (ed) Proc. Journées 1997—Systèmes de Référence Spatio-Temporels, Observatoire de Paris, pp 69–72.
Dehant, V., Defraigne, P. and Wahr, J. M. (1999a), Tides for a convective Earth, J. Geophys. Res. 104, 1035–1058.
Dehant V. et al. (1999b), Considerations concerning the non-rigid Earth nutation theory, Celest. Mech. Dyn. Astron. 72, 245–310.
Dehant, V. (2002), Report of IAU Working Group on ‘Non-rigid Earth rotation theory’, Highlights of Astronomy 12, 117–119.
Deprit, A., Henrard, J. and Rom, A. (1971), Analytical Lunar Ephemeris: Delaunay’s Theory, Astron. J. 76, 269–272.
Deprit, A. and Elipe, A. (1993), Complete reduction of the Euler-Poinsot problem, J. Astronaut. Sci. 41, 603–628.
Dickey, J. O. et al. (2002), Recent Earth Oblateness Variations: Unraveling Climate and Postglacial Rebound Effects, Science, 298, 1975–1977.
D’Hoedt, S. and Lemaitre, A. (2004), The spin-orbit resonant rotation of Mercury: a two degree of freedom Hamiltonian model, Celest. Mech. Dyn. Astron. 89, 267–283.
Dick, W. R. (ed) (2011), IERS Annual Report 2011. Verlag des Bundesamts fr Kartographie und Geodsie, Frankfurt AM.
Efroimsky, M. and Escapa, A. (2009), The theory of canonical perturbations applied to attitude dynamics and to the Earth rotation. Osculating and nonosculating Andoyer variables, Celest. Mech. Dyn. Astron. 98, Issue 4, 251–283.
Escapa, A., Getino, J. and Ferrándiz, J. M. (2001), Canonical approach to the free nutations of a three-layer Earth model, J. Geophys. Res. 106, 11387–11397.
Escapa, A., Getino, J. and Ferrándiz, J. M. (2002), Indirect effect of the triaxiality in the Hamiltonian theory for the rigid Earth nutations, Astron. Astrophys. 389, 1047–1054.
Escapa, A., Ferrándiz, J. M. and Getino, J. (2012), Influence of the inner core on the rotation of the Earth revisited, IAU Joint Discussion 7 “Space-time reference systems for future research”, XXVIIIth General Assembly of the International Astronomical Union.
Ferrándiz, J. and Barkin, Y. (2001), On integrable cases of the Poincaré problem, Astron. Astrophys. Trans. 19, 769–780.
Ferrándiz, J. M., Escapa, A., Navarro, J. F., and Getino, J. (2003), Recent work on theoretical modelling of nutation. In: Richter, B., Schwegmann, W. and Dick, W.R. (eds) Proceedings of the IERS Workshop on Combination Research and Global Geophysical Fluids, IERS Technical Note 30, pp 163–167.
Ferrándiz, J. M., Navarro, J. F., Escapa, A. and Getino, J. (2004), Precession of the Nonrigid Earth: Effect of the Fluid Outer Core, Astron. J. 128, 1407–1411.
Ferrándiz, J. M., Navarro, J. F., Escapa, A., Getino, J. and Baenas, T. (2007), Influence of the mantle elasticity on the precessional motion of a two-layer Earth model, In: Lemaître, A. (ed) The rotation of celestial bodies, Press. Universitaires de Namur, pp 9–14.
Ferrándiz, J. M., Martínez-Ortiz, P. A. and García, D. (2011), Effects of time gravity changes on the Earth nutations, Geophysical Research Abstracts 13, EGU2011-4981.
Ferrándiz, J. M., Baenas, T. and Escapa, A. (2012), Effect of the potential due to lunisolar deformations on the Earth precession, Geophysical Research Abstracts 14, EGU2012-6175.
Ferrándiz, J. M. and Gross, R. S. (2014), The New IAU/IAG Joint Working Group on Theory of Earth Rotation, IAG Symp 143 (to appear).
Fey, A. L., Arias, E. F., Charlot, P., Feissel-Vernier, M., Gontier, A. M., Jacobs, C. S., Li, J. and Macmillan, D. S. (2004), The second extension of the International Celestial Reference Frame: ICRF-EXT. 1, Astron. J. 127, 3587–3608.
Folkner, W. M., Charlot, P., Finger, M. H., Williams, J. G., Sovers, O. J., Newhall, X., Standish, E. M. Jr. (1994), Determination of the extragalactic-planetary frame tie from joint analysis of radio interferometric and lunar laser ranging measurements, Astron. Astroph. 287, 279–289.
Folkner, W. M et al. (2014), JPL Interplanetary Network Progress Report 42–196, (2014) Available at http://ipnpr.jpl.nasa.gov/progress_report/42-196/196C.
Fukushima, T. (2003) A new precession formula, Astron. J. 126, 494–534.
Getino, J. and Ferrándiz, J. M. (1990), A Hamiltonian theory for an elastic earth: Canonical variables and kinetic energy, Celest. Mech. Dyn. Astron. 49, 303–326.
Getino, J. and Ferrándiz, J. M. (1991), A Hamiltonian Theory for an Elastic Earth—First Order Analytical Integration, Celest. Mech. Dyn. Astron. 51, 35–65.
Getino, J. and Ferrándiz, J. M. (1995), On the effect of the mantle elasticity on the Earth’s rotation, Celest. Mech. Dyn. Astron. 61, 117–180.
Getino, J. and Ferrándiz, J. M. (1997), A Hamiltonian approach to dissipative phenomena between the Earth’s mantle and core, and effects on free nutations, Geophys. J. Int. 130, 326–334.
Getino, J. and Ferrándiz, J. M. (2000), Effects of dissipation and a liquid core on forced nutations in Hamiltonian theory, Geophys. J. Int. 142, 703–715.
Getino, J. and Ferrándiz, J. M. (2000b), Advances in the Unified Theory of the Rotation of the Nonrigid Earth. In: Jhonston, T. et al. (ed) Towards models and constants for sub-microarcsecond astrometry, Proc. IAU Col. 180, pp 236–241 Geophys. J. Int. 142, 703–715.
Getino, J. and Ferrándiz, J. M. (2001), Forced nutations of a two-layer Earth model, Mon. Not. R. Astron. Soc. 322, 785–799.
Getino, J., Ferrándiz, J. M. and Escapa, A. (2001), Hamiltonian theory for the non-rigid Earth: semidiurnal terms, Astron. Astroph. 370, 330–341
Getino, J., Escapa, A. and Miguel, D. (2010), General theory of the rotation of the non-rigid Earth at the second order. I. The rigid model in Andoyer variables, Astron. J. 139, 1916–1934.
Gross, R. S. (1992), Correspondence between theory and observations of polar motion, Geophys. J. Int. 109, 162–170.
Gross, R. S., Fukumori, I. and Menemenlis, D. (2005), Atmospheric and oceanic excitation of decadal-scale Earth orientation variations, J. Geophys. Res. 110, B09405.
Gross, R. S. (2007), Earth rotation variations long period, In: Herring TA (ed) Physical Geodesy. Treatise on Geophysics vol 3, Elsevier, Oxford, 239–294.
Henrard, J. (1979), A New Solution to the Main Problem of Lunar Theory, Celest. Mech. 19, 337–355.
Henrard, J. (1986), Algebraic manipulation on computers for lunar and planetary theories. In: Kovalevsky, J. and Brumberg, V. (eds.) Proceedings IAU Symposium, 114, Reidel , pp 59–62.
Hilton, J. L., Capitaine, N., Chapront, J., Ferrndiz, J. M., Fienga, A., Fukushima, T., Getino, J., Mathews, P., Simon, J. L., Soffel, M., Vondrak, J., Wallace, P. and Williams, J. (2006), Report of the Internacional Astronomical Union Division I Working Group on precession and the ecliptic, Celest. Mech. Dyn. Astron. 94, 351–367.
Hohenkerk, C., and the IAU SOFA Board (2010), SOFA Tools for Earth Attitude. IAU. Available at http://www.iausofa.org
Hori, G. (1966), Theory of General Perturbation with Unspecified Canonical Variable, Publ. Astron. Soc. Jpn. 18, 287–296.
Huang, C. L., Jin, W. J. and Liao, X. H. (2001), A new nutation model of a non-rigid earth with ocean and atmosphere, Geophys. J. Int. 146, 126–133.
Huang, C. L., Dehant, V., Liao, X. H., Van Hoolst, T. and Rochester, M. G. (2011), On the coupling between magnetic field and nutation in a numerical integration approach, J. Geophys. Res. 116, B03403, doi:10.1029/2010JB007713.
Jefferys, W. H. (1970), A Fortran-based list processor for Poisson series. Celest. Mech. 2, 474–480.
Jeffreys, H. and Vicente, RO. (1957), The theory of nutation and the variation of latitude: the Roche model core, Month. Not. Roy. Astron. Soc. 117, 162–173.
Kinoshita, H. (1977), Theory of the rotation of the rigid Earth, Celest. Mech. Dyn. Astron. 15, 277–326.
Kinoshita, H. and Souchay, J. (1990), The theory of the nutation for the rigid earth model at the second order, Celest. Mech. Dyn. Astron. 48, 187–265.
Klioner, S. A., Gerlach, E., and Soffel, M. (2009), Relativistic aspects of rotational motion of celestial bodies, In: S. Klioner, K. Seidelmann, M. Soffel (eds.) Relativity in Fundamental Astronomy, Proc. of the IAU Symposium 261, Cambridge University Press, Cambridge, pp 112–123.
Krasinski, G.A. (2006), Numerical theory of rotation of the deformable Earth with the two-layer fluid core. Part 1: Mathematical model, Celest. Mech. Dyn. Astron. 96, 169–217.
Krásná, H., Böhm, K. and Schuh, H. (2013), Free core nutation observed by VLBI, Astron. Astrophys. 555, A29.
Lambert, S. (2007), Empirical model of the Free Core Nutation, Technical note, available at http://syrte.obspm.fr/lambert/fcn/
Leimanis, E. (1965), The general problem of the motion of coupled rigid bodies about a fixed point. Springer-Verlag, Berlin-Heidelberg-New York.
Lieske, J. H., Lederle, T., Fricke, W., and Morando, B. (1977), Expressions for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants, Astron. Astrophys. 58, 1–16.
Mathews, P. M., Herring, T. A., Buffet, B. A. and Shapiro, I. I. (1991a), Forced nutations of the Earth: Influence of inner core dynamics 1. Theory, J. Geophys. Res. 96, 8291–8242.
Mathews, P. M., Herring, T. A., Buffet, B. A. and Shapiro, I. I. (1991b), Forced nutations of the Earth: Influence of inner core dynamics 2. Numerical results and comparisons, J. Geophys. Res. 96, 8243–8257.
Mathews, P. M., Herring, T. A. and Buffet, B. A. (2002), Modelling of nutation and precession: New nutation series for nonrigid Earth and insights into the Earth’s interior, J. Geophys. Res. 107 B4, 2068–2094.
McCarthy, D. D. (ed) (1996), IERS Conventions, IERS Technical Note, 21, Observatoire de Paris, Paris, available at http://www.iers.org/TN21
Moritz, H. (1982), A variational principle for Moledensky’s liquid-core problem, Bull. Geod. 56, 381–400.
Navarro, J. F. and Ferrándiz, J. M. (2002), A new symbolic processor for the Earth rotation theory, Celest. Mech. Dyn. Astron. 82, 243–263.
Navarro, J. F. (2002), Teoría analítica de la rotación de la tierra rígida mediante manipulación simbólica, Doctoral Dissertation.
Newcombe, S. (1892), On the dynamics of the Earth’s rotation, with respect to the periodic variations of latitude, Mon. Not. R. Astron. Soc. 248–249, 336–341.
Newcombe, S. (1898), Sur les formules de nutation basées sur les décisions de la conférence de 1896, Bull. Astron. 15, 241–246.
Nilsson, T., Böhm, J. and Schuh, H. (2010), Sub-diurnal Earth rotation variations observed by VLBI, Artificial Satellites, 45, No. 2.
Petit, G. and Luzum, B., IERS Conventions (2010), IERS Technical Note 36, Verlag des Bundesamtes für Kartographie und Geodäsie, Frankfurt am Main.
Plag, H. P., Gross, R. S. and Rotahacher, M. (2009a), Global geodetic observing system for geohazards and global change, Geosciences, BRGM’s Journal for a Sustainable Earth 9, 96–103.
Plag, H. P. and Pearlman, M. (eds), Global Geodetic Observing System: Meeting the Requirements of a Global Society on a Changing Planet in 2020, Springer-Verlag, Berlin-Heidelberg, (2009b).
Plag, H. P., Rizos, C., Rothacher, M. and Neilan, R., The Global Geodetic Observing System (GGOS): Detecting the Fingerprints of Global Change in Geodetic Quantities. In: Advances in Earth Observation of Global Change, Chuvieco, E., Li, J., Yang, X. (eds.), Springer (2010).
Poincaré, H. (1901), Sur une forme nouvelle des équations de la mécanique, C.R. Acad. Sci. Paris, 132, 369–371.
Poincaré, H. (1910), Sur la précesion des corps déformables, Bull. Astronom. 27, 321–356.
Richardson, D. L. (1989), PARSEC: An interactive Poisson series processor for personal computing systems, Celest. Mech. Dyn. Astron. 45, 267–274.
Rom, A. (1969), Mechanized algebraic operations (MAO), Celest. Mech. 1, 301–319.
Roosbeek, F. and Dehant, V. (1998), RDAN97: An analytical development of rigid Earth nutations series using the torque approach, Celest. Mech. Dyn. Astron. 70, 215–253.
Sasao T., Okubo S., Saito M. (1980), A simple theory on the dynamical effects of a stratified fluid core upon nutational motion of the Earth In Fedorov, E. P., Smith, M. L., Bender, P. L. (eds) Nutation and the Earth’s rotation, Proc. IAU Symp. 78, pp 165–183.
Schastok J. (1997), A new nutation series for a more realistic model Earth, Geophys. J. Int., 130, 137–150.
Schuh, H., Nagel, S. and Seitz, T. (2001), Linear drift and periodic variations observed in long time series of polar motion, J. Geod. 74: 701–710.
Seidelmann, P. K. (1982), 1980 IAU theory of nutation—the final report of the IAU Working Group on Nutation, Celest. Mech. 27, 79–106.
Shirai, T. and Fukushima, T. (2000), Numerical Convolution in the Time Domain and Its Application to the Nonrigid-Earth Nutation Theory, Astron. J., 119, 2475–2480.
Souchay, J. and Kinoshita, H. (1996), Corrections and new developments in rigid earth nutation theory. I. Lunisolar influence including indirect planetary effects, Astron. Astrophys. 312, 1017–1030.
Souchay, J. and Kinoshita, H. (1997), Corrections and new developments in rigid-Earth nutation theory. II. Influence of second-order geopotential and direct planetary effect, Astron. Astrophys. 318, 639–652.
Souchay, J., Losley, B., Kinoshita, H. and Folgueira, M. (1999), Corrections and new developments in rigid Earth nutation theory III. Final tables REN-2000 including crossed-nutation and spin-orbit coupling effects, Astron. Astrophys. Suppl. Ser. 135, 111–131.
Tisserand, F.F. (1891), Traité de Mécanique Céleste, T. II Théorie de la figure des corps célestes et de leur mouvement de rotation. Gauthier Villars, Paris. Reprinted by Jacques Gabay, Paris, 1990.
Urban, S. E. and Seidelmann P. K. (eds) (2013), The Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley.
Vicente, R. O. and Jeffreys, H. (1964), Nearly diurnal nutation of the Earth, Nature 204, 120–121.
Wahr, J. M. (1981), The forced nutations of an elliptical, rotating, elastic and oceanless Earth. Geophys. J. Roy. Astron. Soc. 64, 705–727.
Williams, J. G. (1994), Contributions to the Earth’s obliquity rate, precession, and nutation, Astron. J. 108, 711–724.
Woolard, E. W. (1953a) Theory of the rotation of the Earth around its center of mass, Goddard Space Flight Center.
Woolard, E. W. (1953b) A revedelopment of the theory of nutation, Astron. J. 58, 1–3.
Acknowledgments
The authors acknowledge the valuable suggestions of the anonymous referees. This work has been partially supported by the Spanish government under Grants AYA2010-22039-C02-01 and AYA2010-22039-C02-02 from Ministerio de Economía y Competitividad (MINECO), the University of Alicante under Grant GRE11-08 and the Generalitat Valenciana, Grant GV/2014/072.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Ferrándiz, J.M., Navarro, J.F., Escapa, A. et al. Earth’s Rotation: A Challenging Problem in Mathematics and Physics. Pure Appl. Geophys. 172, 57–74 (2015). https://doi.org/10.1007/s00024-014-0879-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00024-014-0879-7