A Source Model for Induced Earthquakes at the Geysers Geothermal Reservoir

Abstract

The results of a previous study on source mechanisms of small earthquakes at the Geysers geothermal reservoir in northern California are used to investigate an extended crack model for seismic events. The seismic events are characterized by their first-degree moment tensors and interpreted in terms of a model that is a combination of a shear crack and wing cracks. Solutions to both forward and inverse problems are obtained that can be used with either dynamic or static moment tensors. The model contains failure criteria, explains isotropic parts that are commonly observed in induced earthquakes, and produces estimates of crack dimensions and maximum amount of slip. Effects of fluid pressure are easily incorporated into the model as an effective stress. The model is applied to static moment tensors of 20 earthquakes that occurred during a controlled injection project in the northwest Geysers. For earthquakes in the moment magnitude range of 0.9–2.8, the model predicts shear crack radii in the range of 10–150 m, wing crack lengths in the range of 2–25 m, and maximum slips in the range of 0.3–1.1 cm. Only limited results are obtained for the time-dependence of the earthquake process, but the model is consistent with corner frequencies of the isotropic part of the moment tensor being greater than the deviatoric part and waveforms of direct p waves that become more emergent for larger events.

1 Introduction

There are a broad range of human activities that are known to induce earthquakes, including filling of reservoirs, removal of fluids from wells, injection of fluids into wells, and excavation of mines. Added to this list in recent years is production of geothermal energy, hydraulic fracturing, and storage of carbon dioxide. Of the various types of induced earthquakes, those associated with enhanced geothermal systems offer one of the best opportunities to study the cause of induced earthquakes, primarily because of the large amounts of scientific data that are available for these systems. A good example is the Geysers geothermal reservoir in northern California, where induced earthquakes have been studied since the 1970s.

A special opportunity to study earthquakes induced by an enhanced geothermal system occurred recently when a demonstration project began at the Geysers (Rutqvist et al. 2010; Garcia et al. 2012). The project is located in an undeveloped part of the northwest Geysers geothermal reservoir, where water was injected into well Prati 32 (P32) starting on October 6, 2011. The injection takes place in a controlled manner and earthquakes that occur before and during injection are monitored by a dense network of seismographic stations that surround the well. In an attempt to take advantage of this opportunity, Johnson (2014) calculated source mechanisms for some of the induced earthquakes that occurred during this project.

The study of Johnson (2014) characterizes earthquakes in terms of their first-degree moment tensors, which is a general and fairly complete mathematical representation of a seismic source. Having obtained the moment tensors, the next step is to interpret them in terms of physical processes acting at the earthquake source. In the present study, properties of the moment tensors are used to construct a model of the source process for induced earthquakes in enhanced geothermal systems.

In the following section, the demonstration project at the Geysers and the moment tensor results are briefly reviewed. This is followed by a section that describes the source model, a section that interprets the moment tensors in terms of the source model, and a section with further discussion and conclusions. The more mathematical aspects of the source model are contained in two appendices.

2 Moment Tensor Results

A fairly complete discussion of the background of geophysical studies at the Geysers, the demonstration project, the method used in estimating moment tensors, and the moment tensor results can be found in Johnson (2014) and the references contained therein. The only earthquakes considered in that and this study are those with epicenters located within a 1.5 km square area centered on well P32.

Before the beginning of injection into P32, the rate of seismicity in the study area that surrounds it was low with an average of less than one earthquake per day. Figure 1 shows the rate of seismicity for 70 days after injection began. On October 6, 2011 (time 0 in Fig. 1), injection into P32 began with an initial rate of 1,100–1,200 gallons per minute (gpm) for 12 h that was then reduced to 400 gpm. This rate was maintained for 54 days until November 30, 2011, when it was raised to 1,000 gpm. Figure 1 shows a clear increase in seismicity when the rate of injection is increased. The seismicity rate can exceed 30 earthquakes per day.

Fig. 1

Number of earthquakes per day with M _w ≥ 0 and epicenters in the special study area around P32. Time is measured in days from the beginning of injection on October 6, 2011. The dashed line (right hand scale) is the injection rate of water into P32. The symbols at the top denote origin times of events for which moment tensors were estimated

From over 2,000 earthquakes that occurred in the study area around P32 in the 300 days before and after injection began, 20 events were selected for moment tensor inversion and these are listed in chronological order in Table 1. The first five events occurred before injection began. Events 6 through 12 occurred during the time interval shown in Fig. 1 and their origin times are denoted at the top of the figure.

Table 1 Origin times, hypocenters, and magnitudes of events selected for moment tensor inversion

In Johnson (2014), first-degree dynamic moment tensors are estimated for the 20 events listed in Table 1. Estimating dynamic moment tensors at the Geysers is challenging, primarily because of the complicated shallow crust and the limited response of the seismic instrumentation at low frequencies. However, methods have been developed to handle these problems with careful attention given to uncertainty in the results. The spectral modulus of the dynamic moment rate tensor is reliably recovered in the frequency range 1–100 Hz, but uncertainty in the spectral phase limits its use to a few simple results.

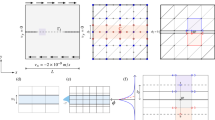
The static moment tensor and its uncertainty are estimated from the low-frequency levels of the spectral modulus of the dynamic moment rate tensor. These static moment tensors are used to construct the focal mechanisms shown in Fig. 2 for all of the events listed in Table 1 along with their locations relative to P32. It is also possible to estimate the scalar moment m _o, isotropic part of the static moment tensor $\tilde{m}_{\rm iso},$ average corner frequency of the deviatoric dynamic moment rate function $\overline{f}_{\rm cd}',$ and corner frequency of the isotropic part of the dynamic moment rate function f _ci. All of this information is listed in Table 2 along with estimated values of uncertainty as expressed by standard deviations.

Fig. 2

Map showing epicenters of events in Table 1 with attached equal area stereographic projections for static moment tensors. The solid line is the surface projection of well P32 with the label at the well head

The results listed in Tables 1 and 2 and displayed in Figs. 1 and 2 summarize some of the results obtained by Johnson (2014) for earthquakes associated with the demonstration project at well P32. These results support a number of conclusions, many of which are consistent with other studies of earthquakes at the Geysers. Injection of water into well P32 clearly causes an increase in seismicity in the vicinity of the well (Fig. 1). The earthquakes exhibit a range of source mechanisms, with spatially related groups of events having very similar mechanisms, but, at the same time, some near-by events have completely different mechanisms (Fig. 2). Most of the events have an isotropic part, with this part well-resolved for about half of the events and marginally resolved for the rest (Table 2; Fig. 2). The isotropic part is predominantly positive and can be as large as 47 % of the scalar moment, but three of the 20 events have smaller, less well-resolved negative isotropic parts (Table 2; Fig. 2). Corner frequencies of the isotropic part of the moment tensor are about 40 % larger than the average for the deviatoric moment tensor (Table 2).

Table 2 Information obtained from dynamic moment tensors

3 Extended Crack Model

A variety of evidence suggests that induced earthquakes associated with enhanced geothermal systems such as the Geysers are different from typical tectonic earthquakes associated with plate boundaries. One type of evidence is that the hypocenters of induced earthquakes generally do not define a through-going fault as in the case of ordinary tectonic earthquakes. Rather, the hypocenters of induced earthquakes often form a cloud of seismicity surrounding the region of fluid injection. This is partly evident in the clustering of events around P32 in Fig. 2 and has been documented in numerous studies (Bufe et al. 1981; Ludwin et al. 1982; Eberhart-Phillips and Oppenheimer 1984; Oppenheimer 1986; Stark 1992; Romero et al. 1994; Majer and Peterson 2007). Another type of evidence is the commonly found isotropic part of the static moment tensor of induced earthquakes as described in Fig. 2, Table 2, and other studies (Kirkpatrick et al. 1996; Ross et al. 1996, 1999; Guilhem et al. 2014). The presence of an isotropic part in a moment tensor implies a change in volume in the source region, and a positive volume change in a compressive environment is not easily explained.

These types of evidence prompt the consideration of a source model for induced earthquakes that is different from the conventional source models that have been developed for tectonic earthquakes. The Geysers geothermal reservoir is highly fractured with the orientation of the fractures generally random (Thompson and Gunderson 1992; Beall and Box 1992), and seismic activity within the reservoir does not appear to be associated with any of the regional fault systems (Eberhart-Phillips and Oppenheimer 1984). So, rather than a through-going fault, consider a volume filled with small, finite cracks. When this volume is subjected to stress, there is a tendency for some of the cracks to slip and extend their length. However, for rocks in compression it is found that the cracks do not extend themselves in their own plane (Scholz 1990). Instead, the cracks extend by developing wing cracks that grow in directions parallel to the most compressive stress. These wing cracks actually fail in tension and are wedged open by the displacement on the original shear crack, which predicts that the moment tensor of such a source will have a positive isotropic part. An important property of this model is that it is possible to have failure in tension and an increase in volume in an environment where all of the principal stresses are compressive.

The basic properties of this extended crack model for induced earthquakes are illustrated in Fig. 3. Following the continuum mechanics convention, the stress τ _ij is defined to be positive in tension. The principal values of the stress tensor at any point are denoted as

$$ \tau_1 \geq \tau_2 \geq \tau_3. $$

(1)

The circular crack in Fig. 3 has a radius r _c and a normal that makes an angle θ with the direction of the most compressive principal stress τ ₃. The normal stress on the crack is (Jager and Cook 1971)

$$ \tau_{\rm n} = \frac{\tau_3 + \tau_1}{2} + \frac{\tau_3 - \tau_1}{2} \cos(2 \theta), $$

(2)

and the shear stress is

$$ \tau_{\rm s} = - \frac{\tau_3 - \tau_1}{2} \sin(2 \theta). $$

(3)

Letting γ be the coefficient of friction, the excess shear stress on the crack is denoted by

$$ \tau_{\rm s}^* = | \tau_{\rm s} | + \gamma \tau_{\rm n}. $$

(4)

The maximum slip d is defined to be the discontinuity in displacement across the shear crack at its center. The wing cracks are assumed to extend parallel to the direction of the maximum compressive stress τ ₃ and have a length ℓ. The ratio L = ℓ/r _c is convenient in expressing the results.

Fig. 3

Sketch of a crack of radius r _c that is extended by wing cracks of length ℓ. The maximum and minimum principal compressive stresses are τ ₃ and τ ₁, respectively, while the intermediate principle stress τ ₂ lies in the plane of the crack. The slip on the crack at its edge is shown as d _c, but the maximum slip is at the center where it has a value d

A quantitative description of the failure process of the crack in Fig. 3 is developed in Appendix A. There it is shown that, given the physical properties of the crack and the state of stress, it is possible to calculate estimates of the shear dislocation on the crack and the length of any wing crack that develops. With this extended crack model, there are two modes of failure. Failure begins when τ ^*_s  > 0 (Eq. 4) with slip only on the shear crack and the amount of maximum slip d given in Eq. 10 with L = 0. This mode of failure continues until k _I = k _Ic (Eq. 11), where k _Ic is a critical stress intensity factor. With a continued increase in stress, the wing crack begins to open and the second mode of failure begins. Setting k _I = k _Ic in Eq. 11 and substituting for d from Eq. 10 results in an implicit equation that can be solved for L and the length of the wing crack ℓ, and this substituted into Eq. 10 yields the maximum displacement d. Given these values of r _c, ℓ, and d, the moment tensor for this type of source is also given in Appendix A. Note that this extended crack model of an earthquake is different from most models of tectonic earthquakes in that it has slip on two non-parallel planes. Also note that when wing cracks are present, the moment tensor has a finite trace, so the source has an isotropic part and that implies a change in volume in the source region.

In applying the extended crack model, two additional pieces of information must be specified. The first is the critical stress intensity factor k _Ic. Li (1987) gives a range of values for rocks in the crust and a reasonable average is $k_{\rm Ic} = 0.001 \; m^{1/2}.$ Also required is the angle θ between the normal to the crack and the direction of maximum compressive stress (Fig. 3). Slip is most likely when this angle has the Coulomb value $\theta = \theta_{\rm c} = 1/2 \; \tan^{-1}[-1/\gamma].$ For θ in the vicinity of θ _c the results are fairly insensitive to its value, so this is a reasonable assumption.

The effect of fluid pressure is easily incorporated into the extended crack model by introducing the effective stress

$$ \hat{\tau}_{ij} = \tau_{ij} + p_{\rm f} \delta_{ij} $$

(5)

where p _f is fluid pressure. This effective stress is then substituted into Eqs. 2, 4, and 10.

There is some precedence for the extended crack model in the seismology literature. A model similar to that described in Appendix A is developed for volcanic earthquakes by Shimizu et al. (1987), and Julian et al. (1998) discuss the moment tensors of sources that combine shear and tensile faulting. However, in neither of these studies is there an attempt to include failure criteria or derive relationships between the dimensions of the shear and tensile cracks. In addition, Miller et al. (1998) summarize results for several types of earthquakes, including those in geothermal areas, where the observational data indicate a source mechanism that is fundamentally different from a simple shear failure.

An example of the application of the extended crack model is shown in Fig. 4. This simulates conditions at a depth of 2,500 m below sea level at the Geysers with principal stresses $\tau_1 = -50 \; {\rm MPa}, \;\; \tau_2 = - 100 \; {\rm MPa}, \;\; \tau_3 = -150 \; {\rm MPa},$ a coefficient of sliding friction γ = 0.6, and a crack with radius r _c = 50 m inclined at an angle θ = 60° to the direction of maximum compressive stress (see Fig. 3). Figure 4 shows how the various parts of the scalar moment develop as a function of fluid pressure. Slip on the shear crack begins when the fluid pressure exceeds a value of 3 MPa and the wing cracks begin to extend when the fluid pressure exceeds 6 MPa. Continued increase in the fluid pressure causes continued increase in the moments of both the shear crack and wing cracks. Note that the hydrostatic fluid pressure at this depth is 31 MPa. Also shown in this figure is the isotropic part of the scalar moment tensor that is associated with the opening of the wing cracks.

Fig. 4

A simulation of the scalar moment released by failure of the extended crack model at a depth of 2,500 m below sea level at the Geysers as a function of the fluid pressure. The part of the moment due to the shear crack is shown as the solid line, the part due to the wing cracks as the long dash line, and the part that is isotropic as the short dash line

Consider the situation that is simulated in Fig. 4 and assume a fluid pressure of 15 MPa. A seismic event will be generated that includes both slip on the shear crack and opening of wing cracks. The theory given in Appendix A produces the dynamic moment tensor shown in Fig. 5. The effects of slip on the shear crack begins at time t = 0, the effects of the opening of the wing cracks begins at t = 0.016 s, and the duration of the entire process is 0.026 s. In the coordinate system of Fig. 3 two of the elements of the moment rate tensor are identically zero (see Eq. 13) and the other four elements all have different time functions.

Fig. 5

The moment rate tensor for a seismic event that is generated for the conditions simulated in Fig. 4 in the case where the fluid pressure is 15 MPa. The indices ij of the moment rate tensor $\dot{m}_{ij}(t)$ are listed on the left and the maximum values in units of GNm/s are listed on the right

Given an appropriate Green's function, the dynamic moment tensor of Fig. 5 can be used to simulate seismograms at any location outside the source region. In Fig. 6 such seismograms are shown at an epicentral distance of 6 km and azimuth of 30° with the calculations using a velocity model and instrument response appropriate for the Geysers (Johnson 2014). The direct p and s waves are the major phases at this distance and are easily identified on the seismograms.

Fig. 6

Simulated seismograms for the moment tensor shown in Fig. 5 at an epicentral distance of 6 km and azimuth of 30°. The velocity model and instrument response used in the simulations are for the Geysers as described in Johnson (2014). Time is measured from the origin time of the event. The directions of motion are radial R (away), transverse T (clockwise), and vertical Z (up). The numbers on the right are maximum values in digital counts

In Appendix B, the solution to the inverse problem for the extended crack model is developed. The moment tensor m(t) is first decomposed into a shear crack moment m _s(t), a wing crack moment m _w(t), and an unmodeled moment m _u(t) that is not consistent with the model. The shear and wing crack moments are then used to estimate the radius of the shear crack r _c, the length of the wing crack ℓ, and the maximum displacement on the shear crack d. Given the dynamic moment tensor m(t), all of these estimates are obtained as functions of time. Given the static moment tensor $\tilde{\bf m},$ these estimates are independent of time and are interpreted as final values of the source process.

As discussed in Johnson (2014), the eigenvectors of the moment tensor determine the T, I, and P axes that are interpreted as principal directions of displacement in the source region. The angle χ derived in Appendix B can then be used to rotate the T, I, and P axes into the directions of τ ₁, τ ₂, and τ ₃, respectively (see Fig. 3). Thus, in principal, the directions of the principal stresses in the source region can also be obtained from the moment tensor. However, the angle χ is a function of the unknown angle θ (Eq. 20a, b, c) that in general cannot be accurately estimated from the moment tensor (McKenzie 1969). This result is consistent with the earlier observation that the results of the forward problem are relatively insensitive to assumed values of θ. In addition, there remains a fundamental ambiguity in choosing the plane of the shear crack from two possible orthogonal planes.

The extended crack model developed in Appendix A explains how slip on a shear crack causes the opening of wing cracks and this leads to a moment tensor with a positive isotropic part in a compressive environment. While this explanation is valid for the majority of the 20 events listed in Table 1, four of these events contain negative isotropic parts. In principle, there seems to be no reason why the extended crack model cannot be operated in a reverse direction whereby pre-existing wing cracks close, shear cracks slip in the reverse direction, and the source has a negative isotropic part. All of the equations of Appendix A are still valid for this reversed model, with the exception of Eq. 11, that is used to determine the length of the wing cracks. Thus, while the physics is not entirely justified, in this study, the extended crack model is also used to interpret moment tensors with negative isotropic parts. The interpretation outlined in Appendix B is performed for m _s(t) and m _w(t) either positive or negative, with positive values indicating opening of the wing cracks with a positive isotropic part, and negative values indicating closing of the wing cracks with a negative isotropic part.

While running the extended crack model in a reverse direction in order to explain the events with negative isotropic parts may be possible in a mathematical sense, it ignores some physical considerations that need further study. If fluids are present, questions about the type of fluid, whether the medium is in a drained or undrained state, and the rate at which fluids can be moved in or out of the cracks are all important. There is also a question about what failure criteria should be used in this case. Finally, note that if failure begins with the closure of the wing cracks, then the time sequence of the shear and wing crack sources shown in Fig. 5 needs to be reversed.

It is important to keep in mind that the long term deformation of the Geysers geothermal field is primarily volumetric contraction, and this would suggest that seismic events with negative isotropic parts should dominate. A discussion of this deformation and the references that describe it can be found in Johnson (2014). What complicates an attempt to relate deformation to seismicity is the fact that the measured deformation is a trend observed over a 20 year period in a large, producing part of the field, while the seismicity of this study is for a period of <1 year in a small, non-producing part of the field.

4 Application of the Extended Crack Model

The model developed in Appendix A and Appendix B is appropriate for the first-degree dynamic moment tensor and has the potential to provide a detailed description of the time-dependence of the source failure process. Unfortunately, in Johnson (2014) there is considerable uncertainty in the spectral phase of the dynamic moment tensors and so the time domain versions of these moment tensors are judged to be of questionable reliability. The complete dynamic interpretation outlined in Appendix B was performed for a few of the events listed in Table 1 with mixed results. In some cases, the time history of source quantities shows the behavior expected for a process that starts with the failure of a shear crack and grows into the extension of wing cracks, but in other cases it is difficult to give a meaningful physical interpretation of the results. The general conclusion, similar to that of Johnson (2014), is that the uncertainty in the dynamic moment tensors prevents a detailed time domain description of the source processes. However, all of the results of Appendix B can be applied to static moment tensors merely by ignoring the time dependence of the expressions.

In Johnson (2014), static moment tensors are obtained for all of the events listed in Table 1 by estimating the mean values of the spectral modulus of the dynamic moment tensor in the frequency interval between 1 Hz and the corner frequency f _c. Using the equations of Appendix B, these static moment tensors are decomposed into shear crack moment, wing crack moment, unmodeled moment, shear crack radius, wing crack length, and maximum displacement. All of these results are listed in Table 3. The fraction of the scalar moment that is not explained by the extended crack model m _u has a maximum of 30 % and an average value of 17 %. The average uncertainty in the scalar moments, as measured by the ratio of the standard deviation of the scalar moment to its value in Table 2, is 11 %, so much of the unmodeled part of the scalar moment is possibly related to its uncertainty.

Table 3 Estimated parameters of the extended crack model

The dimensions of the shear and wing cracks listed in Table 3 are plotted versus the scalar moment in Fig. 7. The shear cracks radii are larger than the wing crack lengths and linear regression gives a reasonable fit with the equation

$$ {\rm log}_{10}[r_{\rm c}] = (0.44 \pm 0.05) + (0.40 \pm 0.02) {\rm log}_{10}[m_{\rm o}]. $$

(6)

The wing crack lengths have more scatter and a regression equation

$$ {\rm log}_{10}[\ell] = (-0.12 \pm 0.09) + (0.37 \pm 0.03) {\rm log}_{10}[m_{\rm o}]. $$

(7)

In Fig. 7, the point with the largest departure from the regression line for both the shear crack radius and wing crack length corresponds to event 7 of Table 2 that has the largest relative isotropic fraction.

Fig. 7

The radius of the shear crack r _c (asterisks and dashed line) and the length of the wing crack ℓ (open circles and solid line) as a function of the scalar moment m _o on a log–log scale. The lines are fit to the data by linear regression

The maximum slip on the shear crack is listed in Table 3 and plotted versus the scalar moment in Fig. 8. Linear regression of these data yields

$$ {\rm log}_{10}[d] = (-2.780 \pm 0.009) + (0.196 \pm 0.003) {\rm log}_{10}[m_{\rm o}] $$

(8)

where d has units of m.

Fig. 8

The maximum slip on the shear crack d as a function of the scalar moment m _o on a log–log scale. The dashed line is fit to the data by linear regression

In Johnson (2014), it is pointed out that, for the 20 events listed in Tables 1 and 2, there are significant differences between the corner frequency of the isotropic part of the dynamic moment rate tensor f _ci and the average corner frequency of the deviatoric dynamic moment rate tensor $\overline{f}_{\rm cd}' .$ The results are listed in Table 2, with a more complete discussion along with plots and linear regression analysis found in Johnson (2014). A basic result is that the average ratio of these two corner frequencies is

$$ \frac{f_{\rm ci}}{\overline{f}_{\rm cd}'} = (1.46 \pm 0.23). $$

(9)

A possible explanation of this result is contained in the extended crack model. In the simulation of Fig. 5, the duration of the motion on the shear crack is 0.026 s (see element 31 in Fig. 5) while the duration of motion on the wing cracks is only 0.010 s (see element 22 in Fig. 5), and this suggests a higher corner frequency for the wing crack part of the source process. Because the isotropic part of the source process is only associated with motion on the wing cracks, and motion on the shear crack is only associated with the deviatoric part, a value of f _ci greater than $\overline{f}_{\rm cd}'$ is implied.

In the process of analyzing the seismic events listed in Table 1 it becomes apparent that the waveform of the direct p wave tends to become more emergent as the scalar moment of the event becomes larger. This is not a problem in the analysis of the direct p wave as the arrival time of the phase can always be identified by magnifying the trace amplitude, but it can increase the difficulty of identifying the arrival time of the direct s wave. Figure 9 is an attempt to illustrate this phenomenon by displaying the direct p wave portion of seismograms recorded at Geysers seismographic station AL4 for all 20 events listed in Table 1. This the closest station to all 20 events with epicentral distances ranging between 0.08 and 0.74 km and azimuths ranging between 33° and 350°E of N. The depths of the 20 events vary somewhat (see Table 1), so small time shifts have been included in the seismograms of Fig. 9 in order to align the first motions, and the polarity of some of the seismograms have been changed so that the direction of first motion is always downward. There is considerable variation in the waveforms that may be related to differences in radiation patterns. However, there is a clear tendency for the p waveform to develop a more gradual beginning as the first trough and first peak move to later times when the size of the event increases. This is particularly clear in the events with scalar moment greater than 2,500 GNm (bottom five traces of Fig. 9) and even more pronounced in events with scalar moments >10,000 GNm (bottom two traces of Fig. 9).

Fig. 9

Plot of the seismograms observed on the vertical component at station AL4 for the 20 events listed in Table 1. The traces are arranged in order of increasing scalar moment from top to bottom with the index number from Table 1 listed on the left and a negative index number indicating that the polarity of the seismogram has been changed. The number on the right is the maximum amplitude in digital counts for the section of the seismogram that is displayed

Figure 9 also presents an opportunity to compare waveforms of events having negative isotropic parts (index numbers 15, 2, 10, and 9) with those having positive isotropic parts. There appears to be no consistent differences in the waveforms of the direct p waves that can be associated with the sign of the isotropic part of the moment tensor. This supplies some limited support for the procedure of using the results of Appendix B to estimate crack parameters for events having both positive and negative isotropic parts.

A simulation of the observed data of Fig. 9 is shown in Fig. 10. For each of the 20 events a moment tensor similar to that of Fig. 5 is constructed using the estimated model parameters of Table 3 and the equations of Appendix A. Then the velocity model and instrument response appropriate for the Geysers (Johnson 2014) are used to calculate synthetic seismograms at a distance of 0.40 km and azimuth of 120° (mean values for the data of Fig. 9). In these simulations the rupture velocities (Eqs. 15a–15d) are v _rs = 0.9 v _s and v _rw = 0.5 v _s where v _s is the shear velocity at the source depth. First note that there is a gradual increase in the duration of the waveforms as the scalar moment increases. This is caused by the corresponding increase in r _c and ℓ shown in Fig. 7 that enters the calculations through Eqs. 15c and 15d and is consistent with the dependence of corner frequency upon scalar moment shown in Fig. 14 of Johnson (2014). Next, note that for scalar moments <500 GNm (top 11 traces of Fig. 10), the waveforms generated by the shear crack and wing crack arrive close enough in time so that what appears to be a single phase is generated in the frequency band of the recording instrument. Trace number 12 of Fig. 10 (corresponding to event 7 of Table 3) is different from all of the other events in that it is the only one with the wing crack part of the moment greater than the shear crack part, and so the contribution from the wing crack dominates the waveform. For scalar moments greater than 1,000 GNm (bottom 8 traces of Fig. 10), the contributions from the shear crack and wing crack become more separated in time and can be identified in the synthetic seismograms. The bottom traces of Fig. 10 show a general similarity to the bottom traces of Fig. 9 in the sense of having an emergent negative beginning that is due to slip on the shear crack followed by a sharper positive pulse caused by motion on the wing cracks and the end of the failure process.

Fig. 10

Simulations of the direct p waves shown in Fig. 9 using the extended crack parameters listed in Table 3

A fairly obvious difference between Figs. 9 and 10 is the general appearance of a higher frequency content in the simulated waveforms. This is to be expected as the simulations are based on only the first-degree moment tensor and thus do not contain any effects of the spatial dimensions of the source that one would expect to be present in the observational data in the form of low-pass filtering (Sato and Hirasawa 1973). When using a representation of the source in terms of moment tensors, these effects of the spatial finiteness of the source can only be obtained by including higher degree moment tensors (Stump and Johnson 1982).

5 Discussion and Conclusions

The source model for induced earthquakes developed in this study is primarily designed to explain seismological waveform data as characterized by first-degree moment tensors. Solutions to both the forward and inverse problem are presented. The formulation of the forward problem starts with the state of stress, contains failure criteria for slip on a shear crack and wing crack, solves for the slip on the shear and wing cracks and the length of the wing crack, and ends with an expression for the dynamic moment tensor. The formulation of the inverse problem starts with an observed first-degree moment tensor and obtains estimates of the shear crack radius, the wing crack length, and the maximum slip on the shear crack. This is only a partial solution to the inverse problem, as a determination of the directions and magnitudes of the principal stresses is not attempted.

The extended crack model developed in this study appears to give a plausible interpretation of the moment tensors estimated for the Geysers in Johnson (2014). It explains the observation of source mechanisms with positive isotropic parts in a compressive environment. It is consistent with the observation that corner frequencies of the isotropic part of the moment tensor are higher than those of the deviatoric part. It provides a possible explanation of waveforms of direct p waves that tend to become more emergent for the larger events. The physics of the model are not entirely justified for the case of a negative isotropic part, but reasonable results are obtained merely by reversing the direction of slip on the shear crack. Additional applications to observational data may help to resolve this matter of a negative isotropic part.

The extended crack model has some important differences with models typically used for tectonic earthquakes. More than one slip surface is involved, different elements of the moment tensor have different time functions, and a volume change is generally present. However, in recent years there have been a number of studies of off-fault seismicity, which consists of the small earthquakes that are invariably found in a zone extending away from tectonic faults (see for instance Poliakov et al. 2002; Rice et al. 2005; Viesca et al. 2008; Sammis et al. 2009; Dieterich and Smith 2009; Powers and Jordan 2010). Thus, while the induced earthquakes and extended crack model of this study may not be appropriate analogs for ordinary tectonic earthquakes, they may be more appropriate analogs for the off-fault seismicity that accompanies tectonic earthquakes.

One of the primary motivations for interpreting seismological data in terms of a source model is that physical properties of the source are produced that can be tested through comparisons with other types of observational data. In this study, these properties are the radius of the shear crack r _c, the length of the wing cracks ℓ, and the maximum slip on the shear crack d. The estimates of these source parameters listed in Table 3 seem reasonable, but the model can only be properly validated by making direct observations of these parameters or at least showing that their values are consistent with other types of observational data. Observed changes in hydrological properties that accompany earthquakes may be one type of datum that can be used to test the extended crack model. Another possibility is a comparison with reservoir modeling calculations of the type that are discussed below.

The extended crack model developed in this study considers a single isolated shear crack with associated wing cracks. However, when cracks of this type are sufficiently near to each other, there will be interactions that need to be considered. Interactions of this type have already been developed by Ashby and Hallam (1986) and Ashby and Sammis (1990), so the extension to interacting cracks appears to be quite feasible and an appropriate topic for further study.

A disappointing aspect of this study is the fact that a complete time domain interpretation of the source failure process has not been obtained, primarily because the dynamic moment tensors of Johnson (2014) have too much uncertainty. While useful results are still recovered from the static moment tensors, details about how slip develops on the shear and wing cracks as a function of time are lacking. An improved velocity model for the shallow crust could possibly be a means of overcoming this problem at the Geysers. In addition, applying the methods of this study to data from other areas of induced earthquakes that have less complicated and better known velocity structures could allow a complete time domain interpretation.

The earthquake model considered in this study starts with the stress field in the vicinity of a pre-existing crack located in a geothermal reservoir. If this model is to make a useful contribution to the production of geothermal energy, it will be necessary to treat the more general problem of how this stress field is generated. Fortunately, considerable progress has been made in the modeling of coupled hydraulic, thermal, and mechanical effects that accompany the injection of water into geothermal reservoirs (Rutqvist et al. 2010, 2013) and local changes in the stress field are produced by these calculations. Thus, it should be possible to use the results of these fairly complete coupled process calculations to test the feasibility of the extended crack model. If this feasibility can be demonstrated, then a variety of further tests and uses of the earthquake model suggest themselves. One is to compare the estimated dimensions of the shear and wing cracks with reservoir models of fracturing. Another is to test whether the orientation of the wing cracks is indeed parallel to the calculated direction of maximum principal stress. The net result could be an improved understanding of the physical mechanisms that cause induced earthquakes in geothermal reservoirs.

Appendices

Appendix A: Extended Crack Model

Analytical equations for slip on a crack that is caused by compressive stresses are derived in Ashby and Hallam (1986). Their results for the three-dimensional problem contain some approximations, but the results agree with the numerical calculations of Nemat-Nasser and Horii (1982). Their results form the starting point for the treatment of damage mechanics by Ashby and Sammis (1990) that has been shown to be useful in studying the generation of elastic waves (Johnson and Sammis 2001).

The basic results needed for the extended crack model are derived in Ashby and Hallam (1986, Appendix A). The necessary elastic parameters are the Lame constants λ and μ and the Poisson ration ν. The maximum slip on the shear crack is

$$ d = \frac{4 }{\sqrt{3 \pi} \mu [1+\nu]} r_{\rm c} \left[ \tau_{\rm s}^* f_1(L) + \frac{5 \pi \sqrt{3}}{8 \cos(\theta)} \tau_1 f_2(L) \right] $$

(10)

where it is to be understood that the slip is zero when the right hand of the equation is negative. The stress intensity factor for the opening of the wing cracks is

$$ k_{\rm I} = [1+\nu]\frac{d}{\sqrt{r_{\rm c}}} f_3(L). $$

(11)

The functions of L = ℓ / r _c found in these results are

$$ f_1(L) = \sqrt{ 1 - (1+L)^{-2} } + (1+L) \sin^{-1}[(1+L)^{-1}], $$

(12a)

$$ f_2(L) = \frac{L^2}{1+L}, $$

(12b)

$$ f_3(L) = \frac{1}{\sqrt{\cos^2(\theta) +(\sin(\theta)+L)^2}}\times \left[ \frac{1 + L \sin(\theta)}{1+L} + \frac{2 L \cos(\theta)}{5 \sqrt{1+L}} \right]. $$

(12c)

Note that Ashby and Hallam (1986) express their results in terms of δ = d/2, KI =  μ k _I, and ψ = π /2 − θ.

The results of Ashby and Hallam (1986) include equations for the dimensions and displacements of both the shear crack and wing cracks, and this is sufficient to construct static moment tensors for both cracks. In addition, if one assumes a kinematic mode of failure in which slip on the shear crack starts at the center and propagates outward at a velocity v _rs while slip on the wing crack propagates at a velocity v _rw, then an estimate of the dynamic moment tensor is also possible. The first-degree moment tensor in the coordinate system of Fig. 3 is

$$ {\bf m}(t) = \left[ \begin{array}{lll} m_{\rm w}(t)+m_{\rm s}(t) \sin(2\theta) & 0 & m_{\rm s} (t) \cos(2\theta) \\ 0 & \frac{\lambda}{\lambda + 2\mu} m_{\rm w}(t) & 0 \\ m_{\rm s}(t) \cos(2\theta) & 0 & \frac{\lambda}{\lambda + 2\mu} m_{\rm w}(t)-m_{\rm s}(t) \sin(2\theta) \\ \end{array} \right] $$

(13)

where

$$ m_{\rm s}(t) = \frac{4}{3} \mu r_{\rm c}^2 d f_1(L) s_{\rm s}(t), $$

(14a)

$$ m_{\rm w}(t) = \frac{5 \pi}{2 \sqrt{3} \cos(\theta)} (\lambda + 2\mu) r_{\rm c}^2 d f_2(L) s_{\rm w}(t), $$

(14b)

$$ s_{\rm s}(t) = \frac{t^3}{(\tau_{\rm s} +\tau_{\rm w})^3} \left[ H(t) - H(t-\tau_{\rm s} -\tau_{\rm w}) \right] + H(t- \tau_{\rm s} - \tau_{\rm w}), $$

(15a)

$$ s_{\rm w}(t) = \frac{t - \tau_{\rm s}}{\tau_{\rm w}} \left[ H(t- \tau_{\rm s}) - H(t - \tau_{\rm s} - \tau_{\rm w}) \right] + H(t- \tau_{\rm s} - \tau_{\rm w}), $$

(15b)

$$ \tau_{\rm s} = \frac{r_{\rm c}}{v_{\rm rs}}, $$

(15c)

$$ \tau_{\rm w} = \frac{\ell}{v_{\rm rw}}. $$

(15d)

Appendix B: Interpretation of the Moment Tensor

Consider the situation where an estimate of the moment tensor m(t) has been obtained from an analysis of waveform data, and the objective is to interpret this moment tensor in terms of the extended crack model described in Appendix A. Required additional information is the ratio of the Lame elastic parameters μ/λ, which can be obtained from knowledge of the elastic velocities at the source depth, the critical stress intensity factor k _Ic, and the angle θ between the normal to the shear crack and the direction of maximum compressive stress (see Fig. 3). An estimate of this latter quantity can be obtained by assuming the Coulomb failure criterion

$$ \tan(2 \theta) = - \frac{1}{\gamma}. $$

(16)

Given this information, the process starts by noting that the eigenvalues of the total moment tensor of Eq. 13 are

$$ \Uplambda_1(t) = \frac{\lambda+\mu}{\lambda+2\mu} m_{\rm w}(t) + \left[ [ \frac{\mu}{\lambda+2\mu} m_{\rm w}(t) + m_{\rm s}(t) \sin(2\theta)]^2 + [m_{\rm s}(t) \cos(2\theta)]^2 \right]^{1/2}, $$

(17a)

$$ \Uplambda_2(t) = \frac{\lambda}{\lambda+2\mu} m_{\rm w}(t), $$

(17b)

$$ \Uplambda_3(t) = \frac{\lambda+\mu}{\lambda+2\mu} m_{\rm w}(t) - \left[ [ \frac{\mu}{\lambda+2\mu} m_{\rm w}(t) + m_{\rm s}(t) \sin(2\theta)]^2 + [m_{\rm s}(t) \cos(2\theta)]^2 \right]^{1/2}. $$

(17c)

Given the eigenvalues, it is possible to obtain the separate contributions of the shear and wing cracks, for it is clear that m _w(t) can be obtained from $\Uplambda_2(t)$ and then m _s(t) can be obtained from the difference $\Uplambda_1(t) - \Uplambda_3(t).$ However, a more general interpretation is to assume that the moment tensor also contains an unmodeled part m _u(t) that is not consistent with the form given in Eq. 13. An interpretation in that case is

$$ m_{\rm w}(t) = \frac{ \lambda + 2 \mu }{3 \lambda + 2 \mu} \left[ \Uplambda_1(t) + \Uplambda_2(t) + \Uplambda_3(t) \right], $$

(18a)

$$ | m_{\rm u}(t) | = {\rm max} \left\{ | \Uplambda_1(t) + \Uplambda_3(t) - \frac{2(\lambda + \mu)}{\lambda + 2\mu} m_{\rm w}(t) | \;, \; | \Uplambda_2(t) - \frac{\lambda}{\lambda + 2\mu} m_{\rm w}(t) | \right\}, $$

(18b)

$$ m_{\rm s}(t) = - \frac{\mu}{\lambda} \Uplambda_2(t) \sin(2\theta) + \left[ [\frac{\Uplambda_1(t) - \Uplambda_3(t)}{2}]^2 - [\frac{\mu}{\lambda} \Uplambda_2(t) \cos(2\theta)]^2 \right]^{1/2}. $$

(18c)

The next step is to note that

$$ \frac{m_{\rm w}(t)}{m_{\rm s}(t)} = \frac{5 \pi \sqrt{3}}{8 \cos(\theta)} \frac{\lambda + 2\mu}{\mu} \frac{L^2}{\sqrt{(1+L)^2 -1} + (1+L)^2 \sin^{-1}[(1+L)^{-1}]}. $$

(19)

This is an implicit equation that can be solved for L. Using this L and Eq. 11 the radius of the shear crack is

$$ r_{\rm c} (t) = \left[ \frac{3 [1+\nu] f_3(L) m_{\rm s}(t) }{4 \mu k_{\rm Ic} f_1(L) } \right]^{2/5}, $$

(19a)

the length of the wing cracks is

$$ \ell (t) = L r_{\rm c}(t), $$

(19b)

and the maximum slip on the shear crack is

$$ d (t) = \frac{k_{\rm Ic}}{[1+\nu] f_3(L)} r_{\rm c}(t)^{1/2}. $$

(19c)

These equations for the crack parameters are strictly valid only for t ≥ τ_s + τ_w. In the special case where m _w(t) = 0 the results of Eq. 19a–19c assume that the stress intensity factor of Eq. 11 is at its critical value k _Ic.

In the case where m _s(t) ≠ 0 the moment tensor is not diagonal so the eigenvectors will not coincide with the axes of the coordinate system assumed in Eq. 13 (the x _i system in Fig. 3). However, one can solve for the eigenvectors and show that with respect to the $\hat{\bf x}_3$ axis, the $\hat{\bf e}_3$ direction is rotated clockwise about the $\hat{\bf x}_2$ axis by an angle

$$ \chi (t) = \tan^{-1} \left[ \frac{ B + m_{\rm s}(t) \sin(2\theta) - R }{m_{\rm s}(t) \cos(2\theta) } \right] $$

(20a)

where

$$ B = \frac{\mu}{\lambda+2\mu} m_{\rm w}(t), $$

(20b)

$$ R = \left[ B^2 +2B m_{\rm s}(t)\sin(2\theta) + m_{\rm s}(t)^2 \right]^{1/2}. $$

(20c)

The $\hat{\bf e}_1$ direction is rotated with respect to the $\hat{\bf x}_1$ axis by this same amount.