Abstract
Global digital elevation models (DEMs) are an invaluable source of information in large area studies. Of particular interest are shuttle radar topography mission (SRTM) data that are freely available for the scientific community worldwide. Prior to any application, global datasets should be evaluated using reference data of higher accuracy. Therefore, the main objective of this study was to assess the accuracy of the SRTM C-band (version 4) DEM and SRTM X-band DEM of mountainous areas located in Poland and to examine the quality of data in relation to topographic parameters, radar beam geometry, initial voids in data and the presence of forest cover. A DEM from the Central National Geodetic and Cartographic Inventory, Poland, served as a reference. The study consisted of three steps: (i) the computation of vertical errors of the SRTM C- and X-band DEMs, (ii) the examination of any systematic bias in the data, and (iii) the analysis of the relationships between the elevation errors and terrain slope, aspect, local incidence angle, occurrence of voids and land cover. We found that the SRTM C- and X-band DEMs have mean errors equal to 4.31 ± 14.09 and 9.03 ± 37.40 m and root mean square errors equal to 14.74 and 38.47 m, respectively. Only 82 % of the C-band DEM and 74 % of the X-band DEM vertical errors had absolute values below 16 m. We found that the most important factors determining the occurrence of high errors were the distribution of initial voids and high slope angles for the C-band DEM, and local incidence angle, slope, aspect and radar beam geometry for the X-band DEM. In both cases, the presence of forest cover increased the mean error by approximately 10 m.
Similar content being viewed by others

Avoid common mistakes on your manuscript.
1 Introduction
In the last decade, global digital elevation models (DEMs) have become an invaluable source of information in large area studies. Knowledge of their accuracy is very important for data analysis and processing. Of particular interest are DEMs acquired from the shuttle radar topography mission (SRTM) (Papasaika et al. 2009; Schindler et al. 2011).
The main objective of the SRTM project was to collect topographic data and create the first-ever DEM with near-global coverage and with absolute horizontal and vertical accuracies better than 20 and 16 m, respectively, with 90 % confidence intervals (Rabus et al. 2003; USGS 2005; Farr et al. 2007; JPL 2009). According to the US National Map Accuracy Standards (NMAS), an absolute vertical accuracy of 16 m within a 90 % confidence interval corresponds to a root mean square error (RMSE) of 10 m, assuming a normal distribution of errors (FGDC 1998; Gesch 2007). These values were accepted as benchmarks for this study.
The SRTM data were acquired from the 11th to the 22nd of February, 2000 with two interferometric synthetic aperture radar sensors. The American SIR-C instrument covered the earth’s surface between latitudes of 60°N and 56°S and provided several observations for most locations. The German–Italian X-SAR sensor, due to its greater resolution, had a narrower ground track and covered approximately half of the area covered by the SIR-C sensor (Rabus et al. 2003; Marschalk et al. 2004; Walker et al. 2007; Jarvis et al. 2008; DLR 2010). The C-band and X-band radar wavelengths of 5.6 and 2.8 cm, respectively, cannot fully penetrate into canopies as they are significantly influenced by vegetation height, structure and density. Due to the presence of various scatterers such as leaves or branches, the resulting DEMs represent, therefore, elevations between the bare ground and the canopy top surface (Hofton et al. 2006; Farr et al. 2007). This means that the DEMs of bare ground have to be produced by filtering the original SRTM data (Jacobsen 2005; Passini and Jacobsen 2007).
The two datasets were processed independently. The SRTM C-band DEM was released by the NASA Jet Propulsion Laboratory (JPL) in 2003 with a spatial resolution of 3 As. The model, however, contained “no-data” holes. As a result, the original DEM was processed to fill the voids and produce more useful data (Reuter et al. 2007). Currently, version 4 can be obtained from the Consultative Group on International Agricultural Research Consortium for Spatial Information (CGIAR-CSI) (Jarvis et al. 2008) as 5° by 5° tiles. The SRTM X-band DEM with a spatial resolution of 1 As was produced by the German Aerospace Centre DLR and has been freely available for scientific purposes since December 2010. Individual tiles cover a geographic area of 10° by 10° (DLR 2010). The multiple coverage of the C-band and the averaging of the height values allowed the production of smoother DEMs than the mostly single-pass X-band DEM, which suffered from radar shadow and layover, especially on steep mountain slopes. The radar shadow was less significant in C-band data where data acquired from several incidence angles could have been used; in contrast, for the X-band DEM, only the areas of swath crossings were covered twice (Marschalk et al. 2004).
The technical report of JPL (Rodriguez et al. 2005) assigns an 8.8 m absolute geolocation error and a 6.2 m absolute elevation error (at 90 % confidence intervals) for SRTM-C band data. Although the accuracy of SRTM DEMs is known, DEMs have been widely examined and assessed. Many studies have been motivated by particular applications in the field of hydrology (Ludwig and Schneider 2006), geomorphology (Gorokhovich and Voustianiouk 2006), glaciology (Kääb 2005; Frey and Paul 2012) or forestry (Walker et al. 2007). SRTM DEMs were compared to elevation data from various sources, including shuttle laser altimeter (SLA) (Sun et al. 2003), advanced spaceborne thermal emission and reflection radiometer (ASTER) stereo-pairs (Nikolakopoulos et al. 2006), elevation data obtained from national resources (Ludwig and Schneider 2006; Zieliński and Chmiel 2007; Shortridge and Messina 2011; Frey and Paul 2012) or field measurements (Gorokhovich and Voustianiouk 2006; Karwel and Ewiak 2006; Karwel 2012; Li et al. 2013). Most of these studies incorporated discrete ground truth data, such as sets of ground control points (GCPs) or terrain profiles measured with a GPS device. The elevation error was, therefore, computed as the difference between the tested DEMs and the reference DEM. Most frequently, statistics such as the mean error (ME), standard deviation (SDE), minimum and maximum error values and RMSE have been used to describe the accuracy of the data.
A number of studies on the accuracy of SRTM DEMs have shown the high quality of these sources as the mean elevation differences from the reference data did not exceed 10 m and horizontal error was lower than 20 m (Strozzi et al. 2003; Sun et al. 2003; Kääb 2005; Marschalk et al. 2004; Gorokhovich and Voustianiouk 2006; Karwel and Ewiak 2006; Ludwig and Schneider 2006; Hirt et al. 2010; Shortridge and Messina 2011; Karwel 2012). Various authors, however, have examined the relationship between the model accuracy and land cover or terrain parameters such as slope, aspect, local incidence angle, initial data voids or elevation (Eineder and Holzner 2000; Sun et al. 2003; Gorokhovich and Voustianiouk 2006; Hoffman and Walter 2006; Karwel and Ewiak 2006; Ludwig and Schneider 2006; Zieliński and Chmiel 2007; Mouratidis et al. 2010; Frey and Paul 2012; Karwel 2012). Eineder and Holzner (2000) stated that radar shadow and layover may degrade the radar signal and, consequently, the accuracy of the elevation data. Sun et al. (2003) noticed only slight increases in C-band DEM elevation error with increasing terrain slope; they also reported a strong positive bias in forested areas. Gorokhovich and Voustianiouk (2006) revealed a significant decrease in SRTM C-band DEM accuracy on slopes steeper than 10° (in the Phuket study area: 5.03 ± 0.35 and 19.20 ± 2.70 m for slope values lesser and greater than 10°, respectively). Moreover, they observed the highest errors on north-western slopes where elevations were underestimated and the lowest errors on south-eastern slopes with mainly overestimated elevations. Hoffman and Walter (2006) confirmed the observations of Falorni et al. (2005), showing that the outliers in the X-band DEM were more frequently found on steep slopes and resulted from the single coverage. Ludwig and Schneider (2006) located one of their test sites in a high alpine environment with rough surfaces, slopes reaching 70° and diverse land cover to analyse the relationship between SRTM X-band elevation errors and parameters such as the local incidence angle of the radar signal, slope, aspect and land cover. They reported that ME increases with slope, reaching over 30 m for a slope of 50° and for a change in aspect towards the north and northwest due to the radar shadow effect. The authors also showed that the local topography and the radar beam geometry strongly influenced the accuracy of SRTM, leading to elevation errors of up to 60 m. Furthermore, they found that slopes facing away from the radar were prone to positive elevation errors, while slopes facing towards the sensor tended to show negative errors. In relation to land cover, forests caused the highest elevation errors. Very high elevation errors in non-vegetated areas were attributed to the fact that these areas were located almost exclusively on steep slopes. Mouratidis et al. (2010) studied all four versions of SRTM C-band DEM and reported high accuracy in each case. They also suggested that slope was the dominant factor that controlled SRTM accuracy, with the critical value at 18°; above this value, the errors increased dramatically. Frey and Paul (2012) noticed lower accuracy of the SRTM C-band DEM in regions with initial voids, even though the voids were filled using interpolation algorithms and auxiliary DEMs if available.
Several studies on the accuracy of SRTM DEMs have been conducted in Poland. Karwel and Ewiak (2006) and Karwel (2012) analysed SRTM C- and X-band DEMs of flat and hilly terrains in Poland and showed positive MEs in both cases. The RMSE for the C-band DEM was equal to 2.9 m for flat terrain and 5.4 m for hilly terrain; for the X-band DEM, the RMSE was equal to 3.6 and 4.1 m for flat and hilly terrains, respectively. Moreover, these studies reported higher errors for flat slopes than for slopes with gradients ranging from 2° to 6°. Zieliński and Chmiel (2007) assessed SRTM C-band DEM version 2 in three test sites with various topographies located in the north, centre and south of Poland and reported that the RMSE of the C-band DEM did not exceed 5.2 m on gentle slopes (below 20°) and reached 6 m on steeper slopes. A recent study by Czubski et al. (2013) focusing on topographical and hydrological modelling in the deep gorge of the Dunajec River (Pieniny Mts., Poland) showed that the largest errors in the SRTM X-band DEM occurred in the most rugged part of the study area where the ME was negative and the RMSE was equal to 12.05 m.
To date, assessments of the accuracy of SRTM DEMs in mountainous areas have been applied mainly in the context of glacier monitoring (Kääb 2005; Berthier et al. 2006; Surazakov and Aizen 2006; Fujita et al. 2008; Frey and Paul 2012), hydrological modelling (Ludwig and Schneider 2006) and terrain morphometry (Gorokhovich and Voustianiouk 2006; Sefercik and Alkan 2009). However, complex investigations of the factors that can potentially influence the accuracy of SRTM DEMs in mountainous areas, especially for the recently released X-band data, are lacking. On the basis of this state-of-the-art technology, it can be assumed that (i) the slope, aspect, combination of slope and aspect and forest cover are correlated with the accuracy of both C- and X-band DEMs; (ii) the proportion and distribution of initial voids are correlated with the accuracy of C-band DEM; and (iii) the combination of radar beam geometry and local topography are correlated with the accuracy of X-band DEM.
For this reason, the main objective of the present study was to assess the accuracy of SRTM C-band version 4 and SRTM X-band DEMs in a mountainous area, and to examine the quality of these measurements in relation to various factors, such as initial proportion of voids, local incidence angle, altitude a.s.l., slope, aspect and forest cover. In the study, the Polish Tatra Mountains were chosen as a test site for three reasons. First, this range is representative of a steep, high-mountain topography of other ranges in the temperate zone. Second, the SRTM C-band DEM version 4 and X-band DEM were available for the entire region. Third, a high-quality reference DEM and other necessary data were available.
The study consisted of three principal steps. First, vertical errors of SRTM C- and X-band DEMs were estimated; then, the presence of systematic errors, such as shift, was examined. Finally, the elevation errors were related to the local incidence angle and the distribution of initial voids, terrain slope, aspect and the occurrence of forest cover.
2 Test Site and Datasets
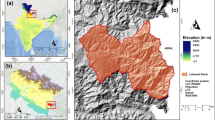
The Tatra Mts. (2,655 m a.s.l.) constitute the highest range of the Carpathians and are located at the border between Poland (Małopolska Province) and Slovakia. The lower parts of the mountains consist predominantly of carbonate rocks, while granite and metamorphic rocks predominate in the highest parts. The alpine character of the relief (Fig. 1) results from glacial processes that formed a system of cliffs and talus slopes. Currently, the relief is strongly influenced by slope and fluvial processes (Kotarba et al. 1987; Kotarba and Pech 2002). Beech-fir and spruce forests, dwarf pine shrubs, grasslands and bare ground are the predominant land cover types, with forests occupying mountain slopes below the timberline at approximately 1,500 m a.s.l.
The test site (Fig. 2) was defined by the boundary of the Polish Tatra National Park (TPN) expanded by a buffer zone 500 m wide. The test site covered 19,729 hectares, with elevations ranging from 902 to 2,540 m a.s.l. The National Park boundary data were obtained from the TPN GIS Section in a shapefile format.
SRTM C-band DEM version 4 and SRTM X-band (Table 1) data consisted of the tiles srtm_40_03 and srtm_41_03 and the tiles E010N40 and E020N40, respectively. For the study area, C-band interferometry observations consisted of multi-pass data, while X-band observations were collected in only one pass of the space shuttle. Therefore, the signal transmission geometry of the SRTM-X DEM should be of higher quality than that of the SRTM-C DEM. Both C- and X-band DEMs were referenced to the WGS84 ellipsoid. The vertical datum for the C-band dataset and the X-band dataset consisted of the EGM96 geoid and the WGS84 ellipsoid, respectively (Farr et al. 2007; Jarvis et al. 2008; JPL 2009; DLR 2010).
The reference data consisted of a section of a DEM available from the national resources of CODGiK (the Central National Geodetic and Cartographic Inventory; CODGiK 2012) as a triangulated irregular network (TIN), which is currently the most accurate DEM covering the entire territory of Poland. These data were acquired in 2002–2005 by the photogrammetric processing of aerial imagery at 0.2 m ground pixel size and included regular points at 10–40 m intervals (depending on the relief), irregular spot heights and breaklines. Only in the areas of dense forest cover, where, neither image matching nor stereoscopic measurement, was possible, was then the model based on contour lines and elevation points digitised from topographic maps at a scale of 1:10,000. The national “1992” projected coordinate system, based on the WGS84 ellipsoid, was used as the reference for horizontal positioning. The data were vertically referenced to the Kronsztad86 elevation system—one of the components of the Polish national reference system.
According to the national standards, the horizontal error of the CODGiK DEM should be less than ±10 m (GUGiK 1980). However, the horizontal accuracy of this product can also be determined as a function of the aerial photo scale and pixel size (Kraus 2007). Taking the respective parameters of the CODGiK DEM into account, the horizontal RMSE should be equal to 0.2 m. The vertical accuracy of the CODGiK DEM was estimated at 1.5 m for open terrain and 2.75 m for forested areas (Gotlib et al. 2006). For the Małopolska Province, Karwel (2007) determined RMSE to be 0.5 m using field data collected along the terrain profiles. For a small case study area located in the Carpathians, Ptak (2008) showed that forested areas had higher MEs than open areas; she also noted that errors occurred exclusively in the former type of land cover.
Considering the predominant types of land cover, we distinguished forests from other land cover types. The forest cover mask was obtained as a vector layer from the TPN GIS Section in a shapefile format. The vector data come from detailed forest surveys that are carried out in Poland for all state forests, including forests in national parks. The vector data only lacked coverage for the westernmost valley of the Polish Tatra Mts. that is a private property; the remaining portion, consisting of approximately 77 % of the study area, was large enough to perform the analysis. The original data included polygons with attribute information on plant species and height, allowing us to distinguish trees from dwarf pines and to exclude dwarf pine shrubs from the forest class.
3 Methods
This study included the following three steps: (i) preparation of the input data; (ii) assessment of the accuracy of each SRTM DEM; and (iii) analysis of the relationships between the accuracy of the SRTM DEMs and various factors, including the initial proportion of voids (only for the C-band DEM), the local incidence angle (only for the X-band DEM), slope, aspect and forest cover occurrence.
3.1 Data Preparation
First, we converted the reference model from TIN to a 10-m grid, with a mean difference between the grid and the TIN equal to −0.15 m. Next, vertical reference systems were unified using the WGS84 ellipsoid as the vertical reference datum. As the WGS84 was the native vertical reference of the SRTM X-band data, the CODGiK DEM and the SRTM C-band data were adjusted for the elevation of the Kronsztad86 elevation system and EGM96 geoid, respectively. Deviations between the Kronsztad86 level and the global EGM96 geoid in the Tatra Mountains reach 10 cm, and both Kronsztad86 and EGM96 have negative deviations from the WGS84 ellipsoid of approximately 42 m. The differences between Kronsztad86/EGM96 and the WGS84 ellipsoid were determined for a sample of regularly distributed points (spacing of 1 As) that were then interpolated to undulation rasters and subsequently added to the respective DEMs. The deviations of the Kronsztad86 from the WGS84 ellipsoid were determined using the official gravity model as implemented in the Geokonwerter software (Numerus 2012), while the EGM96 deviations were computed using the NGA EGM96 Geoid Calculator (NGA 2012).
Next, the SRTM C-band DEM and SRTM X-band DEM tiles were converted to points representing cell centres, with their original elevations written to the attribute table. From the geometry of the original raster files, it was clear that every C-band point had its exact counterpart in the X-band point data. Points were projected to the “1992” Polish national coordinate system. In this way, the problem of different spatial resolution of the datasets (Frey and Paul 2012) was overcome and we avoided raster resampling during the unification of the horizontal reference systems and DEM projection. Finally, reference elevations from the CODGiK DEM were extracted for all points and recorded in the attribute table.
3.2 Accuracy Assessment
The initial accuracy assessment was based on the determination of differences between the SRTM DEMs converted to points and the reference DEM. An elevation error (Sun et al. 2003; Ludwig and Schneider 2006) was computed for each point as:
where H diff is the elevation error, H ex is the elevation of the examined DEM, and H ref is the elevation of the reference DEM. Next, the ME, SDE, RMSE and maximum and minimum error values (Lane et al. 2000; Becek 2008; Liu and Mason 2009; Weisstein 2012) were computed as follows:
SDE and RMSE are measures of surface quality and provide insight into the distribution of deviations on either side of the mean value (Lane et al. 2000; Liu and Mason 2009). Once the elevation deviations and statistics were computed, we determined the percentage of errors with absolute values below 16 m and the threshold value at which more than 10 % of the highest absolute errors occur.
The third task was to detect any systematic horizontal or vertical shift in the data. The iterative closest point (ICP) algorithm (Besl and McKay 1992; Rusinkiewicz and Levoy 2001) was applied to grid points extracted from SRTM C- and X-band DEMs to align them to the reference DEM. The ICP algorithm registers free-form shapes (including point clouds) by the iterative calculation of the local minimum of the least square distance metric and source point cloud transformation (translation and rotation) using the minimisation results (Besl and McKay 1992; Rusinkiewicz and Levoy 2001). The vector of translation indicated the systematic shift between the datasets.
To scale the analysis between the C- and X-band DEMs, we selected every third SRTM X-band DEM point building a 3″ lattice identical to that composed of the SRTM C-band DEM points. We then calculated the differences between the X- and C-band DEMs and the error statistics for the 3″ sample of X-band DEM points to compare this sample with the entire SRTM X-band DEM set.
3.3 Influence of Various Factors on the Accuracy of SRTM DEMs
The accuracy of the SRTM data was assessed with respect to the following factors: initial proportion of voids (for the C-band data only), local incidence angle (for the X-band data only), altitude a.s.l., slope, aspect and forest cover (for both C- and X-band data).
The raw C-band DEM (version 1) within the study area consisted of approximately 2 % of voids located mainly in the vicinity of steep mountain ridges (Fig. 3). To quantify the effect of voids in the original C-band elevation data, statistical analysis was conducted for the SRTM version 4 DEM for two zones determined by the distribution of voids in the original C-band elevation data.
In the case of X-band data, the local incidence angle may impact the accuracy of the DEM output as the geometry of the incidence angle strongly influences the quality of the reflected radar beam. For example, in an extreme situation (such as in a mountainous area), the radar data can be lost on steep slopes that are in shadow due to a radar look angle (Farr 1993). The geometry of the SRTM X-band beam was given by its viewing azimuth angle (147°) and look angle (54.5° at scene centre) (Kramer 2002; Rabus et al. 2003). Following Castel and Oettli (2008), it was assumed that the offset of the two SRTM antennae did not imply geometrical differences.
In the study, the local incidence angle θ loc was derived directly from the output of the Hillshade Algorithm (Hillshade) implemented in the ArcGIS software:
where Hillshade was computed from DEMs for SRTM-X viewing azimuth angle and look angle specified above. Moreover, the hillshade algorithm was customised to address the effects of both local illumination angle and shadows. Shadowed raster cells were assigned a hillshade value of zero and a local incidence angle of 90°. Finally, the local incidence angle was classified into three zones: (i) shadowed parts of terrain, where the local incidence angle was greater than or equal to 90°; (ii) areas where θ loc was greater than 54.5°, indicating a surface opposite to the radar; and (iii) areas where θ loc was less than 54.5°, indicating a surface facing the radar (θ loc equal to 54.5° indicated flat terrain; Fig. 3).
To verify the relationship between elevation errors and altitude, Pearson’s correlation coefficients were computed for the SRTM DEM elevation errors and the reference altitude a.s.l. (Weisstein 2012) for all DEM points after removal of 10 % of the highest absolute errors.
To assess the influence of slope and aspect on the accuracy of SRTM data, the derivatives were calculated from the CODGiK DEM. Errors related to slope were analysed in classes of 1°. Errors related to aspect were analysed in eight 45° zones. Flat areas were not considered due to an insufficiently large sample size.
The quality of the reflected signal in radar-based methods is affected by scattering objects on the earth surface (Ludwig and Schneider 2006). The most significant object within the test site was forest, which covered 70 % of the area. Forests in the TPN cover slopes of various gradients. As the slope gradient itself may influence the elevation errors, to quantify the elevation errors for forested and non-forested areas, we first excluded slopes above 30° to remove the most error-prone areas. The analysis was finally carried out for 50 % of the study area, 70 % of which was forested.
4 Results
4.1 General Quality of the SRTM DEMs
The differences between the SRTM elevation data and the CODGiK DEM resulted in an error value for each point (Figs. 4, 5). A visual inspection of the C-band DEM elevation error showed that the distribution of errors was related to topography. Both the C-band and the X-band DEM elevation errors were distributed irregularly (Fig. 4); however, the C-band positive deviations occurred in valleys while the negative deviations occurred on and near ridges. The highest positive and negative X-band deviations appeared mostly near steep slopes and ridges and were dependent on the terrain aspect. Though visually deviations from the reference DEM might seem to follow a normal distribution (Fig. 5), the frequency of gross errors was in fact higher than in the case of the normal distribution. A slight shift towards positive values was also observed, i.e., the elevation of the SRTM DEMs was often greater than that of the reference DEM. This observation indicated the presence of a constant vertical offset of the SRTM DEMs. The ME, maximum and minimum error, SDE and RMSE were more than twice as large for the SRTM X-band as for the SRTM C-band DEM; in both cases, the RMSE was greater than 10 m (Table 2). A 3″ sample of X-band points showed ME, SDE and RMSE values that were very similar to the values obtained when all the SRTM-X DEM points were taken into account (Table 2).
Absolute values below 16 m were observed for 82 % of the C-band DEM and 74 % of the X-band DEM vertical errors. The thresholds for 10 % of the highest absolute errors were at 19.99 and 29.51 m for the C- and X-band DEM, respectively; these values exceeded the values provided in the official specifications (16 m at 90 % confidence level; USGS 2005; JPL 2009). It was apparent from the high minimum and maximum errors observed (Table 2) that large disparities between the SRTM DEMs and the reference DEM existed. The rather high SDE also showed that the error values were widely dispersed around the average value, especially in the case of the X-band DEM, which confirmed results of initial visual observations of both SRTM DEMs. Furthermore, linear regression analysis revealed strong correlations between the SRTM C-band DEM and the CODGiK DEM, while the X-band DEM data were much more scattered around the regression line (Fig. 6).
Importantly, a systematic offset was detected between both the SRTM DEMs and the CODGiK DEM. For the C-band DEM, the north–south, east–west and vertical shifts were equal to 3.92, −0.88 and 11.14 m, respectively; the shifts for the X-band DEM equalled 14.94, −3.63 and 10.98 m, respectively. Removing horizontal offset in SRTM DEMs slightly decreased ME in both cases and RMSE for X-band data only. However, this offset correction was not included in the further analyses, as location accuracy is a substantial factor of the DEM quality. In both cases, the systematic horizontal offset, equal to 4.02 and 15.37 m for the C- and X-band DEM, respectively, was lower than the mission accuracy constraint of ±20 m (USGS 2005; Farr et al. 2007; JPL 2009).
The mean difference between C- and X-band elevations assessed for a sample of SRTM-X DEM points was equal to −4.69 m. High minimum (−489 m) and maximum (559 m) values of C- and X-band difference, high RMSE (37.14 m) and SDE (36.85 m) indicate significant variations in the differences between these two DEMs.
4.2 Influence of Data Acquisition on the Analysis of the Accuracy of SRTM DEMs
Only 2 % of the test site consisted of no-data values in the original SRTM C-band data. Our results confirmed our expectations that the SRTM C-band DEM errors and the SDE and RMSE were significantly higher in areas of voids in the original SRTM C-band data (Table 3).
For the SRTM X-band DEM, 11 % of the study area consisted of shadowed terrain, 32 % consisted of slopes facing towards the sensor and 57 % represented slopes facing away from the radar. The ME for slopes opposite the radar beam was nearly twice as large as for slopes facing towards the sensor. In both zones, the SDE and RMSE were comparable. There was a significant difference in the error magnitude between slopes that were shadowed and slopes that were illuminated by the radar beam (Table 4). The highest errors occurred in the shadowed parts of the test site where the ME exceeded 36 m and where both the SDE and RMSE were approximately five-times as large as in the illuminated terrain. In the areas affected by the radar shadow, only 18 % of the X-band DEM elevation errors fell into the ME ± 10 m range.
4.3 Influence of Altitude, Slope and Aspect on the Accuracy of SRTM DEMs
The correlation between the SRTM elevation errors and the altitude a.s.l. for all points was −0.02 for the SRTM C-band DEM and −0.16 for the SRTM X-band DEM. If 10 % of the highest errors were removed, the correlation was strong and negative for both the C-band (−0.60) and the X-band data (−0.53).
The analysis of the influence of slope and aspect on the accuracy of SRTM revealed a clear relationship between the magnitude of the elevation error and the terrain slope angle (Fig. 7). A significant decrease in the accuracy of C- and X-band DEM was observed with increasing slope angle, especially for slopes exceeding 40° and 30°, respectively. In terrains steeper than 70°, the ME exceeded 62 m (C-band data) and 108 m (X-band data).
Similarly, terrain aspect was found to have an influence on the magnitude of the SRTM DEMs error. For the SRTM C-band DEM, the highest and lowest errors were observed on slopes with eastern expositions and on south-western slopes, respectively. In contrast, for the SRTM X-band DEM, the highest error values were found in the northwest zones, while the lowest errors occurred on slopes facing south-east (Fig. 8).
4.4 Influence of Forest Cover on the Accuracy of SRTM DEMs
For the SRTM C-band DEM, the ME was significantly higher in forested areas than in non-forested areas where the model underestimated elevation. The SDE values and the range of errors were similar for both land cover types. The RMSE was slightly higher in forested areas, which implies larger deviations from the reference DEM. The results of the X-band DEM were different from the results of the SRTM C-band DEM. The ME showed that SRTM X-band DEM overestimates elevation for both land cover types, though the ME values were significantly higher in the forested areas. The SDE and RMSE were higher in non-forested areas than in forested areas (Table 5).
5 Discussion and Conclusions
The overall goal of this study was to assess the accuracy of the SRTM C- and X-band elevation data in a mountainous area. The quality of SRTM DEMs was assessed in general terms rather than in the application-specific case, with the original mission specifications serving as benchmarks.
The visual evaluation of the distribution of errors for both models allowed us to detect significant differences between the SRTM-C and SRTM-X DEMs and to outline certain generic patterns. While the X-band data were not filtered and smoothed, they included a significant amount of noise. Indeed, the most prominent features of the X-band DEM were large positive elevation errors on steep north and north-western slopes, e.g., areas affected by radar shadow. Because the X-band DEM consisted of a relatively raw dataset, more clear relationships between the X-band DEM errors and the specific factors, especially aspect, were observed. In contrast, the original C-band data were carefully processed to remove artefacts and fill voids by means of interpolation and the use of auxiliary data in SRTM DEM version 4 (Reuter et al. 2007; Jarvis et al. 2008). Therefore, the relationships between the elevation errors and aspects were not as evident for the C-band data. On the other hand, the visual evaluation of the distribution of errors of the C-band DEM proves that it tended to underestimate the elevations of steep ridges frequent at higher elevations and overestimate the elevations of deep gorges and valleys at lower elevations. Paul (2008) and Frey and Paul (2012) claimed that these errors were mainly caused by the relatively low spatial resolution of SRTM C-band data which resulted in smoothing effects and omission of small objects. However, it seems that the processing of the original C-band DEM was also important, as the most suitable method to remove small and medium voids in high altitude areas was the spline interpolation (Jarvis et al. 2008), resulting in smoothing effects and loss of detail.
The results from the visual assessment of differences between the two SRTM DEMs were confirmed by the comparison of differences of pairs of points in the same spatial locations (3″ lattice). The mean difference suggested lower elevation values of the C-band DEM, while the high SDE and range of height differences between C-band and X-band DEMs indicated significant vertical discrepancies between both datasets.
Neither the C-band DEM nor the X-band DEM provided satisfactory results within the study area, as the RMSE of the C- and X-band elevation data were equal to 14.74 and 38.47 m, respectively. In the case of SRTM-C DEM and SRTM-X DEM, 82 and 74 % of errors had absolute values below 16 m, respectively; the mission required that linear vertical absolute elevation errors should be less than 16 m for 90 % of the data (USGS 2005; Farr et al. 2007; JPL 2009). The positive MEs suggest that both SRTM models overestimated elevation in the study area. Other studies carried out in Poland provided various results: Karwel and Ewiak (2006) and Karwel (2012) obtained positive values while Czubski et al. (2013) reported negative ME values for the Pieniny Mts., a small mountain range north-east of the Tatra Mts. A positive ME consistent with results of our study was reported by Hirt et al. (2010) in Australia. Li et al. (2013) reported a negative ME of the C-band DEM in China, but they were unable to explain their result. We believe that the different ME signs in various SRTM studies can be related to regional differences in terrain morphology or to differences in land cover (e.g., presence of forests). The latter factor is crucial for the positive ME obtained in this study, as forests cover 70 % of the Polish Tatra Mountains.
The systematic offset was detected in both datasets in horizontal and vertical directions. The C-band horizontal offset was much smaller than that of the X-band. In contrast to Rodriguez et al. (2005, 2006) who reported geolocation errors throughout Eurasia equal to 8.8 m, the horizontal offset of SRTM DEMs in our study was approximately lower by half for the C-band DEM and twice as high for the X-band DEM; the horizontal offset in C-band data seems therefore negligible. While we were not able to explain the origin of the high horizontal offset in the X-band data, these results suggest that the X-band DEM is clearly an inferior choice to the C-band DEM. We also detected a vertical offset from the reference of approximately 11 m for both SRTM DEMs, though the offset was slightly lower for the X-band DEM. This value is comparable to the mean elevation error of forested areas, confirming the significance of land cover for the error distribution. While the vertical offsets were similar for both DEMs, all other error indicators were higher for the SRTM X-band DEM. We therefore conclude that the higher horizontal shift in the X-band data significantly contributed to higher vertical discrepancies and errors between the SRTM X-band DEM and the reference model than it was in case of the SRTM C-band DEM. In case of SRTM-X DEM we agree with Van Niel et al. (2008) who expressed concerns about the impact of sub-pixel misregistration on DEM errors.
The assessment showed that there was a noticeable relationship between the distribution and magnitude of errors and examined factors, namely altitude a.s.l., slope, aspect, forest cover and characteristics of data acquisition.
The correlation between SRTM errors and altitude a.s.l. was negligible for all points; however, we found a strong negative correlation between SRTM elevation errors and the altitude a.s.l. when gross errors were excluded. Therefore, we assume that elevation errors decreased with increasing altitude, reaching negative values in the highest parts of the study area. This is most likely due to the distribution of forest cover in the lower parts of the study area that caused a positive bias in SRTM data. In addition, the elevation of high mountain ridges were underestimated in most cases, as was detected visually (Fig. 4). On the other hand, a low correlation for all points results from the presence of gross errors that are related to other factors discussed below and that occur at various elevations.
Our results indicating an increase in elevation error with increasing slope are fully consistent with observations of Ludwig and Schneider (2006) and Mouratidis et al. (2010) who examined SRTM X-band and SRTM C-band DEMs, respectively; our results are also generally consistent with findings of Gorokhovich and Voustianiouk (2006) who examined the X-band DEM for two slope classes (below and above 10°) and noted that the elevation error was significantly higher on steeper slopes. Sun et al. (2003) did not notice the effect of slope on the accuracy of SRTM C-band DEM version 1 as their study area was almost completely flat.
We detected a dependence of the ME on aspect, especially in the X-band data. For the X-band DEM, the relationship between error and aspect can be visually detected, as errors increased on the backslopes exposed to the north and north-west. Gorokhovich and Voustianiouk (2006) found that aspect influences not only the magnitude but also the sign of errors (C-band DEM version 4). Similarly, Ludwig and Schneider (2006) detected that the elevations of north-western and south-eastern slopes were, respectively underestimated and overestimated for the X-band DEM in relation to the local incidence angle. Our study does not fully confirm this observation, as we obtained positive ME values regardless of the geometry of the local beam; nonetheless, backslopes were subjected to higher errors than foreslopes, and the positive bias in the SRTM data was, in general, attributable to forest cover.
Higher errors in vegetated areas were confirmed by Jacobsen (2005) and Passini and Jacobsen (2007) who reported that the dominating effect of the vegetation on the positive elevation error was related to the fact that neither C- nor X-band radar wave can fully penetrate forest canopies (Hofton et al. 2006; Farr et al. 2007). The higher bias in vegetated areas was also reported by Sun et al. (2003) who observed that SDEs and RMSEs were significantly higher in regions covered with forest. Contrary to their findings, Ludwig and Schneider (2006) noted that SDE values were twice as high in open areas as in forests. Although this result seems controversial, the partial explanation is the fact that non-forest areas are frequently located on steeper slopes, which are more error-prone. As suggested by Ludwig and Schneider (2006), adjusting elevation values of the SRTM DEM within boundaries of forest patches, e.g., by means of data filtering, should allow users to produce more accurate bare ground elevation data.
On the basis of our findings, we conclude that the most important factors determining the occurrence of high errors for the C-band DEM were the distribution of initial voids and high slope angles. For the X-band DEM, we found that errors were due mostly to the local incidence angle, slope, aspect and radar beam geometry; Ludwig and Schneider (2006) came to similar conclusions. The knowledge of these parameters allows users to exclude areas where the original elevation data are unavailable or unreliable and to preserve the remaining portion of the data where the vertical accuracy is much higher. These findings support the approach proposed by Castel and Oettli (2008) who chose a function of the local incidence angle to model the error distribution in SRTM C-band version 4 elevation data.
Unlike other studies carried out in mountainous areas that reported high vertical accuracy of the SRTM C-band version 4 and X-band data (Gorokhovich and Voustianiouk 2006; Frey and Paul 2012), and in contrast to former expectations (Rabus et al. 2003), the current study shows that the quality of the C- and X-band DEMs in the rugged terrain of the Polish Tatra Mountains is not high; this conclusion is particularly valid for the X-band DEM. Though our results were gathered for a relatively small, specific area of high relief complexity, they were mostly consistent with findings of previous studies examining factors influencing the accuracy of SRTM DEMs conducted at different test sites and on various scales. The global assessment of the SRTM DEM by Rodriguez et al. (2005) also clearly documented that the spatial distribution of errors in SRTM data reflects the global topography and the occurrence of major mountain chains, as detected errors were significantly higher in high mountain areas. Hence, we conclude that because the Tatra Mountains represent alpine relief and vegetation typical of other mountain ranges (especially in the temperate zone, e.g., the Alps, Pyrenees, Caucasus), our results may be applicable to other mountainous areas in the world.
References
Becek, K. (2008), Investigation of elevation bias of the SRTM C- and X-band digital elevation models, Proceedings of the Map Asia 2007 conference, Kuala Lumpur, Malaysia. Online: http://www.gisdevelopment.net/technology/ip/ma07267.htm, available: 10 June 2012.
Berthier, E., Arnaud, Y., Vincent, C., and Remy, F. (2006), Biases of SRTM in High-mountain Areas: Implications for the Monitoring of Glacier Volume Changes. Geophysical Research Letters 33(8): L08502.1–L08502.5.
Besl, P.J., and McKay, N.D. (1992), A method for registration of 3-D shapes, IEEE Transaction on Pattern Analysis and Machine Intelligence 14(2), 239–256.
Castel, T., and Oettli, P. (2008), Sensitivity of the C-band SRTM DEM Vertical Accuracy to Terrain Characteristics and Spatial Resolution, Terrain, 163–176. Online: doi:10.1007/978-3-540-68566-1_10, available: 10 June 2012.
CODGiK (2012), Online: http://www.codgik.gov.pl/, available: 5 June 2012.
Czubski, K., Kozak, J., Kolecka, N. (2013), Topographical and hydrological modelling with SRTM-X and ASTER elevation data: case study of the Pieniny Mts. in Poland. International Journal of Geoinformatics (submitted).
DLR (2010), DLR SRTM Digital Elevation Models, Online: http://www.dlr.de, available: 2 June 2012.
Eineder, M. and Holzner, J. (2000), Interferometric DEMs in alpine terrain—Limits and options for ERS and SRTM, Proceedings of IGARSS, Honolulu, HI, 2000, 3210–3212.
Falorni, G., Teles, V., Vivoni, E. R., Bras, R.L., and Amaratunga, K.S. (2005), Analysis and characterization of the vertical accuracy of digital elevation models from the Shuttle Radar Topography Mission, Journal of Geophysical Research 110(F2), 1–20.
Farr, T.G., Radar interaction with geological surfaces, In Guide to Magellan Image Interpretation (ed. Ford J.P. et al.) (Jet Propul Lab., Pasadena, Calif. 1993), 45–56.
Farr, T. G. et al. (2007), The Shuttle Radar Topography Mission, Reviews of Geophysics 45(2), RG2004.
FGDC (1998), Geospatial Positioning Accuracy Standards. Part 3: National Standard for Spatial Data Accuracy. Federal Geographic Data Committee. USA. Online: http://www.fgdc.gov/standards/standards_publications/, available: 12 June 2012.
Frey, H. and Paul, F. (2012), On the suitability of the SRTM DEM and ASTER GDEM for the compilation of topographic parameters in glacier inventories, International Journal of Applied Earth Observation and Geoinformation 18, 480–490.
Fujita, K., Suzuki, R., Nuimura, T., and Sakai, A. (2008), Performance of ASTER and SRTM DEMs, and their potential for assessing glacial lakes in the Lunana region, Bhutan Himalaya, Journal of Glaciology, 54(185), 220–228.
Gesch, D.B. (2007), The National Elevation Dataset, In: Digital Elevation Model Technologies and Applications: The DEM Users Manual (ed. Maune, D.), 2nd Edition: Bethesda, Maryland, American Society for Photogrammetry and Remote Sensing, 99–118.
Gorokhovich, Y., and Voustianiouk, A. (2006), Accuracy assessment of the processed SRTM-based elevation data by CGIAR using field data from USA and Thailand and its relation to the terrain characteristics, Remote Sensing of Environment 104, 409–415.
Gotlib, D., Iwaniak, A., Olszewski, R. (2006), Budowa krajowej infrastruktury danych przestrzennych w Polsce—harmonizacja baz danych referencyjnych (Creation of the National Spatial Data Infrastructure in Poland—Harmonisation of Reference Databases). Wydawnictwo AR, Wrocław.
GUGiK, (1980), Instrukcja Techniczna K2–Mapy topograficzne do celów gospodarczych, Warszawa.
Hirt, C., Filmer, M.S., Featherstone, W.E. (2010), Comparison and Validation of the Recent Freely Available ASTER-GDEM Ver1, SRTM Ver4.1 and GEODATA DEM-9s Ver3 Digital Elevation Models over Australia. Australian Journal of Earth Sciences 57:337–47.
Hoffman, J., and Walter, D. (2006), How complementary are SRTM-X and -C band Digital Elevation Models? Photogrammetric Engineering & Remote Sensing 72(3), 261–268.
Hofton, M., Dubayah, R., Blair, J. B. and Rabine, D. (2006), Validation of SRTM elevations over vegetated and non-vegetated terrain using medium footprint Lidar. Photogrammetric Engineering and Remote Sensing 72, 279–285.
Jacobsen, K. (2005) Analysis of SRTM Elevation Models, EARSeL 3D-Remote Sensing Workshop, Porto, 2005, on CD+ http://www.ipi.uni-hannover.de/.
Jarvis, A., Reuter, H.I., Nelson, A., Guevara, E. (2008) Hole-filled seamless SRTM data V4, International Centre for Tropical Agriculture (CIAT), available from http://srtm.csi.cgiar.org.
JPL (2009) Shuttle Radar Topography Mission. Technical Fact Sheet, available from http://www2.jpl.nasa.gov/srtm/index.html.
Karwel, A.K. (2007), Estimation of dem accuracy on the area of Poland based on the elevation data of the LPIS project, Archiwum Fotogrametrii, Kartografii i Teledetekcji 17, 357–362.
Karwel, A.K. (2012), Ocena dokładności modelu SRTM-X na obszarze Polski, Archiwum Fotogrametrii, Kartografii i Teledetekcji 23, 139–145.
Karwel, A.K., and Ewiak, I. (2006), Ocena dokładności modelu SRTM na obszarze Polski, Archiwum Fotogrametrii, Kartografii i Teledetekcji 16, 289–296.
Kääb, A. (2005), Combination of SRTM3 and repeat ASTER data for deriving alpine glacier flow velocities in the Bhutan Himalaya, Remote Sensing of Environment 94, 463–474.
Kotarba, A., Kaszowski, L., and Krzemień, K. (1987), High-mountain denudational system of the Polish Tatra Mountains, Wrocław: Ossolineum. The Publishing House of the Polish Academy of Sciences.
Kotarba, A., and Pech P. (2002), The recent evolution of talus slopes in the High Tatra Mountains (with the Pańszczyca Valley as example), Studia Geomorphologica Carpatho-Balcanica 36, 69–76.
Kramer, H. J. (2002), Observation of the earth and its environment: survey of missions and sensors. 4th ed. Berlin: Springer.
Kraus K. (2007), Photogrammetry. Geometry from Images and Laser Scans. Berlin: Walter de Gruyter.
Lane, S.N., James, T.D., and Crowell, M.D., (2000), Application of digital photogrammetry to complex topography for geomorphological research, The Photogrammetric Record 16, 793–821.
Li, P., Shi, C., Li, Z., Muller, J.-P., Drummond, J., Li, X., Li, T., Li, Y., and Liu J. (2013), Evaluation of ASTER GDEM Using GPS Benchmarks and SRTM in China, International Journal of Remote Sensing, 34(5), 1744–1771.
Liu, J.G., and Mason, P.J., Essential Image Processing and GIS for Remote Sensing (John Wiley & Sons, UK 2009).
Ludwig, R., and Schneider, P. (2006), Validation of digital elevation models from SRTM X-SAR for applications in hydrologic modelling. ISPRS Journal of Photogrammetry and Remote Sensing 60, 339–358.
Marschalk, U., Roth, A., Eineder, M. and Suchandt, S. (2004), Comparison of DEMs derived from SRTM/X- and C-band, Proceedings, IGARSS’04 7, 4531–4534.
Mouratidis, A., Briole, P., and Katsambalos, K. (2010), SRTM 3″ DEM (versions 1, 2, 3, 4) validation by means of extensive kinematic GPS measurements: a case study from North Greece, International Journal of Remote Sensing, 31(23), 6205–6222.
Nikolakopoulos, K.G., Kamaratakis, E.K., Chrysoulakis, N. (2006), SRTM vs ASTER Elevation Products. Comparison for Two Regions in Crete, Greece, International Journal of Remote Sensing 27(21), 4819–4838
NGA (2012), NGA EGM96 Geoid Calculator, Online: http://earth-info.nga.mil/GandG/wgs84/gravitymod/egm96/intpt.html, available: 1 June 2012.
Numerus (2012), Geokonwerter, Online: http://www.numerus.net.pl/index.html, available: 2 June 2012.
Papasaika, H., Poli, D., and Baltsavias, E. (2009), Fusion of Digital Elevation Models from Various Data Sources. In Proc. IEEE, The International Conference on Advanced Geographic Information Systems & Web Services, Cancun, Mexico, February, 2009.
Passini, R., Jacobsen, K. (2007), High Resolution SRTM Height Models, ISPRS Hannover Workshop 2007, IntArchPhRS XXXVI Part I/W51, http://www.ipi.uni-hannover.de/.
Ptak A. (2008), Wykorzystanie wysokorozdzielczych modeli wysokości do wyznaczania obszarów zalewowych na przykładzie gminy Ciężkowice. MSc Dissertation, Jagiellonian University, Kraków, Poland.
Paul, F. (2008), Calculation of glacier elevation changes with SRTM: is there an elevation-dependent bias? Journal of Glaciology 54 (188), 945–946.
Rabus, B., Eineder, M., and Bamler, R. (2003), The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar, ISPRS Journal of Photogrammetry and Remote Sensing 57, 241–262.
Reuter, H.I, Nelson, A., and Jarvis, A. (2007), An evaluation of void filling interpolation methods for SRTM data, International Journal of Geographic Information Science 21:9, 983–1008.
Rodriguez, E., Morris, C.S., Belz, J., Chapin, E., Martin, J., Daffer, W., and Hensley, S. (2005), An Assessment of the SRTM Topographic Products, Technical Report JPL D-31639, Jet Propulsion Laboratory, Pasadena, California.
Rodriguez, E., Morris, C.S., and Belz, J.E. (2006), A global assessment of the SRTM performance, Photogrammetric Engineering and Remote Sensing 72 (3), 249–260.
Rusinkiewicz, S., and Levoy, M. (2001), Efficient variants of the ICP Algorithm, Proceedings of the Third International Conference on 3D Digital Imaging and Modeling (2001), 145–152.
Schindler, K., Papasaika, H., Schütz, S., and Baltsavias, E. (2011), Improving Wide-Area DEMs Through Data Fusion—Chances and Limits, Proceedings of the Photogrammetric Week’11, 159–170.
Sefercik, U.G. and Alkan, M. (2009), Advanced analysis of differences between C and X bands using SRTM data for mountainous topography, Journal of the Indian Society of Remote Sensing 3, 335–349.
Shortridge, A., Messina, J. (2011), Spatial structure and landscape associations of SRTM error. Remote Sensing of Environment 115, 1576–1587.
Strozzi, T., Wegmuller, U., Wiesmann, A., and Werner, C. (2003), Validation of the X-SAR SRTM DEM for ERS and JERS SAR geocoding and 2-pass differential interferometry in alpine regions, Proceedings, IGARSS’03, Toulouse, France.
Sun, G., Ranson, K. J., Kharuk, V. I., and Kovacs, K. (2003), Validation of surface height from Shuttle Radar Topography Mission using Shuttle laser altimeter, Remote Sensing of Environment 88(4), 401–411.
Surazakov, A.B, and Aizen, V.B. (2006), Estimating Volume Change of Mountain Glaciers Using SRTM and Topographic Data, IEEE Transactions on Geoscience and Remote Sensing 44, 10, 2991–2995.
USGS (2005), Shuttle radar topography mission, Online: http://srtm.usgs.gov, available: 12 June 2012.
Van Niel, T.G., McVicar, T.R. Li, L., Gallant, J.C., Yang, Q. (2008), The impact of misregistration on SRTM and DEM image differences. Remote Sensing of Environment 112(5), 2430–2442.
Walker, W.S., Kellndorfer, J.M. and Pierce, L.E. (2007), Quality assessment of SRTM C- and X-band interferometric data: Implications for the retrieval of vegetation canopy height, Remote Sensing of Environment 106(4), 428–448.
Weisstein, E.W. (2012) From MathWorld–A Wolfram Web Resource. Online: http://mathworld.wolfram.com/StandardDeviation.html, available: 10 June 2012.
Zieliński, R., and Chmiel, J., Vertical accuracy assessment of SRTM C-band DEM data for different terrain characteristics, In New developments and challenges in remote sensing (ed. Bochenek Z.) (Millpress, Rotterdam 2007), pp. 685–693. Online: http://www.earsel.org/symposia/2006-symposium-Warsaw/pdf/1380.pdf, available: 10 June 2012.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Kolecka, N., Kozak, J. Assessment of the Accuracy of SRTM C- and X-Band High Mountain Elevation Data: a Case Study of the Polish Tatra Mountains. Pure Appl. Geophys. 171, 897–912 (2014). https://doi.org/10.1007/s00024-013-0695-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00024-013-0695-5