1 Introduction

The present study area, the Central India (CI), lies between latitude 18°–26°N and longitude 73°–83°E, and is comprised of Indian provinces, i.e., Madhya Pradesh, a part of Maharashtra, Gujarat, Uttar Pradesh and Chhattisgarh. The major developing cities such as Bhopal, Bhusawal, Nagpur, Rewa, Jabalpur, Indoor, Bharuch and Raipur, etc., fall under this region. Further, the area is tectonically complex and located on both sides of the Son-Narmada-Tapti (SONATA) lineament, an active zone of crustal discontinuity between the Gangetic Plain and the Peninsular India (PI). These cities with large population and sky rising buildings are, therefore, more prone to a high degree of vulnerability to earthquake disasters. Despite the tectonic complexity and higher seismogenic potential of CI, no systematic and comprehensive seismic hazard analyses were carried out for this region. The first seismic hazard zonation map available for PI is the Bureau of Indian Standards (IS 1893), which was upgraded later to the version IS 1893–2002, by merging Zone I and II, and, accordingly, the modified seismic zones are designated as II, III, IV and V with assigned zone factors 0.10, 0.16, 0.24, 0.36 g, respectively. The present study area falls under the seismic zones II and III (IS 1893–2002). The existing seismic zones of India are covering a wider area not properly constrained by site specific ground motion parameters (e.g., site-specific peak ground acceleration (PGA), a soil amplification factor on the surface with respect to bedrock or designed response spectra). To overcome these limitations for quantifying seismic hazard, Bhatia et al. (1999) first carried out the Probabilistic Seismic Hazard Assessment (PSHA) of India and surrounding regions under the Global Seismic Hazard Assessment Programme (GSHAP) and reported the PGA values. Subsequently, Parvez et al. (2003) carried out the Deterministic Seismic Hazard Assessment (DSHA) of India and adjacent regions using structural model data, seismogenic zones, focal mechanisms and earthquake catalogues. Recently, Raghukanth and Iyengar (2006), Jaiswal and Sinha (2007) and Anbazhagan et al. (2009) carried out the PSHA for the cities like Mumbai and Bangalore. Jaiswal and Sinha (2007) reported high seismic hazard, relative to existing code IS 1893–2002, considering a maximum magnitude earthquake of 8.0 which is not complied with the existing history of earthquakes in PI and overestimated the ground motion. Further, several parts of PI are still stable and there is little evidence of only small to moderate magnitude earthquakes. For Central India, smaller seismic zones though were delineated based on the locales of the major earthquakes and seismic lineaments, but some of them are still not well-defined. It is thus imperative to state that the detailed seismic hazard analysis for CI using updated seismotectonic data is still awaited.

There is significant improvement in our knowledge about seismotectonic characterization and relevant data, which in turn envisages that the PSHA may be more informative and meaningful for the purpose of safety measures. The Geological Survey of India (GSI) has generated a reliable “Seismotectonic Atlas of India and its Environs” (Dasgupta et al., 2000), which has helped us to reconstruct a high resolution map over the study area (Fig. 1). In the present study, we carry out PSHA for the area of radius ~300 km centered on Bhopal city, the capital of Madhya Pradesh, and also estimate the spectral acceleration in CI. The response of a structure to the ground vibrations usually depends on the nature of foundation soils, materials, forms, size and mode of construction of structures and also the duration and characteristics of ground motion. Prognosis of seismic hazard thus plays a key role in planning and design of appropriate building codes for earthquake resistant construction of residential buildings, life line structures, important construction, protection of buildings, life lines, industries and other safety considerations of the sensitive structures, and necessitates estimation and quantification of future ground motion. Acceleration response spectra at 5 % damping are estimated on the basis of maximum considered earthquake (MCE) in line with the design-period of the structures and the return period of the earthquakes. These are more useful for engineers and planners for constructing buildings, bridges, dams, nuclear power plants, thermal power plants, etc., for designing earthquake resistant structures and policy making by the insurance sector.

Fig. 1
figure 1

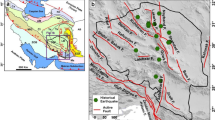
Distributions of earthquakes are shown on the topographic map with elevation varying from 10 m (green colour) to a maximum of 1,000 m from MSL (yellow colour patches) of Central India. The 13-faults and 4-lineaments are also identified (after Dasgupta et al., 2000) in the area. The major faults F1, F3, F5 and F7 are oriented along the Son Narmada North Fault (SNNF), whereas F6, F9, F10 and F11 are located along the Son Narmada South Fault (SNNF). Others are Thargon Fault (F8), Gawilgarh-Barwani Sukta Fault (F2), Jabalpur Fault (F4), Bhilwara Fault (F12), Lucknow subsurface Fault (F13), Azamgarh Subsurface Lineament (L1), Chambal Jamnagar Lineament (L2), Chittorgarh-Machilpur Lineament (L3) and Ajmer Sandia Lineament (L4) shown over the study area in different colours. Inset map on the right top represents the location of the study area. NR Narmada River, TR Tapti River, SR Son River, MRF Mahandragarh Fault. The National Seismic Observatory stations are marked by triangles (yellow) with the station code, BHPL Bhopal, JBL Jabalpur, NGP Nagpur, AKL Akola, BOKR Bokaro, BOM Bombay, PUNE Pune, LATR Latur, AJMR Ajmer. The study area covers the entire states of Madhya Pradesh, and part of Maharashtra, Chhattisgarh, Jharkhand, Orissa, Uttar Pradesh, Rajasthan and Gujarat

Full size image

2 Geology and Tectonic Setup of the Region

Continental India is broadly divided into three distinct tectonic domains, namely, the Himalayas, the Indo-Gangetic Plain and the Indian Peninsular Shield. It is well established in the literature (Minster and Jordan, 1978; Molnar, 1984) that the Himalayas are a convergent front between the Indian and Eurasian Plates and its evolution was initiated ~50 Ma back, because of continent–continent collision (Valdiya, 2001). The present convergence though varied along the Himalayan arc, the average value is estimated to be ~47 mm/year (Bilham, 2004). Due to continued underthrusting of the Indian plate beneath the Eurasian Plate, stresses are accumulating along the deforming zones of the Himalayas and lead to the orogeny being seismically unstable, and triggers great damaging earthquakes (Richter, 1958; Seeber and Armbruster, 1981) for further instability. The accommodation of forceful deformation was presumably started since the initiation of collision of the Indian plate with the Eurasian plate, and undulated the converging Indian lithosphere in the frontal part of the Himalayas. This undulation further allowed the evolution of the Indo-Gangetic plain as the Himalayan fore-deep. The flexural response in conjunction with northwest directed compressive stresses are responsible for sporadic seismicity within the Indian plate interior (Bilham and Szeliga, 2008). The great structural disturbances during the geological past resulted in the development of local zones of weaknesses along which crustal adjustments were likely taking place. The trend of the Aravali Hills in the Indo-Gangetic plain changed the drainage pattern of northwest India drastically during its recent episodic movement (Valdiya, 2002). The Vedic River Saraswati, which flowed from the Himalayas to the present day Rann-of-Kutch in the Holocene period, got desiccated due to tectonic activities in the Indo-Gangetic plain. This E-W trending tectonic basin is characterized by several hidden faults and ridges in the basement of the Ganga basin, and occasionally penetrated into the foot of the Himalaya (Gansser, 1974; Valdiya, 1976). The Delhi-Hardwar ridge, which is demarcated by a pair of faults, is the continuation of the Aravali Mountain into the Himalaya through Hardwar. Similarly, Faizabad ridge and Munger-Saharsa ridge denotes the prolongation of the Bundelkhand and Satpura massifs. All the ridges are bounded by faults and are in tectonic continuation from the Indian shield. The earthquake activity in the Gangetic plain is broadly associated with Strike-slip faulting (Gupta, 2006), and of moderate nature relative to the Himalaya (Quittmeyer and Jacob, 1979). Instead, the earthquake activities in PI are of both rift and non-rift origin, and felt over a much larger area than the Himalaya (Chandra, 1977; Kayal, 2000). One most prominent rift zone in PI is the Kutch rift located at the northwest margin of the Indian shield, and it experienced a number of moderate to great earthquakes in the historical past.

Our study area lies between the Gangetic plain and the PI (Fig. 1), and is principally composed of several formations/tectonic units viz. Vindhyan sediments, Decan volcanics, Cratonic blocks (Bundelkhand and Bastar) and a major SONATA zone. The SONATA zone, a mid-continental rift system, encompassing the Satpura orogenic belt, and is the most conspicuous feature among them. The Central India Tectonic Zone (CITZ), passing all along the SONATA, is considered to have been characterized by a suture between the northern Bundelkhand and the southern Dharwar Protocontinents. It characterizes a consistent ENE–WSW trending CITZ (Fig. 1), delimited by faults on either side, giving rise to a graben and horst structure in the region. The CITZ is bounded by Son Narmada North Fault (SNNF) and the Central India Shear Zone (CISZ) (Yedekar et al., 1990; Nair et al., 1995), forming about a ~120 to 150 km wide distinct tectonic segment. The SONATA zone is also an integral part of the area which includes the Late Achaean to Early Proterozoic Mahakoshal group with occasional patches of relict basement granite-gneisses, Vindhyan Supergroup, Gondwana Supergroup, Lameta Group and the Quaternary/Recent alluvium and laterite. The volcano-sedimentary Mahakoshal fold belt represents a lithological sequence evolved in an intracratonic rift, bounded by the SNNF and SNSF (Son Narmada South Fault). Both the faults have a dormant tectonic history and have also witnessed protracted reactivation since the Precambrian.

3 Historical Seismicity and the Seismogenic Sources

The Central Indian Shield is made up of Cratonic blocks separated by rifts. The major prominent rift that separates the northern and southern peninsular blocks is the Son-Narmada rift about 1,000 km long and 50 km wide. Basement reactivation and associated block faulting took the plate several times along the Son-Narmada rift in the geological past (Kaila et al., 1989; Dasgupta et al., 2000; Kayal, 2000). There are two major deep-seated boundary fault systems; a northerly dipping SNNF and a southerly dipping SNSF. The SNSF was formed by tensional force in the geological past, now reactivated by reverse faulting due to compressional stress for the northeastward movement of the Indian Plate (Kayal, 2000). The region recently experienced the 1997 Mw 5.8 Jabalpur earthquake, which occurred at the base of the Son-Narmada rift basin at a depth of ~35 km in the lower crust through thrust dominated movement. The earthquake was followed by a few aftershocks, and their composite focal mechanism solution shows reverse faulting with left-lateral Strike-slip motion (Bhattacharya et al., 1997; Ramesh and Estabrook, 1998; Singh et al., 1999; Rao and Gupta, 2004). Isoseismal study for this earthquake carried out by the GSI indicates that the maximum intensity was estimated to be of VIII on the MSK scale and the worst affected village was Kosamghat, ~20 km southwest of Jabalpur town. Many of the houses were affected; some suffered total collapse, others are damaged in different degrees in the Jabalpur town. Besides the 1997 Jabalpur earthquake, the region also recorded many historical damaging earthquakes (e.g., 1927 Mw 6.5 Rewal, 1938 Mw 6.3 Satpura, 1957 Mw 5.5 Balaghat and 1970 Mw 5.4 Broach) (Mishra and Gupta, 1997; Gupta et al., 1997; Mohanty, 2010).

The entire above discussion allowed us to consider seventeen faults/lineaments (Fig. 1) as possible source zones for analysis of seismic hazard (Dasgupta et al., 2000) under the present study. The seventeen source zones are (1) Son-Narmada Fault (F1, F3, F5 and F7); (2) Tapti North Fault (F6, F9, F10, F11); (3) Thargon (covered) Fault (F8); (4) Gawilgarh-Barwani Sukta Fault (F2); (5) Jabalpur Fault (F4); (6) Bhilwara Fault (F12); (7) Lucknow subsurface Fault (F13); (8) Azamgarh Subsurface Lineament (L1); (9) Chambal Jamnagar Lineament (L2); (10) Chittorgarh-Machilpur Lineament (L3) and (11) Ajmer Sandia Lineament (L4), respectively.

4 Methodology

The seismic hazard assessment at a site is mainly the function of source, path and site, and therefore, the primary need to identify the causative seismic sources. The source zones may presumably be considered as known faults, those have triggered seismicity in the past. The quantification of seismic potential of the source is normally carried out by assembling an earthquake catalogue containing past events of magnitude M w ≥ 3.0 for the respective seismogenic source. We prepared a comprehensive earthquake catalogue, which has been statistically analyzed to characterize the identified zones in the backdrop of Gutenberg–Richter (Gutenberg and Richter, 1944) recurrence relation and maximum expected earthquake magnitude (M max). The hypocentral distance and the path properties are taken as controlling factors for the attenuation relation of ground motion depending on the quality factor of the intervening rock medium. We estimated the spectral acceleration (S a) and PGA. The effect of local site condition plays a vital role for local enhancement of strong ground motion. The reference site, considered here as an A-type rock site (NEHRP), having average shear wave velocity in the top thirty meters to be greater than 1.5 km/s. Most of the places in central part of India fall under the A-type soil category.

We applied probability theory to estimate the PGA and S a for two different earthquake return periods, say 475 and 2,475 years considering all geological faults in the study area for a future earthquake. The level of confidence itself can be stated as a probability or percentage. At present, the popular way of describing hazard for building design is to specify the value of S a, that will be exceeded by 2 % in every 50 years (B.S.S.C 2001). This is closely related with the returned period T R of an earthquake to generate strong ground motion, which is the average time between consecutive occurrences of the same event in a time series. The events of moment magnitude M w ≥ 4.0 observed around the 300 km radial distance from a centre of site is used to predict the certain ground motion exceeding a certain value y*(say) using the PSHA method for different return periods.

The seismic hazard can be quantified using either the deterministic (DSHA) or probabilistic seismic hazard analysis (PSHA) based on regional geological and seismological information. Sitharam and Anbazhagan (2007) have presented the DSHA method to estimate the ground motion in a site using seismogenic sources and MCE for Bangalore in southern India. The DSHA method to estimate the ground motion at a site is not appropriate because prediction of ground motion in a site with the DSHA method considers just one maximum magnitude scenario earthquake with a shortest source to site (Bommer and Abrahamson, 2006) and neglected the other sources surrounding the site. However, the PSHA method is most appropriate to estimate the future ground motion in a site with consideration of all sources with all observed events around the site of radial distance up to 300 km of it. The goal of PSHA is to quantify the rate or probability of exceeding various ground motion levels at a site or a map of sites given all possible earthquakes (Frankel, 1995). Cornell (1968) first formalized the numerical/analytical approach to PSHA and its computer code was developed by McGuire (1976, 1978) and Algermissen and Perkins (1976). McGuire developed EqRisk in the year 1976 and FRISK in the year 1978. Algermissen and Perkins (1976) developed RISK4a, presently called SeisRisk III. The PSHA study has been addressed in India by many researchers, such as Khattri (1992), Bhatia et al. (1999), Seeber et al. (1999), Iyengar and Ghosh (2004), Jaiswal and Sinha (2007), Raghukanth and Iyengar (2006), Das et al. (2006), etc. This PSHA approach is widely used to estimate seismic-design loads for engineering purposes. The primary output from a PSHA is a hazard curve showing the variation of a selected ground-motion parameter, such as PGA or Sa, against the annual frequency of exceedance (or its reciprocal, return period). The design value is the ground-motion level that corresponds to a preselected design return period (Bommer et al., 2000). The PSHA is able to reflect the actual hazard level due to earthquakes along with bigger and smaller events, which are also important in hazard estimation due to their higher occurrence rates (Das et al., 2006). The PSHA is able to correctly reflect the actual knowledge of seismicity (Orozova and Suhadolc, 1999) and calculates the rate at which different levels of ground motion are exceeded at the site by considering the effects of all possible combinations of magnitude-distance scenarios. In the probabilistic approach, effects of all the earthquakes expected to occur at different locations during a specified life period considered with associated uncertainties, randomness of earthquake occurrences and attenuation of seismic waves. The probability method considers all possible earthquake sources surrounding the target region and then there is developed a probability density function to evaluate the best possible seismic hazard estimation.

5 Data Analyses

5.1 Earthquake Catalogue

An earthquake catalogue is one of the most important records for historical earthquakes. It provides a comprehensive database for numerous studies involving seismotectonics, seismicity, earthquake physics, hazard analysis, etc. It is essential to judge the quality, consistency, and homogeneity of the earthquake data before doing any in-depth study. The best earthquake catalogues are also occasionally heterogeneous and inconsistent in space and time because of the networks’ limitations to detect signals, and accordingly, unraveling and understanding the complexity in the database are still challenging tasks for workers (Woessner and Wiemer, 2005). One of these critical tasks is generally associated with the different magnitude of earthquakes. The India Meteorological Department (IMD) setup first the national seismic observatory in Kolkata, Mumbai and Bhuj in the year 1898 after the incidence of the 1897 M 8.7 Shillong earthquake (Evans, 1964). Since then, IMD is continuously reporting the epicentral parameters of earthquakes with magnitude more than 4.0 for the Himalaya and northeast India and more than 5.0 for rest of India based on analog records. More observatories along with the World Wide Standardized Seismograph Network (WWSSN) were further set up at Shillong, New Delhi, Pune, and Kodaikanal just after the occurrence of the 1950 M 8.6 Sadiya earthquake (Ben-Menahem et al., 1974). The much wider network improved the capability to study the earthquakes and its neighborhoods and boosted seismological research in India (Chakraborty and Tandon, 1961; Tandon and Chaudhury, 1968). After the occurrence of the deadly 1993 Killari earthquake in PI, the Government of India setup more national digital seismographs compatible with other developed countries. At present, India is equipped with ~57 seismic observatories and most of them are of the broadband type. Although the IMD has been reporting the local earthquakes on local magnitude scale (M L) over last more than two decades, we have taken the pre-instrumental earthquake data from the catalogue of the USGS (2011). A working catalogue of duration between 1842 and 2011 (Fig. 2) has been compiled for the present study using the reports of the Coast Geological Survey (presently USGS), events recorded at Jabalpur observatory, i.e., seismological bulletins and works of Primprikar and Rao (2003), GSI and bulletins of the IMD. To make a more comprehensive homogeneous catalogue, we have converted all the M L and the surface wave magnitude (M S) into moment magnitude (M w) using the formulae of Gutenberg and Ritcher (1956), Kanamori (1977) and Scordilis (2006).

Fig. 2
figure 2

Plots illustrate the time-varying occurrences of earthquakes of different magnitudes over the entire study area. The earthquake data were compiled from catalogues of a USGS and IMD for duration 1842–1993, b GSI and IMD for duration 1999–2002, c IMD for duration 1994–2011, and d USGS, IMD, and GSI for duration 1842–2011. Dashed line in d represents events with moment magnitude M w ≥ 4.0

Full size image

5.2 Data and Completeness

A total of 231 historical earthquake events for the duration between 1842 and 2011 having magnitude 3.0 ≤ M w ≤ 6.5 were available for the study area (Table 1). The temporal variation of M w for the dataset taken from IMD, USGS and GSI were explained in Fig. 2a–c. Figure 2d illustrates the complete dataset for duration between 1842 and 2011 reconstructed using IMD, USGS and GSI datasets. The spatial distributions of these events are shown in Fig. 1. The distributions of these events are mainly confined on both sides of the SONATA zone. Few events of magnitude 4.0 ≤ M w ≤ 5.8 are also sporadically distributed to the north of SONATA, and few of lower magnitude (M w < 4.0) are notably observed to the south of the SONATA. The occurrences of all the 231 events were initially examined between 17-decades (Table 1) for the entire duration between 1842 and 2011, and further the whole dataset were categorized into four groups: 3.0 ≤ M w < 4.0, 4.0 ≤ M w < 5.0, 5.0 ≤ M w < 6.0 and M w ≥ 6.0 for assessment of their completeness. The homogeneity of the dataset between specific class intervals (i.e., 3.0 ≤ M w < 4.0, 4.0 ≤ M w < 5.0, 5.0 ≤ M w < 6.0 and M w ≥ 6.0) was tested using the method of Stepp (1972). This method allowed us to determine the average number of events per year in each magnitude range, and the standard deviations of the mean rates are estimated against the sample length (Fig. 3). The deviation of standard deviation from the tangent lines (slope 1/√T, where T is duration) indicates the duration length for completeness of magnitude. Figure 3 also illustrates the stability over smaller time windows for earthquakes of less magnitude and longer windows for large magnitude earthquakes. It is thus clear that the data is complete for 3.0 ≤ M w < 4.0; 4.0 ≤ M w < 5.0; 5.0 ≤ M w ≤ 6.0 and M w ≥ 6.0 for the past 30 (1982–2011); 50 (1962–2011); 90 (1922–2011) and 170 (1842–2011) years, respectively. This analysis thus fulfills the criteria for completeness of the earthquake catalogue for a particular magnitude range and annual rate of activity (Table 2). We still analyze the completeness of earthquake catalogue for magnitude M w ≥ 3.0; events with magnitude M w ≥ 4.0 as the completeness magnitude (M c) (cf. Fig. 2d) were only used for the present PSHA study because of their efficiency for generating ground motion and creating damage to the structures.

Table 1 Number of reported earthquakes in each decade for Central India
Full size table
Fig. 3
figure 3

Plot illustrates the standard deviation of the mean annual number of events as a function of sample length and magnitude class. This alternatively explains the completeness test of earthquakes events over different magnitude ranges and the variation of standard deviation against time interval (years), magnitude and line with slope (1/√T) (after Stepp, 1972)

Full size image
Table 2 Completeness of the earthquake catalogue and activity rate for the study area
Full size table

5.3 Determination of b Values

Ishimoto and Ida (1939) and Gutenberg and Richter (1944) carried out several studies on the frequency-magnitude relationship of earthquakes as a function of time, space, and depth to establish an empirical relationship between frequency of earthquake occurrences and magnitudes in a given region for a finite time-window. Later, Gutenberg and Ritcher (1954) proposed the following empirical equation

$$ {\text{Log }}(N) = a - bM. $$
(1)

For a certain range and time interval, Eq. 1 will provide the number of earthquakes (N) with magnitude (M). The ‘a’ is a measure of seismic activity that depends on the size of the area, length of the observation period, the largest magnitude and stress level of the area, etc. (Allen, 1986). Statistically, the b values (Table 3) are estimated from the slope of the log N–M regression line and is a constant parameter that determines the rate of fall in the frequency of occurrences of events with increasing magnitude. High b values indicate a large number of small earthquakes expected in regions of low strength and large heterogeneity, and low b values indicate high resistance (asperity) and homogeneity of the constituent rock-mass (Tsapanos, 1990; Udias, 1999; Wason et al., 2002; Khan and Chakraborty, 2007; Khan et al., 2011). In natural situations, b values are found to lie between 0.5 and 1.5, depending on the tectonics of a region. The b values were estimated using the above empirical relationship (Eq. 1) considering the earthquake dataset for durations between 1842 and 1960 (M w ≥ 5.0) (Fig. 4a), between 1960 and 2011 (M w ≥ 3.0) (Fig. 4b) and for the entire dataset between 1842 and 2011 (Fig. 4c).

Fig. 4
figure 4

Plots represent the frequency–magnitude distribution of historical earthquakes for the duration between the years a 1842 and 1960, b 1960 and 2011 and c 1842 and 2011, respectively

Full size image
Table 3 Values of ‘b’ are compared with other studies for Peninsular as well as Central India regions
Full size table

6 Probabilistic Seismic Hazard Analysis

Based on the completeness of the earthquake catalogue and the possible threshold value of magnitude (M w ≥ 4.0), earthquakes are classified into three categories, (1) events with magnitudes 4.0 ≤ M w < 5.0 capable of producing ground motion at maximum hypocentral distance of ~50 km assigned to source I, (2) events with magnitudes 5.0 ≤ M w < 6.0 capable of producing ground motion at maximum hypocentral distance of ~100 km assigned to source II, and (3) events with magnitudes M w ≥ 6.0 capable of producing ground motion at maximum hypocentral distance of ~150 km designated to source III, respectively, and weights of 0.5, 0.25 and 0.25 or 50, 25 and 25 % of expectancy are assigned for these earthquake events. The variable weight factors are constrained by the data coverage, instrumental records and earlier studies (Abrahamson and Bommer, 2005; McGuire et al., 2005; Musson et al., 2005). The earthquake data is presumably complete over the period 1982–2011 for source I; 1920–2011 for source II, and 1842–2011 for source III. We choose three models, viz. model I for maximum magnitude M max = 6.8 and b value 0.68, model II with M max = 6.8 and b value 0.76, and model III with M max = 6.8 and b value 0.69 (Fig. 4) for hazard estimation. Similar to all the source areas, we impose the weight factors 0.25, 0.50, 0.25 for model I, model II and model III, respectively. Exceeding ground motion for magnitude M w ≥ 4.0 is obtained using the three predictive ground motion attenuation equations (Fig. 5). The three attenuation relationships were proposed by Atkinson and Boore (1995) for stable continents of the Eastern and Central United States, Fukushima and Tanaka (1990) for Japan and Iyengar and Raghukanth (2004) for PI. Due to a lack of strong motion data, no equations for estimating ground motion were available for PI. However, Iyengar and Raghukanth (2004) investigated the attenuation relationship of PGA with hypocentral distance for PI using the stochastic seismological model of Boore (1983). Boore and Atkinson (1987) and Hwang and Huo (1997) used the seismological models to predict characteristics of ground motion for the central and eastern United States. Though many attenuation relationships are available for various locations, no particular attenuation relation can be used due to its aleatory and epistemic uncertainty. Based on the quality and dependency of attenuation parameters, we impose weight factors of 0.50, 0.25 and 0.25 for data taken from Iyengar and Raghukanth (2004), Atkinson and Boore (1995) and Fukushima and Tanaka (1990), respectively, and, further, we compute the predictive ground motion in a site using a logic-tree concept (Fig. 6). We finally obtain predictive future ground motion in a site considering all possible sources, computed b values and three attenuation equations and generate the probability of the mean annual rate of occurrence of ground motion for the entire study area (Fig. 7).

Fig. 5
figure 5

Plot showing the distributions of PGA in hard rock for different attenuation relationships. Earthquake with M w = 6.0 and focal depth 10 km has been used to estimate hypocentral distances

Full size image
Fig. 6
figure 6

Logic-tree approach for computing the seismic hazard parameters

Full size image
Fig. 7
figure 7

Plot illustrates the generated seismic hazard curves for Central India, and the same is also compared with that of Mumbai region (after Raghukanth and Iyengar, 2006)

Full size image

Peak ground acceleration and S a are usually required at the site for engineering applications. These quantities depend principally on the magnitude of the event and the source distance. Thus, the attenuation relation of S a is a key element in future seismic hazard analysis. Presently, there is no spectral attenuation relation for CI region in compliance with NEHRP soil classification. Here, we use the following attenuation relation (Raghukanth and Iyengar, 2006) to generate the S a at the rock level, a layer whose shear wave velocity is above 3.5 km/s

$$ \ln (y_{\text{br}} ) = C_{1} + C_{2} (M_{\text{w}} - 6) + C_{3} (M_{\text{w}} - 6)^{2} - C_{4} R - \ln R + \ln \varepsilon_{\text{br}}, $$
(2)

where C 1, C 2, C 3, C 4 are correlation coefficients varying with spectral period (Table 4). The y br value is S a/g, \( \ln \varepsilon_{\text{br}} \) is an error terms, M w is moment magnitude and R is hypocentral distance in km. The above attenuation equation is valid at bedrock level with shear wave velocity 3.5 km/s for any stable continental region of the world. The above empirical relation (Eq. 2) developed based on a seismological model was compared by Raghukanth and Iyengar (2007) with the attenuation characteristics of bedrock motion for Eastern North America (Toro et al., 1997; Hwang et al., 1997; Campbell, 2003; Atkinson and Boore, 2006), and noted to be valid for its further use. Later, the recorded data of the 1967 Koyna earthquake at the rock site (A-type) supported the derived spectral acceleration for PI region using Eq. 2. Moreover, the high-frequency components of the recorded data of the 1967 Koyna earthquake were also reflected well in the predicted spectrum of Krishna et al. (1969). The bedrock spectral accelerations are generated between the 0.0 and 4.0 s period using the data shown in Table 4 and PGA values are estimated from the seismic hazard curve (Fig. 7) for two distinguished return periods (T) 475 and 2,475 years (Fig. 8a, b).

Table 4 Coefficients of spectral acceleration (S a) with period at the bedrock level (after Eq. 5 of Raghukanth and Iyengar, 2006) used in the present study
Full size table
Fig. 8
figure 8

a Plot illustrates the response spectrum generated at bedrock with shear wave velocity V s = 3.5 km/s level with 10 % probability of ground motion being exceeded in 50 years and b bedrock response for 2 % probability of being exceeded for ground motion in 50 years for the study area

Full size image

The surface level S a is computed using soil classification (Table 5) of the National Earthquake Hazard Reduction Program for the United States of America (NEHRP-USA 2001). These sites are categorized on the basis of the top 30 m average shear wave velocity, i.e., V s (30). Raghukanth and Iyengar (2006, 2007) established the regression equations (Eqs. 3, 4) to generate the response spectra for different soil categories A, B, C and D. They also opined that rigorous nonlinear site response analysis would be needed for E- and F-type sites with specific local parameters. We thus incorporate the predictive response spectra for E- and F-type soils and derive the soil response spectra for such types of soils having shear wave velocity less than 180 m/s as per NEHRP soil classifications. It is internationally accepted for building coding that E/F-type soil can only be liquefiable and; hence, the responses for such soil are not available. Mandal et al. (2012) reported the variable soil amplification for the Delhi ridge and surrounding regions, and found relatively low V s (30) in the order of 180–160 m/s along the bank of the river Yamuna and its adjacent regions. The frequency dependent soil amplification factor at the surface (F s) was also estimated from a recoded acceleration time series at the rock site using an equivalent linear method (ELM) by Mandal et al. (2012). The F s were determined under the present study for E/F-type soil using the following equations.

$$ y_{\text{s}} = y_{\text{br}} F_{\text{s}} , $$
(3)

and

$$ \ln F_{\text{s}} = a_{1} y_{\text{br}} + a_{2} + \ln (\delta_{\text{s}} ), $$
(4)

where F s is the local soil amplification factor, a 1 and a 2 are regression coefficients and δS is the error term corresponding to site classifications A, B, C, D and E/F. These coefficients along with the standard deviation (σ) of the error ln(δS) vary with periods. The coefficients are estimated from Eqs. (3) and (4) for a period of 0.0–4.0 s (Table 6). Average 5 % damping response spectrum are estimated for A-, B-, C-, D- and E/F-type sites in CI using these correction factors. Cramer and Kumar (2003) using the structural response at thirteen stations during the 2001 Kutch earthquake estimated the Sa for local site conditions at two natural periods 0.4 and 0.75 s at 5 % damping and found a strong correlation with Eq. 4 of Raghukanth and Iyengar (2007).

Table 5 Site classification as per NEHRP USA (B.S.S.C 2001)
Full size table
Table 6 Comparison of hazard parameters for Mumbai, Bangalore and Central India at bedrock level
Full size table

The variation from the mean is characterized by the σ of ln(εs) expressed as,

$$ \sigma \left\{ {\ln (\varepsilon_{\text{s}} )} \right\}^{2} = \sigma \left\{ {\ln (\varepsilon_{\text{br}} )} \right\}^{2}\,+\,\sigma \left\{ {\ln (\delta_{\text{s}} )} \right\}^{2}. $$
(5)

Combined seismic hazard curves for PGA at short period and S a for long period (1.0 s) were computed for A-, B-, C-, D-, and E/F-type soil separately under the present study (Fig. 9a, b). We estimated the soil response spectrum at 5 % damping for A-, B-, C-, D-, E/F-type of soils with respect to bedrock normalized spectrum and convolution of the \( y_{\text{s}} \) values estimated through Eqs. 5–7 for two earthquakes return period, viz., 475 and 2,475 years (Fig. 10a, b). We also constructed the normalized designed response spectrum on the basis of 197 Universal Building Code of NEHRP (B.S.S.C 2001) for soils A, B, C, D, and E/F for MCE of whose return period (T) 2,475 years and compared with the normalized response spectrum of IS 1893–2002 (Fig. 11).

Fig. 9
figure 9

a Mean annual rate of excess is plotted for 10 % probability of excess in 50 years at 5 % damping with peak ground acceleration (g) for A-, B-, C-, D-, E/F-type soils and b mean annual rate of ground motion excess is drawn for 10 % probability of excess in 50 years at 5 % damping with spectral acceleration (S a) in g with structural period, T = 1.0 s for A-, B-, C-, D-, E/F-type soils

Full size image
Fig. 10
figure 10

a Predictive uniform hazard response spectra for 10 % probability of excess in 50 years at 5 % damping, and b response spectra for periods of 2 % probability of excess in 50 years at 5 % damping are drawn for A-, B-, C-, D- and E/F-type soils as per B.S.S.C (2001) soil classification for the study area

Full size image
Fig. 11
figure 11

Plot shows a comparison between normalized response spectra in soil types A, B, C, D and E/F in the present study and rock or hard (Type-I), medium (Type-II) and soft (Type-III) soils of IS 1893–2002 at 5 % soil damping for maximum considered earthquake (MCE) of return period (T) 2,475 years. The characteristic time periods T o and T s (s) are varied with specific site for soil type A, B, C, D and E/F

Full size image

Probabilistic Seismic Hazard Assessment has become a standard tool for estimating the probability of exceeding S a at a site due to all possible future earthquakes over the area under concern. The utility of PSHA in quantifying the safety of man-made structures accounts for assessment of design-based ground motion (Kramer, 1996). Uncertainties in PSHA are usually associated with sources, the method of estimating seismic hazard parameters and the ground motion attenuation models. To overcome these problems, logical quantitative treatment of uncertainties was carried out through the logic-tree approach (Fig. 5). The procedure for carrying out PSHA has also been demonstrated by Iyengar and Ghosh (2004) for Indian regions assuming that the number of earthquakes occurring on faults normally follows a stationary Poisson distribution. The probability that control variable Y exceeds level y* in a time window of T years is given by

$$ P(Y > \mathop y\limits^{*} (T)) = 1 - \exp ( - \mu_{{\mathop y\limits^{*} }} T). $$
(6)

The rate of exceedance, \( \mu_{{\mathop y\limits^{*} }} \) is computed from the following expression

$$ \mu_{{\mathop y\limits^{*} }} = \sum\limits_{i = 1}^{k} {N_{i} } (m_{0} )\int\limits_{{M_{\text{w}} }} {\int\limits_{R} {P(Y > \mathop y\limits^{*} \left| {M_{\text{w}} ,R)P_{R/M} (R\left| {M_{\text{w}} } \right.)} \right.P_{M} (M_{\text{w}} ){\text{d}}R{\text{d}}M_{\text{w}} } }. $$
(7)

Here, K is the number of faults, P M (M w) and P R/M (R/M w) are the probability density functions of the magnitude and hypocentral distance, \( P(Y > y^{*} \left| {M_{\text{w}} ,R} \right) \) is the conditional probability of exceedance of ground motion parameter Y. The return period can be obtained by computing the reciprocal of the annual probability of excess for the corresponding ground motion hazard curve. Equations 6 and 7 are used for generation of seismic hazard curve at the bedrock for the study area (Fig. 7) by computing the mean annual rate of excess \( \mu_{{\mathop y\limits^{*} }} \) for different ground motion values \( \mathop y\limits^{*} \) using all possible demarcated 17-earthquake sources zones (13-faults and 4-lineaments). It was further observed that the seismic hazard for CI region was mainly controlled by SNNF, i.e., the combination of faults F7, F5, F4 and F3 and SNSF includes F8, F6, F2 and F1 faults, respectively. The local soils from A to E/F at a specific site in CI is presumably different against the average shear wave velocity, i.e., V s (30) up to the top 30 m thickness. Generation of V s (30) and its map are helpful to engineers for estimating the parameters of strong ground motion. The site classes assessed from shallow shear wave velocity models are usually important in deriving strong motion prediction equations (Boore et al., 1997) for reconstruction of maps in compliance with site classes under the National Earthquake Hazard Reduction Program (Wills et al., 2000), and, moreover, in applications of building codes to specific sites. The geophysical methods, i.e., Multichannel Analysis of Shear Wave (MASW) techniques, cross hole and down hole test, etc., and the geotechnical investigation are used to determine shear wave velocity for classifying a site. The average shear wave velocity of the top 30 m soil was computed from shear wave travel times for different layers using the following equation

$$ V_{\text{s}} (30) = \frac{30}{{\sum\nolimits_{i = 1}^{n} {\frac{{h_{i} }}{{V_{i} }}} }}, $$
(8)

where \( h{}_{i} \) and \( V{}_{i} \) are thickness and velocity of the ith layer and n is the numbers of layers. Now-a-days many workers carryout survey in the cities for Multichannel Analysis of Shear Wave as per respective interest of studies and finally prepare the V s (30) map for a particular city (Dobry et al., 2000; B.S.S.C 2001; Mandal et al., 2012).

7 Results and Discussion

Three recurrence relations (Fig. 4a–c) established under the present study show that the seismic b values for the region vary from 0.68 to 0.76, and corroborate with the results of Ram and Rathor (1970), Kaila et al. (1972), Rao and Rao (1984) and Jaiswal and Sinha (2007) for PI, CI and Gujarat, Anbazhagan et al. (2009) for the Bangalore region, Seeber et al. (1999) for Maharashtra state and Raghukanth and Iyengar (2006) for the Mumbai region (Table 3). The predictive response spectrum generated at the bedrock level for V s = 3.5 km/s using the analyzed hazard curve (Fig. 7) for 10 and 2 % probability of excess of ground motion in a site for 50 years corresponds to the earthquake of returned period 475 and 2,475 years (Fig. 8a, b). Variation of mean annual rate of excess with PGA and S a at t = 0.1 s for 5 % damping are obtained according to the prescribed designed force of B.S.S.C (2001) for bedrock A-, B-, C-, D- and E/F-type soils (Fig. 9a, b). The uniform hazard response spectra for CI were obtained at different site conditions according to NEHRP’s site classifications for A-, B-, C-, D- and E/F-type soil’s criteria for average shear wave velocity V s (30) up to 30 m depth and the obtained PGA values (Table 8) normally used to characterize the ground motion. However, in recent times, the S a is more useful a parameter for designing the short period (0.2–0.5 s) for residential normal buildings and long period (1.0 s) for monuments like structures. The UHRS are illustrated in Fig. 10a, b for probability of 10 % excess of ground motion at a site for 5 % structure damping in 50 years and probability of 2 % excess of ground motion at a site for 5 % structural damping in 50 years over the study area, respectively. A comparison is made between the normalized designed response spectra in the present study for MCE of soil type A, B, C, D and E/F and the IS 1893–2002 code used by Indian designer (Fig. 11). Indian designer uses only three soil types in IS 1893–2002 code. Type I: rock or hard soil, Type II: medium soils and Type III: soft soils are classified on the basis of N values of the standard penetration test (SPT). It may be stated that the normalized design spectral shapes for Type-I, Type-II and Type-III soils (IS 1893–2002) are similar with C-, D- and E/F-type soils in the present study. Further, as per IS 1893–2002, the normalized response spectra for Type I site corroborates with the C type site’s design response spectra of NEHRP (Fig. 11) instead of its A- or B-type soil, and that essentially overestimates the analysis of design. The zero period acceleration (ZPA) at the bedrock level for 10 % probability for excess for 50 years are compared with the study of Anbazhagan et al. (2009). The result obtained through the present study for ZPA is 0.08 g, which is equivalent to that of Raghukanth and Iyengar (2006) for Mumbai region. The result obtained by Anbazhagan et al. (2009) is slightly higher (Table 7). A comparison between the computed seismic hazard curve under the present study and work done by Raghukanth and Iyengar (2006) for Mumbai are illustrated in Fig. 7. Both the hazard curves are identical at the shorter return period <225 years, however, for returned period greater than 225 years, Raghukanth and Iyengar (2006) the hazard curve has a larger mean annual excess rate for the same ground motion parameters. This is because, the b values obtained by Raghukanth and Iyengar (2006) for Mumbai and also by Seeber et al. (1999) for Maharashtra State, are 0.86 and 0.89, slightly higher than present study for CI (i.e., 0.68–0.76). The differences in b values are possibly due to a different geodynamic setup vis-à-vis seismotectonics of Mumbai and Maharashtra in comparison with the regions along SONATA and its surroundings.

Table 7 Site coefficients are calculated through Eqs. (6) to (8)
Full size table
Table 8 Comparison of hazard parameters for Peninsular India, Mumbai and Present study of Central India
Full size table

The spectral accelerations are also compared for B-, C-type sites with the work of Seeber et al. (1999) for Maharashtra and B-type sites of Raghukanth and Iyengar (2006) for Mumbai for ZPA, S a (at 0.2 s period) and S a (at 1.0 s period) and illustrated in Table 8. Singh et al. (1999) estimated the strong ground motion of 0.15 g at Jabalpur city using the spectral acceleration of 1997 Jabalpur earthquake which is also identical with the present study. The common practices in the studies of dynamic soil responses are confined within 30 m soil to solve the engineering purposes for site characterization (Parvez et al., 2003; Iyengar and Ghosh, 2004; Nath et al., 2008; Anbazhagan et al., 2009). In line with this understanding, the different levels of the Indian Government are encouraged to carryout seismic microzonation study, and accordingly, any structures are designed to reduce the disaster in cities of highest seismic risk on a priority basis and so on. Nath et al. (2008) carried out the seismic microzonation of Guwahati and Sikkim, zones of highest seismic potential (seismic zone V, Bureau of Indian Standard).

In view of the importance of the soil response study, recently, Mandal et al. (2012) carried out the study on soil responses for the National Capital Region (NCR); and they observed that the time history of a local earthquake at a rock site has close correspondence with site specific soil amplification and frequency. Based on this inference, the present PSHA is very important to evaluate the exact soil response at a site with due consideration of the NEHRP soil classifications. It is, therefore, imperative to state that the PSHA for seismic microzonation at the bedrock level is more important for urban or developing cities. Sharma et al. (2003) evaluated the seismic zonation of the Delhi region for Bedrock ground motion. Jaiswal and Sinha (2007) carried out the bedrock PGA for Peninsular India through the Probabilistic method using regional sources for the larger area. Anbazhagan et al. (2009) carried out the seismic microzonation for Bangalore city, first through PSHA at the rock level, and subsequently computed the optimal variation of soil response at the surface level. Similarly, Joshi and Sharma (2011) carried out the PSHA for the Delhi region and reported the bedrock response spectra and uniform hazard response spectra at the bedrock site for different earthquake returned periods.

As mentioned above, our generated hazard parameters under the present study are more precise and relatively comprehensive in comparison to those of previous studies for PI and other regions. Recent studies on PSHA using the concept of logic-tree incorporation and the point source attenuation for the central eastern United States by several researchers (Jaiswal and Sinha, 2007; Toro et al., 1997; Atkinson and Boore, 1995), including the study by Iyengar and Raghukanth (2004) showed higher acceleration values that suggest higher hazardous scenarios jn the area. The generated response spectra for A-, B-, C-, D- and E/F-type sites will, thus, have immense use for the engineers for designing structures for specific soil types. The design spectra developed here incorporate uncertainties in location, magnitude and or recurrence of earthquakes; hence, these are superior to spectra recommended by IS 1893. Influence of the local site condition has been accounted for by providing design spectra for A-, B-, C-, D-, E/F-type sites separately. The result shows that the frequency content of the UHRS varies with local site conditions. The present work has provided requisite parameters for building designers and engineers. The results presented here can be directly used to create a microzonation map for Bhopal (BHPL), Jabalpur (JBP), Nagpur (NGP), Akola (AKL) and other cities of the CI region after getting the detailed shear wave profile for the upper 30 m layer. A micro level seismic hazard map of Bhopal and cities surrounding the SONATA region in CI on a finer grid will be created for the needs of city-level disaster management.

Empirical Power law relationships for ZPA against shear wave velocity at bedrock, A-, B-, C-, D-, E/F-types of soils for the return period of 475 and 2,475 years as \( {\text{ZPA}}_{(T = 475)} = 0.1146\;[V_{\text{s}} (30)]^{ - 0.2924}, \) and \( {\text{ZPA}}_{(T = 2475)} = 0.2053\;[V_{\text{s}} (30)]^{ - 0.2426} \) are established under the present study (Fig. 12). These two equations for ZPA will be very useful to the engineers for estimating the base-shear of a structure using the V s (30) at the top 30 m layers, and moreover, the equations will reduce the uncertainty for categorizing the site class in complex areas for designing purposes. The total design seismic base-shear for the buildings (V B) along each direction due to earthquake is equal to the product of the design horizontal seismic coefficient (A h), total weight of the building (W). Further, the horizontal seismic coefficient (A h) is a function of zone factor (Z), the periodic variation of S a/g, importance factor (I) and the response reduction factor (R) as per IS: 1893–2002. Here, we equate the parameter Z as ZPA. As per the IS 1893–2002 code, Z varies from 0.10 to 0.16 g for seismic zones II and III for all soil Types-I, II and III, respectively. Instead, in the present study, we suggest estimating the Z value from the empirical relations for ZPA using V s (30) values (Eq. 8) prior to the assessment for new sites. Interestingly, we found ZPA as 0.18, 0.23, 0.27, 0.31, 0.35 g for sites A, B, C, D, and E/F, respectively, for MCE of T = 2,475 years (Table 8). The estimated ZPA (Fig. 12) and the normalized designed response spectra (Fig. 11) are helpful to the engineers for selection of useful designed periods of normal residential buildings or tall structures (multistoried buildings, tower, etc.) and lateral long structures such as bridges, moreover, the building code for the study area can be modified accordingly.

Fig. 12
figure 12

Plot illustrates the empirical relation between average shear wave velocity [V s (30)] and zero period acceleration (ZPA) over the study area. Top one curve shows the correlation between V s (30) and ZPA for earthquakes of return period T = 2,475 years used for tall structures design purposes, and the bottom curve shows the correlation between V s (30) and ZPA for earthquakes of return period T = 475 years commonly used for residential low rise normal buildings. Note the ZPA values decrease with increase in shear wave velocity and vice versa

Full size image

8 Limitations

The probability assessment through the logic-tree approach is apparently a relative preference for or degree of belief in an alternative hypothesis and a strong preference is usually represented by logic-tree weights of 0.9 and 0.1 for two alternatives. An equal weight of 0.5 is assigned for no preference in either hypothesis. Increasing weights from 0.5 to 0.9 reflect an increasing preference. Although the logic-tree weights are finally subjective judgments based on available information, it is important to document the data and interpretations that lead to the assessment of parameters and to assign weights. There is an ongoing debate related to the interpretation of branch weights in a logic-tree and whether they are probability or simply subjective indications of relative merit (Abrahamson and Bommer, 2005; McGuire et al., 2005; Musson et al., 2005). However, in their current application as envisioned, for example, in the Senior Seismic Hazard Analysis Committee (SSHAC) frame work (Budnitz et al., 1997), a logic-tree is an implementation of a probability model of uncertainties.

The Poisson process is a random both in time and space, and normally characterizes the occurrences of earthquakes, except the aftershocks, in a seismic source zone, although the occurrence rate of earthquakes over CI is significantly sparse. It thus may be stated that the present analysis is basically a preliminary seismic hazard estimation for the study area. More studies regarding the source characterization and the precise estimation of seismic wave attenuation will provide better results and significantly improve the seismic hazard understanding over the area. Another study has estimated the seismic hazard parameters (e.g., b values) in general, while seventeen faults and lineaments, those considered in the present study, were lacking for any specific hazard parameters. We have considered all possible seismogenic sources to ascertain completeness of the earthquake catalogue. We have compromised with the short duration incomplete database in our analyses, which in turn suggest that the seismic character of the region may not be well represented. Secondly, estimated ‘b’ values using available data without a reliable slip rate for source processes may not be a sole representative of the seismological hazard parameter for the whole area under study. We, however, found that our estimated b values are comparable to earlier studies. Thirdly, the surface level spectral acceleration may be generated more accurately by geotechnical and geophysical investigation at the target sites; besides use of worldwide site classification for average shear wave velocity, i.e., V s (30) for the 30 m depth soil of NEHRP. As the strong motion data is not available over the study area, we were unable to compare our ZPA vs V s (30) relation with the instrumental data. However, Singh et al. (1999) reported the PGA value is ~0.15 g at near the source area using the broadband record of the 1997 Jabalpur earthquake at the rock site. From the microzonation report of Jabalpur city, it was found that the maximum PGA is 0.30 g for shear wave velocities of 150–100 m/s in very loose sedimentary strata and 0.11 g for shear wave velocity of 950–1,000 m/s in hard soil (Project report on Seismic microzonation of Jabalpur Urban area, Madhya Pradesh, 2004).

9 Conclusions

The present article investigates the seismic hazard for CI using the probability theory with a new data set. The seventeen numbers of pertinent faults and lineaments are identified from the seismotectonic map of the area, which have a significant influence on ground motion. Since the slip rate for individual faults is not available, the regional recurrence relation for the region was developed using the historic and instrumental database in this study. Based on our robust relationship between ZPA and V s, the uniform hazard response spectra derived for 10 and 2 % probability of excess in 50 years are assimilated and found to be well-compatible with that of earlier study reported by Seeber et al. (1999) and Raghukanth and Iyengar (2006). The designed spectra developed in this study incorporate uncertainties in location, magnitude and recurrence earthquakes, and, hence, are superior to spectra recommended by IS 1893–2002. Influence of the local site conditions has been accounted for by providing designed spectra for A-, B-, C-, D- and E/F-type sites separately. The result presented here can be directly used to reconstruct a microzonation map for CI through detailed geotechnical investigations. A seismic hazard map covering CI and it’s environs on a finer grid will cater to the needs of precise disaster management.

We infer from this study that seismic hazard assessment is dictated by several seismological factors, including the type of soil and nature of response at the bedrock site. The effort of estimating seismic hazard by evaluating the likelihood of an earthquake occurrence and its magnitude in and around the site of interest is bearing on the severity of strong ground motions expected for a certain return period. The effect of a local site condition plays a vital role for local enhancement of strong ground motion with PGA and spectral acceleration. Seismic hazard assessment is a procedure to indicate on a small scale map in a geographical distribution an estimate of strong ground motion parameters. The assimilated basic seismic hazard information may be useful for improving structural design/building codes for earthquake resistance structures. Such a scientific endeavor may provide a set of guidelines for calculating earthquake insurance premium rates under a disaster risk transfer plan of the area under study. We found that the empirical relationships between ZPA and V s for given return period of earthquakes have effective implications for construction of a structure in a region devoid of observed seismic ground motion parameters. These established relationships are equally important where the occurrence of earthquake is irregular and sporadic, and moreover, have no proper guidelines. We suggest to exercise this approach in other parts of Central India as well as elsewhere in the world having analogous seismotectonic settings.