1 Introduction

Wind noise impinging on an acoustic sensor is dependent on the size of the turbulent eddy whose scale depends on the wind speed (see, e.g., Walker and Hedlin 2010). An arrangement of pipes distributed over a spatial area with a number of ports sampling the atmosphere and connected to a single common sensor can be used to mitigate against the effects of wind noise if the spatial scale of the filter system is larger than those of the turbulent eddy and smaller than those of the acoustic signal of interest. Walker and Hedlin (2010) provide a thorough review of the nature of acoustic noise due to wind turbulence and common mitigation procedures.

Although effective at reducing the contribution of turbulent wind noise on recordings taken from acoustic sensors, it has been established that spatial filters can also have a deleterious influence on the recorded signal of interest. Hedlin et al., (2003) discuss the amplitude attenuation as a function of frequency that will occur as a result of out of phase summing at the sensor due to different propagation path lengths through the various ports. In addition, impedance mis-matches within the acoustic filter system generate internally reflected waves that cause resonances to occur (Alcoverro 2002). Indeed, Alcoverro (2002) using an analogue in electrical circuit theory shows that it is possible to determine the frequency response of a spatial filter system provided the design specifications are known accurately, however, the analysis presented in Alcoverro (2002) assumes vertically incident waves.

In this paper we determine how the plane wave response of a spatial filter impacts the infrasound array response in terms of signal detectability and slowness determination. It should be noted that the analysis presented here does not consider the internal resonances caused by impedance mis-matches internal to the acoustic filter system. It has been shown (Alcoverro 2002) that this resonance will also introduce significant phase shifts and needs to be considered in a complete analysis of the spatial filter response.

In Sect. 2 we derive the plane wave response for infrasound spatial pipe filter systems, and in Sect. 3 determine how it modifies the infrasound array response. Section 4 investigates the effect of the modified array response on the Fischer Statistic and hence the signal detectability, and Sect. 5 determines the effect on the measured back azimuth in terms of the least squares estimate. Section 6 determines the effect on the least squares estimate of signal slowness when low-frequency and high-frequency spatial filters are distributed asymmetrically among the sensors. In Sect. 7 the influence of the spatial filter system on measured signal slowness is simulated using artificial signals that have been contaminated with a realistic pink noise model.

2 The Spatial Filter Plane Wave Response

Elementary considerations show that the addition of two sinusoids A 0 sin (ω(t − t 0)) and A 1 sin (ω(t − t 1)) produces a third sinusoid A sin (ω(t − τ))such that

$$ A_{0} \sin \left( {\omega \left( {t - t_{0} } \right)} \right) + A_{1} \sin \left( {\omega \left( {t - t_{1} } \right)} \right) = A\sin \left( {\omega \left( {t - \tau } \right)} \right) $$
(1)

with \( A = \sqrt {\left( {A_{0} \cos \omega t_{0} + A_{1} \cos \omega t_{1} } \right)^{2} + \left( {A_{0} \sin \omega t_{0} + A_{1} \sin \omega t_{1} } \right)^{2} } \) and \( \tau = \frac{1}{\omega }\arctan \left( {\frac{{A_{0} \sin \omega t_{0} + A_{1} \sin \omega t_{1} }}{{A_{0} \cos \omega t_{0} + A_{1} \cos \omega t_{1} }}} \right). \)

When a monochromatic signal passes through the N-ports of a spatial filter each port presents to the sensor a copy of the signal with a phase shift when compared to the signal recorded on an un-adorned (i.e., filterless) reference sensor at the same location. The phase shift is due to the time delay caused by the different propagation distances and speeds travelled by the signal from each port to the sensor when compared to that of the reference. When the time delay for each port has been determined the resultant signal at the sensor due to the summation of the signal from each port can be found by repeated use of the sinusoidal addition rule given in Eq. 1.

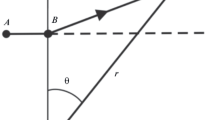
Consider a spatial filter consisting of 4 lengths of pipe in the form of a cross with high-impedance ports placed every metre along each pipe, as shown in Fig. 1. Assume also a monochromatic signal propagating in the +x direction.

Fig. 1
figure 1

Spatial filter in the form of a cross with the summing manifold at the centre with a port placed every metre

Full size image

Acoustic propagation through the spatial filter system consists of a through-air (TA) component and a through pipe (TP) component. We will assume here that all TA propagation is at the trace velocity V of the signal across the array, and all TP propagation is at a speed c determined by Kirchhoff’s transmission line model (Kirchhoff 1868) for sound propagation in a cylindrical conduit, which is presented in Benade (1968) as Eq. 7. If we assume time zero to correspond to the arrival of a surface of constant phase at port 1, the port with the least value of the x-coordinate, then the time difference between the arrival of the surface at the sensor via the TP path to that of the reference is \( \Updelta t_{1} = \frac{{\left| {x_{1} } \right|}}{V} - \frac{{D_{1} }}{c} \) where D 1 is the TP travel distance from port 1 to the sensor. More generally, the delay for a signal travelling via port k is

$$ \Updelta t_{k} = \frac{{\left| {x_{1} } \right|}}{V} - \left( {\frac{{D_{k} }}{c} + \frac{{\left| {x_{k} - x_{1} } \right|}}{V}} \right). $$
(2)

Kirchoff’s analysis treats the propagation of acoustic waves inside a cylinder from the point of view of transmission line theory where a propagation constant \( \Upgamma \left( \omega \right) = \sqrt {\left( {R + i\omega L} \right)\left( {G + i\omega C} \right)} \) is defined as a function of angular frequency ω in the usual manner. Here, R and L are the real and imaginary parts of the impedance, and G and C the real and imaginary parts of the admittance.

For the acoustic problem under consideration these parameters are expressed in terms of the molecular properties of air and the radius a of the cylinder. The reader is directed to Benade (1968) for the exact form of these expressions.

The attenuation constant α and phase constant β are determined according to the usual transmission line formalism as Γ(ω) = α(ω) + iβ(ω) with the phase velocity \( c = \frac{\omega }{\beta } \).

Here, the attenuation constant α is defined to be A x  = A 0e−αx, where A 0 is the amplitude at a reference point, and A x is the amplitude a distance x from the reference.

Tabulated values of the attenuation constant α and phase velocity c as a function of frequency are shown in Table 1 for various pipe radii a, assuming a local sound speed of 343 m/s. These results show that the attenuation constant α is small enough in all cases to be considered to be zero for the remainder of this paper.

Table 1 Acoustic velocity c and attenuation constant α as a function of frequency for sound propagation in a cylinder for three values of the internal radius a
Full size table

The amplitude and phase as a function of frequency for the filter shown in Fig. 1 has been computed and is shown in Fig. 2 for an internal pipe radius a = 1 cm. Here, the amplitude and phase are provided by Eq. 1, and the relative time delay given by Eq. 2.

Fig. 2
figure 2

Phase and amplitude variation as a function of frequency for the spatial filter shown in Fig. 1 with internal pipe radius = 1 cm. Results for five values of the trace velocity V are indicated: black line V = 340 m/s; red line V = 390 m/s; green line V = 440 m/s; blue line V = 490 m/s; pink line V = 540 m/s, and for two values of the incident angle θ = 0.0° and θ = 45.0° from propagation in the +x direction

Full size image

The corresponding results for an internal pipe radius of 5 cm is shown in Fig. 3.

Fig. 3
figure 3

Phase and amplitude variation as a function of frequency for the spatial filter shown in Fig. 1 with internal pipe radius = 5 cm. Results for five values of the trace velocity V are indicated: black line V = 340 m/s; red line V = 390 m/s; green line V = 440 m/s; blue line V = 490 m/s; pink line V = 540 m/s, and for two values of the incident angle θ = 0.0° and θ = 45.0° from propagation in the +x direction

Full size image

Unexpectedly the radius 1.0 cm and radius 5.0 cm curves show good agreement. In both cases for a 0° incident wavefront the phase decreases steadily to around minus 60° at 5 Hz where it stays constant out to 10 Hz, the 45° incident wavefront exhibiting only a fairly small deviation in the phase information. A predicted amplitude attenuation occurs for increasing frequencies, being more pronounced for the 0° incident wavefront above 5 Hz. In both cases, a predicted amplitude attenuation of around 60 % occurs at 5 Hz. The effects are less marked in all cases as the trace velocity increases.

A spatial filter configuration commonly used at infrasound arrays is the rosette-style filter shown in Fig. 4.

Fig. 4
figure 4

The ‘rosette’ spatial filter design in common use at International Monitoring System (IMS) style infrasound arrays (Christie 1999). a Low frequency 144 port 70 m diameter filter. b High frequency 96 port 18 m diameter filter

Full size image

The plane-wave response for both the high-frequency (18 m diameter) and low-frequency (70 m radius) configurations is shown in Fig. 5 and are similar to those discussed in Hedlin et al., (2003).

Fig. 5
figure 5

Phase and amplitude variation as a function of frequency for the rosette filters shown in Fig. 4. a 18 m diameter. b 70 m diameter. Results for five values of the trace velocity V are shown: black line V = 340 m/s; red line V = 390 m/s; green line V = 440 m/s; blue line V = 490 m/s; pink line V = 540 m/s), propagation is in the +x direction

Full size image

The response for the 18 m filter shows a linear phase shift with frequency, being the same for all incident trace velocities, achieving around −70° at 5 Hz. The amplitude attenuation is fairly innocuous, being around 90 % at 5 Hz, and deceasing as the trace velocity increases. The presence of the 70 m filter is significantly distorting the signal. A 180° phase shift and complete amplitude annulment is observed at the characteristic frequency, which is defined by the TA propagation speed divided by the diameter of the spatial filter, which for 340 m/s propagation speed is 4.85 Hz.

3 Modified Array Response

Inclusion of phase and amplitude information of the kind presented in Sect. 2 will likely alter the array response. In this section we determine the modified array response function for an array with spatial filters attached to the sensors.

It can be shown (see, e.g. Kennett 2002) that a plane wave with slowness s and angular frequency ω impinging on an infrasound or seismic array with N sensors is modulated by the array response function

$$ S\left( {{\mathbf{p}} - {\mathbf{s}},\omega } \right) = \sum\limits_{j = 1}^{N} {{\text{e}}^{{i\omega \left( {{\mathbf{p}} - {\mathbf{s}}} \right) \cdot {\mathbf{r}}_{j} }} } $$
(3)

where r j is the position vector of the jth sensor, and p is a point in the slowness plane, so that for the broad-band process \( \psi \left( {{\mathbf{x}},t} \right) \sim \int\nolimits_{{\omega_{1} }}^{{\omega_{2} }} {A\left( \omega \right){\text{e}}^{{i\omega \left( {t - s \cdot {\mathbf{x}}} \right)}} {\text{d}}\omega } \), the normalized signal power P as a function of slowness is given by Eq. 4.

$$ P\left( {p,s} \right) = \left| {\int\limits_{{\omega_{2} }}^{{\omega_{1} }} {A\left( \omega \right)S\left( {p - s,\omega } \right){\text{d}}\omega } } \right|^{2} $$
(4)

For the present analysis we assume that A(ω) is described by the gaussian function \( A\left( \omega \right) = {\text{e}}^{{ - \left( {\omega - \omega_{0} } \right)^{2} }} \) about a central frequency ω 0, thus avoiding purely monochromatic signals, which may tend to prematurely drive an array into spatial aliasing as frequency is increased. Furthermore, we assume that amplitude spectrum is discretely sampled by a finite number of frequency pickets \( \omega_{m} = \omega_{0} 2^{\frac{m}{M}} \) for \( m = \ldots , - 2, - 1,0,1,2, \ldots \) where M is the number of frequency pickets per octave. In this study we assume that \( \omega_{m} = \omega_{0} 2^{\frac{m}{9}} \) for m = −2, −1, 0, 1, 2.

With these constraints, the normalized power as a function of slowness is given by

$$ P = \left| {\sum\limits_{m = - 2}^{2} {A\left( {\omega_{m} } \right)} \sum\limits_{j = 1}^{N} {{\text{e}}^{{i\omega \left( {{\mathbf{p}} - s} \right) \cdot r_{j} }} } } \right|. $$
(5)

Application of spatial filters of the kind considered in Sect. 2, requires the amplitude correction B(ω) and phase shift φ(ω) be included in the expression for the array response. This now becomes the modified array response

$$ \hat{S}\left( {p - {\mathbf{s}},\omega } \right) = \sum\limits_{j = 1}^{N} {B_{j} \left( \omega \right){\text{e}}^{{i\left[ {\omega \left( {p - s} \right) \cdot {\mathbf{r}}_{j} - \phi \left( \omega \right)} \right]}} } $$
(6)

The modified array response given by Eq. 6 has been computed for the test array shown in Fig. 6. This array consists of eight sensors in the form of a low-frequency outer triangle with an inverted high frequency triangle in the centre such that the two inner most sensors are co-located. The low-frequency sensors are equipped with a 70 m rosette filter and the high-frequency sensors are equipped with a 18 m rosette filter of the sort displayed in Fig. 4.

Fig. 6
figure 6

Theoretical eight-element infrasound array with two types of spatial filter, circles indicate sensor locations. Open circles indicate a 70 m diameter 144-port rosette low-frequency spatial filter. Black shaded circles indicate 18 m diameter 96 port rosette high frequency spatial filter. Grey shaded circles indicate co-located sensors, one with a small rosette and one with a large rosette. Indicated distances are in km

Full size image

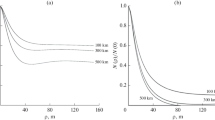
Figure 7 shows the array response (Eq. 3) for an un-adorned array compared to the modified array response (Eq. 6) for the arrangement sensors and filters for the test array in Fig. 6.

Fig. 7
figure 7

Unmodified (left panels) and modified (right panels) normalized array power as a function of slowness for various frequencies for the test array shown in Fig. 6. The signal is assumed to be arriving from the northeast (i.e., 45° from North) at the local sound speed, i.e., there is no vertical component

Full size image

As expected, the modified array response has had a fairly significant effect. This is largely due to the presence of the 70 m spatial filters. The reduction in amplitude is obvious at higher frequencies. The reduction in main lobe amplitude compared with the sidelobes can be significant at higher frequencies, and this is likely to drive the array into spatial aliasing at lower frequencies. To more properly investigate the affect on the array response we need to determine the affect on the measured Fischer Statistic (F-stat) and the least-squares estimate of signal slowness and its variance.

4 Effect on Measured F-stat

An un-adorned or filterless array will cause our test signal ψ to register an infinite F-stat, since by definition ψ represents a purely plane wave. To prevent such infinities from occurring we introduce a slight distortion of the wavefront such that the array response function becomes the modified form

$$ S\left( {p - s,\omega } \right) = \sum\limits_{j = 1}^{N} {{\text{e}}^{{i\left[ {\omega \left( {p - s} \right) \cdot {\mathbf{r}}_{j} + \theta_{j} } \right]}} } \quad {\text{where }}\theta_{j} = 2\pi M \times {\text{rand()}}_{j} $$
(7)

where rand() is a random number between 0 and 1, and M is a multiplier used to set the measured F-stat to a predetermined value, such as 100, for the frequency dependent incident waveform.

The F-stat in the frequency domain can be determined using Shumway’s formula (Shumway 1971)

$$ F\left( {p,s} \right) = \left( {N - 1} \right)\frac{{P\left( {p,s} \right)}}{{P_{T} - P\left( {p,s} \right)}} $$
(8)

where \( P_{T} = \left| {\int\nolimits_{{\omega_{2} }}^{{\omega_{1} }} {A\left( \omega \right){\text{d}}\omega } } \right|^{2} \) is the total signal + noise power.

For the array and filter configuration shown in Fig. 6, and the plane wave ψ impinging upon it, the measured F-stat is modified by the spatial filters as shown in Table 2.

Table 2 The effect of spatial filters on theoretical F-stat values for various frequencies
Full size table

For the theoretical infrasound array and spatial filter arrangement shown in Fig. 6 the predicted affect on the measured F-stat can be significant for signals above 1.0 Hz, although the effect seems to be more pronounced for more coherent signals with higher F-stat; the less coherent signals are not affected to the same extent. Fortunately the broad-band character and generally lower frequency nature of the signals of interest for which the International Monitoring System (IMS) arrays are designed will reduce somewhat the deleterious effect of the spatial filters. These results are of course dominated by the inclusion of the 70 m spatial filters, which was never intended for use at the higher frequencies.

5 Modification to the Least Squares Estimate of Signal Slowness

Assuming our array of n-sensors is distributed in ‘d-dimensions’, where d is either 2 or 3, we can construct a N × d matrix X of unique inter-sensor separations. A vector τ o of observed inter-sensor time delays corresponds to the arrival of a plane wave with d-dimensional vector slowness s through the relationship

$$ \tau_{{\mathbf{o}}} = Xs + \varepsilon $$
(9)

where ε is the error in measuring the time-delays.

The solution in s is found by minimizing the error R 2 = \( \varepsilon^{\text{T}} \varepsilon \), where T indicates matrix transposition.

The least-squares solution to Eq. (9) is found to be (see, e.g., Rao 1973)

$$ \hat{s}_{\text{o}} = C^{ - 1} X^{\text{T}} \tau_{\text{o}} $$
(10)

where C = X T X.

In order to accommodate the inclusion of spatial filters a correction factor μ needs to be subtracted from the vector of observed inter-sensor time delays, so that the ‘correct’ vector τ C = τ O − μ is determined. Note that if the same spatial filter is applied to each sensor then the vector μ = 0 because the same phase delay is applied to each sensor implying that the inter-sensor delays remain unchanged.

With spatial filters attached to each sensor Eq. 10 implies that the least-squares estimate on slowness is given by \( \hat{s}_{\text{o}} = C^{ - 1} X^{\text{T}} \left( {\tau_{\text{c}} + \mu } \right) \), from which the correct slowness vector can be determined to be

$$ {\hat{\mathbf{s}}}_{\text{C}} = {\hat{\mathbf{s}}}_{\text{O}} + \delta {\mathbf{s}} = {\hat{\mathbf{s}}}_{\text{O}} - C^{ - 1} X^{\text{T}} {\varvec{\mu}} $$
(11)

A Cramer–Rao lower bound estimate of the variance in \( {\varvec{\tau}}_{\text{O}} \) is given by (Szuberla and Olson 2004)

$$ \hat{\sigma }_{{\tau_{\text{o}} }}^{2} = \frac{{\tau_{\text{o}}^{\text{T}} \left( {I - R} \right)\tau_{\text{o}} }}{N - r} $$
(12)

where R = XC−1XT, r is the rank of R, and I is the identity matrix. Eq. 11 can be written in terms of the corrected time delays as

$$ \hat{\sigma }_{{\tau_{\text{O}} }} = \hat{\sigma }_{{\tau_{\text{C}} }} + {\varvec{\mu}}^{\text{T}} \left( {I - R} \right){\varvec{\tau}}_{\text{C}} + {\varvec{\tau}}_{\text{C}}^{\text{T}} \left( {I - R} \right){\varvec{\mu}} + {\varvec{\mu}}^{\text{T}} \left( {I - R} \right){\varvec{\mu}} $$
(13)

It can be seen that without accommodating the time delays due to the spatial filters the variance on τ is being over estimated by the factor

$$ A = {\varvec{\mu}}^{\text{T}} \left( {I - R} \right){\varvec{\tau}}_{\text{C}} + {\varvec{\tau}}_{\text{C}}^{\text{T}} \left( {I - R} \right){\varvec{\mu}} + {\varvec{\mu}}^{\text{T}} \left( {I - R} \right){\varvec{\mu}} $$
(14)

The affect on least-squares estimate of slowness for signals recorded on an infrasound array with the sensor and spatial filter configuration shown in Fig. 6 can be estimated via Eqs. 11 and 14. An internal pipe diameter of 1-cm is assumed for the pipe filters in the following analysis.

The array shown in Fig. 6 (assumed to be two-dimensional), being an eight-element array, has 28 possible sensor pairs implying both the vector \( {\varvec{\tau}}_{\text{o}} \) of observed inter-sensor time delays and the correction vector μ is 28-dimensional. Since the array consists of two groups of four sensors with the same spatial filter applied, the vector μ contains 12 elements that are identically zero and 16 identical non-zero elements. The non-zero element of μ is shown in Table 3 as a function of frequency together with components of the slowness correction vector δ s.

Table 3 Estimates of the maximum element of the time correction vector μ to the observed inter-sensor time delay vector, and the correction δs to the least squares estimate of slowness as a function of frequency for the test array shown in Fig. 6, and the asymmetric counterpart shown Fig. 8
Full size table

The correction vector δ s is found to be negligible at all frequencies and so the change in measured back azimuth and trace velocity will be of no consequence, and since the vector μ occurs in each term on the right-hand side of Eq. 14 it also follows that the magnitude of the correction A to the estimate of the variance σ τ to the vector τ will also be negligible.

6 Asymmetric Array

It may perhaps be anticipated that the null result is due to the symmetric nature of the arrangement of the spatial filters in the array, i.e. the small-radius filters placed symmetrically around the centre sensor may reduce the bias in the measured slowness. A second simulation has been performed in which the high-frequency, small-radius spatial filters are placed around one of the corner sensors, as shown in Fig. 8.

Fig. 8
figure 8

Theoretical eight-element infrasound array with two types of spatial filter, circles indicate sensor locations. Open circles indicate a 70 m diameter 144-port rosette low-frequency spatial filter. Black shaded circles indicate 18 m diameter 96 port rosette high frequency spatial filter. Grey shaded circles indicate co-located sensors, one with a small rosette and one with a large rosette. Indicated distances are in km

Full size image

The results are shown in Table 3. The change in the slowness correction vector is significantly larger this time. The change in the back azimuth, δθ, and change in measured speed, δv as a function of signal back azimuth, θ, are shown in Fig. 9. A speed of propagation of 343 m/s was assumed.

Fig. 9
figure 9

Estimated change in the least squares estimate of wave speed δv and back azimuth δθ as a result of applying the asymmetric arrangement of low and high frequency spatial filters shown in Fig. 8 (red line 0.1 Hz, blue line 4.0 Hz). A wave speed of 343 m/s was assumed

Full size image

With this asymmetric arrangement of spatial filters a maximum deviation of 1.5° in the least squares estimate of back azimuth is predicted, together with a corresponding maximum deviation of 10 m/s in the least squares estimate of wave speed.

7 Simulation

In order to test the theoretical predictions, of Sect. 5, a simulation of slowness estimation was arranged for the array depicted in Fig. 6. An ensemble of 104 quasi-monochromatic wave packets corresponding to the frequencies given in Table 1 was prepared. These packets comprised roughly seven full oscillations in a Hanning-tapered window. The packets were then phase shifted to correspond to a planar arrival, from 13.1° back azimuth with a trace velocity of 343 m/s, at each inlet port or sensor. This set of arrival parameters was selected because it is not a function of any symmetry in neither the array nor pipe inlet geometries. Each packet was then sampled at 20 Hz (consistent with CTBT-type infrasound arrays). To simulate noise akin to a realistic infrasound station, each example was contaminated with pink noise (1/f amplitudes, uniformly randomized phases) at 10 dB SNR.

The array shown in Fig. 6 was treated in two different respects: (a) with no pipe array, such that there were seven bare sensors (the co-located center elements would be identical) exposed to the noisy packets, and (b) simulating the effects of the pipe array by further phase shifting the packet at each inlet to correspond with its propagation down the pipes (a = 1.0 cm was used here) at speeds consistent with Table 1. Each sensor response in the latter case was built by summing respective inlet-phase-shifted packets. For each of the two treatments and frequencies, a 95 % confidence ellipse was constructed for the slowness estimates of the noisy packets. These results are shown in Figs. 10 and 11, for two of the frequencies given in Table 3.

Fig. 10
figure 10

Simulation results for wave packets at 0.1 Hz. The nominal slowness, corresponding to 13.1º back azimuth at 343 m/s trace velocity is shown in black. The bare, seven-sensor array is shown in blue, while the eight-element array equipped with spatial filters is shown in green. Confidence ellipses are calculated at the 95 % level for 104 trials at 10 dB SNR, as described in the text

Full size image
Fig. 11
figure 11

Simulation results for wave packets at 4.0 Hz. The nominal slowness, corresponding to 13.1º back azimuth at 343 m/s trace velocity is shown in black. The bare, seven-sensor array is shown in blue, while the eight-element array equipped with spatial filters is shown in green. Confidence ellipses are calculated at the 95 % level for 104 trials at 10 dB SNR, as described in the text

Full size image

In Fig. 10 we show the results for packets at 0.1 Hz. The results at relatively low frequencies such as this are consistent with our intuition, in that the confidence ellipse for the array equipped with spatial filters (shown in green) is smaller than that of the bare sensors, owing to the incoherent noise reduction afforded by the summing of each inlet’s signal at the sensor. The results are also largely unbiased at this relatively high SNR (nominal slowness shown in black).

The results for 4 Hz, shown in Fig. 11 are markedly different, and perhaps not predicted so well by the theory for this configuration of sensors and inlets. The slowness deviation is of order 10−2 s/km. The advantage of incoherent noise reduction is largely lost as we approach the null frequency, as seen by the nearly equal areas of each ellipse. In this case, the inlet-equipped result also exhibits a pronounced bias in slowness that would correspond with 12.6° back azimuth and 341 m/s trace velocity estimates. The uncertainties in these estimates are still relatively small, of order 1° and 1 m/s, so other effects (e.g., winds between the source and array) may easily dominate.

8 Conclusions

The plane wave response for several spatial filter designs, typical of those in use at IMS infrasound stations, has been determined. The analysis incorporated internal acoustic velocities that were specified by the Benade (1968) analysis for sound propagation in a conduit. The determined amplitude and phase response as a function of frequency were incorporated in the usual array response for an arrangement of infrasound sensors. It was found that the incorporation of spatial filters at infrasound stations can have a significant deleterious affect on the signal detectability in terms of the measured Fischer statistic, particularly at frequencies above 2 Hz. Signals with dominant frequency below 1 Hz have only a minor reduction in their detectability. The incorporation of mixed spatial filter types, i.e., spatial filters of different size, and so different phase delays, at infrasound sensors in the same array, can have significant impact on the measured back azimuth and signal speed in term of the least-squares estimate if an asymmetric arrangement of spatial filters is used. However, if a symmetric arrangement of spatial filters is used then there is little impact on the least-squares estimate of signal slowness. Simulation of semi-realistic signals shows that some effects are more pronounced than predicted. The uncertainties arising from these effects are still relatively small compared to other, naturally-caused, perturbations in signal parameter estimation.