Abstract
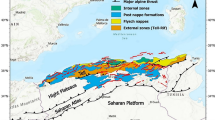
A straightforward Bayesian statistic is applied in five broad seismogenic source zones of the northwest frontier of the Himalayas to estimate the earthquake hazard parameters (maximum regional magnitude M max, β value of G–R relationship and seismic activity rate or intensity λ). For this purpose, a reliable earthquake catalogue which is homogeneous for M W ≥ 5.0 and complete during the period 1900 to 2010 is compiled. The Hindukush–Pamir Himalaya zone has been further divided into two seismic zones of shallow (h ≤ 70 km) and intermediate depth (h > 70 km) according to the variation of seismicity with depth in the subduction zone. The estimated earthquake hazard parameters by Bayesian approach are more stable and reliable with low standard deviations than other approaches, but the technique is more time consuming. In this study, quantiles of functions of distributions of true and apparent magnitudes for future time intervals of 5, 10, 20, 50 and 100 years are calculated with confidence limits for probability levels of 50, 70 and 90 % in all seismogenic source zones. The zones of estimated M max greater than 8.0 are related to the Sulaiman–Kirthar ranges, Hindukush–Pamir Himalaya and Himalayan Frontal Thrusts belt; suggesting more seismically hazardous regions in the examined area. The lowest value of M max (6.44) has been calculated in Northern-Pakistan and Hazara syntaxis zone which have estimated lowest activity rate 0.0023 events/day as compared to other zones. The Himalayan Frontal Thrusts belt exhibits higher earthquake magnitude (8.01) in next 100-years with 90 % probability level as compared to other zones, which reveals that this zone is more vulnerable to occurrence of a great earthquake. The obtained results in this study are directly useful for the probabilistic seismic hazard assessment in the examined region of Himalaya.







Similar content being viewed by others
References
Armbruster, J., Seeber, L. and Jacob, K. H. (1978), The northwestern termination of the Himalayan mountain front: Active tectonics from microearthquakes, J. Geophys. Res. 83, 269–282.
Bhatia, S. C., Kumar, M. R. and Gupta, H. K. (1999), A probabilistic seismic hazard map of India and adjoining regions, Annali di Geofisica 42, 1153–1164.
Benjamin, J. R. (1968), Probabilistic models for seismic forces design, J. Struct. Div., ASCE 94, 5T5, 1175–1196.
Bernard M., Shen-Tu, B., Holt, W. E. and Davis, D. M. (2000), Kinematics of active deformation in the Sulaiman Lobe and Range, Pakistan, J. Geophys. Res., 105, 13253–13297.
BIS., (2002). IS 1893 (part 1)–2002: Indian standard criteria for earthquake resistant design of structures, part 1 – general provisions and buildings, Bureau of Indian Standards, New Delhi.
Campbell, K. W. (1982), Bayesian analysis of extreme earthquake occurrences, Part I. Probabilistic hazard model, Bull. Seismol. Soc. Am. 72, 1689–1705.
Campbell, K. W. (1983), Bayesian analysis of extreme earthquake occurrences, Part II. Application to the San Jacinto fault zone of southern California, Bull. Seismol. Soc. Am. 73, 1099–1115.
Cox, D. R. and Lewis, P. A. W. (1966), The Statistical Analysis of Series of Events, Methuen, London.
Field, E. H., Jackson, D. D. and Dolan, J. F. (1999), A mutually consistent seismic hazard source model for southern California, Bull. Seismol. Soc. Am. 89(3), 559–578.
Galanis, O. C., Tapanos, T. M., Papadopoulos, G.A. and Kiratzi, A.A. (2002), Bayesian extreme values distribution for seismicity parameters assessment in South America. J. Balkan Geophys. Soc. 5, 77–86.
Gansser, A. (1964). Geology of the Himalayas, Inter-Science London.
Gutenberg, B. and Richter, C. F. (1954), Seismicity of the earth and associated phenomena, Princeton University Press, New Jersey (publ.), pp. 310.
Kaila, K. L. and Rao, M. (1979), Seismic zoning maps of Indian sub-continent, Geophys. Res. Bull. 17, 293–301.
Khattri, K. N., Rogers, A. M., Perkins, D. M. and Algermissen, S. T. (1984), A Seismic Hazard Map of India and Adjacent Area, Tectonophysics 108, 93–134.
Kijko, A. (2004), Estimation of the maximum earthquake magnitude M max , Pageoph 161, 1–27.
Kijko, A. and Sellevoll, M. A. (1989), Estimation of Seismic Hazard Parameters from Incomplete Data Files. Part I: Utilization of Extreme and Complete Catalogues with Different Threshold Magnitudes, Bull. Seismol. Soc. Am. 79, 645–654.
Kijko, A. and Sellevoll, M. A. (1992), Estimation of Earthquake Hazard Parameters from Incomplete Data Files. Part II: Incorporation of Magnitude Heterogeneity, Bull. Seismol. Soc. Am. 82 (1), 120–134.
Kijko, A. and Singh, M. (2011), Statistical Tools for Maximum Possible Earthquake Magnitude Estimation, Acta Geophysica, 59 (4), 674–700.
Koulakov, I. and Sobolev, S. (2006), A tomographic image of Indian lithosphere break-off beneath the Pamir-Hindukush region, Geophy. J. Int. 164, 425–440.
Lyubushin, A. A. and Parvez, I. A. (2011), Map of Seismic Hazard of India using Bayesian Approach, Natural Hazard 55(2), 543–556.
Lyubushin, A. A., Tsapanos, T.M., Pisarenko, V. F. and Koravos, G.C. (2002), Seismic hazard for selected sites in Greece: a Bayesian estimates of seismic peak ground acceleration, Natural Hazard 25(1), 83–89.
Mortgat, C. P. and Shah, H. C. (1979), A Bayesian model for seismic hazard mapping, Bull. Seismol. Soc. Am. 69, 1237–1251.
Mueller, C.S. (2010), The influence of maximum magnitude on seismic-hazard estimates in the central and eastern United States, Bull. Seismol. Soc. Am. 100(2), 699–711.
Parvez, I. A. (2007), On the Bayesian analysis of the earthquake hazard in the North-East Indian peninsula, Natural Hazards 40, 397–412.
Parvez, I. A. and Ram, A. (1997), Probabilistic assessment of earthquake hazards in the north-east Indian peninsula and Hindukush regions, Pure Appl. Geophys. 149, 731–746.
Parvez, I. A. and Ram, A. (1999), Probabilistic assessment of earthquake hazards in the Indian subcontinent, Pure Appl. Geophys. 154, 23–40.
Pisarenko, V. F., Lyubushin, A. A., Lysenko, V. B. and Golubeva, T. V. (1996), Statistical estimation of seismic hazard Parameters: Maximum possible magnitude and related parameters, Bull. Seismol. Soc. Am. 86, 691–700.
Pisarenko, V.F. and Lyubushin, A.A. (1997), Statistical estimation of maximal peak ground acceleration at a given point of seismic region, J of Seismology 1, 395–405.
Pisarenko, V.F. and Lyubushin, A.A. (1999), Bayesian approach to seismic hazard estimation: maximum values of magnitudes and peak ground accelerations, Earthq. Res. China (English Edition) 13(1), 45–57.
Rao, C. R. (1965), Linear Statistical Inference and its Application, John Wiley, New York.
Shanker, D. and Papadimitriou, E. E. (2004), Regional time-predictable modeling in Hindukush–Pamir-Himalayas region, Tectonophysics 390, 129–140.
Shanker, D. and Sharma, M. L. (1998), Estimation of seismic hazard parameters for the Himalayas and its vicinity from complete data files, Pure Appl. Geophys. 152, 267–279.
Shanker, D., Yadav R. B. S. and Singh, H. N. (2007), On the seismic risk in the Hindukush–Pamir–Himalaya and their vicinity, Current Science 92, 1625–1630.
Stavrakakis, G. N. and Drakopoulos, J. (1995), Bayesian probabilities of earthquake occurrences in Greece and surrounding areas, Pure Appl. Geophys. 144, 307–319.
Stavrakakjs, G. N. and Tselentis, G. A. (1987), Bayesian probabilistic prediction of strong earthquakes in the main seismogenic zones of Greece, Boll. Geofis. Teor. Applic. 113, 51–63.
Stein, R. S. and Hanks, T. C. (1998), M ≥ 6 earthquakes in southern California during the twentieth century: No evidence for a seismicity or moment deficit, Bull. Seismol. Soc. Am. 88, 3, 635–652.
Thingbaijam, K. K. S., Chingtham, P. and Nath, S. K. (2009). Seismicity in the North-West Frontier Province at the Indian-Eurasian Plate Convergence, Seism. Res. Lett. 80(4), 599–608.
Tinti, S. and Mulargia, F. (1985), Effects of magnitude uncertainties in the Gutenberg-Richter frequency-magnitude law, Bull. Seismol. Soc. Am. 75, 1681–1697.
Tsapanos, T. M. (2003). Appraisal of seismic hazard parameters for the seismic regions of the east circum-Pacific belt inferred from a Bayesian approach, Natural Hazards 30, 59–78.
Tsapanos, T. M. and Christova, C. V. (2003), Earthquake hazard parameters in Crete island and its surrounding area inferred from Bayes statistics: an integration of morphology of the seismically active structures and seismological data, Pure Appl. Geophys. 160, 1517–1536, 2003.
Tsapanos, T. M., Galanis, O. Ch., Koravos, G. Ch. and Musson, R. M. W. (2002), Α method for Bayesian estimation of the probability of the local intensity for some cities of Japan, Annals of Geophysics 45, 657–671.
Tsapanos, T. M., Lyubushin, A. A. and Pisarenko, V. F. (2001), Application of a Bayesian approach for estimation of seismic hazard parameters in some regions of the Circum-Pacific Belt, Pure Appl. Geophys. 158, 859–875.
Wells, D. and Coppersmith, J. K. (1994), New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement, Bull. Seismol. Soc. Am. 84(4), 974–1002.
Wessel, P. and Smith, W.H.F. (1995), New version of the generic mapping tools released, EOS. Trans. Am. Geophys. Un. 76:329.
Wheeler, R. L. (2009), Methods of M max estimation east of the Rocky Mountains, U.S. Geological Survey Open-File Report 2009-1018, 44 pp.
Yadav, R. B. S. (2009), Seismotectonic modeling of NW Himalaya: a perspective on future seismic hazard, Ph. D. thesis, Department of Earthquake Engineering, IIT, Roorkee, India, 198 pp.
Yadav, R. B. S., Shanker, D., Chopra, S. and Singh A. P. (2010), An application of regional time and magnitude predictable model for long-term earthquake prediction in the vicinity of October 8, 2005 Kashmir Himalaya earthquake, Natural Hazards 54 (3), 985–1014.
Yadav, R. B. S., Bayrak, Y., Tripathi, J. N., Chopra, S., Singh, A.P. and Bayrak, E. (2011), A Probabilistic Assessment of Earthquake Hazard Parameters in NW Himalaya and the Adjoining Regions, Pure and Applied Geophysics, doi: 10.1007/s00024-011-0434-8.
Acknowledgments
The authors are thankful to their respective institutes for the support. The first author is thankful to the Director, INCOIS and HoD, ASG, INCOIS for support. Authors, and especially T.M. Tsapanos, would like to express their sincere thanks to Prof. Pisarenko and Prof. A. Lyubushin for introducing the procedure applied here and was developed by them. The collaboration of T.M.T. with Prof. Lyubushin and the cheerful discussions they had some years ago, were very helpful to understand the Bayes approach. Authors are also thankful to Prof. A. Kijko, Editor, PAGEOPH and two anonymous reviewers for constructive comments and suggestions which enhanced quality of the manuscript. The GMT system (Wessel and Smith, 1995) was used to plot some figures. INCOIS contribution no 106.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yadav, R.B.S., Tsapanos, T.M., Bayrak, Y. et al. Probabilistic Appraisal of Earthquake Hazard Parameters Deduced from a Bayesian Approach in the Northwest Frontier of the Himalayas. Pure Appl. Geophys. 170, 283–297 (2013). https://doi.org/10.1007/s00024-012-0488-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00024-012-0488-2