The Differentiability of Horizons Along Their Generators

Abstract

Let H be a (past directed) horizon in a time-oriented Lorentz manifold and $\gamma :[\left( \alpha ,\beta \right) \rightarrow H$ a past directed generator of the horizon, where $[\left( \alpha ,\beta \right)$ is $[\alpha ,\beta )$ or $\left( \alpha ,\beta \right)$. It is proved that either at every point of $\gamma \left( t\right) ,~t\in \left( \alpha ,\beta \right)$ the differentiability order of H is the same, or there is a so-called differentiability jumping point $\gamma \left( t_{0}\right) ,~t_{0}\in \left( \alpha ,\beta \right)$ such that H is only differentiable at every point $\gamma \left( t\right) ,~t\in \left( \alpha ,t_{0}\right)$ but not of class $C^{1}$ and H is exactly of class $C^{1}$ at every point $\gamma \left( t\right) ,~t\in \left( t_{0},\beta \right)$. We will use in the proof a result which shows that every mathematical horizon in the sense of P. T. Chruściel locally coincides with a Cauchy horizon.

1 Introduction

There are different objects in physics which are called horizons. A mathematical definition of horizons was given by P. T. Chruściel in [3], see Definition 1 in this paper. This definition includes, for example, black hole event horizons and Cauchy horizons as well. It turned out that the set of those points at which the horizon is not differentiable cannot be neglected, for references see, for example, the introduction of [5]. First, J. K. Beem and A. Królak in [2] proved that at the interior points of a generator the horizon is differentiable. Moreover, at the possible endpoint p of a generator, H is differentiable if and only if $N\left( p\right) =1$, i.e. p is the endpoint of only 1 generator. Later Chruściel in [3] gave a simpler proof which works for mathematical horizons. The higher-order differentiability properties of the horizon were studied by the author in [5]; it was proved that along a generator the differentiability order of the horizon at the generator points can change only once, see Theorem 4 in this paper. If a change happens, then from simple differentiability it changes to a higher order $C^{k}$, $k\ge 1$ differentiability. Our goal is to show that $k=1$. In [5] a geometric characterization was also given to describe the point at which the differentiability changes with the help of non-injectivity points.

First we recall the definitions, known results and some notations. Then we give the proof in the Minkowski 3-dimensional space-time in which the idea is easy to follow; then we prove the general case. Some technical details are presented in the appendix.

2 Definitions, Known Results

We will use the definitions and notations from the book of J. K. Beem et al. [1], e.g. for the chronological (causal), past (future), causality relations, etc.

We use the definition in [3], to define a horizon in the mathematical sense. Let $\left( M,g\right)$ denote a time-oriented Lorentz manifold throughout the paper.

Definition 1

A subset $H\subset M$ is called a horizon if:

• (1) it is a topological hypersurface;

• (2) it is achronal;

• (3) for every point $p\in H$, there is a past inextendable, past directed, light-like geodesic $\gamma :[0,\alpha )\rightarrow H$, such that $\gamma \left( 0\right) =p$.

An achronal topological hypersurface can be considered as a continuous function graph; for a precise introduction we refer the reader to [5]. Note that in $\left( 2\right)$ we could use local achronality, even in that case the results remain true.

For the sake of simplicity, the notation $[\left( \alpha ,\beta \right)$ will mean the interval $\left( \alpha ,\beta \right)$ or the interval $[\alpha ,\beta )$, where $\alpha ,\beta \in {\mathbb {R}}\cup \left\{ -\infty ,\infty \right\}$

Definition 2

Let $\gamma :[(\alpha ,\beta )\rightarrow H$ be a past directed, past inextendable, light-like geodesic, such that it is future inextendable on the horizon, i.e. there is no $\varepsilon >0$, such that a light-like geodesic $\widetilde{\gamma }:\left( \alpha -\varepsilon ,\beta \right) \rightarrow H$ exists, for which $\widetilde{\gamma }\left( t\right) =\gamma \left( t\right)$ for every $t\in [(\alpha ,\beta )$. Then $\gamma$ is called a generator.

Thus, a generator can be defined on an open interval $\left( \alpha ,\beta \right)$, or on a closed-open one $[\alpha ,\beta )$, depending only on the generator.

Let $N\left( p\right)$ denote the number of the generators at $p\in H$. The achronality of H gives that generators cannot intersect or have branching points except at their possible common endpoint¹, see, for example, [5]. Thus, $N\left( p\right) =1$ must hold if p is an interior point of a generator.

Proposition 3

The following are equivalent:

• H is differentiable at every point of an open set $U\subset H$;

• $\forall p\in U\subset H,~N\left( p\right) =1$;

• every point $p\in U$ is an interior point of a generator;

• H is differentiable at least of class $C^{1}$ at every point $p\in U$.

Proof

See proposition 3.3. in [2], where the proof also works for mathematical horizons. $\square$

We recall shortly what it means that H is differentiable of class $C^{k}$ at a point $p\in H$, the precise description can be found in [5] at the beginning of the section: The differentiability order of horizons. Let N be a topological submanifold in the smooth manifold M. It is differentiable of class $C^{k}$ at $p\in N$ if there is a suitable smooth coordinate chart in a neighbourhood of $p\in M$ such that the coordinate functions of N are k times differentiable at p and the k-th derivatives are continuous at p. It means that in a neighbourhood of p the $\left( k-1\right)$th derivatives of the coordinate functions are continuous, but the continuity of the k-th derivatives is guaranteed only at p. The differentiability class is exactly of class $C^{k},$ if it is of class $C^{k}$ but not of class $C^{k+1}$.

Theorem 4

For every generator $\gamma :[\left( \alpha ,\beta \right) \rightarrow H$, a unique parameter $t_{0}\in [\alpha ,\beta ]$ exists, where $\alpha ,~\beta \in {\mathbb {R}}\cup \left\{ -\infty ,\infty \right\}$, such that there is a $k\ge 1$ for which

• (1) H is exactly of class $C^{k}$ at every $\gamma \left( t\right)$, for which $t>t_{0};$

• (2) H is differentiable, but not of class $C^{1}$ at every $\gamma \left( t\right)$, for which $t\in (\alpha ,t_{0}];$

• (3) H is differentiable at the possible endpoint $\gamma \left( \alpha \right)$ if and only if $N\left( \gamma \left( \alpha \right) \right) = 1$.

Proof

See in [5] Theorem (Structure of the generators). $\square$

Definition 5

Let $\gamma :[\left( \alpha ,\beta \right) \rightarrow H$ be a generator and assume that the point $t_{0}$ defined in Theorem 4 is not equal to $\alpha$ or $\beta$. Then $\gamma \left( t_{0}\right)$ is called the differentiability jumping point of $\gamma$.

Now the main goal of this paper is to sharpen the above theorem, thus

Theorem 6

If on a generator $\gamma :[\left( \alpha ,\beta \right) \rightarrow H$ the differentiability jumping point exists, i.e. $t_{0} \in \left( \alpha ,\beta \right)$, then in Theorem 4, $k=1$.

An immediate consequence is:

Corollary 7

If $\gamma :[(\alpha ,\beta )\rightarrow H$ is a generator and H is of class $C^{k}$, $k\ge 2$ at an interior point $\gamma \left( t\right) ,~t\in \left( \alpha ,\beta \right)$, then H is of class $C^{k}$ at every point $\gamma \left( t\right) ,~t\in \left( \alpha ,\beta \right)$.

An example in [5] is given where the differentiability jumping point exists.

For the proof, we will need the definition of Cauchy horizons, see p. 419 definition 35 in [4]

Definition 8

Let S be an achronal subset in a time oriented Lorentz manifold $\left( M,g\right)$. The future Cauchy development of S is

$$\begin{aligned} D^{+}\left( S\right) \overset{def}{=}\left\{ z\in M\,|\,\text {every past directed inextendable causal curve from }z\text { intersects }S\right\} ; \end{aligned}$$

and the future Cauchy horizon of S is

$$\begin{aligned} H^{+}\left( S\right) \overset{def}{=}\partial D^{+}\left( S\right) -\overline{S}. \end{aligned}$$

It is known that $H^{+}\left( S\right)$ is a horizon in the Lorentz manifold $\left( M\backslash \overline{S},g\right)$, where $\overline{S}$ is the closure of S.

The main idea of the Proof of Theorem 6 is presented first in a Minkowski 3-space in case of a Cauchy horizon because it is easier to understand the idea of the proof in this particular case. Then we will show how to use this idea in the general case.

Fig. 1

The points $r_{n}\in H^{+}\left( S\right) \cap R$ with big curvature converge to $\gamma \left( t^{-}\right)$

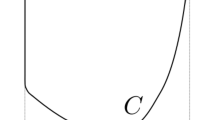
Let $\left( {\mathbb {M}}^{3},g_{M}\right)$ be the standard Minkowski space with the orthonormal basis $e_{1},~e_{2},~e_{3},$ where $e_{1},~e_{2}$ are space-like and $e_{3}$ is time-like. Consider ${\mathbb {R}}^{2}$ the space-like linear subspace spanned by $e_{1}$ and $e_{2}$. Let $S\subset {\mathbb {R}}^{2}$ be an open set. Let $\gamma :$ $[\left( \alpha ,\beta \right) \rightarrow H^{+}\left( S\right)$ be a past directed generator in $H^{+}\left( S\right)$ and assume that $\gamma \left( t_{0}\right)$ is a differentiability jumping point, see Fig. 1. From Theorem 4 we know that $H^{+}\left( S\right)$ is only differentiable at the points of $\gamma |_{\left( \alpha ,t_{0}\right] }$ and it is of class $C^{k},~k\ge 1$ at the points of $\gamma |_{\left( t_{0},\beta \right) }$. By an indirect assumption, assume that $k\ge 2$. Let $t^{-}>t_{0}$ and R an affine subspace at $\gamma \left( t^{-}\right)$, which is parallel to ${\mathbb {R}}^{2}$, see Fig. 1. Since $H^{+}\left( S\right)$ is at least $C^{2}$ at $\gamma \left( t^{-}\right)$, we can use Lemma 11 which gives that the curve $\theta \overset{def}{=}R\cap H^{+}\left( S\right)$ is at least $C^{2}$ at $\gamma \left( t^{-}\right)$.

Let $t^{f}<t^{p}<t_{0}$, then $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) ,~\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ are circles on R touching $\theta$ at $\gamma \left( t^{-}\right)$ with curvatures $0<\kappa ^{f}$ $<\kappa ^{p}$ where the curvature is the common curvature for ${\mathbb {R}}^{2}$ curves. To be able to speak about the curvature, we restrict the metric $g_{M}$ to $R\approx {\mathbb {R}}^{2}$, thus $\left( R,g_{M} |_{R}\right)$ is a Riemannian manifold, where the curvature is the same as on the Euclidean plane ${\mathbb {R}}^{2}$ with the induced Euclidean metric coming from $g_{M}$. Since $H^{+}\left( S\right)$ is only differentiable, but not of class $C^{1}$ at $\gamma \left( t^{p}\right)$, by Proposition 3, there must be a sequence $q_{n}\in H^{+}\left( S\right)$, $q_{n}\rightarrow \gamma \left( t^{p}\right)$ with $N\left( q_{n}\right) \ge 2$. Thus, there are generators $\gamma _{n}^{1},~\gamma _{n}^{2}$ starting at $q_{n}$ which intersect $\theta$ at $p_{n}^{1},~p_{n}^{2}$, since the limit of generators is a generator and the generator at $\gamma \left( t^{p}\right)$ is unique. As $q_{n}\rightarrow \gamma \left( t^{p}\right)$ we have that the curvature $\kappa _{n}$ of the circles $\partial \left( J^{-}\left( q_{n}\right) \cap R\right)$ converges to $\kappa ^{p}$. Since $\left( I^{-}\left( q_{n}\right) \cap R\right) \subset D^{+}\left( S\right)$ and $p_{n}^{1},~p_{n}^{2}\in \theta \subset \partial D^{+}\left( S\right)$ we have that $\theta$ and the circles $\partial \left( J^{-}\left( q_{n}\right) \cap R\right)$ are tangent at $p_{n}^{1}$ and at $p_{n}^{2}$. The curve $\theta$ is differentiable (at least) twice in a neighbourhood of $\gamma \left( t^{-}\right)$; however, we know only that the second derivatives are continuous at $\gamma \left( t^{-}\right)$.

Nevertheless, we can calculate formally the curvature of $\theta$ in the neighbourhood of $\gamma \left( t^{-}\right)$, see Definition 14 in the appendix. To be able to apply this definition and later Lemma 18, we need that the circle piece of $\partial \left( J^{-}\left( q_{n}\right) \cap R\right)$ between $p_{n}^{1}$ and $p_{n} ^{2}$ and the curve piece $\theta |_{p_{n}^{1},p_{n}^{2}}$ can be considered as a function on the plane R. If we take the normal direction of the circle $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$, it will be a transversal direction to $\theta$ at $\gamma \left( t^{-}\right)$. Since $\theta$ is at least $C^{1}$ locally, the lines in R parallel to the normal or very close to the normal direction will be locally transversal to the curve $\theta$ and intersect it only once. So taking a direction $v_{1}$ close to the normal and another one $v_{2}$ such that $v_{1},~v_{2}$ is a basis in R then in the coordinate system on R with origin $\gamma \left( t^{-}\right)$ and basis $v_{1},~v_{2}$ the curve $\theta |_{p_{n}^{1},p_{n}^{2}}$ and the circle piece of $\partial \left( J^{-}\left( q_{n}\right) \cap R\right)$ between $p_{n}^{1}$ and $p_{n}^{2}$ will be a function in the variable corresponding to $v_{2}$, if $p_{n}^{1},~p_{n}^{2}$ are very close to $\gamma \left( t^{-}\right)$.

Since the limit of generators is a generator and $N\left( \gamma \left( t^{p}\right) \right) =1$, we have that $\gamma _{n}^{i}\rightarrow \gamma |_{\left[ t^{p},\beta \right) },~i=1,2$. It follows that $p_{n} ^{1},~p_{n}^{2}\rightarrow \gamma \left( t^{-}\right)$. Therefore, we can apply Lemma 18 to the segment of $\theta$ between $p_{n} ^{1}$ and $p_{n}^{2}$ and to the segment of the circle between $p_{n}^{1}$ and $p_{n}^{2}$ if n is big enough. That lemma gives a point $r_{n}$ on the segment $\theta |_{p_{n}^{1},p_{n}^{2}}$ at which the curvature $\kappa _{\theta }\left( r_{n}\right)$ of $\theta$ is at least the curvature $\kappa _{n}$ of the circle $\partial \left( J^{-}\left( q_{n}\right) \cap R\right)$. As $\theta$ is $C^{2}$ at $\gamma \left( t^{-}\right)$, we have that $\kappa _{\theta }\left( r_{n}\right) \rightarrow \kappa _{\theta }\left( \gamma \left( t^{-}\right) \right)$, where $\kappa _{\theta }\left( \gamma \left( t^{-}\right) \right)$ is the curvature of $\theta$ at $\gamma \left( t^{-}\right)$. Now, since $\kappa _{\theta }\left( r_{n}\right) \ge \kappa _{n}$ and $\kappa _{n}\rightarrow \kappa ^{p}$ we have that

$$\begin{aligned} \kappa _{\theta }\left( \gamma \left( t^{-}\right) \right) \ge \kappa ^{p}>\kappa ^{f}. \end{aligned}$$

By Remark 17 we have that in this case $\theta$ must intersect the interior of the disc $J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R$, which is in $I^{-}\left( \gamma \left( t^{f}\right) \right) \cap R.$ Thus, there is a point $x\in \theta \subset H^{+}\left( S\right) \cap R$ in $I^{-}\left( \gamma \left( t^{f}\right) \right) \cap R$ which contradicts the achronality of $H^{+}\left( S\right)$, since x,$~\gamma \left( t^{f}\right) \in H^{+}\left( S\right)$ cannot be chronologically related.

In the general case we use a similar proof where the steps of the proof are the following. We will use the above-defined notations in these steps.

• 1. Since we examine the horizon locally at the differentiability jumping point, we can chose a suitably small neighbourhood U of $\gamma \left( t_{0}\right)$ and a coordinate system on it, such that the restricted smaller Lorentz manifold $\left( U,g|_{U}\right)$ can be considered as a ball ${\mathbb {B}}^{n}\subset {\mathbb {R}}^{n}$, endowed with a Lorentz metric g which is suitably close to a Minkowski metric. So from now on $\left( U,g|_{U}\right)$ will be identified with $\left( {\mathbb {B}}^{n},g\right)$.

• 2. There is a space-like affine hyperplane ${\mathbb {R}}^{n-1}\subset {\mathbb {B}}^{n}$ with respect to g and a set $S\subset {\mathbb {R}}^{n-1}$ for which the horizon at $\gamma \left( t_{0}\right)$ locally is the same as the Cauchy horizon $H^{+}\left( S\right)$ in $\left( {\mathbb {B}}^{n},g\right)$, see Lemma 9. Thus it is enough to prove the theorem for Cauchy horizons, i.e. we will assume that $H=H^{+}\left( S\right)$.

• 3. Therefore, the intersections $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) ,\dots$ are not circles, because of the higher dimension, nor spheres, but can be arbitrary close to spheres, if $U\simeq {\mathbb {B}}^{n}$ was small enough.

• 4. Let $P\subset R\simeq {\mathbb {R}}^{n-1}$ be a 2-dimensional normal plane of $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$, i.e. $\gamma \left( t^{-}\right) \in P$ and P is parallel to the normal² vector of $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$. The curve $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) \cap P$ is called a normal curve of $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$. If $\gamma \left( t^{p}\right)$ is much closer to R, i.e. to $\gamma \left( t_{0}\right)$, than $\gamma \left( t^{f}\right)$ then there is a constant $\kappa$ such that the curvature at $\gamma \left( t^{-}\right)$ of any normal curve of $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$ is less than $\kappa$ and the curvature at $\gamma \left( t^{-}\right)$ of any normal curve of $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$ is much bigger that $\kappa +1$. To be able to speak about the curvatures, we can equip ${\mathbb {B}}^{n}$ with a Euclidean metric (which induces a Riemannian metric on ${\mathbb {B}}^{n}$) and we consider the restricted metrics on the affine subspaces.

• 5. As previously in the Minkowski case, we can take a sequence $q_{n}\in H^{+}\left( S\right) , q_{n}\rightarrow \gamma \left( t^{p}\right)$ with $N\left( q_{n}\right) \ge 2$, generators $\gamma _{n}^{1},~\gamma _{n}^{2}$ starting at $q_{n}$ and the space-like submanifold $\theta =R\cap H^{+}\left( S\right)$ which is at least of class $C^{1}$ and 1-codimensional in $H^{+}\left( S\right)$ by Lemma 11. Thus, the intersections $p_{n}^{i}=\gamma _{n}^{i}\cap \theta$ exist as before. There is a suitable fixed point $o\in R$ for which the 2-dimensional planes $P_{n}\subset R\simeq {\mathbb {R}}^{n-1}$ defined by $O,~p_{n}^{1},~p_{n}^{2}$ (i.e. $O,~p_{n}^{1},~p_{n}^{2}\in P_{n}$) will have a suitable subsequent which will converge to a normal plane P of $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$.

• 6. The intersections $\partial \left( J^{-}\left( q_{n}\right) \cap R\right) \cap P_{n}$ are curves which are not circles but have curvatures much bigger than $\kappa +1$ if $\gamma \left( t^{p}\right)$ is close enough to R and $q_{n}$ is close enough to $\gamma \left( t^{p}\right)$, i.e. n is big enough, since if $q_{n}$ is close to $\gamma \left( t^{p}\right)$ then the curvatures of $\partial J^{-}\left( q_{n}\right) \cap R$ will be close to the curvatures of $\partial J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R$. Shortly both $\partial J^{-}\left( q_{n}\right) \cap R$ and $\partial J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R$ are diffeomorphic to ${\mathbb {S}}^{n-1}$. So if we fix a Riemannian metric on $R\approx {\mathbb {R}}^{n-1}$ (e.g. the one coming from a Euclidean metric), then both can be considered as Riemannian manifolds $\left( {\mathbb {S}} ^{n-1},g_{q_{n}}\right)$ and $\left( {\mathbb {S}}^{n-1},g_{\gamma \left( t^{p}\right) }\right)$ where the curvature is the same as the classical one considered by the embedding $\partial J^{-}\left( q_{n}\right) \cap R\subset {\mathbb {R}}^{n-1}$. Now if $q_{n}\rightarrow \gamma \left( t^{p}\right)$, then the smooth metric $g_{q_{n}}\rightarrow g_{\gamma \left( t^{p}\right) }$ and all of their derivatives as well, yielding that the curvatures are also converging see Lemma 12.

• 7. The plane curves $\partial \left( J^{-}\left( q_{n}\right) \cap R\right) \cap P_{n}$ and $H^{+}\left( S\right) \cap P_{n}$ are tangent at $p_{n}^{1}$ and $p_{n}^{2}$; moreover, we can apply Lemma 18 to get a point $r_{n}$ in $H^{+}\left( S\right) \cap P_{n}$ where the curvature of the plane curve $H^{+}\left( S\right) \cap P_{n}$ is bigger than $\kappa +1.$

• 8. By the convergence $P_{n}\rightarrow P$ and the continuity of the second order derivatives at $\gamma \left( t^{-}\right)$ the plane curve $P\cap H^{+}\left( S\right)$ must have bigger curvature as $\kappa +1$ at $\gamma \left( t^{-}\right)$.

• 9. The ending is the same, since the curve $P\cap H^{+}\left( S\right)$ must have a point x in the interior of $P\cap \left( I^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) ,$ because the boundary $P\cap \partial \left( I^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) =P\cap \partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right)$ has curvature at most $\kappa$ at $\gamma \left( t^{-}\right)$ and we will apply Remark 17. But this would contradict the achronality of $H^{+}\left( S\right)$ since $x,\gamma \left( t^{f}\right) \in H^{+}\left( S\right)$.

Now we prove the above idea step by step. For the sake of simplicity, a suitable subsequence of $q_{n}$ will be also denoted by $q_{n}$.

Since the statement in Theorem 6 is a local property, we will use a suitable local coordinate system. Let $p\in H$ be a point of the horizon and $U\subset M$ an open suitably small neighbourhood of p such that there is smooth diffeomorphism $\varphi :U\rightarrow {\mathbb {B}}^{n}\subset {\mathbb {R}} ^{n}$, like a coordinate chart. We can consider the Lorentz metric on $\varphi \left( U\right) ={\mathbb {B}}^{n}$ defined by $\varphi$. If U was small enough, then the metric is close to a Minkowski metric. This was step 1. Later for step 5 we will need that the neighbourhood U is nice, i.e. there are no conjugate point pairs in it, which can be achieved if U is a geodetically convex neighbourhood here.

Thus, from here on we will assume that we have a Lorentz metric g on ${\mathbb {B}}^{n}$ and a horizon H in $\left( {\mathbb {B}}^{n},g\right)$.

We will assume that U is so small, that for every point $p\in U$ the causal future (resp. past) of p in $\left( U,g|_{U}\right)$ which is denoted by $J^{+}\left( U,p\right)$ (resp. $J^{-}\left( U,p\right)$) is relatively closed in U and their interiors are $I^{+}\left( U,p\right)$ (resp. $I^{-}\left( U,p\right)$).

Step 2 in the proof of the main theorem is to show that every horizon locally coincides with a local part of a Cauchy horizon:

Lemma 9

Let H be a horizon, then for every $p\in H$ there is an open neighbourhood $U_{p}$ and a Cauchy horizon $H^{+}\left( S\right)$ such that $H\cap U_{p}=H^{+}\left( S\right) \cap U_{p}$.

Proof

Remember that by our assumption we must prove that: if we have a Lorentz metric g on${\mathbb {B}}^{n}$ and a horizon H in $\left( {\mathbb {B}}^{n},g\right)$ , then for every $p\in H$ there is an open neighbourhood $U_{p}$ and a Cauchy horizon $H^{+}\left( S\right)$ such that $H\cap U_{p}=H^{+} \left( S\right) \cap U_{p}$.

Now we will choose neighbourhoods $W_{p},~V_{p},~U_{p}$ of p and an affine hyperplane $F\subset {\mathbb {B}}^{n}$ suitably close to p such that the following hold:

• 1. $U_{p}\subset W_{p}\subset V_{p}$

• 2. $F\cap V_{p}$ is space-like

• 3. $\overline{U_{p}}\cap H$ is compact, where $\overline{U_{p}}$ is the closure of $U_{p}$

• 4. for every point $q\in W_{p}$ every causal past directed and inextendable curve from q intersects $F\cap V_{p}$

• 5. $U_{p}\cap F=\emptyset .$

Consider a Lorentz–Minkowski metric $g_{{\mathbb {M}}^{n}}$ on ${\mathbb {B}}^{n}$ such that $g_{{\mathbb {M}}^{n}}$ has wider time-cones at p as the original Lorentz metric g. Then, by continuity, in a small neighbourhood $Z_{p}$ of p at every point $q\in Z_{p}$ the time-cones of $g_{{\mathbb {M}}^{n}}$ will contain the time-cones of g. Now it is trivial to find the above neighbourhoods for $g_{{\mathbb {M}}^{n}}$ in $Z_{p}$ by taking a time-like line through p and points on it $p_{V}^{-}<<p_{W}^{-}<<p_{U}^{-}<<p^{-}<<p<<p_{U}^{+}<<p_{W}^{+}<<p_{V}^{+}$, choosing a smooth affine space-like hyperplane F through $p^{-}$ and taking the diamonds $U_{p}=I^{+}\left( p_{U}^{-}\right) \cap I^{-}\left( p_{U}^{+}\right) ,~V_{p}=I^{+}\left( p_{V}^{-}\right) \cap I^{-}\left( p_{V}^{+}\right) ,~W_{p}=I^{+}\left( p_{W}^{-}\right) \cap I^{-}\left( p_{W}^{+}\right) .$ If all the points were close enough to p then 1.-5. holds for the metric $g_{{\mathbb {M}}^{n}}$. As the time-cones of g are tide as those of $g_{{\mathbb {M}}^{n}}$ 2., 4. are also true for $W_{p} ,~V_{p},~U_{p},~F$ considering the metric g and 1., 3., 5. will be trivially true. Moreover, we can use the Euclidean metric induced by $g_{{\mathbb {M}}^{n}}$ on F later to define the curvature on F.

Note that for every point $q\in \overline{U_{p}}\cap H$ every generator through q also intersects F and the intersection point is in the past of q. Let

$$\begin{aligned} S\overset{def}{=}\cup _{q\in \overline{U_{p}}\cap H}I^{-} \left( q\right) \cap F, \end{aligned}$$

which is an open achronal set in F, thus, we can consider its Cauchy development $D^{+}\left( S\right)$.

First, we show that

$$\begin{aligned} \overline{U_{p}}\cap H\subset \overline{D^{+}\left( S\right) }. \end{aligned}$$

(1)

If $q\in \overline{U_{p}}\cap H$ and $q^{-}\in I^{-}\left( q\right) \cap W_{p}$ then $J^{-}\left( q^{-}\right) \cap F\subset I^{-}\left( q\right) \cap F\subset S$ and by property 4, we have that $q^{-}\in D^{+}\left( S\right)$. As $q^{-}$ can be arbitrarily close to q, we have $q\in \overline{D^{+}\left( S\right) }$.

Let $q\in \overline{U_{p}}\cap H$ and $\gamma _{q}$ a generator through q (there can be more generators through q). Let $f_{\gamma _{q}} \overset{def}{=}F\cap \gamma _{q}$. Note that $\gamma _{q}$ cannot “return” and have more than one intersection point with F, if U in step 1 is small enough. As $f_{\gamma _{q}}\in J^{-}\left( q\right) \cap F=\overline{I^{-}\left( q\right) \cap F}$, we have that $I^{-}\left( q\right) \cap F\subset S$ yields

$$\begin{aligned} f_{\gamma _{q}}\in \overline{S}. \end{aligned}$$

(2)

We show that $f_{\gamma _{q}}\notin S$. Assume on the contrary that $f_{\gamma _{q}}\in S$. Since $\cup _{q\in \overline{U_{p}}\cap H}I^{-}\left( q\right) \cap F$ is an open cover of S in F, there is a $q^{*} \in \overline{U_{p}}\cap H$ for which $f_{\gamma _{q}}\in I^{-}\left( q^{*}\right) .$ But this would contradict the achronality of H since both $q^{*}$ and $f_{\gamma _{q}}\in \gamma _{q}$ are in H. Therefore, $f_{\gamma _{q}}\notin S$ and by (2) we have that

$$\begin{aligned} f_{\gamma _{q}}\in \partial _{F}S \end{aligned}$$

where the boundary is taken with respect to F. We will show that

$$\begin{aligned} q\in \partial D^{+}\left( S\right) . \end{aligned}$$

(3)

This can be proved by contradiction. If $q\notin \partial D^{+}\left( S\right)$ then by (1) we have $q\in intD^{+} \left( S\right)$. Thus, there would be a point $q^{+}\in I^{+}\left( q\right) \cap D^{+}\left( S\right) \cap W_{p}$. Therefore $I^{-}\left( q^{+}\right) \supset J^{-}\left( q\right)$ would hold and imply $\left( I^{-}\left( q^{+}\right) \cap F\right) \supset \left( J^{-}\left( q\right) \cap F\right) \ni f_{\gamma _{q}}$. By property 4. and by the fact that $S\subset F$, we have $f_{\gamma _{q}}\in \left( I^{-}\left( q^{+}\right) \cap F\right) \subset S$, this would contradict that $f_{\gamma _{q}}\notin S$.

Since $\left( \overline{U_{p}}\cap H\right) \cap F=\emptyset$ by property 5., we have that

$$\begin{aligned} U_{p}\cap H\subset \overline{U_{p}}\cap H\subset \partial D^{+}\left( S\right) -\overline{S}=H^{+}\left( S\right) . \end{aligned}$$

Now as both H and $H^{+}\left( S\right)$ are topological hypersurfaces, $U_{p}\cap H\subset H^{+}\left( S\right)$ and $\overline{U_{p}}\cap H$ is compact (i.e. H “leaves” $U_{p})$, the connected component of $H^{+}\left( S\right) \cap U_{p}$ containing p must coincide with $U_{p}\cap H$. If $U_{p}$ is small enough, then by the achronality of $H^{+}\left( S\right)$ there is only one connected component, yielding that $H\cap U_{p}=H^{+}\left( S\right) \cap U_{p}$. $\square$

Steps 3. and 4. are put together in the following remark.

Remark 10

Let $\left( {\mathbb {B}}^{n},g\right)$ be a Lorentz manifold and $V\subset {\mathbb {B}}^{n}$ a small open set. Let $J^{-}\left( x,V\right)$ be the causal past of x in the restricted smaller Lorentz manifold $\left( V,g|_{V}\right)$. Let R be a hyperplane such that $V\cap R$ is space-like and $x\in V$ a point for which $J^{-}\left( x,V\right) \cap R\subset V$ and $J^{-}\left( x,V\right) \cap R\ne \emptyset$. Since R is a hyperplane, it can be identified with ${\mathbb {R}}^{n-1}$. If x is close enough to R then $\partial \left( J^{-}\left( x,V\right) \cap R\right)$ is smooth and diffeomorphic to a sphere. Therefore, if we equip $R={\mathbb {R}} ^{n-1}$ with a standard Euclidean metric³ then at every point $y\in \partial \left( J^{-}\left( x,V\right) \cap R\right) ~$we can take the inward normal vector $n_{y}$. Let $v\in T_{y}\partial \left( J^{-}\left( x,V\right) \cap R\right)$ be a tangent vector at y and K a 2-dimensional plane through y parallel to $n_{y}$ and v, i.e. a normal plane at y in the direction v. The intersection $\partial \left( J^{-}\left( x,V\right) \cap R\right) \cap K$ is a 2-dimensional curve, called normal curve in the direction of v, which has curvature $\kappa \left( y,v\right)$ with respect to the normal vector $n_{y}$ thus $\kappa \left( y,v\right)$ is the normal curvature of $\partial \left( J^{-}\left( x,V\right) \cap R\right)$ in the direction of v with respect to the inward normal direction $n_{y}$.⁴ This curvature depends on the identification $R\approx {\mathbb {R}}^{n-1}$ and the Euclidean metric on ${\mathbb {R}}^{n-1}$. Let

$$\begin{aligned} \kappa _{x,R}^{\max }\left( y\right) \text { and } \kappa _{x,R}^{\min }\left( y\right) \end{aligned}$$

denote the maximum and minimum of the set $\left\{ \kappa \left( y,v\right) | v\in T_{y}\partial \left( J^{-}\left( x,V\right) \cap R\right) \right\}$ of the normal curvatures at y. By the smoothness and the properties of the exponential map it is clear that for every $0<\kappa$, if x is close enough to F then $\kappa <\kappa _{x,R}^{\min }\left( y\right)$ for every $y\in \partial \left( J^{-}\left( x,V\right) \cap R\right)$.

Now we can proceed with the other steps, which will yield the proof of Theorem 6.

Proof of the Main theorem

By Lemma 9 we can assume that we have a Lorentz manifold $\left( {\mathbb {B}}^{n},g\right)$ a space-like hyperplane F in it and a set $S\subset F$ such that $H^{+}\left( S\right)$ locally coincides with our horizon at $\gamma \left( t_{0}\right)$. Thus it is enough to prove the theorem for $H^{+}\left( S\right)$ at $\gamma \left( t_{0}\right)$.

The proof goes by contradiction. The situation is similar to Fig. 1, but ${\mathbb {R}}^{2}$ is replaced by F, the cones, spheres (circles) are not real cones and spheres only smooth manifolds close to them. Assume that $H^{+}\left( S\right)$ is only differentiable at every $\gamma \left( t\right) ,~t\in \left( \alpha ,t_{0}\right)$ and it is at least of class $C^{2}$ at every $\gamma \left( t\right) ,~t\in \left( t_{0},\beta \right)$. Let $\gamma \left( t^{f}\right) ,~\gamma \left( t^{p}\right) ,~\gamma \left( t^{-}\right) \in \gamma \cap H^{+}\left( S\right)$ such that $t^{f}<t^{p}<t_{0}<t^{-}$ and all these points are close enough to $t_{0}$. Moreover, let R be a hyperplane parallel to F which intersects $\gamma$ at $\gamma \left( t^{-}\right)$. We can assume that $\gamma \left( t^{f}\right)$ and R are so close that $J^{-}\left( \gamma \left( t^{f}\right) \right) \cap F$ is a smooth embedded manifold and $\gamma \left( t^{p}\right)$ is “much closer” to R than $\gamma \left( t^{f}\right)$, thus by Remark 10 (steps 3. and 4.) the following hold. Let $\kappa _{\gamma \left( t^{f}\right) ,R}^{\max }\left( \gamma \left( t^{-}\right) \right)$ be the maximal 2-dimensional curvature of $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right)$ in $R\approx {\mathbb {R}}^{n-1}$ at $\gamma \left( t^{-}\right)$ and $\kappa _{\gamma \left( t^{p}\right) .R}^{\min }\left( \gamma \left( t^{-}\right) \right)$ be the minimal 2-dimensional curvature of $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ in $R\approx {\mathbb {R}}^{n-1}$ at $\gamma \left( t^{-}\right) ,$ then

• P1 $\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) ,~\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ are smooth manifolds in $R\approx {\mathbb {R}}^{n-1}$;

• P2 $0<\kappa _{\gamma \left( t^{f}\right) ,R}^{\max }\left( \gamma \left( t^{-}\right) \right)<\kappa<\kappa +1<\kappa _{\gamma \left( t^{p}\right) .R}^{\min }\left( \gamma \left( t^{-}\right) \right)$ for some $\kappa \in {\mathbb {R}}^{+}$;

Since $H^{+}\left( S\right)$ is only differentiable at $\gamma \left( t^{f}\right)$ but not of class $C^{1}$, by Proposition 3, there is a sequence $q_{n}\in H^{+}\left( S\right)$ for which

$$\begin{aligned} q_{n}\rightarrow \gamma \left( t^{p}\right) ,N\left( q_{n}\right) \ge 2. \end{aligned}$$

Thus, there are at least two different past directed generators $\gamma _{n} ^{1},~\gamma _{n}^{2}$ starting at $q_{n}$. It is easy to see that $\gamma _{n}^{i},~i=1,2$ must converge⁵ to $\overrightarrow{\gamma _{p}}\overset{def}{=}\ \gamma |_{\left[ t^{p},\beta \right) }$, e.g. there is subsequence of $\gamma _{n}^{1}$ which locally converges to a past directed light-like geodesic starting at $\gamma \left( t^{p}\right)$ which must lie on $H^{+}\left( S\right)$, but this is unique, as $N\left( \gamma \left( t^{p}\right) \right) =1$. Therefore, if $p_{n}^{i}\overset{def}{=}\gamma _{n}^{i}\cap R$ then

$$\begin{aligned} p_{n}^{1},~p_{n}^{2}\rightarrow \gamma \left( t^{-}\right) \end{aligned}$$

(4)

as well.

Since $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ is smooth in $R\approx {\mathbb {R}}^{n-1}$, let o be a point in the interior of $J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R$ such that the line $\overline{o\gamma \left( t^{-}\right) }$ is normal to $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right) ,$ i.e. o is on the normal line of $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$. As $q_{n}\rightarrow \gamma \left( t^{p}\right)$ we have that

$$\begin{aligned} \partial J^{-}\left( q_{n}\right) \cap R\rightarrow \partial J^{-} \left( \gamma \left( t^{p}\right) \right) \cap R. \end{aligned}$$

(5)

This is the convergence described in step 6, which is proved in Lemma 12.

For step 5 consider the 2-dimensional plane $P_{n}$ spanned by $o,p_{n}^{1},p_{n}^{2}$ which intersects the smooth manifold $\partial \left( J^{-}\left( q_{n}\right) \cap R\right)$ in a smooth curve and $p_{n}^{1},p_{n}^{2}$ are on this curve⁶. By (4) a suitable subsequent of $P_{n}$ will converge to a normal plane P of $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ at $\gamma \left( t^{-}\right)$.

The continuity of the classical 2-dimensional curvatures, the convergence (5) and property P2 yield that $\partial \left( J^{-}\left( q_{n}\right) \cap R\right)$ has 2-dimensional curvatures bigger than $\kappa +1$ everywhere, if n is big enough. Consider the plane curve $\partial \left( J^{-}\left( q_{n}\right) \cap R\right) \cap P_{n}$ and the (shortest) part of it between its points $p_{n}^{1}$ and $p_{n}^{2}$, see Fig. 2, this curve segment will be denoted by $\phi _{n}$. By Lemma 13, we have that the curvature of $\phi _{n}$ is everywhere at least that of the minimal 2-dimensional curvature of $\partial \left( J^{-}\left( q_{n}\right) \cap R\right)$. By property P2 and by the convergence (5) we have that the curvature of $\phi _{n}$ is at least $\kappa +1$ at every point of $\phi _{n}$ if n is big enough. This proved step 6.

Let $\theta _{n}$ be the segment of the curve $\left( H^{+}\left( S\right) \cap R\right) \cap P_{n}$ between its points $p_{n}^{1}$ and $p_{n}^{2}$ which is twice differentiable if n is big enough, because $H^{+}\left( S\right)$ is at least of class $C^{2}$ at $\gamma \left( t^{-}\right)$ and we have (4).

Note that the manifolds $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ and $H^{+}\left( S\right) \cap R=\partial \left( \overline{D^{+}\left( S\right) }\cap R\right)$ are at least of class $C^{1}$ locally at $\gamma \left( t^{-}\right)$ and since $J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\subset \overline{D^{+}\left( S\right) }\cap R$ they are tangent at $\gamma \left( t^{-}\right)$. Since the line $\overline{o\gamma \left( t^{-}\right) }$ is transversal to the manifolds $\partial \left( J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R\right)$ and $H^{+}\left( S\right) \cap R$, the convergence (5) and a simple continuity argument yield that $\theta _{n}$ and $\phi _{n}$ can be considered as function graphs in $P_{n}$ if n is big enough. Therefore, we can apply Lemma 18 in the appendix to prove step 7. Let $r_{n}\in \theta _{n}$ be the point where the formal curvature is at least the minimal curvature of $\phi _{n}$, see Definition 14 in the appendix. Thus, by step 6. we have that the curvature of $\theta _{n}$ at $r_{n}$ is at least $\kappa +1$.

Step 8. Since $H^{+}\left( S\right)$ is at least of class $C^{2}$ at $\gamma \left( t^{-}\right)$ and $P_{n}\rightarrow P$, we have that the formal curvature expressions of the curves $\theta _{n}$ at $r_{n}$ will converge to the curvature of the curve

$$\begin{aligned} \theta \overset{def}{=}\left( H^{+}\left( S\right) \cap R\right) \cap P \end{aligned}$$

at $\gamma \left( t^{-}\right)$. This gives that the formal curvature of $\theta$ at $\gamma \left( t^{-}\right)$ is at least $\kappa +1$.

What remains is step 9. By property P2 we have that the curvature of the curve $\phi \overset{def}{=}\partial \left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) \cap P$ at $\gamma \left( t^{-}\right)$ is at most $\kappa$. Now in the plane P, we can apply Remark 17 to $\theta$ and $\phi$ at $\gamma \left( t^{-}\right)$ to get a point $x\in \theta \subset H^{+}\left( S\right)$ which is “above” $\phi$, i.e. it must lie in the interior⁷ of $\left( J^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) \cap P$ which is $\left( I^{-}\left( \gamma \left( t^{f}\right) \right) \cap R\right) \cap P$, because $U\approx {\mathbb {R}}^{n}$ in step 1. was suitably small. But then x and $\gamma \left( t^{f}\right)$ are chronological related points on the horizon which contradicts the achronality of $H^{+}\left( S\right)$. $\square$

Fig. 2

The convergence of “big curvature” points $r_{n}$ give a horizon point x in $I^{-}(\gamma (t^{f}))$

2.1 Appendix

In the appendix we collect some technical lemmas. Since their proof is straightforward, we omit some calculations. Most of these lemmas are probably common knowledge, as, for example, the next one using transversality and a general form of the inverse function theorem.

Lemma 11

Let $M\subset {\mathbb {R}}^{n}$ be a hypersurface which is at least of class $C^{1}$ in a neighbourhood of $p\in M$ and S is a k-dimensional affine subspace at p where $k<n$. Assume that S is transversal to M at p. Then $M\cap S$ is a $\left( k-1\right)$-dimensional submanifold locally at p which is at least of class $C^{k}$ at p if M was of class $C^{k}$ at p.

Proof

Since S and M are transversal at p, according to their dimensions, we can have a basis $v_{1},\dots ,v_{n}$ of $T_{p}{\mathbb {R}}^{n}$ such that $v_{1},\dots ,v_{k}$ is a basis of $T_{p}S$ and $v_{1}\notin T_{p}M$, $v_{2},\dots ,v_{k}\in T_{p}M\cap T_{p}S$ and $v_{2,}\dots ,v_{n}$ span $T_{p} M$. Using the canonical isomorphism between $T_{p}{\mathbb {R}}^{n}$ and ${\mathbb {R}}^{n}$ we can consider $v_{1},\dots ,v_{n}$ as a basis in ${\mathbb {R}}^{n}$; thus, we can change the coordinate system of ${\mathbb {R}}^{n}$ such that p is the origin and $v_{1},\dots ,v_{n}$ is the basis, this doesn’t change the differential properties of M. In this coordinate system if ${\mathbb {R}}^{n-1}$ is identified with the linear subspace spanned by $v_{2,}\dots ,v_{n}$ the canonical projection $\Pi :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{n-1},~\left( x_{1},x_{2,}\dots ,x_{n}\right) \mapsto \left( 0,x_{2},\dots ,x_{n}\right)$ can be restricted to M. As M is at least of class $C^{1}$ near p (the new origin) and the projection has full rank at p as $v_{1}$ was a transversal direction to M at p,  there is a neighbourhood $U\subset M$ of $p\in M$ such that the restricted projection $\Pi |_{U}:U\rightarrow {\mathbb {R}}^{n-1}$ is injective. So $\Pi |_{U}^{-1}$ is well defined on $\Pi \left( U\right)$ and we can take the reparametrization $\Pi |_{U}^{-1}:{\mathbb {R}}^{n-1}\supset \Pi \left( U\right) \rightarrow U,~\left( 0,x_{2},\dots ,x_{n}\right) \mapsto \left( f\left( x_{2},\dots ,x_{n}\right) ,x_{2},\dots ,x_{n}\right) \in U$ for a unique well defined function $f:\Pi \left( U\right) \rightarrow {\mathbb {R}}$. As it was shown in the appendix of [5], this reparametrization won’t change the differentiability order (where the fact that M is at least of class $C^{1}$ on U was needed). From this we have that the parametrization of the intersection $S\cap U,~\left( 0,x_{2},\dots ,x_{k},0\,,\dots ,0\right) \mapsto \left( f\left( \left( 0,x_{2},\dots ,x_{k},0\,,\dots ,0\right) \right) ,x_{2},\dots ,x_{k},0\,,\dots ,0\right)$ is at least a $C^{1}$ parametrization which is at least of class $C^{k}$ at p. $\square$

Lemma 12

Let $\left( M,g\right)$ be a Lorentz manifold, Y a smooth small neighbourhood of $y\in M$ and $R\subset Y$ a smooth space-like 1-codimensional submanifold below y, i.e. $y\in I^{+}\left( R\right)$, such that $\partial J^{-}\left( y\right) \cap R$ is diffeomorphic to ${\mathbb {S}}^{n-1}$. If $q_{n}\rightarrow y$ is a converging sequence such that $\partial J^{-}\left( q_{n}\right) \cap R$ is diffeomorphic to ${\mathbb {S}}^{n-1}$, then we can identify $\partial J^{-}\left( y\right) \cap R$ and $\partial J^{-}\left( q_{n}\right) \cap R$ for every $q_{n}$ with the same ${\mathbb {S}}^{n-1}$ and restricted the metrics $g_{y}=g|_{\partial J^{-}\left( y\right) \cap R}$, $g_{q_{n} }=g|_{\partial J^{-}\left( q_{n}\right) \cap R}$ can be considered metrics on the same ${\mathbb {S}}^{n-1}$. As $q_{n}\rightarrow y$ the metrics $g_{q_{n} }\rightarrow g_{y}$ also converge.

Proof

Let $Y\subset U$ be a suitably small neighbourhood of y, where U is a geodetically convex neighbourhood of y. (Note, in step 1 the neighbourhood U in the proof of the main theorem was chosen to be geodetically convex.) Then the map

$$\begin{aligned} \Psi :TY\rightarrow Y\times U,~\left( q,v\right) \mapsto \left( q,\exp _{q}\left( v\right) \right) \text { where }q\in Y,~v\in T_{q}Y \end{aligned}$$

will be of full rank, where it is defined (it is not defined on the whole $Y\times TY$), so it is a smooth diffeomorphism between its domain and image. If Y is small enough then it can be considered as a small ball ${\mathbb {B}}^{n}\subset {\mathbb {R}}^{n}$ and $T_{x}Y\simeq {\mathbb {M}}^{n},~\forall x\in Y$ (the later identification goes by constructing orthogonal vector fields on Y, where one is time-like the others space-like). Thus, we have a nice coordinate system $TY\simeq {\mathbb {B}}^{n} \times {\mathbb {M}}^{n}$. As $\Psi$ is a smooth diffeomorphism, the inverse image $\Psi ^{-1}\left( Y\times R\right)$ is a smooth submanifold. Now as the past directed light-cones in the tangent space can be parametrized smoothly by ${\mathbb {S}}^{n-1} \times {\mathbb {R}}\subset {\mathbb {M}}^{n}$ without their tips, and the smooth submanifold ${\mathbb {B}}^{n}\times {\mathbb {S}}^{n-1} \times {\mathbb {R}}$ (the past light-cones without their tips in TY) is a smooth manifold transversal to $\Psi ^{-1}\left( Y\times R\right)$ (since the light-like geodesics are transversal to R). So we get a smooth parametrization of the intersection with ${\mathbb {B}}^{n}\times {\mathbb {S}}^{n-1}\rightarrow \Psi ^{-1}\left( Y\times R\right) \cap \left( {\mathbb {B}}^{n}\times {\mathbb {S}}^{n-1} \times {\mathbb {R}}\right)$ (where we use that for each $q\in Y$ each past directed light-like geodesic intersects R only once). Now taking the image of $\Psi ^{-1}\left( Y\times R\right) \cap \left( {\mathbb {B}}^{n}\times {\mathbb {S}}^{n-1}\times {\mathbb {R}}\right)$ by the smooth diffeomorphism $\Psi$ we get a smooth parametrization of the intersections $\partial J^{-}\left( q\right) \cap R,~q\in Y$ by ${\mathbb {B}}^{n}\times {\mathbb {S}}^{n-1}\rightarrow R,~\left( q,v\right) \mapsto \gamma _{q,v}\cap R$ where $\gamma _{q,v}$ is the past directed light-like geodesic starting at q in the direction v, i.e. $\gamma _{q,v}^{\prime }\left( 0\right) =v$. For every fixed $q\in Y$ the image of $\left\{ q\right\} \times {\mathbb {S}}^{n-1}$ is $\partial J^{-}\left( q\right) \cap R$ which is a Riemannian submanifold in the space-like R, (where we fixed a Riemannian metric on R). So if $q_{n}\rightarrow \gamma \left( t^{p}\right)$, then the Riemannian manifolds $\partial J^{-}\left( q_{n}\right) \cap R\rightarrow \partial J^{-}\left( \gamma \left( t^{p}\right) \right) \cap R$ meaning that the pulled back metric $g_{q_{n}}$ on ${\mathbb {S}}^{n-1}$ converges smoothly to the pulled back metric $g_{\gamma \left( t^{p}\right) }$ on ${\mathbb {S}}^{n-1}$. This yields that the curvatures will also converge. $\square$

Let $M\subset {\mathbb {R}}^{m}$ be a 1-codimensional smooth submanifold $p\in M$, $v\in T_{p}M$, and $n\perp T_{p}M$ a normal vector of M. Let $S\subset M$ be the 2-dimensional affine plane at p parallel to n and v. Consider the curve $\theta \overset{def}{=}M\cap S$ as a plane curve in S. Let

$$\begin{aligned} \kappa \left( v,M,n\right) \end{aligned}$$

denote the signed curvature of $\theta$ with respect to the base v,  n, which is called the normal curvature in the direction of v with respect to n. Note that n shows the direction in which the curves with positive curvature bend.

Lemma 13

Let $M\subset {\mathbb {R}}^{m}$ be a 1-codimensional smooth submanifold and $P\subset {\mathbb {R}}^{n}$ a 2-dimensional affine plane. Assume that $\phi :\left( -1,1\right) \rightarrow M\cap P$ is a smooth parameterization of a small part of the intersection curve $M\cap P$ and $n\perp T_{\phi \left( 0\right) }M$ is a normal vector for which $\kappa \left( \phi ^{\prime }\left( 0\right) ,M,n\right) \ge 0$. Then the signed curvature of $\phi \subset P\approx {\mathbb {R}}^{2}$ as a plane curve at $\phi ^{\prime }\left( 0\right)$ is at least $\kappa \left( \phi ^{\prime }\left( 0\right) ,M,n\right)$, with respect to the basis $\phi ^{\prime }\left( 0\right) ,~n^{p}$ where $n^{p}$ is the orthogonal projection of n to P.

Proof

(Sketch) Consider the 3-dimensional affine subspace $N\subset {\mathbb {R}}^{m}$ spanned by P and the normal direction of M at $\phi \left( 0\right)$. Since N is transversal to M the intersection $N\cap M$ is locally a smooth submanifold which is a smooth 2-dimensional submanifold in $N\approx {\mathbb {R}}^{3}$ at $\phi \left( 0\right)$ and all our curves lie in N. (Note that the Euclidean metric on ${\mathbb {R}}^{3}$ must be the restriction of the Euclidean metric of ${\mathbb {R}}^{m}$ to be able to speak of the “same” curvatures). We can apply the standard Meusnier theorem to $N\cap M$ in $N\approx {\mathbb {R}}^{3}$ for our curves the following way: the normal section curvature defined by n and $\phi ^{\prime }\left( 0\right)$ is $\kappa \left( \phi ^{\prime }\left( 0\right) ,M,n\right)$. The vectors n and $n^{p}$ have angle $0\le \alpha \le \frac{\pi }{2}$. Then since $\phi$ is a curve in the plane P defined by $\phi ^{\prime }\left( 0\right)$ and $n^{p}$, Meusnier theorem yields

$$\begin{aligned} \kappa \left( \phi ^{\prime }\left( 0\right) ,M,n\right) =\cos \alpha \cdot \kappa \left( 0\right) \end{aligned}$$

where $\kappa \left( t\right)$ is the curvature of $\phi \left( t\right)$. This yields $0\le \kappa \left( \phi ^{\prime }\left( 0\right) ,M,n\right) \le \kappa \left( 0\right)$. $\square$

The curvature of a plane curve is usually defined for $C^{2}$ curves, however we need it for $C^{1}$ curves which second derivatives exist everywhere, but it is not necessarily continuous. But we can define a formal signed curvature also for such curves which has the same geometric properties as the standard one. For the sake of simplicity we will use function graphs.

Definition 14

Let $f:I\rightarrow {\mathbb {R}}$ be a function on the interval I which is twice differentiable at every point of I. The formal curvature of the function graph at $t_{0}\in I$ is

$$\begin{aligned} \kappa _{f}\left( t_{0}\right) \overset{def}{=}\frac{f^{\prime \prime }\left( t_{0}\right) }{\left( 1+f^{\prime }\left( t_{0}\right) ^{2}\right) ^{3/2}}. \end{aligned}$$

The above definition is the usual one, but note that $\kappa \left( t\right)$ is not necessarily continuous. There is a geometric interpretation of the curvature in the $C^{2}$ case which works also in this weaker case.

Definition 15

Let $f:I\rightarrow {\mathbb {R}}$ be a function on the interval I which is twice differentiable at every point of I. Let $r\left( t_{0},t\right)$ be the signed radius of the circle which is tangent to the function graph at $t_{0}$ and contains the point $\left( t,f\left( t\right) \right)$ where the sign is $+$ if the centre of the circle is in the direction $\left( -f^{\prime }\left( t_{0}\right) ,1\right)$ from $\left( t_{0},f\left( t_{0}\right) \right)$, see Fig. 3.

Lemma 16

Let $f:I\rightarrow {\mathbb {R}}$ be a function on the interval I which is twice differentiable at every point of I. Then

$$\begin{aligned} \lim _{t\rightarrow t_{0}}\frac{1}{r\left( t_{0},t\right) }=\kappa _{f}\left( t_{0}\right) \,\ \forall t_{0}\in I. \end{aligned}$$

Thus the limit exists and is equal to the formal curvature.

Proof

By standard geometrical methods indicated on Fig. 3, we can calculate

$$\begin{aligned} r\left( t_{0},t\right) =\frac{2\left\langle \left( -f^{\prime }\left( t_{0}\right) ,1\right) ,\left( \left( t-t_{0}\right) ,\left( f\left( t\right) -f\left( t_{0}\right) \right) \right) \right\rangle \frac{1}{\sqrt{1+f^{\prime }\left( t_{0}\right) ^{2}}}}{\left( t-t_{0}\right) ^{2}+\left( f\left( t\right) -f\left( t_{0}\right) \right) ^{2}}, \end{aligned}$$

where $\left\langle .,.\right\rangle$ is the usual inner product. Since the L’Hospital rule can be applied twice to $\lim _{t\rightarrow t_{0}}\frac{1}{r\left( t_{0},t\right) }$ a standard calculation shows, that the limit exists and is equal to $\kappa _{f}\left( t_{0}\right)$. $\square$

Fig. 3

Left side: the circle in Definition 15 and the signs; Right side: the situation in Remark 17

Now if two function graphs are tangent at some point, the above geometric interpretation of the curvature yields:

Remark 17

Let $f,~g:I\rightarrow {\mathbb {R}}$ be functions on the interval I which are twice differentiable at every point of I and tangent at $t_{0}\in I$. If $\kappa _{f}\left( t_{0}\right) <\kappa _{g}\left( t_{0}\right)$ then there is a $t^{*}\in I$ close enough to $t_{0}$ for which $f\left( t^{*}\right) <g\left( t^{*}\right)$, see Fig. 3.

Lemma 18

Let $f,~g:\left[ \alpha ,\beta \right] \rightarrow {\mathbb {R}}$ be functions which are twice differentiable at every point of $\left[ \alpha ,\beta \right]$ and their function graphs are tangent at $\alpha$ and $\beta$. Assume that $g\left( t\right) \le f\left( t\right) ,~\forall t\in \left[ \alpha ,\beta \right]$. Then there is a $t^{*} \in \left[ \alpha ,\beta \right]$ for which $\min _{t\in \left[ \alpha ,\beta \right] }\kappa _{f}\left( t\right) \le \kappa _{g}\left( t^{*}\right)$.

Proof

Let $0<C$ be the biggest value for which the function graphs of $f-C$ and g have a common point. At this point the graphs must be tangent. Let $t^{*}$ be the parameter at which they are tangent. Since $f\left( t\right) -C\le g\left( t\right)$ locally at $t^{*}$, we must have $\kappa _{f}\left( t^{*}\right) =\kappa _{f-C}\left( t^{*}\right) \le \kappa _{g}\left( t^{*}\right)$ by Remark 17. $\square$