Abstract
The goal of this paper is to make first steps towards the quantisation of integrable nonlinear sigma models using the formalism of affine Gaudin models, by approaching these theories through their conformal limits. We focus mostly on the example of the Klimčík model, which is a two-parameter deformation of the principal chiral model on a Lie group G. We show that the UV fixed point of this theory is described classically by two decoupled chiral affine Gaudin models, encoding its left- and right-moving degrees of freedom, and give a detailed analysis of the chiral and integrable structures of these models. Their quantisation is then explored within the framework of Feigin and Frenkel. We study the quantum local integrals of motion using the formalism of quantised affine Gaudin models and show agreement of the first two integrals with known results in the literature for \(G=\textrm{SU}(2)\). Evidence is given for the existence of a monodromy matrix satisfying the Yang–Baxter algebra for this model, thus paving the way for the quantisation of the non-local integrals of motion. We conclude with various perspectives, including on generalisations of this programme to a larger class of integrable sigma models and applications of the ODE/IQFT correspondence to the description of their quantum spectrum.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Integrable NLSMs and Their Quantisation The integrable nonlinear sigma models (NLSMs) in two space-time dimensions have attracted a lot of attention since several decades. One motivation originated from the observation that the \(\textrm{O}(N)\) symmetric sigma models exhibit quantum phenomena resembling certain features of quantum chromodynamics, e.g. asymptotic freedom in the ultraviolet (UV) and a dynamically generated mass gap [1]. Several subsequent developments have renewed the interest in NLSMs. A major source of motivation for their study is the perturbative approach to string theory. Moreover, important aspects of the AdS/CFT correspondence can be approached by studying NLSMs with targets being anti-de Sitter spaces (see, e.g. the review [2]). NLSMs furthermore offer opportunities to study profound quantum duality phenomena such as the weak/strong coupling dualities between certain sigma models and theories with Toda-like interactions [3, 4].Footnote 1
Some NLSMs are known to be integrable on the classical level, and a lot of evidence has been accumulated for the conjecture that the classical integrability of many of these models survives quantisation. However, a first-principle approach to the quantisation of the NLSMs demonstrating their integrability does not seem to be available yet. For other classes of integrable QFTs, a lot of progress was achieved by applying the quantum inverse scattering method [6]. It is based on the construction of quantum monodromy matrices depending on a spectral parameter and satisfying exchange relations of the R-matrix form. These relations ensure the commutativity of traces of the monodromy matrices and thus the existence of an infinite number of integrals of motion (IMs) in the quantum theory. Moreover, they allow the application of powerful techniques such as the algebraic Bethe ansatz and lattice regularisation for the diagonalisation of these IMs.
In the case of NLSMs, the quantum inverse scattering method faces serious difficulties known as the non-ultralocality problem, which arise from the presence of ambiguities in the Poisson bracket of the monodromy matrices [7, 8]. From this point of view, it is thus currently not well understood how to quantise these matrices and how to use them for the definition of IMs in the quantised integrable NLSMs.
For a few NLSMs, there nevertheless exist precise conjectures about the finite-volume spectra which have been carefully checked in great detail. One of the existing approaches to the study of integrable NLSMs uses the S-matrix bootstrap as a starting point. Based on certain plausible assumptions, one can use the factorised S-matrix as the basis for the thermodynamic Bethe ansatz giving information on the spectrum of some NLSMs in finite volume; see e.g. [9] for an application of this method to the \(\textrm{O}(4)\) sigma model. By combining this approach with other methods, significant results have been obtained in particular for a deformation of the \(\textrm{O}(3)\) sigma model known as the sausage model [5, 10, 11]. A sophisticated blend of several techniques has led to the exact results presented in [12,13,14] on the finite-volume spectrum of a NLSM first introduced by Fateev in [4] and which can be regarded as a two-parameter deformation of the \(\textrm{SU}(2)\) principal chiral model.Footnote 2 These results strongly support the hope that an integrable quantisation exists for all points in the parameter spaces of these NLSMs.
Integrable Structure of Conformal Limits In the search for possible starting points for a more direct approach to the quantisation of integrable NLSMs, one should distinguish between different limits in their parameter spaces. The most natural one may seem to be the classical limit, which is the starting point of many of the traditional approaches to the quantisation of NLSMs. As mentioned above, one may generically expect to encounter severe difficulties related to the non-ultralocality problem in these approaches.
A second type of limit sends the couplings of the model to their values at an RG fixed point. In fortunate circumstances, the resulting theory becomes a non-trivial CFT. One can then exploit the constraints of conformal symmetry and/or integrability to get detailed information on these conformal sigma models. This offers an alternative approach to the investigation of non-conformal NLSMs based on the expansion around the conformal loci. One might hope that the interplay of conformal and integrable structures could provide the basis of powerful techniques for the investigation of quantum integrable sigma models.
The investigation of integrable QFTs with the help of the integrable structures of their conformal limits was initiated in [15]. One of the hallmarks of two-dimensional conformal invariance is the presence of chiral degrees of freedom in the theory. For instance, a CFT in general possesses local chiral currents \(\lbrace {\textsf{W}}^{(\mathrm L)}_s \rbrace \) and \(\lbrace {\textsf{W}}^{(\mathrm R)}_s \rbrace \), labelled in particular by an integer s characterising their respective Lorentz spins \(+s\) and \(-s\). The notations \((\mathrm L)\) and \((\mathrm R)\) used here indicate that \({\textsf{W}}^{(\mathrm L)}_s\) and \({\textsf{W}}^{(\mathrm R)}_s\) are, respectively, left- and right-moving fields, i.e. they satisfy
These sets of chiral fields contain in particular the spin \(\pm 2\) components \({\textsf{W}}^{(\mathrm L)}_2\) and \({\textsf{W}}^{(\mathrm R)}_2\) of the stress–energy tensor. Moreover, the modes of the chiral currents \(\lbrace {\textsf{W}}^{(\mathrm L)}_s \rbrace \) and \(\lbrace {\textsf{W}}^{(\mathrm R)}_s \rbrace \) generate two independent operator algebras, called \({\mathcal {W}}\)-algebras, whose commutation relations are encoded in the operator product expansions of the currents. They define the algebra of extended conformal symmetry of the theory. In particular, the space of states can be represented as a direct sum of irreducible representations of these \({\mathcal {W}}\)-algebras:
Apart from the conformal structure, the CFT can also have an integrable structure described by infinite families of operators acting on each representation \(V^{(\mathrm L)}\) or \(V^{(\mathrm R)}\) that mutually commute. These operators can take the form of both local and non-local IMs, built from the chiral fields of the CFT [16,17,18]. For instance, the local IMs are given by
where \({\textsf{F}}^{(\mathrm L)}_{s+1}\) are specific tensor densities built from the left-moving currents \({\textsf{W}}^{(\mathrm L)}_r\) and their derivatives, while the limits in the integration reflect the fact that we are considering the theory on the space-time cylinder with the space coordinate taking values in the standard segment \(x\in [0,2\pi )\). A similar set \({\textsf{Q}}^{(\mathrm R)}_s\) acts on the second tensor factors in (1.2). There is evidence that these IMs can admit deformations describing the integrable structure of certain massive perturbations of these CFTs, suggesting that the integrable structure of CFTs can offer a useful starting point for the investigation of the integrable structures of their massive deformations.
The construction and simultaneous diagonalisation of commuting families of local and non-local IMs in a CFT is a well-defined mathematical problem in the representation theory of the chiral algebras, which is, however, hard to solve in general. In various cases, there nonetheless exists a systematic construction of local IMs, which characterises them as the observables commuting with specific operators called screening charges [19,20,21,22]. Moreover, non-local IMs can be built in certain examples with the use of monodromy matrices satisfying quantum exchange relations [16,17,18].
ODE/IQFT Correspondence One of the most powerful instruments for the mathematical description of the spectrum of the integrable structures of CFTs is known as the ODE/IQFT correspondence [23,24,25]. This conjectural duality reduces the problem of calculating the eigenvalues of the local and non-local IMs in an integrable CFT to a problem in classical analysis. The simultaneous eigenstates in a representation \(V^{(\textrm{L,R})}\) are in one-to-one correspondence with a class of ordinary differential equations specified by their monodromy properties. The corresponding eigenvalues of the IMs are encoded in the connection coefficients of these ODEs. A prototype of this scenario is the quantum KdV integrable structure, where the ODE is the Schrödinger equation with “monster” potential [23,24,25] (see also [26, 27] for recent results). Other examples have been found and studied extensively in the literature; see the review papers [28, 29] and references therein.
There are a few cases where there exists highly non-trivial evidence for the applicability of the ODE/IQFT correspondence to the conformal limits of NLSMs, namely the UV fixed points of the sausage [11, 30, 31] and Fateev [12,13,14] models in different regimes of the parameters. A particularly striking result of those papers is the existence of a deformation of this description replacing the ODEs by closely related PDEs encoding the finite volume spectrum of the sigma models even away from the conformal limit. This indicates that such a description is not just a peculiarity of the conformal points. However, for more general NLSMs no such descriptions seem to be available yet.
Affine Gaudin Models The ubiquitous appearance of Lie-theoretic structures in the theory of integrable models may offer guidance in the search for a more general framework. In [32], Feigin and Frenkel proposed an ambitious conjecture stating that the ODE/IQFT correspondence covers a large multiparametric class of integrable structures defined in terms of an affine Lie algebra \(\widehat{{\mathfrak {g}}}\). The theories in this class are called affine Gaudin models (AGMs).Footnote 3 In the simplest setting, such a model is built out of N Kac–Moody currents whose modes satisfy the commutation relations of N independent copies of the affine algebra \(\widehat{{\mathfrak {g}}}\) at levels \(\lbrace k_j \rbrace _{j=1}^N\). These copies are attached to points \(\lbrace z_j \rbrace _{j=1}^N \subset \mathbb{C}\mathbb{P}^1\) on the Riemann sphere, called punctures, which are considered to be parameters of the theory. It was conjectured in [32] that AGMs possess an integrable structure, formed by local and non-local commuting IMs built from the Kac–Moody currents and depending on the punctures \(z_j\). Various motivations and checks of this conjecture were presented in that paper. These included the construction of some of these commuting operators, e.g. the first non-local IMs extracted from the expansion of the monodromy matrix as well as local charges quadratic in the Kac–Moody currents. The search for a more systematic construction of higher-degree local IMs was further developed in [34, 35], where more precise conjectures on the form of these operators were formulated and additional examples were explicitly constructed.Footnote 4
It is conjectured in [32] that the eigenvalues of the IMs of AGMs are encoded in certain differential operators called affine opers, which are associated with the Langlands dual affine Lie algebra \({}^{\textrm{L}}\widehat{{\mathfrak {g}}}\). One of the main proposals of [32] is then that these differential operators correspond to the ODEs appearing in the ODE/IQFT correspondence. This conjecture, which relies on an analogy with the case of Gaudin models based on finite-dimensional simple Lie algebras [37,38,39], has first been checked when the Gaudin model becomes equivalent to quantum KdV [32]. Further checks were performed in [40] for higher-rank KdV-type integrable structures, building on the extraction of so-called \(Q{\widetilde{Q}}\) systems from affine opers in refs. [41, 42] as well as the explicit analysis of the \(\widehat{\mathfrak {sl}}(3)\) case from Ref. [43]. The results of the previously mentioned works [34, 35] where the local IMs are systematically studied and refs. [44, 45] on the Kondo problems also give evidence for the conjecture. In the recent paper [46], restricting to the \(\widehat{\mathfrak {sl}}(2)\) case, a generalisation of the AGM is introduced and ODEs describing the spectra of these models are proposed, supported by numerical and analytic verifications.
The proposal of Ref. [32] has furthermore inspired the identification of a large class of relativistic two-dimensional integrable field theories containing most of the known classically integrable NLSMs [47,48,49], driven in part by the appealing possibility [47] of deriving a (massive) ODE/IQFT correspondence for these models. The definition of these field theories, in the following called relativistic AGMs,Footnote 5 uses the classical version (or generalisations thereof) of the set-up described in the work of Feigin and Frenkel as a starting point. While the kinematical basis for the definition of relativistic AGMs is essentially identical to the classical limit of the set-up used in [32], one needs to introduce additional structure in order to define models having an interpretation as relativistic field theories on a two-dimensional space-time. Key ingredients are, in particular, the Hamiltonian and momentum observables, or equivalently the light-cone Hamiltonians. The construction of relativistic AGMs described in [47,48,49] furthermore uses realisations of the Poisson current algebras appearing in the framework of Feigin and Frenkel in terms of the Cauchy data on equal time slices of the fundamental fields of NLSMs.
Quantisation of Relativistic AGMs in Their Conformal Limits Our intention is to make first steps towards a systematic approach to the quantisation of integrable NLSMs through their interpretation as relativistic AGMs. Ambitious questions one may wish to address in this context are, in general:
-
(a)
Does there exist a quantisation of the relativistic two-dimensional AGMs preserving their integrability?
-
(b)
Is it possible to apply the ODE/IQFT correspondence from [32], or some massive generalisation thereof, in order to describe the spectra of these quantised models?
Loosely speaking, our approach amounts to entering the space of quantised relativistic AGMs through the side entrance provided by their conformal limits, for which we will gather some evidences that the answers to the questions (a) and (b) above are positive. We will therefore mostly restrict attention to the loci in the parameter spaces of these models representing fixed points of the RG flow. Our expectation is that, at these fixed points, the classical integrable structure of the relativistic theory decouples into two separate integrable structures built from left- and right-moving degrees of freedom, respectively. These integrable structures of left- and right-movers are moreover described by two decoupled AGMs, which we will refer to as chiral AGMs. We expect the latter to be quantisable in the sense of Feigin and Frenkel [32], which would thus provide a general framework for the study of conformal limits of integrable NLSMs and their ODE/IQFT correspondence. In contrast, for the relativistic AGMs outside of the conformal loci, new qualitative features seem to be required to develop an extension of this scheme, including the treatment of renormalisation of the parameters and of the dynamical generation of a mass. However, we think that understanding the quantisation of the chiral AGMs can offer a useful starting point for the study of these massive cases, for instance through conformal perturbation techniques.
A Case Study In this paper, we will mostly restrict our attention to the conformal limit of a particular example of relativistic AGM introduced in [50, 51] that we will refer to as the Klimčík model. (It is sometimes also called the Bi–Yang–Baxter sigma model in the literature.) It is a two-parameter deformation of the principal chiral model on a Lie group G, which coincides with the Fateev model in the case \(G=\textrm{SU}(2)\), as shown in [52]. This theory provides a good example where the general programme sketched above may be realised, as it exhibits all of its key features while being reasonably simple and well studied in the literature. In particular, the quantisation of this model has been explored in the works [4, 12,13,14, 53] for the case \(G=\textrm{SU}(2)\), hence providing useful checks of the results obtained from the AGM formalism and a fruitful exchange of ideas and techniques between these frameworks.
The relation between the descriptions of the integrable structure of this model provided by the formulation as AGM to the more traditional formulations used in the existing literature turns out to be non-obvious. The basic reason is the use of a gauge symmetry in the formulation of the model of interest as AGM, which is a general feature shared by a large class of AGMs. As observed in many other contexts, the use of a gauge symmetry may allow one to exhibit some aspects of a quantum theory more transparently, while other aspects can be more easily understood in gauge-fixed representations. A similar situation will be found here. While there is a powerful algorithm for the construction of local conserved charges in quantised AGMs, it will turn out that a specific gauge fixing is helpful to employ the results of [53] giving evidence for existence of Yang–Baxter algebraic structure simplifying the construction of non-local conserved quantities considerably. In order to utilise the AGMs as a general framework for the quantisation of certain classes of integrable sigma models, one may expect that it will be important to understand the relation between gauged and gauge-fixed formulations in some detail. This is going to be an important part of what is done in this work.
Outline Let us finally give the outline of the paper, summarising its main results along the way.
In Sect. 2, we review the definition and properties of the classical Klimčík NLSM on an arbitrary Lie group G [50, 51]. This model can be formulated as a theory on \(G\!\times \! G\) with a gauge symmetry by the diagonal subgroup \(G_{\text {diag}}\), following [54]. In particular, we describe the Lax connection underlying the integrability of this model and discuss both its Lagrangian and Hamiltonian formulations.
The first part of Sect. 3 is devoted to the construction of classical relativistic AGMs and mainly consists of a review of [47,48,49]. In particular, we recall the definition of the Hamiltonian, the integrable structure and the Lax connection of these theories. The second part concerns the interpretation of the gauged formulation of the Klimčík NLSM on \(G \! \times \! G / G_{\text {diag}}\) as a relativistic AGM with 4 punctures, based on [47, 55].
In Sect. 4, we initiate the analysis of the conformal limit of the Klimčík model on the group \(\textrm{SU}(2)\), mostly following [53]. We start with a review of the RG flow of this theory [56]. It turns out that in the IR the model becomes strongly coupled, while in the UV the one-loop RG flow equations possess a non-trivial fixed point. A detailed description of the target space in the UV limit of the sigma model is given. Moreover, we discuss the same limit for the Lax connection and describe how its classical integrable structure splits into two decoupled ones, built from left- and right-moving fields, respectively. In particular, we present several convenient choices of gauge for the Lax connection, which are expressed in terms of non-local chiral fields of the model in the UV limit, such as the (classical) parafermions.
We continue the classical analysis of this UV limit in Sect. 5, now focussing on the local conformal and integrable structures. For instance, we describe the \({\mathcal {W}}\)-algebra underlying the theory, i.e. the Poisson algebra formed by its left- or right-moving local currents, as well as a non-trivial relevant subalgebra thereof, called the corner-brane \({\mathcal {W}}\)-algebra. Moreover, we discuss the classical local IMs of the model, which take the form of integrals of particular local chiral densities in this corner-brane \({\mathcal {W}}\)-algebra. Finally, we discuss the characterisation of these \({\mathcal {W}}\)-algebras and local IMs as (Poisson) commutants of specific sets of classical screening charges. Although the classical local IMs of the model turn out to be very simple, this section will serve as a useful warm-up for a subsequent description of quantum local IMs, which are quite less trivial but admit a similar characterisation in terms of quantum screening charges.
The goal of Sect. 6 is to discuss the conformal limit of the Klimčík NLSM from the point of view of AGMs. In particular, we argue in this section that the relativistic AGM with 4 punctures underlying the non-conformal model splits in the UV limit into two decoupled AGMs with 3 punctures, describing, respectively, the left- and right-moving degrees of freedom of the theory. We formalise this phenomenon by introducing the notion of chiral AGMs, in contrast with the relativistic AGMs describing the non-conformal theories. Moreover, we show that various well-chosen gauge fixings of these chiral AGMs give rise to the different chiral Lax connections described in Sect. 4 in terms of parafermionic or screening currents. In particular, the use of AGMs in this context allows the construction of generalisations of these current algebras for higher-rank Lie groups G. Finally, we discuss the \({\mathcal {W}}\)-algebra and local IMs of the model from the point of view of AGMs. Remarkably, we show that this formalism provides a systematic and efficient construction of chiral local currents of the model. The latter form a \(\widehat{{\mathfrak {g}}} \oplus \widehat{{\mathfrak {g}}} / \widehat{{\mathfrak {g}}}\) coset \({\mathcal {W}}\)-algebra, which coincides with the corner-brane algebra of Sect. 5 in the case \(G=\textrm{SU}(2)\).
Starting from Sect. 7, we explore the quantisation of the UV fixed point of the Klimčík model. For instance, Sect. 7 discusses the quantisation of the non-local IMs of this theory. As mentioned earlier, this question is made difficult by the problem of non-ultralocality. However, an observation made in [53] indicates that the existence of a quantum Yang–Baxter algebra can be consistent with having non-ultralocal Poisson brackets on the classical level. More precisely, evidence was given that there exists a quantum monodromy matrix satisfying quantum exchange relations, whose classical limit is a path-ordered exponent over a Lax matrix with a non-ultralocal Poisson bracket. It was shown that this Lax matrix coincides with the one of the Fateev NLSM (\(\textrm{SU}(2)\) Klimčík model) in the conformal limit and in a certain gauge. This means that non-ultralocality may emerge as the result of subtleties in the classical limits of fairly conventional algebraic structures underlying the integrability of many integrable models. We review the results of Ref. [53] in Sect. 7 and explain how it would generalise to higher-rank groups.
Section 8 concerns the study of the quantum \({\mathcal {W}}\)-algebra and local IMs for the case \(G=\textrm{SU}(2)\), which can be characterised by their commutativity with quantum screening charges that are described in the previous section. In particular, we use this approach to describe the first few currents of the \({\mathcal {W}}\)-algebra, its corner-brane subalgebra and the first two local IMs in the quantum Fateev integrable structure.
Section 9 is devoted to the quantisation of the chiral AGMs underlying the UV limit of the Klimčík model, in the framework of Feigin and Frenkel [32]. After recalling some generalities about quantised AGMs, we discuss the quantum \(\widehat{{\mathfrak {g}}} \oplus \widehat{{\mathfrak {g}}} / \widehat{{\mathfrak {g}}}\) coset \({\mathcal {W}}\)-algebra appearing in the theory, focussing mostly on the \(\textrm{SU}(2)\) case for simplicity. Moreover, the (conjectural) construction of an infinite hierarchy of quantum local IMs in this \({\mathcal {W}}\)-algebra is sketched following the proposal of [34, 35] and the first higher-spin charge in this hierarchy is explicitly constructed in the case \(G=\textrm{SU}(2)\). In particular, it is shown that this local IM coincides with the one found in Sect. 8 from screening charges, providing strong support to the proposal that the AGM under consideration describes the quantum Fateev integrable structure.
The paper finishes with the discussion of some perspectives in Sect. 10. The main part concerns the ODE/IQFT correspondence for the conformal model studied in the paper. In particular, it is observed that the differential equation on the ODE side of the ODE/IQFT correspondence conjectured in [12, 13] for the Fateev model in the conformal limit is correctly predicted by the Feigin–Frenkel scheme. This result suggests that this scheme can be used to derive the ODE/IQFT correspondence for the Klimčík model on an arbitrary Lie group. In another part of Sect. 10, we argue that the quantisation programme illustrated here on the example of the Klimčík model should apply to a quite more general class of integrable NLSMs/relativistic AGMs, including for instance models possessing more punctures. In particular, we provide evidence that the conformal limits of these more general models should also be described by decoupled chiral AGMs corresponding to left- and right-moving degrees of freedom. This discussion builds on general results in the literature concerning the light-cone structure of relativistic AGMs [48, 49] and their RG flow [57, 58].
2 The Klimčík Model
2.1 Lagrangian Description
In the work [50], Klimčík introduced a model (sometimes referred to as the Bi–Yang–Baxter sigma model) which is a two-parameter deformation of the principal chiral model on a semi-simple Lie group G. He further proved that this field theory is classically integrable in Ref. [51]. As was shown in [52], when G is taken to be \(\textrm{SU}(2)\), the NLSM coincides with the Fateev sigma model introduced in Ref. [4]. A lot of the technical aspects of the paper concern the \(\textrm{SU}(2)\) case. However, the Lagrangian and Hamiltonian formulations of the theory as well as its Lax connection can be described in a uniform way that does not depend on the particular choice of the Lie group G.
Standard Formulation The configuration space of the Klimčík model is the set of G-valued fields g(t, x). The deformation is achieved by means of the so-called Yang–Baxter operator \({\hat{R}}\), a linear operator acting on the Lie algebra \({\mathfrak {g}}\) that must obey the modified classical Yang–Baxter equation. The latter has many solutions, and different choices of \({\hat{R}}\) generically lead to different classical field theories. We use the standard Drinfel’d-Jimbo R-matrix, which is defined via the Cartan-Weyl decomposition of the complexified Lie algebra \({\mathfrak {g}}^{{\mathbb C}}={\mathfrak {n}}_+\oplus {\mathfrak {h}}\oplus {\mathfrak {n}}_-\). (Here, \({\mathfrak {h}}\) and \({\mathfrak {n}}_\pm \) stand for the Cartan and nilpotent subalgebras, respectively.) Namely,
The action of the Klimčík model, with deformation parameters \(\alpha \) and \(\beta \) as in Ref. [51] and an overall constant prefactor K, reads
By the angular brackets \(\langle \cdot ,\cdot \rangle \) we mean the non-degenerate symmetric form for the semi-simple Lie algebra \({\mathfrak {g}}\), whileFootnote 6
Also, the light-cone derivatives \(\partial _\pm =\frac{1}{2}\,(\partial _t\pm \partial _x)\) are being used.
In the discussion of reality conditions for the target space background, the parameters \(\alpha \) and \(\beta \) controlling the deformation are sometimes assumed to be real numbers. Contrary to this, we will work in the regime with \(\alpha ,\,\beta \) pure imaginary, such that
The action (2.2) describes the propagation of a (1+1)-dimensional field in a Riemannian manifold with non-trivial torsion potential. In the parametric domain (2.4) the metric tensor is real, while the components of the B-field are pure imaginary. Note that for the \(\textrm{SU}(2)\) case the B-field term in the Lagrangian is a total derivative and can be ignored.
Gauged Formulation Important for this work is another formulation of the Klimčík model that was first considered in Ref. [54]. The theory is treated as a coset NLSM on \(G\times G\) gauged by the diagonal subgroup. Practically speaking, one writes \(g=g_1\,g_2^{-1}\) and takes both \(g_1\) and \(g_2\) to be independent fields. This effectively doubles the degrees of freedom. However, there is a redundancy in the description since the gauge transformation
with h an arbitrary G-valued field, leaves the action (2.2) unchanged. The gauge-dependent fields \(g_1\) and \(g_2\) provide one with extra freedom that allows the deformations governed by \(\varepsilon _1\) and \(\varepsilon _2\) to be treated in a symmetric way. For instance, via a simple rearrangement of terms, the classical action (2.2) with \(g=g_1g_2^{-1}\) can be expressed as
This “gauged” formulation of the theory turns out to be important for making connection with classical affine Gaudin models.
Lax Connection The existence of an infinite number of conserved quantities for a classical field theory follows from the zero-curvature representation for the Euler–Lagrange equations:
where \(z\in \mathbb{C}\mathbb{P}^1\) denotes the spectral parameter. To write the explicit form of the Lax connection of the Klimčík model, it is useful to introduce the currents
One then has
with
while the constant \(\xi \) is defined through the relation
The Lax connection is not invariant with respect to the gauge transformation (2.5). Instead, one can easily check that
The above formula requires some comment. In any integrable field theory, the Lax connection is not unique, but is defined up to a conjugation \( {\varvec{\Omega }}^{-1}\,(\partial _\mu + {\mathcal {L}}_\mu )\, {\varvec{\Omega }}\). The specific integrable field theory that we are considering here additionally possesses a gauge symmetry, i.e. a local transformation of the fields that preserves the action of the model. Formula (2.12) shows that the gauge symmetry acts on the Lax connection via conjugation. The equations of motion of the model are equivalent to the zero-curvature representation (2.7). The latter is unchanged under conjugation of \(\partial _\mu + {\mathcal {L}}_\mu \) so that the equations of motion are gauge invariant, as expected. Moreover, it is a standard result in integrable field theories that the integrals of motion extracted from \(\varvec{\Omega }^{-1}(\partial _\mu +{\mathcal {L}}_\mu )\,\varvec{\Omega }\) do not depend on \(\varvec{\Omega }\), thus ensuring in the present case that they are also gauge invariant.
The zero-curvature representation for the equations of motion of the Klimčík model was initially found in Ref. [51]. The corresponding Lax connection is related to the one considered above by
It is straightforward to check that \({\mathcal {L}}_\mu ^{(\textrm{inv})}\) only depends on the combination \(g=g_1g_2^{-1}\) and hence is gauge invariant. Note that for \(G=\textrm{SU}(2)\) the Lax connection turns out to be equivalent to the one obtained in the earlier paper [59] specialised to the Fateev model (see “Appendix B” of Ref. [53] for details).
2.2 Hamiltonian Description
Phase Space The phase space of a sigma model defined on a group manifold G consists of canonical fields valued in the cotangent bundle \(T^*G\). The cotangent space \(T^*_p G\) at any point \(p\in G\) can be naturally identified, through the translation by \(p^{-1}\), with the cotangent space \(T^*_{\text {Id}} G\) at the identity. The latter is by construction the dual \({\mathfrak {g}}^*\) of the Lie algebra \({\mathfrak {g}}\). This then defines a natural trivialisation \(T^*G \simeq G \times {\mathfrak {g}}^*\) of the cotangent bundle. Moreover, the non-degenerate bilinear form \(\langle \cdot ,\cdot \rangle \) provides us with a canonical identification of \({\mathfrak {g}}\) and \({\mathfrak {g}}^*\), yielding an isomorphism \(T^*G \simeq G \times {\mathfrak {g}}\). The phase space of canonical fields on \(T^*G\) can thus be described by a G-valued field g(x) as well as a \({\mathfrak {g}}\)-valued field X(x), which plays the rôle of the canonical momentum. Since the Klimčík model is being viewed here as a coset NLSM on \(G\times G\), two copies \((g_j(x), X_j(x))\), \(j\in \lbrace 1,2 \rbrace \), of these fields are required. Using the standard tensorial notations, the canonical Poisson bracket can be expressed as
with \({{\textsf{C}}}_{2}\) being the quadratic Casimir. We take a moment to explain how the invariant notations look like in a particular basis \(\{\texttt{t}_a\}\in {\mathfrak {g}}\), with \([\texttt{t}_a,\texttt{t}_b]={f_{ab}}^c\,\texttt{t}_c\). We denote by \(\{\texttt{t}^a\}\in {\mathfrak {g}}\) the dual basis with respect to the non-degenerate bilinear form \(\langle \cdot ,\cdot \rangle \), defined by \(\langle \texttt{t}^a, \texttt{t}_b \rangle = \delta ^a_{\;\,b}\). The quadratic Casimir then reads
By expanding the field \(X_j\) into components, \(X_j=X_{j,a}\,\texttt{t}^a\), it is straightforward to check that Eqs. (2.14b) and (2.14c) are equivalent to
respectively.
Constraint and Gauge Symmetry It follows from the action (2.6) that the canonical momenta are given by
where the notation \(\approx \) will be explained below and \(\mathcal {I}_\pm \) are the currents defined in Eq. (2.8). The fact that \(X_1\) and \(X_2\) turn out to be linearly dependent arises from the redundancy in the description of the Klimčík model as a gauged NLSM. In the Hamiltonian picture, following the framework laid out by Dirac [60], this translates to the system being subject to a constraint
Although the physically relevant configurations of the canonical fields are only the ones lying on the surface \(\mathcal {C}(x) \approx 0\), it will also be useful to consider the full phase space. This is the reason behind the introduction of the symbol “\(\approx \)” which denotes weak equalities, true only if the constraint is imposed. In contrast, we keep the standard equals sign “\(=\)” for strong equalities, that hold in the full phase space. According to Dirac’s formalism, the dynamical quantity \(\mathcal {C}(x)\) plays the rôle of the generator of the gauge symmetry (2.5). In particular, it satisfies the first-class condition
which ensures that the constraint \(\mathcal {C} (x) \approx 0\) is stable under gauge transformations. Note that under the gauge symmetry, while \(g_j\) are transformed by right multiplication with h, the canonical momenta are conjugated as
The “physical” phase space is spanned by the pair of gauge-invariant fields (g, X) with
By considering only the gauge-invariant dynamical quantities, one recovers the Hamiltonian description of the Klimčík model as a sigma model on G, with the pair (g, X) encoding the coordinates and canonically conjugate momenta of the theory.
Hamiltonian and Dynamics A direct computation shows that the Hamiltonian associated with the action (2.6) is given by
with \(\mathcal {I}_\pm \) being the currents defined in Eq. (2.8). In order to interpret \(\mathcal {H}\) as the generator of the dynamics in the Hamiltonian framework, it needs to be expressed in terms of the canonical fields \((g_j,X_j)\). We first do this for the currents \(\mathcal {I}_\pm \). This step is actually not unique since there is the freedom of adding a term which vanishes under the constraint \(\mathcal {C} \approx 0\). In order to simplify the comparison with the affine Gaudin model, we will make the following choice:
In particular, one easily checks that this expression is compatible with Eq. (2.16), such that \(K(\mathcal {I}_+ + \mathcal {I}_-) \approx X_1 \approx -X_2\) weakly. Reinserting it in (2.21) gives \(\mathcal {H}\) in terms of the canonical fields \((g_j,X_j)\). As above, one always has the freedom of adding to this expression an arbitrary term proportional to the constraint. According to Dirac’s formalism, in order to define the dynamics of the model on the full phase space, we introduce the “total Hamiltonian”
where the \({\mathfrak {g}}\)-valued field \(\mu (x)\) takes the place of a Lagrange multiplier (in particular, a different choice in the canonical expression of the currents \(\mathcal {I}_\pm \) made in (2.22) would result in an equivalent Hamiltonian through a redefinition of \(\mu \)). In the equations of motion, \(\partial _t\mathcal {O}\approx \{ \mathcal {H}_{\textrm{T}},\mathcal {O}\}\), for any gauge-invariant observable \(\mu \) drops out simply because gauge-invariant quantities Poisson commute with \(\mathcal {C}(x)\). However, say, for \(g_2(x)\):
so that \(\mu \) reflects the ambiguity in the choice of dynamics for the unphysical degrees of freedom.
Lax Matrix For future reference, we give the formula for the x-component of the Lax connection (2.9), (2.10), expressed via \(g_j\) and \(X_j\):
Here, the fields \(\mathcal {I_\pm }\) are given by (2.22),
the constant \(\xi \) is the same as in Eq. (2.11), while \(\lambda (z)\) is an arbitrary function of the spectral parameter that takes into account the freedom of adding a term proportional to the constraint in the expression of \({\mathcal {L}}_x(z)\). (In particular, this term has no effect on the zero-curvature representation, which is to be considered weakly.)
As was already mentioned, the Lax matrix \(\mathcal {L}_x(z)\) in Eq. (2.25) depends on the gauge. In order to obtain a connection in terms of the physical fields (g, X) defined in Eq. (2.20), one can for instance consider \({{\mathcal {L}}}_x^{(\textrm{inv})}(z) = g_2 {\mathcal {L}}_x(z) g_2^{-1} - \partial _x g_2 g_2^{-1}\) (as in Eq. (2.13) in the Lagrangian set-up). This Lax matrix is gauge invariant and can be weakly expressed in terms of \(g=g_1 g_2^{-1}\) and \(X=g_2 X_1 g_2^{-1} \approx - g_2 X_2 g_2^{-1}\) only. It coincides with the one from the work [51], seen in the Hamiltonian framework.
An alternative way of relating \({\mathcal {L}}_x(z)\) with a Lax matrix in terms of the physical fields (g, X) is to impose a gauge fixing condition. The latter should be a second-class constraint, i.e. its Poisson bracket with \(\mathcal {C}\) must define an invertible kernel. A possible choice is \(g_2\equiv \varvec{\Omega }(g,X)\) with \(\varvec{\Omega }\) being some function of g and X. Taking into account this gauge fixing and the initial constraint, all the canonical fields \((g_j,X_j)\) may be expressed in terms of g and X, namely,
With the gauge fixing imposed, we then find
where \({\mathcal {L}}_x^{(\textrm{inv})}\) is as above. In particular, the condition \(g_2 \equiv \text {Id}\) leads to \(\mathcal {L}_x \equiv {\mathcal {L}}_x^{(\textrm{inv})}\).
3 Classical AGMs and Their Relativistic Realisations
In this section, we review the construction of classical affine Gaudin models (AGMs) and their relativistic realisations, following the initial construction [32] of Feigin and Frenkel and the subsequent works [47,48,49]. Moreover, we will explain how the Klimčík model considered before can be interpreted as such a realisation.
3.1 Classical Affine Gaudin Models
Punctures, Levels and Twist Function The main data defining an AGM are the choice of N points \(z_1,\ldots ,z_N\in \mathbb{C}\mathbb{P}^1\) on the Riemann sphere, which we will refer to as punctures, and of N nonzero complex numbers \(\ell _1,\ldots ,\ell _N\in {\mathbb {C}}^\times \), which we will refer to as levels. We encode these parameters in a rational function of the spectral parameter z, called the twist function:
For simplicity, we will suppose here that our choice of coordinate z on \(\mathbb{C}\mathbb{P}^1\) is such that all the punctures \(z_r\) are in the finite complex plane \({\mathbb {C}}\). (See the last paragraph of this subsection for more details on the behaviour of AGMs under a change of coordinate on \(\mathbb{C}\mathbb{P}^1\).)
Kac–Moody Currents and Gaudin Lax Matrix The remaining data entering the definition of an AGM are the choice of a simple Lie algebra \({\mathfrak {g}}\). We attach to each puncture \(z_r\) a \({\mathfrak {g}}^{{\mathbb {C}}}\)-Kac–Moody current with level \(\ell _r\), i.e. a \({\mathfrak {g}}^{{\mathbb {C}}}\)-valued field \({\mathcal {J}}_r(x)\) satisfying the Poisson bracket
In this section, we will consider fields on the circle \({\mathbb {S}}^1\) and thus take the spatial coordinate x to be a periodic variable from 0 to \(2\pi \). In the notations introduced below Eq. (2.14c), expanding \({\mathcal {J}}_r(x) = {\mathcal {J}}_{r,a}(x) \,\texttt{t}^a\) in the dual basis \(\{\texttt{t}^a\}\in {\mathfrak {g}}\), the above bracket translates to
We will denote by \({\mathcal {A}}\) the Poisson algebra generated by the fields \({\mathcal {J}}_{r,a}(x)\) and equipped with the above Poisson bracket, which defines the unreduced algebra of observables of the AGM (see the next paragraph for the explanation of the adjective unreduced). The Kac–Moody currents \({\mathcal {J}}_r(x)\) are encoded in the Gaudin Lax matrix
Constraint and Gauge Symmetry In the previous paragraphs, we defined \(\varphi (z)\) and \(\Gamma (z,x)\) in such a way that the 1-forms \(\varphi (z)\text {d}z\) and \(\Gamma (z,x)\text {d}z\) have singularities at the punctures \(z_r\in {\mathbb {C}}\). To ensure that the finite points \(z_r\in {\mathbb {C}}\) are the only punctures of the AGM, we need to impose that the 1-forms \(\varphi (z)\text {d}z\) and \(\Gamma (z,x)\text {d}z\) are regular at \(z=\infty \). For \(\varphi (z)\text {d}z\), this is equivalent to supposing that the levels \(\ell _r\) satisfy the condition
Similarly, in order to ensure the regularity of \(\Gamma (z,x)\text {d}z\) at infinity, we impose
More precisely, we interpret this equation as a constraint in the Poisson algebra \({\mathcal {A}}\), following the standard formalism of Dirac [60]. In particular, the symbol “\(\approx \)” used here denotes weak equalities, true only when the constraint is imposed. This is similar to the set-up considered in the previous section for the Klimčík model: we refer the reader to that section for a more detailed discussion of constrained Hamiltonian field theories.
It is straightforward to check that the Kac–Moody bracket (3.2) implies that the Poisson bracket of the constraint \({\mathcal {C}}_{G}\) with itself takes the formFootnote 7
This ensures that the constraint \({\mathcal {C}}_{G}\approx 0\) is first class. In particular, according to the general formalism of Dirac, it can be interpreted as the generator of a gauge symmetry. A straightforward computation shows that this gauge symmetry acts on the Kac–Moody currents as
where h is the local G-valued gauge parameter. (Here, G is a connected Lie group whose Lie algebra is the simple algebra \({\mathfrak {g}}\) entering the definition of the AGM.) Equivalently, one sees that the Gaudin Lax matrix, defined as (3.4), transforms as
The algebra of physical observables \({\mathcal {A}}_{\text {red}}\) of the model is defined through the Hamiltonian reduction in the unreduced algebra \({\mathcal {A}}\) with respect to this gauge transformation. This reduced algebra is obtained in two steps: we first impose the constraint \({\mathcal {C}}_{G}\approx 0\) and then restrict to gauge-invariant quantities, i.e. observables that Poisson commute with \({\mathcal {C}}_{G}\).
Lax Matrix and Non-local Charges We define the Lax matrix of the AGM as
Following the standard formalism of integrable field theories, we then construct the monodromy matrix M(z) of \({\mathcal {L}}(z,x)\) and extract charges from it by evaluating conjugacy-invariant functions on M(z). These charges are in general non-local quantities, expressed in terms of the Kac–Moody currents through nested integrals. Moreover, it was argued in [32] that they are pairwise in involution. An alternative proof of this involution property is that the Kac–Moody bracket (3.2) implies
where
We recognise here the so-called \(r\big /s\) bracket introduced by Maillet in refs. [7, 8] with a non-skew-symmetric \({\mathcal {R}}\)-matrix \({\mathcal {R}}(z,w)\). This bracket ensures the involution of the charges extracted from M(z).
It is clear from Eq. (3.9) that under a gauge transformation the Lax matrix transforms according to \(\partial _x+{\mathcal {L}}(z) \mapsto h^{-1}\bigl (\partial _x+{\mathcal {L}}(z)\bigr )h\). This is similar to the discussion around Eq. (2.12) for the Klimčík model: in particular, this property ensures that the non-local charges extracted from conjugacy-invariant functions of M(z) are gauge-invariant.
Local Charges Let us introduce the quantity
We denote by \(\zeta _1,\ldots ,\zeta _{N-2}\in \mathbb{C}\mathbb{P}^1\) the zeroes of the twist function, or more precisely of the 1-form \(\varphi (z)\text {d}z\), which we will suppose are simple. We associate with each of these zeroes a quadratic local charge
Starting from the Kac–Moody bracket (3.2), one then checks that these charges are in involutionFootnote 8
If \(\zeta _i\) is a finite zero, one easily checks that the local charge \({\mathcal {Q}}_i\) can be rewritten as
Moreover, if \(\infty \) is a zero of \(\varphi (z)\text {d}z\), one can derive a similar expression for the corresponding charge in terms of the evaluation of \(\Gamma (z,x)\text {d}z\) at \(z=\infty \), i.e. the evaluation of \(-u^{-2}\Gamma (u^{-1},x)\text {d}u\) at \(u=0\) (note that this 1-form is regular at \(u=0\) on the constrained surface \({\mathcal {C}}_{G}(x) \approx 0\)). The quadratic charges \({\mathcal {Q}}_i\) are in fact the first elements of an infinite hierarchy of local charges in involution, constructed in [61]Footnote 9 (building on the work [62]). Let us quickly summarise this construction here. The main ingredient is an infinite set of invariant polynomials \(\Phi _p\) of degree \(p+1\) on \({\mathfrak {g}}\), first constructed in [62] and labelled by the positive exponents \(p\in {\widehat{E}}\) of the untwisted affine algebra \(\widehat{{\mathfrak {g}}}\) associated with \({\mathfrak {g}}\). (\({\widehat{E}}\) is a specific subset of \({\mathbb {Z}}_{\ge 1}\) which depends on the choice of the Lie algebra \({\mathfrak {g}}\); we refer to [61, 62] for more details.) Similarly to the quadratic charges \({\mathcal {Q}}_i\) defined above, the higher-degree charges are associated with the zeroes \(\zeta _i\) of \(\varphi (z)\text {d}z\). More precisely, if \(\zeta _i\) is a finite zero, they are defined asFootnote 10
If \(\infty \) is a zero of \(\varphi (z)\text {d}z\), one defines the associated charges through a similar expression, in terms of the weak evaluation of \(\Gamma (z,x)\text {d}z\) at \(z=\infty \).
For every simple Lie algebra \({\mathfrak {g}}\), the first exponent in \({\widehat{E}}\) is always 1. The corresponding invariant quadratic polynomial on \({\mathfrak {g}}\) is simply defined by \(\Phi _1(\texttt{a}) = \frac{1}{2}\,\langle \texttt{a},\texttt{a}\rangle \). The first charges \({\mathcal {Q}}_{i,1}\) in the infinite hierarchy then coincide with the quadratic charges \({\mathcal {Q}}_i\) introduced above. Generalising Eq. (3.15) to higher-degree charges, it was proven in [61] that
Moreover, the charges \({\mathcal {Q}}_{i,p}\) Poisson commute weakly with the constraint \({\mathcal {C}}_{G}(x)\) and thus define gauge-invariant quantities. Finally, these local charges are also in involution with the non-local charges extracted from the monodromy matrix of \({\mathcal {L}}(z,x)\).
Integrable Structure Let us summarise the construction so far. In the previous paragraphs, we have constructed non-local charges extracted from the monodromy matrix of \({\mathcal {L}}(z,x)\), as well as local charges naturally associated with the zeroes of \(\varphi (z)\text {d}z\). These charges are all in involution and thus generate a Poisson commutative subalgebra \({\mathcal {Z}}^{(z_r)}\) of the unreduced algebra of observables \({\mathcal {A}}\): in other words, we have built an integrable structure from the Kac–Moody currents generating \({\mathcal {A}}\). Moreover, the charges in \({\mathcal {Z}}^{(z_r)}\) are all gauge-invariant and thus descend to the reduced algebra of observables \({\mathcal {A}}_{\text {red}}\). This defines an integrable structure in the reduced algebra, i.e. a Poisson commutative subalgebra \({\mathcal {Z}}_{\text {red}}^{(z_r)}\) in \({\mathcal {A}}_{\text {red}}\). This is the main output of the affine Gaudin model construction.
Change of Spectral Coordinate In the previous paragraphs, we have defined the affine Gaudin model through the use of the twist function \(\varphi (z)\) and the Gaudin Lax matrix \(\Gamma (z,x)\), working with an explicit choice of coordinate z on the spectral Riemann sphere \(\mathbb{C}\mathbb{P}^1\). Let us then end this subsection with a brief discussion on the behaviour of the model under a change of coordinate on \(\mathbb{C}\mathbb{P}^1\) and in particular on the invariance of the integrable structure. Consider a Möbius transformation
of the spectral parameter. We denote by \({\widetilde{z}}_r=\omega (z_r)\) the position of the punctures of the affine Gaudin model in the new coordinate \({\widetilde{z}}\). For simplicity, we will suppose here that none of the \({\widetilde{z}}_r\)’s are infinite. (Note, however, that such a set-up will be useful for us later, but for the sake of brevity we postpone its discussion to Sect. 9.1.) Let us now describe the affine Gaudin model in the new coordinate \({\widetilde{z}}\). We impose here that the Kac–Moody currents \({\mathcal {J}}_r(x)\) and their levels \(\ell _r\), attached to the punctures of the model, are independentFootnote 11 of the choice of coordinate on \(\mathbb{C}\mathbb{P}^1\). The twist function and Gaudin Lax matrix of the model in the coordinate \({\widetilde{z}}\) are thus
One easily checks that the twist function behaves as a 1-form on \(\mathbb{C}\mathbb{P}^1\):
Note that the right-hand side of the above equation naively contains a pole at \(z=-d/c\), which is not present in the left-hand side. This pole is, however, proportional to \(\sum _{r=1}^N \ell _r\), which we supposed vanishes in Eq. (3.5) to impose the regularity of \(\varphi (z)\text {d}z\) at \(z=\infty \). This condition is thus necessary to ensure that \(\varphi (z)\text {d}z\) behaves as a 1-form.
The situation with the Gaudin Lax matrix is similar but slightly more subtle. Let us start by observing that, since we imposed that the Kac–Moody currents \({\mathcal {J}}_r(x)\) are independent of the choice of coordinate on \(\mathbb{C}\mathbb{P}^1\), the constraint \({\mathcal {C}}_{G}= \sum _{r=1}^N {\mathcal {J}}_r \approx 0\) is the same for both models in coordinates z and \({\widetilde{z}}\). In particular, both these models share the same unreduced and reduced algebras of observables \({\mathcal {A}}\) and \({\mathcal {A}}_{\text {red}}\). Moreover, one easily checks that, up to the constraint \({\mathcal {C}}_{G}\approx 0\), the Gaudin Lax matrix also behaves as a 1-form on \(\mathbb{C}\mathbb{P}^1\) (we note that this property does not hold strongly):
In particular, as both \(\varphi (z)\text {d}z\) and \(\Gamma (z,x)\text {d}z\) are 1-forms, the Lax matrix \({\mathcal {L}}(z,x)=\Gamma (z,x)/\varphi (z)\) behaves as a function on \(\mathbb{C}\mathbb{P}^1\), i.e.
Thus, the non-local charges extracted from the monodromy matrices of \({\mathcal {L}}(z,x)\) and \({\widetilde{{\mathcal {L}}}}({\widetilde{z}},x)\) coincide weakly. This ensures that the non-local quantities in the affine Gaudin model integrable structure are independent of the choice of coordinate on \(\mathbb{C}\mathbb{P}^1\).
Let us now turn our attention to the local charges. It is clear that the quantity \({\mathcal {Q}}(z)\text {d}z\), defined through Eq. (3.13), also behaves as a 1-form (weakly). Thus, the quadratic local charges \({\mathcal {Q}}_i\), introduced as residues of \({\mathcal {Q}}(z)\text {d}z\) at the zeroes of \(\varphi (z)\text {d}z\), are weakly invariant under a change of spectral parameter (indeed, residues of 1-forms are independent of the choice of coordinate). More generally, the higher-degree local charges \({\mathcal {Q}}_{i,p}\) are defined in Eq. (3.17) in terms of the evaluations of \(\Gamma (z,x)\text {d}z\) at the zeroes \(\zeta _i\) of \(\varphi (z)\text {d}z\). One easily checks from Eq. (3.22) that under the change of coordinate \(z\mapsto {\widetilde{z}}=\omega (z)\), these evaluations are multiplied by a factor \(\omega '(\zeta _i)^{-1}\). In the definition (3.17) of the local charges, these terms are compensated by the transformation of the prefactor \(\varphi '(\zeta _i)^{-(p+1)/2}\), ensuring that the local charges are also (weakly) invariant under a change of spectral parameter.
As a conclusion, we thus see that the integrable structures \({\mathcal {Z}}^{(z_r)}\) and \({\mathcal {Z}}^{({\widetilde{z}}_r)}\) built from the affine Gaudin model in the coordinates z and \({\widetilde{z}}\) weakly coincide, i.e. \({\mathcal {Z}}^{(z_r)}\approx {\mathcal {Z}}^{({\widetilde{z}}_r)}\). As a consequence, the integrable structure \({\mathcal {Z}}_{\text {red}}^{(z_r)}={\mathcal {Z}}_{\text {red}}^{({\widetilde{z}}_r)}\) in the reduced algebra \({\mathcal {A}}_{\text {red}}\) is independent of the choice of coordinate on \(\mathbb{C}\mathbb{P}^1\). The affine Gaudin model can thus be seen as associated with the geometric data of a meromorphic 1-form \(\varphi (z)\text {d}z\) on \(\mathbb{C}\mathbb{P}^1\) (here with simple poles). More precisely, the residues \(\ell _r\) of this 1-form define uniquely the unreduced algebra \({\mathcal {A}}\) and its Hamiltonian reduction \({\mathcal {A}}_{\text {red}}\), while the positions of its poles (or more precisely the \(N-3\) Möbius invariants built from these positions) determine the integrable structure \({\mathcal {Z}}_{\text {red}}\) in \({\mathcal {A}}_{\text {red}}\).
3.2 Relativistic Realisations of Classical Affine Gaudin Models
Realisations In the previous subsection, we have defined a classical affine Gaudin model as the data of an integrable structure \({\mathcal {Z}}^{(z_r)}\) in the Poisson algebra \({\mathcal {A}}\) built from Kac–Moody currents \({\mathcal {J}}_r(x)\). In order to relate this formal construction to standard two-dimensional integrable field theories, it is useful to introduce the notion of a realisation of such a model in the algebra \({\mathcal {F}}[T^*Q]\) of fields valued in a cotangent bundle \(T^*Q\). This algebra is generated by canonical fieldsFootnote 12\(\bigl (\pi _i(x),\phi ^j(x)\bigr )_{i,j\in \lbrace 1,\ldots ,\dim \,Q\rbrace }\) and is equipped with the canonical bracket
A realisation of the Gaudin model in \({\mathcal {F}}[T^*Q]\) mainly consists in the choice of a Poisson map \(\rho : {\mathcal {A}}\rightarrow {\mathcal {F}}[T^*Q]\). Concretely, such a realisation is equivalent to constructing \({\mathfrak {g}}^{{\mathbb {C}}}\)-valued currents \({\mathcal {J}}_r^\rho (x)=\rho \bigl ({\mathcal {J}}_r(x)\bigr )\) in \({\mathcal {F}}[T^*Q]\) as combinations of the canonical fields \(\bigl (\pi _i(x),\phi ^j(x)\bigr )\) and their derivatives, in such a way that the canonical bracket implies that these currents satisfy the Kac–Moody bracket (3.2). Given such a realisation, one can “transfer” the integrable structure \({\mathcal {Z}}^{(z_r)}\) of the formal affine Gaudin model to \({\mathcal {F}}[T^*Q]\) and thus obtain charges in involution \(\rho \bigl ({\mathcal {Z}}^{(z_r)}\bigr )\) built from the canonical fields \(\bigl (\pi _i(x),\phi ^j(x)\bigr )\).
Recall that the formal affine Gaudin model in \({\mathcal {A}}\) is subject to the first-class constraint \({\mathcal {C}}_G(x) \approx 0\), generating the gauge symmetry (3.8). It is thus natural to also impose a constraint \({\mathcal {C}}(x) = \rho \bigl ( {\mathcal {C}}_G(x) \bigr ) \approx 0\) in the realisation \({\mathcal {F}}[T^*Q]\) and to consider the Hamiltonian reduction \({\mathcal {F}}[T^*Q]_{\text {red}}\) with respect to the gauge symmetry it generates. By construction, the integrable structure \(\rho \bigl ( {\mathcal {Z}}^{(z_r)} \bigr )\) is gauge-invariant and descends to \({\mathcal {F}}[T^*Q]_{\text {red}}\). Alternatively, one can think of the realisation \(\rho : {\mathcal {A}}\rightarrow {\mathcal {F}}[T^*Q]\) as inducing a realisation \(\rho _{\text {red}}: {\mathcal {A}}_{\text {red}} \rightarrow {\mathcal {F}}[T^*Q]_{\text {red}}\) of the reduced algebra, yielding an integrable structure \(\rho _{\text {red}}\bigl ( {\mathcal {Z}}^{(z_r)}_{\text {red}} \bigr )\) in \({\mathcal {F}}[T^*Q]_{\text {red}}\). In principle, one can consider directly realisations of the Poisson algebra \({\mathcal {A}}_{\text {red}}\), without going through the unreduced one \({\mathcal {A}}\): in practice, it is often easier to work with a gauged model in \({\mathcal {A}}\), subject to the constraint \({\mathcal {C}}(x)\approx 0\) and invariant under the corresponding gauge symmetry.
In order to obtain an integrable two-dimensional field theory in the realisation, one further needs to choose a Hamiltonian \({\mathcal {H}}\in {\mathcal {F}}[T^*Q]\) defining the dynamics \(\partial _t \approx \lbrace {\mathcal {H}}_{\textrm{T}},\cdot \rbrace \). (Following Dirac’s formalism of constrained systems, the time evolution is generated by the total Hamiltonian \({\mathcal {H}}_{\textrm{T}}\), built from \({\mathcal {H}}\) by adding a Lagrange mulitplier term.) This yields a gauged Hamiltonian field theory with fields in \(T^*Q\) and space-time variables \((t,x)\in {\mathbb {R}}\times {\mathbb {S}}^1\). We require that the Hamiltonian (weakly) Poisson commutes with the charges in \(\rho \bigl ({\mathcal {Z}}^{(z_r)}\bigr )\): by construction, these charges are then conserved and in involution, ensuring that the corresponding two-dimensional field theory is integrable. In practice, this last condition is oftenFootnote 13 ensured by choosing the Hamiltonian \({\mathcal {H}}\) to be itself an element of the integrable structure \(\rho \bigl ( {\mathcal {Z}}^{(z_r)} \bigr )\).
Relativistic Realisation We say that a realisation \(\rho : {\mathcal {A}}\rightarrow {\mathcal {F}}[T^*Q]\), with Hamiltonian \({\mathcal {H}}\in {\mathcal {F}}[T^*Q]\), is relativistic if
-
(R1)
the choice of Hamiltonian \({\mathcal {H}}\) is such that the resulting two-dimensional field theory is relativistic;
-
(R2)
the canonical fields \(\bigl (\pi _i(x),\phi ^j(x)\bigr )\) of \({\mathcal {F}}[T^*Q]\) can be reconstructed, up to their initial values at a reference point \(x_0\in {\mathbb {S}}^1\), from the currents \({\mathcal {J}}_r^\rho (x)\) in the realisation \(\rho ({\mathcal {A}})\).
The second condition (R2) in this definition ensures that the Kac–Moody currents of the Gaudin model, when seen in the realisation, capture all the degrees of freedom of the field theory (up to potential integration constantsFootnote 14). As we will see in Sect. 6.1, this is in contrast with what we will define there as chiral realisations, which capture only half of the degrees of freedom of a two-dimensional theory, corresponding to either left-moving of right-moving fields. It is natural at this point to ask whether there exists a systematic way of constructing relativistic realisations of affine Gaudin models. The results of [48, 49] imply that, once we have found a realisation \(\rho : {\mathcal {A}}\rightarrow {\mathcal {F}}[T^*Q]\) which satisfies the point (R2) above, there exists a natural choice of Hamiltonian \({\mathcal {H}}\) in \(\rho ({\mathcal {Z}}^{(z_r)})\) such that the resulting two-dimensional field theory is relativistic and thus satisfies the point (R1). Let us summarise quickly this construction. Recall the quadratic local charges \({\mathcal {Q}}_i\) defined in Eq. (3.14). We introduce
One checks that this observable (weakly) generates the spatial derivative on Kac–Moody currents, i.e. satisfies \(\bigl \{ {\mathcal {P}}_{{\mathcal {A}}}, {\mathcal {J}}_r(x) \bigr \} \approx \partial _x{\mathcal {J}}_r(x)\). By construction, under the realisation \(\rho : {\mathcal {A}}\rightarrow {\mathcal {F}}[T^*Q]\), its image \(\rho ({\mathcal {P}}_{{\mathcal {A}}})\) then generates the spatial derivative on the currents \({\mathcal {J}}_r^\rho (x)\) in \({\mathcal {F}}[T^*Q]\) and thus, by the assumption (R2), on all canonical fields \(\bigl (\pi _i(x),\phi ^j(x)\bigr )\). In other words, \(\rho ({\mathcal {P}}_{{\mathcal {A}}})\) is (weakly) the momentum of \({\mathcal {F}}[T^*Q]\). This property was the main assumptionFootnote 15 made in [48, 49] to construct a Hamiltonian that makes the realisation relativistic.
Following [48, 49], we choose the Hamiltonian \({\mathcal {H}}\) of the realisation as a linear combination of the quadratic charges, in analogy with the above expression for the momentum. More precisely, we define the Hamiltonian as
where the \(s_i\)’s are constant parameters (in particular, the momentum of \({\mathcal {F}}[T^*Q]\) is given by the same expression with all \(s_i\)’s equal to 1). Having expressed the Hamiltonian and momentum of the theory in terms of the quadratic charges \(\rho ({\mathcal {Q}}_i)\) allows one to study the energy–momentum tensor of the model and thus its space-time symmetries. In particular, it was proven in [48, 49] that the theory is relativistic if and only if the coefficients \(s_i\) all square to 1. We thus take
We will further restrict to cases where there are as many coefficients \(s_i\) equal to \(+1\) as ones equal to \(-1\) (indeed, the study of various examples suggests that choices which do not satisfy this condition lead to rather degenerate models, which in particular do not possess a Lagrangian formulation). Let us note, for completeness, that the total Hamiltonian (which generates the dynamics \(\partial _t \approx \lbrace {\mathcal {H}}_{\textrm{T}},\cdot \rbrace \) in the unreduced algebra \({\mathcal {F}}[T^*Q]\)) then takes the form
where \(\mu \) is a Lagrange multiplier.
Integrable \({\sigma }\)-Models Let us illustrate more concretely the ideas presented in the previous paragraphs by discussing how integrable \(\sigma \)-models can arise as relativistic realisations of affine Gaudin models. These theories appear when considering realisations of the Kac–Moody currents of the form
i.e. currents which are linear in the momentum fields \(\pi _i(x)\) and the derivatives \(\partial _x \phi ^{i}(x)\) of the coordinate fields, with coefficients which are local functions of the coordinates only.
For these types of realisations, the Hamiltonian (3.26) is quadratic in the momenta and the derivatives of the coordinates and thus yields a Lagrangian density quadratic in the derivatives \(\partial _t \phi ^i\) and \(\partial _x \phi ^i\). Moreover, the relativistic invariance of the theory further ensures that the Lagrangian density takes the form \(E_{ij}(\phi ^k) \partial _+ \phi ^i \partial _- \phi ^j\), in terms of the light-cone derivatives \(\partial _\pm =\frac{1}{2}\,(\partial _t\pm \partial _x)\) and a 2-tensor \(E_{ij}(\phi ^k)\) on Q. This is the Lagrangian of a nonlinear \(\sigma \)-model.
More precisely, the theory is a gauged \(\sigma \)-model on Q, invariant under a local action of the group G. At the Hamiltonian level, this gauge symmetry is generated by the constraint \({\mathcal {C}}=\sum _{r=1}^N {\mathcal {J}}^\rho _{r}\). For a realisation of the form (3.29) considered here, it is easy to check that this symmetry shifts the coordinate fields \(\phi ^{i}(x)\) by functions of the coordinates only (i.e. independent of the momenta and the derivatives of the coordinates). At the Lagrangian level, this corresponds to a transformation of the fields \(\phi ^i\) which does not depend on the derivatives \(\partial _t\phi ^i\) and \(\partial _x\phi ^i\) and thus to a geometric action of the group G on the configuration space Q. In particular, the physical target space of the \(\sigma \)-model is the quotient \(Q_{\text {red}}=Q/G\). Equivalently, in the Hamiltonian formulation, the reduction thus amounts to passing from the algebra \({\mathcal {F}}[T^*Q]\) to the algebra \({\mathcal {F}}[T^*Q_{\text {red}}]\).
Lax Connection The non-local charges of the formal affine Gaudin model are extracted from the monodromy matrix of the Lax matrix \({\mathcal {L}}(z)\). As explained in the previous subsection, these charges are in involution one with another, as well as with the local ones. In particular, the image of these non-local charges in a relativistic realisation Poisson commute with the Hamiltonian \({\mathcal {H}}\) and are thus conserved. To make the connection with the standard formalism of two-dimensional integrable field theories, it is useful to come back to the proof that the non-local charges are in involution with the local charges. It was shown in [47, 61] that the Hamiltonian flow generated by these local charges acts on the Lax matrix \({\mathcal {L}}(z)\) by a zero-curvature equation, which ensures that the non-local charges extracted from \({\mathcal {L}}(z)\) are invariant under this flow. In particular, in the realisation, the time evolution of the Lax matrix generated by the choice of Hamiltonian takes the form of a zero curvature equation, making the link with the standard Lax formalism of two-dimensional integrable field theories.
Let us quickly describe the Lax connection of the theory. We will work directly in the realisation, i.e. with the Kac–Moody currents \({\mathcal {J}}_r^\rho \) in \({\mathcal {F}}[T^*Q]\). Since we are now considering a two-dimensional field theory, with space-time coordinates x and t, we will denote the Lax matrix in the realisation as \({\mathcal {L}}_x(z)\), to stress that it corresponds to the spatial component of the Lax connection. By construction, we have
This Lax matrix has poles at the zeroes \(\zeta _1,\ldots ,\zeta _{N-2}\) of \(\varphi (z)\text {d}z\). Taking into account the constraint \(\sum _{r=1}^N {\mathcal {J}}_r^\rho \approx 0\), one finds that in the case where all the zeroes \(\zeta _i\) are finite, the partial fraction decomposition of \({\mathcal {L}}_x(z)\) takes the form
where the fields \({\mathcal {B}}_x\) and \({\mathcal {K}}_i\) are linear combinations of the Kac–Moody currents \({\mathcal {J}}_r^\rho \). Following [47, 49], one finds that the time evolution of \({\mathcal {L}}_x(z)\) generated by the Hamiltonian (3.28) takes the form of the zero-curvature equation
with the temporal component of the Lax connection given by
In this equation, the fields \({\mathcal {K}}_i\) are the same as in Eq. (3.31), the coefficients \(s_i\) are the ones entering the definition of the Hamiltonian (3.28) and \({\mathcal {B}}_t\) is a field that contains the Lagrange multiplier \(\mu \). In the case where one of the zeroes \(\zeta _i\) is infinite, the corresponding terms in the sums over \(i\in \lbrace 1,\ldots ,N-2\rbrace \) in the expressions (3.31) and (3.33) of \({\mathcal {L}}_x(z)\) and \({\mathcal {L}}_t(z)\) take the form \({\mathcal {K}}_i\,z\) and \(s_i\,{\mathcal {K}}_i\,z\), respectively. Let us end this paragraph with a quick remark. In the definition of a relativistic realisation made at the beginning of this subsection—see point (R2) in Sect. 3.2—we have required that the canonical fields \(\bigl ( \pi _i, \phi ^{j} \bigr )\) of the realisation can be reconstructed from the currents \({\mathcal {J}}_r^\rho \) of the Gaudin model (up to possible integration constants). Since these currents are all contained in the Lax matrix \({\mathcal {L}}_x(z)\), this assumption thus means that the zero-curvature equation (3.32) encodes all the equations of motion of the theory. This is a standard requirement in integrable field theories, which ensures that the integrable dynamics concerns all the degrees of freedom of the model and not only a subsector.
3.3 The Klimčík Model as a Relativistic Realisation of AGM
In this subsection, we explain how the Klimčík model can be seen as a relativistic realisation of an affine Gaudin model, as first shown in [47], based on the results of [55]. For that, we will use the formulation of the Klimčík model as a gauged \(\sigma \)-model on \(G\times G / G_{\text {diag}}\), as described in Sect. 2. In particular, we will use the notations and conventions of that section.
The Underlying Affine Gaudin Model As explained in Sect. 3.1, a formal affine Gaudin model is defined by the choice of its twist function \(\varphi (z)\). In this subsection, to obtain the Klimčík model, we will take it to be [55]
where K, \(\varepsilon _1\) and \(\varepsilon _2\) are the defining parameters of the Klimčík model introduced in Sect. 2 and \(\xi \) is defined in terms of these parameters by Eq. (2.11). The 1-form \(\varphi (z)\text {d}z\) possesses 4 simple poles
defining the punctures of the affine Gaudin model, and 2 simple zeroes at \(\zeta _1=\infty \) and \(\zeta _2=0\). The levels \(\ell _r\) associated with the punctures are determined by computing the residues of \(\varphi (z)\text {d}z\) at \(z=z_r\) and simply read
The formal affine Gaudin model under consideration is described by 4 commuting Kac–Moody currents \({\mathcal {J}}_r(x)\), with levels \(\ell _r\).
The Realisation In the Hamiltonian formulation, the gauged Klimčík model on \(G\times G/G_{\text {diag}}\) is defined in the extended algebra of observables \({\mathcal {F}}[T^*(G\times G)]\). As explained in Sect. 2.2, this algebra is described by two G-valued fields \(g_1(x),g_2(x)\) and two \({\mathfrak {g}}\)-valued fields \(X_1(x), X_2(x)\), encoding the canonical fields in \(T^*(G\times G)\) and satisfying the Poisson bracket (2.14). In order to interpret the Klimčík model as a realisation of the formal affine Gaudin model considered above, we need to realise the Kac–Moody currents \({\mathcal {J}}_r(x)\), \(r\in \lbrace 1,\ldots ,4\rbrace \), in terms of the fields of \({\mathcal {F}}[T^*(G\times G)]\). This realisation is given by [55, 63]
where \({\hat{R}}:{\mathfrak {g}}\rightarrow {\mathfrak {g}}\) is the Yang–Baxter operator (2.1) entering the definition of the Klimčík model and \({\hat{R}}_g = \text {Ad}_g^{-1}\circ {\hat{R}}\circ \text {Ad}_g\), as in Sect. 2. Starting from the canonical bracket (2.14) and using the fact that \({\hat{R}}\) satisfies the modified classical Yang–Baxter equation, one checks that the fields \({\mathcal {J}}_r^\rho \) are commuting Kac–Moody currents with levels \(\ell _r\), as announced. We note that, when expressed in terms of the canonical fields \((\pi _i,\phi ^{j})\) of \(T^*(G\times G)\) (working in a choice of coordinate chart \((\phi ^{j})\) on the group manifold \(G\times G\)), the currents \(X_{1}\) and \(X_2\) are linear in the momentum fields \(\pi _i\) while the currents \(g_1^{-1}\partial _x g_1\) and \(g_2^{-1}\partial _x g_2\) are linear in the derivatives \(\partial _x \phi ^{\,i}\), so that the Kac–Moody currents are of the form (3.29). Moreover, one can proveFootnote 16 that the canonical fields \((g_i,X_i)\) can be reconstructed from the data of the Kac–Moody currents \({\mathcal {J}}^\rho _r\), up to integration constants, so that the degrees of freedom of the Gaudin model capture all the fields of \(T^*(G\times G)\). The realisation under consideration then satisfies the point (R2) in the definition of a relativistic realisation made in Sect. 3.2.
Formula (3.37) defines a realisation \(\rho : {\mathcal {A}}\rightarrow {\mathcal {F}}[T^*(G\times G)]\) of the unreduced algebra \({\mathcal {A}}\). In particular, the physical model should be understood as subject to the constraint \({\mathcal {C}}= \sum _{r=1}^4 {\mathcal {J}}_r^\rho \approx 0\). It is straightforward to check from the above expression (3.37) of \({\mathcal {J}}_r^\rho \) than in the present case, we have \({\mathcal {C}}= X_1 + X_2\). The constraint and gauge symmetry coming from the affine Gaudin model construction thus coincide with the ones (2.17) and (2.5) of the gauged formulation of the Klimčík model. In particular, the physical observables of the realisation are described by the reduced algebra \({\mathcal {F}}[T^*(G\times G/G_{\text {diag}})] \simeq {\mathcal {F}}[T^*G]\). We will come back to this reduced algebra in the last paragraph of this subsection.
Hamiltonian Recall that the Hamiltonian of a (gauged) relativistic realisation can be built from the quadratic charges \(\rho ({\mathcal {Q}}_i)\) associated with the zeroes \(\zeta _i\) of the twist function. With the choice of twist function (3.34) considered here, the 1-form \(\varphi (z)\text {d}z\) has two zeroes \(\zeta _1=\infty \) and \(\zeta _2=0\). There are thus two local quadratic charges \(\rho ({\mathcal {Q}}_1)\) and \(\rho ({\mathcal {Q}}_2)\), which can be expressed in terms of the canonical fields \((g_i,X_i)\) by a direct computation (starting from the definition (3.14) of these charges in the formal affine Gaudin model and the expression (3.37) of the realised currents \({\mathcal {J}}_r^\rho =\rho ({\mathcal {J}}_r)\)). In particular, one checks that
is the momentum of the algebra \({\mathcal {F}}[T^*(G\times G)]\), in agreement with the general discussion in Sect. 3.2.
The Hamiltonian of a relativistic realisation is defined in Eq. (3.28) in terms of the quadratic charges \(\rho ({\mathcal {Q}}_i)\) and coefficients \(s_i\), which must be either \(+1\) or \(-1\) to ensure the relativistic invariance. In the present case, one thus needs to specify a choice of parameters \(s_1\) and \(s_2\) in \(\lbrace +1,-1 \rbrace \). We required in Sect. 3.2 that there be as many \(s_i\)’s equal to \(+1\) as \(-1\), leaving only two possible choices in the present case, which correspond to two opposite Hamiltonians. In what follows, we will choose \(s_1 = +1\) and \(s_2 = -1\), so that the total Hamiltonian of the gauged model is given by
where \(\mu \) is a Lagrange multiplier. A direct computation shows that this Hamiltonian coincides with the one (2.23) of the gauged Klimčík model, up to a redefinition of the Lagrange multiplier \(\mu \) (which does not impact the theory).
Lax Connection Following Eq. (3.30), the Lax matrix of the theory is given explicitly by
From the explicit expressions (3.34), (3.35) and (3.37) of \(\varphi (z)\), \(z_r\) and \({\mathcal {J}}_r^\rho \) considered in this subsection, it is a straightforward computation to check that this Lax matrix coincides with the one (2.25) of the gauged Klimčík model.Footnote 17 A similar computation shows that the temporal component \({\mathcal {L}}_t(z)\) of the Lax connection built from the affine Gaudin model construction (see previous subsection) agrees with the one of the gauged Klimčík model. This achieves the identification of the present relativistic realisation of the affine Gaudin model with the Klimčík model.
Reduced Algebra and Gauge-Invariant Currents Let us end this subsection with a discussion of the reduced algebra of the model, which describes its physical observables. In terms of the canonical fields \((g_i,X_i)\) of the realisation \({\mathcal {F}}[T^*(G\times G)]\), the reduction is obtained by imposing the constraint \({\mathcal {C}}= X_1 + X_2 \approx 0\) and focussing on gauge-invariant observables. As explained in Sect. 2.2, a generating set of gauge-invariant fields is given by \(g=g_1 g_2^{-1}\) and \(X = g_2 X_1 g_2^{-1} \approx -g_2 X_2 g_2^{-1}\). These satisfy the Poisson bracket of canonical fields on one copy of \(T^*G\) and thus identify the algebra of physical fields of the theory with \({\mathcal {F}}[T^*G]\).
Let us now discuss the reduction in terms of the fields of the affine Gaudin model, namely the Kac–Moody currents \({\mathcal {J}}_r^\rho \). Under a gauge transformation with local parameter \(h\in G\), the latter transform as \({\mathcal {J}}_r^\rho \mapsto h^{-1}{\mathcal {J}}_r^\rho h + \ell _r\,h^{-1}\partial _x h\). To describe the reduction, one needs to build gauge-invariant quantities from these currents. Since the field \(g_2\) transforms as \(g_2 \mapsto g_2h\), one easily checks that the currents
are gauge invariant. Moreover, a straightforward computation starting from the expression (3.37) of \({\mathcal {J}}_r^\rho \) shows that
in terms of the gauge-invariant canonical fields (g, X). These currents \({{\mathcal {J}}}_1^{(\textrm{inv})}\) and \({{\mathcal {J}}}_2^{(\textrm{inv})}\) are also commuting Kac–Moody currents, with levels \(\ell _1=-K/\varepsilon _1\) and \(\ell _2=+K/\varepsilon _1\). On the other hand, the two other gauge-invariant currents \({{\mathcal {J}}}_3^{(\textrm{inv})}\) and \({{\mathcal {J}}}_4^{(\textrm{inv})}\) can be expressed in terms of \({{\mathcal {J}}}_1^{(\textrm{inv})}\) and \({{\mathcal {J}}}_2^{(\textrm{inv})}\) by
and thus do not carry any additional degrees of freedom. Therefore, the Kac–Moody currents \({{\mathcal {J}}}_1^{(\textrm{inv})}\) and \({{\mathcal {J}}}_2^{(\textrm{inv})}\) describe the degrees of freedom of the reduced affine Gaudin model in the algebra \({\mathcal {F}}[T^*G]\) and define a “reduced” realisation \(\rho _{\text {red}}: {\mathcal {A}}_{\text {red}} \rightarrow {\mathcal {F}}[T^*G]\). In particular, the Klimčík model in its standard (non-gauged) formulation can be described in terms of these two currents: this is the formulation put forward in Ref. [53]. (In particular, the Kac–Moody currents \({{\mathcal {J}}}_{1,2}^{(\textrm{inv})}\) coincide, up to an overall factor, with the ones of [53, eqs. (4.9)-(4.13)], where the labels 1, 2 used here correspond to the ones \({\mp }\) in that work.)
4 Klimčík Model in Conformal Limit I: Target Space and Lax Connection for \(\varvec{G=\textrm{SU}(2)}\)
An important part of the paper concerns the investigation of the integrable structures in the CFT underlying the UV fixed point of the Klimčík model. We start by describing the classical field theory that results when the parameters of the Klimčík model are taken to be such that the one-loop \(\beta \) - function vanishes. Here, we focus on the target space and the Lax connection in this limit. The Lie group is set to be \(\textrm{SU}(2)\)—the best studied case in the literature for which many results about the classical/quantum field theory are known. In Sect. 6, some aspects of the generalisation to arbitrary Lie group G will be discussed. The analysis therein will be carried out within the framework of affine Gaudin models. Amongst the goals of the next several sections is to demonstrate how the results for the \(\textrm{SU}(2)\) Klimčík model, based on the approach of the (quantum) inverse scattering method and its variants, fit with those that we obtain via the Gaudin model formalism.
4.1 RG Flow Equations
Choosing a local coordinate frame \(\lbrace \phi ^i \rbrace \) for the target space background, the classical action of a NLSM takes the form
Here, we have decomposed the 2-tensor appearing in the action into a symmetric part \({\textsf{G}}_{ij}={\textsf{G}}_{ji}\) and a skew-symmetric part \({\textsf{B}}_{ij}=-{\textsf{B}}_{ji}\). The symmetric component \({\textsf{G}}_{ij}\) is then interpreted as the metric tensor of the target manifold, while the skew-symmetric one signals the presence of a non-trivial torsion. More precisely, the corresponding torsion tensor is given by
A classical field theory of the type (4.1) describes maps \(\{\phi ^i(t,x)\}\) from the worldsheet to the target manifold, which obey a generalised version of the Laplace equation.
As long as the curvature of the target space is small, the quantisation of the NLSM (4.1) can be considered within the framework of perturbative QFT. As usual, the regularisation of the UV divergent integrals in the perturbative expansion introduces a scale \(\mu \) into the problem. The \(\mu \)-dependence of the physical couplings, which are encoded in \({\textsf{G}}_{ij}\) and \({\textsf{B}}_{ij}\), induces a geometric flow of the target space manifold. The corresponding RG flow equations were first derived to two loops in Refs. [65, 66] for the case with vanishing torsion tensor. The results were extended to a more general set-up in the works [67, 68]. To the lowest perturbative order, one has
where \( \tau =-\frac{1}{2\pi }\,\log (\mu )\) stands for the RG time, \({\textsf{R}}_{ij}\) is the Ricci tensor and \(\nabla _i\) is the covariant derivative. The extra vectors \({\textsf{V}}_i\) and \(\mathsf {\Lambda }_i\) appearing above may be arbitrarily chosen. They take into account possible \(\mu \)-dependent reparameterisations of the coordinates as well as transformations of \({\textsf{B}}_{ij}\) that leave the torsion tensor (4.2) invariant.
In the work [69], the Ricci tensor and torsion potential for a general class of the so-called Poisson–Lie sigma models, which include the Klimčík model as a particular case, are explicitly computed. The results were used by the authors of Ref. [56] to show the one-loop renormalisability of the Klimčík model and to derive the flow of couplings K, \(\varepsilon _1\) and \(\varepsilon _2\) entering into the action (2.2), (2.4). The one-loop RG flow equations read
with
Remarkably, the only dependence on the Lie group G for which the Klimčík model is defined is contained in the dual Coxeter number \(h^\vee \) , which enters as an overall factor in the equation for \(\partial _\tau \varepsilon _1\). It appears as a result of our choice of normalisation for the symmetric form (see footnote 6). Upon setting \(h^\vee =2\), the RG flow equations become equivalent to the ones derived in the earlier work of Fateev [4] for the \(\textrm{SU}(2)\) case.
The model will be considered in the domain with \(K>0\), \(0<\varepsilon _1+\varepsilon _2<1\) and \(|\varepsilon _1-\varepsilon _2|<1\). In the IR limit corresponding to \(\tau \rightarrow +\infty \), the constant K tends to zero, the curvature of the target space blows up and the perturbative approach is no longer valid. In contrast, it turns out that in the UV where \(\tau \rightarrow -\infty \), the curvature of the manifold remains bounded. In this regime, the classical action can be used as a starting point for providing a perturbative definition of the quantum NLSM. The next several sections will be concerned with an analysis of the Klimčík model in the space of couplings corresponding to the UV fixed point. The parameterisation
where \(\nu ^2>0\) is a RG invariant and
will be employed. It is straightforward to check from the differential equations (4.4) that at high energies the running coupling \(\kappa \) tends to one from below. We will refer to
as the “conformal limit” of the field theory (the extra factor multiplying \(K_{\scriptscriptstyle \textrm{UV}}\) has been chosen for future convenience).
4.2 Target Space of the SU(2) Klimčík Model in the Conformal Limit
In studying the Klimčík model, the \(\textrm{SU}(2)\) case serves as an important source of intuition. The corresponding target space manifold already exhibits some important features as \(\kappa \rightarrow 1^-\), which are also expected to be relevant when G is a higher-rank group. Introduce a coordinate frame \((\theta ,v,w)\) through the Euler decomposition of the group element:
where \(\texttt{h}\), \(\texttt{e}_\pm \) obey the standard commutation relations of the \(\mathfrak {sl}(2)\) algebra:
The expression for g, along with the definition (2.2), allows one to write the \(\textrm{SU}(2)\) Klimčík model action in the form of Eq. (4.1). As was mentioned before, in the case under consideration the second term in the integrand that contains the tensor \({\textsf{B}}_{ij}\) is a total derivative and can be ignored. The metric tensor \({\textsf{G}}_{ij}\) depends only on \(\theta \), since v and w turn out to be Killing coordinates. We will avoid presenting the formula for \({\textsf{G}}_{ij}\) as it exists in numerous places in the literature see, e.g. “Appendix A” of Ref. [52].
There is an important feature of the \(\kappa \rightarrow 1^-\) limit that needs to be discussed. It can be motivated by computing the volume of the target space \(V\!ol=\int \sqrt{\textrm{det} \,{\textsf{G}}_{ij}}\). A straightforward calculation yields that
Hence, in the conformal limit the volume diverges. All this suggests that the compact target manifold of the \(\textrm{SU}(2)\) Klimčík model, embedded in Euclidean space, becomes an infinitely extended object in the parameter domain corresponding to the UV fixed point. As such, some care is needed in taking \(\kappa \rightarrow 1^-\). Different coordinate frames must be introduced to cover the various regions of the target manifold, which grow to become an infinite distance apart. For the \(\textrm{SU}(2)\) Klimčík model at least three such regions may be identified. We will define the corresponding charts as follows. First swap \(\theta \in (0,\pi )\) for \(\phi \in (-\infty ,+\infty )\) using the relation
The constant \(\phi _0\) is then set to be
This way as \(1-\kappa \ll 1\) charts II and III will probe the regions of the target space where \(\theta \) is close to zero. It is easy to see from the integrand in Eq. (4.10) that this part of the manifold contributes a divergent amount to \(V\!ol\).
Consider the action (2.2), (2.4) with \(\varepsilon _1\), \(\varepsilon _2\) substituted in favour of \(\nu ^2\) and \(\kappa \) as in Eq. (4.5). Plugging in the expression for g (4.8) with \(\theta \) replaced by \(\phi \) according to Eq. (4.11), and taking the \(\kappa \rightarrow 1^-\) limit yields for the first chart that
Here,
while the decoupled boson \(\chi \) and the field \(\alpha \) are simple linear combinations of v and w:
The matrix elements of g (4.8) in the fundamental representation depend on the Killing coordinates (v, w) through the phase factors \(\text{ e}^{\frac{\textrm{i}}{2}(v+w)}=\text{ e}^\textrm{i}\alpha +\frac{\textrm{i}}{2\nu }\,(1-\nu ^2)\chi \) and \(\text{ e}^{\frac{\textrm{i}}{2}\,(v-w)}=\text{ e}^{\frac{\textrm{i}}{2\nu }\,(1+\nu ^2)\,\chi }\). As a result, the fields \(\alpha \) and \(\chi \) may always be considered to lie in the interval
However, while for the field \(\alpha \) it is possible to prescribe that \(\alpha \sim \alpha +2\pi \), the identifications on \(\chi \) are not so straightforward. For instance, the condition that \(v\sim v+4\pi \) translates to
The action \(\mathcal {A}_{\textrm{cig}}\) defines a field theory that is often referred to as the cigar NLSM [70,71,72]. This comes from the fact that the target manifold can be embedded into three-dimensional space and visualised as the right Hamilton’s cigar:

The tip corresponds to \(\phi =+\infty \), while for \((-\phi )\gg 1\) the non-trivial term in the denominator in (4.14) is negligible and the target space manifold asymptotically approaches the half-infinite cylinder. The coordinate \(\alpha \) goes around the circumference of the cigar and belongs to the segment \([0,2\pi )\), in agreement with Eq. (4.16).
The second coordinate chart corresponds to setting \(\phi _0=\frac{1}{2}\log \big (\frac{1+\kappa }{1-\kappa }\big )\). Then the target space asymptotically approaches an infinite cylinder and the action takes the form \(\lim _{\kappa \rightarrow 1^-}\mathcal {A}= \mathcal {A}_{\textrm{free}}\) with
Finally, for chart III one finds that
where
Notice that for the cigar NLSM with action \({\mathcal {A}}_{\textrm{cig}}[-\phi ,{\tilde{\alpha }}]\), the tip of the target manifold is located at \(\phi =-\infty \), while the infinitely long cylindrical part extends to \(\phi \gg 1\).
As \(1-\kappa \ll 1\) the \(\textrm{SU}(2)\) Klimčík model target space becomes a non-compact manifold of length \(\propto \log (\frac{1+\kappa }{1-\kappa })\). The figure shows a schematic depiction of this manifold, indicating the domains covered by each of the three coordinate charts introduced in Eqs. (4.11) and (4.12). In the first and third charts, the target space is composed of the cigar and a circle of length \(4\pi \,\big /(\nu +\nu ^{-1})\), which are glued together in a topologically non-trivial way. As a result, say, in chart I the coordinates \(\chi ,\alpha \) obey the compactification conditions \((\chi ,\alpha )\sim (\chi ,\alpha +2\pi )\) and \((\chi ,\alpha )\sim (\chi +\tfrac{4\pi \nu }{1+\nu ^2},\alpha +\tfrac{4\pi \nu ^2}{1+\nu ^2})\) and the fundamental domain in the \((\chi ,\alpha )\) plane at fixed \(\phi \) can be chosen to be the parallelogram that is shown in the figure. In chart II, the target space is asymptotically flat and isomorphic to \({\mathbb {R}}\times {\mathbb {S}}^1\times {\mathbb {S}}^1\)
The above analysis of the Klimčík model action for \(\kappa \rightarrow 1^-\) suggests the following picture for the target space manifold. Embedded into Euclidean space, it resembles an infinitely long 3D cylinder \(\cong \) \({\mathbb {R}}\times {\mathbb {S}}^1\times {\mathbb {S}}^1\) with all the curvature concentrated at the tips. These are located at \(\phi =+\infty \) and \(\phi =-\infty \) in charts I and III, respectively. In chart I, the action is that of the cigar NLSM along with an independent Bose field, see Eq. (4.13). However, the corresponding target space is not the Cartesian product \(\textrm{cigar}\times {\mathbb {S}}^1\). The reason is due to the compactification condition (4.17), which involves shifts of both the fields \(\alpha \) and \(\chi \). It corresponds to a gluing of the two components in a topologically non-trivial way. In the coordinate chart III, a similar phenomenon occurs. A sketch of the target space background, emphasising the non-trivial topology, is shown in Fig. 1.
4.3 Conformal Limit for the Lax Connection
The Lax connection was introduced in Sect. 2 for the Klimčík model, viewed as a coset sigma model on \(G\times G\) gauged by the diagonal subgroup. In formulae (2.8)–(2.11), \(\mathcal {L}_\mu \) is given as a gauge-dependent quantity that is not invariant under the transformation \(g_j\mapsto g_j\,h\). In order to simplify the discussion as much as possible, here we work with the gauge-invariant connection \(\mathcal {L}^{(\textrm{inv})}_\mu =g_2\,\mathcal {L}_\mu \,g_2^{-1} - \partial _\mu g_2\,g_2^{-1}\), which depends only on the combination \(g=g_1\,g_2^{-1}\). This is equivalent to fixing the gauge as \(g_2\equiv \text {Id}\) and \(g_1\equiv g\) in formulae (2.8)–(2.11). This subsection is meant as a companion to 6.1 and 6.2, which discuss the chiral limit in the affine Gaudin model framework. Indeed, recall that \(\mathcal {L}_x\) coincides with the Gaudin Lax matrix up to a field independent factor, see Eq. (3.10): the chiral limit of \(\mathcal {L}^{(\textrm{inv})}_\mu \) studied in this subsection thus describes the UV behaviour of the Gaudin Lax matrix in a specific choice of gauge (for \(G=\textrm{SU}(2)\)).
To perform the conformal limit of \(\mathcal {L}^{(\textrm{inv})}_\mu \), there are a couple of points to keep in mind. The first is related to the fact that the target space of the \(\textrm{SU}(2)\) Klimčík model becomes non-compact when \(\kappa \rightarrow 1^-\). As was discussed above, three charts are needed to describe the target manifold, see Fig. 1. In coordinate charts I and III, the action of the corresponding NLSM is the sum of the cigar sigma model action and that of a free boson. In chart II the manifold is asymptotically flat and the dynamics are non-interacting. It turns out that in each of the three charts the conformal limit of the Lax connection is different. Focussing on charts I and II, we will consider \(\lim _{\kappa \rightarrow 1^-} \mathcal {L}^{(\textrm{inv})}_\mu \) and bring it to a form that allows for a simple comparison with the results obtained within the Gaudin formalism. In Sect. 6.2, a “chiral” affine Gaudin model is introduced. It is explained how the Lax matrix of this model, specialised to \(G=\textrm{SU}(2)\), agrees with the conformal limit of \(\mathcal {L}^{(\textrm{inv})}_\mu \) provided suitable gauge-fixing conditions are imposed on the Kac–Moody currents.
The second point is that the spectral parameter z enters into the Lax connection (2.10) always in combination with \(\xi \). From the definition (2.11) of this constant, and swapping \(\varepsilon _{1,2}\) for \(\kappa ,\nu \) according to Eq. (4.5), one finds that \(\xi \sim (1-\kappa )\) as \(\kappa \) tends to one. In order to ensure that a non-trivial dependence on the spectral parameter in the Lax connection remains, we will assume that z tends to infinity in the conformal limit such that \(z^{(\textrm{L})}=\xi z\) is held fixed. Another possibility, which will be commented on briefly, is to keep \(z^{(\textrm{R})}=\xi z^{-1}\) constant.
4.3.1 Chart I
Parameterise the group element g according to Eqs. (4.8) and (4.11) with \(\phi _0=0\). It is straightforward to see from formula (2.10) with \(g_2\equiv \text {Id}\) and \(g_1\equiv g\) that the conformal limit of the Lax connection yields:
with
Here, the currents \(\mathcal {I}_\pm ^{(\scriptscriptstyle \textrm{UV})}\) are given by the same expressions (2.8), where \(g_2\equiv \text {Id}\), \(g_1\equiv g\), but \(\varepsilon _1\) and \(\varepsilon _2\) are substituted for their limiting values. To be fully explicit,
where \(\alpha \) is the \(\textrm{U}(1)\) field of the cigar and \(\chi \) is the decoupled boson, see (4.15) for their definitions. Notice that, since the combination \((\text {Id}\pm \textrm{i}R)\) appearing in formula (4.22) sends \(\texttt{e}_{\mp }\) to zero, \(\mathcal {L}_+^{(0)}\) (\(\mathcal {L}_-^{(0)}\)) is a upper (lower) triangular matrix.
An important feature of the \(\kappa \rightarrow 1^-\) limit of \(\mathcal {L}_\mu ^{(\textrm{inv})}\) is that the “−” component of the resulting Lax connection is independent of the spectral parameter. As a result, there exists a similarity transformation with some field dependent matrix \(\varvec{\Omega }\) that does not depend on \(z^{(\textrm{L})}\), such that
Then, the zero-curvature representation \([\partial _- + \mathcal {L}_-(z),\,\partial _+ + \mathcal {L}_+(z) ]=0\) would turn into the condition that the “\(+\)” component of the flat connection satisfies \(\partial _-\mathcal {L}_+=0\). In other words, as a consequence of the equations of motion \(\mathcal {L}_+(z)=\mathcal {L}_+(z;t+x)\) is a chiral field that moves to the left. The presence of left- and right-moving fields in a 2D (classical) field theory is one of the hallmarks of conformal invariance.
The matrix \(\varvec{\Omega }\) is in general non-local in the sense that its expression involves integrals over the fundamental fields. In the case at hand, it requires one to introduce the so-called dual field \(\alpha ^{(\textrm{D})}\). The cigar NLSM action (4.14) does not contain an explicit dependence on \(\alpha \). This implies the conservation law \(\partial _+ J_-+\partial _- J_+=0\) for the Noether current \(J_\mu =\frac{\partial _\mu \alpha }{1+\text{ e}^{2\phi }}\). The dual field is defined through the relation \(\partial _\pm \alpha ^{(\textrm{D})}=\pm J_\pm \). This way, the conservation of \(J_\mu \) becomes the condition that the partial derivatives \(\partial _\pm \) acting on \(\alpha ^{(\textrm{D})}\) commute, which is necessary for the definition of the dual field to be consistent. Explicitly one has
with \(x_0\) being some arbitrary reference point. Then, the matrix \(\varvec{\Omega }\) such that Eq. (4.24) is satisfied is given by
(the first field independent factor has been included for future convenience).
Applying the similarity transformation to the other connection component, one finds that:
with
where, for compactness, we have specialised the \(\mathfrak {sl}(2)\) generators to their fundamental representation. The boson \(\chi \) is decoupled in the action (4.13) so that the Euler Lagrange equations imply \(\partial _-\partial _+\chi =0\) and the field \(\partial _+\chi \) is left moving. Also, one can check via a brute force computation that
Here and below, the superscript “\(\mathrm{\scriptstyle L}\)” will be awarded to fields that depend only on the combination \(t+x\) of the space-time variables as a consequence of the equations of motion of the classical field theory. Similarly, the superscript “\(\mathrm{\scriptstyle R}\)” will be used to denote right-moving fields that are functions of \(t-x\).
The non-local quantities \(\psi _\pm ^{(\textrm{L})}\) are somewhat special. It turns out that as a consequence of the canonical structure induced by the cigar NLSM action (4.14), they satisfy the closed Poisson bracket algebra:
Since the fields are left moving, the equal-time Poisson bracket relations can be re-interpreted as brackets on the light cone with \(x_+=t+x\) and \(y_+=t+y\). Also, \(\epsilon (x)\) stands for the step function, normalised such that \(\partial _x\epsilon (x)=2\delta (x)\). The quantisation of the above Poisson relations leads to an operator algebra [73, 74] that is satisfied by the fundamental \({\mathbb {Z}}_n\) Fateev–Zamolodchikov parafermions. In the paper [74], these were introduced for integer “n” in the construction of the \({\mathbb {Z}}_n\) CFT models that describe the multicritical points of the \({\mathbb {Z}}_n\) statistical systems (certain generalisations of the \({\mathbb {Z}}_2\) invariant Ising model). For the quantum cigar NLSM, n is identified with the inverse Planck constant and must be considered to be a generic real number. It is worth mentioning, however, that the analysis of the critical behaviour of the \({\mathbb {Z}}_n\) lattice models played a crucial rôle in the quantisation of the so-called 2D sausage in [11], which is a massive deformation of the cigar NLSM formally corresponding to the \(\textrm{SU}(2)\) Klimčík model with \(\nu =0\). This is in spite of the fact that the \({\mathbb {Z}}_n\) CFTs have no direct relation to the NLSM. In Sect. 6.2, a generalisation [75,76,77] of the Poisson algebra (4.30) for any Lie group G is shown to arise naturally from the Gaudin model, see Eq. (6.13). Its quantum version is likewise expected to be important for the study of the quantum Klimčík model for general G.
Finally, let us note that keeping the combination \(z^{(\textrm{R})}=\xi z^{-1}\) fixed in taking the conformal limit would yield a Lax connection where \(\lim _{\kappa \rightarrow 1^-}\mathcal {L}_+^{(\textrm{inv})}\) is independent of the spectral parameter. The other connection component, via a transformation similar to the one in the l.h.s. of Eq. (4.27), can be brought to a form such that it depends only on the right-moving fields \(\partial _-\chi \) and
These right-moving classical parafermions Poisson commute with \(\psi _\pm ^{(\textrm{L})}\) and satisfy Poisson bracket relations similar to (4.30). This way, the theory possesses left- and right-moving fields forming two independent chiral algebras.
4.3.2 Chart II
For the asymptotically flat domain of the target manifold, i.e. chart II, the field \(\theta \) entering into the parameterisation of the group element (4.8) is swapped for \(\phi \) such that \(\theta \sim \sqrt{2(1-\kappa )}\ \text{ e}^{\phi }\). Then, the limit \(\kappa \rightarrow 1^-\) is taken with \(\phi \) assumed to be fixed. As a result of such a limiting procedure, some of the components of \(\mathcal {I}_\pm \) (2.8) with \(g_2\equiv \text {Id}\) and \(g_1\equiv g\) diverge. An explicit computation shows that
where the decomposition \( \mathcal {I}_\sigma =\mathcal {I}_\sigma ^+\ \texttt{e}_++\mathcal {I}_\sigma ^0\ \texttt{h}+\mathcal {I}_\sigma ^-\ \texttt{e}_-\) w.r.t. the \(\mathfrak {sl}(2)\) basis is being used (\(\sigma =\pm \)). Since the currents \(\mathcal {I}_\pm \) enter into the definition of \(\mathcal {L}_\pm ^{(\textrm{inv})}\), extra care is needed to ensure that the conformal limit of the Lax connection is well defined.
It is clear that the following limit exists:
as the similarity transformation compensates the singular behaviour of \(\mathcal {I}_+^A\). For the other component, to get a better idea of what is happening, it is useful to perform an expansion for \(1-\kappa \ll 1\):
Although the part of \(c^{-\frac{\texttt{h}}{4}}\,\mathcal {I}_-\,c^{+\frac{\texttt{h}}{4}}\) proportional to \(\texttt{e}_+\) contains a singularity of order \((1-\kappa )^{-1}\), it lies in the kernel of \((\text {Id}-\textrm{i}R)\) and therefore does not contribute in the limit \(\kappa \rightarrow 1^-\). The \(\texttt{e}_-\) component also tends to zero \(\sim (1-\kappa )\) as follows directly from formula (4.32) and the value of c given in (4.33). This way the conformal limit of \(\mathcal {L}_-^{(\textrm{inv})}\) exists and results in a particularly simple expression:
The obtained connection is somewhat of an intermediate quantity. The comparison to the Gaudin model will be performed with a Lax connection which is related to \(\partial _++\mathcal {L}_{\scriptscriptstyle \textrm{UV}}\) via a similarity transformation. An important point is that, working in chart II, the target space is asymptotically flat and the fields \((v,w,\phi )\) obey the free dynamics. Consequently, they can be written as a sum of a left-moving and right-moving field. In the notation of the work [53], one has
where the reason for the extra factors is to ensure that \(\phi _j^{(\textrm{L})},\phi _j^{(\textrm{R})}\) are all normalised in the same way, see Eq. (4.18). By considering the chiral fields \(\phi _j^{(\textrm{L,R})}\) rather than the original set \((v,w,\phi )\) itself, one has the freedom to perform more general similarity transformations of \(\partial _++\mathcal {L}_{\scriptscriptstyle \textrm{UV}}\) than would otherwise be possible.
Introduce a family of connections, depending on a parameter \(\omega \), as
with
Here, it is assumed that \((v,w,\phi )\) have been replaced by the chiral fields according to Eq. (4.35). The second term in the exponent in \(\varvec{\Omega }^{({\omega })}\) has been chosen to exactly cancel the dependence of \(\mathcal {L}_\mathrm{\scriptscriptstyle UV}^{(\omega )}\) on the right-moving bosons \(\phi _j^{(\textrm{R})}\). As a result,
This has to do with the fact that the corresponding “−” connection component vanishes under the transformation (4.36) and the zero-curvature representation \([\partial _++\mathcal {L}_+,\partial _-+\mathcal {L}_-]=0\) with \(\mathcal {L}_-=0\) leads directly to \(\partial _-\mathcal {L}_+=0\).
The resulting family of Lax connections reads
Here, in line with the notation of Ref. [53], we use the spectral parameter \(\rho ^2\), which is related to the original one via the formula
The fields \(V^{(\omega )}_\pm \) and \(V^{(\omega )}_0\) are expressed in terms of the left-moving bosons as
They turn out to satisfy a closed Poisson bracket algebra of \(\mathfrak {sl}(2)\) type. Starting from the Poisson bracket relations of the free chiral Bose fields
where \(\partial _x\epsilon (x)=2\delta (x)\), one can show thatFootnote 18
For general values of \(\omega \), the above relations are non-local in the sense that they contain the step function \(\epsilon (x_+-y_+)\), which is non-vanishing when \(x_+\) and \(y_+\) are distinct. For the special case when \(\omega = \big (\sqrt{1+\nu ^{-2}}\pm \nu ^{-1})^2\), the coefficient in front of the step function vanishes and the algebra becomes a classical version of the \({\mathfrak {sl}}(2)\) current algebra.
5 Klimčík Model in the Conformal Limit II: \(\varvec{{\mathcal {W}}}\)-Algebra and Local IMs for the \(\varvec{\textrm{SU}(2)}\) Case
Our interest in the conformal limit is partly motivated by the hope that the algebraic structures underlying the integrability of the Klimčík model can be more easily identified there. We are now going to discuss to which extent a paradigm that was recognised in integrable field theories of affine Toda type is realised in the Klimčík model. In both cases, one may exhibit important relations between the integrable structure and the extended conformal symmetry of the field theory. These can be described as follows.
The extension of the conformal symmetry relevant for the models of interest is generated by the modes of collections of left-moving and right-moving local fields, each generating a vertex operator algebra (VOA). The VOAs admit a free field realisation. It turns out that the combinations of the free fields representing generators of the VOA can be characterised by a condition on their commutation relations with a distinguished set of operators called screening charges.Footnote 19 By considering an extended set of screening charges one can define a commutative subalgebra of the VOA. This subalgebra has an infinite number of generators if the model of interest is integrable. The resulting family of commuting operators turn out to coincide with the local IMs of the theory.
The pattern outlined above was exhibited in affine Toda field theories. In this context, the characterisation of the full set of local conserved quantities using the screening charges was achieved by Feigin and Frenkel in [21]. For the case of the \(\textrm{SU}(2)\) Klimčík model, there exists evidence for a similar but in some respects more subtle picture through the dual representation discovered by Fateev [4], see [13].
One of our goals will be to exhibit the integrable structures more directly from the perspective of the sigma model formulation. To this aim, we start by describing the situation on the classical level. Compared to the affine Toda theories, we will see that the \(\textrm{SU}(2)\) Klimčík model displays at least two new features.
First, it turns out that the local conserved quantities are of somewhat limited interest at the classical level. Any classical NLSM of the type (4.1), not necessarily integrable, possesses two sets of local integrals of motion:
with \(m=1,2,\ldots \ \). This is a simple consequence of classical scale invariance. The integrands in the above formula are the mth powers of the Lorentz spin \(\pm 2\) components of the stress–energy momentum tensor. Since these components depend only on \(t\pm x\) for \(\phi ^j\) satisfying the classical equations of motion, it follows immediately that \(\partial _t\,\mathcal {Q}_{2m-1}^{(\textrm{L,R})}=0\) (with suitable boundary conditions imposed). For the \(\textrm{SU}(2)\) Klimčík model at \(\kappa \rightarrow 1^-\) it will turn out that the characterisation based on the classical screening charges yields precisely the IMs \(\mathcal {Q}_{2m-1}^{(\textrm{L,R})}\) defined in (5.1). The fact that these charges are present in any sigma model suggests that their existence by itself is not directly related to the integrability of the classical field theory. The situation will change drastically in the quantum case. We will later describe the procedure for constructing the quantum deformations of \(\mathcal {Q}_{2m-1}^{(\textrm{L,R})}\), which yields integral expressions over non-trivial densities that are not functionally dependent. It is expected that the resulting family of commuting operators appears in the conformal limit of the local conserved charges for the quantum \(\textrm{SU}(2)\) Klimčík model.
The \(\textrm{SU}(2)\) Klimčík model possesses another interesting feature. For a generic field theory, one expects the local charges to be given by integrals over densities formed from the generators of the extended conformal symmetry algebra appearing in the conformal limit. In the case at hand with \(\kappa \rightarrow 1^-\), it will turn out that the conserved charges can be represented as integrals over densities belonging to a (Poisson-)VOA which is strictly smaller than that describing the extended conformal symmetry. The relevance of this feature may not be immediately obvious. In Sect. 6.3, it will be related to a remnant of the gauge symmetry in the affine Gaudin model formulation of the \(\textrm{SU}(2)\) Klimčík model.
Here, we illustrate the basic aspects of this picture on the classical level. The first step is to describe the space of chiral local fields of the \(\textrm{SU}(2)\) Klimčík model in the conformal limit. It follows easily from the relation with the cigar CFT observed above that these generate a \(\textrm{U}(1)\otimes \mathcal {W}_\infty \) algebra, where \(\mathcal {W}_\infty \) is the extended algebra of conformal symmetry of the cigar NLSM. The rest of this section explains how the extended conformal symmetry and the local IMs (5.1) can be characterised in terms of screening charges. The dynamical meaning of the latter will be exhibited, governing the leading deviation between solutions to the equations of motion of the NLSM of our interest and the free fields describing the asymptotic behaviour of the classical solutions at infinite times.
5.1 Classical \(\varvec{{\mathcal {W}}_\infty }\) Algebra
The quantisation of the cigar NLSM results in a unitary CFT possessing a \(\mathcal {W}_\infty ^{(\textrm{L})}\otimes {\mathcal {W}}_\infty ^{(\textrm{R})}\) algebra of extended conformal symmetry with \(\mathcal {W}_\infty ^{(\textrm{L},\textrm{R})}\cong \mathcal {W}_\infty \) being the \(\mathcal {W}\)-algebra studied in Ref. [79]. For the classical field theory, the \(\mathcal {W}_\infty ^{(\textrm{L})}\otimes {\mathcal {W}}_\infty ^{(\textrm{R})}\) algebra is manifest through the presence of an infinite number of fields \(T_m^{(\textrm{L})}\) and \(T_m^{(\textrm{R})}\), which are local tensor densities of integer Lorentz spin m and \(-m\), respectively. Their special property is that, as a consequence of the equations of motion,
so that \(T_m^{(\textrm{L})}=T_m^{(\textrm{L})}(t+x)\) is a left-moving field, while \(T_m^{(\textrm{R})}=T_m^{(\textrm{R})}(t-x)\) is a right-moving field.
The presence of chiral fields in the cigar NLSM has already been observed in Sect. 4.3. However, the classical parafermions \(\psi _\pm ^{(\textrm{L})}\) and \(\psi ^{(\textrm{R})}_\pm \) given by Eqs. (4.28) and (4.31), respectively, are non-local fields. Their definition involves the dual field \(\alpha ^{(\textrm{D})}\), which is given by the integral expression (4.25). Nevertheless, one can consider combinations of the classical parafermions such that the dependence on \(\alpha ^{(\textrm{D})}\) cancels out. For instance,
are Lorentz spin \(\pm 2\) local fields, which coincide with the components of the stress–energy–momentum tensor of the cigar NLSM. There exists a left-moving spin \(+3\) local field, which is independent of \(\partial _+ T_2^{(\textrm{L})}\). Namely,
Parity symmetry yields a right-moving Lorentz spin \((-3)\) field, obtained from \(T_3^{(\textrm{L})}\) via the replacements \(\partial _+\rightarrow \partial _-\) and \(\psi _\pm ^{(\textrm{L})}\mapsto \psi _\pm ^{(\textrm{R})}\). Left-moving fields of spin 4 are \(\big (T_2^{(\textrm{L})}\big )^2\), \(\partial ^2_+T_2^{(\textrm{L })}\), \(\partial _+ T_3^{(\textrm{L})}\), and there is an extra one, \(T_4^{(\textrm{L})}\), which is not expressible as a differential polynomial in terms of the lower-spin fields. It takes the form
Notice that the definition of \(T_4^{(\textrm{L})}\) is ambiguous. One has the freedom of adding any linear combination of the spin 4 fields \(\big (T_2^{(\textrm{L})}\big )^2\), \(\partial ^2_+T_2^{(\textrm{L})}\) and \(\partial _+ T_3^{(\textrm{L})}\) as well as multiplying it by an overall factor. The choice (5.5) for the spin 4 current as well as (5.4) for the spin 3 one is mainly motivated by the fact that, written in terms of the classical parafermions, their expressions happen to be particularly simple. In general, for given \(m=2,3,\ldots \) the space of left moving currents is spanned by composite fields built from \(T^{(\textrm{L})}_j\) with \(j=2,3,\ldots m-1\) and their derivatives, as well as a single independent field \(T_m^{(\textrm{L})}\). A similar statement holds true for the right-moving fields.
The Lagrangian (4.14) induces a Poisson structure. The fields \({T}_m^{(\textrm{L})}\) and \({{T}}_m^{(\textrm{R})}\) turn out to obey a closed Poisson bracket algebra, which can be seen as the classical limit of the commutation relations for the quantum \(\mathcal {W}_\infty ^{(\textrm{L})}\otimes {\mathcal {W}}_\infty ^{(\textrm{R})}\) algebra. The Poisson brackets (PB) of any left-moving field with a right-moving one vanishes. The first few PB relations involving the set \(\{{T}_m^{(\textrm{L})}\}_{m=2}^\infty \) follow from the explicit expressions (5.3)–(5.5) as well as the PBs for the classical parafermions (4.30). A straightforward computation results in:
where the shortcut notation \(T_m = T_m^{(\textrm{L})}\) and \(\partial = \partial _+\) is being used in order to declutter the formula. The left-moving fields have been treated as a function of one variable \(x_+=t+x\) or \(y_+=t+y\). A similar Poisson algebra, obtained from the one above via the replacement \(x\rightarrow -x\) and \(y\rightarrow -y\), is formed by the right-moving fields \(\{{T}_m^{(\textrm{R})}\}_{m=2}^\infty \).
5.2 Free Field Realisation
We are now going to outline how solutions of the equations of motion for the conformal limits of the sigma model can be parameterised by free field data. This will lead us to a characterisation of the chiral local currents of the cigar NLSM as differential polynomials in the free fields satisfying a simple condition on their Poisson brackets with a distinguished observable called the screening charge.
Classical Solutions of the Cigar NLSM Our starting point is the description of the classical solutions to the cigar NLSM equations of motion that were presented in the lecture notes of Lukyanov and Zamolodchikov, published in [80]. It turns out that they can be parameterised by a quadruple of four functions—the classical parafermions that are introduced in Sect. 4.3. Combined with formulae (4.28) and (4.31), which allow one to map the values of \(\phi (t,x)\) and \(\alpha (t,x)\) and their time derivatives at some initial time slice \(t=t_0\) to the parafermions, this solves the Cauchy problem.
As a first step it is useful to observe that the definition of the parafermions in terms of the cigar sigma model coordinate fields \(\phi \) and \(\alpha \) given in (4.28) and (4.31) can be elegantly reformulated using the following \(\textrm{SL}(2)\) matrix
with \({\alpha }^{(\textrm{D})}\) being the dual field defined in (4.25). Namely,
where \(\sigma ^\pm =\frac{1}{2}(\sigma ^x\pm \textrm{i}\sigma ^y)\) and \((\sigma ^x,\sigma ^y,\sigma ^z)\) stand for the usual Pauli matrices. It is important to keep in mind that the classical parafermions are left-/right-moving fields as a consequence of the classical equations of motion, \(\psi _\pm ^{(\textrm{L})}(t,x)=\psi _\pm ^{(\textrm{L})}(t+x)\) and \(\psi _\pm ^{(\textrm{R})}(t,x)=\psi _\pm ^{(\textrm{L})}(t-x)\). Thus, the above formula specifies the light-cone derivatives of \(\varvec{\omega }(t,x)\) in terms of four functions of a single variable. Integrating Eq. (5.8) allows one to reconstruct the \(\textrm{SL}(2)\) matrix directly from \(\psi _\pm ^{(\textrm{L})}\), \(\psi _\pm ^{(\textrm{R})}\) and an integration constant \(\varvec{\omega }_0=\varvec{\omega }(0,0)\)Footnote 20:
Along with formula (5.7) that enables one to extract the fields \(\phi \) and \(\alpha \) from \(\varvec{\omega }(t,x)\), this provides a way of constructing solutions at least locally to the cigar NLSM equations of motion by means of the chiral data \(\psi _{\pm }^{(\textrm{L,R})}\), supplemented by the integration constant \(\varvec{\omega }_0\) needed to fix the zero modes of \(\phi \) and \(\alpha \).
For the Cauchy problem, one has at hand the values of \(\phi \) and \(\alpha \) and their derivatives \(\partial _t\phi \), \(\partial _t\alpha \) at some initial time slice. These are then used to specify the four functions \(\psi _\pm ^{(\textrm{L})}(t+x)\) and \(\psi _\pm ^{(\textrm{R})}(t-x)\) by means of (5.8), or equivalently (4.28) , (4.31) and (4.25), evaluated at \(t=t_0\). One then obtains the solutions \(\phi (t,x)\) and \(\alpha (t,x)\) at all times as functionals of the Cauchy data via Eqs. (5.9) and (5.7).
Free Fields Parameterisation and Scattering Problem Interpretation There is another way of parameterising solutions to the cigar NLSM. It uses the map (5.9) and (5.7) from the classical parafermions to the fundamental fields \((\phi ,\alpha )\), but the functions \(\psi ^{(\textrm{L})}_\pm \) and \(\psi ^{(\textrm{R})}_\pm \) themselves are specified in a different way. One takes
where \(\phi ^{(\textrm{L})},\alpha ^{(\textrm{L})}\) depend only on \(t+x\) and \(\phi ^{(\textrm{R})},\alpha ^{(\textrm{R})}\) on \(t-x\), as suggested by the superscript notation. The motivation for considering such a map has to do with the Hamiltonian structure of the cigar NLSM. Assuming that the fields \(\phi ^{(\textrm{L},\textrm{R})}\) and \(\alpha ^{(\textrm{L},\textrm{R})}\) satisfy the usual PBs for free chiral fields,
where \(\partial _x\epsilon (x)=2\delta (x)\), with vanishing Poisson brackets amongst left- and right-moving fields, one may show that the parafermionic Poisson algebra (4.30) follows from (5.10). For this reason, one sometimes refers to (5.10) as providing a “free field” realisation of the classical parafermions. A more detailed discussion of the Hamiltonian formalism for the cigar NLSM can be found in the lecture notes of Lukyanov and Zamolodchikov from [80].
In the present context, there exists an intuitive physical interpretation of the parameterisation of the classical parafermions using \(\alpha ^{(\textrm{L,R})}\) and \(\phi ^{(\textrm{L,R})}\). It has to do with the fact that the propagation of a classical string on the cigar target space manifold can be interpreted as a scattering process. There exists an important family of solutions to the cigar NLSM equations of motion such that for time \(t\rightarrow - \infty \) the fields take values in the semi-infinite cylindrical end of the cigar, where the average value \(\phi _0(t)=\int \text{ d }x\, \phi (t,x)\) is large and negative. As time increases the classical string approaches the tip of the cigar, gets reflected, and escapes back to the semi-infinite cylindrical end for \(t\rightarrow + \infty \). An illustration of the scattering process is provided in Fig. 2.
Scattering of a string in the cigar NLSM. Starting in the asymptotically flat domain the string (A) approaches the tip with some incoming momentum, (B) scatters and then (C) escapes back to the flat region. The initial (final) states of the scattering process are parameterised by the “in (out)” data \(\phi ^{(\textrm{L},\textrm{R})}\) and \(\alpha ^{(\textrm{L},\textrm{R})}\)
Consider the cigar NLSM action (4.14). In the limits \(t\rightarrow \pm \infty \) when the zero mode \(\phi _0(t)=\int \text{ d }x\, \phi (t,x)\) becomes large and negative, the term \(\text{ e}^{2\phi }\) in the denominator is negligibly small. The solutions of the Euler–Lagrange equations may then be approximated as
where the ellipses denote terms that are suppressed as \(\text{ e}^{2\phi _0}\). The four functions \(\phi ^{(\textrm{L},\textrm{R})}\) and \(\alpha ^{(\textrm{L},\textrm{R})}\) can therefore be used to parameterise the degrees of freedom of an asymptotic “in” state. The relation between the “in” data and the values of the fields \(\phi (t,x)\) and \(\alpha (t,x)\) at finite times is described by a complicated, non-local functional. Determining the latter amounts to an explicit integration of the equations of motion. Formula (5.12) can be understood as an approximation to this functional, valid for \((-\phi _0)\gg 1\) with the next correction being of order \(\text{ e}^{2\phi _0}\).
It is not hard to see that the asymptotic values of \(\phi \) and \(\alpha \) for \(t\rightarrow \pm \infty \) appearing in (5.12) coincide with the fields \(\phi ^{(\textrm{L},\textrm{R})}\) and \(\alpha ^{(\textrm{L},\textrm{R})}\) previously used in the free field realisation of the classical parafermions (5.10), as anticipated in the notations. Indeed, chiral fields such as \(\psi _\pm ^{(\textrm{L})}\) and \(\psi _\pm ^{(\textrm{R})}\) can be considered at \(t\rightarrow \pm \infty \) where the suppression of terms of order \(\text{ e}^{2\phi _0}\) will relate the original expressions for the classical parafermions (4.28),(4.31) to (5.10). The procedure for constructing solutions \((\phi ,\alpha )\) using formulae (5.7), (5.9) with the parafermions as in (5.10) thereby gets interpreted as an explicit description of the scattering functional relating asymptotic data to \(\big (\phi (t,x),\alpha (t,x)\big )\) at any time t.
The interpretation also suggests that the map from the free field data \((\phi ^{(\textrm{L},\textrm{R})},\alpha ^{(\textrm{L},\textrm{R})}, \,\varvec{\omega }_0)\) to solutions \((\phi ,\alpha )\) should define a functional that preserves the Poisson structure. Indeed, the Poisson brackets do not depend on the choice of time slice t at which they are evaluated. As a result, computing them at finite times by means of the canonical bracket for \((\phi ,\alpha )\) should coincide with a calculation performed at \(t\rightarrow \pm \infty \), when the approximation \(\phi (t,x)\approx \phi ^{(\textrm{L})}(x_+)+\phi ^{(\textrm{R})}(x_-)\) and \(\alpha (t,x)\approx \alpha ^{(\textrm{L})}(x_+)+\alpha ^{(\textrm{R})}(x_-)\) with the chiral fields obeying (5.11) is applicable. This could be seen as a “physical” explanation of a point made previously above. Namely, that the PB relations for the classical parafermions give the same result (4.30) whether they are determined via formulae (4.28) with \(\partial _t\phi \) and \(\partial _t\alpha \) substituted in terms of the conjugate momenta or via the realisation (5.10),(5.11).
Free Field Realisation of the \({\mathcal {W}_\infty }\) Algebra and Screening Charges Consider the local fields \(T_m^{(\textrm{L})}\) that generate the \(\mathcal {W}_\infty \) algebra. Taking their expressions (5.3)–(5.5) in terms of the classical parafermions and substituting in the free field realisation (5.10), they can all be rewritten as differential polynomials in \(\partial _+\phi ^{(\textrm{L})}\) and \(\partial _+\alpha ^{(\textrm{L})}\):
An alternative way of obtaining the above formulae is to consider, say, \(T_2^{(\textrm{L})}=\big ((\partial _+\phi )^2+(\partial _+\alpha )^2\big )/(1+\text{ e}^{2\phi })\) at \(t\rightarrow \pm \infty \). Then, the exponential \(\text{ e}^{2\phi }\) can be neglected and \(\phi \), \(\alpha \) replaced by \(\phi ^{(\textrm{L,R})}\) and \(\alpha ^{(\textrm{L,R})}\) by means of (5.12) with the ellipses ignored. Notice that the Poisson bracket relations (5.6) for the \(\mathcal {W}_\infty \) algebra are preserved, i.e. they follow from the free field expressions for \(T_m^{(\textrm{L})}\) combined with the Poisson brackets (5.11).
The scattering map relating the free fields to \((\phi ,\alpha )\) is highly non-local. Arbitrary combinations of \((\phi ^{(\textrm{L},\textrm{R})},\alpha ^{(\textrm{L},\textrm{R})})\) will not map to local fields in the NLSM. In this regard, the currents \(T_m^{(\textrm{L})}\) (5.13) are distinguished. They are differential polynomials built from \(\partial _+\phi ^{(\textrm{L})}\) and \(\partial _+\alpha ^{(\textrm{L})}\) that correspond to chiral fields in the cigar sigma model which are local in the fundamental fields \((\phi ,\alpha )\). Our next goal will be to find a purely algebraic way of finding the differential polynomials that possess this special property. It will be explained how they all can be characterised in terms of their commutation relations with the so-called screening charges.
A key observation is expressed by the following formula displaying the subleading corrections in the relation between the fields \((\phi ^{(\textrm{L},\textrm{R})},\alpha ^{(\textrm{L},\textrm{R})})\) and \((\phi ,\alpha )\) in the limit \(\phi _0\rightarrow -\infty \):
The fields \(V_{\textrm{cig}}^{(\mathrm{L/R})}(x_\pm )\) appearing here are given by
and will turn out to be closely related to the classical analogues of the screening charges relevant for our problem. Formula (5.14) can be verified as follows. One starts with the map between \((\phi ^{(\textrm{L},\textrm{R})},\alpha ^{(\textrm{L},\textrm{R})})\) and \((\phi ,\alpha )\) given by Eqs. (5.7), (5.9) and (5.10) and shows that the matrix \(\varvec{\omega }(t,x)\) can be brought to the form
This, itself, is a consequence of the elementary relations
Since \((\sigma ^y\pm \textrm{i}\sigma ^z)\,V_{\textrm{cig}}^{(\textrm{L,R})}(x_\pm )\) commutes with itself for different values of \(x_\pm \), the path-ordered exponent becomes an ordinary integral as in (5.16). Note that the constant \(\textrm{SL}(2)\) matrix \(\varvec{\omega }_0\) was set to \(\text{ e}^{-\textrm{i}\alpha ^{(\textrm{L})}(0)\,\sigma ^z}\,\text{ e}^{-(\phi ^{(\textrm{L})}(0)+\phi ^{(\textrm{R})}(0)-\log (2))\,\sigma ^x}\text{ e}^{\textrm{i}\alpha ^{(\textrm{R})}(0)\,\sigma ^z}\) in order to simplify the final result, which is equivalent to fixing the zero modes of \(\phi ^{(\textrm{L})}+\phi ^{(\textrm{R})}\) and \(\alpha ^{(\textrm{L},\textrm{R})}\).
We now return to the question that was previously raised: suppose one has a Lorentz spin m differential polynomial \(F_m(x_+)\) in \(\partial _+\alpha ^{(\textrm{L})}\) and \(\partial _+\phi ^{(\textrm{L})}\). Which conditions ensure that the free field realisation of \(F_m(x_+)\) is related to a local expression in the fundamental fields \(\phi \) and \(\alpha \)? A necessary requirement is that the equal-time Poisson brackets of the polynomial \(F_m(t+x)\) with the fundamental fields \(\phi (t,y)\) and \(\alpha (t,y)\) should not contain the step function \(\epsilon (x-y)\). The expression for \(\phi (t,y)\) and \(\alpha (t,y)\) in terms of the free fields \(\phi ^{(\textrm{L},\textrm{R})}\) and \(\alpha ^{(\textrm{L},\textrm{R})}\) can be approximated by (5.14). Inspection of that formula shows that terms proportional to the step function \(\epsilon (x-y)\) could originate from the Poisson bracket of \(F_m(x_+)\) with \(V_{\textrm{cig}}^{(\textrm{L})}\). It takes the form of a sum \(\sum _{j=0}^m C_j(x_+)\, \delta ^{(j)}(x_+-y_+)\) with field dependent coefficients \(C_j(x_+)\) so that if \(C_0(x_+)\) does not vanish a subsequent integration w.r.t. \(y_+\) would yield a step function. Therefore, a necessary condition for locality is that
One can check that the generators \(T_m^{(\textrm{L})}\) of the classical \(\mathcal {W}_\infty ^{(\textrm{L})}\)-algebra, explicitly given for \(m=2,3,4\) in (5.13), satisfy (5.17). It turns out that all solutions to the conditions (5.17) represent elements of the \(\mathcal {W}_\infty ^{(\textrm{L})}\)-algebra.
We may note that (5.17) ensures that the Poisson bracket \(\{F_m(x_+),V_{\textrm{cig}}^{(\textrm{L})}(y_+)\}\) is a total derivative w.r.t. \(y_+\) of an expression that does not contain the \(\epsilon \) - function. This condition is unchanged under the replacement
where \(c_{\textrm{cig}}\) is an arbitrary constant, since the Poisson brackets of \(F_m(x_+)\) with the added term would automatically be a total derivative in \(y_+\). For reasons that will be explained in the next subsection, it is convenient to introduce the dynamical quantity
As discussed above, the requirement on the density (5.17) is unchanged if \(V_{\textrm{cig}}^{(\textrm{L})}\) (5.15) is swapped for \(V_+^{(1)}\). Moreover, by formally integrating both sides of that equation w.r.t. \(y_+\), ignoring any boundary terms, it can be equivalently rewritten as
with the notation \(\sim \) indicating equality up to terms that vanish when \(\text{ e}^{2\phi ^{(\textrm{L})}}\) is periodic. We refer to the obtained formula as the condition of quasi-commutativity with the classical screening charge \(\mathcal {X}_0\). Thus, one arrives at the conclusion that the classical \(\mathcal {W}_\infty ^{(\textrm{L})}\)-algebra can be characterised as the set of differential polynomials formed out of \(\partial _+\phi ^{(\textrm{L})}\) and \(\partial _+\alpha ^{(\textrm{L})}\) that quasi-commute with the classical screening charge.
5.3 Classical Screening Charges and Local IMs
The integrable structure of the Klimčík model induces a set of local and non-local IMs in the field theory underlying its conformal limit. One may use the previous discussion in order to get a Poisson-algebraic characterisation of the local conserved quantities. The key idea is to use an approximate description of the target of the \(\textrm{SU}(2)\) Klimčík model for \(\kappa \) close to 1 as the manifold defined by gluing the two cigars associated to chart I and III to the cylinder representing chart II, see Fig. 1. We will identify the local IMs as the dynamical quantities that are conserved in both of the cigar NLSMs depicted on the left and right sides of that figure. The resulting conditions are then reformulated algebraically in terms of a quasi-commutativity condition with the classical screening charges.
Consider the \(\textrm{SU}(2)\) Klimčík model as described by charts I, II and III that were introduced in the previous section. For \(1-\kappa \) very small we expect that there exist field configurations such that \((\phi ,\alpha )\) take values sufficiently far from the tips of both cigars, where the target space manifold is approximately flat, i.e. in chart II. In that coordinate chart, using the left-moving fields \(\phi ^{(\textrm{L})}_1,\phi ^{(\textrm{L})}_2,\phi ^{(\textrm{L})}_3\) defined in Eq. (4.35), the local IMs can be represented in the form
where \(F_{m}^{\mathrm{(II)}}\) is a differential polynomial of Lorentz spin m in the fields \(\partial _+\phi ^{(\textrm{L})}_1,\partial _+\phi ^{(\textrm{L})}_2,\partial _+\phi ^{(\textrm{L})}_3\).
As long as \(1-\kappa \) is small but non-vanishing, chart II would overlap with chart I. Up to corrections of order \((1-\kappa )^2\), the action in that chart is given by that of the cigar NLSM \(\mathcal {A}_{\textrm{cig}}[\phi ,\alpha ]\) plus free field \(\chi \), see formula (4.13), where the fields \(\alpha \) and \(\chi \) are defined in Eq. (4.15). We expect that the local conserved quantities of the \(\textrm{SU}(2)\) Klimčík model in the conformal limit are contained in a subset of those for the cigar sigma model and free bosonic field:
Staying away from the tip of the cigar NLSM allows one to approximate the expressions for \(T_j^{(\textrm{L})}\) containing factors \((1+\text{ e}^{2\phi })^{-1}\), see for example Eqs. (5.3) and (5.4), by the expressions (5.13) involving the free chiral fields \(\alpha ^{(\textrm{L})}\) and \(\phi ^{(\textrm{L})}=\phi _3^{(\textrm{L})}\). Also, the decoupled boson \(\chi \) can be written as the sum of a left-moving and right-moving field,
up to corrections that vanish for \(1-\kappa \) small. Comparing Eqs. (5.21) and (5.22), with \(\alpha ^{(\textrm{L})}\) and \(\chi ^{(\textrm{L})}\) expressed in terms of \(\phi ^{(\textrm{L})}_1\) and \(\phi ^{(\textrm{L})}_2\), we arrive at a first constraint on the form of \(F_{m}^{\mathrm{(II)}}\).
The key requirement to be imposed is that the local IMs are simultaneously contained in the set of local conserved quantities of the cigar sigma model and free bosonic field associated to chart III. This means that, in the overlap of charts II and III, \(\mathcal {Q}_{m-1}^{(\textrm{L})}\) admits a representation of the form
where \({\tilde{T}}_j^{(\textrm{L})}\) are the left-moving currents for the cigar with action \({\mathcal {A}}_{\textrm{cig}}[-\phi ,{\tilde{\alpha }}]\) (4.14) and \({\tilde{\chi }}\) is given in Eq. (4.20). Using the approximate relations \({\tilde{\alpha }}\asymp {\tilde{\alpha }}^{(\textrm{L})}(x_+)+ {\tilde{\alpha }}^{(\textrm{R})}(x_-)\) and \({\tilde{\chi }}\asymp {\tilde{\chi }}^{(\textrm{L})}(x_+)+ {\tilde{\chi }}^{(\textrm{R})}(x_-)\), and then swapping \(\big ({\tilde{\alpha }}^{(\textrm{L})},{\tilde{\chi }}^{(\textrm{L})}\big )\) in favour of \(\big (\phi ^{(\textrm{L})}_1,\phi ^{(\textrm{L})}_2\big )\) a second ansatz for the form of \(F_{m}^{\mathrm{(II)}}\) is obtained. The agreement of the two expressions holds if the densities appearing in (5.22) and (5.24) coincide up to a total derivative, i.e.
This requirement turns out to be sufficiently strong to fix the local conserved charges completely.
Let us illustrate how this works concretely, starting from (5.22) on the example of \(F_2\). First, one needs at hand the relations between the pairs \(\big (\alpha ^{(\textrm{L})},\chi ^{(\textrm{L})}\big )\), \(\big ({\tilde{\alpha }}^{(\textrm{L})},{\tilde{\chi }}^{(\textrm{L})}\big )\) and \(\big (\phi _1^{(\textrm{L})},\phi _2^{(\textrm{L})}\big )\). These can be easily established from the definitions (4.15), (4.20), (4.35) which yields
Then, the most general form for \(F_2^{\mathrm{(I)}}\), ignoring total derivatives and fixing the overall normalisation, is \(F_2^\mathrm{(I)}=T_2^{(\textrm{L})}+c_2\,(\partial _+\chi )^2\) with \(c_2\) an arbitrary numerical constant and \(T_2^{(\textrm{L})}=(\partial _+\phi ^{(\textrm{L})})^2+(\partial _+\alpha ^{(\textrm{L})})^2\). In a similar way \({F}_2^\mathrm{(III)}=(\partial _+\phi ^{(\textrm{L})})^2+ (\partial _+{\tilde{\alpha }}^{(\textrm{L})})^2+{\tilde{c}}_2\,(\partial _+{\tilde{\chi }})^2\). Rewriting these expressions in terms of \(\phi _j^{(\textrm{L})}\) via formula (5.26), one finds that (5.25) implies \(c_2={\tilde{c}}_2=1\). Hence,
Notice that the integrand is the Lorentz spin \(+2\) component of the stress–energy–momentum tensor considered in chart II.
We are now going to argue that the requirement (5.25) is equivalent to the pair of conditions
Here, the classical screening charges \(\mathcal {X}_0\) and \(\mathcal {X}_1\) are defined as follows
with
Indeed, consider the first of the Poisson quasi-commutativity conditions involving \(\mathcal {X}_0\). The integrand of the screening charge, with \(\phi _1^{(\textrm{L})}\) and \(\phi _2^{(\textrm{L})}\) swapped for \(\chi ^{(\textrm{L})}\) and \(\alpha ^{(\textrm{L})}\) according to Eq. (5.26) takes the form \(V_+^{(1)}=\sqrt{1+\nu ^2}\,\big (\textrm{i}\,\partial _+\phi _3^{(\textrm{L})}+\partial _+\alpha ^{(\textrm{L})}\big )\, \text{ e}^{2\phi _3^{(\textrm{L})}}\). In particular, it contains no dependence on the field \(\chi ^{(\textrm{L})}\), while \(\alpha ^{(\textrm{L})}\) and \(\phi ^{(\textrm{L})} = \phi ^{(\textrm{L})}_3\) appear in the same combination as for \(V_+^{(1)}\) from (5.19). As such, it follows from the discussion in the previous subsection that the condition \(\{F_{m}^{\mathrm{(I)}}(x_+),\mathcal {X}_0\}\,\sim 0\) is solved by densities of the form \(F_{m}^{\mathrm{(I)}}\big [T_j^{(\textrm{L})},\partial _+\chi \big ]\). This way, the first formula in (5.28) is equivalent to the ansatz (5.22). In an analogous way, by noticing that \(V_-^{(1)}= \sqrt{1+\nu ^2}\,\big (\textrm{i}\,\partial _+\phi _3^{(\textrm{L})}+\partial _+{\tilde{\alpha }}^{(\textrm{L})}\big )\, \text{ e}^{-2\phi _3^{(\textrm{L})}}\) one sees that \(\mathcal {X}_1\) is the classical screening charge corresponding to the cigar with action \({\mathcal {A}}_{\textrm{cig}}[-\phi ,{\tilde{\alpha }}]\). Hence, one concludes that \(\{\mathcal {Q}_m^{(\textrm{L})},\mathcal {X}_1\}\,\sim 0\) is equivalent to the representation (5.24). In order to satisfy both conditions at the same time, we need to have (5.25).
Formula (5.28) can be analysed directly. One starts by considering an arbitrary differential polynomial in \(\partial _+\phi _j^{(\textrm{L})}\) of the form
Using the free field Poisson bracket relations for \(\phi _j^{(\textrm{L})}\) (4.42), one computes the PBs of \(F_{m}(x_+)\) with the field \(V_+^{(1)}(y_+)\). Poisson quasi-commutativity with the screening charge \(\mathcal {X}_0\) requires that the term in front of the \(\delta \)-function vanishes, as in Eq. (5.17). This leads to a set of linear relations amongst \(F_{i_1\ldots i_k}^{j_1\ldots j_k}\), which can be used to determine some of the coefficients. The next step involves the screening charge \(\mathcal {X}_1\). Imposing a requirement similar to (5.17) with \(V_+^{(1)}\) swapped for \(V_-^{(1)}\) is too restrictive. The density \(F_{m+1}(x_+)\) can only be expressed in terms of \({\tilde{T}}_j^{(\textrm{L})}\) and \(\partial _+{\tilde{\chi }}\) up to a total derivative, see (5.25), and the Poisson brackets of this derivative term with \(V_-^{(1)}(y_+)\) would lead to a nonzero \(C_0(x_+)\). Nevertheless, it must be the case that
Regarding the above as a condition on the density typically yields an overconstrained system of linear equations on the remaining coefficients \(F_{i_1\ldots i_k}^{j_1\ldots j_k}\) which determines them up to an overall multiplicative factor (that may be zero). Applying the above procedure, one finds that
with \(m=1,2,\ldots \), while there are no local IMs labelled by an even subscript that obey (5.28). Note that the integrand in \(\mathcal {Q}_{2m-1}^{(\textrm{L})}\) is nothing but the mth power of the Lorentz spin \(+2\) component of the stress–energy–momentum tensor for the \(\textrm{SU}(2)\) Klimčík model at \(\kappa \rightarrow 1^-\), as already mentioned in the introduction of this section.
One may find it intriguing to observe that the integrands in (5.29) coincide with the fields \(V_\pm ^{(1)}\) that appear in the connection \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}^{(\omega )}\) at \(\omega =1\), see Eqs. (4.39) and (4.41). We will elaborate on the implications of this observation in Sect. 7.
5.4 Corner-Brane \(\varvec{{\mathcal {W}}}\)-Algebra
It follows from our discussion in Sect. 5.2 that the screening charges describe the leading-order deviations of the dynamics from the free field dynamics, as expressed by (5.14). We have furthermore seen that there is a Poisson-algebraic characterisation of the local charges that remain conserved under these perturbations, expressed by the conditions (5.28). These offer a concise characterisation of the integrable structure in terms of the screening charges, representing a classical analogue of the description developed by Feigin and Frenkel for affine Toda theories in [21] to our case. It seems interesting to note that the local IMs \(\mathcal {Q}_m^{(\textrm{L})}\) possess another characterisation in terms of a second pair of screening charges,
Here, the notation \(V_{\pm }^{(-1)}\) reflects the fact that these fields appear in the matrix elements of the family of Lax connections \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}^{(\omega )}\) (4.39) specialised to \(\omega =-1\), compare the above formula with (4.41). Poisson quasi-commutativity with \(\mathcal {X}_0^{\scriptscriptstyle \mathrm CB}\) gives back a \(\mathcal {W}_\infty \otimes \textrm{U}(1)\) algebra, where the currents are realised differently in terms of the three bosonic fields \(\phi ^{(\textrm{L})}_j\). The two conditions taken together:
yield the same set of local IMs (5.33). Although the form of \(\mathcal {Q}_{2m-1}^{(\textrm{L})}\) is somewhat trivial for the classical field theory, let us mention that the analogue of these statements holds in the quantum case [81]. There it is far from obvious that the set of local IMs of the quantum Fateev integrable structure, which are highly non-trivial densities built from three bosonic fields (see, e.g. “Appendix A” of [81]), can be characterised in these two different ways.
Closely related is the fact that the integrable structure of the \(\textrm{SU}(2)\) Klimčík model has a remarkable feature: the local densities used to construct conserved charges can be taken from an honest subalgebra of \(\mathcal {W}_\infty \otimes \textrm{U}(1)\) which is a non-trivial \(\mathcal {W}\)-algebra of its own. At the classical level, its generators \(W_m\) are defined through the pair of conditions
Notice that the above turns out to be a weaker requirement than simultaneous Poisson quasi-commutativity with \(\mathcal {X}_0\) and \(\mathcal {X}_1\) (5.28) or \(\mathcal {X}^{\scriptscriptstyle \mathrm CB}_0\) and \(\mathcal {X}^{\scriptscriptstyle \mathrm CB}_1\) (5.35). The last two are satisfied only by the integrated quantities \(\mathcal {Q}_{2m-1}^{(\textrm{L})}\), while there exist non-trivial differential polynomials in \(\partial _+\phi _j^{(\textrm{L})}\) that obey (5.36).
As will be pointed out in Sect. 6.3, the Poisson-VOA generated by the densities \(W_m\) is isomorphic to the classical chiral algebra of the coset
The quantum version of this statement has been proven in Ref. [82]. In order to distinguish the two \(\mathcal {W}\)-algebras, whose isomorphism is not obvious, we’ll refer to the one obtained by means of the screening charges as the corner-brane \(\mathcal {W}\)-algebra. This terminology comes from the work [81], where the algebra appeared in the study of a 2D QFT with boundary interaction called the “pillow-brane” model.
As an illustration, we are going to present the first two non-trivial currents satisfying (5.36). Unlike the case of the classical \(\mathcal {W}_\infty \otimes \textrm{U}(1)\) algebra, there is no Lorentz spin \(+1\) field. The simplest left-moving field turns out to be the Lorentz spin \(+2\) component of the stress–energy momentum tensor:
The space of spin \(+3\) local fields is spanned by the “descendent” \(\partial _+ W_2^{(\textrm{L})}\). At spin \(+4\), one has the non-trivial current
Starting directly from the PB relations of the classical \(\mathcal {W}_\infty \) algebra (5.6) one can check by direct calculations that the PBs of the fields \(W_m^{(\textrm{L})}\) form a closed algebra, at least for the first few currents of lowest Lorentz spin (see also Eqs. (6.31) and (6.37)).
The appearance of the coset \(\mathcal {W}\)-algebra (5.37) in the \(\textrm{SU}(2)\) Klimčík model may seem quite surprising. We will later see that the affine Gaudin model formulation offers a natural explanation of this remarkable feature.
6 Klimčík Model in Conformal Limit III: As Chiral AGM
The goal of this section is to revisit the conformal limit of the Klimčík model from the point of view of affine Gaudin models. More precisely, starting from the description made in Sect. 3.3 of the Klimčík model as a relativistic realisation of an AGM, we will show that this structure decomposes into two decoupled AGM realisations in the conformal limit, describing the left-moving and right-moving degrees of freedom of the UV fixed point. In particular, we will explain how the integrable and chiral structures of this conformal limit (described in the previous sections for the \(\textrm{SU}(2)\) case) naturally arise in the formalism of affine Gaudin models.
6.1 Conformal Limit of the AGM Underlying the Klimčík Model
Twist Function and Punctures Recall that the non-chiral Klimčík model, before taking the conformal limit, is described as a relativistic realisation of the AGM with twist function \(\varphi (z)\) defined in Eq. (3.34). In particular, this AGM possesses 4 punctures \(z_r\) and 4 levels \(\ell _r\), given, respectively, by Eq. (3.35) and Eq. (3.36). It is clear from the latter equation and the RG flow (4.4) of the Klimčík model that these levels \(\ell _r\) are RG invariants. In contrast, the punctures \(z_r\) are not invariant and flow to either 0 or \(\infty \) in the conformal limit. Recall, however, from Sect. 4.3 that the coordinate z on \(\mathbb{C}\mathbb{P}^1\) is not the best suited choice of spectral parameter to describe the chiral limit of the Klimčík model: indeed, it was shown in this subsection that one should consider instead the rescaled spectral parameters \(z^{(\mathrm L)}= \xi \,z\) and \(z^{(\mathrm R)}= \xi \,z^{-1}\), which allow one to single out, respectively, the left-moving fields and right-moving fields contained in the Lax matrix in the conformal limit. In particular, since the parameter \(\xi \) tends to 0 in this limit, these rescalings of the spectral parameter have some important consequences on the structure of the AGM underlying the construction and the conformal limit of its punctures.
To describe this more concretely, let us focus for the moment on the spectral parameter \(z^{(\mathrm L)}= \xi \,z\). In this coordinate, the AGM underlying the Klimčík model is described by the twist function \(\xi ^{-1}\varphi \bigl (\xi ^{-1}z^{(\mathrm L)}\bigr )\), with poles at the points \((\xi z_1,\xi z_2,\xi z_3,\xi z_4)\). The latter do not all flow to 0 or \(\infty \), contrarily to the unrescaled punctures \(z_r\), but rather to \((0,4/(1+\nu ^2),0,-4\nu ^2/(1+\nu ^2))\). It will be useful to consider the UV limit of the twist function for the spectral parameter \(z^{(\mathrm L)}\), i.e. the quantity
A direct computation shows that
where \(K_{\scriptscriptstyle {\textrm{UV}}}\) is defined in Eq. (4.7). The 1-form \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\text {d}z^{(\mathrm L)}\) has 3 simple poles, located at
This is quite natural: indeed, we have observed above that the punctures \(\xi z_r\) of the initial AGM flow to these points in the conformal limit. Note that one could have expected \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\text {d}z^{(\mathrm L)}\) to have a double pole at 0, since both \(\xi z_1\) and \(\xi z_3\) flow to 0. Recall, however, that the initial twist function possesses a simple zero at 0: the two simple poles \(\xi z_1\) and \(\xi z_3\) therefore collide with this zero, resulting in only a simple pole at \(z^{(\mathrm L)}_3 = 0\) in the limit. To summarise, the conformal limit makes us pass from a twist function with 4 poles and 2 zeroes to one with 3 poles and 1 zero. This collision procedure and the resulting reduction in the number of punctures will play an important role in the description of the AGM structure underlying the chiral Klimčík model. We will see in Sect. 10.2 that similar phenomena also appear for more general models. One easily checks that the residues \(\displaystyle \ell ^{(\mathrm L)}_r = \mathop {\text {res}\,}_{z^{(\mathrm L)}={z^{(\mathrm L)}_r}} \varphi ^{(\mathrm L)}(z^{(\mathrm L)})\text {d}z^{(\mathrm L)}\) are given by
As one can expect, the first two levels \(\ell ^{(\mathrm L)}_1\) and \(\ell ^{(\mathrm L)}_2\) are, respectively, equal to the levels \(\ell _2\) and \(\ell _4\) of the AGM before taking the conformal limit, while the last one \(\ell ^{(\mathrm L)}_3\) is equal to \(\ell _{1}+\ell _{3}\).
Similar results hold for the AGM considered in the spectral parameter \(z^{(\mathrm R)}= \xi \,z^{-1}\). In particular, one finds
We note that the function \(\varphi ^{(\mathrm R)}\) in fact coincides with the opposite of the function \(\varphi ^{(\mathrm L)}\). This is a particularity of the Klimčík model, whose action (2.2), (2.4) possesses the discrete symmetry \(\varepsilon _{1,2}\mapsto -\varepsilon _{1,2}\) and \(x\mapsto -x\). As a result, the 1-form \(\varphi (z)\text {d}z\) describing the AGM before the UV limit is odd under the transformation \(z\mapsto 1/z\). The 1-form \(\varphi ^{(\mathrm R)}(z^{(\mathrm R)})\text {d}z^{(\mathrm R)}\) then has three simple poles \((z^{(\mathrm R)}_1,z^{(\mathrm R)}_2,z^{(\mathrm R)}_3)\) which are equal to their “left” counterparts \((z^{(\mathrm L)}_1,z^{(\mathrm L)}_2,z^{(\mathrm L)}_3)\) described above, with residues \((\ell ^{(\mathrm R)}_1,\ell ^{(\mathrm R)}_2,\ell ^{(\mathrm R)}_3)\) equal to \(-(\ell ^{(\mathrm L)}_1,\ell ^{(\mathrm L)}_2,\ell ^{(\mathrm L)}_3)\).
Similarly to the above discussion for \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\), the simple pole \(z^{(\mathrm R)}_3 = 0\) arises from the collision in the conformal limit of the two poles \(\xi z_2^{-1}\) and \(\xi z_4^{-1}\) of \(-\xi \,z^{(\mathrm R)}\,^{-2} \varphi \bigl ( \xi \,z^{(\mathrm R)}\,^{-1} \bigr )\) with its zero 0. Let us note that this zero corresponds to the one at \(z=\infty \) in the initial twist function \(\varphi (z)\text {d}z\): in particular, the zero eliminated by the collision procedure in the spectral parameter \(z^{(\mathrm R)}\) is different from the one eliminated in the spectral parameter \(z^{(\mathrm L)}\). (Moreover, the poles that collide with this zero are also different in the two different spectral parameters.)
Gaudin Lax Matrix and Realisation Our main goal in the rest of this subsection is to interpret \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\) and \(\varphi ^{(\mathrm R)}(z^{(\mathrm R)})\) as the twist functions of two distinct AGMs describing the two chiral halves of the UV fixed point of the Klimčík model. The formal AGM corresponding to these twist functions are described by Gaudin Lax matrices
for \(\mathrm M = \mathrm L, \mathrm R\) and where \({\mathcal {J}}_r^{(\mathrm M)}\) are Kac–Moody currents with levels \(\ell ^{(\mathrm M)}_r\), which generate the unreduced algebra of observables \({\mathcal {A}}^{(\mathrm M)}\) of these AGMs. We now want to find how these formal AGMs can be naturally realised in the UV fixed point of the Klimčík model. For that, we will consider the conformal limit of the Gaudin Lax matrix
in the relativistic realisation describing the non-chiral model. The Kac–Moody currents \({\mathcal {J}}_r^\rho \) entering this object are realised in terms of the canonical fields \((g_1,X_1,g_2,X_2)\) in \(T^*(G\!\times \! G)\) as in Eq. (3.37). They depend only on the RG invariants \(K/\varepsilon _{1,2}\) and thus are themselves invariant if we assume that the canonical fields are unaffected by the RG flow. We will suppose that this is the case here and will comment further on this assumption in the next paragraph. As for the twist function, we need to perform the conformal limit working with either \(z^{(\mathrm L)}= \xi \,z\) or \(z^{(\mathrm R)}= \xi \,z^{-1}\) fixed. Focussing on \(z^{(\mathrm L)}\) first, we find
This suggests to interpret this quantity as the realisation of the formal Gaudin Lax matrix \(\Gamma ^{(\mathrm L)}(z^{(\mathrm L)})\) described above and thus to define a realisation \(\rho ^{(\mathrm L)}_\textrm{I}: {\mathcal {A}}^{(\mathrm L)}\rightarrow {\mathcal {F}}\bigl [T^*(G\!\times \! G)\bigr ]\) by
The index \(\textrm{I}\) in this equation will be explained in the next paragraph. The fact that \(\rho ^{(\mathrm L)}_\textrm{I}\) is a Poisson map is ensured by its definition through a limit of \(\Gamma (z)\): indeed, by construction, the fields \({\mathcal {J}}_2^\rho \), \({\mathcal {J}}_4^\rho \) and \({\mathcal {J}}_1^\rho +{\mathcal {J}}_3^\rho \) are Kac–Moody currents in \({\mathcal {F}}\bigl [T^*(G\!\times \! G)\bigr ]\) with respective levels \(\ell ^{(\mathrm L)}_1 = \ell _2\), \(\ell ^{(\mathrm L)}_2 = \ell _4\) and \(\ell ^{(\mathrm L)}_3 = \ell _1+\ell _3\).
One can perform a similar analysis using the spectral parameter \(z^{(\mathrm R)}= \xi \,z^{-1}\). This leads us to define the following realisation \(\rho ^{(\mathrm R)}_\textrm{I}\) of the Kac–Moody currents \({\mathcal {J}}^{(\mathrm R)}_r\):
As expected, these fields are Kac–Moody currents in \({\mathcal {F}}\bigl [T^*(G\!\times \! G)\bigr ]\) with respective levels \(\ell ^{(\mathrm R)}_1 = \ell _1\), \(\ell ^{(\mathrm R)}_2 = \ell _3\) and \(\ell ^{(\mathrm R)}_3 = \ell _2+\ell _4\).
We will refer to \(\rho ^{(\mathrm L)}_\textrm{I}\) and \(\rho ^{(\mathrm R)}_\textrm{I}\) as chiral realisations, as will be justified later in this subsection. Let us observe that in both these chiral realisations, the sum of all three Kac–Moody currents \({\mathcal {J}}_1^{(\mathrm L/R)}+{\mathcal {J}}_2^{(\mathrm L/R)}+{\mathcal {J}}_3^{(\mathrm L/R)}\) is realised as \({\mathcal {C}}= {\mathcal {J}}_1^\rho + {\mathcal {J}}_2^\rho + {\mathcal {J}}_3^\rho + {\mathcal {J}}_4^\rho = X_1+X_2\), i.e. as the constraint of the gauged formulation of the Klimčík model. Thus, the two chiral realisations \(\rho ^{(\mathrm L)}_\textrm{I}\) and \(\rho ^{(\mathrm R)}_\textrm{I}\) share the same constraint and gauge symmetry in the extended algebra \({\mathcal {F}}\bigl [T^*(G\!\times \! G)\bigr ]\) as the initial relativistic realisation.
Realisations in Different Charts Before we study the properties of the chiral realisations \(\rho _\textrm{I}^{(\mathrm L/R)}\) defined in the previous paragraph, let us explain the origin of the index \(\textrm{I}\) in this notation. This is related to the assumption made above that the canonical fields \((g_1,X_1,g_2,X_2)\) entering the currents \({\mathcal {J}}_r^\rho \) are not affected by the RG flow. In particular, this means that we chose a way to extract coordinate fields in the gauge-invariant quantity \(g=g_1 g_2^{-1}\) which does not involve any parameter that flows under the RG. Recall that in the \(\textrm{SU}(2)\) case, the coordinate fields \((\phi ,v,w)\) of the Klimčík model were extracted from g using the Euler angles decomposition (4.8) and the parametrisation (4.11). In particular, this latter equation defined the way we extracted the coordinate \(\phi \) from g, depending on a parameter \(\phi _0\). We then considered various choices of \(\phi _0\) in terms of the parameter \(\kappa \) in Eq. (4.12), leading to the three different charts \(\textrm{I}\), \(\textrm{II}\) and \(\textrm{III}\) for the chiral model in the conformal limit \(\kappa \rightarrow 1^-\). In particular, the choice \(\phi _0=0\) leading to chart \(\textrm{I}\) corresponds to an extraction of the coordinates \((\phi ,v,w)\) in g which does not depend on the parameter \(\kappa \) and which is then unaffected by the RG flow: this is the choice that leads to currents \({\mathcal {J}}_r^\rho \) which are RG invariants and thus to the realisations \(\rho ^{(\mathrm L/R)}_\textrm{I}\) defined in the previous paragraph. These are therefore more precisely realisations of the affine Gaudin models in terms of the fields of the chiral Klimčík model in chart I (and additional non-gauge-invariant degrees of freedom).
This raises the natural question of whether there exist realisations of AGMs corresponding to the charts II and III. We expect the answer to this question to be positive. To construct such realisations, one would first need to express the currents \({\mathcal {J}}_r^\rho \) in terms of the physical fields \((\phi ,v,w)\), but with the choices of the parameter \(\phi _0\) in terms of \(\kappa \) corresponding to charts II and III in Eq. (4.12). It seems likely that these currents do not possess a well-defined UV limit when \(\kappa \rightarrow 1^-\). Following the results of Sect. 4.3, we expect that this can be corrected by first performing a well-chosen \(\kappa \)-dependent conjugation of the currents \({\mathcal {J}}_r^\rho \), ensuring that their limits when \(\kappa \rightarrow 1^-\) stay finite. Since a conjugation of the currents does not change their Kac–Moody Poisson bracket, we expect this different limiting procedure to produce two other realisations \(\rho _\textrm{II}^{(\mathrm L/R)}\) and \(\rho _\textrm{III}^{(\mathrm L/R)}\) of the same underlying formal affine Gaudin models, in terms of the fields in charts II and III, respectively. In practice, this procedure can be difficult to implement since the currents do not depend only on the physical field \(g=g_1 g_2^{-1}\) but also on extra non-gauge-invariant degrees of freedom. We will avoid this difficulty in the next subsection by considering appropriate gauge-fixed models: in particular, this will allow us to discuss realisations in different charts.
Chirality of the Realisations Let us now discuss the chirality properties of the realisations \(\rho _\textrm{I}^{(\mathrm L/R)}\). For the moment, we will focus on the AGM with spectral parameter \(z^{(\mathrm L)}\) and the realisation \(\rho _\textrm{I}^{(\mathrm L)}\). The latter was introduced by considering the UV limit of the Gaudin Lax matrix \(\xi ^{-1} \rho \bigl (\Gamma (\xi ^{-1} z^{(\mathrm L)})\bigr )\). Before taking the limit, the dynamic of \(\rho \bigl (\Gamma (z)\bigr )\) is equivalent to the one of the Lax matrix \({\mathcal {L}}_x(z)\), which takes the form of a zero curvature equation. We will work with the light-cone representation of this equation, in terms of the Lax connection \(\partial _\pm + {\mathcal {L}}_\pm (z)\). As already observed in Sect. 4.3, one checks that in the UV limit, the connection \(\partial _\pm + {\mathcal {L}}_\pm \bigl ( \xi ^{-1} z^{(\mathrm L)}\bigr )\) in the spectral parameter \(z^{(\mathrm L)}\) tends to \(\partial _\pm + {\mathcal {L}}^{(\mathrm L)}_\pm \bigl ( z^{(\mathrm L)}\bigr )\), where the component \({\mathcal {L}}_-^{(\mathrm L)}\) is independent of \(z^{(\mathrm L)}\). As a consequence, this component can be eliminated by a well-chosen gauge transformation with parameter h, which acts on the connection as \(\partial _\pm + {\mathcal {L}}_\pm ^{(\mathrm L)}\mapsto h^{-1}(\partial _\pm +{\mathcal {L}}_\pm ^{(\mathrm L)}\bigr )h\): indeed, since \({\mathcal {L}}_-^{(\mathrm L)}\) is independent of \(z^{(\mathrm L)}\), one can always choose h such that \(h^{-1}(\partial _-+{\mathcal {L}}_-^{(\mathrm L)}\bigr )h=\partial _-\). The remaining component \(h^{-1}(\partial _++{\mathcal {L}}_+^{(\mathrm L)}\bigr )h\) is therefore chiral: more precisely, it is expressed in terms of left-moving fields. In this gauge, the Lax matrix coincides with this light-cone component. We thus deduce that the gauge-transformed Kac–Moody currents \(\rho ^{(\mathrm L)}\bigl ({\mathcal {J}}_r^{(\mathrm L)}\bigr )^h\) are left-moving.
The above results motivate the following definition of a left-moving chiral realisation of an AGM. Consider a formal AGM with Kac–Moody currents \(\bigl ({\mathcal {J}}_1^{(\mathrm L)},\ldots ,{\mathcal {J}}_N^{(\mathrm L)}\bigr )\) forming an unreduced algebra \({\mathcal {A}}^{(\mathrm L)}\) which we realise through a Poisson map \(\rho ^{(\mathrm L)}: {\mathcal {A}}^{(\mathrm L)}\rightarrow {\mathcal {F}}[T^*Q]\). We also suppose that we chose a Hamiltonian \({\mathcal {H}}\in {\mathcal {F}}[T^*Q]\) defining the dynamic \(\partial _t \approx \lbrace {\mathcal {H}}_{\textrm{T}}, \cdot \rbrace \) of a 2d field theory (where \({\mathcal {H}}_{\textrm{T}}\) is built from \({\mathcal {H}}\) by adding a Lagrange multiplier term). We say that this realisation is a left-moving chiral one if:
-
(LM1)
the choice of Hamiltonian \({\mathcal {H}}\) is such that the gauge-invariant fields in \({\mathcal {F}}[T^*Q]\) decompose into left-moving and right-moving fields;
-
(LM2)
there exists a gauge transformation with parameter h such that the gauge-transformed Kac–Moody currents \(\rho ^{(\mathrm L)}\bigl ({\mathcal {J}}_r^{(\mathrm L)}\bigr )^h\) are left-moving. Moreover, all left-moving gauge-invariant fields in \({\mathcal {F}}[T^*Q]\) can be reconstructed from these currents up to integration constants.
It is clear from the previous discussion that the realisation \(\rho ^{(\mathrm L)}_\textrm{I}: {\mathcal {A}}^{(\mathrm L)}\rightarrow {\mathcal {F}}\bigl [T^*(G\!\times \! G)\bigr ]\) defined above for the UV fixed point of the Klimčík model is a left-moving chiral realisation with \(N=3\) punctures. This notion should be compared with the one of relativistic realisation introduced in Sect. 3.2. The condition (R1) in a relativistic realisation that the theory is Lorentz invariant is replaced here by the stronger condition (LM1) that the dynamics decompose the fields into left- and right-movers. Moreover, for a relativistic realisation, the condition (R2) ensured that the fields of the AGM contain all the degrees of freedom of the 2d field theory, while in the case of a chiral realisation the condition (LM2) implies that the fields of the AGM contain only half of the physical degrees of freedom, corresponding to the left-moving fields.
Let us comment on the consequences of this definition. Following the general formalism recalled in Sect. 3.1, the main output of the AGM construction is an integrable structure \({\mathcal {Z}}^{(\mathrm L)}\subset {\mathcal {A}}^{(\mathrm L)}\), composed by local and non-local charges in involution built from the Kac–Moody currents \({\mathcal {J}}_r^{(\mathrm L)}\). As usual, one can consider the image \(\rho ^{(\mathrm L)}\bigl ({\mathcal {Z}}^{(\mathrm L)}\bigr )\) of this integrable structure in the realisation \({\mathcal {F}}[T^*Q]\). Since the charges in this integrable structure are gauge-invariant (see Sect. 3.1), they can equivalently be expressed in terms of the gauge-transformed Kac–Moody currents \(\rho ^{(\mathrm L)}\bigl ({\mathcal {J}}_r^{(\mathrm L)}\bigr )^h\). By the condition (LM2), this ensures that the integrable structure \(\rho ^{(\mathrm L)}\bigl ({\mathcal {Z}}^{(\mathrm L)}\bigr )\) inherited from the AGM is built purely from left-moving fields. We will give a more precise description of this left-moving integrable structure for the case of the Klimčík model in the following subsections.
It is clear that one can define an analogous notion of a right-moving chiral realisation and that the realisation \(\rho ^{(\mathrm R)}_\textrm{I}\) defined in the previous paragraphs for the conformal limit of the Klimčík model belongs to this class. This also motivates the introduction of what we will call a chiral pair of realisations of AGMs. We will define such a pair as the data of a left-moving chiral realisation \(\rho ^{(\mathrm L)}: {\mathcal {A}}^{(\mathrm L)}\rightarrow {\mathcal {F}}[T^*Q]\) and a right-moving chiral realisation \(\rho ^{(\mathrm R)}: {\mathcal {A}}^{(\mathrm R)}\rightarrow {\mathcal {F}}[T^*Q]\) of two AGMs (with observables \({\mathcal {A}}^{(\mathrm L)}\) and \({\mathcal {A}}^{(\mathrm R)}\)) in the same Poisson algebra \({\mathcal {F}}[T^*Q]\) such thatFootnote 21:
-
(CP1)
the Hamiltonian and momentum of the theory take the form \({\mathcal {H}}\approx {\mathcal {Q}}^{(\mathrm L)}+ {\mathcal {Q}}^{(\mathrm R)}\) and \({\mathcal {P}}\approx {\mathcal {Q}}^{(\mathrm L)}- {\mathcal {Q}}^{(\mathrm R)}\) with the charges \({\mathcal {Q}}^{(\mathrm L)}\) and \({\mathcal {Q}}^{(\mathrm R)}\) in the left-moving and right-moving integrable structures \(\rho ^{(\mathrm L)}\bigl ({\mathcal {Z}}^{(\mathrm L)})\) and \(\rho ^{(\mathrm R)}\bigl ({\mathcal {Z}}^{(\mathrm R)})\), respectively;
-
(CP2)
one can reconstruct, up to initial conditions, all canonical fields in \({\mathcal {F}}[T^*Q]\) from the Kac–Moody currents \(\rho ^{(\mathrm L)}\bigl ({\mathcal {J}}^{(\mathrm L)}_r\bigr )\) and \(\rho ^{(\mathrm R)}\bigl ({\mathcal {J}}^{(\mathrm R)}_r\bigr )\) of the two combined realisations.
The charges \({\mathcal {Q}}^{(\mathrm L)}\) and \({\mathcal {Q}}^{(\mathrm R)}\) introduced in the condition (CP1) are the generators of the light-cone derivatives \(\partial _+\) and \(\partial _-\), respectively. The realisations \(\rho ^{(\mathrm L)}_\textrm{I}\) and \(\rho ^{(\mathrm R)}_\textrm{I}\) introduced above for the Klimčík model define such a pair of chiral realisations.
Gauge Symmetries in Chiral Realisations Let us consider an AGM with N Kac–Moody currents forming a Poisson algebra \({\mathcal {A}}^{(\mathrm L)}\) and suppose that we are given a left-moving chiral realisation \(\rho ^{(\mathrm L)}: {\mathcal {A}}^{(\mathrm L)}\rightarrow {\mathcal {F}}[T^*Q]\) as defined in the previous paragraph. The model is subject to a first-class constraint and thus admits a gauge symmetry. The latter plays a role in the definition of the left-moving chiral realisation and in particular in the condition (LM2) above, where we require that the realised Kac–Moody currents are left-moving up to a gauge transformation. This might seem surprising at first as one could have expected the definition of a chiral realisation to require that the Kac–Moody currents themselves are left-moving. This is in fact not a well-defined condition since these currents are not gauge-invariant. Indeed, by construction, non-gauge-invariant fields contain unphysical degrees of freedom which, in the dynamics of the model, contribute as arbitrary functions of space and time coordinates (x, t). (These arbitrary functions are encoded in the Lagrange multiplier appearing in the total Hamiltonian of the theory.) It thus does not make sense to ask for a non-gauge-invariant field to be left-moving or right-moving, i.e. to depend only on the combination \(t+x\) or \(t-x\). This is why the condition (LM2) in the definition of a left-moving chiral realisation requires the chirality of the Kac–Moody currents up to a well-chosen gauge transformation with parameter h: we note that this gauge transformation should then be such that the resulting currents \(\rho ^{(\mathrm L)}\bigl ({\mathcal {J}}_r^{(\mathrm L)}\bigr )^h\) are in fact gauge-invariant quantities, so that the chirality condition makes sense.
Let us also comment on the effects of the constraint and gauge symmetry on the counting of degrees of freedom. To illustrate this, we consider the case of the UV fixed point of the Klimčík model, focussing on the left-moving chiral realisation \(\rho ^{(\mathrm L)}_\textrm{I}: {\mathcal {A}}^{(\mathrm L)}\rightarrow {\mathcal {F}}\bigl [T^*(G\!\times \! G)\bigr ]\). The underlying formal AGM possesses three punctures, corresponding to the three Kac–Moody currents generating the algebra \({\mathcal {A}}^{(\mathrm L)}\). The number of fundamental fields contained in \({\mathcal {A}}^{(\mathrm L)}\) is thus equal to \(3\dim {\mathfrak {g}}\). On the other hand, the map \(\rho ^{(\mathrm L)}_\textrm{I}\) realises these currents in terms of canonical fields \((g_1,X_1,g_2,X_2)\) in \(T^*(G\!\times \! G)\), i.e. in terms of \(4\dim {\mathfrak {g}}\) fields. So far, we have counted all fields in the unreduced algebras \({\mathcal {A}}^{(\mathrm L)}\) and \({\mathcal {F}}[T^*(G\!\times \! G)]\): to count the physical fields of the theory, we now need to take into account the presence of the constraint and the gauge symmetry. Concretely, the former imposes \(\dim {\mathfrak {g}}\) relations between the fields and the latter eliminates an additional \(\dim {\mathfrak {g}}\) fields. Thus, after reduction, the number of physical fields in the AGM is equal to \(3\dim {\mathfrak {g}}-2\dim {\mathfrak {g}}=\dim {\mathfrak {g}}\), while the number of physical fields in the realisation is equal to \(4\dim {\mathfrak {g}}-2\dim {\mathfrak {g}}=2\dim {\mathfrak {g}}\) (corresponding to the gauge-invariant canonical fields (g, X)). This is what we expect for a chiral realisation: indeed, the AGM describes only half of the degrees of freedom of the physical two-dimensional theory, namely the left-moving fields. The remaining \(\dim {\mathfrak {g}}\) fields are then described by the right-moving realisation \(\rho ^{(\mathrm R)}_\textrm{I}\), so that the chiral pair formed by \(\rho ^{(\mathrm L)}_\textrm{I}\) and \(\rho ^{(\mathrm R)}_\textrm{I}\) encodes all the fields of the two-dimensional theory. We note that the reduction in the number of physical fields that occurs when passing from the relativistic realisation of the Klimčík model to the left-moving chiral realisation of its UV fixed point can be traced back to the passage from 4 Kac–Moody currents to only 3 in the conformal limit, and thus to the collision of poles and zeroes in the twist function of the model, which eliminates one pole.
It may seems unnatural to pass through the introduction of non-physical fields \((g_1,X_1,g_2,X_2)\) in the chiral realisation, in particular since the left-moving condition (LM2) concerns only a well-chosen gauge transformation \(\rho ^{(\mathrm L)}\bigl ({\mathcal {J}}_r^{(\mathrm L)}\bigr )^h\) of the Kac–Moody currents which makes them gauge invariant, and which should thus be expressible in terms of the physical fields in (g, X) only (although this can be difficult to do in practice). One can thus wonder whether there is another way to present chiral realisations that would avoid this issue and would rephrase the conditions (LM1) and (LM2) directly in terms of physical fields. One possible approach is to see the gauge transformation by h appearing in condition (LM2) as bringing the Kac–Moody currents to a particular gauge, satisfying a certain gauge-fixing condition. If one is able to interpret this gauge fixing as a condition on the Kac–Moody currents, one can then impose it in the formal AGM itself, before taking a realisation, and thus discuss only the realisation of physical fields. This is the subject of the next subsection.
6.2 Gauge Fixing and Chiral Realisations
In this subsection, we present a different way of thinking about chiral realisations of AGMs which avoid the introduction of non-physical fields in the realisation. The main idea is to focus on physical degrees of freedom already in the formal AGM, before taking a realisation, by considering gauge-fixing conditions in terms of the Kac–Moody currents defining the AGM. As we will see, this will also allow us to gain some insights on the chiral Poisson algebras underlying the UV fixed point of the Klimčík model.
Gauge Fixing Let us consider an AGM with N Kac–Moody currents \({\mathcal {J}}_r\) generating the Poisson algebra \({\mathcal {A}}\), as in Sect. 3.1. The model is subject to the constraint \({\mathcal {C}}= \sum _{r=1}^N {\mathcal {J}}_r \approx 0\) and thus to the gauge symmetry it generates, defining a reduced algebra \({\mathcal {A}}_{\text {red}}\). One efficient way to describe \({\mathcal {A}}_\text {red}\) is to consider a gauge-fixing condition \({\mathcal {F}}\equiv 0\) in \({\mathcal {A}}\), where \({\mathcal {F}}\) is an observable built from the Kac–Moody currents \({\mathcal {J}}_r\). Similarly to weak equalities that we denoted with the symbol \(\approx \), we will use the symbol \(\equiv \) to denote equalities that hold under the gauge-fixing condition, i.e. when we impose \({\mathcal {F}}\equiv 0\) and \({\mathcal {C}}\equiv 0\). This condition should be such that it is always attainable by a gauge transformation, i.e. starting with any configuration of the Kac–Moody currents \({\mathcal {J}}_r\), there always exists a gauge transformation that brings these currents to a configuration that satisfies the condition \({\mathcal {F}}\equiv 0\). We will moreover suppose that this is a complete gauge-fixing condition, i.e. that the gauge transformation leading to \({\mathcal {F}}\equiv 0\) is unique and thus that there are no residual gauge symmetries. In this case, every gauge orbit contains a unique representative satisfying \({\mathcal {F}}\equiv 0\) and one can describe the algebra of reduced observables \({\mathcal {A}}_\text {red}\) as the initial algebra \({\mathcal {A}}\) quotiented by the relations \({\mathcal {C}}\equiv 0\) and \({\mathcal {F}}\equiv 0\). We will denote this quotient by \({\mathcal {A}}_{\text {GF}}\), which is thus isomorphic to \({\mathcal {A}}_\text {red}\). For simplicity, we will still denote by \({\mathcal {J}}_r\) the image of the Kac–Moody currents in the quotient \({\mathcal {A}}_{\text {GF}}\) (and similarly for other observables): we will keep track of the fact that we are working in the quotient by using the symbol \(\equiv \) to denote equalities which hold in \({\mathcal {A}}_{\text {GF}}\).
The Poisson structure of \({\mathcal {A}}_\text {red}\) inherited by the Hamiltonian reduction in \({\mathcal {A}}\) can be described in terms of the gauge-fixed algebra \({\mathcal {A}}_{\text {GF}}\) using the Dirac bracket. Indeed, the assumption made above that \({\mathcal {F}}\equiv 0\) is a complete gauge fixing implies that the combined conditions \({\mathcal {C}}\equiv 0\) and \({\mathcal {F}}\equiv 0\) form a system of second-class constraints in \({\mathcal {A}}\). One can thus define a Dirac bracket \(\lbrace \cdot ,\cdot \rbrace _D\) on \({\mathcal {A}}\), which is a Poisson bracket ensuring that these constraints \({\mathcal {C}}\) and \({\mathcal {F}}\) Poisson commute with all observables in \({\mathcal {A}}\): this bracket is thus compatible with imposing \({\mathcal {C}}\equiv 0\) and \({\mathcal {F}}\equiv 0\). It therefore descends to the quotient \({\mathcal {A}}_{\text {GF}}\), making it isomorphic to \({\mathcal {A}}_\text {red}\) as Poisson algebras.
Recall that the definition of AGMs results in the construction of an integrable structure \({\mathcal {Z}}^{(z_r)}\) in \({\mathcal {A}}\), composed by charges in involution built from the Kac–Moody currents \({\mathcal {J}}_r\). Since these charges are gauge-invariant, their Dirac bracket coincides with their initial bracket and thus vanishes. The integrable structure \({\mathcal {Z}}^{(z_r)}\) thus descends to an integrable structure in the gauge-fixed algebra \({\mathcal {A}}_{\text {GF}}\), which is identified with \({\mathcal {Z}}^{(z_r)}_\text {red}\) in the reduced algebra \({\mathcal {A}}_\text {red}\) through the above isomorphism between \({\mathcal {A}}_{\text {GF}}\) and \({\mathcal {A}}_\text {red}\). In conclusion, we can thus describe the Poisson algebra \({\mathcal {A}}_\text {red}\) and the integrable structure \({\mathcal {Z}}_\text {red}^{(z_r)}\) of the reduced AGM through the gauge fixing, as expected.
Chiral Realisations Through Gauge Fixing Let us now use the formalism of gauge-fixed AGMs to discuss chiral realisations. We will focus on left-moving realisations, the discussion for right-moving ones being completely analogous. Accordingly, we now consider an AGM with Kac–Moody currents \({\mathcal {J}}_r^{(\mathrm L)}\) forming an algebra \({\mathcal {A}}^{(\mathrm L)}\). As in the previous paragraph, we can describe the reduced AGM by choosing a gauge fixing \({\mathcal {F}}^{(\mathrm L)}\equiv 0\) and working with the quotient algebra \({\mathcal {A}}^{(\mathrm L)}_{\text {GF}}\), equipped with the Dirac bracket. We can then consider a realisation of this gauge-fixed AGM in terms of canonical fields in a cotangent bundle \(T^*Q_{\text {red}}\), through a Poisson map \(\rho ^{(\mathrm L)}_{\text {GF}}: {\mathcal {A}}^{(\mathrm L)}_{\text {GF}} \rightarrow {\mathcal {F}}\bigl [T^*Q_{\text {red}}\bigr ]\). Since we consider the gauge-fixed model, this realisation is not subject to any constraint or gauge symmetry and the canonical fields in \(T^*Q_{\text {red}}\) are physical degrees of freedom. We further choose a Hamiltonian \({\mathcal {H}}\in {\mathcal {F}}\bigl [T^*Q_{\text {red}}\bigr ]\) defining the dynamic \(\partial _t = \lbrace {\mathcal {H}}, \cdot \rbrace \). We then say that this realisation is a chiral left-moving one if
-
(LM1’)
the choice of Hamiltonian \({\mathcal {H}}\) is such that the fields in \({\mathcal {F}}[T^*Q_{\text {red}}]\) decompose into left-moving and right-moving fields;
-
(LM2’)
the image \(\rho ^{(\mathrm L)}_{\text {GF}}\bigl ({\mathcal {J}}_r^{(\mathrm L)}\bigr )\) of the (gauge-fixed) Kac–Moody currents are left-moving and all left-moving fields of the theory can be reconstructed from these currents, up to integration constants.
Compared to the condition (LM2) in the previous subsection, we do not need in (LM2’) to require chirality of the Kac–Moody currents up to a gauge transformation, since we have fixed the gauge and are now manipulating purely physical degrees of freedom. As before, such a realisation provides us with an integrable structure \(\rho ^{(\mathrm L)}_{\text {GF}}\bigl ( {\mathcal {Z}}^{(\mathrm L)}\bigr )\) in \({\mathcal {F}}\bigl [T^*Q_{\text {red}}\bigr ]\). Moreover, by construction, this integrable structure is built from the left-moving fields \(\rho ^{(\mathrm L)}_{\text {GF}}\bigl ({\mathcal {J}}_r^{(\mathrm L)}\bigr )\). The notion of left-moving chiral realisation considered here thus corresponds to the gauged-fixed version of the one introduced in the previous subsection.
Applications to the Klimčík Model In the rest of this subsection, our main goal will be to apply the formalism developed in the previous paragraphs to the UV fixed point of the Klimčík model. We have identified the AGM underlying the left-moving part of this model in the previous subsection: it is characterised by the twist function \(\varphi ^{(\mathrm L)}\bigl (z^{(\mathrm L)})\) in Eq. (6.2) and is described by three Kac–Moody currents \({\mathcal {J}}_r^{(\mathrm L)}\), with levels \(\ell _r^{(\mathrm L)}\) given by Eq. (6.4). In the following paragraphs, we will discuss different gauge fixings of this AGM as well as their realisations in terms of the left-moving fields of the UV fixed point of the Klimčík model, in different charts.
Parafermionic Gauge In this paragraph, we will consider the following choice of gauge-fixing condition in terms of the Kac–Moody currents:
where \({{\hat{R}}}: {\mathfrak {g}}^{\mathbb {C}}\rightarrow {\mathfrak {g}}^{\mathbb {C}}\) is the Yang–Baxter operator (2.1). This forces the gauge-fixed current \({\mathcal {J}}^{(\mathrm L)}_1\) to belong to the negative Borel subalgebra \({\mathfrak {h}} \oplus {\mathfrak {n}}_-\) of \({\mathfrak {g}}^{\mathbb {C}}\), while the gauge-fixed current \({\mathcal {J}}^{(\mathrm L)}_2\) belongs to the positive Borel subalgebra \({\mathfrak {h}} \oplus {\mathfrak {n}}_+\) and has a Cartan part which is opposite to the one of \({\mathcal {J}}^{(\mathrm L)}_1\). Finally, using the fact that \({\mathcal {J}}_1^{(\mathrm L)}+{\mathcal {J}}_2^{(\mathrm L)}+{\mathcal {J}}_3^{(\mathrm L)}\equiv 0\), we find that \({\mathcal {J}}_3^{(\mathrm L)}\equiv -{\mathcal {J}}_1^{(\mathrm L)}-{\mathcal {J}}_2^{(\mathrm L)}\) belongs to \({\mathfrak {n}}_+ \oplus {\mathfrak {n}}_-\).
To describe more precisely the gauge-fixed AGM, we will use the root decomposition of \({\mathfrak {g}}^{\mathbb {C}}\). To keep the main text concise, we gather all the relevant definitions, notations and conventions in “Appendix A” . Here, we will mostly need the orthogonal basis \(\lbrace \texttt{h}_i \rbrace _{i= 1,\ldots ,\dim {\mathfrak {h}}}\) of the Cartan subalgebra \({\mathfrak {h}}\), as well as the root vectors \(\lbrace \texttt{e}_\alpha \rbrace _{\alpha \in \Delta }\) forming a basis of \({\mathfrak {n}}_+ \oplus {\mathfrak {n}}_-\) (\(\Delta \) and \(\Delta _\pm \) denote the sets of roots and positive/negative roots). The gauge-fixed currents \({\mathcal {J}}^{(\mathrm L)}_r(x)\) introduced above can then be parametrised in terms of \(\dim {\mathfrak {g}}\) fields \(\lbrace D^{(\mathrm L)}_i(x) \rbrace _{i= 1,\ldots ,\dim {\mathfrak {h}}}\) and \(\lbrace \Psi ^{(\mathrm L)}_\alpha (x) \rbrace _{\alpha \in \Delta }\):
One easily checks that this parametrisation indeed satisfies the constraint \({\mathcal {J}}_1^{(\mathrm L)}+{\mathcal {J}}_2^{(\mathrm L)}+{\mathcal {J}}_3^{(\mathrm L)}\equiv 0\) and the gauge-fixing condition \(\bigl ( {\hat{R}} - \textrm{i}\bigr ) {\mathcal {J}}^{(\mathrm L)}_1 - \bigl ( {\hat{R}} + \textrm{i}\bigr ) {\mathcal {J}}^{(\mathrm L)}_2 \equiv 0\).
The fields \(\lbrace D^{(\mathrm L)}_i(x) \rbrace _{i= 1,\ldots ,\dim {\mathfrak {h}}}\) and \(\lbrace \Psi ^{(\mathrm L)}_\alpha (x) \rbrace _{\alpha \in \Delta }\) generate the gauge-fixed algebra, which we denote in this case by \({\mathcal {A}}^{(\mathrm L)}_P\). To describe its Poisson structure, one needs to determine the Dirac bracket of these fields. We perform this computation in details in “Appendix B” and simply give the final result here. We find
In the above bracket, the numbers \(N^{\alpha ,\beta }\) are defined through the commutation relations of root vectors \(\texttt{e}_\alpha \) and \((\cdot ,\cdot )\) is the standard bilinear form on \({\mathfrak {h}}^*\) (see “Appendix A” for precise definitions).
We will call the Poisson algebra \({\mathcal {A}}^{(\mathrm L)}_P\) generated by the fields \(D^{(\mathrm L)}_i\) and \(\Psi ^{(\mathrm L)}_\alpha \) a parafermionic algebra: the parafermionic currents \(\Psi ^{(\mathrm L)}_\alpha \) were initially introduced in [75, 76] at the quantum level, while their classical bracket (6.13c) was discussed in [77]. A similar analysis can be of course performed for the right-moving AGM: it leads to the description of the gauge-fixed algebra \({\mathcal {A}}^{(\mathrm R)}_P\) in terms of \(\dim {\mathfrak {g}}\) fields \(\lbrace D^{(\mathrm R)}_i(x) \rbrace _{i=1,\ldots ,\dim {\mathfrak {h}}}\) and \(\lbrace \Psi ^{(\mathrm R)}_\alpha (x) \rbrace _{\alpha \in \Delta }\) satisfying the same brackets (6.13) as in the left-moving case but with \(K_{\scriptscriptstyle {\textrm{UV}}}\) replaced by \(-K_{\scriptscriptstyle {\textrm{UV}}}\).
Let us finally discuss the example \(G=\textrm{SU}(2)\). In this case, the Cartan subalgebra is one-dimensional and there is thus a unique Cartan field \(D^{(\mathrm L)}(x)\) in the decomposition (6.12). Moreover, there are only two roots \(\alpha \) and \(-\alpha \), which are opposite one of another, corresponding to two fields \(\Psi ^{(\mathrm L)}_\pm (x)\) in the decomposition (6.12). The brackets (6.13) now read
Parafermionic Realisation Now that we have described a specific gauge fixing of the AGM under consideration, leading to the parafermionic algebra \({\mathcal {A}}^{(\mathrm L)}_P\), let us explain how this algebra can be realised in the UV fixed point of the Klimčík model. We will focus mostly on the case \(G=\textrm{SU}(2)\) and will speculate on the higher-rank one at the end of the paragraph. We thus consider three fields \(D^{(\mathrm L)}(x)\) and \(\Psi ^{(\mathrm L)}_\pm (x)\), satisfying the Poisson algebra (6.14). We have in fact encountered similar fields in the description of the UV fixed point of the \(\textrm{SU}(2)\) Klimčík model in Sect. 4.3. More precisely, using the coordinate fields \((\phi ,\alpha ,\chi )\) of the chart I of this model, we found that the decoupled free boson \(\chi \) induced a left-moving field \(\partial _+ \chi \) satisfying the same Poisson bracket as \(D^{(\mathrm L)}\) up to a constant, while the parafermionic fields \(\psi ^{(\mathrm L)}_\pm \) built from the cigar coordinates \((\phi ,\alpha )\) in Eq. (4.28) satisfied the Poisson brackets (4.30), identical to the ones of \(\Psi ^{(\mathrm L)}_\pm \) also up to a constant. We can thus define a realisation of \({\mathcal {A}}^{(\mathrm L)}_P\) byFootnote 22
As required in the definition of a left-moving chiral realisation made earlier in this subsection, the image of the gauge-fixed Kac–Moody currents in the realisation, which are expressed in terms of \(\rho ^{(\mathrm L)}_P\bigl (D^{(\mathrm L)}\bigr )\) and \(\rho ^{(\mathrm L)}_P\bigl (\Psi ^{(\mathrm L)}_\pm \bigr )\), are left-moving fields. In particular, this ensures that the Lax matrix
induced by this choice of realisation is left-moving. A direct computation shows that
This Lax matrix coincides with the one described in Eq. (4.27). In particular, this ensures that the non-local charges obtained via the Lax matrix from Sect. 4.3 coincide with the ones in the AGM integrable structure \(\rho ^{(\mathrm L)}_P\bigl ({\mathcal {Z}}^{(\mathrm L)}\bigr )\).
Let us note that we are working here in the chart I of the chiral Klimčík model, in terms of the coordinates \((\phi ,\alpha )\) of the left cigar and the decoupled free boson \(\chi \). There exists a similar realisation of the same underlying AGM in the chart III, in terms of the coordinates \((\phi ,{\widetilde{\alpha }})\) of the right cigar and the decoupled free boson \({\widetilde{\chi }}\). Finally, one can also find a realisation in terms of the free bosons \((\phi _1,\phi _2,\phi _3)\) of chart II, see Eq. (5.10).
So far, we have focussed our attention on the case \(G=\textrm{SU}(2)\). Let us say a few words about the case of an arbitrary simple Lie group G. We have described the general gauge-fixed algebra \({\mathcal {A}}^{(\mathrm L)}_P\) in the previous paragraph, in terms of the fields \(\lbrace D^{(\mathrm L)}_i \rbrace _{i= 1,\ldots ,\dim {\mathfrak {h}}}\) and \(\lbrace \Psi ^{(\mathrm L)}_\alpha \rbrace _{\alpha \in \Delta }\) satisfying the bracket (6.13), which is a natural higher-rank generalisation of the \(\textrm{SU}(2)\) set-up considered above. We expect that this algebra can also be realised in terms of left-moving fields of the UV fixed point of the Klimčík model on G and that the corresponding Lax matrix coincides with the one of the Klimčík model in a particular choice of gauge. The concrete implementation of these ideas is out of the scope of the present paper and requires further investigation.
Let us, however, briefly comment on the expected structure of this realisation. It is clear from the Poisson bracket (6.13) that the \(\dim {\mathfrak {h}}\) fields \(D_i^{(\mathrm L)}\) can be realised in terms of the derivatives \(\partial _+\chi ^i\) of \(\dim {\mathfrak {h}}\) free bosons \(\chi ^i\), similar to the boson \(\chi \) in the \(\textrm{SU}(2)\) case above. The remaining fields \(\Psi _\alpha ^{(\mathrm L)}\) form a higher-rank parafermionic algebra [75,76,77], which generalises the parafermions of the cigar model. Recall that the latter can be obtained as the UV fixed point of the sausage model, which itself is identified with the Yang–Baxter deformation of the coset model on \(\textrm{SU}(2)/\textrm{U}(1)\). We expect this higher-rank algebra to describe parafermionic fields in the conformal limit of the Yang–Baxter deformation of the quotient \(G/H_0\), where \(H_0\) is the maximal torus of G (whose Lie algebra is the intersection of the Cartan subalgebra \({\mathfrak {h}}\) with the real form \({\mathfrak {g}}\) of \({\mathfrak {g}}^{\mathbb {C}}\)). For G of rank \(\ell \), the quotient \(G/H_0\) belongs to the class of so-called \({\mathbb {Z}}_{\ell +1}\)-coset spaces, which generalises the class of symmetric spaces, corresponding to \({\mathbb {Z}}_2\)-cosets. The undeformed integrable \(\sigma \)-models on \({\mathbb {Z}}_{\ell +1}\)-cosets for \(\ell >1\) were initially introduced in [83], while the construction of their integrable Yang–Baxter deformations was recently described in [84], generalising the construction of [63] for symmetric spaces. This suggests that the UV fixed point of the Klimčík model on G can be described as the UV fixed point of the deformed coset model on \(G/H_0\) together with \(\dim H_0\) decoupled free bosons. It would be interesting to explore these aspects further.
Let us finally note that another parafermionic algebra defined from a reduction in Kac–Moody currents was studied in [85]. Although it is different from the one considered in this paragraph, we believe that it corresponds to another gauge fixing of the same unreduced algebra \({\mathcal {A}}^{(\mathrm L)}\) considered here. We will comment more on this aspect and the relation to the so-called \(\lambda \)-models in Sect. 10.6, as part of the perspectives and possible extensions of the present work.
\(\omega \)-Gauge Fixing Let us now consider another gauge fixing of the algebra \({\mathcal {A}}^{(\mathrm L)}\).Footnote 23 For that, we introduce the operator \({\hat{\Pi }} = {{\hat{R}}}^2+\text {Id}\), in terms of the Yang–Baxter operator (2.1). It is straightforward to check that \({\hat{\Pi }}\) is the projector along the Cartan subalgebra \({\mathfrak {h}}\) in the decomposition \({\mathfrak {g}}^{\mathbb {C}}= {\mathfrak {h}} \oplus {\mathfrak {n}}_+ \oplus {\mathfrak {n}}_-\). We then consider the gauge-fixing condition
where \(\omega \) is a constant parameter. (The particular dependence on \(\omega \) in the above equation has been introduced to make the comparison with the results of Sect. 4.3 easier.) In this gauge, the currents \({\mathcal {J}}^{(\mathrm L)}_2\) and \({\mathcal {J}}^{(\mathrm L)}_3\) are valued in the Borel subalgebras \({\mathfrak {h}}\oplus {\mathfrak {n}}_-\) and \({\mathfrak {h}}\oplus {\mathfrak {n}}_+\), respectively. Moreover, the current \({\mathcal {J}}^{(\mathrm L)}_1\) is valued in the full algebra \({\mathfrak {g}}^{\mathbb {C}}= {\mathfrak {h}} \oplus {\mathfrak {n}}_+ \oplus {\mathfrak {n}}_-\), except for \(\omega =1+2\nu ^{-2}\), in which case \({\mathcal {J}}^{(\mathrm L)}_1\) has no Cartan component. We will exclude this case here. The physical observables in this gauge can thus be seen as the components of the current \({\mathcal {J}}^{(\mathrm L)}_1\). Using the basis \(\lbrace \texttt{h}_i, \texttt{e}_\alpha \rbrace \) of \({\mathfrak {g}}^{\mathbb {C}}\) introduced in the previous paragraphs (see “Appendix B” for the details), we parametrise these components in terms of \(\dim {\mathfrak {g}}\) fields \(\lbrace \Xi ^{(\mathrm L)}_i \rbrace _{i= 1,\ldots ,\dim {\mathfrak {h}}}\) and \(\lbrace \Xi ^{(\mathrm L)}_\alpha \rbrace _{\alpha \in \Delta }\) according to
The remaining gauge-fixed currents \({\mathcal {J}}^{(\mathrm L)}_2\) and \({\mathcal {J}}^{(\mathrm L)}_3\) can then be expressed as
One checks that these satisfy the gauge-fixing condition (6.18) and \(\sum _r {\mathcal {J}}^{(\mathrm L)}_r \equiv 0\), as expected.
One can determine the Poisson structure of the corresponding gauge-fixed algebra \({\mathcal {A}}^{(\mathrm L)}_\omega \) by computing the Dirac bracket of the components \(\lbrace \Xi ^{(\mathrm L)}_i \rbrace _i= 1,\ldots ,\dim {\mathfrak {h}}\) and \(\lbrace \Xi ^{(\mathrm L)}_\alpha \rbrace _{\alpha \in \Delta }\). The details of this computation are given in “Appendix B”. In the end, we find (for \(\beta \ne -\alpha \))
where the constants \(\rho _\alpha ^i\) are defined through \([ \texttt{e}_\alpha , \texttt{e}_{-\alpha } ] = \sum _i \rho _\alpha ^i\,\texttt{h}_i\) (see “Appendix A” for details), while the parameters \(\ell ^{(\mathrm L)}_1\) and \(\vartheta \) are given by
In the case \(G=\textrm{SU}(2)\), we have one Cartan field \(\Xi _0^{(\mathrm L)}(x)\) and two root fields \(\Xi ^{(\mathrm L)}_\pm (x)\). The above Poisson bracket then becomes
Free Field Realisation in the \(\omega \)-Gauge Let us now discuss the realisation of the gauge-fixed algebra \({\mathcal {A}}^{(\mathrm L)}_\omega \) in the UV fixed point of the Klimčík model. We will focus first on the \(\textrm{SU}(2)\) case and will comment on the higher-rank one at the end of the paragraph. We have in fact encountered a Poisson algebra similar to (6.23) in Sect. 4.3, namely the one (4.43) of the left-moving fields \(V^{(\omega )}_0\), \(V^{(\omega )}_+\) and \(V^{(\omega )}_-\) in the asympotic domain of the \(\textrm{SU}(2)\)-Klimčík model (i.e. chart II). We then define a realisation \(\rho _{\omega }^{(\mathrm L)}\) of \({\mathcal {A}}^{(\mathrm L)}_\omega \) by
One checks from the Poisson brackets (4.43) that this indeed defines a realisation of the algebra (6.23), with the parameters \(\ell ^{(\mathrm L)}_1\) and \(\vartheta \) given by (6.22). In the above equation, \(V^{(\omega )}_0\) and \(V^{(\omega )}_\pm \) should be understood as being defined in terms of the left-moving fields \((\phi _1^{(\textrm{L})},\phi _2^{(\textrm{L})},\phi _3^{(\textrm{L})})\) by Eq. (4.41). Thus \(\rho ^{(\mathrm L)}_\omega \) defines a left-moving free field realisation of the gauge-fixed algebra \({\mathcal {A}}^{(\mathrm L)}_\omega \).
In order to compare the left-moving integrable structure \(\rho ^{(\mathrm L)}_\omega \bigl ({\mathcal {Z}}^{(\mathrm L)}\bigr )\) induced by this realisation with the one described in Sect. 4.3, one needs to look at the Lax matrix
coming from the AGM construction. A direct computation shows that it is given by
Through the relation (4.40) between the spectral parameters \(z^{(\mathrm L)}\) and \(\rho \), this coincides with the Lax matrix (4.39) discussed in Sect. 4.3 that determines the non-local charges built from the left-moving fields in the asymptotic domain of the \(\textrm{SU}(2)\) Klimčík model.
There are a few interesting cases of the \(\omega \)-gauge that deserve special mention. The first one arises for \(\omega =1\). This choice corresponds to \(\vartheta =K_{\scriptscriptstyle {\textrm{UV}}}^{-1}\) and makes the fields \(V^{(\omega )}_\pm \) coincide with the vertex operators entering the definition of the (classical) cigar screening charges (5.29). This means that there is a particular gauge fixing of the AGM considered here which is naturally realised in terms of these vertex operators. A related point is that for \(\omega =-1\), for which \(\vartheta =-\frac{1+\nu ^2}{K_{\scriptscriptstyle {\textrm{UV}}}}\), the components of the Kac–Moody currents \(\Xi ^{(\mathrm L)}_\pm \) can be mapped to \(V^{(-1)}_\pm \). The rôle of these fields is discussed in Sect. 5.4. They appear as the integrands of a second set of classical screening charges which can be used to determine the local IMs, see Eqs. (5.34) and (5.35). Also recall that the combination of charges \(\int \text{ d }x_+ V_+^{(1)}\) and \(\int \text{ d }x_+ V_-^{(-1)}\) defines the corner-brane \(\mathcal {W}\)-algebra, which is a subalgebra of \(\mathcal {W}_\infty \otimes \textrm{U}(1)\). An alternative way of obtaining the local fields belonging to this \(\mathcal {W}\)-algebra, which is coordinate free and uniform in the choice of the Lie group G, will be described in the next subsection. Note that setting \(\omega =1\) in Eq. (6.20), we see that such a gauge fixing corresponds to requiring that the Kac–Moody currents \({\mathcal {J}}^{(\mathrm L)}_2\) and \({\mathcal {J}}^{(\mathrm L)}_3\) are valued, respectively, in the Borel subalgebra \({\mathfrak {h}}\oplus {\mathfrak {n}}_-\) and the nilpotent subalgebra \({\mathfrak {n}}_+\). On the other hand, for \(\omega =-1\) the current \({\mathcal {J}}^{(\mathrm L)}_2\) becomes valued in \({\mathfrak {n}}_-\), while \({\mathcal {J}}^{(\mathrm L)}_3\) is an element of the Borel subalgebra \({\mathfrak {h}}\oplus {\mathfrak {n}}_+\).
The last case we would like to discuss is \(\omega =\bigl (\sqrt{1+\nu ^{-2}} {\mp } \nu ^{-1} \bigr )^2\), for which \(\vartheta =0\). This corresponds to a particular gauge where there are no \(\epsilon \)-distributions in the algebra (6.23) and thus to a gauge where the Gaudin fields are local. More precisely, we get that the gauge-fixed field \({\mathcal {J}}^{(\mathrm L)}_1\) is a standard Kac–Moody current. We finally note that in this case, the realisation of \({\mathcal {J}}^{(\mathrm L)}_1\) in the Klimčík model is particularly simple: indeed, one checks that (6.24) becomes \(\rho ^{(\mathrm L)}_\omega \bigl ({\mathcal {J}}^{(\mathrm L)}_1\bigr )=-\frac{K_{\scriptscriptstyle {\textrm{UV}}}}{\sqrt{1+\nu ^2}}\, \bigl (\pm \frac{1}{2} V^{(\omega )}_0\,\texttt{h} + V^{(\omega )}_+\,\texttt{e}_+ + V^{(\omega )}_-\,\texttt{e}_- \bigr )\).
We expect a realisation similar to (6.24) to exist for higher-rank groups. Finding its explicit expression would, however, first require to properly identify the asymptotic domain of the higher-rank Klimčík model, which has not been described yet in the literature. These aspects are out of the scope of the present work and are interesting future perspectives.
Summary and Comments In this subsection, we have shown that the left-moving fields of the UV fixed point of the Klimčík model naturally form a chiral realisation of the gauge-fixed AGM with twist function \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\). In particular, this sheds some light on the chiral algebra underlying this model, i.e. the Poisson algebra formed by the left-moving fields of the theory. For instance, the left-moving fields in the charts I, II or III naturally form a parafermionic algebra, which can also alternatively be seen as a well-chosen gauge fixing of the AGM Poisson algebra. Moreover, the left-moving fields in the asymptotic domain, i.e. the chiral free bosons in chart II, can be organised into vertex operators or in a Kac–Moody current, also corresponding to two different gauge fixings of the AGM Poisson algebra. By construction, all these chiral Poisson algebras are equivalent to one another. We note, however, that the isomorphisms that relate these algebras are non-local transformations. Moreover, their realisations in general also involve non-local fields.
As a result of having found these realisations, one can construct the corresponding AGM integrable structure in terms of the left-moving fields of the UV fixed point of the Klimčík model. This integrable structure does not depend on the choice of gauge fixing (since it is formed by gauge-invariant charges), and we have checked in the previous paragraphs that the corresponding Lax matrices coincide with the ones described in Sect. 4.3, hence showing that the AGM construction would lead to the same non-local integrals of motion as the ones that would be obtained using the Lax matrices from that subsection.
In addition to non-local chiral fields and integrals of motion, we have also discussed in Sect. 5 the presence of local ones in the UV fixed point of the Klimčík model. Such objects can also be obtained from the AGM construction: this is the subject of the next subsection.
6.3 \(\varvec{{\mathcal {W}}}\)-Algebra and Local Charges
Definition of the \({{\mathcal {W}}}\)-Algebra Let us consider the AGM with twist function \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\) underlying the left-moving half of the Klimčík model. It is subject to the gauge symmetry \({\mathcal {J}}^{(\mathrm L)}_r \mapsto h^{-1} {\mathcal {J}}^{(\mathrm L)}_r h + \ell ^{(\mathrm L)}_r\,h^{-1}\partial _x h\) generated by the constraint \({\mathcal {J}}^{(\mathrm L)}_1 + {\mathcal {J}}^{(\mathrm L)}_2 + {\mathcal {J}}^{(\mathrm L)}_3 \approx 0\). In the previous subsections, we have explained how well-chosen gauge-fixed versions of these currents can be realised in terms of the physical left-moving fields of the Klimčík model, allowing us to describe the chiral algebra underlying this theory. We noted, however, that gauge fixing is in general a non-local procedure and that these chiral fields are thus non-local observables of the theory. To study local chiral fields, let us introduce the \({\mathcal {W}}\)-algebra associated with the AGM. In the formal AGM, with currents \(({\mathcal {J}}^{(\mathrm L)}_1,{\mathcal {J}}^{(\mathrm L)}_2,{\mathcal {J}}^{(\mathrm L)}_3)\), we define it as the set \({\mathcal {W}}^{(\mathrm L)}\) of gauge-invariant differential polynomials in the components of these currents (up to the constraint).
To understand the motivation behind this definition, we now consider the realisation of this AGM in the UV fixed point of the Klimčík model: then the main property of \({\mathcal {W}}^{(\mathrm L)}\) is that its image under the realisation is composed of local left-moving fields. To explain why this is the case, let us consider an element W of \({\mathcal {W}}^{(\mathrm L)}\). Since W is gauge-invariant, its image in the realisation can be computed in any gauge, and in particular in one where the gauge-fixed Kac–Moody currents are left-moving fields, ensuring that W itself is left-moving. Although these gauge-fixed currents are in general non-local fields, their particular combination that forms W turns out to be local. Indeed, the image of W in the realisation can be computed before gauge fixing as well, in which case the currents are realised as local fields of the gauged formulation of the model (see Sect. 6.1). Note that in the previous subsections, we have discussed various left-moving realisations of the AGM in the different charts of the chiral Klimčík model. The \({\mathcal {W}}\)-algebra \({\mathcal {W}}^{(\mathrm L)}\) can thus be used to generate systematically local left-moving fields in these different charts. Of course, one can also define a \({\mathcal {W}}\)-algebra \({\mathcal {W}}^{(\mathrm R)}\) in the AGM with twist function \(\varphi ^{(\mathrm R)}(z^{(\mathrm R)})\), whose realisation then yields local right-moving fields.
We will give a more explicit description of this \({\mathcal {W}}\)-algebra in the next paragraphs. Before that, let us quickly discuss some of its general properties. It is clear that the products and Poisson brackets of gauge-invariant differential polynomials in the currents \({\mathcal {J}}^{(\mathrm L)}_r\) are still gauge-invariant differential polynomials: \({\mathcal {W}}^{(\mathrm L)}\) is thus a Poisson algebra. Its Poisson structure can be either computed using the initial Kac–Moody bracket for the non-gauge-invariant currents \({\mathcal {J}}^{(\mathrm L)}_r\) or using the Dirac bracket of their gauge-fixed versions, since the Dirac bracket of gauge-invariant quantities coincides with the initial one. Let us finally note that in the above definition, we considered the elements of \({\mathcal {W}}^{(\mathrm L)}\) as built from the currents \({\mathcal {J}}^{(\mathrm L)}_r\) up to the constraint \({\mathcal {J}}^{(\mathrm L)}_1 + {\mathcal {J}}^{(\mathrm L)}_2 + {\mathcal {J}}^{(\mathrm L)}_3 \approx 0\): this avoids considering different combinations of these currents that will coincide for physical configurations that respect this constraint and thus avoids overcounting fields in the \({\mathcal {W}}\)-algebra. Since the constraint allows us to express \({\mathcal {J}}^{(\mathrm L)}_3\) in terms of \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\), we can see the elements of \({\mathcal {W}}^{(\mathrm L)}\) as gauge-invariant differential polynomials in the coefficients of \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\) only. The gauge symmetry acting on these two currents is equivalently generated by the sum \({\mathcal {J}}^{(\mathrm L)}_1+{\mathcal {J}}^{(\mathrm L)}_2\), which is itself a Kac–Moody current of level \(\ell ^{(\mathrm L)}_1+\ell ^{(\mathrm L)}_2\). Elements of \({\mathcal {W}}^{(\mathrm L)}\) can thus be regarded as differential polynomials in the components of \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\) that Poisson commute with \({\mathcal {J}}^{(\mathrm L)}_1+{\mathcal {J}}^{(\mathrm L)}_2\). (Note, however, that the latter is not seen here as a constraint.) In this sense, and following the general nomenclature on \({\mathcal {W}}\)-algebras, \({\mathcal {W}}^{(\mathrm L)}\) is then the classical
coset \({\mathcal {W}}\)-algebra.
Explicit Construction of the \({\mathcal {W}}\)-Algebra Let us now give a systematic and explicit construction of the fields in \({\mathcal {W}}^{(\mathrm L)}\). As explained at the end of the previous paragraph, we can see these fields as gauge-invariant differential polynomials in \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\). The key ingredient of our construction is the current
One easily checks that this current is covariant, in the sense that under a gauge transformation \({\mathcal {J}}^{(\mathrm L)}_r \mapsto h^{-1} {\mathcal {J}}^{(\mathrm L)}_r h + \ell ^{(\mathrm L)}_r\,h^{-1}\partial _x h\), it simply transforms as
It is easy to construct elements of \({\mathcal {W}}^{(\mathrm L)}\) using this current. Indeed, if \(\Phi \) is a conjugacy-invariant polynomial on \({\mathfrak {g}}^{\mathbb {C}}\), it is clear that the field \(\Phi \bigl ({\mathcal {K}}^{(\mathrm L)}\bigr )\) is gauge-invariant and thus belongs to the \({\mathcal {W}}\)-algebra \({\mathcal {W}}^{(\mathrm L)}\). In particular, the quadratic density
is the simplest example of a field in \({\mathcal {W}}^{(\mathrm L)}\). One easily checks from the Kac–Moody bracket of \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\) that this field satisfies a closed Virasoro Poisson bracket:
The field \(W_2^{(\mathrm L)}\) is the energy–momentum tensor of the theory and thus plays a particular role in the \({\mathcal {W}}\)-algebra.
The elements of \({\mathcal {W}}^{(\mathrm L)}\) that we have constructed so far are polynomials in \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\) but do not involve any of their derivatives. To also include such terms in the construction, it will be useful to introduce the covariant derivative
The main property of this operator is that the covariant derivative of a covariant current is itself covariant, as one can easily check. Thus, for \(p\in {\mathbb {Z}}_{\ge 0}\), the current \(\nabla ^p_x{\mathcal {K}}^{(\mathrm L)}(x)\) is covariant. This will allow us to construct many elements of \({\mathcal {W}}^{(\mathrm L)}\). Let \(F: ({\mathfrak {g}}^{{\mathbb {C}}})^{\oplus m} \rightarrow {\mathbb {C}}\) be a conjugacy-invariant m-multilinear form on \({\mathfrak {g}}^{\mathbb {C}}\) and \(p_1,\ldots ,p_m \in {\mathbb {Z}}_{\ge 0}\) be non-negative integers. Then, the field
belongs to \({\mathcal {W}}^{(\mathrm L)}\). It is clear that this family of fields include the examples constructed above from invariant polynomials of \({\mathcal {K}}^{(\mathrm L)}\) only. Let us note that the multilinear form F does not have to be symmetric: one can for instance use the completely skew-symmetric form \(F: (X,Y,Z) \mapsto \langle X,[Y,Z] \rangle \). We expect fields of the form (6.33) to span all the \({\mathcal {W}}\)-algebra \({\mathcal {W}}^{(\mathrm L)}\). In principle, starting from the Kac–Moody bracket of \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\), one can compute the Poisson algebra obeyed by these fields: more precisely, the bracket of two such fields should take the form of a linear combination of derivatives \(\partial _x^k\delta (x-y)\) of the Dirac distribution, with coefficients being themselves built from fields of the form (6.33).
Under the chiral realisations \(\rho ^{(\mathrm L)}\) considered in Sect. 6.2, the Kac–Moody currents \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\) in a certain gauge are expressed as left-moving fields in the UV fixed point of the Klimčík model. These fields typically take the form of linear combinations of the derivatives \(\partial _+ \phi ^a\) of the coordinate fields \(\phi ^a\) of the \(\sigma \)-model, with well-chosen coefficients (which can be themselves field dependent). In particular, the currents \(\rho ^{(\mathrm L)}\bigl ({\mathcal {J}}^{(\mathrm L)}_1)\) and \(\rho ^{(\mathrm L)}\bigl ({\mathcal {J}}^{(\mathrm L)}_2\bigr )\) are spin 1 left-moving fields. Since the spatial derivative \(\partial _x\) of a left-moving field coincides with its light-cone derivative \(\partial _+\), we can replace all covariant derivatives acting on these fields by light-cone covariant derivatives
The image of the field (6.33) under the realisation then takes the form
where we have abbreviated \(\rho ^{(\mathrm L)}\bigl ( {\mathcal {K}}^{(\mathrm L)}\bigr )\) as \({\mathcal {K}}^{\rho }\). This is a left-moving field with Lorentz spin \(p_1+\ldots +p_m+m\). Although the realised current \({\mathcal {K}}^{\rho }(x^+)\) is in general non-local, the above combination is such that non-local contributions cancel, yielding in the end a local field.
The \({\mathcal {W}}\)-Algebra for \({\mathfrak {sl}(2)}\) Let us now turn our attention to the case \({\mathfrak {g}}^{\mathbb {C}}=\mathfrak {sl}(2)\). The \({\mathcal {W}}\)-algebra \({\mathcal {W}}^{(\mathrm L)}\) contains only one spin 2 field, namely the energy–momentum tensor \(W^{(\mathrm L)}_2\) defined in Eq. (6.30). Following the general construction outlined in the previous paragraph, we can also construct a spin 3 field in \({\mathcal {W}}^{(\mathrm L)}\) as \(\langle {\mathcal {K}}^{(\mathrm L)}, \nabla {\mathcal {K}}^{(\mathrm L)}\rangle \). Using the ad-invariance of \(\langle \cdot ,\cdot \rangle \), one checks that the commutator term in the covariant derivative \(\nabla {\mathcal {K}}^{(\mathrm L)}\) vanishes when contracted with \({\mathcal {K}}^{(\mathrm L)}\). This spin 3 field is therefore equal to \(\langle {\mathcal {K}}^{(\mathrm L)}, \partial {\mathcal {K}}^{(\mathrm L)}\rangle \) and thus proportional to the derivative \(\partial W_2^{(\mathrm L)}\) of the energy–momentum tensor. There is no new primary spin 3 field.
Let us now turn our attention to spin 4 fields. Up to a constant, the only invariant polynomial of degree 4 on \({\mathfrak {g}}^{\mathbb {C}}=\mathfrak {sl}(2)\) is the square of the bilinear form \(\langle \cdot ,\cdot \rangle \). This yields a spin 4 field in \({\mathcal {W}}^{(\mathrm L)}\) proportional to \(\langle {\mathcal {K}}^{(\mathrm L)}, {\mathcal {K}}^{(\mathrm L)}\rangle ^2\) and thus to \(W_2^{{(\mathrm L)}\,2}\). Let us now look at the spin 4 fields that involve covariant derivatives of \({\mathcal {K}}^{(\mathrm L)}\). We find that there are two, given by \(\langle {\mathcal {K}}^{(\mathrm L)}, \nabla ^2 {\mathcal {K}}^{(\mathrm L)}\rangle \) and \(\langle \nabla {\mathcal {K}}^{(\mathrm L)}, \nabla {\mathcal {K}}^{(\mathrm L)}\rangle \). A direct computation shows that their sum is proportional to the second derivative \(\partial ^2W^{(\mathrm L)}_2\) of the energy–momentum tensor. In the end, there is only one spin 4 field in \({\mathcal {W}}^{(\mathrm L)}\) which is not expressed in terms of \(W^{(\mathrm L)}_2\) and its derivatives, which we can choose as
A similar analysis shows that there are three spin 5 fields in \({\mathcal {W}}^{(\mathrm L)}\), all expressible in terms of \(W^{(\mathrm L)}_2\), \(W^{(\mathrm L)}_4\) and their derivatives, namely \(\partial ^3 W^{(\mathrm L)}_2\), \(W^{(\mathrm L)}_2 \partial W^{(\mathrm L)}_2\) and \(\partial W^{(\mathrm L)}_4\). For spin 6, we find 6 fields expressed in terms of the lower-spin ones and two new ones. A summary is provided in Table 1.
One can compute the Poisson bracket obeyed by these various fields starting from the Kac–Moody bracket of \({\mathcal {J}}^{(\mathrm L)}_1\) and \({\mathcal {J}}^{(\mathrm L)}_2\). We have already pointed out in Eq. (6.31) that \(W^{(\mathrm L)}_2\) satisfies a classical Virasoro algebra. Similarly, we find
with
(the notation \(W_{6A}^{(\textrm{L})}\) and \(W_{6B}^{(\textrm{L})}\) is explained in the last line of Table 1).
Realisation in the Chiral Klimčík Model Let us now express how the \({\mathcal {W}}\)-algebra \({\mathcal {W}}^{(\mathrm L)}\) is realised in the UV fixed point of the Klimčík model for \(G=\textrm{SU}(2)\). For that, we can use the various types of realisations described in the two previous subsections, which in particular can correspond to different charts of the model. For instance, in chart I (corresponding to the left cigar with coordinates \((\phi ,\alpha )\) and the free boson \(\chi \)), one can use the parafermionic realisation \(\rho ^{(\mathrm L)}_P\) defined in Eq. (6.15). The basic building blocks for the fields of the \({\mathcal {W}}\)-algebra are the dynamical quantity \({\mathcal {K}}^{(\textrm{L})}\) (6.28), built out of the Kac–Moody currents, and the covariant derivative (6.34). Applying the map \(\rho ^{(\mathrm L)}_P\), one finds that
Here \(\mathcal {L}_P^{(1)}\) denotes the coefficient of \(z^{(\textrm{L})}\) in the Lax matrix (6.17), while \(\mathcal {L}_P^{(0)}\) is the constant term, i.e.
The formulae (6.30) for the spin 2 current and (6.36) for the spin 4 one yield the expressions (5.38) and (5.39), respectively, that appeared before in Sect. 5.4. Notice that, although the matrix elements of \(\mathcal {L}_P^{(\textrm{L})}\) itself contain the non-local fields \(\psi _\pm \), the currents \(W_2\) and \(W_4\) turn out to be differential polynomials in \(\partial _+\chi \) and \(T_m^{(\textrm{L})}\). Recall that the latter are the special combinations of the classical parafermions (5.3)–(5.5), which are local in the original fields \((\phi ,\alpha ,\chi )\). As before, a similar construction also holds for the right-moving W-currents.
So far, we have focussed on chart I. Similarly, one can realise the \({\mathcal {W}}\)-algebra in the chart III (corresponding to the right cigar with coordinates \((\phi ,{\widetilde{\alpha }})\) and the free boson \({\widetilde{\chi }}\)) and in the chart II (i.e. the asymptotic domain where the currents would be expressed in terms of the left-moving bosons \((\phi _1^{(\textrm{L})},\phi _2^{(\textrm{L})},\phi _3^{(\textrm{L})})\)) using the other realisations described in Sect. 6.2. In conclusion, the AGM construction thus provides an efficient systematic procedure to construct local chiral fields in the different charts of the chiral Klimčík model.
Local Charges So far, we have used the AGM formalism to describe local chiral fields of the model and the closed Poisson algebra \({\mathcal {W}}^{(\mathrm L)}\) that they form. It is also natural to look for local charges built from integrals of chiral fields in \({\mathcal {W}}^{(\mathrm L)}\) that are pairwise in involution and thus part of the integrable structure of the model. We have discussed such local charges in the general formalism of AGMs in Sect. 3.1: in particular, we have recalled that they are naturally associated with the zeroes of the twist function of the AGM—see Eq. (3.17). In the present case, the twist function \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\) is given by Eq. (6.2). The 1-form \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\text {d}z^{(\mathrm L)}\) then possesses one zero, at \(z^{(\mathrm L)}=\infty \). Under the constraint \({\mathcal {J}}^{(\mathrm L)}_1+{\mathcal {J}}^{(\mathrm L)}_2+{\mathcal {J}}^{(\mathrm L)}_3 \approx 0\), one checks that the evaluation of the 1-form \(\Gamma ^{(\mathrm L)}(z^{(\mathrm L)})\text {d}z^{(\mathrm L)}\) at \(z^{(\mathrm L)}=\infty \) is proportional to the current \({\mathcal {K}}^{(\mathrm L)}\) introduced in Eq. (6.28). For this AGM, the local charges discussed in Sect. 3.1 then take the form
where \(p\in {\widehat{E}}\) runs over the exponents of \(\widehat{{\mathfrak {g}}}\), \(\Phi _p\) is a well-chosen invariant polynomial of degree \(p+1\) on \({\mathfrak {g}}\) introduced in Sect. 3.1 and \(\alpha _p\) is an overall normalisation factor. In particular, the quadratic local charge \({\mathcal {Q}}_1^{(\mathrm L)}\) is simply given by the integral of the energy–momentum tensor:
More generally, the density \(\alpha _p \, \Phi _p ( {\mathcal {K}}^{(\mathrm L)})\) of the charge \({\mathcal {Q}}_p^{(\mathrm L)}\) is a local chiral field in the \({\mathcal {W}}\)-algebra \({\mathcal {W}}^{(\mathrm L)}\) (see previous paragraphs). These particular densities are chosen specifically to ensure the involution of the charges \({\mathcal {Q}}_p^{(\mathrm L)}\).
For the case \({\mathfrak {g}}^{\mathbb {C}}=\mathfrak {sl}(2)\), the exponents are all odd numbers \(2\,m-1\), \(m\in {\mathbb {Z}}_{\ge 1}\). The corresponding polynomials \(\Phi _{2m-1}\) have degree 2m and are simply proportional to \(\langle \cdot ,\cdot \rangle ^m\). Thus, the local charges are given by
They coincide with the ones obtained in Sect. 5.3 from screening charges. In particular, they involve only the spin 2 field of the \({\mathcal {W}}\)-algebra and none of the other fields. As we will see in Sect. 9.3, this will not be the case anymore at the quantum level.
7 Quantisation of Non-Local IMs
The problem of quantisation of the non-local IMs for the affine Gaudin model has not been systematically studied yet. (See, however, Ref. [32] for some first results.) For the classical field theory, a well-understood framework exists. The zero-curvature representation for the classical equations of motion implies a one parameter family of conserved quantities generated by the trace of the monodromy M(z). The latter can be thought of as the infinite series:
with \(\mathcal {L}(z;x)=\frac{1}{\varphi (z)}\,\Gamma (z;x)\) so that the corresponding IMs involve multifold ordered integrations of fields built from the Kac–Moody currents \(\mathcal {J}_{i}(x_j)\). While such classical expressions are well defined, providing a meaningful definition of the quantum family of commuting operators runs into problems. As such, although a formula for the simplest of them corresponding to the first term in the expansion of the monodromy at \(z=z_i\) has been proposed in [32], a systematic and rigorous study of the full set of non-local charges, including a proof of their mutual commutativity, is not available at the moment at least for general Lie group G (results for \(G=\textrm{SU}(2)\) may be extracted from the recent paper [46]).
One issue can already be traced at the classical level. It occurs in the derivation of the Poisson algebra satisfied by the matrix elements of the monodromy. The \(r\big /s\) bracket of the Lax matrix at different spatial points x and y contains a term proportional to the generalised distribution \(\delta '(x-y)\), see (3.11). In consequence, when calculating the PBs of two path-ordered exponents (7.1), contact terms arise from the integration of the derivative of the \(\delta \) distribution. These are ambiguous, and their contribution to the final result depends on the regularisation scheme one employs to treat them. This problem was originally studied in detail in the works of Maillet [7, 8]. He introduced a symmetric point-splitting prescription to handle the ambiguities. The computation of the Poisson brackets of the monodromy matrix then resulted in a “new integrable canonical structure”, which did not correspond to the classical limit of any known quantum algebra at the time. In view of this result, it became unclear how to proceed with the quantisation of the monodromy matrix even at the formal algebraic level. The difficulty in quantising a classically integrable system, where the Poisson brackets of the Lax connection contain a \(\delta '(x-y)\) term, has since become known as the problem with non-ultralocality.
A full discussion of the Poisson bracket algebra for M(z) will be reserved for a separate publication. Here our purpose is to review a proposal presented in Ref. [53] that points to a way of making progress in quantising the non-local IMs for the chiral affine Gaudin model discussed in the previous section. In that work, using the representation theory of the quantum affine algebra \({\mathcal {U}}_q\big (\widehat{\mathfrak {sl}}(2)\big )\), a quantum monodromy matrix satisfying the Yang–Baxter algebra is constructed. Based on perturbative computations, it is conjectured that in the classical limit the quantum monodromy becomes a classical one built from the Lax matrix
Here, \(V_s\) with \(s=+,-,0\) are dynamical variables obeying the Poisson bracket algebra
At this point, we note that \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}'\) coincides with the special case \(\omega =1\) of the family of flat connections \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}^{(\omega )}\) from Eq. (4.39), up to a similarity transformation that depends on the spectral parameter \(\rho \), but not on the dynamical fields. In addition, the Poisson brackets for \(V_s\) are the same ones that are satisfied by \(V_s^{(1)}\) in (4.43) upon setting the inessential constant \(K_{\scriptscriptstyle \mathrm UV}\) to one. Recall that \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}^{(\omega )}\) coincides with the Lax matrix obtained from the AGM considered in Sect. 6 for the case \(G=\textrm{SU}(2)\) provided that a particular gauge fixing condition is imposed on the Kac–Moody currents, see Sect. 6.2. The transfer matrix for the corresponding Gaudin model is a gauge-invariant object and is also unaffected by the similarity transformation relating \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}'\) to \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}^{(1)}\). This way, the trace of the quantum monodromy matrix from Ref. [53] provides a potential definition of the quantum non-local IMs for this AGM.
A rigorous proof of the conjectures from [53], as well as their generalisation to higher-rank Lie groups and a general number of punctures, would be valuable for the study of the quantised affine Gaudin model. The aim of this section is to formulate the main statements concisely, and to discuss some consequences relevant for our goals.
7.1 Quantum/Classical Monodromy for \(\varvec{G=\textrm{SU}(2)}\)
Universal R-Matrix The construction of the quantum monodromy matrix in [53], which itself is based on the work [18], uses the representation theory of the quantum affine algebra \({\mathcal {U}}_q\big (\widehat{\mathfrak {sl}}(2)\big )\). The latter is a Hopf algebra with generators \({\textsf{X}}_0,{\textsf{X}}_1\), \({\textsf{Y}}_0, {\textsf{Y}}_1\), \({\textsf{H}}_0\) and \({\textsf{H}}_1\). A summary of the set of relations and the definition of the co-product \(\Delta \) can be found, for example, in [18]. For our purposes, it is enough to mainly focus on the Borel subalgebra \(\mathcal {U}_q(\widehat{{\mathfrak {b}}}_-)\subset {\mathcal {U}}_q(\widehat{\mathfrak {sl}}(2))\) generated by the set \(\{{\textsf{X}}_0\), \({\textsf{X}}_1\), \({\textsf{H}}_0\), \({\textsf{H}}_1\}\). These operators, amongst themselves, satisfy the commutation relations
as well as the quartic Serre relations
with \([m]_q=(q^m-q^{-m})/(q-q^{-1})\). Also note that we set the central element \({\textsf{K}}={\textsf{H}}_0+{\textsf{H}}_1\) to be zero:
The algebra \(\mathcal {U}_q(\widehat{{\mathfrak {b}}}_-)\) turns out to possess an infinite-dimensional commuting subalgebra. It is defined starting from the notion of the universal R-matrix \({{\mathcal {R}}}\). The latter is an element of \({\mathcal {U}}_q(\widehat{{\mathfrak {b}}}_+)\otimes {\mathcal {U}}_q(\widehat{{\mathfrak {b}}}_-)\), where \({\mathcal {U}}_q(\widehat{{\mathfrak {b}}}_+)\) is generated by \({\textsf{Y}}_0\), \({\textsf{Y}}_1\), \({\textsf{H}}_0=-{\textsf{H}}_1\), while \({\mathcal {U}}_q(\widehat{{\mathfrak {b}}}_-)\) is as above. It satisfies the Yang–Baxter equation
with the left- and right-hand sides being valued in three tensor copies of \({\mathcal {U}}_q\big (\widehat{\mathfrak {sl}}(2)\big )\) and the lower two indices indicate to which factors of the tensor product the universal R-matrix belongs. It turns out that expressing \(\mathcal {R}\) in the form:
and requiring \(\overline{{\mathcal {R}}}\) to be a formal series in the nilpotent generators \({\textsf{X}}_0\) and \({\textsf{X}}_1\), is enough to specify the universal R-matrix uniquely. In particular, using the product formula presented in [88], one can develop the series expansion
up to any order in the generators.Footnote 24
“Universal” Monodromy Matrix Consider the evaluation homomorphism from \(\mathcal {U}_q\big (\widehat{\mathfrak {sl}}(2)\big )\) to the loop algebra \(\mathcal {U}_q\big (\mathfrak {sl}(2)\big )[\lambda ,\lambda ^{-1}]\) and further specify a matrix irrep \(\pi \) of \(\mathcal {U}_q\big (\mathfrak {sl}(2)\big )\). With some abuse of notation, we will use the symbols \(\texttt{e}_\pm \), \(\texttt{h}\) for the generators of the quantum algebra specialised to that finite-dimensional representation. Under this map, the elements of \(\mathcal {U}_q\big (\widehat{\mathfrak {sl}}(2)\big )\) become
where
By means of such a homomorphism, one can define the “universal” monodromy matrix:
Up to the factor \(q^{\frac{1}{2}{\textsf{H}}_0\texttt{h}}\), this would be a formal power series in \(\lambda \) with coefficients being matrices, whose entries are polynomials in the unspecified generators \({\textsf{X}}_0\) and \({\textsf{X}}_1\). For instance, according to Eqs. (7.8) and (7.9), the first few terms read
The commutation relations satisfied by the matrix elements of \({\textsf{M}}(\lambda )\) follow from Eqs. (7.4) and (7.5). It turns out to be possible to represent them in the form
with the numerical matrix R being defined as
These is a direct consequence of applying the homomorphism \(\pi _\lambda \otimes \pi _\mu \otimes \textrm{id}\) to both sides of the Yang–Baxter relation (7.7) for the universal R-matrix. Note that, in the case when the representations \(\pi _\lambda \) and \(\pi _\mu \) are chosen to be the fundamental ones, \(R(\lambda )\) coincides with the trigonometric solution of the Yang–Baxter equation associated with the six-vertex model. Namely, up to an overall scalar factor depending on the spectral parameter, \(R(\lambda )\) would be given by
The Yang–Baxter algebra (7.14) yields an infinite family of commuting operators in \(\mathcal {U}_q(\widehat{{\mathfrak {b}}}_-)\), built from the formal generators \({\textsf{X}}_0\), \({\textsf{X}}_1\) and \({\textsf{H}}_0=-{\textsf{H}}_1\). They are obtained by taking a suitable trace of the monodromy over the matrix representation \(\pi \):
Here, as explained in [18], the extra term appearing in the trace, with \(f({\textsf{H}}_0)\) being any function of the generator \({\textsf{H}}_0\), does not spoil the mutual commutativity of the transfer matrices,
The universal monodromy matrix obeys the Yang–Baxter algebra (7.14) as a consequence of the commutation relations (7.4) and the Serre relations (7.5) for the generators of \(\mathcal {U}_q(\widehat{{\mathfrak {b}}}_-)\). Different representations of these generators give rise to commuting families of operators which are associated to different integrable models. The work [18] considers an infinite-dimensional representation, where \({\textsf{X}}_{0,1}\) and \({\textsf{H}}_{0,1}\) act in the (extended) Fock space of one bosonic field. In this case, the transfer matrix (7.17) yields the local and non-local IMs of the quantum KdV integrable structure, provided that the extra factor in the trace is set to be \( q^{\frac{1}{2} f({\textsf{H}}_0)\,\texttt{h}}=q^{\frac{1}{2} {\textsf{H}}_0\,\texttt{h}} \). The KdV case serves as a prototype of the construction from Ref. [53], which is relevant to the \(\textrm{SU}(2)\) Klimčík model. The reader may find the review of the basic case contained in Sect. 2 of that paper as a helpful companion to what is discussed below.
Quantum Monodromy Matrix for the Fateev Integrable Structure The representation of \(\mathcal {U}_q(\widehat{{\mathfrak {b}}}_-)\) first appearing in the works [13, 82] and then considered in Ref. [53] takes three independent copies of the Heisenberg algebra as its starting point:
One groups the generators into bosonic fields
and then constructs the vertex operators
Here, \(n>0\) and \(\varpi >1\) are considered to be parameters of the theory and we assume the standard normal ordering prescriptions (note that the precise way of fixing the ordering of the zero modes \(\hat{\varphi }_0^{(3)}\) and \({\hat{p}}^{(3)}\) in the definition of the exponential field is not essential). Then, the generators of the Borel subalgebra \(\mathcal {U}_q(\widehat{{\mathfrak {b}}}_-)\) are specified to be
while
In writing these formulae, we anticipate the relation between the quantum group parameter q and \((n,\varpi )\), which enter into the vertex operators (7.21):
The Heisenberg algebra generated by \(({\hat{a}}^{(j)}_m,{\hat{p}}^{(j)})\,_{m\ne 0}^{j=1,2,3}\) possesses a highest weight representation, which is commonly referred to as the Fock space. It is built from the highest state, which is an eigenvector of the zero mode momenta \({\hat{p}}^{(j)}\) and is annihilated by the operators \({\hat{a}}_m^{(j)}\) with \(m\ge 1\). The irrep is defined as the linear span of all possible states obtained by acting on the highest state with the creation operators \({\hat{a}}_m^{(j)}\) with \(m\le -1\). We will denote the Fock space as \(\mathcal {F}_{p_1,p_2,p_3}\), where the subscript keeps track of the eigenvalues of \({\hat{p}}^{(j)}\). The generators \({\textsf{X}}_{0,1}\), realised as in (7.22), then act as the intertwiners:
In turn, the matrix elements of the quantum monodromy (7.13) can be understood as operators acting in the extended Fock space \(\bigoplus _{m=-\infty }^\infty \mathcal {F}_{p_1,p_2,p_3+\frac{m\textrm{i}}{\sqrt{n\varpi }}}\).
Recall that the generators \({\textsf{X}}_0\), \({\textsf{X}}_1\) and \({\textsf{H}}_0\) are required to satisfy (7.4) and the Serre relations (7.5). These, in principle, can be investigated from the above definitions and the commutation relations of the Heisenberg algebra (7.19). While the first requirement (7.4) is easily established, checking the Serre relations is subtle. In fact, in even considering monomials built from \({\textsf{X}}_{0,1}\), such as those entering into Eq. (7.5), some clarifications are required. The vertex operators, which are the integrands for \({\textsf{X}}_j\), exhibit singular behaviour whenever two of them come close together:
Upon subsequent integration w.r.t. x and y a divergent result would generically be obtained. Nevertheless, it is possible to define renormalised monomials in \({\textsf{X}}_j\) in the following way.
One may, for example, shift one of the integration contours by a small imaginary amount \(\propto \,\textrm{i}\eta \) such that if \({\textsf{V}}_s(x)\) occurs to the left of \({\textsf{V}}_{s'}(y)\) in the integral, then \(\Im m(x)<\Im m(y)\). Taking the limit \(\eta \rightarrow 0^+\) one expects to get a well-defined result, which could be thought of as a renormalised version of the original monomial. To illustrate, consider one of the simplest cases:
For fixed y belonging to the open interval \(y\in (0,2\pi )\), the integration contour for the x variable can be made to coincide with subsets of \([0,2\pi ]\) outside of the segment \([y-\eta ,y+\eta ]\). The latter may be replaced by \(C_\eta (y)\), the part of the circle of radius \(\eta \) with centre y that is contained in the lower half of the complex x plane. This way,
In order to compute the integration over the semi-circle, one uses the OPE \({\textsf{V}}_+(x)\,{\textsf{V}}_-(y)\), where only the singular part needs to be taken into account. In view of Eq. (7.26), it gives a contribution \(\propto \,\eta ^{-1+\frac{2}{n\varpi }}\). The singularities developed by the integral over \(C_\eta (y)\) in the limit \(\eta \rightarrow 0^+\) exactly cancel the singularities occurring in the first two integrals in the round brackets in (7.28), when upper and lower integration endpoints, respectively, approach the point y.
To verify the Serre relations (7.5), one could represent monomials formed out of the operators \({\textsf{X}}_j\) in a similar way as illustrated by the example in Eq. (7.28). The result can be represented by a multifold integral over \({\textsf{V}}_{s_1}(x_1)\ldots {\textsf{V}}_{s_4}(x_4)\), where the integration variables run over the combination of segments \(x_i\in [0,2\pi ]\cap \{x_i:\ |x_i-x_j|>\eta \}\) along with subtractions that cancel the UV divergences. Then, as explained in Ref. [18], by means of the braiding relations
the order of the vertex operators is rearranged in each integral and the result is expressed in terms of the “renormalised” ordered integrals
with
and the “\(\ldots \)” represent counterterms ensuring the existence of the limit \(\eta \rightarrow 0^+\). It has been observed in Ref. [18] that once the monomials in \({\textsf{X}}_j\) are rewritten using the ordered integrals, the terms \({\textsf{J}}_\eta (s_1,\ldots , s_m)\) cancel each other in the Serre relations. Since the counterterms are determined by the singular part of \({\textsf{J}}_\eta \), one expects that they will mutually cancel each other in the Serre relations as well.
As was first pointed out in the work [18], the full series expansion (7.13) may be brought to the form
If \({\textsf{J}}_{\textrm{ren}}(s_1,\ldots ,s_m)\) had coincided with the usual ordered integral, this would be recognised as a path-ordered exponent:
In the present case, the quantum monodromy can still be understood as a path-ordered exponent over \(\lambda \big ({\textsf{V}}_+\,q^{\frac{\texttt{h}}{2}}\,\texttt{e}_++ {\textsf{V}}_-\, q^{-\frac{\texttt{h}}{2}}\,\texttt{e}_-\big )\), though one must keep in mind that such a representation contains UV divergences that need to be regularised in order to make \({\textsf{M}}(\lambda )\) well defined.
Main Conjecture The main conjecture of Ref. [53] concerns the classical limit of the quantum monodromy \({\textsf{M}}(\lambda )\) described above. This limit is interpreted as sending \(n\,\propto \, \hbar ^{-1} \rightarrow \infty \) so that the deformation parameter q (7.24) tends to one. The fields \(\phi _i^{(\textrm{L})}=\hat{\varphi }_i/(n\varpi )^\frac{1}{2}\) become canonically normalised classical fields satisfying the Poisson bracket relations (4.42) with \(K_{\scriptscriptstyle \mathrm UV}=1\). We keep the superscript “\({\textrm{L}}\)” as a reminder that \(\phi _i^{(\textrm{L})}\) will be identified with the left moving chiral bosons appearing in the asymptotically flat domain of the chiral \(\textrm{SU}(2)\) Klimčík model. Similar to their quantum counterparts \(\hat{\varphi }_i\), they should be taken to be quasi-periodic:
where the dynamical quantity \(P_j\) appears in the \(n\rightarrow \infty \) limit of the operators \({\hat{p}}_j\) from Eq. (7.20). As it follows from (7.21), (7.22) the classical limit of \({\textsf{X}}_0\) and \({\textsf{X}}_1\) yields
where
and
(We use the derivative \(\partial _+\) rather than \(\partial \) since the classical fields \(\phi _i^{(\textrm{L})}\) are being understood as functions of \(t+x\).) Notice that the formula for \(V_\pm \) in terms of the free chiral fields \(\phi ^{(\textrm{L})}_j\) coincides with the first line of (4.41) for \(\omega =1\). Together with the extra field
these dynamical variables obey the classical Poisson algebra (7.3) (in view of the quasi-periodic boundary conditions (7.34) the fields \(V_\pm (x)\) are single valued functions on the universal cover \(x\in {\mathbb {R}}\). In obtaining formula (7.3), it is being assumed that both \(x,y\in [0,2\pi )\), see also discussion below Eq. (7.60)). At this point, we are ready to formulate the main statement of Ref. [53].
Conjecture: The classical limit of the quantum monodromy matrix \({\textsf{M}}(\lambda )\) described by Eqs. (7.13), (7.19)–(7.24) is given by
Here \(V_\pm \) and \(V_0\) are as above with \(\phi _j^{(\textrm{L})}=\lim _{n\rightarrow \infty } \hat{\varphi }_i/(n\varpi )^\frac{1}{2}\) and \(\texttt{h}\), \(\texttt{e}_\pm \) stand for the generators of the \(\mathfrak {sl}(2)\) algebra (4.9). The spectral parameters \(\rho \) and \(\lambda \) are related via a power series of the form
where the higher-order coefficients are non-universal in the sense that they depend on the details of the regularisation needed to assign a precise meaning to \({\textsf{M}}(\lambda )\) and its classical limit. Notice that the monodromy (7.37) is nothing but the path-ordered integral of \(-\mathcal {L}_{\scriptscriptstyle \textrm{UV}}'(\rho )\) from Eq. (7.2) up to the extra factor \(\text{ e}^{-\pi P_3\texttt{h}}\).
The following comment is in order here. Consider the exponent in the r.h.s. of Eq. (7.37). Suppose one were to drop the term \(\propto \rho ^2\, V_0(x)\) and remove the factor \(\frac{1}{1-\rho ^2}\) appearing in front of the integral. Then, the resulting classical monodromy matrix would coincide literally with the classical limit of the path-ordered exponent representation for the quantum monodromy (7.33) with \(\rho =\lambda \). As it happens, the expression (7.33) requires UV regularisation, e.g. by introducing a UV cut-off and performing explicit subtractions of the singular part as described above. The modified form of the r.h.s. of (7.37), including the appearance of the extra field \(V_0(x)\), could be thought of as the result of anomalous contributions coming from the counterterms that remain finite in the double limit where \(\hbar \rightarrow 0\) and the UV regulator goes away.
The Sklyanin Exchange Relations The main conjecture has an important corollary. Since it implies that the classical limit of \({\textsf{M}}(\lambda )\) is well defined, one can take the same limit for both sides of the quantum exchange relations (7.14). As was first observed by Sklyanin [89], assuming that the numerical matrix goes as \(R(\lambda )= \textrm{const}\times \big (\textrm{id}+\textrm{i}\hbar \, r(\lambda )+O(\hbar ^2)\big )\) and using the correspondence principle \([\cdot ,\cdot ]\mapsto \textrm{i}\hbar \{\cdot ,\cdot \}\), one obtains the Poisson algebra
for the classical monodromy \(M(\lambda )=\lim _{n\rightarrow \infty }{\textsf{M}}(\lambda )\) (recall that the Planck constant \(\hbar \propto \, n^{-1}\)). Note that for the \(\mathfrak {sl}(2)\) case, where the R matrix specialised to the fundamental representation is proportional to \(R_{\frac{1}{2}\frac{1}{2}}(\lambda )\) from Eq. (7.16), the matrix \(r(\lambda )\) is given byFootnote 25
Since the quantum monodromy is built from an associative algebra, the Jacobi identity for the commutator \([\cdot ,\cdot ]\) holds. It automatically follows that the Jacobi identity must be valid for the Poisson algebra satisfied by the classical limit of \({\textsf{M}}(\lambda )\). This is equivalent to the classical Yang–Baxter equation for the matrix \(r(\lambda )\) entering into Eq. (7.39). The expression (7.40) is easily recognised to be the trigonometric solution to that equation associated to \(\mathfrak {sl}(2)\).
That the Poisson algebra of the classical monodromy matrix obeys the Sklyanin exchange relations as well as the Jacobi identity is a non-trivial statement in the case at hand. This is because \(M(\lambda )\) takes the form of a path-ordered exponent of the connection \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}'(\rho )\) (7.2), where the fields \(V_\pm (x)\), \(V_0(x)\) entering therein obey the non-ultralocal algebra (7.3). As was mentioned in the preamble, the presence of the \(\delta '(x-y)\) term introduces ambiguities in the computation of the Poisson brackets for the matrix elements of the monodromy. These generically lead to a violation of the Jacobi identity and a modification to the algebra (7.39). The main conjecture essentially implies that there exists a regularisation procedure such that the Jacobi identity and Sklyanin exchange relations are preserved. Note that a way to obtain the Sklyanin exchange relation in a non-ultralocal system was proposed in the work [90]. For the example of the principal chiral model, the authors obtained the Poisson algebra (7.39) where to handle the contact terms a certain “retarded” monodromy matrix was introduced.
Perturbative Checks For the reader’s convenience, we recall and elaborate on the main argument presented in Ref. [53] in support of the conjecture (7.37). In that work, the series expression (7.13) is used as a starting point for taking the classical limit, where the monomials in \({\textsf{X}}_j\) are regularised in some way, e.g. by means of deforming contours as explained above. In general, each term in the expansion for \({\textsf{M}}(\lambda )\) takes the form of a polynomial in the non-commutative variables \({\textsf{X}}_0\) and \({\textsf{X}}_1\) with coefficients depending on the deformation parameter q. To take \(n\,\propto \,\hbar ^{-1}\rightarrow \infty \) one should expand \(q=\text{ e}^{-\frac{\textrm{i}\pi }{n\varpi }}\) for large n, express the result in terms of commutators and then replace the commutators with Poisson brackets using the correspondence principle \( [\,\cdot \,,\,\cdot \,]\mapsto -\frac{2\pi \textrm{i}}{n\varpi }\ \{\,\cdot \,,\,\cdot \,\}\). It is easy to see that with this procedure the first few terms shown in (7.13) become
where \(\texttt{h},\texttt{e}_\pm \) satisfy the commutation relations of the \(\mathfrak {sl}(2)\) algebra. Developing the series expansion for the classical monodromy matrix quickly becomes cumbersome at higher orders. In Ref. [53], a typical computation is illustrated for a term that contributes to (7.41) at fourth order in \(\lambda \). Supported by perturbative computations up to \(\lambda ^5\), it is expected that the series (7.41) exists and can in principle be extended to all orders in the spectral parameter.
In computing the Poisson brackets that appear in the series expansion (7.41) one meets a familiar issue. The integrands of \(\mathcal {X}_0\) and \(\mathcal {X}_1\) satisfy the \(\mathfrak {sl}(2)\) like current algebra given in Eq. (7.3) and those formulae contain a term proportional to the derivative of the delta function. As such when evaluating the PBs involving \(\mathcal {X}_0\), \(\mathcal {X}_1\) one encounters the problem of contact terms that was mentioned before. The appearance of the distribution \(\delta '(x-y)\) and the associated ambiguity in the evaluation of the series (7.41) have an interpretation in the context of the current discussion. They are the classical analogues of the singular behaviour of the vertex operators (7.26) as well as the freedom in the choice of the UV regularisation scheme needed to give meaning to products of \({\textsf{X}}_j\). In principle, once the quantum operator \({\textsf{M}}(\lambda )\) is precisely defined, the corresponding classical expression is fixed completely.
There exists a way of dealing with the contact terms directly at the level of the classical field theory, which goes along the following line. When evaluating nested PBs involving \(\mathcal {X}_0\) and \(\mathcal {X}_1\), one assumes that the Jacobi identity holds true and uses it to reduce the types and number of ambiguous integrals that arise. By means of the Jacobi identity and skew-symmetry it is expected that all of the Poisson brackets appearing in the series expansion may be brought to the form
To give an example, substituting
into
gives rise to the identity
which swaps a nested PB to a sum of two that are of the above type.
In evaluating the reduced class of Poisson brackets (7.42), only three types of ambiguous integrals arise:
Here F(x) and G(x) are arbitrary functions and \(\sigma (x)\) stands for the Heaviside step function so that, in particular, the \(\epsilon (x)\) term in the Poisson algebra (7.3) can be expressed as \(\epsilon (x)=\sigma (x)-\sigma (-x)\). For the first integral it is natural to require that \(\delta '(x_1-x_2)\) be anti-symmetric. This way,
For \(I_2\) some additional care is needed. To illustrate the issue, let’s take the domain of \(x_2\) and \(x_3\) to be \((\eta _{2A},2\pi -\eta _{2B})\) and \((\eta _{3A},2\pi -\eta _{3B})\), respectively, where the infinitesimally small regulators \(\eta _{mA}\) and \(\eta _{mB}\) with \(m=2,3\) are taken to be positive. The last condition ensures that \(|x_2-x_3|<2\pi \) over the full integration domain. This is important, since the Poisson algebra (7.3) that was used to evaluate the nested PBs (7.42) and led to the ambiguous integrals (7.45) is valid when \(|x-y|<2\pi \) and otherwise requires modification to take into account that the fields \(V_\pm (x)\) are quasi-periodic. Then, integrating the expression for \(I_2\) (7.45) w.r.t. \(x_3\) one finds that
A case by case study yields that \(I_2=0\) if \(\eta _{2A}>\eta _{3A}\) and \(I_2=\int _0^{2\pi }\text{ d }x_1 \, F(x_1)\) for \(\eta _{2A}<\eta _{3A}\) (the relative magnitude of \(\eta _{2B}\) and \(\eta _{3B}\) has no effect on the result provided the regulators are taken to be infinitesimal). This way, the value of \(I_2\) is ambiguous and depends on the precise treatment of the endpoints of the integration domain. In what follows, we set
where \(\gamma \) is some undetermined constant. For \(I_3\), there is no issue of contact terms and an integration by parts w.r.t. \(x_2\) or \(x_4\) results in zero so that
Note that the above formulae also specify the value of any ambiguous integrals that can be related to \(I_2\) and \(I_3\) via anti-symmetry of \(\delta '(x_1-x_2)\).Footnote 26
In order to appreciate how the series for the classical monodromy matrix (7.41) could organise into a path-ordered exponent, it is worthwhile performing an explicit computation up to order \(\lambda ^2\). To this end, introduce the ordered integrals over the classical fields
with \(s_j\in \{-1,0,1\}\). The coefficients of \(\texttt{e}_\pm \) and \(\texttt{e}_\pm ^2\) in (7.41) are expressed in terms of these by means of the elementary identities:
while
The non-trivial part concerns the evaluation of \(\{\mathcal {X}_0,\mathcal {X}_1\}\). The Poisson brackets of \(\mathcal {X}_0\) and \(\mathcal {X}_1\) are obtained from those of \(V_+(x)\) and \(V_-(y)\), presented in the first line of Eq. (7.3), by means of integration w.r.t. x and y. A brief inspection of that formula shows that there are three terms that need to be taken into account. One of them is proportional to \(\delta '(x-y)\). It contributes nothing to the end result since the integrated quantity \(\int \text{ d }x\text{ d }y \,\delta '(x-y)\) was prescribed to be zero, see Eqs. (7.45) and (7.46). The part multiplying the delta function yields \(-\int \text{ d }x V_0(x)=-J_{\textrm{cl}}(0)\). For the last term, one uses the fact that by definition \(\epsilon (x)=\sigma (x)-\sigma (-x)\) and hence
As a result, one finds
Notice that the expression in the square brackets coincides with the expansion of a path-ordered exponent for the connection \(\mathcal {L}=-\lambda \,(V_+\texttt{e}_++V_-\texttt{e}_-)-\tfrac{1}{2}\lambda ^2\,V_0(x)+O(\lambda ^3)\). This provides a check of the conjecture 7.37 with \(\rho =\rho (\lambda )\) as in (7.38) to second order in \(\lambda \).
The main piece of evidence for the conjecture is an explicit evaluation of the series (7.41) up to and including \(\lambda ^5\) that was carried out in the work [53]. In the computation of the higher-order terms, in addition to \(I_1\), ambiguous integrals of the form \(I_2\) and \(I_3\) (7.45) arise, which leads to the undetermined constant \(\gamma \) (7.48) entering into the result. The latter turns out to be consistent with the conjecture (7.37), where the spectral parameter \(\rho \) is related to \(\lambda \) as
7.2 Some Comments for the Case of Higher Rank Lie Groups
While the work [53] proposes a direction for quantising the non-local IMs of the three punctured affine Gaudin model for \(G=\textrm{SU}(2)\), we would not have reviewed it here if the arguments were not readily adaptable to the case of arbitrary Lie group G. Indeed, the main ingredients required to carry out the first few steps of the generalisation are already contained in Sect. 6.2.
Consider the Poisson bracket relations (7.3) satisfied by the components of the Lax matrix (7.2). They are essentially the \(\textrm{SU}(2)\) case of the general algebra (6.21) specialised to \(\omega =1\). In simplified notation \(\Xi _\alpha = \Xi _\alpha ^{(\textrm{L})}\), \(\Xi _i = \Xi _i^{(\textrm{L})}\) and setting the inessential constant \(K_{\mathrm{\scriptscriptstyle UV}}\) to be one, the PB relations for general Lie group read:
The conventions for the Lie algebra generators \(\texttt{h}_i\) and \(\texttt{e}_\alpha \) used in this paper as well as the meaning of the symbols \(\alpha (\texttt{h}_i)\), \((\alpha ,\beta )\) and \(N^{\alpha ,\beta }\) are explained in “Appendix A”. Also note that, in our normalisation, \(\rho _\alpha ^i=\frac{1}{2}\,\alpha (\texttt{h}_i)\).
Recall that the dynamical variables \(\Xi _\alpha \) and \(\Xi _j\) possess the interpretation of the components of the Kac–Moody currents in the so-called \(\omega \) gauge for \(\omega =1\), see Eqs. (6.19) and (6.20). The Lax matrix \(\frac{1}{\varphi ^{(\textrm{L})}(z^{(\textrm{L})})}\, \Gamma ^{(\textrm{L})}(z^{(\textrm{L})})\), with the gauge fixing imposed, is expressed linearly in terms of them. Similar to the \(\textrm{SU}(2)\) case, it is convenient to perform an extra similarity transformation to the Lax matrix by a non-dynamical spectral parameter dependent matrix. The latter involves the Weyl coweight \(\texttt{h}_\delta \), whose defining property is that
with \(\ell (\alpha )\) denoting the level of the root \(\alpha \in \Delta \) (see “Appendix A” for additional details). Then introduce
Here, the spectral parameter \(z^{(\textrm{L})}\) is swapped for \(\rho \) according to
which is a simple generalisation of Eq. (4.40), while h is the Coxeter number (e.g. \(h=N\) for \(G=\textrm{SU}(N)\)). By substituting the expressions for the gauge-fixed Kac–Moody currents (6.19), (6.20) into the general formula for the Gaudin Lax matrix (6.6) and (6.3), and making use of the definition (6.2) for the twist function, \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}'\) can be written directly in terms of the component fields \(\Xi _\alpha \) and \(\Xi _i\). This yields
with the first summation being over all the positive roots \(\Delta _+\).
In the usual treatment of the affine Gaudin model, the fields are assumed to be periodic functions of \(x\sim x+2\pi \). The \(G=\textrm{SU}(2)\) case motivates one to consider a generalisation of these boundary conditions, since the classical fields \(\phi _i^{(\textrm{L})}\) entering into the connection had to be quasi-periodic (7.34). We expect it to be possible to broaden the notion of the affine Gaudin model and arrange so that the components \(\Xi _\alpha \) and \(\Xi _j\) of the gauge-fixed currents obey
In turn, the Lax matrix \(\mathcal {L}_{\scriptscriptstyle \textrm{UV}}'\) also becomes quasi-periodic:
(an implicit summation over “j” is being implied in each exponent). Note that the derivation of the Poisson bracket algebra (7.54) assumed periodic boundary conditions. For the case of quasi-periodic fields \(\Xi _\alpha (x)\), they remain valid for \(x,y\in [0,2\pi )\) and can be extended from that domain to the universal cover \(x,y\in {\mathbb {R}}\) in a way that is consistent with Eq. (7.59). Amongst other things, \(\delta (x-y)\) and \(\delta '(x-y)\) should be considered as being periodic distributions, while their coefficients in (7.54) would be modified by factors, e.g. \(\exp \big (2\,(x-y)\,\sum _{j} \rho _\alpha ^j\,P_j\big )\) in the first line of that equation. As for the step function, its extension is given by \(\epsilon (x)=2m+1\) for \(2\pi m<x<2\pi (m+1)\ \ (m\in {\mathbb {Z}})\). A quick analysis of the Poisson bracket algebra (7.54) under the shift \(x\rightarrow x+2\pi \), focussing only on the \(\epsilon (x-y)\) term, shows that the quasi-periodicity factors \(P_j\) must be treated as dynamical variables such that
In a 2D integrable classical field theory defined on the space-time cylinder with \(x\sim x+2\pi \), the transfer matrix T(z) is usually introduced as the Wilson loop integrated along the constant time slice \(0\le x-x_0< 2\pi \). An important property is that T(z) should be independent of the arbitrary constant \(x_0\), i.e. the integration contour needs to close. In the case, when the connection is quasi-periodic as in (7.60), this requires the insertion of an extra factor inside the trace. Choosing some representation for G, we take the monodromy and transfer matrix to be
(note that the index j in \( P_j\,\texttt{h}_j\) is being summed over).
The monodromy matrix \(M(\rho )\) is our candidate, which is expected to appear in the classical limit of a suitable representation of the Yang–Baxter algebra (7.14). Exploring this further in any detail is beyond the scope of the present paper. Nevertheless, we mention some first pieces of evidence, specialising to the case \(G=\textrm{SU}(N)\) in order to avoid unnecessary technical details. Let \(\alpha _j\) be the \(N-1\) simple roots of the Lie algebra and denote by \(\alpha _0\) the negative root with minimum level, i.e.
The inner products \(A_{ij}=(\alpha _i,\alpha _j)\) with \(i,j=0,1,\ldots ,N-1\) are encoded in the extended Cartan matrix:

Also, introduce the notation
Then, one can check that the first two terms in the expansion of the classical monodromy from Eq. (7.62) coincide with
where
It turns out that the series (7.65) appears in the classical limit of the universal monodromy matrix built from the quantum affine algebra \(\mathcal {U}_q\big (\widehat{\mathfrak {sl}}(N)\big )\), similar to what was discussed for the \(\mathfrak {sl}(2)\) case. One should check and eventually prove that it coincides term by term with \(M(\rho )\) from Eq. (7.62). This would be the first step for applying the quantum inverse scattering method to the problem of quantisation of the non-local IMs for the affine Gaudin model with Lax matrix \(\Gamma ^{(\textrm{L})}/\varphi ^{(\textrm{L})}\).
8 Quantum Local IMs and \(\varvec{{\mathcal {W}}}\)-Algebra for \(\varvec{G=\textrm{SU}(2)}\)
The classical algebra of extended conformal symmetry and the classical local IMs are discussed in Sect. 5. It was explained how they admit a representation in terms of free chiral fields \(\partial _+\phi ^{(\textrm{L})}_j\), which is determined through the quasi-commutativity condition (5.28). The classical screening charges entering into that formula are given by Eqs. (5.29), (5.30). One may notice that they coincide with \(\mathcal {X}_0\) and \(\mathcal {X}_1\) from (7.35) and (7.36), which appear in the classical limit of the generators of the Borel subalgebra \({\textsf{X}}_0,{\textsf{X}}_1\in \mathcal {U}_q(\widehat{{\mathfrak {b}}}_-)\subset \mathcal {U}_q\big (\widehat{\mathfrak {sl}}(2)\big )\). This way, accepting the results of the previous section, one is led to conclude that the full classical integrable structure is determined by \(\mathcal {X}_0\) and \(\mathcal {X}_1\). The non-local IMs are given by the trace of the power series (7.41), which involves the classical screening charges and their Poisson brackets, while the local IMs are obtained via the quasi-commutativity condition that was mentioned before.
For the quantum case, the situation is analogous. The rôle of the screening charges is played by \({\textsf{X}}_0\) and \({\textsf{X}}_1\), which are the operators built from the free chiral fields \(\hat{\varphi }_j\) that are given by Eqs. (7.21) and (7.22). These go into the power series expansion for the monodromy \({\textsf{M}}(\lambda )\), see Eq. (7.13), through which the non-local IMs are obtained by taking an appropriate trace (7.17). Note that, at this stage, the generating function \({\textsf{T}}(\lambda )\) is meant as a formal power series expansion in the spectral parameter \(\lambda \), without reference to convergence, whose operator-valued coefficients mutually commute. The quantum local IMs are determined from \({\textsf{X}}_0\) and \({\textsf{X}}_1\) in a way that is a straightforward generalisation of what was discussed for the classical case in Sect. 5.3. It is useful to rephrase this in the language of operator product expansions (OPEs). One starts with a general ansatz for a Lorentz spin m differential polynomial:
Using the free field OPEs
where “\(\text {reg}\)” stands for terms that are regular in \(x-y\), one requires that the OPE of \({\textsf{F}}_{m}(x)\) with the integrand of the screening charge \({\textsf{X}}_0\) obeys
This is easily recognised as the quantum version of (5.17). The result is a set of fields generating a quantum algebra of extended conformal symmetry. A particular subset of them enter as densities for the local IMs. To determine the latter one needs to make use of the second screening charge \({\textsf{X}}_1\). One imposes the further condition that
in direct analogy with Eq. (5.32). This then fixes the coefficients \(F_{i_1\ldots i_k}^{j_1\ldots j_k}\) entering into the density \({\textsf{F}}_m\) up to an overall multiplicative factor (with the possibility that \({\textsf{F}}_m=0\)). The resulting local IM,
can be said to “quasi-commute” with the screening charges:
in the sense that the commutator of \({\textsf{Q}}_{m-1}\) with their integrands \({\textsf{V}}_+(y)\) and \({\textsf{V}}_-(y)\) is a total derivative in y.
In what follows, we perform an explicit analysis of Eqs. (8.3), (8.4) and derive the formula for the first non-trivial local IM of the Fateev integrable structure. This will be important for the next section, where it is checked that the local IMs constructed from the affine Gaudin model following refs. [34, 35] coincides with those obtained through the quasi-commutativity condition with \({\textsf{X}}_0\) and \({\textsf{X}}_1\). Note that the extended algebra of conformal symmetry and the local IMs have been studied in refs. [81, 82] and our discussion uses the results of those papers.
8.1 Quantum \(\varvec{{\mathcal {W}}}\)-Algebra and Local IMs
Consider the first condition (8.3). In finding the densities \({\textsf{F}}_m(x)\), it is useful to introduce the fields \(\hat{\chi }\) and \(\hat{\alpha }\), which are related to \(\hat{\varphi }_1\) and \(\hat{\varphi }_2\) via the orthogonal transformation:
It is easy to see from Eq. (7.21) that \({\textsf{V}}_+\,\propto \, \partial \hat{\alpha }\,\exp (\frac{2\hat{\varphi }_3}{\sqrt{n\varpi }}) \ +\ \mathrm{total\ derivative}\), so that any differential polynomial in \(\partial \hat{\chi }\) trivially satisfies (8.3). By means of the free field OPE (8.2) and repeated use of Wick’s theorem, one analyses that condition for the local densities that are built from the two remaining fields \(\partial \hat{\alpha }\) and \(\partial \hat{\varphi }_3\). Limiting oneself to fields with Lorentz spin \(m=4\) or lower, one obtains the currents:
(every composite field appearing above is assumed to be normal ordered). The formulae above should be compared with Eq. (5.13), which lists the first few classical local left-moving fields of the cigar NLSM in the free field realisation. Taking into account that \(\alpha ^{(\textrm{L})}=\hat{\alpha }/(n\varpi )^{\frac{1}{2}}\) and \(\phi ^{(\textrm{L})}=\hat{\varphi }_3/(n\varpi )^{\frac{1}{2}}\) become canonically normalised fields in the classical limit, one finds that
This way, the currents \({\textsf{T}}_m\) are the first few members of the quantum \(\mathcal {W}_\infty \)-algebra.
Let’s turn to the second condition (8.4). There is an alternative way of stating it. Ignoring total derivatives, the screening charges \({\textsf{V}}_+\) and \({\textsf{V}}_-\) (7.21) are related to each other by the transformation \(\hat{\varphi }_1\mapsto -\hat{\varphi }_1\) and \(\hat{\varphi }_3\mapsto -\hat{\varphi }_3\). Therefore, Eq. (8.4) is equivalent to \({\textsf{F}}_m(x)\) being invariant under a simultaneous flipping of the signs of \(\hat{\varphi }_1\) and \(\hat{\varphi }_3\) up to a total derivative. An analysis yields that \({\textsf{Q}}_{m-1}\) with odd m vanish, while the first few members of the “even” local IMs are given by
with
Here, the constants \(C_j\) read
while  stands for the normal ordered field which can be defined as the first regular term in the OPE of \({\textsf{T}}_2(x){\textsf{T}}_2(0)\). Note that in the classical limit the second line of (8.11), as well as the term
stands for the normal ordered field which can be defined as the first regular term in the OPE of \({\textsf{T}}_2(x){\textsf{T}}_2(0)\). Note that in the classical limit the second line of (8.11), as well as the term  in the first line, dominate. As a result, the local IM \({\textsf{Q}}_3\) becomes proportional to the integral of the square of \(T_2^{(\textrm{L})}+(\partial _+\chi )^2\) and, in particular, contains no dependence on the other classical fields \(T_3^{(\textrm{L})}\) or \(T_4^{(\textrm{L})}\). This was remarked upon at the end of Sect. 5.3.
in the first line, dominate. As a result, the local IM \({\textsf{Q}}_3\) becomes proportional to the integral of the square of \(T_2^{(\textrm{L})}+(\partial _+\chi )^2\) and, in particular, contains no dependence on the other classical fields \(T_3^{(\textrm{L})}\) or \(T_4^{(\textrm{L})}\). This was remarked upon at the end of Sect. 5.3.
8.2 Quantum Corner-Brane \(\varvec{{\mathcal {W}}}\)-Algebra
In Sect. 5.4, the classical corner-brane \(\mathcal {W}\)-algebra was described. Its fields are certain combinations of \(T_m^{(\textrm{L})}\) and \(\partial _+\chi ^{(\textrm{L})}\) that are determined via a commutativity condition with the classical screening charge \(\mathcal {X}^{\scriptscriptstyle \mathrm CB}_1\) (5.34). There is a direct analogue of this in the quantum case. The quantum corner-brane \(\mathcal {W}\)-algebra is generated by the differential polynomials in \(\partial \hat{\varphi }_j\) which, together with \({\textsf{X}}_0\), also quasi-commute with the screening charge:
By analysing the condition similar to (8.3) but with \({\textsf{V}}_+(y)\) replaced by the integrand of \({\textsf{X}}_1^{\scriptscriptstyle \mathrm CB}\), one obtains the spin 2 field:
The extra minus sign here as compared with \({\textsf{T}}_2\) is a matter of convention. It was introduced so that \({\textsf{W}}_2\) satisfies the usual stress–energy–momentum tensor OPE:
with the central charge being
As in the classical case, there is no independent spin 3 field. A straightforward but somewhat lengthy computation yields that the space of Lorentz spin 4 fields is spanned by  , which is defined as the first regular term in the OPE
\({\textsf{W}}_2(x){\textsf{W}}_2(0)\),
\(\partial ^2{\textsf{W}}_2\) and
, which is defined as the first regular term in the OPE
\({\textsf{W}}_2(x){\textsf{W}}_2(0)\),
\(\partial ^2{\textsf{W}}_2\) and
with
Here, the field \({\textsf{F}}_4\) is the same one that appears in (8.11), while the value of the constant \(C_5\) is given in Eq. (8.12). The normalisation of \({\textsf{W}}_4^{(\textrm{PB})}\) has been chosen so that it exactly coincides with the spin 4 current presented in “Appendix A” in the work [81] on the “Pillow Brane” model. The parameters \((\alpha _1,\alpha _2,\alpha _3)\) from that paper should be set to \(\alpha _1=-\sqrt{n\varpi }\), \(\alpha _2=-\textrm{i}\sqrt{n(\varpi -1)}\) and \(\alpha _3=-\textrm{i}\sqrt{n+2}\), while the fields \(\hat{\varphi }_j\) are related to the triple (X, Y, Z) used in that work as \(\hat{\varphi }_1= Y\), \(\hat{\varphi }_2=- Z\) and \(\hat{\varphi }_3=- X\). Note that in the classical limit

where \(W_4^{(\textrm{L})}\) and \(W_2^{(\textrm{L})}\) are the classical corner-brane \(\mathcal {W}\)-algebra currents given in Eqs. (5.38), (5.39) and \(\nu ^2=\lim _{n\rightarrow \infty } \varpi -1\).
The fields \({\textsf{W}}_m(x)\) form a closed algebra. The OPE encoding the commutation relations between the Fourier modes of the currents follow from the explicit formulae presented above and the free field OPEs (8.2). Rather than working with \({\textsf{W}}_4\), it is useful to consider a slightly different spin 4 current:

with
and
Although the expression for \({\textsf{W}}_4\) in terms of the free fields \(\hat{\varphi }_j\) is significantly more complex than that for \({\textsf{W}}_4^{(\textrm{PB})}\), it has the advantage of being a primary field. Namely,
The OPE of \({\textsf{W}}_{4,P}\) with itself gives a cumbersome result that was first presented in Ref. [82], see “Appendix A” of that work. We reproduce it here in our notations in order to make a later comparison with the Gaudin model. It reads

where
and
Recall that the central charge and the constant \(\beta \) were defined in Eqs. (8.16) and (8.22), respectively. Also \({\textsf{W}}_6\) appearing in the last line of the OPE (8.24) is a Lorentz spin 6 field belonging to the quantum corner-brane \(\mathcal {W}\)-algebra that is not expressible as a differential polynomial in \({\textsf{W}}_2\) and \({\textsf{W}}_4\).
Finally, let us note that all the local IMs from the Fateev integrable structure can be written in terms of the fields \({\textsf{W}}_m\) and their “descendents”. In particular, for the first few IMs \({\textsf{Q}}_1\) and \({\textsf{Q}}_3\) presented in (8.10), one finds that
9 Quantised AGM: \(\varvec{{\mathcal {W}}}\)-Algebra and Local IMs
The goal of this section is to discuss the quantisation of affine Gaudin models and their applications to the quantum UV fixed point of the Klimčík model: it is thus meant as a quantisation of the set-up described in the classical case in Sect. 6. Quantised AGMsFootnote 27 were initially introduced in the work [32] of Feigin and Frenkel, motivated by an analogy with Gaudin models based on finite algebras instead of affine ones. In particular, it was argued in [32] that quantised AGMs can provide a systematic formalism to study integrable structures in conformal field theories. Building on these results and ideas, the study of quantised AGMs and their integrable structure was further pursued in the works [34, 35], which focussed on the description of local quantum charges in these models. In this section, we will review the results of [32, 34, 35] and will discuss their applications to the quantisation of the Klimčík model at the UV fixed point. In particular, we will use the formalism of quantised AGMs to describe the quantum \({\mathcal {W}}\)-algebra underlying this model and the quantum local IMs therein, focussing mainly on the \(\textrm{SU}(2)\) case. As we will see, these results agree with the ones obtained from free field realisations and screening charges in Sect. 8 and offer interesting perspectives for future applications in higher rank groups or more general models.
9.1 Quantising Affine Gaudin Models
Reminder: Change of Spectral Parameter in a Classical AGM Our goal in this subsection is to describe the quantisation of an AGM with N punctures \(z_r\), Kac–Moody currents \({\mathcal {J}}_r\) and levels \(\ell _r\). For that, it will be useful to first recall a few facts about the “geometrical” behaviour of this classical model with respect to the spectral parameter \(z\in \mathbb{C}\mathbb{P}^1\), as discussed in Sect. 3.1. In particular, recall that the twist function behaves as a 1-form \(\varphi (z)\text {d}z\) on \(\mathbb{C}\mathbb{P}^1\). In the previous sections, we have always supposed that our choice of spectral parameter z is such that none of the punctures \(z_r\) is situated at infinity. This requires the 1-form \(\varphi (z)\text {d}z\) to be regular at \(z=\infty \) and thus the residues \(\ell _r\) to satisfy the condition (3.5), which we recall here for convenience:
The second main ingredient defining an AGM is the Gaudin Lax matrix, which also defines a 1-form \(\Gamma (z,x)\text {d}z\) on \(\mathbb{C}\mathbb{P}^1\). To ensure the regularity of this 1-form at infinity, we imposed that \({\mathcal {C}}_G(x) = \sum _{r=1}^N{\mathcal {J}}_r(x)\) vanishes, which we interpreted as a constraint \({\mathcal {C}}_G(x) \approx 0\) in the Poisson algebra \({\mathcal {A}}\). Moreover, the condition on the levels (9.1) recalled above ensures that \({\mathcal {C}}_G\) is a first-class constraint and thus that the symmetry it generates is a gauge symmetry. This played an important role in the construction of the AGM. In particular, the integrable structure \({\mathcal {Z}}^{(z_r)}\subset {\mathcal {A}}\) built in this model is formed by gauge-invariant charges and is (weakly) independent of the choice of spectral parameter.
Sending a Puncture at Infinity In the previous sections, we have always supposed for simplicity that our choice of coordinate z on \(\mathbb{C}\mathbb{P}^1\) is such that the punctures \(z_r\) are finite. It will in fact be useful for quantisation to discuss quickly what happens if we perform a change of spectral parameter which sends a puncture to infinity. Up to relabelling, we can always suppose that this is the Nth puncture. We will now work with a coordinate z such that \(z_N = \infty \). The twist function and Gaudin Lax matrix in this coordinate then take the form
In particular, the level \(\ell _N\) and current \({\mathcal {J}}_N\) associated with the Nth puncture do not appear explicitly in these expressions, since \(z_N=\infty \). However, one has
Since the Nth puncture \(z_N\) is at infinity, this residue should coincide with \(\ell _N\), hence \(\ell _N = -\sum _{r=1}^{N-1} \ell _r\). We thus recover in this way the condition (9.1). A similar statement holds for the Gaudin Lax matrix: more precisely, we want to ensure that the residue of \(\Gamma (z,x)\text {d}z\) at infinity coincides with the Kac–Moody current \({\mathcal {J}}_N(x)\) attached to the Nth puncture \(z_N=\infty \). We treat this as a constraint in the algebra \({\mathcal {A}}\) generated by \({\mathcal {J}}_1,\ldots ,{\mathcal {J}}_N\), which then reads
We thus recover the constraint \({\mathcal {C}}_G(x)\approx 0\).
Working with the coordinate z such that the puncture \(z_N\) is at infinity presents a slight advantage. Indeed, the Gaudin Lax matrix is formally independent of the Kac–Moody current \({\mathcal {J}}_N\), which only enters in the model through the constraint (9.4). Thus, the Lax matrix \({\mathcal {L}}(z,x)\) of the model, which allows one to build non-local conserved charges, as well as the local charges built from \(\Gamma (z,x)\) at the zeroes of \(\varphi (z)\) (see Sect. 3.1), are directly expressed in terms of \(N-1\) Kac–Moody currents \({\mathcal {J}}_1,\ldots ,{\mathcal {J}}_{N-1}\) only. In contrast, in another coordinate where all the punctures are finite, all of the N currents \({\mathcal {J}}_r\) enter the explicit definition of these charges. Of course, the dependence of these charges on \({\mathcal {J}}_N\) can be removed weakly, by imposing the constraint to express \({\mathcal {J}}_N\) in terms of the \(N-1\) remaining currents: the charges obtained in this way then coincide with the ones directly built from the coordinate in which \(z_N=\infty \). Working in this coordinate thus has the advantage of describing the integrable structure directly in terms of \(N-1\) Kac–Moody currents, without having to impose the constraint explicitly.
Let us also discuss how the gauge symmetry is implemented in the model with \(z_N=\infty \). The gauge-invariant observables are the ones which weakly Poisson commute with the constraint \({\mathcal {C}}_G = \sum _{r=1}^N {\mathcal {J}}_r\). Since the observables in this model are naturally built from the currents \({\mathcal {J}}_1,\ldots ,{\mathcal {J}}_{N-1}\) only, their Poisson bracket with \({\mathcal {C}}_G(x)\) coincides with their bracket with the current
We can then characterise the physical observables of the model with \(z_N=\infty \) as the quantities built from \({\mathcal {J}}_1,\ldots ,{\mathcal {J}}_{N-1}\) which Poisson commute with \({\mathcal {J}}_{\text {diag}}\). Note, however, that \({\mathcal {J}}_{\text {diag}}\) is not treated here as a constraint: indeed, it is not set to zero. We note also that the set-up considered here formally resembles an AGM with \(N-1\) finite punctures, in which we do not impose that the residues \(-\sum _{r=1}^{N-1}\ell _r\) of \(\varphi (z)\text {d}z\) and \(-{\mathcal {J}}_{\text {diag}}\) of \(\Gamma (z,x)\text {d}z\) vanish, but where we focus on observables invariant under the diagonal symmetry generated by \({\mathcal {J}}_\text {diag}\).Footnote 28 This is reminiscent of the discussion of the classical \({\mathcal {W}}\)-algebra in Sect. 6.3: as we shall see, this will also be useful later in this section for the construction of the quantum \({\mathcal {W}}\)-algebra and the local integrals of motion therein.
Quantum Kac–Moody Currents Consider a basis \(\lbrace \texttt{t}_a \rbrace \) of \({\mathfrak {g}}\), the dual basis \(\lbrace \texttt{t}^a \rbrace \) with respect to the bilinear form \(\langle \cdot ,\cdot \rangle \) and the decomposition \({\mathcal {J}}_r = {\mathcal {J}}_{r,a} \texttt{t}^a\) of the classical Kac–Moody current. The Poisson bracket of these components is then given by Eq. (3.3). This Poisson algebra has a natural quantisation \(\widehat{{\mathcal {A}}}\). Namely, \(\widehat{{\mathcal {A}}}\) is a non-commutative algebra generated by fields \({\textsf{J}}_{r,a}(x)\) satisfying the commutation relations
where \(\eta _{ab}=\langle \texttt{t}_a,\texttt{t}_b\rangle \), \(k_r\) are constant numbers that we will call quantum levels and the factors \(2\pi \) and \(\textrm{i}\) have been introduced for future convenience. To take the classical limit of this algebra, we consider \(\hbar \rightarrow 0\) with
It is then straightforward to check that
with the Poisson bracket \(\lbrace {\mathcal {J}}_{r,a}, {\mathcal {J}}_{s,b} \rbrace \) given by Eq. (3.3). This ensures that the semi-classical limit of the quantum algebra \(\widehat{{\mathcal {A}}}\) is indeed \({\mathcal {A}}\).
Using the language of vertex operator algebras, the commutation relation (9.6) obeyed by the quantum Kac–Moody currents \({\textsf{J}}_{r,a}(x)\) can be rephrased in terms of the following OPE (operator product expansion):
where \(\text {reg}\) designates terms which are regular when \(x\rightarrow y\).
Quantum Twist Function and Gaudin Lax Matrix Let us introduce
We call \(\varphi ^{(\textrm{qt})}(z)\) the quantum twist function and \(\Gamma ^{(\textrm{qt})}(z,x)\) the quantum Gaudin Lax matrix. It is clear from Eq. (9.7) that the behaviour of these objects in the classical limit \(\hbar \rightarrow 0\) is given by
where \(\varphi (z)\) and \(\Gamma (z,x)\) are the twist function and Gaudin Lax matrix of the classical AGM, as defined in Eq. (3.1) and (3.4).
Change of Spectral Parameter in Quantised AGMs Let us now discuss the behaviour of the quantised AGM under a change of spectral parameter \(z \mapsto {\widetilde{z}}\) with \(z=\omega ({\widetilde{z}})\). This question was touched upon indirectly in the work [34], which explored quantised AGMs starting from the conjecture of Feigin and Frenkel [32] stating that the spectrum of these models is encoded in objects called affine opers (we will discuss some of the results of [34] and affine opers later in this section and the next). In particular, the behaviour of affine opers under a change of spectral parameter was studied in [34] and suggests that the twist function is no longer a 1-form at the quantum level. More precisely, it should transform according to the following rule:
where \(h^{\!\vee }\) is the dual Coxeter number of the Lie algebra \({\mathfrak {g}}\). The first term in this equation corresponds to the standard transformation rule of a 1-form under the change of coordinate \(z\mapsto {\widetilde{z}}=\omega ^{-1}(z)\). The second term breaks this property and in fact makes \(-\varphi ^{(\textrm{qt})}(z)\text {d}z\) behave as the component of a meromorphic connection on the line bundle \(\Omega ^{\,h^{\!\vee }}\) over \(\mathbb{C}\mathbb{P}^1\), where \(\Omega ^{k}\) denotes the kth tensor power of the canonical line bundle. This term can be interpreted as a quantum correction: indeed, considering the classical limit \(\hbar \rightarrow 0\) with the scaling property (9.11), we easily see that this term is subdominant in the limit of Eq. (9.12), which reads
recovering that the classical twist function \(\varphi (z)\) behaves as a 1-form when \(\hbar = 0\).
The transformation rule (9.12) has an important consequence. Let us consider the behaviour of the quantum twist function around infinity. For that, we consider the change of variable \(z \mapsto {\widetilde{z}}= z^{-1}\). Applying the rule (9.12), we find that the twist function in the coordinate \({\widetilde{z}}\) is given by
Using the expression (9.10) of \(\varphi ^{(\textrm{qt})}(z)\) in terms of the quantum levels \(k_r\), we find that, around \({\widetilde{z}}=0\),
The fact that the AGM does not possess a puncture at \(z=\infty \) and thus that the twist function \({\widetilde{\varphi }}^{(\textrm{qt})}({\widetilde{z}})\) is regular at \({\widetilde{z}}=0\) then implies
This is the quantum equivalent of the condition (9.1) on the classical levels \(\ell _r\). In fact, it is clear from the scaling behaviour (9.7) of \(k_r\) in the classical limit \(\hbar \rightarrow 0\) that the quantum condition (9.16) reduces to Eq. (9.1) in this limit, as expected. We will discuss the algebraic interpretation of this quantum condition in the following paragraph.
Quantum Gauge Symmetry Recall that in the classical case, we consider the AGM up to the gauge symmetry generated by the constraint \({\mathcal {C}}_G \approx 0\): in particular, the condition (9.1) on the classical levels \(\ell _r\) ensures that this constraint is first class. The quantum equivalent of \({\mathcal {C}}_G\) is the field
which is a Kac–Moody current with level \(\sum _{r=1}^N k_r\). It is thus natural to consider the quantised AGM as gauged with respect to the symmetry generated by this field, which is then seen as a quantum constraint. At the quantum level, this constraint and gauge symmetry should be treated using the BRST formulation. In particular, the consistency of this formulation requires the BRST charge built from the generator of the symmetry to square to zero. For the case of a symmetry generated by a Kac–Moody current, as here, this condition has been studied in [91], where it was proven that it requires the level of the current to be equal to \(-2h^{\!\vee }\). In the case at hand, since the generator (9.17) has level \(\sum _{r=1}^N k_r\), we find that the condition for the consistency of the BRST formulation coincides with the condition (9.16) found above by considering the geometrical behaviour of the quantum twist function. This is the quantum equivalent of the classical condition (9.1), which ensures on the one hand that the classical constraint is first class and on the other hand that the classical twist function behaves as a 1-form.
Setting a Puncture to Infinity As mentioned above, imposing the constraint and the gauge symmetry at the quantum level requires the use of the BRST formalism. There is, however, a way to avoid these technical complications. Indeed, recall from earlier discussions that, in the classical case, considering a set-up in which one of the puncture \(z_N\) is at infinity allows us to build the AGM from the currents \({\mathcal {J}}_1,\ldots ,{\mathcal {J}}_{N-1}\) only and thus avoids having the constraint to be explicitly imposed. We will follow a similar approach in the quantum case and thus suppose from now on that we chose a coordinate z on \(\mathbb{C}\mathbb{P}^1\) such that \(z_N=\infty \).Footnote 29 By construction, the quantum Gaudin Lax matrix \(\Gamma ^{(\textrm{qt})}(z,x)\) in this coordinate then involves only the Kac–Moody currents \({\textsf{J}}_1,\ldots ,{\textsf{J}}_{N-1}\). Observables built from these currents are then gauge invariant if they commute (or equivalently have regular OPE) with the diagonal generator
Since the modes of the Kac–Moody current \({\textsf{J}}_r\) form the affine algebra \(\widehat{{\mathfrak {g}}}_{k_r}\) with level \(k_r\), these gauge-invariant observables then naturally form a
coset algebra.
Quantum Integrable Structure Recall from Sect. 3.1 that the main output of the classical AGM formalism is the construction of an integrable structure \({\mathcal {Z}}^{(z_r)}\), formed by gauge-invariant charges in involution built from the classical Kac–Moody currents. It is natural to expect that a quantum equivalent \(\widehat{{\mathcal {Z}}}^{(z_r)}\) of this integrable structure exists in the quantised AGM described above, corresponding to commuting operators built from the quantum Kac–Moody currents \({\textsf{J}}_r\). This was conjectured and motivated in [32], using an analogy with Gaudin models based on finite algebras, for which the quantum integrable structure is well understood. In particular, some of the commuting operators in \(\widehat{{\mathcal {Z}}}^{(z_r)}\) were discussed in [32], including certain non-local charges and quadratic local charges (as well as higher-degree local charges in specific examples). Building on the results and ideas of [32], the systematic construction of higher degree local charges was also considered in [34, 35], resulting in some conjectures (and first checks thereof) on the form of these charges. We will discuss some of these results as well as a few new ones in Sect. 9.3 and “Appendix D”.
Quantum Realisations So far, we have described a formal quantised AGM, whose algebra of physical observables is a vertex operator algebra built from (the quotient of) abstract quantum Kac–Moody currents \({\textsf{J}}_r\). In order to apply this formalism to the description of integrable two-dimensional quantum field theories, and in particular integrable \(\sigma \)-models, one needs to consider realisations of this algebra in terms of the fields of these theories, as we did in the classical set-up. A natural question at this point is whether any classical realisation of an AGM will be upgraded to a quantum realisation in the above sense: we expect that this is in fact not the case in general. Indeed, there is no guarantee that classical Kac–Moody currents of a two-dimensional field theory will survive quantisation and obey quantum OPEs as in Eq. (9.9).
There is, however, one important set-up where we expect such a quantisation to hold, namely chiral realisations in conformal models. In this case, the currents of the AGM are realised as left- or right-moving fields of the theory (up to gauge symmetry, see Sect. 6). The quantisation of this theory defines a two-dimensional CFT whose chiral algebras of left- and right-moving fields are described by vertex operator algebras: we then expect these chiral algebras to contain a realisation of the corresponding quantised AGM. In this case, we then interpret the quantum fields describing the AGM as functions of the light-cone variable \(x+t\) or \(x-t\). We will see examples of this construction in the next subsection, for the case of the UV fixed point of the \(\textrm{SU}(2)\) Klimčík model. In Sect. 6, we have denoted the quantities in classical chiral AGMs with a label \({(\mathrm L)}\) or \({(\mathrm R)}\), to emphasise that they are realised in terms of left-moving or right-moving fields: to lighten the notations, we will drop this label in the present section. It is, however, important to keep in mind that we expect these quantised AGMs to only be realised in terms of chiral fields of two-dimensional CFTs.
9.2 Quantum \(\varvec{{\mathcal {W}}}\)-Algebra
Generalities As explained in the previous subsection, the physical observables of a quantised AGM with \(N-1\) finite punctures and an infinite one \(z_N=\infty \) can be seen as the quantities built from the Kac–Moody currents \({\textsf{J}}_1,\ldots ,{\textsf{J}}_{N-1}\) which commute with the current \({\textsf{J}}_{\text {diag}}\). Such observables are in general non-local in the currents. We can, however, restrict to local fields satisfying this property, yielding the quantum \({\mathcal {W}}\)-algebra \(\widehat{{\mathcal {W}}}\) underlying the model. More precisely, \(\widehat{{\mathcal {W}}}\) is defined as the set of normal ordered differential polynomials in the components of \({\textsf{J}}_1,\ldots ,{\textsf{J}}_{N-1}\) which have a regular OPE with \({\textsf{J}}_{\text {diag}}\). Such a field \({\textsf{W}}\) is thus built as a linear combination of monomials of the form

(with \(p_k\in {\mathbb {Z}}_{\ge 0}\), \(r_k \in \lbrace 1,\ldots ,N-1\rbrace \) and \(a_k\in \lbrace 1,\ldots ,\dim {\mathfrak {g}}\rbrace \)) and satisfies
We will sometime call these fields W-currents. We note that
\(\widehat{{\mathcal {W}}}\) is a vertex operator subalgebra, in the following sense: for any two fields
\({\textsf{W}}\) and \({\textsf{W}}'\) in \(\widehat{{\mathcal {W}}}\), \(\partial {\textsf{W}}\) and the normal ordered product  belong to \(\widehat{{\mathcal {W}}}\) and the coefficients of the OPE \({\textsf{W}}(x){\textsf{W}}'(y)\) are elements of \(\widehat{{\mathcal {W}}}\).
belong to \(\widehat{{\mathcal {W}}}\) and the coefficients of the OPE \({\textsf{W}}(x){\textsf{W}}'(y)\) are elements of \(\widehat{{\mathcal {W}}}\).
Moreover, \(\widehat{{\mathcal {W}}}\) is a graded vertex operator algebra. The corresponding grading is defined by assigning the weight one to Kac–Moody components \({\textsf{J}}_{r,a}\) and to the derivative \(\partial \), such that the monomial (9.20) has grade \(\sum _{k=1}^m (p_k+1) = p_1+\ldots +p_m+m\). The algebra \(\widehat{{\mathcal {W}}}\) then decomposes into a direct sum
where \(\widehat{{\mathcal {W}}}_p\) is the subspace of W-currents of grade p, which is of finite dimension. Moreover, if \({\textsf{W}}_p\) and \({\textsf{W}}_q\) have respective gradings p and q, then \(\partial {\textsf{W}}_p\) has grading \(p+1\) and  has grading \(p+q\). Finally, let us observe that under a quantum chiral realisation of the AGM in a two-dimensional CFT, this grading coincides with the Lorentz spin of the W-currents if the latter are left-moving fields and to minus their spin if they are right-moving. By a slight abuse of language, we will sometimes refer to a W-current with grade p as a spin p field, having in mind applications to left-moving realisations.
has grading \(p+q\). Finally, let us observe that under a quantum chiral realisation of the AGM in a two-dimensional CFT, this grading coincides with the Lorentz spin of the W-currents if the latter are left-moving fields and to minus their spin if they are right-moving. By a slight abuse of language, we will sometimes refer to a W-current with grade p as a spin p field, having in mind applications to left-moving realisations.
The \({(\widehat{{\mathfrak {g}}}\oplus \widehat{{\mathfrak {g}}})/\widehat{{\mathfrak {g}}}}\) Coset \({\mathcal {W}}\)-Algebra Let us now specialise our set-up by considering an AGM with \(N=3\) punctures, which is the AGM that underlies one of the chiral halves of the UV fixed point of the Klimčík model. In this case, the \({\mathcal {W}}\)-algebra \(\widehat{{\mathcal {W}}}\) is then composed by the differential polynomials in two currents \({\textsf{J}}_1\) and \({\textsf{J}}_2\) which commute with \({\textsf{J}}_{\text {diag}}={\textsf{J}}_1+{\textsf{J}}_2\). It thus forms a \((\widehat{{\mathfrak {g}}}_{k_1}\oplus \widehat{{\mathfrak {g}}}_{k_2})/\widehat{{\mathfrak {g}}}_{k_1+k_2}\) coset \({\mathcal {W}}\)-algebra. In Sect. 6.3, we have given a systematic description of the classical version of this \({\mathcal {W}}\)-algebra, by building classical W-currents from covariant fields and their covariant derivatives. This construction does not seem to straightforwardly generalise to the quantum case considered here: indeed, these classical expressions generally receive quantum corrections which are not directly expressed in terms of the covariant fields.
Let us illustrate this with a simple example, namely the quantum spin 2 W-current \({\textsf{W}}_2\). To find it, one can start with an ansatz as a linear combination of the fields  ,
,  and
and  , where \(\eta ^{ab}\) denotes the inverse of \(\eta _{ab}=\langle \texttt{t}_a, \texttt{t}_b\rangle \). A direct computation shows that the regularity of the OPE \({\textsf{J}}_{\text {diag},a}(x){\textsf{W}}_2(y)\) fixes the corresponding coefficients (up to a global factor), yielding:
, where \(\eta ^{ab}\) denotes the inverse of \(\eta _{ab}=\langle \texttt{t}_a, \texttt{t}_b\rangle \). A direct computation shows that the regularity of the OPE \({\textsf{J}}_{\text {diag},a}(x){\textsf{W}}_2(y)\) fixes the corresponding coefficients (up to a global factor), yielding:

We recognise here the energy–momentum tensor of the Goddard–Kent–Olive (GKO) construction [92, 93]. The overall normalisation has been fixed so that \({\textsf{W}}_2\) satisfies the standard Virasoro OPE:
where the central charge c reads
To study the classical limit of this W-current, let us recall that the levels \(k_r\) and currents \({\textsf{J}}_r\) satisfy the asymptotic property (9.7) when \(\hbar \rightarrow 0\). We then find
is the classical spin 2 W-current. In particular, we see that the shifts of the levels by \(h^{\!\vee }\) in Eq. (9.23) can be interpreted as quantum corrections. Moreover, one checks that the OPE (9.24) gives back, in the classical limit, the Poisson bracket (6.31). Finally, using \({\mathcal {J}}_{\text {diag}}={\mathcal {J}}_1+{\mathcal {J}}_2\), we find that \(W_2\) is proportional to \(\langle {\mathcal {K}},{\mathcal {K}}\rangle \), where \({\mathcal {K}}=\ell _2\,{\mathcal {J}}_1-\ell _1\,{\mathcal {J}}_2\) is the covariant classical current introduced in Eq. (6.28): we thus recover the classical construction (6.30) of \(W_2\) in terms of covariant fields. However, at the quantum level, the expression (9.23) for \({\textsf{W}}_2\) does not seem to be directly expressible in terms of a quantum version of the covariant current \({\mathcal {K}}\). It would be interesting to explore whether a less naive quantisation of the classical procedure outlined in Sect. 6.3 can be found, that would allow a more systematic construction of the quantum \((\widehat{{\mathfrak {g}}}_{k_1}\oplus \widehat{{\mathfrak {g}}}_{k_2})/\widehat{{\mathfrak {g}}}_{k_1+k_2}\) coset \({\mathcal {W}}\)-algebra.
Quantum Corner-Brane \({\mathcal {W}}\)-Algebra Let us finally specialise the set-up even more by considering \({\mathfrak {g}}^{\mathbb {C}}=\mathfrak {sl}(2)\). In this case, \(\widehat{{\mathcal {W}}}\) becomes the corner-brane \({\mathcal {W}}\)-algebra [81, 82]. Its classical version has been discussed in terms of screening charges in Sect. 5.4 and from the point of view of Gaudin models and coset algebras in Sect. 6.3. Its quantisation from screening charges was described in Sect. 8.2. We finally discuss its quantisation as a \(\widehat{\mathfrak {sl}}(2)\oplus \widehat{\mathfrak {sl}}(2)/\widehat{\mathfrak {sl}}(2)\) coset \({\mathcal {W}}\)-algebra in this paragraph and the “Appendix C”.Footnote 30 It was proven in [82] that these two quantisations are equivalent: we refer to this work for a more detailed treatment. For the purpose of the present article, it will be enough to describe the first elements of this algebra and compare them with the free field realisation studied in Sect. 8.2.
This \({\mathcal {W}}\)-algebra contains a unique spin 2 field, the energy–momentum tensor \({\textsf{W}}_2\) described in the previous paragraph for an arbitrary Lie algebra \({\mathfrak {g}}\), as well as a unique spin 3 field \(\partial {\textsf{W}}_2\). The obvious spin 4 fields are  and \(\partial ^2{\textsf{W}}_2\). In the classical case, we found in Sect. 6.3 that there exists an additional independent spin 4 field, built in Eq. (6.36) from the covariant current \({\mathcal {K}}\). As for the energy–momentum tensor \({\textsf{W}}_2\) discussed in the previous paragraph, this construction in terms of \({\mathcal {K}}\) does not directly generalise to the quantum case. We can, however, determine the quantum spin 4 field \({\textsf{W}}_4\) by a brute force computation, solving the linear equation \({\textsf{J}}_{\text {diag}}(x){\textsf{W}}_4(y)=\text {reg}\) starting with a general ansatz for \({\textsf{W}}_4\) in terms of the Kac–Moody currents \({\textsf{J}}_1\) and \({\textsf{J}}_2\). This does not define uniquely \({\textsf{W}}_4\), since we can freely add to it any linear combination of
and \(\partial ^2{\textsf{W}}_2\). In the classical case, we found in Sect. 6.3 that there exists an additional independent spin 4 field, built in Eq. (6.36) from the covariant current \({\mathcal {K}}\). As for the energy–momentum tensor \({\textsf{W}}_2\) discussed in the previous paragraph, this construction in terms of \({\mathcal {K}}\) does not directly generalise to the quantum case. We can, however, determine the quantum spin 4 field \({\textsf{W}}_4\) by a brute force computation, solving the linear equation \({\textsf{J}}_{\text {diag}}(x){\textsf{W}}_4(y)=\text {reg}\) starting with a general ansatz for \({\textsf{W}}_4\) in terms of the Kac–Moody currents \({\textsf{J}}_1\) and \({\textsf{J}}_2\). This does not define uniquely \({\textsf{W}}_4\), since we can freely add to it any linear combination of  and \(\partial ^2{\textsf{W}}_2\) as well as multiply it by an overall constant. Here, we will consider a choice that makes the expression of \({\textsf{W}}_4\) relatively simple and which ensures that we recover the classical spin 4 current (6.36) in the classical limit. Since the end result of this computation is rather convoluted, we give the full expression of \({\textsf{W}}_4\) in “Appendix C”, Eqs. (C.6)–(C.9) (see also Eq. (C.10) for a discussion of its classical limit).
and \(\partial ^2{\textsf{W}}_2\) as well as multiply it by an overall constant. Here, we will consider a choice that makes the expression of \({\textsf{W}}_4\) relatively simple and which ensures that we recover the classical spin 4 current (6.36) in the classical limit. Since the end result of this computation is rather convoluted, we give the full expression of \({\textsf{W}}_4\) in “Appendix C”, Eqs. (C.6)–(C.9) (see also Eq. (C.10) for a discussion of its classical limit).
From this expression, one can moreover compute the OPE of \({\textsf{W}}_2\) with \({\textsf{W}}_4\). We find
where c is the central charge (9.25) and \(\alpha _1\) and \(\alpha _2\) are constant parameters defined in terms of the levels \(k_1\) and \(k_2\), whose explicit expressions we give in “Appendix C”, Eq. (C.12). The presence of poles of order 6, 4 and 3 in this OPE means that \({\textsf{W}}_4\) is not a primary field. One can, however, construct a primary spin 4 field \({\textsf{W}}_{4,P}\) from \({\textsf{W}}_4\), hence satisfying
by adding to it a well-chosen linear combination of the descendant fields  and \(\partial ^2{\textsf{W}}_2\). More precisely, we find
and \(\partial ^2{\textsf{W}}_2\). More precisely, we find

with the parameters \(\alpha _3\) and \(\alpha _4\) defined by Eq. (C.15).
Let us finally describe the OPE of the primary field \({\textsf{W}}_{4,P}\) with itself. A direct computation shows that

where \({\textsf{W}}_6\) is a spin 6 W-current whose explicit expression we will not need and where the parameters \(\beta _i\) and \(\gamma \) are given by
Free Field Realisation in the \({\textrm{SU}(2)}\) Chiral Klimčík Model The OPEs (9.24), (9.28) and (9.30) of \({\textsf{W}}_2\) and \({\textsf{W}}_{4,P}\) then take the exact same form as the ones (8.15), (8.23) and (8.24) found in Sect. 8.2 using free field realisations and screening charges. Recall that in this subsection, the central charge c and the coefficients \(\gamma \) and \(\beta _i\) were expressed in terms of the two parameters n and \(\varpi \) entering the definition of the screening charges—see Eqs. (8.16), (8.25) and (8.26), while in the present case they are expressed in terms of the Kac–Moody levels \(k_1\) and \(k_2\). These expressions exactly coincide under the identification
(Note that the dual Coxeter number of \(\mathfrak {sl}(2)\) is given by \(h^{\!\vee }=2\).) This provides an explicit isomorphism, at least for the first W-currents, between the corner-brane \({\mathcal {W}}\)-algebra defined in terms of screening charges and the \(\widehat{\mathfrak {sl}}(2)_{k_1}\oplus \widehat{\mathfrak {sl}}(2)_{k_2}/\widehat{\mathfrak {sl}}(2)_{k_1+k_2}\) coset \({\mathcal {W}}\)-algebra, as expected in general from the reference [82].Footnote 31
Recall that the description of the corner-brane \({\mathcal {W}}\)-algebra in terms of screening charges in Sect. 8.2 uses chiral free fields \(({\hat{\varphi }}_1,{\hat{\varphi }}_2,{\hat{\varphi }}_3)\). The latter are interpreted as the quantisation of the classical left-moving free fields \((\phi ^{(\mathrm L)}_1,\phi ^{(\mathrm L)}_2,\phi ^{(\mathrm L)}_3)\) of the asymptotic domain of the \(\textrm{SU}(2)\) Klimčík model (in particular, the screening charges considered in Sects. 7 and 8 are the quantum versions of the classical screening charges discussed in Sect. 5 for the \(\textrm{SU}(2)\) Klimčík model). The results of the present subsection and of [82] thus provide us with a free field realisation of the \(\widehat{\mathfrak {sl}}(2)_{k_1}\oplus \widehat{\mathfrak {sl}}(2)_{k_2}/\widehat{\mathfrak {sl}}(2)_{k_1+k_2}\) coset \({\mathcal {W}}\)-algebra in terms of the left-moving quantum fields describing the asymptotic domain of the quantum \(\textrm{SU}(2)\) chiral Klimčík model. As usual, a similar realisation exists in terms of right-moving free fields.
9.3 Quantum Local IMs
Our goal in this subsection is to discuss local Integrals of Motion (IMs) in quantised AGMs and the application of these results to the AGM underlying the quantum UV fixed point of the \(\textrm{SU}(2)\) Klimčík model. For that, it will be useful to first revisit briefly the construction of such local IMs in the classical case.
9.3.1 Revisiting Local Charges in Classical AGMs
Let us consider a classical AGM with N punctures, twist function \(\varphi (z)\) and Gaudin Lax matrix \(\Gamma (z,x)\). To ease the comparison with the quantum case, we will use here the set-up considered in Sect. 9.1, where we have chosen a spectral parameter such that \(z_N=\infty \), i.e. one of the punctures is located a infinity. In this case, the classical observables are built from only \(N-1\) Kac–Moody currents \({\mathcal {J}}_1,\ldots ,{\mathcal {J}}_{N-1}\) and their gauge invariance is equivalent to their Poisson commutativity with the diagonal current \({\mathcal {J}}_{\text {diag}}(x)\) defined in Eq. (9.5).
The construction of local charges in involution in classical AGMs was described in [61] and recalled around Eq. (3.17). In the present set-up, it can be rephrased as follows. For every exponent \(p\in {\widehat{E}}\) of the affine Lie algebra \(\widehat{{\mathfrak {g}}}\), we introduce a density
built by contracting a symmetric invariant \((p+1)\)-tensorFootnote 32\(\tau _p\) on \({\mathfrak {g}}^{\mathbb {C}}\) with the components of the Gaudin Lax matrix \(\Gamma (z,x)\). The local charges are then defined as the quantities
where \(\zeta _1,\ldots ,\zeta _{N-2} \in {\mathbb {C}}\) are the zeroes of the twist function \(\varphi (z)\). The main properties obeyed by the densities \({\mathcal {S}}_{p+1}(z,x)\) are the following:
-
(i)
the Poisson bracket \(\bigl \lbrace {\mathcal {J}}_{\text {diag}}(x), {\mathcal {S}}_{p+1}(z,y) \bigr \rbrace \) is proportional to \(\varphi (z)\);
-
(ii)
the Poisson bracket of two densities take the form
$$\begin{aligned} \bigl \lbrace {\mathcal {S}}_{p+1}(z,x), {\mathcal {S}}_{q+1}(w,y) \bigr \rbrace = {\mathcal {A}}^{(0)}_{p,q}(z,w;y)\,\delta (x-y) + {\mathcal {A}}^{(1)}_{p,q}(z,w;y)\,\delta '(x-y),\nonumber \\ \end{aligned}$$(9.35)where \({\mathcal {A}}^{(0)}_{p,q}(z,w;y)\) is the sum of a derivative with respect to y and terms proportional to \(\varphi (z)\) and \(\varphi (w)\), with coefficients regular at \((z,w)=(\zeta _i,\zeta _j)\) for \(i,j\in \lbrace 1,\ldots ,N-2 \rbrace \).
These properties follow from the Poisson brackets
and require a specific choice of invariant tensors \(\tau _p\) in the definition (9.33) of \({\mathcal {S}}_{p+1}(z,x)\), see [61].
The property (i) ensures that the evaluation \({\mathcal {S}}_{p+1}(\zeta _i,x)\) at a zero \(\zeta _i\) of \(\varphi (z)\) Poisson commutes with \({\mathcal {J}}_{\text {diag}}\) and thus is gauge invariant. In other words, the density \({\mathcal {S}}_{p+1}(\zeta _i,x)\) belongs to the classical \({\mathcal {W}}\)-algebra underlying the AGM (formed by gauge-invariant differential polynomials in the Kac–Moody currents \({\mathcal {J}}_1,\ldots ,{\mathcal {J}}_{N-1}\)). Similarly, the property (ii) ensures that the local charges \({\mathcal {Q}}_{i,p}\) defined in Eq. (9.34) are in involution. Indeed, integrating the bracket (9.35) over x and y and evaluating it at \((z,w)=(\zeta _i,\zeta _j)\), we find that the Poisson bracket of \({\mathcal {Q}}_{i,p}\) and \({\mathcal {Q}}_{j,q}\) is proportional to the integral of \({\mathcal {A}}^{(0)}_{p,q}(\zeta _i,\zeta _j ;y)\), which vanishes by the conditions obeyed by \({\mathcal {A}}^{(0)}_{p,q}(z,w ;y)\) in point (ii).
9.3.2 Local Charges in Quantised AGMs
Conjectured form of the Quantum Charges Let us now consider the quantised AGM, described by quantum Kac–Moody currents \({\textsf{J}}_1,\ldots ,{\textsf{J}}_{N-1}\). We would like to construct the quantisation of the local charges \({\mathcal {Q}}_{i,p}\) discussed above, which would then form commuting operators built from local differential polynomials in these currents. This question was studied in [32, 34, 35]. The approach followed in these references was inspired by the conjecture, first formulated in [32], that the spectrum of these charges is encoded in certain objects called affine opers. Studying these affine opers and their properties, it was conjectured in [34] that the quantum local charges take the following formFootnote 33:
Let us explain the different ingredients entering this formula. The quantity \({\mathcal {P}}(z)\) is defined (up to a global factor) from the quantum twist function \(\varphi ^{(\textrm{qt})}(z)\) by the conditionFootnote 34
Explicitly, in terms of the punctures \(z_r\) and levels \(k_r\), this function is then given by
for a specific choice of the overall constant undetermined by Eq. (9.38). In particular, since the levels \(k_r\) are not necessarily integers, the function \({\mathcal {P}}(z)\) is in general multivalued.
The integration contour \(\gamma \) in Eq. (9.37) is a so-called Pochhammer contour. It is a closed path in \(\mathbb{C}\mathbb{P}^1\) whose main characteristic is that the function \({\mathcal {P}}(z)\) possesses a single-valued branch along \(\gamma \), ensuring that the object \({\mathcal {P}}(z)^{-p/h^{\!\vee }}\) appearing in the integral (9.37) is unambiguously defined along the integration contour. For generic values of the levels \(k_r\), the set P of equivalence classes of independent Pochhammer contours \(\gamma \) (up to smooth deformations which do not change contour integrations over \(\gamma \)) is of size \(N-2\).
Finally, the quantity \({\textsf{S}}_{p+1}(z,x)\) appearing in Eq. (9.37) is a local spin \(p+1\) density built as a differential polynomial in the Gaudin Lax matrix components \(\Gamma ^{(\textrm{qt})}_a(z,x)\), their derivatives with respect to z and the quantum twist function. More precisely, this density is expected to take the form

where \(\tau _p\) is the invariant tensor discussed in Sect. 9.3.1 and the dots represent additional “corrections” of the form

where \(m,n,\alpha _i,\beta _i,\gamma _i\in {\mathbb {Z}}_{\ge 0}\) are non-negative integers such that \(m+n\le p\) and \(m+\sum _{k=1}^m \gamma _k=p+1\) (so that these corrections are of spin \(p+1\)).
To justify and consolidate this conjecture, we need to discuss two main points, following [34, 35]. The first one is the classical limit of the charges \({\textsf{Q}}_{\gamma ,p}\) and its relation to the classical ones \({\mathcal {Q}}_{i,p}\) described in Sect. 9.3.1. The second one is the gauge invariance and commutativity of these quantum charges and the corresponding requirements on the densities \({\textsf{S}}_{p+1}(z,x)\).
Classical Limit We start with the discussion of the classical limit. Recall from Eq. (9.11) that the quantum Gaudin Lax matrix \(\Gamma ^{(\textrm{qt})}(z,x)\) and twist function \(\varphi ^{(\textrm{qt})}(z)\) are of order \(O(\hbar ^{-1})\) when \(\hbar \rightarrow 0\). The first term in the density (9.40) is thus of order \(O(\hbar ^{-p-1})\). Similarly, the corrective term (9.41) is of order \(O(\hbar ^{-m-n})\). Since we supposed \(m+n \le p\) earlier, we thus see that this term is subdominant in the classical limit \(\hbar \rightarrow 0\), allowing us to interpret the dots in Eq. (9.40) as representing quantum corrections. Using the explicit asymptotic (9.11) of \(\Gamma ^{(\textrm{qt})}(z,x)\) in the limit \(\hbar \rightarrow 0\), we then find
where \({\mathcal {S}}_{p+1}(z,x)\) is the classical density defined in Eq. (9.33).
This is suggestive of a relation between the classical limit of the quantum charges \({\textsf{Q}}_{\gamma ,p}\) and the classical charges \({\mathcal {Q}}_{i,p}\). To establish this more precisely, we need to understand the classical limit of the Pochhammer integral in Eq. (9.37). Using the expression (9.39) of \({\mathcal {P}}(z)\) and the classical limit (9.7) of the levels \(k_r\), we find that the term \({\mathcal {P}}(z)^{-p/h^{\!\vee }}\) in this integral obeys the following asymptotic behaviour:
satisfies \(\partial _z \rho (z) = \varphi (z)\). The limit \(\hbar \rightarrow 0\) of the integral (9.37) can then be treated using the well-known saddle-points method (see e.g. [95] for a reference on saddle-points in the context of Pochhammer integrals). In particular, this method implies that the integral localises at the extrema of the function \(\rho (z)\), which are nothing but the zeroes \(\zeta _i\) of the classical twist function \(\varphi (z)=\partial _z \rho (z)\). Thus, with appropriate rescalings by powers of \(\hbar \) and prefactors, the classical limit of the quantum charge \({\textsf{Q}}_{\gamma ,p}\) is expressed as a linear combination of the classical local charges \({\mathcal {Q}}_{i,p}\) defined in Eq. (9.34). We note moreover that the number of Pochhammer contours \(\gamma \in P\) coincides with the number \(N-2\) of zeroes of \(\varphi (z)\), so that the overall counting of local charges agrees at the classical and quantum levels.
Intermezzo: Twisted Derivatives In order to discuss the gauge invariance and commutativity of the quantum charges, we will need to introduce an additional key ingredient, the so-called twisted derivative \(D_{z,p}\). If f(z) is a meromorphic function of z, we define its twisted derivative of degree p as
The fundamental property of this derivative is the following. For any Pochhammer countour \(\gamma \in P\) and any meromorphic function f(z) regular along \(\gamma \), we have
The key observation to prove this fact is that \({\mathcal {P}}(z)^{-p/h^{\!\vee }} D_{z,p} f(z) = \partial _z \bigl ( {\mathcal {P}}(z)^{-p/h^{\!\vee }} f(z) \bigr )\), as one easily checks using \(\partial _z{\mathcal {P}}(z)=\varphi ^{(\textrm{qt})}(z){\mathcal {P}}(z)\). The integrand in the above equation is thus a total derivative. The facts that \({\mathcal {P}}(z)\) is single-valued on the Pochhammer countour \(\gamma \) and that the latter is a closed path then ensure that the integral vanishes, as claimed.
Properties of the Densities Recall that the densities \({\mathcal {S}}_{p+1}(z,x)\) of the classical local charges satisfy the points (i) and (ii) discussed in Sect. 9.3.1. These conditions ensured the gauge invariance and involution of the charges and could be derived from the fundamental Poisson brackets (9.36) obeyed by the Gaudin Lax matrix. In the quantum case, the Poisson bracket of the theory is replaced by the OPE (9.9) of the quantum Kac–Moody currents \({\textsf{J}}_r\). One checks that this OPE implies the following quantum equivalents of the brackets (9.36):
The conditions that we impose on the quantum densities \({\textsf{S}}_{p+1}(z,x)\) are then as follows. Their definition (9.40) in terms of \(\Gamma ^{(\textrm{qt})}(z,x)\) should be such that, using the OPEs (9.46):
-
(i)
the singular part of the OPE \({\textsf{J}}_{\text {diag}}(x) {\textsf{S}}_{p+1}(z,y)\) is a twisted derivative \(D_{z,p}(\dots )\);
-
(ii)
the OPE of any two densities take the form
$$\begin{aligned} {\textsf{S}}_{p+1}(z,x) {\textsf{S}}_{q+1}(w,y) = \sum _{k\in \,{\mathbb {Z}}_{\ge 0}} \frac{{\textsf{A}}^{(k)}_{p,q}(z,w;y)}{(x-y)^{k+1}} + \text {reg}\,, \end{aligned}$$(9.47)where \({\textsf{A}}^{(0)}_{p,q}(z,w;y)\) is a linear combination \(\partial _y(\dots ) + D_{z,p}(\dots )+D_{w,q}(\dots )\) of a spatial derivative and twisted derivatives.Footnote 35
Combined with the fundamental property (9.45) of the twisted derivative \(D_{z,p}\), the condition (i) implies that the quantity \({\textsf{W}}_{\gamma ,p+1}\), obtained as the integral (9.37) of \({\mathcal {P}}(z)^{-p/h^{\!\vee }}{\textsf{S}}_{p+1}(z)\) over \(\gamma \in P\), has a regular OPE with the diagonal current \({\textsf{J}}_{\text {diag}}\). This ensures that \({\textsf{W}}_{\gamma ,p+1}(x)\) is a gauge-invariant local density, or in other words an element of the quantum coset \({\mathcal {W}}\)-algebra \(\widehat{{\mathcal {W}}}\).
Similarly, the condition (ii) implies that, for any two exponents \(p,q\in {\widehat{E}}\) and any two Pochhammer contours \(\gamma ,\gamma '\in P\), the OPE \({\textsf{W}}_{\gamma ,p+1}(x){\textsf{W}}_{\gamma ',q+1}(y)\) has a simple pole \(1/(x-y)\) whose coefficient is a total spatial derivative. This ensures that the local charges \({\textsf{Q}}_{\gamma ,p}\) and \({\textsf{Q}}_{\gamma ',q}\), defined as spatial integrals of \({\textsf{W}}_{\gamma ,p+1}(x)\) and \({\textsf{W}}_{\gamma ',q+1}(y)\), commute as quantum operators, as wanted.
The conditions (i) and (ii) discussed here are the quantum equivalent of the ones discussed in Sect. 9.3.1, in the sense that they ensure the gauge invariance and commutation of the quantum local charges. This can be made more concrete. Recall that in the classical limit, the quantum twist function \(\varphi ^{(\textrm{qt})}(z)\) is of order \(O(\hbar ^{-1})\). The derivative term in the twisted derivative (9.44) is thus subdominant compared to the other term. Hence, a twisted derivative \(D_{z,p}f(z)\) contributes in the classical limit to a term proportional to \(\hbar ^{-1}\varphi (z)f(z)\). The quantum conditions (i) and (ii) then reduce to the classical ones in the limit \(\hbar \rightarrow 0\), as expected, and the derivative terms in the twisted derivatives can be interpreted as quantum corrections.
First Densities and Checks of the Conjectures Let us finally discuss some first checks of the conjectures discussed in this subsection on the existence of densities \({\textsf{S}}_{p+1}(z,x)\) defining commuting quantum local charges, by exhibiting the simplest examples of such densities.
The first exponent of an affine algebra is always \(p=1\), corresponding to a spin 2 density \({\textsf{S}}_2(z,x)\). The latter simply reads

One easily checks by a direct computation that it satisfies the conditions (i) and (ii). We note that the above expression for \({\textsf{S}}_2(z,x)\) coincides with the classical density \({\mathcal {S}}_2(z,x)\), up to the normal ordering of the fields: this density thus does not receive quantum corrections. We note, however, that the local charges defined from it in fact receive such corrections, since they are obtained by integrating \({\textsf{S}}_2(z,x)\) over Pochhammer contours, rather than by a simple evaluation at a zero \(\zeta _i\) of \(\varphi (z)\) as in the classical case. (We will see an explicit example of this phenomenon in the following subsection.)
For higher-rank affine algebras of type A, i.e. \(\widehat{\mathfrak {sl}}(N)\) for \(N \ge 3\), the next exponent is \(p=2\). The corresponding spin 3 density \({\textsf{S}}_3(z,x)\) has been constructed explicitly in [35] and indeed obeys the conditions (i) and (ii) stated above. We will not need its expression here.
In this paper, most of the examples that we explore are based on the algebra \(\widehat{\mathfrak {sl}}(2)\). For this case, there are no cubic charges and the first higher-degree charge is quartic, built from a spin 4 density \({\textsf{S}}_4(z,x)\). This charge was not treated explicitly yet in the literature and thus required some additional analysis. The end result of this computation being a bit involved, we give the explicit expression of \({\textsf{S}}_4(z,x)\) in terms of the Gaudin Lax matrix and the twist function in “Appendix D.1”, Eq. (D.3).
9.3.3 Quantum Local IMs in the AGM Underlying the Chiral \(\varvec{\textrm{SU}(2)}\) Klimčík Model
The Quantised AGM Let us finally apply the results of this subsection to the AGM underlying the left-moving half of the UV fixed point of the Klimčík model. At the classical level, this AGM was described in detail in Sect. 6: in particular it possesses 3 punctures. Recall that in this section, we always started the analysis of the quantum model by performing a change of spectral parameter that sends the last puncture to infinity, to make the treatment of the constraint easier. In the present case, where there are two finite punctures left, one can always use translation and dilation of the spectral parameter to send these points to 0 and 1. The quantum twist function of the AGM under consideration then takes the simple form
where \(k_1\) and \(k_2\) are the quantum levels associated with the punctures 0 and 1, respectively, while the level associated with the third puncture at infinity is equal to \(k_3=-k_1-k_2-2h^{\!\vee }\), according to Eq. (9.16). These levels are related, by the asymptotic property (9.7), to the classical ones, which we recall are given by Eq. (6.4) for the case at hand. In particular, the quantum levels are then such that
where \(\nu \) is the parameter entering the definition of the classical chiral Klimčík model, as in Sect. 4. (This is the main parameter that is needed to relate the classical and quantum physics of the model: indeed, the remaining parameter entering the classical limit of the quantum levels \(k_r\) is the coefficient \(K_{\scriptscriptstyle {\textrm{UV}}}\), which appears as an irrelevant overall prefactor in the classical model.)
Similarly, the quantum Gaudin Lax matrix of the AGM is defined in the present case in terms of two Kac–Moody currents \({\textsf{J}}_1\) and \({\textsf{J}}_2\) and simply reads
Function \({{\mathcal {P}}(z)}\) and Pochhammer Contour Applying Eq. (9.39), we find that in the AGM under consideration here, the function \({\mathcal {P}}(z)\) is simply given by
Of interest for the construction of local charges are the Pochhammer contours, which are defined as the closed paths in \(\mathbb{C}\mathbb{P}^1\) along which \({\mathcal {P}}(z)\) admits a single-valued branch. In the present case, there exists a unique such contour, represented in Fig. 3, which goes around each puncture twice, in opposite directions (ensuring that any non-trivial phase acquired by \({\mathcal {P}}(z)\) after a revolution around a puncture is cancelled by the reverse one).
Quadratic Charge We can now describe the quantum local IMs for the AGM under consideration. The first charge is the quadratic one, whose density is obtained by the integral
where \(\gamma \) is the Pochhammer contour described above and \({\textsf{S}}_2(z,x)\) is defined in terms of \(\Gamma ^{(\textrm{qt})}(z,x)\) by Eq. (9.48). This integral was computed explicitly in [34]. We recall the details of this calculation in “Appendix D.2” and simply summarise the main steps here. Reinserting the expressions (9.51) and (9.52) of \(\Gamma ^{(\textrm{qt})}(z,x)\) and \({\mathcal {P}}(z)\) in the above formula, one reduces the computation to simple integrals of the form
for some real numbers a and b. These integrals can be expressed in terms of the Euler Beta function and satisfy a number of useful recursive identities (with respect to a and b). Using those, we simply find that
where \({\textsf{W}}_2\) is the spin 2 W-current defined in Eq. (9.23) and \(N_2\) is a constant given by
In particular, the terms of the type \(1/(k_r+h^{\!\vee })\) in the expression (9.23) of \({\textsf{W}}_2\) are obtained in the present case by integrals over Pochhamer contours. In the classical limit, these terms simply become \(1/\ell _r\) and arise from an evaluation at the zero of the twist function. This illustrates the type of quantum corrections that one can get when promoting evaluations at zeros to integrations over Pochhammer contours in the quantum model.
As expected from the general discussion in Sect. 9.3.2, the density \({\textsf{W}}_{\gamma ,2}\) belongs to the \(\widehat{{\mathfrak {g}}}_{k_1}\oplus \widehat{{\mathfrak {g}}}_{k_2}/\widehat{{\mathfrak {g}}}_{k_1+k_2}\) coset \({\mathcal {W}}\)-algebra underlying the AGM. In fact, since there is a unique spin 2 current in this algebra, namely the energy–momentum tensor \({\textsf{W}}_2\), we could have expected the density of the quadratic charge to be simply proportional to \({\textsf{W}}_2\).
Quartic Charge for \({\mathfrak {sl}(2)}\) To discuss a less trivial case, let us consider the first higher-order charge for \({\mathfrak {g}}^{\mathbb {C}}=\mathfrak {sl}(2)\). As explained in Sect. 9.3.2, this charge is quartic and is built from the spin 4 field \({\textsf{S}}_4(z,x)\) constructed in “Appendix D.1”, Eq. (D.3). More precisely, the density of this quartic charge is given by
where we have used that \(h^{\!\vee }=2\) for \(\mathfrak {sl}(2)\). By construction, this density should then belong to the \(\widehat{\mathfrak {sl}}(2)_{k_1}\oplus \widehat{\mathfrak {sl}}(2)_{k_2}/\widehat{\mathfrak {sl}}(2)_{k_1+k_2}\) coset \({\mathcal {W}}\)-algebra, i.e. the corner-brane algebra. The latter has been discussed extensively in Sects. 8.2 and 9.2. In particular, it possesses three spin 4 fields, the descendants  and \(\partial ^2{\textsf{W}}_2\) and an additional primary field \({\textsf{W}}_{4,P}\). For the case of the quartic charge, contrarily to the quadratic one, the density \({\textsf{W}}_{\gamma ,4}\) is thus not fixed solely by its belonging to the \({\mathcal {W}}\)-algebra and therefore corresponds to a non-trivial linear combination of
and \(\partial ^2{\textsf{W}}_2\) and an additional primary field \({\textsf{W}}_{4,P}\). For the case of the quartic charge, contrarily to the quadratic one, the density \({\textsf{W}}_{\gamma ,4}\) is thus not fixed solely by its belonging to the \({\mathcal {W}}\)-algebra and therefore corresponds to a non-trivial linear combination of  and \({\textsf{W}}_{4,P}\) (the total derivative \(\partial ^2{\textsf{W}}_2\) is irrelevant for the present discussion since it does not contribute to the local charge, defined as an integral over the space coordinate).
and \({\textsf{W}}_{4,P}\) (the total derivative \(\partial ^2{\textsf{W}}_2\) is irrelevant for the present discussion since it does not contribute to the local charge, defined as an integral over the space coordinate).
The integral (9.57) can be performed explicitly using the same type of techniques as for the quadratic case, in particular using the Beta function identities. We then obtain a rather lengthy expression in terms of normal ordered products of components of the currents \({\textsf{J}}_1\) and \({\textsf{J}}_2\). As expected form the above discussion, we can rewrite this expression in terms of the W-currents \({\textsf{W}}_{4,P}\),  and \(\partial ^2{\textsf{W}}_2\), finally yielding
and \(\partial ^2{\textsf{W}}_2\), finally yielding

Here, the coefficients \(N_4\) and \(\delta _1\) are defined as
with \(\beta \) given in Eq. (9.31). The coefficient \(\delta '_2\) also possesses an explicit expression in terms of \(k_1\) and \(k_2\), which, however, we shall not need here since it multiplies a total derivative, irrelevant for the construction of local charges.
This result is to be compared with the density of the local charge computed in Sect. 8.2 using screening charges, in the free field realisation of the corner-brane \({\mathcal {W}}\)-algebra. According to Eq. (8.27), this density is given by \({\textsf{W}}_4^{(\textrm{PB})}\), which itself can be expressed in terms of the fields \({\textsf{W}}_{4,P}\) and \({\textsf{W}}_2\) and the parameters n and \(\varpi \) entering the screening charges by means of formula (8.20). Recall that in the identification of the corner-brane \({\mathcal {W}}\)-algebra with the \(\widehat{\mathfrak {sl}}(2)_{k_1}\oplus \widehat{\mathfrak {sl}}(2)_{k_2}/\widehat{\mathfrak {sl}}(2)_{k_1+k_2}\) coset \({\mathcal {W}}\)-algebra, these parameters are related to the levels \(k_1\) and \(k_2\) by Eq. (9.32). Using this relation, one easily checks that the two expressions (8.21) and (9.59) of \(\delta _1\) agree and thus that the density \({\textsf{W}}_{\gamma ,4}\) in Eq. (9.58) coincides with the one in Eq. (8.27), up to a global factor and a total derivative. This thus provides a non-trivial check of the identification of the quantum integrable structures defined from screening charges and from the AGM construction.Footnote 36
Let us finally comment briefly on the classical limit of the quartic charge. Using the asymptotic properties (9.7), (9.26) and (C.10) of \(k_r\), \({\textsf{W}}_2\) and \({\textsf{W}}_4\), one checks that the dominant term in the classical limit of the density (9.58) is proportional to \(W_2^2\). We thus recover the fact that, in the classical model, the quartic charge is simply the integral of the energy–momentum tensor squared—see Sects. 5 and 6.3. We moreover see that at the quantum level, this is no longer true as the spin 4 density becomes independent of \({\textsf{W}}_2\), making the quantum integrable structure quite more complicated than the classical one.
10 Summary and Perspectives
This section starts by offering a brief summary of the resulting picture in Sect. 10.1, followed by a discussion of some of the emerging perspectives.
In Sect. 10.2, we point out how the conformal limits considered here can be generalised to the cases with an arbitrary number of punctures. This indicates that the analysis performed in this work can be generalised to more general multiparametric NLSMs.
A key motivation for our work was the perspective to apply the ODE/IQFT correspondence to quantised NLSMs. The existence of the generalised conformal limits suggests that the ODE/IQFT correspondence can be applied to such larger classes of models. These perspectives are discussed in Sect. 10.3.
Another natural direction to explore concerns the study of quantum non-local charges in these models by means of the representation theory of Yang–Baxter algebras. This is discussed in Sect. 10.4.
Some of the most important open questions concern possible existence of deformations away from the conformal limits preserving key aspects of the integrable structures like the ODE/IQFT correspondence and the Yang–Baxter algebra. We will briefly discuss some perspectives in this direction in Sect. 10.5.
Finally, we end in Sect. 10.6 by pointing out the relations between the AGMs studied here to the gauged WZW and \(\lambda \)-models, which are related to the Klimčík model via Poisson–Lie T-duality, indicating that the techniques described in this paper can be useful for the study of these models as well.
10.1 Summary
The goal of our work has been to make first steps towards the quantisation of relativistic AGMs. To this aim, we have considered a locus in the parameter space expected to admit a conformally invariant quantisation. The existence of an extended algebra of conformal symmetry then provides a basis for the investigation of the quantum integrable structures of these theories. These integrable structures can be expected to admit a deformation away from the conformal locus.
In the first step, we considered the conformal limit of the \(\textrm{SU}(2)\) Klimčík model. This corresponds to sending the parameters of the model to their values at the UV fixed point, for which the one-loop beta function vanishes. For the AGM describing the relativistic field theory, two different limiting procedures were introduced. These yielded two decoupled affine Gaudin models encoding the left-moving and right-moving degrees of freedom of the field theory at the RG fixed point. As a result, we were led to introduce the notion of a “chiral” AGM, which should be clearly distinguished from the relativistic AGM we started from, see Sect. 6 for a discussion.
A characteristic feature of the chiral AGM is the existence of an infinite number of fields, built as local combinations of the matrix elements of the Lax connection, which are left/right moving as a consequence of the classical equations of motion. These form a closed (Poisson) algebra which is the algebra of extended conformal symmetry of the model. For the Klimčík NLSM in the conformal limit, we obtained the \({\widehat{{\mathfrak {g}}}}_{\ell _1} \oplus {\widehat{{\mathfrak {g}}}}_{\ell _2}\big /{\widehat{{\mathfrak {g}}}}_{\ell _1+\ell _2}\) coset \(\mathcal {W}\)-algebra in this way. As an illustration, we expressed the first few generating currents in terms of the fundamental fields of the theory, both at the classical and at the quantum level, in the special case with \(G=\textrm{SU}(2)\).
The formulation as AGM offers a powerful framework for the construction of quantum local IMs as integrals over densities formed out of the generators of the coset \(\mathcal {W}\)-algebra [34, 35]. By applying this framework we computed the first non-trivial local IM. Its expression turned out to be consistent with the known results for the Fateev model in the literature, which were obtained by the method of screening charges.
A gauge-fixed description of the chiral AGM has been found to be useful for the study of non-local integrals of motion. Indeed, it has been shown in Sect. 6 that a gauge fixing exists relating the Lax matrix of the AGM to the Lax matrix studied in [53] describing the integrable structure of the conformal limit of the Klimčík model. This should allow us to apply the main results and conjectures of [53] to the quantisation of the non-local IMs in the AGMs studied here. Of particular importance is the conjecture that there exists a quantisation of the monodromy matrix constructed from the gauge-fixed Lax matrix which satisfies commutation relations of Yang–Baxter type. A possible generalisation of this was pointed out in Sect. 7.2, which would be relevant for the study of chiral AGMs associated to Lie algebras of higher ranks.
10.2 More General Chiral Limits of Affine Gaudin Models
It seems likely to us that much more general affine Gaudin models will admit chiral limits similar to the one discussed in this paper. In order to substantiate this claim, let us collect some relevant points, referring to “Appendix E” for more details. To begin with, let us observe that the definition of relativistic AGMs described in Sect. 3.2 was based on a split of the zeroes of the twist function into two subsets of equal cardinality, corresponding to coefficients \(s_i\) equal to, respectively, \(+1\) and \(-1\) in the definition (3.26) of the Hamiltonian. Here, we will consider a natural class of relativistic AGMs generalising the Klimčík model, which are characterised by a set of zeroes \(\{\zeta _1^+,\dots ,\zeta _{M}^+\}\sqcup \{\zeta _1^-,\dots ,\zeta _{M}^-\}\), where the labels ± refer to the aforementioned split, and a set of poles \(\{z_1^+,\dots ,z_{M+1}^+\}\sqcup \{z_1^-,\dots ,z_{M+1}^-\}\) also divided into two subsets (in particular, these AGMs possess \(2M+2\) punctures). We further use the freedom of performing Möbius transformations to fix \(\zeta _M^+=\infty \) and \(\zeta _M^-=0\). In this set-up, the Klimčík model corresponds to the simplest case \(M=1\).
Introducing a scaling parameter \(\xi \) and representing the poles \(z_r^\pm \) and zeroes \(\zeta _i^\pm \) as \(z_r^\pm =\bigl ( z^{{(\mathrm L/R)}}_r / \xi \bigr )^{\pm 1}\) and \(\zeta _i^\pm =\bigl ( \zeta ^{{(\mathrm L/R)}}_i / \xi \bigr )^{\pm 1}\), with fixed \(z_r^{(\mathrm L/R)}\) and \(\zeta _i^{(\mathrm L/R)}\), define a one-parameter flow in the parameter space of this class of AGMs. Letting \(\xi \) tend to 0 allows us to ensure that the poles \(z_r^+\) and zeroes \(\zeta _i^+\) will move to infinity, whereas the poles \(z_r^-\) and zeroes \(\zeta _i^-\) will approach zero. The detailed analysis of this limit is treated in “Appendix E”. In particular, it may then be shown that the limit of the Lax connection of the theory, keeping fixed a rescaled spectral parameter \(z^{(\mathrm L)}=\xi \, z\), satisfies
for some fields \({\mathcal {B}}^{(\mathrm L)}_\pm \) and \({\mathcal {K}}_i^{(\mathrm L)}\) (independent of \(z^{(\mathrm L)}\)). Working in a gauge where \({\mathcal {B}}^{{(\mathrm L)}}_-=0\), one then finds that \({\mathcal {L}}_+(z^{(\mathrm L)}/\xi )\) is a left-moving matrix in the limit \(\xi \rightarrow 0\), as a consequence of the zero-curvature equation. In a similar way, one shows that \({\mathcal {L}}_-(\xi /z^{(\mathrm R)})\) is gauge-equivalent to a right-moving matrix when \(\xi \rightarrow 0\). We conclude that chiral limits similar to the one studied in this paper for the Klimčík model will exist for all AGMs that admit a scaling action of the type considered here. Moreover, one can argue (see “Appendix E” for details) that the left-moving and right-moving Lax matrices obtained through the above procedure arise from chiral realisations of two AGMs, with \(M+2\) punctures each.
In the case of the Klimčík model, corresponding to \(M=1\), it has been observed in Sect. 6.1 that the RG flow of the parameters \(z_r^\pm \) is asymptotically equivalent in the UV to the limit \(\xi \rightarrow 0\) considered above. Based on conjectures and results on the RG flow of general relativistic AGMs [57, 58], there exists numerical evidence for the next simplest case \(M=2\) indicating that a similar behaviour can be found in this case as well (see “Appendix E”). We see this as encouraging indications that many aspects of the chiral limits discussed in this paper in the case of the Klimčík model have fairly natural generalisations to AGMs associated with more complicated twist functions and arbitrary Lie algebras \({\mathfrak {g}}\). We will briefly discuss some of the perspectives for the study of these theories in the next subsections.
Before that, in view of generalisations to more general classes of models, let us note that we have only focussed here on theories which possess gauge symmetries given by an action of the full Lie group G underlying the AGM. It is well known that there exist other types of integrable sigma models which can be described in a gauged formulation where only a specific subgroup H of G is gauged. Typical examples in this class are the sigma models on symmetric spaces G/H and their Yang–Baxter deformations [63]. These can be interpreted as relativistic realisations of a more general type of AGMs, which possess the so-called cyclotomy or dihedrality property [47]. It would be interesting to study the chiral limits of these coset theories using techniques similar to the ones developed in this paper. For instance, relevant examples in this context might be the conformal limits of Yang–Baxter deformations of the \(\textrm{O}(N)\) sigma models and their supersymmetric version, which have been the subject of recent works in the literature [98,99,100], and of the integrable coset sigma models on \(G \times G / H\) [101,102,103,104] whose conformal limit is the Guadagnini–Martellini–Mintchev CFT [105].
10.3 ODE/IQFT Correspondence
One may next note that the quantisation of the chiral limits of AGMs considered in Sect. 10.2 are contained in the class of quantum integrable models discussed in [32]. The main conjectures proposed in [32] imply that the spectra of the models in this class can be described by generalisations of the ODE/IQFT correspondence. This is motivated by hypothetical extensions of the geometric Langlands correspondence from the known cases associated to finite-dimensional simple Lie algebras \({\mathfrak {g}}\) (see for instance [106] for a review) to affine Lie algebras \(\widehat{{\mathfrak {g}}}\). We thus expect that the general ODE/IQFT correspondence conjectured in [32] describes the spectra of the relativistic models considered in Sect. 10.2 in the chiral limits.
In the following, we shall focus on a subclass of the integrable models discussed in [32] which are called affine Gaudin models with regular singularities, abbreviated as regular AGMs. These models are classified by two pieces of data: (i) an affine Lie algebra \(\widehat{{\mathfrak {g}}}\), and (ii) a twist function \(\varphi ^{(\textrm{qt})}\) of the form \(\varphi ^{(\textrm{qt})}(z)=\sum _{r=1}^N\frac{k_r}{z-z_r}\), with \(k_r\), \(r=1,\dots ,N\) satisfying \(\sum _{r=1}^N k_r=-2h^{\!\vee }\). The generalisation of the ODE/IQFT correspondence proposed in [32] would imply that the eigenvalues of the conserved quantities of the regular AGMs associated to the data \((\widehat{{\mathfrak {g}}},\varphi ^{(\textrm{qt})})\) are encoded in a certain class of holomorphic connections on the N-punctured Riemann sphere which have a Lie-algebraic definition based on the Langlands dual \({}^L\widehat{{\mathfrak {g}}}\) of the affine Lie algebra \(\widehat{{\mathfrak {g}}}\). The connections in this class are called affine opers in [32]. For the sake of illustration, we focus here on the case \({\mathfrak {g}}=\mathfrak {sl}(2)\), for which one can characterise the affine opers as connections which are gauge-equivalent to the form
where \({\mathcal {P}}(z)\) is a primitive of the twist function \(\varphi ^{(\textrm{qt})}\) satisfying \(\partial _z\log {\mathcal {P}}(z)=\varphi ^{(\textrm{qt})}(z)\), which can be chosen as \({\mathcal {P}}(z)=\prod _{r=1}^N(z-z_r)^{k_r}\). Instead of the connection \(\nabla _z\), it is often convenient to consider the corresponding second-order differential operator
The function v(z) is allowed to have second-order poles at \(z_r\), \(r=1,\dots ,N\),Footnote 37 and an arbitrary number K of apparent singularities at points \(x_1,\dots , x_K\). The conditions that the singularities at \(x_1,\dots , x_K\) are apparent singularities, equivalent to triviality of the monodromy of \(\nabla _z\) around these points, imply a system of algebraic equations for \(x_1,\dots , x_K\) which is expected to have a discrete set of solutions. The generalised ODE/IQFT correspondence conjectured in [32] predicts that the elements of this set, represented by the corresponding functions v(z) in (10.1), are in one-to-one correspondence with the eigenstates of the quantum affine Gaudin model associated to \((\widehat{{\mathfrak {g}}},\varphi ^{(\textrm{qt})})\).
A refinement of these conjectures was proposed in [34]. It concerns the relation between the affine opers associated with the eigenstates of the relevant affine Gaudin model on the one hand and the eigenvalues \(I_{\gamma ,p}\) of the local conserved charges \({\textsf{Q}}_{\gamma ,p}\) defined in (9.37) on the other hand. The relation proposed in [34] can be represented in the form
which displays a direct correspondence with the definition (9.37) of the local conserved charge \({\textsf{Q}}_{\gamma ,p}\). The densities \(v_p(z)\) in (10.3) can be constructed from the relevant affine opers by an algorithm described in [34]. In the \(\mathfrak {sl}(2)\) case considered here, one obtains a family of differential polynomials of the functions v(z) characterising the affine opers according to (10.1).Footnote 38 This conjecture then takes a form equivalent to a previous proposal made in [12, 13] for the UV fixed point of the \(\textrm{SU}(2)\) Klimčík model (the explicit relation between the approach of [34] and the one of [12, 13] based on WKB expansions follows from the results of [45]).
The results and conjectures from [32, 34] are directly applicable to the chiral AGMs discussed in our paper. The case of the conformal limit of the Klimčík model corresponds to \(N=3\). The function \({\mathcal {P}}(z)\) introduced in Sect. 9.3, Eq. (9.52) is easily seen to be the special case of the function \({\mathcal {P}}(z)\) appearing in (10.1) with \(z_N=\infty \).
Strong support for the validity of the ODE/IQFT correspondence in the case of interest here follows from the detailed investigations described in [12,13,14]. It was proposed in Ref. [4] that the Klimčík model for \(G=\textrm{SU}(2)\) possesses a dual Lagrangian representation with Toda-like interactions. The ODE/IQFT correspondence for the dual model has been thoroughly investigated in [12, 13]. The differential operator defining the ODE studied in these references is easily seen to coincide with the operator \({\mathcal {D}}\) defined in (10.2). For the explicit comparison one may note that the term \(\chi \,{\mathcal {P}}(z)\) in (10.2) corresponds to the function \(\lambda ^2{\mathcal {P}}_{\textrm{BL}}^{}(z)\) considered in [12, 13], defined asFootnote 39
with \(a_i\), \(i=1,2,3\) being the parameters of the dual theory, satisfying \(a_1+a_2+a_3=2\). Relating the parameters \(a_r\) in the expression (10.4) for \({\mathcal {P}}(z)\) to the levels \(k_r\) by the relation \(a_r = k_r + 2\), it is easy to see that \(\chi {\mathcal {P}}(z)=\lambda ^2{\mathcal {P}}_{\textrm{BL}}(z)\) will hold if \(\chi \) is assumed to be a certain function of \(\lambda \) and \(z_1,z_2,z_3\).
The results of our paper clarify the relation between the integrable structures of the chiral limit of the Klimčík model and that of a specific relativistic AGM. The existence of chiral limits in a more general class of relativistic AGMs discussed in Sect. 10.2 opens the perspective to describe the spectra of these chiral models with the help of the generalised versions of the ODE/IQFT correspondence proposed in [32].
10.4 The Yang–Baxter Algebra in Affine Gaudin Models
The problem of quantisation of the non-local conserved charges in the affine Gaudin model was briefly discussed in Sect. 7. It was mentioned that, apart from some early results in Ref. [32], there is no systematic construction of the higher quantum non-local IMs, and a proof of their mutual commutativity is lacking. From the point of view of a semi-classical quantisation of the AGM, one meets two types of problems. First of all, the matrix elements of the Lax connection satisfy non-ultralocal Poisson brackets. This makes it not obvious that there can exist a reasonable definition for the Poisson brackets of the monodromy matrix that obey natural requirements like the Jacobi identity. The other issue is related to the freedom that comes from the gauge symmetry of the AGM. It acts on the Lax connection by conjugation, inducing a corresponding action on the monodromy matrices, which could be field dependent. The Poisson algebra generated by the monodromy matrix elements will therefore generically depend on the choice of gauge. For any result of the Poisson bracket computation, there is always the possibility that a different gauge fixing condition would have led to a Poisson algebra that is of a simpler form, e.g. the Sklyanin exchange relations.
As was pointed out in Sect. 7, a solution to these problems seems to be within reach for the AGM representing the conformal limit of the Klimčík model. We demonstrated that the gauge equivalence class of the classical Lax connection for \(G=\textrm{SU}(2)\) contains the Lax matrix studied in [53]. This was achieved by means of the Dirac bracket computation from Sect. 6, where the Poisson algebra of the AGM Lax matrix elements in a particular gauge turn out to coincide with that for the Lax matrix considered in Ref. [53]. Having established such a relation, one can apply to the AGM of our interest the main conjecture proposed in that work. The latter identifies the monodromy of this Lax connection with the classical limit of an operator-valued monodromy matrix satisfying the Yang–Baxter algebra. The quantum operator from [53] may therefore be regarded as a quantisation of the monodromy of the gauge-fixed AGM Lax connection. This conjecture would further imply that there exists a natural definition of the Poisson brackets for the classical monodromy matrix elements such that the Sklyanin exchange relations hold true.
The above observations suggest that the non-local conserved quantities of the chiral AGM from this paper could be systematically studied within the usual paradigm of the QISM based on Yang–Baxter integrability. That framework would also provide a means of proving the mutual commutativity of the non-local IMs. A first step in this direction is the rigorous proof of the conjecture from Ref. [53]. While it only concerns the \(\mathfrak {sl}(2)\) case, it should also be possible to extend the conjecture to arbitrary simple Lie algebras \({\mathfrak {g}}\), as was briefly mentioned in Sect. 7.2. Another question concerns the definition of the Poisson brackets for the matrix elements of the classical monodromy. It would be interesting to define an explicit prescription for handling the ambiguities that come from the non-ultralocal bracket of the Lax matrix such that the Jacobi identity holds and the Sklyanin exchange relations are obeyed. The existence of such a regularisation procedure would, of course, be a corollary once the proof of the conjecture from Ref. [53], and its generalisations, is achieved.
In view of the underlying Lie-theoretic structures, it seems natural to expect that the integrals of motion of more general AGMs can be understood in a similar way. Quantum monodromy matrices for a so-called generalised affine \(\mathfrak {sl}(2)\) Gaudin model have recently been defined in Ref. [46]. One may hope that similar constructions can be used to study the chiral limits of the AGMs discussed in Sect. 10.2.
10.5 Deforming Away from the Chiral Limits
Some of the most interesting questions in this context concern the possibility that some key features observed in the chiral limits may survive the deformation away from the chiral limit. We have seen two main manifestations of the integrable structures of the AGMs, related to local and non-local charges, respectively. In this subsection, we will briefly discuss prospects for deformations of these manifestations away from the chiral limit.
The ODE/IQFT correspondence appears to describe the eigenvalues of the conserved charges in the chiral limit of the Klimčík model efficiently. It seems very encouraging to observe that the correspondence appearing in this context admits a natural deformation that would encode the spectrum of the IMs for the massive Klimčík model. A key rôle is played by the integrable partial differential equation of the form [12, 13]
whose auxiliary linear problem serves a very similar task as the ODE does in the chiral limit. It is intriguing to note the re-appearance of the function \({\mathcal {P}}(z)\), which suggests that the deformed ODE/IQFT correspondence proposed in [12, 13] admits a natural generalisation to the class of models discussed in Sect. 10.2.
There seem to be a lot of opportunities for generalisations in view of the observation that the ODEs and PDEs which appear to be relevant in this context are simple examples of a large family of classically integrable equations admitting a Lie-algebraic definition related to the Drinfeld–Sokolov classification.
It would furthermore be extremely useful if the Yang–Baxter algebraic structures governing non-local conserved quantities discussed in Sect. 7 would admit a deformation away from the chiral limits. This possibility is known to be realised for affine Toda field theories, where integrable lattice discretisations have been constructed having the property that the structure constants of the exchange relations satisfied by the quantised monodromy matrices are simply mass-independent. This is most transparent in the lattice light-cone approaches going back to [107, 108]. Such an approach has been used in [109] to investigate the chiral limits of the integrable structures of the sinh-Gordon model. These chiral limits are given by variants of the quantum KdV theory associated to the Virasoro algebra with central charge \(c>25\) representing the integrable structures of the Liouville conformal field theory. Integrable lattice regularisations based on Yang–Baxter algebraic structures have been constructed for more general integrable models of affine Toda type in [110, 111]. Such a framework allows us to understand the integrable structures of the massive models as deformations of their chiral limits. Having seen evidence for the existence of Yang–Baxter algebraic structures in the chiral limits of AGMs makes us hope that such structures can also exist in the case of relativistic AGMs.
10.6 Gauged WZW, \(\varvec{\lambda }\)-Models and Poisson–Lie T-Duality
The study of integrable deformations of \(\sigma \)-models has attracted a lot of attention in the past decades. In parallel to the Yang–Baxter deformations, which include the Klimčík model considered in this article, another important class that has been explored is formed by the so-called \(\lambda \)-deformations. The prototypical member of this class has been introduced by Sfetsos in [112] as an integrable deformation of the non-abelian T-dual of the principal chiral model. It was further realised [56, 64, 113] that there exists a deep relation between these two types of deformed models, taking the form of the so-called Poisson–Lie T-duality [114, 115].
In particular, under this correspondence, the Klimčík model is expected to be dual to the \(G\! \times \! G/G\) coset \(\lambda \)-model introduced in [116]Footnote 40. In the language of AGMs, these two theories correspond to two different relativistic realisations of the same underlying AGM: in particular, there exists a map between the parameters of the Klimčík model and the \(\lambda \)-model which allows one to identify their twist function [118]. (More generally, Poisson–Lie T-dual models are canonically equivalent [119] and thus share the same underlying Poisson structure.) The analysis of the Klimčík model carried out in the present paper should thus possess a rather automatic analogue in the \(G\! \times \! G/G\) \(\lambda \)-model. Of particular interest in this analysis is the study of the UV limit of the theory: for the dual \(\lambda \)-model, this limit is the well-known \(G\! \times \! G/G\) gauged Wess–Zumino–Witten model (more generally, \(\lambda \)-deformations can be seen as relevant perturbations of gauged WZW models as has been found in a variety of cases [116, 120,121,122]). The techniques developed in this paper should thus allow the study of classical and quantum integrable structures in this conformal model. It would be interesting to explore these aspects further.
A key role in the study of gauged WZW models is played by theparafermions [77, 85, 123], which are non-local chiral fields. Recall that we have encountered such parafermionic fields in Sects. 4 and 6, for instance through an appropriate gauge fixing of the AGM underlying the chiral Klimčík model. More precisely, we found that this gauge fixing is described by \({\mathfrak {g}}/{\mathfrak {h}}\) parafermions and \(\dim {\mathfrak {h}}\) decoupled free fields, where \({\mathfrak {h}}\) is the Cartan subalgebra of \({\mathfrak {g}}\). At least in the \(\textrm{SU}(2)\) case, this set-up was well suited for the description of the UV fixed point of the Klimčík model. In contrast, on the dual side, one expects the \(G\! \times \! G/G\) gauged WZW model to be naturally described by \({\mathfrak {g}}\oplus {\mathfrak {g}}/{\mathfrak {g}}\) parafermions [85]. The latter are obtainable from a different choice of gauge fixing of the same underlying AGM. We note moreover that they play an important role in the non-conformal \(\lambda \)-model [116]: indeed, the relevant operator driving the perturbation from the conformal point to this model is built as a bilinear in these currents.
Notes
The dual theory for the so-called sausage model [5], which is a one parameter integrable deformation of the \(\textrm{O}(3)\) sigma model, was originally discovered by Al. Zamolodchikov.
This NLSM was introduced to formulate a duality conjecture between a model with three bosonic fields and a sigma model. In case of doubt, we will always refer to the NLSM when using the terminology Fateev model.
The classical version of these models also appeared in the independent work [33].
Let us also mention that an analogue of the Feigin–Frenkel homomorphism for double-loop algebras was recently introduced in [36], partly motivated by potential applications to the study of AGMs.
In the main text, we will more precisely refer to these theories as relativistic realisations of AGMs. By a slight abuse of language, and to avoid the use of heavier terminology in the introduction, we will simply use the name relativistic AGM here.
To fix the normalisation of the symmetric form, if \(\texttt{t}_a\) is a basis for \({\mathfrak {g}}\) with \( [\texttt{t}_a,\texttt{t}_b]= {f_{ab}}^c\,\texttt{t}_c\) then in terms of the structure constants,
$$\begin{aligned} \langle \texttt{t}_a,\texttt{t}_b\rangle =-\tfrac{1}{2h^\vee }\,{f_{ac}}^d\,{f_{bd}}^c\, . \end{aligned}$$The extra factor, with \(h^\vee \) being the dual Coxeter number for the Lie algebra \({\mathfrak {g}}\), has been chosen so that the angular brackets coincide with the negative of the trace over the fundamental representation.
Note that this bracket would generally include a term proportional to \(\bigl (\sum _{r=1}^N \ell _r\bigr )\partial _x\delta (x-y)\). This term vanishes due to the condition (3.5) imposed on the levels. The condition is thus necessary to ensure that the constraint is first class.
This involution property holds only weakly if one of the zeroes \(\zeta _i\) or \(\zeta _j\) is located at infinity in \(\mathbb{C}\mathbb{P}^1\).
Technically, the construction of [61] is restricted to the case of classical Lie algebras \({\mathfrak {g}}\) (of type A, B, C or D). We expect, however, that a similar construction exists for exceptional algebras.
The prefactor \(-\varphi '(\zeta _i)^{-(p+1)/2}\) differs from the conventions of [61] and has been introduced for future convenience.
Although this seems quite natural, let us note here that the situation is more subtle for affine Gaudin models with higher-order poles at the punctures (see [49] for more details).
This description relies on the use of a local coordinate chart \((\phi ^i)_{i\in \lbrace 1,\ldots ,\dim Q\rbrace }\) on the configuration space Q: \(\phi ^i(x)\) are then coordinate fields, while \(\pi _i(x)\) are the corresponding conjugate momentum fields describing the fibres of \(T^*Q\). This is only a local description and a rigorous treatment of \({\mathcal {F}}[T^*Q]\) then requires dealing with globality issues. We will not enter into these details here.
As we will see in Sect. 6.1, the situation will be slightly more subtle in the case of a chiral realisation.
As we will see on explicit examples, the currents \({\mathcal {J}}_r^\rho (x)\) in the realisation are often expressed in terms of the derivatives \(\partial _x\phi ^i(x)\) of the coordinate fields and thus do not contain the data of their initial conditions \(\phi ^i(x_0)\).
Let us give a sketch of this proof, focussing on the fields \((g_1,X_1)\) and the currents \({\mathcal {J}}_1^\rho \) and \({\mathcal {J}}^\rho _2\). Here, it is useful to perform an analytic continuation and work in the domain where \(\textrm{i}\varepsilon _1\) is real. In this case, the currents \({\mathcal {J}}_1^\rho \) and \({\mathcal {J}}_2^\rho \) are complex conjugate of one another. Their path-ordered exponentials are then complex conjugate elements of the complexified group \(G^{{\mathbb {C}}}\). Following [64], their Iwasawa decompositions, along the factorisation \(G^{{\mathbb {C}}}=G\cdot B_\pm \), then allows one to reconstruct the fields \(g_1\) and \(X_1\), up to the initial value \(g_1(x_0)\) at a reference point \(x_0\in {\mathbb {S}}^1\) (corresponding to integration constants in the path-ordered exponentials).
For a specific choice of the function \(\lambda (z)\) which was considered as arbitrary in Eq. (2.25) since it encoded the freedom of adding any term proportional to the constraint in the Hamiltonian expression of \({\mathcal {L}}_x(z)\).
In Sect. 7 quasi-periodic boundary conditions will be considered, where the space coordinate is compactified \(x\sim x+2\pi \) and \(\phi _j^{(\textrm{L})}(x_++2\pi )=\phi _j^{(\textrm{L})}(x_+)+2\pi P_j\). In that case \(x_+\) and \(y_+\) in the Poisson algebra (4.43) should be understood as belonging to the universal cover \(x_+,y_+\in {\mathbb {R}}\) and the Poisson brackets are modified if either of the light-cone variables lie outside the segment \([0,2\pi )\), see discussion below Eq. (7.60). The same applies to the Poisson algebra (4.30) if the classical parafermions are taken to be quasi-periodic fields.
This terminology goes back to the work of Dotsenko and Fateev [78] on free field representations of the minimal models.
Technically, we also require that the constraints \(\sum _{r=1}^N \rho ^{(\mathrm L)}\bigl ( {\mathcal {J}}^{(\mathrm L)}_r \bigr )\) and \(\sum _{r=1}^N \rho ^{(\mathrm R)}\bigl ( {\mathcal {J}}^{(\mathrm R)}_r \bigr )\) coincide in \({\mathcal {F}}[T^*Q]\) so that these two realisations share the same gauge symmetry and physical observables.
Here, we have expressed the realisation in terms of the light-cone derivatives \(\partial _+\phi \), \(\partial _+\alpha \) and \(\partial _+\chi \) of the fields of the Klimčík model. Replacing time derivatives in favour of the conjugate momenta of these fields yields an expression of the realisation in terms of canonical fields \((\phi ,\alpha ,\chi ,\pi _\phi ,\pi _\alpha ,\pi _\chi )\).
Let us mention that the methods and results described in this paragraph share some similarities with the works [63, 86, 87], which discuss the appearance of semi-classical limits of the finite and affine quantum groups \({\mathcal {U}}_q({\mathfrak {g}})\) and \({\mathcal {U}}_q(\widehat{{\mathfrak {g}}})\) in certain integrable \(\sigma \)-models. We note moreover that the results obtained in the present subsection will serve as the starting point in Sect. 7 for the discussion of a quantum affine Borel group structure \({\mathcal {U}}_q(\widehat{{\mathfrak {b}}})\) underlying the quantisation of the monodromy of the AGM. It would be interesting to explore in more details the potential relations between these approaches.
There is an ambiguity in the definition of the classical R-matrix. An additive shift by the identity matrix \(r(\lambda )\mapsto r(\lambda )+f(\lambda )\,\textrm{id}\), where \(f(\lambda )\) is any function of \(\lambda \), has no effect on the Sklyanin exchange relations (7.39). This ambiguity is fixed in formula (7.40) by requiring that the trace of \(r(\lambda )\) be zero.
Defining the Poisson algebra for \(\mathcal {X}_{0,1}\), along the lines of the above discussion, would require the specification of all possible integrals involving \(\delta '(x-y)\) that could appear in nested PBs of \(\mathcal {X}_{0,1}\). This would lead to the introduction of further undertermined constants parameterising the ambiguities, similar to \(\gamma \) from Eq. (7.48). However, skew-symmetry and the Jacobi identity imposes constraints on the constants that may even fix them completely. A systematic study is beyond the scope of the present work.
Here and below, we use the terminology of “quantised” affine Gaudin models rather than “quantum” affine Gaudin models to avoid any confusion: indeed, the algebraic structure underlying this quantum model is still a standard affine algebra \(\widehat{{\mathfrak {g}}}\), and not a quantum (deformed) one \(\mathcal {U}_q(\widehat{{\mathfrak {g}}})\).
For completeness, one should then prove that the quantised AGM constructed in this set-up is equivalent to the one that would be constructed in a coordinate where none of the punctures are at infinity. This would in particular require a treatment in the BRST formalism and is beyond the scope of this paper.
Most of the OPE computations presented in this paragraph and the appendix were performed using the Mathematica package “OPEdefs” by K. Thielemans [94].
Let us mention for completeness that this \({\mathcal {W}}\)-algebra is also isomorphic to a reduction in the affine superalgebra \({\widehat{D}}(2|1;\alpha )\) by a maximal nilpotent subalgebra, as shown in [82].
In the notations of Eq. (3.17), this tensor is in one-to-one correspondence with the invariant polynomial \(\Phi _p\) through \(\Phi _p(X) = \tau _p^{a_1 \ldots a_{p+1}}X_{a_1} \ldots X_{a_{p+1}}\) for any \(X=X_a\,\texttt{t}^a \in {\mathfrak {g}}^{\mathbb {C}}\).
This conjecture can also be motivated by the so-called ODE/IQFT correspondence. We will come back briefly to this point in Sect. 10.3.
Let us briefly comment on this definition of \({\mathcal {P}}(z)\). As we have mentioned in Sect. 9.1, the transformation rule (9.12) of the quantum twist function \(\varphi ^{(\textrm{qt})}(z)\) under a change of spectral parameter means that \(\partial _z - \varphi ^{(\textrm{qt})}(z)\) is a connection on the line bundle \(\Omega ^{\,h^{\!\vee }}\). The condition (9.38) can then be interpreted as defining \({\mathcal {P}}(z)\) as a (multivalued) section of the bundle \(\Omega ^{\,h^{\!\vee }}\) which is flat with respect to this connection. In particular, this means that the object \({\mathcal {P}}(z)\,(\text {d}z)^{h^{\!\vee }}\) behaves as an order \(h^{\!\vee }\) differential with respect to the spectral parameter, i.e. that \({\mathcal {P}}(z)^{1/h^{\!\vee }}\text {d}z\) is a 1-form.
Technically, one also needs to impose that the quantities of which we take the spatial or twisted derivatives are regular when \(z=w\).
Let us mention that this integrable structure also appeared recently in [96], where it is studied using the framework of toroidal algebras. Remarkably, it was pointed out in [97] that the spectrum of some integrable systems arising from toroidal algebras can be described by Bethe ansatz equations of affine Gaudin type. It would be interesting to explore the potential relations between our results and this framework.
Note that one puncture is located at infinity in the conventions of [32], whereas we will here assume \(z_r\ne \infty \) for all r in the following discussion.
The coefficients of these differential polynomials also involve the function \({\mathcal {P}}(z)\), which depends only on the AGM considered and not on the choice of eigenstate.
The Klimčík model can in fact be Poisson–Lie T-dualised in two ways, corresponding to its left and right deformed Poisson–Lie symmetries. Dualising with respect to one of these symmetries yields the so-called generalised \(\lambda \)-model [56, 117]. A second dualisation with respect to the other Poisson–Lie symmetry is then expected to give the \(G\! \times \! G/G\) coset \(\lambda \)-model.
The components \(N_{ab}\) and \(N'_{ab}\) are entries of the inverse of the \((2\dim {\mathfrak {g}})\times (2\dim {\mathfrak {g}})\) matrix built from all Poisson brackets of \({\mathcal {C}}^a\) and \({\mathcal {F}}^a\). The top-left block of this matrix is zero since \(\lbrace {\mathcal {C}}^a,{\mathcal {C}}^b\rbrace \equiv 0\), so its inverse has a vanishing bottom-right block.
More rigorously, one should think of the fields \({\mathcal {J}}_r\) as distributions on \({\mathbb {S}}^1\) rather than functions, since they possess an infinite Fourier series which does not necessarily converge in the standard functional sense. In particular, the field \({\mathcal {J}}_r\) is more technically valued in a completion of \({\mathcal {A}}\otimes {\mathcal {L}}{\mathfrak {g}}\), which allows for such infinite series (converging with respect to a certain valuation associated with loop modes in \({\mathcal {A}}\) and \({\mathcal {L}}{\mathfrak {g}}\)). We will not enter in these subtleties here and refer to [47] for details on similar considerations.
Let us note for completeness that this reformulation can be naturally interpreted by seeing the Kac–Moody bracket as the Kirillov–Kostant bracket of the affine algebra \(\widehat{{\mathfrak {g}}}\), whose dual is identified with the space \({\mathbb {C}}\partial \rtimes {\mathcal {L}}{\mathfrak {g}}\) of \({\mathfrak {g}}^{\mathbb {C}}\)-connections on \({\mathbb {S}}^1\).
In the main text, the Kac–Moody currents were denoted as \({\mathcal {J}}_r^{(\mathrm L)}\) to emphasise that they correspond to a left-moving affine Gaudin model. To lighten the notations, we have dropped the labels \({(\mathrm L)}\) in this appendix.
For completeness, we should mention that there is in fact a redundancy in the ansatz that we took for \({\textsf{W}}_4\), since certain terms are not independent. For instance, we have
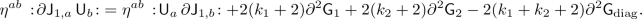 (C.9a)
(C.9a)Here, we use this redundancy to obtain an expression for the coefficients \(\lambda ^{(n)}_\bullet \) and \(\rho ^{(n)}_\bullet \) which is as simple and “symmetric” as possible.
The fact that the resulting density \({\textsf{S}}_4(z,x)\) also satisfies the condition (ii) was checked explicitly in the recent work [124], which appeared shortly after the first version of this article. We thank T. Franzini and C. A. S. Young for interesting discussions on this subject.
Recall also from Sect. 3.2 that these two sets have the same size, which is thus equal to M.
Based on the experience of the Klimčík model, we know, however, that this question can in general be a subtle one. Indeed, in this example, we could consider different ways of parametrising the coordinates and conjugate momenta of the realisation in terms of the parameters of the AGM, giving rise to different limits of the Kac–Moody currents (sometimes requiring fine-tuned conjugations), corresponding to different charts of the target space in the limit. We will not enter into these considerations here.
For the proof of the property (CP2), one has to use the fact that the initial relativistic realisation we are starting with contains all the canonical fields of the theory up to initial values, as assumed in the condition (R2) defining a relativistic realisation—see Sect. 3.2.
The corresponding coefficients \((b_0,b_1,b_2)\) are thus in general arbitrary, except if one has fixed the freedom of performing Möbius transformations, for instance by sending some of the points \((z_r^\pm ,\zeta _i^\pm )\) to specific positions. We are in the latter situation here, as we have imposed \((\zeta _M^+,\zeta _M^-)=(\infty ,0)\). In this case, the parameters \((b_0,b_1,b_2)\) are then non-arbitrary and take specific values which ensure that the RG flow (E.15) preserves this choice.
References
Polyakov, A.M.: Interaction of Goldstone particles in two dimensions. Applications to ferromagnets and massive Yang–Mills fields. Phys. Lett. B 59, 79 (1975). https://doi.org/10.1016/0370-2693(75)90161-6
Beisert, N., et al.: Review of AdS/CFT integrability: an overview. Lett. Math. Phys. 99, 3 (2012). https://doi.org/10.1007/s11005-011-0529-2. [arXiv:1012.3982]
Fateev, V.A.: The duality between two-dimensional integrable field theories and sigma models. Phys. Lett. B 357, 397 (1995). https://doi.org/10.1016/0370-2693(95)00883-M
Fateev, V.A.: The sigma model (dual) representation for a two-parameter family of integrable quantum field theories. Nucl. Phys. B 473, 509 (1996). https://doi.org/10.1016/0550-3213(96)00256-8
Fateev, V.A., Onofri, E., Zamolodchikov, A.B.: Integrable deformations of the O(3) sigma model. The sausage model. Nucl. Phys. B 406, 521 (1993). https://doi.org/10.1016/0550-3213(93)90001-6
Faddeev, L.D., Sklyanin, E.K., Takhtajan, L.A.: The quantum inverse problem method. I. Theor. Math. Phys. 40, 688 (1980). https://doi.org/10.1007/BF01018718
Maillet, J.M.: Kac–Moody algebra and extended Yang–Baxter relations in the \(O(N)\) non-linear sigma model. Phys. Lett. Ser. B162, 137 (1985). https://doi.org/10.1016/0370-2693(85)91075-5
Maillet, J.M.: New integrable canonical structures in two-dimensional models. Nucl. Phys. Ser. B269, 54 (1986). https://doi.org/10.1016/0550-3213(86)90365-2
Gromov, N., Kazakov, V., Vieira, P.: Finite volume spectrum of 2D field theories from Hirota dynamics. JHEP 12, 060 (2009). https://doi.org/10.1088/1126-6708/2009/12/060. [arXiv:0812.5091]
Fateev, V.A.: Integrable deformations of Sine–Liouville conformal field theory and duality. SIGMA 13, 080 (2017). https://doi.org/10.3842/SIGMA.2017.080. [arXiv:1705.06424]
Bazhanov, V.V., Kotousov, G.A., Lukyanov, S.L.: Quantum transfer-matrices for the sausage model. JHEP 01, 021 (2018). https://doi.org/10.1007/JHEP01(2018)021. [arXiv:1706.09941]
Lukyanov, S.L.: ODE/IM correspondence for the Fateev model. JHEP 12, 012 (2013). https://doi.org/10.1007/JHEP12(2013)012. [arXiv:1303.2566]
Bazhanov, V.V., Lukyanov, S.L.: Integrable structure of quantum field theory: classical flat connections versus quantum stationary states. JHEP 09, 147 (2014). https://doi.org/10.1007/JHEP09(2014)147. [arXiv:1310.4390]
Bazhanov, V.V., Kotousov, G.A., Lukyanov, S.L.: Winding vacuum energies in a deformed O(4) sigma model. Nucl. Phys. B 889, 817 (2014). https://doi.org/10.1016/j.nuclphysb.2014.11.005. [arXiv:1409.0449]
Zamolodchikov, A.B.: Integrable field theory from conformal field theory. Adv. Stud. Pure Math. 19, 641 (1989). https://doi.org/10.2969/aspm/01910641
Bazhanov, V.V., Lukyanov, S.L., Zamolodchikov, A.B.: Integrable structure of conformal field theory, quantum KdV theory and thermodynamic Bethe ansatz. Commun. Math. Phys. 177, 381 (1996). https://doi.org/10.1007/BF0210189. [arXiv:hep-th/9412229]
Bazhanov, V.V., Lukyanov, S.L., Zamolodchikov, A.B.: Integrable structure of conformal field theory. 2. Q operator and DDV equation. Commun. Math. Phys. 190, 247 (1997). https://doi.org/10.1007/s002200050240. [arXiv:hep-th/9604044]
Bazhanov, V.V., Lukyanov, S.L., Zamolodchikov, A.B.: Integrable structure of conformal field theory. 3. The Yang–Baxter relation. Commun. Math. Phys. 200, 297 (1999). https://doi.org/10.1007/s002200050531. [arXiv:hep-th/9805008]
Fateev, V.A., Zamolodchikov, A.B.: Conformal quantum field theory models in two-dimensions having Z(3) symmetry. Nucl. Phys. B 280, 644 (1987). https://doi.org/10.1016/0550-3213(87)90166-0
Fateev, V.A., Lukyanov, S.L.: The models of two-dimensional conformal quantum field theory with Z(n) symmetry. Int. J. Mod. Phys. A 3, 507 (1988). https://doi.org/10.1142/S0217751X88000205
Feigin, B., Frenkel, E.: Free field resolutions in affine Toda field theories. Phys. Lett. B 276, 79 (1992). https://doi.org/10.1016/0370-2693(92)90544-E
Feigin, B., Frenkel, E.: Integrals of motion and quantum groups. Lect. Notes Math. 1620, 349 (1996). https://doi.org/10.1007/BFb0094794. [arXiv:hep-th/9310022]
Dorey, P., Tateo, R.: Anharmonic oscillators, the thermodynamic Bethe ansatz, and nonlinear integral equations. J. Phys. A 32, L419 (1999). https://doi.org/10.1088/0305-4470/32/38/102. [arXiv:hep-th/9812211]
Bazhanov, V.V., Lukyanov, S.L., Zamolodchikov, A.B.: Spectral determinants for Schroedinger equation and Q operators of conformal field theory. J. Stat. Phys. 102, 567 (2001). https://doi.org/10.1023/A:1004838616921. [arXiv:hep-th/9812247]
Bazhanov, V.V., Lukyanov, S.L., Zamolodchikov, A.B.: Higher level eigenvalues of Q operators and Schroedinger equation. Adv. Theor. Math. Phys. 7, 711 (2003). https://doi.org/10.4310/ATMP.2003.v7.n4.a4. [arXiv:hep-th/0307108]
Conti, R., Masoero, D.: Counting monster potentials. JHEP 02, 059 (2021). https://doi.org/10.1007/JHEP02(2021)059. [arXiv:2009.14638]
Conti, R., Masoero, D.: On solutions of the Bethe Ansatz for the quantum KdV model. arXiv:2112.14625
Dorey, P., Dunning, C., Tateo, R.: The ODE/IM correspondence. J. Phys. A 40, R205 (2007). https://doi.org/10.1088/1751-8113/40/32/R01. [arXiv:hep-th/0703066]
Dorey, P., Dunning, C., Negro, S., Tateo, R.: Geometric aspects of the ODE/IM correspondence. J. Phys. A 53, 223001 (2020). https://doi.org/10.1088/1751-8121/ab83c9. [arXiv:1911.13290]
Bazhanov, V.V., Lukyanov, S.L., Runov, B.A.: Vacuum energy of the Bukhvostov–Lipatov model. Nucl. Phys. B 911, 863 (2016). https://doi.org/10.1016/j.nuclphysb.2016.08.031. [arXiv:1607.04839]
Bazhanov, V.V., Lukyanov, S.L., Runov, B.A.: Bukhvostov–Lipatov model and quantum-classical duality. Nucl. Phys. B 927, 468 (2018). https://doi.org/10.1016/j.nuclphysb.2017.12.022. [arXiv:1711.09021]
Feigin, B., Frenkel, E.: Quantization of soliton systems and Langlands duality. In: Exploration of New Structures and Natural Constructions in Mathematical Physics. Advanced Studies in Pure Mathematics, vol. 61, pp. 185–274 (2011). https://doi.org/10.1142/e032. [arXiv:0705.2486]
Levin, A.M., Olshanetsky, M.A., Zotov, A.: Hitchin systems–symplectic Hecke correspondence and two-dimensional version. Commun. Math. Phys. 236, 93 (2003). https://doi.org/10.1007/s00220-003-0801-0. [arXiv:nlin/0110045]
Lacroix, S., Vicedo, B., Young, C.A.S.: Affine Gaudin models and hypergeometric functions on affine opers. Adv. Math. 350, 486 (2019). https://doi.org/10.1016/j.aim.2019.04.032. [arXiv:1804.01480]
Lacroix, S., Vicedo, B., Young, C.A.S.: Cubic hypergeometric integrals of motion in affine Gaudin models. Adv. Theor. Math. Phys. 24, 155 (2020). https://doi.org/10.4310/ATMP.2020.v24.n1.a5. [arXiv:1804.06751]
Young, C.A.S.: An analog of the Feigin–Frenkel homomorphism for double loop algebras. J. Algebra 588, 1 (2021). https://doi.org/10.1016/j.jalgebra.2021.07.031. [arXiv:2011.01648]
Gaudin, M.: Diagonalisation d’une classe d’hamiltoniens de spin. J. Phys. France 37, 1087 (1976). https://doi.org/10.1051/jphys:0197600370100108700
Gaudin, M.: La fonction d’onde de Bethe. Masson, Paris (1983)
Feigin, B., Frenkel, E., Reshetikhin, N.: Gaudin model, Bethe ansatz and correlation functions at the critical level. Commun. Math. Phys. 166, 27 (1994). https://doi.org/10.1007/BF02099300. [arXiv:hep-th/9402022]
Frenkel, E., Hernandez, D.: Spectra of quantum KdV Hamiltonians, Langlands duality, and affine opers. Commun. Math. Phys. 362, 361 (2018). https://doi.org/10.1007/s00220-018-3194-9. [arXiv:1606.05301]
Masoero, D., Raimondo, A., Valeri, D.: Bethe Ansatz and the spectral theory of affine Lie algebra-valued connections I. The simply-laced case. Commun. Math. Phys. 344, 719 (2016). https://doi.org/10.1007/s00220-016-2643-6. [arXiv:1501.07421]
Masoero, D., Raimondo, A., Valeri, D.: Bethe Ansatz and the spectral theory of affine Lie algebra-valued connections II: the non simply-laced case. Commun. Math. Phys. 349, 1063 (2017). https://doi.org/10.1007/s00220-016-2744-2. [arXiv:1511.00895]
Bazhanov, V.V., Hibberd, A.N., Khoroshkin, S.M.: Integrable structure of W(3) conformal field theory, quantum Boussinesq theory and boundary affine Toda theory. Nucl. Phys. B 622, 475 (2002). https://doi.org/10.1016/S0550-3213(01)00595-8. [arXiv:hep-th/0105177]
Gaiotto, D., Lee, J.H., Wu, J.: Integrable Kondo problems. JHEP 04, 268 (2021). https://doi.org/10.1007/JHEP04(2021)268. [arXiv:2003.06694]
Gaiotto, D., Lee, J.H., Vicedo, B., Wu, J.: Kondo line defects and affine Gaudin models. JHEP 01, 175 (2022). https://doi.org/10.1007/JHEP01(2022)175. [arXiv:2010.07325]
Kotousov, G.A., Lukyanov, S.L.: ODE/IQFT correspondence for the generalized affine \( \mathfrak{sl} \)(2) Gaudin model. JHEP 09, 201 (2021). https://doi.org/10.1007/JHEP09(2021)201. [arXiv:2106.01238]
Vicedo, B.: On integrable field theories as dihedral affine Gaudin models. Int. Math. Res. Not. Ser. 2020, 15 (2020). https://doi.org/10.1093/imrn/rny128. [arXiv:1701.04856]
Delduc, F., Lacroix, S., Magro, M., Vicedo, B.: Assembling integrable \(\sigma \)-models as affine Gaudin models. JHEP Ser. 06, 017 (2019). https://doi.org/10.1007/JHEP06(2019)017. [arXiv:1903.00368]
Lacroix, S.: Constrained affine Gaudin models and diagonal Yang–Baxter deformations. J. Phys. Ser. A53, 255203 (2020). https://doi.org/10.1088/1751-8121/ab876e. [arXiv:1907.04836]
Klimčík, C.: On integrability of the Yang–Baxter sigma-model. J. Math. Phys. 50, 043508 (2009). https://doi.org/10.1063/1.3116242. [arXiv:0802.3518]
Klimčík, C.: Integrability of the Bi–Yang–Baxter sigma-model. Lett. Math. Phys. 104, 1095 (2014). https://doi.org/10.1007/s11005-014-0709-y. [arXiv:1402.2105]
Hoare, B., Roiban, R., Tseytlin, A.A.: On deformations of \(AdS_n\times S^n\) supercosets. JHEP 06, 002 (2014). https://doi.org/10.1007/JHEP06(2014)002. [arXiv:1403.5517]
Bazhanov, V.V., Kotousov, G.A., Lukyanov, S.L.: On the Yang–Baxter Poisson algebra in non-ultralocal integrable systems. Nucl. Phys. B 934, 529 (2018). https://doi.org/10.1016/j.nuclphysb.2018.07.016. [arXiv:1805.07417]
Hoare, B.: Towards a two-parameter q-deformation of \(\text{ AdS}_3 \times S^3 \times M^4\) superstrings. Nucl. Phys. B 891, 259 (2015). https://doi.org/10.1016/j.nuclphysb.2014.12.012. [arXiv:1411.1266]
Delduc, F., Lacroix, S., Magro, M., Vicedo, B.: On the Hamiltonian integrability of the Bi–Yang–Baxter sigma-model. JHEP 03, 104 (2016). https://doi.org/10.1007/JHEP03(2016)104. [arXiv:1512.02462]
Sfetsos, K., Siampos, K., Thompson, D.C.: Generalised integrable \(\lambda \)- and \(\eta \)-deformations and their relation. Nucl. Phys. B 899, 489 (2015). https://doi.org/10.1016/j.nuclphysb.2015.08.015. [arXiv:1506.05784]
Delduc, F., Lacroix, S., Sfetsos, K., Siampos, K.: RG flows of integrable \(\sigma \)-models and the twist function. JHEP Ser. 02, 065 (2021). https://doi.org/10.1007/JHEP02(2021)065. [arXiv:2010.07879]
Hassler, F.: RG flow of integrable \({\cal{E} }\)-models. Phys. Lett. B 818, 136367 (2021). https://doi.org/10.1016/j.physletb.2021.136367. [arXiv:2012.10451]
Lukyanov, S.L.: The integrable harmonic map problem versus Ricci flow. Nucl. Phys. B 865, 308 (2012). https://doi.org/10.1016/j.nuclphysb.2012.08.002. [arXiv:1205.3201]
Dirac, P.A.M.: Lectures on Quantum Mechanics. Yeshiva University, Belfer Graduate School of Science (1964)
Lacroix, S., Magro, M., Vicedo, B.: Local charges in involution and hierarchies in integrable sigma-models. JHEP 1709, 117 (2017). https://doi.org/10.1007/JHEP09(2017)117. [arXiv:1703.01951]
Evans, J.M., Hassan, M., MacKay, N.J., Mountain, A.J.: Local conserved charges in principal chiral models. Nucl. Phys. B 561, 385 (1999). https://doi.org/10.1016/S0550-3213(99)00489-7. [arXiv:hep-th/9902008]
Delduc, F., Magro, M., Vicedo, B.: On classical \(q\)-deformations of integrable \(\sigma \)-models. JHEP Ser. 1311, 192 (2013). https://doi.org/10.1007/JHEP11(2013)192. [arXiv:1308.3581]
Vicedo, B.: Deformed integrable \(\sigma \)-models, classical R-matrices and classical exchange algebra on Drinfel’d doubles. J. Phys. A 48, 355203 (2015). https://doi.org/10.1088/1751-8113/48/35/355203. [arXiv:1504.06303]
Friedan, D.: Nonlinear models in \(2+\epsilon \) dimensions. Phys. Rev. Lett. 45, 1057 (1980). https://doi.org/10.1103/PhysRevLett.45.1057
Friedan, D.: Nonlinear models in \(2+\epsilon \) dimensions. Annals Phys. 163, 318 (1985). https://doi.org/10.1016/0003-4916(85)90384-7
Fradkin, E.S., Tseytlin, A.A.: Quantum string theory effective action. Nucl. Phys. B 261, 1 (1985). https://doi.org/10.1016/0550-3213(85)90559-0
Callan, C.G., Jr., Martinec, E.J., Perry, M.J., Friedan, D.: Strings in background fields. Nucl. Phys. B 262, 593 (1985). https://doi.org/10.1016/0550-3213(85)90506-1
Valent, G., Klimcik, C., Squellari, R.: One loop renormalizability of the Poisson–Lie sigma models. Phys. Lett. B 678, 143 (2009). https://doi.org/10.1016/j.physletb.2009.06.001. [arXiv:0902.1459]
Hamilton, R.S.: The Ricci flow on surfaces. In: Mathematics and General Relativity, Contemporary Mathematics, vol. 71. Amer. Math. Soc., Providence, p. 237 (1988)
Elitzur, S., Forge, A., Rabinovici, E.: Some global aspects of string compactifications. Nucl. Phys. B 359, 581 (1991). https://doi.org/10.1016/0550-3213(91)90073-7
Witten, E.: On string theory and black holes. Phys. Rev. D 44, 314 (1991). https://doi.org/10.1103/PhysRevD.44.314
Lepowsky, J., Wilson, R.L.: The structure of standard modules, I: universal algebras and the Rogers–Ramanujan identities. Invent. Math. 77, 199 (1984). https://doi.org/10.1007/BF01388447
Fateev, V.A., Zamolodchikov, A.B.: Parafermionic currents in the two-dimensional conformal quantum field theory and selfdual critical points in Z(n) invariant statistical systems. Sov. Phys. JETP 62, 215 (1985)
Ninomiya, M., Yamagishi, K.: Nonlocal SU(3) current algebra. Phys. Lett. B 183, 323 (1987). https://doi.org/10.1016/0370-2693(87)90972-5
Gepner, D.: New conformal field theories associated with lie algebras and their partition functions. Nucl. Phys. B 290, 10 (1987). https://doi.org/10.1016/0550-3213(87)90176-3
Bardakci, K., Crescimanno, M.J., Rabinovici, E.: Parafermions From coset models. Nucl. Phys. B 344, 344 (1990). https://doi.org/10.1016/0550-3213(90)90365-K
Dotsenko, V.S., Fateev, V.A.: Conformal algebra and multipoint correlation functions in two-dimensional statistical models. Nucl. Phys. B 240, 312 (1984). https://doi.org/10.1016/0550-3213(84)90269-4
Bakas, I., Kiritsis, E.: Beyond the large N limit: non-linear \(W_\infty \) as symmetry of the SL(2, R)/U(1) coset model. Int. J. Mod. Phys. A 7, 55 (1992). https://doi.org/10.1142/S0217751X92003720. [arXiv:hep-th/9109029]
Dorey, P., Korchemsky, G., Nekrasov, N., Schomerus, V., Serban, D., Cugliandolo, L. (eds.): Integrability: From Statistical Systems to Gauge Theory. Oxford University Press (2019)
Lukyanov, S.L., Zamolodchikov, A.B.: Integrable boundary interaction in 3D target space: the “pillow-brane’’ model. Nucl. Phys. B 873, 585 (2013). https://doi.org/10.1016/j.nuclphysb.2013.05.008
Feigin, B.L., Semikhatov, A.M.: The sl(2) + sl(2)/sl(2) coset theory as a Hamiltonian reduction of D(2 \(|\)1 alpha) superalgebra. JETP Lett. 74, 59 (2001). https://doi.org/10.1134/1.1402208. [arXiv:hep-th/0102078]
Young, C.A.S.: Non-local charges, Z(m) gradings and coset space actions. Phys. Lett. B 632, 559 (2006). https://doi.org/10.1016/j.physletb.2005.10.090. [arXiv:hep-th/0503008]
Hoare, B.: Integrable deformations of sigma models. J. Phys. A 55, 093001 (2022). https://doi.org/10.1088/1751-8121/ac4a1e. [arXiv:2109.14284]
Bardakci, K., Crescimanno, M.J., Hotes, S.: Parafermions from nonabelian coset models. Nucl. Phys. B 349, 439 (1991). https://doi.org/10.1016/0550-3213(91)90332-R
Kawaguchi, I., Matsumoto, T., Yoshida, K.: The classical origin of quantum affine algebra in squashed sigma models. JHEP 04, 115 (2012). https://doi.org/10.1007/JHEP04(2012)115. [arXiv:1201.3058]
Delduc, F., Kameyama, T., Magro, M., Vicedo, B.: Affine \(q\)-deformed symmetry and the classical Yang–Baxter \(\sigma \)-model. JHEP 03, 126 (2017). https://doi.org/10.1007/JHEP03(2017)126. [arXiv:1701.03691]
Khoroshkin, S.M., Stolin, A.A., Tolstoi, V.N.: Gauss decomposition of trigonometric R matrices. Mod. Phys. Lett. A 10, 1375 (1995). https://doi.org/10.1142/S0217732395001496. [arXiv:hep-th/9404038]
Sklyanin, E.K.: On the complete integrability of the Landau–Lifshitz equation, preprint LOMI E-3-79 (1979). https://cds.cern.ch/record/121210
Duncan, A., Nicolai, H., Niedermaier, M.: On the Poisson bracket algebra of monodromy matrices. Z. Phys. C 46, 147 (1990). https://doi.org/10.1007/BF02440845
Hlousek, Z., Yamagishi, K.: An approach to BRST formulation of Kac–Moody algebra. Phys. Lett. B 173, 65 (1986). https://doi.org/10.1016/0370-2693(86)91231-1
Goddard, P., Kent, A., Olive, D.I.: Virasoro algebras and coset space models. Phys. Lett. B 152, 88 (1985). https://doi.org/10.1016/0370-2693(85)91145-1
Goddard, P., Kent, A., Olive, D.I.: Unitary representations of the virasoro and supervirasoro algebras. Commun. Math. Phys. 103, 105 (1986). https://doi.org/10.1007/BF01464283
Thielemans, K.: A mathematica package for computing operator product expansions. Int. J. Mod. Phys. C 2, 787 (1991). https://doi.org/10.1142/S0129183191001001
Reshetikhin, N., Varchenko, A.: Quasiclassical asymptotics of solutions to the KZ equations. arXiv:hep-th/9402126
Feigin, B., Jimbo, M., Mukhin, E.: Towards trigonometric deformation of \(\widehat{\mathfrak{sl} }_2\) coset VOA. J. Math. Phys. 60, 073507 (2019). https://doi.org/10.1063/1.5081799. [arXiv:1811.02056]
Feigin, B., Jimbo, M., Mukhin, E.: Integrals of motion from quantum toroidal algebras. J. Phys. A 50, 464001 (2017). https://doi.org/10.1088/1751-8121/aa8e92. [arXiv:1705.07984]
Fateev, V.A., Litvinov, A.V.: Integrability, duality and sigma models. JHEP 11, 204 (2018). https://doi.org/10.1007/JHEP11(2018)204. [arXiv:1804.03399]
Litvinov, A.V., Spodyneiko, L.A.: On dual description of the deformed \(O(N)\) sigma model. JHEP 11, 139 (2018). https://doi.org/10.1007/JHEP11(2018)139. [arXiv:1804.07084]
Alfimov, M., Feigin, B., Hoare, B., Litvinov, A.: Dual description of \(\eta \)-deformed OSP sigma models. JHEP 12, 040 (2020). https://doi.org/10.1007/JHEP12(2020)040. [arXiv:2010.11927]
Bardakci, K., Bernardo, L.M., Sochen, N.: Integrable generalized Thirring model. Nucl. Phys. Ser. B487, 513 (1997). https://doi.org/10.1016/S0550-3213(96)00715-8. [arXiv:hep-th/9607018]
Georgiou, G., Sfetsos, K.: A new class of integrable deformations of CFTs. JHEP 03, 083 (2017). https://doi.org/10.1007/JHEP03(2017)083. [arXiv:1612.05012]
Arutyunov, G., Bassi, C., Lacroix, S.: New integrable coset sigma models. JHEP 03, 062 (2021). https://doi.org/10.1007/JHEP03(2021)062. [arXiv:2010.05573]
Levine, N., Tseytlin, A.A.: Integrability vs. RG flow in \(G \times G\) and \(G \times G /H\) sigma models. JHEP 05, 076 (2021). https://doi.org/10.1007/JHEP05(2021)076. [arXiv:2103.10513]
Guadagnini, E., Martellini, M., Mintchev, M.: Scale invariant sigma models on homogeneous spaces. Phys. Lett. Ser. B194, 69 (1987). https://doi.org/10.1016/0370-2693(87)90771-4
Frenkel, E.: Lectures on the Langlands program and conformal field theory. In: Frontiers in Number Theory, Physics, and Geometry II, p. 387. Springer, Berlin, (2007). https://doi.org/10.1007/978-3-540-30308-4_11 [arXiv:hep-th/0512172]
Faddeev, L.D., Volkov, A.Y.: Quantum inverse scattering method on a space-time lattice. Theor. Math. Phys. 92, 837 (1992). https://doi.org/10.1007/BF01015552
Bazhanov, V., Bobenko, A., Reshetikhin, N.: Quantum discrete sine-Gordon model at roots of 1: integrable quantum system on the integrable classical background. Commun. Math. Phys. 175, 377 (1996). https://doi.org/10.1007/BF02102413
Bytsko, A., Teschner, J.: The Integrable structure of nonrational conformal field theory. Adv. Theor. Math. Phys. 17, 701 (2013). https://doi.org/10.4310/ATMP.2013.v17.n4.a1. [arXiv:0902.4825]
Ridout, D., Teschner, J.: Integrability of a family of quantum field theories related to sigma models. Nucl. Phys. B 853, 327 (2011). https://doi.org/10.1016/j.nuclphysb.2011.07.019. [arXiv:1102.5716]
Meneghelli, C., Teschner, J.: Integrable light-cone lattice discretizations from the universal \(\rm R \)-matrix. Adv. Theor. Math. Phys. 21, 1189 (2017). https://doi.org/10.4310/ATMP.2017.v21.n5.a3. [arXiv:1504.04572]
Sfetsos, K.: Integrable interpolations: from exact CFTs to non-Abelian T-duals. Nucl. Phys. B 880, 225 (2014). https://doi.org/10.1016/j.nuclphysb.2014.01.004. [arXiv:1312.4560]
Hoare, B., Tseytlin, A.A.: On integrable deformations of superstring sigma models related to \(AdS_n \times S^n\) supercosets. Nucl. Phys. B 897, 448 (2015). https://doi.org/10.1016/j.nuclphysb.2015.06.001. [arXiv:1504.07213]
Klimcik, C., Severa, P.: Dual non-abelian duality and the Drinfeld double. Phys. Lett. B 351, 455 (1995). https://doi.org/10.1016/0370-2693(95)00451-P. [arXiv:hep-th/9502122]
Klimcik, C., Severa, P.: Poisson–Lie T-duality and loop groups of Drinfeld doubles. Phy s. Lett. B 372, 65 (1996). https://doi.org/10.1016/0370-2693(96)00025-1. [arXiv:hep-th/9512040]
Sfetsos, K., Siampos, K.: Integrable deformations of the \(G_{k_1} \times G_{k_2}/G_{k_1+k_2}\) coset CFTs. Nucl. Phys. B 927, 124 (2018). https://doi.org/10.1016/j.nuclphysb.2017.12.011. [arXiv:1710.02515]
Klimčík, C.: Poisson–Lie T-duals of the Bi–Yang–Baxter models. Phys. Lett. B 760, 345 (2016). https://doi.org/10.1016/j.physletb.2016.06.077. [arXiv:1606.03016]
Georgiou, G., Sfetsos, K., Siampos, K.: Strong integrability of \(\lambda \)-deformed models. Nucl. Phys. B 952, 114923 (2020). https://doi.org/10.1016/j.nuclphysb.2020.114923. [arXiv:1911.07859]
Sfetsos, K.: Canonical equivalence of nonisometric sigma models and Poisson–Lie T duality. Nucl. Phys. B 517, 549 (1998). https://doi.org/10.1016/S0550-3213(97)00823-7. [arXiv:hep-th/9710163]
Itsios, G., Sfetsos, K., Siampos, K.: The all-loop non-Abelian Thirring model and its RG flow. Phys. Lett. B 733, 265 (2014). https://doi.org/10.1016/j.physletb.2014.04.061. [arXiv:1404.3748]
Appadu, C., Hollowood, T.J.: Beta function of k deformed \(\text{ AdS}_{5}\)\(\times \)\(\text{ S}^{\,5}\) string theory. JHEP 11, 095 (2015). https://doi.org/10.1007/JHEP11(2015)095. [arXiv:1507.05420]
Georgiou, G., Sfetsos, K., Siampos, K.: \(\lambda \)-Deformations of left–right asymmetric CFTs. Nucl. Phys. B 914, 623 (2017). https://doi.org/10.1016/j.nuclphysb.2016.11.022. [arXiv:1610.05314]
Karabali, D., Schnitzer, H.J.: BRST quantization of the gauged WZW action and coset conformal field theories. Nucl. Phys. B 329, 649 (1990). https://doi.org/10.1016/0550-3213(90)90075-O
Franzini, T., Young, C.A.S.: Quartic Hamiltonians, and higher Hamiltonians at next-to-leading order, for the affine \(\mathfrak{sl}_2\) Gaudin model. arXiv:2205.15815
Delduc, F., Magro, M., Vicedo, B.: Integrable double deformation of the principal chiral model. Nucl. Phys. B 891, 312 (2015). https://doi.org/10.1016/j.nuclphysb.2014.12.018. [arXiv:1410.8066]
Bassi, C., Lacroix, S.: Integrable deformations of coupled \(\sigma \)-models. JHEP 05, 059 (2020). https://doi.org/10.1007/JHEP05(2020)059. [arXiv:1912.06157]
Acknowledgements
The authors would like to thank B. Vicedo for useful and interesting discussions. G.K. also acknowledges V.V. Bazhanov and S.L. Lukyanov for fruitful and stimulating interactions and S.L. similarly thanks F. Delduc, T. Franzini, M. Magro, K. Siampos and C. A. S. Young. The work of G.K. and J.T. is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC 2121 “Quantum Universe”—390833306. S.L. is supported by Dr. Max Rössler, the Walter Haefner Foundation and the ETH Zürich Foundation.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Antti Kupiainen.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Conventions on Lie Algebras and Root Decompositions
Root Decomposition Let us consider the complexified simple Lie algebra \({\mathfrak {g}}^{\mathbb {C}}\) and its decomposition \({\mathfrak {g}}^{\mathbb {C}}={\mathfrak {h}}\oplus {\mathfrak {n}}_+\oplus {\mathfrak {n}}_-\), where \({\mathfrak {h}}\) is a Cartan subalgebra and \({\mathfrak {n}}_\pm \) are positive/negative nilpotent subalgebras. We denote by \(\Delta = \Delta _+ \sqcup \Delta _- \subset {\mathfrak {h}}^*\) the root system of \({\mathfrak {g}}^{\mathbb {C}}\), decomposed in positive roots \(\Delta _+\) and negative ones \(\Delta _-\). For each \(\alpha \in \Delta _\pm \), let \(\texttt{e}_\alpha \) be the corresponding root vector lying in \({\mathfrak {n}}_\pm \). We then have
We normalise these vectors such that
where \(\langle \cdot ,\cdot \rangle \) is our choice of non-degenerate bilinear form on \({\mathfrak {g}}^{\mathbb {C}}\). If two roots \(\alpha ,\beta \in \Delta \) are such that \(\alpha +\beta \) is also a root, then there exists a nonzero number \(N^{\alpha ,\beta }\) such that \(\bigl [ \texttt{e}_\alpha , \texttt{e}_\beta \bigr ] = N^{\alpha ,\beta } \, \texttt{e}_{\alpha +\beta }\). If \(\alpha +\beta \) is not a root, we set \(N^{\alpha ,\beta }=0\).
Let us also fix an orthogonal basis \(\lbrace \texttt{h}_i \rbrace _{i=1,\ldots ,\dim {\mathfrak {h}}}\) of the Cartan subalgebra \({\mathfrak {h}}\) of \({\mathfrak {g}}^{\mathbb {C}}\). It will be convenient to normalise it so that
The family \(\lbrace \texttt{h}_i \rbrace _{i=1,\ldots ,\dim {\mathfrak {h}}} \sqcup \lbrace \texttt{e}_\alpha \rbrace _{\alpha \in \Delta }\) then forms a basis of \({\mathfrak {g}}^{\mathbb {C}}\), in which the Lie bracket reads
where \(i,j\in \lbrace 1,\ldots ,\dim {\mathfrak {h}} \rbrace \) and \(\alpha ,\beta \in \Delta \) with \(\alpha +\beta \ne 0\). In the last equation, a sum over the repeated index \(i \in \lbrace 1,\ldots ,\dim {\mathfrak {h}} \rbrace \) is implied and the numbers \(\rho _\alpha ^i\) are given in our normalisation by \(\rho _\alpha ^i=\frac{1}{2}\,\alpha (\texttt{h}_i)\). Finally, the split quadratic Casimir of \({\mathfrak {g}}^{\mathbb {C}}\) reads
Root Levels and Coxeter Number Let \(\lbrace \alpha _i \rbrace _{i=1}^{\dim {\mathfrak {h}}}\) be the simple roots of \({\mathfrak {g}}^{\mathbb {C}}\). They form a basis of \({\mathfrak {h}}^*\) such that any positive root \(\alpha \in \Delta _+\) can be written as
for some non-negative integers \(m_i\in {\mathbb {Z}}_{\ge 0}\). We then define the level of \(\alpha \) as
One similarly defines the level of a negative root, which is then a negative number.
There exists a unique positive root \(\theta \in \Delta _+\) with maximal level, which we call the highest root of \({\mathfrak {g}}^{\mathbb {C}}\). The so-called Coxeter number h of the algebra is then defined as
For any positive root \(\alpha \in \Delta _+\), we thus have \(0< \ell (\alpha ) < h\).
Let us finally define the Weyl coweight \(\texttt{h}_\delta \) of the Lie algebra \({\mathfrak {g}}^{\mathbb {C}}\). It is the unique element \(\texttt{h}_\delta \in {\mathfrak {h}}\) in the Cartan subalgebra such that
By construction, this object then satisfies \(\alpha (\texttt{h}_\delta ) = \ell (\alpha )\) for any root \(\alpha \in \Delta \). It is thus characterised by the property
Bilinear Form on \({\mathfrak {h}}^*\) The restriction of \(-\langle \cdot ,\cdot \rangle \) to \({\mathfrak {h}}\) defines a non-degenerate bilinear form. By duality, it then induces a non-degenerate bilinear form on \({\mathfrak {h}}^*\) as well, which we will denote by \((\cdot ,\cdot )\). Let us describe it more explicitly. For any linear forms \(\alpha ,\beta \in {\mathfrak {h}}^*\), we have
Recall that we have normalised the bilinear form \(\langle \cdot ,\cdot \rangle \) with respect to the Killing form as (see footnote 6)
where \(h^{\!\vee }\) is the dual Coxeter number of \({\mathfrak {g}}^{\mathbb {C}}\). This choice corresponds to asking that \((\theta ,\theta )=2\) for \(\theta \in \Delta _+\) the highest root of \({\mathfrak {g}}^{\mathbb {C}}\).
B Gauge Fixings and Dirac Brackets
The goal of this appendix is to compute Dirac brackets coming from appropriate gauge fixings of Kac–Moody currents. Before considering this, it will be useful to revisit the case of gauge fixings in mechanical systems with a finite number of degrees of freedom, to gain some intuition on how to treat the field theory case. This will be the subject of the first subsection. The Dirac brackets of Kac–Moody currents are then covered in the remaining parts of this appendix.
1.1 B.1 Gauge Fixings and Dirac Brackets in Mechanics
Constraints and Reduction Let us consider a finite-dimensional phase space P. The algebra of functions F[P] on P is then naturally equipped with a Poisson bracket \(\lbrace \cdot ,\cdot \rbrace \). We suppose here that P admits a Hamiltonian action of a simple Lie group G, generated by a moment map \({\mathcal {C}}: P \rightarrow {\mathfrak {g}}\) (where \({\mathfrak {g}}\) is the Lie algebra of G). This moment map can be seen as an element of \(F[P]\otimes {\mathfrak {g}}\) that generates the infinitesimal action of \({\mathfrak {g}}\) on F[P]. Namely, the action of \(\epsilon \in {\mathfrak {g}}\) on an observable \(f\in F[P]\) is given by
where \(\langle \cdot ,\cdot \rangle \) is our choice of invariant bilinear form on \({\mathfrak {g}}\). The condition that this infinitesimal action satisfies the commutation relations of \({\mathfrak {g}}\) translates to the fact that \({\mathcal {C}}\) can be made to satisfy the Kirillov–Kostant bracket
where we used tensorial notations and where \({{\textsf{C}}}_{2} \in {\mathfrak {g}}\otimes {\mathfrak {g}}\) is the split quadratic Casimir of \({\mathfrak {g}}\).
In this set-up, one can consider the Hamiltonian reduction with respect to the G-symmetry generated by \({\mathcal {C}}\). For that, we treat this moment map as a constraint and thus impose \({\mathcal {C}}\approx 0\) (here, we use the sign \(\approx \) to denote weak equalities). The Kirillov–Kostant bracket (B.2) ensures that \({\mathcal {C}}\approx 0\) is a first-class constraint, since \(\lbrace {\mathcal {C}}\begin{array}{c} \otimes \\ , \end{array}{\mathcal {C}}\rbrace \approx 0\). The action of G is then treated as a gauge symmetry and the reduced phase space \(P_{\text {red}}\) is obtained by considering the quotient of the constrained surface by this action. This reduced phase space is equipped with the Marsden–Weinstein symplectic structure.
Gauge Fixing and Dirac Bracket One concrete way to describe the reduced phase space is to consider a gauge-fixing condition. We treat the latter as an additional constraint \({\mathcal {F}}\equiv 0\) (as in the main text, the symbol \(\equiv \) then denotes equalities that hold under both the initial constraint \({\mathcal {C}}\equiv 0\) and the gauge-fixing condition \({\mathcal {F}}\equiv 0\)). For this additional constraint to be a good gauge-fixing condition, one needs it to be always attainable by a gauge transformation, i.e. each G-orbit should contain a representative satisfying this condition. Moreover, we will suppose here that this is a complete gauge-fixing condition, in the sense that there is a unique such representative in each orbit and thus that there are no residual gauge symmetries. Let us note that \({\mathcal {F}}\equiv 0\) should then in fact encode \(\dim {\mathfrak {g}}\) gauge-fixing conditions: for simplicity, we will suppose here that these can be organised in such a way that \({\mathcal {F}}\) is a \({\mathfrak {g}}\)-valued observable, i.e. an element of \(F[P]\otimes {\mathfrak {g}}\). It is clear that the reduced phase space \(P_{\text {red}}\) is isomorphic to the subset \(P_{\text {GF}}\) of points in P which satisfy \({\mathcal {C}}\equiv 0\) and \({\mathcal {F}}\equiv 0\).
In order to describe the reduced symplectic structure in terms of the gauged-fixed space \(P_{\text {GF}}\), it is useful to define the notion of a Dirac bracket. For that, let us introduce the decompositions \({\mathcal {C}}= {\mathcal {C}}^a \,{\textsf{t}}_a\) and \({\mathcal {F}}= {\mathcal {F}}^a\, {\textsf{t}}_a\) of the \({\mathfrak {g}}\)-valued observables \({\mathcal {C}}\) and \({\mathcal {F}}\) in a basis \(\lbrace {\textsf{t}}_a \rbrace \) of \({\mathfrak {g}}\). We then define the matrices of Poisson brackets
as well asFootnote 41
In particular, the components of N satisfy \(M^{ac}N_{cb}\equiv \delta ^a_{\;\,b}\) and \(N_{ac}M^{cb}\equiv \delta _a^{\;\,b}\). The fact that M is invertible is due to the property that \({\mathcal {F}}\equiv 0\) is a complete gauge fixing, which implies that the set of constraint \(({\mathcal {C}}^a,{\mathcal {F}}^a)\) is second-class. We note that \(M'\) and \(N'\) are skew-symmetric matrices, in the sense that \(M'^{ab}=-M'^{\,ba}\) and \(N'_{ab}=-N'_{ba}\).
Using these notations, the Dirac bracket of two observables \(f,g\in F[P]\) is defined as
It is clear that it is skew-symmetric and satisfies the Leibniz rule. Moreover one can show that it also obeys the Jacobi identity. The main additional property of this bracket is that the constraints \({\mathcal {C}}^a\) and \({\mathcal {F}}^a\) have a vanishing Dirac bracket with all observables in F[P]. Indeed, one easily checks from the above definition and the properties of N and \(N'\) that
This means that the Dirac bracket is compatible with the constraints \({\mathcal {C}}\equiv {\mathcal {F}}\equiv 0\). It thus descends to the gauge-fixed phase space \(P_{\text {GF}}\) and defines a Poisson bracket on the algebra \(F[P_{\text {GF}}]\), making \(P_{\text {GF}}\) isomorphic to the Marsden–Weinstein quotient \(P_{\text {red}}\) as a symplectic manifold.
Reformulation in Terms of Linear Operators To gain some useful intuition for the computation of Dirac brackets in affine Gaudin models in the next subsections, it will be useful to reformulate slightly the classical mechanics case described above. For that, let us introduce linear operators \({\widehat{N}}: {\mathfrak {g}}\rightarrow {\mathfrak {g}}\) and \({\widehat{N}}': {\mathfrak {g}}\rightarrow {\mathfrak {g}}\), defined by the following action on the basis \(\lbrace {\textsf{t}}_a \rbrace \):
where \(\eta ^{ab}\) denotes the inverse of the matrix \(\eta _{ab}=\langle {\textsf{t}}_a, {\textsf{t}}_b \rangle \). In other words, the linear operators \({\widehat{N}}\) and \({\widehat{N}}'\) are characterised by
We note that the skew-symmetry of the coefficients \(N'_{ab}\) implies \(^t{\widehat{N}}'=-{\widehat{N}}'\), where t denotes the transpose with respect to the bilinear form \(\langle \cdot ,\cdot \rangle \). In terms of these operators, the Dirac bracket (B.5) can be rephrased in a basis-independent way:
Recall that the coefficients \(N_{ab}\) and \(N'_{ab}\) defining the operators \({\widehat{N}}\) and \({\widehat{N}}'\) were originally introduced in Eq. (B.4) in terms of the quantities \(M^{ab}\) and \(M'^{\,ab}\) built from Poisson brackets of the constraints \({\mathcal {C}}^a\) and \({\mathcal {F}}^a\). There is also a basis-independent reformulation of this definition. For that, let us introduce the operators \({\widehat{M}}: {\mathfrak {g}}\rightarrow {\mathfrak {g}}\) and \({\widehat{M}}': {\mathfrak {g}}\rightarrow {\mathfrak {g}}\) defined through
Then, we can reformulate Eq. (B.4) as
Moreover, the definition (B.3) of the coefficients \(M^{ab}\) and \(M'^{\,ab}\) can berephrased in terms of the operators \({\widehat{M}}\) and \({\widehat{M}}'\) using the Poisson brackets of the constraints \({\mathcal {C}}\) and \({\mathcal {F}}\) in tensorial notations. Namely,
where we recall that \({\textsf{C}}_2\) is the split quadratic Casimir \({\textsf{C}}_2 = \eta ^{ab} \, {\textsf{t}}_a \otimes {\textsf{t}}_b\). We note that the skew-symmetry \(^t{\widehat{M}}'= -{\widehat{M}}'\) of the operator \({\widehat{M}}'\) encodes the skew-symmetry of the bracket \(\lbrace {\mathcal {F}}\begin{array}{c} \otimes \\ , \end{array}{\mathcal {F}}\rbrace \), using the identity \(\bigl ( {\widehat{O}} \otimes \text {Id}\bigr ) {\textsf{C}}_2 = \bigl ( \text {Id}\otimes ^t{\widehat{O}} \bigr ) {\textsf{C}}_2\) true for any linear operator \({\widehat{O}}: {\mathfrak {g}}\rightarrow {\mathfrak {g}}\).
To summarise, the formalism introduced in this paragraph allows one to reformulate every step in the definition of the Dirac bracket in a basis-independent way. Concretely, one starts by writing the Poisson bracket of the constraints \({\mathcal {C}}\) and \({\mathcal {F}}\) in the form (B.12), thereby defining the two operators \({\widehat{M}}\) and \({\widehat{M}}'\). We then introduce the operators \({\widehat{N}}\) and \({\widehat{N}}'\) through the equation (B.11). Finally, we define the Dirac bracket by the formula (B.9). A similar formulation will be useful to compute Dirac brackets in affine Gaudin models in the next subsections. Let us finally note for completeness that the Kirillov–Kostant bracket (B.2) can also be naturally written in an “operatorial” form, similar to the one of Equation (B.12):
Here, \(\text {ad}_{{\mathcal {C}}}: {\mathfrak {g}}\rightarrow {\mathfrak {g}}\) is the standard adjoint action of \({\mathcal {C}}\) on \({\mathfrak {g}}\).
1.2 B.2 Preliminaries: Kac–Moody Currents and Loop Algebra
Loop Algebra Let us now come back to the case of an affine Gaudin model. Such a theory is described by a Poisson algebra \({\mathcal {A}}\), generated by N Kac–Moody currents \({\mathcal {J}}_r(x)\) with levels \(\ell _r\), satisfying the Poisson bracket (3.2). Moreover, the model is subject to the first-class constraint \({\mathcal {C}}(x) = \sum _{r=1}^N {\mathcal {J}}_r(x) \approx 0\). The main difference with the mechanical set-up considered in the previous subsection is that here, \({\mathcal {C}}\) is a field on the circle \({\mathbb {S}}^1\) and the constraint \({\mathcal {C}}(x) \approx 0\) holds for all \(x\in {\mathbb {S}}^1\). To develop an approach similar to the one of the previous subsection in this field theory case, it will be useful to see this constraint in a “functional” sense, interpreting the field \({\mathcal {C}}\) as belonging to an infinite-dimensional Lie algebra composed of functions on \({\mathbb {S}}^1\), called the loop algebra \({\mathcal {L}}{\mathfrak {g}}\): one then formally imposes \({\mathcal {C}}\approx 0\), encoding the infinitely many constraints \({\mathcal {C}}(x)\approx 0\). We introduce the necessary formalism for that in this preliminary subsection.
Formally, we can think of the Kac–Moody current \({\mathcal {J}}_r\) as an element of the space \({\mathcal {A}}\otimes {\mathcal {L}}{\mathfrak {g}}\), i.e. as a dynamical observable valued in the loop algebra \({\mathcal {L}}{\mathfrak {g}}\). We define the latter as the space of functionsFootnote 42 on the circle \({\mathbb {S}}^1\) valued in \({\mathfrak {g}}^{\mathbb {C}}\). An element \(A\in {\mathcal {L}}{\mathfrak {g}}\) can be evaluated at points \(x\in {\mathbb {S}}^1\), yielding objects A(x) valued in the finite algebra \({\mathfrak {g}}^{\mathbb {C}}\). One defines a Lie algebra structure on \({\mathcal {L}}{\mathfrak {g}}\) by extending the Lie bracket of \({\mathfrak {g}}^{\mathbb {C}}\) pointwise in \({\mathbb {S}}^1\), i.e. such that \([A,B](x)=[A(x),B(x)]\). We will denote by \(\partial \) the formal derivation operator acting on \({\mathcal {L}}{\mathfrak {g}}\) (such that \((\partial A)(x) = \partial _x A(x)\) under evaluation of \(A\in {\mathcal {L}}{\mathfrak {g}}\) at the point \(x\in {\mathbb {S}}^1\)).
Bilinear Form on the Loop Algebra The Lie algebra \({\mathcal {L}}{\mathfrak {g}}\) possesses a non-degenerate invariant bilinear form  , defined in terms of the one \(\langle \cdot ,\cdot \rangle \) on the finite algebra \({\mathfrak {g}}^{\mathbb {C}}\) by
, defined in terms of the one \(\langle \cdot ,\cdot \rangle \) on the finite algebra \({\mathfrak {g}}^{\mathbb {C}}\) by

More algebraically, this bilinear form can be seen as pairing the Fourier coefficient of \(e^{inx}\) in A with the Fourier coefficient of \(e^{-inx}\) in B (up to a factor \(2\pi \)).
Let \({\widehat{O}}:{\mathcal {L}}{\mathfrak {g}}\rightarrow {\mathcal {L}}{\mathfrak {g}}\) be a linear operator on the loop algebra. We will denote by \(^{{\textsf{T}}}{\widehat{O}}\) its transpose with respect to the bilinear form  , which satisfies
, which satisfies  for all \(A,B\in {\mathcal {L}}{\mathfrak {g}}\). Here, we used a symbol different from the transpose t on the finite Lie algebra \({\mathfrak {g}}^{\mathbb {C}}\), to avoid confusion. Note, however, that if \({\widehat{O}}\) is a linear operator on \({\mathfrak {g}}^{\mathbb {C}}\) that we extend to \({\mathcal {L}}{\mathfrak {g}}\) pointwise in \({\mathbb {S}}^1\), then \(^{{\textsf{T}}}{\widehat{O}}=^t{\widehat{O}}\). Let us finally point out that the derivation operator \(\partial :{\mathcal {L}}{\mathfrak {g}}\rightarrow {\mathcal {L}}{\mathfrak {g}}\) is skew-symmetric with respect to the transpose \({\textsf{T}}\). Indeed, one easily checks that \(^{{\textsf{T}}}\partial =-\partial \) using the functional definition (B.14) of
for all \(A,B\in {\mathcal {L}}{\mathfrak {g}}\). Here, we used a symbol different from the transpose t on the finite Lie algebra \({\mathfrak {g}}^{\mathbb {C}}\), to avoid confusion. Note, however, that if \({\widehat{O}}\) is a linear operator on \({\mathfrak {g}}^{\mathbb {C}}\) that we extend to \({\mathcal {L}}{\mathfrak {g}}\) pointwise in \({\mathbb {S}}^1\), then \(^{{\textsf{T}}}{\widehat{O}}=^t{\widehat{O}}\). Let us finally point out that the derivation operator \(\partial :{\mathcal {L}}{\mathfrak {g}}\rightarrow {\mathcal {L}}{\mathfrak {g}}\) is skew-symmetric with respect to the transpose \({\textsf{T}}\). Indeed, one easily checks that \(^{{\textsf{T}}}\partial =-\partial \) using the functional definition (B.14) of  and an integration by part.
and an integration by part.
Casimir of the Loop Algebra One can canonically construct a split quadratic Casimir \({\mathcal {L}}{\textsf{C}}_2\) associated with the non-degenerate bilinear form  . It is an element of (a completion of) \({\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\) which satisfies
. It is an element of (a completion of) \({\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\) which satisfies

where the index \({\underline{2}}\) means that we are applying  on the second tensor factor in \({\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\). Functionally, this loop Casimir can be seen as the distribution
on the second tensor factor in \({\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\). Functionally, this loop Casimir can be seen as the distribution
Here, (x, y) means that we are evaluating the first and second tensor factors in \({\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\) at the points \(x\in {\mathbb {S}}^1\) and \(y\in {\mathbb {S}}^1\), respectively, \({\textsf{C}}_2 \in {\mathfrak {g}}\otimes {\mathfrak {g}}\) is the split Casimir of the finite algebra \({\mathfrak {g}}\) and \(\delta (x-y)\) is the Dirac \(\delta \)-distribution on \({\mathbb {S}}^1\). This identity can be verified by a direct computation, using the functional expression (B.14) of the bilinear form  . Indeed, for any \(A\in {\mathcal {L}}{\mathfrak {g}}\), we have
. Indeed, for any \(A\in {\mathcal {L}}{\mathfrak {g}}\), we have

thus checking the characterisation (B.15) of \({\mathcal {L}}{\textsf{C}}_2\) (here, we have used the property \(\langle {\textsf{C}}_2, {\textsf{a}} \rangle {_{\underline{2}}} = {\textsf{a}}\) of the finite Casimir \({\textsf{C}}_2\), true for all \({\textsf{a}}\in {\mathfrak {g}}^{\mathbb {C}}\)).
Let us finally note that for any linear operator \({\widehat{O}}:{\mathcal {L}}{\mathfrak {g}}\rightarrow {\mathcal {L}}{\mathfrak {g}}\) on the loop algebra, the loop Casimir satisfies the following identity:
Kac–Moody Brackets As we will now see, the rather abstract formalism we have just introduced will be useful to describe the algebra of the Kac–Moody currents \({\mathcal {J}}_r\) in a compact way. For that, we introduce the following linear operator on \({\mathcal {L}}{\mathfrak {g}}\):
where \(\text {ad}_{{\mathcal {J}}_r} = [ {\mathcal {J}}_r,\cdot ]\) denotes the adjoint action of \({\mathcal {J}}_r\) on \({\mathcal {L}}{\mathfrak {g}}\). One then checks that the Kac–Moody bracket (3.2) can be rephrased as the following tensorial bracket in \({\mathcal {A}}\otimes {\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\)Footnote 43:
The last equality in this equation encodes the skew-symmetry of the Kac–Moody bracket and follows from \(^{{\textsf{T}}}\nabla _r = -\nabla _r\) and the identity (B.18).
1.3 B.3. Gauge Fixing and Dirac Brackets in Affine Gaudin Models
Constraint and Gauge Fixing in the Loop Algebra The constraint in an affine Gaudin model is given by \({\mathcal {C}}\approx 0\), where we see \({\mathcal {C}}= \sum _r {\mathcal {J}}_r\) as an element of \({\mathcal {A}}\otimes {\mathcal {L}}{\mathfrak {g}}\), i.e. an observable valued in the loop algebra \({\mathcal {L}}{\mathfrak {g}}\). Recall that the levels \(\ell _r\) of the currents \({\mathcal {J}}_r\) are taken to satisfy the condition \(\sum _r \ell _r = 0\) – see Eq. (3.5). In the notations introduced in the previous subsection, we then get from the Kac–Moody algebra (B.20) that \({\mathcal {C}}\) satisfies the bracket
This is the equivalent of Eq. (B.13) in the mechanical case, but where the constraint \({\mathcal {C}}\) is now valued in the infinite-dimensional loop algebra \({\mathcal {L}}{\mathfrak {g}}\). We note that in analogy with equation (B.1) in the mechanical case, the infinitesimal gauge symmetry generated by the constraint \({\mathcal {C}}\) acts on an observable \(f\in {\mathcal {A}}\) by

where \(\epsilon \in {\mathcal {L}}{\mathfrak {g}}\) is the infinitesimal local parameter of the transformation.
Let us now consider a gauge-fixing condition for this model. In analogy with the mechanical case, we will suppose here that this condition can be phrased as \({\mathcal {F}}\equiv 0\), for some observable \({\mathcal {F}}\in {\mathcal {A}}\otimes {\mathcal {L}}{\mathfrak {g}}\), built from the Kac–Moody currents \({\mathcal {J}}_r\) and also valued in the loop algebra. We then work in the gauge-fixed algebra \({\mathcal {A}}_{\text {GF}}\), in which we impose \({\mathcal {C}}\equiv {\mathcal {F}}\equiv 0\).
Dirac Bracket To describe the Poisson structure of \({\mathcal {A}}_{\text {GF}}\), one needs to define the Dirac bracket. We will do this using a formalism very close to the one developed in terms of linear operators around Eq. (B.9) for the mechanical case. We first introduce two linear operators \({\widehat{M}}: {\mathcal {L}}{\mathfrak {g}}\rightarrow {\mathcal {L}}{\mathfrak {g}}\) and \({\widehat{M}}': {\mathcal {L}}{\mathfrak {g}}\rightarrow {\mathcal {L}}{\mathfrak {g}}\), defined through the following brackets of the constraint and the gauge-fixing condition, in analogy with Eq. (B.12):
One can argue that such operators always exist. We then let
similarly to Eq. (B.11) in the mechanical case. Finally, we define the Dirac bracket as the following “loop” generalisation of Eq. (B.9):

where f and g are observables in \({\mathcal {A}}\). One checks from this definition that this bracket is such that \(\lbrace {\mathcal {C}}, f \rbrace _D \equiv \lbrace {\mathcal {F}}, f \rbrace _D \equiv 0\) for all \(f\in {\mathcal {A}}\), as expected from a Dirac bracket. This ensures that \(\lbrace \cdot ,\cdot \rbrace _D\) is compatible with the constraints \({\mathcal {C}}\equiv {\mathcal {F}}\equiv 0\) and thus descends to the algebra \({\mathcal {A}}_{\text {GF}}\).
Linear Gauge Fixing In all the examples studied in this article, we consider a gauge-fixing condition which is linear in the Kac–Moody currents \({\mathcal {J}}_r\). More precisely, this condition takes the form \({\mathcal {F}}\equiv 0\), with
for some non-dynamical linear operators \({\widehat{O}}_r: {\mathfrak {g}}^{\mathbb {C}}\rightarrow {\mathfrak {g}}^{\mathbb {C}}\) on the finite Lie algebra (in the examples we consider, these operators \({\widehat{O}}_r\) will typically be expressed in terms of the Yang–Baxter operator \({{\hat{R}}}\)). Starting from the Kac–Moody bracket (B.20), we find
Similarly,
where we used the identity (B.18). Comparing to Eq. (B.23), we find
In principle, we then have all the necessary information to determine the operators \({\widehat{N}}\) and \({\widehat{N}}'\) in Eq. (B.24) and thus write down the Dirac bracket (B.25).
Dirac Bracket of Kac–Moody Currents Let us consider two Kac–Moody currents \({\mathcal {J}}_r\) and \({\mathcal {J}}_s\). We would like to compute their Dirac bracket \(\lbrace {\mathcal {J}}_r \begin{array}{c} \otimes \\ , \end{array}{\mathcal {J}}_s \rbrace _D\) under the linear gauge fixing introduced above. Since these currents are \({\mathcal {L}}{\mathfrak {g}}\)-valued observables themselves, the intermediate computations in the Dirac bracket will involve objects in a 3-fold tensor product \({\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\). To simplify the presentation, we will denote, for any \(A\in {\mathcal {L}}{\mathfrak {g}}\),
We will use similar notations to express on which tensor factor in \({\mathcal {L}}{\mathfrak {g}}^{\otimes 3}\) linear operators act. Also, we will denote the three possible embeddings of \({\mathcal {L}}{\textsf{C}}_2\in {\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\) in \({\mathcal {L}}{\mathfrak {g}}^{\otimes 3}\) as \({\mathcal {L}}{\textsf{C}}_{\underline{12}}\), \({\mathcal {L}}{\textsf{C}}_{\underline{13}}\) and \({\mathcal {L}}{\textsf{C}}_{\underline{23}}\), dropping the index 2 to lighten the notations. Finally, we indicate by indices \({\underline{i}}\) along which tensor factors bilinear forms  are applied. With these conventions, Eq. (B.25) implies
are applied. With these conventions, Eq. (B.25) implies

We then use
where we used the identity (B.18). By repeated use of this identity again, we can move all operators in the above Dirac bracket to the first and second tensor spaces, yielding

where we also used \(^{{\textsf{T}}}{\widehat{N}}'=-{\widehat{N}}'\). Using the property (B.15) of the loop Casimir, we then get
We can now drop the notation with tensor indices \({\underline{i}}\) and treat this bracket as we dealt with \({\mathcal {L}}{\mathfrak {g}}\otimes {\mathcal {L}}{\mathfrak {g}}\)-valued bracket before. We then rewrite the above equation as
where
The computation of the Dirac bracket then mostly amounts to determining this quantity \({\textsf{T}}_2^{(rs)}\). Recall that \({\widehat{N}}= {\widehat{M}}^{-1}\) and \({\widehat{N}}'={\widehat{M}}^{-1}\circ {\widehat{M}}'\circ ^{{\textsf{T}}}{\widehat{M}}^{-1}\). Acting with \({\widehat{M}}\otimes {\widehat{M}}\) on the above definition, we see that \({\textsf{T}}_2^{(rs)}\) is characterised by the following equation:
1.4 B.4 Parafermionic Gauge Fixing
Parafermionic Gauge-Fixing Condition Let us now apply the formalism developed above to the explicit examples of gauge fixings treated in the main text, for which we consider an affine Gaudin model with \(N=3\) Kac–Moody currents. We start with the parafermionic gauge-fixing condition (6.11), which we recall here for the reader’s convenienceFootnote 44:
where \({{\hat{R}}}\) is the standard R-matrix (2.1). This takes the form of a linear gauge fixing (B.26) as considered in the previous subsection, with the operators \({\widehat{O}}_r\) chosen here to be
where
Let us introduce \({\mathcal {J}}=({\mathcal {J}}_1-{\mathcal {J}}_2)/2\textrm{i}\). The gauge-fixing condition (B.38) and the constraint \({\mathcal {J}}_1+{\mathcal {J}}_2+{\mathcal {J}}_3\equiv 0\) then imply that
In particular, \({\mathcal {J}}_1\) and \({\mathcal {J}}_2\) are valued, respectively, in the Borel subalgebras \({\mathfrak {h}}\oplus {\mathfrak {n}}_-\) and \({\mathfrak {h}}\oplus {\mathfrak {n}}_+\), while \({\mathcal {J}}_3\) is valued in \({\mathfrak {n}}_+\oplus {\mathfrak {n}}_-\).
It will also be useful for us to define the projector \({\hat{\Pi }}\) on the Cartan subalgebra \({\mathfrak {h}}\) in the decomposition \({\mathfrak {g}}^{\mathbb {C}}= {\mathfrak {h}} \oplus {\mathfrak {n}}_+ \oplus {\mathfrak {n}}_-\). One easily checks that this operator can be expressed in terms of the R-matrix as
Moreover, it satisfies \({\hat{\Pi }}^2={\hat{\Pi }}\) and \(^t{\hat{\Pi }}={\hat{\Pi }}\). In particular, this operator can be used to project the split quadratic Casimir \({\textsf{C}}_2 \in {\mathfrak {g}}\otimes {\mathfrak {g}}\) of the finite algebra on \({\mathfrak {h}}\otimes {\mathfrak {h}}\), defining
Operators \({{\widehat{M}}}\) and \({{\widehat{M}}'}\) For the choice of \({\widehat{O}}_r\) in Eq. (B.39), corresponding to the parafermionic gauge fixing, the operators \({\widehat{M}}\) and \({\widehat{M}}'\) (given in general by Eq. (B.29)) take the form
where we have used \(^{{\textsf{T}}}{{\hat{R}}}^\pm = -{{\hat{R}}}^{\mp }\). Recall that \(\nabla _r = \ell _r \partial + \text {ad}_{{\mathcal {J}}_r}\). We then rewrite \({\widehat{M}}'\) as
where we used the gauge-fixed expression (B.41) of \({\mathcal {J}}_1\) and \({\mathcal {J}}_2\). Using the action (2.1) of \({{\hat{R}}}\) on the decomposition \({\mathfrak {g}}^{{\mathbb {C}}} = {\mathfrak {h}} \oplus {\mathfrak {n}}_+ \oplus {\mathfrak {n}}_-\) and the commutation relations \([{\mathfrak {h}},{\mathfrak {h}}]=0\) and \([{\mathfrak {h}}, {\mathfrak {n}}_\pm ] \subset {\mathfrak {n}}_\pm \), one finds that \({{\hat{R}}}^- \circ \text {ad}_{{{\hat{R}}}^+{\mathcal {J}}} \circ {{\hat{R}}}^+ = {{\hat{R}}}^+ \circ \text {ad}_{{{\hat{R}}}^-{\mathcal {J}}} \circ {{\hat{R}}}^- = 0\). Moreover, one has \({{\hat{R}}}^+\circ {{\hat{R}}}^- = {\hat{\Pi }}\). We then simply get
Similarly, we have
Reasoning as above, we find that the operators \({{\hat{R}}}^\pm \circ \text {ad}_{{{\hat{R}}}^{\mp }{\mathcal {J}}}\) act trivially on the Cartan subalgebra \({\mathfrak {h}}\). Moreover, \({{\hat{R}}}^\pm \) acts as \(\pm \textrm{i}\,\text {Id}\) on \({\mathfrak {h}}\). We thus have
where \({\mathcal {L}}{\mathfrak {h}}\) is formed by the elements in the loop algebra \({\mathcal {L}}{\mathfrak {g}}\) valued in the Cartan subalgebra \({\mathfrak {h}}\). These identities will be useful to compute the Dirac brackets below.
Dirac Bracket of \({{\mathcal {J}}_3}\) Let us now compute the Dirac bracket of \({\mathcal {J}}_3\) with itself under this gauge fixing. From the general result (B.35) found in the previous subsection, we have
where the tensor \({\textsf{T}}_2^{(33)}\) is characterised by Eq. (B.37). In the case at hand, since \({\widehat{O}}_3=0\) and \({\widehat{M}}'\) is given by (B.46), the latter simply takes the form
We now want to solve this equation for \({\textsf{T}}_2^{(33)}\). From the functional expression (B.16) of \({\mathcal {L}}{\textsf{C}}_2\), we find that the evaluation of the right-hand side at \((x,y)\in S^1\times S^1\) is \((\ell _1+\ell _2)\,{\textsf{H}}_{2}\,\partial _x\delta (x-y)\), with the tensor \({\textsf{H}}_{2}\) defined as in Eq. (B.43). It is then natural to take an ansatz for \({\textsf{T}}_2^{(33)}\) which is itself proportional to \({\textsf{H}}_{2}\). More precisely, we will take the following ansatz:
where f(x, y) is a distribution to be determined. Recall from Eq. (B.48) that \({\widehat{M}}\) acts very simply on Cartan-valued functions. The above equation on \({\textsf{T}}_2^{(33)}\) then becomes
To solve for f, we introduce the \(\epsilon \)-distribution, which satisfies
It is then clear that
where the last equality follows from the explicit expression (6.4) of the levels \(\ell _r\) in the affine Gaudin model considered here. To summarise, we then get that the Dirac bracket of \({\mathcal {J}}_3\) simply reads
where by \(\epsilon \) we mean the formal distribution whose evaluation at (x, y) is \(\epsilon (x-y)\).
Analysis of the Dirac Bracket of \({{\mathcal {J}}_3}\) Let us now analyse the Dirac bracket (B.55). Evaluating it at (x, y) and reinserting \(\nabla _3 = \ell _3\,\partial + \text {ad}_{{\mathcal {J}}_3} = - K_{\scriptscriptstyle {\textrm{UV}}}\partial + \text {ad}_{{\mathcal {J}}_3}\), we get
Writing down the initial Kac–Moody bracket of \({\mathcal {J}}_3\) in the first term and developing the various derivatives in the second one, using the identity (B.53) obeyed by the \(\epsilon \)-distribution, we get
Recall that the gauge-fixing condition (B.38) implies that \({\mathcal {J}}_3=-2{{\hat{R}}}{\mathcal {J}}\)—see Eq. (B.41)—and thus that \({\mathcal {J}}_3\) is valued in \({\mathfrak {n}}_+\oplus {\mathfrak {n}}_-\). One checks that the form of the above bracket ensures that the right-hand side is valued in \(({\mathfrak {n}}_+\oplus {\mathfrak {n}}_-)\otimes ({\mathfrak {n}}_+\oplus {\mathfrak {n}}_-)\). For instance, the shift by \(-{\textsf{H}}_{2}\) in the term proportional to \(\partial _x\delta (x-y)\) removes the part valued in the Cartan subalgebra. One shows a similar statement for the remaining terms using \([{\mathfrak {h}},{\mathfrak {h}}]=0\) and \([{\mathfrak {h}}, {\mathfrak {n}}_\pm ] \subset {\mathfrak {n}}_\pm \). This shows the consistency of the gauge-fixing procedure and the computation of the Dirac bracket and is an alternative check of the vanishing of the Dirac bracket on constraints.
As explained in Eq. (6.12), we parametrise \({\mathcal {J}}_3\) as \(-\sum _{\alpha \in \Delta } \Psi _\alpha \,\mathtt e_{-\alpha }\), where \(\mathtt e_\alpha \) are root vectors of the algebra \({\mathfrak {g}}^{\mathbb {C}}\) (see “Appendix A” for conventions). Recall also that we introduced an orthogonal basis \(\lbrace \mathtt h_i\rbrace \) of the Cartan subalgebra \({\mathfrak {h}}\), with normalisation \(\langle \texttt{h}_i, \texttt{h}_j \rangle = -2\,\delta _{ij}\). We then have
One can then extract the Poisson brackets of the components \(\Psi _\alpha \) from the Dirac bracket (B.57), using the commutation relations (A.4) of the basis \(\lbrace \mathtt e_\alpha , \mathtt h_i \rbrace \) and the relation (A.11). We then get
Dirac Bracket of Cartan Fields Recall that \({\mathcal {J}}_3\) has no Cartan component and is expressed only in terms of the fields \(\Psi _\alpha \) associated with root vectors \(\mathtt e_\alpha \). On the other hand, the gauge-fixed current \({\mathcal {J}}_1\) and \({\mathcal {J}}_2\) are in the Borel subalgebras \({\mathfrak {h}}\oplus {\mathfrak {n}}_{\mp }\) and in particular contain fields \(D_i\) associated with the Cartan basis \(\lbrace \mathtt h_i \rbrace \)—see Eq. (6.12). Let us then introduce
We now want to compute the Dirac brackets of \({\mathcal {D}}\) with itself and the current \({\mathcal {J}}_3\). This can be done in a similar, although slightly more complicated, way than the Dirac brackets computed above. For conciseness, we will not enter into the details of these computations here. Let us mention, however, a few useful identities, which serve as important steps in the determination of these Dirac brackets. First of all, combining equations (B.46) and (B.48), we find
Together with the definition (B.24) of \({\widehat{N}}\) and \({\widehat{N}}'\), this implies
Moreover, using the fact that the gauge-fixed current \({\mathcal {J}}_1\) is valued in \({\mathfrak {h}}\oplus {\mathfrak {n}}_-\) with the commutation relations \([{\mathfrak {h}},{\mathfrak {h}}]=0\) and \([{\mathfrak {h}}, {\mathfrak {n}}_\pm ] \subset {\mathfrak {n}}_\pm \), one finds
Finally, the following Poisson brackets are useful:
Combining these results, one computes the Dirac brackets involving \({\mathcal {D}}\). In particular, we find
where the coefficient in the second equation originates from
Using the decomposition (B.60) of \({\mathcal {D}}\) in the basis \(\lbrace \mathtt h_i\rbrace \) and \({\textsf{H}}_{2}= - \frac{1}{2} \sum _i\mathtt h_i\otimes \mathtt h_i\), we finally get
1.5 B.5 \(\omega \)-Gauge Fixing
Gauge-Fixing Condition Let us now consider the \(\omega \)-gauge-fixing condition (6.18). Dropping the \({(\mathrm L)}\) labels as in the previous subsection, we will write it in this appendix as
where we recall that \({{\hat{R}}}^\pm = {{\hat{R}}} \pm \textrm{i}\) and we introduced
Here, \(\omega \) is a constant parameter and \({\hat{\Pi }}\) is the projection on the Cartan subalgebra \({\mathfrak {h}}\), as above. This gauge-fixing condition implies that the currents \({\mathcal {J}}_2\) and \({\mathcal {J}}_3\) are valued in the Borel subalgebras \({\mathfrak {h}}\oplus {\mathfrak {n}}_-\) and \({\mathfrak {h}}\oplus {\mathfrak {n}}_+\), respectively. In contrast, the current \({\mathcal {J}}_1\) has non-trivial components in all the factors of the decomposition \({\mathfrak {g}}^{{\mathbb {C}}} = {\mathfrak {h}}\oplus {\mathfrak {n}}_+\oplus {\mathfrak {n}}_-\), except when \(\omega =1+2\nu ^{-2}\) in which case \({\mathcal {J}}_1\) has no Cartan component. Outside of this case, all the degrees of freedom in the gauge-fixed currents \({\mathcal {J}}_r\) are then contained in \({\mathcal {J}}_1\) and we can compute the corresponding gauge-fixed Poisson structure by computing the Dirac bracket of \({\mathcal {J}}_1\) with itself.
The condition (B.68) takes the form of a linear gauge fixing (B.26), as considered in the previous subsections, with the operators \({\widehat{O}}_r\) given by
From these data and Eq. (B.29), we can compute the operators \({\widehat{M}}\) and \({\widehat{M}}'\). By a reasoning similar to the one detailed in the previous subsection for the parafermionic gauge (see Eq. (B.44) and the discussion below), one finds
and
Dirac bracket of \({{\mathcal {J}}_1}\) Let us then compute the Dirac bracket of \({\mathcal {J}}_1\) in the \(\omega \)-gauge. Applying the general result (B.35), this bracket is given by
where the tensor \({\textsf{T}}_2^{(11)}\) is characterised by Eq. (B.37). In the present case, since \({\widehat{O}}_1=0\) and \({\widehat{M}}'\) is given by (B.71), this equation simply takes the form
The resolution of this equation is very similar to the one of Eq. (B.50) in the parafermionic gauge, using an ansatz for \({\textsf{T}}_2^{(11)}\) proportional to \({\textsf{H}}_{2}\) together with equation (B.72). In the end, we find
where \(\epsilon (x,y)=\epsilon (x-y)\) and
The second equality in the above equation comes from the definition (B.69) of \(\mu \) and expression (6.4) of the levels \(\ell _r\) for the affine Gaudin model under consideration here.
Analysis of the Dirac Bracket of \({{\mathcal {J}}_1}\) Reinserting the expression found above for \({\textsf{T}}_2^{(11)}\) in Eq. (B.73), one writes down the Dirac bracket of \({\mathcal {J}}_1\) with itself in the \(\omega \)-gauge. More precisely, we get
Let us recall that in the main text, we decompose \({\mathcal {J}}_1\) in the basis \(\lbrace \mathtt h_i, \mathtt e_\alpha \rbrace \) as in Eq. (6.19), which we recall here for the reader’s convenience:
Reinserting in the above Dirac bracket and using the commutation relations (A.4) and the expression of \({\textsf{C}}_2\) and \({\textsf{H}}_{2}\) in the basis \(\lbrace \mathtt h_i, \mathtt e_\alpha \rbrace \), one extracts the Poisson bracket of the components \(\Xi _i\) and \(\Xi _\alpha \). More precisely, we find
C Quantum \({\varvec{\hat{\mathfrak {sl}}(2)\oplus \hat{\mathfrak {sl}}(2)/\hat{\mathfrak {sl}}(2)}}\) coset \(\varvec{{\mathcal {W}}}\)-Algebra
Our goal in this appendix is to describe the first fields in the quantum \(\widehat{\mathfrak {sl}}(2)\oplus \widehat{\mathfrak {sl}}(2)/\widehat{\mathfrak {sl}}(2)\) coset \({\mathcal {W}}\)-algebra in terms of the \(\mathfrak {sl}(2)\)-Kac–Moody currents \({\textsf{J}}_1\) and \({\textsf{J}}_2\).
Segal–Sugawara Fields and Energy–Momentum Tensor Let us define

for \(r\in \lbrace 1,2 \rbrace \). We recognise in this expression the Segal–Sugawara fields associated with the Kac–Moody currents \({\textsf{J}}_r\) and \({\textsf{J}}_{\text {diag}}\) (note that the dual Coxeter number of \(\mathfrak {sl}(2)\) is given by \(h^{\!\vee }=2\)). In particular, in terms of these fields, the energy–momentum tensor \({\textsf{W}}_2\) of the \(\widehat{\mathfrak {sl}}(2)\oplus \widehat{\mathfrak {sl}}(2)/\widehat{\mathfrak {sl}}(2)\) coset \({\mathcal {W}}\)-algebra, defined in Eq. (9.23), can simply be rewritten as
As explained in the main text, this field \({\textsf{W}}_2\) is the quantisation of the classical spin 2 current defined in Eq. (6.30).
Quantum Spin 4 Current We now want to describe the quantisation of the classical spin 4 current (6.36). It will be useful for that to first rewrite this classical current in a more concrete form. Let us then introduce the classical commutator field \({\mathcal {U}} = \bigl [ {\mathcal {J}}_1, {\mathcal {J}}_2 ] = f^{bc}_{\,\,a} \,{\mathcal {J}}_{1,b}\,{\mathcal {J}}_{2,c}\,\texttt{t}^a\), where \(f^{bc}_{\,\,a}\) are the structure constants of the dual basis \(\lbrace \texttt{t}^a \rbrace \) of the Lie algebra. In terms of this field, the covariant derivative of the current \({\mathcal {K}}\) considered in Sect. 6.3 reads
In particular, the classical spin 4 W-current defined in Eq. (6.36) can then be expressed as
We define the quantum equivalent of \({\mathcal {U}}_a\) as

We then search for the quantum spin 4 W-current in the following form

where the \(\lambda ^{(n)}_{\bullet }\)’s are constant coefficients to be determined (and whose notation will be explained in a future discussion of the classical limit—see below). The first term in this equation is a natural quantisation of the classical expression (C.4), taking into account the non-commutativity of the quantum fields. It is, however, not enough to capture the full quantum spin 4 field, which necessitates the introduction of a quantum correction \({\textsf{W}}^{{(\mathrm corr)}}_4\). Here, we will take the following ansatz for this correction, in terms of the Segal–Sugawara fields \({\textsf{G}}_r\) and \({\textsf{G}}_{\text {diag}}\):

with some coefficients \(\rho ^{(n)}_{\bullet }\) to be determined. Note that we did not include the fields  and \(\partial ^2{\textsf{G}}_{\text {diag}}\) in this ansatz, since these terms can always be eliminated by well-chosen shifts by
and \(\partial ^2{\textsf{G}}_{\text {diag}}\) in this ansatz, since these terms can always be eliminated by well-chosen shifts by  and \(\partial ^2{\textsf{W}}_2\), which are the obvious spin 4 currents in the \({\mathcal {W}}\)-algebra.
and \(\partial ^2{\textsf{W}}_2\), which are the obvious spin 4 currents in the \({\mathcal {W}}\)-algebra.
To proceed, we impose that the above ansatz for \({\textsf{W}}_4\) belongs to the quantum \({\mathcal {W}}\)-algebra, i.e. is such that the OPE \({\textsf{J}}_{\text {diag},a}(x){\textsf{W}}_4(y)\) is regular. This translates into a system of linear equations on the coefficients \(\lambda ^{(n)}_\bullet \) and \(\rho ^{(n)}_\bullet \), which we can then solveFootnote 45 up to an overall multiplicative factor that we fix here for convenience. Explicitly, we find
while the coefficients \(\rho ^{(n)}_{\bullet }\) read
Classical Limit of \({{\textsf{W}}_4}\) Now that we have constructed the quantum spin 4 field \({\textsf{W}}_4\), let us quickly discuss its classical limit. Recall that when \(\hbar \rightarrow 0\), the quantum Kac–Moody currents \({\textsf{J}}_r\) and levels \(k_r\) are of order \(O(\hbar ^{-1})\) and more precisely obey the asymptotic (9.7). Reinserting this in equations (C.6) and (C.7), we find that the terms in \({\textsf{W}}_4\) multiplying the coefficients \(\lambda ^{(n)}_{\bullet }\) and \(\rho ^{(n)}_\bullet \) are of order \(O(\hbar ^{-n})\) (for instance, the field  , with coefficient \(\lambda ^{(2)}_1\) in Eq. (C.6), is of order \(O(\hbar ^{-2})\)). The asymptotic behaviour of the coefficients \(\lambda ^{(n)}_{\bullet }\) and \(\rho ^{(n)}_\bullet \) themselves can be computed in a similar way from their expressions (C.9) in terms of \(k_r\) (for instance, \(\lambda ^{(2)}_1=k_2(3k_2-5)\) is of order \(O(\hbar ^{-2})\)). Combining all this, we find that the dominant term in \({\textsf{W}}_4\) is of order \(O(\hbar ^{-4})\). More precisely, we get
, with coefficient \(\lambda ^{(2)}_1\) in Eq. (C.6), is of order \(O(\hbar ^{-2})\)). The asymptotic behaviour of the coefficients \(\lambda ^{(n)}_{\bullet }\) and \(\rho ^{(n)}_\bullet \) themselves can be computed in a similar way from their expressions (C.9) in terms of \(k_r\) (for instance, \(\lambda ^{(2)}_1=k_2(3k_2-5)\) is of order \(O(\hbar ^{-2})\)). Combining all this, we find that the dominant term in \({\textsf{W}}_4\) is of order \(O(\hbar ^{-4})\). More precisely, we get
with \(W_4\) the classical spin 4 field (C.4), ensuring that the latter is indeed recovered in the classical limit of \({\textsf{W}}_4\). In particular, during this computation, one finds that the term \({\textsf{W}}^{{(\mathrm corr)}}_4\), defined in Eq. (C.7), is of order \(O(\hbar ^{-3})\) and is thus subdominant in the classical limit: this confirms the interpretation of this term as a quantum correction.
Primary Spin 4 Field Using the explicit expression of the quantum spin 4 field \({\textsf{W}}_4\), we can determine its OPE with the energy–momentum tensor \({\textsf{W}}_2\). A direct computation gives
where c is the central charge (9.25) and the coefficients \(\alpha _1\) and \(\alpha _2\) are defined in terms of \(k_1\) and \(k_2\) as
In particular, this means that the W-current \({\textsf{W}}_4\) is not primary. To construct such a primary field, we consider a linear combination

This field is automatically in the \({\mathcal {W}}\)-algebra, since both \({\textsf{W}}_4\) and \({\textsf{W}}_2\) belong to it. We then ask that it is a primary field by imposing the OPE
This translates into a system of linear equations on \(\alpha _3\) and \(\alpha _4\), whose solution reads
D Quantum Local IMs in Affine Gaudin Models
1.1 Quartic Density for \(\varvec{\mathfrak {sl}(2)}\)
In this appendix, we describe the spin 4 density \({\textsf{S}}_4(z,x)\) from which we construct the quantum quartic charges in AGMs based on the Lie algebra \({\mathfrak {g}}^{\mathbb {C}}=\mathfrak {sl}(2)\). The classical version of this density is given by
where \(\tau _3^{abcd}\) is a symmetric tensor of degree 4 on \(\mathfrak {sl}(2)\). This tensor is unique up to an overall multiplicative constant and can be written in terms of the degree 2 tensor \(\eta ^{ab}\):
In particular, this implies that the classical spin 4 density (D.1) is simply proportional to \(\langle \Gamma (z,x),\Gamma (z,x) \rangle ^2\), i.e. to the square of the quadratic one.
To search for the quantum spin 4 density \({\textsf{S}}_4(z,x)\), we start with a general ansatz in terms of the quantum Gaudin Lax matrix \(\Gamma ^{(\textrm{qt})}(z,x)\) and the twist function \(\varphi ^{(\textrm{qt})}(z)\), formed by the normal ordered quantum version of Eq. (D.1) plus corrective terms of the form (9.41). To constrain the coefficients of these terms, we then impose that the density \({\textsf{S}}_4(z,x)\) satisfies the conditions (i) and (ii) stated after Eq. (9.46). As it turns out, the condition (i) is sufficient to fix \({\textsf{S}}_4(z,x)\), up to twisted derivatives with respect to z and a total spatial derivative proportional to \(\partial ^2_x{\textsf{S}}_2(z,x)\), which do not contribute to the local charges \({\textsf{Q}}_{\gamma ,3}\) built from \({\textsf{S}}_4(z,x)\).Footnote 46 One can use this freedom to simplify the final expression of \({\textsf{S}}_4\), which we now present. To declutter this formula, we omit the labels \((\textrm{qt})\) on the quantum Gaudin Lax matrix \(\Gamma ^{(\textrm{qt})}(z,x)\) and the quantum twist function \(\varphi ^{(\textrm{qt})}(z)\). We then get

1.2 D.2 Quadratic Charge for 3 Punctures
In this appendix, following [34], we perform explicitly the integral (9.53) over the Pocchammer contour \(\gamma \), giving the density \({\textsf{W}}_{\gamma ,2}(x)\) of the quadratic charge in the case of an AGM with 3 punctures at 0, 1 and \(\infty \). Using expression (9.48) of \({\textsf{S}}_2(z,x)\), we rewrite this integral as

Reinserting Eqs. (9.51) and (9.52), i.e. \(\Gamma ^{(\textrm{qt})}(z) = \dfrac{{\textsf{J}}_1}{z} + \dfrac{{\textsf{J}}_2}{z-1}\) and \({\mathcal {P}}(z) = z^{k_1} (z-1)^{k_2}\), and developing the products, we get

where we defined
This integral can be expressed in terms of the Euler Beta function. Here, we will not need this explicit expression. Instead, we will use some recursive identities obeyed by B(a, b), which follow either from the above integral expression (see e.g. [35, Lemma 6.1]) or from the relation of the Beta function to the Gamma function. For any a and b, we have
from which we get
as well as a similar expression for \(B(a,b-2)/B(a,b)\). Let us then define
Noting that the integral in \(N_2\) is equal to \(B(-k_1/h^{\!\vee },-k_2/h^{\!\vee })\) and using the identities (D.8), we can rewrite Eq. (D.5) as

Using \({\textsf{J}}_{\text {diag}}={\textsf{J}}_1+{\textsf{J}}_2\) to rewrite the crossed term, we find

We recognise here the spin 2 W-current defined in Eq. (9.23), multiplied by \(N_2\).
E Chiral Limits of General Relativistic AGMs
We have seen in Sect. 3.3 that the Klimčík model can be identified as a relativistic realisation of an AGM with 4 punctures and in Sect. 6 that its conformal limit splits it into two decoupled AGMs with 3 punctures each, corresponding to the left-moving and right-moving fields of the chiral model. The goal of this appendix is to argue that a similar phenomenon should occur for more general relativistic realisations of AGMs, in particular with a higher number of punctures.
Zeroes of the Twist Function in a Relativistic Realisation Let us then consider an AGM with \(2M+2\) punctures (we restrict here to the case of regular punctures, i.e. simple poles, for simplicity; however, most of the discussion can be generalised to the irregular case). Its twist function \(\varphi (z)\text {d}z\) then possesses 2M zeroes \(\zeta _i\), which we will suppose here are simple. As explained in Sect. 3.2, there exists a general scheme to obtain a relativistic two-dimensional integrable field theory from this AGM by considering a realisation \(\rho \) of its Kac–Moody currents in terms of the canonical fields on a cotangent bundle \(T^*Q\), with Q of dimension \((M+1)\dim {\mathfrak {g}}\). In particular, recall from Eq. (3.27) that the relativistic invariance of this realisation requires that the coefficients \(s_i\) entering the Hamiltonian (3.26) are equal to either \(+1\) or \(-1\). Since these coefficients are naturally associated with the zeroes \(\zeta _i\) of the twist function, in practice, this has for effect to separate these zeroes into two sets, depending on whether the corresponding coefficient \(s_i\) is \(+1\) or \(-1\). For simplicity, we then adapt slightly our notation and now write these two sets of zeroes asFootnote 47\(\lbrace \zeta _i^+ \rbrace _{i=1}^M\) and \(\lbrace \zeta _i^- \rbrace _{i=1}^M\). Acting with a Möbius transformation, we can further assume that \(\zeta _M^+=\infty \) and \(\zeta _M^-=0\) without loss of generality. In particular, the set-up considered here is then a natural generalisation of the Klimčík model, which corresponds in the present notation to the case \(M=1\) (see Sect. 3.3).
The separation of the zeroes into the subsets \(\lbrace \zeta _i^+ \rbrace _{i=1}^M\) and \(\lbrace \zeta _i^- \rbrace _{i=1}^M\) reflects the light-cone structure of the relativistic model. For instance, the “light-cone Hamiltonians” \({\mathcal {P}}_\pm \), which generate the derivatives \(\partial _\pm = \frac{1}{2}(\partial _t\pm \partial _x) = \lbrace {\mathcal {P}}_\pm ,\cdot \rbrace \), take the form
with \({\mathcal {Q}}(z)\) defined by Eq. (3.13). Thus, only the zeroes \(\lbrace \zeta _i^+ \rbrace _{i=1}^M\), resp. \(\lbrace \zeta _i^- \rbrace _{i=1}^M\), contribute to \({\mathcal {P}}_+\), resp. \({\mathcal {P}}_-\). Similarly, from expressions (3.31) and (3.33) of the spatial and temporal components of the Lax connection in the relativistic realisation, one finds that the light-cone components take the form
for some \({\mathfrak {g}}^{\mathbb {C}}\)-valued fields \({\mathcal {B}}_\pm \) and \({\mathcal {K}}_{i,\pm }\). In particular, we see that the separation of the zeroes into \(\lbrace \zeta _i^+ \rbrace _{i=1}^M\) and \(\lbrace \zeta _i^- \rbrace _{i=1}^M\) directly appears in the analytical structure of the light-cone Lax connection as a meromorphic function of the spectral parameter z and more precisely in the position of its poles (note that the zero \(\zeta _M^+\), being situated at infinity, contributes to a term linear in z in \({\mathcal {L}}_+(z)\) rather than a simple fraction). For future convenience, it will be useful to write down explicitly the expression of the currents \({\mathcal {K}}_{i,\pm }\) appearing in Eq. (E.2):
Chiral Limit: Colliding Zeroes and Poles The form (E.2) of the light-cone Lax connection is suggestive of a general scheme to obtain chiral limits of the relativistic realisation. Schematically, since only the zeroes \(\lbrace \zeta _i^\pm \rbrace \) appear in the analytical structure of the component \({\mathcal {L}}_\pm (z)\), one can intuitively expect that in order to decouple the \((\pm )\)-chirality in the AGM, one needs to “eliminate” these zeroes. In order to implement this idea, we will consider a limit of the parameters of the AGM in which the punctures collide with the zeroes. More precisely, we ask that the limit is such that half of the poles collide with the zeroes associated with the \((-)\)-chirality in a certain choice of spectral parameter \(z^{{(\mathrm L)}}\), which is built from the initial one z by a Möbius transformation that is degenerate in the limit, while the remaining poles collide with the zeroes associated with the \((+)\)-chirality in another choice of spectral parameter \(z^{{(\mathrm R)}}\).
This is reminiscent of the conformal limit of the Klimčík model discussed in Sect. 6.1. In the general case considered here, a natural scheme to construct such a limit would thus be to follow the RG flow of the relativistic realisation towards an RG fixed point (if it exists). In practice, this can be difficult to implement precisely as the exact form of this RG flow can in general be quite complicated. Therefore, we will not follow this approach here and instead will build explicitly a simple flow of the parameters that fits the characteristics described above and which thus sends the classical theory to a chiral one. Although it will not coincide with the RG flow, we expect that it has a similar asymptotic behaviour (at least for well-chosen initial conditions of the parameters), so that the end point of this flow will coincide with a RG fixed point. We will come back to the RG flow of the theory and its comparison with the chiral limit considered here at the end of this appendix.
To define the limit we first split the punctures of the AGM into two subsets, which we will denote \(\lbrace z_r^+ \rbrace _{r=1}^{M+1}\) and \(\lbrace z_r^- \rbrace _{r=1}^{M+1}\). We then consider the following parametrisation of the punctures \(z_r^\pm \) and zeroes \(\zeta _i^\pm \):
in terms of a real positive parameter \(\xi \) and \(4\,M\) points \(z_1^{(\textrm{L}/\textrm{R})},\ldots ,z_{M+1}^{(\textrm{L}/\textrm{R})}\) and \(\zeta _1^{(\textrm{L}/\textrm{R})},\ldots ,\zeta _{M-1}^{(\textrm{L}/\textrm{R})}\) which we take to be all distinct, finite and different from 0. We then make the parameter \(\xi \) flow to 0, while keeping these points fixed (more generally, one could consider a limit where the latter are not fixed but simply stay finite and pairwise distinct). It is clear that in the limit \(\xi \rightarrow 0\), the punctures and zeroes all collide either at \(z=\infty \) or at \(z=0\). Moreover, we can refine this collision phenomenon by “zooming-in” on 0 or \(\infty \) while taking the limit. For instance, working with the rescaled spectral parameter \(z^{{(\mathrm L)}} = \xi \, z\), the points \(\lbrace \xi \, z_r^- \rbrace _{r=1}^{M+1}\) and \(\lbrace \xi \, \zeta _i^- \rbrace _{i=1}^{M}\) still all collide together at 0 while the remaining points \(\lbrace \xi \, z_r^+ \rbrace _{r=1}^{M+1}\) and \(\lbrace \xi \, \zeta _i^+ \rbrace _{i=1}^{M}\) stay pairwise distinct. Similarly, for another choice of rescaled spectral parameter \(z^{{(\mathrm R)}} = \xi /z\), the points \(\lbrace \xi / z_r^- \rbrace _{r=1}^{M+1}\) and \(\lbrace \xi / \zeta _i^- \rbrace _{i=1}^{M}\) stay pairwise distinct while \(\lbrace \xi / z_r^+ \rbrace _{r=1}^{M+1}\) and \(\lbrace \xi / \zeta _i^+ \rbrace _{i=1}^{M}\) all collide. This is very similar to the Klimčík model set-up discussed in Sect. 6.1, which we recall corresponds here to \(M=1\).
Limits of the Twist Function Let us now consider the limit of the twist function \(\varphi (z)\) in the rescaled spectral parameters \(z^{{(\mathrm L)}}\) and \(z^{{(\mathrm R)}}\). For that, it will be useful to first write \(\varphi (z)\) in the following way:
Here, we chose to parametrise the overall coefficient as \(K/\xi ^2\) to facilitate the limit: indeed, in order to obtain the expected behaviour when \(\xi \rightarrow 0\), we will need to keep the parameter K fixed, or at least finite and nonzero (this can also be expected from the example of the Klimčík model). Keeping this in mind, let us then take the limit explicitly, focussing first on the spectral parameter \(z^{{(\mathrm L)}}=\xi \,z\). For this choice of coordinate on \(\mathbb{C}\mathbb{P}^1\), the twist function before the limit is given by \(\xi ^{-1} \varphi \bigl ( \xi ^{-1}z^{{(\mathrm L)}})\). A direct computation then yields
This corresponds to the twist function of an AGM with \(M+2\) punctures \(\lbrace z_r^{(\mathrm L)}\rbrace _{r=1}^{M+2}\), where we defined \(z_{M+2}^{(\mathrm L)}=0\). A similar analysis can be performed for the spectral parameter \(z^{(\mathrm R)}=\xi /z\). Explicitly, we find
This also corresponds to the twist function of an AGM with \(M+2\) punctures.
Our main goal in the rest of this appendix will be to show that the theory obtained when \(\xi \rightarrow 0\) is chiral, in the sense that it splits into decoupled left-moving and right-moving sectors, and that the latter are chiral realisations of two AGMs with respective twist functions \(\varphi ^{{(\mathrm L)}}\bigl ( z^{(\mathrm L)}\bigr )\) and \(\varphi ^{{(\mathrm R)}}\bigl ( z^{(\mathrm R)}\bigr )\).
Levels It will be useful to study the levels of the model and their behaviour in the limit. In the original relativistic AGM, we have \(2M+2\) such levels \(\ell _r^\pm \), defined as the residues of \(\varphi (z)\text {d}z\) at \(z=z_r^\pm \), for \(r\in \lbrace 1,\ldots ,M+1\rbrace \). From this definition and expression (E.5) of \(\varphi (z)\), one easily expresses these levels in terms of the parameters K, \(\xi \), \(z_r^{{(\mathrm L/R)}}\) and \(\zeta _i^{{(\mathrm L/R)}}\). Making the parameter \(\xi \) flow to 0 as in the previous paragraph, we find that the levels \(\ell _r^\pm \) do not stay fixed in this process, but importantly converge to a finite and nonzero value. In fact, their limits coincide with the residues of the functions \(\varphi ^{(\mathrm L)}\bigl (z^{(\mathrm L)}\bigr )\) and \(\varphi ^{(\mathrm R)}\bigl (z^{(\mathrm R)}\bigr )\) obtained above. More precisely, for \(r\in \lbrace 1,\ldots ,M+1 \rbrace \), we have
We thus expect the limiting values of \(\ell _r^+\) and \(\ell _r^-\) to define the levels of the left-moving and right-moving chiral AGMs describing the theory at \(\xi = 0\).
Limit of the Lax Connection Let us now discuss the limit of the Lax connection of the theory. For the initial relativistic model, it is given by Eq. (E.2). In order to take the limit of this quantity, we will need to study the behaviour of the currents \({\mathcal {K}}_{i,\pm }\) when \(\xi \rightarrow 0\), using their expression (E.3). The latter uses the Gaudin Lax matrix \(\rho \bigl (\Gamma (z)\bigr )\) in the realisation, which is defined as
in terms of the realised Kac–Moody currents \({\mathcal {J}}^\rho _{r,\pm }\). In order to proceed further, we will have to suppose that these currents have a finite and nonzero limit when \(\xi \rightarrow 0\). This assumption would require a more in-depth analysis but appears sensible thanks to the observation made in the previous paragraph that the levels \(\ell _r^\pm \) of these currents stay finite and nonzero in the limitFootnote 48. Using this hypothesis to study the behaviour of the Gaudin Lax matrix in the limit \(\xi \rightarrow 0\) and combining these results with an analysis of the term \(\varphi '(\zeta _i^\pm )\) in Eq. (E.3), a slightly lengthy but straightforward computation shows that the currents \({\mathcal {K}}_{i,+}\) and \({\mathcal {K}}_{i,-}\), \(i\in \lbrace 1,\ldots ,M-1\rbrace \), respectively, diverge and tend to zero in the limit. More precisely, we find
for some non-vanishing fields \({\mathcal {K}}^{(\textrm{L}/\textrm{R})}_{i}\), expressed in terms of the limit of the Kac–Moody currents and the parameters \(\bigl (K,z_r^{(\mathrm L/R)},\zeta _i^{(\mathrm L/R)}\bigr )\) (the sign and prefactor in the second equation have been introduced for further convenience). Similarly, one can study the limit of the currents \({\mathcal {K}}_{M,\pm }\) from the second part of Eq. (E.3) (in particular the behaviour of the current \({\mathcal {K}}_{M,+}\) is different from the one of the other currents \({\mathcal {K}}_{i,+}\) since it is associated with a zero at infinity). In the end, we find two fields \({\mathcal {K}}^{(\textrm{L}/\textrm{R})}_{M}\) such that
Using the above results on the asymptotic behaviour of the currents \({\mathcal {K}}_{\pm ,i}\) when \(\xi \rightarrow 0\), it is then easy to compute the limit of the Lax connection (E.2) in the rescaled spectral parameters \(z^{(\mathrm L)}= \xi \,z\) and \(z^{(\mathrm R)}= \xi /z\). Namely, defining
we get, for some fields \({\mathcal {B}}_\pm ^{{(\mathrm L/R)}}\),
Chirality Let us now analyse the properties of the Lax connection \({\mathcal {L}}_\pm ^{(\mathrm L)}(z^{(\mathrm L)})\) obtained in the limit \(\xi \rightarrow 0\), using the spectral parameter \(z^{(\mathrm L)}\). As can be seen in Eq. (E.12a), its main characteristic is the fact that the “−” component \({\mathcal {L}}_-^{(\mathrm L)}(z^{(\mathrm L)})\) becomes independent of the spectral parameter in the limit. This is reminiscent of the situation described in Sects. 4 and 6 for the conformal limit of the Klimčík model. As discussed there, the main consequence of this observation is that there exists a gauge transformation \(\partial _\pm +{\mathcal {L}}^{(\mathrm L)}_\pm \mapsto h(\partial _\pm +{\mathcal {L}}^{(\mathrm L)}_\pm )h^{-1}\) (independent of the spectral parameter) which eliminates the constant term \({\mathcal {B}}^{{(\mathrm L)}}_-\) in the component \({\mathcal {L}}_-^{(\mathrm L)}(z^{(\mathrm L)})\). In this gauge, the zero-curvature equation then simply states that the “\(+\)” component of the Lax connection is a left-moving field. Thus, there exists h such that the gauge-transformed currents \({\mathcal {B}}^{{(\mathrm L)}\,h}_+\) and \({\mathcal {K}}_{i}^{{(\mathrm L)}\,h}\) are left-moving.
Of course, a similar analysis shows that one can eliminate the “\(+\)” component of the connection \({\mathcal {L}}_\pm ^{(\mathrm R)}(z^{(\mathrm R)})\) by a gauge transformation \(\partial _\pm +{\mathcal {L}}^{(\mathrm R)}_\pm \mapsto h'\,(\partial _\pm +{\mathcal {L}}^{(\mathrm R)}_\pm )h'^{-1}\). As a result, the gauge-transformed currents \({\mathcal {B}}^{{(\mathrm R)}\,h'}_+\) and \({\mathcal {K}}_{i}^{{(\mathrm R)}\,h'}\) are right-moving fields. We thus showed that the theory obtained when \(\xi \rightarrow 0\) splits into a left-moving sector and a right-moving one, as expected. Based on this, we will now refer to \(\xi \rightarrow 0\) as a chiral limit.
Chiral Realisations In the initial relativistic model, the Lax matrix satisfies a \(r\big /s\) bracket with twist function \(\varphi (z)\), characteristic of the underlying AGM structure. Applying the limit \(\xi \rightarrow 0\) to this bracket, we find that the limit of the Lax matrix in the spectral parameter \(z^{(\mathrm L)}\) satisfies a \(r\big /s\) bracket with twist function \(\varphi ^{(\mathrm L)}(z^{(\mathrm L)})\). This means that the Lax matrix \({\mathcal {L}}^{(\mathrm L)}(z^{(\mathrm L)})\) arises from a realisation of the AGM with this twist function. Moreover, the discussion of the previous paragraph shows that the fields entering this realisation are left-moving, up to a well-chosen gauge transformation. This is the main property entering the condition (LM2) in the definition of a left-moving chiral realisation of an AGM in Sect. 6.1. We thus proved that the limit \(\xi \rightarrow 0\) produces such a left-moving chiral realisation.
Similarly, one can argue that the Lax matrix \({\mathcal {L}}^{(\mathrm R)}(z^{(\mathrm R)})\) obtained in the spectral parameter \(z^{(\mathrm R)}\) arises from a right-moving chiral realisation of the AGM with twist function \(\varphi ^{(\mathrm R)}(z^{(\mathrm R)})\). Together, they form a chiral pair of realisations, as defined in Sect. 6.1. In particular, through a careful analysis using similar computations to the one performed earlier in this appendix, one can show that these two realisations indeed satisfy the technical conditions (CP1) and (CP2) entering the definition of a chiral pair.Footnote 49
Sigma Models Realisations So far, we have only used the general properties of the relativistic AGM to discuss its chiral limit, independently of the concrete choice of realisation. Let us then comment on this aspect and the form of the integrable two-dimensional field theories that we obtain by this construction. We will focus on realisations in terms of canonical fields in \(T^*Q\) that give rise to a sigma model, corresponding to Kac–Moody currents linear in the momentum fields and the spatial derivative of the coordinate fields (see Sect. 3.2 for more details). The property (R2) in the definition of a relativistic realisation requires that there are as many degrees of freedom in the realisation that there are in the Kac–Moody currents of the AGM, so that \(\dim \,T^*Q = 2(M+1)\dim {\mathfrak {g}}\), since the AGM possesses \(2(M+1)\) punctures. This describes the unreduced degrees of freedom of the theory: one further needs to impose the constraint and quotient by the corresponding gauge symmetry, effectively eliminating \(2\dim {\mathfrak {g}}\) Hamiltonian fields. The physical degrees of freedom of the theory can then be seen as canonical fields on \(T^*Q_{\text {red}}\), where \(Q_{\text {red}}=Q/G\) is of dimension \(\dim \,Q_{\text {red}}=M\dim {\mathfrak {g}}\). The space \(Q_{\text {red}}\) then plays the role of the target space of the integrable sigma model obtained through the realisation. In the chiral limit discussed above, the AGM underlying this theory splits into a pair of chiral realisations, each possessing \(M+2\) punctures. After reduction, these chiral AGMs are then described by \(M\dim {\mathfrak {g}}\) Hamiltonian fields each, i.e. half of the dimension of \(T^*Q_{\text {red}}\): this is exactly what we expect, since these two chiral AGMs describe the left-moving and right-moving halves of the theory in the chiral limit.
In principle, there can exist many different realisations of the Kac–Moody currents, which would give rise to various types of target spaces \(Q_{\text {red}}\). For concreteness, let us discuss one possible class of interesting examples that naturally generalise the Klimčík model. In the notations of this appendix, these are built by realising separately the \(M+1\) pairs of Kac–Moody currents \(\bigl ({\mathcal {J}}_{r,+},{\mathcal {J}}_{r,-}\bigr )\) associated with the punctures \((z_r^+,z_r^-)\). More precisely, we will express each of these pairs through a so-called Yang–Baxter realisation, in terms of canonical fields in a cotangent bundle \(T^*G\), where G is a connected Lie group with Lie algebra \({\mathfrak {g}}\). These realisations are expressed using the Drinfel’d-Jimbo R-matrix on \({\mathfrak {g}}\) and coincide with the ones considered in Eq. (3.37) for the Klimčík model when the levels \((\ell _r^+,\ell _r^-)\) attached to the punctures are opposite. When these levels are generic, one needs to consider a deformation of this realisation [125] which involves a field related to the Wess–Zumino term on G. Through this construction, we then naturally obtain a realisation in \({\mathcal {F}}[T^*Q]\) with \(Q=G^{M+1}\). Moreover, the form of the Yang–Baxter realisations is such that the gauge symmetry of the AGM simply takes the form of the diagonal right multiplication on Q, so that the physical target space of the sigma model is \(Q_{\text {red}} = G^{M+1} / G_{\text {diag}} \simeq G^M\). The theory then describes M coupled G-valued fields each possessing a Wess–Zumino term, with non-trivial interactions between the copies and subject to \(M+1\) deformations of Yang–Baxter type controlled by the R-matrix. This class then consists of coupled multi-copy versions of the Klimčík model. We refer to [49, 126] for an explicit description of some of these coupled deformed sigma models.
Let us finally mention an interesting subclass of the AGMs considered here, which is defined through a certain symmetry property under the inversion of the spectral parameter \(z\mapsto z^{-1}\). More precisely, we will require that the 1-form \(\varphi (z)\text {d}z\) is odd under this transformation. In the notations of the appendix, this is achieved by requiring that the poles \(z_r^\pm \) and the zeroes \(\zeta _i^\pm \) of \(\varphi (z)\text {d}z\) satisfy \(z_r^- = 1/z_r^+\) and \(\zeta _i^- = 1/\zeta _i^+\), or equivalently that \(z_r^{(\mathrm L)}=z_r^{(\mathrm R)}\) and \(\zeta _i^{(\mathrm L)}=\zeta _i^{(\mathrm R)}\). In particular, this means that the transformation \(z\mapsto z^{-1}\) sends the zeroes \(\lbrace \zeta _i^+ \rbrace _{i=1}^M\) associated with the \((+)\)–chirality of the model to the zeroes \(\lbrace \zeta _i^- \rbrace _{i=1}^M\) associated with the \((-)\)–chirality. This transformation then encodes a certain parity symmetry \(x\mapsto -x\) of the theory, which exchanges these two chiralities. Another effect of the oddness of \(\varphi (z)\text {d}z\) under \(z\mapsto z^{-1}\) is that the levels \((\ell _r^+,\ell _r^-)\) are ensured to be opposite one to another. In the class of Yang–Baxter deformed coupled sigma models considered in the previous paragraph, this translates to the absence of Wess–Zumino terms for each of the G-valued fields in the theory.
RG Flow and Conformality So far, we have discussed only classical aspects of the chiral limit. However, we expect it to be intimately related to the RG flow of the model and its properties of quantum conformal invariance. Let us finally comment on these aspects. Recently, a conjecture has been proposed in [57] for a universal formula describing the 1-loop RG flow of relativistic realisations of AGMs in terms of their twist function \(\varphi (z)\). This conjecture was initially spelled out for AGMs without gauge symmetries, corresponding to the presence of a double pole at infinity in \(\varphi (z)\text {d}z\). It has been checked on various examples [57] and proven in the case of a twist function with simple poles in the complex plane [58]. There exists a natural generalisation of this conjecture for the case of AGMs with gauge symmetries, which we present here. To phrase it, it will be useful to first describe the inverse of the twist function. By construction, it has poles at the points \(\zeta _i^\pm \). A simple analysis of its analytical structure then shows that it satisfies the following partial fraction decomposition:
for some coefficients \((a_0,a_1,a_2)\) whose explicit expression we will not need. Note that the second term corresponds to the contribution of the zero \(\zeta _M^-=0\) (in particular, \(\varphi '(0)={\widetilde{K}}/\xi ^2\)) and the first term to the contribution of the zero \(\zeta _M^+=\infty \).
We now define a closely related, although slightly different, function f(z):
where, compared to Eq. (E.13), we have changed the sign of the contribution of \(\zeta _i^-\) and the coefficients of the polynomial terms of degree up to 2. The conjectured 1-loop RG flow of the relativistic realisations of the AGM with twist function \(\varphi (z)\) then simply reads
where \(\tau =-\frac{1}{2\pi }\,\log (\mu )\) is the RG time, as in Sect. 4.1. We note that the right-hand side of the RG flow (E.15) formally takes the form of the variation of \(\varphi (z)\) under an infinitesimal transformation \(z \mapsto z +\hbar h^{\!\vee }\,f(z)\text {d}\tau \) of the spectral parameter. This can seem surprising at first: indeed, the AGM is invariant under biholomorphic changes of the spectral parameter (see Sect. 3.1), and one could thus naively conclude that the above RG flow leaves the AGM invariant. This is in fact not the case, as one should expect, since \(z \mapsto z +\hbar h^{\!\vee }\,f(z)\text {d}\tau \) is not the infinitesimal version of a biholomorphic transformation on \(\mathbb{C}\mathbb{P}^1\), i.e. of a Möbius transformation, due to the poles of f(z) at \(z=\zeta ^\pm _i\). The RG flow (E.15) thus does not integrate to a global invertible transformation \(z \mapsto {\widetilde{z}}(\tau )\) and hence does not leave the model invariant. We note, however, that the infinitesimal variations corresponding to Möbius transformations take the form \(\delta z=\epsilon _0 +\epsilon _1 z + \epsilon _2 z^2\): the polynomial term \(b_0 + b_1 z + b_2 z^2\) in the definition (E.14) of f(z) then contributes only to a genuine biholomorphism of z in the RG flow (E.15) and is therefore inconsequentialFootnote 50.
Let us now discuss the behaviour of the RG flow (E.15) in the chiral limit considered in this appendix. For that we will first consider the model in the rescaled spectral parameter \(z^{(\mathrm L)}=\xi \,z\): we can then apply the RG flow formula (E.15) for the corresponding twist function \(\xi ^{-1}\varphi \bigl (\xi ^{-1}z^{(\mathrm L)}\bigr )\), using an equivalent of the function f(z) for this choice of spectral parameter. We will denote by \(\varphi ^{(\mathrm L)}\bigl ( z^{(\mathrm L)}\bigr )\) and \(f^{(\mathrm L)}\bigl (z^{(\mathrm L)}\bigr )\) the limit of these functions when \(\xi \rightarrow 0\). As explained earlier, the main property of the chiral limit in the coordinate \(z^{(\mathrm L)}\) is that it eliminates the zeroes \(\lbrace \xi \,\zeta _i^- \rbrace _{i=1}^{M+1}\) by making them collide with poles. As a result, the contribution of these zeroes to \(f^{(\mathrm L)}\bigl (z^{(\mathrm L)}\bigr )\) disappear in the limit and this function then coincides with the inverse of \(\varphi ^{{(\mathrm L)}}\bigl (z^{(\mathrm L)}\bigr )\), up to polynomial terms of degrees up to 2, as can be seen from the formulas (E.13) and (E.14) translated to the spectral parameter \(z^{(\mathrm L)}\). In other words, we have
for some coefficients \((a_{L,0},a_{L,1},a_{L,2})\). Reinserting this is in the RG equation (E.15) for \(\xi \rightarrow 0\), we find that the term \(\varphi ^{(\mathrm L)}\bigl (z^{(\mathrm L)}\bigr )^{-1}\) in \(f^{(\mathrm L)}\bigl (z^{(\mathrm L)}\bigr )\) does not contribute to the flow. Since the remaining polynomial term corresponds simply to a Möbius transformation of \(z^{(\mathrm L)}\), we then get that the twist function \(\varphi ^{(\mathrm L)}\bigl (z^{(\mathrm L)}\bigr )\) in the limit has a trivial RG flow and thus that the physical parameters of the left-moving chiral AGM do not run under the flow (at least at 1-loop).
One can apply a similar reasoning in the spectral parameter \(z^{(\mathrm R)}= \xi /z\), hence proving that the physical parameters of the right-moving chiral AGM also have a vanishing 1-loop \(\beta \)-function. Together, the pair of chiral AGMs encode all the parameters of the full two-dimensional theory obtained in the limit and we thus conclude that the latter defines a conformal theory.
Although we have argued that the theory in the limit \(\xi \rightarrow 0\) is conformal, i.e. defines a fixed point of the RG, let us recall that the flow in the parameter space that we considered above will in general not coincide exactly with the RG flow itself. Indeed, we have taken here the limit \(\xi \rightarrow 0\) while keeping the other parameters \(\bigl (K,z_r^{(\mathrm L/R)},\zeta _i^{(\mathrm L/R)}\bigr )\) fixed. In general, we expect that the RG flow of the theory, at least for well-chosen initial conditions of the parameters, will also send the parameter \(\xi \) to zero in the UV, but keeping \(\bigl (K,z_r^{(\mathrm L/R)},\zeta _i^{(\mathrm L/R)}\bigr )\) finite and nonzero rather than fixed. Let us note moreover that a striking property of the RG equation (E.15) is that the levels \(\ell _r^\pm \) of the model, which are complicated combinations of \(\bigl (K,\xi ,z_r^{(\mathrm L/R)},\zeta _i^{(\mathrm L/R)}\bigr )\), stay fixed under the RG flow. As mentioned earlier, this is not the case for the limit \(\xi \rightarrow 0\): however, the latter was such that \(\ell _r^+\) and \(\ell _r^-\) converge to finite nonzero values which coincide with the levels of the left-moving and right-moving chiral AGMs, respectively. The asymptotic behaviour of the levels is thus similar to the one expected in the UV limit.
More generally, we have mentioned at a few points in this appendix that a limit in which the parameters \(\bigl (K,z_r^{(\mathrm L/R)},\zeta _i^{(\mathrm L/R)}\bigr )\) stay finite and nonzero rather than fixed would have a qualitative behaviour very similar to the one we considered and that most of the computations would readily apply to this case as well. In other words, we expect this chiral limit to have a similar asymptotic behaviour to the UV limit of the theory (for well-chosen initial conditions). This is motivated by the example of the Klimčík model for \(M=1\), which indeed behaves in such a manner. Moreover, we have performed some numerical checks using the conjectured RG flow (E.15) for a higher number of punctures, namely for \(M=2\), showing that this expectation is indeed true when one starts with initial parameters in a well-chosen regime. We thus think that the chiral realisations in these conformal limits can be studied and quantised using techniques similar to the ones discussed in this article for the case of the Klimčík model.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kotousov, G.A., Lacroix, S. & Teschner, J. Integrable Sigma Models at RG Fixed Points: Quantisation as Affine Gaudin Models. Ann. Henri Poincaré 25, 843–1006 (2024). https://doi.org/10.1007/s00023-022-01243-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-022-01243-4