Abstract
In open quantum systems, the quantum Zeno effect consists in frequent applications of a given quantum operation, e.g., a measurement, used to restrict the time evolution (due, for example, to decoherence) to states that are invariant under the quantum operation. In an abstract setting, the Zeno sequence is an alternating concatenation of a contraction operator (quantum operation) and a \(C_0\)-contraction semigroup (time evolution) on a Banach space. In this paper, we prove the optimal convergence rate \(\mathcal {O}(\tfrac{1}{n})\) of the Zeno sequence by proving explicit error bounds. For that, we derive a new Chernoff-type \(\sqrt{n}\)-Lemma, which we believe to be of independent interest. Moreover, we generalize the convergence result for the Zeno effect in two directions: We weaken the assumptions on the generator, inducing the Zeno dynamics generated by an unbounded generator, and we improve the convergence to the uniform topology. Finally, we provide a large class of examples arising from our assumptions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In its original form, the quantum Zeno effect is defined for closed finite quantum systems. Misra and Sudarshan predicted that “an unstable particle which is continuously observed to see whether it decays will never be found to decay!” [30, Abst.]. In a more general setup, frequent measurements enable a change in the time evolution and convergence to the so-called Zeno dynamics. Experimentally, the Zeno effect is verified for instance in [14, 24]. In addition to its theoretical value, the quantum Zeno effect is used in error correction schemes to suppress decoherence in open quantum systems [1, 3, 15, 23, 29]. The idea is to frequently measure the quantum state and thereby force the evolution to remain within the code space. With an appropriate measurement, one can even decouple the system from its environment [5, 12] and show that appropriately encoded states can be protected from decoherence with arbitrary accuracy [7, 9]. Moreover, the quantum Zeno effect has been used in commercial atomic magnetometers [26].
Introduced by Beskow and Nilsson [4] and later named by Misra and Sudarshan after the Greek philosopher Zeno of Elea, the quantum Zeno effect in its simplest form can be stated as follows: given a projective measurement P and a unitary time evolution generated by a Hamiltonian H acting on a finite-dimensional Hilbert space \(\mathcal {H}\) [30]: For \(n\rightarrow \infty \)
Since the seminal works [4, 30], the result was extended in many different directions (overviews can be found in [13, 24, 35]). Recently, the convergence in Eq. (1) was proven in the strong topology for unbounded Hamiltonian under the weak assumption that PHP is the generator of a \(C_0\)-semigroup [11]. Earlier approaches used the so-called asymptotic Zeno condition [10, 30, 35], which assumes \((\mathbbm {1}-P)e^{itH}P\) and \(Pe^{itH}(\mathbbm {1}-P)\) to be Lipschitz continuous at \(t=0\). This condition is natural in the sense that it is related to the boundedness of the first moment of the Hamiltonian in the initial state and is efficiently verifiable in practice. With the works [1, 5, 31], the quantum Zeno effect was generalized to open and infinite-dimensional quantum systems equipped with general quantum operations and uniformly continuous time evolutions. Note that in open quantum systems, we are dealing with operators acting on the Banach space \(\mathcal {T}_1(\mathcal {H})\) of trace class operators. More recently, Becker, Datta, and Salzmann generalized the Zeno effect further and interpreted the Zeno sequence as a product formula consisting of a contraction M (quantum operation) and a \(C_0\)-contraction semigroup (quantum time evolution) on an abstract Banach space. Under a condition of uniform power convergence of the power sequence \(\{M^k\}_{k\in \mathbb {N}}\) toward a projection P and boundedness of \(M\mathcal {L}\) and \(\mathcal {L}M\), they proved a quantitative bound on the convergence rate [2]:
for \(n\rightarrow \infty \) and all \(x\in \mathcal {D}(\mathcal {L})\). However, the optimality of (2) was left open.Footnote 1
Main contributions In this paper, we achieve the optimal convergence rate \(\mathcal {O}(n^{-1})\) of the Zeno sequence consistent with the finite-dimensional case [5] by providing an explicit bound which recently attracted interest in finite closed quantum systems [19, Theorem 1]. Moreover, we generalize the results of [2] in two complementary directions:
In Theorem 5.1, we assume a special case of the uniform power convergence assumption on M, that is \(\Vert M^n-P\Vert \le \delta ^n\) for some \(\delta \in (0,1)\), and weaken the assumption on the semigroup to the uniform asymptotic Zeno condition inherited from the unitary setting of [35]: for \(t\rightarrow 0\)
Therefore, we prove the convergence of a non-trivial Zeno sequence in open quantum systems to a Zeno dynamics described by a possibly unbounded generator.
Second, Theorem 6.1 is stated under slightly weaker assumptions as Theorem 3 in [2] and improves the result to the optimal convergence rate and to the uniform topology.
In order to achieve these results, we prove a modified Chernoff \(\sqrt{n}\)-Lemma in Lemma 4.2, find a quantitative convergence rate for \({\text {exp}}\big ({nP(e^{\frac{1}{n}t\mathcal {L}}-\mathbbm {1})P}\big )P-{\text {exp}}(tP\mathcal {L}P)P\) as \(n \rightarrow \infty \), where \(P\mathcal {L}P\) is possibly unbounded, and prove the upper semicontinuity of parts of the spectrum of \(Me^{t\mathcal {L}}\) under tight assumptions.
Organization of the paper In Sect. 2, we provide a short recap on bounded and unbounded operator theory. We expose our main results in Sect. 3. Section 4 deals with the modified Chernoff \(\sqrt{n}\)-Lemma and some of its implications as regards to Trotter–Kato’s product formula. Then, we prove our main theorems under the weakest possible assumptions on the \(C_0\)-semigroup in Sect. 5, and under the weakest possible assumptions on M in Sect. 6. Our results are illustrated by three large classes of examples in finite- and infinite-dimensional quantum systems in Sect. 7. Finally, we discuss some remaining open questions in Sect. 8.
2 Preliminaries
Let \((\mathcal {X},\Vert \cdot \Vert )\) be a Banach space and \(({\mathcal {B}}(\mathcal {X}),\Vert \cdot \Vert _{\infty })\) be the associated space of bounded linear operators over \(\mathbbm {C}\) equipped with the operator norm, i.e., \(\Vert C\Vert _{\infty }{:}{=}\sup _{x\in \mathcal {X}\backslash \{0\}}\frac{\Vert Cx\Vert }{\Vert x\Vert }\), and the identity \(\mathbbm {1}\in {\mathcal {B}}(\mathcal {X})\). By a slight abuse of notation, we extend all densely defined and bounded operators by the bounded linear extension theorem to bounded operators on \(\mathcal {X}\) [27, Theorem 2.7–11]. A sequence \((C_k)_{k\in \mathbbm {N}}\subset {\mathcal {B}}(\mathcal {X})\) converges uniformly to \(C\in {\mathcal {B}}(\mathcal {X})\) if \(\lim _{k\rightarrow \infty }\Vert C_k-C\Vert _\infty =0\) and strongly if \(\lim _{k\rightarrow \infty }\Vert C_kx-Cx\Vert =0\) for all \(x\in \mathcal {X}\). The integral over bounded vector-valued maps, e.g., \([a,b]\rightarrow \mathcal {X}\) or \([a,b]\rightarrow {\mathcal {B}}(\mathcal {X})\) with \(a<b\), is defined by the Bochner integral, which satisfies the triangle inequality, is invariant under linear transformations and satisfies the fundamental theorem of calculus if the map is continuously differentiable [22, Sect. 3.7–8, 28, Sect. A.1–2].
We define the resolvent set of \(C\in {\mathcal {B}}(\mathcal {X})\) by \(\rho (C){:}{=}\{z\in \mathbbm {C}\;|\;(z-C)\text { bijective}\}\) and its spectrum by \(\sigma (C){:}{=}\mathbbm {C}\backslash \rho (C)\). Then, we define the resolvent of C by \(R(z,C){:}{=}(z-C)^{-1}\) for all \(z\in \rho (C)\). Note that the resolvent is continuous in z [25, Theorem 3.11] and thereby uniformly bounded on compact intervals. A point \(\lambda \in \sigma (C)\) is called isolated if there is a neighborhood \(V\subset \mathbbm {C}\) of \(\lambda \) such that \(V\cap \sigma (C)=\lambda \). The spectrum is separated by a curve \(\Gamma :I\rightarrow \rho (C)\) if \(\sigma (C)=\sigma _1\cup \sigma _2\), the subsects \(\sigma _1\), \(\sigma _2\) have disjoint neighborhoods \(V_1\), \(V_2\), and the curve is simple, closed, rectifiableFootnote 2, and encloses one of the neighborhoods without intersecting \(V_1\) and \(V_2\) [25, Sects. III, 6.4]. This definition can be generalized to a finite sum of subsets separated by curves. An example for a simple, closed, and rectifiable curve is the parametrization of the boundary of a complex ball around the origin with radius r. We denote the open ball by \(\mathbbm {D}_r\) and its boundary by \(\partial \mathbbm {D}_r\).
We define the spectral projection \(P\in {\mathcal {B}}(\mathcal {X})\) with respect to a separated subset of \(\sigma (C)\) enclosed by a curve \(\Gamma \) via the holomorphic functional calculus [36, Theorem 2.3.1–3]
As the name suggests, \(P\in {\mathcal {B}}(\mathcal {X})\) satisfies the projection property, \(P^2=P\). We denote the complementary projection \(\mathbbm {1}-P\) by \(P^\perp \). If \(\Gamma \) encloses the isolated one-point subset \(\{\lambda \}\subset \sigma (C)\), then \(CP=\lambda P+N\) with the quasinilpotent operator [36, Theorem 2.3.5]
A quasinilpotent operator \(N\in {\mathcal {B}}(\mathcal {X})\) is characterized by \(\lim \nolimits _{n\rightarrow \infty }\Vert N^n\Vert _\infty ^{\frac{1}{n}}=0\).
The time evolution in the Zeno sequence is described by a \(C_0\)-contraction semigroup [8, Definition 5.1]. A family of operators \((T_t)_{t\ge 0}\subset {\mathcal {B}}(\mathcal {X})\) is called a \(C_0\)-semigroup if the family satisfies the semigroup properties, namely: (i) \(T_tT_s=T_{t+s}\) for all \(t,s\ge 0\), (ii) \(T_0=\mathbbm {1}\), and (iii) \(t\mapsto T_t\) is strongly continuous in 0. The generator of a \(C_0\)-semigroup is a possibly unbounded operator defined by taking the strong derivative in 0, that is
for all \(x\in \mathcal {D}(\mathcal {L}){:}{=}\{x\in \mathcal {X}\;|\;t\mapsto T_tx\text { differentiable}\}\) and is denoted by \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) (cf. [8, Ch. II.1]). Since the generator defines the \(C_0\)-semigroup uniquely, we denote it by \((e^{t\mathcal {L}})_{t\ge 0}\), although the series representation of the exponential is not well defined (cf. [25, Sects. IX, 1]). A semigroup is called contractive if \(\sup _{t\ge 0}\Vert e^{t\mathcal {L}}\Vert _\infty \le 1\). Note that the linear combination and concatenation of two unbounded operators \((\mathcal {K},\mathcal {D}(\mathcal {K}))\) and \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) is defined on \(\mathcal {D}(\mathcal {K}+\mathcal {L})=\mathcal {D}(\mathcal {K})\cap \mathcal {D}(\mathcal {L})\) and \(\mathcal {D}(\mathcal {K}\mathcal {L})=\mathcal {L}^{-1}(\mathcal {D}(\mathcal {K}))\) (cf. [25, Sects. III, 5.1]). The following lemma summarizes some properties of \(C_0\)-semigroups which are used in this work:
Lemma 2.1
([8, Lemma II.1.3]). Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of the \(C_0\)-semigroup \((e^{t\mathcal {L}})_{t\ge 0}\) defined on \(\mathcal {X}\). Then, the following properties hold:
-
(1)
If \(x\in \mathcal {D}(\mathcal {L})\), then \(e^{t\mathcal {L}}x\in \mathcal {D}(\mathcal {L})\) and
$$\begin{aligned} \frac{\partial }{\partial t}e^{t\mathcal {L}}x=e^{t\mathcal {L}}\mathcal {L}x=\mathcal {L}e^{t\mathcal {L}}x\qquad \text {for all } t\ge 0\,. \end{aligned}$$ -
(2)
For every \(t\ge 0\) and \(x\in \mathcal {X}\), one has
$$\begin{aligned} \int _{0}^{t}e^{\tau \mathcal {L}}xd\tau \in \mathcal {D}(\mathcal {L})\,. \end{aligned}$$ -
(3)
For every \(t\ge 0\), one has
$$\begin{aligned} e^{t\mathcal {L}}x-x&=\mathcal {L}\int _{0}^{t}e^{\tau \mathcal {L}}xd\tau \quad \text { for all }x\in \mathcal {X}\\&=\int _{0}^{t}e^{\tau \mathcal {L}}\mathcal {L}xd\tau \quad \text { if }x\in \mathcal {D}(\mathcal {L}). \end{aligned}$$
Additionally, a general integral formulation for the difference of two semigroups is discussed in the following lemma (cf. [8, Cor. III.1.7]).
Lemma 2.2
(Integral equation for semigroups). Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) and \((\mathcal {K},\mathcal {D}(\mathcal {K}))\) be the generators of two \(C_0\)-semigroups on a Banach space \(\mathcal {X}\) and \(t\ge 0\). Assume \(\mathcal {D}(\mathcal {L})\subset \mathcal {D}(\mathcal {K})\) and \([0,t]\ni s\mapsto e^{s\mathcal {K}}(\mathcal {K}-\mathcal {L})e^{(t-s)\mathcal {L}}x\) is continuous for all \(x\in \mathcal {D}(\mathcal {L})\). Then, for all \(x\in \mathcal {D}(\mathcal {L})\)
Proof
Assume \(x\in \mathcal {D}(\mathcal {L})\). In the first part, we follow the proof of Corollary III.1.7 in [8]. By definition, the vector-valued maps \([0,t]\ni s\mapsto e^{s\mathcal {K}}x\) and \([0,t]\ni s\mapsto e^{(t-s)\mathcal {L}}x\) are continuously differentiable and \(\mathcal {D}(\mathcal {L}) \) is invariant under the second map. Then, Lemma B.16 in [8] shows
By assumption, the above derivative is continuous in \(s\in [0,t]\), so that the fundamental theorem of calculus proves the integral equation. \(\square \)
Corollary 2.3
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-semigroup on a Banach space \(\mathcal {X}\), \(t\ge 0\), and \(A\in {\mathcal {B}}(\mathcal {X})\). Then, the unbounded operator \(\mathcal {K}=\mathcal {L}+A\) defined on \((\mathcal {L}+A,\mathcal {D}(\mathcal {L}))\) is the generator of a \(C_0\)-semigroup. If additionally the semigroup \(t\mapsto e^{t\mathcal {L}}\) is quasi-contractive, i.e., \(\Vert e^{t\mathcal {L}}\Vert _\infty \le e^{tw}\) for a \(w\in \mathbbm {R}\), then
Proof
By Theorem 13.2.1 and the corollary afterward in [22], the operator \((\mathcal {L}+A,\mathcal {D}(\mathcal {L}))\) is the generator of a quasi-contractive \(C_0\)-semigroup, i.e., \(\Vert e^{t(\mathcal {L}+A)}\Vert _\infty \le e^{t\tilde{w}}\) with \(\tilde{w}=w+\Vert A\Vert _\infty \). Moreover, \([0,t]\ni s\mapsto e^{s\mathcal {K}}Ae^{(t-s)\mathcal {L}}x\) is continuous by [8, Lemma B.15] so that Lemma 2.2 shows
\(\square \)
3 Main Results
In this section, we list the main results achieved in the paper. Since the quantum Zeno effect consists of a contraction operator \(M\in {\mathcal {B}}(\mathcal {X})\) (e.g., measurement) and a \(C_0\)-semigroup (e.g., quantum time evolution), the assumptions on the contraction operator and on the \(C_0\)-semigroup influence each other. We first start with weak assumptions on the semigroup and stronger assumption on the contraction operator:
Theorem I
(stated as Theorem 5.1 in main text). Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\), \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction, and P a projection satisfying
for \(\delta \in (0,1)\) and all \(n\in \mathbbm {N}\). Moreover, assume there is \(b\ge 0\) so that for all \(t\ge 0\)
If \((P\mathcal {L}P,\mathcal {D}(\mathcal {L}P))\) is the generator of a \(C_0\)-semigroup, then for any \(t\ge 0\) and all \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
for some constant \(c(t,b)>0\) depending on t and b, but independent of n .
Remark
Note that the assumption on M is a special case of the so-called uniform power convergence assumption (q.v. Eq. 9) and the assumption (6) on the \(C_0\)-semigroup is a generalization of the uniform asymptotic Zeno condition which implies the convergence in the case of a unitary evolution frequently measured by a projective measurement [35, Sect. 3.1]. Note that in that specific case, [11] recently managed to remove the asymptotic Zeno condition. Moreover, the assumption that \((P\mathcal {L}P,\mathcal {D}(\mathcal {L}P))\) is a generator can be relaxed to the assumption that \(P\mathcal {L}P\) is closeable and its closure defines a generator (q.v. remark after Lemma 5.6). The famous Generation Theorem by Hille and Yosida provides a sufficient condition under which \(\overline{P\mathcal {L}P}\) is a generator [8, Theorem 3.5–3.8].
The following example confirms the optimality of the achieved convergence rate.
Example 1
Let \(\left\{ \vert 1 \rangle ,\vert 2 \rangle ,\vert 3 \rangle \right\} \) be an orthonormal basis of \(\mathbbm {R}^3\) and \(\delta \in (0,1)\). We define,
Then, \(P=\vert 1 \rangle \langle 1 \vert \), \((\mathbbm {1}-P) M=\delta \vert 3 \rangle \langle 3 \vert \), \(M\mathcal {L}=\mathcal {L}M\), and \(\mathcal {L}^2=0=\mathcal {L}P\), \(\Vert M^n-P\Vert _\infty \le \delta ^n\). Using these properties, \(Me^{\frac{t}{n}\mathcal {L}}=M +\frac{t}{n}\mathcal {L}\) and for \(t\in [0,\infty )\)
Therefore,
which shows the optimality of our convergence rate in Theorem 5.1.
Beyond the proven asymptotics, we find explicit error bounds in Lemmas 5.2, 5.5, and 5.6, which simplify if \(\mathcal {L}\) is bounded to the following explicit convergence bound depending on the generator \(\mathcal {L}\), the projection P, the spectral gap \(\delta \), and the time t:
Proposition 3.1
Let \(\mathcal {L}\in {\mathcal {B}}(\mathcal {X})\) be the generator of a contractive uniformly continuous semigroup and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction satisfying
for a projection \(P\in {\mathcal {B}}(\mathcal {X})\), \(\delta \in (0,1)\), and all \(n\in \mathbbm {N}\). Then, for all \(t\ge 0\) and \(n\in \mathbbm {N}\),
where \(c_{p}{:}{=}\Vert \mathbbm {1}-P\Vert _\infty \) and \(e^{\tilde{b}}=\sup _{s\in [0,t]}\Vert e^{sP\mathcal {L}P}\Vert _\infty \).
Note that the above proposition can be easily extended to the case of an unbounded generator with the assumption that \(\mathcal {L}M\) and \(M\mathcal {L}\) are densely defined and bounded. Another advantage of our setup is the freedom it provides for choosing the Banach space \(\mathcal {X}\), which allows us to treat open quantum systems (\(\mathcal {X}=\mathcal {T}(\mathcal {H})\) the trace class operators over a Hilbert space) and closed quantum systems (\(\mathcal {X}=\mathcal {H}\) a Hilbert space) on the same footing. In the case of finite-dimensional closed quantum systems, Proposition 3.1 reduces to the following bound, which was independently proven in [19, Theorem 1] (up to a change of the numerical constant in the quadratic term from \(\tfrac{5}{2}\) to 2):
Corollary 3.2
Let \(\mathcal {H}\) be a Hilbert space, \(H\in {\mathcal {B}}(\mathcal {H})\) be a Hermitian operator, and \(P\in {\mathcal {B}}(\mathcal {H})\) a Hermitian projection. Then,
To achieve the bound above, one inserts \(\delta =0\) and \(\mathcal {L}=iH\) in Proposition 3.1. Note that PHP is Hermitian and \(\Vert e^{siPHP}\Vert _\infty =1\) for all \(s\ge 0\).
Next, we consider convergence rates under a slight weakening of the condition on the map M:
Corollary 3.3
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction satisfying
for some projection P, \(\delta \in (0,1)\), \(\tilde{c}\ge 0\) and all \(n\in \mathbbm {N}\). Moreover, assume there is \(b\ge 0\) so that
If \((P\mathcal {L}P,\mathcal {D}(\mathcal {L}P))\) is the generator of a \(C_0\)-semigroup, then there exists a constant \(c>0\) and \(n_0\in \mathbbm {N}\) so that \(\tilde{c}\delta ^{n_0}{=}{:}\tilde{\delta }<1\) and for all \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
The above corollary follows by the choice \(n_0\) such that \(\tilde{c}\delta ^{n_0}<1\) and applying Theorem I to \(\tilde{M}{:}{=}M^{n_0}\). A more physically motivated result treating the same generalization as the corollary above is provided in the next result:
Proposition II
(stated as Proposition 5.7 in main text). Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction such that
for some projection P, \(\delta \in (0,1)\) and \(\tilde{c}\ge 0\). Moreover, we assume that there is \(b\ge 0\) so that
where \(M^\perp =(\mathbbm {1}-P)M\). If \((P\mathcal {L}P,\mathcal {D}(\mathcal {L}P))\) generates a \(C_0\)-semigroup, then there is an \(\epsilon >0\) such that for all \(t\ge 0\), \(n\in \mathbbm {N}\) satisfying \(t\in [0,n\epsilon ]\), \(\tilde{\delta }\in (\delta ,1)\), and \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
for some constants \(c_1,c_2\ge 0\) depending on t, b, the difference \(\tilde{\delta }-\delta \), and \(\tilde{c}\).
As in Proposition 3.1, we also get a more explicit bound in the case of bounded generators in the following proposition:
Proposition 3.4
Let \(\mathcal {L}\in {\mathcal {B}}(\mathcal {X})\) be the generator of a contractive uniformly continuous semigroup and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction satisfying
for a projection \(P\in {\mathcal {B}}(\mathcal {X})\), \(\delta \in (0,1)\), \(\tilde{c}>1\), and all \(n\in \mathbbm {N}\). Then, there is \(\epsilon >0\) such that for all \(t\ge 0\), \(n\in \mathbbm {N}\) satisfying \(t\in [0,n\epsilon ]\), and \(\tilde{\delta }\in (\delta ,1)\)
where \(c_{p}{:}{=}\Vert \mathbbm {1}-P\Vert _\infty \) and \(e^{\tilde{b}}=\sup _{s\in [0,t]}\Vert e^{sP\mathcal {L}P}\Vert _\infty \).
Finally, we extend the assumption on M (q.v. Eqs. 5, 7) to the uniform power convergence introduced in [2]. Let \(\{P_j,\lambda _j\}_{j=1}^J\) be a set of projections satisfying \(P_jP_k=1_{j=k} P_j\) and associated eigenvalues on the unit circle \(\partial \mathbbm {D}_1\). Then, M is called uniformly power convergent with rate \(\delta \in (0,1)\) if \(M^n-\sum _{j=1}^{J}\lambda ^n_jP_j=\mathcal {O}(\delta ^n)\) uniformly for \(n\rightarrow \infty \). To prove our result in this case, we also need to assume that \(M\mathcal {L}\) and \(\mathcal {L}P_\Sigma \) with \(P_\Sigma {:}{=}\sum _{j=1}^{J}P_j\) are densely defined and bounded (cf. [2]) and \(P_j\) is a contraction for all \(j\in \{1,...,J,\Sigma \}\):
Theorem III
(stated as Theorem 6.1 in main text). Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction satisfying the following uniform power convergence: There is \(\tilde{c}>0\) so that
for a set of projections \(\{P_j\}_{j=1}^J\) satisfying \(P_jP_k=1_{j=k}P_j\), eigenvalues \(\{\lambda _j\}_{j=1}^J\subset \partial \mathbbm {D}_1\), and a rate \(\delta \in (0,1)\). For \(P_\Sigma {:}{=}\sum _{j=1}^{J}P_j\), we assume that \(M\mathcal {L}\) and \(\mathcal {L}P_\Sigma \) are densely defined and bounded by \(b\ge 0\) and \(\Vert P_j\Vert _\infty =1\) for all \(j\in \{1,...,J,\Sigma \}\). Then, there is an \(\epsilon >0\) such that for all \(n\in \mathbbm {N}\), \(t\ge 0\) satisfying \(t\in [0,n\epsilon ]\), and \(\tilde{\delta }\in (\delta ,1)\)
for some constants \(c_1,c_2\ge 0\) depending on all involved parameters except from n.
In comparison with Theorem 3 in [2], Theorem 6.1 achieves the optimal convergence rate and is formulated in the uniform topology under slightly weaker assumptions on the generator.
Remark
A natural way to weaken the above assumption is to assume that the power converges is in the strong topology (cf. [2, Theorem 2]).
4 Chernoff \(\sqrt{n}\)-Lemma and Trotter–Kato’s Product Formula
In the previous works [2, 31], Chernoff’s \(\sqrt{n}\)-Lemma [6, Lemma 2], which we restate here, is used as a proof technique to approximate the Zeno product by a semigroup (q.v. Eq. 13).
Lemma 4.1
(Chernoff \(\sqrt{n}\)-Lemma). Let \(C\in {\mathcal {B}}(\mathcal {X})\) be a contraction. Then, \((e^{t(C-\mathbbm {1})})_{t\ge 0}\) is a uniformly continuous contraction semigroup and for all \(x\in \mathcal {X}\)
Remark
In Lemma 2.1 in [40], the dependence on n is improved to \(n^\frac{1}{3}\). This is crucial in the proof of the convergence rate in [2, Lemmas 5.4–5.5]. Unfortunately, we found an inconsistency in the proof of [40, Lemma 2.1], i.e., Inequality 2.3 is not justified. An update and more Chernoff bounds can be found in [41]. Following the proof by Becker, Datta, and Salzmann, one can achieve a convergence rate of order \(\tfrac{1}{\sqrt{n}}\) in the bounded generator case [2, Theorem 1] and of order \(\tfrac{1}{\root 4 \of {n}}\) in the unbounded generator case [2, Theorem 3].
In the case of the quantum Zeno effect (see Lemmas 5.5 and 6.4) for bounded generators, the contraction C is a vector-valued map \(t\mapsto C(t)\) on \(\mathcal {X}\) satisfying \(\Vert C(\tfrac{1}{n})-\mathbbm {1}\Vert _\infty =\mathcal {O}(n^{-1})\). By Chernoff’s \(\sqrt{n}\)-Lemma
here we chose the bounded generator case for the sake of simplicity. Nevertheless, the argument can be extended to unbounded generator as well (see Lemmas 5.5, 6.4, and C.1). Next, we prove a modified bound, which allows us to achieve the optimal rate in the quantum Zeno effect.
Lemma 4.2
(Modified Chernoff Lemma). Let \(C\in {\mathcal {B}}(\mathcal {X})\) be a contraction and \(n\in \mathbbm {N}\). Then, \((e^{t(C-\mathbbm {1})})_{t\ge 0}\) is a contraction semigroup and for all \(x\in \mathcal {X}\)
Remark
At first glance, this seems to be worse than the original Chernoff \(\sqrt{n}\)-Lemmas in [6]. However, if C is a vector-valued map satisfying \(\Vert C(\tfrac{1}{n})-\mathbbm {1}\Vert _\infty =\mathcal {O}(n^{-1})\), then the modified Chernoff lemma gives
which is the key idea to prove the optimal convergence rate of the quantum Zeno effect for bounded generators and contractions M satisfying the uniform power convergence (q.v. Lemma 5.5).
Proof of Lemma 4.2
Similar to Chernoff’s proof [6, Lemma 2], \((e^{t(C-\mathbbm {1})})_{t\ge 0}\) is a contraction semigroup. We define \(C_t{:}{=}(1-t)\mathbbm {1}+tC=\mathbbm {1}+t(C-\mathbbm {1})\) for \(t\in [0,1]\), which itself is a contraction as a convex combination of contractions, and we use the fundamental theorem of calculus so that
which proves the lemma. \(\square \)
In [6, p. 241], Chernoff proves the convergence of Trotter’s product formula by approximating the product using the Chernoff \(\sqrt{n}\)-Lemma. For bounded generators, Chernoff’s proof gives a convergence rate of order \(n^{-\frac{1}{2}}\). Following his proof and using our modified Chernoff Lemma, we achieve the well-known optimal convergence rate of order \(n^{-1}\) [20, Theorem 2.11, 32, p. 1-2]:
Proposition 4.3
([6, Theorem 1]). Let \(F:\mathbbm {R}_{\ge 0}\rightarrow {\mathcal {B}}(\mathcal {X})\) be a continuously differentiable function (in the uniform topology) satisfying \(\sup _{t\in \mathbbm {R}_{\ge 0}}\Vert F(t)\Vert _\infty \le 1\). Assume that \(F(0)=\mathbbm {1}\) and denote the derivative at \(t=0\) by \(\mathcal {L}\in {\mathcal {B}}(\mathcal {X})\). Then, for all \(t\ge 0\)
Proof
The case \(t=0\) is clear. For \(t>0\), applying Lemma 4.2, we get
For the second term above, we apply Lemma 2.2:
where we use \(\Vert F(\tfrac{t}{n})\Vert _\infty \le 1\) and that \(e^{sn(F({{\tfrac{t}{n}}})-\mathbbm {1})}\) is a contraction semigroup.
\(\square \)
Applying the proposition to the case of Trotter’s product formula, we achieve the well-known optimal convergence rate for bounded generators on Banach spaces [20, Theorem 2.11, 32, p. 1–2]:
Corollary 4.4
([20, Theorem 2.11]). Let \(\mathcal {L}_1\) and \(\mathcal {L}_2\) be bounded generators of two uniformly continuous contraction semigroups. Then, for \(n\rightarrow \infty \)
Proof
We define \(F(\tfrac{1}{n})\, {:}{=}\, e^{\frac{1}{n}\mathcal {L}_1}e^{\frac{1}{n}\mathcal {L}_2}\) for which
holds. Moreover,
and
and the statement follows from Proposition 4.3. \(\square \)
5 Strongly Continuous Zeno Dynamics
We proceed with the statement and proof of our first main result, namely Theorem 5.1, which we restate here for the sake of clarity of conciseness:
Theorem 5.1
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\), \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction, and P a projection satisfying
for \(\delta \in (0,1)\) and all \(n\in \mathbbm {N}\). Moreover, assume there is \(b\ge 0\) so that for all \(t\ge 0\)
If \((P\mathcal {L}P,\mathcal {D}(\mathcal {L}P))\) is the generator of a \(C_0\)-semigroup, then for any \(t\ge 0\) and all \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
for a constant \(c(t,b)>0\) depending on t and b, but independent of n .
5.1 Proof of Theorem 5.1
We assume for the sake of simplicity that \(t=1\) and split our proof into three parts:
for all \(x\in \mathcal {D}((\mathcal {L}P)^2)\).
Upper bound on Equation (12) The following lemma uses similar proof strategies as Lemma 3 in [5] and extends the result to infinite dimensions in the strong topology.
Lemma 5.2
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction satisfying the assumptions in Theorem 5.1. Then, for all \(x\in \mathcal {X}\)
The proof of the above lemma relies on a counting method: More precisely, we need to count the number of transitions in a binary sequence. This is related to the urn problem, where k indistinguishable balls are placed in l distinguishable urns [37, Chapter 1.9]. Then, there are
possibilities to distribute the balls so that each urn contains at least one ball.
Definition 5.3
Let \(S=\{A,B\}\), \(j,n,k\in \mathbbm {N}\), and \(n\ge 1\). We define
In words, N(j, n, k) counts the number of sequences consisting of k A’s and \(n-k\) B’s with the restriction that A changes to B or vice versa j times.
Example 2
Let \(S=\{A,B\}\), \(n=4\), and \(k=2\). Then,
Lemma 5.4
Let \(S=\{A,B\}\) and \(n,k,j\in \mathbbm {N}\) with \(k\le n\). Then,
for \(j\in \{0,...,2\min \{k,n-k\}-1_{2k=n}\}\). Otherwise \(N(j,n,k)=0\).
Proof
If \(j\ge 2\min \{n-k,k\}-1_{2k=n}\), then \(N(j,n,k)=0\) by Definition 5.3. Next we assume that \(j=0\), the only possible sequences are \(A^n\) (\(k=n\)) and \(B^n\) (\(k=0\)) so that \(N(0,n,k)=1_{k\in \{0,n\}}\). In the following, we assume that \(1\le j\le 2\min \{n-k,k\}-1_{2k=n}\), then there is a \(s\in S_{n,k}\) so that s includes exactly j transitions AB or BA so that \(N(j,n,k)>0\). In the odd case \(j=2l-1\) for \(l\in \{1,...,\min \{k,n-k\}\}\), the element s is constructed by l blocks of A’s and l blocks of B’s:
Identifying these blocks with distinguishable urns and the elements A and B with indistinguishable balls (q.v. Eq. 15), the task is to count the possibilities of placing k A’s in l urns and vice versa \(n-k\) B’s in l urns with the additional assumption that each urn must contain at least one A or one B. By changing the roles of A and B, we get twice the number of possible combinations. Therefore, one of the Twelvefold Ways [37, Chapter 1.9] shows
In the even case \(j=2l\) for \(l\in \{1,...,\min \{k,n-k\}-1_{2k=n}\}\), we argue similarly to the odd case. The only difference is that s is constructed by \(l+1\) blocks of A’s and l blocks of B’s or vice versa:
Then, the Twelvefold Ways [37, Chap. 1.9] proves the statement by
With the help of this counting method, we are ready to prove Lemma 5.2. In what follows, we identify the couple (A, B) with the product AB by slight abuse of notations.
Proof of Lemma 5.2
Assume w.l.o.g. \(P\ne 0\), then \(MP=PM=P\) because for all \(n\in \mathbbm {N}\)
and \(\left\| P \right\| _\infty \le 1\) holds by a similar argument because for all \(n\in \mathbbm {N}\)
The main idea is to split \(M=P+M^\perp \) with \(M^\perp {:}{=}P^\perp M\) and order the terms after expanding the following polynomial appropriately. Let \(A\, {:}{=}\, M^\perp e^{\frac{1}{n}\mathcal {L}}\) and \(B\, {:}{=}\, Pe^{\frac{1}{n}\mathcal {L}}\) so that
where elements in \(S_{n,k}\) are identified with sequences of concatenated operators and denoted by s. Then, we partition summands by the number of transitions from A to B or vice versa and use
The number of summands with j transitions is equal to N(j, n, k) given by Lemma 5.4 for \(j\in \{1, ..., m\}\) and \(m \, {:}{=}\, 2\min \{k,n-k\}-1_{2k=n}\). Then, the inequality above shows
In (1) above, we used the upper bound \(\left( {\begin{array}{c}n\\ k\end{array}}\right) \le \frac{n^k}{k!}\) to show
Additionally, we increase the upper index to \(\lfloor \frac{n}{2} \rfloor \) and upper-bound
Applying the assumptions again to
finishes the lemma:
\(\square \)
Remark
By the counting method introduced above, we can approximate \((Me^{\frac{1}{n}\mathcal {L}})^n\) by \((Pe^{\frac{1}{n}\mathcal {L}}P)^n\), which is independent of \(M^\perp \). In the previous works [2, 31], the operators considered in similar proof steps as Eqs. (13) and (14) depended on \(M^\perp \).
Upper bound on Eq. (13): In the next step, we apply our modified Chernoff Lemma 4.2:
Lemma 5.5
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(P\in {\mathcal {B}}(\mathcal {X})\) be a projection. Assume that both operators satisfy the same assumption as in Theorem 5.1. Then, for all \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
Proof
The proof relies on the modified Chernoff Lemma (q.v. Lemma 4.2) applied to the contraction \(C(\tfrac{1}{n})=Pe^{\frac{1}{n}\mathcal {L}}P\) on \(P\mathcal {X}\). Then, for all \(x\in \mathcal {X}\)
Moreover, the asymptotic Zeno condition (11) and the continuity of the norm imply
for all \(x\in \mathcal {D}(\mathcal {L}P)\). Hence, \(P^\perp \mathcal {L}P\) is a bounded operator with \(\Vert P^\perp \mathcal {L}P\Vert _\infty \le b\). Next, given \(x\in \mathcal {D}(\mathcal {L}P)\), the \(C_0\)-semigroup properties (q.v. Lemma 2.1) imply
Note that \(\int _{0}^{1}e^{\frac{\tau _1}{n}\mathcal {L}}P\mathcal {L}Px\) belongs to \(\mathcal {D}(\mathcal {L})\) by Lemma 2.1, but not necessarily to \(\mathcal {D}(\mathcal {L}P)\). However, for all \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
which proves Lemma 5.5. \(\square \)
Remark
As regards to the convergence rate of the quantum Zeno effect, Lemma 5.5 constitutes our main improvement compared to the work [2]. The modified Chernoff lemma allows to improve the convergence rate to \(n^{-1}\).
Upper bound on Eq. (14): Finally, we prove an upper bound on Equation (14), which can be interpreted as a modified Dunford–Segal approximation [18].
Lemma 5.6
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(P\in {\mathcal {B}}(\mathcal {X})\) be a projection. Assume that both operators satisfy the assumptions of Theorem 5.1. Then, for all \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
with \(e^{\tilde{b}}{:}{=}\sup _{s\in [0,1]}\Vert e^{sP\mathcal {L}P}P\Vert _\infty <\infty \).
Proof
The proof relies on the integral equation for semigroups from Lemma 2.2. We start by proving the continuity of
Since for all \(s\in [0,1]\) and \(x\in \mathcal {D}(\mathcal {L}P)\)
the vector-valued function defined in Equation (19) is equal to
and, thereby, well defined and continuous in s. Therefore, Lemma 2.2 gives for all \(x\in \mathcal {D}(\mathcal {L}P)\)
Moreover, for all \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
Finally, we use \(\sup _{s\in [0,1]}\Vert e^{sP\mathcal {L}P}P\Vert _\infty <\infty \), which holds by the principle of uniform boundedness (q.v. proof of Proposition 4.3), the property that \((e^{s nP(e^{\frac{1}{n}\mathcal {L}}-\mathbbm {1})P})_{s\ge 0}\) is a contraction, and the upper bounds \(\Vert P^\perp \mathcal {L}P\Vert _\infty \le b\) and \(\Vert Pe^{s\mathcal {L}}P^\perp \Vert _\infty \le sb\) so that
for all \(x\in \mathcal {D}((\mathcal {L}P)^2)\) and \(e^{\tilde{b}}=\sup _{s\in [0,1]}\Vert e^{sP\mathcal {L}P}P\Vert _\infty \). \(\square \)
The above approximation of \(e^{P\mathcal {L}P}\) by \(e^{nP(e^{\frac{1}{n}\mathcal {L}}-\mathbbm {1})P}\) is similar to the Dunford–Segal approximation, which would be given by \({\text {exp}}\big (n({\text {exp}}({\frac{1}{n}P\mathcal {L}P})-\mathbbm {1})\big )\): for the generator \((\mathcal {K},\mathcal {D}(\mathcal {K}))\) of a bounded \(C_0\)-semigroup, Gomilko and Tomilov proved [18, Corollary 1.4]
for all \(x\in \mathcal {D}(\mathcal {K}^2)\) and \(\tilde{b}{:}{=}\sup _{t\ge 0}\Vert e^{t\mathcal {K}}\Vert _\infty \). In our case, it is not clear whether \((e^{sP\mathcal {L}P})_{s\ge 0}\) is uniformly bounded.
Remark
The specificity of the last step stems from the fact that \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) is unbounded. In the previous works [2, 31], a similar step exits but in both papers \(\mathcal {L}\) was assumed to be bounded. Moreover, Equation (20) is the only step in the proof of Theorem 5.1, which deals with the operator \(P\mathcal {L}P\). If \(P\mathcal {L}P\) is closable, \(P\mathcal {L}Px=\overline{P\mathcal {L}P}x\) for all \(x\in \mathcal {D}(\mathcal {L}P)\) so that it is enough to ask for the closure of \(P\mathcal {L}P\) to define a generator. The same reasoning works for Proposition 5.7 and Corollary 3.3.
End of the proof of Theorem 5.1: We combine Lemmas 5.2, 5.5, and 5.6 to prove Theorem 5.1.
Proof of Theorem 5.1
Let \(x\in \mathcal {D}((\mathcal {L}P)^2)\). Then,
Redefining \(\mathcal {L}\) by \(t\mathcal {L}\) and b by tb, we achieve
with an appropriate constant \(c>0\) and \(e^{\tilde{b}}=\sup _{s\in [0,t]}\Vert e^{sP\mathcal {L}P}\Vert _\infty \). \(\square \)
Remark
The upper bound in Theorem 5.1 can be formulated for all \(x\in \mathcal {D}(\mathcal {L}P)\). For this, one must stop at an earlier stage of the proof and express the error terms by appropriate integrals. One possible bound would be the following:
5.2 Proof of Proposition 3.1 and Corollary 3.2
Proof of Proposition 3.1
Since \(\Vert P\Vert _\infty \le 1\) (17) and \(t\mapsto e^{t\mathcal {L}}\) is a uniformly continuous contraction semigroup, the generator is defined on \(\mathcal {X}\) and bounded, i.e., \(\Vert \mathcal {L}\Vert _\infty <\infty \), so that
where \(c_{p}{:}{=}\Vert \mathbbm {1}-P\Vert _\infty \le 2\). Then, we simplify the bounds found in Lemma 5.2, 5.5, and 5.6 to
where \(e^{\tilde{b}}=\sup _{s\in [0,t]}\Vert e^{sP\mathcal {L}P}\Vert _\infty \). By redefining \(\mathcal {L}\) by \(t\mathcal {L}\), b by tb, and using \(b\le \Vert \mathcal {L}\Vert _\infty c_{p}\),
which proves the statement. \(\square \)
Proof of Corollary 3.2
In closed quantum systems \(\mathcal {X}=\mathcal {H}\) equipped with the operator norm induced by the scalar product, which shows \(\Vert U\Vert _\infty =1\) for all unitaries \(U\in {\mathcal {B}}(\mathcal {H})\). Particularly, \(e^{\tilde{b}}=\sup _{s\in [0,t]}\Vert e^{sP\mathcal {L}P}\Vert _\infty =1\) because \(\Vert P\Vert _\infty =1\) is equivalent to \(P=P^\dagger \) [36, Theorem 2.1.9] so that PHP is Hermitian. Moreover, \(P=P^\dagger \) implies \((\mathbbm {1}-P)^\dagger =(\mathbbm {1}-P)\) which shows \(c_{p}=\Vert \mathbbm {1}-P\Vert _\infty \le 1\). Finally, the choice \(M=P\) implies \(\delta =0\) which proves the corollary by inserting the constants into Proposition 3.1. \(\square \)
5.3 Proof of Proposition 5.7
In this subsection, we weaken the assumptions (10) on the contraction M at the cost of stronger assumptions on the \(C_0\)-semigroup. For that, we combine techniques from holomorphic functional calculus with the semicontinuity of the spectrum of M perturbed by the semigroup under certain conditions. We refer to Appendix A for details on the tools needed to prove the main result of this section.
Proposition 5.7
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction such that
for some projection P, \(\delta \in (0,1)\) and \(\tilde{c}\ge 0\). Moreover, we assume that there is \(b\ge 0\) so that
where \(M^\perp =(\mathbbm {1}-P)M\). If \((P\mathcal {L}P,\mathcal {D}(\mathcal {L}P))\) generates a \(C_0\)-semigroup, then there is \(\epsilon >0\) such that for all \(t\ge 0\), \(n\in \mathbbm {N}\) satisfying \(t\in [0,n\epsilon ]\), \(\tilde{\delta }\in (\delta ,1)\), and \(x\in \mathcal {D}((\mathcal {L}P)^2)\)
for some constants \(c_1,c_2\ge 0\) depending on t, b, the difference \(\tilde{\delta }-\delta \), and \(\tilde{c}\).
The only difference to the proof of Theorem 5.1 is summarized in the question: How can we upper-bound \(\Vert (M^\perp e^{\frac{t}{n}\mathcal {L}})^k\Vert _\infty \) for all \(k\in \{1,...,n\}\) with the weaker assumption (21) on M? For that, we replace the argument in the proof of Lemma 5.2, which only works for the case \(\tilde{c}=1\).
Proof
Since the bounds found in Lemmas 5.5 and 5.6 are independent of the value of \(\tilde{c}\), it is enough to improve Lemma 5.2:
with \(e^{\tilde{b}}=\sup _{s\in [0,t]}\Vert e^{sP\mathcal {L}P}\Vert _\infty <\infty \). Since the assumption (21) on M is a special case of the uniform power convergence (q.v. Eq. (26)), Proposition B.1 shows the equivalence of the uniform power convergence of M to the spectral gap assumption, that is
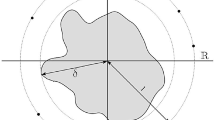
where the quasinilpotent operator corresponding to the eigenvalue 1 vanishes. Therefore, the eigenprojection P w.r.t. 1 satisfies \(MP=PM=P\) and the curve \(\gamma :[0,2\pi ]\rightarrow \mathbbm {C},\varphi \mapsto \tilde{\delta }e^{i\varphi }\) encloses the spectrum of \(M^\perp {:}{=}MP^\perp \) (q.v. Fig. 1). Together with the second bound in (22), Lemma A.2 shows that there exists \(\epsilon >0\) so that the spectrum of \(M^\perp e^{s\mathcal {L}}\) can be separated by \(\gamma \) for all \(s\in [0,\epsilon ]\). Therefore, the holomorphic functional calculus (q.v. Proposition A.1) shows for all \(t\in [0,n\epsilon ], k\in \mathbbm {N}\)
Let \(t\ge 0\), \(n\in \mathbbm {N}\) so that \(t\in [0,n\epsilon ]\). By the principle of stability of bounded invertibility [25, Theorem IV.2.21], \(R(z,M^\perp e^{s\mathcal {L}})\) is well defined and bounded for all \(z\in \gamma \) and \(s\in [0,\epsilon ]\). More explicitly, using the second Neumann series for the resolvent [25, p. 67], we have
where we have applied the assumption (22) and the following upper bound on s (q.v. Eq. 50):
to compute the geometric series. Combining Eqs. (23) and (24) shows for all \(k\in \{1,...,n\}\)
Next, we define \(A{:}{=}M^\perp e^{\frac{{t}}{n}\mathcal {L}}\) and \(B{:}{=}Pe^{\frac{{t}}{n}\mathcal {L}}\) and expand
The above \(n^{\text {th}}\) power can be expanded in terms of sequences of the form
Similar to Lemma 5.2, we can upper-bound every sequence w.r.t. the number of transitions AB or BA using the assumptions (22) on the \(C_0\)-semigroup as well as the inequality (25). The only difference to the proof of Lemma 5.2 is the constant \(c_2\) in the inequality so that
where \(m\, {:}{=}\, 2\min \{k,n-k\}-1_{2k=n}\). Then, for all \(x\in \mathcal {D}((\mathcal {L}P)^2)\) and an appropriate \(c_1\ge 0\)
\(\square \)
Proof of Proposition 3.4
Similar to Proposition 3.1,
where \(e^{\tilde{b}}=\sup _{s\in [0,t]}\Vert e^{sP\mathcal {L}P}\Vert _\infty \) and \(c_2{:}{=}\sup _{z\in \gamma }\left\| R(z,M^\perp ) \right\| _\infty \frac{2+2\tilde{\delta }^2}{1+2\tilde{\delta }^2}\) (see Eq. (24)). The constant \(c_2\) can be bounded with the help of the first von Neumann series [25, p. 37] and the geometric series:
so that
which finishes the proof of the proposition. \(\square \)
6 Uniform Power Convergence with Finitely Many Eigenvalues
In this section, we weaken the assumption on M to the uniform power convergence assumption (q.v. Eq. 26), that is we allow for finitely many eigenvalues \(\{\lambda _j\}_{j=1}^J\) and associated projections \(\{P_j\}_{j=1}^J\) satisfying \(P_jP_k=1_{j=k}P_j\). Similar to Theorem 3 in [2], we strengthen the assumptions on the \(C_0\)-semigroup to \(M\mathcal {L}\) and \(\mathcal {L}P_\Sigma \) being densely defined and bounded by \(b\ge 0\), where \(P_\Sigma {:}{=}\sum _{j=1}^{J}P_j\). Under those assumptions, we can prove the Zeno convergence in the uniform topology:
Theorem 6.1
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction satisfying the following uniform power convergence: There is \(\tilde{c}>0\) so that
for a set of projections \(\{P_j\}_{j=1}^J\) satisfying \(P_jP_k=1_{j=k}P_j\), eigenvalues \(\{\lambda _j\}_{j=1}^J\subset \partial \mathbbm {D}_1\), and a rate \(\delta \in (0,1)\). For \(P_\Sigma {:}{=}\sum _{j=1}^{J}P_j\), we assume that \(M\mathcal {L}\) and \(\mathcal {L}P_\Sigma \) are densely defined and bounded by \(b\ge 0\) and \(\Vert P_j\Vert _\infty =1\) for all \(j\in \{1,...,J,\Sigma \}\). Then, there is an \(\epsilon >0\) such that for all \(n\in \mathbbm {N}\), \(t\ge 0\) satisfying \(t\in [0,n\epsilon ]\), and \(\tilde{\delta }\in (\delta ,1)\)
for some constants \(c_1,c_2\ge 0\) depending on all involved parameters except from n.
6.1 Proof of Theorem 6.1
Similar to the papers [31] and [2], we use the holomorphic functional calculus to separate the spectrum of the contraction \(Me^{t\mathcal {L}}\) appearing in the Zeno sequence. In contrast to [2] where the \(C_0\)-semigroup is approximated by a sequence of uniformly continuous semigroups, we instead crucially rely upon the uniform continuity of the perturbed contraction to recover the optimal convergence rate. We upper-bound the following terms:
where the definitions of the perturbed spectral projection \(P_j(\tfrac{t}{n})\) and the Chernoff contraction \(C_{j}(\tfrac{t}{n})\) are postponed to Lemma 6.4.
Approximation of the Perturbed Spectral Projection In the following result, we consider an operator A uniformly perturbed by a vector-valued map \(t\mapsto B(t)\) in the following way:
Under certain assumptions on the perturbation controlled by t, we construct the associated perturbed spectral projection for which we obtain an approximation bound (cf. [2, Lemma 5.3]). The key tools are the holomorphic functional calculus and the semicontinuity of the spectrum under uniform perturbations. The statements are summarized in Proposition A.1 and Lemma A.2.
Lemma 6.2
Let \(A\in {\mathcal {B}}(\mathcal {X})\), \(t\mapsto B(t)\) be a vector-valued map on \({\mathcal {B}}(\mathcal {X})\) which is uniformly continuous at \(t=0\) with \(\sup _{t\ge 0}\Vert B(t)\Vert _\infty \le b\), and \(\Gamma :[0,2\pi ]\rightarrow \rho (A)\) be a curve separating \(\sigma (A)\). Then, there exists an \(\epsilon >0\) so that for all \(t\in [0,\epsilon ]\)
defines a projection with \(\left\| P(t) \right\| _\infty \le \tfrac{d|\Gamma |}{2\pi }\) and derivative at \(t=0\) given by
with \(\Vert P'\Vert _\infty \le \frac{R^2b|\Gamma |}{2\pi }\). The zeroth-order approximation of \(t\mapsto P(t)\) can be controlled by
and the first-order approximation by
Above \(|\Gamma |\) denotes the length of the curve \(\Gamma \), P abbreviates the unperturbed spectral projection P(0), \(R{:}{=}\sup _{z\in \Gamma }\Vert R(z,A)\Vert _\infty <\infty \), and \(d=R\inf _{z\in \Gamma }\frac{2+2|z|^2}{1+2|z|^2}\).
Proof
Since \(t\mapsto B(t)\) is uniformly continuous at \(t=0\), the vector-valued map \(t\mapsto A+tB(t)\) is uniformly continuous as well. Then, Lemma A.2 states that there exists an \(\epsilon >0\) such that \(\sigma (A+tB(t))\) is separated by \(\Gamma \) for all \(t\in [0,\epsilon ]\) and Proposition A.1 shows that
defines a projection on \(\mathcal {X}\) for all \(t\in [0,\epsilon ]\). Let \(R{:}{=}\sup _{z\in \Gamma }\Vert R(z,A)\Vert _\infty <\infty \), then using the same steps as in Eq. (24), we have that for all \(\eta \in \Gamma \)
Therefore, the perturbed resolvent is uniformly bounded. To prove the explicit representation of the derivative and the quantitative approximation, we follow the ideas of [2, Lemma 5.2–5.3]:
which uses the second resolvent identity, i.e., \(R(z,A+tB(t))tB(t)R(z,A)=R(z,A)-R(z,A+tB(t))\) for all \(z\in \Gamma \) and \(t\in [0,\epsilon ]\) and proves Equation (30) by Lebesgue’s dominated convergence theorem [22, Theorem 3.7.9]. Moreover, the above equation proves Eq. (31). Finally,
where \(|\Gamma |\) denotes the length of the curve \(\Gamma \). \(\square \)
Now, we are ready to prove Theorem 6.1.
Upper bound on Equation (27):
Lemma 6.3
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction with the same assumption as in Theorem 6.1 and \(c_p{:}{=}\Vert \mathbbm {1}-P_\Sigma \Vert _\infty \). Then, there is an \(\epsilon _1>0\) and \(c_2\ge 0\) so that for all \(t\ge 0\) and \(n\in \mathbbm {N}\) satisfying \(t\in [0,n\epsilon _1]\)
Proof
As in the proof of Proposition 5.7, B.1 shows that the uniform power convergence assumption (26), that is \(\Vert M^n-\sum _{j=1}^J\lambda _j^{{ n}}P_j\Vert _\infty \le \tilde{c}\,\delta ^n\) for all \(n\in \mathbbm {N}\), is equivalent to the spectral gap assumption (q.v. Appx. B),
with corresponding quasinilpotent operators being zero. Therefore, the curve \(\gamma :[0,2\pi ]\rightarrow \mathbbm {C},\varphi \mapsto \tilde{\delta }e^{i\varphi }\), with \(\tilde{\delta }\in (\delta ,1)\), encloses the spectrum of \(M^\perp {:}{=}MP_\Sigma ^\perp =P_\Sigma ^\perp M\), where \(P_\Sigma =\sum _{j=1}^JP_j\) and \(P_\Sigma ^\perp =\mathbbm {1}-P_\Sigma \) (q.v. Fig. 2). By Lemma 2.1
with \(c_{p}{:}{=}\Vert P_{\Sigma }^\perp \Vert _\infty \). Therefore, \(M^\perp e^{s\mathcal {L}}\) converges uniformly to \(M^\perp \) for \(s\downarrow 0\). Hence, Lemma A.2 shows that there exists an \(\epsilon _1>0\) such that the spectrum of \(M^\perp e^{s\mathcal {L}}\) can be separated by \(\gamma \) for all \(s\in [0,\epsilon _1]\). Therefore, we can apply the holomorphic functional calculus (Proposition A.1) to conclude that for all \(t\in [0,n\epsilon _1]\)
where \(k\in \{1,..,n\}\). By Equation (24) and with \(c_2{:}{=}\sup _{z\in \gamma }\Vert R(z,M^\perp )\Vert _\infty \frac{2+2\tilde{\delta }^2}{1+2\tilde{\delta }^2}\),
Moreover, by the assumptions \(\Vert P_\Sigma \Vert _\infty =1\), \(\Vert M\mathcal {L}\Vert _\infty \le b\), \(\Vert \mathcal {L}P_\Sigma \Vert _\infty \le b\), and Lemma 2.1
By the same expansion of \((Me^{\frac{t}{n}\mathcal {L}})^n=(P_\Sigma Me^{\frac{t}{n}\mathcal {L}}+M^\perp e^{\frac{t}{n}\mathcal {L}})^n\) as in the proof of Proposition 5.7,
Finally, Lemma 2.1 shows
so that
which finishes the proof. \(\square \)
Upper bound on Eq. (28) As in Lemma 5.5, we apply the modified Chernoff Lemma (4.2) to upper-bound the second term (28). However, our proof strategy includes two crucial improvements compared to Theorem 3 in [2]. Firstly, we show that the spectrum of the perturbed contraction is upper semicontinuous under certain assumptions on M and the \(C_0\)-semigroup. Therefore, we can use the holomorphic functional calculus and apply the modified Chernoff Lemma with respect to each eigenvalue separately, which allows us to achieve the optimal convergence as in Lemma 5.5.
Lemma 6.4
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction satisfying the same assumption as in Theorem 6.1. Then, there is an \(\epsilon _2>0\), and a \(\tilde{d}_1\ge 0\) so that for all \(t\ge 0\) and \(n\in \mathbbm {N}\) satisfying \(t\in [0,n\epsilon _2]\)
where \(C_{j}(\tfrac{1}{n}){:}{=}\bar{\lambda }_jP_{j}(\tfrac{1}{n})P_\Sigma Me^{\frac{1}{n}\mathcal {L}}P_\Sigma P_{j}(\tfrac{1}{n})\) and \(P_\Sigma {:}{=}\sum _{j=1}^{J}P_j\).
Proof
By Proposition B.1, the uniform power convergence (26) shows that the \(P_j\)’s are the eigenprojections of M so that \(P_\Sigma M=MP_\Sigma =\sum _{j=1}^{J}\lambda _jP_j\) and the spectrum \(\sigma (P_\Sigma M)\) consists of J isolated eigenvalues on the unit circle separated by the curves \(\Gamma _j:[0,2\pi ]\rightarrow \mathbbm {C},\phi \mapsto \lambda _j+re^{i\phi }\) (q.v. Sect. 2 and Fig. 3) with radius
Note that we use the curve interchangeably with its image and denote the formal sum of all curves around the eigenvalues \(\{\lambda _j\}_{j=1}^J\) by \(\Gamma \). In the following, we define the vector-valued function:
Since \(M\mathcal {L}\) is bounded, the defined vector-valued map converges in the uniform topology to \(P_\Sigma M\). Moreover, Lemma 2.1 shows that \(s\mapsto B(s)\) is uniformly bounded and continuous in \(s=0\) because
where we have used the assumption \(\Vert P_\Sigma \Vert _\infty \le 1\). Then, we can apply Lemma 6.2 which shows that there exists an \(\epsilon _2>0\) such that for all \(s\in [0,\epsilon _2]\)
defines the perturbed spectral projection w.r.t. \(\lambda _j\). Next, let \(t\ge 0\), \(n\in \mathbbm {N}\) such that \(t\in [0,n\epsilon _2]\). By Lemma 6.2 and Equation (37), the perturbed spectral projection can be approximated by
where \(R_j{:}{=}\sup _{z\in \Gamma _j}\Vert R(z,P_\Sigma M)\Vert _\infty \), \(d_j{:}{=}R_j\inf _{z\in \Gamma _j}\frac{2+2|z|^2}{1+2|z|^2}+\frac{1}{2}\), and we use that \(|\Gamma _j|=2\pi r\). Note that the defined \(d_j\) is not exactly the d in Lemma 6.2. Moreover, note that \(\Vert P_j(\tfrac{t}{n})\Vert _\infty \le d_jr\) and \(\Vert P'_j\Vert _\infty \le R_j^2br\). By the spectral decomposition,
Next, we aim at applying the modified Chernoff Lemma 4.2 to \(C_{j}(\tfrac{t}{n}){:}{=}\bar{\lambda }_jP_{j}(\tfrac{t}{n})P_\Sigma Me^{\frac{1}{n}\mathcal {L}}P_\Sigma P_{j}(\tfrac{1}{n})\) for all \(j\in \{1,..,J\}\), which has to be adapted since it is no longer clear that \(\Vert C_j(\tfrac{1}{n})\Vert _\infty =1\). We start by bounding the difference in norm between \(C_t(\tfrac{t}{n})\) and \(P_j(\tfrac{t}{n})\). By the fundamental theorem of calculus and the facts \(\Vert P_j(\tfrac{t}{n})\Vert _\infty \le d_jr\), \(\Vert P_{\Sigma }M\mathcal {L}\Vert _\infty \le b\), \(\Vert e^{s\mathcal {L}}\Vert _\infty \le 1\), \(|\lambda _j|=1\)
In the next step, we focus on the second term and prove a higher-order approximation then needed because in Lemma 6.5 we will reuse this calculation. In the following calculation, we use the bounds from above, in particular Equations (38) and (39). Moreover, we use the product rule for derivatives, which shows \(P_j'=P_jP_j'+P_j'P_j\) by \(\tfrac{\partial }{\partial s}P_j(s)=\tfrac{\partial }{\partial s}P_j(s)^2\) (cf. [31, Lemma 3]).
Combining Eqs. (41), (42), and \(\tfrac{t}{n}\le \epsilon _2\) shows
In Eqs. (38) and (44), we have proven that \(\Vert P_j(\tfrac{t}{n})-P_j\Vert \le \tfrac{t}{n}v_j\), \(\Vert C_j(\tfrac{t}{n})-P_j(\tfrac{t}{n})\Vert \le \tfrac{t}{n}w_j\) and note that \(\Vert P_j\Vert _\infty =1\), \(P_j(\tfrac{t}{n})C_j(\tfrac{t}{n})=C_j(\tfrac{t}{n})P_j(\tfrac{t}{n})=C_j(\tfrac{t}{n})\) holds by definition. Then, we can apply the approximate version of the modified Chernoff Lemma C.1 to \(C_j(\tfrac{t}{n})\). This shows
Combining Eqs. (40) and (44) and writing out the constants \(v_j\) and \(w_j\) gives
Finally, we define \(\tilde{d}_1=\max \nolimits _{j\in \{1,...,J\}}v_j+2w_j\), which finishes the proof. \(\square \)
Upper bound on Eq. (29):
Lemma 6.5
Let \((\mathcal {L},\mathcal {D}(\mathcal {L}))\) be the generator of a \(C_0\)-contraction semigroup on \(\mathcal {X}\) and \(M\in {\mathcal {B}}(\mathcal {X})\) a contraction with the same assumption as in Theorem 6.1. Then, there exists a constant \(\tilde{d}_2\ge 0\) such that
Proof
For ease of notation, we absorb the time parameter t into the generator \(\mathcal {L}\) and b. In order to prove the convergence of the generator, Equation (42) proves:
where \(R_j\, {:}{=}\, \sup _{z\in \Gamma _j}\Vert R(z,P_\Sigma M)\Vert _\infty \), \(d_j{:}{=}R_j\inf _{z\in \Gamma _j}\frac{2+2|z|^2}{1+2|z|^2}+\frac{1}{2}\), and r is the radius of the curves \(\Gamma _j\) defined in Equation (35). Then, we apply Lemmas 2.1 and 6.2 on the first term:
where we used Equation (38) in the last step and the assumption that \(M\mathcal {L}\) and \(\mathcal {L}P_{\Sigma }\) are bounded by b and all the inequalities discussed before Equation (43). In combination with Lemma 2.2
for all \(j\in \{1,..J\}\) and where \(w_j\) is defined in Equation (43). With one more application of Equation (38), this shows
where we choose \(\tilde{d}_2\ge 0\) appropriately and redefine \(\mathcal {L}\) by \(t\mathcal {L}\) and b by bt. \(\square \)
End of the Proof of Theorem 6.1 Finally, we combine the upper bounds found in the lemmas in order to finish the proof of Theorem 6.1.
Proof of Theorem 6.1
Lemmas 6.3, 6.4, and 6.5 show for all \(t\in [0,n\epsilon ]\) with \(\epsilon {:}{=}\min \{\epsilon _1,\epsilon _2\}\)
For an appropriate constant \(c_1\ge 0\), we finish the proof of Theorem 6.1. \(\square \)
7 Examples
In this section, we present two classes of examples, which illustrate the range of applicability of our results. In the examples, we denote by \(\rho ,\sigma \) quantum states.
Example 3
(Finite-dimensional quantum systems). We choose \(\mathcal {X}={\mathcal {B}}(\mathcal {H})\) to be the algebra of linear operators over a finite-dimensional Hilbert space \(\mathcal {H}\) endowed with the trace norm \(\Vert x\Vert _1=\textrm{tr}|x|\), \(M:{\mathcal {B}}(\mathcal {H})\rightarrow {\mathcal {B}}(\mathcal {H})\) a quantum channel, i.e., a completely positive, trace preserving linear map, and \(\mathcal {L}\) the generator of a semigroup of quantum channels over \({\mathcal {B}}(\mathcal {H})\), also known as a quantum dynamical semigroup. In finite dimension, it is know that every quantum channel is a contraction [38, Cor. 3.40], the spectrum includes the eigenvalue 1 [39, Theorem 3], and every linear operator in finite dimension has a discrete spectrum. Moreover, the nilpotent part of a quantum channel is zero [21, Lemma A.1]. Therefore, there exist \(\delta \in (0,1)\), \(\tilde{c}>0\), and a set of eigenvalues and projections \(\{\lambda _j,P_j\}_{j=1}^J\) such that for all \(n\in \mathbbm {N}\)
Note that the assumptions on the semigroup are satisfied due to the finiteness of the system and the contraction property of the \(P_j\) must be assumed additionally.
In the following example class, we calculate \(\delta \) directly.
Example 4
(Power convergence via strong data processing inequalities). As in Example 3, we define \(\mathcal {X}={\mathcal {B}}(\mathcal {H})\) endowed with the trace norm \(\Vert x\Vert _1\), \(M:{\mathcal {B}}(\mathcal {H})\rightarrow {\mathcal {B}}(\mathcal {H})\) a quantum channel, and \(\mathcal {L}\) the generator of a quantum dynamical semigroup. Here, we further assume the existence of a projection \(P:{\mathcal {B}}(\mathcal {H})\rightarrow \mathcal {N}\) onto a subalgebra \(\mathcal {N}\subset {\mathcal {B}}(\mathcal {H})\) with \(MP=PM\) and such that the following strong data processing inequality holds for some \(\hat{\delta }\in (0,1)\): for all states \(\rho \in \mathcal {X}\),
where we recall that the relative entropy between two quantum states, i.e., positive, trace-one operators on \(\mathcal {H}\), is defined as \(D(\rho \Vert \sigma ):=\textrm{tr}[\rho \log \rho -\rho \log \sigma ]\), whenever \({\text {supp}}(\rho )\subseteq {\text {supp}}(\sigma )\). Equation (45) was recently shown to hold under a certain detailed balance condition for M in [16]: There exists a full-rank state \(\sigma \) such that for any two \(x,y\in {\mathcal {B}}(\mathcal {H})\),
Here, \(x^*\), resp. \(M^*\), denotes the adjoint of x w.r.t. the inner product on \(\mathcal {H}\), resp. the adjoint of M w.r.t. the Hilbert–Schmidt inner product on \({\mathcal {B}}(\mathcal {H})\). In finite dimensions, the quantity \(\sup _\rho \,D(\rho \Vert P(\rho ))<\infty \) is called the Pimsner–Popa index of P [33]. Using Pinsker’s inequality, we see that the assumption of Theorem 6.1 is satisfied: for all \(x=x^*\in {\mathcal {B}}(\mathcal {H})\) with \(\Vert x\Vert _1\le 1\) and decomposition \(x=x_+-x_-\) into positive and negative parts and corresponding states \(\rho _{\pm }=x_{\pm }/\textrm{tr}[x_{\pm }]\),
Then, we can apply Proposition 3.4 which proves that there is an \(\epsilon >0\) such that for all \(n\in \mathbbm {N}\), \(t\in [0,n\epsilon ]\), and \(\tilde{\delta }\in (\delta ,1)\)
for \(n\rightarrow \infty \).
Example 5
(Infinite-dimensional quantum systems and unbounded generators). Here, we pick \(\mathcal {H}=L^2(\mathbb {R})\), denote by I the identity operator on \(\mathcal {H}\), let \(\sigma \) be a quantum state on \(\mathcal {H}\) and M a generalized depolarizing channel of depolarizing parameter \(p\in (\frac{1}{2},1)\) and fixed point \(\sigma \):
It is clear by convexity that M satisfies the uniform strong power convergence with projection \(P(\rho )=\textrm{tr}(\rho )\,\sigma \) and parameter \(\delta =2(1-p)<1\),
Let \(\mathcal {L}\) be a generator of a \(C_0\)-contraction semigroup such that \(\sigma \in \mathcal {D}(\mathcal {L})\). For example, let \(\mathcal {H}\) be the Fock space spanned by the Fock basis \(\{\vert 0 \rangle ,\vert 1 \rangle ,\vert 2 \rangle ,...\}\), a and \(a^\dagger \) be the annihilation and creation operator defined by \(a\vert 0 \rangle =0\), \(a\vert j \rangle =\sqrt{j}\vert j-1 \rangle \) for all \(j\in \mathbbm {N}_{\ge 1}\), and \(a^\dagger \vert j \rangle =\sqrt{j+1}\vert j+1 \rangle \) for all \(j\in \mathbbm {N}_{\ge 0}\). Then, define \(e^{t\mathcal {L}}(\rho ){:}{=}e^{-itH}\rho e^{itH}\) where \(H=a^\dagger a+\tfrac{1}{2}\) (\(H=-\Delta +x^2\)) is the Hamiltonian of the harmonic oscillator as in [2] and
Then, we have that for all \(t\ge 0\):
Moreover, by duality and the unitality of the maps \(e^{t\mathcal {L}^*}\) we have that
Therefore, the assumptions of Theorem 5.1 are satisfied and we find the convergence rate \(\mathcal {O}(n^{-1})\). Interestingly, this answers a conjecture of [2, Ex. 3, 5] for the Hamiltonian evolution generated by the one-dimensional harmonic oscillator. There, the authors had numerically guessed the optimal rate which we prove here. However, their analytic bounds could only provide a decay of order \(\mathcal {O}(n^{-\frac{1}{4}})\) (q.v. remark after Lemma 4.1) and for a restriction of H to a finite-dimensional stable subspace, which effectively assumed the boundedness of the generator.
The depolarizing noise considered in the previous example is artificial. In an infinite-dimensional bosonic system, a more natural model of noise is the photon loss channel, which we consider in the next example.
Example 6
(Bosonic beam splitter). We define the bosonic one-mode system by the algebra generated by the creation and annihilation operators \(a^*\) and a which satisfy the canonical commutation relation (CCR):
The associated Fock basis \(\{\vert 0 \rangle ,\vert 1 \rangle ,\vert 2 \rangle ,...\}\) is orthonormal and defined by
where the vacuum state \(\vert 0 \rangle \) satisfies \(a\vert 0 \rangle =0\). The Fock basis spans a Hilbert space called Fock space on which the operators from the CCR algebra are defined. A bosonic quantum state is a semidefinite operator in the CCR algebra with trace 1. A bosonic 2-mode system is defined by the CCR algebra generated by \(\{a,b,a^*,b^*\}\), which satisfy, additionally to the canonical commutation relation, \([a,b]=0\). Next, we consider the quantum beam splitter for \(\lambda \in [0,1)\)
where \(\textrm{tr}_2\) denotes the partial trace over the second register, \(U_\lambda {:}{=} e^{(a^* b-b^* a){\text {arcos}}(\sqrt{\lambda })}\), an environment state \(\sigma \), and y an element in the CCR algebra generated by \(\{a^*, a\}\). Moreover, \(P(y){:}{=}\textrm{tr}[y]\sigma \) defines a projection which satisfies \(PM_\lambda =M_\lambda P=P\) with the adjoint \(P^*(x)=\textrm{tr}[\sigma x]\mathbbm {1}\).
In order to establish, for example, the uniform power convergence of Theorem 5.1 in the topology of the trace distance, we would need to consider a convergence in the form of \(\Vert M_\lambda ^n(\rho )-\sigma \Vert _1\rightarrow 0\) in the limit of large n and uniformly in the initial state \(\rho \). Such property is notoriously hard to prove even in the classical setting [34]. Instead, we will consider a different metric on the set of quantum states which turns out to be more easy to work with.
We write \({\mathcal {B}}_{{N}}\) for the linear space of all N-bounded operators, where \( N= a^\dagger a\) corresponds to the photon number operator. That is the vector space of linear operators X on \(L^2(\mathbb {R})\) such that for any \(|\psi \rangle \in {\text {dom}}(N)\), \(|\psi \rangle \in {\text {dom}}(X)\) and there are some positive constants a, b such that
We define the Bosonic Lipschitz constant of a \(X\in {\mathcal {B}}_{{N}}\) as [17]
where the suppremum is over all pure states \(|\psi \rangle ,|\varphi \rangle \in {\text {dom}}({N})\) of norm 1. By duality, we then define the Bosonic Wasserstein norm of a linear functional f over \(\mathcal {B}_N\) with \(f(\mathbbm {1})=0\) as
where the supremum is over all N-bounded, self-adjoint operators X. We then choose our Banach space \(\mathcal {X}\) as the closure of the set of such linear functionals such that \(\Vert f\Vert _{W_1}<\infty \). In particular, whenever \(f\equiv f_{\rho -\sigma }\) is defined in terms of the difference between two quantum states \(\rho ,\sigma \) as \(f_{\rho -\sigma }(X)=\textrm{tr}((\rho -\sigma ) X)\), we denote the Wasserstein distance associated with the norm \(\Vert .\Vert _{W_1}\) as (see also [17]):
These definitions extend the classical Lipschitz constant \(\Vert \nabla f\Vert :=\sup _{x\in \mathbb {R}^2}|\nabla f(x)|\) of a real, continuously differentiable function f of 2 variables as well as the dual Wasserstein distance over probability measures on \(\mathbb {R}^2\).
In order to relate the Wasserstein distance to the statistically more meaningful trace distance, we seek for an upper bound on the trace distance in terms of \(W_{1}\). By duality of both metrics, this amounts to finding an upper bound on the Lipschitz constant \(\Vert \nabla X\Vert \) of any bounded operator X in terms of its operator norm \(\Vert X\Vert _\infty \). However, a bound of that sort does not exist (as classically, one can easily think of bounded observables which are not smooth). In the classical setting, the problem can be handled by first smoothing the function f, e.g., by convolving it with a Gaussian density g. In that case, one proves that there exists a finite constant \(C>0\) such that \(\Vert \nabla (f*g)\Vert \le C\Vert f\Vert _\infty \). In analogy with the classical setting, we can prove that for any two states \(\rho _1,\rho _2\) and \(\lambda \in [0,1)\) (see also [17, Proposition 6.4]),
where \(C^2:=(\Vert [a,\sigma ]\Vert _1^2+\Vert [a^*,\sigma ]\Vert _1^2)\lambda {(1-\lambda )^{-1}}\).
With a slight abuse of notations, we also write \(M_\lambda (f)\) for \(f\circ \mathcal {B}^*_\lambda \). It remains to prove the uniform power convergence. Proposition 6.2 from [17] gives
The uniform power convergence follows by \(P(f)(X)\equiv f\circ P^*(X)=\textrm{tr}(\sigma X)f(\mathbbm {1})=0\). Moreover, the asymptotic Zeno condition (11) is satisfied if \(\sigma \in \mathcal {D}(\mathcal {L})\) so that Theorem 5.1 is applicable.
As illustrated here, our asymptotic Zeno condition is easily verifiable and provides a rich class of examples. More examples for which our optimal convergence rate holds can be found in [2].
8 Discussion and Open Questions
In this paper, we proved the optimal convergence rate of the quantum Zeno effect in two results: Theorem 5.1 focuses on weakening the assumptions of the \(C_0\)-semigroup to the so-called asymptotic Zeno condition. Hence, Theorem 5.1 allows strongly continuous Zeno dynamics which is novel for open systems. In Theorem 6.1 instead, we weaken the assumption on M to the uniform power convergence as in [2, Theorem 3]. Additionally, we presented an example which shows the optimality of the achieved convergence rate. This brings up the question whether our assumptions are optimal and how the assumption on the contraction correlates with the assumption on the \(C_0\)-semigroup. For example, is it possible to weaken the uniform power convergence in Theorem 5.1 or Proposition 5.7 to finitely many eigenvalues on the unit circle without assuming stronger assumption on the semigroup? Following our proof strategy (q.v. Lemma 5.2), this question is related to the conjecture of a generalized version of Trotter’s product formula for finitely many projections under certain assumptions on the generator,
Another line of generalization would be to weaken the assumption on M to the strong topology as in Theorem 2 in [2]. There, the authors assume that \(M^n\) converges to P in the strong topology and that the semigroup is uniformly continuous. It would be interesting to know whether an extension to \(C_0\)-semigroups is possible. Finally, another important line of generalization would be to extend our results to time-dependent semigroups as in [31].
References
Barankai, N., Zimborás, Z.: Generalized Quantum Zeno Dynamics and Ergodic Means. arxiv:1811.02509 (2018)
Becker, S., Datta, N., Salzmann, R.: Quantum zeno effect in open quantum systems. In: Annales Henri Poincaré, vol. 22, pp. 3795–3840. Springer, New York (2021). https://doi.org/10.1007/s00023-021-01075-8
Beige, A., Braun, D., Tregenna, B., Knight, P.L.: Quantum computing using dissipation to remain in a decoherence-free subspace. Phys. Rev. Lett. 85, 1762–1765 (2000). https://doi.org/10.1103/PhysRevLett.85.1762
Beskow, A., Nilsson, J.: The concept of wave function and irreducible representations of the Poincaré group. II. Unstable systems and exponential decay law. In: Inst. of Theoretical Physics, Goteborg (1967)
Burgarth, D.D., Facchi, P., Nakazato, H., Pascazio, S., Yuasa, K.: Quantum zeno dynamics from general quantum operations. Quantum (2020). https://doi.org/10.22331/q-2020-07-06-289
Chernoff, P.R.: Note on product formulas for operator semigroups. J. Funct. Anal. 2, 238–242 (1968). https://doi.org/10.1016/0022-1236(68)90020-7
Dominy, J.M., Paz-Silva, G.A., Rezakhani, A.T., Lidar, D.A.: Analysis of the quantum Zeno effect for quantum control and computation. J. Phys. A Math. Theor. (2013). https://doi.org/10.1088/1751-8113/46/7/075306
Engel, K.-J., Nagel, R.: One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics, vol. 194. Springer, New York, London (2000). https://doi.org/10.1007/b97696
Erez, N., Aharonov, Y., Reznik, B., Vaidman, L.: Correcting quantum errors with the Zeno effect. Phys. Rev. A Atomic Mol. Opt. Phys. 69, 1050–2947 (2004). https://doi.org/10.1103/PhysRevA.69.062315
Exner, P.: One more theorem on the short-time regeneration rate. J. Math. Phys. (1989). https://doi.org/10.1063/1.528536
Exner, P., Ichinose, T.: Note on a product formula related to quantum zeno dynamics. In: Annales Henri Poincaré, vol. 22. Springer, New York (2021). https://doi.org/10.1007/s00023-020-01014-
Facchi, P., Lidar, D.A., Pascazio, S.: Unification of dynamical decoupling and the quantum Zeno effect. Phys. Rev. A At. Mol. Opt. Phys. (2004). https://doi.org/10.1103/PhysRevA.69.032314
Facchi, P., Pascazio, S.: Quantum Zeno dynamics: mathematical and physical aspects. J. Phys. Math. Theor. (2008). https://doi.org/10.1088/1751-8113/41/49/493001
Fischer, M.C., Gutiérrez-Medina, B., Raizen, M.G.: Observation of the quantum zeno and anti-zeno effects in an unstable system. Phys. Rev. Lett. (2001). https://doi.org/10.1103/PhysRevLett.87.040402
Franson, J.D., Jacobs, B.C., Pittman, T.B.: Quantum computing using single photons and the Zeno effect. Phys. Rev. A At. Mol. Opt. Phys. (2004). https://doi.org/10.1103/PhysRevA.70.062302
Gao, L., Rouzé, C.: Complete entropic inequalities for quantum Markov chains. Arch. Ration. Mech. Anal. (2022). https://doi.org/10.1007/s00205-022-01785-1
Gao, L., Rouzé, C.: Ricci Curvature of Quantum Channels on Non-commutative Transportation Metric Spaces. arXiv: 2108.10609 [quant-ph] (2021)
Gomilko, A., Tomilov, Y.: On convergence rates in approximation theory for operator semigroups. J. Funct. Anal. (2014). https://doi.org/10.1016/j.jfa.2013.11.012
Hahn, A., Burgarth, D., Yuasa, K.: Unification of Random Dynamical Decoupling and the Quantum Zeno Effect. arXiv: 2112.04242 [quant-ph] (2021)
Hall, B.C.: Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Graduate texts in mathematics, vol. 222, 2nd edn. Springer, New York (2015). https://doi.org/10.1007/978-3-319-13467-3
Hasenöhrl, M., Wolf, M.M.: Interaction-Free Channel Discrimination. arXiv: 2010.00623 [quant-ph] (2020)
Hille, E., Phillips, R.S.: Functional Analysis and Semi-groups. Reviewed and Expanded Edition, Vol. 31. Colloquium Publications. Providence, Rhode Island, American Mathematical Society (2000). https://doi.org/10.1090/coll/031
Hosten, O., Rakher, M.T., Barreiro, J.T., Peters, N.A., Kwiat, P.G.: Counterfactual quantum computation through quantum interrogation. Nature 439, 949–952 (2006). https://doi.org/10.1038/nature04523
Itano, W.M., Heinzen, D.J., Bollinger, J.J., Wineland, D.J.: Quantum zeno effect. Phys. Rev. A At. Mol. Opt. Phys. 41(5), 2295–2300 (1990). https://doi.org/10.1103/physreva.41.2295
Katō, T.: Perturbation Theory for Linear Operators. A Series of Comprehensive Studies in Mathematics, vol. 132, 2nd edn. Springer, New York (1995)
Kominis, I.K.: Quantum zeno effect explains magnetic-sensitive radical-ion-pair reactions. Phys. Rev. E (2009). https://doi.org/10.1103/PhysRevE.80.056115
Kreyszig, E.: Introductory Functional Analysis with Applications. Wiley, New York (1989)
Liu, W., Röckner, M.: Stochastic Partial Differential Equations: An Introduction. Springer, New York (2015)
Luchnikov, I.A., Filippov, S.N.: Quantum evolution in the stroboscopic limit of repeated measurements. Phys. Rev. A (2017). https://doi.org/10.1103/PhysRevA.95.022113
Misra, B., Sudarshan, G.: The Zeno’s paradox in quantum theory. J. Math. Phys. 18(4), 756–763 (1977). https://doi.org/10.1063/1.523304
Möbus, T., Wolf, M.M.: Quantum Zeno effect generalized. J. Math. Phys. (2019). https://doi.org/10.1063/1.5090912
Neidhardt, H., Stephan, A., Zagrebnov, V.A.: Operator-norm convergence of the trotter product formula on hilbert and banach spaces: a short survey. In: Rassias, T. (ed.) Current Research in Nonlinear Analysis, vol. 135, pp. 229–247. Springer, New York (2018). https://doi.org/10.1007/978-3-319-89800-1_9
Pimsner, M., Popa, S.: Entropy and index for subfactors. Ann. Sci. l’Ecole Norm. Supér. 19(1), 57–106 (1986)
Polyanskiy, Y., Wu, Y.: Dissipation of information in channels with input constraints. IEEE Trans. Inf. Theory 62(1), 35–55 (2016). https://doi.org/10.1109/TIT.2015.2482978
Schmidt, A.U.: Mathematics of the quantum zeno effet. In: Benton, C.V. (ed.) Mathematical Physics Research on the Leading Edge, pp. 113–143. Nova Science Publishers, New York (2004)
Simon, B.: Operator Theory. A comprehensive course in analysis, vol. 4. American Mathematical Society, Providence, Rhode Island (2015)
Stanley, R.P.: Enumerative Combinatorics. Springer, Boston, MA (1986). https://doi.org/10.1007/978-1-4615-9763-6
Watrous, J.: The Theory of Quantum Information. Cambridge University Press, Cambridge (2018)
Wolf, M.M., Perez-Garcia, D.: The Inverse Eigenvalue Problem for Quantum Channels. arXiv: 1005.4545v1 [quant-ph] (2010)
Zagrebnov, V.: Comments on the Chernoff \(\sqrt{n}\)-Lemma. In: Dittrich, J., Kovařík, H., Laptev, A. (eds.) Functional Analysis and Operator Theory for Quantum Physics. EMS Series of congress reports, European Mathematical Society, Zurich Switzerland (2017)
Zagrebnov, V.A.: Notes on the Chernoff Estimate. https://doi.org/10.48550/arXiv.2205.04794 (2022)
Acknowledgements
We would like to thank Michael Wolf and Markus Hasenöhrl for their support on this project. Moreover, we would like to thank Valentin A. Zagrebnov for his helping out with questions on the Chernoff Lemma and the anonymous reviewers for their constructive and detailed feedback. T.M. and C.R. acknowledge the support of the Munich Center for Quantum Sciences and Technology, and C.R. that of the Humboldt Foundation.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Alain Joye.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Holomorphic Functional Calculus and Semicontinuous Spectra
In this section, we introduce the holomorphic functional calculus and consider some continuity properties of the spectrum of perturbed operators. These two methods are used in Proposition 5.7 and Theorem 6.1 in the main text. Let’s start with the holomorphic functional: To be precise, the holomorphic functional calculus defines f(A) for \(A\in {\mathcal {B}}(\mathcal {X})\) and a function \(f:\mathbbm {C}\rightarrow \mathbbm {C}\) holomorphic on a neighborhood of \(\sigma (A)\) in such a way that, if the spectrum is separated into two sets, then the functions restricted to the separated subsets can be treated independently. This in turn is used to define spectral projections of A. More details on this topic can be found in Section 2.3 of [36]. We use the holomorphic functional calculus to introduce an integral representation of f(A) for a holomorphic function f, as well as its associated spectral projections:
Proposition A.1
(Holomorphic Functional Calculus [36, Theorem 2.3.1–3]). Let \(A\in {\mathcal {B}}(\mathcal {X})\), \(\Gamma :[0,2\pi ]\rightarrow \mathbbm {C}\) be a curve around \(\sigma (A)\), and f be a function that is holomorphic in the neighborhood of \(\sigma (A)\). Then,
is independent of \(\Gamma \). If a subset \(\tilde{\sigma }\) of the spectrum is separated by a curve \(\Gamma \), the spectral projection w.r.t. the enclosed subset is defined as
and satisfies \(P^2=P\) and \(PA=AP\). If \(\tilde{\sigma }=\{\lambda _0\}\) is an isolated eigenvalue, the following nilpotent operator
satisfies \(NP=PN=N\) and \(AP=\lambda _0P+N\).
In our case, M has finitely many isolated eigenvalues on the unit circle. However, if the semigroup perturbs those eigenvalues, the following lemma states a condition under which the separation of the spectrum is maintained.
Lemma A.2
(Semicontinuous Spectra [25, Sect. IV.3.1]). Let \(b\ge 0\) and \(M:\mathbbm {R}_{\ge 0}\rightarrow {\mathcal {B}}(\mathcal {X})\) be a vector-valued function which satisfies
Moreover, assume that \(\sigma (M(0))=\sigma _1\cup \sigma _2\) is a disjoint union separated by a curve \(\gamma :[0,2\pi ]\rightarrow \rho (M(0))\). For \(\epsilon >0\) satisfying
the spectrum of \(\sigma (M(t))\) is separated by \(\gamma \) for all \(t\in [0,\epsilon ]\).
Proof
Firstly, we show that Equation (50) is well defined—i.e., the value \(\epsilon >0\) exists. The compactness of the image of \(\gamma \) and the continuity of the resolvent [25, Theorem II.1.5] show that \(\sup _{z\in \gamma }\Vert R(z,M(0))\Vert _\infty <\infty \) and \(\epsilon >0\) exists. Then, we can apply Theorem 3.16 from [25, Sect. IV], which proves the lemma. \(\square \)
Remark
It is possible to generalize the lemma above to uniformly continuous vector-valued maps. This case, however, we loose the explicit bound on \(\epsilon \).
Appendix B. Spectral Gap Assumption
In the proofs of Proposition 5.7 and Theorem 6.1, we use the equivalence [2, Prop. 3.1] of the uniform power convergence and the spectral gap assumption with corresponding quasinilpotent operators being zero, that is there are eigenvalues \(\{\lambda _j\}_{j=1}^J\subset \partial \mathbbm {D}_1\) and a gap \(\delta \in (0,1)\) so that
Moreover, the quasinilpotent operators are assumed to be zero, that is
for \(\Gamma _{j}:[0,2\pi )\ni \varphi \mapsto \lambda _j+\frac{1}{2}\min \nolimits _{k,l\in \{1,..,J\}}\{\vert \lambda _k-\lambda _l \vert ,1-\delta \}e^{i\varphi }\) (q.v. Eq. 4). Additionally, the projections defined in the uniform power convergence are equal to the spectral projections
for all \(j\in \{1,...,J\}\) (q.v. Eq. 3). Since \(N_j=0\), \(P_jM=MP_j=\lambda _jP_j\) [36, Theorem 2.3.5]. The equivalence between the uniform power convergence and the spectral gap assumption with corresponding quasinilpotent operators being zero is given in [2, Proposition 3.1].
Proposition B.1
([2, Proposition 3.1]). Let \(M\in {\mathcal {B}}(\mathcal {X})\) be a contraction, \(J\in \mathbbm {N}\), \(\delta \in (0,1)\), and \(\{\lambda \}_{j=1}^J\subset \partial \mathbbm {D}_1\). Then, the following statements are equivalent:
-
(1)
The contraction M satisfies the spectral gap assumption w.r.t. \(\{\lambda _j\}_{j=1}^J\), the gap \(\delta \), and the corresponding quasinilpotent operators being zero.
-
(2)
There are projections \(\{P_j\}_{j=1}^J\), \(\delta \in (0,1)\) and \(\tilde{c}\ge 0\) such that \(MP_j=\lambda _j P_j\) for all \(j=\{1,...,J\}\) and
$$\begin{aligned} \left\| M^n-\sum _{j=1}^{J}\lambda _j^nP_j \right\| _\infty \le \,\tilde{c}\,\delta ^n. \end{aligned}$$ -
(3)
There are contractions \(\{C_j\}_{j=1}^J\) so that \(\lim \nolimits _{n\rightarrow \infty }\Vert M^n-\sum _{j=1}^{J}\lambda _j^nC_j\Vert _\infty =0\).
If any of the conditions above holds true, \(C_j=P_j\) and \(P_j\) are the eigenprojectors w.r.t. to the eigenvalue \(\lambda _j\).
Appendix C. Approximate Modified Chernoff \(\sqrt{n}\) Lemma
Lemma C.1
(Approximate Modified Chernoff Lemma). Let \(\epsilon >0\), \(P\in {\mathcal {B}}(\mathcal {X})\) a projection with \(\Vert P\Vert _\infty =1\), and \([0,\epsilon ]\ni t\mapsto P(t)\in {\mathcal {B}}(\mathcal {X})\), \([0,\epsilon ]\ni t\mapsto C(t)\in {\mathcal {B}}(\mathcal {X})\) be two vector-valued maps with the properties \(P(t)^2=P(t)\), \(P(t)C(t)=C(t)P(t)=C(t)\), \(\Vert P(t)-P\Vert _\infty \le tv\), and \(\Vert C(t)-P(t)\Vert _\infty \le tw\) for some \(v,w\ge 0\) and all \(t\in [0,\epsilon ]\). Then, for all \(n\in \mathbbm {N}\) with \(\frac{1}{n}\in [0,\epsilon ]\)
Proof
Similar to the proof of Lemma 4.2, we define \(C_t(\tfrac{1}{n}){:}{=}P(\tfrac{1}{n})+t(C(\tfrac{1}{n})-P(\tfrac{1}{n}))\) for \(t\in [0,1]\) and \(n\in \mathbbm {N}\) and we use the fundamental theorem of calculus so that
In the fourth inequality (51), we used
which proves the lemma. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Möbus, T., Rouzé, C. Optimal Convergence Rate in the Quantum Zeno Effect for Open Quantum Systems in Infinite Dimensions. Ann. Henri Poincaré 24, 1617–1659 (2023). https://doi.org/10.1007/s00023-022-01241-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-022-01241-6