Abstract
The bosonic signature operator is defined for Klein–Gordon fields and massless scalar fields on globally hyperbolic Lorentzian manifolds of infinite lifetime. The construction is based on an analysis of families of solutions of the Klein–Gordon equation with a varying mass parameter. It makes use of the so-called bosonic mass oscillation property which states that integrating over the mass parameter generates decay of the field at infinity. We derive a canonical decomposition of the solution space of the Klein–Gordon equation into two subspaces, independent of observers or the choice of coordinates. This decomposition endows the solution space with a canonical complex structure. It also gives rise to a distinguished quasi-free state. Taking a suitable limit where the mass tends to zero, we obtain corresponding results for massless fields. Our constructions and results are illustrated in the examples of Minkowski space and ultrastatic spacetimes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum field theory in globally hyperbolic spacetimes plays an important role in describing physical systems in the presence of gravitation fields, with applications to quantum effects near black holes and to cosmology. Furthermore, it can be regarded as an intermediate step towards quantum gravity, i.e. a unified description of spacetime and matter in the quantum realm. In the framework of algebraic quantum field theory, the quantization scheme consists of two steps (see for example [2, 7, 29]). First, one associates to a physical system a unital \(*\)-algebra \({\mathcal {A}}\), whose elements are interpreted as observables and which encodes structural properties such as causality and the canonical commutation or anti-commutation relations. In the second step, one chooses a state, defined as a positive linear functional \(\omega :{\mathcal {A}}\rightarrow {\mathbb {C}}\). Out of the pair \(({\mathcal {A}},\omega )\) one recovers the standard probabilistic interpretation of quantum theory via the GNS theorem, which gives a representation of the algebra by operators on a Hilbert space.
From the variety of states, one wants to select those states which are physically sensible. These states are characterized mathematically by the so-called Hadamard condition, a constraint on the wavefront set of the underlying two point distribution (see [7, 29] for recent surveys on this topic). While the existence of Hadamard states can be shown abstractly with glueing constructions (see [27, 28]), these methods are not explicit. Therefore, the construction of Hadamard states is an ongoing subject of intensive research. In recent years, two methods for constructing Hadamard states have been developed: the pseudo-differential operator approach [30,31,32] and the holographic method [3, 10,11,12]. The first method gives a whole class of states. The second method does give a distinguished state, but it has the shortcoming that it relies on conformal methods which only apply to massless fields.
For Dirac fields, a distinguished state which does not depend on observers or the choice of coordinates is the so-called fermionic projector state. Its construction uses the splitting of the Dirac solution space corresponding to the sign of the spectrum of the so-called fermionic signature operator  . This construction goes back to the perturbative treatment of the Dirac sea in [17]. The fermionic signature operator was first introduced in spacetimes of finite lifetime in [22]. The construction has been extended in [23] to spacetimes of infinite lifetime, making use of the so-called mass oscillation property. This construction has been proven to be useful for the construction of Hadamard states [9, 20, 24]. Moreover, the fermionic signature operator respects the spacetime symmetries [25] and is a suitable starting point for spectral geometry with Lorentzian signature [19]. Generalizations and related constructions can be found in [15, 21, 26].
. This construction goes back to the perturbative treatment of the Dirac sea in [17]. The fermionic signature operator was first introduced in spacetimes of finite lifetime in [22]. The construction has been extended in [23] to spacetimes of infinite lifetime, making use of the so-called mass oscillation property. This construction has been proven to be useful for the construction of Hadamard states [9, 20, 24]. Moreover, the fermionic signature operator respects the spacetime symmetries [25] and is a suitable starting point for spectral geometry with Lorentzian signature [19]. Generalizations and related constructions can be found in [15, 21, 26].
It is the goal of the present paper to adapt the construction of the fermionic signature operator to bosonic fields. For simplicity, we restrict attention to scalar fields, i.e. to the Klein–Gordon equation
and the massless wave equation
with real parameters m and \(\xi \). In this context, similar constructions in spacetimes of finite lifetime give rise to so-called SJ-states (see [5, 35, 40] and [6, 16]). In spacetimes of infinite lifetime, the only related constructions concern the analysis of Feynman propagators in [13]. In the present paper, we introduce the mass oscillation property for the Klein–Gordon field and construct the corresponding bosonic signature operator. As an application, we show that the bosonic signature operator endows the solution space of the Klein–Gordon equation with a canonical complex structure. It also gives rise to a distinguished quasi-free state, the bosonic projector state. Moreover, we show that, under suitable assumptions, one can take the limit \(m \searrow 0\) to extend the results to massless fields. We remark that our methods and results generalize in a straightforward way to other bosonic equations, in particular to the wave equation in the presence of gauge fields.
The main obstacle for adapting the constructions from the Dirac field to the Klein–Gordon field is that, on the space of solutions of the Klein–Gordon equation, there is no canonical scalar product, but instead the symplectic form \(\sigma _m\) defined by
where \(\mathscr {N}\) is an arbitrary Cauchy surface. As a consequence, the solution space does not carry a natural topology. In order to get a canonical scalar product and topology, we want to make use of the \(L^2\)-scalar product in spacetime after integrating over the mass parameter. Our goal is to derive a mass decomposition of this scalar product of the form
where \((\phi _m)_{m \in I}\) and \(({\tilde{\phi }}_m)_{m \in I}\) are families of solutions of the Klein–Gordon equation for a mass parameter \(m \in I\) with \(0 \not \in {\overline{I}}\) with suitable regularity properties (for details see Sect. 3). We remark that the factors m and \(m'\) in the above integrals can be understood from the fact that the Klein–Gordon equation only involves the mass squared. Therefore, it is preferable to integrate over the square of the mass \(a:=m^2\), which in view of the transformation law \(da = 2m \,\mathrm{d}m\) of the integration measures gives rise to the factor of m.
Once the decomposition (1.2) has been obtained, the scalar product \(\langle .|. \rangle _m\) in the integrand on the right hand side endows the solution space of the Klein–Gordon equation of mass m with the desired canonical Hilbert space structure. The main technical difficulty in implementing this method is that a Hilbert space structure on the solution space is needed right from the beginning in order to derive the above mass decomposition. In order to overcome this difficulty, we introduce an auxiliary scalar product of the form
where \((A_m)_{m \in I}\) is a suitable family of operators on the symplectic space (for details see again Sect. 3). Then we construct the mass decomposition 1.2 and show that it is indeed independent of the choice of the auxiliary scalar product. Moreover, we prove that the bosonic signature operator is uniquely defined as a bounded linear operator on the Hilbert space  .
.
In order to illustrate our methods and results, we consider two explicit examples: The Klein–Gordon equation in Minkowski space and the Klein–Gordon equation in an ultrastatic spacetimes. By explicit computation, we obtain in both cases that the bosonic signature operator reproduces the splitting of the solution space into solutions of positive and negative frequency. In this way, we obtain consistency with the usual construction of states in these spacetimes. The main benefit of using the bosonic signature operator is that the construction applies also in situations when spacetime is not ultrastatic, giving rise to a distinguished quantum state which is defined using the global geometry of spacetime. Other future applications include the study of the entanglement entropy in the absence of Killing fields.
The paper is organized as follows. In Sect. 2 we provide the necessary background on globally hyperbolic spacetimes and the Klein–Gordon equation. In Sect. 3 the bosonic mass oscillation property is defined and the corresponding mass decomposition is derived. In Sect. 4, the resulting bosonic signature operator is introduced, and it is shown that it gives rise to a canonical complex structure on the solution space of the Klein–Gordon equation as well as to the bosonic projector state. In Sect. 5, it is explained how the massless case can be treated by taking a suitable limit \(m \searrow 0\). In Sect. 6 it is shown that in flat Minkowski space, the bosonic signature operator has eigenvalues \(\pm 1\), and that the corresponding eigenspaces are the subspaces of positive and negative frequency, respectively. In Sect. 7 it is shown that this holds true in general ultrastatic spacetimes.
2 Preliminaries
Let \((\mathscr {M}, g)\) be a smooth, globally hyperbolic Lorentzian manifold of dimension \(k \ge 2\). For the signature of the metric we use the convention \((+ ,-, \ldots , -)\). As proven in [4], \(\mathscr {M}\) admits a smooth foliation \((\mathscr {N}_t)_{t \in {\mathbb {R}}}\) by Cauchy hypersurfaces. Thus \(\mathscr {M}\) is diffeomorphic to the product of \({\mathbb {R}}\) with a \((k-1)\)-dimensional manifold. We denote the wave operator on \((\mathscr {M}, g)\) by \(\Box _g\),
where \(\phi \in C^\infty (\mathscr {M}) = C^\infty (\mathscr {M}, {\mathbb {C}})\) is a smooth, complex scalar field. The Klein–Gordon operator \(P_m\) is defined by
where m is the rest mass and \(\xi \in {\mathbb {R}}\) is a dimensionless coupling constant to scalar curvature \(R_g\). We denote the solutions of the Klein–Gordon equation by \(\mathrm {Sol}_m(\mathscr {M})\). For clarity we remark that we always consider complex-valued fields.
The Cauchy problem for the Klein–Gordon equation is well-posed. This can be seen either by considering energy estimates for symmetric hyperbolic systems (see for example [34] or [18, Chapter 13]) or alternatively by constructing the Green’s kernel (see for example [1]). These methods also show that the Klein–Gordon equation is causal, meaning that the solution of the Cauchy problem only depends on the initial data in the causal past or future. In particular, if the initial data on \(\mathscr {N}_t\) has compact support, the solution \(\phi \) also has compact support on any other Cauchy hypersurface. This leads us to consider solutions \(\phi _m\) in the class \(C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_m(\mathscr {M})\) of smooth functions with spatially compact support. On solutions in this class, one introduces the symplectic form \(\sigma _\mathscr {N}\) by
where \(\nu \) denotes the future-directed normal. One immediately verifies that the symplectic form is sesquilinear and skew-symmetric, i.e.
Moreover, it does not depend on the choice of the Cauchy surface \(\mathscr {N}\). In order to see this, we let \(\mathscr {N}'\) be another Cauchy surface and \(\Omega \) the spacetime region enclosed by \(\mathscr {N}\) and \(\mathscr {N}'\). We then obtain
where in the last step we used that \(\Box \) and \(P_m\) differ by a real-valued multiplication operator. Integrating over \(\Omega \) and applying the Gauß divergence theorem, we find that \(\sigma _\mathscr {N}(\psi _m, \phi _m) = \sigma _{\mathscr {N}'}(\psi _m, \phi _m)\). In view of the independence of the choice of the Cauchy surface, we also denote the symplectic form (2.2) by \(\sigma _m(.,.)\).
The retarded and advanced Green’s operators \(S_m^\wedge \) and \(S_m^\vee \) are formal adjoints of each other (with respect to the \(L^2\)-scalar product on \(\mathscr {M}\)) and linear mappings (for details see for example [1, 37])
where \(C^\infty _0(\mathscr {M})\) denotes the vector space of smooth functions with compact support. They satisfy the defining equation of the Green’s operator
Moreover, they are uniquely determined by the condition that the support of \(S_m^\wedge \phi \) (or \(S_m^\vee \phi \)) lies in the causal future (respectively the causal past) of \({{\,\mathrm{supp}\,}}\phi \).
The causal fundamental solution is defined as the difference of the advanced and retarded Green’s operators
note that it maps to solutions of the Klein–Gordon equation. The fundamental solution gives rise to a sesquilinear form, which we again denote by \(G_m\),
In the next lemma, this sesquilinear is related to the symplectic form.
Lemma 2.1
For any \(f,g \in C^\infty _0(\mathscr {M})\)
Proof
Knowing that the definition of the symplectic form (2.2) does not depend on the choice of the Cauchy surface, it suffices to compute it for a Cauchy surface \(\mathscr {N}\) which lies in the future of the supports of f and g. Then, using (2.4) and the causal properties of the Green’s operators, we obtain
Choosing \(\Omega \) as the past of \(\mathscr {N}\), we can apply the Gauss divergence theorem and proceed as in (2.3) to obtain
This gives the result. \(\square \)
This lemma shows in particular that \(G_m\) is skew-symmetric, i.e.
3 The Bosonic Mass Oscillation Property
We consider the mass parameter in a bounded open interval, \(m \in I := (m_L, m_R)\) with \(0 \not \in {\overline{I}}\). We consider families of solutions \((\phi _m)_{m \in I}\) which are smooth and have spatially compact support, i.e. \(\phi _m \in C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_m(\mathscr {M})\) for all \(m \in I\). Moreover, we assume that the family depends smoothly on the mass parameter and vanishes identically for m outside a compact subset of \((m_L, m_R)\). Writing the mass parameter as an additional argument (i.e. \(\phi (x,m) = \phi _m(x)\)), we summarize these properties by writing
where \(C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\) denotes the smooth wave functions with spatially compact support which are also compactly supported in I. We denote the operator of multiplication with m by T,
Moreover, we denote the operation of integrating over m by \({\mathfrak {p}}\),
where, as explained after (1.2), we work with the integration measure \(m\,\mathrm{d}m\) (and \(\mathrm{d}m\) is the Lebesgue measure). We assume that \({\mathfrak {p}}\) maps to the square-integrable functions in spacetime, i.e.
(this assumption will be justified by the bosonic mass oscillation property to be introduced below). This makes it possible to introduce on \(C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\) a positive semi-definite sesquilinear form  by
by

Dividing out the null space and forming the completion gives a Hilbert space . We denote the corresponding norm by
. We denote the corresponding norm by  . We also refer to the scalar product
. We also refer to the scalar product  as the spacetime scalar product.
as the spacetime scalar product.
We now introduce an auxiliary scalar product on the solutions of the Klein–Gordon equation.
Definition 3.1
For every \(m \in I\) we let \(A_m\) be a linear operator on \(C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_m(\mathscr {M})\). The family \((A_m)_{m \in I}\) is referred to as a family of auxiliary operators if the following conditions holds:
-
(i)
The sesquilinear form \(\langle .|. \rangle _{A_m}\) defined by
$$\begin{aligned} \langle \phi _m \,|\, {\tilde{\phi }}_m \rangle _{A_m} := i \sigma _m \big ( \phi _m, A_m {\tilde{\phi }}_m \big ) \end{aligned}$$(3.2)is positive semi-definite.
-
(ii)
The operators \(A_m\) are uniformly bounded in the sense that there is a constant \(c>0\) such that
$$\begin{aligned} \big | \sigma _m \big ( A_m \phi _m, A_m \phi _m \big ) \big | \le c\, i \sigma (\phi _m, A_m \phi _m) \qquad \text {for all}~\phi \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}) \,. \end{aligned}$$(3.3) -
(iii)
For any \(\phi , {\tilde{\phi }} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\), the function
$$\begin{aligned} \sigma _m(\phi _m, A_m {\tilde{\phi }}_m) \qquad \text {is continuous in}~m \in I\,. \end{aligned}$$(3.4)
We remark that a sesquilinear, positive semi-definite form is Hermitian in the sense that
Thus, dividing out the null space, the sesquilinear form \(\langle .|.\rangle _{A_m}\) defines a scalar product. Forming the completion gives the Hilbert spaces  . We denote the corresponding norm by \(\Vert .\Vert _{A_m}\).
. We denote the corresponding norm by \(\Vert .\Vert _{A_m}\).
Let us explain the above assumptions. The positivity of (3.2) implies that the operator \(A_m\) is symmetric on  , as the following consideration shows. For any \(\phi _m \in C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_m(\mathscr {M})\),
, as the following consideration shows. For any \(\phi _m \in C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_m(\mathscr {M})\),
where in the last step we took the complex conjugate and used that, according to (2.2), taking the complex conjugate of the symplectic form flips its arguments and gives a minus sign. Polarizing (3.5), we conclude that
As a consequence,
giving the desired symmetry of \(A_m\) on  . Using this symmetry property, the inequality (3.3) simply means that the operators \(A_m\) are uniformly bounded on
. Using this symmetry property, the inequality (3.3) simply means that the operators \(A_m\) are uniformly bounded on  . In order to see this, we first note that uniform boundedness on
. In order to see this, we first note that uniform boundedness on  can be expressed by demanding that for all \(\phi \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\) and \(m \in I\),
can be expressed by demanding that for all \(\phi \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\) and \(m \in I\),
Expressing the scalar products via (3.2) in terms of the symplectic form gives precisely the inequality (3.3).
Next, on families of solutions \(\psi , \phi \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\) we introduce the auxiliary scalar product by integrating over the mass parameter,
Forming the completion gives the Hilbert space  . This Hilbert space can also be understood as the direct integral of the Hilbert space
. This Hilbert space can also be understood as the direct integral of the Hilbert space  ,
,

Now the methods in [23] apply, giving the following results.
Theorem 3.2
The following statements are equivalent:
-
(i)
There is a constant \(c>0\) such that for all \(\phi , {\tilde{\phi }} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\),
$$\begin{aligned} \big | \langle {\mathfrak {p}}\phi | {\mathfrak {p}}{\tilde{\phi }} \rangle _{L^2(\mathscr {M})} \big | \le c \int _I \, \Vert \phi _m\Vert _{A_m}\, \Vert {\tilde{\phi }}_m\Vert _{A_m}\, m\,\mathrm{d}m \,. \end{aligned}$$ -
(ii)
There is a constant \(c>0\) such that for all \(\phi , {\tilde{\phi }} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\), the following two relations hold:
$$\begin{aligned} \big | \langle {\mathfrak {p}}\phi | {\mathfrak {p}}{\tilde{\phi }} \rangle _{L^2(\mathscr {M})} \big |&\le c\, \Vert \phi \Vert _A\, \Vert {\tilde{\phi }}\Vert _A \end{aligned}$$(3.7)$$\begin{aligned} \langle {\mathfrak {p}}T \phi | {\mathfrak {p}}{\tilde{\phi }} \rangle _{L^2(\mathscr {M})}&= \langle {\mathfrak {p}}\phi | {\mathfrak {p}}T {\tilde{\phi }} \rangle _{L^2(\mathscr {M})}\,. \end{aligned}$$(3.8) -
(iii)
There is a family of linear operators
 which are uniformly bounded,
which are uniformly bounded,  (3.9)
(3.9)such that
$$\begin{aligned} \langle {\mathfrak {p}}\phi | {\mathfrak {p}}{\tilde{\phi }} \rangle _{L^2(\mathscr {M})} = \int _I \langle \phi _m \,|\, Q_m \,{\tilde{\phi }}_m\rangle _{A_m}\, m\,\mathrm{d}m \qquad \forall \, \phi , {\tilde{\phi }} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\,.\nonumber \\ \end{aligned}$$(3.10)
Proof
Follows exactly as the proof of [23, Theorem 4.2]. \(\square \)
The following proposition is proved exactly as [23, Proposition 4.2].
Proposition 3.3
(uniqueness of \(Q_m\)). The family \((Q_m)_{m \in I}\) in the statement of Theorem 3.2 can be chosen such that for all \(\phi , {\tilde{\phi }} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\), the expectation value \( f_{\phi , {\tilde{\phi }}}(m) := \langle \phi _m | Q_m {\tilde{\phi }}_m\rangle _{A_m}\) is continuous in m,
The family \((Q_m)_{m \in I}\) with the properties (3.10) and (3.11) is unique. Moreover, choosing two intervals \({\check{I}}\) and I with \(m \in {\check{I}} \subset I\) and \(0 \not \in {\overline{I}}\), and denoting all the objects constructed in \({\check{I}}\) with an additional check, we have
After these preparations, we are ready to represent the spacetime scalar product in terms of the symplectic form.
Definition 3.4
The Klein–Gordon operator \(P_m\) on the globally hyperbolic manifold \((\mathscr {M}, g)\) has the bosonic mass oscillation property with respect to the auxiliary operators \((A_m)_{m \in I}\) if the following conditions hold:
-
(i)
The operator T is symmetric on
 , i.e.
, i.e.  (3.13)
(3.13) -
(ii)
The norms on
 and
and  are equivalent, i.e. there is a constant \(c>0\) such that
are equivalent, i.e. there is a constant \(c>0\) such that  (3.14)
(3.14)
Theorem 3.5
Assume that the bosonic mass oscillation property holds with respect to the auxiliary operators \((A_m)_{m \in I}\). Then there is a unique family of operators  on
on  with the following properties:
with the following properties:
-
(i)
The spacetime scalar product is related to the symplectic form by
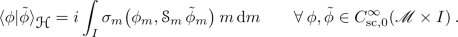 (3.15)
(3.15) -
(ii)
For any \(\phi , {\tilde{\phi }} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\), the expectation value
 is continuous in m.
is continuous in m. -
(iii)
The family of linear operators
 are uniformly bounded,
are uniformly bounded,  (3.16)
(3.16)
Moreover, the operator  does not depend on the choice of I, in the sense that choosing two intervals \({\check{I}}\) and I with \(m \in {\check{I}} \subset I\), then
does not depend on the choice of I, in the sense that choosing two intervals \({\check{I}}\) and I with \(m \in {\check{I}} \subset I\), then  for all \(m \in {\check{I}}\).
for all \(m \in {\check{I}}\).
Proof
Using Cauchy-Schwarz, the second inequality in (3.14) yields (3.7). Moreover, (3.13) gives (3.8). Therefore, Theorem 3.2 applies, giving the mass decomposition (3.10). Combining this formula with (3.2) yields

Therefore, we obtain (3.15) with  . The operators
. The operators  are uniformly bounded in m because of the uniform boundedness of \(A_m\) and \(Q_m\) (see (3.2) and Definition 3.1 (ii)). \(\square \)
are uniformly bounded in m because of the uniform boundedness of \(A_m\) and \(Q_m\) (see (3.2) and Definition 3.1 (ii)). \(\square \)
It remains to show that our results do not depend on the choice of the auxiliary operators.
Theorem 3.6
(independence of the choice of \(A_m\)). Let \((A_m)_{m \in I}\) and \((A'_m)_{m \in I}\) be two families of auxiliary operators. Then the corresponding Hilbert space norms are equivalent, i.e. there is a constant \(C>0\) such that
In other words, the Hilbert spaces  and
and  are equivalent as topological vector spaces. Moreover, the operators
are equivalent as topological vector spaces. Moreover, the operators  corresponding to the choices of auxiliary operators \((A_m)_{m \in I}\) and \((A'_m)_{m \in I}\) coincide.
corresponding to the choices of auxiliary operators \((A_m)_{m \in I}\) and \((A'_m)_{m \in I}\) coincide.
Proof
For clarity, we denote the operator  corresponding to the auxiliary operators \((A_m)\) by
corresponding to the auxiliary operators \((A_m)\) by  . Then, combining (3.6) with (3.2),
. Then, combining (3.6) with (3.2),
and similarly for \(A'_m\). Using that, according to (3.14), the corresponding norms are both equivalent to the norm  , we conclude that there is a constant c such that
, we conclude that there is a constant c such that
Let \({\tilde{\phi }}_m \in C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_m(\mathscr {M})\). We extend \({\tilde{\phi }}_m\) to a family \({\tilde{\phi }} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\). Next, we let \(\eta _\ell \in C^\infty _0(I)\) be a Dirac sequence which converges to the Dirac measure at m. Then, choosing \(\phi _m = \sqrt{\eta _\ell (m)}\, {\tilde{\phi }}_m\), we conclude that
functions \(\Vert {\tilde{\phi }}_m\Vert ^2_{A_m}\) and \(\Vert {\tilde{\phi }}_m\Vert ^2_{A'_m}\) are both continuous in m. Therefore, we can take the limit \(\ell \rightarrow \infty \) to obtain the pointwise inequality
This establishes the desired equivalence of the norms. Hence we can identify  and
and  as topological vector spaces.
as topological vector spaces.
In order to show uniqueness, we consider the representations (3.15) corresponding to \(A_m\) and \(A'_m\),

Here the integrand is again continuous in m, because for example

which is continuous in view of (3.11). Therefore, choosing again \(\phi _m = \sqrt{\eta _\ell (m)} \, {\tilde{\phi }}_m\), we may take the limit \(\ell \rightarrow \infty \) to obtain the pointwise identity

Polarizing and using a denseness argument, we conclude that  on
on  . \(\square \)
. \(\square \)
The integrand of (3.15) gives a canonical scalar product on \(C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_m(\mathscr {M})\),

Again dividing out the null space and taking the completion, we get the Hilbert spaces  . Taking their direct integrals gives back the Hilbert space
. Taking their direct integrals gives back the Hilbert space  ,
,

It follows immediately from the above results that the norms of the Hilbert spaces  and
and  are equivalent.
are equivalent.
We finally remark that, if one can prove the existence or give an explicit expression for a family of operators  satisfying (3.15), then the bosonic mass oscillation property given in Definition 3.4 follows immediately by choosing
satisfying (3.15), then the bosonic mass oscillation property given in Definition 3.4 follows immediately by choosing  .
.
4 The Bosonic Signature Operator and Applications
The constructions of the previous section gave us for any \(m \in I\) a Hilbert space of solutions  with a canonical scalar product (3.17). We now choose m as the physical mass; from now on it will be kept fixed. The operator
with a canonical scalar product (3.17). We now choose m as the physical mass; from now on it will be kept fixed. The operator  appearing in the definition of this scalar product is a bounded symmetric linear operator on
appearing in the definition of this scalar product is a bounded symmetric linear operator on  which is uniquely defined by the mass decomposition (3.15).
which is uniquely defined by the mass decomposition (3.15).
Definition 4.1
The operator  is referred to as the bosonic signature operator.
is referred to as the bosonic signature operator.
4.1 A Canonical Complex Structure
Being a bounded symmetric operator, we obtain the spectral decomposition

with a projection-valued spectral measure dE. Assume that the operator  has a trivial kernel,
has a trivial kernel,

Then the operator J given by

defines a canonical complex structure on the solution space of the Klein–Gordon equation. Indeed, the projection operators to its eigenspaces
map to subspaces of  referred to as the holomorphic and anti-holomorphic subspaces, respectively.
referred to as the holomorphic and anti-holomorphic subspaces, respectively.
4.2 The Bosonic Projector State
The canonical complex structure give rise to a distinguished quasi-free state, as we now outline. Following the algebraic approach, we define the algebra of fields \({\mathcal {A}}(\mathscr {M})\) as the free algebra generated by complex-valued test functions in \({\mathbb {C}}_{0}(\mathscr {M})\) divided by the ideal generated by the canonical commutation relations
(here G is again the causal fundamental solution (2.5)). A state \(\omega \) is a normalized and positive linear functional on the algebra of fields, i.e.
A state \(\omega \) is called quasi-free (or Gaussian) if the associated odd n-point functions all vanish, while the even ones can be computed with the Wick rule
where \({\mathcal {P}}\) denotes all possible permutations of the set \(\{1,\dots ,2n\}\) into a collection of elements \(\{\sigma (1),\dots ,\sigma (2n)\}\) such that \(\sigma (2k-1)<\sigma (2k)\) for all \(k=1,\dots ,n\). According to this formula, a quasi-free state is uniquely determined by its two-point function \(\omega _2\). For the bosonic projector state we choose
where \(\chi ^{\mathrm{hol}}\) is the projection to the holomorphic component (4.2).
Proposition 4.2
The two-point function given in (4.4) defines a quasi-free bosonic state.
Proof
Our task is to verify the positivity statement in (4.3) and the compatibility with the canonical commutation relations. Before beginning, we form the real Hilbert space  formed of the real-valued solutions. Restricting attention to these real-valued solutions, the scalar product and the symplectic form in (3.17) are both real. Therefore, the operator
formed of the real-valued solutions. Restricting attention to these real-valued solutions, the scalar product and the symplectic form in (3.17) are both real. Therefore, the operator  maps
maps  to itself. Using the spectral calculus, the same is true for the complex structure in (4.1),
to itself. Using the spectral calculus, the same is true for the complex structure in (4.1),

As a consequence, for real-valued f and g, we can decompose (4.4) into its real and imaginary parts,

In particular, we conclude that the real part is positive semi-definite, and that the imaginary part satisfies the relation
Now we can apply Proposition 5.2.23 (b) in the textbook [7] to obtain the result. \(\square \)
5 The Limiting Case of Massless Fields
In the constructions so far, it was essential that the scalar field was massive. Indeed, we cannot expect that integrating over the mass generates the desired decay for large times if we integrate over arbitrary small masses. This is the reason why we assumed that the interval I did not intersect a neighborhood of the origin. However, in many situations the bosonic signature operator  can be defined for all \(m>0\). If this is the case, one can hope to extend the results to the massless case by taking the limit \(m \searrow 0\).
can be defined for all \(m>0\). If this is the case, one can hope to extend the results to the massless case by taking the limit \(m \searrow 0\).
In order to relate the solution spaces for different masses, we let \(\mathscr {N}\) be an arbitrary Cauchy surface (we will show later that our results do not depend on the choice of this Cauchy surface). We identify a solution \(\phi _m \in C^\infty _{{\mathrm{sc}}}(\mathscr {M})\) with the corresponding Cauchy data
Clearly, the symplectic form (2.2) can be expressed in terms of the Cauchy data; we write for clarity \(\sigma _\mathscr {N}(\Phi , {\tilde{\Phi }})\). Moreover, the symplectic form is continuous with respect to the Sobolev norm
In what follows, it suffices to consider this norm locally on compact subsets of \(\mathscr {N}\).
Definition 5.1
The Klein–Gordon operator \(P_m\) is infrared regular on the Cau-chy surface \(\mathscr {N}\) if for every compact subset \(K \subset \mathscr {N}\), the restrictions of the bosonic signature operators to K converge in norm, i.e. if the limit

Under the above assumptions, we can define the sesquilinear form

Being the limit of scalar products, this sesquilinear form is positive semi-definite. Dividing out the null space and taking the completion, we obtain a Hilbert space, which we denote by  .
.
Proposition 5.2
If the Klein–Gordon operator \(P_m\) is infrared regular on the Cauchy surface \(\mathscr {N}\), then it is also infrared regular on any other Cauchy surface. Moreover, the limit in (5.1) does not depend on the choice of the Cauchy surface.
Proof
Let \(\mathscr {N}'\) be another Cauchy surface. We describe the time evolution operators from \(\mathscr {N}\) to \(\mathscr {N}'\) and from \(\mathscr {N}'\) to \(\mathscr {N}\) by
These mappings are symplectomorphisms. Moreover, standard energy estimates show that these mappings are continuous in \(H^{1,2}_\mathrm{{loc}}\oplus L^2_\mathrm{{loc}}\) on the respective Cauchy surfaces (for details see for example [34, Section 5.3] or [18, Chapter 13]).
Suppose we consider the symplectic forms in (5.1) on the Cauchy surface \(\mathscr {N}'\). Using that the time evolution operator preserves the symplectic form, we can also compute it on \(\mathscr {N}\),

Due to causality, there is a compact set \(K \subset \mathscr {N}'\) (which clearly depends on \(\Phi \) and \({\tilde{\Phi }}\)) such that the supports of all the waves on the right hand side of the last equation are contained in K for all m. Therefore, we can take the limit \(m \searrow 0\) using that these vectors converge in the Hilbert space in \(H^{1,2}(K) \oplus L^2(K)\), and that the operators  converge in norm on this Hilbert space. \(\square \)
converge in norm on this Hilbert space. \(\square \)
As a result of the above construction, we have two sesquilinear forms on the massless solutions \(C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_0(\mathscr {M})\): The symplectic form \(\sigma _0\) and the scalar product \(\langle .|. \rangle _0\). Since we took a rather weak limit, it is a-priori not clear whether these sesquilinear forms are bounded relative to each other. If they are, one can express one sesquilinear form relative to the other, giving rise to operators on the respective spaces. The spectral decompositions of these operators again give rise to a splitting of the solution space into distinguished subspaces. In order to illustrate how this can be done, assume that the symplectic form is bounded pointwise by the scalar product, i.e. that for every \(\phi _0 \in C^\infty _{{\mathrm{sc}}}(\mathscr {M}) \cap \mathrm {Sol}_0(\mathscr {M})\) there is a constant \(c>0\) such that

Then the Fréchet-Riesz theorem gives a symmetric linear operator

which is uniquely defined by the property

Other variations of this constructions can be used depending on the specific properties of the resulting sesquilinear forms.
For clarity, we finally point out that the above constructions are not conformally invariant in the sense that, even when applied to the conformal wave equation, the resulting scalar product \(\langle .|. \rangle _0\) will transform in an intricate (in general nonlocal) way under conformal transformations. This can be understood from the fact that the mass oscillation property makes it necessary to consider families of massive solutions, thereby breaking the conformal symmetry.
6 Example: Minkowski Space
In this section, we verify by direct computation that the bosonic mass oscillation property holds in Minkowski space. Moreover, we derive an explicit formula for the bosonic signature operator. As we shall see, the resulting canonical complex structure will give us back the usual frequency splitting. This is an important check showing that the bosonic signature operator gives physically sensible results.
We consider Minkowski space, i.e. the spacetime \(\mathscr {M}={\mathbb {R}}\times {\mathbb {R}}^3\) with the line element
We let \(\phi _m\) be a solution of the Klein–Gordon equation for a given mass \(m>0\),
For initial data on \({\mathbb {R}}^3\) at time \(t=0\) denoted by
the Cauchy problem has a unique solution (here \({\mathbf {x}}=(x^1, x^2, x^3) \in {\mathbb {R}}^3\), and \(\pi _{m,0}({\mathbf {x}})\) is the canonical momentum).
For our purposes, it is most convenient to write the solution of the Klein–Gordon equation as a Fourier integral over the upper and lower mass shell,
Then initial data is computed by
where \(\omega _k := \sqrt{{\mathbf {k}}^2+m^2}\). Next, the symplectic form (1.1) takes the form
Applying Plancherel’s theorem in the spatial variables, we obtain
We next consider a family of solutions \(\phi = (\phi _m)_{m \in I} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\). Integrating over the mass according to (3.1) gives
(note that the assumption \(\phi = (\phi _m)_{m \in I} \in C^\infty _{{\mathrm{sc}},0}(\mathscr {M}\times I)\) implies that the function \(\varphi _m(k)\) vanishes unless \(\sqrt{k^2} \in I\)). Applying Plancherel’s theorem in spacetime, it follows that
Comparing with (6.3), we conclude that

where the operator  acts on the solutions of positive and negative frequency by
acts on the solutions of positive and negative frequency by

We finally rewrite the bosonic signature operator as an operator acting on the initial data. To this end, from (6.1) and (6.2) we read off that
where \({\hat{\phi }}_{m,0}\) and \({\hat{\pi }}_{m,0}\) denote the spatial Fourier transforms. Thus, using (6.4),

We thus obtain the simple formula

The scalar product (3.17) can be computed most easily by using (6.4) in (6.3). We thus obtain
This is positive definite and Lorentz invariant, as desired. Moreover, one sees immediately that in the limit \(m \searrow 0\), this scalar product as well as the bosonic signature operators converge to

Using the notion of Definition 5.1, the Klein–Gordon equation in Minkowski space is infrared regular. Moreover, the operator  is again bounded on
is again bounded on  . Therefore, all our results apply as well to the scalar wave equation in Minkowski space.
. Therefore, all our results apply as well to the scalar wave equation in Minkowski space.
7 Example: Ultrastatic Spacetimes
In this section we prove that the bosonic mass oscillation property holds for the Klein–Gordon operator in ultrastatic spacetimes. We also compute the bosonic signature operator explicitly and verify that the resulting canonical complex structure reproduces the usual frequency splitting. For simplicity, we only consider the case \(\xi =0\) without coupling to scalar curvature. Thus we let \((\mathscr {M},g)\) be a k-dimensional globally hyperbolic spacetime which is ultrastatic in the sense that it is the product \(\mathscr {M}= {\mathbb {R}}\times \mathscr {N}\) with a metric of the form
where \(g_\mathscr {N}\) is a Riemannian metric on \(\mathscr {N}\). The global hyperbolicity of \((\mathscr {M}, g)\) implies that \((\mathscr {N}, g_\mathscr {N})\) is complete. In preparation, we formulate the Klein–Gordon equation in the Hamiltonian form, following the procedure in [14]. We denote spacetime points \(x \in \mathscr {M}\) by \(x=(t,{\mathbf {x}})\) with \({\mathbf {x}}\in \mathscr {N}\). We introduce the two-component vector \(\Phi _m\) by
Then the Klein–Gordon equation can be written as
with the Hamiltonian \(H_m\) given by
Moreover, the symplectic form (2.2) takes the form
In what follows, we shall work with the spectral calculus for the operator
with domain \(C^\infty _0(\mathscr {N})\) on the Hilbert space \(L^2(\mathscr {N})= L^2(\mathscr {N}, \mathrm{d}\mu _\mathscr {N})\). Using Chernoff’s method [8], one sees that the operator \(K_m^2\) is essentially self-adjoint (for details see [36, Theorem 7.1] or [38]). We denote the self-adjoint extension again by \(K_m^2\). Taking the square root, we obtain the spectral decomposition
where \(E_k\) is a projection-valued spectral measure. Moreover, we know that
Consequently, the Hamiltonian has the spectral decomposition
By direct computation, one verifies that
where we introduced the notation
Hence, given initial data \(\Phi _{m,0} \in C^\infty _0(\mathscr {N})^2\), the solution of the Cauchy problem takes the form
In order to simplify the following computation, we restrict attention to the case of non-compact Cauchy surface (the case of compact Cauchy surfaces can be treated similarly by replacing the \(\omega \)-integrals by sums). The spectral measure is absolutely continuous with respect to the Lebesgue measure, i.e. \(\mathrm{d}E_k = E_k \,dk\) (for details see [41]). Introducing \(\omega \) as an integration variable, we obtain
where \(k_\omega := \sqrt{\omega ^2-m^2}\). Therefore, the Fourier transform in t is computed by
Hence
where we transformed back to a k-integral and set \(m_k= \sqrt{\omega ^2-k^2}\). Now we can apply Plancherel’s theorem in the time variable to obtain

with

In the case of Minkowski space, this formula gives back (6.5). The eigenspaces of this operator are precisely the solutions of positive and negative energy, respectively.
Now the scalar product (3.17) takes the form
This is positive definite, as desired. Similar as described at the end of the previous section in Minkowski space, in an ultrastatic spacetime the Klein–Gordon equation is again infrared regular. More precisely, in the limit \(m \searrow 0\) of the scalar product and the bosonic signature operator converge to

In this way, in ultrastatic spacetimes all our results apply to the scalar wave equation as well.
8 Discussion and Outlook
In the present paper we gave a general construction of the bosonic signature operator in globally hyperbolic spacetimes. For the case of ultrastatic spacetimes, the complex structure defined by the bosonic signature operator in (4.1), i.e.

agrees with the usual frequency splitting as obtained in in [36, 39]. As a consequence, the resulting bosonic projector state is a Hadamard state. The main advantage of working with the bosonic signature operator is that the construction also applies to general time-dependent situations, in which the time evolution is not unitarily implementable Hamiltonian (see [33]). The only condition needed is that the bosonic mass oscillation property holds (see Definition 3.4). In this way, we obtain a canonical quantum state which does not depend on an observer. Instead, this state is determined by the global geometry of spacetime. We remark that, in the setting of a scattering process, the bosonic signature state does not coincide with the vacuum of the observer in the past or future, but instead it can be considered as being an “interpolation” between the scattering states (for a discussion of this point in the fermionic context see [17, Section 5]).
In the time-dependent situation, it is unknown whether the bosonic projector state is a Hadamard state. At present, there is no general argument to prove the Hadamard property (in particular, due to the dependence on the global geometry, it does not seem possible to apply gluing arguments as in [27, 28]). Also, at present there is no general method for verifying if a given spacetime has the bosonic mass oscillation property by constructing a suitable family of auxiliary operators \((A_m)_{m \in I}\). Instead, both the bosonic mass oscillation property and the Hadamard property must be verified for different classes of spacetimes in a case to case study. We expect that, similar as proven in the fermionic case in [9, 20, 24, 26], the bosonic projector state should be Hadamard in many physically interesting situations. These questions are part of an ongoing research program. Another direction of research is to extend our construction to spacetimes with bifurcate Killing horizons, as studied in the fermionic case in [15, 21, 26].
References
Bär, C., Ginoux, N., Pfäffle, F.: Wave Equations on Lorentzian Manifolds and Quantization, ESI Lectures in Mathematics and Physics. European Mathematical Society (EMS), Zürich (2007). arXiv:0806.1036 [math.DG]
Benini, M., Dappiaggi, C., Hack, T.-P.: Quantum field theory on curved backgrounds–a primer. Int. J. Mod. Phys. A 28(17), 1330023 (2013). 49. arXiv:1306.0527 [gr-qc]
Benini, M., Dappiaggi, C., Murro, S.: Radiative observables for linearized gravity on asymptotically flat spacetimes and their boundary induced states. J. Math. Phys. 55(8), 082301 (2014). 28. arXiv:1404.4551 [gr-qc]
Bernal, A.N., Sánchez, M.: On smooth Cauchy hypersurfaces and Geroch’s splitting theorem. Commun. Math. Phys. 243(3), 461–470 (2003). arXiv:gr-qc/0306108
Bombelli, L., Lee, J., Meyer, D., Sorkin, R.D.: Space-time as a causal set. Phys. Rev. Lett. 59(5), 521–524 (1987)
Brum, M., Fredenhagen, K.: ‘Vacuum-like’ Hadamard states for quantum fields on curved spacetimes. Class. Quant. Gravity 31(2), 025024 (2014). 16. arXiv:1307.0482 [gr-qc]
Brunetti, R., Dappiaggi, C., Fredenhagen, K., Yngvason, J. (eds.): Advances in Algebraic Quantum Field Theory. Math. Phys. Stud., Springer (2015)
Chernoff, P.R.: Essential self-adjointness of powers of generators of hyperbolic equations. J. Funct. Anal. 12, 401–414 (1973)
Dappiaggi, C., Finster, F., Murro, S., Radici, E.: The fermionic signature operator in De Sitter space-time. J. Math. Anal. Appl. 485(2), 123808 (2020). arXiv:1902.09144 [math-ph]
Dappiaggi, C., Hack, T.-P., Pinamonti, N.: Approximate KMS states for scalar and spinor fields in Friedmann-Robertson-Walker spacetimes. Ann. Henri Poincaré 12(8), 1449–1489 (2011). arXiv:1009.5179 [gr-qc]
Dappiaggi, C., Moretti, V., Pinamonti, N.: Rigorous steps towards holography in asymptotically flat spacetimes. Rev. Math. Phys. 18(4), 349–415 (2006). arXiv:gr-qc/0506069
Dappiaggi, C., Siemssen, D.: Hadamard states for the vector potential on asymptotically flat spacetimes. Rev. Math. Phys. 25(1), 1350002 (2013). 31. arXiv:1106.5575 [gr-qc]
Dereziński, J., Siemssen, D.: An evolution equation approach to the Klein-Gordon operator on curved spacetime. Pure Appl. Anal. 1(2), 215–261 (2019). arXiv:1709.03911 [math-ph]
Dimock, J., Kay, B.S.: Classical and quantum scattering theory for linear scalar fields on the Schwarzschild metric. Ann. Phys. I 175(2), 366–426 (1987)
Drago, N., Murro, S.: A new class of fermionic projectors: Møller operators and mass oscillation properties. Lett. Math. Phys. 107(12), 2433–2451 (2017). arXiv:1607.02909 [math-ph]
Fewster, C.J., Verch, R.: On a recent construction of ‘vacuum-like’ quantum field states in curved spacetime. Class. Quant. Gravity 29(20), 205017 (2012). 20. arXiv:1206.1562 [math-ph]
Finster, F.: Definition of the Dirac sea in the presence of external fields. Adv. Theor. Math. Phys. 2(5), 963–985 (1998). arXiv:hep-th/9705006
Finster, F., Kindermann, S., Treude, J.-H.: An Introductory Course on Causal Fermion Systems, in preparation. www.causal-fermion-system.com/intro-public.pdf
Finster, F., Müller, O.: Lorentzian spectral geometry for globally hyperbolic surfaces. Adv. Theor. Math. Phys. 20(4), 751–820 (2016). arXiv:1411.3578 [math-ph]
Finster, F., Murro, S., Röken, C.: The fermionic projector in a time-dependent external potential: Mass oscillation property and Hadamard states. J. Math. Phys. 57(7), 072303 (2016). arXiv:1501.05522 [math-ph]
Finster, F., Murro, S., Röken, C.: The fermionic signature operator and quantum states in Rindler space-time. J. Math. Anal. Appl. 454(1), 385–411 (2017). arXiv:1606.03882 [math-ph]
Finster, F., Reintjes, M.: A non-perturbative construction of the fermionic projector on globally hyperbolic manifolds I: space-times of finite lifetime. Adv. Theor. Math. Phys. 19(4), 761–803 (2015). arXiv:1301.5420 [math-ph]
Finster, F., Reintjes, M.: A non-perturbative construction of the fermionic projector on globally hyperbolic manifolds II: space-times of infinite lifetime. Adv. Theor. Math. Phys. 20(5), 1007–1048 (2016). arXiv:1312.7209 [math-ph]
Finster, F., Reintjes, M.: The fermionic signature operator and Hadamard states in the presence of a plane electromagnetic wave. Ann. Henri Poincaré 18(5), 1671–1701 (2017). arXiv:1609.04516 [math-ph]
Finster, F., Reintjes, M.: The fermionic signature operator and space-time symmetries. Adv. Theor. Math. Phys. 22(8), 1907–1937 (2018). arXiv:1708.09643 [math-ph]
Finster, F., Röken, C.: The fermionic signature operator in the exterior Schwarzschild geometry. Ann. Henri Poincaré 20(10), 3389–3418 (2019). arXiv:1812.02010 [math-ph]
Fulling, S.A., Narcowich, F.J., Wald, R.M.: Singularity structure of the two-point function in quantum field theory in curved spacetime. II. Ann. Phys. 136(2), 243–272 (1981)
Fulling, S.A., Sweeny, M., Wald, R.M.: Singularity structure of the two-point function quantum field theory in curved spacetime. Commun. Math. Phys. 63(3), 257–264 (1978)
Gérard, C.: An introduction to quantum field theory on curved spacetimes. Asymptotic Analysis in General Relativity, London Math. Soc. Lecture Note Ser., vol. 443, Cambridge Univ. Press, Cambridge, pp. 171–218 (2018)
Gérard, C., Wrochna, M.: Construction of Hadamard states by pseudo-differential calculus. Commun. Math. Phys. 325(2), 713–755 (2014). arXiv:1209.2604 [math-ph]
Gérard, C., Wrochna, M.: Hadamard states for the linearized Yang-Mills equation on curved spacetime. Commun. Math. Phys. 337(1), 253–320 (2015). arXiv:1403.7153 [math-ph]
Gérard, C., Wrochna, M.: Construction of Hadamard states by characteristic Cauchy problem. Anal. PDE 9(1), 111–149 (2016)
Helfer, A.D.: The Hamiltonians of linear quantum fields: I. Existence theory, arXiv:hep-th/9908011 (1999)
John, F.: Partial Differential Equations. fourth ed., Applied Mathematical Sciences, vol. 1, Springer-Verlag, New York (1991)
Johnston, S.: Feynman propagator for a free scalar field on a causal set. Phys. Rev. Lett. 103, 180401 (2009). arXiv:0909.0944 [hep-th]
Kay, B.S.: Linear spin-zero quantum fields in external gravitational and scalar fields. I. A one particle structure for the stationary case. Commun. Math. Phys. 62(1), 55–70 (1978)
Kay, B.S., Wald, R.M.: Theorems on the uniqueness and thermal properties of stationary, nonsingular, quasifree states on spacetimes with a bifurcate Killing horizon. Phys. Rep. 207(2), 49–136 (1991)
Much, A., Oeckl, R.: Self-adjointness in Klein-Gordon theory on globally hyperbolic spacetimes. Math. Phys. Anal. Geom. 24(1), 14 (2021). Paper No. 5. arXiv:1804.07782 [math-ph]
Much, A., Oeckl, R.: Complex structures for Klein-Gordon theory on globally hyperbolic spacetimes. Class. Quant. Gravity 39, 37 (2022). Paper No. 025015. arXiv:1812.00926 [math-ph]
Sorkin, R.D.: Scalar field theory on a causal set in histories form. J. Phys. Conf. Ser. 306, 012017 (2011). arXiv:1107.0698 [gr-qc]
Xavier, F.: Convexity and absolute continuity of the Laplace-Beltrami operator. Math. Ann. 282(4), 579–585 (1988)
Acknowledgements
We are grateful for support by the German Science Foundation (DFG) within the Priority Program SPP 2026 “Geometry at Infinity.” We would like to thank the referees for valuable comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Karl-Henning Rehren.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Finster, F., Much, A. A Canonical Complex Structure and the Bosonic Signature Operator for Scalar Fields in Globally Hyperbolic Spacetimes. Ann. Henri Poincaré 24, 1185–1209 (2023). https://doi.org/10.1007/s00023-022-01236-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-022-01236-3



 which are uniformly bounded,
which are uniformly bounded, 
 , i.e.
, i.e. 
 and
and  are equivalent, i.e. there is a constant
are equivalent, i.e. there is a constant 
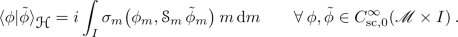
 is continuous in m.
is continuous in m. are uniformly bounded,
are uniformly bounded, 