Abstract
The main result of this paper is a complete proof of a new Lieb–Thirring-type inequality for Jacobi matrices originally conjectured by Hundertmark and Simon. In particular, it is proved that the estimate on the sum of eigenvalues does not depend on the off-diagonal terms as long as they are smaller than their asymptotic value. An interesting feature of the proof is that it employs a technique originally used by Hundertmark–Laptev–Weidl concerning sums of singular values for compact operators. This technique seems to be novel in the context of Jacobi matrices.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this note, we prove a conjecture of Hundertmark and Simon [2] concerning a sharp Lieb–Thirring inequality for Jacobi matrices. We denote the symmetric Jacobi matrix with diagonal entries \(\{ b_n\}_{n=-\infty }^\infty \) and off-diagonal entries \(\{a_n\}_{n=-\infty }^\infty \) by
It is assumed that the \(a_n\) tend to 1 as \(n \rightarrow \pm \infty \) which yields the interval \([-2,2]\) as the essential spectrum of this Jacobi matrix. We denote by \(E_j^+(J)\) the eigenvalues of J that are larger than 2 and by \(E_j^-(J)\) the eigenvalues of J that are less than \(-2\). Hundertmark and Simon proved that
and observed that this inequality is sharp. Indeed, in the absence of the potential, they noted that the Jacobi matrix with all entries \(a_n=1\) except for a single one that is chosen to be larger than one yields asymptotic equality in (1.1). They then conjectured the improved version of (1.1) in which \(|a_n-1|\) is replaced by \((a_n-1)_+\), where we use the notation \((a)_+\) to mean a if \(a>0\) and 0 if \(a \le 0\). We have the following theorem.
Theorem 1.1
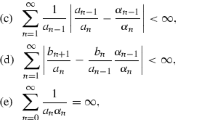
Assume that \(\sum _n |b_n| < \infty \), \( \sum _n (a_n-1)_+ < \infty \) and \(\lim _{n \rightarrow \pm \infty } a_n = 1\). Then we have the bound on the eigenvalue sum
The following consequence provides another justification for this short note. Generally, the proof of Lieb–Thirring inequalities is patterned after the ones for the continuum in which case the kinetic energy is given by \(-\Delta \). The discrete Laplacian requires that all \(a_n=1\). It is, however, of some interest that in the case of Jacobi matrices this needs not be the case. This is a distinguishing feature of Lieb–Thirring inequalities for Jacobi matrices. Further, it was shown in [5], (see also [7]) that
where \(G(a) = a^2-1-\log |a|^2\) and \(F(E) = \beta ^2 -\beta ^{-2} - \log |\beta |^2\) and \(E=\beta +\beta ^{-1}\) with \(|\beta |>1\).
In [6], one of us proved that if \(a_n\equiv 1\) then the inequality (1.1) implies (1.3). Using this argument and Theorem 1.1, we obtain as a consequence
Theorem 1.2
Let \(\gamma >1/2\). Assume that \(\sum _n b_n^{\gamma +1/2} < \infty \) and that \(a_n\ge 0\) for all \(n \in {\mathord {{\mathbb {Z}}}}\) with \(\lim _{n \rightarrow \pm \infty } a_n = 1\) and \(\sum _n (a_n-1)_+^{\gamma +1/2}<\infty \). Then with \(\mathrm {B}(x,y)\) denoting the Beta function
For \(\gamma =3/2\), the left-hand side coincides with \(\frac{1}{2}\sum _{j}F(E_j^\pm (J))\). The function \(G(a) \ge 0\) equals zero if and only if \(a= \pm 1\) and hence (1.4) is an improvement over (1.3) for the case where \(0 \le a_n \le 1\).
Remark
As proved in [6], the left-hand side in (1.4) is bounded from below by
and by
Thus, (1.4) improves on the corresponding Lieb–Thirring inequalities in [2]. Note that in [2, p.121] an argument is given that allows to replace \((a_n-1)\) in their results by \((a_n-1)_+\) for \(\gamma \ge 1\) but importantly not for \(1/2<\gamma <1\) and not in the case of the main result (1.2).
In order to prove Theorem 1.1, we reduce the problem (as in [2]) to the discrete Schrödinger operator. When treating terms \(0 \le a_n \le 1\), we use some additional convexity property.
2 The Proof of the Main Result
We follow Hundertmark and Simon except for one key step. Using norm resolvent convergence, we may assume that only finitely many of the \(a_n\) are not equal to one and finitely many \(b_n\) are not equal to zero. Likewise, we may assume that \(b_n \ge 0\). We also write
with the understanding that A contains only the off-diagonal terms and B the diagonal terms of the Jacobi matrix. If the off-diagonal terms are all equal to one, we denote the corresponding matrix by \(A_1\). The essential spectrum is given by the interval \([-2,2]\) which follows from Weyl’s theorem. Let us denote the eigenvalues that are strictly greater than 2 by \(E^+_1(A+B) \ge E^+_2(A+B) \ge E^+_3(A+B) \ge \cdots \). In what follows, the eigenvalues that are strictly less than \(-2\) can be treated in a similar fashion.
Treating \(a_n>1\): Consider the window of the matrix A that contains an off-diagonal term \(a>1\) and use the elementary inequalities
Applying it to all \(a_n>1\), we obtain
where
where \([x]_\pm = \max \{\pm x,0\}\). This implies
and similarly
This reduces the problem to the case \(a_n\le 1\), \(n\in {\mathbb {Z}}\).
Treating \(a_n\le 1\): Assuming \(a_n\le 1\), we consider the Birman–Schwinger operator
where \(\beta >2\) and list the eigenvalues of the Birman–Schwinger operator, \(E_j(B^{1/2} (\beta - A)^{-1} B^{1/2})\), in decreasing order. The Birman–Schwinger principle states that the j-th eigenvalue of \( B^{1/2} (E^+_j(A+B) - A)^{-1} B^{1/2}\) is one.
Let us decompose the matrix A in a certain fashion. Consider the following window of the general matrix \(A_\kappa \),
The distinct notation \(\kappa \) indicates that we concentrate on this particular position of the matrix. Denote by U the infinite diagonal matrix that consists of \(+1\) on the diagonal above the position of \(\kappa \) and of \(-1\) below \(\kappa \), i.e., its window is given by
It has the effect that the corresponding window of the matrix \(U \,A_\kappa \,U\) is given by
i.e., the entry \(\kappa \) changes sign and all others are unchanged. Since U is unitary, the matrices A and \(UA\,U\) are unitarily equivalent and have the same spectrum. With a slight abuse of notation, we now identify the matrices with their window. If we assume that \(0\le \kappa <1\), we may write
or if we denote by \(A'\) the first matrix displayed above we can write
Repeating this for all the off-diagonal elements that are strictly less than one we find
where off-diagonal elements of \(A_1\) are equal one and where \( \lambda _j \ge 0, \, \sum _j \lambda _j = 1\). Since the matrices U(j) are diagonal and have the matrix elements \(\pm 1\), the matrices \( A_1\) and \(U(j) A_1 U(j)\) have the same eigenvalues.
The key observation is the following lemma.
Lemma 2.1
Let \(\beta I > X\). Then the function
is operator convex, i.e., if \(0\le \lambda \le 1\) then
Proof
We follow [1]. Let \(Y_j = \beta - X_j\), \(j=1,2\). It amounts to showing that for two positive and invertible self-adjoint operators \(Y_1\) and \(Y_2\), we have
This is equivalent to
or
which is equivalent to
This is an inequality in terms of the positive, invertible and self-adjoint operator \(Y= Y_2^{-1/2} Y_1Y_2^{-1/2}\), i.e.,
which reduces the whole problem to positive numbers on account of the spectral theorem. For positive numbers, the inequality is obvious. \(\square \)
Applying now Lemma 2.1 to (2.2), we find
If we set \(\beta = \mu + \frac{1}{\mu }\) and introduce the operator,
we find
The operator \( L_\mu (A_1) \) has the matrix representation
where once more
Denote by \(S_n(\mu )\) the sum of the n largest eigenvalues of \(\sum _j \lambda _j U(j) L_\mu (A_1) U(j) \).
Lemma 2.2
for \(\nu \ge \mu \).
We will present two proofs of this Lemma.
Proof of Lemma 2.2 following Hundertmark and Simon
[2]. Pick any bounded sequence \(\{ \mu _n\}_{n=-\infty }^\infty \) and consider the matrix
where
Now we fix some integer n and set \(\mu _n = \mu \). All the other ones are fixed. The matrix \(\sum _j \lambda _j U(j) L_{\{\mu _n\}}U(j) \) is an affine function of \(\mu \) with a diagonal that is independent of \(\mu \) and hence the matrix is of the form
Now we consider the sum of the top n eigenvalues of this matrix and denote this function by \(f(\mu )\). This function is convex. Moreover, if we consider the diagonal matrix \(V: \ell ^2 \rightarrow \ell ^2\) given by
we find that
since the matrix V is also diagonal and commutes with the U(j). This matrix has the same spectrum but is of the form
and hence \(f(\mu )\) is even. Thus, f, being convex, is monotone for \(\mu >0\). \(\square \)
Remark
The above proof is closely related to the proof of a similar result from [4] except for using some symmetry property rather than perturbation at the spectral point zero.
Proof of Lemma 2.2 following Hundertmark, Laptev and Weidl
[3]. We aim to use the following abstract result of [3] concerning the sum \(\Vert T\Vert _n\) of the largest n singular values of a compact operator T,
The result is an immediate consequence of \(\Vert T\Vert _n\) defining a norm by Ky-Fan’s inequality.
Lemma 2.3
Let T be a non-negative compact operator on a Hilbert space \(\mathcal {G}\), let g be a probability measure on \(\Omega \), and let \(\{V(k)\}_{k\in \Omega }\) be a family of unitary operators on \(\mathcal {G}\). Then, for any \(n\in {\mathord {{\mathbb {N}}}}\),
To apply the above result to \(L_\mu (A_1)\), we recall the unitary map \(\mathcal {F}:L^2([-\pi ,\pi ])\rightarrow \ell ^2({\mathord {{\mathbb {Z}}}})\) onto the Fourier coefficients
By means of the transform \(\mathcal {F}\), the free operator W with \(a_n\equiv 1, b_n\equiv 0\) is unitarily equivalent to the operator \(2\cos k\) on \(L^2([-\pi ,\pi ])\). Defining \(g_\mu \) to be the non-negative function
and denoting by T the rank one operator onto \(b_n^{1/2}\), and by V(k) the unitary operator \((V(k)u)_n=\mathrm{e}^{-\mathrm{i}n k} u_n\), we can thus write
To obtain some more properties of \(g_\mu \), we note that its Fourier transform is given by \((\widehat{g}_\mu )_n=\mu ^{|n|}\). This can in particular be used to establish the aforementioned matrix representation of \(L_\mu (A_1)\). For our purposes, we note that for \(0<\mu<\nu < 1\) clearly
Since \({g}_{\mu }\) is smooth and periodic in k, the pointwise identity
holds and the properties (2.3) imply
for all \(0<\mu<\nu < 1\). The convolution identity is understood in the sense that
which is well-defined since all three functions are periodic. Using this identity together with the fact that \(V(k'+k'')=V(k')V(k'')\) and that \(V(k')\) and U(j) commute as both are multiplication operators, we obtain
By periodicity, the operator
is independent of \(k'\) and thus we can apply Lemma 2.3 to obtain the desired monotonicity. The special case \(\nu =1\) is an immediate consequence of Lemma 2.3. \(\square \)
Remark
The above proof is closely related to the continuous case [3] with the established convolution identity for \(g_\mu \) replacing the fact that the Cauchy distribution is a convolution semigroup. Using the parametrization \(\mu =\mathrm{e}^{-\sigma }, \nu =\mathrm{e}^{-\tau }\) with \(\sigma>\tau >0\), the above identity may also be written in the more similar form \(\frac{g_{\tau }}{\sqrt{2\pi }}*\frac{g_{\sigma -\tau }}{\sqrt{2\pi }}=\frac{g_{\sigma }}{\sqrt{2\pi }}\).
Because of the Birman–Schwinger principle, \(E_j(K(A;E_j^+))\), the j-the eigenvalue of \(K(A; E_j^+)\), equals 1 and hence
where \(\mu _j+\frac{1}{\mu _j} = E^+_j\). Now, again, we proceed as in Hundertmark–Simon [2] and get the estimate
where \(S_{N^+}(\mu _n)\) includes all the eigenvalues of \(\widetilde{J}\) that are greater than 2. In other words
As shown in [2], the Jacobi matrices
are unitarily equivalent and hence it follows that
which together with the previous estimate proves Theorem 1.1.
As a corollary, we obtain Theorem 1.2.
Proof of Theorem 1.2
Let \(\chi _{\{c,d\}}\) be the characteristic function of the interval (c, d). Then, recalling \(J\le \widetilde{J}^+\), we have
Applying first the variational principle and then the main result, we obtain
and the proof is complete. \(\square \)
References
Hiai, F., Petz, D.: Introduction to Matrix Analysis and Applications. Springer, Universitext, Berlin (2014)
Hundertmark, D., Simon, B.: Lieb–Thirring inequalities for Jacobi matrices. J. Approx. Theory 118(1), 106–130 (2002)
Hundertmark, D., Laptev, A., Weidl, T.: New bounds on the Lieb–Thirring constants. Invent. Math. 140, 693–704 (2000)
Hundertmark, D., Lieb, E.H., Thomas, L.E.: A sharp bound for an eigenvalue moment of the one-dimensional Schrödinger operator. Adv. Theor. Math. Phys. 2(4), 719–731 (1998)
Killip, R., Simon, B.: Sum rules for Jacobi matrices and their applications to spectral theory. Ann. Math. (2) 158(1), 253–321 (2003)
Schimmer, L.: Spectral inequalities for Jacobi operators and related sharp Lieb–Thirring inequalities on the continuum. Commun. Math. Phys. 334, 473–505 (2015)
Simon, B.: Szegö’s theorem and its descendants, M. B. Porter Lectures, Princeton University Press, Princeton, NJ. Spectral theory for \(L^2\) perturbations of orthogonal polynomials (2011)
Acknowledgements
Work of Michael Loss was partially supported by US National Science Foundation grant DMS 1856645; Ari Laptev was partially supported by RSF grant 18-11-0032. Lukas Schimmer was supported by Vetenskapsrådet, grant 2017-04736. Michael Loss would like to thank Institute Mittag-Leffler for its generous hospitality.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Alain Joye.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Laptev, A., Loss, M. & Schimmer, L. On a Conjecture by Hundertmark and Simon. Ann. Henri Poincaré 23, 4057–4067 (2022). https://doi.org/10.1007/s00023-022-01169-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-022-01169-x