Abstract
The spectrum of a real and symmetric \(N\times N\) matrix determines the matrix up to unitary equivalence. More spectral data is needed together with some sign indicators to remove the unitary ambiguities. In the first part of this work, we specify the spectral and sign information required for a unique reconstruction of general matrices. More specifically, the spectral information consists of the spectra of the N nested main minors of the original matrix of the sizes \(1,2,\ldots ,N\). However, due to the complicated nature of the required sign data, improvements are needed in order to make the reconstruction procedure feasible. With this in mind, the second part is restricted to banded matrices where the amount of spectral data exceeds the number of the unknown matrix entries. It is shown that one can take advantage of this redundancy to guarantee unique reconstruction of generic matrices; in other words, this subset of matrices is open, dense and of full measure in the set of real, symmetric and banded matrices. It is shown that one can optimize the ratio between redundancy and genericity by using the freedom of choice of the spectral information input. We demonstrate our constructions in detail for pentadiagonal matrices.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The answer to the question posed in the title is definitely: No! The spectrum determines the matrix up to unitary equivalence. The question is then, what additional spectral information is required for this purpose. This question accompanies Mathematical Physics already for a long time, and it is usually referred to as the spectral inversion or spectral reconstruction problems [1, 2]. The related reconstruction methods have a wide scope of applications in different areas of Physics, Materials Science and Engineering. They appear, e.g., in studies of mechanical systems near equilibrium, where one tries to construct a quadratic Hamiltonian model [3], or in atomic, molecular and nuclear physics where spectra are measured, with the hope that they will provide information on the underlying interactions. In most cases, the Hamiltonian operator is expressed as an ODE or PDE acting on an appropriate function spaces. A prime example is the Sturm Liouville operator which appears in various guises [4]. In other cases, the systems are described in terms of discrete models, so that finite-dimensional matrices are the operators under study. In the present paper, we shall consider this case.
Recent applications of inverse methods in experiments are numerous. We mention briefly a partial list. A model mechanical problem concerns a spring-mass system where the spring constants and masses can be deduced from the knowledge of system’s eigenfrequencies [1, 5]. More complex problems include studying vibrating beams [6] or the composition of strings [7, 8]. Another paper [9] studies neutrino oscillations by reconstructing the so-called mixing matrix in matter from the spectra of its main \((N-1)\times (N-1)\)-minors. There, the relevant identity is the so-called eigenvector–eigenvalue identity [10]. Other types of eigenvector–eigenvalue identities have been used for parameter estimation in spin chain Hamiltonians [11] and Markov Models [12].
In the present paper, the spectral information about the matrix comes from the spectra of its N nested main minors. Such a spectral information determines the matrix up to a finite (a prori large) number of possibilities. The reconstruction can be then made unique by providing additional discrete data encoded in the signs of certain expressions involving entries of the desired matrix. We devote much attention to the study of this sign problem. This may seem like a small subtlety, but the difficulty related to correctly choosing different types of signs in the study of the inverse matrix problems is often identified as one of the main factors that makes the practical use of the theoretical methods hard. Gladwell in his book [1] describes the subtle role played by different types of signs in the following way: “Signs, positive and negative, lie at the heart of any deep discussion of inverse problems.”
Arguably, the reconstruction methods have been most successful for symmetric tridiagonal matrices often referred to as Jacobi matrices [4]. For an N-dimensional Jacobi matrix, the number of unknown entries is \(2N-1\) and the spectral information necessary for the reconstruction is the spectrum with N eigenvalues, to which one adds the spectrum of the \(N-1\)-dimensional minor obtained by removing the last column and row from the original matrix (also called a main minor of order \(N-1\)). This data provides the diagonal elements (with their signs), but only the absolute value of the off diagonal entries can be recovered [13,14,15]. Thus, the related sign problem is particularly simple—it suffices to know the signs of the off-diagonal entries of the desired Jacobi matrix.
When more general matrices which are less sparse are considered, the number of unknown entries is larger, and naturally, the number of input spectral data has to increase. This is accompanied by the sign problem becoming more acute. The sign indicators needed in the general case are not necessarily the signs of the individual entries. However, they are absolutely needed to resolve the ambiguity due to spectral invariance of the main minors under similarity with diagonal matrices with entries arbitrarily chosen from \(\{-1,+1\}\). Various methods were developed for recovering banded or full matrices [10, 16,17,18,19,20,21,22]. Most of them provide only an exemplary matrix satisfying the spectral data and stop short of resolving the sign-related or other ambiguities. One of the common strategies for reconstructing banded symmetric matrices relies on fixing the spectra of a few largest main minors (specifically \(d+1\) main minors of orders N, \(N-1\), \(\ldots \), \(N-d\) for a \((2d+1)\)-banded matrix) and using the Lanczos algorithm in order to bring the reconstructed matrix to a \((2d+1)\)-banded form [16,17,18,19]. Importantly, the Lanczos algorithm changes the spectra of all remaining main minors and thus this method differs from the approach presented in this work. Similar problems have been considered for matrices with complex entries. A reconstruction algorithm using spectra of all \(2^{N}-1\) main minors has been developed [23]. The algorithm produces an example of a complex matrix whose main minors have the given spectra and, under some regularity assumptions, the result is unique up to similarity transformations by nonsingular diagonal matrices and the transposition operation [20]. Even more general settings concerning matrices with entries from an algebraically closed field have been considered. In particular, it has been shown that there exists a finite number of square \(N\times N\) matrices with a prescribed spectrum and prescribed off-diagonal entries [21]. A different approach to the problem is presented in [24] where any Hermitian matrix can be reconstructed from its spectrum and the spectra of a suitable number of its perturbations. Recently, there has been some revived interest in the so-called eigenvector–eigenvalue identity [10] which allows one to find the amplitudes of eigenvector’s entries of a hermitian matrix using the spectra of its \((N-1)\times (N-1)\)-minors and the spectrum of the full matrix itself. As the authors of [10] point out, the eigenvector–eigenvalue identity appears in different guises in many places in the literature (see e.g., [25]—the authors of [10] also provide a thorough review of the relevant literature). In the present paper, we derive (“Appendix B”) an identity which bears some similarity to the eigenvector–eigenvalue identity. This identity was proved previously [16,17,18] using a different method.
The present paper consists of three sections. The first deals with the inverse problem of full, real and symmetric matrices of dimension N, where the number of unknown entries is \(\frac{1}{2}N(N+1)\). The spectral data to be used is the union of the spectra of the first N nested main minors of the matrix of the sizes \(1,2,\ldots ,N\), and \(\frac{1}{2}N(N-1)\) sign indicators needed for the complete reconstruction. The precise definition of the sign indicators will be given below. The actual construction is inductive: given a matrix A and a minor \(A^{(n)}\) of dimension n, its next neighbor \(A^{(n+1)}\) is obtained by computing the \((n+1)\)’th column from the given spectra and sign indicators. The uniqueness of the resulting solution is proved. Thus, the matrix unfolds like a telescope, hence its name—the telescopic construction. The fly in the ointment is that the computation of the sign indicators is rather cumbersome.
The second section uses the telescopic method restricted to banded matrices with band width \(D=2d+1\) much smaller than N. The spectral input exceeds the number of unknowns, but this redundancy enables circumventing the need to compute the sign indicators, and the only sign information required consists of the signs of the off-diagonal matrix elements in the diagonal which is d steps away from the main diagonal, just as it was the case for the Jacobi matrices. The proposed method is proved to provide a unique solution only for generic D-diagonal matrices. Namely, this subset is open, dense and of full measure in the set of real, symmetric and banded matrices specified by entries in \({{\mathbb {R}}}^{ ( N-d/2)(d +1) } \). An explicit criterion which distinguishes non-generic cases is proposed.
Finally, in the last section, it is shown that the large redundancy which exists in the telescopic approach can be reduced appreciably by studying a different construction: One considers only the \(d+1\) dimensional principal minors \(M^{(n)}\) which are distinguished by the position of their upper corner of \(M^{(n)}\) along the diagonal. Their spectra and appropriate sign indicators are used to compute successive minors in a recursive process. This method will be referred to as the sliding-minor construction. Also in the sliding-minor construction, we are able to introduce certain redundancy by considering \((d+2)\)-dimensional sliding minors. Then, we show that the required sign data typically reduces to the signs of the off-diagonal matrix elements in the first row. The application of the last two methods for banded matrices requires a special treatment of the upper \(d\times d\) main minor, as will be explained in detail for each case. To allow a smooth flow of the main ideas, some of the more technical proofs of lemmas and theorems which are stated in the text are deferred to the appendices.
We believe that turning the focus to generic rather than to unconditionally applicable methods increases the domain of practical application and the scope of the study of inverse problems.
1.1 Notations and Preliminaries
Before turning to the main body of the paper, the present subsection introduces notations and conventions that will be used throughout.
Let A be a symmetric real \(N\times N\) matrix. Denote by \(A^{(n)}\) its \(n\times n\) upper main diagonal minor, so that \(A^{(1)}= A_{1,1}\) and \(A^{(N)}= A\). The upper suffix (n) will be used throughout for the dimension of the subspace under discussion.
The Dirac notation for vectors is used. That is, given a list \(x^{(n)} = \{ x^{(n)}_j \}_{j=1}^n\), then \({|{x^{(n)}}\rangle }\) denotes the column vector in dimension n with entries \( x^{(n)}_j\). Its transpose (row) will be denoted by \({\langle {x^{(n)} }|}\) so that the scalar product is \({\langle {x^{(n)} | y^{(n)}}\rangle }\). It is convenient also to introduce the unit vectors \({|{e^{(n)}(j)}\rangle },\ \ 1\le j\le n\) whose entries all vanish but for the j’th which is unity. Thus, clearly \({\langle {e^{(n)}(j) |x^{(n)}}\rangle } = x^{(n)}_j \), and \(A^{(n )}_{i,j}:={\langle {e^{(n )}(i) | A^{(n )} | e^{(n )}(j)}\rangle }\).
For every minor \(A^{(n)}, \ 1\le n\le (N-1)\) define the upper off-diagonal part of the next column
The spectra of \(A^{(n)}\) for \(1\le n \le N\) will be denoted by \(\sigma ^{(n)} = \{\lambda ^{(n)}_j \}_{j=1}^n \), with \(\lambda ^{(n)}_k \ge \lambda ^{(n)}_j\ \forall \ k\ge j\), and the corresponding normalized eigenvectors (determined up to an overall sign) are \(\left\{ {|{v^{(n)}(j) }\rangle }\right\} _{j=1}^n\). In general, the choice of eigenvectors is ambiguous. In the following, we will often remove this ambiguity by fixing the choice of eigenvectors of \( A^{(n)}\). If the spectrum is non-degenerate, this is done, for instance by demanding the last entry of each \({|{v^{(n)}(j) }\rangle }\) to be positive. For a fixed choice of eigenvectors, the overlaps of \( {|{a^{(n)}}\rangle }\) with the eigenvectors of \( A^{(n )}\) will be denoted by \( s^{(n)}_j \xi ^{(n)}_j\) where
The \( s^{(n)}_j\) will play the role of the sign indicators in what follows. However, the arbitrary choice of the overall signs of the vectors \({|{v^{(n)}(j)}\rangle }\) will not have any effect on the results, as long as the chosen signs are not altered throughout the proof. The choice of the sign indicators can be geometrically interpreted as specifying the orthant in \(\mathbb {R}^{n}\) where the vector \({|{a^{(n)}}\rangle }\) lies. Indeed, the normalized eigenvectors \( A^{(n)}\) form an orthonormal basis of \(\mathbb {R}^{n}\) and the signs \(\left\{ s^{(n)}_j\right\} _{j=1}^n\) specify the orthant relative to this basis.
2 Inversion by the Telescopic Construction
Given the spectra \(\sigma ^{(n)}\) for \(1\le n \le N\), one can use very simple arguments to derive the following information on the matrix A, without relaying on any sign information. They are known in different guises, see e.g., references [16,17,18,19]. We bring them here for completeness and as a background necessary for the ensuing developments.
Theorem 1
The spectra \(\sigma ^{(n)}\) for \(1\le n \le N\) suffice to determine the diagonal elements of A and the norms of the vectors \(|a^{(n)}\rangle \).
Proof
The minor \(A^{(n+1)}\) is different from \(A^{(n)}\) by the added diagonal entry \(A^{(n+1)}_{n+1,n+1} \) to be denoted by h, and the off-diagonal column \({|{a^{(n)}}\rangle }\) . Clearly,
Hence, h is deduced directly from the spectral data. Also,
Thus, h and the value of \(\left| a^{(n)}\right| ^2\) can be computed for all n. \(\square \)
Remark 1
This result can be considered as the inverse of the Gerschgorin theorem [26], which for symmetric matrices states that given a symmetric matrix A, its spectrum lies in the union of real intervals centered at the points \(A_{n,n}\) and are of lengths \(2\sum _{k=1} ^N |A_{n,k}|\). Theorem 1 states that given the spectra of the successive minors, the diagonal elements of the matrix are determined precisely, and the vectors of off-diagonal elements \(a^{(a)}\) are restricted to a sphere of a radius determined by (3).
Remark 2
If A is a Jacobi (symmetric, tridiagonal) matrix, only the nth component of \(a^{(n)}\) is different from zero, and therefore the off-diagonal entries are determined up to a sign. In other words, one has to provide their signs so that the Jacobi matrix could be heard.
The following identities are similar in spirit to the former ones, and can be proven by similar ways. They will be used in the sequel.
and
which is valid if 0 is not in the spectrum of \(A^{(n)}\). (If \(0\in \sigma ^{(n)} \) one can add to A a constant multiple of the identity which renders all the spectra non-vanishing, without affecting any of the proofs or the results derived in the sequel.)
The identities (3,4,5) are quadratic in the n components of the vector \(|a^{(n)}\rangle \). When A is assumed to be a pentadiagonal (\(D=5\)), only the last two components of \(|a^{(n)}\rangle \) do not vanish, and the quadratic forms describe three concentric curves—a circle and two conic sections in \({{\mathbb {R}}}^2\). Their mutual intersections are candidates for the solution for the inversion problem. This is discussed in detail in Sect. 3.2.2.
2.1 A General Algorithm
Unlike the case of tridiagonal matrices where the signature indicators required are just the signs of the off diagonal entries (see Remark 2), for the general case, one requires the sign indicators \(\left\{ \ s^{(n)}_j\right\} _{j=1}^n \) defined in (1).
In the following, it will often be convenient to assume certain regularity properties of the matrix A.
Definition 2
(Regular matrix). A real \(N\times N\) symmetric matrix is called regular if and only if the following conditions are satisfied.
-
(i)
The multiplicity of all eigenvalues of each \(A^{(n)}\) is one.
-
(ii)
The successive spectra do not share a common value, \(\sigma ^{(n)}\cap \sigma ^{(n+1)}=\emptyset \) for \(n=1,\ldots ,N-1\).
Remark 3
The following theorem was kindly provided by Percy Deift [27], and it is quoted without proof.
Theorem 3
(Deift). The subset of regular matrices is open, dense and of full measure in the set of real and symmetric matrices.
Let A be an \(N\times N\) real symmetric and regular matrix. We prove
Theorem 4
Given the spectra \(\left\{ \sigma ^{(n)}\right\} _{n=1} ^N\) and the sign indicators \(\left\{ s^{(n)}\right\} _{n=1} ^N\) as defined in (1.1). Then, these data suffice to construct the original matrix A uniquely.
(Irregular matrices will be discussed in a subsequent subsection).
Consider two successive minors \(A^{(n)}\) and \(A^{(n+1)}\). Cauchy’s spectral interlacing theorem guarantees that
For regular matrices, the inequality signs above are strict.
Lemma 5
The vector \({|{a^{(n)}}\rangle }\) and the diagonal element \(h:=A^{(n+1)}_{n+1,n+1}\) , as well as the (normalized) eigenvectors of the minor \(A^{(n+1)}\), \(\left\{ {|{v^{(n+1)}(j) }\rangle } \right\} _{j=1}^{n+1}\), are uniquely determined by the following data.
-
(i)
The full spectral data of \(A^{(n)}\), i.e., its spectrum \(\sigma ^{(n)}\) and eigenvectors \(\left\{ {|{v^{(n)}(j) }\rangle } \right\} _{j=1}^n\).
-
(ii)
The spectrum \(\sigma ^{(n+1)}\) of \(A^{(n+1)}\),
-
(iii)
The sign indicators \(s^{(n)}_j\), \(j=1,\ldots ,n\).
Proof
The value of h is determined by (2). The next steps are based on the relation between the two spectra \(\sigma ^{(n)}\) and \(\sigma ^{(n+1)}\) which is used in the proof of (6). Define an auxiliary matrix \({\tilde{A}}^{(n+1)} \) with \( A^{(n)}\) being its main \(n\times n\) minor, \(\tilde{A}^{(n+1)}_{n+1,n+1}= h\), and whose off diagonal entries of the \((n+1)\)’th column and row all vanish. Then, the two matrices of dimension \((n+1)\), \( A^{(n+1)}\) and \( {\tilde{A}}^{(n+1)}\) differ by a matrix of rank 2.
The spectrum of \({\tilde{A}}^{(n+1)}\) consists of \(\sigma ^{(n)}\cup \{h\}\) . Correspondingly, the eigenvectors of \({\tilde{A}}^{(n+1)}\) are obtained by increasing the dimension of each of the eigenvectors of \(A^{(n)}\) by adding a 0 in the \((n+1)\)’th position and adding the eigenvector \({|{e^{(n+1)}(n+1)}\rangle }\). These eigenvectors will be denoted by \(\left\{ {|{{\tilde{v}}^{(n+1)}(j)}\rangle } \right\} _{j=1}^{n+1}\), where
To express the spectrum and eigenvalues of \( A^{(n+1)}\), expand any of its eigenvectors in the basis \(\left\{ {|{{\tilde{v}}^{(n+1)}(j)}\rangle } \right\} _{j=1}^{n+1}\), so that
Replacing \(A^{(n+1)}\) by its form (7), one easily finds that the expansion coefficients \( \{ b_{k,r} \}_{r=1}^{n+1}\) of the kth eigenvector satisfy
From these relations and the definitions above, we conclude that:
-
(i)
for \(r=n+1\)
$$\begin{aligned} ( \lambda ^{(n+1)}_k -h ) b_{k,n+1} = \sum _{j=1}^n b_{k,j} {\langle { a^{(n)} | v^{(n)}(j) }\rangle }\ , \end{aligned}$$(10) -
(ii)
for \(r\le n\)
$$\begin{aligned} ( \lambda ^{(n+1)}_k -\lambda ^{(n)}_r ) b_{k,r} = b_{k,n+1} {\langle { v^{(n)}(r) |a^{(n)}}\rangle }\ . \end{aligned}$$(11)
Since by the conditions of the theorem, \( \lambda ^{(n+1)}_k \ne \lambda ^{(n)}_r \) for all the pairs \(1\le r \le n,\ 1\le k \le n+1 \), one can write
Moreover, all minors are assumed to be of full rank, and both \(\sigma ^{(n+1)}\) and \(\sigma ^{(n)}\) are given. Therefore, one can consider (13) as a set of linear equations from which the unknown n parameters
could be computed and none vanishes as shown in (15). However, the number of equations exceeds by 1 the number of unknowns, and therefore there exists a solution only if the equations are consistent. To prove consistency, we start by obtaining an explicit solution of the first n equations in (13). Introducing the Cauchy matrix
the unknown parameters \(\{ (\xi ^{(n)}_r) ^2 \}_{r=1}^n \) then read (see “Appendix B”):
The consistency of the linear \(n+1\) equations (10) and (11) could be proved by substituting the \((\xi ^{(n)}_r) ^2\) computed above in the last equation in (13), and showing that the resulting equation
is satisfied identically. An explicit expression for \( \left( C^{-1}\right) _{r,k}\) is given in [28] :
The identities which are proved in “Appendix A” show that equation (16) is satisfied identically provided that \(h=\sum _{k=1}^{n+1}\lambda ^{(n+1)}_k -\sum _{r=1}^{n}\lambda ^{(n )}_r \) as is the case in the present context.
To recapitulate, the solution of equations (13) exists, and it provides the \((\xi ^{(n)}_r)^2\) in terms of the spectra in a unique way as shown in (15). This information together with the sign indicators determine \( \langle a^{(n)}|v^{(n)}(r)\rangle = s^{(n)}_r\xi ^{(n)}_r \), and the vector \({|{a^{(n)}}\rangle }\) is obtained by an orthogonal change of basis. Moreover, the possible \(2^n\) combinations of the sign indicators encapsulate all possible choices of the overall signs of the eigenvectors of \(A^{(n)}\). Thus, an a priori choice of the overall phases of the eigenvectors does not result with any loss of generality or the loss of solutions. \(\square \)
Remark 4
Formula (15) from the proof of Lemma 5 can also be found in earlier works [16,17,18], and the recursive relation for the eigenvectors (12) has been also used in [17]. Similarly, one can combine (12) with (15) to obtain (after requiring the eigenvectors of \(A^{(n+1)}\) to be normalized to one) the following expression for the coefficients \( \left| b_{k,n+1}\right| ^2\)
(18) is an instance of the eigenvector–eigenvalue identity from [10] which allows one to compute the amplitudes \(\left| {\langle {e_{r}^{(n+1)}|\tilde{v}^{(n+1)}(k)}\rangle }\right| \) directly from the spectra of the n main minors of \(A^{(n+1)}\) of the size \(n\times n\). Here, we are using only one \(n\times n\) minor (namely, \(A^{(n)}\)), thus we recover only the last squared entry of each eigenvector. By combining (18) with (12), we can express the coefficients \(b_{k,r}\) in terms of the spectra of \(A^{(n)}\) and \(A^{(n+1)}\), but the resulting formulae will be different from the eigenvector–eigenvalue identity [10] as we use different spectral data and the entries refer to the basis of the eigenvectors of \(A^{(n)}\) only.
Remark 5
A complementary result to the above was recently reported in [29]. Using another approach, it is proved that given a real symmetric matrix \({\tilde{A}}^{(n)}\) whose spectrum \({\tilde{\sigma }} ^{(n)}\) is simple (no multiplicities) and a list \(\mu ^{(n+1)}\) of \((n+1)\) arbitrary numbers which interlace with \({\tilde{\sigma }} ^{(n)}\), one can construct a column vector \(|{\tilde{a}}^{(n)}\rangle \) and a real \({\tilde{h}}\) which, when used to complete \({\tilde{A}}{(n)}\) to \({\tilde{A}}^{(n+1)}\) yields \({\tilde{A}}^{(n+1)}\) with the spectrum \(\mu ^{(n+1)}\). Moreover, \(|{\tilde{a}}^{(n)}\rangle \) can be constructed uniquely once an orthant (whose choice provides the sign indicators) is prescribed in the n-dimensional space spanned by the eigenvectors of \({\tilde{A}}^{(n)}\). It is also proved that the assignment of \(|{\tilde{a}}^{(n)}\rangle \) and \({\tilde{h}}\) to \(\mu ^{(n+1)}\) is a homeomorphism onto its image and a differomorphism.
The knowledge of the overlaps \({\langle {a|v^{(n)}(r)}\rangle }\) with their signs enables the use of (12) to obtain the coefficients of the eigenvectors of \(A^{(n+1)}\) up to the constant factor \(b_{k,n+1}\) which can be determined by requiring a proper normalization.
Proof
(of Theorem 4). The proof proceeds by a recursive construction: Start with a known \(A^{(1)}\) and with the known spectrum of \(A^{(2)}\). Clearly, \(\lambda ^{(1)}_1=A_{1,1},\ \mathrm{and} \ v^{(1)}=1\). Furthermore,
Hence, (15) gives
Therefore, we get two possible solutions for \(A^{(2)}\) corresponding to choosing \(s^{(1)}_1=+1\) or \(s^{(1)}_1=-1\), which written explicitly read
The normalized eigenvectors can be computed from (12). In the standard basis, their forms read
Thus, the theorem is valid for \(n=1,2\). Note also that one can show that (13) is satisfied—which is not clear at first sight but can be easily checked. The lemma provides the final stage of the inductive proof. \(\square \)
The above inductive procedure is optimal for generic matrices whose all entries are typically nonzero. However, the requirement of providing signs of projections of the unknown column to the eigenvectors of \(A^{(n)}\) seems awkward for practical use. However, when one wants to apply this result to banded matrices, it turns out that there is large redundancy which can be used to our advantage. In particular, as we argue in the following sections, the inductive reconstruction procedure for banded matrices can be improved so that the number of required sign data can be tremendously reduced.
2.1.1 Explicit Reconstruction of \(A^{(3)}\).
It is instructive to work out the above inductive procedure explicitly for \(n=3\). The results will prove useful in the following sections.
Consider the problem of reconstructing a regular \(3\times 3\) real symmetric matrix, \(A^{(3)}\), given its spectrum \(\lambda _1^{(3)}<\lambda _2^{(3)}<\lambda _3^{(3)}\) and its \(2\times 2\) top-left minor \(A^{(2)}\). It has a spectral decomposition
where
and
with \(s={\mathrm {Sign}}\left( A^{(2)}_{1,2}\right) \). The unknown entries of the matrix \(A^{(3)}\) read
where \(\{\xi ^{(2)}_r\}_{r=1}^2\) are given by (15). Thus, there are four possible solutions for the last column of \(A^{(3)}\) corresponding to different choices of signs \(s_i\). Next, let us show how to determine \(s_i\) directly from the sign of a certain expression involving only matrix elements of \(A^{(3)}\). Using (15) and (21), we get that
This allows us to express \(s^{(2)}_1\) and \(s^{(2)}_2\) as
Because the denominators of the above expressions are positive numbers, we finally get
The main advantage of these expressions is that they provide expressions for the signatures \(s^{(2)}_1,s^{(2)}_2\) in terms of data directly available from the matrix.
2.2 Non-regular Matrices
In this subsection, we show that non-regular matrices that have degeneracy in \(\sigma ^{(n)}\) or where the overlaps \(\sigma ^{(n)}\cap \sigma ^{(n+1)}\) are nonempty can be effectively treated using the methods developed above for regular matrices. We consider the situation where there is a single block of degeneracy in \(\sigma ^{(n)}\), i.e., for some \(1\le l\le n\) and \(m\ge 0\), we have \(\lambda _l^{(n)}=\lambda _{l+1}^{(n)}=\cdots =\lambda _{l+m}^{(n)}:=\lambda \) and other eigenvalues of \(A^{(n)}\) are non-degenerate. Let us denote the respective degeneracy indices by
The interlacing property (6) dictates the following possibilities for the respective degeneracy indices \(\mathcal {D}^{(n+1)}(l,m)\) (see Fig. 1):
In what follows, we assume that the eigenvalues \(\lambda _{k}^{(n+1)}\) with \(k\notin \mathcal {D}^{(n+1)}(l,m)\) are non-degenerate. Furthermore, the degenerate eigenspaces of \(A^{(n)}\) and \(A^{(n+1)}\) will be denoted by \(V^{(n)}(\lambda )\) and \(V^{(n+1)}(\lambda )\), respectively, and their respective orthogonal complements in \({{\mathbb {R}}}^{n}\) and \({{\mathbb {R}}}^{n+1}\) by \(V^{(n)}(\lambda )^\perp \) and \(V^{(n+1)}(\lambda )^\perp \). We will also embed \({{\mathbb {R}}}^{n}\) into \({{\mathbb {R}}}^{n+1}\) by appending a zero at the end of every vector. With a slight abuse of notation, we will also denote by \(V^{(n)}(\lambda )\) and \(V^{(n)}(\lambda )^\perp \) the images of these spaces under the above embedding.
Theorem 6 shows how to reduce each of the above four degenerate cases to a regular problem, where Theorem 4 can be applied. Interestingly, each case requires a different procedure.
Theorem 6
Assume that the spectra of \(A^{(n)}\) and \(A^{(n+1)}\) as well as the eigenvectors \(\left\{ {|{v^{(n)}(r)}\rangle }\right\} _{r=1}^n\) of \(A^{(n)}\) are given and fixed. Assume that the spectra have single degeneracy blocks with the eigenvalue \(\lambda \) given by degeneracy indices \(\mathcal {D}^{(n)}(l,m)\) and \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_i^{(n+1)}(l,m)\) for some \(i\in \{I,II,III,IV\}\), respectively. The matrix \(A^{(n+1)}\) is reconstructed from the above spectral data as follows:
-
I.
The vector \({|{a^{(n)}}\rangle }\) as well as the non-degenerate eigenvectors of \(A^{(n+1)}\) belong to the space \(V^{(n)}(\lambda )^\perp \). They are constructed by applying Theorem 4 to the truncated regular matrices
 and
and 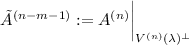 . The degenerate eigenvectors of \(A^{(n+1)}\)$$\begin{aligned}{|{{\tilde{v}}^{(n+1)}(k)}\rangle }=b_{n+1,k}{|{e^{(n+1)}}\rangle }+\sum _{r=1}^nb_{k,r} {|{v^{(n)}(r),0}\rangle },\quad k\in \mathcal {D}_{I}^{(n+1)}(l,m)\end{aligned}$$
. The degenerate eigenvectors of \(A^{(n+1)}\)$$\begin{aligned}{|{{\tilde{v}}^{(n+1)}(k)}\rangle }=b_{n+1,k}{|{e^{(n+1)}}\rangle }+\sum _{r=1}^nb_{k,r} {|{v^{(n)}(r),0}\rangle },\quad k\in \mathcal {D}_{I}^{(n+1)}(l,m)\end{aligned}$$have coefficients
$$\begin{aligned}b_{k,r}=\frac{{\langle { a^{(n)}|v^{(n)}(r)}\rangle }}{\lambda -\lambda _r^{(n)}}b_{k,n+1},\quad r\notin \mathcal {D}^{(n)}(l,m), \quad k\in \mathcal {D}_{I}^{(n+1)}(l,m).\end{aligned}$$The remaining coefficients \(b_{k,n+1}\) and \(b_{r,k}\) with \(k\in \mathcal {D}_I^{(n+1)}(l,m)\) and \(r\notin \mathcal {D}^{(n)}(l,m)\) can be arbitrary so that the resulting eigenvectors form an orthonormal set.
-
II.
The vector \({|{a^{(n)}}\rangle }\) as well as the non-degenerate eigenvectors of \(A^{(n+1)}\) belong to the space \(V^{(n)}(\lambda )^\perp \). They are constructed by applying Theorem 4 to the truncated regular matrices
 and
and  . The degenerate eigenvectors of \(A^{(n+1)}\) form an orthonormal basis of \(V^{(n)}(\lambda )\).
. The degenerate eigenvectors of \(A^{(n+1)}\) form an orthonormal basis of \(V^{(n)}(\lambda )\). -
III.
The same as case II above.
-
IV.
The space \(V^{(n+1)}(\lambda )\) is a subspace of \(V^{(n)}(\lambda )\) of codimension one. The degenerate eigenvectors of \(A^{(n+1)}\), \({|{{\tilde{v}}^{(n+1)}(k)}\rangle }\), \(k\in \mathcal {D}^{(n+1)}(l,m)\) can be freely chosen as any orthonormal subset of \(V^{(n)}(\lambda )\). They determine the embedding \(\phi :\ V^{(n+1)}(\lambda )\subset V^{(n)}(\lambda )\). The vector \({|{a^{(n)},0}\rangle }\) as well as the remaining eigenvectors of \(A^{(n+1)}\) belong to the orthogonal complement of the image of the embedding \(\phi \) in \({\mathbb {R}}^{n+1}\), \(\phi (V^{(n+1)}(\lambda ))^\perp \). They are constructed using Theorem 4 applied to the regular matrices
 and
and  .
.
The proof of Theorem 6 is deferred to “Appendix C”.
3 Applications to Banded Matrices
In the present chapter, we shall discuss the application of the above formalism for banded matrices. The fact that the spectral data exceeds the number of unknowns will be shown to provide stringent constraints on the sign distribution of the off diagonal elements, so that generically their signs are determined up to an overall sign per column. If not stated otherwise, we will assume that the considered matrices are regular.
3.1 Tridiagonal Matrices
In Remark 1, we have shown that the present construction applies for the tridiagonal case. However, it is certainly not efficient since the two spectra and the signs of the off-diagonal matrix elements suffice for the purpose—as is well-known [30].
3.2 Pentadiagonal Matrices
The next simple case which illustrates however the main ingredients of the general case are the \(D=5\)—banded matrices a.k.a. the pentadiagonal matrices. Here,
hence, the inductive step requires solving a number of equations in the two real variables \(a^{(n)}_{n }\ \mathrm{and}\ a^{(n)}_{n-1}.\) We shall address the subject using two different approaches. In the first, we shall apply the method based on Theorem 4. In the second, we shall use the quadratic forms (4, 5), which give an alternative point of view that applies exclusively for pentadiagonal matrices.
Note that for both approaches, one should compute the upper \(3 \times 3 \) minor using the procedure outlined in Sect. 2.1.1. Alternatively, it suffices to provide as input the spectrum and the eigenvectors of the upper \(3 \times 3 \) minor, and use this data as the starting data for the ensuing inductive steps.
3.2.1 Applying Theorem 4 to the Pentadiagonal Case
In this subsection, we will focus on answering the following two questions:
-
(i)
Given that the spectra \(\sigma ^{(n)}\), \(n=1,\ldots ,N\) correspond to a pentadiagonal matrix, what additional information is needed to uniquely reconstruct the matrix?
-
(ii)
What are the necessary conditions for a matrix \(A^{(n)}\) and the spectrum \(\sigma ^{(n+1)}\) of \(A^{(n+1)}\) so that \(A^{(n+1)}\) is a pentadiagonal matrix?
Starting with the first question, the general answer is given by Theorem 4. However, we will make use of the redundant information to show that typically, one can do away with the computation of the sign indicators as prescribed in the theorem. It will be shown that the vectors \(|a^{(n)} \rangle \) are determined up to an overall sign, which is uniquely provided by the easily available signs of the entries in the upper diagonal.
Consider the inductive step, where \(A^{(n)}\) and the spectrum \(\sigma ^{(n+1)}\) are known. All vectors \({|{a^{(n)}}\rangle }\) have the same norm determined by (3). Hence,
Furthermore, the solutions of (15) imply that
for every \(r=1,\ldots ,n\). Thus, every \({|{a^{(n)}}\rangle }\) belongs to the intersection of one of the above lines (for every r) with the circle of radius \(R^{(n)}\) (recall also that \(\xi _r^{(n)}\) were defined to be positive).
By the assumption of Theorem 4, \(\sigma ^{(n)}\) is non-degenerate and none of the elements of \(\sigma ^{(n)}\) belongs to \(\sigma ^{(n+1)}\). By (15), this implies that \(\xi _r ^{(n)} > 0\) for all \(r=1,\ldots ,n\). Then, (24) defines two distinct parallel lines for each r. Moreover, for a fixed r, the intersection of the two lines with the circle occurs at two distinct pairs of points, where a single pair consists of a point and its antipode (see Fig. 2).
Intersecting lines from (24) with the circle. The blue line corresponds to the line with \( \xi _r^{(n)} \) as the constant, while the green line corresponds to the choice of \(- \xi _r^{(n)}\). Dashed lines connect the antipodal solutions (Color figure online)
Since the spectral data comes from a pentadiagonal matrix, each of the lines from (24) must have an intersection point \({|{{\tilde{a}}^{(n)}}\rangle }\) or \(-{|{{\tilde{a}}^{(n)}}\rangle }\) where \({|{\tilde{a}^{(n)}}\rangle }\) is the nth column (with only two nonzero entries) of the original matrix (see Fig. 3).
A typical situation showing the result of intersecting lines from (24) with the circle for \(r=1,2,3\). Blue lines correspond to the line with \( \xi _r^{(n)} \) as the constant, while green lines correspond to the choice of \(- \xi _r^{(n)}\) (Color figure online)
However, there exist special situations when such intersections with the circle give more than just one solution up to a sign. These are highly degenerate cases where all the lines are determined by a fixed pair of parallel lines \((l_+,l_-)\). More precisely, for every r, the lines from (24) are either equal to \((l_+,l_-)\) or to another fixed pair of lines \((l'_+,l'_-)\) where \(l'_{+/-}\perp l_{+/-}\) (see Fig. 4).
A typical situation where intersecting all lines from (24) with the circle leads to four solutions for \({|{a^{(n)}}\rangle }\)
The precise conditions when that happens are as follows. Let us denote the slope of \(l_{+/-}\) by \(\alpha \). Then, the slope of \(l'_{+/-}\) is \(-\frac{1}{\alpha }\). Thus, for every r the slopes of the lines from (24) are either \(\alpha \) or \(-\frac{1}{\alpha }\), i.e.,
Define the subsets \(\mathcal {I},\mathcal {J}\subset \{1,\ldots ,n\}\), \(\mathcal {I}\cap \mathcal {J}=\emptyset \) by
Note that, we can never have \(\mathcal {I}=\emptyset \) or \(\mathcal {J}=\emptyset \), because this implies that the eigenvectors of \(A^{(n)}\) are linearly dependent, which is a contradiction. Furthermore, because the eigenvectors of \(A^{(n)}\) are orthonormal, we necessarily have
Using \(\alpha \), we can express \(v^{(n)}_{r,n-1}\) by \(v^{(n)}_{r,n}\) and obtain that
where
It is straightforward to see that
Finally, note that conditions (25) readily imply that intersecting the lines (24) with the circle results with only four points and it is not necessary to look at the free coefficients of the lines. This is because we assume that the spectral data comes from an existing pentadiagonal matrix and hence all the lines must intersect in at least one common point.
To sum up, we have the following theorem.
Theorem 7
For a regular pentadiagonal matrix, the inductive step leads to at most four solutions for \({|{a^{(n)}}\rangle }\). Typically, by intersecting the lines from (24), there exists only one solution for \({|{a^{(n)}}\rangle }\), up to an overall sign. However, there are two possible solutions for \({|{a^{(n)}}\rangle }\), up to an overall sign, if and only if the spectral data satisfies the following condition (which we call the \(\alpha \)-condition): there exists a nonempty subset \(\mathcal {I}\subset \{1,\ldots ,n\}\), \(\mathcal {I}\ne \{1,\ldots ,n\}\), such that for all \(r=1,\ldots ,n\), we have \( \frac{v^{(n)}(r)_{n-1}}{v^{(n)}(r)_{n}}=\alpha \) if \(r\in \mathcal {I}\) and \( \frac{v^{(n)}(r)_{n-1}}{v^{(n)}(r)_{n}}=-\frac{1}{\alpha }\) if \(r\notin \mathcal {I}\) for \(\alpha \) defined by
Remark 6
The set of matrices satisfying the \(\alpha \)-condition from Theorem 7 is a subset of all pentadiagonal symmetric matrices of codimension at least one. This explains the results of simulations where sets of a few millions of randomly chosen pentadiagonal matrices of dimensions up to \(n=10\) where tested, and none satisfied the \(\alpha \)-condition. This fact can be understood by noting that the matrices satisfying the \(\alpha \)-condition satisfy certain polynomial equations, as explained in Sect. 3.2.2. Thus, the set of matrices which do not satisfy the \(\alpha \)-condition is of a full dimension, and thus, it is a full-measure set.
Another outcome of the above analysis provides the answer to the second question stated at the beginning of the section: It provides a set of necessary conditions that ensures that the spectral data indeed belong to a pentadiagonal matrix. The conditions are that the distance of each line from (24) from the origin must be no greater than \(R^{(n)}\), i.e.,
3.2.2 Using the Conic Sections for Recovering Pentadiagonal Matrices
Before proceeding to the general case, we shall show that using the three quadratic forms from Eqs. (3), (4) and (5) typically allows one to reconstruct a pentadiagonal matrix from its spectral data up to an overall sign of each of its columns. For a pentadiagonal matrix, we have that \({|{a^{(n)}}\rangle }\) has only two nonzero entries, and the quadratic forms from Eqs. (4) and (5) describe either ellipses or hyperbolae (a.k.a. conic sections). Their explicit forms read
where
The three conic sections are centered at (0, 0), thus each of the curves from (29) and (30) typically intersects the circle given by (28) at exactly four points (or none). There may also be only two intersection points in certain degenerate cases. If any of the intersections is empty or both intersections have zero overlap, then there is no pentadiagonal matrix \(A^{(n+1)}\) whose top-left main minor is \(A^{(n)}\). If such a pentadiagonal matrix \(A^{(n+1)}\) exists, then the three conic sections intersect at at-least two points which yield \(a^{(n)}\) up to an overall sign. However, in certain non-generic cases, it may happen that the three conic curves intersect at four points (see Fig. 5).
Then, one cannot decide which of the intersection points give a correct solution. This happens if and only if the principal axes of the two conic sections are identical. This can be written as a condition for the eigenvectors of the quadratic forms defining the conic sections. Namely, both sets of eigenvectors must be the same (up to a scalar factor) [31]. This in turn happens if and only if the matrices of both quadratic forms commute. This boils down to the following algebraic condition for the coefficients defining the conic intersections (29)–(30).
In the special case, when \(n=2\), (31) is automatically satisfied and all four points of intersection give correct solutions for \(a^{(n)}\). For \(n>2\), the set of pentadiagonal \(n\times n\) matrices satisfying condition (31) is a strict subset of the set of all \(n\times n\) pentadiagonal matrices of codimension one. Thus, a typical (generic) pentadiagonal matrix can be completely reconstructed using the above conic curves’ method. However, considering non-generic cases brings in a few subtleties. In particular, satisfying the \(\alpha \)-condition from Theorem 7 implies satisfying (31), but the converse statement is not true. The set of \(n\times n\) pentadiagonal matrices satisfying the \(\alpha \)-condition is of codimension at least one, but it is a strict subset of the set of matrices satisfying (31). Thus, in the non-generic cases, only Theorem 7 can give a definite answer about the possible solutions (see Fig. 6).
Conic curves (29)–(30) for a random \(5\times 5\) pentadiagonal matrix satisfying the degeneracy condition (31). The green lines are lines from (24) which determine the correct solutions for the column \(a^{(5)}\). Despite (31) being satisfied, only one pair of antipodal points gives solutions for \(a^{(5)}\) (Color figure online)
3.3 A Finite Algorithm for Reconstructing a D-Diagonal Matrix
Given that the spectra \(\sigma ^{(n)}\), \(n=1,\ldots ,N\) correspond to a D-diagonal real symmetric matrix, we provide a finite algorithm which produces the set of possible D-diagonal matrices whose main minors have the given spectra \(\{\sigma ^{(n)}\}_{n=1}^N\). By definition, the nth column of a D-diagonal matrix satisfies \(a^{(n)}_1=\cdots =a^{(n)}_{n-d}=0\), where \(d:=\frac{1}{2}\left( D-1\right) \).
The algorithm starts by computing \(|\xi _r|=\left| {\langle {a^{(n)}|v^{(n)}(r)}\rangle }\right| \) from (15). By choosing the sign indicators \(\mathbf {s}:=(s_1,\ldots ,s_n)\), we obtain \(2^n\) potential solutions for \({|{a^{(n)}}\rangle }\) which read
For the inductive steps involving the main minors of size \(n=1,\ldots ,d\) these are all valid solutions. However, if \(n>d\), we have additional constraints for \({|{a^{(n)}}\rangle }\) of the form
The above equations are satisfied only by some choices of \(\mathbf {s}\) which determine the valid solutions in the nth inductive step. Alternatively, one can verify the solutions by demanding that vector \({|{a^{(n)}(\mathbf {s})}\rangle }\) belongs to the \((d-1)\)-dimensional sphere, i.e.,
where \(R^{(n)}\) depends only on the spectral input data via (3). Thus, we have the following algorithm for realizing the inductive step of constructing \(A^{(n+1)}\) from \(A^{(n)}\) (Algorithm 1).

One can see that the main contribution to the numerical complexity of the above inductive step relies on the loop going through all \(2^n\) choices of the possible signs. Thus, the complexity scales like \(poly_{n,d}2^n\), where the polynomial factor \(poly_{n,d}\) comes from the necessity of evaluating expressions from (32) and (33) in each step of the loop. What is more, heuristics shows that the required numerical accuracy \(\epsilon \) grows with d and n, as the potential solutions tend to bunch close to the surface of the sphere.
Let us next argue that for generic input data, the result of Algorithm 1 for \(\epsilon \) sufficiently small is just two antipodal solutions for \(a^{(n)}\). To this end, consider the hyperplanes
The procedure of intersecting lines with the circle from Sect. 3.2 for \(d>2\) generalizes here to a procedure involving the study of intersections of hyperplanes \(H_r^{(n),\pm }\) with the (hyper)sphere of radius \(R^{(n)}\). As before, typically, as a result of such a procedure, one obtains only a single pair of antipodal solutions for \(a^{(n)}\). Non-typical situations arise when some hyperplanes are perpendicular to each other. This requires the existence of certain relations between the eigenvectors of \(A^{(n)}\) analogously to the relations stated in Theorem 7. However, the precise form of these conditions seems to be much more complicated, and we leave this problem open for future research. For an illustration of the intersection procedure for a typical heptadiagonal matrix (\(d=3\)), see Fig. 7.
Result of intersecting eight hyperplanes \(H_r^{(n),\pm }\), \(r=1,2,3,4\) for a typical random heptadiagonal matrix. Intersecting one of the hyperplanes with the sphere of radius \(R^{(n)}\) results with a single circle. The common points where n circles meet (here \(n=4\)) determine the solutions for the vector \(a^{(n)}\) (the red dots). As one can see, typically, there are just two such points which lie on the opposite sides of the sphere. The orange and blue colors were used to mark the relevant groups of intersecting circles (Color figure online)
Similarly to the pentadiagonal case, one can find necessary conditions for the spectral data to correspond to a D-diagonal matrix. Every hyperplane \(H_r^{(n),\pm }\) must have a nontrivial intersection with the sphere of radius \(R^{(n)}\); hence, its distance from the origin must be no greater than \(R^{(n)}\).
Remark 7
Using Theorem 6, we can apply the above methodology mutatis mutandis to non-regular banded matrices. In particular, whenever the dimension of the smaller truncated matrix from Theorem 6 is greater than d, we can use the same redundancy effects to our advantage when dealing with typical matrices.
4 Improved Strategies for D-Diagonal Matrices: The Sliding Minor Construction
The number of independent non-vanishing entries of a D-diagonal real symmetric matrix is
The spectral data for all the main minors of a D-diagonal \(N\times N\) matrix is \(N_{N-1}\), which exceeds \(N_D\) by far. In this section, we provide two alternative methods for reconstructing D-diagonal matrices and which use much less spectral data. The first utilizes the minimum number of spectral parameters needed for the purpose, together with the necessary sign indicators. The second method makes use of \(N-d-1\) more spectral data. This introduces enough redundancy to render the method much more straight forward to use at the cost of being applicable only for generic matrices.
4.1 Inverse Method with Minimal Spectral Input
The number of non-vanishing data needed to write a D-diagonal matrix, \(N_D\), can also be written as \( N_{D}=\frac{1}{2}d(d+1)+(d+1)(N-d)\). It can be interpreted as the sum of two terms:
-
(i)
The spectra of the minors \(A^{(1)}=A_{1,1}\), \(A^{(2)}\), \(\ldots \), \(A^{(d)}\) which give a total of \(\frac{1}{2}d(d+1)\) numbers needed to reconstruct the first \(d\times d\) minor.
-
(ii)
The spectra of \((N-d)\) minors of size \((d+1)\times (d+1)\) with upper diagonal entry at successive positions along the diagonal of A which are denoted by \(M_1^{(d+1)}=A^{(d+1)}\), \(M_2^{(d+1)}\), \(\ldots \), \(M_{N-d}^{(d+1)}\) (see (35) for an example with \(N=6\) and \(d=2\)). The "sliding minors" in the present construction are the \(\left\{ M_k^{(d+1)}\right\} _{k=2}^{N-d}\) minors.
 (35)
(35)
The reconstruction algorithm consists of the following steps.
-
(1)
Reconstruct \(A^{(d+1)}\) from the spectral data of \(A^{(1)}\) through \(A^{(d)}\) and the sign indicators (\(\frac{1}{2}d(d+1)\) signs in total) as described in the inductive procedure from the proof of Theorem 4.
-
(2)
The matrix elements of the \(d\times d\) minor \(M_2^{(d)}\) starting with the upper diagonal \(A_{2,2}\) are obtained from the known spectral decomposition of \(A^{(d+1)}=M_1^{(d+1)}\). The eigenvalues and eigenvectors of \(M_2^{(d)}\) are then computed.
-
(3)
Use Theorem 4 to reconstruct \(M_2^{(d+1)}\) from the spectral decomposition of \(M_2^{(d)}\) and appropriate sign indicator data.
-
(4)
Repeat the previous two steps recursively to procedure the successive minors \(M_{3}^{(d+1)},\cdots , M_{N-d}^{(d+1)}\).
The main drawback of this method is the need to provide the sign indicators at each step. To overcome this, one can also introduce minimal redundancy to the above sliding minor method so that for a typical matrix the required sign data reduces only to the overall signs of columns of \(A^{(N)}\). This applies only for generic matrices, as explained in the previous section.
4.2 Inverse Method with Optimal Spectral Input
Here, the sliding minors are the \(\left\{ M_k^{(d+2)}\right\} _{k=2}^{N-d-1}\) minors (see (36)). The increase in their dimension amounts also to the vanishing of the \((1,d+2)\) and \((d+2,1)\) entries. This enables turning the redundant information to impose constraints, which for generic matrices remove the need for computing the sign indicators required in the previous construction.

The inversion algorithm consists of the following steps.
-
(1)
Reconstruct \(A^{(d+1)}\) from the spectral data of \(A^{(1)}\) through \(A^{(d)}\) and the sign indicators (\(\frac{1}{2}d(d+1)\) signs in total) as described in the inductive procedure from the proof of Theorem 4.
-
(2)
The matrix elements of the \((d+2)\times (d+2)\) minor \(M_1^{(d+2)}\) starting at the upper diagonal \(A_{1,1}\) are computed using the algorithm proposed in Sect. 3.3. The only sign indicator needed is the sign of the entry \(A_{1,d+1}\).
-
(3)
The \((d+1) ,(d+1) \) minor \(M_2^{(d+1)}\) is extracted from the computed \(M_1^{(d+2)}\). Its eigenvalues and eigenvectors are then computed. (\(M_2^{(d+1)}\) is the \(d+1\times d+1\) minor with \(A_{2,2}\) as its upper diagonal entry)
-
(4)
Use Theorem 4 to reconstruct \(M_3^{(d+2)}\) from the spectral decomposition of \(M_2^{(d+1)}\) and the sign of the entry \(A_{1,d+1}\).
-
(5)
Repeat the previous two steps recursively to produce the successive minors \(M_{3}^{(d+1)},\cdots , M_{N-d-1}^{(d+2)}\).
In order to minimize further the set of exceptional matrices where this strategy fails, one could choose a larger dimension for the sliding minor. In choosing an “optimum” strategy, one has to weigh computational effort against minimizing the exceptional set. This is an individual decision left for the discretion of the practitioner.
4.3 Pentadiagonal Matrices
The first inversion strategy for regular pentadiagonal matrices (\(d=2\)) is a combination of two steps which we have already analyzed in detail in the previous sections. The first step of reconstructing \(A^{(2)}\) has been described in the proof of Theorem 4 (see (19) and (20)). The second as well as all other steps rely on reconstructing \(3\times 3\) matrices \(\left\{ M_k^{(3)}\right\} _{k=2}^{N-2}\) from their top-left \(2\times 2\) minors. This has been done explicitly in Sect. 2.1.1. In total, the \(2\times 2\rightarrow 3\times 3\) steps require the following sign data.
-
(i)
The sign of the matrix element \(A_{1,2}\).
-
(ii)
A pair of signs from (23) applied to each minor \(\left\{ M_k^{(3)}\right\} _{k=2}^{N-2}\).
The second inversion strategy which uses the larger \(4\times 4\) sliding minor gives extra redundancy and, as explained above, it typically reduces the required sign data to the overall signs of columns of \(A^{(N)}\). Here, the notion of typicality is particularly straightforward to state. Namely, all the sliding minors of a typical matrix do not satisfy the \(\alpha \)-condition from Theorem 7. The computation of the spectral decomposition of the \((3\times 3)\) minors can be carried out analytically.
5 Summary
We revisited here the question of how much spectral data is needed to determine a real symmetric matrix. In principle, a matrix is determined by its spectrum only up to unitary equivalence. Hence, more spectral information is needed in order to reconstruct a non-diagonal matrix. Heuristically, the number of spectral data should match the number of unknowns. Hence, for a generic real symmetric \(N\times N\) matrix, we need \(N(N+1)/2\) numbers coming from the spectral data. In our work, these numbers come from the spectra of the main minors. Given such spectra, we provide a finite algorithm that reconstructs the matrix up to a finite number of possibilities. The construction can be made unique by supplementing additional sign data as stated in Theorem 4 which comprises of \(N(N-1)/2\) signs in total. However, the signs are not easily deduced from the matrix itself; therefore, the requirement of supplementing the signs is a notable limitation to our procedure. Thus, in further parts of this paper, we focus on ways of reducing the required sign data in the case of banded matrices. For \((2d+1)\)-banded matrices, there are less unknowns, hence one can find a smaller optimal set of \((d+1)\times (d+1)\) minors whose spectra allow one to reconstruct the matrix up to a finite number of possibilities. As before, some additional sign information is required to make the construction unique. By analyzing the case of pentadiagonal matrices, we compare both methods of reconstruction. We find that the redundant information coming from the spectra of all main minors in a typical case (where the notion of typicality has been made precise in Sect. 3.2) allows one to reduce the number of required signs to \(N-1\) that are just the overall signs of columns of the upper-triangular part of \(A^{(N)}\), while using the optimal amount of spectral information requires \(2N-1\) signs. In Sect. 4, we argue that this is a general fact, i.e., the redundancy coming from all main minors typically allows one to uniquely reproduce a general banded matrix from the spectral data using only the overall signs of columns of the upper-triangular part of \(A^{(N)}\).
References
Gladwell, G.M.L.: Inverse Problems in Vibration. Kluwer Academic Publishers (2004)
Marchenko, V.: Inverse Problems in the Theory of Small Oscillations, Translations of Mathematical Monographs, vol. 247. AMS (2018)
Gantmacher, F.R., Krein, M.G.: Oszillationsmatrizen, Oszillations-keme und kleine Schwingungen mechanischer Systeme. Akademie-Verlag, Berlin (1960)
Gesztesy, F.: Inverse spectral theory as influenced by Barry Simon. In: Gesztesy, F., Deift, P., Galvez, C., Perry, P., Schlag, W. (eds.) Spectral Theory and Mathematical Physics: A Festschrift in Honor of Barry Simon’s 60th Birthday. ISBN-10: 0-8218-3783-4 (2010) Article electronically published on February 18, (2021)
Gladwell, G.M.L., Morassi, A. (eds.): Dynamical Inverse Problems: Theory and Application, vol. 529. CISM International Centre for Mechanical Sciences, Springer-Verlag, Wien (2011)
Gladwell, G.M.L.: The inverse problem for the vibrating beam. Proc. R. Soc. Lond. Ser. A 393, 277–295 (1984)
Cox, Steven J., Embree, Mark, Hokanson, Jeffrey M.: One can hear the composition of a string: experiment with an inverse eigenvalue problem. SIAM Rev. 54, 157–178 (2012)
Pivovarchik, V., Rozhenko, N., Tretter, C.: Dirichlet–Neumann inverse spectral problem for a star graph of Stieltjes strings. Linear Algebra Appl. 439, 2263–2292 (2013)
Denton, P.B., Parke, S.J., Zhang, X.: Neutrino oscillations in matter via eigenvalues. Phys. Rev. D 101, 093001 (2020)
Denton, P.B., Parke, S.J., Tao, T., Zhang, X.: Eigenvectors from eigenvalues: a survey of a basic identity in linear algebra. Bull. Amer. Math. Soc. 59, 31–58 (2022)
Burgarth, D., Ajoy, A.: Evolution-free Hamiltonian parameter estimation through Zeeman markers. Phys. Rev. Lett. 119, 030402 (2017)
Burgarth, D.: Identifying combinatorially symmetric hidden Markov models. Electron. J. Linear Algebra 34, 393–398 (2018)
Hochstadt, H.: On some inverse problems in matrix theory. Arch. Math. 18, 201–207 (1967)
Hochstadt, H.: On the construction of a Jacobi matrix from spectral data. Linear Algebra Appl. 8, 435446 (1974)
Hald, Ole H.: Inverse Eigenvalue problems for Jacobi matrices. Linear Algebra Appl. 14, 63–85 (1976)
Boley, D., Golub, G.H.: Inverse eigenvalue problems for band matrices. In: Watson, G.A. (ed.) Numerical Analysis. Lecture Notes in Mathematics, vol. 630. Springer, Berlin (1978)
Biegler-König, F.W.: Construction of band matrices from spectral data. Linear Algebra Appl. 40, 79–87 (1981)
Boley, D., Golub, G.H.: A survey of matrix inverse eigenvalue problems. Inverse Probl. 3, 595 (1987)
Chu, M., Golub, G.: Inverse Eigenvalue Problems: Theory, Algorithms, and Applications. Oxford University Press (2005)
Loewy, R.: Principal minors and diagonal similarity of matrices. Linear Algebra Appl. 78, 23–64 (1986)
Friedland, Shmuel: Matrices with prescribed off-diagonal elements. lsrael J. Math. 11, 184–189 (1972)
Martin, R.S., Wilkinson, J.H.: Symmetric decomposition of positive definite band matrices. Numer. Math. 7, 355–361 (1965)
Griffin, Kent, Tsatsomeros, Michael J.: Principal minors, part II: the principal minor assignment problem. Linear Algebra Appl. 419, 125–171 (2006)
Kotlyarov, V.P., Marchenko, V.A., Slavin, V.V.: Reconstruction of the Hermitian matrix by its spectrum and spectra of some number of its perturbations. Doklady Math. 94(2), 529–531 (2016)
Deift, P., Li, L., Nanda, T., Tomei, C.: The Toda flow on a generic orbit is integrable. Commun. Pure Appl. Math. 39, 183–232 (1986)
Gerschgorin, S.: Über die Abgrenzung der Eigenwerte einer Matrix. Izv. Akad. Nauk. USSR Otd. Fiz.-Mat. Nauk 6, 749–754 (1931)
Deift, P.: Private communication (2021)
Gow, R.: Cauchy’s matrix, the Vandermonde matrix and polynomial interpolation. Irish Math. Soc. Bull 28, 45–52 (1992)
Leite, R.S., Tomei, C.: The geometry of spectral interlacing. arXiv:2108.06285 (2021)
Anderson, L.: On the effective determination of the wave operator from given spectral data in the case of a difference equation corresponding to a Sturm–Liouville differential equation. Math. Anal. A 29, 467497 (1970)
Ayoub, A.B.: The central conic sections revisited. Math. Mag. 66(5), 322–325 (1993)
See https://proofwiki.org/wiki/VandermondeMatrixIdentityforCauchyMatrix
Knuth, D.E.: Art of Computer Programming, The: Volume 1: Fundamental Algorithms, 3rd edn. Addison-Wesley (1997)
Acknowledgements
We would like to thank Professor Raphael Loewy for suggestions and critical comments during the first stages of the present work. Professor Percy Deift accompanied the work since its beginning and offered critique and advise in many instances. We are obliged for his invaluable help and in particular for his permission to quote an unpublished theorem quoted in Remark 3. Professor Carlos Meite is acknowledged for bringing to our attention his work (Remark 5) before its publication. We also thank Professor Jon Keating for useful suggestions and Doctor Yotam Smilansky for helpful comments on the manuscript. The inspiration for the work came by listening to a seminar by Professor Christiane Tretter within the webinar series “Spectral Geometry in the Clouds.” Thanks Christiane. The seminar is organized by Doctors Jean Lagacé and Alexandre Girouard whom we thank for initiating and running such successful seminar during the miserable Corona days.
Funding
TM’s funding was provided by the University of Bristol (Vice-Chancellor’s fellowship).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jan Derezinski.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Identities for Cauchy Matrices
For two sequences of real numbers, \({{\varvec{x}}}:=\{x_i\}_{i=1}^n\) and \({{\varvec{y}}}:=\{y_i\}_{i=1}^n\), define the Cauchy matrix \(C({{\varvec{x}}},{{\varvec{y}}})\) as \(\left( C({{\varvec{x}}},{{\varvec{y}}})\right) _{i,j}:=\frac{1}{x_i-y_j}\). The matrix \(C({{\varvec{x}}},{{\varvec{y}}})\) has the following symmetry
C will be used to denote \(C({{\varvec{x}}},{{\varvec{y}}})\) by default. An explicit expression for \(C^{-1}\) reads [28]
The sum of the matrix elements of \(C^{-1}\) is known to be [32]
We aim to prove the following identities:
Note first that the LHS identities imply the RHS identities by symmetry A.1. Hence, it is enough to prove the LHS identities. To this end, we write them down as the following matrix vector products
where vectors \({|{1^{(n)}}\rangle }\), \({|{\frac{1}{x}^{(n)}}\rangle }\) and \({|{y^{(n)}}\rangle }\) are defined as
We will use the following lemma.
Lemma 8
(Vandermonde Matrix Identity for Cauchy Matrix [28, 33]). \(C({{\varvec{x}}},{{\varvec{y}}})\) has the following decomposition
where P and Q are diagonal matrices defined as
with
and \(V_x\), \(V_y\) are the Vandermonde matrices
By Lemma 8, we have
Next, we define the vectors \({|{\phi _1}\rangle }\), \({|{\phi _y}\rangle }\) and \({|{\phi _x}\rangle }\) as
Calculation of A.6 boils down to computing overlaps
Let us start with finding \({|{\phi _x}\rangle }\). A straightforward calculation using (A.7) shows
In order to compute the sums in (A.8), we use the following Lemma [33].
Lemma 9
(Summation of Powers over Product of Differences). Let \((t_1,t_2,\ldots ,t_n)\) be a sequence of real numbers. Then,
By Lemma 9, we have \({\langle {e_j^{(n)}|\phi _x}\rangle }=\) for \(j\ge 2\). The only nonzero entry is
which is evaluated in the following proposition.
Proposition 10
Let \((t_1,t_2,\ldots ,t_n)\) be a sequence of real numbers. Then,
Proof
Consider the following complex integral over a circle of radius \(R>\max \{|t_i|:\ 1\le i\le n\}\)
Because the integrand is a regular function at \(z=\infty \), we have \(I_R(t_1,\ldots ,t_n)=0\). On the other hand, the integrand has simple poles at \(z=0\), \(z=t_1\), \(\ldots \), \(z=t_n\). Hence, the residue theorem asserts that
which finishes the proof. \(\square \)
Next, let us compute the vectors \({|{\phi _1}\rangle }\) and \({|{\phi _y}\rangle }\). Note first that because the first entry of \({|{\phi _x}\rangle }\) is its only nonzero entry, we only need to find the first entries of \({|{\phi _1}\rangle }\) and \({|{\phi _y}\rangle }\). By (A.7), the desired vectors are solutions to the following linear equations
We use now Crammer’s rule.
Applying the Laplace expansion of both determinants with respect to their first columns.
where
Using the expression for the determinant of a Vandermonde matrix, we have
It follows that
After application of the above result, the desired expressions read
As the final step, we use the following expansion of p(t).
where \(e_{n+1-l}\left( \{x_1,\ldots ,x_n\}\right) \) is the \((n+1-l)\)th Viete sum in variables \(\{x_1,\ldots ,x_n\}\). Plugging the above expansion into (A.10), we get
By Lemma 9, we get that
Finally, after making use of Proposition 10 and expanding Viete sums \(a_1=(-1)^n x_1\cdot \ldots \cdot x_n\) and \(a_n=-(x_1+\cdots +x_n)\)
The result follows now directly by multiplying the above expressions by \({\langle {e_1^{(n)}|\phi _x}\rangle }\) from (A.9).
The identity which is used in the discussion of (16) follows by combining (A.4) and (A.5) to give
Appendix B: Derivation of the Formula for \(({\xi _r}^{(n)}) ^2\).
The aim is to prove the identity used in (15) which reads
where \(C=C({{\varvec{x}}},{{\varvec{y}}})\) is a Cauchy matrix and \(h:=\sum _{k=1}^{n+1}x_k-\sum _{k=1}^ny_n\). Note first that
Next, let us use Lemma 8 to find that \(C^{-1}=-QV_Y^{-1}V_xP^{-1}\). By a reasoning relying on the use of Lemma 9 (which is analogous to the one used in (A.9)), we obtain that
The next step is the multiplication by \(V_y^{-1}\). To this end, we apply the following result concerning the inverse of a Vandermonde matrix [33].
Lemma 11
Let \(V^{(n)}_t\) be the Vandermonde matrix of size n in variables \(t_1,\ldots ,t_n\), i.e., \(V_{i,j}=t_i^{j-1}\), \(1\le i,j\le n\). Then,
where \(e_m\) denotes the mth Viete sum.
We only need the last two columns of \((V_y)^{-1}\), because using (B.3), we get
By Lemma 11, the necessary matrix elements of \(V_y^{-1}\) forms read
Plugging the above results to the LHS of (B.1) yields
which after substituting expressions for h and \(p(y_r)\) yields the desired result.
Appendix C: Non-regular Matrices—Proof of Theorem 6
Let us start with the simplest situation where for some n, we have \(\left| \sigma ^{(n)}\cap \sigma ^{(n+1)}\right| =1\) and both spectra are non-degenerate. The other cases can be analyzed by essentially repeating and slightly adjusting the proof of the simple case. By the interlacing property (6), the scenario described above happens if and only if there exists a single \(l\in \{1,\ldots ,n\}\) such that either \(\lambda _l^{(n)}=\lambda _l^{(n+1)}\) or \(\lambda _l^{(n)}=\lambda _{l+1}^{(n+1)}\). (11) applied to \(k=r=l\), gives \(b_{l,n+1}\xi _l^{(n)}=0\), i.e., i) \(b_{l,n+1}=0\) or ii) \(\xi _l^{(n)}=0\). The two cases are analyzed separately.
-
(i)
\(b_{l,n+1}=0\). (11) applied to \(k=l\) and \(r\ne l\) gives \((\lambda _l^{(n+1)}-\lambda _r^{(n)})b_{l,r}=0\), which in turn implies that \(b_{l,r}\) for \(r\ne l\) (recall that \(\lambda _l^{(n+1)}\ne \lambda _r^{(n)}\) by the assumption that \(\left| \sigma ^{(n)}\cap \sigma ^{(n+1)}\right| =1\)). Thus, the eigenvector \({|{{\tilde{v}}^{(n+1)}(l)}\rangle }={|{v^{(n)}(l),0}\rangle }\). (10) applied for \(k=l\) implies \({\langle {v^{(n)}(l)|a^{(n)}}\rangle }=0\), thus \(b_{l,n+1}=0\) leads to \(\xi _l^{(n)}=0\).
-
(ii)
\(\xi _l^{(n)}=0\) and \(b_{l,n+1}\ne 0\). Here, we will show that this is in contradiction with the assumption that \(\left| \sigma ^{(n)}\cap \sigma ^{(n+1)}\right| =1\). To this end, we combine Equations (11) for \(r\ne l\) with Equations (10) to obtain the following reduced set of equations involving a Cauchy matrix
$$\begin{aligned} \lambda ^{(n+1)}_k -{\tilde{h}} = \sum _{r=1,r\ne l}^n \frac{\left( \xi _r^{(n)}\right) ^2}{\lambda ^{(n+1)}_k-\lambda ^{(n)}_r}, \quad \forall \ \ 1\le k \le n+1, \end{aligned}$$(C.1)where \({\tilde{h}}=\sum _{k=1,k\ne l}^{n+1}\lambda ^{(n+1)}_k-\sum _{k=1,k\ne l}^{n}\lambda ^{(n)}_k\). Note that Equations (C.1) for \(k\ne l\) can be viewed as a set equations for the regular spectra \({\tilde{\sigma }}^{(n-1)}:=\sigma ^{(n)}/\{\lambda _{l}^{(n)}\}\) and \({\tilde{\sigma }}^{(n)}:=\sigma ^{(n+1)}/\{\lambda _{l}^{(n+1)}\}\). Thus, solutions for \(\left( \xi _r^{(n)}\right) ^2\), \(r\ne l\) read
$$\begin{aligned} (\xi ^{(n)}_r)^2 =-\frac{\prod _{k=1,k\ne l}^{n+1}\left( \lambda ^{(n)}_r-\lambda ^{(n+1)}_k\right) }{\prod _{k=1,k\notin \{r,l\}}^n \left( \lambda ^{(n)}_r-\lambda ^{(n)}_k\right) }. \end{aligned}$$(C.2)However, the above formula for \(\left( \xi _r^{(n)}\right) ^2\) has to be consistent with (C.1) for \(k=l\). By denoting \(\lambda _l^{(n)}=\lambda _l^{(n+1)}:=\lambda \), this boils down to the following condition:
$$\begin{aligned} \left( \lambda -{\tilde{h}}\right) =\sum _{r=1,r\ne l}^n -\frac{1}{\lambda -\lambda ^{(n)}_r}\frac{\prod _{k=1,k\ne l}^{n+1}\left( \lambda ^{(n)}_r-\lambda ^{(n+1)}_k\right) }{\prod _{k=1,k\notin \{r,l\}}^n\left( \lambda ^{(n)}_r-\lambda ^{(n)}_k\right) }, \end{aligned}$$(C.3)We view (C.3) as a polynomial equation for \(\lambda \). It turns out that (C.3) can be simplified to the equation \(\prod _{k=1,k\ne l}^{n+1}\left( \lambda -\lambda ^{(n+1)}_k\right) =0\). This is in contradiction with the regularity assumption, because it implies that \(\lambda =\lambda ^{(n+1)}_{l+1}\).
Summing up the above analysis of the simplest case where \(\lambda _l^{(n)}=\lambda _l^{(n+1)}\) for a single l and both spectra are non-degenerate, we have obtained that we necessarily have \(\xi _l^{(n)}=0\) and \({|{\tilde{v}^{(n+1)}(l)}\rangle }={|{v^{(n)}(l),0}\rangle }\). The remaining solutions for \(\left( \xi _r^{(n)}\right) ^2\), \(r\ne l\) are given by (C.2). Moreover, (11) applied for \(k\ne l\) yields \(b_{k,r}=0\) whenever \(r=l\) and \(k\ne l\). Thus, the expressions for the eigenvectors \({|{{\tilde{v}}^{(n+1)}(r)}\rangle }\), \(r\ne l\), of the matrix \(A^{(n+1)}\) are formally identical with the expressions for the eigenvectors of a regular matrix \({\tilde{A}}^{(n)}\) obtained by removing the eigenspaces corresponding to the eigenvalue \(\lambda _l^{(n)}\) in \(A^{(n)}\) and \(A^{(n+1)}\).
Let us next consider the situation where there is a single degeneracy block in \(\sigma ^{(n)}\) and \(\sigma ^{(n+1)}\). Note first that whenever \(k\in \mathcal {D}^{(n+1)}(l,m)\) and \(r\in \mathcal {D}^{(n)}(l,m)\), then (11) implies that \(b_{k,n+1}\xi _r^{(n)}=0\). Thus, we have two possibilities for each \(k\in \mathcal {D}^{(n+1)}(l,m)\):
-
(i)
\(b_{k,n+1}=0\) or
-
(ii)
\(b_{k,n+1}\ne 0\) and \(\xi _r^{(n)}=0\) for all \(r\in \mathcal {D}^{(n)}(l,m)\).
As the following Lemma states, case (ii) is only relevant when \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_{I}^{(n+1)}(l,m)\).
Lemma 12
Assume that the spectrum \(\sigma ^{(n)}\) has degeneracy indices \(\mathcal {D}^{(n)}(l,m)\) and denote the degenerate eigenvalue by \(\lambda \). If the degeneracy indices in the spectrum \(\sigma ^{(n+1)}\) are of the form \(\mathcal {D}_{II}^{(n+1)}(l,m)\), \(\mathcal {D}_{III}^{(n+1)}(l,m)\) or \(\mathcal {D}_{IV}^{(n+1)}(l,m)\), then for every \(k\in \mathcal {D}^{(n+1)}(l,m)\) we have \({\langle {\tilde{v}^{(n+1)}(k)|e^{(n+1)}(n+1)}\rangle } =0\), i.e., the coefficient \(b_{k,n+1}=0\).
Proof
(Ad absurdum.) Assume that \(b_{k,n+1}\ne 0\) for some \(k\in \mathcal {D}^{(n+1)}(l,m)\) and \(\mathcal {D}^{(n+1)}(l,m)\) is of the form \(\mathcal {D}_i^{(n+1)}(l,m)\) with \(i\in \{\mathrm{II},\mathrm{III},\mathrm{IV}\}\). Denote \(\mathcal {K}':=\{k\in \mathcal {D}^{(n+1)}(l,m):\ b_{k,n+1}\ne 0\}\). Then, (11) applied for any \(k\in \mathcal {K}'\) and \(r\in \mathcal {D}^{(n)}(l,m)\) implies that \(\xi _r^{(n)}=0\) for all \(r\in \mathcal {D}^{(n)}(l,m)\). On the other hand, for any \(k\in \mathcal {K}'\cup \left( \{1,\ldots ,n+1\}/\mathcal {D}^{(n+1)}(l,m)\right) \), (11) gives
This in turn combined with (10) for the same k yields
In particular, we can use the Cauchy matrix method to solve the above equations for \(\sum _{r\in \mathcal {D}^{(n)}(l,m)}\left( \xi _r^{(n)}\right) ^2\) or \(\left( \xi _r^{(n)}\right) ^2\) with \(r\notin \mathcal {D}^{(n)}(l,m)\). However, each case with \(D^{(n)}_i\), \(i\in \{\mathrm{II},\mathrm{III},\mathrm{IV}\}\) has to be treated separately.
-
(i)
\(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)\). Consider the set of Equations (C.4) for \(k\in \{1,\ldots ,n+1\}/\mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)\). They are Cauchy equations for the regular spectra of a reduced dimension \({\tilde{\sigma }}^{(n-m+1)}=\{\lambda _k^{(n+1)}:\ k\in \{1,\ldots ,n+1\}/\mathcal {D}_{IV}^{(n+1)}(l,m)\}\) and \({\tilde{\sigma }}^{(n-m)}=\{\lambda \}\cup \{\lambda _k^{(n)}:\ k\in \{1,\ldots ,n\}/\mathcal {D}_4^{(n)}(l,m)\}\) with \(\left( {\tilde{\xi }}_1^{(n-m)}\right) ^2:=\sum _{r\in \mathcal {D}^{(n)}(l,m)}\left( \xi _r^{(n)}\right) ^2\). In analogy to (15), we solve (C.4) to obtain
$$\begin{aligned} \left( {\tilde{\xi }}_1^{(n-m)}\right) ^2= -\frac{\prod _{k=1,k\notin \mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)}^{n+1}\left( \lambda -\lambda _k^{(n+1)}\right) }{\prod _{k=1,k\notin \mathcal {D}^{(n)}(l,m)}^n\left( \lambda -\lambda _k^{(n)}\right) }. \end{aligned}$$(C.5)As we mentioned earlier, \(\mathcal {K'}\ne \emptyset \) implies \(\left( {\tilde{\xi }}_1^{(n-m)}\right) ^2=0\), thus the above expression implies that \(\lambda _k^{(n+1)}=\lambda \) for some \(k\notin \mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)\), which is in contradiction with the Lemma’s assumptions.
-
(ii)
\(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_{II}^{(n+1)}(l,m)\) or \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_{\mathrm{III}}^{(n+1)}(l,m)\) Consider the set of Equations (C.4) for \(k\in \{1,\ldots ,n+1\}/\mathcal {D}^{(n+1)}(l,m)\) with \(\xi _r^{(n)}=0\) whenever \(r\in \mathcal {D}^{(n)}(l,m)\). They are Cauchy equations for the regular spectra of a reduced dimension \({\tilde{\sigma }}^{(n-m)}=\{\lambda _k^{(n+1)}:\ k\in \{1,\ldots ,n+1\}/\mathcal {D}^{(n+1)}(l,m)\}\) and \({\tilde{\sigma }}^{(n-m-1)}=\{\lambda _k^{(n)}:\ k\in \{1,\ldots ,n\}/\mathcal {D}^{(n)}(l,m)\}\). In analogy to (15), we solve (C.4) to obtain
$$\begin{aligned} (\xi ^{(n)}_r)^2 =-\frac{\prod _{k=1,k\notin \mathcal {D}^{(n+1)}(l,m)}^{n+1}\left( \lambda ^{(n)}_r-\lambda ^{(n+1)}_k\right) }{\prod _{k=1,k\notin \mathcal {D}^{(n)}(l,m),k\ne r}^n\left( \lambda ^{(n)}_r-\lambda ^{(n)}_k\right) },\quad r\in \{1,\ldots ,n\}/\mathcal {D}^{(n)}(l,m). \nonumber \\ \end{aligned}$$(C.6)The above expressions for \((\xi ^{(n)}_r)^2\) have to be compatible with (C.4) applied to \(k\in \mathcal {K}'\). This is in full analogy to (C.3) which we treated as a polynomial equation for \(\lambda \). This polynomial equation is equivalent to
$$\begin{aligned}\prod _{k=1,k\notin \mathcal {D}^{(n+1)}(l,m)}^{n+1}\left( \lambda -\lambda ^{(n+1)}_k\right) =0.\end{aligned}$$This in turn implies that \(\lambda _k^{(n+1)}=\lambda \) for some \(k\notin \mathcal {D}^{(n+1)}(l,m)\), which is in contradiction with this Lemma’s assumptions.
\(\square \)
Thus, whenever \(\mathcal {D}^{(n+1)}(l,m)\ne \mathcal {D}_{\mathrm{I}}^{(n+1)}(l,m)\), we have \(b_{k,n+1}=0\) for all \(k\in \mathcal {D}^{(n+1)}(l,m)\). Let us now focus on this particular case. By (11), we get that for every \(k\in \mathcal {D}^{(n+1)}(l,m)\) and \(r\notin \mathcal {D}^{(n)}(l,m)\) \(b_{k,r}=0\). Thus, vector \({|{{\tilde{v}}^{(n+1)}(k)}\rangle }\) effectively belongs to the degenerate subspace of \(A^{(n)}\), i.e.,
Depending on the precise form of the set \(\mathcal {D}^{(n+1)}(l,m)\), the dimension of the degenerate subspace of \(A^{(n+1)}\) can be:
-
(i)
equal to the dimension of the degenerate subspace of \(A^{(n)}\); this happens when \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_i^{(n+1)}(l,m)\) with \(i=\mathrm{II},\mathrm{III}\)
-
(ii)
one dimension smaller than the degenerate subspace of \(A^{(n)}\); this happens when \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)\).
If \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_i^{(n+1)}(l,m)\) with \(i=\mathrm{II},\mathrm{III}\), then (C.7) effectively describes just a change of basis. Thus, coefficients \(b_{r,k}\) with \(r\in \mathcal {D}^{(n)}(l,m)\) and \(k\in \mathcal {D}^{(n+1)}(l,m)\) form an orthogonal matrix. If \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)\), then (C.7) geometrically means that the degenerate eigenspace of \(A^{(n+1)}\) can be any subspace of the degenerate eigenspace of \(A^{(n)}\) of codimension one. (10) yields the condition that \({\langle {{\tilde{v}}^{(n+1)}(k)|a^{(n)}}\rangle }=0\) for all \(k\in \mathcal {D}^{(n+1)}(l,m)\), i.e.,
If \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_i^{(n+1)}(l,m)\) with \(i=\mathrm{II},\mathrm{III}\), the dimensionality of the degenerate eigenspaces together with (C.8) forces \(\xi _r^{(n)}=0\) for all \(r\in \mathcal {D}^{(n)}(l,m)\). This together with (11) imply that any eigenvector of \(A^{(n+1)}\) corresponding to a non-degenerate eigenvalue is orthogonal to the degenerate eigenspace of \(A^{(n)}\). Thus, we have effectively reduced the dimension of the problem by \(m+1\) and we can apply Theorem 4 for the regular reduced matrices \({\tilde{A}}^{(n-m-1)}\) and \({\tilde{A}}^{(n-m)}\) with the degenerate eigenspaces removed. In particular,
and \(b_{k,r}=0\) for \(k\notin \mathcal {D}^{(n+1)}(l,m)\) otherwise.
Let us next move to the case when \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)\). The geometric interpretation of (C.8) is that \({|{a^{(n)}}\rangle }\) is orthogonal to the degenerate eigenspace of \(A^{(n+1)}\) embedded in the degenerate eigenspace of \(A^{(n)}\). Consider next (C.4) from the proof of Lemma 12 applied for \(k\notin \mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)\). This is a set of \(n-m+1\) equations involving regular spectra of a reduced dimension \({\tilde{\sigma }}^{(n-m+1)}=\{\lambda _k^{(n+1)}:\ k\in \{1,\ldots ,n+1\}/\mathcal {D}_{\mathrm{IV}}^{(n+1)}(l,m)\}\) and \({\tilde{\sigma }}^{(n-m)}=\{\lambda \}\cup \{\lambda _k^{(n)}:\ k\in \{1,\ldots ,n\}/\mathcal {D}^{(n)}(l,m)\}\). The reduced regular matrix \({\tilde{A}}^{(n-m+1)}\) is obtained from \(A^{(n+1)}\) by removing the entire degenerate eigenspace with eigenvalue \(\lambda \). The reduced regular matrix \({\tilde{A}}^{(n-m)}\) is determined by the embedding of the degenerate eigenspace of \(A^{(n+1)}\) into the degenerate eigenspace of \(A^{(n)}\)—the image of this embedding is removed. Next, we use the familiar method of Theorem 4 applied the above regular matrices. However, in contrast to the previous case, the coefficients \(\xi _r^{(n)}\) and \(b_{k,r}\) for \(r\in \mathcal {D}^{(n)}(l,m)\) and \(k\notin \mathcal {D}^{(n+1)}(l,m)\) may be nonzero and are determined by the choice of the embedding of eigenspaces.
Finally, let us consider \(\mathcal {D}^{(n+1)}(l,m)=\mathcal {D}_{\mathrm{I}}^{(n+1)}(l,m)\). Firstly, note that \(|\mathcal {D}_{\mathrm{I}}^{(n+1)}(l,m)|=|\mathcal {D}^{(n)}(l,m)|+1=m+2\), thus the degenerate eigenspace of \(A^{(n+1)}\) cannot be spanned only by the vectors \({|{v^{(n)}(r),0}\rangle }\) with \(r\in \mathcal {D}^{(n)}(l,m)\). Hence, we necessarily have \(b_{k,n+1}\ne 0\) for some \(k\in \mathcal {D}_{\mathrm{I}}^{(n+1)}(l,m)\). By (11), this implies that \(\xi _r^{(n)}=0\) for all \(r\in \mathcal {D}^{(n)}(l,m)\), i.e., \({|{a^{(n)}}\rangle }\) is orthogonal to the degenerate eigenspace of \(A^{(n)}\). This in turn implies that for any \(k\notin \mathcal {D}_{\mathrm{I}}^{(n+1)}(l,m)\), we have \(b_{k,r}=0\) whenever \(r\in \mathcal {D}^{(n)}(l,m)\), i.e., the non-degenerate eigenvectors of \(A^{(n+1)}\) are orthogonal to the degenerate eigenspace of \(A^{(n)}\). Thus, we consider the regular matrices \({\tilde{A}}^{(n-m)}\) and \({\tilde{A}}^{(n-m-1)}\) which are the original matrices truncated to the space defined as the orthogonal complement of the degenerate eigenspace of \(A^{(n)}\). They have the regular spectra \({\tilde{\sigma }}^{(n-m)}=\{\lambda \}\cup \{\lambda _k^{(n+1)}:\ k\in \{1,\ldots ,n+1\}/\mathcal {D}_{\mathrm{I}}^{(n+1)}(l,m)\}\) and \({\tilde{\sigma }}^{(n-m-1)}=\{\lambda _k^{(n)}:\ k\in \{1,\ldots ,n\}/\mathcal {D}^{(n)}(l,m)\}\). Thus, we use Theorem 4 to find the vector \({|{a^{(n)}}\rangle }\) as well as the non-degenerate eigenvectors of \(A^{(n+1)}\). What is left to find are the remaining \(m+2\) degenerate eigenvectors of \(A^{(n+1)}\) corresponding to the eigenvalue \(\lambda \). Their coefficients \(b_{k,r}\) with \(r\notin \mathcal {D}^{(n)}(l,m)\) are proportional to \(b_{k,n+1}\) as stated in (11), i.e.,
Note that the equations
are now automatically satisfied by the above expressions for \(b_{k,r}\). The unknown coefficients \(b_{k,n+1}\) and \(b_{r,k}\) with \(k\in \mathcal {D}_{\mathrm{I}}^{(n+1)}(l,m)\) and \(r\notin \mathcal {D}^{(n)}(l,m)\) are completely free to choose so that the resulting vectors \(\left\{ {|{{\tilde{v}}^{(n+1)}(k)}\rangle }\right\} _{k\in \mathcal {D}_{\mathrm{I}}^{(n+1)}(l,m)}\) form an orthonormal basis of the degenerate eigenspace.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Macia̧żek, T., Smilansky, U. Can One Hear a Matrix? Recovering a Real Symmetric Matrix from Its Spectral Data. Ann. Henri Poincaré 23, 1791–1829 (2022). https://doi.org/10.1007/s00023-021-01135-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-021-01135-z




 and
and 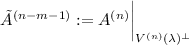 . The degenerate eigenvectors of
. The degenerate eigenvectors of  and
and  . The degenerate eigenvectors of
. The degenerate eigenvectors of  and
and  .
.





