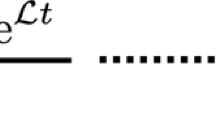Abstract
We introduce a notion of absorption operators in the context of quantum Markov processes. The absorption problem in invariant domains (enclosures) is treated for a quantum Markov evolution on a separable Hilbert space, both in discrete and continuous times: We define a well-behaving set of positive operators which can correspond to classical absorption probabilities, and we study their basic properties, in general, and with respect to accessibility structure of channels, transience and recurrence. In particular, we can prove that no accessibility is allowed between the null and positive recurrent subspaces. In the case, when the positive recurrent subspace is attractive, ergodic theory will allow us to get additional results, in particular about the description of fixed points.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multiple motivations naturally drive to reflect on a quantum notion of absorption probability, which is a concept with its own peculiar interest and with many significant connections. Indeed, starting from the generalization of absorption probabilities, we shall be able to revisit and extend to the non-commutative case some classical steps of this theory, to stress peculiar behaviors of the non-commutative case and to analyze some implications in asymptotic theory and, more in general, in some structure property of the evolution. In particular, accessibility among different domains, or relations with communication properties, transience and recurrence, which are still delicate and unclear themes in the non-commutative world, will be involved. Moreover, as well-known classical probability results teach us, under suitable conditions, the fixed points can be described through absorption probabilities in appropriate subsets of the domain.
Quantum Markov semigroups are widely used in physical models since years, from quantum optics to quantum information and computation. From a mathematical viewpoint, they can be seen as a non-commutative counterpart of Markov semigroups on commutative spaces of functions in classical probability. The basic objects we will deal with are quantum channels, a single one or a family forming a semigroup to describe evolution with time.
Various fields of applications to quantum physics motivate the study of these channels and, in particular, of absorption operators and fixed points (see [1, 13, 32, 33, 37]), but the approach we shall follow here comes from classical and quantum probability. In a first step, a central theme which stimulated this work is the study of the fixed points of a quantum channel: This theme has been widely investigated, with satisfactory results for the case of positive recurrent channels, i.e., channels with an invariant faithful density (see [5, 7, 9, 10, 19, 27]), but information is lacking and yet useful in the general case [1, 2, 24]. Once the construction of the mathematical object clearly appeared, we realized that it could be a useful tool to tackle the different aforementioned subjects.
To be more precise in the description of the mathematical environment, we fix a quantum system described by a separable Hilbert space \({{\mathcal {H}}}\), and we denote by \(B({{\mathcal {H}}})\) the algebra of bounded operators acting on \({{\mathcal {H}}}\), so containing the observables, and by \(L^1({{\mathcal {H}}})\) its predual, the space of trace class operators, which contains the densities.
A quantum channel, in the Heisenberg picture, is then a completely positive identity preserving normal map \(\varPhi \) on \(B({{\mathcal {H}}})\). This map is sometimes called a Markov operator, and it is contractive [6, Corollary 3.2.6]. Its predual \(\varPhi _*\) will be a completely positive trace preserving map acting on \(L^1({{\mathcal {H}}})\) and describing the Schrodinger picture.
By a quantum Markovian evolution, we mean here an evolution described by a semigroup \({{\mathcal {P}}}=({{\mathcal {P}}}_t)_{t\in {{\mathfrak {T}}}}\) of quantum channels. For discrete time models, we shall essentially consider \({{\mathfrak {T}}}=\mathbb {N}\) and the semigroup \({{\mathcal {P}}}\) will consist of powers of a single quantum channel \(\varPhi \), i.e., \({{\mathcal {P}}}=(\varPhi ^n)_{n\ge 0}\), while, in the continuous time case, \({{\mathfrak {T}}}=[0,+\infty )\) and \({{\mathcal {P}}}\) is generally considered as a quantum dynamical semigroup, so also with some continuity properties (see Sect. 2). We immediately underline that the conditions on \({{\mathcal {P}}}\) and on the domain can be easily relaxed for many of our results, either for positivity or for continuity conditions, but we are not going to detail this here anyway, because these assumptions are standard for most applications.
In the next section, we shall be more precise in notations and definitions, and here, we aim to give a brief outline of the absorption operators and of the contents of the paper. First, we need to consider appropriate absorbing domains: By “absorbing,” we informally mean that the evolution cannot escape from this domain, even if it is not obliged to enter in it. These kinds of domains are usually called invariant subspaces or enclosures in the literature (see Definition 1). We denote by \({{\mathcal {V}}}\) such a domain and by \(p_{{\mathcal {V}}}\) the projection on \({{\mathcal {V}}}\), which is always a subharmonic projection for the semigroup \({{\mathcal {P}}}\). Then, we define the corresponding absorption operator \(A({{\mathcal {V}}})\) by the relation
The choice of this name is due to the fact that they are the quantum counterpart of absorption probabilities and they coincide with these probabilities for the minimal dilations: see Remark 3 for the parallel with the classical commutative picture. These operators contain the same kind of information as absorption probabilities, and they mimic some of their nice properties in a non-commutative setting. In particular, for any vector u in \({{\mathcal {H}}}\),
so that \(A({{\mathcal {V}}})\) describes the quantity of mass that the evolution asymptotically sends to \({{\mathcal {V}}}\) starting in the pure state u.
Section 2 will be first devoted to the construction of absorption operators, to their characterization as fixed points and to the study of some basic general properties related to the structure of the channels (Proposition 6); accessibility rules between \({{\mathcal {V}}}\), \({{\mathcal {V}}}^\perp \) and other enclosures associated with the spectral resolution of absorption operators (Proposition 4) will also be investigated.
Section 3 will focus on the relations between absorbing properties and transience and recurrence. Similarly as in the classical case, the absorption operators \(A({{\mathcal {V}}})\) will be particularly relevant in the case when \({{\mathcal {V}}}\) is a minimal recurrent enclosure (i.e., a recurrent class, for a classical Markov chain). We recall that, for a classical Markov chain valued in a discrete set V, a vertex j in V is recurrent if, starting from j, the chain almost surely returns to it; otherwise, the vertex is transient. Among recurrent vertices, we call positive (or fast) recurrent the vertices for which the return times are averagely finite, while other vertices are called null (or slow) recurrent. Transience and (null and positive) recurrence are invariant properties for communicating vertices and positive recurrent vertices consist of the support of invariant probabilities. We refer, for instance, to [31] for a complete introduction to classical Markov chains.
Here, we shall briefly summarize the main definitions to characterize quantum recurrence using potentials, introduced in [18, 35]), and we shall prove that the orthogonal complement of an enclosure inside the recurrent space is again an enclosure (Theorem 9). This is maybe the main result of the section, due to its various implications: It will be the main instrument to analyze the properties of absorption operators with respect to transience and recurrence (Theorem 14), and in addition, as a by-product, it implies that the null recurrent subspace is an enclosure or, equivalently, that it reduces the Markov evolution (a problem of non-accessibility between quantum null and positive recurrent spaces left open in [35]).
In Sect. 4, we concentrate on the case when the positive recurrent subspace is attractive. This trivially includes the situation when the semigroup has an invariant faithful state, already extensively studied [5, 9, 10, 19, 27], but allows to consider infinite-dimensional models with non-trivial transient subspaces, for which results are still lacking in general. The existence of a normal conditional expectation which projects the space of observables on the positive recurrent part [23] allows to gain supplementary results about absorption operators and create a bridge to analyze the structure of fixed points in general (Theorem 22) and to characterize the cases when it is an algebra. It is then immediate to deduce some more details about the links with the asymptotic/ergodic properties of the evolution.
Finally, in Sect. 5, we consider some models in order to see the application of our results: We consider both continuous and discrete time cases, examples in which the positive recurrent space is absorbing or not, finite and infinite-dimensional examples.
2 Absorption Operators
In this section, after some brief preliminary description of the context, we are going to define the absorption operators and to prove the basic properties, essentially involving the spectral structure and accessibility relations between subspaces.
By quantum channel, we mean a completely positive identity preserving normal map acting on \(B({{\mathcal {H}}})\). We already specified that we consider the evolutions described by a Markov semigroup \({{\mathcal {P}}}=({{\mathcal {P}}}_t)_{t\in {{\mathfrak {T}}}}\), that is a semigroup of quantum channels, indexed in discrete or continuous time, i.e.:
-
\({{\mathfrak {T}}}\) is equal \({\mathbb N}\) or \([0,+\infty )\);
-
\({{\mathcal {P}}}_t\) is a quantum channel for any t;
-
\({{\mathcal {P}}}_0=\mathrm {Id}\) and \({{\mathcal {P}}}_t\circ {{\mathcal {P}}}_s = {{\mathcal {P}}}_{t+s}\) for all times t and s.
-
When time is continuous, we shall suppose that \({{\mathcal {P}}}\) is a quantum dynamical semigroup, i.e., a \(\hbox {weak}^*\)-continuous semigroup of completely positive unital maps.
When we are interested in one single channel \(\varPhi \), we can naturally associate it to the discrete time semigroup \((\varPhi ^n)_{n\ge 0}\). In this section, we do not really need the additional continuity assumptions on the semigroup nor complete positivity, but these conditions are generally considered the standard ones, so we shall not worry about this (see Remark 8).
The predual operator of a channel \(\varPhi \) will be denoted by \(\varPhi _*\) and is a completely positive trace preserving operator acting on the space \(L^1({{\mathcal {H}}})\) of trace class operators. \(L^1({{\mathcal {H}}})\) contains the density operators, i.e., the nonnegative operators with unit trace; we shall call states these density operators, identifying, by standard duality arguments, the densities with the normal non-commutative probability measures.
As we have previously remarked in Introduction, in order to analyze the absorption problems, we need to define the proper “absorbing” domains, for which it makes sense to define absorption. These subspaces of \({{\mathcal {H}}}\) are sometimes called enclosures or invariant subspaces [5, 37], and they are informally characterized by the fact that the evolution cannot decrease the quantity of mass inside these domains.
More precisely, we write the following.
Definition 1
A subspace \({{\mathcal {V}}}\) of \({{\mathcal {H}}}\) is an enclosure for a channel \(\varPhi \) if, for any state \(\rho \),
\({{\mathcal {V}}}\) is an enclosure for a semigroup \({{\mathcal {P}}}=({{\mathcal {P}}}_t)_t\) when it is an enclosure for any channel \({{\mathcal {P}}}_t \) of the family \({{\mathcal {P}}}\).
Under different names or viewpoints, enclosures have been deeply investigated and widely used, in order to study the reducibility/irreducibility of quantum processes; the literature is huge, both in theoretical [14, 17, 20, 26]) and applicative contexts [5, 13, 37]. Enclosures are exactly the range of a so-called reducing or subharmonic projection for the channel and they identify hereditary subalgebras. The jungle of different terminologies have sometimes given difficulties to interplay between the various visions, but it is useful to keep in mind all of them, because this will allow to exploit all the potentialities. We rapidly sum up here some of these parallel different definitions. For a subspace \({{\mathcal {V}}}\) of \({{\mathcal {H}}}\), we denote by \(p_{{\mathcal {V}}}\) the projection on \({{\mathcal {V}}}\), and then, the following facts are equivalent (see [10, Section 3]):
-
\({{\mathcal {V}}}\) is an enclosure, or stationary domain, or invariant subspace for the channel \(\varPhi \),
-
\(p_{{\mathcal {V}}}\) is a reducing or subharmonic projection for \(\varPhi \), i.e., \(\varPhi (p_{{\mathcal {V}}})\ge p_{{\mathcal {V}}}\)
-
\(p_{{\mathcal {V}}}L^1({{\mathcal {H}}})p_{{\mathcal {V}}}\) is hereditary for \(\varPhi _*\), i.e., \(\varPhi _*(p_{{\mathcal {V}}}L^1({{\mathcal {H}}})p_{{\mathcal {V}}})\subseteq p_{{\mathcal {V}}}L^1({{\mathcal {H}}})p_{{\mathcal {V}}}\), i.e., a weak-closed face preserved by \(\varPhi _*\).
-
\(p_{{{\mathcal {V}}}^\perp }{\mathcal B}({{\mathcal {H}}})p_{{{\mathcal {V}}}^\perp }\) is hereditary for \(\varPhi \).
When \({{\mathcal {V}}}\) is an enclosure, \(p_{{\mathcal {V}}}L^1({{\mathcal {H}}})p_{{\mathcal {V}}}\) is hereditary for \(\varPhi _*\), so we can define the restricted quantum channel \(\varPhi ^{{\mathcal {V}}}\) on the subsystem \({{\mathcal {V}}}\), that is an operator acting on the set \(p_{{\mathcal {V}}}B({{\mathcal {H}}})p_{{\mathcal {V}}}\simeq B({{\mathcal {V}}})\) of bounded operators on \({{\mathcal {V}}}\), \(\varPhi ^{{{\mathcal {V}}}} : p_{{\mathcal {V}}}B({{\mathcal {H}}})p_{{\mathcal {V}}} \rightarrow p_{{\mathcal {V}}}B({{\mathcal {H}}})p_{{\mathcal {V}}},\)
and the restricted predual channel \(\varPhi ^{{\mathcal {V}}}_*:=\varPhi _{*| p_{{\mathcal {V}}}L^1({{\mathcal {H}}})p_{{\mathcal {V}}}}: p_{{\mathcal {V}}}L^1({{\mathcal {H}}})p_{{\mathcal {V}}} \rightarrow p_{{\mathcal {V}}}L^1({{\mathcal {H}}})p_{{\mathcal {V}}}\)
From now on, we shall use the same notation, \({{\mathcal {V}}}\) , for instance, for a subspace of \({\mathcal {H}}\) and for the projection on the same subspace when the distinction is clear from the context.
An immediate consequence of the definition is that when \({{\mathcal {V}}}\) is an enclosure for \({{\mathcal {P}}}\), since the corresponding projection is subharmonic and \({{\mathcal {P}}}\) is positivity preserving, the family \(({{\mathcal {P}}}_t({\mathcal {V}}))_{t \in {{\mathfrak {T}}}}\) is an increasing family of positive operators bounded above by the identity operator. So (Lemma 2.4.19 in [6]) it converges weak* to its least upper bound. This makes the following definition consistent.
Definition 2
Consider an enclosure \({{\mathcal {V}}}\) for a Markov semigroup \({{\mathcal {P}}}\). We can define the absorption operator associated with \({\mathcal {V}}\) as the \(\hbox {weak}^*\) limit
In the case, \({{\mathcal {V}}}\) is an enclosure for a quantum channel \(\varPhi \), defined as before \({{\mathcal {P}}}=(\varPhi ^n)_{n \in \mathbb {N}}\).
Obviously, the limit in (2) does not exist when \({{\mathcal {V}}}\) is replaced by a general operator, but it is true at least for enclosures and we shall deduce the same for a wider class of operators in the sequel (see Theorem 22).
Remark 3
A classical Markov chain \(X=(X_n)_{n\in {\mathbb N}}\) with transition matrix Q on the set V can be thought of as the diagonal/classical restriction of a dilated quantum channel acting on \(B({\mathbb C}^{|V|})\). An enclosure for X is then a subset C of V which is closed under the evolution, i.e., such that \(Q_{ij}=0\) whenever \(i\in C\) and \(j\notin C\), or, equivalently, such that, for any probability law \(\mu \) supported in C, \(\mu Q\) is still supported in C. The absorption operator for the enclosure C will be defined by (2) as \(A(C)=\lim _{n \rightarrow +\infty }Q^n(1_C)\), so that A(C) is a bounded function defined on the set V representing the absorption probabilities for a classical Markov chain, i.e.,
This parallel can suggest some expected properties of an absorption operator, starting from the classical probability context, replacing bounded functions with bounded operators, complementary sets with orthogonal complement and so on.
Proposition 4
Let \({{\mathcal {V}}}\) be an enclosure.
-
1.
\(A({{\mathcal {V}}})\) is a well-defined bounded operator, and it is a fixed point for the semigroup and \(0\le A({{\mathcal {V}}})\le 1\).
-
2.
If \(\lambda \) is an eigenvalue of \(A({{\mathcal {V}}})\) with norm one eigenvector x, then
$$\begin{aligned} \lambda = \lim _{t \rightarrow +\infty } \mathrm {Tr}({{\mathcal {V}}} {{\mathcal {P}}}_{*t}(|x\rangle \langle x|)). \end{aligned}$$In particular, the kernel of \(A({{\mathcal {V}}})\) consists of all vectors x such that
$$\begin{aligned} \mathrm{Enc}(x):=\sup _{t \in {{\mathfrak {T}}}}\{\mathrm{supp}({{\mathcal {P}}}_{*t}(|x\rangle \langle x|))\}\subset \mathcal {V}^\perp . \end{aligned}$$ -
3.
The eigenspaces of \(A({{\mathcal {V}}})\) corresponding to the eigenvalues 0 and 1 are enclosures.
The previous proposition shows some first elementary properties that we can expect from absorption classical probabilities. In particular, we can characterize the kernel of \(A({{\mathcal {V}}})\) as the space generated by vectors x such that if the system starts in the pure state \(|x\rangle \langle x|\), zero probability is given to the enclosure \({{\mathcal {V}}}\) along the whole evolution. The space \(\mathrm{Enc}(x)\) introduced above can be proved to be the smallest enclosure containing x (see [9]). Notice that, when working in a non-commutative context, some classical rules are missing; for instance, \(\mathrm{Enc}(x)\not \perp \mathcal {V}\) is not a sufficiently strong condition to ensure that x is in the support of \(A({{\mathcal {V}}})\) and we cannot hope that \({{\mathcal {V}}}\subset \mathrm{Enc}(x)\) holds for all x in the support of \(A({{\mathcal {V}}})\). For a counterexample to the latter fact, we can consider models for which there exist enclosures which do not contain \({{\mathcal {V}}}\) and that are not orthogonal to it (see Examples 5.1 or 5.3).
Proof
-
1.
We already remarked that the definition given in relation (2) is consistent. Moreover, since \({{\mathcal {V}}}\) is a projection and \({{\mathcal {P}}}\) is positivity and identity preserving,
$$\begin{aligned} 0 \le {{\mathcal {V}}} \le 1 \qquad \Rightarrow \qquad 0\le {{\mathcal {P}}}_t({{\mathcal {V}}}) \le 1 \quad \forall t \in {{\mathfrak {T}}} \end{aligned}$$and passing to the \(\hbox {weak}^*\) limit, we preserve the inequalities. Moreover, \(A({{\mathcal {V}}})\) is a fixed point due to the normality of the channels \({{\mathcal {P}}}_t\).
-
2.
When x is a norm one eigenvector pertaining \(\lambda \), then we immediately deduce
$$\begin{aligned} \lambda = \langle x, A({{\mathcal {V}}}) x \rangle =\lim _{t \rightarrow +\infty } \mathrm {Tr}({{\mathcal {V}}} {{\mathcal {P}}}_{*t}(|x\rangle \langle x|)). \end{aligned}$$In particular, when \(\lambda =0\), this implies that, for x in the kernel of \(A({{\mathcal {V}}})\),
$$\begin{aligned} \lim _{t \rightarrow +\infty } \mathrm {Tr}({{\mathcal {V}}} {{\mathcal {P}}}_{*t}(|x\rangle \langle x|))=0; \end{aligned}$$but, since \({{\mathcal {V}}}\) is an enclosure, the trace \(\mathrm {Tr}({{\mathcal {V}}} {{\mathcal {P}}}_{*t}(|x\rangle \langle x|))\) is a nonnegative increasing function of t, so that the previous gives
$$\begin{aligned} \mathrm {Tr}({{\mathcal {V}}} {{\mathcal {P}}}_{*t}(|x\rangle \langle x|))=0 \qquad \text{ for } \text{ all } t \in {{\mathfrak {T}}} \end{aligned}$$(3)and the conclusion follows.
-
3.
We first show that the kernel of \(A({{\mathcal {V}}})\) is an enclosure. \(A({{\mathcal {V}}})\) is positive and harmonic; hence, for \(\rho \in L^1({{\mathcal {H}}})\) such that \(\mathrm{supp}(\rho )\subset \ker (A({{\mathcal {V}}}))\), we have that for all \( t \in {{\mathfrak {T}}}\)
$$\begin{aligned} \mathrm {Tr}(A({{\mathcal {V}}}){{\mathcal {P}}}_{*t}(\rho ))=\mathrm {Tr}({{\mathcal {P}}}_t(A({{\mathcal {V}}}))\rho )= \mathrm {Tr}(A({{\mathcal {V}}})\rho )=0, \end{aligned}$$so \(\mathrm{supp}({{\mathcal {P}}}_{*t}(\rho ))\subset \ker (A({{\mathcal {V}}}))\) and the kernel of \(A({{\mathcal {V}}})\) is an enclosure. We can repeat similar computations replacing \(A({{\mathcal {V}}})\) with the operator \(X:=1-A({{\mathcal {V}}})\) and prove that its kernel, which is exactly the eigenspace of \(A({{\mathcal {V}}})\) corresponding to the eigenvalue 1, is an enclosure.
\(\square \)
In the next result and in the following pages, we shall repeatedly use the following well-known property of positive operators: Let Y be a positive bounded operator and p an orthogonal projection such that \(pYp=0\); then \(pY(1-p)=(1-p)Yp=0\).
Lemma 5
For any enclosure \({\mathcal {V}}\) and for any \(t\in {{\mathfrak {T}}}\),
or equivalently
Moreover, for any enclosure \({\mathcal W}\) orthogonal to \({\mathcal {V}}\),
Proof
Since \({\mathcal {V}}\) is an enclosure, \({{\mathcal {V}}} \le {{\mathcal {P}}}_t({{\mathcal {V}}}) \le 1\), so \({{\mathcal {V}}} = {{\mathcal {V}}} {{\mathcal {P}}}_t({{\mathcal {V}}}) {{\mathcal {V}}}\). Moreover, this implies that, for any \(t \in {{\mathfrak {T}}}\), \({{\mathcal {P}}}_t({{\mathcal {V}}}) -{{\mathcal {V}}}\) is a positive operator such that \({{\mathcal {V}}}({{\mathcal {P}}}_t({{\mathcal {V}}}) -{{\mathcal {V}}}){{\mathcal {V}}}=0\), and so
which immediately implies \( {{\mathcal {V}}}{{\mathcal {P}}}_t({{\mathcal {V}}})(1-{{\mathcal {V}}})=(1-{{\mathcal {V}}}){{\mathcal {P}}}_t({{\mathcal {V}}}){{\mathcal {V}}}=0. \)
For the last assertion, simply notice that \(0\le {{\mathcal {V}}}\le 1-{\mathcal W}\), so the positivity and unitality of \({{\mathcal {P}}}\) give
where the last equality follows from the application of the first part of the statement to the enclosure \({\mathcal W}\). \(\square \)
Proposition 6
-
1.
For any enclosure \({{\mathcal {V}}}\)
$$\begin{aligned} {{\mathcal {V}}}A({{\mathcal {V}}}){{\mathcal {V}}}={{\mathcal {V}}}, \qquad {{\mathcal {V}}}A({{\mathcal {V}}})(1-{{\mathcal {V}}})= (1-{{\mathcal {V}}})A({{\mathcal {V}}}){{\mathcal {V}}}=0. \end{aligned}$$ -
2.
\({\mathcal W} A({{\mathcal {V}}}){\mathcal W} = 0\) for any enclosure \({\mathcal W}\) orthogonal to \({\mathcal {V}}\). In fact, the kernel of \(A({{\mathcal {V}}})\) is the maximal enclosure orthogonal to \({{\mathcal {V}}}\).
-
3.
\(A({{\mathcal {V}}})\) is the minimal fix point x of the semigroup \({{\mathcal {P}}}\) such that
$$\begin{aligned} 0\le x\le 1 \qquad \text{ and } \qquad {{\mathcal {V}}}x{{\mathcal {V}}}={{\mathcal {V}}}. \end{aligned}$$(4)
Proof
The first and second points are evident using the previous lemma and simply passing to the limit. For the last assertion of point 2, also remember that we already know that \(\text{ ker }A({{\mathcal {V}}})\) is an enclosure by Proposition 4.
Now, consider a fixed point satisfying relations (4). Then, since \((1-x)\) is a positive operator such that \({{\mathcal {V}}}(1-x){{\mathcal {V}}}=0\), by positivity,
Applying the semigroup, we obtain for any t
This concludes the proof. \(\square \)
Example 7
As a first example, we consider a model simple enough to allow an easy intuition and explicit calculations. It displays anyway interesting characteristics of infinite-dimensional systems with respect to absorption and fixed points, and even if it seems to behave pretty much like in the classical case, with little variations, it can present features which arise only in the non-commutative setting, but we shall come back to this later, in Sect. 5. This model is an open quantum random walks (OQRW) as introduced in [3]. Such processes are a possible non-commutative generalization of classical Markov Chains and have applications in quantum computing, quantum optics, biology; they have been intensively studied in the recent years (see the bibliography in [9, 10, 32]).
Let us consider a homogeneous OQRW [8] on \(\mathbb {Z}\) with local space \(\mathbb {C}^3\), hence the state space is \({{\mathcal {H}}}=\ell ^2(\mathbb {Z}) \otimes \mathbb {C}^3\). We consider the local transition operators
and the related OQRW \(\varPhi :B({{\mathcal {H}}})\rightarrow B({{\mathcal {H}}})\),
In order for the map to be Markov, we have the following constraints on the coefficients:
Let \(\{e_i\}_{i=0}^2\) be the canonical basis for \(\mathbb {C}^3\) and \(E_i\) be the projection \(\bigoplus _{j\in \mathbb {Z}}|e_i\rangle \langle e_i|\otimes |j\rangle \langle j| \) for \(i=0,1,2\). \(E_2\) is a minimal subharmonic projection, and the reduced process is essentially a symmetric random walk on \(\mathbb {Z}\). \(E_0\) is a subharmonic projection too, and the corresponding reduced process is again a random walk. So it will be significant to compute the absorption operators \(A(E_0)\) and \(A(E_2)\). Since we are interested in a model showing non-trivial absorption dynamics, we assume that
which means that any state supported in \(E_1\) will have the possibility to flow both to \(E_0\) and \(E_2\). Due to Proposition 6, we know that the absorption operators are fixed points and have a block diagonal structure, \(A(E_k)=E_k+E_1A(E_k)E_1\), \(k=0,2\). So it is immediate to compute explicitly
where \(p=\frac{\sum _{\varepsilon =-,+} |b_\varepsilon |^2}{\sum _{\varepsilon =-,+} |b_\varepsilon |^2+|d_\varepsilon |^2}\in (0,1)\).
We shall further consider this model in the last section.
Remark 8
All the properties in this section rely on the (simple) positivity of the quantum Markov semigroup \({{\mathcal {P}}}\). This can be significant to remark, because of discussions emerging in the physicists’ community, even if the assumption of complete positivity remains surely the most popular. However, if we use complete positivity, we can study how absorption influences the structure of the Kraus operators of the channels. It is well known that, for any quantum channel \(\varPhi \), there exists a denumerable family of bounded operators \(\{V_i\}_{i \in I}\) such that, for every \(x \in B({{\mathcal {H}}})\),
We can reformulate the accessibility relations implied by Proposition 4 in terms of the \(V_i\)’s. Consider an enclosure \({{\mathcal {V}}}\), and let us define \(p_{\mathcal K}\) the projection onto \(\ker (A({{\mathcal {V}}}))\) and q the range projection of \(A({{\mathcal {V}}})-{{\mathcal {V}}}\). Indeed, we have that
-
\( p_{{\mathcal {V}}}V_i p_{\mathcal K}=p_{\mathcal K}V_i p_{{\mathcal {V}}}=0\) for every \(i \in I\);
-
\(p_{{\mathcal {V}}}V_i q \ne 0\) for some \(i \in I\) if \(q \ne 0\).
In the continuous time setting, when we are treating a quantum dynamical semigroup with a Lindblad generator, similar relations can be obtained for the operators appearing in the Lindblad form and this had essentially already been observed in [17].
3 Absorption and Recurrence
In this section, we study the relations of absorption operators with transience and recurrence. We shall see how the classical relations can be generalized in a someway expected manner, reflecting the classical situations in the case when the channel has only orthogonal minimal enclosures, and with appropriate variations when the channel displays the typically quantum feature of non-orthogonal minimal enclosures. The absorption operators \(A({{\mathcal {V}}})\) turn out to have additional interesting properties in the case when \({{\mathcal {V}}}\) is a minimal recurrent enclosure (i.e., a recurrent class, for a Markov chain). We study this in Theorem 14.
As a by-product, absorption can enrich our knowledge about enclosures and transience and recurrence. In particular, we can prove that the orthogonal complement of an enclosure in the recurrent space is again an enclosure (Theorem 9): This was previously known only in the positive recurrent case, and apart from its intrinsic value, it is usually considered a significant starting step in reduction problems [5, 10] for the finite and infinite-dimensional cases, respectively). In addition, a paramount consequence of Theorem 9 is that the null recurrent subspace is an enclosure. The fact that positive recurrent configurations are not accessible from null recurrent ones is indeed a well-known fact for classical Markov chains, but still not proven for quantum chains. This was one of the main questions left open in [35] (see Remark 12 for more details).
For the convenience of the reader, we shall collect below the basic definitions about quantum recurrence and transience. The positive recurrent space \({\mathcal R}_+\) has been identified and characterized as the supremum of the ranges of invariant states since the 70s (see, for instance, [23]),
where we recall that a normal state is called invariant for \({{\mathcal {P}}}\) when it is a fixed point for \({{\mathcal {P}}}_*\). For the finite-dimensional case, the transient space was simply identified by its orthogonal complement; but a deep and comprehensive study of the infinite-dimensional case, which could introduce transience and (not necessarily positive) recurrence, was structured only more recently, in [18, 35]. The original exposition is in continuous time, but everything can be proved also in discrete time, as one can see in [24]. We indeed use both discrete and continuous time settings, and we denote by m a measure on the time set, which will coincide with the counting measure in the case \({{\mathfrak {T}}}=\mathbb {N}\) and with the Lebesgue measure in the case \({{\mathfrak {T}}}\) is a real interval.
Following [35], for every positive bounded operator x, we call form-potential of x the quadratic form \(\mathfrak {U}(x)\)
We denote by \({\mathcal B}({{\mathcal {H}}})_\text {int}\) the set of positive bounded linear operators x such that \(\mathfrak {U}(x)\) is bounded; for such x, one can consider the corresponding selfadjoint bounded linear operator \({\mathcal U}(x)\) (the potential of x). The transient subspace \({\mathcal T}\) is then given by [35]
and consequently
-
the recurrent subspace \({\mathcal R}:={\mathcal T}^\perp \) is given by the orthogonal complement of the transient subspace
-
and the null (or slow) recurrent subspace \({\mathcal R}_0:={\mathcal R} \cap {\mathcal R}_+^\perp \) by the orthogonal complement of the positive recurrent subspace inside the recurrent one.
Similarly as what we made for other subspaces, even for \({\mathcal R}_0\), \({\mathcal R}_+\), \({\mathcal R}\), \({\mathcal T}\), we shall use the same symbol for both the space and the projection any time the distinction is anyway clear from the context.
We can now prove the first main result of this section: The orthogonal complement of an enclosure inside a recurrent enclosure is itself an enclosure.
Theorem 9
If \({{\mathcal {V}}},{\mathcal Z}\) are increasing enclosures included in \({\mathcal R}\), i.e., such that \({{\mathcal {V}}}\subseteq {\mathcal Z} \subseteq {\mathcal R}\), then \({\mathcal Z}\cap {{\mathcal {V}}}^\perp \) is an enclosure.
In particular, \({\mathcal R}\cap {{\mathcal {V}}}^\perp \) is an enclosure and the null recurrent space \({\mathcal R}_0\) is an enclosure.
We divide the proof of the theorem in two steps; the first and central point, Lemma 10, proves that if a pure state can take mass to an orthogonal enclosure, then the corresponding vector is transient.
Lemma 10
Let \({{\mathcal {V}}}\) be an enclosure, w a norm one vector in \({{\mathcal {V}}}^\perp \). If there exist \({\bar{t}} \in {{\mathfrak {T}}}\) and \(\varepsilon >0\) such that \({{\mathcal {P}}}_{{\overline{t}}}({{\mathcal {V}}})\ge \varepsilon |w \rangle \langle w|\), then \(w\in {\mathcal T}\).
Proof
Let us call
By hypothesis, we know that \( {{\mathcal {P}}}_{\overline{t}}({{\mathcal {V}}})\ge \epsilon |w\rangle \langle w|\) and, since \(A({{\mathcal {V}}})\ge {{\mathcal {P}}}_{\overline{t}}({{\mathcal {V}}})\) by construction, w belongs to \( \ker (A({{\mathcal {V}}}))^\perp \) and therefore to the space \({\mathcal W}:={{\mathcal {V}}}^\perp \cap (\mathrm{Ker}A({{\mathcal {V}}}))^\perp \) (\(w\in {{\mathcal {V}}}^\perp \) by assumption). Recalling that \({{\mathcal {V}}}\) is contained in the range of \(A({{\mathcal {V}}})\), \({\mathcal W}^\perp := (\mathrm{Ker}A({{\mathcal {V}}}))\oplus {{\mathcal {V}}}\) is an enclosure as sum of two orthogonal enclosures. Consequently, the projection on \(\mathcal W\), always denoted with the same symbol \({\mathcal W}\) below, is superharmonic and we have, for \(t\ge {\overline{t}}\),
Thus, for \(s\ge {{\overline{t}}}\), we get
This guarantees that \({{\mathfrak {U}}}(|w\rangle \langle w|)\) is bounded and its support is contained in the transient subspace, defined in (6). In order to conclude, we just have to remark that the support of \({{\mathfrak {U}}}(|w\rangle \langle w|)\) contains w. Indeed, \(\lambda _0(w)=1\), and in discrete time, \({\mathfrak U}(|w\rangle \langle w|)[w] \ge \lambda _0(w)\), while, in the continuous time setting, since the function \(t \mapsto \langle w , {{\mathcal {P}}}_t(|w\rangle \langle w|)w\rangle \) is continuous and positive and it is equal to 1 for \(t=0\), it is true that \({{\mathfrak {U}}}(|w\rangle \langle w|) [w] > 0\). \(\square \)
Proof
(of Theorem 9) We define the projection \({\mathcal W}={\mathcal Z}-{{\mathcal {V}}}\subseteq {\mathcal R}\). By previous lemma, we have, for any time t,
Indeed, by contradiction, let us suppose that this is not true. So there would exist a time \({{\overline{t}}}\), a norm 1 vector \(w\in {{\mathcal {V}}}^\perp {\setminus }{\mathcal W}^\perp \) and \(\varepsilon >0\) such that \({{\mathcal {P}}}_{{\overline{t}}}({{\mathcal {V}}})\ge \varepsilon |w \rangle \langle w|\), by Lemma 5. Then, by Lemma 10, \(w\in {\mathcal T}\perp {\mathcal R}\supset {\mathcal W}\), which is a contradiction.
Now, we know that \({{\mathcal {V}}}\) and \({\mathcal Z}\) are enclosures included in \({\mathcal R}\), so, by Lemma 5, we deduce
and this guarantees that \({\mathcal W}\) is an enclosure.
Now, that the first statement is proven, the others easily follow using first only \({\mathcal Z}={\mathcal R}\) and then also \({{\mathcal {V}}}={\mathcal R}_+\). \(\square \)
Remark 11
In the particular case, when \({\mathcal R}={\mathcal R}_+\), the previous result reduces to the second part of Proposition 5.2 in [9].
Remark 12
It was already shown that \({\mathcal R}_+\) and \({\mathcal R}\) are enclosures (see, for instance, [15, Section 3] and [35, Corollary 2]). Showing that \({\mathcal R}_0\) is an enclosure, Theorem 9 provides the answer to two questions left open in [35]:
-
1.
the reduced semigroup \({{\mathcal {P}}}^{\mathcal R}\) can be decomposed into a slow recurrent \({{\mathcal {P}}}^{{\mathcal R}_0}\) and a fast recurrent \({{\mathcal {P}}}^{{\mathcal R}_+}\) semigroups, completing the decomposition of quantum Markov semigroups given in [35, Theorem 9];
-
2.
starting from a state supported in the slow recurrent subspace \({\mathcal R}_0\), the semigroup cannot leave \({\mathcal R}_0\).
Theorem 9 also highlights that the mass collected by an enclosure (not necessarily a recurrent one) always comes from the transient subspace. This fact reflects in the structure of absorption operators.
Corollary 13
For any enclosure \({{\mathcal {V}}}\) and any time t,
In particular, \({{\mathcal {V}}}\) is a recurrent enclosure for \({{\mathcal {P}}}\) if and only if the associated projection is harmonic for the reduced semigroup \({{\mathcal {P}}}^{\mathcal R}\).
Proof
We denote by \({\mathcal S}_t\) the space \(\mathrm{supp}({{\mathcal {V}}}^\perp {{\mathcal {P}}}_t({{\mathcal {V}}}) {{\mathcal {V}}}^\perp ) = (\mathrm{supp}{{\mathcal {P}}}_t({{\mathcal {V}}}))\cap {{\mathcal {V}}}^\perp \). Then, by Lemma 5, we have
But, due to Lemma 10, \({\mathcal S}_t\subset {\mathcal T}\), and this implies relation (8).
Now, if \({{\mathcal {V}}}\) is a recurrent enclosure for \({{\mathcal {P}}}\), then, by (8),
so \({{\mathcal {V}}}\) is harmonic for \({{\mathcal {P}}}^{\mathcal R}\). Conversely, if \({{\mathcal {V}}}\) is a harmonic projection for \({{\mathcal {P}}}^{\mathcal R}\), i.e., \({{\mathcal {V}}}\le {\mathcal R}\) and \({\mathcal R}{{\mathcal {P}}}_t({{\mathcal {V}}}){\mathcal R}={{\mathcal {V}}}\), then
by positivity of \({{\mathcal {P}}}_t({{\mathcal {V}}})\). Furthermore, since \(\Vert {{\mathcal {P}}}_t({{\mathcal {V}}})\Vert \le 1\), if we consider any two norm one vectors v in \({{\mathcal {V}}}\) and u in \({\mathcal T}\) and any \(\varepsilon \in {\mathbb C}\), we have
this implies \(\langle v, {{\mathcal {P}}}_t({{\mathcal {V}}}) u\rangle =0\), so that we conclude
i.e., \({{\mathcal {V}}}\) is an enclosure for \({{\mathcal {P}}}\). \(\square \)
Now, we are able to improve Proposition 6 for absorption operators in relation to transience and recurrence.
Theorem 14
Absorption operators.
-
1.
For any \({{\mathcal {V}}}\) enclosure,
$$\begin{aligned} A({{\mathcal {V}}}) = {{\mathcal {V}}} + {\mathcal T} A({{\mathcal {V}}}) {\mathcal T} = {{\mathcal {V}}} + {\mathcal T}{{\mathcal {V}}}^\perp A({{\mathcal {V}}}){{\mathcal {V}}}^\perp {\mathcal T} \quad \text{ and } \quad {\mathcal R}{{\mathcal {V}}}^\perp A({{\mathcal {V}}}){{\mathcal {V}}}^\perp {\mathcal R}=0. \end{aligned}$$Further, \(X=A({{\mathcal {V}}})-{{\mathcal {V}}}\) is a superharmonic operator supported in \({\mathcal T}\) and such that \({{\mathcal {P}}}_t(X)\downarrow 0\) in the weak* topology.
-
2.
Suppose that \({{\mathcal {V}}}\) is an enclosure included in the recurrent space \({\mathcal R}\). Then, \(A({{\mathcal {V}}})\) is the minimal fix point x of the semigroup \({{\mathcal {P}}}\) such that \(0\le x\le 1\), \({{\mathcal {V}}}x{{\mathcal {V}}}={{\mathcal {V}}}\), \(({\mathcal R}-{{\mathcal {V}}})x({\mathcal R}-{{\mathcal {V}}})=0\). It is the unique fix point with such features when \({\mathcal H}\) is finite dimensional or, more in general, when the recurrent projection \({\mathcal R}\) is attractive (i.e., \(A({\mathcal R})=1\)).
Remark 15
If not immediately evident, we stress that this theorem proves the quantum counterpart of well-known properties for classical absorption probabilities. Indeed, for a classical Markov chain X, recovering the notations of Remark 3 and denoting \(a_j:=A(C)_j\), it is known that \(a=(a_j)_{j \in V}\) is the minimal bounded function on V such that \(0\le a_j\le 1\), verifying
and the last equation, given the first two conditions, is equivalent to write \(a_j=(Qa)_j\), i.e., the function a is harmonic for Q.
Proof
-
1.
The first part is obtained by Eq. (8) passing to the limit for \( t \rightarrow +\infty \). For the second part, notice that X is superharmonic being the difference of a harmonic and a subharmonic operators. Hence, \(({{\mathcal {P}}}_t(X))_{t \in {{\mathfrak {T}}}}\) is a monotone decreasing net of positive operators whose limit is 0 because of the definition of absorption operator.
-
2.
Consider an operator x as in the statement, then \(x={{\mathcal {V}}} + {\mathcal T} x {\mathcal T} ={{\mathcal {P}}}_t(x)\) so \(x={{\mathcal {P}}}_t(x)\ge {{\mathcal {P}}}_t({{\mathcal {V}}}) \) for any \(t \in {{\mathfrak {T}}}\), and then, passing to the limit, we conclude \(x\ge A({{\mathcal {V}}})\). Finally, we can also write
$$\begin{aligned}&x-A({{\mathcal {V}}})=w^*-\lim _{t \rightarrow +\infty } {{\mathcal {P}}}_t(x-{{\mathcal {V}}}) =w^*-\lim _{t \rightarrow +\infty } {{\mathcal {P}}}_t({\mathcal T} x {\mathcal T}) \\&\qquad \le w^*-\lim _{t \rightarrow +\infty } {{\mathcal {P}}}_t({\mathcal T}) \end{aligned}$$and the right-hand side is null if and only if \({\mathcal R}\) is attractive.
\(\square \)
Remark 16
Since \({\mathcal R}\) is an enclosure, the absorption operator \(A({\mathcal R})\) is well defined and, proceeding according to a “probabilistic” approach, it is natural to read the operator
as representing the probability for the evolution to remain forever in the transient subspace \({\mathcal T}\). By point 2 of the previous theorem, used with \({{\mathcal {V}}}={\mathcal R}\), the operator U is the maximal harmonic operator y such that \(0\le y\le 1\) and \({\mathcal T}y{\mathcal T}=y\).
Another consequence of Theorem 9 is that every recurrent enclosure \({{\mathcal {V}}}\subset {\mathcal R}\) is diagonal in the block representation induced by \({\mathcal R}_0\) and \({\mathcal R}_+\).
Corollary 17
Every enclosure \({{\mathcal {V}}}\subset {\mathcal R}\) is of the form \({{\mathcal {V}}}={\mathcal R}_+{{\mathcal {V}}}{\mathcal R}_++ {\mathcal R}_0{{\mathcal {V}}}{\mathcal R}_0\).
Proof
By contradiction, let \({{\mathcal {V}}}\subset {\mathcal R}\) be an enclosure such that \({\mathcal R}_+{{\mathcal {V}}}{\mathcal R}_0 \ne 0\). We can assume that \({{\mathcal {V}}}\cap {\mathcal R}_+=\{0\}\). Indeed, if this is not the case, we can replace it with the space
which is an enclosure as intersection of the two enclosures \({{\mathcal {V}}}\) and \(({\mathcal R}\cap ({{\mathcal {V}}}\cap {\mathcal R}_+)^\perp )\) (the latter by Theorem 9), and always included in \({\mathcal R}\). Furthermore, \({{\mathcal {V}}}^\prime \cap {\mathcal R}_+=\{0\}\) and \({\mathcal R}_+{{\mathcal {V}}}^\prime {\mathcal R}_0={\mathcal R}_+{{\mathcal {V}}}{\mathcal R}_0 \ne 0\). Hence, by taking \({{\mathcal {V}}}^\prime \) as \({{\mathcal {V}}}\), we can assume that \({{\mathcal {V}}}\cap {\mathcal R}_+=\{0\}\).
Now, since \({\mathcal R}_+{{\mathcal {V}}}{\mathcal R}_0 \ne 0\), by the definition of \({\mathcal R}_+\), there exists an invariant state \(\rho \) with \(\mathrm{supp}(\rho ) \not \perp {{\mathcal {V}}}\), i.e., such that \({{\mathcal {V}}}\rho {{\mathcal {V}}}\ne 0\). We call \({\tilde{{{\mathcal {V}}}}} = {\mathcal R}\cap {{\mathcal {V}}}^\perp \), which is an enclosure by Theorem 9. Then, for every \(t \in {{\mathfrak {T}}}\), as \(\rho \) is supported in \({\mathcal R}_+\subseteq {\mathcal R}={{\mathcal {V}}}\oplus {\tilde{{{\mathcal {V}}}}}\), we can use Proposition 5.2 in [9] to obtain
where the second equality is due to the invariance of \(\rho \). This implies that
is an invariant state supported in \({{\mathcal {V}}}\) and we get to the contradiction \({{\mathcal {V}}}\cap {\mathcal R}_+\ne \{0\}\). \(\square \)
Remark 18
There are some features of absorption operators that can be interpreted in the potential theory framework of [18, 35]:
-
1.
a positive bounded operator y is said to be a potential if there exists \(x \in {\mathcal B}({{\mathcal {H}}})_\text {int}\) such that \(y={\mathcal U}(x)\). The first point of Theorem 14 shows that for every enclosure \({{\mathcal {V}}}\), \(A({{\mathcal {V}}})-{{\mathcal {V}}}\) is a potential (see [18, Theorem 4]);
-
2.
it is not hard to see that \(\ker (A({{\mathcal {V}}}))=\{u \in D(\mathfrak {U}({{\mathcal {V}}})):\mathfrak {U}({{\mathcal {V}}})[u]=0\}\).
4 Absorption Operators to Describe Fixed Points
In this section, we are mainly concerned with the description of the fixed points of a semigroup of quantum channels. In order to have a full description, we shall need to add the extra condition that the positive recurrent space is attractive for the evolution. Let \({\mathcal F}({{\mathcal {P}}})\) be the set of the fixed points (or harmonic operators) of the quantum Markov semigroup \({{\mathcal {P}}}\), i.e.,
The structure of the set \({\mathcal F}({{\mathcal {P}}})\) is well known when there exists a faithful normal invariant state (i.e., the semigroup is positive recurrent): In such a case, it is an atomic \(W^*\)-algebra, since it is in the multiplicative domain and it is the range of a \({{\mathcal {P}}}\)-invariant normal conditional expectation (see, for instance, [21, 22, 29] and more recent developments in [4, 7, 19]).
When we have no faithful invariant state, we do not have general results and the problem becomes substantially different and more complicated; for instance, \({\mathcal F}({{\mathcal {P}}})\) does not need to be an algebra in general. Examples are easy to find, also in classical probability, just considering models with a transient state having access to more than one recurrent class.
Abandoning the condition on the existence of an invariant faithful state means considering non-purely positive recurrent Markov evolutions. If we try to weaken this condition, one natural first step can be assuming that the positive recurrent subspace \({\mathcal R}_+\) is anyway attractive, i.e.,
In the following of this section, we shall always work under this additional assumption of having an attractive fast recurrent space. This condition is quite popular in relation to ergodic theory and extensively used [23, 24]. It is not too restrictive: It holds true for every finite-dimensional Hilbert space \({{{\mathcal {H}}}}\); furthermore, as pointed out already in [23], there is a wide class of quantum Markov semigroups for which checking its validity reduces to an analogous problem for a classical Markov chain.
We point out some immediate consequences of condition \(A({\mathcal R}_+) =1\).
-
There exists at least one invariant state, since \({\mathcal R}_+\ne 0\) (otherwise, we would have \(A({\mathcal R}_+)=0\)).
-
The evolution passes a finite amount of time in the transient subspace (\(U=0\) by Remark 16).
-
Similarly as in the commutative case, this assumption implies that there are no null recurrent vectors, i.e., \({\mathcal R}_+={\mathcal R}\). Indeed, since \({\mathcal R}_0\) is an enclosure and, by definition, \({\mathcal R}_0\le {\mathcal R}_+^\perp \), for every \(t \in \mathfrak {T}\), we have that \({{\mathcal {P}}}_t({\mathcal R}_0)\le {{\mathcal {P}}}_t({\mathcal R}_+^\perp )\) and consequently
$$\begin{aligned} 0 \le A({\mathcal R}_0)=w^*-\lim _{t \rightarrow +\infty } {{\mathcal {P}}}_t({\mathcal R}_0)\le w^*-\lim _{t \rightarrow +\infty } {{\mathcal {P}}}_t({\mathcal R}_+^\perp ) = 1- A({\mathcal R}_+)= 0, \end{aligned}$$which implies \( A({\mathcal R}_0)=0\). So \({\mathcal R}_0=0\) since \(0 \le {\mathcal R}_ 0 \le A({\mathcal R}_0)=0\).
We recap here some equivalent conditions for \(A({\mathcal R}_+) =1\), and we recall that this condition assures the mean ergodicity of the semigroup.
Theorem 19
(Theorem 2.1, [23]) For a quantum Markov semigroup \({{\mathcal {P}}}\), the following are equivalent:
-
(i)
\(A({\mathcal R}_+) = 1\);
-
(ii)
there exists a normal \({{\mathcal {P}}}\)-invariant norm one projection \(\mathcal {E}\) of \({\mathcal B}({{{\mathcal {H}}}})\) onto \({\mathcal F}({{\mathcal {P}}})\);
-
(iii)
\(\mathcal {E}_*(\phi ):= w-\lim \frac{1}{t} \int _0^t {{\mathcal {P}}}_{*s}(\phi )\mathrm{d}m(s)\) exists for every \(\phi \in L^1({{{\mathcal {H}}}})\);
-
(iv)
\({\mathcal F}({{\mathcal {P}}}_*)\) separates \({\mathcal F}({{\mathcal {P}}})\).
If the above conditions are satisfied, then \(\mathcal {E}\) is given by
The set of quantum channels is convex and closed in the point-weak* topology; therefore, \(\mathcal {E}\) is a quantum channel.
At least for all enclosures \({{\mathcal {V}}}\), we know that \(\{{{\mathcal {P}}}_t({{\mathcal {V}}})\}_{t \in {{\mathfrak {T}}}}\) converges monotonically to \(A({{\mathcal {V}}})\), so the net of the Cesaro’s means will have the same limit and \(\mathcal {E}({{\mathcal {V}}})=A({{\mathcal {V}}})\). This is true in particular for \({{\mathcal {V}}}={\mathcal R}_+\), and indeed condition (i) is written as \(\mathcal {E}({\mathcal R}_+)=1\) in the original version of the previous theorem.
Remark 20
If \(A({\mathcal R}_+) = 1\), \(\mathcal R\) must be contained in any other attractive projection; indeed, consider an orthogonal projection Q, then \(\mathcal {E}(Q) =1\) if and only if Q contains \({\mathcal R}\) (i.e., \(Q\ge {\mathcal R}\)). Notice that Q is not necessarily subharmonic. One implication is obvious, for the other, just notice that, if \(\mathcal {E}(Q) =1\), then, for any invariant density \(\sigma \), we have \(\sigma =\mathcal {E}_*(\sigma )\) so
and this implies that \(Q\ge {\mathcal R}\) because \({\mathcal R}\) is the supremum of all supports of invariant densities.
Under the assumption \(A({\mathcal R}_+) =1\), the set of fixed points of \({{\mathcal {P}}}\) is controlled by the set of fixed points of the restricted semigroup \({{\mathcal {P}}}^{\mathcal R_+}={{\mathcal {P}}}^{\mathcal R}\), defined accordingly to (1). This is still a quantum Markov semigroup because \({\mathcal R}_+\) is an enclosure, and it is positive recurrent by construction.
The following proposition is a consequence of the mean ergodic theorem in [23], partially appearing also in [30, Theorem 3, Corollary 4] and [24, Proposition 8.2, Theorem 8.3]. We provide here a compact alternative proof which is adapted to our setting and makes use of the multiplicative algebra.
Proposition 21
[23, 24, 30] Let \({{\mathcal {P}}}\) a completely positive quantum Markov semigroup, \(A({\mathcal R}_+) = 1\). Then,
-
1.
if \(y \in {\mathcal F}({{\mathcal {P}}})\) is such that \({\mathcal R}y{\mathcal R}=0\), then \(y=0\);
-
2.
\({\mathcal R}\mathcal {F}({{\mathcal {P}}}) {\mathcal R}=\mathcal {F}({{\mathcal {P}}}^{\mathcal R})\);
-
3.
\(\mathcal {F}({{\mathcal {P}}})\) and \(\mathcal {F}({{\mathcal {P}}}^{{\mathcal R}})\) are homeomorphic considering both the weak* and the norm topologies; the homeomorphism is linear and is given by the restriction \({\tilde{\mathcal {E}}}\) of \(\mathcal {E}\) to \(\mathcal {F}({{\mathcal {P}}}^{{\mathcal R}})\) and \(\mathcal {E}({\mathcal R}x{\mathcal R})={\mathcal E}(x)=x\) for any fixed point x.
We remark that this result is true also for weaker positivity conditions on the semigroup, that is assuming 2-positivity instead of complete positivity.
Proof
Let us consider the operators
Both of them are norm continuous and normal, and we shall prove that \({\mathcal R}{\mathcal F}({{\mathcal {P}}}) {\mathcal R}\subset {\mathcal F}({{\mathcal {P}}}^{\mathcal R})\) and that \({\mathcal R}\cdot {\mathcal R}={\tilde{\mathcal E}}^{-1}\), in order to obtain statement 3.. First, for any fixed point y of \({{\mathcal {P}}}\), we have \( {{\mathcal {P}}}_t^{\mathcal R}({\mathcal R}y{\mathcal R})={\mathcal R}{{\mathcal {P}}}_t(y){\mathcal R} = {\mathcal R} y {\mathcal R}; \) so \({\mathcal R} y {\mathcal R}\) is a fixed point for \({{\mathcal {P}}}^{\mathcal R}\) and \({\mathcal R}\mathcal {F}({{\mathcal {P}}}) {\mathcal R}\subset \mathcal {F}({{\mathcal {P}}}^{\mathcal R})\).
For any bounded operator x, due to the multiplication property of the projection \({\mathcal R}\) for the channel \({\mathcal E}\) (see [12] or also [7] and references therein),
When x is a fixed point for \({{\mathcal {P}}}\), the previous implies that \(\mathcal {E}({\mathcal R}x{\mathcal R})={\mathcal E}(x)=x,\) which means that \({\mathcal E} \circ ({\mathcal R} \cdot {\mathcal R})= id_{{\mathcal F}({{\mathcal {P}}})}\) and that \({\mathcal R} \cdot {\mathcal R}\) is injective (1. is proved).
Take now \(y={\mathcal R}y{\mathcal R}\) an element in \(\mathcal {F}({{\mathcal {P}}}^{\mathcal R})\), then, by [23],
which is in \({\mathcal R}\mathcal {F}({{\mathcal {P}}}) {\mathcal R}\) since \(\mathcal {E}(y)\in \mathcal {F}({{\mathcal {P}}})\). Therefore, we proved that \(({\mathcal R}\cdot {\mathcal R} )\circ {\mathcal E}=id_{{\mathcal F}({{\mathcal {P}}}^{\mathcal R})}\) and also in particular point 2. This concludes the proof. \(\square \)
We can now give a characterization of the harmonic operators in terms of absorption operators when the fast recurrent subspace is attractive and prove that the ergodic limit exists for all the fixed points of the restricted semigroup.
Theorem 22
Suppose \(A(\mathcal {R}_+)=1\). Then, the following facts hold:
-
1.
the fixed points are spanned by absorption operators, and more precisely
$$\begin{aligned} \overline{{{\,\mathrm{span}\,}}\{A({{\mathcal {V}}})\}}^{w^*}_{\{\mathcal {V}\subset \mathcal {R} \text { enclosure}\}}= \mathcal {F}({{\mathcal {P}}}) =\mathcal {F}({{\mathcal {P}}}^{{\mathcal R}}) \oplus {{\mathcal {T}}}{\mathcal {F}({{\mathcal {P}}})} {{\mathcal {T}}}; \end{aligned}$$ -
2.
for every \(x\in {\mathcal F}({{\mathcal {P}}}^{{\mathcal R}})\), there exists the limit \(\; w^*-\lim _{t \rightarrow +\infty }{{\mathcal {P}}}_t(x) = \mathcal {E}(x).\)
Proof
-
1.
Since \(\mathcal {F}({{\mathcal {P}}}^{\mathcal R})\) is a W*-algebra, it is the weak*-closure of the space spanned by its projections, which are exactly the projections onto the positive recurrent enclosures of \({{\mathcal {P}}}\) by virtue of Corollary 13, so \( \mathcal {F}({{\mathcal {P}}}) ={\tilde{\mathcal {E}}}(\mathcal {F}({{\mathcal {P}}}^{\mathcal R})) \) is the weak*-closure of the space
$$\begin{aligned} \mathrm{span}\; {\tilde{\mathcal {E}}}\{{{\mathcal {V}}}\in \mathcal {F}({{\mathcal {P}}}^{\mathcal R}), {{\mathcal {V}}}\; \mathrm{projection}\} = \mathrm{span} \{A({{\mathcal {V}}}), {{\mathcal {V}}}\; \mathrm{pos.}\, \mathrm{rec.}\, \mathrm{enclosure}\} \end{aligned}$$and this directly implies the first equality in the thesis. The second equality follows from the block structure of the absorption operators proven in Theorem 14.
-
2.
It is enough to prove that the limit is well defined for positive elements of \({\mathcal F}({{\mathcal {P}}}^{\mathcal R})\) since it is a W*-algebra. Let us, then, consider a positive \(x\in {\mathcal F}({{\mathcal {P}}}^{\mathcal R})\), then \(x=\lim _K x^{(K)}\) (in operator norm), for some increasing sequence \((x^{(K)})_K\), with \(x^{(K)}=\sum _{k\in J_K} x_k {{\mathcal {V}}}_k\) for some finite set of indices \(J_K\). Then,
$$\begin{aligned} \mathcal {E}(x^{(K)})=\sum _{k\in J_K} x_k A({{\mathcal {V}}}_k) = w^*-\lim _{t \rightarrow +\infty }{{\mathcal {P}}}_t(x^{(K)}), \quad \text{ and } \quad \lim _K\, \mathcal {E}(x^{(K)})=\mathcal {E}(x), \end{aligned}$$where the last equality is due to the boundedness of \(\mathcal {E}\). Then, for any operator \(\sigma \) in \(L^1({{\mathcal {H}}})\) and for all K,
$$\begin{aligned} |\mathrm {Tr}(\sigma ({{\mathcal {P}}}_t(x)-\mathcal {E}(x)))|\le & {} |\mathrm {Tr}( \sigma ({{\mathcal {P}}}_t-\mathcal {E})(x^{(K)})))| + |\mathrm {Tr}(\sigma ({{\mathcal {P}}}_t-\mathcal {E})(x-x^{(K)})))| \\\le & {} |\mathrm {Tr}( \sigma ({{\mathcal {P}}}_t-\mathcal {E})(x^{(K)})))| + 2 \Vert \sigma \Vert _1 \Vert x-x^{(K)} \Vert _\infty , \end{aligned}$$so we can easily conclude.
\(\square \)
In Corollary 17, we proved that in the recurrent case, subharmonic projections commute with the projections on fast and null recurrent subspaces; now, we can improve the result under the assumption \(A({\mathcal R}_+) =1\).
Proposition 23
Assume \(A({\mathcal R}_+)=1\) and let \({{\mathcal {V}}}\) be an enclosure, then
where \({\mathcal R}{{\mathcal {V}}}{\mathcal R}\) is a recurrent enclosure and \({\mathcal T}{{\mathcal {V}}}{\mathcal T} \le A({\mathcal R}{{\mathcal {V}}}{\mathcal R})-{\mathcal R}{{\mathcal {V}}}{\mathcal R}\).
Moreover, when \({{\mathcal {V}}}\) is minimal, it is positive recurrent and \(A({{\mathcal {V}}})\) is the unique harmonic operator such that
Proof
Consider the block decomposition of \(B({{\mathcal {H}}})\) induced by the recurrent and the transient subspaces; \(A({{\mathcal {V}}})-{{\mathcal {V}}}\) and \(A({{\mathcal {V}}})\) are diagonal because of points 1 of Theorems 14 and 22, respectively; therefore, \({{\mathcal {V}}}\) is diagonal too. Since \({{\mathcal {V}}}\) and \({\mathcal R}\) are enclosures, \({\mathcal R}{{\mathcal {V}}}{\mathcal R}\) is an enclosure too. Notice that
and hence \(A({\mathcal R}{{\mathcal {V}}}{\mathcal R})=A({{\mathcal {V}}})\ge {{\mathcal {V}}}={\mathcal R}{{\mathcal {V}}}{\mathcal R}+{\mathcal T}{{\mathcal {V}}}{\mathcal T}\). Therefore \(A({\mathcal R}{{\mathcal {V}}}{\mathcal R})-{\mathcal R}{{\mathcal {V}}}{\mathcal R}\ge {\mathcal T}{{\mathcal {V}}}{\mathcal T}\) and if \({{\mathcal {V}}}\ne 0\), \({\mathcal R}{{\mathcal {V}}}{\mathcal R}\) cannot be 0; otherwise, \(0=A({\mathcal R}{{\mathcal {V}}}{\mathcal R})=A({{\mathcal {V}}})\ge {{\mathcal {V}}}\).
Hence, if \({{\mathcal {V}}}\) is minimal, it must be \({{\mathcal {V}}}={\mathcal R}{{\mathcal {V}}}{\mathcal R}\) and the conclusion follows by point 2 of Theorem 14. \(\square \)
Remark 24
The second point in previous proposition is particularly useful from a computational viewpoint, especially when there is not an analytic way to compute the limit defining absorption operators (see, for instance, Example 5.1). In the parallel with the classical case, already described in Remark 15, we can now add that the solution of the system (9) is unique. Even if it can be not immediate to recognize, similar forms of this result for particular models already appeared in [13, Proposition 7] for finite-dimensional quantum systems.
Moreover, Proposition 21 shows that every fixed point \(x \in {\mathcal F}({{\mathcal {P}}})\) is completely determined by its recurrent restriction \({\mathcal R}x{\mathcal R}\); in addition, Theorem 22 proves that \(x={\mathcal R}x{\mathcal R} + {\mathcal T}x{\mathcal T}\). It is therefore possible to express \({\mathcal T}x{\mathcal T}\), and consequently x, as a function of \({\mathcal R}x{\mathcal R}\): There exists a superoperator
such that, for every \(x \in {\mathcal F}({{\mathcal {P}}})\), we can write
Since
we can find a first expression for \(\varPsi \):
As \({\mathcal E}\) is not commonly given in a model, it can be useful to find alternative expressions for \(\varPsi \) using directly the semigroup. If the semigroup is continuous time, we consider the infinitesimal generator \({\mathcal L}\), while if it is discrete time, we replace it by \(\varPhi -\mathrm {Id}\). For any fixed point x, we know that \({\mathcal T}x{\mathcal T}\) is the unique solution \(y\in {\mathcal T}B({{\mathcal {H}}}){\mathcal T}\) of
due to either Propositions 21 or 23. Then, the operator \({\mathcal L}\), though not invertible in general, admits a unique inverse image if applied to the right-hand side of the previous equation and we can provide a further expression for \(\varPsi \),
which is the same already found in [1, Proposition 3] for the finite-dimensional case.
We have already remarked that in general \({\mathcal F}({{\mathcal {P}}})\) is only a weak*-closed and selfadjoint subspace of \({\mathcal B}({{\mathcal {H}}})\), while \({\mathcal F}({{\mathcal {P}}}^{\mathcal R})\) is a W*-algebra encoding important information about the dynamic induced by the semigroup. We briefly recall the results about fixed points set when there is a faithful invariant state. (The proof can be recovered in [27].)
Proposition 25
There exists a decomposition as a direct sum of orthogonal enclosures of the fast recurrent subspace \({\mathcal R}_+=\bigoplus _{j \in J} \mathcal {V}_j\) and there exist Hilbert spaces \({\mathcal H}_j^{(1)}\), \({\mathcal H}_j^{(2)}\) and unitary operators \(U_j:{{\mathcal {V}}}_j \rightarrow {\mathcal H}_j^{(1)}\otimes {\mathcal H}_j^{(2)}\) such that
Hence, \({\mathcal F}({{\mathcal {P}}}^{{\mathcal R}_+})\) is an atomic \(W^*\)-algebra and \({{\mathcal {V}}}_j\) are the central projections.
Moreover, for any \(j \in J\), there exists a (unique and faithful) state \(\rho _j\) on \({\mathcal H}_j^{(2)}\) such that all the invariant normal states for \({{\mathcal {P}}}\) can be written in the form
For every \(j \in J\), the restriction of the semigroup acts in the following way
where \({\mathcal Q}_t^j\) is an irreducible positive recurrent semigroup acting on \({\mathcal B}({{\mathcal {H}}}_j^{(2)})\) with faithful invariant state \(\rho _j\).
When \(\dim ({{\mathcal {H}}}_j^{(1)})=1\) for some j, then \({{\mathcal {V}}}_j\) is a minimal central projection and it is also a minimal enclosure, while if \(\dim ({{\mathcal {H}}}_j^{(1)})>1\), Eq. (13) tells us that \({{\mathcal {V}}}_j\) is a minimal central projection, but it is not a minimal enclosure and indeed it admits an infinite number of decompositions as direct sum of minimal orthogonal enclosures.
More precisely, in this case, for any complete orthonormal system \(\{e^j_i\}_{i\in I_j}\) for \({{\mathcal {H}}}_j^{(1)}\), the projections \({{\mathcal {V}}}_{j,i}:=U_j^*(|e^j_i\rangle \langle e^j_i| \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}_j})U_j\) are minimal enclosures and \({{\mathcal {V}}}_j=\oplus _{i\in I_j} {{\mathcal {V}}}_{j,i}\). Further, for any couple of minimal enclosures \({{\mathcal {V}}}_{j,i}\) and \({{\mathcal {V}}}_{j,k}\), for \(j\ne k\), we know that there exists a partial isometry \(Q_{j,i,k}:=U_j^*(|e^j_i\rangle \langle e^j_k| \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}_j})U_j\) between them; this operator is a fixed point of the reduced dynamic and allows to express the dynamic of the semigroup restricted to \({{\mathcal {V}}}_{j,i}\) and the minimal invariant state supported on it in terms of the dynamic restricted to \({{\mathcal {V}}}_{j,k}\) and the invariant state supported on it (see [9]). The dynamic on \({{\mathcal {V}}}_{j,i}\) (and all the other isometric enclosures) is described by the semigroup \({\mathcal Q}^j\) (modulo \(U_j\)), and \(U_j^*(|e^j_i\rangle \langle e_i^j| \otimes \rho _j)U_j\) is the unique extremal invariant state with support \({{\mathcal {V}}}_{j,i}\).
Coming back now to the case of non-trivial transient space, many easy examples show that the symmetries of the reduced positive recurrent dynamic do not extend to the whole semigroup \({{\mathcal {P}}}\) and consequently that it is not possible to recover \(A({{\mathcal {V}}}_{j,k})\) from \(A({{\mathcal {V}}}_{j,i})\) (see examples in Sect. 5).
Nevertheless, the following result holds. Recall that by definition \(Q_{j,i,i}\) coincides with the projection \({{\mathcal {V}}}_{j,i}\).
Proposition 26
Consider the decomposition in Eq. (13), and for any orthonormal system \(\{e^j_i\}_{i\in I_j}\) for \({{\mathcal {H}}}_j^{(1)}\), define \(Q_{j,i,k}:=U_j^*(|e^j_i\rangle \langle e^j_k| \otimes \mathbb {I}_{{{\mathcal {H}}}_j^{(2)}})U_j\) as before. Then,
In particular, if \({\mathcal W}\) is a positive recurrent minimal enclosure, then \({\mathcal W}=U_j^*(|f\rangle \langle f| \otimes \mathbb {I}_{{{\mathcal {H}}}_j^{(2)}})U_j\) for some index j and for some f in \({{\mathcal {H}}}_j^{(1)}\) and
A positive recurrent enclosure \({\mathcal W}\) is minimal if and only if for every \(x \in {\mathcal F}({{\mathcal {P}}})\) such that \(0 \le x \le A({\mathcal W})\), there exists \(\lambda \in [0,1]\) such that \(x =\lambda A({\mathcal W})\).
Proof
The first part easily follows from the normality of \({\tilde{\mathcal {E}}}\) and from the fact that the space spanned by \(\{|e^j_i\rangle \langle e_k^j|\}_{i,k \in I_j}\) is weak*-dense in \({\mathcal B}({{\mathcal {H}}}^{(1)}_j)\) for any \(j \in J\).
Every positive recurrent minimal enclosure \({\mathcal W}\) is contained in a subspace of \({{\mathcal {H}}}^{(1)}_j\) for some index \(j \in J\), hence we can drop the index j for simplicity. \({\mathcal W}\) is then trivially of the form \(U^*(|f\rangle \langle f| \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}})U\) for some \(f \in {{\mathcal {H}}}^{(1)}\) and \(|f\rangle \langle f| \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}}\overset{(w^*)}{=} \sum _{i,k} \overline{\langle f, e^j_i\rangle } \langle f, e^j_k\rangle |e^j_i\rangle \langle e^j_k| \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}}\). The second statement follows again by linearity and weak*- continuity of \({\tilde{\mathcal {E}}}\).
If the positive recurrent enclosure \({\mathcal W}\) is not minimal, then there exists another enclosure \(0<{{\mathcal {V}}}< {\mathcal W}\) and \(A({{\mathcal {V}}})\) is a fix point, \(0<A({{\mathcal {V}}})\le A({\mathcal W})\), but not proportional to \(A({\mathcal W})\), since \({\mathcal W}-{{\mathcal {V}}}\) is again an enclosure, \({\mathcal W}-{{\mathcal {V}}}\subset \ker (A({{\mathcal {V}}}))\), while \(({\mathcal W}-{{\mathcal {V}}})A({\mathcal W})({\mathcal W}-{{\mathcal {V}}})={\mathcal W}-{{\mathcal {V}}}\ne 0\).
On the other hand, let \({\mathcal W}\) be a minimal positive recurrent enclosure and suppose there exists a fixed point x such that \(0\le x\le A({\mathcal W})\); then either \(x=0\) or \(0<{\mathcal R}x{\mathcal R}={\mathcal W}x{\mathcal W}\le {\mathcal W}\). Being \({{\mathcal {P}}}^{\mathcal W}\) positive recurrent and irreducible and \({\mathcal W}x{\mathcal W}\) a fixed point of the reduced semigroup, there must be a \(\lambda \in (0,1]\) such that \({\mathcal W}x{\mathcal W}=\lambda {\mathcal W}\). Hence, \(x={\mathcal E}({\mathcal W}x{\mathcal W})=\lambda A({\mathcal W})\). \(\square \)
Links with ergodic theorems. Absorption operators, by construction, register features of the limit behavior of the semigroup. It is then natural that they have some explicit relations with ergodic theory. If assumption \(A({\mathcal R}_+) =1\) holds, by Theorem 19, we know that the limit
exists for every \(\phi \in L^1({{{\mathcal {H}}}})\), and since it is an invariant state for \({{\mathcal {P}}}\), it will be written in the form of Eq. (14), i.e.,
for some \(\sigma _j(\phi )\) state on \({\mathcal H}^{(1)}_j\), and real numbers \(\lambda _j(\phi )\ge 0\) with \( \sum _{j \in J}\lambda _j(\phi )=1\). The coefficients \(\sigma _j(\phi )\), \(\lambda _j(\phi )\), \(j\in J\), are immediately identified knowing absorption operators and the operators \(\mathcal {E}(Q_{j,i,k})\) generating \({{\mathcal {F}}}({{\mathcal {P}}})\). Indeed, the mass flowing to the enclosure \({{\mathcal {V}}}_j\) (introduced in Proposition 25) is
and, introducing as before an orthonormal basis \(\{e^j_i\}_{i\in I_j}\) for \({{\mathcal {H}}}_j^{(1)}\), we can represent \(\sigma _j(\phi )=\sum _{k,m}(\sigma _j(\phi ))_{km}|e_k\rangle \langle e_m|\), where
since \(\sigma _j(\phi )\) is meaningful only when \(\lambda _j(\phi )\ne 0\), the previous completely identifies \(\sigma (\phi )\). Passing to the Heisenberg picture and considering \(x \in {\mathcal B}({{\mathcal {H}}})\), we shall similarly obtain an expression for the ergodic mean of the form
and here it is evident again that \(\mathcal {E}(x)\) depends only on \({\mathcal R}x{\mathcal R}\). In the easiest case, when there is a unique decomposition in orthogonal minimal enclosures of the fast recurrent subspace, the isometries \(U_j\) are trivial and the invariant states are convex combinations of the invariant states \(\rho _j\) supported in the minimal enclosures, with weights \(\mathrm {Tr}(\phi A({{\mathcal {V}}}_j))\); thus, we have
If we look at quantum trajectories and at the pathwise versions of the ergodic theorems [28], we shall obtain similar relations, but absorption operators register a someway “mean” behavior anyway. For simplicity, assume here the time set to be discrete, i.e., \({{\mathfrak {T}}}=\mathbb {N}\), and the semigroup to be generated by a quantum channel \(\varPhi \). The same ideas will work for the continuous time case. We consider an associated state valued stochastic process \((\Theta _n)_n\) which is a homogeneous Markov process describing the quantum trajectories. (We follow the same notations as in [28].) Once chosen a set of Kraus operators \(\{V_i\}_{i \in I}\) for \(\varPhi \), every initial state \(\phi \in L^1({{\mathcal {H}}})\) uniquely determines a probability measure on the set \(\varOmega =I^\infty \) through the condition
The Markov chain \((\Theta _n)\) is defined in the following way:
and it verifies by construction that, for every \(n<m\), \(n,m \in \mathbb {N}\), \(\mathbb {E}^\phi [\Theta _m|{\mathcal F}_n]=\varPhi ^{m-n}_*(\Theta _n)\), where \(({\mathcal F}_n)_{n \in \mathbb {N}}\) is the filtration generated by the coordinate process. If \({{\mathcal {H}}}\) is finite dimensional, Kummerer and Maassen proved that
where \(\Theta _\infty \) is a random equilibrium state such that \(\mathbb {E}[\Theta _\infty ]=\lim _{N\rightarrow +\infty }\frac{1}{N}\sum _{k=0}^{N-1}\varPhi ^k_*(\Theta _0)\). So, for any enclosure \({{\mathcal {V}}}\) and state \(\phi \in L^1({{\mathcal {H}}})\) we have
Being a random invariant state for \(\varPhi \), \(\Theta _\infty \) is of the form
with \(\lambda _j=1\) and \(\sigma _j\) random variables now, \(\lambda _j \ge 0\), \(\sum _{j \in J}\lambda _j=1\) and \(\sigma _j \in L^1({{\mathcal {H}}}_j^{(1)})\), verifying (computations as 16)
where again \((\sigma _j)_{mk}\) are the matrix entries of \(\sigma _j\).
Multiplicative properties of the fixed points The multiplicative structure of the fixed points is strictly connected to the ergodic behavior of the semigroup of quantum channels (see, for instance, [23]). Moreover, the difference between observables which are not disturbed by a measurement and those which are compatible with it relies again on whether the fixed points set is an algebra or not [2]. If the fixed points space \({\mathcal F}({{\mathcal {P}}})\) is an algebra, there are some constraints on the absorption operators which have a nice probabilistic interpretation.
Proposition 27
If \({\mathcal F}({{\mathcal {P}}})\) is an algebra, the following facts hold true:
-
1.
for every enclosure \({{\mathcal {V}}}\), \(A({{\mathcal {V}}})\) is a projection;
-
2.
for every pair of orthogonal enclosures \({{\mathcal {V}}}\) and \({\mathcal W}\), \(A({{\mathcal {V}}})\) and \(A({\mathcal W})\) are orthogonal projections and their supports are orthogonal enclosures.
By the second point, we can informally say that when \({\mathcal F}({{\mathcal {P}}})\) is an algebra, no transient state can reach two different orthogonal enclosures.
Proof
-
1.
Since \({\mathcal F}({{\mathcal {P}}})\) is a W*-algebra, \(Q:={1}_{\{1\}}(A({{\mathcal {V}}}))\) is a fixed point too. Notice that \(0 \le Q \le A({{\mathcal {V}}})\le 1\) and that \({{\mathcal {V}}}Q{{\mathcal {V}}}={{\mathcal {V}}}\), therefore, by point 3 in Proposition 6, \(Q=A({{\mathcal {V}}})\) and \(A({{\mathcal {V}}})\) is a projection.
-
2.
If \({{\mathcal {V}}}\) and \({\mathcal W}\) are orthogonal enclosures, then \(A({{\mathcal {V}}})+A({\mathcal W})=A({{\mathcal {V}}}+{\mathcal W})\), which are projections by point 1. If the sum of two projections is again a projection, they must be orthogonal. For the last statement, since \(A({{\mathcal {V}}})\) is a projection, \(\mathrm{supp}(A({{\mathcal {V}}}))\) coincides with the eigenspace corresponding to the eigenvalue 1 and is an enclosure by Proposition 4. The same will hold for \(A({\mathcal W})\).
\(\square \)
We can prove that if assumption \(A({\mathcal R}_+) =1\) holds true, 1. and 2. are equivalent and each one of them implies that \({\mathcal F}({{\mathcal {P}}})\) is an algebra. However, in general we cannot hope to get the same result, since we can easily find an example even in the abelian case where 2. holds, but 1. does not.
Example 28
Consider the Markov chain on \(\mathbb {N}\cup \{a_i\}_{i=0}^k\) for some \(k \in \mathbb {N}\) with the following transition probabilities:
The only enclosures are the singletons \(\{a_i\}\) for \(0\le i \le k\) ; \(A(\{a_i\})={1}_{\{a_i\}}\) for \(i>0\), while \(\mathrm{supp}(A(\{a_0\}))=\{a_0\}\cup \mathbb {N}\), hence 2. holds true. However, \(A(\{a_0\})\) is not a projection; denoting with \(f=\mathbb {I}_{\{a_0\}}\), it is easy to see that for \(N \ge 1\):
Proposition 29
Assume that \(A({\mathcal R}_+)=1\). If, for every pair of orthogonal enclosures \({{\mathcal {V}}}, {\mathcal W} \subset {\mathcal R}\), it is true that \(A({{\mathcal {V}}})A({\mathcal W})=0\), then \({\mathcal F}({{\mathcal {P}}})\) is an algebra and \({\tilde{\mathcal {E}}}\) is an isomorphism of W*-algebras.
Proof
For every enclosure \({{\mathcal {V}}}\subset {\mathcal R}\), \(A({{\mathcal {V}}})^2=A({{\mathcal {V}}})(A({\mathcal R})-A({\mathcal R}-{{\mathcal {V}}}))=A({{\mathcal {V}}})\), thus \(A({{\mathcal {V}}})\) is a projection. In particular, it is a harmonic projection; hence, it is in the decoherence-free algebra
\({\mathcal N}\) is a W*-algebra, so it is \(w^*\)-closed and, since by Theorem 22, \({\mathcal F}({{\mathcal {P}}})\) is the \(w^*\)-closure of the linear span of the absorption operators, \({\mathcal F}({{\mathcal {P}}}) \subset {\mathcal N}\). Hence, (see always [7, 12]) fixed points enjoy the multiplication property, \({{\mathcal {P}}}_t(x_1^*x_2 )={{\mathcal {P}}}_t(x_1^*){{\mathcal {P}}}_t(x_2)=x_1^*x_2 \) for \(x_1,x_2 \in {\mathcal F}({{\mathcal {P}}})\), and thus, \({\mathcal F}({{\mathcal {P}}})\) is a \(*\)-algebra. Moreover, always for \(x_1,x_2 \in {\mathcal F}({{\mathcal {P}}})\), by Proposition 21 and Theorem 22, \(x_i={\mathcal R}x_i{\mathcal R}+{\mathcal T}x_i{\mathcal T}={\tilde{\mathcal {E}}}({\mathcal R}x_i{\mathcal R})\) for \(i=1,2\), and we have
(\((*)\) because \(x_1x_2\) is a fixed point too). Therefore, \(\tilde{{\mathcal E}}\) preserves multiplication and is an isomorphism of W*-algebras. \(\square \)
Remark 30
The example in Sect. 5.3 shows that when the decomposition in orthogonal minimal enclosures of the fast recurrent space is non-unique, it is not enough to check that the absorption operators are projections only for a chosen decomposition to ensure that the fixed points set is an algebra.
Remark 31
We remark that in [11], some results of the present section were proved for a specific class of quantum Markov semigroups (sometimes called generic semigroups) under the stronger hypothesis that the semigroup is ergodic and not only mean ergodic. The techniques used there are quite different and rely on a link between this special family of quantum models and the associated classical Markov chains, which allows to use classical probability tools.
If assumption \(A({\mathcal R}_+) =1\) holds and \({\mathcal F}({{\mathcal {P}}})\) is an algebra, the dynamic restricted to the fast recurrent subspace strongly determines the global evolution.
Proposition 32
If \(A({\mathcal R}_+)=1\) and \({\mathcal F}({{\mathcal {P}}})\) is an algebra, then
-
1.
\({\mathcal F}({{\mathcal {P}}})\) is atomic and it is isomorphic as a W*-algebra to \({\mathcal F}({{\mathcal {P}}}^{\mathcal R})\);
-
2.
its central projections are the absorption operators corresponding to the central projections of \({\mathcal F}({{\mathcal {P}}}^{\mathcal R})\);
-
3.
let \({\mathcal K}\) be a minimal central projection of \({\mathcal F}({{\mathcal {P}}})\), then there exist Hilbert spaces \({{\mathcal {H}}}^{(1)}\), \({{\mathcal {H}}}^{(2)}\) and an isometry \(U:{\mathcal K} \rightarrow {{\mathcal {H}}}^{(1)} \otimes {{\mathcal {H}}}^{(2)}\) such that the restriction of the semigroup \({{\mathcal {P}}}^{\mathcal K}\) acts in the following way:
$$\begin{aligned} {{\mathcal {P}}}^{\mathcal K}(U^*(A \otimes B)U)=U^*(A \otimes {\mathcal Q}_t(B))U \quad A \in {\mathcal B}({{\mathcal {H}}}^{(1)}), B \in {\mathcal B}({{\mathcal {H}}}^{(2)}) \end{aligned}$$where \({\mathcal Q}\) is a quantum Markov semigroup acting on \(B({{\mathcal {H}}}^{(2)})\) with a unique invariant state \(\rho \in L^1({{\mathcal {H}}}^{(2)})\) and such that \(w^*-\lim _{t \rightarrow +\infty }{\mathcal Q}_t(\mathrm{supp}(\rho ))= \mathbb {I}_{{{\mathcal {H}}}^{(2)}}\).
With the usual abuse of notation, we use the same symbol \(\mathrm{supp}(\rho )\) for the space and for the corresponding projection.
In general, \({\mathcal F}({{\mathcal {P}}}^{{\mathcal R}_+})\) and \({\mathcal F}({{\mathcal {P}}})\) are not isometrically isomorphic.
Proof
-
1.
\({\mathcal F}({{\mathcal {P}}}^{\mathcal R})\) is an atomic W*-algebra, and it can be proved to be isomorphic to \({\mathcal F}({{\mathcal {P}}})\) as in the proof of Proposition 29.
-
2.
Central projections are preserved by isomorphism of W*-algebras, and we showed the isomorphism maps projections of \({\mathcal F}({{\mathcal {P}}}^{\mathcal R})\) into the corresponding absorption operators.
-
3.
\({\mathcal K}{\mathcal F}({{\mathcal {P}}}){\mathcal K}\) is a type I factor, and hence, there exist Hilbert spaces \({{\mathcal {H}}}^{(1)}\), \({{\mathcal {H}}}^{(2)}\) and an isometry \(U:{\mathcal K} \rightarrow {{\mathcal {H}}}^{(1)} \otimes {{\mathcal {H}}}^{(2)}\) such that
$$\begin{aligned} {\mathcal K}{\mathcal F}({{\mathcal {P}}}){\mathcal K}=U^* (B({{\mathcal {H}}}^{(1)}) \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}}) U. \end{aligned}$$For every \(t \in {{\mathfrak {T}}}\), \(A \in {\mathcal B}({{\mathcal {H}}}^{(1)})\) and \(B \in {\mathcal B}({{\mathcal {H}}}^{(2)})\),
$$\begin{aligned}&{{\mathcal {P}}}_t(U^*(A\otimes B)U)=U^*(A \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}})U{{\mathcal {P}}}_t(U^*(\mathbb {I}_{{{\mathcal {H}}}^{(2)}}\otimes B)U)\\&={{\mathcal {P}}}_t(U^*(\mathbb {I}_{{{\mathcal {H}}}^{(2)}}\otimes B)U)U^*(A \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}})U. \end{aligned}$$It implies that \({{\mathcal {P}}}_t(\mathbb {I}_{{{\mathcal {H}}}^{(1)}} \otimes B)\in {{\mathcal B}({{\mathcal {H}}}^{(1)}) \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}}}^\prime =\mathbb {I}_{{{\mathcal {H}}}^{(1)}}\otimes {\mathcal B}({{\mathcal {H}}}^{(2)})\) and so \({{\mathcal {P}}}^{\mathcal K}_t=id_{{{\mathcal {H}}}^{(1)}} \otimes {\mathcal Q}_t\) with \({\mathcal Q}\) quantum Markov semigroup acting on \(B({{\mathcal {H}}}^{(2)})\). Since \({\mathcal F}({{\mathcal {P}}})\) is the range of a normal conditional expectation from a type I factor, \({\mathcal Q}\) admits a unique invariant state \(\rho \in L^1({{\mathcal {H}}}^{(2)})\) (see Lemma 2 in [7]), and it is easy to see that \({{\mathcal {V}}}=U^*({{\mathcal {H}}}^{(1)} \otimes \mathrm{supp}(\rho ))\), where \({{\mathcal {V}}}\) is the central projection of \({\mathcal F}({{\mathcal {P}}}^{\mathcal R})\) such that \({\mathcal K}=A({{\mathcal {V}}})\). Therefore,
$$\begin{aligned} \mathbb {I}_{{{\mathcal {H}}}^{(1)}} \otimes {\mathcal Q}_t(\mathrm{supp}(\rho ))=U{{\mathcal {P}}}_t({{\mathcal {V}}})U^* \rightarrow _{t\rightarrow +\infty } UA({{\mathcal {V}}})U^*=\mathbb {I}_{{{\mathcal {H}}}^{(1)}} \otimes \mathbb {I}_{{{\mathcal {H}}}^{(2)}} \end{aligned}$$and this concludes the proof.
\(\square \)
Remark 33
For every \({\mathcal K}\) minimal central projection of \({\mathcal F}({{\mathcal {P}}})\), consider \({{\mathcal {H}}}^{(1)}\), \({{\mathcal {H}}}^{(2)}\) as in point 3 of Proposition 32. For every \(w,v \in {{\mathcal {H}}}^{(1)}\), \(Q_{w,v}=U^*(|w\rangle \langle v| \otimes \mathbb {I}_{H^{(2)}})U\) is a symmetry of the semigroup \({{\mathcal {P}}}\), i.e.,
Remark 34
As we mentioned in Introduction, some results of the paper can be extended to the case when \({{\mathcal {P}}}\) acts on more general W*- algebras. This is not true anyway, for instance, for Propositions 26 and 32 because the proofs rely on the fact that \({\mathcal F}({{\mathcal {P}}}^{{\mathcal R}_+})\) is isomorphic to a central direct sum of factors of type I, which is a consequence of the existence of a normal conditional expectation \({\mathcal E}\) from a type I factor onto \({\mathcal F}({{\mathcal {P}}}^{{\mathcal R}_+})\) (see the proof of [34, Theorem 5]).
5 Examples and Applications
In this section, we have collected some models where absorption operators can be studied. We searched for processes with various characteristics: continuous or discrete time, finite- and infinite-dimensional system spaces, different situations for the existence and structure of the positive recurrent projection.
5.1 Excitation Transport in a Unitary Quantum Walk
The physical model discussed in [36] describes the coherent transport of excitation along a finite ring of coupled quantum systems with a sink located at one vertex of the ring which absorbs the excitation; it presents both a non-trivial transient subspace and multiple recurrent enclosures, and hence, it is an interesting example for studying absorption dynamic. Although the simple structure, we shall see that the explicit expression for absorption operators is not easy to write.
The state space \({{\mathcal {H}}}={{\mathcal {H}}}_P\otimes {{\mathcal {H}}}_C\) is the tensor product of the position space \({{\mathcal {H}}}_P=\mathrm{span}\{e_m: m=-N,\dots ,N\}\), for some \(N=1,2,3,\dots \), and the internal state or coin space \({{\mathcal {H}}}_C=\mathrm{span}\{u_0, u_1\}\). The graph on which the excitation moves is a finite line with two sinks in N and \(-N\). The evolution of the system can be described by the quantum channel
where \(V_1=(|e_{-N}\rangle \langle e_{-N}|+|e_N\rangle \langle e_N|) \otimes \mathbb {I}_C\) and \(V_2=S(\mathbb {I}_P \otimes C)\) is the composition of the change of position
and the coin toss, which in the basis \(\{u_0,u_1\}\) is represented by the following matrix:
The model described in [36] really specifies only the Kraus operator \(V_2\) (the action on the transient space), while the choice of \(V_1\) is not uniquely determined.
We can roughly say that if the system starts from the pure state \(u_0\otimes e_k\) [resp.ly \(u_1\otimes e_k\)], \(k\ne \pm N\), it will move to the left [right] with probability 1. \(\rho ^2\) represents the probability of keeping the same direction of the previous step, while \({\tilde{\rho }}^2\) is the probability of changing direction with respect to the previous shift on the lattice.
First, we remark that the recurrent space \({\mathcal R}\) coincides with the subspace \({\mathcal W}:=\mathrm{span}\{e_{-N}, e_N\}\otimes {{\mathcal {H}}}_C\). Indeed, by direct computation, we have that, for \(\psi \in {\mathcal W}\),
and this proves both that \(\psi \) is recurrent and that \(\mathrm{span}\{\psi \}\) is an enclosure. Then, \({\mathcal W}\) is an enclosure too and it is contained in \({\mathcal R}\).
Moreover, if \(\psi \) is instead in \({\mathcal W}^\perp =\mathrm{span}\{e_{-N+1},\ldots , e_{N-1}\}\otimes {{\mathcal {H}}}_C\), then
and the last operator is non-null for n big enough. This proves that such \(\psi \) is in the transient space due to Lemma 10 and consequently \({\mathcal R}={\mathcal W}\).
Since the model is finite dimensional, there is no null recurrent subspace and the (fast) recurrent space is attractive, i.e., \(A({\mathcal R_+})=1\). As mentioned above, the action of the quantum channel on \({\mathcal R}\) is trivial, and hence, any one-dimensional subspace of \({\mathcal R}\) is an enclosure. These are the only minimal enclosures of the channel (but not the only non-trivial enclosures!).
In this physical model, an explicit formula for the absorption operators for every dimension and every enclosure of the chain seems hard to be found. However, there is a general way of computing them: Given an enclosure \({{\mathcal {V}}}\), we know that \(A({{\mathcal {V}}})=A({\mathcal R}{{\mathcal {V}}}{\mathcal R})={\mathcal R}{{\mathcal {V}}}{\mathcal R}+{\mathcal T}A({{\mathcal {V}}}){\mathcal T}\) is the only fixed point of the channel with this structure (Theorem14), so recalling Remark 24, \({\mathcal T}A({{\mathcal {V}}}){\mathcal T}\) is the unique solution \(x \in B({\mathcal T})\) of the linear system
Notice that the latter is a discrete Lyapunov equation and that the operator \(V_2\) is a “sparse matrix.”
For some particular enclosures, determining the absorption operators is immediate. Indeed, we can easily see that
hence, such enclosures do not collect any mass coming from the transient space.
In general, Eq. 18 gives us an easy inductive procedure to find the solution, but, as we wrote before, giving the precise formula of the absorption operators is complicated. It is anyway immediate to see that if we consider enclosures which are not contained in \(\mathrm{span}\{e_{N-1}\otimes C u_1,e_{1-N}\otimes C u_0 \}\), then the support of the corresponding absorption operator will spread all over the ring.
In particular, we can also show that some absorption operators have eigenspaces corresponding to the eigenvalue 1 which are bigger than the associated recurrent enclosure:
are the eigenspaces corresponding to the eigenvalue 1 of \(A(|e_N\rangle \langle e_N|\otimes |u_1\rangle \langle u_1|)\) and \(A(|e_{-N}\rangle \langle e_{-N}|\otimes |u_0\rangle \langle u_0|)\), respectively. (Recall that \(B_N\) and \(B_{-N}\) will be enclosures, by Proposition 4.)
Already in the simplest case \(N=1\), it is anyway evident that symmetries among minimal enclosures of the recurrent dynamic do not extend to the whole channel \(\varPhi \); for instance, there is no way of reconstructing \(A(|e_N \otimes u_1\rangle \langle e_N \otimes u_1|)\) from \(A(|e_N \otimes u_0\rangle \langle e_N \otimes u_0|)\) knowing only the action of the quantum channel on the recurrent space: Changing the value of \(\rho \), C varies accordingly and so does \(A(|e_N \otimes u_1\rangle \langle e_N \otimes u_1|)\), while \(A(|e_N \otimes u_0\rangle \langle e_N \otimes u_0|)\) and \(\varPhi ^{\mathcal R}\) stay the same.
5.2 A Homogeneous Open Quantum Random Walk
We reconsider the model in Example 7. Now that we have recalled transience and recurrence, we can discuss more properties of this model. \(E_2\) is always a minimal slow recurrent enclosure, but, according to the different choices of the involved parameters, the situations and the possible communication and so absorption phenomena can significantly change. \(E_0\), for instance, will be always an enclosure, as already written, but it is not necessarily minimal (only if \(a_-,a_+\ne 0\)), and it will be slow recurrent when \(|a_+|^2=|a_-|^2\); otherwise, it is transient. As for \(E_1\), in general, under the mentioned conditions (5), it is not an enclosure, but it could be when all the parameters \(b_\varepsilon \) and \(d_\varepsilon \) are null, and in that case, it will not necessarily be minimal. So, this simple model, can really be instructive to understand what happens for different reduction of the space, because it offers examples of both transient and recurrent minimal enclosures, situations with a more complex structure of the recurrent subspace. Different absorption operators can then be considered. In particular, it is anyway never true that \(A({\mathcal R}_+)=1\) and it can happen that \(U\ne 0\).
Whenever \(a_-,a_+\ne 0\) and (5) hold, it is easy to show that absorption operators are able to completely describe the fixed points set of the quantum channel, i.e., even if the fast recurrent space is not attractive, and so the hypotheses of Theorem 22 are not satisfied, the conclusion holds true and the fixed points set coincides with the \(w^*\)-closure of the set of absorption operators \(A({{\mathcal {V}}})\), for \({{\mathcal {V}}}\) enclosure. In particular, if \(a_+=\mathrm{e}^{i\theta }1/\sqrt{2}\) and \(a_-=\mathrm{e}^{-i\theta }1/\sqrt{2}\) with \(\theta \in [-\pi ,\pi ]\), the recurrent restriction of the quantum channel has infinitely many non-orthogonal minimal enclosures and the fixed points set of the restricted channel is isomorphic to \(M_{2 \times 2}(\mathbb {C})\). For all the other values of \(a_\pm \), \(E_0\) and \(E_2\) are the only minimal subharmonic projections ([10, Section 6]) and the corresponding absorption operators generate the fixed points.
5.3 A Continuous Time Model: Two-Photon Absorption [24]
We describe here an infinite-dimensional model, with a not uniquely reducible attractive fast recurrent space, but for which we can explicitly compute any absorption operator relative to a fast recurrent enclosure. We consider the Hilbert space \({{\mathcal {H}}}=l^2({\mathbb N})\) with orthonormal basis \((e_n)_{n\ge 0}\) and denote the creation and annihilation operators by \(a^\dag \) and a, respectively,
The two-photon absorption model described in [16] can be represented with the Lindblad generator \({{\mathcal {L}}}\), defined on a dense subspace of \(B({{\mathcal {H}}})\) by
where \(\omega \) is a real constant and \(\mu ^2\) is the absorption rate. Such a master equation arises as the weak coupling limit of a one-mode electromagnetic field with a Bosonic Gaussian zero-temperature reservoir of two-photon absorbing atoms [16, 25]. In order to have an intuition about some properties of this model, it can be useful to recall that the diagonal restriction of the generator \({{\mathcal {L}}}\) coincides with the generator of a classical continuous time Markov chains with values in \({\mathbb N}\) for which the only possible jumps are the ones from k to \(k-2\) for all \(k\ge 2\). More precisely, using (20) for a diagonal x, \(x=\sum _{k\ge 0} f_k |e_k \rangle \langle e_k|\) in the domain of \({{\mathcal {L}}}\), we have
This tells that the diagonal restriction of \({{\mathcal {L}}}\) is a classical generator Q with transition rates
Many properties of this model have been deeply investigated in [16], so we know that the normal invariant states of this generator consist of all the density operators with support included in the positive recurrent space \({\mathcal R}_+={\text{ span }}\{e_0,e_1\}\). It is immediate to see that any vertex k is accessible from all vertices \(k+2j\) with \(j\ge 0\) and this implies that all the \(e_k\) are transient for \(k\ge 2\). Moreover, it is an easy exercise on classical processes to verify that the Markov chain X with generator Q is absorbed in \(\{0,1\}\) and consequently
in particular
Really we know even more, because due to [16, Proposition 3.2 and Corollary 7.1], we have
Proposition 35
The invariant states of this generator are all the density operators of the form
with \(\alpha \in [0,1]\), \(|z|^2 \le \alpha (1-\alpha )\).
For any state \(\sigma =\sum _{k,l\ge 0}\sigma _{kl} |e_k \rangle \langle e_l|\), we denote
where \(c_k = 2^{-2k}\sqrt{2k+1}\frac{(2k)!}{k!} \prod _{j=1}^k(j-\frac{i\omega }{\mu ^2})^{-1}\). The attraction domain of \(\rho _{\alpha ,z}\) is given by
For any minimal enclosure \({{\mathcal {V}}}\) in \({\mathcal R}_+\), \({\mathcal V}\) is spanned by a vector u which is linear combination of \(e_0\) and \(e_1\), \(u=u_0e_0+u_1e_1\), and the previous proposition allows us to conclude that, for any state \(\sigma \),
so that
It is immediate to see some properties of absorption operators.
-
The operator \(A(|u\rangle \langle u|)\) is a projection if and only if u is proportional to \(e_0\) or \(e_1\) (21). When u is not proportional to \(e_0\) or to \(e_1\), i.e., when \(u_0u_1\ne 0\), the precise spectral representation of \(A(|u\rangle \langle u|)\) is easy to write explicitly and its support contains the entire transient space in this case. Indeed, for u as before with \(u_0u_1\ne 0\), \(A(|u\rangle \langle u|)\) has eigenvalues 0 and 1, which are simple: u is eigenvector for 1 and \(u^\perp := {\bar{u}}_1 e_0 - {\bar{u}}_0 e_1\) generates the kernel. While when \(\lambda \ne 0,1\), \(v=\sum _j v_j e_j\), we trivially have
$$\begin{aligned}&A(|u\rangle \langle u|)v = \lambda v \Leftrightarrow \left\{ \begin{array}{l} v_{2k+1}= \frac{ (\lambda -|u_0|^2) }{c_k u_0 {\bar{u}}_1}v_{2k} \\ ((|u_1|^2 -\lambda ) (\lambda -|u_0|^2) + | {\bar{c}}_k {\bar{u}}_0 u_1|^2) v_{2k} = 0 \end{array}\right. \quad \text{ for } \text{ all } k,\\&\quad \text{ which } \text{ gives } \qquad A(|u\rangle \langle u|) = \sum _k \lambda _k |w^{k}\rangle \langle w^{k}|, \quad \text{ where } \end{aligned}$$– \(\lambda _{2k}, \lambda _{2k+1}\) are the two distinct solutions of equations
$$\begin{aligned} \lambda ^2 - \lambda + |u_0 u_1|^2 (1 - | c_k|^2)=0 \end{aligned}$$– and the pertaining eigenvectors are such that \(w^{2k}\) and \( w^{2k+1}\) are orthogonal norm one vectors in \( \text{ span }\{e_{2k},e_{2k+1}\}\) completely determined by the previous linear system.
-
\((A(|u\rangle \langle u|))^2\) is not a fixed point when \(u_0u_1\ne 0\) (direct computation), so the fixed points do not form an algebra.
-
\(A({\mathcal R}_+)=1\), so all results of Sect. 4 can be applied to this model and in particular the structure of fixed points is described by Theorem 22.
-
Since \(A(|e_0 \rangle \langle e_0|)\) and \(A(|e_1 \rangle \langle e_1|)\) are projections, the set of fixed points for the classical diagonal process is instead an algebra.
-
As we already remarked in previous sections and as in Example 5.1, when the decomposition in minimal enclosures is not unique, the behavior of the absorption operators related to different minimal enclosures cannot be controlled by the absorption operators associated with a generating basis, as \(A(|e_0\rangle \langle e_0|)\) and \(A(|e_1\rangle \langle e_1|)\) here.
5.4 Dissipation-Induced Decomposition
The definition of absorption operators recalls the dissipation-induced decomposition (DID) introduced in [13, 33] for finite-dimensional quantum Markov semigroups in order to tackle the problem of establishing whether an invariant subspace is attractive. In [13], for instance, the authors consider a single quantum channel \(\varPhi \); given an enclosure \({{\mathcal {V}}}\), they provide an algorithm that, using a choice of Kraus operators for \(\varPhi \), decomposes the state space
for some finite \(N \in \mathbb {N}\). DID highlights the one-step accessibility relations: Starting from a state supported in \({{\mathcal {H}}}_n\), \({{\mathcal {V}}}\) is reached in exactly n-steps, while \({{\mathcal {H}}}_R\) does not have access to \({{\mathcal {V}}}\). Then, exploiting the obvious relations
we could rewrite the previous decomposition in our notations as
Notice that since the dimension of the state space is finite,
References
Albert, V.: Asymptotics of quantum channels: conserved quantities, an adiabatic limit, and matrix product states. Quantum 3, 151 (2019)
Arias, A., Gheondea, A., Gudder, S.: Fixed points of quantum operations. J. Math. Phys. 43(12), 5872–5881 (2002)
Attal, S., Petruccione, F., Sabot, C., Sinayskiy, I.: Open quantum random walks. J. Stat. Phys. 147(4), 832–852 (2012)
Bátkai, A., Groh, U., Kunszenti-Kovács, D., Schreiber, M.: Decomposition of operator semigroups on \({\rm W}^*\)-algebras. Semigroup Forum 84(1), 8–24 (2012)
Baumgartner, B., Narnhofer, H.: The structures of state space concerning quantum dynamical semigroups. Rev. Math. Phys. 24(2), 1250001 (2012). 30
Bratteli, O., Robinson, D.W.: Operator Algebras and Quantum-Statistical Mechanics. I. \(C^*\)- and \(W^*\)-Algebras. Symmetry Groups. Decomposition of States, Texts and Monographs in Physics. Springer, Berlin (1987)
Carbone, R., Jenčová, A.: On period, cycles and fixed points of a quantum channel. Ann. Henri Poincaré 21(1), 155–188 (2020)
Carbone, R., Pautrat, Y.: Homogeneous open quantum random walks on a lattice. J. Stat. Phys. 160(September), 1125–1153 (2015)
Carbone, R., Pautrat, Y.: Irreducible decompositions and stationary states of quantum channels. Rep. Math. Phys. 77(June), 293–313 (2016)
Carbone, R., Pautrat, Y.: Open quantum random walks: reducibility, period, ergodic properties. Ann. Henri Poincaré 17(January), 99–135 (2016)
Carbone, R., Sasso, E., Umanitá, V.: On the asymptotic behavior of generic quantum Markov semigroups. Infin. Dimens. Anal. Quantum. Probab. Relat. Top. 17(1), 1450001 (2014)
Choi, M.D.: A Schwarz inequality for positive linear maps on \(C^{\ast } \)-algebras. Illinois J. Math. 18, 565–574 (1974)
Cirillo, G.I., Ticozzi, F.: Decompositions of Hilbert spaces, stability analysis and convergence probabilities for discrete-time quantum dynamical semigroups. J. Phys. A 48(8), 085302 (2015). 28
Evans, D.E.: Irreducible quantum Markov semigroups. Commun. Math. Phys. 54, 293–297 (1977)
Evans, D.E., Hoegh-Krohn, R.: Spectral properties of positive maps on c*-algebras. J. Lond. Math. Soc. 17, 345–355 (1978)
Fagnola, F., Quezada, R.: Two-photon absorption and emission process. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 8(4), 573–591 (2005)
Fagnola, F., Rebolledo, R.: Subharmonic projections for a quantum Markov semigroup. J. Math. Phys. 43(2), 1074–1082 (2002)
Fagnola, F., Rebolledo, R.: Transience and recurrence of quantum Markov semigroups. Probab. Theory Related Fields 126(2), 289–306 (2003)
Fagnola, F., Sasso, E., Umanità, V.: The role of the atomic decoherence-free subalgebra in the study of quantum Markov semigroups. J. Math. Phys. 60(7), 072703 (2019). 15
Farenick, D.R.: Irreducible positive linear maps on operator algebras. Proc. Am. Math. Soc. 124(11), 3381–3390 (1996)
Frigerio, A.: Quantum dynamical semigroups and approach to equilibrium. Lett. Math. Phys., 2(2):79–87 (1977/78)
Frigerio, A.: Stationary states of quantum dynamical semigroups. Commun. Math. Phys. 63(3), 269–276 (1978)
Frigerio, A., Verri, M.: Long-time asymptotic properties of dynamical semigroups on \(W^{\ast } \)-algebras. Math. Z. 180(2), 275–286 (1982)
Gärtner, A., Kümmerer, B.: A coherent approach to recurrence and transience for quantum markov operators. ArXiv e-prints (Nov. 2012)
Gilles, L., Knight, P.L.: Two-photon absorption and nonclassical states of light. Phys. Rev. A 48, 1582–1593 (1993)
Groh, U.: The peripheral point spectrum of Schwarz operators on \(C^{\ast } \)-algebras. Math. Z. 176(3), 311–318 (1981)
Jenčová, A., Petz, D.: Sufficiency in quantum statistical inference. Commun. Math. Fisica 263(1), 259–276 (2006)
Kümmerer, B., Maassen, H.: A pathwise ergodic theorem for quantum trajectories. J. Phys. A 37(49), 11889–11896 (2004)
Kümmerer, B., Nagel, R.: Mean ergodic semigroups on \(W^{\ast } \)-algebras. Acta Sci. Math. (Szeged) 41(1–2), 151–159 (1979)
Luczak, A.: Ergodic projection for quantum dynamical semigroups. In: Proceedings of the International Quantum Structures Association, Quantum Structures ’94 (Prague, 1994), vol. 34, pp. 1533–1540 (1995)
Norris, J.R.: Markov Chains. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge (1997)
Sinayskiy, I., Petruccione, F.: Efficiency of open quantum walk implementation of dissipative quantum computing algorithms. Quantum Inf. Process. 11(5), 1301–1309 (2012)
Ticozzi, F., Lucchese, R., Cappellaro, P., Viola, L.: Hamiltonian control of quantum dynamical semigroups: stabilization and convergence speed. IEEE Trans. Automat. Control 57(8), 1931–1944 (2012)
Tomiyama, J.: On the projection of norm one in \(W^*\)-algebras III. Tohoku Math. J. 2(11), 125–129 (1959)
Umanità, V.: Classification and decomposition of quantum Markov semigroups. Probab. Theory Relat. Fields 134(4), 603–623 (2006)
Štefaňák, M., Novotný, J., Jex, I.: Percolation assisted excitation transport in discrete-time quantum walks. New J. Phys. 18, 023040 (2016)
Wolf, M.: Quantum Channels and Operations Guided Tour. Online Lecture Notes (2012)
Acknowledgements
The authors acknowledge the support of the INDAM GNAMPA Project 2020 “Evoluzioni markoviane quantistiche” and of the Italian Ministry of Education, University and Research (MIUR) for the FFABR 2017 program and for the Dipartimenti di Eccellenza Program (2018– 2022)—Dept. of Mathematics “F. Casorati,” University of Pavia.
Funding
Open access funding provided by Università degli Studi di Pavia.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Alain Joye.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carbone, R., Girotti, F. Absorption in Invariant Domains for Semigroups of Quantum Channels. Ann. Henri Poincaré 22, 2497–2530 (2021). https://doi.org/10.1007/s00023-021-01016-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-021-01016-5
Keywords
- Quantum channel
- Quantum Markov semigroup
- Absorption probabilities
- Ergodic theory
- Quantum recurrence
- Fixed points