1 Introduction

This paper continues the study of the so-called detectable subspace of an operator in Hilbert space started in [7,8,9,10]. The detectable subspace of a (generally) non-self-adjoint operator is defined in terms of boundary triples [5, 12, 21]. The problem of its determination is physically motivated, as it addresses the important inverse problem of determining the part of the physical model which is ‘visible’ from boundary measurements. Therefore, it determines what partial information on the system is available in many standard experimental settings. Roughly speaking, the detectable subspace is the reducible subspace corresponding to the part of the operator which is ‘visible’ from the boundary behaviour of the solutions of the formal spectral equations (see the rigorous definition below). The analysis of its structure, in particular the question of detectability (the coincidence of the detectable subspace with the whole Hilbert space), is very important in the study of various types of inverse problems.

By the nature of the problem, finding the detectable subspace is very technically involved. Therefore, consideration of particular examples, such as the Friedrichs model considered here, is relevant and important in understanding the phenomena of ‘visibility’ or ‘cloaking’ in various fields such as in quantum mechanics, wave propagation theory and questions related to metamaterials and homogenisation.

Friedrichs model operators are perturbations of the multiplication operator by an integral operator. They were introduced by Friedrichs in 1948 [15] as a first rigorous model for scattering theory and enabled L.D. Faddeev’s famous results on multi-particle Schrödinger operators [14]. Via the Fourier transform, Friedrichs model operators allow the study of Schrödinger operators with so-called separable potentials, see [11] for a detailed discussion of the scattering theory for such operators. Moreover, according to L.D. Faddeev, they provide a simple model for renormalisation theory in physics.

In the previous papers [7, 9, 10], the analysis of Friedrichs model operators showed how complicated the structure of the detectable subspace may be, even in the seemingly simple case of a rank one perturbation. Therefore, considering various special cases for the perturbation can provide an important step in understanding the nature of the whole problem. In [10], the technique of Hankel operators was used for the analysis of the detectable subspace under special conditions on the rank one perturbation in terms of Hardy classes [20]. In the current paper, we consider another wide class of perturbations, again of rank one, where the theory of Toeplitz operators appears as the main tool. We stress that the paper does not add any new results in the theory of Toeplitz operators, but shows a new application of the theory to the detectable subspace problem for a class of operators.

The paper is organised as follows. Section 2 contains a collection of basic facts on the generalised Weyl–Titchmarsh function (or Dirichlet-to-Neumann map), the abstract boundary triple approach and the definition of the detectable subspaces. Section 3 briefly discusses the main properties of the Friedrichs model, including its boundary triple set-up. The main results are presented in Sect. 4, where, using the canonical factorisation of a Toeplitz operator’s symbol, the indices (the codimensions of the detectable subspaces) are explicitly calculated (Theorem 4.7). The section also contains a few examples illustrating the main theorems.

2 Background: Boundary Triples and the Detectable Subspace

For the convenience of the reader and to keep this article as self-contained as reasonably possible, in this section and the next, we give an introduction to concepts and notation that will be used throughout the article. We make the following basic assumptions.

  1. (1)

    A, \( {\widetilde{A}}\) are closed, densely defined operators in a Hilbert space H.

  2. (2)

    A and \( {\widetilde{A}}\) are an adjoint pair, i.e. \(A^*\supseteq {\widetilde{A}}\) and \( {\widetilde{A}}^*\supseteq A\).

Then, see [21], there exist ‘boundary spaces’ \({{\mathcal {H}}}\), \({{\mathcal {K}}}\) and ‘trace operators’

$$\begin{aligned}&\Gamma _1:{\mathrm {Dom\,}}( {\widetilde{A}}^*)\rightarrow {{\mathcal {H}}},\quad \Gamma _2:{\mathrm {Dom\,}}( {\widetilde{A}}^*)\rightarrow {{\mathcal {K}}},\\&\quad {\widetilde{\Gamma }}_1:{\mathrm {Dom\,}}(A^*)\rightarrow {{\mathcal {K}}}\quad \hbox { and }\quad {\widetilde{\Gamma }}_2:{\mathrm {Dom\,}}(A^*)\rightarrow {{\mathcal {H}}}\end{aligned}$$

such that for \(u\in {\mathrm {Dom\,}}( {\widetilde{A}}^*) \) and \(v\in {\mathrm {Dom\,}}(A^*)\) we have an abstract Green formula

$$\begin{aligned} \left\langle {\widetilde{A}}^* u, v\right\rangle _H - {\Big \langle u,A^*v \Big \rangle _H} = \left\langle \Gamma _1 u, {\widetilde{\Gamma }}_2 v\right\rangle _{{\mathcal {H}}}- \left\langle \Gamma _2 u, {\widetilde{\Gamma }}_1v\right\rangle _{{\mathcal {K}}}. \end{aligned}$$
(2.1)

The trace operators \(\Gamma _1\), \(\Gamma _2\), \({\widetilde{\Gamma }}_1\) and \( {\widetilde{\Gamma }}_2 \) are bounded with respect to the graph norm. The pair \((\Gamma _1,\Gamma _2)\) is surjective onto \({{\mathcal {H}}}\times {{\mathcal {K}}}\) and \(({\widetilde{\Gamma }}_1,{\widetilde{\Gamma }}_2)\) is surjective onto \({{\mathcal {K}}}\times {{\mathcal {H}}}\). Moreover, we have

$$\begin{aligned}&{\mathrm {Dom\,}}(A)= {\mathrm {Dom\,}}( {\widetilde{A}}^*)\cap \ker \Gamma _1\cap \ker \Gamma _2 \ \hbox { and } \ {\mathrm {Dom\,}}( {\widetilde{A}})= {\mathrm {Dom\,}}(A^*)\cap \ker {\widetilde{\Gamma }}_1\!\cap \\&\ker {\widetilde{\Gamma }}_2. \end{aligned}$$

The collection \(\{{{\mathcal {H}}}\oplus {{\mathcal {K}}}, (\Gamma _1,\Gamma _2), ({\widetilde{\Gamma }}_1,{\widetilde{\Gamma }}_2)\}\) is called a boundary triple for the adjoint pair \(A, {\widetilde{A}}\).

Remark 2.1

There has been an explosion of interest in boundary triples in the last decade, in particular around their application to partial differential equations usually in the self-adjoint case (see, e.g. [1,2,3, 5, 12, 16,17,18,19, 22, 23]). Generalisations to relations have been studied in [13].

We next define Weyl M-functions associated with boundary triples (see, e.g. [5, 12]). Given bounded linear operators \(B\in {\mathcal {L}}({{\mathcal {K}}},{{\mathcal {H}}})\) and \({\widetilde{B}}\in {\mathcal {L}}({{\mathcal {H}}},{{\mathcal {K}}})\), consider extensions of A and \( {\widetilde{A}}\) (respectively) given by

$$\begin{aligned} A_B:= {\widetilde{A}}^*\vert _{\ker (\Gamma _1-B\Gamma _2)} \hbox { and } {\widetilde{A}}_{\widetilde{B}}:=A^*\vert _{\ker ({\widetilde{\Gamma }}_1-{\widetilde{B}}{\widetilde{\Gamma }}_2)}. \end{aligned}$$

In the following, we assume the resolvent set \(\rho (A_B)\ne \emptyset \), in particular \(A_B\) is a closed operator. For \(\lambda \in \rho (A_B)\), define the M-function via

$$\begin{aligned} M_B(\lambda ):{\mathrm {Ran\,}}(\Gamma _1{-}B\Gamma _2)\rightarrow {{\mathcal {K}}},\ M_B(\lambda )(\Gamma _1{-}B\Gamma _2) u{=}\Gamma _2 u \hbox { for all } u\in \ker ( {\widetilde{A}}^*{-}\lambda ) \end{aligned}$$

and for \(\lambda \in \rho ( {\widetilde{A}}_{\widetilde{B}})\), we define

$$\begin{aligned} {\widetilde{M}}_{\widetilde{B}}(\lambda ):{\mathrm {Ran\,}}({\widetilde{\Gamma }}_1{-}{\widetilde{B}}{\widetilde{\Gamma }}_2)\rightarrow {{\mathcal {H}}},\ {\widetilde{M}}_{\widetilde{B}}(\lambda )({\widetilde{\Gamma }}_1{-}{\widetilde{B}}{\widetilde{\Gamma }}_2) v{=}{\widetilde{\Gamma }}_2 v \hbox { for all } v\in \ker (A^*{-}\lambda ). \end{aligned}$$

For \(\lambda \in \rho (A_B)\), the linear operator \(S_{\lambda ,B}:{\mathrm {Ran\,}}(\Gamma _1-B\Gamma _2)\rightarrow \ker ( {\widetilde{A}}^*-\lambda )\) given by

$$\begin{aligned} ( {\widetilde{A}}^*-\lambda )S_{\lambda ,B} f=0,\ (\Gamma _1-B\Gamma _2)S_{\lambda ,B} f=f \end{aligned}$$
(2.2)

is called the solution operator. For \(\lambda \in \rho ( {\widetilde{A}}_B^*)\), we similarly define the linear operator \( {\widetilde{S}}_{\lambda ,B^*}:{\mathrm {Ran\,}}({\widetilde{\Gamma }}_1-B^*{\widetilde{\Gamma }}_2)\rightarrow \ker (A^*-\lambda )\) by

$$\begin{aligned} (A^*-\lambda ) {\widetilde{S}}_{\lambda ,B^*} f=0,\ ({\widetilde{\Gamma }}_1-B^*{\widetilde{\Gamma }}_2) {\widetilde{S}}_{\lambda ,B^*} f=f. \end{aligned}$$
(2.3)

The operators \(M_B(\lambda )\), \(S_{\lambda ,B}\), \( {\widetilde{M}}_{\widetilde{B}}(\lambda )\) and \( {\widetilde{S}}_{\lambda ,B^*} \) are well defined for \(\lambda \in \rho (A_B)\) and \(\lambda \in \rho ( {\widetilde{A}}_{\widetilde{B}})\), respectively.

We are now ready to define one of the main concepts of the paper, the detectable subspaces, introduced in [7]. Fix \(\mu _0\not \in \sigma (A_B)\). Then, define the spaces

$$\begin{aligned}&{\mathcal {S}}_B := {\mathrm {Span\,}}_{\delta \not \in \sigma (A_B)}(A_B-\delta I)^{-1} \text{ Ran }(S_{\mu _0,B}), \end{aligned}$$
(2.4)
$$\begin{aligned}&{\mathcal {T}}_B := {\mathrm {Span\,}}_{\mu \not \in \sigma (A_B)} \text{ Ran }(S_{\mu ,B}), \end{aligned}$$
(2.5)

and similarly the ‘adjoint’ pair of linear sets

$$\begin{aligned}&\widetilde{ {\mathcal {S}}}_{B^*} := \text{ Span}_{\delta \not \in \sigma ({\tilde{A}}_{B^*})} ({\tilde{A}}_{B^*}-\delta I)^{-1}\text{ Ran }({\tilde{S}}_{\overline{\mu }_0,B^*}), \end{aligned}$$
(2.6)
$$\begin{aligned}&\widetilde{ {\mathcal {T}}}_{B^*} := \text{ Span}_{\mu \not \in \sigma ({\tilde{A}}_{B^*})} \text{ Ran }({\tilde{S}}_{\mu ,B^*}). \end{aligned}$$
(2.7)

Remark 2.2

In many cases of the Friedrichs model, we will be considering, the spaces \(\overline{ {\mathcal {S}}_B}\) and \(\overline{ {\mathcal {T}}_B}\) coincide and are independent of B. This follows from [7] or [9, Proposition 2.9]. To avoid cumbersome notation, in many places we shall denote all these spaces by \( {\overline{\mathcal {S}}}\). We will refer to \( {\overline{\mathcal {S}}}\) as the detectable subspace.

In [7, Lemma 3.4], it is shown that \(\overline{ {\mathcal {S}}}\) is a regular invariant subspace of the resolvent of the operator \(A_B\): that is, \(\overline{(A_B-\mu I)^{-1}\overline{ {\mathcal {S}}}} = \overline{ {\mathcal {S}}}\) for all \(\mu \in \rho (A_B)\). From (2.4) and [5, Proposition 3.9], we get that the orthogonal complement of \( {\overline{\mathcal {S}}}\) is

$$\begin{aligned} {\mathcal {S}}^\perp =\bigcap _{B\in {\mathcal {L}}({{\mathcal {K}}},{{\mathcal {H}}})}\ \bigcap _{\lambda \in \rho (A_B)}\ker (S_{\lambda ,B}^*)=\bigcap _{B\in {\mathcal {L}}({{\mathcal {K}}},{{\mathcal {H}}})}\ \bigcap _{\lambda \in \rho (A_B)}\ker \left( {\widetilde{\Gamma }}_2( {\widetilde{A}}_{B^*}-\overline{\lambda })^{-1}\right) . \end{aligned}$$

3 Basic Properties of the Friedrichs Model

In this section, we briefly introduce the Friedrichs model and collect some results. More details and proofs of the results can be found in [7].

Let \(\phi \), \(\psi \) be in \(L^2({\mathbb {R}})\). We consider in \(L^2({\mathbb {R}})\) the operator A with domain

$$\begin{aligned} {\mathrm {Dom\,}}(A) {=} \left\{ f\in L^2({\mathbb {R}}) \, \Big \vert \, xf(x)\in L^2({\mathbb {R}}), \lim _{R\rightarrow \infty }\int _{{-}R}^{R}f(x)dx \;\; \text{ exists } \text{ and } \text{ is } \text{ zero }\right\} , \end{aligned}$$

given by the expression

$$\begin{aligned} (Af)(x) = x f(x) + \langle f,\phi \rangle \psi (x). \end{aligned}$$
(3.1)

Observe that since the constant function \({{\mathbf {1}}}\) does not lie in \(L^2({\mathbb {R}})\) the domain of A is dense. The adjoint of A is given on the domain

$$\begin{aligned} {\mathrm {Dom\,}}(A^*) = \left\{ f\in L^2({\mathbb {R}}) \, | \, \exists c_f\in {\mathbb {C}}: xf(x)-c_f{{\mathbf {1}}} \in L^2({\mathbb {R}})\right\} , \end{aligned}$$
(3.2)

by the formula

$$\begin{aligned} (A^*f)(x) = x f(x) - c_f +\langle f,\psi \rangle \phi (x). \end{aligned}$$
(3.3)

Note that \({\mathrm {Dom\,}}(A)\subseteq {\mathrm {Dom\,}}(A^*)\) and that \(c_f=0\) for \(f\in {\mathrm {Dom\,}}(A)\).

We introduce an operator \(\widetilde{A}\) in which the roles of \(\phi \) and \(\psi \) are exchanged: \({\mathrm {Dom\,}}( {\widetilde{A}})={\mathrm {Dom\,}}(A)\) and

$$\begin{aligned} ( {\widetilde{A}}f)(x) = x f(x) + \langle f,\psi \rangle \phi {(x)}. \end{aligned}$$
(3.4)

We immediately see that \({\mathrm {Dom\,}}( {\widetilde{A}}^*) = {\mathrm {Dom\,}}(A^*)\) and that

$$\begin{aligned} {( {\widetilde{A}}^*f)(x)} = x f(x) - c_f +\langle f,\phi \rangle {\psi (x)}. \end{aligned}$$
(3.5)

Thus, \( {\widetilde{A}}^*\) is an extension of A, while \(A^*\) is an extension of \( {\widetilde{A}}\).

Since \(c_f=\lim _{R\rightarrow \infty }(2R)^{-1} \int _{-R}^R xf(x)\ dx\) is uniquely determined, we can define trace operators \(\Gamma _1\) and \(\Gamma _2\) on \({\mathrm {Dom\,}}(A^*)\) as follows:

$$\begin{aligned} \Gamma _1 u = \lim _{R\rightarrow \infty } \int _{-R}^R u(x) dx,\;\;\; \Gamma _2 u = c_u. \end{aligned}$$
(3.6)

Note that the limit in (3.6) always exists and that \(\Gamma _1 u= \int _{{\mathbb {R}}} (u(x) - c_u\mathrm{sign}(x)\)\((x^2+1)^{-1/2})dx\), which is the expression used in [7].

Then,

$$\begin{aligned} A = \left. {\widetilde{A}}^*\right| _{\ker (\Gamma _1)\cap \ker (\Gamma _2)} \;\;\; \hbox { and } \;\;\; {\widetilde{A}}= \left. A^*\right| _{\ker (\Gamma _1)\cap \ker (\Gamma _2)}; \end{aligned}$$
(3.7)

moreover, the following Green’s formula holds

$$\begin{aligned} \langle A^*f,g\rangle - \langle f, {\widetilde{A}}^*g \rangle = \Gamma _1 f \overline{\Gamma _2 g} - \Gamma _2 f \overline{\Gamma _1 g}, \end{aligned}$$
(3.8)

showing that we have constructed a boundary triple for the pair A, \( {\widetilde{A}}\).

We can now determine the M-function and the resolvent. Suppose that \(\mathfrak {I}\lambda \ne 0\). Then, \(f\in \ker ( {\widetilde{A}}^*-\lambda )\) if

$$\begin{aligned} f {(x)} = (\Gamma _2f) \left[ \frac{1}{x-\lambda }-\frac{\langle (t-\lambda )^{-1},\phi \rangle }{D(\lambda )}\frac{\psi {(x)}}{x-\lambda }\right] . \end{aligned}$$
(3.9)

Here, the perturbation determinant D is the function

$$\begin{aligned} D(\lambda ) = 1 + \int _{{\mathbb {R}}}\frac{1}{x-\lambda }\psi (x)\overline{\phi (x)}dx, \quad \lambda \not \in {\mathbb {R}}. \end{aligned}$$
(3.10)

Moreover, the Weyl-function \(M_B(\lambda )\) is given by the scalar function

$$\begin{aligned} M_B(\lambda )= & {} \left[ \text{ sign }(\mathfrak {I}\lambda ) \pi i -\frac{ {\langle (t-\lambda )^{-1},\overline{\psi }\rangle \langle (t-\lambda )^{{-}1},\phi \rangle } }{D(\lambda )} {-} B\right] ^{{-}1}\!,\lambda \not \in {\mathbb {R}}. \end{aligned}$$
(3.11)

For the resolvent, we have that \((A_B-\lambda )f=g\) if and only if

$$\begin{aligned} f(x)= & {} \frac{g(x)}{x-\lambda } -\frac{1}{ D(\lambda )}\frac{\psi (x)}{x-\lambda } \left\langle \frac{g}{t-\lambda },\phi \right\rangle \nonumber \\&\quad + c_f\left[ \frac{1}{x-\lambda }-\frac{1}{ D(\lambda )}\frac{\psi (x)}{x-\lambda } \left\langle \frac{1}{t-\lambda },\phi \right\rangle \right] , \end{aligned}$$
(3.12)

in which the coefficient \(c_f\) is given by

$$\begin{aligned} c_f = M_B(\lambda )\left[ -\left\langle \frac{1}{t-\lambda },\overline{g}\right\rangle + \frac{1}{ D(\lambda )}\left\langle \frac{g}{t-\lambda },\phi \right\rangle \left\langle \frac{1}{t-\lambda },\overline{\psi }\right\rangle \right] . \end{aligned}$$
(3.13)

Remark 3.1

There is another approach to the Friedrichs model via the Fourier transform, which turns the perturbed multiplication operator into a rank one perturbation of a first-order differential operator with an appropriate matching condition at 0. See [10] for more details.

4 Spectra of Toeplitz Operators and Detectability

In our previous paper on detectable subspaces for Friedrichs model operators [10], Hankel operators played a special role in the analysis of determining the detectable subspace. However, for another class of examples of the Friedrichs model, the theory of Toeplitz operators is the main instrument of our analysis. We will discuss this type of examples and the related detectability problem here.

We first introduce some notation. Let \(H^+_p({\mathbb {C}}_+)\) and \(H^-_p({\mathbb {C}}_-)\), \(1\le p\le \infty \), denote the Hardy spaces of p-integrable functions, analytic in the upper and lower half-plane, respectively, where the norm is given by

$$\begin{aligned} \left\| f\right\| _{H_p^\pm }=\sup _{y>0}\left( \int _{\mathbb {R}}|f(x\pm iy)|^p\ dx\right) ^{1/p} \hbox { for } p<\infty \quad \hbox {and} \left\| f\right\| _{H_\infty ^\pm }=\sup _{z\in {\mathbb {C}}_\pm } |f(z)|. \end{aligned}$$

Functions in the Hardy spaces can be identified with their boundary values on the real line which lie in \(L^p({\mathbb {R}})\) (see [20] for more details). In what follows we will use this identification without further comment and denote the Hardy spaces simply by \(H^+_p\) and \(H^-_p\).

The operators \(P_\pm :L^2({\mathbb {R}})\rightarrow H_2^\pm \) given by

$$\begin{aligned} P_\pm f(k) =\pm \frac{1}{2\pi i}\lim _{\varepsilon \rightarrow 0}\int _{\mathbb {R}}\frac{f(x)}{x-(k\pm i\varepsilon )}dx \end{aligned}$$
(4.1)

are the Riesz projections where the limit is to be understood in \(L^2({\mathbb {R}})\) (see [20]).

We next give a characterisation of the space \(\overline{ {\mathcal {S}}}\), or, more precisely, its orthogonal complement for the Friedrichs model which is taken from [9, Proposition 7.2]. The proof is based on the definition of \(\overline{ {\mathcal {S}}}\) using (2.5) and the results from Sect. 3.

Proposition 4.1

Let \(P_\pm \) be the Riesz projections defined in (4.1) and \(D(\lambda )\) be as in (3.10). Denote by \(D_\pm (\lambda )\) its restriction to \({\mathbb {C}}_\pm \) and by \(D_\pm \) the boundary values of these functions on \({\mathbb {R}}\) (which exist a.e., cf. [20, 24]).

  1. (1)

    Let \(\phi ,\psi \in L^2({\mathbb {R}})\). Then, \(g\in \overline{ {\mathcal {S}}}^\perp \) if and only if

    $$\begin{aligned}&P_+ \overline{g}-\frac{2\pi i}{D_+}(P_+\overline{\phi })P_+(\psi \overline{g})=0\; \hbox { and }\; P_- \overline{g}+\frac{2\pi i}{D_-}(P_-\overline{\phi })P_-(\psi \overline{g})=0, \end{aligned}$$
    (4.2)

    if and only if

    $$\begin{aligned}&{\left\{ \begin{array}{ll} \mathrm {(i)}\ \frac{(P_+\overline{\phi })P_+(\psi \overline{g})}{D_+}\in H_2^+, \; \mathrm {(ii)}\ \frac{(P_-\overline{\phi })P_-(\psi \overline{g})}{D_-}\in H_2^-, \\ \mathrm {(iii)}\ \overline{g}-\frac{2\pi i}{D_+}(P_+\overline{\phi })P_+(\psi \overline{g})+\frac{2\pi i}{D_-}(P_-\overline{\phi })P_-(\psi \overline{g})=0\ (a.e.). \end{array}\right. } \end{aligned}$$
    (4.3)
  2. (2)

    If \(\phi \in L^2({\mathbb {R}}),\psi \in L^2({\mathbb {R}})\cap L^\infty ({\mathbb {R}})\) or \(\phi ,\psi \in L^2({\mathbb {R}})\cap L^4({\mathbb {R}})\), then \( g\in \overline{ {\mathcal {S}}}^\perp \) if and only if any of the following three equivalent conditions holds:

    $$\begin{aligned}&\left[ D_+- 2\pi i(P_+\overline{\phi })\psi \right] \overline{g}= 2\pi i\overline{\phi }[\psi P_-\overline{g}-P_-(\psi \overline{g})]\ (a.e.), \end{aligned}$$
    (4.4)
    $$\begin{aligned}&\left[ D_+- 2\pi i(P_+\overline{\phi })\psi \right] \overline{g}= 2\pi i\overline{\phi }[-\psi P_+\overline{g}+P_+(\psi \overline{g})]\ (a.e.), \end{aligned}$$
    (4.5)
    $$\begin{aligned}&\left[ D_+- 2\pi i(P_+\overline{\phi })\psi \right] \overline{g}= 2\pi i\overline{\phi }[P_+(\psi P_-\overline{g})-P_-(\psi P_+\overline{g})]\ (a.e.). \end{aligned}$$
    (4.6)

We see from the proposition, e.g. from (4.2), that the operator \(u\mapsto (P_+\overline{\phi })P_+(\psi u)\) will play an important role in determining the detectable subspace. Therefore, under the assumption that \(\overline{\phi }\in H^+_2\), we will study the operator

$$\begin{aligned} T:L^2({\mathbb {R}})\rightarrow L^2({\mathbb {R}}), \quad Tu:={\overline{\phi }} P_+(\psi u). \end{aligned}$$

It is closely related to the Toeplitz operator

$$\begin{aligned} T_a:H^+_2\rightarrow H^+_2, \quad T_a u :=P_+(au), \end{aligned}$$

with symbol \(a:=\psi {\overline{\phi }}\) which can be found, e.g. in [4].

Throughout this section, we will make the following assumptions.

Assumption 4.2

Let \(\phi ,\psi \in L^2({\mathbb {R}})\) be such that

  1. (i)

    for \(k\in {\mathbb {R}}\), \(a(k):=\psi (k){\overline{\phi }} (k) \in H_1^-\backslash \{0\}\),

  2. (ii)

    \(\phi \in H_2^-\) and

  3. (iii)

    \(\phi ,\psi \in L^\infty ({\mathbb {R}})\).

Remark 4.3

  1. (1)

    All three assumptions are independent of each other.

  2. (2)

    From (i), it follows from the Uniqueness Theorem [20, 24] that both \(\phi \) and \(\psi \) are nonzero a.e. on \({\mathbb {R}}\).

  3. (3)

    Under the above assumptions, we have \(D_+(\lambda )\equiv 1\) and \(P_+\overline{\phi }=\overline{\phi }\), \(P_-\overline{\phi }=0\). In particular, from (3.12), we get that the corresponding Friedrichs model operator has no spectrum in \({\mathbb {C}}_+\).

  4. (4)

    The majority of functions \(a\in H_1^-\) can be decomposed as in assumption (i). To see this, choose \(\phi =(x-i)^{-\frac{1}{2}-\varepsilon }\) for some \(\varepsilon >0\) and a suitable choice of the branch cut. Then, we have \(\phi \in H_2^-\). To satisfy the first assumption, we then require \(\psi (x):=a(x)(x+i)^{\frac{1}{2}+\varepsilon }\in L^2({\mathbb {R}})\), or \(a\in L^2({\mathbb {R}}; (1+x^2)^{\frac{1}{2}+\varepsilon })\). Therefore, the assumption that \(\phi \in H^-_2\) only imposes a mild extra condition on the decay of a at infinity.

  5. (5)

    The third assumption is only introduced for the sake of convenience and may be significantly relaxed. However, this would introduce more technical details which would obscure the main results. It means that \(a\in H_\infty ^-\), that the operator T is a bounded operator in \(L^2({\mathbb {R}})\) and \(T_a\) in \(H^+_2\), in particular, the operators are defined on the whole space.

  6. (6)

    Under the first assumption, we can express the operator \(T_a\) by \(T_a u =P_+(aP_+u)\).

We will now analyse the spectral properties of the operators T and \(T_a\); by \(\sigma _p\) we denote the set of eigenvalues of an operator. The proofs of parts (1)–(4) are very similar to the corresponding proofs for Toeplitz operators, e.g. in [4].

Proposition 4.4

Let \(\phi \), \(\psi \) satisfy Assumptions 4.2. Define the operators T on \(L^2({\mathbb {R}})\) and \(T_a:H^+_2\rightarrow H^+_2\) as above. Then,

  1. (1)

    \(\sigma _p(T)\supseteq {\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)\).

  2. (2)

    \(\sigma _p(T)=\{\mu \in {\mathbb {C}}\ |\ (a-\mu ) \text{ is } \text{ not } \text{ an } \text{ outer } \text{ function } \text{ in } {\mathbb {C}}_-\}\cup \{0\}\).

  3. (3)

    \(\mu \not \in \overline{ {\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)}\) implies \(\mu \) belongs to the resolvent set \(\rho (T)\).

  4. (4)

    The spectrum of T is given by \(\sigma (T)=\overline{\sigma _p(T)}=\overline{ {\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)}.\)

  5. (5)

    \(\sigma _p(T)\setminus \{0\}= \sigma _p(T_a)\setminus \{0\}\).

  6. (6)

    \(0\in \sigma _p(T_a)\) if and only if a is not an outer function in \({\mathbb {C}}_-\).

Proof

Proof of (1): Take \(u(k)=\tfrac{ \overline{\phi }(k)}{k-z_1}\), \(k\in {\mathbb {R}}\), \(z_1\in {\mathbb {C}}_-\). Then, \(u\in H_2^+\) and

$$\begin{aligned} Tu(k)= & {} {\overline{\phi }} (k) P_+ \Big ( \dfrac{\psi {\overline{\phi }} }{k-z_1} \Big )\ = {\overline{\phi }} (k) P_+\Big ( \dfrac{a(k)}{k-z_1} \Big ) \\= & {} {\overline{\phi }} (k) P_+\Big ( \dfrac{ a(k)-a(z_1)}{k-z_1}+\dfrac{a(z_1)}{k-z_1}\Big )\ = \dfrac{a(z_1)}{k-z_1}{\overline{\phi }}(k)=a(z_1)u(k) \end{aligned}$$

since the first term acted on by \(P_+ \) is analytic in \({\mathbb {C}}_-\), in \(L^2({\mathbb {R}})\) and is easily seen to lie in \(H_2^-\), while the second is in \(H_2^+\) since \(z_1\in {\mathbb {C}}_-\).

Proof of (2): We first consider \(\mu =0\). Choosing \(\overline{g}=\overline{\phi }h\) for \(h\in H_2^-\), we get \(T\overline{g}= \overline{\phi } P_+ \psi \overline{\phi }h =0,\) since \(\psi \overline{\phi }h \in H_2^-\), due to \(a\in H_\infty ^-\). Hence, all functions in \(\overline{\phi }H_2^-\) are eigenfunctions to the eigenvalue 0.

Now let \(\mu \ne 0\) and assume that \((a-\mu )\) is an outer function in \({\mathbb {C}}_-\) (see, e.g. [20] for the definition). We use that if \(f\in H^-_\infty \), then f is outer if and only if the closure of the set \(fH_2^-\) is \(H_2^-\) (Beurling Theorem, see [20]) and that the functions \((k-z_0)^{-1}\) for \(z_0\in {\mathbb {C}}_+\) span \(H_2^-\). Therefore,

$$\begin{aligned} {\mathrm {clos\,}}\left( {\mathrm {Span\,}}_{z_0\in {\mathbb {C}}_+}\frac{a(k)-\mu }{k-z_0}\right) =H^-_2. \end{aligned}$$

Now assume there exists \(g\in L^2({\mathbb {R}})\setminus \{0\}\) with \(T\overline{g}=\mu \overline{g}\) and set \(h=\psi \overline{g}\). Then, \(h\in (L^1\cap L^2)({\mathbb {R}})\setminus \{0\}\) and \(aP_+h=\mu h\), or \((a-\mu )P_+h=\mu P_-h\). Let \(z\in {\mathbb {C}}_+\), then

$$\begin{aligned} \int _{\mathbb {R}}(a-\mu )P_+h \frac{dk}{k-z} =\mu \int _{\mathbb {R}}P_-h \frac{dk}{k-z}\equiv 0. \end{aligned}$$

Therefore, \(P_+h\perp \frac{\overline{a}-\overline{\mu }}{k-\overline{z}}\) for all \(z\in {\mathbb {C}}_+\), i.e.

$$\begin{aligned} P_+h\perp {\mathrm {clos\,}}\left( {\mathrm {Span\,}}_{\overline{z}\in {\mathbb {C}}_-} \frac{\overline{a}-\overline{\mu }}{k-\overline{z}}\right) = H^+_2. \end{aligned}$$

This implies \(P_+h=0\), and since \(\mu \ne 0\) we get \(P_-h=0\), so \(h=0\). As \(\psi \) is nonzero a.e., we have \(g=0\), so \(\mu \) is not an eigenvalue of T.

Next let \(\mu \ne 0\) and assume that \((a-\mu )\) is not an outer function in \({\mathbb {C}}_-\). This implies that there exists \(h\in H^-_2\setminus \{0\}\) such that \(h\perp (a-\mu )H^-_2\). Now

$$\begin{aligned} h\perp (a-\mu )H^-_2\Longleftrightarrow & {} \overline{h}\perp (\overline{a}-\overline{\mu }) H^+_2 \Longleftrightarrow \ (a-\mu ) \overline{h}\in H^-_2, \end{aligned}$$

so \(P_+((a-\mu )\overline{h})=0\) and \(P_+(a\overline{h})=\mu P_+ \overline{h} = \mu \overline{h}\) (as \(\overline{h}\in H^+_2\)). This implies that \(T(\overline{\phi }\overline{h})= \overline{\phi }P_+(\psi \overline{\phi }\overline{h})=\mu \overline{\phi }\overline{h}.\) As \(\phi \in L^\infty ({\mathbb {R}})\), \(\overline{\phi }\overline{h}\in L^2({\mathbb {R}})\) and it is not identically zero (as \(\phi \not \equiv 0\) and h is nonzero a.e. by the uniqueness theorem, see [20]), so \(\mu \in \sigma _p(T)\) with the nonzero eigenfunction \(\overline{\phi }\overline{h}\).

Proof of (3): We first note that as \(a\in H_1^-\) we have that \(\mu \not \in \overline{ {\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)}\) implies \(\mu \ne 0\) and that \(\inf _{z\in {\mathbb {C}}_-}|a(z)-\mu |>0.\) We want to calculate the resolvent of T at \(\mu \). Consider \((T-\mu )g=v\) with \(v\in L^2({\mathbb {R}})\). Since \(\psi \ne 0\) a.e. and \((a-\mu )\vert _{{\mathbb {R}}}\) is invertible we get (all equalities hold a.e.)

$$\begin{aligned} (T-\mu )g{=}v\Longleftrightarrow & {} \psi \overline{\phi }P_+(\psi g) {-} \mu \psi g{=} \psi v \ \Longleftrightarrow \ (a-\mu )P_+(\psi g)- \mu P_-(\psi g) {=} \psi v \nonumber \\\Longleftrightarrow & {} P_+(\psi g) {=}\frac{\psi }{a-\mu }v {+} \frac{\mu }{a-\mu } P_-(\psi g) \quad \hbox { in } L^2({\mathbb {R}}). \end{aligned}$$
(4.7)

Note that, as \(\frac{\mu }{a-\mu }\in H^-_\infty \), the last term lies in \(H^-_2\). Applying \(P_+\) and \(P_-\) to (4.7), we get

$$\begin{aligned} P_+(\psi g)= P_+\frac{\psi v}{a-\mu }, \quad \quad 0=P_-\frac{\psi v}{a-\mu }+ \frac{\mu }{a-\mu } P_-(\psi g). \end{aligned}$$

Thus,

$$\begin{aligned} \psi g = P_+(\psi g) +P_-(\psi g)= P_+\frac{\psi v}{a-\mu } - \frac{a-\mu }{\mu }P_-\frac{\psi v}{a-\mu } \end{aligned}$$

and

$$\begin{aligned} g =\frac{1}{\psi } P_+\frac{\psi v}{a-\mu } - \frac{a-\mu }{\psi \mu }P_-\frac{\psi v}{a-\mu }= \frac{v}{a-\mu }-\frac{a}{\mu \psi }P_-\frac{\psi v}{a-\mu }. \end{aligned}$$

Formally, we have for arbitrary \(v\in L^2({\mathbb {R}})\) that

$$\begin{aligned} g=(T-\mu )^{-1} v = \frac{v}{a-\mu }-\frac{\overline{\phi }}{\mu }P_-\frac{\psi v}{a-\mu }. \end{aligned}$$
(4.8)

Since \(\phi ,\psi \in L^\infty ({\mathbb {R}})\), the operator defined by the r.h.s. is bounded in \(L^2({\mathbb {R}})\). Checking the formal calculation of the resolvent for any \(v\in L^2({\mathbb {R}})\),

$$\begin{aligned}&(T-\mu )\left( \frac{v}{a-\mu }-\frac{\overline{\phi }}{\mu }P_-\frac{\psi v}{a-\mu }\right) \\&\quad = \overline{\phi } P_+\frac{\psi v}{a-\mu } - \frac{\mu v}{a-\mu } - \frac{\overline{\phi }}{\mu } \underbrace{P_+ \left( a P_- \frac{\psi v}{a-\mu }\right) }_{=0} +\overline{\phi } P_- \frac{\psi v}{a-\mu } \\&\quad = \overline{\phi } \frac{\psi v}{a-\mu } - \frac{\mu v}{a-\mu } = v. \end{aligned}$$

Therefore, the r.h.s. of (4.8) is the right inverse of the operator \((T-\mu )\). Similarly we see that the same expression gives the left inverse,

$$\begin{aligned}&\frac{(T-\mu ) v}{a-\mu }-\frac{\overline{\phi }}{\mu }P_-\frac{\psi (T-\mu ) v }{a-\mu }\\&\quad = \frac{\overline{\phi }P_+(\psi v)}{a-\mu } - \frac{\mu v}{a-\mu }-\frac{\overline{\phi }}{\mu }P_-\left[ \frac{\psi \overline{\phi }P_+(\psi v) }{a-\mu } - \frac{\mu \psi v }{a-\mu }\right] \\&\quad = \frac{\overline{\phi }P_+(\psi v)}{a-\mu } - \frac{\mu v}{a-\mu }-\frac{\overline{\phi }}{\mu }P_-\left[ \frac{a P_+(\psi v) }{a-\mu } - \frac{\mu (P_+(\psi v)+P_-(\psi v)) }{a-\mu }\right] \\&\quad = \frac{\overline{\phi }P_+(\psi v)}{a-\mu } - \frac{\mu v}{a-\mu }-\frac{\overline{\phi }}{\mu }P_-\left[ P_+(\psi v) - \frac{\mu P_-(\psi v) }{a-\mu }\right] \\&\quad = \frac{\overline{\phi }P_+(\psi v)}{a-\mu } - \frac{\mu v}{a-\mu }+\frac{\overline{\phi }}{a-\mu } P_-(\psi v) \\&\quad = \frac{\overline{\phi }\psi v}{a-\mu } - \frac{\mu v}{a-\mu } \ =\ v, \end{aligned}$$

so \(T-\mu \) is invertible, proving (3).

Now, (4) follows from (1) and (3), as \(\sigma (T)\subseteq \overline{ {\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)} \subseteq \overline{\sigma _p(T)} \subseteq \sigma (T),\) so all three sets must coincide.

Proof of (5): We again solve \(T\overline{g}=\mu \overline{g}.\) As \(\psi \ne 0\) a.e., this is equivalent to \(aP_+(\psi \overline{g}=\mu \psi \overline{g}\). Setting \(h=\psi \overline{g}\) this gives \(aP_+h=\mu h\).

Note that if \(h\in L^2({\mathbb {R}})\) and \(\mu \ne 0\) with \(aP_+h=\mu h\), then \(h=\psi \frac{\overline{\phi }P_+h}{\mu }\in \psi L^2({\mathbb {R}})\), so \(\overline{g}=h/\psi \in L^2({\mathbb {R}})\). Thus, for nonzero \(\mu \), \(T\overline{g}=\mu \overline{g}\) is equivalent to \(aP_+h=\mu h\). This reduces the problem to considering Toeplitz operators:

$$\begin{aligned} aP_+h=\mu h \Longleftrightarrow \left\{ \begin{array}{rcl} P_+(a P_+ h) &{}=&{} \mu P_+h, \\ P_-(aP_+h) &{}=&{} \mu P_-h, \end{array}\right. \ \Longleftrightarrow \ \left\{ \begin{array}{l} P_+(a P_+ h) = \mu P_+h, \\ P_-h = \frac{1}{\mu }P_-(aP_+h). \end{array}\right. \end{aligned}$$

Thus, \(P_+h\) determines \(P_-h\) uniquely and we only need to consider the first equation in \(H^+_2\) which shows equality of the point spectra of T and \(T_a\) away from 0.

Proof of (6): Consider \(T_a h=0\) for \(h\in H_2^+\setminus \{0\}\). Then,

$$\begin{aligned} P_+(ah)=0\Longleftrightarrow & {} ah\perp H_2^+ \ \Longleftrightarrow \ h\perp \overline{a} H_2^+ \ \Longleftrightarrow \ \overline{h}\perp a H_2^-. \end{aligned}$$

The existence of such a non-trivial h is then equivalent to a not being an outer function in \({\mathbb {C}}_-\). \(\square \)

Example 4.5

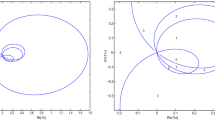
We illustrate Proposition 4.4 (4) with an example: We consider a case where we have no nonzero eigenvalues on the boundary of \(\sigma _p(T)\), as \((a-\mu )\) is outer. Let \(\overline{\phi }(k)=(k+i)^{-1}\) and \(\psi (k)=(k+i)(k-i)^{-4}\). Then, \(\phi ,\psi \in L^2({\mathbb {R}})\cap L^\infty ({\mathbb {R}})\), \(\phi \in H^-_2\) and \(a(z)=(z-i)^{-4}\in H^-_1\), so Assumptions 4.2 are satisfied. To determine \({\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)\), we consider \(a(t), t\in {\mathbb {R}}\) and take the inside of the curve (Fig. 1).

Fig. 1
figure 1

The range of \(a(t)=(t-i)^{-4}\) for \(t\in {\mathbb {R}}\) with the section around the origin enlarged

Full size image

Let

$$\begin{aligned} x+iy:=\frac{1}{(t-i)^4}=\frac{(t+i)^4}{(t^2+1)^4} = \frac{t^4-6t^2+1}{(t^2+1)^4} + i \frac{4t(t^2-1)}{(t^2+1)^4}. \end{aligned}$$

We first check that all nonzero points inside the inner curve are in the range. If \(y=0\) and x is small and negative (so \(\root 4 \of {-x}>0\)),

$$\begin{aligned} \frac{1}{(z-i)^4} = x \Longleftrightarrow (z-i)^4=\frac{1}{x} \Longleftrightarrow z-i=\frac{1}{\root 4 \of {-x}}e^{\frac{i(\pi +2\pi m)}{4}}, \ m\in {\mathbb {Z}}, \end{aligned}$$

so, e.g. for \(m=2\), \(z=i+\frac{1}{\root 4 \of {-x}}e^{\frac{5i\pi }{4}}\in {\mathbb {C}}_-\) for |x| sufficiently small, so the point x lies in \({\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)\). Similarly, we see that all points between the inner and outer curve lie in \({\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)\). Next, we check the points on the inner curve (corresponding to \(|t|>1\)): Let \(t>1\) and \((t-i)^{-4}=(z-i)^{-4}\). Then, \(z-i=(t-i)e^{i\frac{2\pi m}{4}}\), \(m\in {\mathbb {Z}}\). With \(m=3\), \(z=i+(t-i)(-i)=-1+(1-t)i\in {\mathbb {C}}_-.\)

Therefore, the boundary of the set \({\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-} a(z)\) consists of the outer curve (\(|t|\le 1\)) together with the isolated point 0 (corresponding to \(t=\infty \)). For these \(\mu \), the function \((a-\mu )\) is outer in \({\mathbb {C}}_-\). For \(\mu =0\) this is clear. For all other such \(\mu \), \((a-\mu )\) takes values outside a cone. This implies that \((a-\mu )^k\) is outer for some sufficiently small positive k which implies that \((a-\mu )\) is outer, since any Herglotz function (i.e. analytic functions on \({\mathbb {C}}_+\) with positive imaginary part) is outer.

We finally consider the behaviour at \(t=\pm 1\) and \(t=\pm \infty \). As \(t\rightarrow \pm \infty \), \(x\sim t^{-4}\) and \(y\sim 4t^{-5}\), so \(y\sim 4x^{5/4}\). At \(t=1\), \(x\sim \frac{-4-8(t-1)}{16}\), \(y\sim \frac{8(t-1)}{16}\), so \(y\sim -x-\frac{1}{4}\), and using symmetry of the range of a w.r.t. complex conjugation, we get a cone of angle \(\pi /2\) at this point.

Example 4.6

The next example shows that in statement (2) of Proposition 4.4, it is necessary to add the point \(\{0\}\), as it is not always contained in the set \(\{\mu : (a-\mu ) \hbox { is outer}\}\): Let \(\alpha _0\in {\mathbb {R}}\) and consider

$$\begin{aligned} \psi (z) = \frac{(z-\alpha _0)(z+i)}{(z-i)^3}e^{\frac{i}{z}}, \quad \overline{\phi }(z)=\frac{1}{z+i}, \quad \mathfrak {I}z\le 0. \end{aligned}$$

Then, \(\phi \in H_2^-\), \(\phi , \psi \in (L^2\cap L^\infty )({\mathbb {R}})\),

$$\begin{aligned} a(z)= \frac{z-\alpha _0}{(z-i)^3}e^{\frac{i}{z}}\in H_1^-\cap H^-_\infty \end{aligned}$$

and \(0\notin {\mathrm {Ran\,}}_{z\in {\mathbb {C}}_-}a(z)\). Due to the singular exponential factor, \(a=(a-0)\) is not an outer function.

In our main theorem on detectability, we will make use of the canonical Riesz–Nevanlinna factorisation theorem (see [20, Chapter IV]). The factorisation into inner and outer functions was actually first published in 1928 in a paper by V.I. Smirnov (see [25]). For the reader’s convenience, we state it here for functions in the lower half plane: If \(f\not \equiv 0\), \(f\in H_p^-\) for \(p\ge 1\), then up to constant multiples, f can be factorised uniquely as \( f(z)=B(z)\Sigma (z)G(z), \) where B(z) is a Blaschke product with

$$\begin{aligned} B(z) = \prod _k\left( e^{i\theta _k} \frac{z-z_k}{z-\overline{z_k}}\right) \hbox { for } \mathfrak {I}z<0 , \end{aligned}$$

where \(z_k\) are all the roots of f in \({\mathbb {C}}_-\) counted with their multiplicity and the real \(\theta _k\) are chosen so that \(e^{i\theta _k}(i-z_k)/(i-\overline{z_k})\ge 0,\) i.e. \(e^{i\theta _k}\) is a normalising factor; \(\Sigma (z)\) is the singular factor given by

$$\begin{aligned} \Sigma (z) = \exp \left( \frac{1}{\pi }\int _{-\infty }^\infty \left( \frac{i}{z-t}+\frac{it}{t^2+1}\right) \ d\sigma (t) \right) \end{aligned}$$

with \(d\sigma (t)\ge 0\) a singular measure (w.r.t. Lebesgue measure) satisfying \(\int _{-\infty }^\infty \)\(\frac{d\sigma (t)}{t^2+1}<\infty \); and G(z) is the outer factor given by

$$\begin{aligned} G(z)=\exp \left( -\frac{i}{\pi }\int _{-\infty }^\infty \left( \frac{1}{z-t}+\frac{t}{t^2+1}\right) \log |f(t)| \ dt \right) . \end{aligned}$$

We next introduce a scaling factor (or coupling constant) \(\alpha \in {\mathbb {C}}\setminus \{0\}\) and replace \(\psi \) by \(\alpha \psi \). We denote the corresponding detectable subspace by \( {\mathcal {S}}_\alpha \). This allows us to study the detectable subspace while we vary the parameter \(\alpha \). Moreover, we introduce the defect \({\mathrm {def\,}}( {\mathcal {S}}_\alpha )\) to be the dimension of the orthogonal complement \( {\mathcal {S}}_\alpha ^\perp \), i.e.

$$\begin{aligned} {\mathrm {def\,}}( {\mathcal {S}}_\alpha ):=\dim {\mathcal {S}}^\perp _\alpha . \end{aligned}$$

Theorem 4.7

Let \(\phi ,\psi \) satisfy Assumption 4.2. Define the operators T on \(L^2({\mathbb {R}})\) and \(T_a:H^+_2\rightarrow H^+_2\) as above and let \(\mu _\alpha =(2\pi i \alpha )^{-1}\). Then,

  1. (1)

    \({\mathrm {def\,}}( {\mathcal {S}}_\alpha )= \dim \ker \left( T_a-\mu _\alpha \right) \). Moreover,

    $$\begin{aligned} {\mathcal {S}}^\perp _\alpha =\left( \ker (T-\mu _\alpha )\right) ^*=[\psi ^{-1}(\mu _\alpha P_+ + P_-aP_+)\ker \left( T_a-\mu _\alpha \right) )]^*. \end{aligned}$$

    Here, we use \(\left( \ker (T-\mu _\alpha )\right) ^*\) to denote the set of complex conjugates of functions in \(\ker (T-\mu _\alpha )\). This will be used to distinguish it from the closure of a set in cases where the meaning may be ambiguous.

  2. (2)

    We have that \( {\mathcal {S}}^\perp _\alpha = \phi \left( H_2^-\ominus (a(z)-\mu _\alpha ) H_2^-\right) \). In particular, this implies that the space \(\phi \left( H_2^-\ominus (a(z)-\mu _\alpha ) H_2^-\right) \) is a closed subspace.

  3. (3)

    Consider the canonical factorisation of \((a(z)-\mu _\alpha )=B_\alpha (z) \Sigma _\alpha (z)G_\alpha (z)\) in \({\mathbb {C}}_-\) for a fixed \(\alpha \in {\mathbb {C}}\setminus \{0\}\) where \(B_\alpha \) is a Blaschke product containing all zeros of \((a(z)-\mu _\alpha )\) in \({\mathbb {C}}_-\) counted with their multiplicity, \(\Sigma _\alpha \) is the singular part and \(G_\alpha \) is an outer function. Then,

    $$\begin{aligned} \overline{(a-\mu _\alpha )H_2^-}=\overline{ B_\alpha (z) \Sigma _\alpha (z)H_2^-} \equiv B_\alpha (z) \Sigma _\alpha (z)H_2^-. \end{aligned}$$

    and

    $$\begin{aligned} {\mathrm {def\,}}( {\mathcal {S}}_\alpha )=\left\{ \begin{array}{cc} \infty &{} \text{ if } \Sigma _\alpha \not \equiv 1, \\ \text{ number } \text{ of } \text{ roots } \text{ of } B_\alpha (z) &{} \text{ if } \Sigma _\alpha \equiv 1. \end{array} \right. \end{aligned}$$
    (4.9)

    Note that the number of roots of \(B_\alpha (z)\) is counted with multiplicity and may be infinite.

Proof

Proof of (1): As \(a(z) \in H^-_1\backslash \{0\}\), we have \(\phi ,\psi \ne 0\) a.e. Moreover, for \(g\in L^2({\mathbb {R}})\) we have from (4.2) and using \(\overline{\phi }\in H^+_\infty \)

$$\begin{aligned} g\in {\mathcal {S}}_\alpha ^\perp\Longleftrightarrow & {} P_+ \overline{g}= 2\pi i\alpha \overline{\phi }P_+(\psi \overline{g})\ \hbox { and }\ P_- \overline{g}=0 \quad \Longleftrightarrow \quad \overline{g}= 2\pi i\alpha \overline{\phi }P_+(\psi \overline{g}). \end{aligned}$$

We rewrite this as

$$\begin{aligned} T\overline{g}=\overline{\phi } P_+ (\psi \overline{g})=\mu _\alpha \overline{g}, \end{aligned}$$
(4.10)

giving \( {\mathcal {S}}^\perp _\alpha =\left( \ker (T-\mu _\alpha )\right) ^*\).

Next let \(g\in {\mathcal {S}}_\alpha ^\perp \) and set \(h=\psi \overline{g}\). Then, as \(\psi \in L^\infty ({\mathbb {R}})\) and is nonzero a.e., we have \(h\in L^2({\mathbb {R}})\) and

$$\begin{aligned} g\in {\mathcal {S}}_\alpha ^\perp\Longleftrightarrow & {} \psi \overline{\phi } P_+ h = \mu _\alpha h,\ h\in L^2({\mathbb {R}}) \ \Longleftrightarrow aP_+h=\mu _\alpha h \\\Longleftrightarrow & {} \left\{ \begin{array}{ccc} P_+(aP_+h)&{}=&{}\mu _\alpha P_+h, \\ P_-(aP_+h)&{}=&{}\mu _\alpha P_-h. \end{array}\right. \end{aligned}$$

For the first equivalence, we note that any \(L^2\)-solution h of \(\psi \overline{\phi } P_+ h = \mu _\alpha h\) with \( \mu _\alpha \ne 0\) is divisible by \(\psi \) and \(h/\psi \in L^2({\mathbb {R}})\).

This shows that \(P_+h\) uniquely determines \(P_-h\) via \(P_-h=\frac{1}{\mu _\alpha }P_-(aP_+h)\) and it is sufficient to consider \(P_+(aP_+h)=\mu _\alpha P_+h\) which gives \( {\mathcal {S}}^\perp _\alpha \subseteq [\psi ^{-1}(\mu _\alpha P_+ + P_-aP_+)\ker \left( T_a-\mu _\alpha \right) ]^*\). On the other hand, given \(h_+\in \ker \left( T_a-\mu _\alpha \right) \), set \(\overline{g}=\overline{\phi }h_+\). Then,

$$\begin{aligned} T\overline{g}= \overline{\phi } P_+ (\psi \overline{g})= \overline{\phi } P_+ (a h_+) = \mu _\alpha \overline{\phi } h_+ = \mu _\alpha \overline{g}\end{aligned}$$

gives the reverse inclusion, since \( {\mathcal {S}}^\perp _\alpha =\left( \ker (T-\mu _\alpha )\right) ^*\).

Proof of (2): Using the characterisation (4.10), we need to study the equation

$$\begin{aligned} (T-\mu _\alpha )\overline{g}=\overline{\phi } P_+(\psi \overline{g}) -\mu _\alpha \overline{g}=0. \end{aligned}$$

We consider the equation pointwise and multiply by \(\psi \). Setting \(h=\psi \overline{g}\), we get \(h\in L^2({\mathbb {R}})\) and

$$\begin{aligned} aP_+h-\mu _\alpha h =0. \end{aligned}$$
(4.11)

By virtue of (4.11), the fact that a is divisible by \(\psi \) and \(\mu _\alpha \ne 0\), \(h/\psi =\overline{g}\in L^2({\mathbb {R}})\). Now, using \(h=P_+h+P_-h\), we find \((a-\mu _\alpha )P_+h=\mu _\alpha P_-h.\) Thus, \((a-\mu _\alpha )P_+h\perp H^+_2\), or \(P_+h\perp (\overline{a}-\overline{\mu _\alpha })H^+_2\), which implies \(P_+h\in H^+_2\ominus (\overline{a}-\overline{\mu _\alpha })H^+_2\). From (4.11), this implies

$$\begin{aligned} h \in \frac{a}{\mu _\alpha } \left( H^+_2\ominus (\overline{a}-\overline{\mu _\alpha })H^+_2\right) \end{aligned}$$

and dividing by \(\psi \) (which is nonzero a.e.), we get

$$\begin{aligned} \overline{g}\in \frac{\overline{\phi }}{\mu _\alpha }\left( H^+_2\ominus (\overline{a}-\overline{\mu _\alpha })H^+_2\right) =\overline{\phi } \left( H^+_2\ominus (\overline{a}-\overline{\mu _\alpha })H^+_2\right) . \end{aligned}$$

Taking complex conjugates and using \((H_2^+)^*=H_2^-\) implies one set inclusion. Conversely, let \(\overline{g}\in \overline{\phi } \left( H^+_2\ominus (\overline{a}-\overline{\mu _\alpha })H^+_2\right) .\) Then, \(\overline{g}=\overline{\phi }f_+\) for some \(f_+\in H^+_2\ominus (\overline{a}-\overline{\mu _\alpha })H^+_2\). Then,

$$\begin{aligned} \overline{\phi } P_+(\psi \overline{g}) -\mu _\alpha \overline{g}= & {} \overline{\phi } P_+(\psi \overline{\phi }f_+) -\mu _\alpha \overline{\phi }f_+\ =\ \overline{\phi } (P_+af_+ -\mu _\alpha f_+) \\= & {} \overline{\phi } P_+((a -\mu _\alpha )f_+) \ =\ 0, \end{aligned}$$

as \((a -\mu _\alpha )f_+ \in H^-_2\). Hence, \(g\in {\mathcal {S}}_\alpha ^\perp \) by part (1).

Proof of (3): Since \((a-\mu _\alpha )\in H^-_\infty \), we have the canonical factorisation

$$\begin{aligned} a(z)-\mu _\alpha =B_\alpha (z) \Sigma _\alpha (z)G_\alpha (z). \end{aligned}$$

In \({\mathbb {C}}_-\), \(B_\alpha \Sigma _\alpha \) is an inner function and \(G_\alpha \) is an outer function. As \(G_\alpha \) is outer, by Beurling’s Theorem, the closure

$$\begin{aligned} \overline{(a-\mu _\alpha )H^-_2}= B_\alpha (z) \Sigma _\alpha (z)H^-_2. \end{aligned}$$

Thus, by part (2), \( {\mathcal {S}}^\perp _\alpha = \phi \left( H_2^-\ominus B_\alpha (z) \Sigma _\alpha (z)H^-_2\right) \). This gives (4.9), since \(\phi \ne 0\) a.e. \(\square \)

We conclude the paper by showing by an explicit construction that the defect number \({\mathrm {def\,}}( {\mathcal {S}}_\alpha )\) may take any positive integer value, as well as zero and infinity.

Example 4.8

We need to construct the parameters \(\phi ,\psi \) of our Friedrichs model appropriately. In a first step, we construct the symbol a. For fixed \(\alpha \in {\mathbb {C}}\setminus \{0\}\), we consider a canonical decomposition of \((a-\mu _\alpha )\) in \({\mathbb {C}}_-\) of the following form: Choose any \(B_a\) with zeroes in a finite box and the singular measure in \(\Sigma _a\) with bounded support. Then, \(B_a\Sigma _a \rightarrow 1\) at infinity. Choose

$$\begin{aligned} G_a(z)= -\mu _\alpha \frac{(z-a_1)(z+\sigma )}{z^2+\tau z+\rho }, \end{aligned}$$

where \(a_1\in {\mathbb {C}}_+,\sigma \in {\mathbb {C}}_-,\tau \in {\mathbb {C}}_-\) and real \(\rho<<-1\).

Being contractive in \({\mathbb {C}}_-\), the product \(B_a\Sigma _a\) behaves like \(e^{\frac{b}{z}}\) with \(b\in {\mathbb {C}}_+\) at \(\infty \). We can choose the constants above such that \(a_1-\sigma =b-\tau \in {\mathbb {C}}_+\). Therefore, \(a(z)=O(1/z^2)\) at \(\infty \). Defining \(\phi (z)=(z-i)^{-1}\in H_2^-\), we have \(\phi \sim 1/z\) at \(\infty \) , so \(\psi :=a/\overline{\phi }= O(1/z)\) belongs to \(L^2({\mathbb {R}})\).

Choosing \(\rho \) sufficiently negative, we get that both roots of \(z^2+\tau z+\rho \), approximately \(-\tau /2\pm \sqrt{-\rho }\), lie in \({\mathbb {C}}_+\). This gives \(G_a\in H^-_\infty \) and since both its roots \(a_1\) and \(-\sigma \) lie in \({\mathbb {C}}_+\), \(G_a\) is outer in \({\mathbb {C}}_-\). By Theorem 4.7, the number of roots of \(B_a\) in \({\mathbb {C}}_-\) equals \({\mathrm {def\,}} {\mathcal {S}}\) provided \(\Sigma _a\equiv 1\) and therefore all natural numbers and infinity are possible as indices by proper choice of the Blaschke factor \(B_a\).