Location of Eigenvalues of Non-self-adjoint Discrete Dirac Operators

Abstract

We provide quantitative estimates on the location of eigenvalues of one-dimensional discrete Dirac operators with complex $\ell ^p$-potentials for $1\le p \le \infty$. As a corollary, subsets of the essential spectrum free of embedded eigenvalues are determined for small $\ell ^1$-potential. Further possible improvements and sharpness of the obtained spectral bounds are also discussed.

Appendix: Illustrative and Comparison Plots

1.1 A: Plots of the Spectral Enclosures from Theorem 2

The spectral enclosure for the $\ell ^{1}$-potentials from Theorem 1 was displayed already in the introduction in Fig. 1. Similarly, we provide several plots illustrating the spectral enclosures from Theorem 2 in Fig. 2 below. Namely, the plots show the boundary curves given by the equation

$$\begin{aligned} g_p(\lambda ,m) \Vert V\Vert _p=1, \end{aligned}$$

for $m=1$, $\Vert V\Vert _p=\frac{j}{4}$, $j\in \{1,2,\dots ,7\}$, and four choices of $p\in \{3/2,2,3,5\}$.

Fig. 2

The plots of the expanding boundary curves corresponding to the spectral enclosure from Theorem 2 for $m=1$, $\Vert V\Vert _p=\frac{j}{4}$, $j\in \{1,2,\dots ,7\}$, and four choices of the parameter $p>1$

Fig. 3

Boundary curves for the spectral enclosures Theorem 1 (dashed blue lines) compared to the corresponding result of Theorem 3 (solid red/green lines) with $m=1/2$. Green color demonstrates the partial optimality in the sense of Theorem 5 (color figure online)

1.2 B: Comparison Plots for the $\ell ^{1}$-Bounds of Theorems 1 and 3 and Optimality

Next set of plots show the boundary curve of the spectral enclosure from Theorem 1 together with the corresponding improved result of Theorem 3 for a comparison. Moreover, the boundary curve of the improved spectral enclosure is made in two colors distinguishing the parts that are eigenvalues of some discrete Dirac operators as discussed in Theorem 5.

More concretely, in Fig. 3, we plot the boundary curve of Theorem 1 by blue dashed lines for $m=1/2$ and several choices of $\Vert V\Vert _{1}$. At the same time, we add a plot of the curve defined by the equation

$$\begin{aligned} \max \{|T_{0}(k)|,|T_{1}(k)|\}\Vert V\Vert _{1}=1, \end{aligned}$$

by red or green solid lines for the same choice of parameters. The parts of the curve made in green belong to the set $\mathcal {D}$ and hence these points are eigenvalues of some discrete Dirac operators with $\ell ^{1}$-potentials. The remaining parts are made in red.

1.3 C: Comparison Plots for the $\ell ^{p}$-Bounds from Theorems 2, 3, and Corollary 2

In the next plots, we compare the spectral enclosures given in Theorems 2 and 3 for $\ell ^{p}$-potentials with $p>1$. As an extra, we add also the spectral enclosure of Corollary 2 into these plots. In this numerical comparison, we exclude the result of Theorem 4 due to its complexity and non-reliability of the numerical computations. Note that it is clear from the proofs that Theorem 4 is an improvement of Theorem 2.

The comparison is made in plots in Fig. 4 where the boundary curve of the spectral enclosure from Theorem 2 is made in solid yellow lines, from Theorem 3 in red dashed lines, and from Corollary 2 in blue dotted lines for $m=1$, $\Vert V\Vert _{p}=0.7$, and four choices of the parameter $p\in \{3/2,2,3,5\}$.

It is by no means evident whether one of the spectral enclosures of Theorems 2 and 3 is better than the other. However, numerical experiments indicate that none is better than the other, i.e.  none is a subset of the other, in general.

Fig. 4

Boundary curves of spectral enclosures of Theorem 2 (solid yellow lines), Theorem 3 (red dashed lines), and Corollary 2 (blue dotted lines) for $m=1$, $\Vert V\Vert _{p}=0.7$, and four choices of the parameter $p>1$

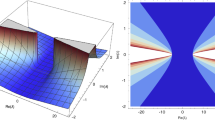
1.4 D: A Plot for Remark 6

Finally, as an illustration for Remark 6, Fig. 5 shows for what k’s within the unit disk the norm of the diagonal element $T_{0}(k)$ of the resolvent (2.1) is not dominant.

Fig. 5

The blue subregion of the unit disk indicates the set of k’s for which $|T_0(k)|<|T_1(k)|$ when $m=1/8$