Abstract
Cherednik’s type A quantum affine Knizhnik–Zamolodchikov (qKZ) equations form a consistent system of linear q-difference equations for \(V_n\)-valued meromorphic functions on a complex n-torus, with \(V_n\) a module over the \(\mathrm{GL}_n\)-type extended affine Hecke algebra \({\mathcal {H}}_n\). The family \(({\mathcal {H}}_n)_{n\ge 0}\) of extended affine Hecke algebras forms a tower of algebras, with the associated algebra morphisms \({\mathcal {H}}_n\rightarrow {\mathcal {H}}_{n+1}\), in the Hecke algebra descending of arc insertion at the affine braid group level. In this paper, we consider qKZ towers \((f^{(n)})_{n\ge 0}\) of solutions, which consist of twisted-symmetric polynomial solutions \(f^{(n)}\) (\(n\ge 0\)) of the qKZ equations that are compatible with the tower structure on \(({\mathcal {H}}_n)_{n\ge 0}\). The compatibility is encoded by the so-called braid recursion relations: \(f^{(n+1)}(z_1,\ldots ,z_{n},0)\) is required to coincide up to a quasi-constant factor with the push-forward of \(f^{(n)}(z_1,\ldots ,z_{n})\) by an intertwiner \(\mu _{n}{:}\,V_{n}\rightarrow V_{n+1}\) of \({\mathcal {H}}_{n}\)-modules, where \(V_{n+1}\) is considered as an \({\mathcal {H}}_{n}\)-module through the tower structure on \(({\mathcal {H}}_n)_{n\ge 0}\). We associate with the dense loop model on the half-infinite cylinder with nonzero loop weights, a qKZ tower \((f^{(n)})_{n\ge 0}\) of solutions. The solutions \(f^{(n)}\) are constructed from specialized dual non-symmetric Macdonald polynomials with specialized parameters using the Cherednik–Matsuo correspondence. In the special case that the extended affine Hecke algebra parameter is a third root of unity, \(f^{(n)}\) coincides with the (suitably normalized) ground state of the inhomogeneous dense O(1) loop model on the half-infinite cylinder with circumference n.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum Knizhnik–Zamolodchikov (qKZ) equations are consistent systems of linear q-difference equations that naturally arise in the context of representation theory of quantum affine algebras [14] and affine Hecke algebras [5]. They appear as consistency equations for form factors and correlation functions of various integrable models (see e.g., [19, 26] for the first examples). In this paper, we focus on Cherednik’s qKZ equations associated with the \(\mathrm{GL}_n\)-type extended affine Hecke algebra \({\mathcal {H}}_n\). This case relates to integrable one-dimensional lattice models with quasiperiodic boundary conditions, with the integrability governed by the extended affine Hecke algebra \({\mathcal {H}}_n\). Important examples, also in the context of the present paper, are the XXZ spin-\(\frac{1}{2}\) chain and the dense loop model.
The collection \(({\mathcal {H}}_n)_{n\ge 0}\) of extended affine Hecke algebras forms a tower of algebras with respect to algebra morphisms \({\mathcal {H}}_n\rightarrow {\mathcal {H}}_{n+1}\) that arise as descendants of arc insertion morphisms \({\mathcal {B}}_n\rightarrow {\mathcal {B}}_{n+1}\) for the groups \({\mathcal {B}}_n\) of affine n-braids, cf. [1, 3, 15]. In this paper, we study families \((f^{(n)})_{n\ge 0}\) of solutions \(f^{(n)}\) of qKZ equations taking values in \({\mathcal {H}}_n\)-modules \(V_n\) that are naturally compatible with the tower structure.
It leads us to introducing the notion of a tower \((f^{(n)})_{n\ge 0}\) of solutions of qKZ equations. The constituents \(f^{(n)}\) of the tower are polynomials in n complex variables \(z_1,\ldots ,z_n\), taking values in a finite-dimensional \({\mathcal {H}}_n\)-module \(V_n\). They are twisted-symmetric solutions of Cherednik’s qKZ equations interrelated by the so-called braid recursion relations, meaning that \(f^{(n+1)}(z_1,\ldots ,z_{n},0)\) coincides, up to a quasi-constant factor, with the push-forward of \(f^{(n)}(z_1,\ldots ,z_{n})\) by an \({\mathcal {H}}_n\)-intertwiner \(\mu _{n}{:}\,V_{n}\rightarrow V_{n+1}\), where \(V_{n+1}\) is regarded as an \({\mathcal {H}}_{n}\)-module through the tower structure of \(({\mathcal {H}}_n)_{n\ge 0}\). In the terminology of [3], the collection \(\{(V_n,\mu _n)\}_{n\ge 0}\) of \({\mathcal {H}}_n\)-modules \(V_n\) and \({\mathcal {H}}_n\)-intertwiners \(\mu _n{:}\,V_n\rightarrow V_{n+1}\) is a tower of extended affine Hecke algebra modules. From this perspective, towers of solutions of qKZ equations are naturally associated with towers of extended affine Hecke algebra modules. The braid recursion relations are then determined by the module tower up to the quasi-constant factors.
In [3], the first and third authors constructed a family of module towers, called link pattern towers, which depends on a twist parameter v. The link pattern tower actually descends to a tower of extended affine Temperley–Lieb algebra modules. The representations \(V_n\) are realized on spaces of link patterns on the punctured disk, which alternatively can be interpreted as the quantum state spaces for the dense \(O(\tau )\) loop models on the half-infinite cylinder (with n the circumference of the cylinder). The intertwiners \(\mu _n\) in the link pattern tower are constructed skein theoretically (for even n this goes back to [11]), and are in fact closely related to arc insertion morphisms in a relative version of the Roger and Yang [25] skein module in the presence of a pole (see [3, Rem. 8.11]). In this paper, we construct towers \((f^{(n)})_{n\ge 0}\) of solutions of qKZ equations relative to the link pattern tower with twist parameter one and describe the corresponding quasi-constant factors in the braid recursion relations explicitly. We consider two cases.
We show that the (suitably normalized) ground states \(f^{(n)}\) of the inhomogeneous dense O(1) loop model on the half-infinite cylinder with circumference n form a tower of solutions relative to the link pattern tower. In this case, the associated affine Hecke algebra parameter is a third root of unity. This generalizes results from [11], where the braid recursion relations relating \(f^{(2k+1)}(z_1,\ldots ,z_{2k},0)\) to \(f^{(2k)}(z_1,\ldots ,z_{2k})\) were derived under the implicit additional assumption that a unique normalized ground state for the inhomogeneous dense O(1) loop model exists when one of the rapidities is set equal to zero (the latter is not guaranteed, since the transfer operator is no longer stochastic when one of the rapidities is set equal to zero). In an upcoming paper [2], the full set of braid recursion relations for the ground states is used to derive explicit formulas for various observables of the dense O(1) loop model on the infinite cylinder.
We generalize this example by constructing a tower of solutions \((f^{(n)})_{n\ge 0}\) for twist parameter one and for all values of the affine Hecke algebra parameter for which the loop weights of the associated dense loop model are nonzero. In this case, the constituents \(f^{(n)}\) are constructed using the Cherednik–Matsuo correspondence [22, 27]. The Cherednik–Matsuo correspondence, relating solutions of qKZ equations to common eigenfunctions of Cherednik’s commuting Y-operators, can be applied in the present context since the link pattern modules are principal series modules, as we shall show in Theorem 6.6. It leads to the construction of the constituents \(f^{(n)}\) of the tower in terms of non-symmetric Macdonald polynomials. Subtle issues arise here since the two parameters of the associated double affine Hecke algebra satisfy an algebraic relation that breaks down the semisimplicity of the Y-operators. We resort to Kasatani’s [20] work to deal with these issues. See [21] for an alternative approach to construct polynomial twisted-symmetric solutions \(f^{(n)}\) of the qKZ equations using Kazhdan–Lusztig bases.
In both towers, the constituent \(f^{(n)}\) is a nonzero twisted-symmetric homogeneous polynomial solution of the qKZ equations of total degree \(\frac{1}{2}n(n-1)\). In fact, this property characterizes \(f^{(n)}\) up to a nonzero scalar multiple, a result that plays a crucial role in establishing the explicit braid recursion relations. In particular, it allows us to prove the braid recursion relations for the suitably normalized ground states of the inhomogeneous dense O(1) loop models without addressing the issue of the existence of a unique normalized ground state when the rapidities are outside the stochastic regime.
The content of the paper is as follows. In Sect. 2, we recall the definitions of extended affine Hecke algebras and qKZ equations and introduce the notion of a qKZ tower of solutions. In Sect. 3, we recall from [3] the definition of the link pattern tower. In Sect. 4, we determine necessary conditions for the existence of nonzero twisted-symmetric homogeneous polynomial solutions \(f^{(n)}\) of total degree \(\frac{1}{2}n(n-1)\) of the qKZ equations with values in the link pattern modules. We show that the existence implies that \((f^{(n)})_{n\ge 0}\) forms a tower of solutions relative to the link pattern tower, and we explicitly write down the corresponding braid recursion relations. The construction of the tower of solutions when the Hecke algebra parameter is a third root of unity is discussed in Sect. 5. The general case is discussed in Sect. 6. We derive a dual version of the braid recursion relations in Sect. 7. Lastly, in “Appendix A” we discuss uniqueness properties for various classes of twisted-symmetric solutions to qKZ equations, some of which were considered before in [8, 11, 21].
2 Towers of Solutions of qKZ Equations
In this section, we begin by recalling the extended affine Hecke algebra, the qKZ equations, and introduce what we call a qKZ tower of solutions. The extended affine Hecke algebra can be defined using two different presentations. We make use of both presentations as one is more convenient for defining qKZ equations, while the other is more suitable for relating the algebra to the extended affine Temperley–Lieb algebra.
2.1 Extended Affine Hecke Algebras
Let \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\).
Definition 2.1
Let \(n\ge 3\). The extended affine Hecke algebra \({\mathcal {H}}_n={\mathcal {H}}_n(t^{\frac{1}{2}})\) of type \({\widehat{A}}_{n-1}\) is the complex associative algebra with generators \(T_i\) (\(i\in {\mathbb {Z}}/n{\mathbb {Z}}\)) and \(\rho ,\rho ^{-1}\) and defining relations
where the indices are taken modulo n. For \(n=2\), the extended affine Hecke algebra \({\mathcal {H}}_2={\mathcal {H}}_2(t^{\frac{1}{2}})\) is the algebra generated by \(T_0,T_1,\rho ^{\pm 1}\) with defining relations (2.1) but with the third relation omitted. For \(n=1\), we set \({\mathcal {H}}_1:={\mathbb {C}}[\rho ,\rho ^{-1}]\) to be the algebra of Laurent polynomials in one variable \(\rho \), and for \(n=0\) we set \({\mathcal {H}}_0:={\mathbb {C}}[X]\), the polynomial algebra in the variable X.
Note that \(T_i\) is invertible with inverse \(T_i^{-1}=T_i -t^{-\frac{1}{2}} + t^{\frac{1}{2}}\). For \(n\ge 1\), the element \(\rho ^n\in {\mathcal {H}}_n\) is central.
For \(n\ge 2\), the affine Hecke algebra\({\mathcal {H}}_n^a={\mathcal {H}}_n^a(t^{\frac{1}{2}})\) of type \({\widehat{A}}_{n-1}\) is the subalgebra of \({\mathcal {H}}_n\) generated by \(T_i\) (\(i\in {\mathbb {Z}}/n{\mathbb {Z}}\)). For \(n\ge 3\), the first three relations of (2.1) are the defining relations of \({\mathcal {H}}_n^a\) in terms of these generators (for \(n=2\) the first two relations are the defining relations). Furthermore, \({\mathcal {H}}_n\) is isomorphic to the crossed product algebra \({\mathbb {Z}}\ltimes {\mathcal {H}}_n^a\), where \(m \in {\mathbb {Z}}\) acts on \({\mathcal {H}}^a_n\) by the algebra automorphism \(T_i\mapsto T_{i+m}\) (with the indices modulo n). Equivalently, \(m\in {\mathbb {Z}}\) acts by restricting the inner automorphism \(h\mapsto \rho ^mh\rho ^{-m}\) of \({\mathcal {H}}_n\) to \({\mathcal {H}}_n^a\). For \(n\ge 2\), the (finite) Hecke algebra of type \(A_{n-1}\) is the subalgebra \({\mathcal {H}}^0_n\) of \({\mathcal {H}}^a_n\) generated by \(T_1,\dots , T_{n-1}\). The defining relations of \({\mathcal {H}}_n^0\) in terms of the generators \(T_1,\ldots ,T_{n-1}\) are given again by the first three relations of (2.1), restricted to those indices that they make sense.
Bernstein and Zelevinsky [23] obtained the following alternative presentation of the extended affine Hecke algebra (see also [18] for a detailed discussion).
Theorem 2.2
Let \(n\ge 2\) and define \(Y_j\in {\mathcal {H}}_n\) for \(j=1,\ldots ,n\) by
Then, \({\mathcal {H}}_n\) is generated by \(T_1,\ldots ,T_{n-1},Y_1^{\pm 1},\ldots ,Y_n^{\pm 1}\). The defining relations of \({\mathcal {H}}_n\) in terms of these generators are given by
Note that \(\rho \in {\mathcal {H}}_n\) can be expressed as
with respect to the Bernstein–Zelevinsky presentation of \({\mathcal {H}}_n\). Let \({\mathcal {A}}_n\) be the commutative subalgebra of \({\mathcal {H}}_n\) generated by \(Y_1^{\pm 1},\ldots ,Y_n^{\pm 1}\).
More can be said about the structure of \({\mathcal {H}}_n\) in terms of the Bernstein–Zelevinsky presentation (see [18, 23]). Let \(f\in {\mathbb {C}}[{\mathbf {z}}^{\pm 1}]:={\mathbb {C}}[z_1^{\pm 1},\ldots ,z_n^{\pm 1}]\) be a Laurent polynomial in n variables \(z_1,\ldots ,z_n\). Let \(f=\sum _{\alpha \in {\mathbb {Z}}^n}c_\alpha {\mathbf {z}}^\alpha \) (\(c_\alpha \in {\mathbb {C}}\)) be its expansion in monomials \({\mathbf {z}}^\alpha :=z_1^{\alpha _1}\ldots z_n^{\alpha _n}\). Then, we write \(f(Y):=\sum _{\alpha \in {\mathbb {Z}}^n}c_\alpha Y^\alpha \in {\mathcal {A}}_n\), where \(Y^\alpha :=Y_1^{\alpha _1}\ldots Y_n^{\alpha _n}\). The map \(f\mapsto f(Y)\) defines an isomorphism \({\mathbb {C}}[{\mathbf {z}}^{\pm 1}]\overset{\sim }{\longrightarrow } {\mathcal {A}}_n\) of commutative algebras. In addition, the multiplication map
is a linear isomorphism.
In [3, §8], it was shown that there exists a unique unit-preserving algebra map \(\nu _n: {\mathcal {H}}_n\rightarrow {\mathcal {H}}_{n+1}\) satisfying for \(n\ge 2\),
satisfying \(\nu _1(\rho )=t^{-\frac{1}{4}}\rho T_1^{-1}\) for \(n=1\), and satisfying \(\nu _0(X)=t^{\frac{1}{4}}\rho +t^{-\frac{1}{4}}\rho ^{-1}\) for \(n=0\). The \(\nu _n\) was obtained in [3, §8] as the Hecke algebra descent of an algebra homomorphism \({\mathbb {C}}[{\mathcal {B}}_n]\rightarrow {\mathbb {C}}[{\mathcal {B}}_{n+1}]\), with \({\mathcal {B}}_n\) the extended affine braid group on n strands, defined topologically by inserting an extra braid going underneath all the other braids it meets. At the end of this section, we require the algebra maps \(\nu _n\) in constructing towers of \({\mathcal {H}}_n\)-modules and qKZ towers of solutions.
2.2 qKZ Equations
We consider Cherednik’s [5, 6] qKZ equations of type \(\mathrm{GL}_n\). We will follow closely [27], and we will restrict attention to twisted-symmetric solutions of qKZ equations. The notations \((m,k,\xi )\) in [27, §4.3] correspond to our \((n,-t^{\frac{1}{2}},\rho )\). The qKZ equations depend on an additional parameter q, which we for the moment take to be an arbitrary nonzero complex number.
Recall that for \(n\ge 1\) and \(t^{\frac{1}{2}}=1\), the extended affine Hecke algebra \({\mathcal {H}}_n(1)\) is isomorphic to the group algebra \({\mathbb {C}}[W_n]\) of the extended affine symmetric group \(W_n\simeq S_n\ltimes {\mathbb {Z}}^n\). Writing \(s_i\) (\(i\in {\mathbb {Z}}/n{\mathbb {Z}}\)) and \(\rho \) for the (Coxeter type) generators of \(W_n\), acting on \({\mathbb {C}}[{\mathbf {z}}^{\pm 1}]\) and \({\mathbb {C}}({\mathbf {z}}):={\mathbb {C}}(z_1,\ldots ,z_n)\) by
cf. Definition 2.1. Note that the \(W_n\)-action on \({\mathbb {C}}[{\mathbf {z}}^{\pm 1}]\) is by graded algebra automorphisms, with the grading defined by the total degree. In addition, \(W_n\) preserves the polynomial algebra \({\mathbb {C}}[{\mathbf {z}}]:={\mathbb {C}}[z_1,\ldots ,z_n]\).
Define for \(n\ge 1\) and \(i\in {\mathbb {Z}}/n{\mathbb {Z}}\),
which we view as rational \({\mathcal {H}}_n(t^{\frac{1}{2}})\)-valued function in x. The key point in the construction of qKZ equations is the fact that for any \({\mathcal {H}}_n(t^{\frac{1}{2}})\)-module \(V_n\) with representation map \(\sigma _n{:}\,{\mathcal {H}}_n(t^{\frac{1}{2}})\rightarrow \mathrm{End}(V_n)\) and for \(q\in {\mathbb {C}}^*\), the formulas
define a left \(W_n\)-action on the space \(V_n({\mathbf {z}}):={\mathbb {C}}({\mathbf {z}})\otimes V_n\) of \(V_n\)-valued rational functions in \(z_1,\ldots ,z_n\), where the \(W_n\)-action in the right-hand side is the action on the variables as given by (2.4). For \(n=0\), we simply take \(\nabla =\sigma _0\) acting on \(V_0\). The fact that (2.5) defines a \(W_n\)-action is a consequence of the following identities for the R-operators \({\widetilde{R}}_i(x)\),
with the indices taken modulo n. The first equation is the Yang–Baxter equation [13, Vol. 5] in braid form.
Note that in (2.4) and (2.5) the action of \(s_0\) is determined by the action of \(s_i\) (\(1\le i<n\)) and of \(\rho \), and hence does not have to be specified. We will often omit the explicit formula for the action of \(s_0\) in the remainder of the paper. Following [27], we call the subspace \(V_n({\mathbf {z}})^{\nabla (W_n)}\) of \(\nabla (W_n)\)-invariant elements in \(V_n({\mathbf {z}})\), the space of twisted-symmetric solutions of the qKZ equations on \(V_n\). We need a more refined class of qKZ solutions, defined as follows.
Definition 2.3
Let \(q\in {\mathbb {C}}^*\) and \(c\in {\mathbb {C}}\). Fix a \({\mathcal {H}}_n(t^{\frac{1}{2}})\)-module \(V_n\) with representation map \(\sigma _n{:}\,{\mathcal {H}}_n(t^{\frac{1}{2}}) \rightarrow {\text {End}}(V_n)\). For \(n\ge 2\) write \(\mathrm{Sol}_n(V_n;q,c)\subseteq V_n[{\mathbf {z}}]\) for the \(V_n\)-valued polynomials \(f\in V_n[{\mathbf {z}}]\) in the variables \(z_1,\ldots ,z_n\) satisfying
For \(n=1\), we write \(\mathrm{Sol}_1(V_1;q,c)\) for the \(V_1\)-valued polynomials \(f\in V_1[z]\) in the single variable z satisfying the q-difference equation \(\sigma _1(\rho )f(q^{-1}z)=c\,f(z)\). Finally, for \(n=0\) write \(\mathrm{Sol}_0(V_0;q,c)\subseteq V_0\) for the eigenspace of \(\sigma _0(X)\in \mathrm{End}(V_0)\) with eigenvalue c.
If \(n\ge 1\) and \(\mathrm{Sol}_n(V_n;q,c)\not =\{0\}\), then necessarily \(c\in {\mathbb {C}}^*\). In this case,
with \(V_n^{(c)}\) denoting the vector space \(V_n\) endowed with the twisted action \(\sigma _n^{c}: {\mathcal {H}}_n\rightarrow \mathrm{End}(V_n)\) defined by \(\sigma _n^{c}(T_i):=\sigma _n(T_i)\) for \(i\in {\mathbb {Z}}/n{\mathbb {Z}}\) and \(\sigma _n^{c}(\rho ):=c^{-1}\sigma _n(\rho )\). We call c a twist parameter.
For \(n\ge 2\), let \(\pi _{n}^{t^{\frac{1}{2}},q}: {\mathcal {H}}_n(t^{\frac{1}{2}}) \rightarrow {\text {End}}({\mathbb {C}}[{\mathbf {z}}^{\pm 1}])\) be Cherednik’s [7] basic representation, defined by
(see [27, Thm. 3.1] with \((m,k_i,\xi )\) replaced by \((n,-t^{\frac{1}{2}},\rho )\) and specializing to type A as in [27, §4.3]). For \(n=1\), we define the basic representation \(\pi _1^{t^{\frac{1}{2}},q}{:}\,{\mathcal {H}}_1(t^{\frac{1}{2}})\rightarrow \mathrm{End} \bigl ({\mathbb {C}}[{\mathbf {z}}^{\pm 1}]\bigr )\) by \(\pi _1^{t^{\frac{1}{2}},q}(\rho ):=\rho \). Note that \({\mathbb {C}}[{\mathbf {z}}]\) is a \(\pi _n^{t^{\frac{1}{2}},q}({\mathcal {H}}_n)\)-submodule of \({\mathbb {C}}[{\mathbf {z}}^{\pm 1}]\).
By [27, Prop. 3.10] (see also [24, §4.1] and [22]), we have for \(n\ge 1\) and \(c\in {\mathbb {C}}^*\) the following alternative description of \(\mathrm{Sol}_n(V_n;q,c)\):
where \(J{:}\,{\mathcal {H}}_n(t^{-\frac{1}{2}})\rightarrow {\mathcal {H}}_n(t^{\frac{1}{2}})\) is the unique anti-algebra isomorphism satisfying \(J(T_i):=T_i^{-1}\) (\(i\in {\mathbb {Z}}/n{\mathbb {Z}}\)) and \(J(\rho ):=\rho ^{-1}\). Here, the basic representation \(\pi _n^{t^{-\frac{1}{2}},q}\) acts on the first tensor component of \(V_n[{\mathbf {z}}]={\mathbb {C}}[{\mathbf {z}}]\otimes V_n\). More concretely,
where one needs to be well aware that the action on the variables through the basic representation is with respect to the extended affine Hecke algebra \({\mathcal {H}}_n(t^{-\frac{1}{2}})\) and the action on \(V_n\) through \(\sigma _n\) is with respect to the extended affine Hecke algebra \({\mathcal {H}}_n(t^{\frac{1}{2}})\).
Before we can conclude this section with the introduction of the notion of a qKZ tower of solutions we need to establish some notation. Let A be a complex associative algebra and write \({\mathcal {C}}_A\) for the category of left A-modules. Write \(\mathrm{Hom}_A(M,N)\) for the space of morphisms \(M\rightarrow N\) in \({\mathcal {C}}_A\), which we will call intertwiners. Suppose that \(\eta {:}\,A\rightarrow B\) is a (unit preserving) morphism of \({\mathbb {C}}\)-algebras, then we write \(\mathrm{Ind}^{\eta }{:}\,{\mathcal {C}}_A\rightarrow {\mathcal {C}}_B\) and \(\mathrm{Res}^{\eta }{:}\,{\mathcal {C}}_B\rightarrow {\mathcal {C}}_A\) for the corresponding induction and restriction functor. Concretely, if M is a left A-module, then
with B viewed as a right A-module by \(b\cdot a:=b\eta (a)\) for \(b\in B\) and \(a\in A\). If N is a left B-module, then \(\mathrm{Res}^{\eta }(N)\) is the complex vector space N, viewed as an A-module by \(a\cdot n:=\eta (a)n\) for \(a\in A\) and \(n\in N\).
For a left \({\mathcal {H}}_{n+1}\)-module \(V_{n+1}\), we use the shorthand notation \(V^{\nu _n}_{n+1}\) for the left \({\mathcal {H}}_n\)-module \(\mathrm{Res}^{\nu _n} (V_{n+1})\). The following lemma introduces the concept of the module lift of a qKZ solution.
Lemma 2.4
Let \(n\ge 0\). Let \(V_n\) be a left \({\mathcal {H}}_n(t^{\frac{1}{2}})\)-module and \(V_{n+1}\) a left \({\mathcal {H}}_{n+1}(t^{\frac{1}{2}})\)-module, with representation maps \(\sigma _n\) and \(\sigma _{n+1}\), respectively. Let \(\mu _n \in \mathrm{Hom}_{{\mathcal {H}}_n}(V_n,V^{\nu _n}_{n+1})\) be an intertwiner. Extend \(\mu _n\) to a \({\mathbb {C}}[\mathbf{z }]\)-linear map \(V_n[{\mathbf {z}}]\rightarrow V_{n+1}^{\nu _n}[{\mathbf {z}}]\), which we still denote by \(\mu _n\). Then, its restriction to \(\mathrm{Sol}_n(V_n;q,c_n)\) is a linear map
Proof
This is immediate from the intertwining property
Indeed, if \(f\in \mathrm{Sol}_n(V;q,c_n)\), then it follows for \(n\ge 1\) from (2.9) that
for \(1\le i<n\) and
hence \(\mu _n(f)\in \mathrm{Sol}_n(V_{n+1}^{\nu _n};q,c_n)\). For \(n=0\) and \(f\in \mathrm{Sol}_0(V_0;q,c_0)\), i.e., \(f\in V_0\) satisfying \(\sigma _0(X)f=c_0f\), we have
hence \(\mu _0(f)\in \mathrm{Sol}_0(V_1^{\nu _0};q,c_0)\). \(\square \)
By the intertwiner \(\mu _n\) a qKZ solution \(f^{(n)}({\mathbf {z}}) \in \mathrm{Sol}_n(V_n;q,c_n) \) gets lifted to a solution in \(\mathrm{Sol}_n(V^{\nu _n}_{n+1} ;q,c_n)\), taking values in the \({\mathcal {H}}_{n+1}\)-module \(V_{n+1}\). Along with this upward module lift, there is also a downward descent of a solution, which reduces the number of variables. It is defined as follows.
Recall the algebra map \(\nu _{n}{:}\,{\mathcal {H}}_{n} \rightarrow {\mathcal {H}}_{n+1}\) defined by (2.3).
Lemma 2.5
Let \(n\ge 0\) and let \(V_{n+1}\) be a left \({\mathcal {H}}_{n+1}(t^{\frac{1}{2}})\)-module with associated representation map \(\sigma _{n+1}\). Then, for \(n\ge 1\) and \(f \in \mathrm{Sol}_{n+1}(V_{n+1};q,c_{n+1})\),
and for \(n=0\) and \(f\in \mathrm{Sol}_1(V_1;q,c_1)\),
Proof
Let \(n\ge 1\) and \(f \in \mathrm{Sol}_{n+1}(V_{n+1};q,c_{n+1})\). Set \(g(z_1,\ldots ,z_n):=f(z_1,\ldots ,z_n,0)\). For \(1\le i<n\), we have
Hence, to prove that \(g\in \mathrm{Sol}_n(V_{n+1}^{\nu _n};q,-t^{-\frac{3}{4}}c_{n+1})\) it remains to show that
To prove (2.10), first note that
Setting \(z_{n+1}=0\) and using that \({\widetilde{R}}_n(\infty ):=\lim _{x\rightarrow \infty }{\widetilde{R}}_n(x)= -t^{\frac{1}{2}}T_n^{-1}\), we get
Then, (2.10) follows from the fact that \(\nu _n(\rho )=t^{-\frac{1}{4}}\rho T_n^{-1}\).
For \(n=0\) and \(f\in \mathrm{Sol}_1(V_1;q,c_1)\), we have
hence \(f(0)\in \mathrm{Sol}_0(V_1^{\nu _0};q,t^{\frac{1}{4}}c_1+t^{-\frac{1}{4}}c_1^{-1})\). \(\square \)
By lifting solutions of qKZ equations by intertwiners \(\mu _n\) and descending solutions of qKZ equations by setting variables equal to zero, we can connect qKZ solutions of different ranks. This leads to the definition of a qKZ tower of solutions. The starting point is the following definition of a tower of extended affine Hecke algebra modules (compare with [3], where this notion was introduced for modules over extended affine Temperley–Lieb algebras, see also Sect. 3).
Definition 2.6
A tower
of extended affine Hecke algebra modules is a sequence \(\{(V_n,\mu _n)\}_{n\in {\mathbb {Z}}_{\ge 0}}\) with \(V_n\) a left \({\mathcal {H}}_n\)-module and \(\mu _n\in \mathrm{Hom}_{{\mathcal {H}}_n}\bigl (V_n,V_{n+1}^{\nu _n}\bigr )\).
To lift this notion of a tower to solutions of qKZ equations, it is convenient to disregard quasiperiodic (with respect to the action of \(\rho \)) symmetric normalization factors h, i.e., polynomials \(h\in {\mathbb {C}}[{\mathbf {z}}]^{S_n}\) satisfying \(\rho h=\lambda h\) for some \(\lambda \in {\mathbb {C}}^*\). We call such h a \(\lambda \)-recursion factor, and \(\lambda \) the scale parameter. We write \({\mathcal {T}}_{n,\lambda }\subset {\mathbb {C}}[{\mathbf {z}}]\) for the space of \(\lambda \)-recursion factors. Note that \(hf\in \mathrm{Sol}_n(V_n;q,\lambda c_n)\) if \(f\in \mathrm{Sol}_n(V_n;q,c_n)\) and \(h\in {\mathcal {T}}_{n,\lambda }\). By convention, we define the space \({\mathcal {T}}_{0,\lambda }\) of \(\lambda \)-recursion factors for \(n=0\) to be \({\mathbb {C}}\) if \(\lambda =1\) and \(\{0\}\) otherwise.
If q is a root of unity, then we write \(e\in {\mathbb {Z}}_{>0}\) for the smallest natural number such that \(q^e=1\). We take \(e=\infty \) if q is not a root of unity.
Lemma 2.7
Let \(n\ge 1\). Then, \({\mathcal {T}}_{n,\lambda }=\{0\}\) unless \(\lambda =q^{-m}\) for some \(0\le m<e\). If \(0\le m<e\), then
The latter formula should be read as \({\mathcal {T}}_{n,q^{-m}}=\mathrm{span}_{{\mathbb {C}}}\{(z_1\ldots z_n)^m\}\) if \(e=\infty \).
Proof
Let \(\alpha \in {\mathbb {Z}}_{\ge 0}^n\). It suffices to show that \(\sum _{\beta \in S_n\alpha }{\mathbf {z}}^\beta \in {\mathbb {C}}[{\mathbf {z}}]^{S_n}\) is a \(\lambda \)-recursion factor if and only if there exists a \(0\le m<e\) such that \(\lambda =q^{-m}\) and \(\alpha _i\equiv m\) mod e for all i (where the latter condition for \(e=\infty \) is read as \(\alpha _i=m\) for all i).
Note that
hence \(\sum _{\beta \in S_n\alpha }z^\beta \in {\mathcal {T}}_{n,\lambda }\) if and only if \(\lambda =q^{-\alpha _i}\) for all \(i=1,\ldots ,n\). This is equivalent to \(\lambda =q^{-m}\) and \(\alpha _i\equiv m\) mod e for some \(0\le m<e\). \(\square \)
The following lemma shows that by rescaling a nonzero symmetric polynomial solution of the qKZ equations by an appropriate recursion factor, it will remain nonzero if one of its variables is set to zero.
Lemma 2.8
Let \(n\ge 1\) and let \(V_n\) be a left \({\mathcal {H}}_n\)-module with representation map \(\sigma _n\). If \(0\not =f\in \mathrm{Sol}_n(V_n;q,c_n)\), then there exists a unique \(m\in {\mathbb {Z}}_{\ge 0}\) and \(g\in \mathrm{Sol}_n(V_n;q,q^mc_n)\) such that \(f({\mathbf {z}})=(z_1\ldots z_n)^mg({\mathbf {z}})\) and \(g(z_1,\ldots ,z_{n-1},0)\not \equiv 0\).
Proof
Recall that the existence of a nonzero \(f\in \mathrm{Sol}_n(V_n;q,c_n)\) guarantees that \(c_n\not =0\). Suppose that \(f(z_1,\ldots ,z_{n-1},0)\equiv 0\). Using \(\sigma _n(\rho )f(z_2,\ldots ,z_n,q^{-1}z_1)= c_nf({\mathbf {z}})\) repeatedly, we conclude that \(f(\dots ,z_{i-1},0,z_{i+1},\dots )\equiv 0\). Hence, \(f({\mathbf {z}})\) is divisible by the \(q^{-1}\)-recursion factor \(z_1\dots z_n\) in \(V_n[{\mathbf {z}}]\). Now divide this factor out and apply induction to the total degree of f. \(\square \)
Definition 2.9
(qKZ tower). Let \(\{(V_n,\mu _n)\}_{n\in {\mathbb {Z}}_{\ge 0}}\)be a tower of extended affine Hecke algebra modules. We call \((f^{(n)})_{n\ge 0}\) an associated qKZ tower of solutions with twisting parameters \(c_n\in {\mathbb {C}}^*\) (\(n\ge 1\)) if there exist recursion factors \(h^{(n)}\in {\mathcal {T}}_{n,\lambda _n}\) (\(n\ge 0\)) such that
- (a) :
-
\(0\not =f^{(n)}\in \mathrm{Sol}_n(V_n;q,c_n)\) for \(n\ge 0\), with \(c_0:= t^{\frac{1}{4}}c_1+t^{-\frac{1}{4}}c_1^{-1}\).
- (b) :
-
\(f^{(n+1)}(z_1,\ldots ,z_n,0)\not \equiv 0\) for all \(n\ge 0\).
- (c) :
-
For all \(n\ge 0\), we have
$$\begin{aligned} f^{(n+1)}(z_1,\ldots ,z_n,0)=h^{(n)}(z_1,\dots ,z_n)\mu _n(f^{(n)}(z_1,\ldots ,z_n)). \end{aligned}$$(2.11)We call (2.11) the braid recursion relations for the qKZ tower \((f^{(n)})_{n\ge 0}\) of solutions.
Note that by Lemmas 2.4 and 2.5, we necessarily must have the compatibility condition
between the twist and scale parameters in a qKZ tower of solutions (note that for \(n=0\) we have \(t^{\frac{1}{4}}c_1+t^{-\frac{1}{4}}c_1^{-1}=c_0\) by definition).
3 Extended Affine Temperley–Lieb Algebra
The qKZ towers we construct are built using modules of the extended affine Temperley–Lieb algebra, which is a quotient of \({\mathcal {H}}_n\). In this section, we recall the definition of the extended affine Temperley–Lieb algebra and discuss the relevant tower of extended affine Temperley–Lieb algebra modules, following [3].
The extended affine Temperley–Lieb algebras arise as the endomorphism algebras of the skein category of the annulus, see [3] and references therein. We first give the definition of the extended affine Temperley–Lieb algebra in terms of generators and relations and then discuss its relation to \({\mathcal {H}}_n\) and the qKZ equations. For more details on the theory discussed in this section, see [3] and references within.
Definition 3.1
Let \(n\ge 3\). The extended affine Temperley–Lieb algebra\(\mathcal {TL}_n=\mathcal {TL}_n(t^{\frac{1}{2}})\) is the complex associative algebra with generators \(e_i\) (\(i\in {\mathbb {Z}}/n{\mathbb {Z}}\)) and \(\rho ,\rho ^{-1}\), and defining relations
where the indices are taken modulo n. For \(n=2\), the extended affine Temperley–Lieb algebra \(\mathcal {TL}_2=\mathcal {TL}_2(t^{\frac{1}{2}})\) is the algebra generated by \(e_0,e_1,\rho ^{\pm 1}\) with the defining relations (3.1) but with the third relation omitted. For \(n=1\), we set \(\mathcal {TL}_1={\mathcal {H}}_1={\mathbb {C}}[\rho ,\rho ^{-1}]\), and for \(n=0\) we set \(\mathcal {TL}_0={\mathcal {H}}_0={\mathbb {C}}[X]\).
The affine Temperley–Lieb algebra is the subalgebra \(\mathcal {TL}^a_n\) of \(\mathcal {TL}_n\) generated by \(e_i\) (\(i\in {\mathbb {Z}}/n{\mathbb {Z}}\)). The first three relations in (3.1) are the defining relations in terms of these generators (the first relation is the defining relation when \(n=2\)). The (finite) Temperley–Lieb algebra is the subalgebra \(\mathcal {TL}^0_n\) of \(\mathcal {TL}^a_n\) generated by \(e_1,\dots ,e_{n-1}\). The first three relations in (3.1) for the relevant indices are then the defining relations. Note that the dependence on the parameter \(t^{\frac{1}{2}}\) of \(\mathcal {TL}_n\) is actually a dependence on \(t^{\frac{1}{2}}+t^{-\frac{1}{2}}\).
It is well known that for \(n\ge 2\) the assignments
for \(i\in {\mathbb {Z}}/n{\mathbb {Z}}\) extend to a surjective algebra homomorphism \(\psi _n{:}\,{\mathcal {H}}_n(t^{\frac{1}{2}})\twoheadrightarrow \mathcal {TL}_n(t^{\frac{1}{2}})\) see e.g., [3, Prop. 7.2] and references therein. For \(n=1\) and \(n=0\), we take \(\psi _n{:}\,{\mathcal {H}}_n\rightarrow \mathcal {TL}_n\) to be the identity map.
Via the map \(\psi _n\), the R-operators \(R_i(x):=\psi _n({\widetilde{R}}_i(x))\) (\(i\in {\mathbb {Z}}/n{\mathbb {Z}}\)) on the extended affine Temperley–Lieb level are
as rational \(\mathcal {TL}_n\)-valued function in x, with \(a(x)=a(x;t^{\frac{1}{2}})\) and \(b(x)=b(x;t^{\frac{1}{2}})\) given by
Note that the \(R_i(x)\) (\(i\in {\mathbb {Z}}/n{\mathbb {Z}}\)) satisfy the Yang–Baxter-type equations (2.6) in \(\mathcal {TL}_n\). The weights a(x) and b(x) will play an important role in the next section, where they appear as the Boltzmann weights of the dense loop model.
We can now define the following analog of the qKZ solution space \(\mathrm{Sol}_n(V_n;q,c)\) (Definition 2.3) for left \(\mathcal {TL}_n\)-modules \(V_n\). For \(n\ge 2\), it is the space of \(V_n\)-valued polynomials \(f\in V_n[{\mathbf {z}}]\) in the variables \(z_1,\ldots ,z_n\) satisfying
where \(\sigma _n\) is the representation map of the \(\mathcal {TL}_n\)-module \(V_n\). For \(n=1\), it is the space of \(V_1\)-valued polynomials f in the single variable z satisfying \(\sigma _1(\rho )f(q^{-1}z)=cf(z)\). For \(n=0\), it is the eigenspace of \(\sigma _0(X)\) with eigenvalue c. By a slight abuse of notation, we will denote this space of solutions again by \(\mathrm{Sol}_n(V_n;q,c)\). No confusion can arise, since \(\mathrm{Sol}_n(V_n;q,c)\) for the left \(\mathcal {TL}_n\)-module \(V_n\) coincide with \(\mathrm{Sol}_n({\widetilde{V}}_n;q,c)\), where \({\widetilde{V}}_n\) is the \({\mathcal {H}}_n\)-module obtained by endowing \(V_n\) with the lifted \({\mathcal {H}}_n\)-module structure with representation map \(\sigma _n\circ \psi _n\).
From [3, Prop. 6.3], we have an algebra homomorphism \({\mathcal {I}}_n{:}\,\mathcal {TL}_n(t^{\frac{1}{2}})\rightarrow \mathcal {TL}_{n+1}(t^{\frac{1}{2}})\) for \(n\ge 0\) defined by \({\mathcal {I}}_0(X)=t^{\frac{1}{4}}\rho +t^{-\frac{1}{4}}\rho ^{-1}\) and
for \(n\ge 1\). In particular, \({\mathcal {I}}_n(\rho ^{-1})=(t^{\frac{1}{4}}e_n+t^{-\frac{1}{4}})\rho ^{-1}\). Note that we have a commutative diagram

Following [3, Def. 7.1], we say that \(\{(V_n,\mu _n)\}_{n\in {\mathbb {Z}}_{\ge 0}}\) is a tower of extended affine Temperley–Lieb modules if \(V_n\) is a left \(\mathcal {TL}_n\)-module and \(\mu _n\in \mathrm{Hom}_{\mathcal {TL}_n}\bigl (V_n,V_{n+1}^{{\mathcal {I}}_n}\bigr )\) for all \(n\ge 0\). We sometimes write the tower as
Note that (3.5) implies that an intertwiner \(\mu _n\in \mathrm{Hom}_{\mathcal {TL}_n}(V_n,V_{n+1}^{{\mathcal {I}}_n})\) is also an intertwiner \({\widetilde{V}}_n\rightarrow {\widetilde{V}}_{n+1}^{\nu _n}\) of the associated \({\mathcal {H}}_n\)-modules. Hence, the tower \(\{(V_n,\mu _n)\}_{n\ge 0}\) of extended affine Temperley–Lieb algebra modules gives rise to the tower \(\{({\widetilde{V}}_n,\mu _n)\}_{n\ge 0}\) of extend affine Hecke algebra modules. Conversely, if \(\{({\widetilde{V}}_n,\mu _n)\}_{n\ge 0}\) is a tower of extended affine Hecke algebra modules and the representation maps \({\widetilde{\sigma }}_n{:}\,{\mathcal {H}}_n\rightarrow \mathrm{End}(V_n)\) factorize through \(\psi _n\), then the tower descends to a tower of extended affine Temperley–Lieb algebra modules. We will freely use these lifts and descents of towers in the sequel of the paper.
The tower of extended affine Temperley–Lieb modules relevant for the dense loop model is constructed from the skein category \({\mathcal {S}}={\mathcal {S}}(t^{\frac{1}{4}})\) of the annulus, defined in [3]. We shortly recall here the basic features of the category \({\mathcal {S}}\). For further details, we refer to [3, §3].
The category \({\mathcal {S}}\) is the complex linear category with objects \({\mathbb {Z}}_{\ge 0}\) and with the space of morphisms \(\mathrm{Hom}_{{\mathcal {S}}}(m,n)\) being the linear span of planar isotopy classes of (m, n)-tangle diagrams on the annulus \(A:=\{z\in {\mathbb {C}} \,\, | \,\, 1\le |z|\le 2\}\), with m and n marked ordered points on the inner and outer boundary, respectively, modulo the Kauffman skein relation

and the (null-homotopic) loop removal relation

We consider here planar isotopies that fix the boundary of A pointwise. The ordered marked points on the boundary are \(\xi _m^{i-1}\) (\(1\le i\le m\)) and \(\xi _n^{j-1}\) (\(1\le j\le n\)) with \(\xi _\ell :=e^{2\pi \mathrm {i}/\ell }\). In these equations, the disk shows the local neighborhood in the annulus where the diagrams differ. Let L be an (l, m)-tangle diagram and \(L'\) an (m, n)-tangle diagram. The composition \([L'] \circ [L]\) of the corresponding equivalence classes in \({\mathcal {S}}\) is \([L'\circ L]\), with \(L'\circ L\) the (l, n)-tangle diagram obtained by placing L inside \(L'\) such that the outer boundary points of L match with the inner boundary points of \(L'\). For example,

By [17, Prop. 2.3.7] and [3, Thm. 5.3], we have an isomorphism \(\theta _n{:}\,\mathcal {TL}_n(t^{\frac{1}{2}})\overset{\sim }{\longrightarrow } \mathrm{End}_{{\mathcal {S}}(t^{\frac{1}{4}})}(n)\) of algebras for \(n\ge 0\), with the algebra isomorphism \(\theta _n\) for \(n\ge 1\) determined by

and for \(n=0\) by

Moreover, in [3, Def. 6.1] an arc insertion functor \({\mathcal {I}}{:}\,{\mathcal {S}}\rightarrow {\mathcal {S}}\) is defined using a natural monoidal structure on \({\mathcal {S}}\). It maps n to \(n+1\) and, on morphisms, it inserts on the level of link diagrams a new arc connecting the inner and outer boundary while going underneath all arcs it meets (the particular winding of the new arc is subtle, see [3, §6] for the details). The resulting algebra homomorphisms \({\mathcal {I}}|_{\mathrm{End}_{{\mathcal {S}}}(n)}{:}\,\mathrm{End}_{{\mathcal {S}}}(n)\rightarrow \mathrm{End}_{{\mathcal {S}}}(n+1)\) coincides with the algebra homomorphism \({\mathcal {I}}_n\) by the identification of \(\mathrm{End}_{{\mathcal {S}}}(n)\) with \(\mathcal {TL}_n(t^{\frac{1}{2}})\) through the isomorphism \(\theta _n\), see [3, Prop. 8.3].
Let \(v\in {\mathbb {C}}^*\) and set \(u:=t^{\frac{1}{4}}v+t^{-\frac{1}{4}}v^{-1}\). The one-parameter family of link pattern towers
of extended affine Temperley–Lieb algebra modules is now defined as follows (see [3, §10]). For \(n=2k\), the \(\mathcal {TL}_{2k}\)-module \(V_{2k}(u)\) is defined as
where \(\mathrm{Hom}_{{\mathcal {S}}}(0,2k)\) is endowed with its canonical \((\mathcal {TL}_{2k},\mathcal {TL}_0)\)-bimodule structure and \({\mathbb {C}}_0^{(u)}\) denotes the one-dimensional representation of \(\mathcal {TL}_0={\mathbb {C}}[X]\) defined by \(X\mapsto u\). For \(n=2k-1\), the \(\mathcal {TL}_{2k-1}\)-module \(V_{2k-1}(v)\) is defined as
with \({\mathbb {C}}_1^{(v)}\) denoting the one-dimensional representations of \(\mathcal {TL}_1={\mathbb {C}}[\rho ^{\pm 1}]\) defined by \(\rho \mapsto v\). For \(Y\in \mathrm{Hom}_{{\mathcal {S}}}(0,2k)\), we write \(Y_u:=Y\otimes _{\mathcal {TL}_0}1\) for the corresponding element in \(V_{2k}(u)\). Similarly, for \(Z\in \mathrm{Hom}_{{\mathcal {S}}}(1,2k-1)\) we write \(Z_v:=Z\otimes _{\mathcal {TL}_1}1\) for the corresponding element in \(V_{2k-1}(v)\). We sometimes omit the dependence of the representations \(V_{2k}(u)\) and \(V_{2k-1}(v)\) on \(u=t^{\frac{1}{4}}v+t^{-\frac{1}{4}}v^{-1}\) and v, if it is clear from context.
The intertwiners \(\phi _n\) (\(n\ge 0\)) are defined as follows. Consider the skein element

Then,
for a (0, 2k)-link diagram L and a \((1,2k-1)\)-link diagram \(L^\prime \).
Example 3.2

The rather peculiar form of the intertwiners \(\phi _{2k-1}\) can be explained in terms of a Roger and Yang [25]-type graded algebra structure on the total space \(V_0(u)\oplus V_1(v)\oplus V_2(u)\oplus \cdots \) of the link pattern tower, see [3, Rem. 8.11].
Let \({\mathbb {D}}=\{z\in {\mathbb {C}} \,\, | \,\, |z|\le 2\}\) and \({\mathbb {D}}^*:={\mathbb {D}}{\setminus } \{0\}\). A punctured link pattern of size 2k is a perfect matching of the 2k equally spaced marked points \(2\xi _{2k}^{i-1}\) (\(1\le i\le 2k\)) on the boundary of \({\mathbb {D}}^*\) by k non-intersecting arcs lying within \({\mathbb {D}}^*\). A punctured link pattern of size \(2k-1\) is a perfect matching of the 2k marked points \(2\xi _{2k-1}^{j-1}\) (\(1\le j<2k\)) and 0 by k non-intersecting arcs lying within \({\mathbb {D}}\). Only the endpoints of the arcs are allowed to lie on \(\{0\}\cup \partial {\mathbb {D}}\). Two link patterns are regarded the same if they are planar isotopic by a planar isotopy fixing 0 and the boundary \(\partial {\mathbb {D}}\) of \({\mathbb {D}}\) pointwise. The arc connecting 0 to the outer boundary of \({\mathbb {D}}\) is called the defect line. An arc that connects two points on the boundary are sometimes referred to as an arch, and an arch that connects two consecutive points that does not contain the puncture is called a little arch. We denote the set of punctured link patterns of size n by \({\mathcal {L}}_{n}\). As an example, the following punctured link patterns

constitute \({\mathcal {L}}_3\).
For twist parameter \(v=1\), we can naturally identify the nth representation space \(V_n\) in the link pattern tower with \({\mathbb {C}}[{\mathcal {L}}_n]\) as a vector space by shrinking the hole \(\{z\in {\mathbb {C}} \,\, | \,\, |z|\le 1\}\) of the annulus to 0. The resulting action of \(\mathcal {TL}_n\) on \({\mathbb {C}}[{\mathcal {L}}_n]\) can be explicitly described skein theoretically, see [3, §8].
4 qKZ Equations on the Space of Link Patterns
In this section, we fix \(v=1\). We discuss the qKZ equations associated with the \(\mathcal {TL}_n\)-modules \(V_n\simeq {\mathbb {C}}[{\mathcal {L}}_n]\) (\(n\ge 0\)) from the link pattern tower, and we derive necessary conditions for the existence of qKZ towers of solutions. The existence of qKZ towers of solutions will be the subject of later sections.
Let \(L_{\cap }=L_\cap ^{(n)} \in {\mathcal {L}}_n\) denote the link patterns

for \(n=2k\) and \(2k-1\), respectively. We call \(L_\cap \in {\mathcal {L}}_n\) the fully nested diagram. For \(g^{(n)}({\mathbf {z}})=\sum _{L\in {\mathcal {L}}_n}g_L^{(n)}({\mathbf {z}})L\in V_n({\mathbf {z}})\), we call \(g_{L_\cap }^{(n)}({\mathbf {z}})\) the fully nested component of \(g^{(n)}({\mathbf {z}})\).
The fully nested component plays an important role in the analysis of polynomial twisted-symmetric solutions \(g^{(n)}({\mathbf {z}})\in V_n^{(c)}({\mathbf {z}})^{\nabla (W_n)}\) of the qKZ equations. In [11, §2.2] and [21, §3.5.2], it was remarked that such solutions are uniquely determined by their fully nested component, and an explicit expression for the fully nested component was determined in case the solution is polynomial of total degree \(\frac{1}{2}n(n-1)\) (existence of such a solution is a subtle issue). We recall these results here extend them to qKZ solutions taking values in \(V_{n+1}^{{\mathcal {I}}_n}\) and show how these results combined lead to explicit braid recursion relations.
Lemma 4.1
Let \(n\ge 1\), \(q,c\in {\mathbb {C}}^*\) and let
with coefficients \(g_L^{(n)}({\mathbf {z}})\in {\mathbb {C}}({\mathbf {z}})\) (\(L\in {\mathcal {L}}_n\)). Then, \(g^{(n)}({\mathbf {z}})\in V_n^{(c)}({\mathbf {z}})^{\nabla (W_n)}\) if and only if for all \(L\in {\mathcal {L}}_n\) and \(1\le i<n\),
where \(e_iL^\prime \sim L\) means that L is obtained from \(e_iL^\prime \) by removing the loops in \(e_iL^\prime \) (there is in fact at most one loop). The coefficient \(\gamma _{L^\prime ,L}^{(i)}\) is
Proof
This follows directly by rewriting the qKZ equations
component-wise. \(\square \)
For the following lemmas concerning the uniqueness of solutions, we need to impose that the loop weights \(-(t^{\frac{1}{2}}+t^{-\frac{1}{2}})\) and \(t^{\frac{1}{4}}+t^{-\frac{1}{4}}\) are both nonzero.
Lemma 4.2
Let \(n\ge 1\), \(q,c\in {\mathbb {C}}^*\) and \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\) with \((t^{\frac{1}{2}}+1)(t+1)\not =0\). Let
(a) If \(g_{L_\cap }^{(n)}({\mathbf {z}})=0\), then \(g^{(n)}({\mathbf {z}})=0\).
(b) If \(g_{L_\cap }^{(n)}({\mathbf {z}})\in {\mathbb {C}}[{\mathbf {z}}]\) is a homogeneous polynomial of total degree m, then so is \(g_L^{(n)}({\mathbf {z}})\) for all \(L\in {\mathcal {L}}_n\).
Proof
In “Appendix A,” we show by induction that, given \(g_{L_\cap }({\mathbf {z}})\), the recursion relations (4.1) determine the other coefficients \(g_L^{(n)}({\mathbf {z}})\) (\(L\in {\mathcal {L}}_n\)) uniquely. For this, the first equation in (4.1) is used in the following way: for \(L^\prime \in {\mathcal {L}}_n\) and \(1\le i<n\) such that \(L^\prime \) does not have a little arch between i and \(i+1\), denote by \(L\in {\mathcal {L}}_n\) the link pattern such that \(e_iL^\prime \sim L\), then \(g_{L^\prime }^{(n)}({\mathbf {z}})\) can be computed from other base components by the formula
since \(\gamma _{L^\prime ,L}^{(i)}\not =0\). By substituting the explicit expressions of the weights a(x) and b(x), this can be rewritten as
from which it is clear that \(g_{L^\prime }^{(n)}({\mathbf {z}})\) will be a homogeneous polynomial of total degree m if \(g_L^{(n)}({\mathbf {z}})\) and \(g_{L^{\prime \prime }}^{(n)}({\mathbf {z}})\) are homogeneous polynomials of total degree m. \(\square \)
A similar result holds true for the restricted modules \(V_{n+1}^{{\mathcal {I}}_n}\):
Lemma 4.3
Let \(n\ge 1\), \(q,c\in {\mathbb {C}}^*\) and \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\) such that \((t^{\frac{1}{2}}+1)(t+1)\not =0\). Let
(a) If \(g_{L_\cap }^{(n)}({\mathbf {z}})=0\) with \(L_\cap =L_\cap ^{(n+1)}\in {\mathcal {L}}_{n+1}\) the fully nested diagram, then \(g^{(n)}({\mathbf {z}})=0\).
(b) If \(g_{L_\cap }^{(n)}({\mathbf {z}})\in {\mathbb {C}}[{\mathbf {z}}]\) is a homogeneous polynomial of total degree m, then so is \(g_L^{(n)}({\mathbf {z}})\) for all \(L\in {\mathcal {L}}_{n+1}\).
Proof
The proof is similar to the proof of the previous lemma, but the check that the recursion relations coming from the qKZ equations for the representation \(V_{n+1}^{{\mathcal {I}}_n,(c)}\) determine all components in terms of the fully nested component \(g_{L_\cap ^{(n+1)}}^{(n)}({\mathbf {z}})\) is more subtle. The details are given in “Appendix A.” \(\square \)
Corollary 4.4
Let \(n\ge 1\) and
Then,
with \(C_n({\mathbf {z}})\in {\mathbb {C}}({\mathbf {z}})^{S_n}\). If in addition \(g_{L_\cap }^{(n)}({\mathbf {z}})\) is a homogeneous polynomial of total degree m and \((t^{\frac{1}{2}}+1)(t+1)\not =0\), then \(m\ge \frac{1}{2}n(n-1)\) and \(C_n({\mathbf {z}})\) is a homogeneous symmetric polynomial of total degree \(m-\frac{1}{2}n(n-1)\).
Proof
Note that \(L_\cap \) does not have a little arch connecting i and \(i+1\) for \(1\le i<n\). By the recursion relation (4.1), it follows that
for \(1\le i<n\). The first result now follows immediately.
For the second statement, suppose that \(g_{L_\cap }^{(n)}({\mathbf {z}})\) is a homogeneous polynomial of total degree m. Then, (4.2) and \(t^2\not =1\) imply that \(g_{L_\cap }^{(n)}({\mathbf {z}})\) is divisible by \(t^{\frac{1}{2}}z_{2}-t^{-\frac{1}{2}}z_1\) in \({\mathbb {C}}[{\mathbf {z}}]\) and the resulting quotient is invariant under interchanging \(z_1\) and \(z_{2}\). One now proves by induction on r that \(g_{L_\cap }^{(n)}({\mathbf {z}})\) is divisible by \(\prod _{1\le i<j\le r}(t^{\frac{1}{2}}z_j-t^{-\frac{1}{2}}z_i)\) in \({\mathbb {C}}[{\mathbf {z}}]\) and the resulting quotient is symmetric in \(z_1,\ldots ,z_r\). The second statement then follows by taking \(r=n\). \(\square \)
It follows from the previous result that if the loop weights are nonzero and if there exists a nonzero \(g^{(n)}\in \mathrm{Sol}_n(V_n;q,c_n)\) with coefficients being homogeneous of total degree \(\frac{1}{2}n(n-1)\), then it is unique up to a nonzero scalar multiple and
for some \(\kappa \in {\mathbb {C}}^*\).
The following lemma is important in the analysis of qKZ towers of solutions relative to the link pattern tower \(\{(V_n,\phi _n)\}_{n\ge 0}\).
Lemma 4.5
For \(L\in {\mathcal {L}}_n\), consider the expansion
of \(\phi _n(L)\) in terms of the linear basis \({\mathcal {L}}_n\) of \(V_n\). Then, \(c_{L,L_\cap ^{(n+1)}}=t^{-\frac{1}{4}\lfloor n/2\rfloor }\delta _{L,L_\cap ^{(n)}}\).
Proof
For \(n=2k\), consider a link pattern \(L\in {\mathcal {L}}_{2k}\) that has a little arch connecting \(i,i+1\) for some \(i\in \{1,\ldots ,2k-1\}\). All the link patterns in the image \(\phi _{2k}(L)\) also contain the same little arch since the inserted defect line at the skein module level does not cross it (possibly after an appropriate number of applications of Reidemeister II moves). The only link pattern that does not contain a little arch connecting \(i,i+1\) for any \(1\le i <2k\) is \(L_\cap \). By the mapping \(\phi _{2k}\), we have at the skein module level

and note that the image has k under-crossings. Resolving all the crossings using the Kauffman skein relations gives a linear combination of link patterns. The contribution to link pattern \(L_\cap \in {\mathcal {L}}_{2k+1}\) comes from taking the smoothing  for each crossing
for each crossing  . Each of these contributions gives a factor \(t^{-\frac{1}{4}}\), which establishes the result for n even.
. Each of these contributions gives a factor \(t^{-\frac{1}{4}}\), which establishes the result for n even.
For the case \(n=2k-1\) odd the first step of the argument is similar. The only link pattern that does not contain a little arch connecting \(i,i+1\) for any \(1\le i <2k-1\) is \(L_\cap \). By the mapping \(\phi _{2k-1}\), we have at the skein module level

and note that each term in the image has \(k-1\) under-crossings. Resolving all the crossings using Kauffman’s skein relations gives a linear combination of link patterns. The contributions to the link pattern \(L_\cap \in {\mathcal {L}}_{2k}\) come from taking the smoothing  for each crossing
for each crossing  in the first term. Each of these contributions gives a factor \(t^{-\frac{1}{4}}\), which establishes the result for n odd.
in the first term. Each of these contributions gives a factor \(t^{-\frac{1}{4}}\), which establishes the result for n odd.
\(\square \)
The next lemma provides necessary conditions on the parameters \(q,c_n\) for the existence of a qKZ tower of solutions of minimal degree relative to the link pattern tower.
Lemma 4.6
Let \(v=1\) and \(q,c_n, t^{\frac{1}{4}}\in {\mathbb {C}}^*\)\((n\ge 1)\) with \((t^{\frac{1}{2}}+1)(t+1)\not =0\). Suppose that for each \(n\ge 1\) there exists a \(g^{(n)}\in \mathrm{Sol}_n(V_n;q,c_n)\) with
Write \(g^{(0)}:=1\in V_0\).
Then, the following two statements are equivalent:
- (a) :
-
\(\bigl (g^{(n)}\bigr )_{n\ge 0}\) is a qKZ tower of solutions relative to the link pattern tower \(\{(V_n,\phi _n)\}_{n\ge 0}\).
- (b) :
-
\(q=t^{\frac{3}{2}}\), \(c_n=\bigl (-t^{-\frac{3}{4}}\bigr )^{n-1}\) (\(n\ge 1\)) and \(c_0=t^{\frac{1}{4}}+t^{-\frac{1}{4}}\).
If these equivalent conditions are satisfied, then \(\lambda _n:=q^{-1}\)\((n\ge 1)\), \(\lambda _0=1\),
and \(h^{(0)}=1\). In other words, the corresponding braid recursion relations are then given by
Proof
Note that for \(n\ge 1\),
since \(\rho ^n\) acts as the identity on \(V_n\) and \(g^{(n)}\) is homogeneous of total degree \(\frac{1}{2}n(n-1)\). Hence, \((c_n)^n=q^{-\frac{1}{2}n(n-1)}\) (\(n\ge 1\)). Furthermore, \(c_1=1\) since \(g^{(1)}\) is constant.
By the rank descent lemma, we have
while the representation lift lemma gives \(\phi _n(g^{(n)}(z_1,\ldots ,z_n))\in \mathrm{Sol}_n\bigl (V_{n+1}^{{\mathcal {I}}_n};q,c_n)\). The fully nested component of \(g^{(n+1)}(z_1,\ldots ,z_n,0)\) is
Using Lemma 4.5, the fully nested component of \(\phi _n(g^{(n)}(z_1,\ldots ,z_n))\) is
(a)\(\Rightarrow \)(b): assume that \((g^{(n)})_{n\ge 0}\) is a qKZ tower of solutions. Then, the above analysis of the fully nested components implies that \(\lambda _n=q^{-1}\) and
for \(n\ge 1\), while \(\lambda _0=1\), \(h^{(0)}=1\) for \(n=0\). Hence, the corresponding braid recursion takes on the explicit form (4.3). Note that \(c_0=t^{\frac{1}{4}}+t^{-\frac{1}{4}}\) since \(g^{(0)}=1\). For \(n\ge 1\), the left-hand side of (4.3) lies in \(\mathrm{Sol}_n(V_{n+1}^{{\mathcal {I}}_n};q,-t^{-\frac{3}{4}}c_{n+1})\), while the right-hand side lies in \(\mathrm{Sol}_n(V_{n+1}^{{\mathcal {I}}_n};q,q^{-1}c_n)\); hence, the twist parameters \(c_n\) must satisfy \(c_{n+1}=-q^{-1}t^{\frac{3}{4}}c_n\) (\(n\ge 1\)). Since \(c_1=1\), we conclude that
Combined with (4.4), we obtain for \(n\ge 1\),
which is satisfied if and only if \(q=t^{\frac{3}{2}}\). It follows that \(c_n=(-t^{-\frac{3}{4}})^{n-1}\) for \(n\ge 1\), as desired.
(b)\(\Rightarrow \)(a) in view of Lemmas 4.2 and 4.3 we only have to show that under the parameter conditions as stated in (b), the fully nested components of the left- and right-hand side of (4.3) match. This can be confirmed by a direct computation. \(\square \)
We can now state the main theorem of the paper.
Theorem 4.7
Let \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\) with \((t^{\frac{1}{2}}+1)(t+1)\not =0\) and set \(v=1\), \(q=t^{\frac{3}{2}}\). There exists, for all \(n\ge 1\), a unique solution \(g^{(n)}({\mathbf {z}})\in \mathrm{Sol}_n\bigl (V_n;t^{\frac{3}{2}}, (-t^{-\frac{3}{4}})^{n-1}\bigr )\) homogeneous of total degree \(\frac{1}{2}n(n-1)\), such that
Then, \((g^{(n)})_{n\ge 0}\), with \(g^{(0)}:=1\in \mathrm{Sol}_0(V_0;t^{\frac{3}{2}},t^{\frac{1}{4}}+t^{-\frac{1}{4}})\), is a qKZ tower of solutions, with the associated braid recursion relations given by (4.3).
The proof of the theorem will be given in Sect. 6. The key step is the construction of \(g^{(n)}({\mathbf {z}})\) for generic \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\) in terms of specialized non-symmetric dual Macdonald polynomials using the Cherednik–Matsuo correspondence [27] and using results of Kasatani [20]. The generic conditions on \(t^{\frac{1}{4}}\) can then be removed by noting that the constructed solution \(g^{(n)}({\mathbf {z}})\) is well defined over \({\mathbb {C}}(t^{\frac{1}{4}})\) and the fact that the coefficients \(g_L^{(n)}({\mathbf {z}})\) for \(L\in {\mathcal {L}}_n\) are regular at the values \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\) for which \((t^{\frac{1}{2}}+1)(t+1)\not =0\). Indeed, \(g_{L_\cap }^{(n)}({\mathbf {z}})\) is clearly regular at \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\). By the recursion relations expressing \(g_L^{(n)}({\mathbf {z}})\) in terms of \(g_{L_\cap }^{(n)}({\mathbf {z}})\) (see the proof of Lemma 4.2 and “Appendix A”), it then follows inductively that all coefficients \(g_L^{(n)}({\mathbf {z}})\) (\(L\in {\mathcal {L}}_n\)) are regular at the values \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\) for which \((t^{\frac{1}{2}}+1)(t+1)\not =0\).
Remark 4.8
Note that for \(t^{\frac{1}{4}}=\exp (\pi \mathrm {i}/3)\), we have \(t^{\frac{3}{2}}=1\) and \(-t^{\frac{1}{2}}-t^{-\frac{1}{2}}=1=t^{\frac{1}{4}}+t^{-\frac{1}{4}}\). The resulting qKZ tower of solutions \((g^{(n)})_{n\ge 0}\) from Theorem 4.7 is closely related to the inhomogeneous dense O(1) loop model on the half-infinite cylinder, see Sect. 5 and [11]. In fact, the constituents \(g^{(n)}\in \mathrm{Sol}_n\bigl (V_n;1,1\bigr )\) then are the renormalized ground states of the inhomogeneous O(1) dense loop models on the half-infinite cylinder. In this case, the braid recursion relations reduce to
5 Existence of Solution for \(t^{\frac{1}{4}}= \exp (\pi \mathrm {i} /3)\)
In this section, we recall the construction of the polynomial solutions \(g^{(n)}({\mathbf {z}}) \in \mathrm{Sol}_n(V_n(1);1,1)\) of degree \(\frac{1}{2}n(n-1)\) for \(v=1\) and \(t^{\frac{1}{4}}=\exp (\pi \mathrm {i}/3)\) (see Theorem 4.7). In this special case, the construction of the qKZ tower of solutions is facilitated by the fact that the underlying integrable model, the inhomogeneous dense O(1) loop model on the half-infinite cylinder, is stochastic. This allows one to construct \(g^{(n)}({\mathbf {z}})\) as a suitably renormalized version of the ground state of the inhomogeneous dense O(1) loop model, following [11].
The section begins with discussing the Temperley–Lieb transfer operator, and then we specialize the analysis to the inhomogeneous dense O(1) loop model on the half-infinite cylinder. In this section \(v=1\).
5.1 Transfer Operator
The transfer operator \({\widehat{T}}^{(n)} :={\widehat{T}}(x; z_1,\dots ,z_n){:}\,{\mathbb {C}}[{\mathcal {L}}_n] \rightarrow {\mathbb {C}}[{\mathcal {L}}_n] \) can be defined as follows [9, 11]. For \(n>0\) consider the following two tiles

which we denote by \(\tau ^{\text{ n }w}\) and \(\tau ^{\text{ n }e}\), respectively, where ‘nw’ and ‘ne’ indicate that the north edge of the tile is connected to the west or east edge by an arc. Then, \({\widehat{T}}^{(n)}(x;{\mathbf {z}})={\widehat{T}}^{(n)}(x;z_1,\ldots ,z_n)\) is defined by

where \(\tau _i \in \{\tau ^{\text{ n }w}, \tau ^{\text{ n }e}\}\),
Note that the inner boundary of the annulus is always taken as the north edge of the tile. Moreover, for the case \(n=1\), tiling the annulus is done by stretching the tile so that the east and west edges are identified. The string of tiles covering the annulus can immediately be interpreted as an element in \({\mathcal {S}}_n(t^{\frac{1}{4}})\). Hence, by the algebra isomorphism \(\theta _n{:}\,\mathcal {TL}_n(t^{\frac{1}{2}})\overset{\sim }{\longrightarrow } \mathrm{End}_{{\mathcal {S}}(t^{\frac{1}{4}})}(n)\) we have \({\widehat{T}}^{(n)}(x;{\mathbf {z}}) \in {\mathbb {C}}(x,{\mathbf {z}}) \otimes \mathcal {TL}_n(t^{\frac{1}{2}}).\)
The case \(n=0\) is special. We define \({\widehat{T}}^{(0)} := \theta _0(X)\) (recall that \(\mathcal {TL}_0={\mathbb {C}}[X]\)). We also point out that since \(\mathcal {TL}_1={\mathbb {C}}[\rho ,\rho ^{-1}]\) we have
We will drop the isomorphism \(\theta _n\) when it is clear from context. Using diagrams, we write the R-operator as

and also as

where we view the crossing in the annulus as a weighted sum of the two diagrams given in (5.1). Using the diagram description of the R-operator, the Yang–Baxter equations and inversion relation [lines 1 and 3 of (2.6)] can be depicted as

respectively. The area within the dotted lines is a local neighborhood in the annulus.
The transfer operator can now be defined in terms of the R-operators \(R_i(x)\) for \( i \in {\mathbb {Z}}/n{\mathbb {Z}}\) as follows. Let
be the monodromy operator where we view the auxiliary point as \(n+1\equiv 0\) (modulo \(n+1\)). Then,
where \(\mathrm{cl}_0\) corresponds to the tangle closure [16] at the auxiliary point 0. In this specific case, \(\mathrm{cl}_0\) amounts to disconnecting the two arcs from the inner- and outer boundary points labeled ‘0’ and connecting them in \(\mathrm{End}_{{\mathcal {S}}}(n)\) by an arc that under-crosses all arcs one meets.
The transfer operators with different values of x commute in \(\mathcal {TL}_n\),
This can be shown by interlacing two T operators with R-operators. In the literature, it is usually shown diagrammatically using the inversion relation and Yang–Baxter equation (5.2) of the R-operators. For an example of this technique, we refer the reader to [9] for dense loop models and [4] in general. Using the Yang–Baxter equation and the relations involving \(\rho \) [see (3.1)], one shows that
In [11], the authors made the crucial observation that the R-operators \(R_i(0), R_i(\infty )\in \mathcal {TL}_n\) can be interpreted as a single crossing in the skein description of the element,

Consequently,

Noting this over-crossing and recalling the algebra map \({\mathcal {I}}_{n-1}{:}\,\mathcal {TL}_{n-1} \rightarrow \mathcal {TL}_n\) arising from the arc insertion functor, we obtain the following braid recursion relation for the transfer operator, which is due to [11, §2.4]:
Proposition 5.1
For \(n\ge 1\),
5.2 The Inhomogeneous Dense O(1) Loop Model
The transfer operator \({\widehat{T}}^{(n)}(x;{\mathbf {z}})\in \mathcal {TL}_n\) acting on the link pattern tower representation \(V_n\) in the special case \(v=1\) is by definition the transfer operator \(T^{(n)}(x;{\mathbf {z}})\in \mathrm{End}(V_n)\) of the inhomogeneous dense \(\mathrm{O}(-t^{\frac{1}{2}}-t^{-\frac{1}{2}})\) loop model on the punctured disk [11, 21]. We specialize in this section further to the case \(t^{\frac{1}{4}}=\exp (\pi \mathrm {i}/3)\), in which case
This means that all loops can be removed by a factor 1. As we shall discuss in a moment, the resulting \(\mathrm{O}(1)\)-model is not only Bethe integrable but also stochastic. We identify \(V_n\) with \({\mathbb {C}}[{\mathcal {L}}_n]\) as vector spaces (see the end of Sect. 3).
In [11], the authors stated the existence and uniqueness of a suitably normalized ground state of the inhomogeneous dense \(\mathrm{O}(1)\) loop model, with \({\mathbf {z}}\) regarded as formal variables. For the convenience of the reader, we provide a full proof of this result. It uses the irreducibility and stochasticity of the transfer operator \({\widehat{T}}^{(n)}(x;{\mathbf {z}})\) for a particular parameter regime, and it uses the algebraic dependence of \({\widehat{T}}^{(n)}(x;{\mathbf {z}})\) on x and \({\mathbf {z}}\).
Consider the matrix \(A^{(n)}(x;{\mathbf {z}}):=(A_{LL'} (x;{\mathbf {z}}))_{L,L' \in {\mathcal {L}}_n}\) of \(T^{(n)}(x;{\mathbf {z}})\) with respect to the link pattern basis,
The coefficients \(A_{LL^\prime }(x;{\mathbf {z}})\) depend rationally on \(x,z_1,\ldots ,z_n\). For the special value \(t^{\frac{1}{4}}=\exp (\pi \mathrm {i}/3)\) the Boltzmann weights a(x) and b(x) [see (3.3)] satisfy
hence \(\sum _{L\in {\mathcal {L}}_n}A_{LL^\prime }(x;{\mathbf {z}})=1\) for all \(L^\prime \in {\mathcal {L}}_n\). Furthermore, \(0<a(x)<1\) if \(x=e^{\mathrm {i}\theta }\) with \(0<\theta <2\pi /3\), hence \(A^{(n)}(x;{\mathbf {z}})\) is left-stochastic if \(x/z_j=e^{\mathrm {i}\theta _j}\) with \(0<\theta _j<2\pi /3\) for \(j=1,\ldots ,n\). In this situation, \(A^{(n)}(x;{\mathbf {z}})\) is irreducible; this follows from the fact that each \(L\in {\mathcal {L}}_n\) is a cyclic vector for the \(\mathcal {TL}_n\)-module \(V_n\), which can be proven as follows.
For \(n=2k\) even, let \(L_{ln}\in {\mathcal {L}}_{2k}\) be the least-nested link pattern, which is the link pattern that has little arches connecting boundary points \((2i-1,2i)\) for \(1\le i \le k\) such that the little arches do not contain the puncture. All \(L\in {\mathcal {L}}_n\) can be mapped to \(L_{ln}\) by acting with \(e_{1} e_{3} \ldots e_{2k-1}\). In turn, \(L_{ln}\) can be mapped to the fully nested link pattern \(L_\cap \) by the action of \(\rho ^{k}g_kg_{k-1}\ldots g_2\) with \(g_i:=e_{i}e_{i+2}\ldots e_{2k-i}\). Lastly, by the inductive argument in “Appendix A,” \(L_\cap \) can be mapped to any \(L\in {\mathcal {L}}_n\). The case for n odd is analogous.
Lemma 5.2
Let \(v=1\), \(q=1\) and \(t^{\frac{1}{4}}=\exp (\pi \mathrm {i}/3)\). There exists a unique \({\widehat{g}}^{(n)}({\mathbf {z}})=\sum _{L\in {\mathcal {L}}_n}{\widehat{g}}^{(n)}_L({\mathbf {z}})L\) with \({\widehat{g}}_L^{(n)}({\mathbf {z}})\in {\mathbb {C}}({\mathbf {z}})\) such that
for all \(x\in {\mathbb {C}}\) and such that \(\sum _{L\in {\mathcal {L}}_n}{\widehat{g}}^{(n)}_L({\mathbf {z}})=1\). Furthermore,
Proof
Consider \(A^{(n)}({\mathbf {z}}):=A^{(n)}(1;{\mathbf {z}})\). Since the matrix coefficients \(A_{LL^\prime }({\mathbf {z}}):=A_{LL^\prime }(1;{\mathbf {z}})\) satisfy \(\sum _{L\in {\mathcal {L}}_n}A_{LL^\prime }({\mathbf {z}})=1\), we have \(\mathrm{det}\bigl (A^{(n)}({\mathbf {z}})-1\bigr )=0\) and hence there exists a nonzero vector \(\kappa ({\mathbf {z}})=\bigl (\kappa _L({\mathbf {z}})\bigr )_{L\in {\mathcal {L}}_n}\) with \(\kappa _L({\mathbf {z}})\in {\mathbb {C}}({\mathbf {z}})\) such that \(A^{(n)}({\mathbf {z}})\kappa ({\mathbf {z}})=\kappa ({\mathbf {z}})\). Consider
Note that \(A^{(n)}({\mathbf {z}})\) is irreducible left-stochastic if \(z_j=e^{-\mathrm {i}\theta _j}\) with \(0<\theta _j<2\pi /3\); hence, for generic specialized values of the rapidities in this stochastic parameter regime, \(A^{(n)}({\mathbf {z}})\) has a one-dimensional eigenspace with eigenvalue 1, spanned by the Frobenius–Perron eigenvector \(v^{\mathrm{FP}}({\mathbf {z}})\), and the Frobenius–Perron eigenvector \(v^{\mathrm{FP}}({\mathbf {z}})\) (normalized such that the sum of the coefficients is one) has the property that all its coefficients are \(>0\). Hence, for generic values of the rapidities in the stochastic parameter regime, \(N({\mathbf {z}})\not =0\). In particular, \(N({\mathbf {z}})\in {\mathbb {C}}({\mathbf {z}}){\setminus }\{0\}\), and we may set \({\widehat{g}}^{(n)}({\mathbf {z}}):=\sum _{L\in {\mathcal {L}}_n}g_L^{(n)}({\mathbf {z}})L\) with \({\widehat{g}}^{(n)}_L({\mathbf {z}}):=\kappa _L({\mathbf {z}})/N({\mathbf {z}})\in {\mathbb {C}}({\mathbf {z}})\). Then,
and \(\sum _{L\in {\mathcal {L}}_n}{\widehat{g}}_L^{(n)}({\mathbf {z}})=1\). It follows from restricting to the stochastic parameter regime again that these two properties determine \({\widehat{g}}^{(n)}({\mathbf {z}})\) uniquely.
Let \(x\in {\mathbb {C}}\) and set
Write
with \({\widehat{g}}_L^{(n)}(x;{\mathbf {z}})\in {\mathbb {C}}({\mathbf {z}})\). Since \([T^{(n)}(1;{\mathbf {z}}), T^{(n)}(x;{\mathbf {z}})]=0\), we have
Since \(\sum _{L\in {\mathcal {L}}_n}A_{LL^\prime }(x;{\mathbf {z}})=1\) for all \(L^\prime \in {\mathcal {L}}_n\), we furthermore have \(\sum _{L\in {\mathcal {L}}_n}{\widehat{g}}_L^{(n)}(x;{\mathbf {z}})=1\). Hence, \({\widehat{g}}^{(n)}(x;{\mathbf {z}})={\widehat{g}}^{(n)}({\mathbf {z}})\), i.e.,
This completes the proof of the uniqueness and existence of \({\widehat{g}}_n({\mathbf {z}})\).
For the second statement, let \(1\le i<n\) and set \(h_i({\mathbf {z}}):=R_i(z_{i+1}/z_i){\widehat{g}}^{(n)}(s_i{\mathbf {z}})\). Then, by the first formula of (5.3),
and the sum of the coefficients of \(h_i({\mathbf {z}})\) is one since \(a(x)+b(x)=1\). Hence, \(h_i({\mathbf {z}})={\widehat{g}}^{(n)}({\mathbf {z}})\), i.e.,
In the same way, one shows that \(\rho {\widehat{g}}^{(n)}(z_2,\ldots ,z_n,z_1)={\widehat{g}}^{(n)}({\mathbf {z}})\), now using the second equality of (5.3). This completes the proof of the lemma. \(\square \)
Now, we are ready to prove Theorem 4.7 in the special case that \(t^{\frac{1}{4}}= \exp (\pi i/3)\). By Corollary 4.4, the fully nested component is of the form
with \(0\not =C_n({\mathbf {z}})\in {\mathbb {C}}(z)^{S_n}\). Since in the present situation \(q=1\) and \(C_n({\mathbf {z}})\) is symmetric, we have that the renormalized function
is also a symmetric solution of the qKZ equations, \(g^{(n)}({\mathbf {z}})\in \bigl ({\mathbb {C}}({\mathbf {z}})\otimes V_n\bigr )^{\nabla (W_n)}\). Now, \(g^{(n)}({\mathbf {z}})\) has fully nested component
By Lemma 4.2, we conclude that \(g^{(n)}({\mathbf {z}})\in \mathrm{Sol}_n(V_n;1,1)\) is a homogeneous polynomial solution of total degree \(\frac{1}{2}n(n-1)\), which completes the proof of Theorem 4.7 in the special case that \(t^{\frac{1}{4}}=\exp (\pi i/3)\).
Remark 5.3
From Proposition 5.1, it follows immediately that
when \(t^{\frac{1}{4}}=\exp (\pi i/3)\). In [11], the authors use this equation to prove the braid recursion relation for \(v=1\), \(1=q\)\(t^{\frac{1}{4}}=\exp (\pi i/3)\) and n even (see Remark 4.8). However, they implicitly assume that \(g^{(n+1)}({\mathbf {z}},0)\) is uniquely characterized as ground state of \({\widehat{T}}^{(n+1)}(1;{\mathbf {z}},0)\), which is though not clear since there is no stochastic parameter regime when one of the rapidities is set equal to zero. We have circumvented this problem here by using the characterization of \(g^{(n)}({\mathbf {z}})\) as a twisted-symmetric solution of qKZ equations.
6 Existence of Solutions for Generic \(t^{\frac{1}{4}}\)
In this section, we construct for generic \(t^{\frac{1}{4}}\) (i.e., for values \(t^{\frac{1}{4}}\) in a nonempty Zariski open subset of \({\mathbb {C}}\)) nontrivial polynomial twisted-symmetric solutions to the qKZ equations for link pattern modules, leading to the proof of Theorem 4.7 for generic \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\). As we remarked in the paragraph following Theorem 4.7, the generic condition on \(t^{\frac{1}{4}}\) can subsequently be weakened to the condition that the loop weights are nonzero.
A major difference between the generic case and the case that \(t^{\frac{1}{4}}=\exp (\pi \mathrm {i} /3)\) is that we do not have the argument of a stochastic matrix to construct \(g^{(n)}\) using the Frobenius–Perron theorem. We instead use the Cherednik–Matsuo correspondence [27]. This is different from the approach in [21], where Kazhdan–Lusztig bases are used.
In order to be able to apply the Cherednik–Matsuo correspondence, we first need to identify the link pattern representations \(V_n\) with principal series representations. This is done in the first subsection, for general twist parameter v. In the subsequent subsection, we recall the Cherednik–Matsuo correspondence and rephrase it in terms of dual Y-operators. In the last subsection, we prove Theorem 4.7 by constructing the polynomial solution of the qKZ equation from dual non-symmetric Macdonald polynomials with specialized parameters.
For fixed \(v \in {\mathbb {C}}^*\), the link patterns \({\mathcal {L}}_n\) form a (non-canonical) basis of \(V_n\). We can naturally identify \(V_n\) with \({\mathbb {C}}[{\mathcal {L}}_n]\) as a vector space by shrinking the hole \(\{ z \in {\mathbb {C}}\; |\; |z| \le 1\}\) of the annulus to 0. A choice needs to be made for the winding of the defect line, unless \(v=1\).
6.1 \(V_n\) as a Principal Series Module
In this section, we take \(n\ge 2\), and we fix \(v\in {\mathbb {C}}^*\). We recall first the definition of the principal series representation \(M^I(\gamma )\) of the affine Hecke algebra \({\mathcal {H}}_n={\mathcal {H}}_n(t^{\frac{1}{2}})\).
Let \(\epsilon _i\) (\(1 \le i \le n\)) denote the standard basis of \({\mathbb {R}}^n\). Set \(R_0:= \{ \epsilon _i-\epsilon _{j} | 1\le i\ne j \le n\}\), the root system of type \(A_{n-1}\). We take \(R_0^{+}:= \{ \epsilon _i-\epsilon _{j} | 1\le i<j\le n \}\) the set of positive roots. The corresponding simple roots are \(\alpha _i:= \epsilon _i - \epsilon _{i+1} \) (\(1 \le i <n\)). We write \(s_\alpha \) (\(\alpha \in R_0\)) for the reflection in \(\alpha \). Then, the simple reflections \(s_i:=s_{\alpha _i}\) (\(1 \le i<n\)) correspond to the simple neighboring transpositions \(i\leftrightarrow i+1\). For \(\alpha =\epsilon _i-\epsilon _j\in R_0\) we write \({\mathbf {z}}^\alpha =z_i/z_j\) and \(Y^\alpha =Y_i/Y_j\) in \({\mathbb {C}}[{\mathbf {z}}^{\pm 1}]\) and \({\mathcal {H}}_n\), respectively.
For \(I \subseteq \{ 1, \dots , n-1 \}\), we write
For \(\gamma \in T^I\), let \(\chi _{\gamma }^I:={\mathcal {H}}_I(t^{\frac{1}{2}})\rightarrow {\mathbb {C}}\) be the one-dimensional representation of the parabolic subalgebra \({\mathcal {H}}_I={\mathcal {H}}_I(t^{\frac{1}{2}}):= {\mathbb {C}}\langle Y^{\pm 1}_j, T_i | i \in I, j=1\dots ,n \rangle \) of \({\mathcal {H}}_n(t^{\frac{1}{2}})\) satisfying \(\chi _\gamma ^I(Y_j)=\gamma _j\) (\(1\le j\le n\)) and \(\chi _\gamma ^I(T_i)=t^{-\frac{1}{2}}\) (\(i\in I\)). It is well defined since \(\gamma \in T^I\). The corresponding principal series module \(M^I(\gamma )\) with central character \(\gamma \) is
Comparing with the notations from [27, §4.3]: \((k,m,\zeta ,H(k))\) correspond to our \((-t^{\frac{1}{2}},n,\rho ,{\mathcal {H}}_n(t^{\frac{1}{2}}))\). The principal series module \(M^I(\gamma )\) then corresponds to the principal series module \(M^{-t^{\frac{1}{2}},-,I}(\gamma )\) from [27, Lem. 2.5].
Let \(S_{n,I}=\langle s_i\,\, | \,\, i\in I\rangle \subseteq S_n\) be the standard parabolic subgroup generated by the simple neighboring transpositions \(s_i\) (\(i\in I\)), and \(S_n^I\) the minimal coset representatives of \(S_n/S_{n,I}\). For \(w\in S_n\), let \(T_w\in {\mathcal {H}}_n^0\) be the element \(T_w=T_{i_1}T_{i_2}\ldots T_{i_r}\) if \(w=s_{i_1}s_{i_2}\ldots s_{i_r}\) is a reduced expression. This is well defined since the \(T_i\)’s satisfy the braid relations. A linear basis of \(M^I(\gamma )\) is given by \(\{v_w^I(\gamma ):=T_w\otimes _{{\mathcal {H}}_I}1_{\chi _\gamma ^I}\}_{w\in S_n^I}\).
For a finite-dimensional left \({\mathcal {H}}_n\)-module V and \(\xi \in ({\mathbb {C}}^*)^n\), we define the subspace of vectors of weight \(\xi \) by
The module V is said to be calibrated if \(V=\bigoplus _{\xi }V_\xi \).
For \(1 \le i < n\) set
The following theorem is well known, see [27, Thrm. 2.8, Cor. 2.9] and references therein.
Theorem 6.1
For \(w\in S_n\) and \(w=s_{i_1}s_{i_2}\ldots s_{i_r}\) a reduced expression,
is well defined (independent of the choice of reduced expression). Furthermore, for all \(f({\mathbf {z}})\in {\mathbb {C}}[{\mathbf {z}}^{\pm 1}]\) and \(w\in S_n\) we have
in \({\mathcal {H}}_n\), with
If V is a left \({\mathcal {H}}_n\)-module, then the previous theorem implies that \(I_w(V_\xi )\subseteq V_{w\xi }\) for \(w\in S_n\) and \(\xi \in ({\mathbb {C}}^*)^n\).
It is known that \(M^I(\gamma )\) is calibrated for generic \(\gamma \in T^I\) with corresponding weight decomposition
with \(b_w^I(\gamma ):=I_w\otimes _{{\mathcal {H}}_I}1_{\chi _\gamma ^I}\) (see e.g., [27, Prop. 2.12], for the specific additional conditions on \(\gamma \)).
We now view the \(\mathcal {TL}_n\)-module \(V_n\) from the link pattern tower as an \({\mathcal {H}}_n\)-module through the surjective algebra map \(\psi _n{:}\,{\mathcal {H}}_n\twoheadrightarrow \mathcal {TL}_n\) satisfying \(\psi _n(T_i)=e_i+t^{-\frac{1}{2}}\) (\(1\le i<n\)) and \(\psi _n(\rho )=\rho \). The aim is to show that \(V_n\) is isomorphic to \(M^I(\gamma )\) for an appropriate subset \(I\subseteq \{1,\ldots ,n-1\}\) and \(\gamma \in T^I\) for generic \(t^{\frac{1}{4}}\). As a first step, we create explicit weight vectors in \(V_n\).
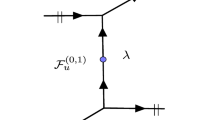
Write \(k=\lfloor \frac{n}{2}\rfloor \) and let \(J \subseteq \{ 1,\dots ,k \}\) be a subset, say \(J =\{ j_1, \dots ,j_r \}, 1 \le j_1< \cdots < j_r\le k\). Let \(D^{n}_J\) be the element in \(V_{n}\) shown in Fig. 1. Note that in the definition of \(D^{n}_J\), the arches \((2m-1, 2m)\) include the hole of the annulus if \(m \in J\), and \((2j_{s+1}-1, 2j_{s+1})\) is positioned over \((2j_{s}-1, 2j_{s})\). Furthermore, \(D^{2k+1}_J\) is obtained from \(D^{2k}_J\) by inserting the defect line at \(2k+1\), which is positioned over all other paths.
We require the skein theoretic description of \(\psi _n(Y_j) \in \mathcal {TL}_n\). From the expression \(Y_j=T_{j-1}^{-1}\ldots T_1^{-1}\rho T_{n-1}\ldots T_j\), we obtain
with \({\widehat{Y}}_j \in \mathcal {TL}_n\simeq \mathrm{End}_{{\mathcal {S}}}(n)\) the skein class of

Set \(\epsilon _n:=(-1)^n\).
Lemma 6.2
Write \({\underline{\eta }}=(\eta _1,\ldots ,\eta _{\lfloor n/2\rfloor })\) with \(\eta _j\in \{v^{\epsilon _n},t^{-\frac{1}{2}}v^{-\epsilon _n}\}\). Let \({\widehat{\xi }}({\underline{\eta }})\in ({\mathbb {C}}^*)^n\) be given by
and write for \(J\subseteq \{1,\ldots ,\lfloor n/2\rfloor \}\),
Then, \({\widehat{Y}}_jQ_n({\underline{\eta }})={\widehat{\xi }}_j({\underline{\eta }})Q_n({\underline{\eta }})\) in \(V_n\) for \(j=1,\ldots ,n\), where
In particular, we have \(Q_n({\underline{\eta }})\in V_{n,\xi ({\underline{\eta }})}\) with weight
Proof
It suffices to show that \({\widehat{Y}}_jQ_n({\underline{\eta }})= {\widehat{\xi }}_j({\underline{\eta }})Q_n({\underline{\eta }})\). Write \(k:=\lfloor n/2\rfloor \). There are three cases to consider, \(j=2i,2i-1\) (for \(1\le i \le k\)) and, if n is odd, \(j=n=2k+1\). We consider first \(j=2i\). Note that by the definition of \(D^{n}_J\) an arch is placed on top of the previous arch if they both encircle the hole of the annulus. For \({\widehat{Y}}_{2i}D_j^n\), the path connected to 2i that is wound around the diagram passes over all paths connected to \(l < 2i\) and under all paths connected to \(l >2i\). Due to these properties, the action of \({\widehat{Y}}_{2i}\) on \(D_J^n\) will only affect the arch \((2i-1,2i)\) and leave the others unchanged.
Consider now \({\widehat{Y}}_{2i}Q_{n}({\underline{\eta }})\) and combine the terms J and \(J\cup \{i\}\) for subsets J not containing i,
Focusing on the action of \({\widehat{Y}}_{2i}\) on the terms in the bracket, we claim that
for all \(J \subseteq \{1, \dots ,k\} {\backslash } \{i\}\). Since \(\eta _i\) satisfies
it then follows that \({\widehat{Y}}_{2i}Q_n({\underline{\eta }})=\eta _iQ_n({\underline{\eta }})\). To prove the claim, we show
for \(J\subseteq \{1,\ldots ,\lfloor n/2\rfloor \}{\setminus }\{i\}\). These equalities follow from the following diagrammatic calculations, in which we omit all paths that are not involved in the computation. The first diagrammatic computation is for \({\widehat{Y}}_{2i}D^{2k}_{J}\) in \(V_{2k}\), the second for \({\widehat{Y}}_{2i}D^{2k+1}_{J}\) in \(V_{2k+1}\) (note that the defect line creates a subtle difference) and the third for \({\widehat{Y}}_{2i} D^{n}_{J\cup \{i\}}\) in \(V_n\) (in this case the defect line does not affect the calculation):

The check that \({\widehat{Y}}_{2i-1}Q_n({\underline{\eta }})=\eta _i^{-1}Q_n({\underline{\eta }})\) is analogous.
The proof that \({\widehat{Y}}_{2k+1}Q_{2k+1}({\underline{\eta }})=vQ_{2k+1}({\underline{\eta }})\) with \(n=2k+1\) odd is simpler. All that the operator \({\widehat{Y}}_{2k+1}\) does is wind the defect line a full turn around the hole of the annulus. The operator keeps the defect line above all other curves. This full turn in \(V_{2k+1}\) can then be removed by the multiplicative factor v. \(\square \)
From now on, we choose
and we write \(Q_n\), \(\xi \) and \({\widehat{\xi }}\) for the corresponding \(Q_n({\underline{\eta }})\), \(\xi ({\underline{\eta }})\) and \({\widehat{\xi }}({\underline{\eta }})\). Concretely,
and
Lemma 6.3
\(Q_n \ne 0\) for generic \(t^{\frac{1}{4}}\).
Proof
Consider first \(n=2k\) even. Let \(Z_{2k}\in \mathrm{Hom}_{{\mathcal {S}}}(2k,0)\) be the skein class of the (2k, 0)-link diagram with little arches connecting \(2i-1\) and 2i for \(1\le i\le k\). Composing on the left with \(Z_{2k}\) defines a linear map \(\mathrm{Hom}_{{\mathcal {S}}}(0,2k)\rightarrow \mathrm{End}_{{\mathcal {S}}}(0)\) that descends to a well-defined linear map \(Z_{2k}: V_{2k}\rightarrow V_0\simeq {\mathbb {C}}\). Then,
which is a nonzero Laurent polynomial in \(t^{\frac{1}{4}}\) (look at its highest order term).
For \(n=2k+1\) odd, we apply a similar argument, now using the element \(Z_{2k+1}\in \mathrm{Hom}_{{\mathcal {S}}}(2k+1,1)\) which is the skein class of the \((2k+1,1)\)-link diagram with little arches connecting the inner boundary points \(2i-1\) and 2i (\(1\le i\le k\)) and with a defect line connecting the inner boundary point at \(2k+1\) to the outer boundary point at 1. Then, the resulting linear map \(Z_{2k+1}{:}\,V_{2k+1}\rightarrow V_1\simeq {\mathbb {C}}\) maps \(Q_{2k+1}\) to
for some \(\kappa \in {\mathbb {Z}}\), which again is a nonzero Laurent polynomial in \(t^{\frac{1}{4}}\) (the factor for the removal of a closed loop around the hole with a defect line running over it is \((v^{-1}t^{\frac{1}{4}}+vt^{-\frac{1}{4}})\), as shown in the proof of the previous lemma). \(\square \)
To establish an identification \(V_n\simeq M^I(\gamma )\) as \({\mathcal {H}}_n\)-modules, we will use \(Q_n\) and the intertwiners \(I_w\) (\(w\in S_n\)) to construct the corresponding cyclic vector in \(V_n\). But first we determine what the subset \(I\subseteq \{1,\ldots ,n-1\}\) should be.
Set
The associated parabolic subgroup \(S_{n,I^{(n)}}\) of \(S_n\) is isomorphic to \(S_k\times S_k\) if \(n=2k\) even, and \(S_{k}\times S_{k-1}\) if \(n=2k-1\) is odd.
Lemma 6.4
\(\mathrm{Dim}(V_{n}) = \#(S_{n}/S_{n,I^{(n)}}) = \# S_n^{I^{(n)}}\).
Proof
For \(n=2k\) even, \({\mathcal {L}}_{2k}\) is in bijective correspondence with the set of binary words of length 2k with letters \(\alpha ,\beta \) of length 2k such that k letters are \(\alpha \). The bijection is as follows. Orient the outer boundary of the punctured disk anticlockwise. Given \(L\in {\mathcal {L}}_{2k}\), orient the arcs in L in such a way that the closed oriented loop obtained by adding a piece of the oriented outer boundary of the punctured disk, is enclosing the puncture. Then, the word of length 2k in the letters \(\{\alpha ,\beta \}\) is obtained by putting \(\alpha \) as the ith letter if the orientation of the arc at i is away from i, and \(\beta \) if it is toward i.
In the odd case \(n=2k-1\), we create a bijective correspondence of \({\mathcal {L}}_{2k-1}\) with the set of binary words of length \(2k-1\) with letters \(\alpha ,\beta \) such that k letters are \(\alpha \) by a similar procedure, with the only addition that \(\alpha \) is assigned to the outer boundary point that is connected to the puncture.
Clearly, the cardinality of the set of such binary words is equal to \(\#(S_n/S_{n,I^{(n)}})\). \(\square \)
Remark 6.5
The minimal coset representatives \(S_n^{I^{(n)}}\) are described as the set of permutations \(\sigma \in S_n\) such that \(\ell (\sigma s_i)=\ell (\sigma )+1\) for all \(i\in I^{(n)}\), where \(\ell \) is the length function of \(S_n\). It follows that \(S_n^{I^{(n)}}\) is the set of permutations \(\sigma \in S_n\) such that
We define \(w_n\in S_n\) as follows:
Note that \(w_{2k}=\iota _{2k-1}(w_{2k-1})\) with \(\iota _n{:}\,S_{n-1}\hookrightarrow S_n\) the natural group embedding extending \(\sigma \in S_{n-1}\) to a permutation of \(\{1,\ldots ,n\}\) by \(\sigma (n)=n\). Note that
It follows that \(w_n^{-1}\in S_n^{I^{(n)}}\), cf. Remark 6.5. We now define \(\gamma =\gamma ^{(n)}\in ({\mathbb {C}}^*)^n\) by
with \(\xi \) the weight of \(V_n\) as given by (6.2). Concretely, we have
Note that \(\gamma \in T^{I^{(n)}}\), and hence we have the associated principal series module \(M^{I^{(n)}}(\gamma )\).
Theorem 6.6
For generic \(t^{\frac{1}{4}}\), we have \(M^{I^{(n)}}(\gamma )\simeq V_n\) as left \({\mathcal {H}}_n\)-modules, with the isomorphism \(M^{I^{(n)}}(\gamma )\overset{\sim }{\longrightarrow } V_n\) mapping \(v_e^{I^{(n)}}(\gamma )\in M^{I^{(n)}}(\gamma )_\gamma \) to \(I_{w_n}Q_n\in V_{n,\gamma }\), where e is the unit element of the symmetric group \(S_n\).
Proof
We have \(I_{w_n}Q_n\in V_{n,\gamma }\) by Lemma 6.2 and Theorem 6.1. Furthermore, by Theorem 6.1 again,
and
for generic \(t^{\frac{1}{4}}\), since \(R_0^+\cap w_n^{-1}R_0^-\) consists of the roots \(\epsilon _{2l}-\epsilon _{2m-1}\) (\(l<m\)). Hence, \(I_{w_n}Q_n\not =0\) for generic \(t^{\frac{1}{4}}\). Consider now the vectors
Then, for \(w\in S_n^{I^{(n)}}\) we have
by Theorem 6.1. Furthermore, \(e_w(\gamma )\not =0\) for generic \(t^{\frac{1}{4}}\) since for \(w\in S_n^{I^{(n)}}\) we have
for \(w\in S_n^{I^{(n)}}\), in view of Remark 6.5. It follows that \(0\not =u_w\in V_{n,w\gamma }\) for all \(w\in S_n^{I^{(n)}}\). Hence, by Lemma 6.4, for generic \(t^{\frac{1}{4}}\),
with \(V_{n,w\gamma }={\mathbb {C}}u_w\) for all \(w\in S_n^{I^{(n)}}\), since the \(w\gamma \)’s (\(w\in S_n^{I^{(n)}}\)) are pairwise different for generic \(t^{\frac{1}{4}}\). It remains to show that \(T_iu_e=t^{-\frac{1}{2}}u_e\) for \(i\in I^{(n)}\) and generic \(t^{\frac{1}{4}}\). Fix \(i\in I^{(n)}\). Then, \(I_iu_e\in V_{n,s_i\gamma }=\{0\}\) since
for generic \(t^{\frac{1}{4}}\). By the explicit expression of the intertwiner \(I_i\) (see (6.1)), we then obtain
Hence, \(T_iu_e=t^{-\frac{1}{2}}u_e\), as desired. \(\square \)
6.2 The Cherednik–Matsuo Correspondence
Now that we have identified the link pattern modules \(V_n\) with principal series representations, we can apply the Cherednik–Matsuo correspondence to analyze the existence of polynomial solutions of the associated qKZ equations.
The Cherednik–Matsuo correspondence gives a bijective correspondence between meromorphic twisted-symmetric solution to qKZ equations associated with a principal series module and suitable classes of meromorphic common eigenfunctions for the action of the Y-operators under the basic representation [22, 27].
The version of the Cherednik–Matsuo correspondence we need is as follows. If \(I\subseteq \{1,\ldots ,n-1\}\) and \(w\in S_n\), then we write \({\underline{w}}\in S_{n,I}\) and \({\overline{w}}\in S_n^I\) for the unique elements such that \(w={\overline{w}}{\underline{w}}\). Let \(w_0\in S_n\) be the longest Weyl group element, mapping j to \(n+1-j\) for \(j=1,\ldots ,n\). Let \(I^*:=\{i^*\,\, | \,\, i\in I\}\) with \(i^*\in \{1,\ldots ,n-1\}\) such that \({\overline{w}}_0(\alpha _i)=\alpha _{i^*}\).
Theorem 6.7
Fix \(c\in {\mathbb {C}}^*\), \(I \subseteq \{ 1, \dots , n-1 \}\) and \(\zeta \in T^I\). Then, we have a linear isomorphism
with \(\mathrm{CM}_{I,\zeta }\) given by
Proof
For \(c=1\), this is an easy consequence of [27, Cor. 4.4 & Thm. 4.14]. For general c, it then follows using the fact that \(M^I(c^{-1}\zeta )\simeq M^I(\zeta )^{(c^{-1})}\) with isomorphism given by \(v_w^I(c^{-1}\zeta )\mapsto v_w^I(\zeta )\) for \(w\in S_n^{I}\), and
\(\square \)
We want to re-express the common eigenspace for \(\pi ^{t^{-\frac{1}{2}},q}(Y_j)\)-operators in the left-hand side of (6.5) in terms of the dual Cherednik operators, in order to apply the results of [20] in the next subsection. The dual Y-operators are defined by
cf. [20, §2.2]. The relation to our commuting Y-operators
is as follows.
Lemma 6.8
We have in \({\mathcal {H}}_n\),
Proof
The first identity is well known. For the second identity, it suffices to show that
This follows using \(\rho T_i=T_{i+1}\rho \) and the fact that
are two reduced expressions for \(w_0\in S_n\). \(\square \)
Returning to the Cherednik–Matsuo correspondence (see Theorem 6.7), we can reformulate it as follows.
Corollary 6.9
Fix \(c\in {\mathbb {C}}^*\), \(I \subseteq \{ 1, \dots , n-1 \}\) and \(\zeta \in T^I\). Then, we have a linear isomorphism
with \(\overline{\mathrm{CM}}_{I,\zeta }\) given by
Proof
By the previous lemma, \(\pi ^{t^{-\frac{1}{2}},q}(T_{w_0}^{-1})\) restricts to a linear isomorphism from the space defined by the left-hand side of (6.6) onto the space defined by the left-hand side of (6.5). Hence, it suffices to note that
which follows from the fact that for all \(w\in S_n^I\),
\(\square \)
6.3 Dual Non-symmetric Macdonald Polynomials
In this subsection, we take \(n\ge 2\). The next step will be to introduce the polynomial eigenfunctions of the dual Cherednik operators \(\pi ^{t^{-\frac{1}{2}},q}({\overline{Y}}_j)\) (\(1\le j\le n\)), called the dual non-symmetric Macdonald polynomials. We follow Kasatani [20]: The \((t^{\frac{1}{2}},\omega ,Y_j)\) in [20] corresponds to our \((-t^{-\frac{1}{2}},\rho ^{-1},{\overline{Y}}_j)\).
For \(\lambda \in {\mathbb {Z}}^n\) let
Then, \(2 \rho ( \lambda ) = \sum ^{n}_{i=1} d_i(\lambda ) \epsilon _i\) with
Write
i.e., \(s_{\lambda }=(s_{\lambda ,1},\ldots ,s_{\lambda ,n})\) with \(s_{\lambda ,i}=\bigl (-t^{-\frac{1}{2}}\bigr )^{d_i(\lambda )}q^{\lambda _i}\).
For generic q and \(t^{\frac{1}{4}}\) (or indeterminates), the monic dual non-symmetric Macdonald polynomial
of degree \(\lambda \in {\mathbb {Z}}^n\) is the unique Laurent polynomial satisfying the eigenvalue equations
such that the coefficient of \({\mathbf {z}}^\lambda \) in the expansion of \(E_\lambda \) in monomials \(\{{\mathbf {z}}^\nu \}_{\nu \in {\mathbb {Z}}^n}\) is one. It is well known that \(E_\lambda \) is homogeneous of total degree \(|\lambda |:=\lambda _1+\cdots +\lambda _n\). In addition, \(E_\lambda \in {\mathbb {C}}[{\mathbf {z}}]\) if and only if \(\lambda \in {\mathbb {Z}}_{\ge 0}^n\). The intertwiners with respect to the dual Y-operators are defined by
cf. [20, Lemma 2.6]. Then, for \(1\le i<n\),
if \(\lambda \in {\mathbb {Z}}^n\) and \(\lambda _{i}>\lambda _{i+1}\).
Kasatani [20] analyzed the dual non-symmetric Macdonald polynomials \(E_\lambda \) with parameters specialized to \(t^{-k-1}q^{r-1}=1\) with \(1\le k\le n-1\) and \(r\ge 2\). In our situation, we are going to need the special case that \(k=2\) and \(r=3\), i.e., when \(t^{-3}q^2=1\) (cf. Theorem 4.7). In fact, for our purposes it suffices to take \(q=t^{\frac{3}{2}}\). We recall some key results from [20] in this special case.
Definition 6.10
We say \(\lambda \in {\mathbb {Z}}^n\) has a neighborhood if it has a pair of indices (i, j) such that conditions 1 and 2 are satisfied:
-
(1)
\(\rho (\lambda )_i - \rho (\lambda )_j = 2,\)
-
(2)
-
(a)
\(\lambda _i - \lambda _j \le 1,\) or
-
(b)
\(\lambda _i - \lambda _j =2\) and \(j<i\).
-
(a)
Write
By [20, Thm. 3.11], the dual non-symmetric Macdonald polynomial \(E_\lambda \) can be specialized at \(q=t^{\frac{3}{2}}\) if \(\lambda \in B^{(2,3)}\). For \(q=t^{\frac{3}{2}}\) write
and define the ideal \(I^{(2,3)}\subseteq {\mathbb {C}}[{\mathbf {z}}]\) by
Then, for \(q=t^{\frac{3}{2}}\) and generic \(t^{\frac{1}{4}}\), the ideal \(I^{(2,3)}\) is a \(\pi _n^{t^{-\frac{1}{2}},t^{\frac{3}{2}}}({\mathcal {H}}_n(t^{-\frac{1}{2}}))\)-submodule of \({\mathbb {C}}[{\mathbf {z}}^{\pm 1}]\) and
by [20, Thm. 3.11].
Remark 6.11
The conditions \(f({\mathbf {z}})=0\) for \({\mathbf {z}}\in Z^{(2,3)}\) are known as wheel conditions. It originally appeared in [12] (see also [21]).
We recall now the notion of a (2, 3)-wheel in \(\lambda \in {\mathbb {Z}}^n\), following [20, Def. 3.5].
Definition 6.12
Let \(q=t^{\frac{3}{2}}\) and fix \(\lambda \in {\mathbb {Z}}^n\). A three-tuple \((i_1,i_2,i_3)\) with distinct \(i_1,i_2,i_3\in \{1,\ldots ,n\}\) is called a (2, 3)-wheel in \(\lambda \) if there exists \(r_1,r_2\in {\mathbb {Z}}_{\ge 0}\) such that
with \(r_1+r_2\le 1\), and \(i_a<i_{a+1}\) if \(r_a=0\) (\(a=1,2\)).
Two wheels \((i_1,i_2,i_3)\) and \((j_1,j_2,j_3)\) in \(\lambda \) are said to be equivalent if there exists a \(\sigma \in S_3\) such that \(i_a=j_{\sigma ^{-1}(a)}\) for \(a=1,2,3\). We write \(\#^{(2,3)}(\lambda )\) for the number of equivalence classes of (2, 3)-wheels in \(\lambda \). Note that (still under the assumption that \(q=t^{\frac{3}{2}}\)) we have \(\#^{(2,3)}(\lambda )=0\) if and only if \(s_\lambda ^{-1}\in Z^{(2,3)}\). Furthermore, from [20, §3] (Definition 3.7) we have
6.4 Proof of Theorem 4.7
Let \(n\ge 2\) and specialize throughout this subsection \(v=1\) and \(q=t^{\frac{3}{2}}\). Furthermore, we set
cf. Theorem 4.7. Recall the notation \(I^{(n)}=\{1,\ldots ,\lceil n/2\rceil -1, \lceil n/2\rceil +1,\ldots ,n-1\}\) and the central character \(\gamma =\gamma ^{(n)}\in T^{I^{(n)}}\) with \(v=1\) (see (6.4)), so
In the even \(n=2k\) case, the decomposition \(w_0={\overline{w}}_0{\underline{w}}_0\) of the longest element \(w_0\in S_{2k}\) as a product of \({\overline{w}}_0\in S_{2k}^{I^{(2k)}}\) and \({\underline{w}}_0\in S_{2k,I^{(2k)}}\) gives the expressions
Hence, for \(n=2k\) even, we have \(I^{(2k),*}=I^{(2k)}\) and
In the odd \(n=2k-1\) case, the decomposition \(w_0={\overline{w}}_0{\underline{w}}_0\) of the longest element \(w_0\in S_{2k-1}\) as a product of \({\overline{w}}_0\in S_{2k-1}^{I^{(2k-1)}}\) and \({\underline{w}}_0\in S_{2k-1,I^{(2k-1)}}\) gives the expressions
Therefore, \(I^{(2k-1),*}=\{1,\ldots ,k-2,k,k+1,\ldots ,2k-2\}\) and
Hence, it follows from Theorem 6.6 and Corollary 6.9 that for generic \(t^{\frac{1}{4}}\), we have
with \(\widetilde{\mathrm{CM}}_n\) given by
In the next lemma, we relate the spectral point \(c_n^{-1}({\underline{w}}_0\gamma )\) to the spectrum of the dual non-symmetric Macdonald polynomials.
Lemma 6.13
For \(q=t^{\frac{3}{2}}\),
with \(\lambda ^{(n)}\in {\mathbb {Z}}^n\) given by
Proof
By a direct computation, for \(q=t^{\frac{3}{2}}\),
\(\square \)
Hence, we have for generic \(t^{\frac{1}{4}}\),
Next, we need to verify that the dual non-symmetric Macdonald polynomials \(E_{\lambda ^{(n)}}\) are nonzero under the specialization \(q=t^{\frac{3}{2}}\).
Lemma 6.14
\(S_{n}\lambda ^{(n)}\cap B^{(2,3)}= \{\sigma \lambda ^{(n)}\,\,\, | \,\,\, \sigma \in S_{n}^{I^{(n)}} \}\). In particular, \(\lambda ^{(n)}\in B^{(2,3)}\), and for generic \(t^{\frac{1}{4}}\),
is well defined, homogeneous of total degree \(\frac{1}{2}n(n-1)\), and satisfies
Proof
Note that by Remark 6.5 and the definition of \(\lambda ^{(n)}\),
Now suppose that \(\mu \in S_n\lambda ^{(n)}\cap B^{(2,3)}\) and \(\mu _i-\mu _j=2\). By (6.7),
Since \(\mu \in B^{(2,3)}\), this implies that \(i<j\). By (6.12), we conclude that \(\mu \in \{\sigma \lambda ^{(n)}\,\, | \,\, \sigma \in S_n^{I^{(n)}}\}\).
Conversely, suppose that \(\mu \in \{\sigma \lambda ^{(n)}\,\, | \,\, \sigma \in S_n^{I^{(n)}}\}\). Suppose that \(\rho (\mu )_i-\rho (\mu )_j=2\). By (6.7), this implies that
It follows that \(\mu _i>\mu _j\), and hence
forcing \(\mu _i-\mu _j=2\). By (6.12), this implies that \(i<j\), and hence \(\mu \in S_n\lambda ^{(n)}\cap B^{(2,3)}\). The remaining statements now follow immediately (note that the degree of \(E_{\lambda ^{(n)}}({\mathbf {z}})\) is \(\sum _{i=1}^n\lambda _i^{(n)}=\frac{1}{2}n(n-1)\)). \(\square \)
Proposition 6.15
For generic \(t^{\frac{1}{4}}\), we have
In particular, there exists a unique \(\kappa _n\in {\mathbb {C}}^*\) such that
has fully nested component
Proof
For the first statement, fix \(i\in I^{(n)}\). In fact, for \(n=2k\) even the (2, 3)-wheels in \(s_i\lambda ^{(2k)}\) are \((i,i+1,k+i+1)\) and \((k+i+1,i,i+1)\) if \(1\le i<k\) and \((i,i+1,i-k)\), \((i-k,i,i+1)\) if \(k+1\le i<2k\). For \(n=2k-1\), the (2, 3)-wheels in \(s_i\lambda ^{(2k-1)}\) are \((i,i+1,k+i)\), \((k+i,i,i+1)\) if \(1\le i<k\) and \((i,i+1,i-k+1)\), \((i-k+1,i,i+1)\) if \(k+1\le i<2k-1\). Hence, \(\#^{(2,3)}(s_i\lambda ^{(n)})=1\).
By [20, Lemma 4.13], it follows from \(\#^{(2,3)}(s_i\lambda ^{(n)})=1\) that \(E_{s_i\lambda ^{(n)}}({\mathbf {z}};-t^{-\frac{1}{2}},q)\) can be specialized to \(q=t^{\frac{3}{2}}\) for generic \(t^{\frac{1}{4}}\). By (6.8), we then obtain
since \(s_{\lambda ^{(n)},i+1}/s_{\lambda ^{(n)},i}=t^{-1}\) and \(\lambda _{i}^{(n)}>\lambda _{i+1}^{(n)}\). Substituting the explicit expression of \(B_i\) then gives
hence \(\pi _n^{t^{-\frac{1}{2}},t^{\frac{3}{2}}}(T_i)E_{\lambda ^{(n)}}(\cdot ;-t^{-\frac{1}{2}},t^{\frac{3}{2}})= t^{\frac{1}{2}}E_{\lambda ^{(n)}}(\cdot ;-t^{-\frac{1}{2}},t^{\frac{3}{2}})\) for \(i\in I^{(n)}\).
It follows that
is homogeneous of total degree \(\frac{1}{2}n(n-1)\). By Corollary 4.4,
for some \(\kappa _n\in {\mathbb {C}}^*\), hence the result. \(\square \)
With the last proposition, we have completed the proof of Theorem 4.7 for generic \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\) (note that uniqueness follows from Lemma 4.2 and that for \(n=1\) the desired unique solution \(g^{(1)}\) is simply given by the constant function \(g^{(1)}\equiv 1\)). The remark following Theorem 4.7 then completes the proof of Theorem 4.7 for all values \(t^{\frac{1}{4}}\in {\mathbb {C}}^*\) for which \((t^{\frac{1}{2}}+1)(t+1)\not =0\).
7 The Dual Braid Recursion
The extended affine Temperley–Lieb algebra \(\mathcal {TL}_n(t^{\frac{1}{2}})\) is invariant under the inversion \(t^{\frac{1}{4}} \rightarrow t^{-\frac{1}{4}}\). In this last section of the article, we discuss how this symmetry results in a dual braid recursion for the qKZ towers of solutions \((g^{(n)})_{n\ge 0}\) from Theorem 4.7. We set \(v=1\) in this section.
First, we discuss the inversion on the Kauffman skein relation (3.6). If we invert \(t^{\frac{1}{4}}\) and then rotate the diagrams by ninety degrees, we have

Comparing this to the original equation, we see that all the over-crossings swap to under-crossings and vice versa. Hence, in the identification of \(\mathcal {TL}_n(t^{\frac{1}{2}})\) with \(\mathrm{End}_{{\mathcal {S}}}(n)\), the inversion \(t^{\frac{1}{4}}\rightarrow t^{-\frac{1}{4}}\) amounts to replacing under-crossings by over-crossing and vice versa.
Let \({\mathcal {I}}_n^\iota {:}\,\mathcal {TL}_n\rightarrow \mathcal {TL}_{n+1}\) be the algebra map \({\mathcal {I}}_n\) with the role of \(t^{\frac{1}{4}}\) replaced by \(t^{-\frac{1}{4}}\). Hence, in the skein theoretic description, the arc insertion is now done by over-crossing all arcs its meets, instead of under-crossing. Similarly, we write
for the intertwiner obtained from replacing in the construction of \(\phi _n\in \mathrm{Hom}_{\mathcal {TL}_n}\bigl (V_n,V_{n+1}^{{\mathcal {I}}_n}\bigr )\) the parameter \(t^{\frac{1}{4}}\) by \(t^{-\frac{1}{4}}\) and the role of \({\mathcal {I}}_n\) by \({\mathcal {I}}_n^\iota \).
Theorem 7.1
With the assumptions as in Theorem 4.7, let \(g^{(n)}\in \mathrm{Sol}_n(V_n,t^{\frac{3}{2}}, (-t^{-\frac{3}{4}})^{n-1})\) for \(n\ge 1\) be the homogeneous polynomial solution qKZ of degree \(\frac{1}{2}n(n-1)\) with fully nested component
and set \(g^{(0)}:=1\in \mathrm{Sol}_0(V_0,t^{\frac{3}{2}},t^{\frac{1}{4}}+t^{-\frac{1}{4}})\). Write
Then, \({\widetilde{g}}^{(n)}({\mathbf {z}})\in V_n[{\mathbf {z}}]\) is a \(V_n\)-valued homogeneous polynomial of total degree \(\frac{1}{2}n(n-1)\) and
Proof
Let \(R_i^\iota (x)\in \mathcal {TL}_n\) be the R-operator \(R_i(x)\) with \(t^{\frac{1}{4}}\) replaced by \(t^{-\frac{1}{4}}\),
Note that \(R_i^\iota (x)=R_i(x^{-1})\), from which it follows that
for \(1\le i<n\). Furthermore, with \(q=t^{\frac{3}{2}}\),
Hence, \({\widetilde{g}}^{(n)}({\mathbf {z}})\) is a twisted-symmetric solution of the qKZ equation with respect to the action \(\nabla ^\iota \) of \(W_n\) obtained from \(\nabla \) by inverting \(t^{\frac{1}{4}}\) and setting \(q=t^{\frac{3}{2}}\). Furthermore, the fully nested component of \({\widetilde{g}}^{(n)}({\mathbf {z}})\) is
As in Lemma 4.2, it follows that \({\widetilde{g}}^{(n)}({\mathbf {z}})\), as symmetric solution of these qKZ equations, is determined by the fully nested component and that all coefficients \({\widetilde{g}}^{(n)}_L({\mathbf {z}})\) are homogeneous polynomials in \(z_1,\ldots , z_n\) of total degree \(\frac{1}{2}n(n-1)\). In particular,
with \(\mathrm{Sol}_n^\iota \bigl (V_n;q,d_n)\) being the polynomial \(V_n\)-valued functions \(f({\mathbf {z}})\in V_n[{\mathbf {z}}]\) satisfying
Using slightly modified versions of Lemmas 2.4 and 2.5 one now shows that
Furthermore, a modified version of Lemma 4.5 yields
with \(d_{L,L_\cap ^{(n+1)}}=\delta _{L,L_\cap ^{(n)}}t^{\frac{1}{4}\lfloor n/2\rfloor }\). Hence, \({\widetilde{g}}^{(n+1)}(z_1,\ldots ,z_n,0)\) and \(t^{\frac{1}{4}(2n-\lfloor n/2\rfloor )}z_1\ldots z_n \phi _n^\iota \bigl ({\widetilde{g}}^{(n)}({\mathbf {z}})\bigr )\) have the same fully nested component. The properly modified version of Lemma 4.3 then shows that they are equal. \(\square \)
References
Al Harbat, S.: Markov trace on a tower of affine Temperley–Lieb algebras of type \({\tilde{A}}\). J. Knot Theory Ramif. 249(9), 1550049 (2015)
Al Qasimi, K., Jacobsen, J., Nienhuis, B.: Observables of the TL \({\rm O}(1)\) model on the infinite cylinder: current and nesting number. In preparation
Al Qasimi, K., Stokman, J.V.: The Skein Category of the Annulus (2017). ArXiv e-prints arXiv:1710.04058
Baxter, R.J.: Exactly Solved Models in Statistical Mechanics. Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], London (1982)
Cherednik, I.: Quantum Knizhnik–Zamolodchikov equations and affine root systems. Commun. Math. Phys. 150(1), 109–136 (1992)
Cherednik, I.: Integration of quantum many-body problems by affine Knizhnik–Zamolodchikov equations. Adv. Math. 106(1), 65–95 (1994)
Cherednik, I.: Double affine Hecke algebras. In: London Mathematical Society Lecture Note Series, vol. 319. Cambridge University Press, Cambridge (2005)
De Gier, J., Pyatov, P.: Factorized solutions of Temperley–Lieb qKZ equations on a segment. Adv. Theor. Math. Phys. 14(3), 795–877 (2010)
Di Francesco, P., Zinn-Justin, P.: Around the Razumov–Stroganov conjecture: proof of a multi-parameter sum rule. Electron. J. Combin. 12, 6 (2005)
Di Francesco, P., Zinn-Justin, P.: Quantum Knizhnik–Zamolodchikov equation: reflecting boundary conditions and combinatorics. J. Stat. Mech. Theory Exp. 12, P12009 (2007)
Di Francesco, P., Zinn-Justin, P., Zuber, J.-B.: Sum rules for the ground states of the \({\rm O} (1)\) loop model on a cylinder and the xxz spin chain. J. Stat. Mech. Theory Exp. 8, P08011 (2006)
Feigin, B., Jimbo, M., Miwa, T., Mukhin, E.: Symmetric polynomials vanishing on the shifted diagonals and Macdonald polynomials. Int. Math. Res. Not. 18, 1015–1034 (2003)
Françoise, J.-P., Naber, G.L., Tsou, S.T. (eds.): Encyclopedia of Mathematical Physics, vol. 1, 2, 3, 4, 5. Academic Press/Elsevier Science, Oxford (2006)
Frenkel, I.B., Reshetikhin, N.Y.: Quantum affine algebras and holonomic difference equations. Commun. Math. Phys. 146(1), 1–60 (1992)
Gainutdinov, A.M., Saleur, H.: Fusion and Braiding in Finite and Affine Temperley–Lieb Categories, ArXiv e-prints (2016). arXiv:1606.04530
Goodman, F.M., Hauschild, H.: Affine Birman–Wenzl–Murakami algebras and tangles in the solid torus. Fund. Math. 190, 77–137 (2006)
Green, R.M.: On representations of affine Temperley–Lieb algebras. In: Algebras and Modules, II (Geiranger, 1996), pp. 245–265 (1998)
Haines, T.J., Pettet, A.: Formulae relating the Bernstein and Iwahori–Matsumoto presentations of an affine Hecke algebra. J. Algebra 252(1), 127–149 (2002)
Jimbo, M., Miwa, T.: Algebraic analysis of solvable lattice models. In: CBMS Regional Conference Series in Mathematics, vol. 85, Published for the Conference Board of the Mathematical Sciences, Washington; by the American Mathematical Society, Providence (1995)
Kasatani, M.: Subrepresentations in the polynomial representation of the double affine Hecke algebra of type \({\rm GL}_n\) at \(t^{k+1}q^{r-1}=1\). Int. Math. Res. Not. 28, 1717–1742 (2005)
Kasatani, M., Pasquier, V.: On polynomials interpolating between the stationary state of a \({\rm O}(n)\) model and a Q.H.E. ground state. Commun. Math. Phys. 276(2), 397–435 (2007)
Kasatani, M., Takeyama, Y.: The quantum Knizhnik–Zamolodchikov equation and non-symmetric Macdonald polynomials. Funkcial. Ekvac. 50(3), 491–509 (2007)
Lusztig, G.: Affine Hecke algebras and their graded version. J. Am. Math. Soc. 2(3), 599–635 (1989)
Pasquier, V.: Quantum incompressibility and Razumov Stroganov type conjectures. Ann. Henri Poincaré 7(3), 397–421 (2006)
Roger, J., Yang, T.: The skein algebra of arcs and links and the decorated Teichmüller space. J. Differ. Geom. 96(1), 95–140 (2014)
Smirnov, F.A.: Form Factors in Completely Integrable Models of Quantum Field Theory, Advanced Series in Mathematical Physics, vol. 14. World Scientific Publishing Co., Inc., River Edge (1992)
Stokman, J.V.: Quantum affine Knizhnik–Zamolodchikov equations and quantum spherical functions, I. Int. Math. Res. Not. IMRN 5, 1023–1090 (2011)
Acknowledgements
We thank Eric Opdam for a comment leading to the precise conditions on the affine Hecke algebra parameter for which the main theorem of the paper (Theorem 4.7) holds true. The work by Kayed Al Qasimi is supported by the Ministry of Education of the United Arab Emirates under Scholarship No. 201366644. Diagrams were coded using PSTricks.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nikolai Kitanine.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Recursion Relations for Link Pattern Components of qKZ Solutions
Appendix A: Recursion Relations for Link Pattern Components of qKZ Solutions
In this section, we prove Lemma 4.2(a) and Lemma 4.3(b), i.e., we show that twisted-symmetric solutions of qKZ equations with values in link pattern modules are determined by the fully nested component. This proof is done for three different representations of \({\mathcal {H}}_n\): link patterns \({\mathbb {C}}[\mathrm{LP}_{2k}]\) (when \(n=2k\)), punctured link patterns \({\mathbb {C}}[{\mathcal {L}}_{n}]\simeq V_n\) (Lemma 4.2) and the restricted modules \(V^{\nu _n}_{n+1}\) (Lemma 4.3). The first two cases have been considered before in the literature, see [8, 11, 21]. We recall these here in detail, since the technicalities play an important role in proving the most delicate third case.
A link pattern of size 2k is a diagram with 2k equally spaced points on the boundary of the disk \({\mathbb {D}}\) that are connected by k non-intersecting curves lying within the disk. To establish convention, the points are numbered 1 to 2k going counterclockwise around the disk. We denote the set of link patterns of size 2k by \(\mathrm{LP}_{2k}\). As an example, \(\mathrm{LP}_6\) consists of the following link patterns:

Link patterns can also be drawn by placing the endpoints on a horizontal line such that the k non-intersecting curves lie above it. To establish convention, the points are numbered in increasing order from left to right. As an example, the link patterns of \(\mathrm{LP}_6\) can be drawn as

respectively. Due to this form, the curves are sometimes referred to as arches and a little arch is one that connects two consecutive points.
A Dyck path of length 2k is a lattice path from (0, 0) to (2k, 0) with steps (1, 1) called a rise and \((1,-1)\) called a fall, which never falls below the x-axis. We denote the set of Dyck paths of length 2k by \(DP_{2k}\). As an example, \(DP_{6}\) consists of the following Dyck paths:

A Dyck path can also be encoded by a string of 2k numbers \((a_1,\dots , a_{2k})\) where \(a_j\) for \(1\le j \le 2k\) is the height of the path after step j. Furthermore, for a Dyck path L we define its content |L| to be the number of boxes within the gray triangle that lie above the path. For example, if \(L \in DP_{6}\) denotes the last Dyck path in the example above, then \(|L|=3\).
There exists a bijection between \(\mathrm{LP}_{2k}\) and \(DP_{2k}\). To go from link patterns to Dyck paths, consider the link pattern drawn on a horizontal line and traverse along the line from left to right. Each point i that is the beginning/end of an arch corresponds to a rise/fall at step i in the Dyck path. To go from Dyck paths to link patterns, for each rise draw the start of an arch and for each fall an end, and then complete the diagram by connecting a start with an end such that the arches do not intersect. For example, the ordered lists of elements in \(\mathrm{LP}_6\) and \(DP_6\) are the same under the bijective correspondence.
The bijection allows us to establish a containment ordering on link patterns. For two link patterns \(L,L' \in \mathrm{LP}_{2k}\), we say that L contains \(L'\) if the entire corresponding Dyck path of \(L'\) can be drawn along or below the Dyck path of L. More formally, let L and \(L'\) correspond to the Dyck paths \((a_1,\dots a_{2k})\) and \((b_1,\dots b_{2k})\), respectively. Then, L contains \(L'\) if \(a_j \ge b_j\) for all \(1\le j \le 2k\). As an example, in the list of Dyck paths in \(DP_6\) the first path contains all other paths. Furthermore, note that if L contains \(L'\) then \(|L| \le |L'|\).
Using the disk diagrams, one can define the action of \(\mathcal {TL}_{2k}\) on \({\mathbb {C}}[\mathrm{LP}_{2k}]\) similarly to that on \({\mathbb {C}}[{\mathcal {L}}_{2k}]\), one just ignores the puncture so we do not have the loop removal rule for non-contractible loops. Using the horizontal line diagrams is more suitable when discussing the action of the finite Temperley–Lieb algebra \(\mathcal {TL}^f_{2k}\). The induced action of \(\mathcal {TL}^f_{2k}\) on \({\mathbb {C}}[DP_{2k}]\) can then be described as follows.
At step i for \(1 \le i \le 2k-1\), a Dyck path can have one of three different local situations:
-
(1)
Steps \(i,i+1\) form a local maximum, i.e., a rise followed by a fall;
-
(2)
Steps \(i,i+1\) form a local minimum, i.e., a fall followed by a rise;
-
(3)
Steps \(i,i+1\) form a slope, i.e., two consecutive rises or falls.
If steps \(i,i+1\) form a local maximum, then the action of \(e_i\) acts as a scalar, leaving the path unchanged and multiplying by a factor \(-(t^{\frac{1}{2}}+t^{-\frac{1}{2}})\) (line 1, Fig. 2). If steps \(i,i+1\) form a local minimum, then \(e_i\) changes it into a local maximum (line 2, Fig. 2). For a slope, if it is two consecutive rises, say with heights \(a_i=m\) and \(a_{i+1}=m+1\), then let \(j>i+1\) be the first step that is a fall with \(a_j=m\). The action of \(e_i\) then changes step \(i+1\) into fall and j into a rise, creating a local maximum at \(i,i+1\) and decreasing the height of the path between i and j by two (line 3, Fig. 2). This decrease in height shifts the internal path down, and we refer to it as a collapse. If the slope is downwards with height \(a_i=m,a_{i+1}=m-1\), let \(j<i\) be the last rise with \(a_j=m+1\). Then, the action of \(e_i\) changes step i and j to a rise and fall, respectively. This creates a local maximum at \(i,i+1\) and causes a collapse decreasing \(a_l\) by two for \(j\le l<i\). Note that a collapse leads to a smaller Dyck path in the inclusion order.
Figure 2 shows a diagrammatic definition of the action on Dyck paths. The dotted frame indicates the section of the paths where they differ, and the dotted line in the third mapping represents a Dyck path of length \(j-i-2\). The case for two consecutive falls is the same as the third line but with the diagrams reflected across a vertical line in the middle of the diagrams.
1.1 A.1. Link Patterns
Let \(L_{0}\in DP_{2k}\) denote the Dyck path with k rises followed by k falls, i.e., \((1,2,\dots ,k,k-1,\dots ,0)\). Note that \(L_{0}\) contains all Dyck paths in \(DP_{2k}\) and \(|L_0|=0\). We show that the solution \(g^{(2k)}({\mathbf {z}}) \in \mathrm{Sol}_{2k}({\mathbb {C}}[\mathrm{LP}_{2k}];q,c_{2k})\) is determined by its base component \(g^{(2k)}_{L_{0}}({\mathbf {z}})\).
We prove this by showing that if \(g^{(2k)}_{L_{0}}({\mathbf {z}}) \equiv 0 \), then we have \( g^{(2k)}_L({\mathbf {z}}) \equiv 0\) for all \(L \in DP_{2k}\). This is done using the qKZ equations (4.1), which give for \(1\le j <2k\),
where \(e_jL^\prime \sim L\) means that L is obtained from \(e_jL^\prime \) by removing the loops in \(e_jL^\prime \) (there is in fact at most one loop). The coefficient \(\gamma _{L^\prime ,L}^{(j)}\) is defined by
We begin with the inductive hypothesis,
where \(m \in {\mathbb {Z}}_{\ge 0}\). Now consider a Dyck path L such that \(|L| =m\) with a local maximum at, say, step i with \(a_i>1\) (if such a local maximum does not exist, then L is the unique Dykh path with maximal content |L|, and hence there is nothing to prove). We use Eq. (A.1) for \(j=i\) and examine the pre-images \(L'\) in the sum on the right-hand side. We find that besides L there is only one pre-image that is contained by L. This is the pre-image that has a local minimum turned into a local maximum by the action of \(e_i\). Let us denote this particular Dyck path by N. Switching a local minimum to a local maximum is equivalent to removing a box, so we have \(|N| = m+1\). Furthermore, all other pre-images \(L' \ne N\) contain L so \(|L'| \le m\) and \(g^{(2k)}_{L'}({\mathbf {z}}) \equiv 0\). Thus, \(g^{(2k)}_{N}({\mathbf {z}}) \equiv 0\) with \(|N|=m+1\) by (A.1). Since \(|L_{0}|=0\), it provides the base case of the induction and determines all other components.
Remark A.1
The algorithm of this proof can be viewed as collapsing the local maxima till we end up at the last component, which has k local maxima with height 1. Since a Dyck path cannot fall below the x-axis we cannot collapse a local maximum with a height 1. Thus, the algorithm never uses (A.1) at j if the height \(a_j\) is one. This is an important remark for the proofs that follow.
Remark A.2
The Dyck path \(L_{0}\) corresponds to the link pattern that connects point i with \(2k-i+1\). The same arguments used in this proof can be found in [10] where they prove the unique solution for the model with reflecting boundaries.
1.2 A.2: Punctured Link Patterns
Here, we present the proof to Lemma 4.2. Let \(L_\cap \) denote the link pattern

in \({\mathcal {L}}_{2k}\) and \({\mathcal {L}}_{2k+1}\), respectively. A little arch in a punctured link patterns is an arch connecting points \(j,j+1\) that does not contain the puncture. For example, \(L_\cap \) only has one little arch, it connects points \(2k+1 \) to 1.
We show that the solution \(g^{(n)}({\mathbf {z}}) \in \mathrm{Sol}_{n}({\mathbb {C}}[{\mathcal {L}}_{n}];q,c_n)\) is determined by its base component \(g^{(n)}_{L_\cap }({\mathbf {z}})\). The qKZ equations written component-wise are
where \(e_iL^\prime \sim L\) means that L is obtained from \(e_iL^\prime \) by removing the loops in \(e_iL^\prime \) (there is in fact at most one loop), see (4.1). The coefficient \(\gamma _{L^\prime ,L}^{(i)}\) is
We treat the even and odd case separately.
1.2.1 A.2.1. Case \(n=2k\)
Let \(\mathrm{LP}^{(*,j)}_{2k}\) denote the set of punctured link patterns in \({\mathcal {L}}_{2k}\) such that the puncture could be connected to a point on the boundary between points j and \(j+1\) (modulo 2k) without crossing a line. Then, \({\mathcal {L}}_{2k} = \bigcup _{j=1}^{2k} \mathrm{LP}^{(*,j)}_{2k}\) (not necessarily disjoint) and \(\rho {:}\,\mathrm{LP}^{(*,j)}_{2k} \rightarrow \mathrm{LP}^{(*,j+1)}_{2k}\). Note that \(L_\cap \) is in \(\mathrm{LP}^{(*,k)}_{2k}\) and if we define \(L_{2k}:= \rho ^k \cdot L_\cap \) then \(L_{2k} \in \mathrm{LP}^{(*,2k)}_{2k}\). Define a bijection from \(\mathrm{LP}^{(*,2k)}_{2k}\) to \(\mathrm{LP}_{2k}\) by simply removing the puncture. This mapping preserves the action of \(\mathcal {TL}^f_{2k}\). Furthermore, it maps \(L_{2k} \in \mathrm{LP}^{(*,2k)}_{2k}\) to \(L_0 \in \mathrm{LP}_{2k}\).
To prove that \(g^{(2k)}_{L_\cap }({\mathbf {z}})\) determines the solution, we have the following steps. First, if \(g^{(2k)}_{L_\cap }({\mathbf {z}}) \equiv 0\) then by using Eq. (A.3) k times we have \(g^{(2k)}_{L_{2k}}({\mathbf {z}}) \equiv 0\). Second, by the mapping from \(\mathrm{LP}^{(*,2k)}_{2k}\) to \(\mathrm{LP}_{2k}\) and the proof on \(\mathrm{LP}_{2k}\) we have \(g^{(2k)}_{L}({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,2k)}_{2k}\). Last, we use Eq. (A.3) to show that if \(g^{(2k)}_{L}({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,i)}_{2k}\) then \(g^{(2k)}_{L'}({\mathbf {z}}) \equiv 0\) for all \(L' \in \mathrm{LP}^{(*,i+1)}_{2k}\).
There is one key subtlety that we have ignored, which we point out and address. There is a difference between Eq. (A.1) and (A.2); in the latter equation, the pre-images are in \({\mathcal {L}}_{2k}\) and not just \(\mathrm{LP}_{2k}\). So when determining all the components for \(L \in \mathrm{LP}^{(*,2k)}_{2k}\) we must check that all the pre-images \(L'\) are also in \(\mathrm{LP}^{(*,2k)}_{2k}\). Recall Remark A.1; each step of the algorithm is on a local maximum, which corresponds to a little arch in a link pattern. For the equation \(e_i\cdot L'=L\), the only case where we have \(L' \not \in \mathrm{LP}^{(*,2k)}_{2k}\) is if the little arch in L is on the boundary of the domain that contains the puncture. Such a little arch corresponds to a local maximum of height 1. Recalling again Remark A.1, we do not collapse such local maxima, and therefore we do not have this case and can conclude all pre-images are in \(\mathrm{LP}^{(*,2k)}_{2k}\). If \(L \in \mathrm{LP}^{(*,2k)}_{2k}\) has a little arch \((i,i+1)\) on the boundary of the domain containing the puncture, then \(L' \not \in \mathrm{LP}^{(*,2k)}_{2k}\) is the link pattern identical to L but with the puncture inside the little arch.
1.2.2 A.2.2. Case \(n=2k+1\)
Let \(\mathrm{LP}^{(*,j)}_{2k+1}\) denote the set of punctured link patterns in \({\mathcal {L}}_{2k+1}\) such that the defect line connects the puncture to point j on the boundary. Then, we have \({\mathcal {L}}_{2k+1} = \bigsqcup _{j=1}^{2k+1} \mathrm{LP}^{(*,j)}_{2k+1}\) and \(\rho : \mathrm{LP}^{(*,j)}_{2k+1} \rightarrow \mathrm{LP}^{(*,j+1)}_{2k+1}\). Note that \(L_\cap \) is in \(\mathrm{LP}^{(*,k+1)}_{2k}\) and if we define \(L_{2k+1}:= \rho ^k \cdot L_\cap \) then \(L_{2k+1} \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\). Define a bijection from \(\mathrm{LP}^{(*,2k+1)}_{2k+1}\) to \(\mathrm{LP}_{2k}\) by simply removing the defect line, puncture and boundary point \(2k+1\). This mapping preserves the action of \(\mathcal {TL}^f_{2k}\). Furthermore, it maps \(L_{2k+1} \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\) to \(L_0 \in \mathrm{LP}_{2k}\).
Now to prove that \(g^{(2k+1)}_{L_\cap }({\mathbf {z}})\) determines the solution we have the following steps. First, if \(g^{(2k+1)}_{L_\cap }({\mathbf {z}}) \equiv 0\) then by using Eq. (A.3) k times we have \(g^{(2k+1)}_{L_{2k+1}}({\mathbf {z}}) \equiv 0\). Second, by the mapping from \(\mathrm{LP}^{(*,2k+1)}_{2k+1}\) to \(\mathrm{LP}_{2k}\) and the proof on \(\mathrm{LP}_{2k}\) we have \(g^{(2k)}_{L}({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\). Last, by Eq. (A.3), if \(g^{(2k+1)}_{L}({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,i)}_{2k+1}\) then \(g^{(2k+1)}_{L'}({\mathbf {z}}) \equiv 0\) for all \(L' \in \mathrm{LP}^{(*,i+1)}_{2k+1}\).
The same subtle issue occurs in this case and the argument is identical. The only case a pre-image \(L'\) is not in \(\mathrm{LP}^{(*,2k+1)}_{2k+1}\) is when the little arch in L is on the boundary of the domain that contains the puncture. Such a little arch corresponds to a local maximum of height 1. Again, recalling Remark A.1, we do not collapse such local maxima, and therefore we do not have this case and can conclude all pre-images are in \(\mathrm{LP}^{(*,2k+1)}_{2k+1}\). If \(L \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\) has a little arch \((i,i+1)\) on the boundary of the domain containing the puncture, then \(L' \not \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\) is the link pattern with either point i or \(i+1\) connected to the puncture and the other to the point \(2k+1\).
1.3 A.3. The Restricted Module \(V^{\nu _n}_{n+1}\)
Here, we present the proof to Lemma 4.3. Let \(g^{(n)}({\mathbf {z}}) \in \mathrm{Sol}_n(V^{\nu _n}_{n+1};q,c_n)\). The qKZ equations associated with the representation \(V^{\nu _n}_{n+1}\) written component-wise are
for \(1\le j<n\). It is important to note that the link patterns are in \({\mathcal {L}}_{n+1}\) but the first equation is only for \(1\le j < n\); there is one equation less than in the previous cases. Note furthermore that (A.5) follows from the fact that \({\mathcal {I}}_n(\rho )=\rho (t^{-\frac{1}{4}}e_n+t^{\frac{1}{4}})\).
The proof for the even and odd case are treated separately.
1.3.1 A.3.1. The Case \(n=2k\)
Note that for the case \(n=2k\) the link patterns are in \({\mathcal {L}}_{2k+1}\). Recall from “Appendix A.2” the definitions for \(L_\cap ,L_{2k+1} \in {\mathcal {L}}_{2k+1}\) and \(\mathrm{LP}^{(*,j)}_{2k+1}\). We show the solution \(g^{(2k)}({\mathbf {z}})\) is determined by its base component \(g_{L_\cap }^{(2k)}({\mathbf {z}})\) in three steps.
First, consider Eq. (A.5) for \(L=L_\cap \). Since \(L_\cap \) does not have a little arch connecting \((2k,2k+1)\) there is no pre-image \(L'\) such that \(e_{2k}\cdot L'\sim L_{\cap }\). Therefore, there are no terms in the sum (over \(L'\)) on the left-hand side of the equation, and if \(g_{L_\cap }^{(2k)}({\mathbf {z}}) \equiv 0\) then \(g_{\rho \cdot L_\cap }^{(2k)}({\mathbf {z}}) \equiv 0\). Continuing this way, we conclude that \(g_{\rho ^iL_\cap }^{(2k)}({\mathbf {z}})\equiv 0\) for all \(0\le i\le 2k\). But then we have covered all the possible rotations of \(L_\cap \), so \(g_{\rho ^iL_\cap }^{(2k)}({\mathbf {z}})\equiv 0\) for all \(i\in {\mathbb {Z}}\). In particular, \(g_{L_{2k+1}^{(2k)}}({\mathbf {z}}) \equiv 0\).
The second step is identical to “Appendix A.2.” By the mapping from \(\mathrm{LP}^{(*,2k+1)}_{2k+1}\) to \(\mathrm{LP}_{2k}\) and the proof on \(\mathrm{LP}_{2k}\), we have \(g^{(2k)}_{L}({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\). The fact that we have one equation less does not play a role here as the mapping from \(\mathrm{LP}^{(*,2k+1)}_{2k+1}\) to \(\mathrm{LP}_{2k}\) decreases the size of the link patterns by one.
The last step is to use Eq. (A.5). However, this is not as simple as “Appendix A.2” because Eq. (A.5) has an extra term on the left-hand side. It is a sum over pre-images for the action of \(e_n\). We will refer to it as the pre-image sum. Consider Eq. (A.5) for \(L\in \mathrm{LP}^{(*,2k)}_{2k+1}\). Since L has the defect line connected to point 2k there are no pre-images \(L'\) such that \(e_{2k}\cdot L'\sim L\). Therefore, the pre-image-sum of (A.5) does not give a contribution and \(g^{(2k)}_{L} ({\mathbf {z}}) \equiv 0\) because \(g^{(2k)}_{\rho \cdot L}({\mathbf {z}}) \equiv 0\) as \(\rho \cdot L \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\). Now consider (A.5) for \( L \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\). By the same argument, the pre-image-sum gives no contribution and \(g^{(2k)}_{\rho \cdot L} ({\mathbf {z}}) \equiv 0\). Since each \(L' \in \mathrm{LP}^{(*,1)}_{2k+1}\) is of the form \(\rho \cdot L\) for some \(L \in \mathrm{LP}^{(*,2k+1)}_{2k+1}\) we have \(g^{(2k)}_{L} ({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,1)}_{2k+1}\).
Having shown that \(g^{(2k)}_{L}({\mathbf {z}}) \equiv 0\) for \(L \in \mathrm{LP}^{(*,1)}_{2k+1} \sqcup \mathrm{LP}^{(*,2k)}_{2k+1}\sqcup \mathrm{LP}^{(*,2k+1)}_{2k+1}\), we now use an inductive argument to complete the proof. The induction hypothesis is
for some \(1 \le i <2k\). Consider Eq. (A.5) for \(L \in \mathrm{LP}^{(*,i)}_{2k+1}\). If L does not have a little arch connecting \((2k,2k+1)\), then we have the same argument used before: There are no pre-images and the pre-image sum does not give a contribution, and hence \(g^{(2k)}_{L}({\mathbf {z}}) \equiv 0\) for \(L \in \mathrm{LP}^{(*,i+1)}_{2k+1}\). If L does have a little arch connecting \((2k,2k+1)\), then the pre-image \(L'\) must have the defect line connected to points i, 2k or \(2k+1\). The case that the link pattern \(L'\) in the pre-image lies in \(\mathrm{LP}^{(*,i)}_{2k+1}\) is obvious. For the other two cases, the parts of the pre-images connected to \(i, 2k, 2k+1\) are shown in Fig. 3. It follows that the pre-image \(L'\) is in \( \mathrm{LP}^{(*,2k)}_{2k+1}\sqcup \mathrm{LP}^{(*,2k+1)}_{2k+1} \sqcup \mathrm{LP}^{(*,i)}_{2k+1}\) and the pre-image sum is equivalently zero. Hence, in both cases \(g^{(2k)}_{\rho \cdot L}({\mathbf {z}}) \equiv 0 \) and since \(\rho {:}\,\mathrm{LP}^{(*,i)}_{2k+1} \rightarrow \mathrm{LP}^{(*,i+1)}_{2k+1}\) we have \(g^{(2k)}_{ L}({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,i+1)}_{2k+1}\). This completes the induction and the base case is \(i=1\) which was discussed in the previous paragraph.
1.3.2 A.3.2. The Case \(n=2k-1\) (\(k\ge 1\))
Note that for the case \(n=2k-1\) the link patterns are in \({\mathcal {L}}_{2k}\) Recall from “Appendix A.2” the definitions for \(L_\cap ,L_{2k} \in {\mathcal {L}}_{2k}\) and \(\mathrm{LP}^{(*,j)}_{2k}\). We show the solution \(g^{(2k-1)}({\mathbf {z}})\) is determined by its base component \(g_{L_\cap }^{(2k-1)}({\mathbf {z}})\) in three steps.
The first step is identical to the case \(n=2k\). The link pattern \(L_\cap \) does not have a little arch connecting \((2k-1,2k)\) and neither do the link patterns \(\rho ^j \cdot L_\cap \) for \(1\le j \le k\). So if \(g_{L_\cap }^{(2k-1)}({\mathbf {z}}) \equiv 0\), then \(g_{L_{2k}}^{(2k-1)}({\mathbf {z}}) \equiv 0\).
The second step is similar to “Appendix A.2”; however, there is a new subtle issue to note; we have one equation less. By the mapping from \(\mathrm{LP}^{(*,2k)}_{2k}\) to \(\mathrm{LP}_{2k}\) and the proof on \(\mathrm{LP}_{2k}\), we have \(g^{(2k-1)}_{L}({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,2k)}_{2k}\). Indeed, Eq. (A.4) with \(1\le j<2k-1\) suffices since a local maximum at step \(2k-1\) must have height one, cf. Remark A.1.
For the final step, consider Eq. (A.5) for \(L\in \mathrm{LP}^{(*,2k-1)}_{2k}\). Since L does not have a little arch connecting points \((2k-1,2k)\), there is no pre-image \(L'\) and hence the pre-image sum does not give a contribution. Therefore, we have \(g^{(2k-1)}_{L}({\mathbf {z}}) \equiv 0\) for all \(L \in \mathrm{LP}^{(*,2k-1)}_{2k}\) since \(\rho \cdot L \in \mathrm{LP}^{(*,2k)}_{2k}\). Next, consider the equation for \(L\in \mathrm{LP}^{(*,2k-2)}_{2k}\). If L has a little arch connecting points \((2k-1,2k)\), then L is also in \(\mathrm{LP}^{(*,2k)}_{2k}\) so \(g^{(2k-1)}_L \equiv 0\). If L does not have a little arch connecting points \((2k-1,2k)\), then there are no pre-images \(L'\) and the pre-image sum does not give a contribution, so \(g^{(2k-2)}_L ({\mathbf {z}})\equiv 0\) because \(\rho \cdot L \in \mathrm{LP}^{(*,2k-1)}_{2k}\).
Now consider Eq. (A.5) for \(L \in \mathrm{LP}^{(*,2k)}_{2k}\). All the possible pre-images of L with respect to the action of \(e_{2k-1}\) are in \(\mathrm{LP}^{(*,j)}_{2k}\) for \(j=2k-2,2k-1,2k\). Therefore, the pre-image sum gives no contribution and \(g^{(2k-1)}_L({\mathbf {z}}) \equiv 0\) for \(L \in \mathrm{LP}^{(*,1)}_{2k}\). We now use an induction argument. The hypothesis is
for some \(1\le i <2k-2\). Consider Eq. (A.5) for \(L \in \mathrm{LP}^{(*,i)}_{2k}\). If L does not have a little arch connecting points \((2k-1,2k)\), then we have the same argument as before: There are no pre-images and the pre-image sum gives no contribution, and hence \(g^{(2k-1)}_{\rho L} \equiv 0\) and \(g_{L^{\prime \prime }}^{(2k-1)}({\mathbf {z}})\equiv 0\) for all \(L^{\prime \prime }\in \mathrm{LP}_{2k}^{(*,i+1)}\). If L does have a little arch connecting points \((2k-1,2k)\), then we examine the pre-images of L with respect to action of \(e_{2k-1}\). We find that
(see Fig. 4). Therefore, the pre-image sum is equivalently zero and since \(g^{(2k-1)}_L({\mathbf {z}}) \equiv 0\) and \(\rho \cdot L \in \mathrm{LP}^{(*,i+1)}_{2k}\), we have \(g^{(2k-1)}_L({\mathbf {z}}) \equiv 0\) for \(L \in \mathrm{LP}^{(*,i+1)}_{2k}\). This completes the inductive step, and the base case is \(i=1\) which was discussed in the beginning of this paragraph.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Al Qasimi, K., Nienhuis, B. & Stokman, J.V. Towers of Solutions of qKZ Equations and Their Applications to Loop Models. Ann. Henri Poincaré 20, 3743–3797 (2019). https://doi.org/10.1007/s00023-019-00836-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-019-00836-w