Geodesics orbiting a singularity

Abstract

We study the behaviour of geodesics on a Riemannian manifold near a generalized conical or cuspidal singularity. We show that geodesics entering a small neighbourhood of the singularity either hit the singularity or approach it to a smallest distance $\delta$ and then move away from it, winding around the singularity a number of times. We study the limiting behaviour $\delta \rightarrow 0$ in the second case. In the cuspidal case the number of windings goes to infinity as $\delta \rightarrow 0$, and we compute the precise asymptotic behaviour of this number. The asymptotics have explicitly given leading term determined by the warping factor that describes the type of cuspidal singularity. We also discuss in some detail the relation between differential and metric notions of conical and cuspidal singularities.

1 Introduction

Geodesics in Riemannian manifolds are among the most fundamental objects of differential geometry. Besides their intrinsic interest as locally shortest curves, or as trajectories of a free particle, they are used to define normal coordinates, which are of great utility. Also, they play an essential role in studying solutions of the wave equation, whose singularities propagate along geodesics (see [10], for instance).

In this paper we study the behaviour of geodesics near an isolated conical or cuspidal singularity of a Riemannian space. The precise definition of such singularities is given below, but for a first illustration of our results consider the example of the surface in ${\mathbb {R}}^3$ generated by rotating the curve $x=z^2$, $z\ge 0$, around the z-axis, see the bottom left picture in Fig. 1. It has a cuspidal singularity at the origin $p=0$.

Fig. 1

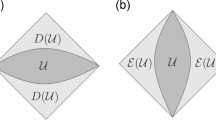
Illustrations of Theorem C for a conical metric $f(r)=r$ (above) and a cuspidal metric $f(r)=r^2$ (below). The right hand pictures show the product space $(0,R)\times Y$ while the left hand pictures illustrate the geometric situation. In all cases, $R=1.5$ and $\delta =0.3$. The r resp. z direction is upwards. Only the downward moving part of the geodesic is shown in the cuspidal case

Consider the geodesics entering the neighbourhood $U=\{z<1\}$ of p at any given point. It is quite obvious that one of these will hit p after a finite time. Any other geodesic will move downward, reach a lowest point at $z=\delta$ say, then move up again, and finally leave U (this can be seen using the classical Clairaut integral, for example, but we will prove it in greater generality). Inside U this geodesic will wind around p a number of times, as illustrated in Fig. 1. In this special case, our results (see Theorem C) imply that the number of windings is asymptotic to $\frac{\pi }{C} \delta ^{-1}$ as $\delta \rightarrow 0$, with $C=\int _{-\pi /2}^{\pi /2} \sqrt{\cos (\vartheta )}\, d\vartheta \approx 2.4$.

Our setting and results are more general than this example in the following ways: we allow more general profile functions $x=f_0(z)$ instead of $z^2$, including $f_0(z)=z$ and $f_0(z)=e^{-1/z}$, for example. We also consider the natural generalization of rotation surfaces to product manifolds $(0,R)\times Y$ in any dimension with warped product metrics, where the cross section Y is any closed Riemannian manifold (generalizing $Y=S^1$ in the surface case, where $f_0$ roughly corresponds to the warping function), and we also allow perturbations of such warped products. See below for the precise setting.

Our Main Theorems A, B, C are stated in Sect. 1.2 below. They can be roughly summarized as follows.

Theorem 1

(Rough summary of all results). Consider a space with a conical or cuspidal singularity p, with cross section Y. Any geodesic $\gamma$ in a neighbourhood of p is either radial, i.e. it hits the singularity, or it approaches p, to a smallest distance $\delta$, and then moves away from p, while winding around p. For a winding geodesic $\gamma$ with small $\delta$ we have:

• The distance of $\gamma$ to p behaves as for a radial geodesic up to an error of order $\delta$.

• The Y-component of $\gamma$ closely follows a geodesic in Y.

• The length of this geodesic in Y (generalizing the number of windings in the case $Y=S^1$) is asymptotic (as $\delta \rightarrow 0$) to $C_f/f'(\delta )$, for a constant $C_f$ only depending on f.

1.1 Setting

We now give a rough definition of the spaces that we consider in this paper. We refer to Sect. 2 for the precise definitions of a Riemannian space with isolated conical or cuspidal singularity along with technical assumptions. The key point is that the metric has generalized warped product form near the singularity, which we define as follows.

Definition 2

Let Y be a compact manifold and $R>0$. A generalized warped product metric on $(0,R)\times Y$ is a smooth Riemannian metric of the form, with r the coordinate on (0, R),

$$\begin{aligned} g=dr^2+f(r)^2\, h_r\,,\qquad h_r = h(r,y)dy^2 \end{aligned}$$

(1)

where $f:(0,R)\rightarrow (0,\infty )$ is continuously differentiable and $h_r$ is a Riemannian metric¹ on Y for each $r\in [0,R)$, depending continuously differentiably on r. The function f is called the warping function. If h does not depend on r then g is called a warped product metric.

Of course, in (1) the factor $f^2$ could be incorporated into h, but we will be interested in the case where $f(r)\rightarrow 0$ as $r\rightarrow 0$ while h stays non-degenerate. In this case distances between points (r, y) and $(r',y')$ tend to zero as $r\rightarrow 0$, $r'\rightarrow 0$, so geometrically one may complete the metric at $r=0$ by adding a single point, which we call the singularity. We call the resulting metric space including the singularity a Riemannian space with isolated singularity. Figure 1 illustrates the idea.

Definition 3

In the setting of Definition 2, assume

the function f extends to a continuously differentiable map

$$\begin{aligned} f:[0,R) \rightarrow [0,\infty ) \nonumber \end{aligned}$$

which satisfies

$$\begin{aligned} f(0)=0\,,\quad f \text { convex}. \end{aligned}$$

(2)

If $f'(0)>0$ then we speak of a conical singularity, while if $f'(0)=0$ then we speak of a cuspidal singularity.

Remark 4

The convexity of f is not needed in the conical case if f extends to a $C^2$-function $f:[0,R)\rightarrow [0,\infty )$. See Remark 8 (a)-(c) below. See Remark 8 (d) for some typical examples of warping functions covered by this work.

1.2 Results

We give a detailed description of the geodesics in the pointed neighbourhood $(0,R)\times Y$ of the conical/cuspidal singularity. We write geodesics as

$$\begin{aligned} \gamma :I\rightarrow (0,R)\times Y,\qquad \gamma (t)=(r(t),y(t)), \end{aligned}$$

$I\subset {\mathbb {R}}$ an interval, and assume unit speed, $\vert \dot{\gamma }\vert _g\equiv 1$, i.e. $\dot{r}^2 + f(r)^2 |\dot{y}|^2 \equiv 1$, where a dot always indicates the derivative with respect to t and $|\dot{y}|$ is the length with respect to $h_r$.

First, we have the following dichotomy.

Theorem A

(Radial and winding geodesics). Let g be a generalized warped product metric on $(0,R)\times Y$ as in (1). Then any geodesic is of one of the following types.

radial:

y is constant, and $\dot{r}$ is constant equal to 1 or $-1$.

winding:

$\dot{y}(t)\ne 0$ for all t.

If the warping function satisfies (2) and if $R>0$ is small enough, then any maximal winding geodesic $\gamma :I\rightarrow (0,R)\times Y$ satisfies in addition:

• (a) The function $t\mapsto r(t)$ is strictly convex.

• (b) $\gamma$ has finite length, i.e. $I=(T_-,T_+)$ with $T_\pm \in {\mathbb {R}}$.

• (c) $\gamma$ enters and leaves at $r=R$, i.e. $r(t)\rightarrow R$ as $t\rightarrow T_\pm$.

In the warped product case, $t\mapsto y(t)$ is a time reparametrised geodesic of (Y, h).

In the sequel, all geodesics will be assumed to be maximal, i.e. their domain I cannot be enlarged.

We now give a more precise description of the winding geodesics $\gamma =(r,y)$. By (a) and (c) above, r assumes its minimum at a unique time, which we may and will always take to be $t=0$. We write $\delta =r(0)$ for the minimum. Since geodesics are uniquely determined by their initial point, we get a parametrisation

$$\begin{aligned} (0,R) \times SY \rightarrow \{\text {winding geodesics}\} \,,\quad (\delta , y_0,v_0)\mapsto \gamma _{\delta ,y_0,v_0} \end{aligned}$$

(3)

where $SY=\{(y,v)\in TY:\ |v|_{h_0}=1\}$ is the unit tangent bundle and $\gamma _{\delta ,y_0,v_0}$ is the maximal geodesic starting at $(\delta ,y_0)$ in direction $(0,v_0)\in T_{(\delta ,y_0)}((0,R)\times Y)$.

The next two theorems describe the behaviour of winding geodesics as $\delta \rightarrow 0$. Theorem B describes how the radial component $r_{\delta }$ behaves, including a comparison theorem. Theorem C describes the Y component $y_{\delta }$, in particular the asymptotics of its length.

Theorem B

(Radial component of geodesics). Let (X, d) be a Riemannian space with an isolated conical or cuspidal singularity, and assume R is small enough so (8) is satisfied.

• (a) Let $\gamma _\delta =(r_\delta ,y_\delta ):I_\delta \rightarrow (0,R)\times Y$, $\delta \in (0,R)$, be any family of unit speed geodesics, with $\min _t r_\delta (t)=r_\delta (0)=\delta >0$, with maximal interval of existence $I_\delta$.

  As $\delta \rightarrow 0$ we have $I_\delta \rightarrow (-R,R)$ (i.e. the endpoints of $I_\delta$ converge to $\pm R$) and

  $$\begin{aligned} r_\delta (t) \rightarrow |t| \text { for all } t\in (-R,R). \end{aligned}$$

• (b) In the case of a warped product with convex warping function f, the following comparison principle holds. If $\gamma$, $\overline{\gamma }$ are two unit speed geodesics which both reach their lowest point at $t=0$, and if $r(0)<\overline{r}(0)$, then $r(t)<\overline{r}(t)$ for all time t.

In fact, we have precise error estimates for the convergence in (a), see Lemma 15. Note that combining (a) and (b) we obtain

$$\begin{aligned} r(t)> |t| \text { for all }t \end{aligned}$$

in the warped product case, for any winding geodesic. This is not obvious even for a conical surface.

Theorem C

(Angular component of geodesics) Assume the setup of Theorem B, and let $\gamma _\delta =(r_\delta ,y_\delta )$ be a family of geodesics as in part (a) of that theorem. Assume that the warping function f satisfies the non-oscillation condition (7).

• (a) The length of the Y-projection of $\gamma _\delta$,

  $$\begin{aligned} \ell (y_{\delta }):= \int _{I_\delta } \vert \dot{y}_{\delta }(t) \vert _{h}\, dt \end{aligned}$$

  satisfies

  $$\begin{aligned} \ell (y_{\delta })\sim \frac{C_f}{f'(\delta )}, \end{aligned}$$

  (4)

  where $\sim$ means that the quotient of the left hand side by the right hand side tends to one as $\delta \rightarrow 0$ and

  $$\begin{aligned} C_f:= \int _{-\frac{\pi }{2}}^{\frac{\pi }{2}} \mathfrak {F}\left( \frac{1}{\cos (\vartheta )}\right) \, d\vartheta \end{aligned}$$

  with $\mathfrak {F}$ defined in (7). The constant $C_f$ satisfies

  $$\begin{aligned} 2\le C_f\le \pi , \end{aligned}$$

  with $C_f=\pi$ in the conical case and $C_f\rightarrow 2$ for $f(x)=x^{\alpha }$ as $\alpha \rightarrow \infty$. The sharper the cusp, the smaller is $C_f$ (see (40) for a precise statement).

• (b) Suppose that $y_\delta (0)\rightarrow y_0$, $f(\delta )\dot{y}_\delta (0)\rightarrow v_0$ as $\delta \rightarrow 0$ for some $(y_0,v_0)\in SY$. Let $\tilde{y}:\tilde{I}\rightarrow Y$ be the unit speed geodesic in $(Y,h_0)$ satisfying $\tilde{y}(0)=y_0$, $\dot{\tilde{y}}(0)=v_0$, where

  $$\begin{aligned}{} & {} \tilde{I}=(-\frac{\pi }{2},\frac{\pi }{2}) \text { in the conical case with } f'(0)=1, \\{} & {} \tilde{I}={\mathbb {R}}\text { in the cuspidal case.} \end{aligned}$$

  Then $y_\delta$ converges after unit speed reparametrisation to $\tilde{y}$, uniformly on compact subsets of $\tilde{I}$.

More explicitly, the statement in (b) is: Define the rescaled time $\tau$ by $\tau (0)=0$ and

$$\begin{aligned} \frac{d\tau }{dt} = |\dot{y}_\delta | \end{aligned}$$

(5)

Then for $\tilde{I}_\delta =\tau (I_\delta )$ and $\tilde{y}_\delta :\tilde{I}_\delta \rightarrow Y$ defined by $\tilde{y}_{\delta }(\tau (t))=y_{\delta }(t)$ we have, as $\delta \rightarrow 0$,

$$\begin{aligned} \tilde{I}_\delta \rightarrow \tilde{I}, \quad \text {and} \quad \tilde{y}_\delta \rightarrow \tilde{y}\text { uniformly on compact subsets of}\ \tilde{I}. \end{aligned}$$

The asymptotic length in (4) behaves as follows, as $\delta \rightarrow 0$:

$$\begin{aligned} \frac{C_f}{f'(\delta )}\rightarrow \frac{\pi }{f'(0)} \ \text { (conical case)},\quad \frac{C_f}{f'(\delta )} \rightarrow \infty \ \text { (cuspidal case).} \end{aligned}$$

This shows that parts (a) and (b) of the theorem are consistent, since $|\tilde{I}_\delta |=\ell (\gamma _\delta )$.

In particular, Theorem C(b) implies that every compact segment of a geodesic on Y (having length less than $\pi /f'(0)$ in the conical case) is the uniform limit of the Y-parts of some family $(\gamma _\delta )$ of geodesics on X.

Remark 5

• (1) It is worth stressing that the constant on the right hand side of (4) only depends on f, and not on h, the dimension, or any detailed description of $\gamma _{\delta }$. We discuss the function $\mathfrak {F}$ and the constant $C_f$ in more detail in Sect. 5, including bounds and several examples.

• (2) In the case of $Y=S^1$ of length $2\pi$ Equation (4) means that a geodesic which almost hits the singularity winds roughly $\frac{C_f}{2\pi }\cdot \frac{1}{f'(\delta )}$ times around the singularity before leaving. See Fig. 1 for a couple of illustrations.

• (3) The assumed convergence of the initial conditions of $y_\delta$ in part (b) of Theorem C is always satisfied after passing to a subsequence, by compactness.

1.3 Methods, outline of proofs

We formulate the geodesic equations as a Hamiltonian system of first order ODEs. In the warped product case, the equations for r completely decouple and depend only on f. The motion in the r-direction then determines the speed in the Y-direction via the unit speed condition. This allows us to study the asymptotic behaviour quite explicitly. In the generalized warped case, the equations of motion almost decouple. In particular, the leading order behaviour turns out to be the same as in the warped case, and we derive bounds which imply that the generalized warped case has the same asymptotic behaviour as the warped one.

Perhaps the most surprising of our results is the length asymptotics (4). Here is a quick rough explanation for the appearance of the term $f'(\delta )$, in the case of a cuspidal warped product metric: Denote by $\theta \in (-\frac{\pi }{2},\frac{\pi }{2})$ the angle between $\dot{\gamma }$ and the ‘circle’ of latitude $r=$ const, for a given geodesic $\gamma =\gamma _\delta$. Then $|\dot{\gamma }|=1$ implies $\cos \theta =f(r)|\dot{y}|$, $\sin \theta =\dot{r}$. The well-known Clairaut relation (which we rederive) says that $f(r)\cos \theta$ is constant along $\gamma$. Differentiating it in t we obtain $\dot{\theta }=f'(r)|\dot{y}|$, or $|\dot{y}|dt = \frac{1}{f'(r)}d\theta$. The length of $\gamma$ is obtained by integrating this, and (4) essentially follows from the fact that r is on the order of $\delta$ when $\theta$ is bounded away from $\pi /2$.

The structure of the paper is as follows. We start by describing the geometry of the spaces we work with in some more detail in Sect. 2. We proceed by stating the geodesic equations as a Hamiltonian system in Sect. 3. Here we also introduce several useful variables and deduce a Clairaut-like relation. Section 4 is the heart of the paper, where we analyse the equations of motion and prove Theorem A, B and C. Section 5 deals with the constant $C_f$ appearing in the length asymptotics (4), including explicit computations of it and the necessity of assuming convexity and that (7) exists. Section 6 relates our notion of conical/cuspidal spaces to metric-free definitions of such spaces. Here we also present some families of spaces for which our assumptions hold.

1.4 Related work and further remarks

Our results are new only in the cuspidal case but give a unified treatment of conical and cuspidal case. The conical case was treated by Melrose and Wunsch in [14, Definition 1.4, Lemma 1.5] in the context of wave propagation, after early work by Stone [16]. The first author discusses conical metrics in detail in [8].

The family of geodesics hitting the singularity was analysed for a more general class of k-cuspidal (i.e. $f(r)=r^k$, $k\ge 2$) metrics – those arising from differential k-cuspidal singularities, see Subsection 6.2 and in particular (48) – by Grandjean and the first author [6]. By Theorem A, the geodesics hitting the singularity are simply given by constant y, for generalized warped product metrics. In [6] it is shown that metrics on k-cuspidal singularities are not of generalized warped product form (see Subsection 6.2 and in particular (45) in the present work), and that the family of geodesics hitting the singularity has a more complicated structure in this setting.

Previously, Bernig and Lytchak [1] obtained first order information for geodesics on general real algebraic sets $X\subset {\mathbb {R}}^n$, by showing that any geodesic reaching a singular point p of X in finite time must have a limit direction at p.

For more on warped products and geodesics, one can consult [3, Section 7] and [15, Chapter 7].

2 Generalized warped product geometry

We start by being a bit more precise about the family of metrics $h_r$ in our definition of generalized warped products.

Assumption 6

(Regularity assumption) The metrics $h_r$ in the generalized warped product metric of Definition 2 are uniformly positive definite and depend uniformly $C^1$ on r. These uniformity conditions are equivalent to

$$\begin{aligned} -2c h \le \partial _r h \le 2c h \end{aligned}$$

(6)

for all $r\in (0,R)$, for some constant $c\ge 0$.

This implies that the family extends to a continuous family of metrics on $r\in [0,R]$.

Next, we introduce singular Riemannian spaces whose singularities are modelled on generalized warped products as defined above.

Definition 7

A metric space (X, d) is called a Riemannian space with an isolated conical or cuspidal singularity at $p\in X$ if

• $X\setminus \{p\}$ is a smooth manifold, and the metric d is induced by a Riemannian metric $g_X$ on $X\setminus \{p\}$;

• there is a neighbourhood U of p in X, a number $R>0$ and a compact manifold Y, and a continuous map

  $$\begin{aligned} \beta :[0,R) \times Y \rightarrow U \end{aligned}$$

  which sends $\{0\}\times Y$ to p and restricts to an isometry $\bigl ((0,R) \times Y, g\bigr ) \rightarrow \bigl (U\setminus \{p\},g_X\bigr )$ where g is a generalized warped product metric as in (1) and where f satisfies the conditions of Definition 3. As in that definition, if $f'(0)>0$ then we speak of a conical singularity, while if $f'(0)=0$ then we speak of a cuspidal singularity.

See Sect. 6 for examples, in particular for the proof that surfaces of revolution as indicated above fit into this framework, and for the relation of this notion of conical/cuspidal singularity to other natural such notions.

Remark 8

• (a) As remarked above, the warping function f is not uniquely determined by the metric g: Replacing f by af and h by $a^{-2}h$, where a is positive and $C^1$ on [0, R), yields the same metric. This is the only freedom, by the conditions on h. Thus, if we call two warping functions equivalent if they differ by such a factor a then g determines the equivalence class [f] of f, and it makes sense to speak of a singularity of type [f].

• (b) If f vanishes to finite order k at zero and is $C^{k+1}$ on [0, R) then it is equivalent to $f_k(r)=r^k$.

• (c) We use convexity of f in several arguments. However, if f is non-convex but there is an equivalent function af which is convex then it follows that Theorems A, B(a) hold verbatim and Theorem C holds with f replaced by af. For instance, this is true in the $C^2$ conical case. Note that convexity of f implies $f'(r)>0$ for $r>0$.

  The example of Sect. 5.3 demonstrates that the asymptotics of Theorem C can change without convexity. Convexity of f implies that the angle $\theta$ between a geodesic and the level sets $\{r\}\times Y$ increases in r, see (20). See also Remark 12 for an interpretation of the convexity of f in terms of curvature.

• (d) Some classes of functions f to have in mind are²

  • $f(x)=x^{\alpha }$ for $\alpha \in [1,\infty )$.

  • $f(x)=\exp \left( -\ln \left( \frac{1}{x}\right) ^{\mu }\right)$ for $\mu \in [1,\infty )$.

  • $f(x)= \exp \left( -\frac{1}{x^\beta }\right)$ for $\beta \in (0,\infty )$.

We will identify $U\setminus \{p\}$ with $(0,R)\times Y$. The map $\beta$ should be thought of as a generalization of polar coordinates: For $X={\mathbb {R}}^2$ the map

$$\begin{aligned} \beta :[0,\infty )\times S^1\rightarrow {\mathbb {R}}^2,\quad (r,\phi ) \mapsto (r\cos \phi ,r\sin \phi ) \end{aligned}$$

is an isometry over $r>0$ for the metric $dr^2+r^2d\phi ^2$ on $(0,\infty )\times S^1$ (where $S^1={\mathbb {R}}/2\pi {\mathbb {Z}}$) and the Euclidean metric on ${\mathbb {R}}^2\setminus \{0\}$. So $0\in {\mathbb {R}}^2$ can be considered a conical singularity in this sense, and the same is true for any smooth point of a Riemannian manifold (with Y equal to the sphere). The space $[0,\infty )\times Y$ is sometimes called the blow-up of X in p, and the map $\beta$ the blow-down map.

Note that, while g is a Riemannian metric in $r>0$, it is only positive semi-definite at $r=0$, with any two points at $r=0$ having distance zero with respect to g. This reflects the fact that the map $\beta$ crunches all points at $r=0$ to the single point p. The warping function determines the ’speed’ at which the crunching happens as $r\rightarrow 0$. Also, note that the form (1) of the metric implies that r is the distance to the singularity p.

Remark 9

There is no unique answer to the question what the ’correct’ definition of a Riemannian space with an isolated singularity is. While our notion of singularity is quite general in terms of f and $h_r$, it is somewhat restrictive in requiring that there are no mixed terms in the metric (1), i.e. that coordinates r, y can be chosen so that the lines $y=$ const are perpendicular to the hypersurfaces $r=$ const. See Sect. 6.2.2 for a natural example where this is not satisfied. We leave it for future work to analyse the geodesic flow for some of these more general metrics.

For Theorem C, we need f to satisfy the following condition:

Assumption 10

(Non-oscillation condition). For the inverse function $F:= f^{-1}$ the limit

$$\begin{aligned} \mathfrak {F}(\sigma ):= \lim _{\epsilon \rightarrow 0} \frac{F'(\sigma \epsilon )}{F'(\epsilon )} \end{aligned}$$

(7)

exists for $\sigma \in [1,\infty )$, and the convergence is uniform on compact subsets.

This condition is satisfied for the examples above. See Lemma 19 for a family of cuspidal examples where it is not satisfied. Furthermore, we need (except in Sect. 3) to limit the variation of $h_r$ over the interval (0, R):

Assumption 11

(Small perturbation condition). The constant c in (6) can be chosen so that

$$\begin{aligned} Rc<1. \end{aligned}$$

(8)

Of course this can be achieved by shrinking R. The condition (8) is used to prove (20) below, which in turn gets used implicitly several times.

Remark 12

The small perturbation condition along with the convexity of f has an interpretation in terms of the mean curvature of the level sets of r: A standard computation shows that the mean curvature vector of $\{r\}\times Y\subset (0,R)\times Y$ is $H=H_0\partial _r$ where

$$\begin{aligned} H_0 =-\dim (Y)\frac{f'}{f} - \frac{1}{2} \text {Tr}_h(\partial _r h). \end{aligned}$$

By the bound (6), we can bound $H_0$ as

$$\begin{aligned} -\dim (Y)\left( \frac{f'}{f}+c\right) \le H_0\le -\dim (Y) \left( \frac{f'}{f}-c\right) \end{aligned}$$

The convexity of f and $f(0)=0$ imply $\frac{f'(r)}{f(r)}\ge \frac{1}{r}\ge \frac{1}{R}$ (see Lemma 14), so the small perturbation condition implies a negative upper bound for the scalar mean curvature,

$$\begin{aligned} H_0\le -\frac{\dim (Y)}{R}(1-Rc)<0. \end{aligned}$$

We will not use this geometric interpretation directly.

3 Geodesic equations

In this section we analyse the geodesic equations for generalized warped product metrics of the type (1), but without extra conditions on the warping function f.

3.1 Review of the Hamiltonian approach

We use the Hamiltonian description of the geodesic flow. Recall that this means that (constant speed) geodesics on a Riemannian manifold (Y, h) are the projections to Y of curves in the cotangent bundle $T^*Y$, which are the integral curves of the Hamiltonian vector field for the Hamilton function ${\mathcal {H}}_h:T^*Y\rightarrow {\mathbb {R}}$,

$$\begin{aligned} {\mathcal {H}}_h(y,\eta ) = \frac{1}{2} |\eta |^2_{h_y} ,\quad \eta \in T^*_yY \end{aligned}$$

where by $h_y$ we also denote the metric on $T^*_yY$ dual to the metric $h_y$ on $T_yY$. In coordinates, $|\eta |^2_{h_y} = h^{ij}(y)\eta _i\eta _j$ where $(h^{ij})$ is the inverse matrix of $(h_{ij})$. Often we write simply $|\eta |_h$ or $|\eta |$. The Hamilton vector field is, in coordinates,

$$\begin{aligned} {\mathcal {X}}_h = \frac{\partial {\mathcal {H}}_h}{\partial \eta }\partial _y - \frac{\partial {\mathcal {H}}_h}{\partial y} \partial _\eta \end{aligned}$$

so its integral curves, also called lifted geodesics, are solutions $t\mapsto (y(t),\eta (t))$ of the system of differential equations

$$\begin{aligned} \dot{y}= \frac{\partial {\mathcal {H}}_h}{\partial \eta }(y,\eta )\qquad \dot{\eta }= - \frac{\partial {\mathcal {H}}_h}{\partial y} (y,\eta ) . \end{aligned}$$

Geodesics are then the y(t) parts of solutions of this system. It is a basic fact that the Hamiltonian function is constant along integral curves, i.e. ${\mathcal {H}}_h(y(t),\eta (t))=$ const. Note that

$$\begin{aligned} \frac{\partial {\mathcal {H}}_h}{\partial \eta } (y,\eta ) = \eta ^\sharp \end{aligned}$$

where $\eta \mapsto \eta ^\sharp$, $T^*Y\rightarrow TY$ is the isomorphism induced by the metric. In coordinates, $(\eta ^\sharp )^i =h^{ij} \eta _j$. So for a geodesic $t\mapsto y(t)$ its lift is the curve $(y(t),\eta (t))$ where $\eta ^\sharp (t)=\dot{y}(t)$, and this explains the relationship of the Hamiltonian approach to geodesics (with lift in the cotangent bundle) to the more standard approach where the lift is the curve $(y(t),\dot{y}(t))$ in the tangent bundle.

3.2 Geodesic equations for generalized warped product metrics

We apply this general discussion with Y replaced by $(0,R)\times Y$, with the metric g in (1). Points are denoted (r, y), and the dual cotangent variables are denoted $(\xi ,\eta )$, so $\xi \in {\mathbb {R}}$, $\eta \in {\mathbb {R}}^{n-1}$ in coordinates. The Hamilton function is

$$\begin{aligned} {\mathcal {H}}_g=\frac{1}{2} \left( \xi ^2 +\frac{\vert \eta \vert ^2_h}{f(r)^2}\right) \end{aligned}$$

(9)

As mentioned above, ${\mathcal {H}}_g$ is constant along integral curves. We will always consider unit speed geodesics, i.e. integral curves lying on the hypersurface ${\mathcal {H}}_g=\frac{1}{2}$, or

$$\begin{aligned} 1 = \xi ^2 + \frac{\vert \eta \vert ^2_h}{f(r)^2}. \end{aligned}$$

(10)

We calculate the Hamilton vector field for ${\mathcal {H}}_g$. Since ${\mathcal {H}}_g$ depends on $y,\eta$ only through $|\eta |^2_h$ we have

$$\begin{aligned} {\mathcal {X}}_g = {\mathcal {X}}_{\textrm{rad}}+ \frac{1}{f(r)^2} {\mathcal {X}}_h \end{aligned}$$

(11)

where ${\mathcal {X}}_{\textrm{rad}}= \frac{\partial {\mathcal {H}}_g}{\partial \xi }\partial _r -\frac{\partial {\mathcal {H}}_g}{\partial r}\partial _\xi$ governs the radial motion and ${\mathcal {X}}_h$ is the Hamilton vector field of ${\mathcal {H}}_h$, hence governs the motion in the Y directions. Recall that the latter depends parametrically on r since h does, and as such defines a family of vector fields on Y.

We first observe that ${\mathcal {X}}_g$ is tangential to the submanifold $\{\eta =0\}$ since the $\partial _\eta$ coefficient, which is $-f(r)^{-2}\partial |\eta |^2_{h_y} / \partial y$, vanishes at $\eta =0$. This implies that any integral curve of ${\mathcal {X}}_g$ satisfies

$$\begin{aligned} \text {either}\ \eta (t)=0\ \text {for all}\ t\ \text {or} \ \eta (t)\ne 0\ \text {for all}\ t. \end{aligned}$$

The Hamilton equations for $\dot{r}$ and $\dot{y}$ are

$$\begin{aligned} \dot{r}= \frac{\partial {\mathcal {H}}_g}{\partial \xi } = \xi , \quad \dot{y}= \frac{\partial {\mathcal {H}}_g}{\partial \eta } = \frac{1}{f(r)^2}\frac{\partial {\mathcal {H}}_h}{\partial \eta } = \frac{1}{f(r)^2}\eta ^\sharp . \end{aligned}$$

From this we deduce the first part of Theorem A: Geodesics with $\eta \equiv 0$ have constant y, and $\dot{r}=\xi \equiv \pm 1$ by the unit speed condition (10), so they are radial. All other geodesics have $\dot{y}(t)\ne 0$ for all t, so they are winding.

We now consider winding geodesics, i.e. $\eta (t)\ne 0$ for all t, and derive the full Hamilton equations for them. Calculating $\frac{\partial {\mathcal {H}}_g}{\partial r} = \frac{\vert \eta \vert ^2_h}{f(r)^2} \left( -\frac{f'(r)}{f(r)} + \frac{\partial _r|\eta |}{|\eta |}\right)$ and using (10) we get

$$\begin{aligned} {\mathcal {X}}_{\textrm{rad}}= \xi \partial _r + (1-\xi ^2) \left( \frac{f'(r)}{f(r)} - \tfrac{\partial _r|\eta |}{|\eta |}\right) \partial _\xi \end{aligned}$$

(12)

We write $\tfrac{\partial _r|\eta |}{|\eta |}$ in small font to emphasize that it is to be considered as a small perturbation (it vanishes in the warped product case). Correspondingly, the lifted geodesics are solutions $t\mapsto (r(t),y(t),\xi (t),\eta (t))$ of the system

$$\begin{aligned} \dot{r}&=\xi \quad \dot{\xi }=(1-\xi ^2)\left( \frac{f'(r)}{f(r)} -\tfrac{\partial _r|\eta |}{|\eta |}\right) \end{aligned}$$

(13)

$$\begin{aligned} \dot{y}&=f(r)^{-2} \,\partial _\eta {\mathcal {H}}_h \quad \dot{\eta }=-f(r)^{-2}\, \partial _y {\mathcal {H}}_h \end{aligned}$$

(14)

By (10), (2), and the assumption $\eta (t)\ne 0$ for all t, the variable $\xi$ is constrained to lie in $(-1,1)$, so we may introduce a new variable $\theta$ (i.e. coordinate on the hypersurface ${\mathcal {H}}_g=\frac{1}{2}$) by

$$\begin{aligned} \xi = \sin \theta ,\qquad \theta \in \left( -\frac{\pi }{2},\frac{\pi }{2}\right) . \end{aligned}$$

This will simplify the calculations below. The equations (13) then turn into

$$\begin{aligned} \dot{r}= \sin \theta \quad \dot{\theta }= \left( \frac{f'(r)}{f(r)} - \tfrac{\partial _r|\eta |}{|\eta |}\right) \cos \theta \end{aligned}$$

(13')

and the unit speed condition (10) turns into

$$\begin{aligned} f(r) \cos \theta = |\eta |\,. \end{aligned}$$

(15)

Note that $\dot{r}=\sin \theta$, $|\dot{\gamma }|=1$ implies that $\theta$ is the angle between $\dot{\gamma }$ and the ’circle of latitude’ $\{r\}\times Y$.

3.3 The warped product case; Clairaut’s integral

In the warped product case, i.e. where h does not depend on r, two simplifications happen: The vector field ${\mathcal {X}}_{\textrm{rad}}$ is independent of $\eta$ since the term $\partial _r|\eta |$ vanishes, and the vector field ${\mathcal {X}}_h$ is independent of r.

This means that lifted geodesics $t\mapsto (r(t),\theta (t),y(t),\eta (t))$ are given as follows:

• (1) $(r(t),\theta (t))$ solves the system (13’)

• (2) $(y(t),\eta (t))$ is an integral curve for the Hamilton vector field ${\mathcal {X}}_h$, but with time reparametrised using the factor $f(r)^{-2}$ with $r=r(t)$ obtained in step 1.

Here we use that the vector field ${\mathcal {H}}_h$ and the time-dependent vector field $\frac{1}{f(r(t))^2}{\mathcal {H}}_h$ on Y have the same integral curves except for time reparametrisation. We also see that, along each integral curve,

$$\begin{aligned} f(r)\cos \theta = {\textrm{const}}\,, \end{aligned}$$

(16)

either by direct calculation from (13’) or using (15) and the fact that $|\eta |$ is constant along integral curves for ${\mathcal {X}}_h$. The relation (16) completely determines the solutions of the $r,\theta$ system up to time parametrisation.

The expression on the left of (16) is known as Clairaut’s integral in the context of surfaces of revolution.

3.4 Estimates for the deviation from the warped product case

If h depends on r then the ‘Clairaut integral’ $f(r)\cos \theta$ is not constant along geodesics, but we can estimate its variation.

By (15) the Clairaut integral equals $|\eta |$, so we consider this quantity. Note that $|\eta |=|\eta |_h$ depends on r through h.

We recall that Assumption 6 says

$$\begin{aligned} -2ch \le \partial _r h \le 2ch \end{aligned}$$

(6')

for a constant $c\ge 0$.

Lemma 13

With c as above, we have for any $\eta \in T^*Y\setminus \{0\}$:

$$\begin{aligned} -c\le \tfrac{\partial _r \vert \eta \vert }{\vert \eta \vert } \le c\,. \end{aligned}$$

(17)

Furthermore, along any lifted geodesic we have

$$\begin{aligned} \left| \frac{d}{dt}|\eta | \right| \le c|\eta | \, \vert \sin \theta \vert \end{aligned}$$

(18)

Estimate (18) quantifies the fact that lifted geodesics are tangent to $\{\eta =0\}$.

Proof

Let $h^{-1}$ denote the inverse of h considered as a matrix in some local coordinates. We multiply (6’) by $h^{-1}$ from left and right to get $-2ch^{-1} \le \partial _r h^{-1} \le 2ch^{-1}$ and therefore $-2c\vert \eta \vert ^2 \le \partial _r \vert \eta \vert ^2\le 2c\vert \eta \vert ^2$. This implies (17).

Lifted geodesics are integral curves of ${\mathcal {H}}_g$, and along such a curve we have

$$\begin{aligned} \frac{d}{dt}{\mathcal {H}}_h&= (\partial _y {\mathcal {H}}_h) \dot{y}+ (\partial _\eta {\mathcal {H}}_h) \dot{\eta }+ (\partial _r {\mathcal {H}}_h) \dot{r}\\&= (\partial _r {\mathcal {H}}_h) \dot{r}\end{aligned}$$

using (14), and this gives $\frac{d}{dt}|\eta | = \partial _r|\eta | \sin \theta$ from which we deduce (18) using (17). $\square$

4 Proofs of the main theorems

In this section we use the results from the previous section in combination with the properties (2) of f to prove Theorems A, B, and C.

First, we supplement the estimates in Lemma 13 by estimates that use the special properties of f.

Lemma 14

A warping function f as in (2) satisfies

$$\begin{aligned} \frac{f'(r)}{f(r)} \ge \frac{1}{r} \end{aligned}$$

(19)

Furthermore, if $R<\frac{1}{c}$ (with c satisfying (6)) then along any lifted winding geodesic we have

$$\begin{aligned} \dot{\theta }> 0 \end{aligned}$$

(20)

Proof

(19) follows from $f(0)=0$ and the convexity of f: $f(r)=\int _0^r f'(s)\,ds \le r f'(r)$.

The equation (13’) for $\dot{\theta }$ along with (19) and (17) imply $\dot{\theta }\ge (\frac{1}{r}-c)\cos \theta$. Also $\cos \theta >0$ for winding geodesics, which gives the second claim. $\square$

Proof of Theorem A

By the Clairaut-like relation (15), we see that $\cos \theta \ne 0$ for winding geodesics. From $\dot{r}=\sin \theta$ and (20) we get

$$\begin{aligned} \ddot{r}=\dot{\theta }\cos \theta > 0, \end{aligned}$$

so r is strictly convex. Then (b), (c) follow easily since geodesics exist as long as $r<R$.

The statement about reparametrisation in the warped product case was explained in Sect. 3.3. $\square$

For the proof of Theorem B it is useful to introduce two new variables $\rho$ and u (i.e. functions on $(0,R)\times Y$, resp. its cotangent bundle), defined by the identities:

$$\begin{aligned} \rho&= f(r) \nonumber \\ \rho \sin \theta&= f(u) \end{aligned}$$

(21)

We will use the following bounds on the variation of $\eta$ and r along a geodesic.

Lemma 15

Assume $R<\frac{1}{c}$, with c defined in (6). Let $\gamma _\delta$ be a family of geodesics as in Theorem B(a). Then

$$\begin{aligned}&f(\delta )e^{-c(r_\delta -\delta )}\le \vert \eta _\delta \vert \le f(\delta )e^{c(r_\delta -\delta )}. \end{aligned}$$

(22)

$$\begin{aligned}&(1-C\delta )\,\vert t\vert \le r_{\delta }(t) \le \vert t\vert +\delta \end{aligned}$$

(23)

holds for all time t and all $\delta$. Here $C=ce^{cR}$.

Proof of Lemma 15

We will drop all $\delta$-subscripts, writing $r=r_{\delta }$ and so on. We may assume $t>0$. Then $\theta >0$ since $\theta (0)=0$ and $\dot{\theta }>0$ by (20).

We first prove (22). We rewrite (18) as $\bigl |\frac{d}{dt}\log |\eta |\bigr | \le c \sin \theta = c\dot{r}$, so

$$\begin{aligned} -c\dot{r}\le \frac{d}{dt}\log |\eta | \le c\dot{r}. \end{aligned}$$

We integrate this from $t=0$ and exponentiate. Using $r(0)=\delta$ and $|\eta (0)| = f(\delta )$ (from (15) since $\theta (0)=0$) we get (22).

We now prove (23). The unit speed condition implies $\vert \dot{r}(t)\vert \le 1$, so

$$\begin{aligned} r(t)-\delta =r(t)-r(0)=\int _0^t \dot{r}(s)\, ds\le t. \end{aligned}$$

This gives the upper bound in (23)

For the lower bound we first consider the warped product case, for which $c=0$, hence $C=0$, so we need to show

$$\begin{aligned} \vert t\vert \le r_{\delta }(t). \end{aligned}$$

(24)

Differentiating $f(u)=f(r)\sin \theta$ in t we get

$$\begin{aligned} \dot{u}f'(u) = \dot{r}f'(r)\sin \theta + \dot{\theta }f(r)\cos \theta \end{aligned}$$

(25)

which by virtue of $\dot{r}=\sin \theta$, $\dot{\theta }=\frac{f'(r)}{f(r)}\cos \theta$ simplifies to

$$\begin{aligned} \dot{u}f'(u) = f'(r) \end{aligned}$$

(26)

Now $f(u)\le f(r)$ by (21), so $u\le r$ since f is strictly increasing. Then $f'(u)\le f'(r)$ since $f'$ is increasing. So (26) implies

$$\begin{aligned} \dot{u}\ge 1. \end{aligned}$$

From $u(0)=0$ we now get $t\le u(t)\le r(t)$ as claimed.

Now we prove the lower bound in (23) for the generalized warped product case. In fact, we will prove the stronger lower bound

$$\begin{aligned} \left( 1-C\frac{f(\delta )}{f'(\delta )}\right) |t| \le r_\delta (t) \end{aligned}$$

(27)

which implies (23) by (19).

We use (25) again, but now we have the extra summand $-\frac{\partial _r|\eta |}{|\eta |}\cos \theta$ in $\dot{\theta }$ (see (13’)), which equals $-\frac{\partial _r|\eta |}{f(r)}$ by (15). Therefore, (26) is replaced by

$$\begin{aligned} \dot{u}f'(u) = f'(r) - \partial _r|\eta |\,\cos \theta = f'(r)\left[ 1-\frac{\partial _r|\eta |}{f'(r)} \cos \theta \right] \end{aligned}$$

This implies (27) by the same argument as in the warped case, provided

$$\begin{aligned} 1-\frac{\partial _r|\eta |}{f'(r)} \cos \theta \ge 1 -C\frac{f(\delta )}{f'(\delta )}\,. \end{aligned}$$

Finally, this inequality follows from $f'(r)\ge f'(\delta )$ (since $r\ge \delta$ and $f'$ is increasing), $\cos \theta \le 1$, and $\partial _r|\eta | \le C f(\delta )$. The latter inequality follows from (17) and (22), with $C=c e^{cR}$. $\square$

Proof of Theorem B

By symmetry, it suffices to consider the $t>0$ part of the geodesics. Then $\theta >0$ since $\theta (0)=0$ and $\dot{\theta }>0$. We write $I_{\delta }=(T_-^{\delta },T_+^{\delta })$. By Theorem A part (b) and (c), we have $r_{\delta }(T_{\pm }^{\delta }):= \lim _{t\rightarrow T_{\pm }^{\delta }} r_{\delta }(t)=R$. By Lemma 15, we therefore have

$$\begin{aligned} (1-C\delta )\vert T_{\pm }^{\delta }\vert \le R \le \vert T_{\pm }^{\delta }\vert +\delta , \end{aligned}$$

and sending $\delta \rightarrow 0$ gives

$$\begin{aligned} T_{\pm }^{\delta }\xrightarrow {\delta \rightarrow 0} \pm R. \end{aligned}$$

Also $r_\delta (t)\rightarrow |t|$ follows from (23).

It remains to prove (b) in the warped product case. So let $\gamma =(r,y)$ and $\overline{\gamma }=(\overline{r},\overline{y})$ be two geodesics with $\delta =r(0)$, $\overline{\delta } =\overline{r}(0)$ and $\delta < \overline{\delta }$. We write u and $\overline{u}$ for the function defined in (21) associated to r and $\overline{r}$ respectively. By the Clairaut-like relation (16) and the definition of u (21) we have

$$\begin{aligned} f(r)^2=f(u)^2+f(\delta )^2 \end{aligned}$$

(28)

and similarly for $f(\overline{r})$. Since $\partial _r h=0$, we may use (26) to find

$$\begin{aligned} \frac{d}{dt}f(u)=f'(r). \end{aligned}$$

(29)

and similarly for $f(\overline{u})$. The convexity of f then implies

$$\begin{aligned} \frac{d}{dt}\left( f(\overline{u})-f(u)\right) \ge 0 \end{aligned}$$

for all t such that $\overline{r}(t)\ge r(t)$. Assume for contradiction that there is a maximal $t_0<T_{\delta }$ such that $\overline{r}(t)>r(t)$ on $[0,t_0)$. By continuity, $r(t_0)=\overline{r}(t_0)$. By (29), we therefore have

$$\begin{aligned} f(\overline{u}(t_0))-f(u(t_0))=\int _0^{t_0} f'(\overline{r}(t)) -f'(r(t))\, dt\ge 0. \end{aligned}$$

Inserting this into (28), we find

$$\begin{aligned} f(\overline{r}(t_0))^2-f(\overline{\delta })^2 =f(\overline{u}(t_0))^2\ge f(u(t_0))^2=f(r(t_0))^2-f(\delta )^2 \end{aligned}$$

which rearranges to yield

$$\begin{aligned} f(\overline{r}(t_0))^2-f(r(t_0))^2 \ge f(\overline{\delta })^2-f(\delta )^2>0. \end{aligned}$$

This shows $\overline{r}(t_0)>r(t_0)$, contradicting the maximality of $t_0$. $\square$

Remark 16

The proof of the comparison theorem might seem a bit indirect, using f(u(t)) instead of r(t). The reason being that it is in general false that $\overline{r}(t)-r(t)$ is increasing. Indeed, for the conical case $f(r)=r$, one can solve the equation of motion explicitly to find $r(t)=\sqrt{t^2+\delta ^2}$, and $\overline{r}(t)-r(t)$ is strictly decreasing but never 0 when $\overline{\delta }>\delta$. The auxiliary function f(u(t)) is in this conical case simply $f(u(t))=t=f(\overline{u}(t)$, so $f(\overline{u}(t))-f(u(t))=0$ is increasing.

Proof of the first part of Theorem C

We will use the coordinates $\rho =f(r)$ and $\sin \theta =\xi$ again. We will drop the $\delta$-subscripts on all the variables. Since (20) says $\dot{\theta }>0$, we can and will parametrise using $\theta$ instead of t. From the equation of motion (14), and the Clairaut-like relation (16), we have

$$\begin{aligned} \vert \dot{y}\vert =\frac{\cos (\theta )}{\rho } \end{aligned}$$

(30)

(we write $\vert \dot{y}\vert = \vert \dot{y}\vert _h:= \vert \dot{y}\vert _{h_{r_\delta (t)}}$).

Recall that F is the inverse function of f. Using the equation of motion (13’), $\partial _r = f'(r)\partial _\rho$ and $\frac{1}{f'(r)}=F'(\rho )$ we can write the measure as

$$\begin{aligned} \vert \dot{y}\vert dt=\frac{F'(\rho )}{1-\rho \partial _\rho \log \vert \eta \vert )}\, d\theta \,. \end{aligned}$$

(31)

We again start by assuming h does not depend on r, since the argument becomes more transparent in this case. In this case the formula (31) simplifies to the elegant

$$\begin{aligned} \vert \dot{y}\vert dt =F'(\rho )\,d\theta , \end{aligned}$$

and one can use the Clairaut-like relation (16) to find

$$\begin{aligned} \rho =\frac{\rho _0}{\cos (\theta )}, \end{aligned}$$

where $\rho _0:= f(\delta )$. Hence

$$\begin{aligned} f'(\delta ) \vert \dot{y}\vert dt=\frac{1}{F'(\rho _0)}\vert \dot{y}\vert dt=\frac{F'\left( \frac{\rho _0}{\cos \theta }\right) }{F'(\rho _0)}\, d\theta . \end{aligned}$$

(32)

When f is convex, $F'$ is decreasing, and the right hand integrand is bounded by 1. So by the dominated convergence theorem and the non-oscillation condition (7),

$$\begin{aligned} \lim _{\delta \rightarrow 0} f'(\delta )\int _{T_-}^{T_+} \vert \dot{y}\vert dt=\int _{-\pi /2}^{\pi /2} \lim _{\rho _0\rightarrow 0} \frac{F'\left( \frac{\rho _0}{\cos \theta }\right) }{F'(\rho _0)}\, d\theta =\int _{-\pi /2}^{\pi /2} \mathfrak {F} \left( \frac{1}{\cos \theta }\right) \, d\theta =C_f. \end{aligned}$$

This proves part (a) when h is independent of r. For the general case, we return to (31). Using the bounds (17) again results in

$$\begin{aligned} \frac{F'(\rho )}{1+c\rho F'(\rho )}\, d\theta \le \vert \dot{y}\vert dt\le \frac{F'(\rho )}{1-c\rho F'(\rho )}\, d\theta . \end{aligned}$$

Since F is concave and $F(0)=0$, we have $\rho F'(\rho )\le F(\rho )$, thus

$$\begin{aligned} \frac{F'(\rho )}{1+c F(\rho )}\, d\theta \le \vert \dot{y}\vert dt\le \frac{F'(\rho )}{1-c F(\rho )}\, d\theta \,. \end{aligned}$$

(33)

We therefore need bounds on both sides of (33). Recall that $\rho$ is a function of $\delta$ and $\theta$. We consider its behaviour as $\delta \rightarrow 0$ for fixed $\theta$. The bounds (22) say, since $|\eta |=\rho \cos \theta$,

$$\begin{aligned} \frac{f(\delta )}{\cos \theta } e^{-c({r}-\delta )}\le {\rho } \le \frac{f(\delta )}{\cos \theta } e^{c({r}-\delta )}, \end{aligned}$$

(34)

so

$$\begin{aligned} \lim _{\delta \rightarrow 0} {\rho (\theta )}=0 \end{aligned}$$

for every $\theta \in (-\frac{\pi }{2},\frac{\pi }{2})$. But then also ${r}=F({\rho })\xrightarrow {\delta \rightarrow 0}0$. Hence, using (34) and $f(\delta )=\rho _0$ we get

$$\begin{aligned} \lim _{\delta \rightarrow 0} \frac{{\rho }}{\rho _0}\cos \theta =1. \end{aligned}$$

Since, per assumption,

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \frac{F'(\epsilon \sigma )}{F'(\epsilon )} =\mathfrak {F}(\sigma ) \end{aligned}$$

and the convergence is uniform on compacts, we have

$$\begin{aligned} \lim _{\delta \rightarrow 0} \frac{F'({\rho })}{F'(\rho _0)(1\pm cF({\rho }))} =\lim _{\delta \rightarrow 0} \frac{F'\left( \frac{{\rho }}{\rho _0} \cos \theta \cdot \frac{\rho _0}{\cos \theta }\right) }{F'(\rho _0)} =\mathfrak {F}\left( \frac{1}{\cos \theta }\right) . \end{aligned}$$

Both the upper and lower bounds in (33) are bounded functions, hence integrable. By the dominated convergence theorem again, we find

$$\begin{aligned} \int _{-\pi /2}^{\pi /2} \mathfrak {F} \left( \frac{1}{\cos \theta }\right) \, d\theta \le \lim _{\delta \rightarrow 0} f'(\delta ) \ell (y_{\delta }) \le \int _{-\pi /2}^{\pi /2} \mathfrak {F} \left( \frac{1}{\cos \theta }\right) \, d\theta . \end{aligned}$$

This proves part (a) in general. $\square$

We now turn to the second part of Theorem C. We will rescale the time $\tau$ according to (5),

$$\begin{aligned} \frac{d\tau }{dt}=\vert \dot{y}_{\delta }\vert =\frac{\vert \eta \vert }{f(r(t))^2}. \end{aligned}$$

subject to $\tau (0)=0$. We also introduce the rescaled angular momentum variable

$$\begin{aligned} \overline{\eta }(t):= \frac{\eta (t)}{f(\delta )}, \end{aligned}$$

(35)

which by (14) implies $\overline{\eta }^{\#}(0)=f(\delta )\dot{y}(0)$. We recall our convention for the time-rescaled variables,

$$\begin{aligned} \tilde{y}(\tau (t)):= y(t), \quad \tilde{\eta }(\tau (t)) :=\overline{\eta }(t). \end{aligned}$$

For most of the proof, we will not write out the $\delta$-subscript on $y,\tilde{y},\eta ,\tilde{\eta }$. We will use a slash $'$ for $\tau$-derivatives and a dot $\dot{}$ for t-derivatives. Recall that we assume $\tilde{\eta }(0)=\overline{\eta }(0)=f(\delta ) \dot{y}(0)\rightarrow v_0$ as $\delta \rightarrow 0$.

Proof of the second part of Theorem C

By the unit speed parametrisation, the length of the time interval is the same as the length of the Y-component of the geodesic

$$\begin{aligned} \Delta \tau =\int _{T_-^{\delta }}^{T_+^{\delta }} \frac{d\tau }{dt} \, dt=\ell (y_\delta ). \end{aligned}$$

By the first part of Theorem C, this has the asymptotic behaviour

$$\begin{aligned} \Delta \tau \sim \frac{C_f}{f'(\delta )}. \end{aligned}$$

(36)

The equations of motion (14) get rescaled by $\frac{dt}{d\tau }$ and read

$$\begin{aligned} \tilde{\eta }'(\tau )=\frac{\dot{\eta }(t)}{f(\delta )\vert \dot{y}\vert }=-\frac{\partial _y \vert \tilde{\eta }\vert ^2}{2\vert \tilde{\eta } \vert } \quad \qquad \tilde{y}' = \frac{\tilde{\eta }^\sharp }{|\tilde{\eta }^\sharp |}\,. \end{aligned}$$

(37)

We stress that $\tilde{\eta }$ is both a rescaled and time-reparametrised quantity. We first observe that the bound (22) tells us

$$\begin{aligned} C'\le \vert \tilde{\eta }\vert \le C \end{aligned}$$

uniformly in $\tau$ and $\delta$, where $C'>0$. Furthermore, since h is $C^1$ in the y-directions and uniformly non-degenerate down to $r=0$, we can find a constant $\tilde{c}\ge 0$ such that

$$\begin{aligned} \left| \partial _y \vert \tilde{\eta }\vert ^2\right| \le 2\tilde{c}\vert \tilde{\eta }\vert ^2, \end{aligned}$$

hence, by the unit speed condition and equation of motion (37) respectively,

$$\begin{aligned} d( \tilde{y}_{\delta }(\tau ),\tilde{y}_{\delta }(\sigma )) \le \int _{\sigma }^{\tau } \left| \tilde{y}_{\delta }' (\upsilon )\right| \, d\upsilon \le \vert \tau -\sigma \vert , \end{aligned}$$

and

$$\begin{aligned} \vert \tilde{\eta }_{\delta }(\tau )-\tilde{\eta }_{\delta } (\sigma )\vert =\left| \int _{\sigma }^{\tau } \tilde{\eta }_{\delta }'(\upsilon )\, d\upsilon \right| \le \tilde{C} \vert \tau -\sigma \vert . \end{aligned}$$

This shows that the families $\tilde{y}_{\delta },\tilde{\eta }_{\delta }$ are uniformly (in $\tau$ and $\delta$) Lipschitz continuous. Let $K\subset \tilde{I}_{\delta }$ be any compact subset. By the Arzelà-Ascoli theorem, there is a subsequence $\delta _n\rightarrow 0$ such that $(\tilde{y}_{\delta _n}, \tilde{\eta }_{\delta _n})\rightarrow (\tilde{y}, \tilde{\eta })$ in $C(K;T^*Y)$. Since we can rewrite the differential equations (37) as integral equations, the limit $(\tilde{y}, \tilde{\eta })$ satisfies the same equations, with respect to the metric $h_0$ and with initial condition $\tilde{y}(0)=y_0$ and $\tilde{\eta }(0)=v_0$. By the same argument, any subsequence of $(\tilde{y}_\delta ,\tilde{\eta }_\delta )$ has a convergent subsequence, whose limit must be the same $(\tilde{y}, \tilde{\eta })$ since it satisfies the same initial conditions and same equations. By a standard argument, this implies the convergence of $(\tilde{y}_\delta ,\tilde{\eta }_\delta )$ to $(\tilde{y}, \tilde{\eta })$. $\square$

5 Discussion

5.1 The function $\mathfrak {F}$ and the constant $C_f$

Recall that the constant $C_f$ in the length asymptotics of Theorem C is given by

$$\begin{aligned} C_f=\int _{-\pi /2}^{\pi /2} \mathfrak {F} \left( \frac{1}{\cos (\vartheta )}\right) \, d\vartheta \quad \text { where }\ \mathfrak {F}(\sigma )=\lim _{\epsilon \rightarrow 0} \frac{F'(\sigma \epsilon )}{F'(\epsilon )}\ \text { for } \sigma \ge 1 \end{aligned}$$

with F the inverse function of f, see Assumption 10. We now discuss properties of $\mathfrak {F}$ and $C_f$ and their dependency on f.

It is useful to introduce a new variable z defined by $x=e^{-z}$, so that $x\rightarrow 0$ corresponds to $z\rightarrow \infty$. We do this change of variable in both the domain and the range of f. That is, for given f we consider the conjugated function

$$\begin{aligned} \phi := \overline{\exp }^{-1} \circ f \circ \overline{\exp },\quad \overline{\exp }(z) = e^{-z} \end{aligned}$$

or explicitly $\phi (z) = - \log f(e^{-z})$. For the examples in Remark 8 we get, with $\Phi$ the inverse function of $\phi$:

$$\begin{aligned} \begin{array}{c|c|c|c} f(x)\quad &{} \quad \phi (z)\quad &{} \quad \Phi (w)\quad &{} \quad \text {parameter range}\quad \\ \hline x^\alpha \quad &{} \quad \alpha z\quad &{} \quad \frac{1}{\alpha }w\quad &{} \quad \alpha \ge 1\quad \\ \exp \left( -\ln \left( \frac{1}{x}\right) ^{\mu }\right) \quad &{} \quad z^\mu \quad &{} \quad w^{1/\mu }\quad &{} \quad \mu> 1\quad \\ \exp \left( -\frac{1}{x^\beta }\right) \quad &{} \quad e^{\beta z}\quad &{} \quad \frac{1}{\beta }\log w \quad &{} \quad \beta > 0\quad \end{array} \end{aligned}$$

(38)

This displays the relative rates of vanishing as $x\rightarrow 0$ of f very clearly since they correspond to rates of growth of $\phi$ as $z\rightarrow \infty$: the rate increases with the parameter in each row, and from top to bottom.

Lemma 17

• (a) Assume f satisfies (2) and $\mathfrak {F}$ exists. Then

  $$\begin{aligned} \frac{1}{\sigma }\le \mathfrak {F}(\sigma )\le 1 \end{aligned}$$

  (39)

  for all $\sigma \ge 1$ and

  $$\begin{aligned} 2\le C_f\le \pi . \end{aligned}$$

• (b) Assume f, ${\tilde{f}}$ satisfy (2) and $\mathfrak {F}$, $\widetilde{\mathfrak {F}}$ exist. Then

  $$\begin{aligned} f = O({\tilde{f}}) \text { near zero } \ \Longrightarrow \ \mathfrak {F}\le \widetilde{\mathfrak {F}}\,,\ \text { hence } C_f \le C_{{\tilde{f}}} \end{aligned}$$

  (40)

Proof

(a) Since f is increasing and convex, F is increasing and concave, so $F'$ is positive and decreasing. This implies $\mathfrak {F}\le 1$. By L’Hôpital’s rule,

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \frac{F(\sigma \epsilon )}{F(\epsilon )} =\sigma \lim _{\epsilon \rightarrow 0} \frac{F'(\sigma \epsilon )}{F'(\epsilon )} =\sigma \mathfrak {F}(\sigma ). \end{aligned}$$

(41)

Now F is increasing and $\sigma \ge 1$, so $\frac{F(\sigma \epsilon )}{F(\epsilon )}\ge 1$, which implies $\sigma \mathfrak {F}(\sigma )\ge 1$.

Integration yields the inequalities for $C_f$.

(b) The inverse functions $F,\Phi$ of $f,\phi$ are related by $\Phi =\overline{\exp }^{-1} \circ F \circ \overline{\exp }$, or $F=\overline{\exp }\circ \Phi \circ \overline{\exp }^{-1}$, i.e. $F(\varepsilon )=\exp (-\Phi (\log \frac{1}{\varepsilon }))$. From this and (41) we get for each $s\ge 0$

$$\begin{aligned} \lim _{w\rightarrow \infty }\left( \Phi (w+s) - \Phi (w) \right) =\log \left( \sigma \mathfrak {F}(\sigma )\right) ,\quad \sigma =e^s. \end{aligned}$$

This means that $\Phi (w)$ has approximate linear growth as $w\rightarrow \infty$ at the rate $\frac{1}{s}\log \left( \sigma \mathfrak {F}(\sigma )\right)$. Now let $f=O({\tilde{f}})$. Since the existence and value of $\mathfrak {F}$ are not changed when multiplying f by a constant, we may assume $f\le {\tilde{f}}$ near zero. This implies $\phi \ge \tilde{\phi }$, so $\Phi \le \tilde{\Phi }$ near infinity. Assume for contradiction that $\mathfrak {F}(\sigma )>\widetilde{\mathfrak {F}}(\sigma )$ for some $\sigma >1$ (they are equal to one for $\sigma =1$). Then $\Phi$ would have a higher linear growth rate than $\tilde{\Phi }$, so $\Phi (w)>\tilde{\Phi }(w)$ for large w, contradicting $\Phi \le \tilde{\Phi }$. $\square$

For the examples in (38) we now get:

• If $f(x)=x^\alpha$ then $\mathfrak {F}(\sigma )= \sigma ^{\frac{1}{\alpha }-1}$, hence $C_{f}= B(1-\tfrac{1}{2\alpha },\tfrac{1}{2})$ where B is the Beta function.

• In particular, in the conical case $f(x)=x$ we have $\mathfrak {F}(\sigma )= 1$, so $C_f= \pi$, and for ‘sharp cusps’, i.e. $f(x)=x^\alpha$ with $\alpha \rightarrow \infty$, we get $\mathfrak {F}(\sigma )\rightarrow \frac{1}{\sigma }$, so $C_f\rightarrow 2$.

• The monotonicity (40) now implies that $\mathfrak {F}(\sigma )=\frac{1}{\sigma }$, so $C_f=2$, for the examples in the second and third row of (38).

Remark 18

The monotonicity formula (40) shows that $C_f=2$ for any worse singularity than the ones in (38). For instance, define $\exp _{k+1}=\exp \circ \exp _k$ with $\exp _0(x)=x$. Let $k\ge 0$. Then

$$\begin{aligned} f(x)=\exp \left( -\exp _k\left( \frac{1}{x}\right) \right) \end{aligned}$$

satisfies (2) and by (40), $C_f=2$ for any $k\ge 0$.

5.2 Example of $\mathfrak {F}$ failing to exist

The idea is to add a fast but suitably small oscillation to $F=f^{-1}$, preventing convergence. We perturb a family F(x) tending to 0 as $x^{\alpha }$ for $\alpha \in (0,1)$.

Lemma 19

Let $\alpha \in (0,1)$ and $c\ge \frac{2-\alpha }{1-\alpha }\cdot \frac{1+\alpha }{\alpha }$. Define

$$\begin{aligned} F(x)=x^{\alpha }\left( c+\sin (\log (x))\right) = cx^\alpha +\tfrac{1}{2i} x^{\alpha +i}-\tfrac{1}{2i} x^{\alpha -i}. \end{aligned}$$

Here $i=\sqrt{-1}$. Then F is positive, increasing and concave, but $\lim \limits _{\epsilon \rightarrow 0} \frac{F'(\epsilon \sigma )}{F'(\epsilon )}$ fails to exist unless $\log (\sigma )= 2n\pi$ for some $n\in {\mathbb {N}}_0$.

Proof

We compute

$$\begin{aligned}{} & {} F'(x)= x^{\alpha -1}\left( \alpha c+\alpha \sin \log x+\cos \log x\right) , \\{} & {} F''(x)= x^{\alpha -2}\left( \alpha (\alpha -1)c+(\alpha ^2-\alpha -1) \sin \log x+(2\alpha -1)\cos \log x\right) . \end{aligned}$$

$F'(x)>0$ clearly holds if $c>\frac{1+\alpha }{\alpha }$, which is true since $c\ge \frac{2-\alpha }{1-\alpha }\cdot \frac{1+\alpha }{\alpha }$. Similarly, since $\alpha ^2-\alpha -1<0$ and $|2\alpha -1|<1$,

$$\begin{aligned} F''(x)\le x^{\alpha -2}\left( \alpha (\alpha -1)c -(\alpha ^2-\alpha -1)+1\right) \le 0 \end{aligned}$$

if $c\ge \frac{2-\alpha }{1-\alpha }\cdot \frac{1+\alpha }{\alpha }$.

To see that the limit fails to exist, assume it did. Then, by L’Hôpital’s rule, the limit $\lim \limits _{\epsilon \rightarrow 0} \frac{F(\epsilon \sigma )}{F(\epsilon )}$ would also exist. But

$$\begin{aligned} \frac{F(\epsilon \sigma )}{F(\epsilon )}=\sigma ^{\alpha } \frac{c+\sin \log (\epsilon \sigma ) }{ c+\sin \log \epsilon } =\sigma ^{\alpha } \frac{c+\sin \left( \log \epsilon +\log (\sigma )\right) }{c+\sin \log \epsilon }, \end{aligned}$$

and the existence of the limit as $\epsilon \rightarrow 0$ is equivalent to the existence of the limit

$$\begin{aligned} \lim _{x\rightarrow \infty } \frac{c+\sin (x+y)}{c+\sin (x)} \end{aligned}$$

for all $y=\log (\sigma )\ge 0$. Consider the sequence $x_n=\frac{\pi }{2}+n\pi$. Then

$$\begin{aligned} \frac{c+\sin (x_n+y)}{c+\sin (x_n)} =\frac{c+(-1)^n \cos y}{c+(-1)^n}, \end{aligned}$$

and this converges only if $\cos y=1$, i.e. $y=\log (\sigma ) \in 2\pi {\mathbb {N}}_0$. The converse follows from

$$\begin{aligned} \frac{F'(\sigma \epsilon )}{F'(\epsilon )}=\sigma ^{\alpha -1} \end{aligned}$$

whenever $\log (\sigma )\in 2\pi {\mathbb {N}}_0$. $\square$

We formulate a small question concerning $\mathfrak {F}$.

Question 1

Assume f satisfies (2), and additionally, that

$$\begin{aligned} \lim _{x\rightarrow 0} \frac{f(x)}{x^{\alpha }}=0 \end{aligned}$$

for all $\alpha \ge 1$.

Does $\mathfrak {F}$ exist and is $\mathfrak {F}(\sigma )=\frac{1}{\sigma }$?

5.3 Why convexity?

One possible extension of our work is to relax the assumptions on f. One could for instance ask what happens when f is concave instead of convex? What one will notice then is that the bounds on $\mathfrak {F}$ are no longer true, and $C_f$ might very well be infinite. When $f(x)=x^{\alpha }$ with $0<\alpha <1$, $\mathfrak {F}(\sigma )=\sigma ^{\frac{1-\alpha }{\alpha }}$ is unbounded, and $C_f$ is infinite for $\alpha \le \frac{1}{2}$. The border case $\alpha =\frac{1}{2}$ can be explicitly solved in the warped case. The formula (32) holds for arbitrary positive and increasing f, hence also for $f(x)=\sqrt{x}$. Here $F(\rho )=\rho ^2$, so

$$\begin{aligned} f'(\delta )\ell (y_{\delta })=\int _{-\Theta _{\delta }}^{\Theta _{\delta }} \frac{d\theta }{\cos \theta }, \end{aligned}$$

where $\cos \Theta _{\delta }=\sqrt{\frac{\delta }{R}}.$ The integral is explicitly computable, and the result is

$$\begin{aligned} f'(\delta )\ell (y_{\delta })=2 \log \left( \frac{R+\sqrt{R^2-\delta ^2}}{\sqrt{\delta }}\right) . \end{aligned}$$

The essential point here is that the length behaves as

$$\begin{aligned} f'(\delta )\ell (y_{\delta }) \sim \log \delta ^{-1}, \end{aligned}$$

so the asymptotic behaviour has become more complicated.

6 Metrics on isolated singularities

Singular spaces typically arise in one of the following ways:

• as subsets of smooth manifolds M, e.g. as solution sets $\{x\in M:F(x)=0\}$ of (systems of) equations, where $F:M\rightarrow N$ is a smooth map to a manifold N and singularities may arise at points p where the differential $dF_{|p}$ is not surjective; an important class of examples are algebraic varieties;

• as quotients of smooth spaces by non-free group actions; important classes of examples are orbifolds and moduli spaces.

These spaces are often equipped with natural metrics. For example, complex projective algebraic varieties carry metrics induced by the Fubini-Study metric, and the Riemannian moduli space carries a natural metric, which has (non-isolated) cuspidal singularities.

However, in this section we carefully distinguish non-metric and metric aspects of singularities. The discussion will be summarized in Subsection 6.3.

6.1 Singularities of type [s]

We focus on singular spaces arising as subsets of manifolds and only consider isolated singularities which are described by a profile (or ’shrinking’) function s of a single variable, in the sense described below. First, we define:

Definition 20

Let M be a manifold and $X\subset M$. Let $p\in X$. We say that p is an isolated singularity of X if $X_0=X\setminus \{p\}$ is a submanifold of M and p lies in the closure of $X_0$.

We define a profile function to be a $C^1$ function $s:[0,\varepsilon )\rightarrow [0,\infty )$ for some $\varepsilon >0$ which satisfies

$$\begin{aligned} s(0)=0,\ s(z)>0\text { for }z>0. \end{aligned}$$

We call two profile functions $s,\tilde{s}$ equivalent if $\tilde{s}= as$ near 0, where a is positive and $C^1$ on some interval $[0,\epsilon )$. Denote the equivalence class of s by [s].

Let us say that two curves $\gamma$, $\overline{\gamma }$ in M with $\gamma (0)=\overline{\gamma }(0)=p$ and $\dot{\gamma }(0)\ne 0\ne \dot{\overline{\gamma }}(0)$ are s-tangent at p if $|\gamma (t)-\overline{\gamma }(t)|=O(s(t))$ near $t=0$ in one (hence any) local coordinate system. If $s(z)=z^k$, $k\in {\mathbb {N}}$, then this corresponds to tangency of order $k-1$. Roughly, we will say that X has a singularity of type s at p if it is a union of curves which are pairwise s-tangent at p, but not tangent to higher order (i.e. also $|\gamma (t)-\overline{\gamma }(t)|\ge cs(t)$ for a constant $c>0$).

6.1.1 The cuspidal case

We call a profile function s cuspidal if $s'(0)=0$. For a cuspidal profile function s the s-blow-down map $\beta _s$ is defined by

$$\begin{aligned} \beta _s:[0,\varepsilon )\times {\mathbb {R}}^{N-1}\rightarrow [0,\varepsilon ) \times {\mathbb {R}}^{N-1}\,,\quad (z,u) \mapsto (z,s(z)u) \end{aligned}$$

(42)

It shrinks the hyperplane at height z by the factor s(z). In particular the boundary plane $z=0$ is collapsed to the origin.

Definition 21

Let M be a manifold and $X\subset M$. Let $p\in X$, and let s be a cuspidal profile function. We say that X has a cuspidal singularity of type [s] at p if there are coordinates $(z,x):U\rightarrow {\mathbb {R}}\times {\mathbb {R}}^{N-1}$ on a neighbourhood $U\subset M$ of p, mapping p to the origin, in terms of which

$$\begin{aligned} X\cap U=\beta _s(\tilde{X})\,,\quad \tilde{X}:= \bigcup _{z\in [0,\varepsilon )} \{z\} \times Y_z \end{aligned}$$

(43)

where $\beta _s$ is the s-blow-down map and $Y_z\subset {\mathbb {R}}^{N-1}$ are closed submanifolds varying smoothly³ with $z\in [0,\varepsilon )$. We call $\tilde{X}$ a resolution of X.

The curve $z\mapsto (z,0)$ is called axis of the singularity. We also call the germ of $X\subset M$ at p a singularity of type [s].

These singularities are natural generalizations of surfaces of rotation in ${\mathbb {R}}^3={\mathbb {R}}\times {\mathbb {R}}^2$ with profile function s, for which $Y_z=S^1\subset {\mathbb {R}}^2$ for each z (see also Example 25). Compared to isolated singularities of algebraic sets they allow more flexibility in that s can vanish to infinite order at zero, but are also more restricted since the blow-down map shrinks each point $u\in Y_z$ by the same factor s(z). For example, the set $\{(z,x,y):\, (\frac{x}{z})^2 + (\frac{y}{z^2})^2 = 1\,,\ z>0\}\cup \{0\}\subset {\mathbb {R}}^3$ is not of this type. See [5] for more on this.

The singularity type is an equivalence class [s] because equivalent profile functions define the same class of singularities: if $\tilde{s}=as$ then $s, (Y_z)$ define the same X as $\tilde{s}, (a(z)^{-1}Y_z)$.

It follows from the cusp condition $s'(0)=0$ that a cuspidal singularity (X, p) has a well-defined tangent direction at p, which is a ray in $T_pM$. This is the set of tangents at p of curves in X starting at p, and is equal to the tangent cone in the sense of [1], for instance.

Note that this notion of singularity type is purely differential, i.e. there is no metric involved. It is also natural in the sense that if the condition holds in one coordinate system then it holds in any other having the same axis.⁴

6.1.2 Conical singularities

Conical singularities can be defined in essentially the same way, where the profile function is $s(z)=z$ or equivalent to this. However, while cuspidal singularities always lie in a half space since they have a unique tangent direction at p, it would be unnatural to require this for a cone. Therefore, we define a conical singularity in the same way as in Definition 21, except that we replace the map $\beta _s$ above by the polar coordinates map

$$\begin{aligned} \beta _{\textrm{conic}}: [0,\infty ) \times {\mathbb {S}}^{N-1}\rightarrow {\mathbb {R}}^N\,, \quad (z,\omega )\mapsto z\omega \end{aligned}$$

(44)

and take a smooth family of closed submanifolds $Y_z\subset {\mathbb {S}}^{N-1}$. The space $[0,\infty ) \times {\mathbb {S}}^{N-1}$ is called the blow-up of ${\mathbb {R}}^N$ at the point 0 and $\beta _{\textrm{conic}}$ the blow-down map, and the definition can be restated by saying that X is resolved by blowing up p. The map $\beta _s$ in (42), with $s(z)=z$, then is $\beta _{\textrm{conic}}$ written in one of the projective coordinate systems. See [12] or [7] for details on this.

If $s(z)=z^k$ then the map $\beta _s$ is the blow-down map for a quasi-homogeneous blow-up (in projective coordinates; see [9, 11]), so for general s we have defined a generalized notion of quasi-homogeneous blow-up.

The other remarks above carry over to the conical case. In particular, this notion of conical singularity is differential, not metric.

6.2 Metrics on singularities of type [s]

It is natural to consider metrics on X which are induced by smooth metrics on M.

Definition 22

Let $(M,g_M)$ be a smooth Riemannian manifold and $X\subset M$. Assume that X has an isolated singularity at $p\in X$. The induced metric for X, denoted $g_X$, is the Riemannian metric on $X_0=X\setminus \{p\}$ obtained by restriction of $g_M$ to $TX_0$. The induced distance on X, denoted $d_X$, is the distance function on X defined by $g_X$.

That is, if $q,q'\in X$ then $d_X(q,q')=\inf \ell (\gamma )$ where the infimum is taken over all curves $\gamma :(0,1)\rightarrow X_0$ with $\lim _{t\rightarrow 0}\gamma (t)=q$, $\lim _{t\rightarrow 1}\gamma (t)=q'$. This is sometimes called the intrinsic distance on X, and is to be distinguished from the extrinsic distance, which is the restriction of the distance function $d_M$ (defined on $M\times M$ by $g_M$) to $X\times X$.

To understand the geometry of (X, g), e.g. the behaviour of geodesics near p, it is useful to have a normal form of the metric. Specifically, we ask under which conditions the induced distance makes X a Riemannian space with conical or cuspidal singularity at p as in Definition 7. This turns out to be rather subtle even for spaces with cuspidal or conical singularity as defined above. We discuss this now.

6.2.1 Warped products

In order to get a warped product metric on X (rather than just a generalized one) one expects to have to impose rather rigid conditions. We will consider the case where $M={\mathbb {R}}^N$ with the Euclidean metric, and where the resolution $\tilde{X}$ (defined using standard coordinates (z, x) on ${\mathbb {R}}^N$) is a product $[0,\varepsilon )\times Y$.

Proposition 23

Let $X\subset {\mathbb {R}}^N$ have an isolated singularity at 0. Let $g_X$ be the metric on $X_0$ induced by the Euclidean metric on ${\mathbb {R}}^N$, and $d_X$ the induced distance.

• (a) (Cuspidal case) If X has a cuspidal singularity of type [s], and if, in (43),

  $$\begin{aligned} Y_z=Y \ \forall z\ \text { where } Y\subset {\mathbb {R}}^{N-1} \text { is contained in the unit sphere } {\mathbb {S}}^{N-2} \text { centered at }0 \end{aligned}$$

  (45)

  then $g_X$ is a warped product metric. The warping function is determined by

  $$\begin{aligned} f(r(z))=s(z)\ \text { where }\ r(z)=\int _0^z \sqrt{1+(s'(w))^2}\,dw\,, \end{aligned}$$

  (46)

  and h is the metric on Y induced by the Euclidean metric on ${\mathbb {R}}^{N-1}$. Also, $f(r)\sim s(r)$ as $r\rightarrow 0$, and f is convex iff s is convex, so $(X,d_X)$ is a Riemannian space with an isolated cuspidal singularity in this case.

• (b) (Conical case) If X has a conical singularity, and if

  $$\begin{aligned} Y_z=Y \ \forall z \ \text { for some}\ Y\subset {\mathbb {S}}^{N-1} \end{aligned}$$

  (47)

  then $g_X$ is a warped product metric with warping function $f(r)=r$, so $(X,d_X)$ is a Riemannian space with an isolated conical singularity. The metric h is the metric on Y induced by the standard metric on ${\mathbb {S}}^{N-1}$.

Note that in the cuspidal case there is an additional condition, $Y\subset {\mathbb {S}}^{N-2}$, on the cross section Y, while in the conical case there isn’t. See also the remark after Theorem 27. Condition (47) says that X is a ‘straight’ cone with an arbitrary base Y.

The idea of the proof of part (a) is that r(z) is arc length along the curve $z\mapsto (z,s(z)u)$ for any fixed u with $|u|=1$. The unit sphere condition is needed to ensure that mixed terms vanish, i.e. that the curves $u= {\textrm{const}}.$ are orthogonal to the level sets $z= {\textrm{const}}$.

Proof

• (a) We calculate the induced Riemannian metric on $X_0=X\setminus \{0\}$. First, we write the Euclidean metric on ${\mathbb {R}}^N$ in coordinates z, u, i.e. we pull it back under the map $\beta _s$, see (42). The differential of $s(z)u_i$ is

  $$\begin{aligned} d(s(z)u_i) = s(z)\,du_i + s'(z)u_i\,dz , \end{aligned}$$

  so we get

  $$\begin{aligned} \beta _s^*(g_{\textrm{eucl}})&= dz^2 + \sum _{i=1}^{N-1} \left( d(su_i)\right) ^2\\&= (1+(s')^2 |u|^2)\,dz^2 + 2 ss' dz \sum _{i=1}^{N-1}u_i\,du_i + s^2 \sum _{i=1}^{N-1} du_i^2 \end{aligned}$$

  where $s=s(z)$ etc. Now we restrict to Y. From $Y\subset {\mathbb {S}}^{N-2}$ we have that $|u|^2$ is constant equal to 1 on Y. In particular, the mixed term, which is $ss'\,dz\,d(|u|^2)$, vanishes when pulled back to Y, so we get

  $$\begin{aligned} g_{X_0} = (1+(s')^2)\,dz^2 + s^2 \,h. \end{aligned}$$

  With r defined in (46) we have $dr = \sqrt{1+(s')^2} \,dz$ and $s(z)=f(r)$. So in r, u coordinates the metric is $dr^2 + f(r)^2 \,h$ as claimed.

  From $s'(0)=0$ we get $r(z)\sim z$ as $z\rightarrow 0$, hence $f(r)\sim s(r)$ as $r\rightarrow 0$. Finally, one calculates

  $$\begin{aligned} f'(r(z)) = \frac{s'(z)}{\sqrt{1+(s'(z))^2}} \end{aligned}$$

  and since the function $z\mapsto r(z)$ as well as the function $\sigma \mapsto \frac{\sigma }{\sqrt{1+\sigma ^2}}$ (and hence also their inverses) are strictly increasing, it follows that $f'$ is increasing iff $s'$ is increasing, so f is convex iff s is convex.

• (b) It is well-known that the Euclidean metric on ${\mathbb {R}}^N$ reads $\beta _{\textrm{conic}}^*(g_{\textrm{eucl}}) = dr^2 + r^2 g_{{\mathbb {S}}^{N-1}}$ in polar coordinates (where we write r instead of z in (44)). Since $\tilde{X}$ is $\beta ^{-1}(X)=[0,R)\times Y$ in polar coordinates, it follows that $g=dr^2+r^2 h$.

$\square$

Remark 24

Proposition 23 implies that our results on geodesics apply in the cuspidal case if (45) holds and s is convex, and in the conical case if (47) holds. There are also other cases where one obtains conical warped product metrics:

• (a) X is as in Proposition 23(a), except that $s'(0)>0$, and s is convex.

  Note in particular the additional condition $Y\subset {\mathbb {S}}^{N-2}$ in (45). However, this condition is not needed if $s(z)=cz$ with a constant $c>0$ since then X can be expressed as in Proposition 23(b) (with a different Y).⁵

  Note that if $s'(0)>0$ and s is $C^2$ then f is also $C^2$, so by Remark 8 (c) one does not need to require convexity of s then.

• (b) X is as in Proposition 23(a), except that $s(z)=z^{\alpha }$ with $\alpha \in (0,\frac{2}{3}]$.

  (Note that s is not even differentiable at zero then.) The reason is that

  $$\begin{aligned} r(z)= & {} \int _0^z \sqrt{1+\alpha ^2 w^{2\alpha -2}}\, dw=\sum _{k=0}^{\infty } \frac{c_k \alpha ^{1-2k}}{2k(1-\alpha )+\alpha }z^{2k(1-\alpha )+\alpha }\\= & {} z^\alpha +\beta z^{2-\alpha }+\dots , \end{aligned}$$

  where $c_k$ are the coefficients of the Taylor series of $\sqrt{1+x}$ at $x=0$, so $\beta =\frac{1}{2\alpha (2-\alpha )}>0$. This implies $f(r)=r-\beta r^{\gamma }+\dots$ where $\gamma =\frac{2-\alpha }{\alpha }$, which is conical but not convex. However, if $\alpha \le \frac{2}{3}$ then it is $C^2$ down to 0, so f is equivalent to a convex function.

  For example, if $s(z)=\sqrt{z}$ and $Y={\mathbb {S}}^{N-2}$ then X is in fact smooth at p.

Example 25

If $X\subset {\mathbb {R}}^3$ is a surface of revolution with profile function s then it has a cuspidal warped product metric if s is cuspidal and a conical warped product metric if s is $C^1$ at zero and $s'(0)>0$, or if $s(z)=z^\alpha$ with $\alpha \in (0,\frac{2}{3}]$.

6.2.2 Generalized warped products

If we use more general metrics on M near p or do not impose the product type condition $Y_z=Y\,\forall z$ then we cannot expect the induced metric on X to have warped product structure. We discuss what is known in the conical and k-cuspidal case, i.e. $f(r)=r^k$ for some $k\in {\mathbb {N}}$, $k\ge 1$.

First, in the conical case one always gets a generalized warped product, as shown by Melrose and Wunsch.

Theorem 26

([14]). Let $X\subset M$ have a conical singularity as defined above. Let $g_M$ be a Riemannian metric on M and $d_X$ the induced distance function on X.

Then $(X,d_X)$ is a Riemannian space with an isolated conical singularity at p, as in Definition 7.

Theorem 26 is proven in two steps: First one uses normal polar coordinates in M, centred at p, to write the induced metric as $g = dr^2 + r^2 h$ on $\tilde{X}=[0,R)\times Y$, where all $Y_z$ are identified with a fixed Y and h is a smooth 2-tensor on $\tilde{X}$ restricting to a metric on $\{0\}\times Y$. However, this is more general than (1) since h may involve $dr^2$ terms and also mixed $dr\, dy$ terms. In a second, more difficult step one proves that one can change coordinates so that these terms are removed, i.e. g takes the form (1). For this one shows that for each $q\in Y$ there is a unique geodesic in $(0,R)\times Y$ hitting the boundary at (0, q), and that these geodesics together define a fibration $\Phi :[0,R')\times Y\rightarrow U$ of a neighbourhood $U\subset \tilde{X}$ of $r=0$. Then $\Phi$ is the desired coordinate system.

The k-cuspidal case was analysed by Grandjean and Grieser in [6], with more detail and a correction given in [2]. Let X be given as in (43) with $s(z)=z^k$, $k\ge 2$, and let $g_M$ be any Riemannian metric on M. First, by [6, Proposition 7.3] and [2] a trivialization $U\cong [0,r_0)\times {\partial \tilde{X}}$ of a neighbourhood U of ${\partial \tilde{X}}$ can be chosen so that the induced metric on X, pulled back to $\tilde{X}$, has the form

$$\begin{aligned} g =(1+S(z,u) z^{k})\,dz^2 +z^{2k}h \end{aligned}$$

(48)

for a smooth function S and a smooth 2-tensor h on $\tilde{X}$ restricting to a metric $h_0$ on $\{0\}\times \partial \tilde{X}=Y_0$.⁶

This cannot be improved in general: Consider the subspace ${\mathcal {N}}\subset C^\infty ([0,r_0)\times {\partial \tilde{X}})$ of functions f satisfying $d_{\partial \tilde{X}}f = O(z^{k-1})$, and denote by $S_0$ the equivalence class of S modulo ${\mathcal {N}}$. For example, if $k=2$ then $S_0$ can be identified with the restriction of S to ${\partial \tilde{X}}$ modulo constants, so it vanishes if and only if $S_{|{\partial \tilde{X}}}$ is constant. By [6, Lemma 2.2] and [2] the class $S_0$ is an invariant of the singularity and metric. In particular, if $S_0$ is non-zero then the metric can not be put in generalized warped product form by any choice of coordinates on $\tilde{X}$. However, if $S_0$ vanishes then an argument using geodesics hitting p, similar to the argument in [14], shows:

Theorem 27

(Theorem 1.2 + Remark 3.4 in [6]). Suppose X has a k-cuspidal singularity as discussed above. If the equivalence class $S_0$ defined above vanishes then the metric on X is a generalized warped product metric with warping factor $f(r)=r^k$.

For example, if $M={\mathbb {R}}^N$ with the Euclidean metric then $S_0(z,u)=z^{k-2}|u|^2$, with u restricted to $Y_0\subset {\mathbb {R}}^{N-1}$. This shows that the additional condition on Y in (45) is necessary, up to a constant factor.

In [6] the geodesics hitting ${\partial \tilde{X}}$ were analysed also in the more general case where $S(z,u)=z^{k-2}\tilde{S}(u) + O(z^{k-1})$ with $\tilde{S}$ a Morse function on ${\partial \tilde{X}}$.

6.3 Summary of Sect. 6

We distinguish differential and metric notions of conical/cuspidal singularities.

The differential notion refers to subsets X of a manifold M with isolated singularity $p\in X$. It is based on the idea of s-tangency of curves, where s is a profile function.

The metric notion is based on the idea of generalized warped product metrics. It is related to the differential notion as follows. Given a Riemannian metric $g_M$ on M, the induced metric $g_X$ on X is

• conical if X has a conical singularity in the differential sense

• cuspidal if X has a cuspidal singularity in the differential sense and if it satisfies additional requirements in its relation to $g_M$, like the vanishing of $S_0$ in Theorem 27.

Thus, in the cuspidal case, the metric notion is more restrictive than the differential notion.

We also mention that there are other notions of conical singularity in the literature. For example, the notion of corner domain introduced by Dauge in [4] refers to subsets of ${\mathbb {R}}^N$ which arise from ’straight’ conical spaces as in Proposition 23(b) by local diffeomorphisms of the ambient space ${\mathbb {R}}^N$. This is more special than our notion of conical singularity given in Sect. 6.1.2. (However, corner domains also include non-isolated singularities such as those arising from the base Y having corner domain singularities itself.)