Power sum polynomials and the ghosts behind them

Abstract

The power sum polynomial associated to a multi-subset of the projective plane $\text {PG}(2,q)$ is the sum of the $(q-1)$-th powers of the Rédei factors of the points in the multi-subset. The classification of multi-subsets having the same power sum polynomial passes through the determination of those multi-subsets associated to the zero polynomial, called ghosts. In this paper we provide new classes of ghosts and compute the dimension of the ghost subspace by exploiting the linear code generated by the lines of $\text {PG}(2,q)$ and its dual. Moreover, we explicitly enumerate and classify ghosts for planes of order 2, 3, 4.

1 Introduction

A well investigated research field in the framework of finite geometries is the study of the interplay between subsets of a projective space and polynomials over finite fields (see for instance [3, 5]). In [14], Sziklai defines the notion of power sum polynomial of a point set S contained in the n-dimensional projective space $\text {PG}(n,q)$: it is a homogeneous polynomial given by the sum of the $(q-1)$-th powers of the Rédei factors associated to the points of S. It is a hard task in general to determine all sets sharing the same power sum polynomial.

In [12], the authors give some general results on the classification and the size of the point sets of $\text {PG}(2,q)$ associated to a given power sum polynomial. More precisely, the right environment to study such a problem is the set of multi-subsets of $\text {PG}(2,q)$, denoted by $p^{\text {PG}(2,q)}$, where by multi-subset we mean a point subset of $\text {PG}(2,q)$, with each point counted with a certain multiplicity modulo p (the field characteristic). Motivated by the description of ghosts in discrete tomography (see for instance [9]), the authors prove that multisets associated to a same power sum polynomial can be obtained one from the other by a suitable multiset sum modulo p with sets whose power sum polynomial is identically zero, which are called ghosts themselves. Reducing to simple sets, i.e., with no multiple points, ghosts are exactly the generalized Vandermonde sets defined in [14]. Moreover, in [12] the size of the subset of ghosts when $q=p$, namely, for prime fields, is determined.

In the present paper we find new classes of simple ghosts. Moreover, we prove that the set of multi-subsets of $\text {PG}(2,q)$ may be endowed with the structure of vector space over $\mathbb {F}_p$. In particular, ghosts constitute a vector subspace, whose dimension may be computed, providing the number of ghosts for any q. As a consequence, all the multi-subsets of $\text {PG}(2,q)$ sharing the same power sum polynomial constitute an affine subspace of $p^{\text {PG}(2,q)}$, which is precisely the translate of the ghost vector space through a peculiar multi-subset. In this way a partition of $p^{\text {PG}(2,q)}$ into affine subspaces, each representing a given power sum polynomial, of a same dimension and parallel to the ghost subspace, is obtained.

The dimension of the ghost space is computed by exploiting a link between multi-subsets of $\text {PG}(2,q)$ and the code of points and lines of the projective plane [11]. It results that, exactly when q is a prime, all ghosts may be obtained as multiset sums of lines, which in this case constitute a set of generators for the space of ghosts. It is not true for $q=p^h$, $h>1$, where other configurations arise. These are thoroughly enumerated and studied for $q=4$ in the last part of the paper.

The paper is organized as follows. In the next section we recall the basic definitions and the results obtained in [12], while in Sect. 3 we present new classes of simple ghosts. In Sect. 4 the link to coding theory is investigated and exploited to get the dimension of the ghost subspace. Section 5 is devoted to the classification and enumeration of ghosts in the smallest three projective planes, namely, of order 2, 3, 4. Section 6 shows possible extensions of the present work and concludes the paper.

2 Definitions and previous results

Let $\mathbb {F}_q$ denote the finite field of order a prime power $q=p^h$, $h\ge 1$. Write $\text {PG}(n,q)$ for the n-dimensional projective space over $\mathbb {F}_q$.

We are interested in assigning a peculiar polynomial to a subset of $\text {PG}(n,q)$. Given a point $P=(p_0,\ldots ,p_{n})\in \text {PG}(n,q)$, its Rédei factor is the linear polynomial $P\cdot {\textbf{X}}= p_0X_0+\cdots +p_{n}X_{n}$. The zeros of a Rédei factor corresponding to a point P represent the hyperplanes through P.

Definition 1

Let $S\subseteq \text {PG}(n,q)$. The power sum polynomial of S is defined as

$$\begin{aligned} G^S({\textbf{X}}):=\sum _{P\in S}(P\cdot {\textbf{X}})^{q-1}. \end{aligned}$$

The power sum polynomial is a homogeneous polynomial of degree $q-1$ in the variables $X_0,\ldots ,X_{n}$. Denote by $\mathbb {F}_q[X_0,\ldots ,X_{n}]_{q-1}$ the set of homogeneous polynomials of degree $q-1$ with coefficients in $\mathbb {F}_q$, together with the null polynomial. It is a vector space over $\mathbb {F}_q$ of dimension $\left( {\begin{array}{c}n+q-1\\ n\end{array}}\right)$. For $n=2$, we write $\mathbb {F}_q[X,Y,Z]_{q-1}$. If a hyperplane $(x_0,\ldots ,x_{n})$ intersects S in m points, then

$$\begin{aligned} G^S(x_0,\ldots ,x_{n})=\left| S\right| -m. \end{aligned}$$

As a consequence, a hyperplane is a zero of the power sum polynomial if and only if the size of its intersection with S equals $\left| S\right|$ modulo p.

Example

([14], Exercise 7.6). Consider the point set S of the parabola ${\mathcal {C}}:X^2-YZ=0$ in $\text {PG}(2,q)$. It results that $G^S(X,Y,Z)=-\left( X^2-4YZ\right) ^{\frac{q-1}{2}}$. Geometrically, a line $\ell$ is a zero of the power sum polynomial if and only if $\left| S\right| -\left| S\cap \ell \right| =0\mod p$, that is, if and only if $\left| S\cap \ell \right| =1\mod p$. This means that $G^S$ is the envelope of the tangent lines to the parabola.

For q odd, the envelope is a conic counted $\frac{q-1}{2}$ times. If q is even, then all tangent lines to a conic are through the nucleus, and therefore the envelope is a line (i.e., a reducible conic) counted $q-1$ times (indeed, $G^S(X,Y,Z)=X^{q-1}$).

In [12] links were constructed between the problem of characterising subsets of $\text {PG}(2,q)$ sharing the same power sum polynomial and the two-dimensional tomographic problem. The following definition was given.

Definition 2

A subset $S\subseteq \text {PG}(2,q)$ is a ghost of $\text {PG}(2,q)$ when $G^S\equiv 0$.

A nice characterization follows immediately from [14, Theorem 13.5].

Theorem 3

Ghosts of $\text {PG}(2,q)$ are exactly those sets intersecting each line in a constant number (modulo p) of points.

In discrete tomography, a ghost (i.e., a function with null projections along a given set of directions) may be added to a function to obtain another function having the same projections as the previous one (see [9]). Ghosts of $\text {PG}(2,q)$ act similarly; the operation in this case is the multiset sum modulo p (denoted by $\uplus _p$).

As a consequence, the characterization of ghosts is a necessary step in the investigation of sets associated to a same power sum polynomial. The environment to study ghosts is $p^{\text {PG}(2,q)}$, namely, the set of multi-subsets of $\text {PG}(2,q)$, where each point is counted up to $p-1$ times. Note that $\left| p^{\text {PG}(2,q)}\right| =p^{q^2+q+1}$.

For any $S\in p^{\text {PG}(2,q)}$ and any $P\in S$, denote by $m_S(P)$ the multiplicity of P in S. Therefore,

$$\begin{aligned} \left| S\right| =\sum _{P\in S}m_S(P)=\sum _{P\in \text {PG}(2,q)}m_S(P), \end{aligned}$$

where the second equality holds since points not in S have multiplicity zero in S. As a consequence, for any pair S, T of multisets we have

$$\begin{aligned} \left| S\cap T\right| =\sum _{P\in \text {PG}(2,q)}\min \{m_S(P),\,m_T(P)\}. \end{aligned}$$

For a subset A of a multiset B, the complement of A in B is the multiset where each element $b\in B$ is counted $m_B(b)-m_A(b)$ times. A multi-subset is said to be simple (i.e., a subset) if it contains no multiple points.

In [12] the following results have been proven.

Theorem 4

([12]). The following facts hold:

• (i) $(p^{\text {PG}(2,q)},\uplus _p)$ is an abelian p-group, and ghosts form a subgroup ${\mathcal {G}}$ of it. In particular, multiset sums of ghosts are still ghosts;

• (ii) the complement of a ghost is a ghost;

• (iii) lines are ghosts;

• (iv) for $q=p$ prime, the size of the ghost subgroup is $p^{\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) +1}$.

3 New classes of ghosts

The previous theorem points out that multi-subsets constitute a group. The following result states that they are endowed with a richer structure.

Lemma 5

The set $p^{\text {PG}(2,q)}$ is a vector space over $\mathbb {F}_p$ of dimension $q^2+q+1$. Therefore, ${\mathcal {G}}$ is a vector subspace of $p^{\text {PG}(2,q)}$.

Proof

Both $p^{\text {PG}(2,q)}$ and ${\mathcal {G}}$ are abelian groups by Theorem 4. Since the ground field is $\mathbb {F}_p$, multiplication by a scalar corresponds to a repeated sum. The dimension of $p^{\text {PG}(2,q)}$ is obtained from the fact that its size is $p^{q^2+q+1}$. $\square$

The dimension of ${\mathcal {G}}$ will be computed in the next section.

In [12] the focus was mainly on the case $q=p$, and examples of simple ghosts were provided in such case, as lines and affine planes. However, there are well-known structures which turn out to be ghosts and do not exist in the prime case.

Definition 6

Let q be a square. A Baer subplane is a subplane of $\text {PG}(2,q)$ of order $\sqrt{q}$. A unital of $\text {PG}(2,q)$ is a set of $q\sqrt{q}+1$ points, intersecting each line in either 1 or $\sqrt{q}+1$ points.

Lemma 7

Let q be a square. Then Baer subplanes and unitals are ghosts of $\text {PG}(2,q)$.

Proof

The definition of unital reported above satisfies the characterization given by Theorem 3. Baer subplanes intersect every line in either 1 or $\sqrt{q}+1$ points as well. $\square$

Indeed, it results that unitals may be seen as multiset sums of lines if and only if they are Hermitian (see [4]). The justification of this fact is due to the link to coding theory we will investigate in the next section.

In even characteristic, another example of ghost arises.

Lemma 8

Let q be even. Then hyperovals are ghosts.

Proof

A hyperoval is a set of $q+2$ points intersecting every line in either 0 or 2 points. So a hyperoval has constant intersection size with lines ($0\mod 2$) and therefore it is a ghost. $\square$

In the next section, we exploit an elegant correspondence between codewords and multisets to get further information about the space ${\mathcal {G}}$ of ghosts.

4 A coding theory perspective

From [7] on, linear codes constructed from the incidence relation between subspaces of projective spaces have been extensively studied (see [11] for an overview of the topic). In this section we rephrase our setting into a coding-theoretical one, so that the multiset sum modulo p becomes the usual vector sum over $\mathbb {F}_p$ and known properties of codes reveal useful to shed light on the dimension of the space of ghosts.

Each vector ${\textbf{v}}$ of $\mathbb {F}_p^{q^2+q+1}$, whose entries get values in $\mathbb {F}_p$, can be associated to a multi-subset of $p^{\text {PG}(2,q)}$, where each point is counted a number of times equal to the corresponding entry of ${\textbf{v}}$. We say that a vector is a ghost if the corresponding multi-subset is.

Consider the incidence matrix of points and lines of $\text {PG}(2,q)$, whose rows are indexed by the lines and the columns by the points. Denote by C the linear code generated by the rows of the matrix. It has dimension $\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h+1$ (see [13]). Since lines are ghosts, we have that C is isomorphic to a subspace of ${\mathcal {G}}$.

For $q=p$ prime, the dimension of C is $\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) +1$, so, by Theorem 4, there are no other ghosts outside C.

Remark 9

The fact that ${\mathcal {G}}=C$ for prime fields means that all ghosts are multiset sums of lines: for instance, affine planes are obtained as the multiset sum of q lines through a common point. In particular, simple ghosts can only be: the empty set, lines, affine planes and $\text {PG}(2,q)$ itself.

For $h>1$ the situation is different, since there are ghosts which are not multiset sums of lines, as we will show in a while.

The inner product between a vector of C and any other vector ${\textbf{v}}\in \mathbb {F}_p^{q^2+q+1}$ counts the number of intersections of the multiset corresponding to ${\textbf{v}}$ with multiset sums of lines. This leads us to consider the dual code $C^{\perp }$. It has been widely investigated (see for instance [11]) and may be interpreted as the subspace of those multi-subsets of $\text {PG}(2,q)$ having zero modulo p points in common with each line. Therefore, by Theorem 3 vectors of $C^{\perp }$ are ghosts. Examples of ghosts in $C^{\perp }\cap C$ are affine planes, while, for $q>2$ even, hyperovals are in $C^{\perp }\backslash C$. However, not all ghosts are in $C^{\perp }$; for instance, the complements of ghosts of $C^{\perp }$, which have $p-1$ intersections with each line, are not in $C^{\perp }$.

Let ${\textbf{j}}$ denote the all-one vector. Note that it corresponds to $\text {PG}(2,q)$.

Theorem 10

The space of ghosts is isomorphic to $\langle C^{\perp },{\textbf{j}}\rangle$. Moreover, $\langle C^{\perp },{\textbf{j}}\rangle =\langle C^{\perp },C\rangle$.

Proof

A vector ${\textbf{u}}$ in $\langle C^{\perp },{\textbf{j}}\rangle =C^{\perp }\oplus \langle {\textbf{j}}\rangle$ is a combination of vectors whose corresponding multisets have constant intersection size with lines, so also ${\textbf{u}}$ has. Therefore, ${\textbf{u}}$ is a ghost.

On the other side, let A be the incidence matrix of points and lines of $\text {PG}(2,q)$. A vector ${\textbf{u}}$ is a ghost if and only if

$$\begin{aligned} \exists \lambda \in \mathbb {F}_p\,:\,A{\textbf{u}}=\lambda {\textbf{j}}. \end{aligned}$$

(1)

Combining the fact that $\lambda {\textbf{j}}$ itself is a solution of (1) with the fact that vectors of $C^{\perp }$ constitute the kernel of A, it results that for each vector ${\textbf{u}}$ corresponding to a ghost there exist $\lambda \in \mathbb {F}_p$ and ${\textbf{w}}\in C^{\perp }$ such that

$$\begin{aligned} {\textbf{u}}=\lambda {\textbf{j}}+{\textbf{w}}, \end{aligned}$$

which proves the other inclusion. Thus, the space of ghosts is isomorphic to $\langle C^{\perp },{\textbf{j}}\rangle$ and

$$\begin{aligned} \dim {\mathcal {G}}=\dim C^{\perp }+1. \end{aligned}$$

Since ${\textbf{j}}\in C\setminus C^{\perp }$, we can conclude that $\langle C^{\perp },{\textbf{j}}\rangle =\langle C^{\perp },C\rangle$. $\square$

Remark 11

Therefore, all ghosts may be found in $\langle C^{\perp },{\textbf{j}}\rangle$ and

$$\begin{aligned} {\mathcal {G}}=C^{\perp }\sqcup \left( C^{\perp }+{\textbf{j}}\right) \sqcup \left( C^{\perp }+2{\textbf{j}}\right) \sqcup \cdots \sqcup \left( C^{\perp }+(p-1){\textbf{j}}\right) , \end{aligned}$$

where each of these affine subspaces $C^{\perp }+\lambda {\textbf{j}}$, $\lambda \in \{0,\ldots ,p-1\}$, may be seen as the set of those ghosts intersecting each line in $\lambda$ points.

The dimension of the space of ghosts is

$$\begin{aligned} \dim {\mathcal {G}}=q^2+q+1-\left( \left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h+1\right) +1=q^2+q+1-\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h. \end{aligned}$$

(2)

Following [12], let $\varphi :p^{\text {PG}(2,q)}\rightarrow \mathbb {F}_q[X,Y,Z]_{q-1}$ denote the morphism mapping a multi-subset of $\text {PG}(2,q)$ to the corresponding power sum polynomial. It results from (2) that

$$\begin{aligned} \dim \text {im}\varphi =\dim p^{\text {PG}(2,q)}-\dim {\mathcal {G}}=\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h. \end{aligned}$$

Corollary 12

Multi-subsets of $\text {PG}(2,q)$ sharing the same power sum polynomial fill affine subspaces of the affine space $p^{\text {PG}(2,q)}$, which are precisely the translates of the ghost space through given multi-subsets.

All such spaces have the same dimension, given by (2).

Again, for $q=p$ it results

$$\begin{aligned} \dim {\mathcal {G}}=\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) +1=\dim C, \end{aligned}$$

so all ghosts may be obtained as multiset sums of lines. In particular, we have that $C^{\perp }\le C$.

Differently, to treat the case $h>1$ we need the following result.

Lemma 13

Let p be a prime, h a positive integer. Then

$$\begin{aligned} \left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h\le \left( {\begin{array}{c}p^h+1\\ 2\end{array}}\right) \end{aligned}$$

(3)

and equality holds if and only if $h=1$.

Proof

For $h=1$, the statement is clearly true and equality holds. We prove that strict inequality holds for $h\ge 2$, which also provides as a consequence that equality in (3) implies $h=1$.

Note that

$$\begin{aligned} \left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h<\left( {\begin{array}{c}p^h+1\\ 2\end{array}}\right) \end{aligned}$$

is equivalent to

$$\begin{aligned} \frac{p+1}{2}<\root h \of {\frac{p^h+1}{2}}. \end{aligned}$$

The above relation is the power mean inequality, which holds since the root index of the right-hand side (i.e., h) is greater than that of the left-hand side (i.e., 1) and is strict since $p>1$ (namely, the two terms are not equal). $\square$

The strict inequality in (3) for $h>1$ implies that

$$\begin{aligned} \dim \mathbb {F}_q[X,Y,Z]_{q-1}=\left( {\begin{array}{c}p^h+1\\ 2\end{array}}\right) >\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h=\dim \text {im}\varphi , \end{aligned}$$

so the map $\varphi$ is onto if and only if q is prime.

As a consequence of Lemma 13, for $h>1$ we get

$$\begin{aligned} \dim C^{\perp }= & {} p^{2h}+p^h-\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h \\> & {} p^{2h}+p^h-\left( {\begin{array}{c}p^h+1\\ 2\end{array}}\right) = \left( {\begin{array}{c}p^h+1\\ 2\end{array}}\right) \\> & {} \left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h, \end{aligned}$$

which means that $\dim {\mathcal {G}}=\dim C^{\perp }+1>\left( {\begin{array}{c}p+1\\ 2\end{array}}\right) ^h+1=\dim C$ and thus there exist ghosts which are not multiset sums of lines.

5 Classification of ghosts for small q

In this section we explicitly enumerate ghosts in $\text {PG}(2,q)$ for $q=2,3,4$. Our aim is to underline the different construction of ghosts when q is a prime and when it is not.

Denote by $\theta (m,q)$ the number of configurations of m points (or dually, lines) in general position in $\text {PG}(2,q)$. In particular, $\theta (3,q)=\frac{(q^2+q+1)(q^2+q)q^2}{3!}$ and $\theta (4,q)=\frac{(q^2+q+1)(q^2+q)q^2(q-1)^2}{4!}$.

5.1 Ghosts in $\text {PG}(2,2)$

For the Fano plane no multiplicities are allowed. Therefore there are $2^7$ subsets of $\text {PG}(2,2)$ and $\dim {\mathcal {G}}=\left( {\begin{array}{c}2+1\\ 2\end{array}}\right) +1=4$. The 16 ghosts of ${\mathcal {G}}$ are the empty set, the seven lines of $\text {PG}(2,2)$, the seven corresponding affine planes and $\text {PG}(2,2)$ itself.

As proven above, each ghost can be seen as a multiset sum of lines: zero lines for the empty set, one for the line ghosts, two for the affine planes and three lines through a common point for the whole projective plane. Note further that in this case hyperovals and affine planes coincide.

5.2 Ghosts in $\text {PG}(2,3)$

If we see $\text {PG}(2,3)$ as a multiset, it consists of 26 points and has $3^{13}$ multi-subsets. The dimension of the space of ghosts is $\left( {\begin{array}{c}3+1\\ 2\end{array}}\right) +1=7$ and therefore $\left| {\mathcal {G}}\right| =3^7=2187$. We group the multiset sums of lines according to the number of lines involved. Here, a line can be counted at most twice.

Given a ghost S, its complement is a ghost of size $26-\left| S\right|$, so it suffices to argue on configurations of size up to 13 or on the corresponding complements when more convenient. Note that, when moving to the complement, simple points remain simple, double points are not counted and conversely points which were not included become double. As a consequence, ghosts of size 13 are self-complementary.

We have 14 ghosts deriving from taking either zero or one line: the empty set and the lines of $\text {PG}(2,3)$, respectively. Multiset sums of two lines involve two cases: either the two lines are distinct, or one line is counted twice. We have $\left( {\begin{array}{c}13\\ 2\end{array}}\right) =78$ possibilities for the first case and 13 for the second one.

Concerning three lines, three subcases are allowed.

• (3.1) There are three distinct lines of a pencil. This corresponds to an affine plane contained in $\text {PG}(2,3)$, counted once and of size 9, and therefore ghosts of this kind are 13.

• (3.2) The three distinct lines do not pass through a common point, so the configuration has size 12: there are 6 simple points and 3 double points. The number of such configurations is $\theta (3,3)=234$.

• (3.3) There are two distinct lines, and one of them is counted twice (configuration with 3 simple points and 3 double points, size 9). The two lines are distinguishable, so there are $13\cdot 12=156$ possibilities.

Multiset sums of four lines lead to a larger number of subcases.

• (4.1) If the four lines belong to a pencil, we get the whole projective plane (counted once and of size 13). There is just one allowed case and it is self-complementary.

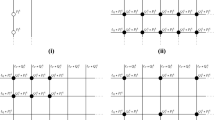
• (4.2) If the four lines are distinct and three of them belong to a pencil, we obtain the same configuration as case (4.4) (see Fig. 1).

• (4.3) In the case of four lines, no three in a pencil, there are 4 points counted once and 6 points counted twice (size 16). This configuration appears $\theta (4,3)=234$ times.

• (4.4) If one line is counted twice and other two lines once, and the three lines belong to a pencil, we obtain a configuration consisting of 7 points counted once and 3 points counted twice (size 13). The double line can be chosen in 13 ways, the first simple line in 12 and the second one in 2 ways. The simple lines are undistinguishable, so this case gives $\frac{13\cdot 12\cdot 2}{2!}=156$ ghosts. This case is self-complementary.

• (4.5) If one line is counted twice and other two lines once, and the three lines do not belong to a pencil, there are 4 points counted once and 3 points counted twice (size 10). This case is the complement of the case (4.3).

• (4.6) In the case of two lines counted twice, there are $\left( {\begin{array}{c}13\\ 2\end{array}}\right) =78$ occurrences. This case consists of 6 double points and 1 simple point (size 13) and is self-complementary.

Fig. 1

Equivalence of cases (4.2) (left) and (4.4) (right). Simple lines are full, while the double line is dashed. Double points are circled. Note that in a three lines intersect in the vertex of the pencil, which so vanishes, while in b one point is counted $4=1\mod 3$ times

Up to this point, the found ghosts are

$$\begin{aligned} 2\cdot \left( 14+78+13+13+234+156+234\right) +\left( 1+156+78\right) =1719. \end{aligned}$$

The remaining 468 are retrieved as follows. When considering five or more lines, the only cases which have not been previously considered, or are not the complement of a previous case, are the multiset sum of three double lines not in a pencil ($\theta (3,3)=234$ occurrences) and its complement. In the first case there are 3 simple points and 6 double points (size 15), while the complement has size 11, consists of 3 simple points and 4 double points and may be seen as the multiset sum of two double lines and a simple line not in a pencil. Such cases contribute with 468 ghosts, so the classification of ghosts in $\text {PG}(2,3)$ is complete.

The kinds of ghosts of size at most 13 are summarized in Table 1.

Table 1 Ghosts of $\text {PG}(2,3)$ with size up to 13

According to Remark 11, each ghost of $\text {PG}(2,3)$ is in exactly one of the cosets $C^{\perp },C^{\perp }+{\textbf{j}},C^{\perp }+2{\textbf{j}}$. In particular, the multiset sum of $\lambda$ lines, $\lambda =0,1,2\mod 3$, is in $C^{\perp }+\lambda {\textbf{j}}$.

5.3 Ghosts in $\text {PG}(2,4)$

Being $p=2$, points can be counted up to once, and there are $2^{21}$ subsets. Also, $\text {PG}(2,4)$ is the smallest plane having ghosts which are not multiset sums of lines. In fact, the ghost space has dimension $21-\left( {\begin{array}{c}2+1\\ 2\end{array}}\right) ^2=12$, greater than $\dim C=\left( {\begin{array}{c}2+1\\ 2\end{array}}\right) ^2+1=10$. Furthermore, $\dim C^{\perp }=11$.

We first report the ghosts in $\text {PG}(2,4)$ which are multiset sums of lines:

• the empty set;

• sets consisting of one line (21 occurrences);

• multiset sums of two lines, consisting of 8 points. Their number is $\left( {\begin{array}{c}21\\ 2\end{array}}\right) =210$;

• three lines of a pencil. This configuration consists of 13 points and is the complement of the multiset sum of two lines;

• unitals, consisting of $2^3+1=9$ points. All unitals in $\text {PG}(2,4)$ are Hermitian (see [10]), so, by [4], they may be seen as multiset sums of lines (three lines not in a pencil in this case). It is known that there are 280 unitals of $\text {PG}(2,4)$.

Note that the previous cases correspond exactly to the weight distribution presented in [11]. There are no cases left in C, since

$$\begin{aligned} 2\cdot (1+21+210+280)=2^{10}. \end{aligned}$$

Ghosts outside C are as follows:

• hyperovals (168 occurrences, see [10]). Recall that all hyperovals of $\text {PG}(2,4)$ are regular, namely, they consist of 6 points, each being the nucleus of the conic through the remaining five points. It is worth noting that its complement has size 15 and a suitable coordinatization makes it isomorphic to $\text {PG}(3,2)$ (see [2] for the nice construction);

• Baer subplanes (size 7, 360 occurrences, see [6, 8]);

• multiset sums of ghosts of the previous kinds. We focus on the configuration consisting of the multiset sum of a hyperoval and an external line (11 points) and show that there are no cases left. There are six external lines to a given hyperoval, and a configuration is reached by exactly one choice for each object (a hyperoval is a cap). Therefore, there are $168\cdot 6=1008$ ghosts which are the multiset sum of a hyperoval and an external line. Note that the complement of the previous configuration is an affine plane $\pi$ minus a hyperoval H entirely contained in $\pi$, so, in characteristic two, it is the multiset sum of $\pi$ and H.

We now sum the occurrences of the kinds of ghosts we have previously found, together with their complements:

$$\begin{aligned} 2\cdot (1+21+210+280+168+360+1008)=4096=2^{12}. \end{aligned}$$

It is the total number of ghosts of $\text {PG}(2,4)$, so the search is complete. This means that multiset sums of other ghosts will fall in one of the previous kinds, or in the corresponding complement.

To make the picture clearer, we now group ghosts with respect to $C^{\perp }$. The intersection of C and $C^{\perp }$ has dimension 9 and consists of 512 (vectors corresponding to) multiset sums of lines intersecting each line in an even number of points, namely, multiset sums of an even number of lines. This leads to consider multiset sums of: zero lines (the empty set: one case); two lines (210 cases); four lines in a pencil (an affine plane: 21 cases); three lines in a pencil and a transversal line. The latter case is the complement of a unital, obtained by taking the other two lines of the pencil and the transversal line, and so contributes with 280 cases. There are no cases left in $C\cap C^{\perp }$.

Vectors in $C^{\perp }\backslash C$ are $2^{11}-2^9=1536$, distributed as follows:

• 168 hyperovals;

• 360 complements of Baer subplanes, which are blocking sets of (maximal) size 14. A complement of a Baer subplane may be seen as the multiset sum of a hyperoval and two external lines;

• 1008 multiset sums of an affine plane $\pi$ and a hyperoval contained in $\pi$, as seen above.

The remaining $2^{11}$ ghosts not corresponding to vectors of $C^{\perp }$, i.e., those in $C^{\perp }+{\textbf{j}}$, are simply the complements of the previous ones, intersecting each line in an odd number of points. More precisely, $C^{\perp }+{\textbf{j}}$ consists of:

• ghosts also belonging to C, which are multiset sums of an odd number of lines. Since $\left( C^{\perp }+{\textbf{j}}\right) \cap C=\left( C^{\perp }\cap C\right) +{\textbf{j}}$, these ghosts are exactly the complements of those in $C^{\perp }\cap C$, namely: multiset sums of five lines in a pencil ($\text {PG}(2,4)$), three lines in a pencil, three lines delimiting a triangle (unital), one line;

• ghosts in $\left( C^{\perp }+{\textbf{j}}\right) \backslash C=\left( C^{\perp }\backslash C\right) +{\textbf{j}}$. They are complements of ghosts in $C^{\perp }\backslash C$ listed above, namely, complements of hyperovals, Baer subplanes and the multiset sums of a hyperoval and an external line.

Note that the elements of $C^{\perp }+{\textbf{j}}$ different from the complements of hyperovals and $\text {PG}(2,4)$ may be obtained as the multiset sum of a Baer subplane and a hyperoval, according to the size m of their intersection:

• if $m=0$, the ghost has size 13 and corresponds to the multiset sum of three lines in a pencil;

• if $m=1$, the resulting ghost (size 11) is the multiset sum of a hyperoval and an external line;

• if $m=2$, the configuration has size 9 and represents a unital;

• if $m=3$, the size is 7, so the obtained ghost is another Baer subplane;

• if $m=4$ (size 5), one obtains a line. In this case the hyperoval intersects the Baer subplane in a sub-hyperoval (an affine plane of the Baer subplane).

When m is even (respectively, odd), the corresponding ghost belongs to $\left( C^{\perp }+{\textbf{j}}\right) \cap C$ (respectively, $\left( C^{\perp }+{\textbf{j}}\right) \backslash C$). Note further that the multiset sum of a Baer subplane and a secant line gives a hyperoval, and conversely a Baer subplane may be obtained as the multiset sum of a hyperoval and a secant line. In a sense, we can say that the class of Baer subplanes differs from that of hyperovals by the multiset sum of suitable secant lines.

The sizes of the ghosts of $\text {PG}(2,4)$ range from 5 to 16, together with sizes 0 and 21. Indeed, it is known (see [1]) that the minimum weight of the code of points and lines of $\text {PG}(2,q)$ is $q+1$, so there are no ghosts of $\text {PG}(2,q)$ of size in the interval [1, 4] (and symmetrically in [17, 20]).

6 Conclusions

This paper moves from [12] and goes on studying the structure of multisets whose power sum polynomial is the null one, called ghosts. We have proven that ghosts constitute a vector subspace of the space of multi-subsets of $\text {PG}(2,q)$ modulo p, and therefore multi-subsets associated to a same power sum polynomial belong to an affine subspace, whose corresponding vector space is the ghost space. The dimension of the ghost space has been determined by employing a known link to the code C of points and lines of $\text {PG}(2,q)$, where the multiset sum is replaced by the vector sum. Emphasis has been given on the different behavior for q prime or not: only in the first case, in fact, lines constitute a generator set for the space of ghosts.

Furthermore, we have determined new classes of simple ghosts: unitals, Baer subplanes and hyperovals. The projective plane $\text {PG}(2,4)$ unveils to be particularly rich of the above kinds of ghosts.

The research proposed in the present paper could be extended by finding new classes of (simple) ghosts, possibly by investigating projective planes of higher order, where other rich structures arise. Other objects that could be worth studying in such a perspective are linear sets. Also, moving to higher dimensions would reveal possible non-planar ghosts.