Continuous flattening of the 2-dimensional skeleton of a regular 24-cell

Abstract

Bellow theorem says that any polyhedron with rigid faces cannot change its volume even if it is flexible. The problem on continuous flattenig of polyhedra with non-rigid faces proposed by Demaine et al. was solved for all convex polyhedra by using the notion of moving creases to change some of the faces. This problem was extended to a problem on continuous flattening of the 2-dimensional skeleton of higher dimensional polytopes. This problem was solved for all regular polytopes except three types, the 24-cell, the 120-cell, and the 600-cell. This article addresses the 24-cell and gives a continuous flattening motion for its 2-skeleton, which is related to the Jitterbug by Buckminster Fuller.

1 Introduction

We use the term polyhedron for a closed polyhedral surface that is permitted to touch but not cross itself. We assume a polyhedron can always be folded by creases like a piece of paper ignoring its thickness, but not allowing stretching. A flat folding of a polyhedron is a folding by creases into a multi-layered planar shape so that the number of creases is finite. In [2] it was proved that any polyhedron of genus zero has a flat folded state. The topic presented here is related to the problem by Demaine et al. [4] (Open Problems 18.1 and 18.3 in [5]): Can every flat folded state of a polyhedron be reached by a continuous folding process?

An important limitation to continuous flattening is Bellow theorem [3, 13] that the volume of any polyhedron with rigid faces is invariant, even if the dihedral angles can be changed by hinges so that the polyhedron is flexible. Hence, to obtain a flat folded state of a polyhedron continuously, the polyhedral surface should change by moving creases (edges).

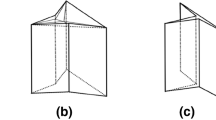
For example, a rectangular box can be flat folded by creases as shown in Fig. 1. The problem asks to find a continuous motion to reach the flat folded state from the original box. The long-dotted line segments are moving creases used in [8].

Fig. 1

From left to right: a rectangular box, the moving creases shown by long-dotted line segments, and its flat folded state

We say a polyhedron Q is isometric to a polyhedron P with respect to the intrinsic metric if there is a polyhedron $P'$ obtained from P by subdividing some faces of P (i.e., some faces of $P'$ may be included in the same face of P, but $P'$ is congruent to P) such that Q is combinatorially equivalent to $P'$ and the corresponding faces of $P'$ and Q are congruent. In [8] the authors defined a continuous flat-folding motion of a polyhedron P by a family of polyhedra $\{P_t: 0 \le t \le 1 \}$ such that each $P_t$ is isometric to P with respect to the intrinsic metric, and $P_t$ converges to $P_1$ continuously, where $P_0=P$ and $P_1$ is a flat folded state of P.

The first paper [8] on continuous flattening of polyhedra gives results for the Platonic polyhedra, and we explain more in detail the continuous motion of the regular octahedron in Sect. 2, which will be used for the proof of Theorem 4.1. The case of any convex polyhedron was solved by two methods [1, 11]. However, the set of moving creases in those two methods covers almost the entire surface of a convex polyhedron, but the method used in [8], namely the kite method, only requires small portions of the convex polyhedron’s surface, and maximizes the number of rigid edges and faces in some sense. So, we use the kite method in this article because of these advantages.

This problem was extended to higher dimensional polytopes in [9, 10].

Problem

Find a continuous flat-folding motion of the 2-dimensional skeleton (2-skeleton for short), denoted by C(P), of any given polytope P.

We concentrate on regular polytopes. There are three types of n-dimensional regular polytopes for $n \ge 5$, that is, the hypercube, the simplex, and the cross-polytope, and three more types for $n=4$, that is, the 24-cell, the 120-cell, and the 600-cell. We showed in [9] that for any given hypercube there is a continuous flat-folding motion of the 2-skeleton onto any of its square face F such that all square faces parallel to F are rigid, that is, have no crease during the motion, and in [10] that for any given regular simplex or cross-polytope there is a continuous flat-folding motion of the 2-skeleton such that at least two thirds of the edges and two ninths of the triangular faces are rigid.

Here we address the regular 24-cell. Let P be a regular 24-cell. Then P has 24 regular octahedral facets. First, we show that the 2-skeleton of P can be continously folded onto any of its octahedral facets (Theorem 4.1). We show that the 2-skeleton of P contains the eight triangular faces of a cuboctahedron, denoted by Q, and Q can be continuously transformed into an octahedron so that all edges are rigid. Such motion of Q is same as the motion of the Jitterbug by Buckminster Fuller [6, 7]. We give a precise calculation of this motion in Sect. 4, which is used to prove Theorem 4.1. Next, we show the existence of a continuous flattening motion of the 2-skeleton of P onto any of its triangular face F such that 54 out of the 96 edges and all triangular faces parallel to F are rigid during the motion (Theorem 5.1).

2 Continuous flattening of a regular octahedron

We denote by |uv| length of the line segment uv. The following property, called the kite property, plays a key role for continuous flattening of a regular octahedron.

Definition 2.1

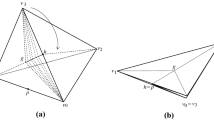
Let $K=abcd$ be a kite with $|ab|=|ad|$, $|cb|=|cd|$, and h the midpoint of bd. Let q and $q'$ be points on bh and dh, respectively, so that $|qh|=|q'h|$. Fold K by valley creases along dh, aq, bq, and cq, and mountain creases along ah, ch, and hq so that the point q attaches to the point $q'$ (Fig. 2). We call the resulting figure a folded kite with wing-shape at q. This figure is flexible. If the distances of two pairs of diagonal vertices of K in the resulting figure are given, such as $dist(a, c) = l$ and $dist(b, d) = m$, the resulting figure is uniquely determined up to congruence. We denote it by K(l, m).

Proposition 2.2

[8, 12]. Let $K=abcd$ be a kite with $|ab|=|ad|$, $|cb|=|cd|$, and h the midpoint of bd. For any pair $\{l, m\}$ with $||ah|-|ch|| \le l \le |ac|$ and $0 \le m \le |bd|$, there is a unique point q in the line segment bh so that one of its folded kites with wing-shape at q is congruent to K(l, m). For any two folded kites $K(l_1,m_1)$ and $K(l_2,m_2)$ there is a family $\{K(l_t,m_t): 1 \le t \le 2\}$ such that $K(l_t,m_t)$ converges to $K(l_2,m_2)$ as t increases from 1 to 2.

We denote by S(p, r) the sphere with center p of radius r in ${\mathbb {R}}^3$ with the xyz-axes. (We will use the same symbols to spheres in higher dimensional Euclidean spaces.) We denote by $v'$ the point symmetric to a point v about the origin in ${\mathbb {R}}^3$. For any real number $t \, (0 \le t \le 1)$, we denote by p(t) the position of a point p in the space considered.

Let W be the regular octahedron with vertices $v_1=(1, 0, 0), v_2=(0, 1, 0)$, $v_3=(0,0, 1)$, and its symmetric vertices $v'_i \, (1 \le i \le 3)$, respectively, about the origin O (Fig. 3a). The length of each edge of W is $\sqrt{2}$ and the distance between two parallel triangular faces is $2/ \sqrt{3}$.

Proposition 2.3

[8, 10]. A regular octahedron can be continuously flattened onto any of its faces F by rotation and translation of its parallel face toward F, such that 9 of the 12 edges and two parallel faces are rigid (Fig. 3).

Proof

For the regular octahedron W we call $\triangle v_1v_2v_3$ and $\triangle v'_1v'_2v'_3$ the top and bottom faces, respectively and other faces the side faces. We can choose the bottom face as an arbitrary face F.

Fig. 2

A folded kite with wing-shape: a a kite abcd with $|ab|=|ad|$, $|cb|=|cd|$, h the midpoint of bd, and q and $q'$ be points on bh and dh with $|qh|=|q'h|$, respectively, where dotted line segments denote valley crease and solid line segments denote mountain crease; b a folded kite; c another slant view of the folded kite, where $dist(a, c) = l$ and $dist(b, d) = m$

Fix the bottom face $F=\triangle v'_1v'_2v'_3$. Let l be the line segment connecting the centroids of the top face and the bottom face F, and T be the cylinder over the circumcircle of F (Fig. 3b where l and T are described as a point and a circle, respectively). Rotate and translate the top face toward F so that the centroid of the top face moves on l and the top face is parallel to F at all times. Then the top face slides down, touching T. There are two possibilities, either the vertex $v_2$ moves to $v'_1$ or $v'_3$. Choose the former case. More precisely, the vertex $v_2$ moves to $v'_1$ along the minar (shorter) part of the curve, divided into two parts by $v_2$ and $v'_1$, which is obtained as the intersection of the cylinder T and the sphere $S(v'_3, \sqrt{2})$, that is,

$$\begin{aligned} v_2(t) \in T \cap S(v'_3, \sqrt{2}). \end{aligned}$$

There are six side faces and they compose three folded rhombuses $R_1=v_3v_2v'_3v'_1$, $R_2=v_1v_3v'_1v'_2$, and $R_3=v_2v_1v'_2v'_3$. Applying the kite property to those folded rhombuses, we can continuously fold the octahedron onto $\triangle v'_1v'_2v'_3$ with moving creases shown in Fig. 3c. $\square$

Remark

In the above proof since $v_2$ moves to $v'_1$, the edge $v_2v'_1$ is folded in half at its midpoint h. For the midpoint h there are two possibilities, either h moves to the midpoint of $v'_1v'_2$ or $v'_1v'_3$. In the former case as shown in Fig. 3, the midpoint h moves on the minar arc of the circle so that

$$\begin{aligned} h(t) \in S\Big (v'_1, \frac{1}{\sqrt{2}}\Big ) \bigcap S\Big (v'_3, \sqrt{\frac{3}{2}}\Big ). \end{aligned}$$

Fig. 3

A continuous flattening of an octahedron: a the octahedron W in ${\mathbb {R}}^3$ with vertices $v_1=(1, 0, 0), v_2=(0, 1, 0)$, $v_3=(0,0, 1)$, and their symmetric vertices $v'_i \, (1 \le i \le 3)$, respectively, about the origin O; b the view from the top face $\triangle v_1v_2v_3$, together with its circumscribed cylinder with its central axis l connecting centroids of $\triangle v_1v_2v_3$ and $\triangle v'_1v'_2v'_3$, and the motion of vertices $v_i \, (1 \le i \le 3)$; c the moving creases where h and p are the midpoints of $v_2v'_1$ and $v'_1v'_2$, respectively; d the flat folded state

We use the motion of the regular octahedron mentioned in the proof of Proposition 2.3 later, so we describe it as a function of the time $t \,(0 \le t \le 1)$. Let $\theta (t) =(\pi /3)t$ be the rotation angle of $\triangle v_1v_2v_3$ and denote by l(t) the distance of two centroids of $\triangle v_1(t)v_2(t)v_3(t)$ and $\triangle v'_1v'_2v'_3$ in the motion. Since the edge length is $\sqrt{2}$, the radius of the circumcircle of $\triangle v_1v_2v_3$ is $\sqrt{2/3}$.

Lemma 2.4

The following holds

$$\begin{aligned} l(t)=\sqrt{ 2- \frac{8}{3} \Big ( \sin \frac{(1+t)\pi }{6} \Big )^2 }. \end{aligned}$$

Proof

Let $v^{*}_2(t)$ be the orthogonal projection of $v_2(t)$ on the plane including $\triangle v'_1v'_2v'_3$. Then $\angle v'_3gv^{*}_2(t) = \pi /3 + \theta (t)$ where g is the centroid of $\triangle v'_1v'_2v'_3$ (Fig. 4).

Fig. 4

The orthogonal projection $v^{*}_2(t)$ of $v_2(t)$ to the plane including $\triangle v'_1v'_2v'_3$

Since $v'_3$ is fixed, that is, $v'_3(t)=v'_3$ and $|v_2(t)v^{*}_2(t)|=l(t)$, by the Pythagorean theorem

$$\begin{aligned} | v_2(t)v'_3|^2=|v'_3v^{*}_2(t)|^2 + |v_2(t)v^{*}_2(t)|^2 = |v'_3v^{*}_2(t)|^2 +\{l(t)\}^2. \end{aligned}$$

By the rigidity of $v_2v'_3$, we have $|v_2(t)v'_3| = |v_2v'_3| = \sqrt{2}$. From this, the above equation, and

$$\begin{aligned} |v'_3v^{*}_2(t)|=2 \sqrt{\frac{2}{3}} \sin \Big ( \frac{\pi }{6} + \frac{\theta (t)}{2} \Big ), \end{aligned}$$

we have

$$\begin{aligned} 2=\Big \{ 2\sqrt{\frac{2}{3}} \sin \Big ( \frac{\pi }{6} +\frac{\theta (t)}{2} \Big ) \Big \}^2 + l(t)^2. \end{aligned}$$

Substituting $\theta (t)= (\pi /3)t$, we get the equality in Lemma 2.4. $\square$

3 Regular 24-cell

Let P be a regular n-polytope in ${\mathbb {R}}^n$ and $C=C(P)$ the 2-skeleton of P. For C, we call a 2-skeleton $C'$ a folded C if $C'$ is intrinsically isometric to C, is composed of flat polygons, allowed to touch each other without self-crossing.

Definition 3.1

We say the 2-skeleton C of a regular n-polytope P is folded continuously to a folded C, which we call $C_1$, if there is a continuous family of $\{C_t: 0 \le t \le 1 \}$ satisfying the following conditions:

• (1) for each t, $C_t$ is a folded C,

• (2) $C_0 =C$ and the mapping from $t \in \{0\le t \le 1\}$ to $C_t$ is continuous.

Moreover, if $C_1$ is a flat folded state of C, we say C is flat folded continuously. We also call the family $\{C_t: 0 \le t \le 1 \}$ a continuous folding (or flat-folding) process from C to $C_1$.

In the definition above, the stacking order of the flat folded state $C_1$ is not taken into account, but in this paper we take care of it for the case of a regular 24-cell P by first folding the 2-skeleton C onto an octahedral facet of P in $R^4$.

A regular 24-cell has 24 regular octahedral facets. We can realize it in ${\mathbb {R}}^4$ with vertices (x, y, z, w) such that two of the coordinates are 1 or $-1$ and the others 0, we denote it by P through this section. Then there are 24 vertices in P. The edges of P are the line segments joining two vertices of distance $\sqrt{2}$, and there are 96 edges. The 2-skeleton is the set of the triangular faces of P, and there are 96 triangular faces.

For a point u in the hyperplane $w=0$, we use the symbol $u'$ for the point symmetric to u about the origin, and $u^{+} (u^{-})$ for the points translated to the hyperplane $w=1 \, (w=-1)$ along the w-axis by one unit. We denote by $W^0$ the octahedron with vertices $v_1=(1,0,0,0)$, $v_2=(0,1,0,0)$, $v_3=(0,0,1,0)$, and $v'_i \, (1 \le i \le 3)$.

The intersection of P with the hyperplane $w=1$ is the octahedron with vertices $v^{+}_i= (v_i)^{+}$ and $v'^{+}_i= (v'_i)^{+}$ $(1 \le i \le 3)$, denoted by $W^{+}$. We denote by $W^{-}$ the corresponding octahedron $P \cap \{w=-1 \}$.

The intersection of P with the hyperplane $w=0$ is the cuboctahedron with 12 vertices $a_1=(1,0,1,0)$, $a_2=(1,1,0,0)$, $a_3=(0,1,1,0)$, $a_4=(1,0,-1,0)$, $a_5=(0,-1,1,0)$, $a_6=(-1,1,0,0)$, and $a'_i$ $(1\le i \le 6)$ (Fig. 5a). The intersection of the 2-skeleton C(P) with $w=0$ is the set of triangular faces of the cuboctahedron, and we denote it by Q.

Note that the vertices of $W^0$ are the centroids of six square faces of the cuboctahedron, and $W^{+}$ and $W^{-}$ are images of $W^0$ by translation parallel to the w-axis with $+1$ and $-1$, respectively (Fig. 5b).

Hence the 24 vertices of C(P) are $a_i,\,a'_i \, (1\le i \le 6)$ and ${v_i}^{\pm }, \, {v'_i}^{\pm }$ $(1 \le i \le 3)$. For each triangular face F of Q, there is a unique triangular face G of $W^{+}$ $(W^{-})$ parallel to F with distance $2/ \sqrt{3}$, so that F and G compose an octahedral facet of P, e.g., $F=\triangle a_1a_2a_3$ and $G=\triangle v^{+}_1v^{+}_2v^{+}_3$ in Fig. 5. We denote it by W(F, G). Therefore, there are 16 octahedral facets mentioned above. For each square hole of Q, say $a_1a_2a_4a'_6$ with center $v_1$, composes an octahedral facet with ${v_1}^{+}$ and ${v_1}^{-}$. Since there are 6 holes in Q, there are 6 octahedral facets mentioned above. Adding $W^{+}$ and $W^{-}$, there are exactly 24 octahedral facets in P.

We denote by T(F) the 3-dimensional cylinder over the circumcircle of a triangle F, where the cylinder means a cylenderical surface, e.g. if F is a triangle with the circumcircle $\{(x,y,0,0): x^2 +y^2 =1\}$, then $T(F)=\{(x,y,z,w): x^2+y^2=1 \}$.

Fig. 5

The regular 24-cell P: a The cuboctahedron $P \cap \{w=0 \}$ and the vertices $v_1, v_2, v_3$ of the regular octahedron $W^{0}$; b the regular octahedron $W^{+}$, the translation of W in the hyperplane $w=1$

Lemma 3.2

The cylinders $T(\triangle a_1a_2a_3)$ and $T(\triangle v_1v_2v_3)$ in the hyperplane $w=0$ are identical, and they include all vertices of the octahedron $W^0$.

Proof

Since the line joining centroids of $\triangle a_1a_2a_3$ and $\triangle v_1v_2v_3$ is orthogonal to those triangles, the first statement of the lemma holds. Since both $W^0$ and $T(\triangle a_1a_2a_3)$ are symmetric about the origin, all vertices $v_i, \, v'_i \, (1 \le i \le 3)$ of $W^0$ are on the cylinder. $\square$

Lemma 3.2 holds for any pair of parallel triangular faces, one in Q and the other in $W^0$.

4 From the 24-cell onto an octahedron

We prove that the 2-skeleton of a regular 24-cell can be continuously folded onto any of the octahedral facets.

Theorem 4.1

Let P be a regular 24-cell. There is a continuous folding process from the 2-dimensional skeleton of P onto any of the octahedral facets of P so that 72 edges are rigid and each of the other 24 edges is folded at its midpoint, and furthermore, the 24 faces are rigid during the motion.

Without loss of generality, we can assume that a regular 24-cell is the 24-cell P described in the previous section and $W^{+}$ is the chosen facet. We fix $W^0$ and translate $W^{+}$ to $W^0$ in the following motion. We divide the proof into three steps. First, we define the motion of each vertex in P and then, we determine the motion of each triangular face in P so as to synchronize the motion of the vertices. Finally, combining those two motions we prove that the 2-skeleton of P can be continuously folded onto $W^0$ so that all requirements in the theorem are satisfied.

We first define the motion of vertices of Q. Figure 6 shows the edge graph of the cuboctahedron together with vertices of $W^0$. The (curved) dotted line segment with arrow shows where each vertex in Q moves, precisely, $a_1$ and $a_4$ to $v_1$, $a_2$ and $a_6$ to $v_2$, $a_3$ and $a_5$ to $v_3$, $a'_1$ and $a'_4$ to $v'_1$, $a'_2$ and $a'_6$ to $v'_2$, and $a'_3$ and $a'_5$ to $v'_3$.

Lemma 4.2

There is a continuous motion of Q (the cuboctahedron without square faces) shown in Fig. 5a onto the octahedron $W^0$ satisfying the following conditions for each face F of Q, e.g. $F=\triangle a_1a_2a_3$.

• (1) F is rotated and moved toward $\triangle v_1v_2v_3$ along the line l joining the centroids of F and $\triangle v_1v_2v_3$.

• (2) F always touches the cylinder T(F), that is, F is always orthogonal to l.

Proof

Fix the vertices $v_i$ and $v'_i$ $(1\le i \le 3)$. Let $F_i$ $(1 \le i \le 4)$ be four triangular faces $F_1=\triangle a_1a_2a_3$, $F_2=\triangle a_3a_6a'_4$, $F_3=\triangle a'_4a'_2a_5$, and $F_4=\triangle a_1a_5a'_6$ (Fig. 6). Then the central axes of those four cylinders $T(F_i)$ $(1\le i \le 4)$ meet at the origin O, so that any pair of them makes the angle $\arccos (1/3)$ at O, same as the supplement of the angle made by the two vectors from the center of a regular tetrahedron to any two vertices. Note that the intersection of any pair of those cylinders are two ellipsoids (Fig. 7a).

Choose the ellipsoid in $T(F_1) \cap T(F_4)$ including the vertices $a_1$ and $v_1$. Move the vertex $a_1$ along the shorter curve joining $a_1$ and $v_1$ of the ellipsoid divided by $a_1$ and $v_1$. Move $a_2$ and $a_3$ by a congruent motion of $a_1$, and move $a'_i \, (1 \le i \le 3)$ by a symmetric motion of $a_i$ about O. Since $F_1$ and $F_4$ move onto $\triangle v_1v_2v_3$ and $\triangle v_1v'_2v_3$, respectively, there are no self-crossing for $F_1$ and $F_4$ during the motion. For any other pair of triangular faces having a common vertex in Q, there are no self-crossing by a similar reason. Therefore, there are no self-crossings during the motion of Q onto $W^0$. $\square$

Note that the motion of Q mentioned above is same as the one used in the model, so-called, Octabug or Jitterbug [6, 7].

Let $\theta (t) = (\pi /3) t$ for $1 \le t \le 1$ be the rotation angle of the face $F=F_1=\triangle a_1a_2a_3$ in the motion defined in the proof of Lemma 4.2 (Fig. 7b). Denote by m(t) the distance between $\triangle a_1(t)a_2(t)a_3(t)$ and $\triangle v_1v_2v_3$.

Lemma 4.3

The following holds

$$\begin{aligned} m(t)= \displaystyle { \frac{2}{\sqrt{3}} \cos \Big {(} \frac{\pi }{3} t} \Big {)} - \frac{1}{\sqrt{3}}. \end{aligned}$$

Fig. 6

The edge graph of Q with vertices of $W_0$ and motion of the vertices of Q shown in line segments with arrows

Proof

Let E be the ellipsoid in $T(F_1) \cap T(F_4)$ defined in the proof of Lemma 4.2. Since the central axes of $T(F_1)$ and $T(F_4)$ makes the angle $\alpha = \arccos 1/3$, the angle

$$\begin{aligned} \beta = \frac{\pi }{2} - \frac{\alpha }{2} \end{aligned}$$

is the angle of the plane including E and the plane, setting H, including O and parallel to $F_1$, and let $a^{*}_1(t)$ be the orthogonal projection of $a_1(t)$ to H (Fig. 7b).

Denote by $g_1$ and $g_2$ the centroids of $F_1$ and $\triangle v_1v_2v_3$, respectively and $m(t)=|g_1(t) - g_2|$. Since the radius of the circumcircle of $F_1$ is $r=\sqrt{2/3}$ and the distance between the centroid of $\triangle v_1v_2v_3$ and the origin O is $1/\sqrt{3}$,

$$\begin{aligned} m(t)&=|a_1(t)a^{*}_1(t)| - \frac{1}{\sqrt{3}} = r \cos \theta (t) \tan \beta - \frac{1}{\sqrt{3}} \\&= \displaystyle {\sqrt{\frac{2}{3}} \cos \Big {(} \frac{\pi }{3} t \Big {)} \tan \Big {(}\frac{\pi }{2}-\frac{\alpha }{2}\Big {)} - \frac{1}{\sqrt{3}}}. \end{aligned}$$

By $\cos \alpha = 1/3$, we have

$$\begin{aligned} \tan \frac{\alpha }{2}= \sqrt{\frac{1-\cos \alpha }{1+ \cos \alpha }} =\frac{1}{\sqrt{2}}. \end{aligned}$$

Substituting this in the above, we get the equality required. $\square$

Fig. 7

a The intersection of two cylinders over the circumcircles of $F=\triangle a_1a_2a_3$ and $\triangle a_1a'_5a'_6$; b the height of $a_1(t)$ from the plane parallel to F including O

Next, we will define the motion of octahedron $W^{+}$ (resp. $W^{-}$) as translation along the w-axis so that the coordinate of the centroid (0, 0, 0, w(t)) (resp., $(0,0,0, -w(t))$) for $0 \le t \le 1$ is

$$\begin{aligned} w(t)^2=l(t)^2 - m(t)^2, \end{aligned}$$

where l(t) and m(t) are defined in Lemmas 2.4 and 4.3 , respectively.

Lemma 4.4

The distance between the centroid of $\triangle a_1(t)a_2(t)a_3(t)$ and

$\triangle v^{+}_1(t)v^{+}_2(t)v^{+}_3(t)$ (resp. $v^{-}_1(t)v^{-}_2(t)v^{-}_3(t)$) is l(t).

Proof

Let $c_1, \, c_2=c_2(t)$ and $c_3=c_3(t)$ be the centroids of $\triangle v_1v_2v_3$,

$\triangle a_1(t)a_2(t)a_3(t)$, and $\triangle v^{+}_1(t)v^{+}_2(t)v^{+}_3(t)$, respectively. Then $c_3$ is the translate of $c_1$ along the w-axis with w(t). Since the line segment $c_1c_2$ in the hyperplane $w=0$ is orthogonal to the w-axis, $\triangle c_1c_2c_3$ is an orthogonal triangle with right angle at $c_1$. By the Pythagorean theorem,

$$\begin{aligned} |c_2c_3|^2 = |c_1c_2|^2 + |c_1c_3|^2 = m(t)^2 + w(t)^2 =l(t)^2. \end{aligned}$$

$\square$

Finally, we define the motion of triangular faces in $\{0< w < 1\}$ and $\{-1< w < 0\}$, each of which is folded in half or folded with moving creases such as $\triangle v_2v'_1v'_3$ or $\triangle v_2v'_1v_3$, respectively, in Fig. 3c.

Denote

$$\begin{aligned} F=F_1=\triangle a_1a_2a_3, \,\,\, G=\triangle v^{+}_1v^{+}_2v^{+}_3. \end{aligned}$$

Consider the octahedral facet W(F, G) with F and G. We denote by F(t) and G(t) the position of F and G, respectively for $0 \le t \le 1$.

Fact

Let $\Pi$ be any given plane in ${\mathbb {R}}^4$. For two vectors $\mathbf{u_1}$ and $\mathbf{u_2 }$ orthogonal to $\Pi$ any linear combination of $\mathbf{u_1}$ and $\mathbf{u_2 }$ is orthogonal to any plane parallel to $\Pi$.

Denote by $c_1$, $c_2(t)$, and $c_3(t)$ the centroids of $\triangle v_1v_2v_3$, F(t), and G(t), respectively. Since $c_1c_3(t)$ is parallel to the w-axis, it is orthogonal to both F(t) and G(t). Since $c_1c_2$ is orthogonal to $F=\triangle a_1a_2a_3$ and $\triangle v_1v_2v_3$, it is also orthogonal to both F(t) and G(t). Since the vector $c_2(t)c_3(t)$ is a linear combination of the vectors $c_1c_2(t)$ and $c_1c_3(t)$, it is orthogonal to F(t) and G(t) by the above fact.

Apply the flattening motion defined in Proposition 2.3 to the octahedral facet W(F, G). Since $v^{+}_i$ and $a_i$ move to $v_i$ for $1 \le i \le 3$, the three edges $a_iv^{+}_i$ are folded in half at their midpoints. Let h be the midpoint of the edge $a_1v^{+}_1$. Since the edge $a_1a_3$ moves to the edge $v_1v_3$ of $W^{0}$, move h to the midpoint of $a_1(1)a_3(1)$, and hence to the midpoint of $v_1v_3$.

Moreover, since $a_1v^{+}_1$ is the common edge of W(F, G) and

$W(\triangle a_1a'_6a_5 , \, \, \triangle v^{+}_1v'^{+}_2v_3^{+})$, we choose h(t) as one of the two points obtained as the intersection of four spheres in ${\mathbb {R}}^4$, that is, for $0< t < 1$

$$\begin{aligned} h(t) \, \in \, S\Big (v^{+}_2 (t), \frac{\sqrt{3}}{\sqrt{2}}\Big ) \bigcap S\Big (v'^{+}_2 (t), \frac{\sqrt{3}}{\sqrt{2}}\Big ) \bigcap S\Big (v^{+}_1(t), \frac{1}{\sqrt{2}}\Big ) \bigcap S\Big (a_1(t), \frac{1}{\sqrt{2}}\Big ), \end{aligned}$$

so that for each fixed t the position of h is defined as in Proposition 2.3 and Remark.

There are three triangular faces with the edge $a_1v^{+}_1$, precisely, $H_1=\triangle a_1a_2{v_1}^{+}$, $H_2=\triangle a_1a'_6{v_1}^{+}$, and $H_3=\triangle a_1{v_1}^{+}{v_3}^{+}$ (see Figs. 5, 6), since the facet W(F, G) includes $H_1$ and $H_3$, and the facet $W(F^{*}, G^{*})$ includes $H_2$ and $H_3$, where $F^{*}=F_4=\triangle a_1a_5a'_6$ and $G^{*}=\triangle {v_1}^{+}{v'_2}^{+}{v_3}^{+}$.

Since the midpoint h of $a_1{v_1}^{+}$ moves to the midpoint of $v_1v_3$, $H_1$ and $H_2$ are folded in half and the other one $H_3$ is folded with moving creases as shown in Fig. 3. More precisely, $H_3$ can be continuously flat-folded as a part of the rhombus, obtained together with either $H_1$ or $H_2$, by the kite property.

Move each of the other triangular faces in $\{0<w<1\}$ and $\{-1<w <0\}$ as was done with faces with the edge $a_1v^{+}_1$, as defined above. There is no self-crossing during the motion; because for any pair $E_1, E_2$ of rigid edges in $\{0<w <1 \}$ there is a hyperplane $\Gamma$ such that $E_1$ and $E_2$ are included in the different half-spaces divided by $\Gamma$, and each edge moves in the one of the half-spaces. For example, when $E_1=v_1^{+}a_2$ and $E_2=v_1^{+}a'_6$, $\Gamma$ is the hyperplane determined by $\triangle a_1v_1v_3$ and $v_1^{+}$ (see Figs. 5, 6).

Proof of Theorem 4.1

By defining the motion of P onto $W_0$ as mentioned in Steps 1 through Step 3, there are no self-crossings. For any given octahedral facet of P we can assume, without loss of generality that it is $W^{+}$. In this motion, 24 edges in

$$\begin{aligned} E=\{a_1{v_1}^{\pm }, \, a_2{v_2}^{\pm }, \, a_3{v_3}^{\pm }, \, a_4{v_1}^{\pm },a_5{v_3}^{\pm }, \, a_6{v_2}^{\pm } \} \end{aligned}$$

and $E'$ obtained from E by replacing $a_i$ and $v_i$ to $a'_i$ and $v'_i$, respectively for $1 \le i \le 6$, are folded at their midpoints and the other 72 edges are rigid (see Figs. 5 and  6). So the proof of Theorem 4.1 has completed. $\square$

Remark

In the proof of Theorem 4.1, since the 2-skeleton C, of the regular 24-cell P, are folded so that two octahedral facets $W^+$ and $W^-$ move onto different sides of $W^0$, the stacking order of the resulting figure can be determined in such process. The remaining triangular faces of P in the half-space $\{w>0\}$ (respectively,$\{w<0\}$) are folded between $W^0$ and $W^+$ (respectively, $W^-$), according to the motion defined in the proof of Proposition 2.3.

5 Flattening the 24-cell

Theorem 5.1

Let P be a regular 24-cell. There is a continuous folding process from the 2-dimensional skeleton of P onto any of its faces F, so that 54 edges and all six faces parallel to F are rigid during the motion.

Proof

Combining Theorem 4.1 and Proposition 2.3 we can prove the result, because each edge of the resulting octahedron is a sextuple and hence 18 edges are folded at their midpoints to flatten the octahedron. Therefore 54 edges are rigid and six parallel faces are rigid during the motion. $\square$