1 On spherical geometry

Let \(S^d\) be the unit sphere in the \((d+1)\)-dimensional Euclidean space \(E^{d+1}\), where \(d\ge 2\). By a great circle of \(S^d\) we mean the intersection of \(S^d\) with any two-dimensional subspace of \(E^{d+1}\). The common part of the sphere \(S^d\) with any hyper-subspace of \(E^{d+1}\) is called a \((d-1)\)-dimensional great sphere of \(S^d\). By a pair of antipodes of \(S^d\) we mean any pair of points of intersection of \(S^d\) with a straight line through the origin of \(E^{d+1}\).

Clearly, if two different points \(a, b \in S^d\) are not antipodes, there is exactly one great circle containing them. By the arc ab connecting a with b we mean the shorter part of the great circle containing a and b. By the spherical distance |ab|, or shortly distance, of these points we mean the length of the arc connecting them. The diameter \(\mathrm{diam}(A)\) of a set \(A \subset S^d\) is the number \(\mathrm{sup}_{a, b \in A} |ab|\). By a spherical ball \(B_{\rho }(r)\)of radius \(\rho \in (0, {\pi \over 2}]\), or shorter a ball, we mean the set of points of \(S^d\) having distance at most \(\rho \) from a fixed point, called the center of this ball. Spherical balls of radius \(\pi \over 2\) are called hemispheres. Two hemispheres whose centers are antipodes are called opposite hemispheres.

We say that a subset of \(S^d\) is convex if it does not contain any pair of antipodes and if together with every two points a, b it contains the arc ab. By a convex body, or shortly body, on \(S^d\) we mean any closed convex set with non-empty interior.

Recall a few notions from [6]. If for a hemisphere H containing a convex body \(C \subset S^d\) we have \(\mathrm{bd}(H) \cap C \not = \emptyset \), then we say that H supports C. If hemispheres G and H of \(S^d\) are different and not opposite, then \(L = G \cap H\) is called a lune of \(S^d\). The \((d-1)\)-dimensional hemispheres bounding the lune L and contained in G and H, respectively, are denoted by G/H and H/G. We define the thickness of a lune \(L = G \cap H\) as the spherical distance of the centers of G/H and H/G. For a hemisphere H supporting a convex body \(C \subset S^d\) we define the width \(\mathrm{width}_H(C)\)of C determined by H as the minimum thickness of a lune of the form \(H \cap H'\), where \(H'\) is a hemisphere, containing C. If for all hemispheres H supporting C we have \(\mathrm{width}_H(C) = w\), we say that C is of constant width w.

2 Spherical complete bodies

Similarly to the traditional notion of a complete set in the Euclidean space \(E^d\) (for instance, see [1,2,3] and [10]) we say that a set \(K \subset S^d\) of diameter \(\delta \in (0, \pi )\) is complete provided \(\mathrm{diam}(K \cup \{x\}) > \delta \) for every \(x \not \in K.\)

Theorem 1

An arbitrary set of diameter \(\delta \in (0, \pi )\) on the sphere \(S^d\) is a subset of a complete set of diameter \(\delta \) on \(S^d\).

We omit the proof since it is similar to the proof by Lebesgue [9] in \(E^d\) (it is recalled in Part 64 of [1]). Let us add that earlier Pál [12] proved this for \(E^2\) by a different method.

The following fact permits to use the term a complete convex body for a complete set.

Lemma 1

Let \(K \subset S^d\) be a complete set of diameter \(\delta \). Then K coincides with the intersection of all balls of radius \(\delta \) centered at points of K. Moreover, K is a convex body.

Proof

Denote by I the intersection of all balls of radius \(\delta \) with centers in K.

Since \(\mathrm{diam}(K) = \delta \), then K is contained in every ball of radius \(\delta \) whose center is a point of K. Consequently, \(K \subset I\).

Let us show that \(I \subset K\); so let us show that \(x \not \in K\) implies \(x \not \in I\). Really, from \(x \not \in K\) we get \(|xy| > \delta \) for a point \(y \in K\), which means that x is not in the ball of radius \(\delta \) with center y, and thus \(x \not \in I\).

The first thesis implies that K is a convex body. \(\square \)

Lemma 2

If \(K \subset S^d\) is a complete body of diameter \(\delta \), then for every \(p \in \mathrm{bd}(K)\) there exists \(p' \in K\) such that \(|pp'|=\delta \).

Proof

Suppose the contrary, i.e., that \(|pq| < \delta \) for a point \(p \in \mathrm{bd}(K)\) and for every point \(q \in K\). Since K is compact, there is an \(\varepsilon > 0\) such that \(|pq| \le \delta - \varepsilon \) for every \(q \in K\). Hence there is a point \(s \not \in K\) in a positive distance from p which is smaller than \(\varepsilon \) such that \(|sq| \le \delta \) for every \(q \in K\). Thus \(\mathrm{diam}(K \cup \{s\}) = \delta \), which contradicts the assumption that K is complete. Consequently, the thesis of our lemma holds true. \(\square \)

For different points \(a, b \in S^d\) at a distance \(\delta < \pi \) from a point \(c \in S^d\) define the piece of the circle \(P_c(a,b)\) as the set of points \(v \in S^d\) such that cv has length \(\delta \) and intersects ab.

We show the next lemma for \(S^d\) despite we apply it later only for \(S^2\).

Lemma 3

Let \(K \subset S^d\) be a complete convex body of diameter \(\delta \). Take \(P_c(a,b)\) with |ac| and |bc| equal to \(\delta \) such that \(a, b \in K\) and \(c \in S^d\). Then \(P_c(a,b) \subset K\).

Proof

First let us show the thesis for a ball B of radius \(\delta \) in place of K. There is unique \(S^2 \subset S^d\) with \(a, b, c \in S^2\). Consider the disk \(D= B \cap S^2\). Take the great circle containing \(P_c(a,b)\) and points \(a^*, b^*\) of its intersection with the circle bounding D. There is a unique \(c^* \in S^2\) such that \(P_c(a,b) \subset P_{c^*}(a^*,b^*)\). Clearly, \(P_{c^*}(a^*,b^*) \subset D \subset B\). Hence \(P_c(a,b) \subset B.\)

By the preceding paragraph and Lemma 1 we obtain the thesis of the present lemma. \(\square \)

3 Complete and constant width bodies on \(S^d\) coincide

Here is our main result presenting the spherical version of the classic theorem in \(E^d\) proved by Meissner [11] for \(d=2,3\) and by Jessen [5] for arbitrary d.

Theorem 2

A body of diameter \(\delta \) on \(S^d\) is complete if and only if it is of constant width \(\delta \).

Proof

(\(\Rightarrow \)) Let us prove that if a body \(K \subset S^d\) of diameter \(\delta \) is complete, then K is of constant width \(\delta \).

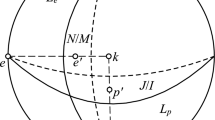
Suppose the opposite, i.e., that \(\mathrm{width}_I(K) \not = \delta \) for a hemisphere I supporting K. By Theorem 3 and Proposition 1 of [6] \(\mathrm{width}_I(K) \le \delta \). So \(\varDelta (K) < \delta \). By lines 1-2 of p. 562 of [6] the thickness of K is equal to the minimum thickness of a lune containing K. Take such a lune \(L = G \cap H\), where G, H are different and non-opposite hemispheres. Denote by g, h the centers of G/H and H/G, respectively. Of course, \(|gh| < \delta \). By Claim 2 of [6] we have \(g, h \in K\). By Lemma 2 there exists a point \(g' \in K\) in the distance \(\delta \) from g. Since the triangle \(ghg'\) is non-degenerate, there is a unique two-dimensional sphere \(S^2 \subset S^d\) containing \(g, h, g'\). Clearly, \(ghg'\) is a subset of \(M= K \cap S^2\). Hence M is a convex body on \(S^2\). Denote by F this hemisphere of \(S^2\) such that \(hg' \subset \mathrm{bd}(F)\) and \(g \in F\). There is a unique \(c \in F\) such that \(|ch| =\delta = |cg'|\). By Lemma 3 for \(d=2\) we have \(P_c(h,g') \subset M\).

We intend to show that c is not on the great circle E of \(S^2\) through g and h. In order to see this, for a while suppose the opposite, i.e. that \(c \in E\). Then from \(|g'g| = \delta \), \(|g'c| =\delta \) and \(|hc| = \delta \) we conclude that \(\angle gg'c = \angle hcg'\). So the spherical triangle \(g'gc\) is isosceles, which together with \(|gg'|= \delta \) gives \(|cg| = \delta \). Since \(|gh| = \varDelta (L) = \varDelta (K) >0\) and g is a point of ch different from c, we get a contradiction. Hence, really, \(c \not \in E\).

By the preceding paragraph \(P_c(h,g')\) intersects \(\mathrm{bd}(M)\) at a point \(h'\) different from h and \(g'\). So the non-empty set \(P_c(h,g') \setminus \{h,h'\}\) is out of M. This contradicts the result of the paragraph before the last. Consequently, K is a body of constant width \(\delta \).

(\(\Leftarrow \)) Let us prove that if K is a spherical body of constant width \(\delta \), then K is a complete body of diameter \(\delta \). In order to prove this, it is sufficient to take any point \(r \not \in K\) and to show that \(\mathrm{diam}(K \cup \{r\}) > \delta \).

Take the largest ball \(B_{\rho }(r)\) disjoint with the interior of K. Since K is convex, \(B_{\rho }(r)\) has exactly one point p in common with K. By Theorem 3 of [8] there exists a lune \(L \supset K\) of thickness \(\delta \) with p as the center of one of the two \((d-1)\)-dimensional hemispheres bounding this lune. Denote by q the center of the other \((d-1)\)-dimensional hemisphere. By Claim 2 of [6] also \(q \in K\). Since p and q are the centers of the two \((d-1)\)-dimensional hemispheres bounding L, we have \(|pq|= \delta \). From the fact that rp and pq are orthogonal to \(\mathrm{bd}(H)\) at p, we see that \(p \in rq\). Moreover, p is not an endpoint of rq and \(|pq| = \delta \), Hence \(|rq| > \delta \). Thus \(\mathrm{diam}(K \cup \{r\}) > \delta \). Since \(r \not \in K\) is arbitrary, K is complete. \(\square \)

We say that a convex body \(D \subset S^d\) is of constant diameter \(\delta \) provided \(\mathrm{diam}(D) = \delta \) and for every \(p \in \mathrm{bd}(D)\) there is a point \(p' \in \mathrm{bd}(D)\) with \(|pp'| = \delta \) (see [8]). The following fact is analogous to the result in \(E^d\) given by Reidemeister [13].

Theorem 3

Bodies of constant diameter on \(S^d\) coincide with complete bodies.

Proof

Take a complete body \(D \subset S^d\) of diameter \(\delta \). Let \(g \in \mathrm{bd}(D)\) and G be a hemisphere supporting D at g. By Theorem 2 the body D is of constant width \(\delta \). So \(\mathrm{width}_G(D) = \delta \) and there exists a hemisphere H such that the lune \(G \cap H \supset D\) has thickness \(\delta \). By Claim 2 of [6] the centers h of H/G and g of G/H belong to D. So \(|gh| =\delta \). Thus D is of constant diameter \(\delta \).

Consider a body \(D \subset S^d\) of constant diameter \(\delta \). Let \(r \not \in D\). Take the largest \(B_{\rho }(r)\) whose interior is disjoint with D. Denote by p the common point of \(B_{\rho }(r)\) and D. A unique hemisphere J supports \(B_{\rho }(r)\) at p. Observe that \(D \subset J\) (if not, there is a point \(v \in D\) out of J; clearly vp passes through \(\mathrm{int}B_{\rho }(r)\), a contradiction). Since D is of constant diameter \(\delta \), there is \(p' \in D\) with \(|pp'| =\delta \). Observe that \(\angle rpp' \ge \frac{\pi }{2}\). If it is \(\frac{\pi }{2}\), then \(|rp'| > \delta \). If it is larger than \(\frac{\pi }{2}\), the triangle \(rpp'\) is obtuse and then by the law of cosines \(|rp'| > |pp'|\) and hence \(|rp'| > \delta \). By \(|rp'| > \delta \) in both cases we see that D is complete. \(\square \)

Theorem 2 permits to change “complete” to “constant width” in Theorem 3. This form is proved earlier as follows. In [8] it is shown that any body of constant width \(\delta \) on \(S^d\) is of constant diameter \(\delta \) and the inverse is argued for \(\delta \ge \frac{\pi }{2}\), and for \(\delta < \frac{\pi }{2}\) if \(d=2\). By [4] the inverse holds for any \(\delta \). Our short proof of Theorem 3 is quite different from the considerations in [4, 8] and [7].