Linear Instability of Symmetric Logarithmic Spiral Vortex Sheets

Abstract

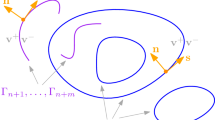
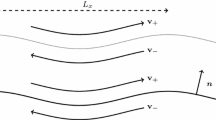
We consider Alexander spirals with $M\ge 3$ branches, that is symmetric logarithmic spiral vortex sheets. We show that such vortex sheets are linearly unstable in the $L^\infty$ (Kelvin–Helmholtz) sense, as solutions to the Birkhoff–Rott equation. To this end we consider Fourier modes in a logarithmic variable to identify unstable solutions with polynomial growth in time.

Appendix

Here we show some more properties of the notion of the finite part (recall (2.1)), and we prove (2.4) in Proposition 6.3 below.

Lemma 6.1

(Finite part of a regular or p.v. integral). If $f(t) = g(t)(t-x)^{2}$ then

$$\begin{aligned} \mathrm {f.p.}\int _{a}^{b} \frac{f(t)}{(t-x)^{2}}\,\textrm{d}t = \int _{a}^{b} g(t)\,\textrm{d}t, \end{aligned}$$

and if $f(t) = g(t)(t-x)$ then

$$\begin{aligned} \mathrm {f.p.}\int _{a}^{b} \frac{f(t)}{(t-x)^{2}}\,\textrm{d}t = \mathrm {p.v.}\int _{a}^{b}\frac{g(t)}{t-x}\,\textrm{d}t \end{aligned}$$

for every $x\in (a,b)$ and every $g\in C^{\infty }((a,b),\mathbb {R})$.

Proof

For the first claim we recall the definition (2.1) to get

$$\begin{aligned} \mathrm {f.p.}\int _{a}^{b} \frac{f(t)}{(t-x)^{2}}\,\textrm{d}t&= \lim _{\varepsilon \rightarrow 0^{+}} \left( \int _{a}^{x-\varepsilon }\frac{g(t)(t-x)^{2}}{(t-x)^{2}}\,\textrm{d}t + \int _{x+\varepsilon }^{b}\frac{g(t)(t-x)^{2}}{(t-x)^{2}}\,\textrm{d}t -\frac{g(x+\varepsilon )\varepsilon ^{2}+g(x-\varepsilon )(-\varepsilon )^{2}}{\varepsilon }\right) \\&=\lim _{\varepsilon \rightarrow 0^{+}} \left( \int _{a}^{x-\varepsilon } g(t)\,\textrm{d}t + \int _{x+\varepsilon }^{b}g(t) \,\textrm{d}t-(g(x+\varepsilon )\varepsilon -g(x-\varepsilon )\varepsilon )\right) = \int _{a}^{b}g(t)\,\textrm{d}t , \end{aligned}$$

and for the second claim we have

$$\begin{aligned}&\mathrm {f.p.}\int _{a}^{b} \frac{f(t)}{(t-x)^{2}}\,\textrm{d}t = \lim _{\varepsilon \rightarrow 0^{+}} \left( \int _{a}^{x-\varepsilon }\frac{g(t)(t-x)}{(t-x)^{2}}\,\textrm{d}t + \int _{x+\varepsilon }^{b}\frac{g(t)(t-x)}{(t-x)^{2}}\,\textrm{d}t -\frac{g(x+\varepsilon )\varepsilon +g(x-\varepsilon )(-\varepsilon )}{\varepsilon }\right) \\&\qquad = \lim _{\varepsilon \rightarrow 0^{+}} \left( \int _{a}^{x-\varepsilon }\frac{g(t)}{t-x}\,\textrm{d}t + \int _{x+\varepsilon }^{b}\frac{g(t)}{t-x}\,\textrm{d}t-(g(x+\varepsilon ) - g(x-\varepsilon ))\right) =\mathrm {p.v.}\int _{a}^{b}\frac{g(t)}{t-x}\,\textrm{d}t. \end{aligned}$$

as desired. $\square$

We now consider a bit more general denominator, and we characterize the finite part from Definition 2.1 as the derivative of the principal value integral.

Lemma 6.2

(FP vs. PV). For any $x\in (a,b)$, the following equality holds

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}x}\left( \mathrm {p.v.}\int _{a}^{b}\frac{f(t)}{\gamma (t)-\gamma (x)}\,\textrm{d}t\right) = \gamma '(x)\,\mathrm {f.p.}\int _{a}^{b} \frac{f(t)}{(\gamma (t)-\gamma (x))^{2}}\,\textrm{d}t, \end{aligned}$$

(6.1)

where $\gamma :[a,b]\rightarrow \mathbb {C}$ is a smooth curve such that $\gamma '(t)\ne 0$ for $t\in [a,b]$.

Proof

Let us observe that

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}x}\left( \int _{a}^{x-\varepsilon }\frac{f(t)}{\gamma (t)-\gamma (x)}\,\textrm{d}t + \int _{x+\varepsilon }^{b}\frac{f(t)}{\gamma (t)-\gamma (x)}\,\textrm{d}t\right) = \int _{a}^{x-\varepsilon }\frac{\gamma '(x)f(t)\,\textrm{d}t}{(\gamma (t)-\gamma (x))^{2}} + \int _{x+\varepsilon }^{b}\frac{\gamma '(x)f(t)\,\textrm{d}t}{(\gamma (t)-\gamma (x))^{2}} \\&\quad +\frac{f(x-\varepsilon )}{\gamma (x-\varepsilon )-\gamma (x)} - \frac{f(x+\varepsilon )}{\gamma (x+\varepsilon )-\gamma (x)}. \end{aligned}$$

Then we have the following asymptotics as $\varepsilon \rightarrow 0$

$$\begin{aligned}&-\frac{\varepsilon f(x+\varepsilon )\gamma '(x)}{(\gamma (x+\varepsilon )-\gamma (x))^{2}} + \frac{f(x+\varepsilon )}{\gamma (x+\varepsilon )-\gamma (x)} = -\frac{f(x+\varepsilon )(\varepsilon \gamma '(x) - \gamma (x+\varepsilon ) + \gamma (x))}{(\gamma (x+\varepsilon )-\gamma (x))^{2}} \\&\qquad = -\frac{f(x+\varepsilon )(\frac{1}{2}\gamma ''(x)\varepsilon ^{2} + o(\varepsilon ^{2}))}{(\gamma (x+\varepsilon )-\gamma (x))^{2}} =-\frac{1}{2}\frac{f(x+\varepsilon )\gamma ''(x)\varepsilon ^{2}}{(\gamma (x+\varepsilon )-\gamma (x))^{2}} + o(1) \end{aligned}$$

and furthermore

$$\begin{aligned}&-\frac{\varepsilon f(x-\varepsilon )\gamma '(x)}{(\gamma (x-\varepsilon )-\gamma (x))^{2}} - \frac{f(x-\varepsilon )}{\gamma (x-\varepsilon )-\gamma (x)} = \frac{f(x-\varepsilon )(-\varepsilon \gamma '(x) - \gamma (x-\varepsilon ) + \gamma (x))}{(\gamma (x-\varepsilon )-\gamma (x))^{2}} \\&\qquad = \frac{f(x-\varepsilon )(\frac{1}{2}\gamma ''(x)\varepsilon ^{2} + o(\varepsilon ^{2}))}{(\gamma (x-\varepsilon )-\gamma (x))^{2}} =\frac{1}{2}\frac{f(x-\varepsilon )\gamma ''(x)\varepsilon ^{2}}{(\gamma (x-\varepsilon )-\gamma (x))^{2}} + o(1). \end{aligned}$$

Since the limits in the definition of $\mathrm {p.v.}$ and $\mathrm {f.p.}$ are uniform with respect to x in compact subsets of (a, b), it follows that

$$\begin{aligned}&\frac{\textrm{d}}{\textrm{d}x}\left( \mathrm {p.v.}\int _{a}^{b}\frac{f(t)}{\gamma (t)-\gamma (x)}\,\textrm{d}t\right) - \gamma '(x)\,\mathrm {f.p.}\int _{a}^{b} \frac{f(t)}{(\gamma (t)-\gamma (x))^{2}}\,\textrm{d}t\\&\qquad = \lim _{\varepsilon \rightarrow 0}\left( -\frac{1}{2}\frac{f(x+\varepsilon )\gamma ''(x)\varepsilon ^{2}}{(\gamma (x+\varepsilon )-\gamma (x))^{2}} + \frac{1}{2}\frac{f(x-\varepsilon )\gamma ''(x)\varepsilon ^{2}}{(\gamma (x-\varepsilon )-\gamma (x))^{2}} \right) = 0, \end{aligned}$$

and the proof of lemma is completed. $\square$

In the following proposition we prove the integration by parts formula (2.4).

Proposition 6.3

(FP vs. PV via integration by parts). Let us assume that $\gamma :[a,b]\rightarrow \mathbb {C}$ is a smooth curve satisfying $\gamma '(t)\ne 0$ for $t\in [a,b]$. Then, for any $x\in (a,b)$, we have

$$\begin{aligned} \mathrm {f.p.}\int _{a}^{b} \frac{f(t)\,\textrm{d}t}{(\gamma (t)\!-\!\gamma (x))^{2}} = \mathrm {p.v.}\int _{a}^{b}\frac{\left( f(t)/\gamma '(t)\right) '\textrm{d}t}{\gamma (t)-\gamma (x)} - \frac{f(b)}{\gamma '(b)(\gamma (b)\!-\!\gamma (x))} + \frac{f(a)}{\gamma '(a)(\gamma (a)\!-\!\gamma (x))}. \end{aligned}$$

(6.2)

Proof

Let us define

$$\begin{aligned} I(\varepsilon ):=\frac{\varepsilon }{(\gamma (x+\varepsilon )-\gamma (x))^{2}}\quad \text {and}\quad J(\varepsilon ):=\frac{1}{\gamma '(x+\varepsilon )(\gamma (x+\varepsilon )-\gamma (x))},\quad \varepsilon \in \mathbb {R}\setminus \{0\}. \end{aligned}$$

Then we have

$$\begin{aligned}&\int _{a}^{x-\varepsilon }\frac{f(t)\,\textrm{d}t}{(\gamma (t)-\gamma (x))^{2}} = -\int _{a}^{x-\varepsilon }\frac{f(t)}{\gamma '(t)} \left( \frac{1}{\gamma (t)-\gamma (x)}\right) '\,\textrm{d}t \\&\qquad = \int _{a}^{x-\varepsilon } \left( \frac{f(t)}{\gamma '(t)}\right) '\frac{\textrm{d}t}{\gamma (t)-\gamma (x)} -f(x-\varepsilon )J(-\varepsilon ) + \frac{f(a)}{\gamma '(a)(\gamma (a)-\gamma (x))} \end{aligned}$$

and similarly

$$\begin{aligned} \int _{x+\varepsilon }^{b}\frac{f(t)\,\textrm{d}t}{(\gamma (t)-\gamma (x))^{2}} = \int _{x+\varepsilon }^{b} \left( \frac{f(t)}{\gamma '(t)}\right) '\frac{dt}{\gamma (t)-\gamma (x)} +f(x+\varepsilon )J(\varepsilon ) - \frac{f(b)}{\gamma '(b)(\gamma (b)-\gamma (x))}. \end{aligned}$$

Let us write

$$\begin{aligned} R(\varepsilon )&:=-f(x+\varepsilon )I(\varepsilon ) + f(x-\varepsilon )I(-\varepsilon ) +f(x+\varepsilon )J(\varepsilon ) - f(x-\varepsilon )J(-\varepsilon ),\quad \varepsilon \in \mathbb {R}\setminus \{0\}. \end{aligned}$$

By the formula (2.3), to prove (6.2), it is enough to show that $R(\varepsilon ) = o(1)$ as $\varepsilon \rightarrow 0$. To this end we observe that

$$\begin{aligned} \begin{aligned} R(\varepsilon )&= f(x+\varepsilon )(J(\varepsilon )-I(\varepsilon )) + f(x-\varepsilon )(I(-\varepsilon ) - J(-\varepsilon )) \\&= f(x)(J(\varepsilon )-I(\varepsilon )) + f(x)(I(-\varepsilon ) - J(-\varepsilon )) \\&\quad - O(\varepsilon )(J(\varepsilon )-I(\varepsilon )) + O(\varepsilon )(I(-\varepsilon ) - J(-\varepsilon ))\quad \text { as }\quad \varepsilon \rightarrow 0. \end{aligned} \end{aligned}$$

(6.3)

Then we have

$$\begin{aligned} \begin{aligned} J(\varepsilon )-I(\varepsilon )&= \frac{\gamma (x+\varepsilon )-\gamma (x) - \varepsilon \gamma '(x+\varepsilon )}{\gamma '(x+\varepsilon )(\gamma (x+\varepsilon )-\gamma (x))^{2}} = \frac{\gamma '(x)\varepsilon +o(\varepsilon ) - \varepsilon (\gamma '(x)+\gamma ''(x)\varepsilon + o(\varepsilon ))}{\gamma '(x+\varepsilon )(\gamma (x+\varepsilon )-\gamma (x))^{2}} \\&= \frac{o(\varepsilon ) - \gamma ''(x)\varepsilon ^{2} + \varepsilon o(\varepsilon )}{\gamma '(x+\varepsilon )(\gamma (x+\varepsilon )-\gamma (x))^{2}},\quad \varepsilon \rightarrow 0, \end{aligned} \end{aligned}$$

(6.4)

which after changing of variables $\varepsilon \mapsto -\varepsilon$ gives

$$\begin{aligned} \begin{aligned} I(-\varepsilon ) - J(-\varepsilon ) = \frac{o(\varepsilon ) - \gamma ''(x)\varepsilon ^{2} - \varepsilon o(\varepsilon )}{\gamma '(x-\varepsilon )(\gamma (x-\varepsilon )-\gamma (x))^{2}}, \quad \varepsilon \rightarrow 0. \end{aligned} \end{aligned}$$

(6.5)

Combining (6.3), (6.4) and (6.5) provides

$$\begin{aligned} R(\varepsilon ) = f(x)(J(\varepsilon )-I(\varepsilon )) + f(x)(I(-\varepsilon ) - J(-\varepsilon )) + o(1),\quad \varepsilon \rightarrow 0. \end{aligned}$$

(6.6)

Let us observe that

$$\begin{aligned} \begin{aligned}&(J(\varepsilon )-I(\varepsilon ) + I(-\varepsilon ) - J(-\varepsilon ))(\gamma (x-\varepsilon )-\gamma (x)) ^{2}(\gamma (x+\varepsilon )-\gamma (x))^{2}\gamma '(x+\varepsilon )\gamma '(x-\varepsilon ) \\&\quad = -(\gamma (x-\varepsilon )-\gamma (x))(\gamma (x+\varepsilon )-\gamma (x))^{2}\gamma '(x+\varepsilon ) \\&\qquad +(\gamma (x-\varepsilon )-\gamma (x))^{2}(\gamma (x+\varepsilon )-\gamma (x))\gamma '(x-\varepsilon ) \\&\qquad -\varepsilon (\gamma (x-\varepsilon )-\gamma (x))^{2}\gamma '(x+\varepsilon )\gamma '(x-\varepsilon ) \\&\qquad -\varepsilon (\gamma (x+\varepsilon )-\gamma (x))^{2}\gamma '(x+\varepsilon )\gamma '(x-\varepsilon ) \\&\quad = K_{1}(\varepsilon ) - K_{1}(-\varepsilon ) + K_{2}(\varepsilon )-K_{2}(-\varepsilon ) \end{aligned} \end{aligned}$$

(6.7)

for $\varepsilon \in \mathbb {R}\setminus \{0\}$, where we define

$$\begin{aligned} K_{1}(\varepsilon )&:= -(\gamma (x-\varepsilon )-\gamma (x))(\gamma (x+\varepsilon )-\gamma (x))^{2}\gamma '(x+\varepsilon ) \\ K_{2}(\varepsilon )&:= -\varepsilon (\gamma (x-\varepsilon )-\gamma (x))^{2}\gamma '(x+\varepsilon )\gamma '(x-\varepsilon ). \end{aligned}$$

We show that $K_{1}(\varepsilon ) - K_{1}(-\varepsilon ) + K_{2}(\varepsilon )-K_{2}(-\varepsilon )=o(\varepsilon ^{4})$ as $\varepsilon \rightarrow 0$. To this end, we observe that

$$\begin{aligned} K_{1}(\varepsilon )&= - (-\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2 + o(\varepsilon ^{2}))(\varepsilon \gamma '(x)+\gamma ''(x)\varepsilon ^{2}/2 + o(\varepsilon ^{2}))^{2}(\gamma '(x) + \gamma ''(x)\varepsilon +o(\varepsilon ))\\&= - (-\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2)(\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2 + o(\varepsilon ^{2}))^{2}(\gamma '(x) + \gamma ''(x)\varepsilon ) + o(\varepsilon ^{4}) \\&= - (-\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2)(\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2)^{2}(\gamma '(x) + \gamma ''(x)\varepsilon ) + o(\varepsilon ^{4}) \\&= - (-\varepsilon ^{2}\gamma '(x)^{2} + \gamma ''(x)^{2}\varepsilon ^{4}/4)(\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2)(\gamma '(x) + \gamma ''(x)\varepsilon ) + o(\varepsilon ^{4}) \\&= \varepsilon ^{2}\gamma '(x)^{2}(\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2)(\gamma '(x) + \gamma ''(x)\varepsilon ) + o(\varepsilon ^{4}) \\&= \varepsilon ^{-2}\gamma '(x)^{3}(\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2) + \varepsilon ^{4}\gamma '(x)^{2}(\gamma '(x) + \gamma ''(x)\varepsilon /2) \gamma ''(x) + o(\varepsilon ^{4}), \end{aligned}$$

as $\varepsilon \rightarrow 0$, and consequently

$$\begin{aligned} \begin{aligned}&K_{1}(\varepsilon ) - K_{1}(-\varepsilon )= \varepsilon ^{2}\gamma '(x)^{3}(\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2) - \varepsilon ^{2}\gamma '(x)^{3}(-\varepsilon \gamma '(x) + \gamma ''(x)\varepsilon ^{2}/2)\\&\quad + \varepsilon ^{4}\gamma '(x)^{2}(\gamma '(x)+\gamma ''(x)\varepsilon /2)\gamma ''(x) -\varepsilon ^{4}\gamma '(x)^{2}(\gamma '(x)-\gamma ''(x)\varepsilon /2) \gamma ''(x) + o(\varepsilon ^{4}) \\&= \varepsilon ^{3}\gamma '(x)^{4} + \varepsilon ^{4}\gamma '(x)^{3}\gamma ''(x)/2 + \varepsilon ^{3}\gamma '(x)^{4} - \varepsilon ^{4}\gamma '(x)^{3}\gamma ''(x)/2 + o(\varepsilon ^{4}) \\&= 2\varepsilon ^{3}\gamma '(x)^{4} + o(\varepsilon ^{4})\quad \text { as }\quad \varepsilon \rightarrow 0. \end{aligned} \end{aligned}$$

(6.8)

Furthermore we have

$$\begin{aligned} K_{2}(\varepsilon )&= -\varepsilon (-\gamma '(x)\varepsilon + \gamma ''(x)\varepsilon ^{2}/2 + o(\varepsilon ^{2}))^{2}(\gamma '(x) + \gamma ''(x)\varepsilon + o(\varepsilon ))(\gamma '(x) - \gamma ''(x)\varepsilon +o(\varepsilon ))\\&= -\varepsilon (-\gamma '(x)\varepsilon + \gamma ''(x)\varepsilon ^{2}/2 + o(\varepsilon ^{2}))^{2}(\gamma '(x) + \gamma ''(x)\varepsilon )(\gamma '(x) - \gamma ''(x)\varepsilon ) + o(\varepsilon ^{4}) \\&= -\varepsilon (-\gamma '(x)\varepsilon + \gamma ''(x)\varepsilon ^{2}/2 + o(\varepsilon ^{2}))^{2}\gamma '(x)^{2} + o(\varepsilon ^{4}) \\&= -\varepsilon (-\gamma '(x)\varepsilon + \gamma ''(x)\varepsilon ^{2}/2 )^{2}\gamma '(x)^{2} + o(\varepsilon ^{4}) \\&= -\varepsilon ^{3}\gamma '(x)^{4} +\varepsilon ^{4}\gamma '(x)^{3}\gamma ''(x) + o(\varepsilon ^{4})\quad \text { as }\quad \varepsilon \rightarrow 0, \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned} K_{2}(\varepsilon )-K_{2}(-\varepsilon )&=-\varepsilon ^{3}\gamma '(x)^{4} +\varepsilon ^{4}\gamma '(x)^{3}\gamma ''(x)-\varepsilon ^{3}\gamma '(x)^{4} -\varepsilon ^{4}\gamma '(x)^{3}\gamma ''(x)+o(\varepsilon ^{4}) \\&= -2\varepsilon ^{3}\gamma '(x)^{4}+ o(\varepsilon ^{4})\quad \text { as }\quad \varepsilon \rightarrow 0. \end{aligned} \end{aligned}$$

(6.9)

Combining (6.6), (6.7), (6.8) and (6.9) we obtain

$$\begin{aligned} R(\varepsilon )&= \frac{K_{1}(\varepsilon ) - K_{1}(-\varepsilon ) + K_{2}(\varepsilon )-K_{2} (-\varepsilon )}{(\gamma (x-\varepsilon )-\gamma (x))^{2}(\gamma (x+\varepsilon ) -\gamma (x))^{2}\gamma '(x+\varepsilon )\gamma '(x-\varepsilon )} + o(1) \\&= \frac{o(\varepsilon ^{4})}{(\gamma (x-\varepsilon )-\gamma (x))^{2}(\gamma (x+\varepsilon ) -\gamma (x))^{2}\gamma '(x+\varepsilon )\gamma '(x-\varepsilon )} + o(1) = o(1) \end{aligned}$$

as $\varepsilon \rightarrow 0$ and the proof of the proposition is completed. $\square$