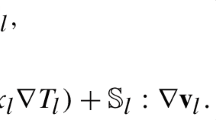Feedback Stabilization of a Two-Fluid Surface Tension System Modeling the Motion of a Soap Bubble at Low Reynolds Number: The Two-Dimensional Case

Abstract

The aim of this paper is to design a feedback operator for stabilizing in infinite time horizon a system modeling the interactions between a viscous incompressible fluid and the deformation of a soap bubble. The latter is represented by an interface separating a bounded domain of $\mathbb {R}^2$ into two connected parts filled with viscous incompressible fluids. The interface is a smooth perturbation of the 1-sphere, and the surrounding fluids satisfy the incompressible Stokes equations in time-dependent domains. The mean curvature of the surface defines a surface tension force which induces a jump of the normal trace of the Cauchy stress tensor. The response of the fluids is a velocity trace on the interface, governing the time evolution of the latter, via the equality of velocities. The data are assumed to be sufficiently small, in particular the initial perturbation, that is the initial shape of the soap bubble is close enough to a circle. The control function is a surface tension type force on the interface. We design it as the sum of two feedback operators: one is explicit, the second one is finite-dimensional. They enable us to define a control operator that stabilizes locally the soap bubble to a circle with an arbitrary exponential decay rate, up to translations, and up to non-contact with the outer boundary.

1 Introduction

In this paper we consider a model that describes the time evolution of an interface $\Gamma (t)$ separating a bounded fluid domain $\Omega \subset \mathbb {R}^2$ into two connected components. The fluid is assumed to be viscous and incompressible. This interface represents a soap bubble, and is subject to surface tension forces. Surface tension is the result of intermolecular forces in fluids (air or liquid, see [64]). We consider the low Reynolds number case, that is the inertia forces are assumed to be negligible compared to the other involved forces (viscosity effects, surface tension, electric field, etc...), which is typically the case of blood flows [39] containing globules [9]. We will also neglect the temperature effects. Our aim is to stabilize the deformations of this soap bubble such that this latter converges to a circle, with a prescribed exponential decay rate, via the design of a feedback operator acting on the interface. Our contribution falls within the modeling and mathematical aspects of the motion of bubbles out of equilibrium.

1.1 The Model

Due to incompressibility, the volume contained inside the soap bubble remains constant, and any sphere of this volume, strictly contained in $\Omega$, can be considered as the sphere of reference $\Gamma _s$. Denoting by $X(\cdot ,t)$ the Lagrangian deformation of this sphere, the deformed soap bubble is given by $\Gamma (t) = X(\Gamma _s,t)$, with the initial condition $X_0 = X(\cdot ,0)$, and separates the whole domain $\Omega$ into two subdomains $\Omega ^+(t)$ and $\Omega ^-(t)$, corresponding to the exterior and the interior of the soap bubble, respectively. The geometric description and notation are given in Fig. 1.

Fig. 1

Deformation of the soap bubble, from the reference configuration $\Gamma _s$, to $\Gamma (t)$ at time t

We will assume throughout the paper that $\Gamma (t)$ is a Jordan curve, that $X(\cdot ,t)$ is invertible and orientation preserving, and the non-contact condition, that is $\Gamma (t) \subset \mathring{\Omega }$. This can be guaranteed by assuming the data smooth and sufficiently small, in particular $X_0$ close enough to the identity, implying that $X(\cdot ,t)$ stays close to the identity as well. With this condition, we then have $\Gamma (t) = \partial \Omega ^{-}(t)$ and $\partial \Omega ^+(t) = \partial \Omega \cup \Gamma (t)$ (disjoint union), and $\Omega ^+(t)$ is connected. The deformation X and the velocity/pressure couples $(u^+,p^+)$, $(u^-,p^-)$ constitute the unknowns of the following system

$$\begin{aligned} - {{\,\textrm{div}\,}}\sigma (u^+,p^+) = f^+{} & {} \text {in } \Omega ^+(t), \ t \in (0,\infty ), \\ - {{\,\textrm{div}\,}}\sigma (u^-,p^-) = f^-{} & {} \text {in } \Omega ^-(t), \ t \in (0,\infty ), \\ {{\,\textrm{div}\,}}u^+ = 0{} & {} \text {in } \Omega ^+(t), \ t \in (0,\infty ), \\ {{\,\textrm{div}\,}}u^- = 0{} & {} \text {in } \Omega ^-(t), \ t \in (0,\infty ), \\ u^+ = 0{} & {} \text {on } \partial \Omega \times (0,\infty ), \\ u^+ = u^- = \frac{\partial X}{\partial t} \left( X(\cdot ,t)^{-1},t\right) ,{} & {} \text {on } \Gamma (t), \ t \in (0,\infty ), \\ \sigma (u^+,p^+)n^+ + \sigma (u^-,p^-)n^- = \mu \kappa n^- + g{} & {} \text {on } \Gamma (t), t \in (0,\infty ), \\ X(\cdot ,0) = X_0{} & {} \text {on } \Gamma _s, \end{aligned}$$

where $\Gamma (t) = X(\Gamma _s,t)$ splits $\Omega$ into $\Omega ^+(t)$ and $\Omega ^-(t)$. We adopt the Lagrangian formalism for describing the interface $\Gamma (t)$: Particles of coordinates $x\in \Gamma (t)$ are obtained uniquely from particles $y \in \Gamma _s$ as $x = X(y,t)$, and their velocity writes $\displaystyle \frac{\partial X}{\partial t}(y,t)$. On the other hand, the Eulerian velocities $u^+$ or $u^-$ describe the velocity field of particles occupying position $x \in \Omega ^+(t)$ or $\Omega ^-(t)$ at time t. Therefore from the equality of particle velocities on $\Gamma (t)$ we have the relation $\displaystyle \frac{\partial X}{\partial t}(y,t) = u^+(X(y,t),t) = u^-(X(y,t),t)$, leading to the equality of Eulerian velocities on $\Gamma (t)$ above, by using $y = X(x,t)^{-1}$. The pressure variables $p^+$ and $p^-$ play the role of Lagrange multipliers for the zero divergence conditions, referring to the incompressibility of the fluid. We have introduced the Cauchy stress tensor $\sigma (u,p):= 2\nu \varepsilon (u) -p \textrm{Id}$, where $\varepsilon (u):= \textrm{Sym}(\nabla u) = \frac{1}{2}(\nabla u + \nabla u^T)$, and the viscosity $\nu >0$ is constant and assumed to be the same in $\Omega ^+(t)$ and $\Omega ^-(t)$, for the sake of simplicity, but without loss of generality. We denoted by $n^+$ and $n^-$ the outward unit normal of $\Omega ^+(t)$ and $\Omega ^-(t)$, respectively. By default we denote $n=n^- = -n^+$. The parameter $\mu >0$ is a given constant surface tension coefficient, and $\kappa$ denotes the mean curvature of $\Gamma (t)$, with the convention $\kappa <0$ for the 1-sphere. In dimension 2, the mean curvature is simply called the curvature. The right-hand-sides $f^+$ and $f^-$ are given volume forces, representing for example the effect of an electric field [71], or some density contribution like in the case gravity Stokes flows [32], leading to the so-called Stokes-transport system [40, 43]. The function g is a surface tension type force, acting on the interface $\Gamma (t)$. It will be considered as the control function, and will be chosen in the form of a feedback operator. For the sake of concision, we rewrite the system above as follows:

$$\begin{aligned} - {{\,\textrm{div}\,}}\sigma (u^\pm ,p^\pm ) = f^\pm \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0{} & {} \text {in } \Omega ^\pm (t), \ t \in (0,\infty ), \end{aligned}$$

(1a)

$$\begin{aligned} u^+ = 0{} & {} \text {on } \partial \Omega \times (0,\infty ), \end{aligned}$$

(1b)

$$\begin{aligned} u^\pm = \frac{\partial X}{\partial t}\left( X(\cdot ,t)^{-1},t\right) \quad \text { and } \quad -\left[ \sigma (u,p)\right] n = \mu \kappa n + g{} & {} \text {on } \Gamma (t), \ t \in (0,\infty ), \end{aligned}$$

(1c)

$$\begin{aligned} X(\cdot ,0) = X_0{} & {} \text {on } \Gamma _s. \end{aligned}$$

(1d)

We have denoted by $[\varphi ] = \varphi ^+ - \varphi ^-$ the jump across $\Gamma (t)$ of a vector/matrix field, and by $\varphi ^\pm$ when we consider $\varphi ^+$ and $\varphi ^-$ separately, simultaneously, and respectively. In (1c), the control function g and the surface tension force $\mu \kappa n$ induces the jump of $\sigma (u,p)n$ across $\Gamma (t)$, and the response of the surrounding fluid is the trace of the velocity field on the interface $\Gamma (t)$, governing the time evolution of the latter via the time derivative of $X(\cdot ,t)$. Recall that mapping $X(\cdot ,t)$ determines the interface $\Gamma (t)$, and therefore also the domains $\Omega ^\pm (t)$ in which the Stokes equations are set, as well as the mean curvature that satisfies the relation $\kappa n = \Delta _{\Gamma (t)} \textrm{Id}$, involving the Laplace-Beltrami operator. Thus system (1) couples in a nonlinear manner the geometry given by $X(\cdot ,t)$ and the state variables of the fluid, namely $(u^\pm ,p^\pm )$.

Existence of solutions for such a model in the context of two fluids separated by a closed free interface has been studied by Denisova and Solonnikov [21, 24], in line with prior contributions [19, 20, 22, 23, 61], based on the work of Rivkind [54,55,56,57]. More recently Prüss and Simonett revisited wellposedness questions in the context of the $L^p$-maximal regularity [46,47,48], addressing also the case of phase transitions [49,50,51]. Modeling aspects, leading to the transmission equations on $\Gamma (t)$, were first introduced in [58], as far as we know. Addressing advanced wellposedness questions for systems of type (1) can be a difficult task, as for example global existence of solutions for the Navier-Stokes model is still an open problem (see for example [28] dealing with the notion of varifold solutions). We refer to [25] for an exploration in this direction. Note that in this article the equality of velocities in (1c) which governs the time evolution of the interface will be treated as Dirichlet-type boundary conditions, but we could also represent the flow of surfaces $\Gamma (t)$ via the Peskin formulation [45], the so-called immersed boundary method, which consists in writing this equality as an integral supported by a delta function. In this fashion, recent wellposedness contributions were provided in [31, 33, 34, 44, 59]. At low Reynolds number, namely for the Stokes model, let us mention the recent contributions [41, 42]. Let us also mention that stability questions were addressed in [32, 67]. In the present article we will only be interested in the stabilizability question, and will address wellposedness only for the linearized system as well as for the feedback-control-stabilized nonlinear system (1).

1.2 Main Result

Note that the volume enclosed by $\Gamma (t)$ is constant and prescribed by the one enclosed by the reference circle $\Gamma _s$, due to incompressibility. Since any circle of the same volume, strictly included inside $\Omega$, is a stationary state (see Lemma 2.1), we can decide to stabilize system (1) around any of these circles, and thus stabilization around the sphere is understood up to elements of the following space

$$\begin{aligned} \mathcal {C}_{\Gamma _s}= \left\{ X_c \in \textbf{H}^2(\Gamma _s) \text { such that } X_c(\Gamma _s) \subset \mathring{\Omega } \text { is a circle of the same radius as }\Gamma _s \right\} . \end{aligned}$$

The initial configuration $\Gamma _0$ is represented via the deformation $X_0$ of $\Gamma _s$, so that $\Gamma _0 = X_0(\Gamma _s)$. Since we need smallness assumptions on the data, in particular $X_0$, in practice we can choose $X_c\in \mathcal {C}_{\Gamma _s}$ such that $\Vert X_0-X_c\Vert _{\textbf{H}^2(\Gamma _s)}$ is minimal, for example by restricting $\mathcal {C}_{\Gamma _s}$ to translations. We refer to Remark 2.1 in Sect. 2.2 for further comments. This amounts to say that $\Gamma _0$ is close to a circle of the same radius as $\Gamma _s$. The main result of the present article is Theorem 1.1:

Theorem 1.1

Choose $X_c \in \mathcal {C}_{\Gamma _s}$. Let be $X_0 \in \textbf{H}^2(\Gamma _s)/\mathbb {R}^2$ and $f^\pm = f_{|\Omega ^\pm (t)}$ such that $f\in \textrm{L}^2(0,\infty ;\textbf{L}^2(\Omega ))$. For all $\lambda >0$, there exists a finite-dimensional linear operator $\mathcal {K}_{\lambda }$, depending only on $\lambda$, $\Gamma _s$, $\nu$ and $\mu$, such that if the quantities $\Vert X_0-X_c\Vert _{\textbf{H}^2(\Gamma _s)}$ and $\Vert e^{\lambda t}f\Vert _{\textrm{L}^2(0,\infty ;\textbf{L}^2(\Omega ))}$ are small enough, then the solution of system (1) with

$$\begin{aligned} g = \left( (\textrm{det}\mathfrak {g})^{-1/2} \left( {{\,\textrm{div}\,}}_{\Gamma _s}\big ((\tau _s \otimes \tau _s) \nabla _{\Gamma _s}(X-X_c) \big )+ \mathcal {K}_{\lambda }\nabla _{\Gamma _s}(X-X_c)\right) \right) \circ X^{-1} \end{aligned}$$

satisfies

$$\begin{aligned} \left\| e^{\lambda t} (X-X_c) \right\| _{\textrm{L}^2(0,\infty ;\textbf{H}^{5/2}(\Gamma _s)/\mathbb {R}^2)\cap \textrm{H}^1(0,\infty ; \textbf{H}^{3/2}(\Gamma _s)/\mathbb {R}^2)} \le C\Vert X_0-X_c\Vert _{\textbf{H}^2(\Gamma _s)}, \end{aligned}$$

Where $\tau _s$ denotes the tangent vector of  $\Gamma _s$, $C>0$ is a constant, and $\mathfrak {g}$ denotes the metric tensor of $\Gamma (t)$.

This result implies the asymptotic convergence towards a stationary state corresponding to an immobile circle, up to a translation in $\mathbb {R}^2$. Note that in the choice of g, we need two different operators, one explicit, namely ${{\,\textrm{div}\,}}_{\Gamma _s}\big ((\tau _s \otimes \tau _s) \nabla _{\Gamma _s}(X-X_c) \big )$, and one of finite dimension. Both deal with the tangential derivative of $X-X_c$. This feedback stabilization result is in line with many others obtained for other fluid–structure models, for example [13, 14, 53]. But as far as we know, there are very few mathematical contributions that address control-related questions for models involving surface tension forces: The models considered in [2, 8, 11, 18, 30] deal with free boundary problems, that do not involve jump conditions like in (1c). However, other non-mathematical references explain the practical realization of surface tension controls on a small scale [12, 52].

1.3 Method

Like in [13, 14, 53], our method is based on the feedback stabilization of the linearized system. For deriving the latter, we first need to rewrite system (1) in cylindrical domains, in order to uncouple the fluid domains and the state variables, in particular the deformation X. Since this surface deformation is initially defined on $\Gamma _s$ only, we need to define a suitable extension to the whole domain, which leads us to study the non-trivial question of extension of diffeomorphisms from boundaries. This is realized in Sect. 3.1, and the corresponding proof relies on recent results on the harmonic extensions of diffeomorphisms (see Appendix A.1).

Concerning the model, for the sake of simplicity, in the fluid domain we choose to consider the linear stationary Stokes system, which corresponds to a low Reynolds number fluid. Considering fluid models at average or high Reynolds number would introduce other difficulties. For example, in [16, 17] the authors consider the Euler system, and existence of solutions is obtained with high-order energy estimates, without any operator formulation that could be used for designing a possible feedback operator. On the other hand, addressing the Navier–Stokes system consists classically in deriving an operator formulation of the linearized system, involving the non-stationary Stokes system, for which a lifting method is used. For the present model, based on jump conditions, it is not clear how a lifting method would enable us to derive an operator formulation. Still in the case of the non-stationary Stokes equations with transmission conditions, the respective authors of [47] and [21] first reduced the interface to a straight line, and derived existence and uniqueness results via pseudo-differential calculus techniques, which lead to a space-time operator for describing the solution. In practice, such approaches can not be used in a infinite-horizon stabilization problem, moreover dealing with general surfaces. Further, the unique continuation argument used in our case for obtaining approximate controllability and stabilizability of the linearized system does not apply to the case of the non-stationary Stokes system, as the latter would necessitate taking into consideration zeros of spherical harmonics, leading to difficulties that go beyond the scope of this article.

Therefore we adopt the stationary Stokes equations, as we prefer to focus on the time-evolution of the interface displacement, more specifically an operator formulation that involves the time derivative of the interface displacement only. For the linearized system, involving the Stokes system in time-independent domains, we describe the solution via a stationary Poincaré-Steklov operator denoted by $\mathcal {P}_{\Gamma _s}$, of Neumann-to-Dirichlet type, mapping the different transmission conditions. The existence of this operator is obtained via the Ladyzhenskaya-Babuška-Brezzi condition. Next the operator formulation for time-evolution of the interface displacement is obtained, involving $\mathcal {P}_{\Gamma _s}$, as follows

$$\begin{aligned} \frac{\partial Z}{\partial t} - \mu \mathcal {P}_{\Gamma _s}({{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{n_s}_{\Gamma _s} Z) = \mathcal {P}_{\Gamma _s}G \text { on } \Gamma _s \times (0,\infty ), \quad Z(\cdot ,0) = X_0-\textrm{Id}\text { on } \Gamma _s, \end{aligned}$$

where $Z = X-\textrm{Id}$ represents the displacement of the interface, $\nabla ^{n_s}_{\Gamma _s}:= (n_s \otimes n_s)\nabla _{\Gamma _s}$, and G represents a control function to be chosen in a feedback form. Since $\nabla ^{n_s}_{\Gamma _s}$ is not coercive (see Sect. 2.3), we define a first feedback operator as $\mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{\tau _s}_{\Gamma _s} Z$, where $\nabla ^{\tau _s}_{\Gamma _s}Z:= (\tau _s \otimes \tau _s)\nabla _{\Gamma _s} Z$, so that $Z \mapsto -\mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{n_s}_{\Gamma _s}Z - \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{\tau _s}_{\Gamma _s} Z = -\Delta _{\Gamma _s} Z$ is coercive. This operator is explicit, and supported on the tangent to $\Gamma _s$, which is compatible with possible practical realization. The resulting operator generates an analytic semigroup of contractions, with compact resolvent. Next we prove approximate controllability for the linear system via a unique continuation argument. Since the spectrum of the operator is discrete, the number of unstable modes is of finite number, and thus we can reduce the problem to a finite-dimensional control problem where approximate controllability implies stabilizability by a finite-dimensional feedback operator satisfying a Riccati equation. This feedback operator is re-used for defining another control function that stabilizes locally the nonlinear system, via a fixed-point argument, provided that the perturbations of the steady state are sufficiently small.

One of the main reasons why we restricted our study to dimension 2 is due to theoretical difficulties that arise in dimension 3 when trying to extend diffeomorphisms. Another reason lies in the fact that the linear evolution equation above, involving the operator $\nabla ^{n_s}_{\Gamma _s}$, would be a priori more complex in dimension 3. All these reasons are explained in Sect. 7. Nevertheless, the methodology adopted in the present article for designing in practice the feedback operator is still valid in dimension 3. Throughout the paper we try to keep as much as possible a formalism that is not restricted to dimension 2.

The paper is organized as follows: Notation and functional spaces are defined in Sect. 2. Comments and important properties of the model are described in Sect. 2.2. A change of variable is introduced in Sect. 3.1, enabling us to rewrite in Sect. 3.2 the main system in time-independent domains. Section 4 is devoted to the study of the corresponding linearized system, where in particular in Sect. 4.1 we define operator $\mathcal {P}_{\Gamma _s}$, leading in Sect. 4.2 to an operator formulation. In Sect. 5 we design a linear feedback operator that stabilizes the linear system. In Sect. 6 we deduce another feedback operator that stabilizes the nonlinear system, and thus prove the main result. Questions related with the extension to dimension 3 of the present work are posed in Sect. 7. Finally, technical proofs of intermediate results are given in the Appendix.

2 Functional Setting and Preliminaries

2.1 Function Spaces and Notation

Denote by $\textrm{L}^2$, $\textrm{H}^s$ and $\textrm{W}^{k,p}$ the standard Lebesgue/Sobolev spaces of real-valued functions, and their multi-dimensional versions for $d=2$ as follows:

$$\begin{aligned} \textbf{L}^2(\Omega _s^\pm ) = [\textrm{L}^2(\Omega _s^\pm )]^d, \quad \mathbb {L}^2(\Omega _s^\pm ) = [\textrm{L}^2(\Omega _s^\pm )]^{d\times d}, \quad \mathbb {L}^2(\Gamma _s) = [\textrm{L}^2(\Gamma _s)]^{d\times (d-1)}. \end{aligned}$$

The notation $\mathbb {L}^2(\Gamma _s)$ applies when considering for example tangential gradients on $\Gamma _s$. Naturally we transpose the same type of notation for other types of spaces and domains. Recall the notation $\textbf{H}^{-1/2}(\Gamma _s) = \textbf{H}^{1/2}(\Gamma _s)'$. For matrix fields $A,\ B$ of $\mathbb {R}^{2\times 2}$ we recall the inner product $A:B = \textrm{trace}(A^TB)$ and the corresponding Euclidean norm satisfies $|AB|_{\mathbb {R}^{2\times 2}} \le |A|_{\mathbb {R}^{2\times 2}}|B|_{\mathbb {R}^{2\times 2}}$. We will denote $\textrm{Sym}(A) = \frac{1}{2}(A+A^T)$. Denote by $\textrm{cof}(A)$ the cofactor matrix of any matrix field A, and note that in dimension 2 the mapping $A\mapsto \textrm{cof}(A)$ is linear. Given two vectors a and b of $\mathbb {R}^2$, the tensor product $a\otimes b$ denotes the matrix of $\mathbb {R}^{2\times 2}$ defined by $(a\otimes b)_{ij} = a_ib_j$.

For $0< T \le \infty$, the displacements $Z=X-\textrm{Id}$ of $\Gamma _s$ will be considered in the following space

$$\begin{aligned} \mathcal {Z}_{T}(\Gamma _s) := \textrm{L}^2(0,T; \textbf{H}^{5/2}(\Gamma _s)/\mathbb {R}^2) \cap \textrm{H}^1(0,T; \textbf{H}^{3/2}(\Gamma _s)/\mathbb {R}^2), \end{aligned}$$

where quotient spaces have been introduced for considering displacements Z up to a constant of $\mathbb {R}^2$. This is equivalent to consider deformations $X = Z+\textrm{Id}$ up to translations of $\mathbb {R}^2$. Note that the translations of $\mathbb {R}^2$ are also elements of the space $\mathcal {C}_{\Gamma _s}$. For any Banach space B and subset $I \subset B$, we define $\displaystyle \Vert Z\Vert _{B/I} = \inf _{Z_I \in I}\Vert Z -Z_I\Vert _B$. Subsequently, because of (1c), we will consider the velocity/pressure variables in the respective spaces

$$\begin{aligned} \begin{array} {l} \mathcal {U}_{T}(\Omega _s^+) := \left\{ u\in \textrm{L}^2(0,T; \textbf{H}^2(\Omega _s^\pm ))\mid u_{| \partial \Omega } = 0\right\} , \\ \mathcal {U}_{T}(\Omega _s^-) := \textrm{L}^2(0,T; \textbf{H}^2(\Omega _s^-)), \quad \mathcal {Q}_{T}(\Omega _s^\pm ) := \textrm{L}^2(0,T; \textrm{H}^1(\Omega _s^\pm )/\mathbb {R}). \end{array} \end{aligned}$$

We endow the spaces $\mathcal {U}_{T}(\Omega _s^\pm )$ with the classical norms, and $\mathcal {Q}_{T}(\Omega _s^\pm )$ with $\Vert p^\pm \Vert _{\mathcal {Q}_{T}(\Omega _s^\pm )}:= \Vert \nabla p^\pm \Vert _{\textrm{L}^2(0,T;\textbf{L}^2(\Omega _s^\pm ))}$. Note that the pressures in $\mathcal {Q}_{T}(\Omega _s^\pm )$ are determined up to a constant. Actually these constants are the residual static pressures $p_s^\pm$ corresponding to the stationary state. We refer to Lemma 2.1 for more details. Still for $0<T\le \infty$, the data will be considered in the following spaces

$$\begin{aligned} \mathcal {F}_{T}(\Omega _s^\pm ) := \textrm{L}^2(0,T; \textbf{L}^2(\Omega _s^\pm )), \quad \mathcal {G}_{T}(\Gamma _s) := \textrm{L}^2(0,T; \textbf{H}^{1/2}(\Gamma _s)), \quad \mathcal {Z}_0(\Gamma _s) := \textbf{H}^2(\Gamma _s)/\mathbb {R}^2. \end{aligned}$$

Note that $\mathcal {Z}_0(\Gamma _s)$ is the trace space of $\mathcal {Z}_{T}(\Gamma _s)$, and we recall that the following continuous embedding holds:

$$\begin{aligned} \mathcal {Z}_{\infty }(\Gamma _s) \hookrightarrow \mathcal {C}_b([0,\infty ); \textbf{H}^2(\Gamma _s)). \end{aligned}$$

The interest of this regularity framework is that we can define extensions $\tilde{X}$ of mappings X that are continuous in time with values in $\textbf{H}^{5/2}(\Omega _s^\pm )\hookrightarrow \mathcal {C}^1(\overline{\Omega _s^\pm })$. More specifically, extensions $\tilde{X}$ of X will be considered in the following space:

$$\begin{aligned} \mathcal {X}_{\infty }(\Omega _s^\pm ) := \textrm{L}^{\infty }(0,\infty ; \textbf{H}^{5/2}(\Omega _s^\pm )). \end{aligned}$$

Besides, the extensions $\tilde{X}$ are such that $\nabla {\tilde{X}} \in \textrm{L}^{\infty }(0,\infty ;\mathbb {H}^{3/2}(\Omega _s^\pm ))$. The same property holds for the inverse of $\nabla \tilde{X}$ (Corollary 3.1), which is convenient for deriving Lipschitz estimates when stabilizing the nonlinear system in Sect. 6, as the space $\mathbb {H}^{3/2}(\Omega _s^\pm )$ is an algebra (see [35, Proposition B.1, page 283]). In the same fashion, the space $\mathbb {H}^1(\Gamma _s)$ is also an algebra.

Recall the Petree-Tartar lemma [27, Lemma A.38 page 469], that we will use several times.

Lemma

(Petree-Tartar lemma). Let $B_1$, $B_2$ and $B_3$ be Banach spaces. Let $A \in \mathcal {L}(B_1,B_2)$ be an injective operator, and let $C \in \mathcal {L}(B_1,B_3)$ be a compact operator. Assume that there exists a positive constant¹$C>0$ such that for all $\varphi \in B_1$ we have

$$\begin{aligned} \Vert \varphi \Vert _{B_1} \le C\left( \Vert A\varphi \Vert _{B_2}+\Vert C\varphi \Vert _{B_3}\right) . \end{aligned}$$

Then there exists $C>0$ such that

$$\begin{aligned} \Vert \varphi \Vert _{B_1} \le C\Vert A\varphi \Vert _{B_2} \end{aligned}$$

for all $\varphi \in B_1$.

2.2 On the Surface Tension Model and the Stationary States

The surface tension force is generated by the mean curvature vector of the surface $\Gamma (t)$. It is related to the Laplace-Beltrami operator via the following relation (see [68, p. 151, Exercise 2]):

$$\begin{aligned} \kappa n = \Delta _{\Gamma (t)} \textrm{Id}. \end{aligned}$$

Using [1, Theorem 2.6], the following energy estimate holds, showing that the surface tension force derives from a potential energy quantified by the area of $\Gamma (t)$:

This energy is dissipated with the help of the viscosity terms. From [66, page 18], the kernel of $\varepsilon$ is reduced to the tangent space of the special Euclidean group SE(2), namely the functions of type $u^\pm (x) = h^\pm + \omega ^\pm x^\perp$, where $h^\pm \in \mathbb {R}^2$ and $\omega ^\pm \in \mathbb {R}$ are constant. Using $u^+ = 0$ on $\partial \Omega$, we deduce $h^+ = 0$ and $\omega ^+ = 0$, which also implies $h^- = 0$ and $\omega ^- =0$ when we have $u^+ = u^-$ on $\Gamma (t)$. Therefore, the first Korn’s inequality combined with the Rellich-Kondrachov theorem and the Petree-Tartar lemma yields the following general result:

Lemma 2.0

Let $\Omega ^\pm$ be any smooth subdomains of $\Omega$ split by a closed smooth curve $\Gamma = \partial \Omega ^-$ such that $\Gamma \subset \mathring{\Omega }$. Then, for all $u^\pm \in \textbf{H}^1(\Omega ^\pm )$ such that $u^+ = 0$ on $\partial \Omega$ and $u^+ = u^-$ on $\Gamma$, we have

$$\begin{aligned} \Vert u^+\Vert _{\textbf{H}^1(\Omega ^+)} + \Vert u^- \Vert _{\textbf{H}^1(\Omega ^-)} \le C \left( \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega ^+)}^2 + \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega ^-)}^2 \right) , \end{aligned}$$

where $C>0$ is independent of $u^\pm$.

Since our approach is based on the study of the linearized system that involves ${{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{n_s}_{\Gamma _s}(X-\textrm{I})$ (see Sect. 3.2), we will rather focus on the different differential operators rather than on the mean curvature. The curve $\Gamma _s$ is considered as a Riemannian manifold, and due to its regularity, we claim that the trace spaces $\textbf{H}^s(\Gamma _s)$ coincide with the definition of Sobolev spaces given on Riemannian manifolds [37, section 2.2]. For a circle $\Gamma _s \subset \mathring{\Omega }$ of given radius r we adopt the parameterization by arc length

$$\begin{aligned} X_s: [0,2\pi r) \ni \xi \mapsto \left( r\cos (\xi /r) , r\sin (\xi /r) \right) ^T \in \Gamma _s \subset \mathbb {R}^2. \end{aligned}$$

Denoting $\tau _s$ the tangent vector of $\Gamma _s$, we have

$$\begin{aligned} n_s \circ X_s = \left( \cos (\xi /r) , \sin (\xi /r) \right) ^T, \quad \tau _s \circ X_s = \left( \sin (\xi /r) , -\cos (\xi /r) \right) ^T \end{aligned}$$

Recall the notation for the tangential gradient $\nabla _{\Gamma _s}$ and the tangential divergence ${{\,\textrm{div}\,}}_{\Gamma _s}$. In the particular case of a circle, with the parameterization $X_s$ chosen above, the metric tensor $\mathfrak {g}_s$ of $\Gamma _s$ is scalar-valued, equal to $|\nabla _{\xi } X_s|_{\mathbb {R}^2}^2 = 1$. Therefore, for all $\varphi \in \textbf{H}^1(\Gamma _s)$, these operators simply write

$$\begin{aligned} \begin{array} {rcl} (\nabla _{\Gamma _s} \varphi )\circ X_s &{} = &{} \nabla _{\xi } (\varphi \circ X_s), \\ ({{\,\textrm{div}\,}}_{\Gamma _s})\circ X_s &{} = &{} \displaystyle (\textrm{det}\mathfrak {g}_s)^{-1/2} \frac{\partial }{\partial \xi }\left( (\textrm{det}\mathfrak {g}_s)^{1/2} (\varphi \circ X_s) \right) = \nabla _{\xi }(\varphi \circ X_s) = (\nabla _{\Gamma _s} \varphi )\circ X_s. \end{array} \end{aligned}$$

We will still use the general notation $\nabla _{\Gamma _s}$ and ${{\,\textrm{div}\,}}_{\Gamma _s}$, for the sake of consistency with higher dimension. Recall the Frenet-Serret formulas:

$$\begin{aligned} \nabla _{\Gamma _s} n_s = -\frac{1}{r}\tau _s, \quad \nabla _{\Gamma _s} \tau _s = \frac{1}{r} n_s. \end{aligned}$$

The integrals on $\Gamma _s$ have to be understood as surface integrals. We recall the Stokes formula on smooth manifolds without boundary, that we will use in this article only for the 1-sphere $\Gamma _s$. For all $\varphi , \psi \in \textbf{H}^{1/2}(\Gamma _s)$, we have

$$\begin{aligned} \langle \Delta _{\Gamma _s} \varphi , \psi \rangle _{\textbf{H}^{-1/2}(\Gamma _s), \textbf{H}^{1/2}(\Gamma _s)} = - \langle \nabla _{\Gamma _s} \varphi , \nabla _{\Gamma _s} \psi \rangle _{\mathbb {L}^2(\Gamma _s)}, \end{aligned}$$

where we recall the definition $\Delta _{\Gamma _s} = {{\,\textrm{div}\,}}_{\Gamma _s} \circ \nabla _{\Gamma _s}$ of the Laplace-Beltrami operator on $\Gamma _s$. More generally, for all matrix field $\Sigma \in \mathbb {H}^1(\Gamma _s)$ and vector field $\varphi \in \textbf{H}^1(\Gamma _s)$ we have

$$\begin{aligned} \langle {{\,\textrm{div}\,}}_{\Gamma _s} \Sigma , \varphi \rangle _{\textbf{H}^{-1/2}(\Gamma _s), \textbf{H}^{1/2}(\Gamma _s)} = - \langle \Sigma , \nabla _{\Gamma _s} \varphi \rangle _{\mathbb {L}^2(\Gamma _s)}. \end{aligned}$$

(2)

We define admissible deformations, summarizing the basic assumptions we consider for mappings X, as well as the set of admissible deformations transforming the circle $\Gamma _s$ into another circle of the same radius and orientation:

Definition 2.1

We say that $X\in \textbf{H}^2(\Gamma _s)$ is admissible if X is invertible, orientation-preserving and volume-preserving, that is that the volume contained by $\Gamma _s$ is the same as the one contained by $X(\Gamma _s)$, and if $X(\Gamma _s) \subset \mathring{\Omega }$. Further, we define

$$\begin{aligned} \mathcal {C}_{\Gamma _s}= \left\{ X \in \textbf{H}^2(\Gamma _s)\mid \ X(\Gamma _s) \subset \mathring{\Omega } \text { is a circle of the same radius as }\Gamma _s \right\} . \end{aligned}$$

The relation $X(\Gamma _s) \subset \mathring{\Omega }$ is the condition of non-contact with the outer boundary, that is $X(\Gamma _s) \cap \partial \Omega = \emptyset$.

Remark 2.1

Note that any volume-preserving deformation $X\in \textbf{H}^2(\Gamma _s)$ that is close enough to the identity and volume-preserving is admissible. Relaxing the non-contact condition, remark that the space $\mathcal {C}_{\Gamma _s}$ contains elements of the special Euclidean group SE(2), made of proper rigid transformations $X_R$, namely direct isometries, composed of translations and rotations, as $X_R:\mathbb {R}^2 \ni y \mapsto h + \textbf{R}y \in \mathbb {R}^2,$ where $h\in \mathbb {R}^2$ and $\textbf{R}$ is an orthogonal matrix with $\textrm{det}\textbf{R} = 1$. The space $\mathcal {C}_{\Gamma _s}$ also includes the group $\textrm{Diff}^+(\Gamma _s)$ of direct diffeomorphisms of the circle $\Gamma _s$. We claim that $\mathcal {C}_{\Gamma _s}$ can be generated by composing elements of SE(2) with elements of $\textrm{Diff}(\Gamma _s)$. Finally, we note that we can obtain the circle $X(\Gamma _s)$ globally—as geometric object—from $\Gamma _s$ simply by composing the latter by a translation of SE(2). But for the sake of completeness we introduce $\mathcal {C}_{\Gamma _s}$ as above for describing all the possible stationary states.

We derive a series of lemmas, that will be used several times throughout the paper. The first one characterizes the stationary states, given by system (4):

Lemma 2.1

Let be subdomains $\Omega ^\pm \subset \Omega$ like in Lemma 2.0. If $g\in \textbf{H}^{-1/2}(\Gamma )$ is the right-hand-side of the following system

$$\begin{aligned} \left\{ \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0 &{} &{} \text {in } \Omega ^\pm , \\ u^+ = 0 &{} &{} \text {on } \partial \Omega , \\ u^\pm = 0 \quad \text { and } \quad -\left[ \sigma (u,p) \right] n = g &{} &{} \text {on } \Gamma , \end{array} \right. \end{aligned}$$

(3)

then necessarily $g = c n$, where c is a constant equal to the difference [p] of constant pressures. In particular, the admissible mappings X such that $X(\Gamma _s)\subset \mathring{\Omega }$ splits $\Omega$ into two subdomains denoted by $\Omega _{X(\Gamma _s)}^\pm = \Omega ^\pm$, like in Lemma 2.0, and satisfying

$$\begin{aligned} \left\{ \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0 &{} &{} \text {in } \Omega _{X(\Gamma _s)}^\pm , \\ u^+ = 0 &{} &{} \text {on } \partial \Omega , \\ u^\pm = 0 \quad \text { and } \quad -\left[ \sigma (u,p) \right] n = \mu \Delta _{X(\Gamma _s)}\textrm{Id}&{} &{} \text {on } X(\Gamma _s), \end{array} \right. \end{aligned}$$

(4)

describe the set $\mathcal {C}_{\Gamma _s}$. That is, $X(\Gamma _s)$ is a circle of the same radius $r>0$ as $\Gamma _s$. The velocities $u^\pm$ are equal to zero everywhere, and the pressures $p^\pm$ are constant, equal to the static pressures $p_s^\pm$ such that $[p_s]n_s = \mu \Delta _{X(\Gamma _s)} \textrm{Id}= \kappa _s n_s$ (namely the so-called Young-Laplace equation), where $\kappa _s = -1/r<0$ is the curvature of $X(\Gamma _s)$, implying that $p_s^- > p_s^+$.

Proof

Taking the scalar product of the first equation of (3), and integrating by parts leads to $\Vert \varepsilon (u^\pm )\Vert _{\mathbb {L}^2(\Omega _{X(\Gamma _s)}^\pm )} = 0$, and from Lemma 2.0, to $u^\pm = 0$ in $\textbf{H}^1(\Omega ^\pm )$. Then we also deduce $\nabla p^\pm = 0$ in the first equation, that yields that $p^\pm$ are both constant, equal to the static pressures $p_s^\pm$. Thus $g = \left[ 2\nu \varepsilon (u) - p \textrm{I}\right] n = -\left[ p_s\right] n$, where $\left[ p_s\right]$ is a constant, which completes the first part of the proof. Next, using this result for system (4) with $\Omega ^\pm = \Omega _{X(\Gamma _s)}^\pm$, $\Gamma = \Gamma _{X(\Gamma _s)}$ and $g = \mu \Delta _{X(\Gamma _s)} \textrm{Id}$, the constant $\left[ p\right]$ obtained previously corresponds to $\left[ p\right] n = \mu \Delta _{X(\Gamma _s)} \textrm{Id}$. Actually $\mu \Delta _{X(\Gamma _s)} \textrm{Id}= \kappa n$, where $\kappa$, namely the (mean) curvature of $X(\Gamma _s)$, is constant, equal to $\kappa _s = -1/r$. Therefore $X(\Gamma _s)$ is a circle, and since X is assumed to be admissible, this condition yields that $X(\Gamma _s)$ and $\Gamma _s$ have the same radius r, and so the same mean curvature $-1/r$. Therefore X lies necessarily in $\mathcal {C}_{\Gamma _s}$, and conversely, which completes the proof. $\square$

The stationary states are then obtained from the reference circle $\Gamma _s$ via transformations of $\mathcal {C}_{\Gamma _s}$. The deformations X of $\Gamma _s$ will be then compared to an element $X_c \in \mathcal {C}_{\Gamma _s}$, and the corresponding displacements writes $X-X_c$. For the sake of simplicity we will rather consider $X-\textrm{Id}$ in what follows, by keeping in mind that $\textrm{Id}$ is to be replaced by any given $X_c \in \mathcal {C}_{\Gamma _s}$. From there, we will use the notation

$$\begin{aligned} Z = X- \textrm{Id}\end{aligned}$$

for the displacements, keeping in mind that ultimately we shall consider $Z=X-X_c$ with $X_c \in \mathcal {C}_{\Gamma _s}$. Next we introduce the following differential operator

$$\begin{aligned} \nabla ^{n_s}_{\Gamma _s} = (n_s \otimes n_s) \nabla _{\Gamma _s}. \end{aligned}$$

Operator $\nabla ^{n_s}_{\Gamma _s}$ appears in the linearized system (22) (see Sect. 3.2 for its derivation). Note that the matrix field $n_s \otimes n_s$ is never invertible.

2.3 The Kernel of $\nabla ^{n_s}_{\Gamma _s}$ and the Lack of Coercivity

The operator ${{\,\textrm{div}\,}}_{\Gamma _s}\nabla ^{n_s}_{\Gamma _s}$ appears in the linearization of $(\kappa n) \circ X$ (see Sect. 3.2). The description of the kernel of $\nabla _{\Gamma _s}$ is then central for the methodology we adopted, namely the wellposedness of the corresponding linearized system (Sect. 4), and the unique continuation argument (Sect. 5.1). Unfortunately there are non-trivial mappings $X = Z+\textrm{Id}$ that are smooth, orientation-preserving, volume-preserving, transforming the circle into a Jordan curve, that can be chosen arbitrarily close to the identity, and such that $\nabla ^{n_s}_{\Gamma _s} Z = 0$.

Indeed, $\nabla ^{n_s}_{\Gamma _s} Z = (\nabla _{\Gamma _s}Z \cdot n_s)n_s= 0$ implies that $\nabla _{\Gamma _s} Z$ is tangent to $\Gamma _s$. There exists a function $\xi \mapsto \alpha (\xi )$ such that $\nabla _{\Gamma _s} Z = \alpha \tau _s$. Decompose $\alpha$ with its Fourier series:

$$\begin{aligned} \alpha (\xi ) = \sum _{k=2}^{\infty } \big ( a_{1,k} \cos (k\xi /r) + a_{2,k} \sin (k\xi /r) \big ). \end{aligned}$$

The modes $k=0$ and $k=1$ are not considered, as they introduce constants that are necessarily equal to 0, because of the periodicity of Z, meaning that $(\textrm{Id}+Z)(\Gamma _s)$ is a closed curve ($Z(X_s(0)) = Z(X_s(2\pi r))$). Integrating the equality $\nabla _{\Gamma _s} Z = \alpha \tau _s$ leads us to

$$\begin{aligned} Z(X_s(\xi )) = \sum _{k=2}^{\infty } \frac{1}{k^2-1} \Big ( \big ( a_{1,k} \cos (k\xi /r) + a_{2,k} \sin (k\xi /r) \big ) n_s + \big ( -a_{2,k}k \cos (k\xi /r) + a_{1,k}k \sin (k\xi /r) \big )\tau _s \Big ), \end{aligned}$$

up to a constant that corresponds to a translation. Several examples of such displacements are represented in Fig. 2 below, corresponding to $k \in \{2,3,4,5,6,7\}$ and coefficients $a_k, b_k \in \{0,1\}$.

Fig. 2

Different deformations $X(\Gamma _s)$ of the circle such that $\nabla ^{n_s}_{\Gamma _s} (X-\textrm{Id}) =0$

In order to define a linear operator whose the kernel is reduced to a trivial set, we need to regularize the operator ${{\,\textrm{div}\,}}_{\Gamma _s}\nabla ^{n_s}_{\Gamma _s}$.

2.4 Regularization

Instead of considering $\mu {{\,\textrm{div}\,}}_{\Gamma _s}\nabla ^{n_s}_{\Gamma _s}$ alone, we add a regularizing term, namely

$$\begin{aligned} \mu {{\,\textrm{div}\,}}_{\Gamma _s}\nabla ^{\tau _s}_{\Gamma _s} = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \circ \big ( (\tau _s \otimes \tau _s) \nabla _{\Gamma _s} \big ), \end{aligned}$$

so that the linear system studied in Sect. 4 involves the following operator

$$\begin{aligned} Z\mapsto -\mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{n_s}_{\Gamma _s} Z -\mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{\tau _s}_{\Gamma _s} Z = -\mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z = -\mu \Delta _{\Gamma _s} Z. \end{aligned}$$

For the Laplace-Beltrami operator $-\Delta _{\Gamma _s}$ we recall a rigidity result combined with Gårding-type inequalities.

Proposition 2.1

Assume that $Z\in \textbf{H}^\ell (\Gamma _s)$ with $\ell \ge 1$ satisfies $\Delta _{\Gamma _s} Z =0$. Then Z is a constant of $\mathbb {R}^2$. Moreover, the following estimates hold:

$$\begin{aligned} \Vert Z\Vert _{\textbf{H}^1(\Gamma _s)/\mathbb {R}^2} \le C \Vert \nabla _{\Gamma _s} Z\Vert _{\mathbb {L}^2(\Gamma _s)}{} & {} \text {for all } Z \in \textbf{H}^1(\Gamma _s), \end{aligned}$$

(5)

$$\begin{aligned} \Vert Z\Vert _{\textbf{H}^{5/2}(\Gamma _s)/\mathbb {R}^2} \le C \Vert \nabla _{\Gamma _s} Z\Vert _{\mathbb {H}^{3/2}(\Gamma _s)}{} & {} \text {for all } Z \in \textbf{H}^{5/2}(\Gamma _s), \end{aligned}$$

(6)

$$\begin{aligned} \Vert Z\Vert _{\textbf{H}^{3/2}(\Gamma _s)/\mathbb {R}^2} \le C \Vert \nabla _{\Gamma _s} Z\Vert _{\mathbb {H}^{1/2}(\Gamma _s)}{} & {} \text {for all } Z \in \textbf{H}^{3/2}(\Gamma _s). \end{aligned}$$

(7)

Furthermore, if $Z\in \textbf{H}^2(\Gamma _s)$, the following estimate holds:

$$\begin{aligned} \Vert Z\Vert _{\textbf{H}^2(\Gamma _s)/\mathbb {R}^2} \le C \Vert \Delta _{\Gamma _s}Z \Vert _{\textbf{L}^2(\Gamma _s)}. \end{aligned}$$

(8)

Proof

See for example [37, section 2.8]. Estimate (5) is deduced from the Poincaré inequality combined with the Petree-Tartar lemma. The same inequality applies to high-order derivatives of Z, and consequently estimates (6)–(7) are deduced by interpolation. Finally, estimate (8) is classically obtained by using Fourier series on the circle. $\square$

We deduce a unique continuation result that is used for proving Proposition 5.1.

Lemma 2.2

The mappings $X \in \textbf{H}^1(\Gamma _s)$ satisfying the following system

$$\begin{aligned} \left\{ \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0 &{} &{} \text {in } \Omega _s^\pm , \\ u^+ = 0 &{} &{} \text {on } \partial \Omega , \\ u^\pm = 0 \quad \text { and } \quad -\left[ \sigma (u,p) \right] n = \mu \Delta _{\Gamma _s} (X-\textrm{Id}) &{} &{} \text {on } \Gamma _s, \end{array} \right. \end{aligned}$$

(9)

are translations of $\mathbb {R}^2$.

Proof

By using Lemma 2.1 with $\Omega ^\pm = \Omega _s^\pm$, $\Gamma = \Gamma _s$ and $g = \mu \Delta _{\Gamma _s} (X-\textrm{Id})$, we deduce $\Delta _{\Gamma _s} (X-\textrm{Id}) = cn_s$, where c is a constant equal to the difference of constant pressures. Recall that the static pressures introduced in Lemma 2.1 satisfy $\mu \Delta _{\Gamma _s} \textrm{Id}= [p_s]n_s$. Therefore we can assume that the constant pressures mentioned above are such that $c = 0$, and so $\Delta _{\Gamma _s} (X-\textrm{Id}) = 0$. Since $\Gamma _s$ is a compact manifold, it follows that $X-\textrm{Id}$ is a constant, and X is a translation. $\square$

Remark 2.2

In the proof of Lemma 2.2, another argument for deducing $c=0$ would have consisted in restricting the deformation X to volume-preserving deformations. Since $n_s = -r \Delta _{\Gamma _s} \textrm{Id}$, we would have deduced $\Delta _{\Gamma _s} (X-\textrm{Id}+cr\textrm{Id}) = 0$, implying that $X+ (cr-1)\textrm{Id}$ is a constant. Assuming that X is volume-preserving then leads to $c=0$. This also amounts saying that the difference of static pressures remains the same after deformation by X.

The third lemma is an energy estimate that holds for an unsteady linear system:

Lemma 2.3

Let be $T>0$ and $\lambda >0$. Assume that Z satisfies

$$\begin{aligned} \left\{ \begin{array} {llll} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0 &{} &{} \text {in } \Omega _s^\pm \times (0,T), \\ u^+ = 0 &{} &{} \text {on } \partial \Omega \times (0,T), \\ u^\pm = \displaystyle \frac{\partial Z}{\partial t} -\lambda Z \quad \text { and } \quad -\left[ \sigma (u,p) \right] n = \mu \Delta _{\Gamma _s} Z + g &{} &{} \text {on } \Gamma _s \times (0,T), \\ Z(\cdot ,0) = Z_0 &{} &{} \text {on } \Gamma _s. \end{array} \right. \end{aligned}$$

(10)

Then the following identity holds almost everywhere in (0, T):

$$\begin{aligned} \frac{\mu }{2}\frac{\partial }{\partial t} \Vert \nabla _{\Gamma _s} Z \Vert _{\mathbb {L}^2(\Gamma _s)}^2 + 2\nu \left( \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega _s^+)}^2 + \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega _s^-)}^2\right) = \lambda \Vert \nabla _{\Gamma _s} Z \Vert _{\mathbb {L}^2(\Gamma _s)}^2 + \left\langle g ; u^\pm \right\rangle _{\textbf{L}^2(\Gamma _s)}. \end{aligned}$$

(11)

In particular, if $g=0$ and $Z_0 = 0$ in $\textbf{H}^1(\Gamma _s)$, then $Z\equiv 0$ up to a constant of $\mathbb {R}^2$.

Proof

Taking the scalar product of the first equation of (10) by $u^\pm$, and integrating by parts yields

$$\begin{aligned} 2\nu \left( \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega _s^+)}^2 + \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega _s^-)}^2\right) = \mu \left\langle \frac{\partial Z}{\partial t}-\lambda Z , \Delta _{\Gamma _s} Z \right\rangle _{\textbf{L}^2(\Gamma _s)} +\left\langle g , u^\pm \right\rangle _{\textbf{L}^2(\Gamma _s)}. \end{aligned}$$

The Stokes formula (2) shows that ${{\,\textrm{div}\,}}_{\Gamma _s}^{*} =-\nabla _{\Gamma _s}$, so we deduce

$$\begin{aligned} \begin{array} {rcl} \displaystyle \left\langle \frac{\partial Z}{\partial t}-\lambda Z ,\mu \Delta _{\Gamma _s} Z \right\rangle _{\textbf{L}^2(\Gamma _s)} &{} = &{} - \displaystyle \left\langle \frac{\partial \nabla _{\Gamma _s} Z}{\partial t}-\lambda \nabla _{\Gamma _s}Z , \mu \nabla _{\Gamma _s} Z \right\rangle _{\mathbb {L}^2(\Gamma _s)} \\ &{} = &{} \displaystyle -\frac{\mu }{2}\frac{\partial }{\partial t} \Vert \nabla _{\Gamma _s}Z \Vert ^2_{\mathbb {L}^2(\Gamma _s)} + \lambda \Vert \nabla _{\Gamma _s}Z \Vert ^2_{\mathbb {L}^2(\Gamma _s)}, \end{array} \end{aligned}$$

and thus (11) follows. By integrating in time this identity, with $g=0$, we obtain $\Vert \nabla _{\Gamma _s} Z \Vert _{\mathbb {L}^2(\Gamma _s)}^2 \le \Vert \nabla _{\Gamma _s} Z_0 \Vert _{\mathbb {L}^2(\Gamma _s)}^2 = 0$, which yields $\nabla _{\Gamma _s}Z=0$, and Proposition 2.1 enables us to complete the proof. $\square$

Note that the energy estimate (11) is also valid for any geometric configuration satisfying the non-contact condition, but we will use it only for $\Gamma _s$.

3 Extension of Diffeomorphisms and Change of Variables

In order to rewrite (1) in time-independent domains, we need to define in the whole domain $\Omega$ a change of variable that coincides with X on $\Gamma _s$. Therefore the question of the extension of X in $\Omega _s^\pm$ arises.

3.1 Extension of Diffeomorphisms

Let us define an extension of X which inherits its regularity properties. We state the following result:

Proposition 3.1

Let be $X-\textrm{Id}\in \mathcal {Z}_{\infty }(\Gamma _s)$ such that for all $t\ge 0$ the mapping $X(\cdot ,t)$ is a diffeomorphism from $\Gamma _s$ onto $\Gamma (t)$. There exists a mapping $\tilde{X}$ defined in $\Omega \times (0,\infty )$ such that for all $t \ge 0$ we have $\tilde{X}(\cdot ,t)_{| \Omega _s^\pm } \in \textbf{H}^{5/2}(\Omega _s^\pm )$, $\tilde{X}_{|\partial \Omega } = \textrm{Id}$, $\tilde{X}_{|\Gamma _s} = X$, $\tilde{X}(\cdot ,t)_{| \Omega _s^-}$ is a diffeomorphism from $\Omega _s^-$ onto $\Omega ^-(t)$, and that satisfies

$$\begin{aligned} \Vert \tilde{X} - \textrm{Id}\Vert _{\mathcal {X}_{\infty }(\Omega _s^\pm )} \le C \Vert X - \textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}, \end{aligned}$$

(12)

where the constant $C>0$ is independent of X. Furthermore, given $X_1-\textrm{Id}, \, X_2-\textrm{Id}\in \mathcal {Z}_{\infty }(\Gamma _s)$, the respective extensions $\tilde{X}_1$ and $\tilde{X}_2$ so obtained satisfy

$$\begin{aligned} \Vert \tilde{X}_1 - \tilde{X}_2 \Vert _{\mathcal {X}_{\infty }(\Omega _s^\pm )} \le C \Vert X_1 - X_2 \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}. \end{aligned}$$

(13)

The $\textbf{H}^{5/2}(\Omega _s^\pm )$ regularity implies in particular that for every $t\ge 0$ the mapping $\tilde{X}( \cdot ,t)_{|\Omega _s^\pm }$ is of class $\mathcal {C}^1$ on $\overline{\Omega _s^\pm }$. The proof of Proposition 3.1 combines different results that are not related to the main result of the paper. Therefore it is given in Appendix A.1. Note that the domains $\Omega ^\pm (t)$ defined as the two connected components of $\Omega {\setminus } \Gamma (t)$ are also described as $\Omega ^\pm (t) = \tilde{X}(\Omega _s^\pm ,t)$, due to conexity. By choosing $X-\textrm{Id}$ small enough, we can define a local inverse for $\tilde{X}_{|\Omega _s^+}(\cdot ,t)$. We deduce regularity for the inverse of the Jacobian matrix of $\tilde{X}(\cdot ,t)_{| \Omega _s^\pm }$.

Corollary 3.1

Given the assumptions of Proposition 3.1, the inverse $\tilde{Y}(\cdot ,t)$ of mapping $\tilde{X}(\cdot ,t)_{|\Omega _s^\pm }$, so that

$$\begin{aligned} \tilde{X}(\tilde{Y}(x,t),t) = x, \text { for } x\in \Omega ^\pm (t), \ t\in (0,\infty ), \qquad \tilde{Y}(\tilde{X}(y,t),t) = y \text { for } (y,t) \in \Omega _s^\pm \times (0,\infty ), \end{aligned}$$

satisfies the following estimate, provided that $\Vert X - \textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}$ is small enough:

$$\begin{aligned} \Vert \nabla \tilde{Y}(\tilde{X}) - \textrm{I}\Vert _{\textrm{L}^\infty (0,\infty ; \mathbb {H}^{3/2}(\Omega _s^\pm ))} \le C \Vert X - \textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}. \end{aligned}$$

(14)

Denoting by $\tilde{Y}_1$ and $\tilde{Y}_2$ the respective inverses of $\tilde{X}_1$ and $\tilde{X}_2$, extensions of $X_1$ and $X_2$ respectively, we have

$$\begin{aligned} \Vert \nabla \tilde{Y}_1(\tilde{X}_1) - \nabla \tilde{Y}_2(\tilde{X}_2) \Vert _{\textrm{L}^\infty (0,\infty ; \mathbb {H}^{3/2}(\Omega _s^\pm ))} \le C \Vert X_1 - X_2 \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}, \end{aligned}$$

(15)

provided that $\Vert X_1 - \textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}$ and $\Vert X_2 - \textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}$ are small enough.

Proof

Even if $\tilde{X}_{|\Omega _s^+}(\cdot ,t)$ is not globally invertible, we still use the notation $\nabla \tilde{Y}(\tilde{X})$ for the inverse of $\nabla \tilde{X}$, for the sake of simplicity. Recall that $\mathbb {H}^{3/2}(\Omega _s^\pm )$ is an algebra. The identity $\nabla \tilde{Y}(\tilde{X})-\textrm{I}= (\textrm{I}- \nabla \tilde{X})(\nabla \tilde{Y}(\tilde{X}) - \textrm{I}) + (\textrm{I}- \nabla \tilde{X})$ yields

$$\begin{aligned} \Vert \nabla \tilde{Y}(\tilde{X})-\textrm{I}\Vert _{\textrm{L}^\infty (0,\infty ; \mathbb {H}^{3/2}(\Omega _s^\pm ))} \le \frac{\Vert \nabla \tilde{X}-\textrm{I}\Vert _{\textrm{L}^\infty (0,\infty ; \mathbb {H}^{3/2}(\Omega _s^\pm ))}}{1- C \Vert \nabla \tilde{X}-\textrm{I}\Vert _{\textrm{L}^\infty (0,\infty ; \mathbb {H}^{3/2}(\Omega _s^\pm ))}} \end{aligned}$$

which, combined with (12), implies (14). Further, the identity

$$\begin{aligned} \nabla \tilde{Y}_1(\tilde{X}_1)- \nabla \tilde{Y}_2(\tilde{X}_2) = \big (\nabla \tilde{Y}_1(\tilde{X}_1) - \nabla \tilde{Y}_2(\tilde{X}_2)\big ) (\textrm{I}- \nabla \tilde{X}_1) - (\nabla \tilde{Y}_2(\tilde{X}_2) - \textrm{I})(\nabla \tilde{X}_1 - \nabla \tilde{X}_2) -(\nabla \tilde{X}_1 - \nabla \tilde{X}_2) \end{aligned}$$

enables us to derive (15) similarly, by using (12) for controlling $(\textrm{I}-\nabla \tilde{X}_1)$, (14) for controlling $(\nabla \tilde{Y}_2(\tilde{X}_2) - \textrm{I})$, and (13) for controlling $(\nabla \tilde{X}_1 - \nabla \tilde{X}_2)$, completing the proof. $\square$

Remark 3.1

In case we would consider stabilizing X around some $X_c \in \mathcal {C}_{\Gamma _s}$, instead of $\textrm{Id}$, we would need to define an extension $\tilde{X}_c \in \textbf{H}^{5/2}(\Omega _s^\pm )$ of $X_c \in \textbf{H}^2(\Gamma _s)$. Such an extension is provided by Proposition A.1 in Appendix A.1, and the Lipschitz estimates (12) and (14) would then be

$$\begin{aligned} \begin{array} {rcl} \Vert \tilde{X} - \tilde{X}_c \Vert _{\mathcal {X}_{\infty }(\Omega _s^\pm )} \le C \Vert X - X_c \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)},&\,&\Vert \nabla \tilde{Y}(\tilde{X}) - (\nabla \tilde{X}_c)^{-1} \Vert _{\textrm{L}^\infty (0,\infty ; \mathbb {H}^{3/2}(\Omega _s^\pm ))} \le C \Vert X - X_c \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}, \end{array} \end{aligned}$$

respectively.

We now have the tools for rewriting system (1) in cylindrical domains. The Lipschitz estimates of Proposition 3.1 and Corollary 3.1 are used in Sect. 6.

3.2 Change of Variables and System Transformation

We introduce the change of variables

$$\begin{aligned} \begin{array} {ll} \tilde{u}^\pm (y,t) := u^{\pm }(\tilde{X}(y,t),t), &{} \tilde{p}^\pm (y,t) := p^{\pm }(\tilde{X}(y,t),t), \quad (y,t) \in \Omega _s^\pm \times (0,\infty ), \\ u^\pm (x,t) = \tilde{u}^\pm (\tilde{Y}(x,t),t), &{} p^\pm (x,t) = \tilde{p}^\pm (\tilde{Y}(x,t),t), \quad (x,t) \in \displaystyle \bigcup _{t\in (0,\infty )} \Omega ^\pm (t) \times \{t\}, \\ &{} \tilde{f}^\pm (y,t) := (\textrm{det}\nabla \tilde{X}(y,t) )f^{\pm }(\tilde{X}(y,t),t), \quad (y,t) \in \Omega _s^\pm \times (0,\infty ), \\ &{} \tilde{g}(y,t) : = |\textrm{cof}(\nabla \tilde{X}(y,t))n_s |\, g(X(y,t),t), \quad (y,t) \in \Gamma _s \times (0,\infty ). \end{array} \end{aligned}$$

Implicitly, on $\Gamma _s$, $\nabla \tilde{X}$ refers to $\nabla \tilde{X}^-$. Composing system (1) by $\tilde{X}$ and using the Piola’s identity, we obtain

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}\left( \left( \sigma (u^\pm ,p^\pm ) \circ \tilde{X}\right) \textrm{cof}(\nabla \tilde{X}) \right) = \tilde{f}^\pm \quad \text { and } \quad {{\,\textrm{div}\,}}\left( \textrm{cof}(\nabla \tilde{X})^T \tilde{u} \right) = 0 &{} &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ \tilde{u}^+ = 0 &{} &{} \text {on } \partial \Omega \times (0,\infty ), \\ \tilde{u}^\pm = \displaystyle \frac{\partial X}{\partial t} \quad \text { and } \quad -\left[ \left( \sigma (u,p)\circ X\right) \right] \textrm{cof}\nabla {\tilde{X}} n_s = \mu |\textrm{cof}\nabla {\tilde{X}} n_s| (\Delta _{\Gamma (t)} \textrm{Id}) \circ X + \tilde{g} &{} &{} \text {on } \Gamma _s \times (0, \infty ), \\ X(\cdot ,0) = X_0 &{} &{} \text {on } \Gamma _s, \end{array} \end{aligned}$$

(16)

where

$$\begin{aligned} \sigma (u,p) \circ \tilde{X} = \nu \, \textrm{Sym}(\nabla \tilde{u} \nabla \tilde{Y}(\tilde{X})) - \tilde{p}\, \textrm{I}=: \tilde{\sigma }(\tilde{u},\tilde{p}), \end{aligned}$$

and where we used $n\circ X = \textrm{cof}\nabla {\tilde{X}} n_s/|\textrm{cof}\nabla {\tilde{X}} n_s|$. Let us develop $(\Delta _{\Gamma (t)} \textrm{Id}) \circ X$. The parameterization $X_s: \ [0,2\pi r) \ni \xi \mapsto X_s(\xi ) \in \Gamma _s$ of $\Gamma _s$ introduced in Sect. 2.2 enables us to define $X\circ X_s$ as a parameterization of $\Gamma (t)$. We denote by $\mathfrak {g}_s$, $\mathfrak {g}(t)$ the metric tensors of $\Gamma _s$ and $\Gamma (t)$, respectively. We have, in local coordinates, and using the Einstein notation²:

$$\begin{aligned} \begin{array} {rcl} (\Delta _{\Gamma (t)} \textrm{Id})_i \circ X \circ X_s= & {} (\textrm{det}\mathfrak {g}(t))^{-1/2} \displaystyle \frac{\partial }{\partial \xi _j} \left( (\textrm{det}\mathfrak {g}(t))^{1/2} \frac{\partial (X\circ X_s)_i}{\partial \xi _k} (\mathfrak {g}(t)^{-1})_{kj} \right) . \end{array} \end{aligned}$$

(17)

Volume forms considerations yield

$$\begin{aligned} (\textrm{det}\mathfrak {g}(t))^{1/2} = |\textrm{cof}\nabla \tilde{X} n_s| (\textrm{det}\mathfrak {g}_s)^{1/2} \end{aligned}$$

(see for instance [7, Lemma 6.23, p. 135]), and when $X-\textrm{Id}$ is small, we write

$$\begin{aligned} \begin{array} {rcl} \mathfrak {g}(t) &{} = &{} \nabla _{\xi } (X\circ X_s)^T \nabla _{\xi }(X\circ X_s) = \mathfrak {g}_s + \nabla _{\xi } (X\circ X_s)^T \nabla _{\xi }(X\circ X_s) - \nabla _{\xi }X_s^T \nabla _{\xi } X_s \\ &{} = &{} \mathfrak {g}_s + 2\, \textrm{Sym}\left( \nabla _{\xi }X_s^T \nabla _{\xi } ( (X-\textrm{Id})\circ X_s) \right) + \mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} ), \\ \mathfrak {g}(t)^{-1} &{} = &{} \mathfrak {g}_s^{-1} - 2\, \mathfrak {g}_s^{-1} \textrm{Sym}\left( \nabla _{\xi }X_s^T \nabla _{\xi } ( (X-\textrm{Id})\circ X_s) \right) \mathfrak {g}_s^{-1} + \mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} ) \\ &{} = &{} \mathfrak {g}_s^{-1} - 2\, \mathfrak {g}_s^{-1} \left( \nabla _{\xi }X_s^T \nabla _{\xi } ( (X-\textrm{Id})\circ X_s) \right) \mathfrak {g}_s^{-1} + \mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} ) \\ \textrm{det}\mathfrak {g}(t) &{} = &{} \textrm{det}\mathfrak {g}_s + 2\, \textrm{cof}\mathfrak {g}_s : \textrm{Sym}\left( \nabla _{\xi }X_s^T \nabla _{\xi } ( (X-\textrm{Id})\circ X_s) \right) + \mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} )\\ &{} = &{} (\textrm{det}\mathfrak {g}_s)\left( 1+ 2\, \mathfrak {g}_s^{-1} : \left( \nabla _{\xi }X_s^T \nabla _{\xi } ( (X-\textrm{Id})\circ X_s) \right) \right) + \mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} ) , \\ (\textrm{det}\mathfrak {g}(t))^{1/2} &{} = &{} (\textrm{det}\mathfrak {g}_s)^{1/2}\left( 1 + \mathfrak {g}_s^{-1} : \left( \nabla _{\xi }X_s^T \nabla _{\xi } ( (X-\textrm{Id})\circ X_s) \right) \right) +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} ),\\ \displaystyle \frac{\partial (X\circ X_s)_i}{\partial \xi _k} &{} = &{} (\nabla _{\xi }X_s)_{ik} + \displaystyle \frac{\partial ((X-\textrm{Id})\circ X_s)_i}{\partial \xi _k}, \end{array} \end{aligned}$$

where we have used the symmetry of $\mathfrak {g}_s$ and $\mathfrak {g}(t)$, and where the Landau’s notation $\mathcal {O}$ applies when $\nabla \tilde{X} - \textrm{I}$ is small in the algebra $\mathbb {H}^{1}(\Gamma _s)$. Further, let us make some simplifications provided by dimension 2, using the parameterizaion by arc length given in Sect. 2.2: The metric tensor $\mathfrak {g}_s$ is scalar valued, equal to $| \nabla _{\xi }X_s|^2 = 1$, and the tangent space of $\Gamma _s$ is made of the tangent vectors $\tau _s$ such that $\tau _s \circ X_s = -\nabla _{\xi }X_s/|\nabla _{\xi } X_s| = - \nabla _{\xi } X_s$. We then have

$$\begin{aligned} \begin{array} {rcl} \mathfrak {g}(t)^{-1} &{} = &{} \mathfrak {g}_s^{-1} - 2 \displaystyle \frac{\langle \nabla _{\xi } X_s, \nabla _{\xi }((X-\textrm{Id})\circ X_s) \rangle _{\mathbb {R}^2}}{|\nabla _{\xi } X_s |^2} +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} )\\ &{} = &{} \mathfrak {g}_s^{-1} + 2 \displaystyle \langle \tau _s\circ X_s, \nabla _{\xi }((X-\textrm{Id})\circ X_s) \rangle _{\mathbb {R}^2} +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} ),\\ (\textrm{det}\mathfrak {g}(t))^{1/2} &{} = &{} (\textrm{det}\mathfrak {g}_s)^{1/2}\left( 1 + \displaystyle \frac{\langle \nabla _{\xi } X_s, \nabla _{\xi }((X-\textrm{Id})\circ X_s) \rangle _{\mathbb {R}^2}}{|\nabla _{\xi } X_s |^2} \right) +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} )\\ &{} = &{} (\textrm{det}\mathfrak {g}_s)^{1/2}\left( 1 - \displaystyle \langle \tau _s\circ X_s, \nabla _{\xi }((X-\textrm{Id})\circ X_s) \rangle _{\mathbb {R}^2} \right) +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} ),\\ \displaystyle \frac{\partial (X\circ X_s)_i}{\partial \xi _k} &{} = &{} -(\tau _s\circ X_s)_i + \displaystyle \nabla _{\xi }((X-\textrm{Id})\circ X_s)_i . \end{array} \end{aligned}$$

Linearizing (17), we deduce

$$\begin{aligned} \begin{array}{rcl} (\Delta _{\Gamma (t)} \textrm{Id}) \circ (X\circ X_s) &{} = &{} |\textrm{cof}\nabla \tilde{X} n_s|^{-1}\big (\Delta _{\Gamma _s} \textrm{Id}+ {{\,\textrm{div}\,}}_{\Gamma _s}(\nabla _{\Gamma _s} (X-\textrm{Id})) \big ) \circ X_s \\ &{} &{} \left. -|\textrm{cof}\nabla \tilde{X} n_s|^{-1} (\textrm{det}\mathfrak {g}_s)^{-1/2}\displaystyle \frac{\partial }{\partial \xi }\left( (\textrm{det}\mathfrak {g}_s)^{1/2} \displaystyle \big ((\tau _s \otimes \tau _s)\circ X_s\big ) \nabla _{\xi }((X-\textrm{Id})\circ X_s) \right) \right) \\ &{} &{} +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} )\\ &{} = &{} |\textrm{cof}\nabla \tilde{X} n_s|^{-1} \Big ( \Delta _{\Gamma _s} \textrm{Id}+ {{\,\textrm{div}\,}}_{\Gamma _s}(\nabla _{\Gamma _s} (X-\textrm{Id})) - {{\,\textrm{div}\,}}_{\Gamma _s}((\tau _s \otimes \tau _s)\nabla _{\Gamma _s} (X-\textrm{Id})) \Big )\circ X_s \\ &{} &{} +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)}) ,\\ (\Delta _{\Gamma (t)} \textrm{Id}) \circ X &{} = &{} |\textrm{cof}\nabla \tilde{X} n_s|^{-1}\big (\Delta _{\Gamma _s} \textrm{Id}+ {{\,\textrm{div}\,}}_{\Gamma _s}\left( (n_s \otimes n_s)\nabla _{\Gamma _s} (X-\textrm{Id})\right) \big ) +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)}), \end{array} \end{aligned}$$

as $n_s \otimes n_s= \textrm{I}- \tau _s \otimes \tau _s$ is the projection operator on $n_s$. Thus, recalling the notation $\nabla ^{n_s}_{\Gamma _s} = (n_s \otimes n_s) \nabla _{\Gamma _s}$, the fourth equation of (16) writes

$$\begin{aligned} \begin{array} {rcl} -\left[ \tilde{\sigma }(\tilde{u},\tilde{p}) \right] \textrm{cof}\nabla {\tilde{X}} n_s = \mu \Delta _{\Gamma _s} \textrm{Id}+ {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{n_s}_{\Gamma _s}(X-\textrm{Id}) + \tilde{g} +\mathcal {O}(\Vert \nabla \tilde{X}-\textrm{I}\Vert ^2_{\mathbb {H}^1(\Gamma _s)} )&\,&\text {on } \Gamma _s \times (0, \infty ). \end{array} \end{aligned}$$

The interest of (16) lies in the fact that the space domains domains $\Omega _s^\pm$ are time-independent. The price to pay is the nonlinear operators with respect to X that appear above. Recall that $\Delta _{\Gamma _s} \textrm{Id}= [p_s]n_s$, where $p_s^\pm$ are the constant static pressures introduced in Lemma 2.1. Further, we introduce the following unknowns:

$$\begin{aligned} \begin{array}{rcl} \hat{u}^\pm = e^{\lambda t} \tilde{u}^\pm , \quad \hat{p}^\pm = e^{\lambda t} (\tilde{p}^\pm - p_s^\pm ), \quad \hat{f}^\pm = e^{\lambda t} \tilde{f} &{} &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ \hat{Z}(\cdot ,t) = e^{\lambda t}(X(\cdot ,t)-\textrm{Id}), \quad \hat{g} = e^{\lambda t} \tilde{g} &{} &{} \text {on } \Gamma _s\times (0,\infty ). \end{array} \end{aligned}$$

(18)

The idea here is to find a control $\hat{g}$ that will make the variables $(\hat{u}^\pm ,\hat{p}^\pm ,\hat{Z})$ bounded, so that the original unknwon will decrease exponentially with $\lambda$ as decay rate. The system satisfied by $(\hat{u}^\pm ,\hat{p}^\pm ,\hat{X})$ is the following:

$$\begin{aligned} \begin{array} {rcl} - {{\,\textrm{div}\,}}(\sigma (\hat{u}^\pm , \hat{p}^\pm ) = \hat{f}^\pm + F(\hat{u}^\pm ,\hat{p}^\pm , \hat{Z}) \quad \text { and } \quad {{\,\textrm{div}\,}}\hat{u} = {{\,\textrm{div}\,}}H(\hat{u}^\pm , \hat{Z}) &{} &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ \hat{u}^+ = 0 &{} &{} \text {on } \partial \Omega \times (0,\infty ), \\ \hat{u}^\pm = \displaystyle \frac{\partial \hat{Z}}{\partial t} - \lambda \hat{Z}, \ \text { and } \ -\left[ \sigma (\hat{u},\hat{p})\right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s}\nabla ^{n_s}_{\Gamma _s}\hat{Z} + \hat{g} + G(\hat{u}^+, \hat{p}^+, \hat{u}^-, \hat{p}^-, \hat{Z}) &{} &{} \text {on } \Gamma _s \times (0,\infty ), \\ \hat{Z}(\cdot ,0) = X_0-\textrm{Id}&{} &{} \text {on } \Gamma _s, \end{array} \end{aligned}$$

(19)

where we have introduced

$$\begin{aligned} F(\hat{u}^\pm ,\hat{p}^\pm , \hat{Z})= & {} {{\,\textrm{div}\,}}\left( \tilde{\sigma }(\hat{u}^\pm ,\hat{p}^\pm ) (\textrm{cof}\nabla \tilde{X}-\textrm{I}) \right) + 2\nu {{\,\textrm{div}\,}}\left( \textrm{Sym}\left( \nabla \hat{u} (\tilde{Y}(\tilde{X})-\textrm{I})\right) \right) , \end{aligned}$$

(20a)

$$\begin{aligned} G(\hat{u}^+, \hat{p}^+, \hat{u}^-, \hat{p}^-, \hat{Z})= & {} \left[ \tilde{\sigma }(\hat{u},\hat{p})\right] (\textrm{cof}\nabla \tilde{X}-\textrm{I}) n_s + 2\nu \left[ \textrm{Sym}\left( \nabla \hat{u} (\tilde{Y}(\tilde{X})-\textrm{I}) \right) \right] n_s \nonumber \\{} & {} + \Vert \nabla \tilde{X}\Vert _{\mathbb {H}^1(\Gamma _s)} \mathcal {O}(\Vert \nabla \tilde{X}-I \Vert _{\mathbb {H}^1(\Gamma _s)}), \end{aligned}$$

(20b)

$$\begin{aligned} H(\hat{u}^\pm , \hat{Z})= & {} (\textrm{I}- \textrm{cof}\nabla \tilde{X})^T\hat{u}^\pm . \end{aligned}$$

(20c)

In Sect. 6 we deduce regularity for the functions F, G and H. Note that the condition $\hat{u}^+_{|\partial \Omega } = 0$ on the outer boundary implies that $H(\hat{u}^+,Z)_{|\partial \Omega } = 0$, and so we will consider in particular $H(\hat{u}^+,Z) \in \mathcal {U}_{\infty }(\Omega _s^+)$. In system (19), the linear part is on the left-hand-side, and the nonlinear part is represented by the right-hand-sides F, G and H. Considering small data, the displacements $X-\textrm{Id}$ remain small, and the nonlinearities F, G and H too (see Sect. 6). Therefore we first study the stabilizability of the linearized system.

4 On the Linearized System

From (19) we deduce the linearized system with $(u^\pm , p^\pm )$ and Z as unknowns:

$$\begin{aligned} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0{} & {} \text {in } \Omega _s^\pm \times (0,\infty ), \nonumber \\ u^+ = 0{} & {} \text {on } \partial \Omega \times (0,\infty ), \nonumber \\ u^+ = u^- = \frac{\partial Z}{\partial t} - \lambda Z \quad \text { and } \quad -\left[ \sigma (u,p) \right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{n_s}_{\Gamma _s} Z + G{} & {} \text {on } \Gamma _s \times (0,\infty ), \nonumber \\ Z(\cdot ,0 ) = Z_0{} & {} \text {on } \Gamma _s. \end{aligned}$$

(21)

As explained in Sect. 2.3, the operator $\nabla ^{n_s}_{\Gamma _s}$ is non-coercive, and we define a first feedback operator $Z\mapsto \mu {{\,\textrm{div}\,}}_{\Gamma _s} \big ( (\tau _s \otimes \tau _s)\nabla _{\Gamma _s} Z\big ) = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{\tau _s}_{\Gamma _s} Z = G$, such that the resulting elliptic operator in (21) becomes

$$\begin{aligned} Z\mapsto \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{n_s}_{\Gamma _s} Z + \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla ^{\tau _s}_{\Gamma _s} Z = {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z = \Delta _{\Gamma _s} Z. \end{aligned}$$

Given $T\in (0,\infty )$, this section is devoted to wellposedness and operator formulation for the following linear system:

$$\begin{aligned} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0{} & {} \text {in } \Omega _s^\pm \times (0,T), \end{aligned}$$

(22a)

$$\begin{aligned} u^+ = 0{} & {} \text {on } \partial \Omega \times (0,T), \end{aligned}$$

(22b)

$$\begin{aligned} u^+ = u^- = \frac{\partial Z}{\partial t} - \lambda Z \quad \text { and } \quad -\left[ \sigma (u,p) \right] n_s = \mu \Delta _{\Gamma _s} Z + G{} & {} \text {on } \Gamma _s \times (0,T), \end{aligned}$$

(22c)

$$\begin{aligned} Z(\cdot ,0 ) = Z_0{} & {} \text {on } \Gamma _s. \end{aligned}$$

(22d)

The data are assumed to satisfy $G \in \mathcal {G}_T(\Gamma _s)=\textrm{L}^2(0,T;\textbf{H}^{1/2}(\Gamma _s))$, $Z_0 \in \mathcal {Z}_0(\Gamma _s)= \textbf{H}^{2}(\Gamma _s)/\mathbb {R}^2$. Our approach consists in writing (22) as an abstract evolution equation with Z as the only unknown. The other unknowns $(u^\pm ,p^\pm )$ can be then deduced as solutions of standard Stokes problems with the Dirichlet boundary condition of (22c).

4.1 A Poincaré-Steklov Operator

For $G\in \textbf{H}^{1/2}(\Gamma _s)$ given, in this subsection we are interested in the following linear transmission problem:

$$\begin{aligned} -{{\,\textrm{div}\,}}\sigma (u^{\pm }, p^{\pm }) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^{\pm } = 0{} & {} \text {in } \Omega _s^{\pm }, \end{aligned}$$

(23a)

$$\begin{aligned} u^+ = 0{} & {} \text {on } \partial \Omega , \end{aligned}$$

(23b)

$$\begin{aligned} \left[ u\right] = 0 \quad \text { and } \quad -\left[ \sigma (u,p)\right] n_s = G{} & {} \text {on } \Gamma _s. \end{aligned}$$

(23c)

Following the approach of [15], the equality of velocities in (23c) leads us to introduce a boundary velocity $\phi \in \textbf{H}^{1/2}(\Gamma _s)$, and we obtain a weak solution of (23) as a critical point of the following Lagrangian functional:

$$\begin{aligned} \begin{array} {rcl} \mathcal {L}(u^+,p^+,u^-,p^-, \lambda ^+,\lambda ^-,\phi ) &{} = &{} 2\nu \Vert \varepsilon (u^+)\Vert ^2_{\mathbb {L}^2(\Omega _s^+)} + 2\nu \Vert \varepsilon (u^-)\Vert ^2_{\mathbb {L}^2(\Omega _s^-)} \\ &{} &{} - \langle p^+ ,{{\,\textrm{div}\,}}u^+\rangle _{\textrm{L}^2(\Omega _s^+)} - \langle p^- , {{\,\textrm{div}\,}}u^-\rangle _{\textrm{L}^2( \Omega _s^-)} \\ &{} &{} -\langle \lambda ^+,u^+-\phi \rangle _{\textbf{H}^{-1/2}(\Gamma _s):\textbf{H}^{1/2}(\Gamma _s)} - \langle \lambda ^- , u^- -\phi \rangle _{\textbf{H}^{-1/2}(\Gamma _s):\textbf{H}^{1/2}(\Gamma _s)} \\ &{} &{} - \langle G , \phi \rangle _{\textbf{H}^{-1/2}(\Gamma _s):\textbf{H}^{1/2}(\Gamma _s)} . \end{array} \end{aligned}$$

Note that the variable $\phi$ also plays the role of a multiplier for the transmission condition (23c). Let us introduce

$$\begin{aligned} \begin{array} {l} \textbf{V}^+ = \displaystyle \left\{ v \in \textbf{H}^1(\Omega _s^+) \mid v_{|\partial \Omega } = 0 \right\} , \quad \textbf{V}^- = \textbf{H}^1(\Omega _s^-)/\mathbb {R}^2, \quad Q^\pm = \textrm{L}^2(\Omega _s^\pm ) /\mathbb {R}, \\ \textbf{W} = \displaystyle \left\{ v\in \textbf{H}^{1/2}(\Gamma _s) \mid \langle v, n \rangle _{\textbf{L}^2(\Gamma _s)} = 0 \right\} . \end{array} \end{aligned}$$

Relying on the Korn’s inequality and the Petree-Tartar lemma, we equip $\textbf{V}^\pm$ with the norms $\Vert v\Vert _{\textbf{V}^\pm }:= \Vert \varepsilon (v)\Vert _{\mathbb {L}^2(\Omega _s^\pm )}$. For the sake of brevity we denote

$$\begin{aligned}{} & {} \mathfrak {u} = (u^+,p^+,u^-,p^-,\lambda ^+,\lambda ^-,\phi ),\quad \mathfrak {v} = (v^+,q^+,v^-,q^-,\mu ^+,\mu ^-,\varphi ),\\{} & {} \mathfrak {V} = \textbf{V}^+\times Q^+\times \textbf{V}^-\times Q^-\times \textbf{W}' \times \textbf{W}' \times \textbf{W}. \end{aligned}$$

A weak solution of (23) satisfies the variational formulation given by the first order optimality condition for functional $\mathcal {L}$:

$$\begin{aligned} \begin{array}{l} \text {Find }\mathfrak {u}\,\in \,\mathfrak {V},\text { such that for all } \mathfrak {v}\,\in \,\mathfrak {V}:\\ \left\{ \begin{array} {rcl} \displaystyle \langle \sigma (u^\pm ,p^\pm ),\varepsilon (v^\pm )\rangle _{\mathbb {L}^2(\Omega _s^\pm )} -\langle \lambda ^\pm , v^\pm \rangle _{\textbf{W}';\textbf{W}} = 0, &{} &{} \displaystyle -\langle q^\pm ,{{\,\textrm{div}\,}}u^\pm \rangle _{\textrm{L}^2(\Omega _s^\pm )} = 0,\\ \displaystyle -\langle \mu ^\pm , u^\pm -\Phi \rangle _{\textbf{W}';\textbf{W}} = 0, &{} &{} \displaystyle \langle \lambda ^+ + \lambda ^- - G, \varphi \rangle _{\textbf{W}';\textbf{W}} = 0. \end{array} \right. \end{array} \end{aligned}$$

(24)

By integration by parts, we easily see that at the optimality we have $\lambda ^\pm = \sigma (u^\pm ,p^\pm )n^\pm$. We rewrite the variational problem (24) more compactly, as follows:

$$\begin{aligned}&\text {Find }\mathfrak {u}\,\in \,\mathfrak {V}\text { such that} \quad \mathcal {M}(\mathfrak {u};\mathfrak {v}) = \mathcal {G}(\mathfrak {v})\quad \forall \mathfrak {v} \in \mathfrak {V},\\&\begin{array}{rcl} \text {where}\quad \mathcal {M}(\mathfrak {u};\mathfrak {v}) &{} := &{} 2\nu \langle \varepsilon (u^+),\varepsilon (v^+)\rangle _{\mathbb {L}^2(\Omega _s^+)} + 2\nu \langle \varepsilon (u^-):\varepsilon (v^-)\rangle _{\mathbb {L}^2(\Omega _s^-)} \\ &{} &{} - \langle p^+,{{\,\textrm{div}\,}}v^+\rangle _{\textrm{L}^2(\Omega _s^+)} -\langle q^+,{{\,\textrm{div}\,}}u^+ \rangle _{\textrm{L}^2(\Omega _s^+)} - \langle p^-,{{\,\textrm{div}\,}}v^-\rangle _{\textrm{L}^2(\Omega _s^-)} - \langle q^-,{{\,\textrm{div}\,}}u^- \rangle _{\textrm{L}^2(\Omega _s^-)} \\ &{} &{} - \langle \lambda ^+ ,v^+-\varphi \rangle _{\textbf{W}';\textbf{W}} - \langle \mu ^+ , u^+ - \Phi \rangle _{\textbf{W}';\textbf{W}} - \langle \lambda ^- ,v^--\varphi \rangle _{\textbf{W}';\textbf{W}} - \langle \mu ^-, u^- - \Phi \rangle _{\textbf{W}';\textbf{W}}, \\ \mathcal {G}(\mathfrak {v}) &{} := &{} \left\langle G, \varphi \right\rangle _{\textbf{W}';\textbf{W}}. \end{array} \end{aligned}$$

The existence and uniqueness of a solution for (24) is equivalent to the Ladyzhenskaya-Babuška-Brezzi inf-sup condition. In that sense we state the following result:

Proposition 4.1

There exists a constant $C >0$ such that

$$\begin{aligned} \inf _{\mathfrak {u} \in \mathfrak {V}\setminus \{0\}} \sup _{\mathfrak {v} \in \mathfrak {V}\setminus \{0\}} \frac{\mathcal {M}(\mathfrak {u};\mathfrak {v})}{\Vert \mathfrak {u} \Vert _{\mathfrak {V}} \Vert \mathfrak {v} \Vert _{\mathfrak {V}}}\ge & {} C. \end{aligned}$$

The proof of this proposition is given in Appendix A.2. The consequence of this result is the existence and uniqueness of a weak solution for system (23).

Corollary 4.1

Assume that $G \in \textbf{W}$. System (23) admits a unique solution $(u^+,p^+,u^-,p^-)$ in $\textbf{V}^+\times Q^+\times \textbf{V}^- \times Q^-$. Moreover, there exists a constant $C >0$, depending only on $\Omega _s^+$ and $\Omega _s^-$, such that

$$\begin{aligned} \Vert u^+\Vert _{\textbf{H}^1(\Omega _s^+)} + \Vert p^+\Vert _{\textrm{L}^2(\Omega _s^+)/\mathbb {R}} + \Vert u^-\Vert _{\textbf{H}^1(\Omega _s^-)} + \Vert p^-\Vert _{\textrm{L}^2(\Omega _s^-)/\mathbb {R}}\le & {} C \Vert G \Vert _{\textbf{H}^{-1/2}(\Gamma _s)}. \end{aligned}$$

The proof of Corollary 4.1 is also given in Appendix A.2. Thus, considering the trace on $\Gamma _s$ of the solution $u^\pm$ of system (23), we have defined the operator

$$\begin{aligned} \begin{array} {rccl} \mathcal {P}_{\Gamma _s}: &{} \textbf{W}' &{} \rightarrow &{} \textbf{W} \\ &{} G &{} \mapsto &{} u^\pm _{|\Gamma _s} \end{array} \end{aligned}$$

(25)

mapping the jump condition in the right side of (23c) to the velocity trace on $\Gamma _s$. From Proposition 4.1 and Corollary 4.1, we can deduce more regularity for system (23), and consequently for operator $\mathcal {P}_{\Gamma _s}$ restricted to $\textbf{H}^{1/2}(\Gamma _s)$.

Proposition 4.2

Assume that $\partial \Omega$ is of class $C^1$, and that $G \in \textbf{H}^{1/2}(\Gamma _s)$. Then system (23) admits a unique solution $(u^+, p^+, u^-, p^-)$ in $\textbf{H}^2(\Omega _s^+) \times \textrm{H}^{1}(\Omega _s^+)\times \textbf{H}^2(\Omega _s^-) \times \textrm{H}^{1}(\Omega _s^-)$, and it satisfies the estimate

$$\begin{aligned} \Vert u^+\Vert _{\textbf{H}^2(\Omega _s^+)} + \Vert p^+\Vert _{\textrm{H}^1(\Omega _s^+)/\mathbb {R}} + \Vert u^-\Vert _{\textbf{H}^2(\Omega ^-)} + \Vert p^-\Vert _{\textrm{H}^1(\Omega _s^-)/\mathbb {R}}\le & {} C\Vert G \Vert _{\textbf{H}^{1/2}(\Gamma _s)}, \end{aligned}$$

where the constant $C >0$ depends only $\Omega _s^+$ and $\Omega _s^-$.

Proof

The proof of the regularity theorem of [36, Theorem 9.19, p. 278], can be repeated in our context, and the regularity of $u^\pm$ in $\textbf{H}^2(\Omega _s^\pm )$ follows, as well as those of $p^\pm$ in $\textrm{H}^1(\Omega _s^\pm )/\mathbb {R}$. $\square$

Therefore $\mathcal {P}_{\Gamma _s}$ maps $\textbf{H}^{1/2}(\Gamma _s)$ onto $\textbf{H}^{3/2}(\Gamma _s)$. Finally, we state the following properties for the Neumann-to-Dirichlet operator $\mathcal {P}_{\Gamma _s}$:

Proposition 4.3

Operator $\mathcal {P}_{\Gamma _s}$ is self-adjoint and non-negative, and $\textrm{Ker}(\mathcal {P}_{\Gamma _s}) = \textrm{span}(n_s)$.

Proof

Let be $G_1$, $G_2 \in \textbf{H}^{-1/2}(\Gamma _s)$, and denote by $(u^\pm _1,p^\pm _1)$ and $(u^\pm _2,p^\pm _2)$ the solutions of system (23) corresponding to $G_1$ and $G_2$ respectively. By integration by parts, we obtain

$$\begin{aligned} \langle G_2,\mathcal {P}_{\Gamma _s}G_1 \rangle _{\textbf{H}^{-1/2}(\Gamma _s);\textbf{H}^{1/2}(\Gamma _s)}= & {} \langle -\left[ \sigma (u_2,p_2)\right] n_s, u^\pm _1\rangle _{\textbf{H}^{-1/2}(\Gamma _s);\textbf{H}^{1/2}(\Gamma _s)} \\= & {} \langle \sigma (u^+_2,p^+_2)n^+_s + \sigma (u_2^-,p_2^-)n_s^-, u^\pm _1\rangle _{\textbf{H}^{-1/2}(\Gamma _s);\textbf{H}^{1/2}(\Gamma _s)}\\= & {} 2\nu \left( \langle \varepsilon (u^+_1), \varepsilon (u^+_2) \rangle _{\mathbb {L}^2(\Omega _s^+)} + \langle \varepsilon (u^-_1), \varepsilon (u^-_2) \rangle _{\mathbb {L}^2(\Omega _s^-)} \right) . \end{aligned}$$

This symmetric form shows that $\mathcal {P}_{\Gamma _s}$ is self-adjoint. Further, with $G = G_1 = G_2$, we have

$$\begin{aligned} \langle G,\mathcal {P}_{\Gamma _s}G \rangle _{\textbf{H}^{-1/2}(\Gamma _s);\textbf{H}^{1/2}(\Gamma _s)} = 2\nu \left( \Vert \varepsilon (u_1^+)\Vert ^2_{\textbf{L}^2(\Omega _s^+)} + \Vert \varepsilon (u_1^-)\Vert ^2_{\textbf{L}^2(\Omega _s^-)} \right) \ge 0, \end{aligned}$$

and $\langle G, \mathcal {P}_{\Gamma _s}G \rangle _{\textbf{H}^{-1/2}(\Gamma _s);\textbf{H}^{1/2}(\Gamma _s)} = 0$ if and only if $u_1^\pm \equiv 0$ from Lemma 2.0. Finally, Lemma 2.1 also describes the kernel of $\mathcal {P}_{\Gamma _s}$, finishing the proof. $\square$

4.2 The Semi-homogeneous System

Using the operator $\mathcal {P}_{\Gamma _s}$, we rewrite system (22) with $\lambda =0$ as the following abstract evolution equation

$$\begin{aligned} \frac{\partial Z}{\partial t} - \mathcal {P}_{\Gamma _s}(\mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z) = \mathcal {P}_{\Gamma _s} G \quad \text { in } (0,T), \qquad Z(0) = Z_0, \end{aligned}$$

(26)

with $Z_0 \in \textbf{H}^{2}(\Gamma _s)/\mathbb {R}^2$. Composing (26) by $\nabla _{\Gamma _s}$, we obtain an equation dealing with $\nabla _{\Gamma _s}Z$ as unknown:

$$\begin{aligned} \frac{\partial \nabla _{\Gamma _s} Z}{\partial t} - \mu \nabla _{\Gamma _s}\mathcal {P}_{\Gamma _s}({{\,\textrm{div}\,}}_{\Gamma _s}\nabla _{\Gamma _s} Z) = \nabla _{\Gamma _s}\mathcal {P}_{\Gamma _s} G \quad \text { in } (0,T), \qquad \nabla _{\Gamma _s}Z(0) = \nabla _{\Gamma _s}Z_0. \end{aligned}$$

(27)

The interest of this formulation is that the following unbounded linear operator

$$\begin{aligned} \begin{array} {rccl} \mathcal {A}: &{} \nabla _{\Gamma _s}\textbf{H}^{3/2}(\Gamma _s) &{} \rightarrow &{} \nabla _{\Gamma _s}\textbf{H}^{3/2}(\Gamma _s) \\ &{} \nabla _{\Gamma _s} Z &{} \mapsto &{} \mu \nabla _{\Gamma _s} \mathcal {P}_{\Gamma _s}({{\,\textrm{div}\,}}_{\Gamma _s}\nabla _{\Gamma _s} Z) \end{array}, \end{aligned}$$

(28)

with domain $D(\mathcal {A}):=\nabla _{\Gamma _s}\textbf{H}^{5/2}(\Gamma _s)$, is self-adjoint. For $\nabla _{\Gamma _s} Z \in \nabla _{\Gamma _s}\textbf{H}^{\ell }(\Gamma _s)$ we consider the norm $\Vert \nabla _{\Gamma _s} Z \Vert _{\mathbb {H}^{\ell -1}(\Gamma _s)}$, with $\ell \ge 1$. Let us derive the fundamental properties of $\mathcal {A} = \mu \nabla _{\Gamma _s} \mathcal {P}_{\Gamma _s} {{\,\textrm{div}\,}}_{\Gamma _s}$.

Proposition 4.4

The operator $(\mathcal {A}, D(\mathcal {A}))$ is self-adjoint, dissipative, and thus infinitesimal generator of an analytic semigroup on $\nabla _{\Gamma _s}\textbf{H}^{5/2}(\Gamma _s)$.

Proof

The Green’s formula (2) shows that $(\nabla _{\Gamma _s})^*$ $= -{{\,\textrm{div}\,}}_{\Gamma _s}$. For $Z_1$,  $Z_2 \in \textbf{H}^{5/2}(\Gamma _s)$ we have

$$\begin{aligned} \begin{array}{rcl} \langle \mathcal {A}\nabla _{\Gamma _s} Z_1 , \nabla _{\Gamma _s} Z_2 \rangle _{\mathbb {L}^2(\Gamma _s)} &{} = &{} \mu \langle \mathcal {P}_{\Gamma _s}({{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z_1) , (\nabla _{\Gamma _s})^{*} \nabla _{\Gamma _s} Z_2 \rangle _{\textbf{L}^2(\Gamma _s)}\\ &{} = &{} -\mu \langle \mathcal {P}_{\Gamma _s}({{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z_1) , {{\,\textrm{div}\,}}_{\Gamma _s}\nabla _{\Gamma _s} Z_2 \rangle _{\textbf{L}^2(\Gamma _s)}\\ &{} = &{} -\mu \langle \mathcal {P}_{\Gamma _s}(\Delta _{\Gamma _s} Z_1) , \Delta _{\Gamma _s} Z_2 \rangle _{\textbf{L}^2(\Gamma _s)}. \end{array} \end{aligned}$$

Using Proposition 4.3, we see that $\mathcal {A}$ is self-adjoint and dissipative. Consequently, from [10, Chapter 1, Proposition 2.11], the operator $(\mathcal {A},D(\mathcal {A}))$ generates an analytic semigroup, completing the proof. $\square$

We prove now that $\mathcal {A}$ is maximal monotone, and has compact resolvent.

Proposition 4.5

The operator $\mathcal {A}$ generates an analytic semigroup of contractions, and has compact resolvent.

Proof

Let us show that there exists $\lambda \in \mathbb {R}$ such that $\lambda \textrm{Id}- \mathcal {A}$ is invertible. Let be $\nabla _{\Gamma _s}W\in \nabla _{\Gamma _s} \textbf{H}^{5/2}(\Gamma _s) \subset \mathbb {H}^{3/2}(\Gamma _s)$ and consider the following resolvent equation:

$$\begin{aligned} \lambda \nabla _{\Gamma _s}Z - \mathcal {A}\nabla _{\Gamma _s}Z = \nabla _{\Gamma _s} W. \end{aligned}$$

(29)

Taking the scalar product of this equation by $\nabla _{\Gamma _s}Z$, and using the Green’s formula (2), we obtain

$$\begin{aligned} \lambda \Vert \nabla _{\Gamma _s}Z \Vert _{\mathbb {L}^2(\Gamma _s)}^2 +\mu \langle \mathcal {P}_{\Gamma _s}({{\,\textrm{div}\,}}_{\Gamma _s}\nabla _{\Gamma _s} Z) , {{\,\textrm{div}\,}}_{\Gamma _s}\nabla _{\Gamma _s}Z\rangle _{\textbf{L}^2(\Gamma _s)} = \langle \nabla _{\Gamma _s} W , \nabla _{\Gamma _s} Z \rangle _{\mathbb {L}^2(\Gamma _s)}. \end{aligned}$$

Further, from the definition of $\mathcal {P}_{\Gamma _s}$, we introduce $u^\pm$ the solution of

$$\begin{aligned} \left\{ \begin{array} {lcl} -{{\,\textrm{div}\,}}\sigma (u^\pm ,p^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0 &{} &{} \text {in } \Omega _s^\pm , \\ u^+ = 0 &{} &{} \text {on } \partial \Omega , \\ \left[ u\right] = 0 \quad \text { and } \quad -\left[ \sigma (u,p)\right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z &{} &{} \text {on } \Gamma _s, \end{array} \right. \end{aligned}$$

(30)

and by integration by parts we deduce

$$\begin{aligned} \lambda \Vert \nabla _{\Gamma _s}Z \Vert _{\mathbb {L}^2(\Gamma _s)}^2 + 2\nu \left( \Vert \varepsilon (u^+)\Vert ^2_{\mathbb {L}^2(\Omega ^+)}+ \Vert \varepsilon (u^-)\Vert ^2_{\mathbb {L}^2(\Omega ^-)} \right) = \langle \nabla _{\Gamma _s} W , \nabla _{\Gamma _s} Z \rangle _{\mathbb {L}^2(\Gamma _s)}. \end{aligned}$$

(31)

Introduce the bilinear form

$$\begin{aligned} \begin{array} {rccl} a: &{} \nabla _{\Gamma _s} \textbf{H}^1(\Gamma _s) \times \nabla _{\Gamma _s} \textbf{H}^1(\Gamma _s) &{} \rightarrow &{} \mathbb {R}\\ &{} (\nabla _{\Gamma _s} Z_1 , \nabla _{\Gamma _s} Z_2) &{} \mapsto &{} \lambda \langle \nabla _{\Gamma _s}Z_1, \nabla _{\Gamma _s}Z_2 \rangle _{\mathbb {L}^2(\Gamma _s)}\\ &{} &{} &{} + 2\nu \left( \langle \varepsilon (u_1^+),\varepsilon (u_2^+\rangle _{\mathbb {L}^2(\Omega ^+)}+ \langle \varepsilon (u_1^-), \varepsilon (u_2^-)\rangle _{\mathbb {L}^2(\Omega ^-)} \right) , \end{array} \end{aligned}$$

where $u_1^\pm$ and $u_2^\pm$ are solutions of (30) corresponding to $Z=Z_1$ and $Z= Z_2$, respectively. It satisfies

$$\begin{aligned} a(\nabla _{\Gamma _s}Z,\nabla _{\Gamma _s}Z) \ge \lambda \Vert \nabla _{\Gamma _s} Z \Vert _{\mathbb {L}^2(\Gamma _s)}^2 , \end{aligned}$$

and thus, for $\lambda >0$, it is coercive. From Proposition 4.4, it is sufficient to study the resolvent equation (29) for $\lambda =1$ for example. Introduce the linear form $b:\nabla _{\Gamma _s} \textbf{H}^1(\Gamma _s) \ni \nabla _{\Gamma _s} Z \mapsto \langle \nabla _{\Gamma _s} W, \nabla _{\Gamma _s} Z \rangle _{\mathbb {L}^2(\Gamma _s)}$, which is clearly continuous. We consider the variational formulation of (29) as follows:

$$\begin{aligned} \text {Find }\nabla _{\Gamma _s}Z\,\in \,\nabla _{\Gamma _s}\textbf{H}^1(\Gamma _s) \text { such that }a(\nabla _{\Gamma _s}Z,\,\nabla _{\Gamma _s}\,\tilde{Z})\,=\, b(\nabla _{\Gamma _s}\tilde{Z})\text { for all }\nabla _{\Gamma _s}\tilde{Z} \in \,\nabla _{\Gamma _s}\textbf{H}^1(\Gamma _s). \end{aligned}$$

(32)

From the Lax-Milgram theorem there exists a unique $\nabla _{\Gamma _s}Z \in \nabla _{\Gamma _s}\textbf{H}^1(\Gamma _s)$ solution of (32), and so satisfying (29). Note that it is sufficient to assume $\nabla _{\Gamma _s} W \in \nabla _{\Gamma _s}\textbf{H}^1(\Gamma _s)$ for obtaining $\nabla _{\Gamma _s}Z \in \nabla _{\Gamma _s} \textbf{H}^1(\Gamma _s)$. Choosing $\nabla _{\Gamma _s}\tilde{Z}= \nabla _{\Gamma _s} Z$ in (32), with the Cauchy-Schwarz inequality we get the following estimate

$$\begin{aligned} \Vert \nabla _{\Gamma _s} Z\Vert _{\mathbb {L}^2(\Gamma _s)} \le C \Vert \nabla _{\Gamma _s} W\Vert _{\mathbb {L}^2(\Gamma _s)}. \end{aligned}$$

(33)

Next, if we assume $\nabla _{\Gamma _s} W \in \nabla _{\Gamma _s} \textbf{H}^{2}(\Gamma _s)$, let us prove that $\nabla _{\Gamma _s} Z \in \nabla _{\Gamma _s} \textbf{H}^{2}(\Gamma _s)$ too. Since $\nabla _{\Gamma _s}Z \in \nabla _{\Gamma _s} \textbf{H}^1(\Gamma _s)$, the identity

$$\begin{aligned} -\mathcal {A} \nabla _{\Gamma _s}Z = \nabla _{\Gamma _s} W -\nabla _{\Gamma _s}Z \end{aligned}$$

yields

$$\begin{aligned} \Vert \nabla _{\Gamma _s} \mathcal {P}_{\Gamma _s} {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z\Vert _{\mathbb {L}^2(\Gamma _s)} = \Vert \mathcal {A} \nabla _{\Gamma _s} Z\Vert _{\mathbb {L}^2(\Gamma _s)} \le \Vert \nabla _{\Gamma _s} W\Vert _{\mathbb {L}^2(\Gamma _s)} + \Vert \nabla _{\Gamma _s} Z \Vert _{\mathbb {L}^2(\Gamma _s)} \le C\Vert \nabla _{\Gamma _s} W\Vert _{\mathbb {L}^2(\Gamma _s)}, \end{aligned}$$

(34)

where we used (33). Therefore $\mathcal {P}_{\Gamma _s} {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z \in \textbf{H}^1(\Gamma _s)$, which means that $u^\pm _{|\Gamma _s} \in \textbf{H}^1(\Gamma _s)$ in system (30), leading to $u^\pm \in \textbf{H}^{3/2}(\Omega _s^\pm )$, and consequently to $-\left[ \sigma (u,p)\right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z \in \textbf{L}^2(\Gamma _s)$. Furthermore, using classical elliptic estimates for Stokes problems with prescribed non-homogeneous Dirichlet boundary conditions (see [29, Lemma 6.1, Chapter IV], the estimates in fractional spaces can be obtained by linear interpolation), we estimate

$$\begin{aligned} \begin{array} {rcl} \Vert \Delta _{\Gamma _s}Z \Vert _{\textbf{L}^2(\Gamma _s)} = \Vert {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z\Vert _{\textbf{L}^2(\Gamma _s)} &{} = &{} \Vert \left[ \sigma (u,p)\right] n_s \Vert _{\textbf{L}^2(\Gamma _s)} \\ &{} \le &{} C \left( \Vert u\Vert _{\textbf{H}^{3/2}(\Omega _s^\pm )/\mathbb {R}^2} + \Vert \nabla p\Vert _{\textrm{H}^{-1/2}(\Omega _s^\pm )/\mathbb {R}^2} \right) \\ &{} \le &{} C\Vert u^\pm _{|\Gamma _s} \Vert _{\textbf{H}^1(\Gamma _s)/\mathbb {R}^2} = C\Vert \mathcal {P}_{\Gamma _s} {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s}Z \Vert _{\textbf{H}^1(\Gamma _s)/\mathbb {R}^2} \\ &{} \le &{} C\Vert \nabla _{\Gamma _s} \mathcal {P}_{\Gamma _s} {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s}Z \Vert _{\mathbb {L}^2(\Gamma _s)} = C\Vert \mathcal {A} \nabla _{\Gamma _s}Z \Vert _{\mathbb {L}^2(\Gamma _s)} \\ &{} \le &{} C\Vert \nabla _{\Gamma _s} W\Vert _{\mathbb {L}^2(\Gamma _s)}, \end{array} \end{aligned}$$

where we have used the Poincaré inequality (5) and estimate (34) above. Next, using (8), we deduce

$$\begin{aligned} \Vert \nabla _{\Gamma _s} Z \Vert _{\mathbb {H}^1(\Gamma _s)} \le \Vert Z\Vert _{\textbf{H}^2(\Gamma _s)/\mathbb {R}^2} \le C\Vert \nabla _{\Gamma _s} W \Vert _{\mathbb {L}^2(\Gamma _s)}. \end{aligned}$$

(35)

We proceed similarly in order to estimate

$$\begin{aligned} \begin{array} {rcl} \Vert \nabla _{\Gamma _s} Z\Vert _{\mathbb {H}^2(\Gamma _s)} \le \Vert Z\Vert _{\textbf{H}^3(\Gamma _s)} \le \Vert \Delta _{\Gamma _s}Z \Vert _{\textbf{H}^1(\Gamma _s)} &{} = &{} \Vert \left[ \sigma (u,p)\right] n_s \Vert _{\textbf{H}^1(\Gamma _s)} \\ &{} \le &{} C \left( \Vert u\Vert _{\textbf{H}^{5/2}(\Omega _s^\pm )/\mathbb {R}^2} + \Vert \nabla p\Vert _{\textrm{H}^{1/2}(\Omega _s^\pm )/\mathbb {R}^2} \right) \\ &{} \le &{} C\Vert u^\pm _{|\Gamma _s} \Vert _{\textbf{H}^2(\Gamma _s)/\mathbb {R}^2} = C\Vert \mathcal {P}_{\Gamma _s} {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s}Z \Vert _{\textbf{H}^2(\Gamma _s)/\mathbb {R}^2} \\ &{} \le &{} C\Vert \nabla _{\Gamma _s} \mathcal {P}_{\Gamma _s} {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s}Z \Vert _{\mathbb {H}^1(\Gamma _s)} = C\Vert \mathcal {A} \nabla _{\Gamma _s}Z \Vert _{\mathbb {H}^1(\Gamma _s)}. \end{array} \end{aligned}$$

Again, the identity $-\mathcal {A} \nabla _{\Gamma _s}Z = \nabla _{\Gamma _s} W - \nabla _{\Gamma _s}Z$ yields

$$\begin{aligned} \Vert \mathcal {A} \nabla _{\Gamma _s} Z\Vert _{\mathbb {H}^1(\Gamma _s)} \le \Vert \nabla _{\Gamma _s} W\Vert _{\mathbb {H}^1(\Gamma _s)} + \Vert \nabla _{\Gamma _s} Z \Vert _{\mathbb {H}^1(\Gamma _s)} \le C\Vert \nabla _{\Gamma _s} W\Vert _{\mathbb {H}^1(\Gamma _s)}, \end{aligned}$$

where we have used (35), and thus we deduce

$$\begin{aligned} \Vert \nabla _{\Gamma _s} Z\Vert _{\mathbb {H}^2(\Gamma _s)} \le C \Vert \nabla _{\Gamma _s} W\Vert _{\mathbb {H}^1(\Gamma _s)}. \end{aligned}$$

(36)

Combining (35) and (36), by interpolation we obtain

$$\begin{aligned} \Vert \nabla _{\Gamma _s} Z\Vert _{\mathbb {H}^{3/2}(\Gamma _s)} \le C \Vert \nabla _{\Gamma _s} W\Vert _{\mathbb {H}^{1/2}(\Gamma _s)}, \end{aligned}$$

which proves that $\textrm{Id}- \mathcal {A}$ is surjective. Hence, from the Lumer-Phillips theorem, the analytic semigroup that $\mathcal {A}$ generates is of contractions. Further, since the embedding $\nabla _{\Gamma _s} \textbf{H}^{5/2} \hookrightarrow \nabla _{\Gamma _s} \textbf{H}^{3/2}$ is compact, the last estimate above shows that the resolvent $(\textrm{Id}-\mathcal {A})^{-1}$ exists and is compact, which completes the proof. $\square$

We deduce wellposedness for system (26).

Theorem 4.1

Let be $0<T<\infty$. For $G \in \mathcal {G}_T(\Gamma _s)$ and $Z_0 \in \mathcal {Z}_0(\Gamma _s)$, the following system

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}(u^\pm , p^\pm ) = 0, \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0 &{} &{} \text {in } \Omega _s^\pm \times (0,T), \\ u^+ = 0 &{} &{} \text {on } \partial \Omega \times (0,T), \\ u^\pm = \displaystyle \frac{\partial Z}{\partial t} \quad \text { and } \quad -\left[ \sigma (u,p)\right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z + G &{} &{} \text {on } \Gamma _s \times (0,T), \\ Z(\cdot ,0) = Z_0 &{} &{} \text {on } \Gamma _s, \end{array} \end{aligned}$$

admits a unique solution $Z\in \mathcal {Z}_T(\Gamma _s)$. Moreover, there exists a constant $C>0$, non-decreasing with respect to T, such that

$$\begin{aligned} \Vert Z \Vert _{\mathcal {Z}_T(\Gamma _s)} + \Vert Z \Vert _{\textrm{L}^{\infty }(0,T;\textbf{H}^2(\Gamma _s))} \le C \left( \Vert Z_0\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert G \Vert _{\mathcal {G}_T(\Gamma _s)} \right) . \end{aligned}$$

Proof

See for example [65, Proposition 3.3], that provides for (27) existence and uniqueness of $\nabla _{\Gamma _s} Z$ satisfying

$$\begin{aligned} \Vert \nabla _{\Gamma _s} Z \Vert _{\textrm{L}^{2}(0,T;\mathbb {H}^{3/2}(\Gamma _s))\cap \textrm{H}^{1}(0,T;\mathbb {H}^{1/2}(\Gamma _s))} + \Vert \nabla _{\Gamma _s} Z \Vert _{\textrm{L}^{\infty }(0,T;\mathbb {H}^1(\Gamma _s))} \le C \left( \Vert Z_0\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert G \Vert _{\mathcal {G}_T(\Gamma _s)} \right) . \end{aligned}$$

From $\nabla _{\Gamma _s} Z$, we retrieve Z up to a constant, by using estimates (5)–(7) of Proposition 2.1, leading to the announced result. $\square$

4.3 The Non-homogeneous System

We now address system (22) in finite-time horizon, for general right-hand-sides, and any $\lambda \ge 0$.

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = F^\pm \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = {{\,\textrm{div}\,}}H^\pm &{} &{} \text {in } \Omega _s^\pm \times (0,T), \\ u^+ = 0 &{} &{}\text {on } \partial \Omega \times (0,T), \\ u^+ = u^- = \displaystyle \frac{\partial Z}{\partial t} - \lambda Z \quad \text { and } \quad -\left[ \sigma (u,p) \right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z + G &{} &{} \text {on } \Gamma _s \times (0,T), \\ Z(\cdot ,0 ) = Z_0 &{} &{} \text {on } \Gamma _s. \end{array} \end{aligned}$$

(37)

With $0<T<\infty$, we assume that $F^\pm \in \mathcal {F}_T(\Omega _s^\pm )$, $G \in \mathcal {G}_T(\Gamma _s)$, $H^\pm \in \mathcal {U}_T(\Omega _s^\pm )$, and $Z_0 \in \mathcal {Z}_0(\Gamma _s)$. We use a lifting method: Let us describe a solution of (37) as

$$\begin{aligned} u^\pm = v^\pm + w^\pm , \quad p^\pm = q^\pm + \pi ^\pm , \end{aligned}$$

where $(w^\pm , \pi ^\pm )$ are solutions of the following Stokes problems

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}(w^\pm , \pi ^\pm ) = F^\pm \quad \text { and } \quad {{\,\textrm{div}\,}}w^\pm = {{\,\textrm{div}\,}}H^\pm &{} &{} \text {in } \Omega _s^\pm \times (0,T), \\ w^+ = 0 &{} &{}\text {on } \partial \Omega \times (0,T), \\ w^+ = w^- = 0 &{} &{} \text {on } \Gamma _s \times (0,T), \end{array} \end{aligned}$$

(38)

and $(v^\pm , q^\pm )$ satisfy

$$\begin{aligned} \begin{array} {llll} -{{\,\textrm{div}\,}}\sigma (v^\pm , q^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}v^\pm = 0 &{} &{} \text {in } \Omega _s^\pm \times (0,T), \\ v^+ = 0 &{} &{}\text {on } \partial \Omega \times (0,T), \\ v^+ = v^- = \displaystyle \frac{\partial Z}{\partial t} - \lambda Z \quad \text { and } \quad -\left[ \sigma (v,q) \right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s}\nabla _{\Gamma _s} Z + G + \left[ \sigma (w,\pi ) \right] n_s &{} &{} \text {on } \Gamma _s \times (0,T), \\ Z(\cdot ,0 ) = Z_0 &{} &{} \text {on } \Gamma _s. \end{array} \end{aligned}$$

(39)

Note that the equations of (38) are uncoupled, as both Stokes systems can be considered in $\Omega _s^+$ and $\Omega _s^-$ independently. By considering $\overline{w}^\pm := w^\pm - H^\pm$, we eliminate the non-homogeneous divergence condition, and we reduce (38) to standard Stokes problems with non-homogeneous Dirichlet condition:

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (\overline{w}^\pm , \pi ^\pm ) = F^\pm + 2\nu {{\,\textrm{div}\,}}\varepsilon (H^\pm ) \quad \text { and } \quad {{\,\textrm{div}\,}}\overline{w}^\pm = 0 &{} &{} \text {in } \Omega _s^\pm , \\ \overline{w}^+ = 0 &{} &{}\text {on } \partial \Omega , \\ \overline{w}^\pm = - H^\pm &{} &{} \text {on } \Gamma _s. \end{array} \end{aligned}$$

(40)

It is well-known that for almost every $t\in (0,T)$ there exists a unique solution $(\overline{w}^\pm ,\pi ^\pm )$ satisfying

$$\begin{aligned} \Vert \overline{w}^\pm \Vert ^2_{\textbf{H}^{2}(\Omega _s^\pm )} + \Vert \pi \Vert ^2_{\textbf{H}^1(\Omega _s^\pm )/\mathbb {R}} \le C\left( \Vert F^\pm \Vert ^2_{\textbf{L}^2(\Omega _s^\pm )} + \Vert {{\,\textrm{div}\,}}\varepsilon (H^\pm )\Vert ^2_{\textbf{L}^2(\Omega _s^\pm )} + \Vert H^\pm \Vert ^2_{\textbf{H}^{3/2}(\Gamma _s)} \right) . \end{aligned}$$

See for example [29, Lemma 6.1, Chapter IV]. We deduce the same estimate for $(w^\pm ,\pi ) = (\overline{w}^\pm + H^\pm , \pi )$. Further, integrating in time this estimate, it follows from the trace theorem the following estimate

$$\begin{aligned} \Vert \left[ \sigma (w,\pi ) \right] n_s \Vert _{\mathcal {G}_T(\Gamma _s)} \le C\left( \Vert F^\pm \Vert _{\mathcal {F}_T(\Omega _s^\pm )} + \Vert H^\pm \Vert _{\mathcal {U}_T(\Omega _s^\pm )} \right) . \end{aligned}$$

(41)

On the other side, equation (39) admits the following operator formulation

$$\begin{aligned} \frac{\partial Z}{\partial t} - \lambda Z - \mathcal {P}_{\Gamma _s}(\mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z) = \mathcal {P}_{\Gamma _s}\big (G + \left[ \sigma (w,\pi ) \right] n_s \big ) \quad \text {in (0,T),} \quad Z(0) = Z_0. \end{aligned}$$

Following Proposition 4.5 and Theorem 4.1, system (39) admits a unique solution, satisfying

$$\begin{aligned} \Vert Z \Vert _{\mathcal {Z}_T(\Gamma _s)} \le C\left( \Vert Z_0\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert G\Vert _{\mathcal {G}_T(\Gamma _s)} + \Vert \left[ \sigma (w,\pi )\right] n_s\Vert _{\mathcal {G}_T(\Gamma _s)} \right) . \end{aligned}$$

Combined with (41), this estimate yields

$$\begin{aligned} \Vert Z \Vert _{\mathcal {Z}_T(\Gamma _s)} \le C\left( \Vert Z_0\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert G\Vert _{\mathcal {G}_T(\Gamma _s)} + \Vert F^\pm \Vert _{\mathcal {F}_T(\Omega _s^\pm )} + \Vert H^\pm \Vert _{\mathcal {U}_T(\Omega _s^\pm )} \right) . \end{aligned}$$

(42)

Wellposedness of the linear system (37) is stated as follows:

Proposition 4.6

For $0<T<\infty$, if $F^\pm \in \mathcal {F}_T(\Omega _s^\pm )$, $H^\pm \in \mathcal {U}_T(\Omega _s^\pm )$, $G \in \mathcal {G}_T(\Gamma _s)$ and $Z_0 \in \mathcal {Z}_0(\Gamma _s)$, then there exists a unique solution $Z\in \mathcal {Z}_T(\Gamma _s)$ to system (37). It satisfies (42).

Proof

Existence is provided by the lifting method described above. For proving uniqueness, we use the linearity of the system, and assume $F^\pm = H^\pm = G = Z_0 = 0$. Then from Lemma 2.3 we obtain (11) with $g=0$, namely the following identity

$$\begin{aligned} \frac{\mu }{2}\frac{\textrm{d}}{\textrm{d}t} \Vert \nabla _{\Gamma _s} Z \Vert ^2_{\mathbb {L}^2(\Gamma _s)} +2\nu \left( \Vert \varepsilon (u^+) \Vert ^2_{\mathbb {L}^2(\Omega _s^+)} + \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega _s^-)} \right) = \lambda \Vert \nabla _{\Gamma _s} Z \Vert ^2_{\mathbb {L}^2(\Gamma _s)}. \end{aligned}$$

The Grönwall’s lemma combined with $Z_0 =0$ yields $Z\equiv 0$ (up to a constant of $\mathbb {R}^2$), and concludes the proof. $\square$

5 Feedback Operator for the Linear System

This section is devoted to the design of a feedback operator that stabilizes system (22) in infinite time horizon. Let us first study its controllability properties in finite time horizon.

5.1 Approximate Controllability

Let be $0<T<\infty$. We consider system (22) with control G, with null data and initial condition:

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (u^\pm ,p^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = 0 &{} &{} \text {in } \Omega _s^\pm \times (0,T), \\ u^+ = 0 &{} &{} \text {on } \partial \Omega \times (0,T), \\ u^\pm = \displaystyle \frac{\partial Z}{\partial t} \quad \text { and } \quad -\left[ \sigma (u,p)\right] n = \mu \Delta _{\Gamma _s} Z + G &{} &{} \text {on } \Gamma _s \times (0,T), \\ Z(\cdot ,0) = 0 &{} &{} \text {on } \Gamma _s. \end{array} \end{aligned}$$

(43)

Recall the definition of approximate controllability and exact controllability for linear evolution equations of type (43), that we state in our context as follows:

Definition 5.1

Define the reachable set as

$$\begin{aligned} R(T) := \left\{ Z(\cdot ,T)\text { such that }Z\text { is solution of }(43) \mid G \in \mathcal {G}_T(\Gamma _s) \right\} . \end{aligned}$$

We say that system (43) is approximately controllable if R(T) is dense in $\textbf{L}^2(\Gamma _s)/\mathbb {R}^2$, or equivalently if $R(T)^{\perp } = \mathbb {R}^2$. We say that (43) is exactly controllable if $R(T)=\textbf{L}^2(\Gamma _s)/\mathbb {R}^2$.

We obtain the following key result:

Proposition 5.1

System (43) is approximately controllable.

Proof

Introduce $Z_T \in R(T)^\perp$, and the following adjoint system

$$\begin{aligned} \begin{array} {rcl} \displaystyle - {{\,\textrm{div}\,}}\sigma (\phi ^\pm , \psi ^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}\phi ^\pm = 0 &{} &{} \text {in } \Omega _s^\pm \times (0,T),\\ \phi ^+ = 0 &{} &{} \text {on } \partial \Omega \times (0,T), \\ \phi ^\pm = \displaystyle -\frac{\partial \zeta }{\partial t} \quad \text { and } \quad -\left[ \sigma (\phi , \psi )\right] n_s = \mu \Delta _{\Gamma _s} \zeta &{} &{} \text {on } \Gamma _s \times (0,T), \\ \zeta (T) = Z_T &{} &{} \text {on }\Gamma _s, \end{array} \end{aligned}$$

(44)

with $(\phi ^+,\psi ^+, \phi ^-, \psi ^-, \zeta )$ as unknowns. Now consider $(u^+, p^+, u^-,p^-, Z)$ the solution of (43). Taking the inner product in $\textrm{L}^2(0,T;\textbf{L}^2(\Omega _s^\pm ))$ of the left equation in the first line of (44) by $u^\pm$, by integration by parts we obtain for all $G \in \mathcal {G}_T(\Gamma _s)$

$$\begin{aligned} \mu \left\langle \nabla _{\Gamma _s} Z_T, \nabla _{\Gamma _s} Z(T)\right\rangle _{\mathbb {L}^2(\Gamma _s)} = \int _0^T \left\langle G, \frac{\partial \zeta }{\partial t}\right\rangle _{\textbf{L}^2(\Gamma _s)} \textrm{d}t. \end{aligned}$$

Since $Z_T \in R(T)^\perp$, this identity implies that $\displaystyle \frac{\partial \zeta }{\partial t} = 0$ in $\textrm{L}^2(0,T;\textbf{L}^2(\Gamma _s))$. System (44) then becomes system (9) of Lemma 2.2, which yields that $\zeta$ is a constant of $\mathbb {R}^2$, and therefore $Z_T$ too, completing the proof. $\square$

5.2 Feedback Operator

Theorem 5.1

For all $\lambda >0$ and $Z_0 \in \mathcal {Z}_0(\Gamma _s)$, there exists a finite-dimensional subspace $\mathbb {H}_u^{(\lambda )}$ of $\nabla _{\Gamma _s}\textbf{H}^{5/2}(\Gamma _s)$, with orthogonal projection $P_{\lambda }: \nabla _{\Gamma _s}\textbf{H}^{5/2}(\Gamma _s) \rightarrow \mathbb {H}_u^{(\lambda )}$, a finite-dimensional space $\Xi \subset \textbf{H}^{1/2}(\Gamma _s)$ and a linear operator $\Pi _{\lambda } \in \mathcal {L}\left( \mathbb {H}_u^{(\lambda )}, (\mathbb {H}_u^{(\lambda )})^{*}\right)$ defining the feedback operator

$$\begin{aligned} \mathcal {K}_{\lambda } := -\mathcal {P}_{\Gamma _s} (\nabla _{\Gamma _s})^{*}\Pi _{\lambda }P_{\lambda } \in \mathcal {L} \left( \nabla _{\Gamma _s}\textbf{H}^{5/2}(\Gamma _s) , \Xi \right) \end{aligned}$$

such that the solution Z of system (22) with $G = \mathcal {K}_{\lambda }\nabla _{\Gamma _s}Z$ satisfies $\left\| Z \right\| _{\mathcal {Z}_{\infty }(\Gamma _s)} \le C_0$, where the constant $C_0$ depends only on $Z_0$. Further, the operator $\Pi _{\lambda }$ is the solution of the following finite-dimensional algebraic Riccati equation

$$\begin{aligned} \Pi _{\lambda } = \Pi _{\lambda }^{*} \succeq 0, \quad \Pi _{\lambda } \mathcal {A}_{\lambda } + \mathcal {A}_{\lambda }^{*} \Pi _{\lambda } - \Pi _{\lambda } \mathcal {B}_{\lambda } \mathcal {B}_{\lambda }^{*} \Pi _{\lambda } + \textrm{I}= 0, \end{aligned}$$

(45)

where we have introduced $\mathcal {A}_{\lambda } = P_{\lambda }\mathcal {A} P_{\lambda } \in \mathcal {L}(\mathbb {H}_u^{(\lambda )}, \mathbb {H}_u^{(\lambda )})$ and $\mathcal {B}_{\lambda } = P_{\lambda }\nabla _{\Gamma _s} \mathcal {P}_{\Gamma _s} \in \mathcal {L}(\textbf{H}^{1/2}(\Gamma _s),\mathbb {H}_u^{(\lambda )})$.

Proof

Let us consider the operator formulation of system (22), namely

$$\begin{aligned} \frac{\partial \nabla _{\Gamma _s}Z}{\partial t} - (\mathcal {A}+\lambda \textrm{Id}) \nabla _{\Gamma _s}Z = \nabla _{\Gamma _s}\mathcal {P}_{\Gamma _s}G \quad \text { in } (0,T), \qquad \nabla _{\Gamma _s}Z(0) = \nabla _{\Gamma _s}Z_0, \end{aligned}$$

(46)

where $\mathcal {A}$ is defined in (28). Recall that from $\nabla _{\Gamma _s}Z$ we can retrieve Z (up to a constant) via Proposition 2.1. We can choose $\lambda$ in the resolvent of $\mathcal {A}$, without loss of generality. From Proposition 4.4, the spectrum of $\mathcal {A}$ is a discrete set of complex eigenvalues $(\lambda _i)_{i\in \mathbb {N}}$, contained in an angular domain $\left\{ z\in \mathbb {C}{\setminus } \{0\} \mid \textrm{arg}(\theta - z) \in (-\alpha , \alpha ) \right\}$ where $\theta \in (0, \pi /2)$ and $\alpha \in \mathbb {R}$. We can order them such that

$$\begin{aligned} \dots< \Re (\lambda _{N+1})< - \lambda< \Re (\lambda _{N})< \cdots< \Re (\lambda _{2})< \Re (\lambda _{1}) < 0. \end{aligned}$$

Furthermore, the generalized eigenspace associated with each eigenvalue is of finite dimension (see for instance [38, Chapter III, Theorem 6.29 page 187]). Denoting by $\Lambda (\lambda _i)$ the real generalized eigenspace of $\lambda _i$ or $(\lambda _i, \overline{\lambda _i})$ whether $\Im (\lambda _i) = 0$ or not, respectively, we introduce the Hilbert spaces

$$\begin{aligned} \mathbb {H}_u^{(\lambda )} = \bigoplus _{i=1}^N \Lambda (\lambda _i), \quad \mathbb {H}_s^{(\lambda )} = \bigoplus _{i=N+1}^\infty \Lambda (\lambda _i). \end{aligned}$$

Let us explain what we mean by real generalized eigenspace: If $(e_j(\lambda _i))_{1\le j \le m(\lambda _i)}$ is a basis of the complex generalized eigenspace of $\lambda _i$, where $m(\lambda _i)$ denotes its multiplicity, then $\Lambda (\lambda _i)$ is generated by the family $\left\{ \Re (e_j(\lambda _i)), \Im (e_j(\lambda _i)) \mid 1\le j \le m(\lambda _i)\right\}$. Note that $\mathbb {H}_u^{(\lambda )}$, the space of unstable modes, is of finite dimension. Both $\mathbb {H}_u^{(\lambda )}$ and $\mathbb {H}_s^{(\lambda )}$ are invariant under $\mathcal {A}$. Denote by $P_{\lambda }$ the orthogonal projection on $\mathbb {H}_u^{(\lambda )}$, parallel to $\mathbb {H}_s^{(\lambda )}$. Projecting equation (46), with $\lambda = 0$, on $\mathbb {H}_u^{(\lambda )}$ yields

$$\begin{aligned} \frac{\partial P_{\lambda }\nabla _{\Gamma _s}Z}{\partial t} - P_{\lambda }\mathcal {A}P_{\lambda }\nabla _{\Gamma _s}Z = P_{\lambda } \nabla _{\Gamma _s}\mathcal {P}_{\Gamma _s}G \quad \text { in } (0,T), \qquad P_{\lambda }\nabla _{\Gamma _s}Z(0) = P_{\lambda } \nabla _{\Gamma _s}Z_0. \end{aligned}$$

(47)

The approximate controllability of system (43) obtained in Proposition 5.1 implies that (47) too is approximately controllable. Its reachable set is dense in $\mathbb {H}_u^{(\lambda )}$, and since this space is of finite dimension, it is actually equal to $\mathbb {H}_u^{(\lambda )}$. This means that equation (47) is exactly controllable. From there, we use for instance the result of [70, Chapter I, Theorem 2.9, page 35] stating that there exists a linear operator $K_{\lambda }$ defined on $\mathbb {H}_u^{(\lambda )}$ such that $P_{\lambda }\mathcal {A}P_{\lambda } + P_{\lambda } \nabla _{\Gamma _s}\mathcal {P}_{\Gamma _s} K_{\lambda }$ is exponentially stable with $\lambda$ as a decay rate. Since the same property holds for $\mathcal {A}(\textrm{Id}- P_{\lambda })$, we merely set $\mathcal {K}_{\lambda } = \Re K_{\lambda }P_{\lambda }$ and $\Xi = \Re K_{\lambda }(\mathbb {H}_u^{(\lambda )})$. Further, following [62] (more specifically Lemma 8.4.1 page 381 and Theorem 41 page 384), we consider the following infinite time horizon optimal control problem:

$$\begin{aligned} \displaystyle \inf _{G\in \Xi } \left\{ \mathcal {J}(Z,G)\mid \,Z\text { satisfies }(43) \right\} , \end{aligned}$$

(48)

with $\mathcal {J}(Z,G) = \displaystyle \frac{1}{2}\int _0^\infty \Vert P_{\lambda }\nabla _{\Gamma _s}Z\Vert _{\mathbb {H}_u^{(\lambda )}}^2 \textrm{d}t + \frac{1}{2} \int _0^{\infty } \Vert G\Vert _{\Xi }^2 \textrm{d}t$. The first-order optimality conditions for Problem (48) lead to $G = - \mathcal {P}_{\Gamma _s}^{*}(\nabla _{\Gamma _s})^{*} \Pi _{\lambda } P_{\lambda } \nabla _{\Gamma _s}Z =\mathcal {P}_{\Gamma _s} {{\,\textrm{div}\,}}_{\Gamma _s} \Pi _{\lambda } P_{\lambda } \nabla _{\Gamma _s}Z$, where $\Pi _{\lambda } = \Pi _{\lambda }^{*} \succeq 0$ satisfies the Riccati equation (45), finishing the proof. $\square$

We deduce an estimate for the stabilized linear system with non-homogeneous right-hand-sides.

Corollary 5.1

Assume $Z_0 \in \mathcal {Z}_0(\Gamma _s)$, $F^\pm \in \mathcal {F}_{\infty }(\Omega _s^\pm )$, $H^\pm \in \mathcal {U}_{\infty }(\Omega _s^\pm )$, and $G \in \mathcal {G}_{\infty }(\Gamma _s)$. Using the feedback operator $\mathcal {K}_{\lambda }$ obtained in Theorem 5.1, there exists a unique solution $Z \in \mathcal {Z}_{\infty }(\Gamma _s)$ to the following system

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = F^\pm \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = {{\,\textrm{div}\,}}H^\pm &{} &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ u^+ = 0 &{} &{}\text {on } \partial \Omega \times (0,\infty ), \\ u^+ = u^- = \displaystyle \frac{\partial Z}{\partial t} - \lambda Z \quad \text { and } \quad -\left[ \sigma (u,p) \right] n = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z + \mathcal {K}_{\lambda }\nabla _{\Gamma _s}Z + G &{} &{} \text {on } \Gamma _s \times (0,\infty ), \\ Z(\cdot ,0 ) = Z_0 &{} &{} \text {on } \Gamma _s, \end{array} \end{aligned}$$

(49)

and it satisfies

$$\begin{aligned} \begin{array} {l} \Vert u^+\Vert _{\mathcal {U}_{\infty }(\Omega _s^+)} + \Vert p^+\Vert _{\mathcal {Q}_{\infty }(\Omega _s^+)} + \Vert u^-\Vert _{\mathcal {U}_{\infty }(\Omega _s^-)} + \Vert p^-\Vert _{\mathcal {Q}_{\infty }(\Omega _s^-)} + \Vert Z\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \\ \quad \le C_s(1+\lambda ) \left( \Vert Z_0\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert F^+\Vert _{\mathcal {F}_{\infty }(\Omega _s^+)} + \Vert F^-\Vert _{\mathcal {F}_{\infty }(\Omega _s^-)} + \Vert H^+\Vert _{\mathcal {U}_{\infty }(\Omega _s^+)} + \Vert H^-\Vert _{\mathcal {U}_{\infty }(\Omega _s^-)} + \Vert G\Vert _{\mathcal {G}_{\infty }(\Gamma _s)} \right) ,\qquad \end{array} \end{aligned}$$

(50)

where the constant $C_s >0$ depends only on $\Gamma _s$.

Proof

The lifting method of Sect. 4.3 can be used here: Introduce $u^\pm = v^\pm + w^\pm$ and $p^\pm = q^\pm + \pi ^\pm$, where $(w^\pm ,\pi ^\pm )$ satisfy the Stokes problems (38) with (0, T) replaced by $(0,\infty )$, and where $(v^\pm , q^\pm , Z)$ satisfies

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (v^\pm , q^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}v^\pm = 0 &{} &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ v^+ = 0 &{} &{}\text {on } \partial \Omega \times (0,\infty ), \\ v^\pm = \displaystyle \frac{\partial Z}{\partial t} - \lambda Z \ \text { and } \ -\left[ \sigma (v,q) \right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z + \mathcal {K}_{\lambda }\nabla _{\Gamma _s}Z + G + \left[ \sigma (w,\pi ) \right] n_s &{} &{} \text {on } \Gamma _s \times (0,\infty ), \\ Z(\cdot ,0 ) = Z_0 &{} &{} \text {on } \Gamma _s. \end{array} \end{aligned}$$

(51)

We formulate system (51) as

$$\begin{aligned} \begin{array} {rcl} \displaystyle \frac{\partial \nabla _{\Gamma _s}Z}{\partial t} -\lambda \nabla _{\Gamma _s}Z - \nabla _{\Gamma _s}\mathcal {P}_{\Gamma _s}(\mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s} Z) - \mathcal {K}_{\lambda } \nabla _{\Gamma _s}Z &{} = &{} \nabla _{\Gamma _s}\mathcal {P}_{\Gamma _s}\left( G+ \left[ \sigma (w,\pi )\right] n_s\right) ,\\ \displaystyle \frac{\partial \nabla _{\Gamma _s}Z}{\partial t} -(\lambda \textrm{Id}+ \mathcal {A} + \mathcal {K}_{\lambda }) \nabla _{\Gamma _s}Z &{} = &{} \nabla _{\Gamma _s}\mathcal {P}_{\Gamma _s}\left( G+ \left[ \sigma (w,\pi )\right] n_s\right) , \end{array} \end{aligned}$$

and since the operator $\lambda \textrm{Id}+ \mathcal {A} + \mathcal {K}_{\lambda }$ is the infinitesimal generator of an analytic semigroup of negative type, a consequence of [10, Theorem 3.1 page 143, Part II] and Proposition 2.1 is the existence of $Z\in \mathcal {Z}_{\infty }(\Gamma _s)$, satisfying

$$\begin{aligned} \Vert Z \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \le C\left( \Vert Z_0\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert G\Vert _{\mathcal {G}_{\infty }(\Gamma _s)} + \Vert \left[ \sigma (w,\pi )\right] n_s\Vert _{\mathcal {G}_{\infty }(\Gamma _s)} \right) . \end{aligned}$$

Next, the steps of Sect. 4.3 can be repeated to obtain the existence and uniqueness of Z, which satisfies

$$\begin{aligned} \Vert Z\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \le C \left( \Vert Z_0\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert F^+\Vert _{\mathcal {F}_{\infty }(\Omega _s^+)} + \Vert F^-\Vert _{\mathcal {F}_{\infty }(\Omega _s^-)} + \Vert H^+\Vert _{\mathcal {U}_{\infty }(\Omega _s^+)} + \Vert H^-\Vert _{\mathcal {U}_{\infty }(\Omega _s^-)} + \Vert G\Vert _{\mathcal {G}_{\infty }(\Gamma _s)} \right) . \end{aligned}$$

(52)

Further, $(u^\pm ,p^\pm )$ are also obtained uniquely as the solutions of the classical Stokes problems with Dirichlet boundary conditions and non-homogeneous divergence condition, namely

$$\begin{aligned} \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (u^\pm , p^\pm ) = F^\pm \quad \text { and } \quad {{\,\textrm{div}\,}}u^\pm = {{\,\textrm{div}\,}}H^\pm &{} &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ u^+ = 0 &{} &{}\text {on } \partial \Omega \times (0,\infty ), \\ u^\pm = \displaystyle \frac{\partial Z}{\partial t} - \lambda Z &{} &{} \text {on } \Gamma _s \times (0,\infty ). \end{array} \end{aligned}$$

Up to considering $u^\pm - H^\pm$, from [29, Lemma 6.1, Chapter IV] they satisfy the estimate

$$\begin{aligned} \begin{array}{rcl} \Vert u^\pm \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} + \Vert p^\pm \Vert _{\mathcal {Q}_{\infty }(\Omega _s^\pm )} &{} \le &{} C \left( \left\| \displaystyle \frac{\partial Z}{\partial t} - \lambda Z\right\| _{\textrm{L}^2(0,\infty ;\textbf{H}^{3/2}(\Gamma _s))} + \Vert H^\pm \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} \right) \\ &{} \le &{} \left( (1+\lambda )\Vert Z\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} + \Vert H^\pm \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} \right) \end{array} \end{aligned}$$

which, combined with (52), leads to (50), and thus the announced result. $\square$

6 Feedback Stabilization of the Nonlinear System

In this section we prove Theorem 1.1. We first prove wellposedness of system (19)–(20) when $\hat{g}$ is replaced by $\mu {{\,\textrm{div}\,}}_{\Gamma _s}\big ( (\tau _s \otimes \tau _s) \nabla _{\Gamma _s}\hat{Z}\big ) + \mathcal {K}_{\lambda } \nabla _{\Gamma _s}\hat{Z}$ in (19):

$$\begin{aligned} \begin{array} {rl} - {{\,\textrm{div}\,}}(\sigma (\hat{u}^\pm , \hat{p}^\pm )) = \hat{f}^\pm + F(\hat{u}^\pm ,\hat{p}^\pm , \hat{Z}) \quad \text { and } \quad {{\,\textrm{div}\,}}\hat{u} = {{\,\textrm{div}\,}}H(\hat{u}^\pm , \hat{Z}) &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ \hat{u}^+ = 0 &{} \text {on } \partial \Omega \times (0,\infty ), \\ \hat{u}^\pm = \displaystyle \frac{\partial \hat{Z}}{\partial t} - \lambda \hat{Z}, \ \text { and } \ -\left[ \sigma (\hat{u},\hat{p})\right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s}\hat{Z} + \mathcal {K}_{\lambda }\nabla _{\Gamma _s} \hat{Z} + G(\hat{u}^+, \hat{p}^+, \hat{u}^-, \hat{p}^-, \hat{Z}) &{} \text {on } \Gamma _s \times (0,\infty ), \\ \hat{Z}(\cdot ,0) = X_0-\textrm{Id}&{} \text {on } \Gamma _s. \end{array} \end{aligned}$$

(53)

Denote

$$\begin{aligned} \mathcal {H}(\Omega _s^+,\Omega _s^-,\Gamma _s) := \mathcal {U}_{\infty }(\Omega _s^+) \times \mathcal {Q}_{\infty }(\Omega _s^+) \times \mathcal {U}_{\infty }(\Omega _s^-) \times \mathcal {Q}_{\infty }(\Omega _s^-) \times \mathcal {Z}_{\infty }(\Gamma _s), \end{aligned}$$

that we equip with the norm that goes without saying. A solution for system (53) is obtained as a fixed point of the mapping

$$\begin{aligned} \begin{array} {rccc} \mathcal {N}: &{} \mathcal {H}(\Omega _s^+,\Omega _s^-,\Gamma _s) &{} \rightarrow &{} \mathcal {H}(\Omega _s^+,\Omega _s^-,\Gamma _s) \\ &{} (\hat{u}_1^+,\hat{p}_1^+,\hat{u}_1^-,\hat{p}_1^-,\hat{Z}_1) &{} \mapsto &{} (\hat{u}_2^+,\hat{p}_2^+,\hat{u}_2^-,\hat{p}_2^-,\hat{Z}_2), \end{array} \end{aligned}$$

where $(\hat{u}_2^+,\hat{p}_2^+,\hat{u}_2^-,\hat{p}_2^-,\hat{Z}_2)$ is the solution of (49) with $F^\pm$, $H^\pm$ and G replaced by $F(\hat{u}_1^\pm ,\hat{p}_1^\pm , \hat{Z}_1)$, $H(\hat{u}_1^\pm , \hat{Z}_1)$ and $G(\hat{u}_1^+, \hat{p}_1^+, \hat{u}_1^-, \hat{p}_1^-, \hat{Z}_1)$, respectively:

$$\begin{aligned} \begin{array} {ll} - {{\,\textrm{div}\,}}(\sigma (\hat{u}_2^\pm , \hat{p}_2^\pm )) = \hat{f}^\pm + F(\hat{u}_1^\pm ,\hat{p}_1^\pm , \hat{Z}_1) \quad \text { and } \quad {{\,\textrm{div}\,}}\hat{u}_2 = H(\hat{u}_1^\pm , \hat{Z}_1) &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ \hat{u}_2^+ = 0 &{} \text {on } \partial \Omega \times (0,\infty ), \\ \hat{u}_2^\pm = \displaystyle \frac{\partial \hat{Z}_2}{\partial t} - \lambda \hat{Z}_2 &{} \text {on } \Gamma _s \times (0,\infty ), \\ -\left[ \sigma (\hat{u}_2,\hat{p}_2)\right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s}\hat{Z}_2 + \mathcal {K}_{\lambda }\nabla _{\Gamma _s} \hat{Z}_2 + G(\hat{u}_1^+, \hat{p}_1^+, \hat{u}_1^-, \hat{p}_1^-, \hat{Z}_1) &{} \text {on } \Gamma _s \times (0,\infty ), \end{array} \end{aligned}$$

Estimate (50) of Corollary 5.1 yields

$$\begin{aligned} \begin{array} {rcl} \Vert (\hat{u}_2^+,\hat{p}_2^+,\hat{u}_2^-,\hat{p}_2^-,\hat{Z}_2)\Vert _{\mathcal {H}(\Omega _s^+,\Omega _s^-,\Gamma _s)} &{} \le &{} C_s(1+\lambda ) \Big ( \Vert X_0-\textrm{Id}\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert \hat{f}^+\Vert _{\mathcal {F}_{\infty }(\Omega _s^+)} + \Vert \hat{f}^-\Vert _{\mathcal {F}_{\infty }(\Omega _s^-)}\\ &{} &{} +\Vert F(\hat{u}_1^+,\hat{p}_1^+, \hat{Z}_1)\Vert _{\mathcal {F}_{\infty }(\Omega _s^+)} + \Vert F(\hat{u}_1^-,\hat{p}_1^-, \hat{Z}_1)\Vert _{\mathcal {F}_{\infty }(\Omega _s^-)} \\ &{} &{} +\Vert H(\hat{u}_1^+, \hat{Z}_1)\Vert _{\mathcal {U}_{\infty }(\Omega _s^+)} + \Vert H(\hat{u}_1^-, \hat{Z}_1)\Vert _{\mathcal {U}_{\infty }(\Omega _s^-)} \\ &{} &{} +\Vert G(\hat{u}_1^+, \hat{p}_1^+, \hat{u}_1^-, \hat{p}_1^-, \hat{Z}_1)\Vert _{\mathcal {G}_{\infty }(\Gamma _s)} \Big ). \end{array} \end{aligned}$$

(54)

Consider the following closed subset of $\mathcal {Z}_{\infty }(\Gamma _s)$

$$\begin{aligned} \begin{array} {rcl} \mathcal {B}_\rho:= & {} \left\{ (\hat{u}^+,\hat{p}^+,\hat{u}^-,\hat{p}^-,\hat{Z}) \in \mathcal {H}_{\infty }(\Omega _s^+,\Omega _s^-,\Gamma _s) \mid \Vert (\hat{u}^+,\hat{p}^+,\hat{u}^-,\hat{p}^-,\hat{Z}\Vert _{\mathcal {H}(\Omega _s^+,\Omega _s^-,\Gamma _s)} \le 2C_s(1+\lambda )\rho \right\} , \end{array} \end{aligned}$$

where

$$\begin{aligned} \rho := \Vert X_0 - \textrm{Id}\Vert _{\mathcal {Z}_0(\Gamma _s)} + \Vert \hat{f}^+ \Vert _{\mathcal {F}_{\infty }(\Omega _s^+)} + \Vert \hat{f}^- \Vert _{\mathcal {F}_{\infty }(\Omega _s^-)}, \end{aligned}$$

and $C_s$ is the constant of estimate (50). Let us prove that $\mathcal {N}$ is a contraction in $\mathcal {B}$, provided that $\Vert X_0-\textrm{Id}\Vert _{\mathcal {Z}_0(\Gamma _s)}$ and $\Vert \hat{f}^\pm \Vert _{\mathcal {F}_{\infty }(\Omega _s^\pm )}$ are small enough. Since the different nonlinearities in the right-hand-side of (54) are polynomial, from [35, Proposition B.1, page 283] we can address them with estimates of type

$$\begin{aligned} \Vert \nabla \tilde{Y}(\tilde{X}) \nabla \hat{u} \Vert _{\mathbb {H}^1(\Omega _s^\pm )} \le C \Vert \nabla \tilde{Y}(\tilde{X}) \Vert _{\mathbb {H}^{3/2}(\Omega _s^\pm )} \Vert \nabla \hat{u} \Vert _{\mathbb {H}^1(\Omega _s^\pm )}. \end{aligned}$$

Combined with the Lipschitz estimates of Proposition 3.1 and Corollary 3.1, we deduce

$$\begin{aligned} \begin{array} {rcl} \Vert F(\hat{u}^\pm ,\hat{p}^\pm , \hat{Z})\Vert _{\textbf{L}^2(\Omega _s^\pm )} &{} \le &{} C\Vert \nabla \tilde{Y}(\tilde{X}) \Vert _{\mathbb {H}^{3/2}(\Omega _s^\pm )} \left( \Vert \nabla \hat{u} \Vert _{\mathbb {H}^1(\Omega _s^\pm )} + \Vert \hat{p} \Vert _{\textrm{H}^1(\Omega _s^\pm )}\right) \Vert \nabla \tilde{X}-\textrm{I}\Vert _{\mathbb {H}^{3/2}(\Omega _s^\pm )}, \\ \Vert F(\hat{u}^\pm ,\hat{p}^\pm , \hat{Z})\Vert _{\mathcal {F}_{\infty }(\Omega _s^\pm )} &{} \le &{} C\left( 1+\Vert X-\textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}\right) \left( \Vert \hat{u} \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )}+ \Vert \hat{p} \Vert _{\mathcal {Q}_{\infty }(\Omega _s^\pm )} \right) \Vert X-\textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \\ &{} \le &{} C\left( 1+\Vert e^{-\lambda t} \hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}\right) \left( \Vert \hat{u} \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )}+ \Vert \hat{p} \Vert _{\mathcal {Q}_{\infty }(\Omega _s^\pm )} \right) \Vert e^{-\lambda t}\hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \\ \Vert H(\hat{u}^\pm , \hat{Z})\Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} &{} \le &{} C\Vert \hat{u} \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} \Vert X-\textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \le C\Vert \hat{u} \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} \Vert e^{-\lambda t}\hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} , \\ \Vert G(\hat{u}^+, \hat{p}^+, \hat{u}^-, \hat{p}^-, \hat{Z})\Vert _{\mathcal {G}_{\infty }(\Gamma _s)} &{} \le &{} C\left( 1+\Vert e^{-\lambda t}\hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}\right) \left( \Vert \hat{u} \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )}+ \Vert \hat{p} \Vert _{\mathcal {Q}_{\infty }(\Omega _s^\pm )} \right) \Vert e^{-\lambda t}\hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}\\ &{} &{} + \mathcal {O}(\Vert \nabla \tilde{X}-I\Vert ^2_{\mathbb {H}^1(\Gamma _s)}) \\ &{} \le &{} C\left( 1+\Vert e^{-\lambda t}\hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}\right) \left( \Vert \hat{u} \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )}+ \Vert \hat{p} \Vert _{\mathcal {Q}_{\infty }(\Omega _s^\pm )} \right) \Vert e^{-\lambda t}\hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}\\ &{} &{} +C\Vert e^{-\lambda t}\hat{Z} \Vert ^2_{\mathcal {Z}_{\infty }(\Gamma _s)} . \end{array} \end{aligned}$$

We see easily that $\Vert e^{-\lambda t}\hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \le C(1+\lambda )\Vert \hat{Z} \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}$. Consequently, if $(\hat{u}_1^+,\hat{p}_1^+,\hat{u}_1^-,\hat{p}_1^-, \hat{Z}_1) \in \mathcal {B}_\rho$, from (54) we obtain

$$\begin{aligned} \begin{array} {rcl} \Vert (\hat{u}_2^+,\hat{p}_2^+,\hat{u}_2^-,\hat{p}_2^-,\hat{Z}_2)\Vert _{\mathcal {H}(\Omega _s^+,\Omega _s^-,\Gamma _s)}\le & {} C_s(1+\lambda )\left( \rho + C\rho ^2(1+\lambda )^3(1+(1+\lambda ) + \rho (1+\lambda )^2) \right) . \end{array} \end{aligned}$$

Therefore $\mathcal {N}$ is well-defined, and if $\rho$ is small enough, that is

$$\begin{aligned} C\rho ^2(1+\lambda )^3(1+(1+\lambda ) + \rho (1+\lambda )^3) \le \rho , \end{aligned}$$

the ball $\mathcal {B}$ is left invariant under $\mathcal {N}$. Next, let be

$$\begin{aligned} (\hat{u}_{i}^+,\hat{p}_{i}^+,\hat{u}_{i}^-,\hat{p}_{i}^-,\hat{Z}_{i}) \in \mathcal {B}_\rho \end{aligned}$$

for $i\in \{1,2\}$. The difference

$$\begin{aligned} (\overline{u}^+,\overline{p}^+,\overline{u}^-,\overline{p}^-,\overline{Z}) := \mathcal {N}(\hat{u}_{1}^+,\hat{p}_{1}^+,\hat{u}_{1}^-,\hat{p}_{1}^-,\hat{Z}_{1})- \mathcal {N}(\hat{u}_{2}^+,\hat{p}_{2}^+,\hat{u}_{2}^-,\hat{p}_{2}^-,\hat{Z}_{2}) \end{aligned}$$

satisfies

$$\begin{aligned} \begin{array} {rcl} - {{\,\textrm{div}\,}}(\sigma (\overline{u}^\pm , \overline{p}^\pm )) = \overline{F}^\pm \quad \text { and } \quad {{\,\textrm{div}\,}}\overline{u} = {{\,\textrm{div}\,}}\overline{H}^\pm &{} &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ \overline{u}^+ = 0 &{} &{} \text {on } \partial \Omega \times (0,\infty ), \\ \overline{u} = \displaystyle \frac{\partial \overline{Z}}{\partial t} - \lambda \overline{Z}, \quad \text { and } \quad -\left[ \sigma (\overline{u},\overline{p})\right] n_s = \mu {{\,\textrm{div}\,}}_{\Gamma _s} \nabla _{\Gamma _s}\overline{Z} + \mathcal {K}_{\lambda }\nabla _{\Gamma _s} \overline{Z} + \overline{G} &{} &{} \text {on } \Gamma _s \times (0,\infty ), \\ \overline{Z}(\cdot ,0) = 0 &{} &{} \text {on } \Gamma _s, \end{array} \end{aligned}$$

(55)

where we have introduced

$$\begin{aligned} \begin{array}{rcl} \overline{F}^\pm &{} := &{} F(\hat{u}_{1}^\pm ,\hat{p}_{1}^\pm , \hat{Z}_1) - F(\hat{u}_{2}^\pm ,\hat{p}_{2}^\pm , \hat{Z}_2), \\ \overline{H}^\pm &{} := &{} H(\hat{u}^\pm _{1}, \hat{Z}_1)-H(\hat{u}^\pm _{2}, \hat{Z}_2), \\ \overline{G} &{} := &{} G(\hat{u}^+_1, \hat{p}^+_1, \hat{u}^-_1, \hat{p}^-_1, \hat{Z}_1) - G(\hat{u}^+_2, \hat{p}^+_2, \hat{u}^-_2, \hat{p}^-_2, \hat{Z}_2). \end{array} \end{aligned}$$

Using the Lipschitz estimates of Proposition 3.1 and Corollary 3.1, they satisfy

$$\begin{aligned} \begin{array} {rcl} \Vert \overline{F}^\pm \Vert _{\mathcal {F}_{\infty }(\Omega _s^\pm )} + \Vert \overline{G}\Vert _{\mathcal {G}_{\infty }(\Gamma _s^\pm )} &{} \le &{} C\left( \Vert e^{-\lambda t}( \hat{Z}_1-\hat{Z}_2)\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} + \Vert \hat{u}_1 - \hat{u}_2\Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} + \Vert \hat{p}_1 - \hat{p}_2\Vert _{\mathcal {Q}_{\infty }(\Omega _s^\pm )} \right) \\ &{} &{} \times \left( \displaystyle \sum _{i=1}^2 \Vert \hat{u}_i \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} + \Vert \hat{p}_i \Vert _{\mathcal {Q}_{\infty }(\Omega _s^\pm )} +\Vert e^{-\lambda t}\hat{Z}_i\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \right) \\ &{} &{} \times \left( 1+ \Vert e^{-\lambda t} \hat{Z}_1\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} + \Vert e^{-\lambda t} \hat{Z}_2\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}\right) ,\\ \Vert \overline{H}^\pm \Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} &{} \le &{} C\left( \Vert e^{-\lambda t}( \hat{Z}_1-\hat{Z}_2)\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} + \Vert \hat{u}_1 - \hat{u}_2\Vert _{\mathcal {U}_{\infty }(\Omega _s^\pm )} \right) \\ &{} &{} \times \left( \Vert \hat{u}_2\Vert _{\mathcal {U}_{\infty }(\Omega ^\pm _s)} +\Vert e^{-\lambda t} \hat{Z}_1\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)} \right) . \end{array} \end{aligned}$$

Combined with estimate (50) of Corollary 5.1, we then obtain

$$\begin{aligned} \begin{array} {rcl} \Vert (\overline{u}^+,\overline{u}^+,\overline{u}^-,\overline{p}^-,\overline{Z}) \Vert _{\mathcal {H}(\Omega _s^+,\Omega _s^-,\Gamma _s)} &{} \le &{} C_s(1+\lambda ) \Big ( \Vert \overline{F}^+\Vert _{\mathcal {F}_{\infty }(\Omega _s^+)} + \Vert \overline{F}^-\Vert _{\mathcal {F}_{\infty }(\Omega _s^-)} \\ &{} &{} +\Vert \overline{H}^+\Vert _{\mathcal {U}_{\infty }(\Omega _s^+)} + \Vert \overline{H}^-\Vert _{\mathcal {U}_{\infty }(\Omega _s^-)} +\Vert \overline{G}\Vert _{\mathcal {G}_{\infty }(\Gamma _s)} \Big ) \\ &{} \le &{} C(1+\lambda )^2\rho (1+(1+\lambda )\rho ) \\ &{} &{} \times \Vert (\hat{u}_{1}^+ -\hat{u}_2^+,\hat{p}_{1}^+-\hat{p}_2^+,\hat{u}_{1}^- -\hat{u}_2^-,\hat{p}_{1}^--\hat{p}_2^-,\hat{Z}_{1}-\hat{Z}_2)\Vert _{\mathcal {H}(\Omega _s^+,\Omega _s^-,\Gamma _s)}. \end{array} \end{aligned}$$

Choosing once again $\rho$ small enough, that is $C(1+\lambda )^2\rho (1+(1+\lambda )\rho ) < 1$, we obtain that $\mathcal {N}$ is a contraction in $\mathcal {B}_\rho$. Therefore wellposedness for (53) is a consequence of the Banach fixed-point theorem. Furthermore, $\Vert \hat{Z}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}$ is bounded. Recall that in (18) we introduced $\hat{Z} = e^{\lambda t} (X-\textrm{Id})$, where $\textrm{Id}$ can be replaced by any deformation $X_c \in \mathcal {C}_{\Gamma _s}$. In (53) we have chosen

$$\begin{aligned} \begin{array} {rcl} \hat{g} &{} = &{} \mu {{\,\textrm{div}\,}}_{\Gamma _s}\big ( (\tau _s \otimes \tau _s) \nabla _{\Gamma _s}\hat{Z}\big ) +\mathcal {K}_{\lambda } \nabla _{\Gamma _s}\hat{Z}\\ &{} = &{} \mu e^{\lambda t} {{\,\textrm{div}\,}}_{\Gamma _s}\big ( (\tau _s \otimes \tau _s)\nabla _{\Gamma _s}(X-X_c)\big ) + e^{\lambda t} \mathcal {K}_{\lambda }\nabla _{\Gamma _s}(X-X_c). \end{array} \end{aligned}$$

Still following Sect. 3.2, we note that system (53) is equivalent to (1) by choosing

$$\begin{aligned} \begin{array} {rcl} g &{} = &{} \big (|\textrm{cof}\nabla \tilde{X} n_s |^{-1} \tilde{g} \big ) \circ X^{-1} = \big (|\textrm{cof}\nabla \tilde{X} n_s |^{-1} e^{-\lambda t}\hat{g} \big ) \circ X^{-1} \\ &{} = &{} \left( |\textrm{cof}\nabla \tilde{X} n_s |^{-1}\left( {{\,\textrm{div}\,}}_{\Gamma _s} \big ( (\tau _s \otimes \tau _s) \nabla _{\Gamma _s} (X-X_c) \big ) + \mathcal {K}_{\lambda }\nabla _{\Gamma _s}(X-X_c) \right) \right) \circ X^{-1}. \end{array} \end{aligned}$$

Since $(\textrm{det}\mathfrak {g}(t))^{1/2}$ $= |\textrm{cof}\nabla \tilde{X} n_s | (\textrm{det}\mathfrak {g}_s)^{1/2}$, and $(\det \mathfrak {g}_s)^{1/2} = 1$ is constant, we consider

$$\begin{aligned} g = \left( (\textrm{det}\mathfrak {g})^{-1/2}\left( {{\,\textrm{div}\,}}_{\Gamma _s} \big ( (\tau _s \otimes \tau _s) \nabla _{\Gamma _s} (X-X_c) \big ) +\mathcal {K}_{\lambda }\nabla _{\Gamma _s}(X-X_c)\right) \right) \circ X^{-1}. \end{aligned}$$

Thus the result announced in Theorem 1.1 follows.

7 Comments on a Possible Extension to Dimension 3

Some results obtained in the present paper could certainly and straightforwardly be extended to the three-dimensional case, like the study of the Poincaré-Steklov operator for example, or the design of the feedback operator. Higher-order Sobolev spaces may be considered for guaranteeing the $C^1$ regularity and stability of Sobolev spaces by product. However, some geometric aspects would deserve a careful investigation. Let us make comments on the difficulties that appear in dimension 3:

• About the stationary state obtained in Lemma 2.1: In dimension 2, the interface $\Gamma (t)$ is a curve, and its mean curvature is simply called the curvature. From the fundamental theorem of curves, this curvature determines entirely $\Gamma (t)$, up to proper rigid deformations. In the case of dimension 3, the interface $\Gamma (t)$ is then a surface, and this is the Gaussian curvature which characterizes the metric of the surface. We say that this is an intrinsic property of the surface $\Gamma (t)$ (cf. the Gauss’s Theorem Egregium). More precisely, two surfaces with the same Gaussian curvature differ only up to proper rigid deformations, we say that they are congruent. The mean curvature which appears in the surface-tension model is only extrinsic in dimension 3, which means that two surfaces with the same mean curvature could not be congruent. However, when restricting the framework to closed surfaces, the Alexandrov’s theorem [3] (see [4] for an English translation) provides a positive result: Two closed surfaces with the same mean curvature are identical, up to essential transformations. Essential transformations refer to proper rigid deformations and dilatation. In the incompressible case, the volume contained inside the surface is constant, and thus this notion reduces to proper rigid deformations, like in dimension 2.

• About the linearized system in dimension 3: Simplifications specific to dimension 2 have been made in Sect. 3.2 when linearizing the mean curvature of $\Gamma (t)$ for small displacements. The expression so obtained involves the operator $\nabla ^{n_s}_{\Gamma _s}$. A priori the linear operator which appears in dimension 3 is more complex, and discussions of Sect. 2.3 about the kernel of $\nabla ^{n_s}_{\Gamma _s}$ would no longer be relevant.

• About the extension of diffeomorphisms on the sphere into the ball: This question is less simple in the case of a 2-sphere. In [69, system (8.3), section 8], the author gave comments on conditions under which we could extend a diffeomorphism defined on a boundary of a given domain. A sufficient condition is that the set of diffeomorphisms of this boundary preserving the orientation is connected. In $\mathbb {R}^2$, this sufficient condition is always fulfilled and thus the answer is positive. In $\mathbb {R}^3$, things are more delicate, and counter-examples to this sufficient condition exist. However, in the case of the sphere, Smale provided a positive answer in [60]. The result requires a $C^\infty$ regularity, and we do not know whether it could be used for obtaining an extension with the same properties as in Sect. 3.1. Further comments on these geometric questions would go beyond the scope of the present article.

A Appendix

1.1 A.1 Proof of Proposition 3.1

Harmonic extension of X. Let us first discuss of how to extend X from the circle $\Gamma _s$ into the unit ball $\Omega _s^-$. In dimension 2, one way of extending diffeomorphisms of the circle is to consider the Douady-Earle extension [26], which is harmonic, and therefore inherits of the elliptic regularity from its Dirichlet boundary condition. It relies on the Radó-Kneser-Choquet theorem, and more specifically the Poisson integral formula. Many generalizations of such a result have been obtained afterwards, in particular requiring the strong Choquet condition, namely that $X(\Gamma _s)$ shall be convex. But more recently it has been extended in [5, 6] to the case of homeomorphisms from the unit circle onto a simple closed curve of $\mathbb {R}^2$. We state [5, Theorem 1.3] in our context as follows:

Lemma A.1

Let $X:\Gamma _s \rightarrow X(\Gamma _s)$ be an orientation preserving diffeomorphism of class $C^1$ onto a simple closed curve $X(\Gamma _s)$. Let D be the bounded domain such that $\partial D = X(\Gamma _s)$. Denote by $X_{\textrm{RKC}}$ the solution of the Dirichlet problem

$$\begin{aligned} \left\{ \begin{array} {rcl} \Delta X_{\textrm{RKC}} = 0 &{} &{} \text {in } \Omega _s^-, \\ X_{\textrm{RKC}} = X &{} &{} \text {on } \Gamma _s. \end{array} \right. \end{aligned}$$

(56)

When $X_{\textrm{RKC}} \in C^1(\overline{\Omega _s^-})$, it is a diffeomorphism of $\overline{\Omega _s^-}$ onto $\overline{D}$ if and only if $\textrm{det}\nabla X_{\textrm{RKC}} >0$ everywhere on $\Gamma _s$.

The condition $X_{\textrm{RKC}} \in C^1(\overline{\Omega _s^-})$ is satisfied when the elliptic regularity of (56) provides a solution in a Sobolev space that is embedded in $C^1(\overline{\Omega _s^-})$, in our case $\textbf{H}^{5/2}(\Omega _s^\pm )$. The condition $\textrm{det}\nabla X_{\textrm{RKC}} >0$ can be guaranteed by assuming the data X close enough to the identity. The estimates provided in the next step shows this.

Elliptic regularity, Lipschitz estimates and invertibility. The interest of extending X via the Dirichlet problem (56) lies in the linearity and simplicity of the latter. Therefore we derive straightforwardly the following result, leading to Proposition 3.1:

Proposition A.1

If $X \in \mathcal {Z}_{\infty }(\Gamma _s)$, the solutions $\tilde{X}^\pm$ of

$$\begin{aligned} \left\{ \begin{array} {rcl} \Delta \tilde{X}^\pm = 0 &{} &{} \text {in } \Omega _s^\pm \times (0,\infty ), \\ \tilde{X}^\pm = X &{} &{} \text {on } \Gamma _s \times (0,\infty ), \\ \tilde{X}^+ = \textrm{Id}&{} &{} \text {on } \partial \Omega \times (0, \infty ), \end{array} \right. \end{aligned}$$

(57)

satisfy

$$\begin{aligned} \Vert \tilde{X}^\pm - \textrm{Id}\Vert _{\mathcal {X}_{\infty }(\Omega _s^\pm )} \le C\Vert X- \textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}. \end{aligned}$$

(58)

If $\Vert X-\textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}$ is small enough, the extension $\tilde{X}^+$ is locally invertible, and $\tilde{X}^-$ is globally invertible. Furthermore, given two mappings $X_1-\textrm{Id}, \, X_2-\textrm{Id}\in \mathcal {Z}_{\infty }(\Gamma _s)$, the respective solutions $\tilde{X}^\pm _1, \, \tilde{X}^\pm _2$ of (57) satisfy

$$\begin{aligned} \Vert \tilde{X}^\pm _1 - \tilde{X}^\pm _2 \Vert _{\mathcal {X}_{\infty }(\Omega _s^\pm )} \le C\Vert X_1 - X_2 \Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}. \end{aligned}$$

(59)

Without ambiguity we omit the notation $\tilde{X}^\pm$ for keeping only $\tilde{X}$.

Proof

Estimates (58) and (59) are straightforwardly deduced from the elliptic regularity of system (57) in $\textbf{H}^{5/2}(\Omega _s^\pm )$. Next, recalling that the differential of $A \mapsto \textrm{det}A$ is $H\mapsto \textrm{cof}(A):H$, and that in dimension 2 the mapping $A\mapsto \textrm{cof}(A)$ is linear, for all $t\ge 0$ we deduce from the mean value theorem

$$\begin{aligned} \begin{array}{rcl} |\textrm{det}\nabla \tilde{X}(y,t) - 1 |_{\mathbb {R}} &{} \le &{} \displaystyle \sup _{\alpha \in [0,1]} |\textrm{cof}(\alpha y + (1-\alpha )\tilde{X}(y,t)) |_{\mathbb {R}^{2\times 2}} | \tilde{X}(y,t) - y |_{\mathbb {R}^{2\times 2}}, \\ \Vert \textrm{det}\nabla \tilde{X}(\cdot ,t) -1 \Vert _{\mathcal {C}(\overline{\Omega _s^\pm })} &{} \le &{} C\left( 1 + \Vert \tilde{X}(\cdot ,t) \Vert _{\textbf{L}^{\infty }(\Omega _s^\pm )} \right) \Vert X-\textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}. \end{array} \end{aligned}$$

Therefore, assuming $\Vert X-\textrm{Id}\Vert _{\mathcal {Z}_{\infty }(\Gamma _s)}$ small enough shows that $\textrm{det}\nabla \tilde{X}(y,t)> C>0$ for all $(y,t) \in \Omega _s \times (0,\infty )$. Then the local invertibility of $\tilde{X}_{|\Omega _s^+}$ is due to the inverse function theorem, and the global invertibility of $\tilde{X}_{|\Omega _s^-}$ follows from Lemma A.1. $\square$

1.2 A.2 Proof of Proposition 4.1 and Corollary 4.1

We start by recalling the two following lemmas that are needed for what follows. The first one can be deduced from [29, Exercise 3.4, Chapter III].

Lemma A.2

For $p^{\pm } \in \textrm{L}^2(\Omega _s^{\pm })$, there exists $v_p^{\pm } \in \textbf{H}^1_0(\Omega _s^{\pm })$ satisfying

$$\begin{aligned} -{{\,\textrm{div}\,}}v_p^{\pm } = p^{\pm } \quad \text {in } \Omega _s^{\pm }, \qquad v_p^{\pm } = 0 \quad \text {on } \partial \Omega _s^{\pm }, \end{aligned}$$

(60)

and

$$\begin{aligned} \Vert v_p^{\pm } \Vert _{\textbf{H}^1(\Omega _s^{\pm })} \le C \Vert p^{\pm }\Vert _{\textrm{L}^2(\Omega _s^{\pm })}. \end{aligned}$$

(61)

The second lemma is given in [29, Theorem 1.1, Chapter IV].

Lemma A.3

For $h^{\pm } \in \textbf{W}$, there exists a unique solution $(v_h^\pm ,q_h^\pm )$ in $\textbf{V}^\pm \times Q^\pm$ to the Stokes problem

$$\begin{aligned} \left\{ \begin{array} {rcl} -{{\,\textrm{div}\,}}\sigma (v_h^\pm ,q_h^\pm ) = 0 \quad \text { and } \quad {{\,\textrm{div}\,}}v_h^\pm = 0 &{} &{} \text {in } \Omega _s^{\pm }, \\ v_h^+ = 0 &{} &{} \text {on } \partial \Omega , \\ v_h^{\pm } = h^{\pm } &{} &{} \text {on } \Gamma _s. \end{array} \right. \end{aligned}$$

(62)

Moreover, it satisfies

$$\begin{aligned} \Vert v_h^{\pm } \Vert _{\textbf{H}^1(\Omega _s^{\pm })} + \Vert q_h^{\pm } \Vert _{\textrm{L}^2(\Omega _s^{\pm })}\le & {} C \Vert h^{\pm }\Vert _{\textbf{H}^{1/2}(\Gamma _s)}. \end{aligned}$$

(63)

We are now in position to prove Proposition 4.1 and Corollary 4.1.

1.2.1 Proof of Proposition 4.1

We adopt the method used for proving [63, Lemma 6, p. 144]. Recall the definition of the bilinear form

$$\begin{aligned} \begin{array} {rcl} \mathcal {M}(\mathfrak {u},\mathfrak {v}) &{} = &{} 2\nu \langle \varepsilon (u^+),\varepsilon (v^+)\rangle _{\mathbb {L}^2(\Omega _s^+)} + 2\nu \langle \varepsilon (u^-),\varepsilon (v^-)\rangle _{\mathbb {L}^2(\Omega _s^-)} \\ &{} &{} - \langle p^+,{{\,\textrm{div}\,}}v^+ \rangle _{\textrm{L}^2(\Omega _s^+)} - \langle q^+{{\,\textrm{div}\,}}u^+ \rangle _{\textrm{L}^2(\Omega _s^+)} - \langle p^-,{{\,\textrm{div}\,}}v^- \rangle _{\textrm{L}^2(\Omega _s^-)} -\langle q^-,{{\,\textrm{div}\,}}u^-\rangle _{\textrm{L}^2(\Omega _s^-)} \\ &{} &{} - \langle \lambda ^+ , v^+-\varphi \rangle _{\textbf{W}';\textbf{W}} - \langle \mu ^+, u^+ - \phi \rangle _{\textbf{W}';\textbf{W}} - \langle \lambda ^- , v^--\varphi \rangle _{\textbf{W}';\textbf{W}} - \langle \mu ^-, u^- - \phi \rangle _{\textbf{W}';\textbf{W}}, \end{array} \end{aligned}$$

with the notation $\mathfrak {u} = (u^+,p^+,u^-,p^-,\lambda ^+,\lambda ^-,\phi )$ and $\mathfrak {v} = (v^+,q^+,v^-,q^-,\mu ^+,\mu ^-,\varphi ) \in \mathfrak {V}$.

Step 1. Choose $\mathfrak {v}_1 = (u^+,-p^+,u^-,-p^-,-\lambda ^+,-\lambda ^-,\phi )$. Then

$$\begin{aligned} \mathcal {M}(\mathfrak {u},\mathfrak {v}_1)= & {} 2\nu \left( \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega _s^+)}^2 + \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega _s^-)}^2\right) . \end{aligned}$$

(64)

Step 2. Choose $\mathfrak {v}_2 = (v^+_p,0,v^-_p,0,0,0,0)$, where $v_p^{\pm } \in \textbf{H}^1_0(\Omega _s^{\pm })$ is the solution of system (60) corresponding to $p^\pm$, satisfying (61). Then, using successively the Cauchy-Schwarz and the Young’s inequalities for any $\alpha >0$, we obtain

$$\begin{aligned} \mathcal {M}(\mathfrak {u},\mathfrak {v}_2)= & {} 2\nu \langle \varepsilon (u^+),\varepsilon (v_p^+)\rangle _{\mathbb {L}^2(\Omega _s^+)} + 2\nu \langle \varepsilon (u^-),\varepsilon (v_p^-)\rangle _{\mathbb {L}^2(\Omega _s^-)} + \Vert p^+\Vert ^2_{\textrm{L}^2(\Omega _s^+)} + \Vert p^-\Vert ^2_{\textrm{L}^2(\Omega _s^-)} \\\ge & {} \Vert p^+\Vert ^2_{\textrm{L}^2(\Omega _s^+)} + \Vert p^-\Vert ^2_{\textrm{L}^2(\Omega _s^-)} - \alpha \nu \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega _s^+)}^2 - \alpha \nu \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega _s^-)}^2 \\{} & {} - \frac{\nu }{\alpha }\Vert \varepsilon (v_p^+) \Vert _{\mathbb {L}^2(\Omega _s^+)}^2 - \frac{\nu }{\alpha }\Vert \varepsilon (v_p^-) \Vert _{\mathbb {L}^2(\Omega _s^-)}^2. \end{aligned}$$

Furthermore, combining the Korn’s inequality for $v_p^{\pm }$ and the estimate (61), we deduce

$$\begin{aligned} \mathcal {M}(\mathfrak {u},\mathfrak {v}_2)\ge & {} \left( 1 - \frac{C\nu }{\alpha } \right) \left( \Vert p^+\Vert ^2_{\textrm{L}^2(\Omega _s^+)} + \Vert p^-\Vert ^2_{\textrm{L}^2(\Omega _s^-)} \right) - \alpha \nu \left( \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega _s^+)}^2 + \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega _s^-)}^2 \right) , \end{aligned}$$

(65)

where the constant $C>0$ is independent of $\alpha >0$.

Step 3. Choose $\mathfrak {v}_3 = (v_{h_n}^+,q_{h_n}^+,v_{h_n}^-,q_{h_n}^-,0,0,0)$, where $(v_{h_n}^{\pm },q_{h_n}^{\pm })$ is the solution of the Stokes system (62) with ${v^{\pm }_{h_n}}_{|\Gamma } = \Vert \lambda ^\pm \Vert _{\textbf{W}'} h_n^\pm$ as data, where the sequences $(h_n^\pm )_n$ are such that $\Vert h_n^\pm \Vert _{\textbf{W}} = 1$ and $-\langle \lambda ^\pm , h_n^\pm \rangle _{\textbf{W}';\textbf{W}} \rightarrow \Vert \lambda ^\pm \Vert _{\textbf{W}'}$. Then for some $\beta >0$, the same combination of the Cauchy-Schwarz and Young’s inequalities yields

$$\begin{aligned} \mathcal {M}(\mathfrak {u},\mathfrak {v}_3)= & {} 2\nu \langle \varepsilon (u^+),\varepsilon (v_{h_n}^+)\rangle _{\mathbb {L}^2(\Omega _s^+)} + 2\nu \langle \varepsilon (u^-),\varepsilon (v_{h_n}^-)\rangle _{\mathbb {L}^2(\Omega _s^-)} \\{} & {} -\langle q_{h_n}^+,{{\,\textrm{div}\,}}u^+ \rangle _{\textrm{L}^2(\Omega _s^-)} -\langle q_{h_n}^-,{{\,\textrm{div}\,}}u^- \rangle _{\textrm{L}^2(\Omega _s^-)} - \langle \lambda ^+,h_n^+ \rangle _{\textbf{W}',\textbf{W}} - \langle \lambda ^-,h_n^- \rangle _{\textbf{W}',\textbf{W}} \\\ge & {} - \langle \lambda ^+,h_n^+ \rangle _{\textbf{W}',\textbf{W}} - \langle \lambda ^-,h_n^- \rangle _{\textbf{W}',\textbf{W}} \\{} & {} -\frac{1}{\beta }\left( \nu \Vert \varepsilon (v_{h_n}^+) \Vert _{\mathbb {L}^2(\Omega _s^+)}^2 + \Vert q^+_{h_n}\Vert ^2_{\textrm{L}^2(\Omega _s^+)} + \nu \Vert \varepsilon (v_{h_n}^-) \Vert _{\mathbb {L}^2(\Omega _s^-)}^2 + \Vert q^-_{h_n}\Vert ^2_{\textrm{L}^2(\Omega _s^-)} \right) \\{} & {} - \beta \left( \nu \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega _s^+)}^2 + \Vert {{\,\textrm{div}\,}}u^+\Vert ^2_{\textrm{L}^2(\Omega _s^+)} + \nu \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega _s^-)}^2 + \Vert {{\,\textrm{div}\,}}u^-\Vert ^2_{\textrm{L}^2(\Omega _s^-)} \right) . \end{aligned}$$

Estimate (63) yields $\Vert v_{h_n} \Vert _{\textbf{H}^1(\Omega _s^\pm )} + \Vert q^\pm _{{h_n}}\Vert _{\textrm{L}^2(\Omega _s^\pm )} \le C\Vert \lambda ^\pm \Vert _{\textbf{W}'}$, and by passing to the limit we deduce

$$\begin{aligned} \mathcal {M}(\mathfrak {u},\mathfrak {v}_3)\ge & {} \left( 1-\frac{C}{\beta } \right) \left( \Vert \lambda ^+ \Vert _{\textbf{W}'}^2 + \Vert \lambda ^- \Vert _{\textbf{W}'}^2 \right) - C\beta \nu \left( \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega ^+)}^2 + \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega ^-)}^2 \right) , \end{aligned}$$

(66)

where here again the generic constant $C>0$ is independent of $\beta >0$.

Step 4. Choose $\mathfrak {v}_4 = (0,0,0,0,\phi ,\phi ,0)$. With the Young’s inequalities we estimate

$$\begin{aligned} \mathcal {M}(\mathfrak {u},\mathfrak {v}_4)= & {} 2\Vert \phi \Vert ^2_{\textbf{W}} - \langle \phi , u^+ \rangle _{\textbf{W}';\textbf{W}} - \langle \phi , u^- \rangle _{\textbf{W}';\textbf{W}} \ge 2\Vert \phi \Vert ^2_{\textbf{W}} - \Vert \phi \Vert _{\textbf{W}'} \Vert u^+\Vert _{\textbf{W}} - \Vert \phi \Vert _{\textbf{W}'} \Vert u^-\Vert _{\textbf{W}}, \nonumber \\ \mathcal {M}(\mathfrak {u},\mathfrak {v}_4)\ge & {} \Vert \phi \Vert ^2_{\textbf{W}}- \frac{1}{2} \left( \Vert u^+\Vert ^2_{\textbf{W}} + \Vert u^-\Vert ^2_{\textbf{W}} \right) , \nonumber \\ \mathcal {M}(\mathfrak {u},\mathfrak {v}_4)\ge & {} \Vert \phi \Vert ^2_{\textbf{W}}- C \left( \Vert u^+\Vert ^2_{\textbf{V}} + \Vert u^-\Vert ^2_{\textbf{V}} \right) , \end{aligned}$$

(67)

where $C>0$ is deduced from the constant of the trace operators and those of the Korn’s inequality.

Step 5. Choose $\mathfrak {v} = \mathfrak {v}_1 + \gamma _2 \mathfrak {v}_2 + \gamma _3\mathfrak {v}_3 + \gamma _4 \mathfrak {v}_4$, for some positive constants $\gamma _2$, $\gamma _3$ and $\gamma _4$. Then, the estimates (64)–(67) yields

$$\begin{aligned} \mathcal {M}(\mathfrak {u},\mathfrak {v})\ge & {} \left( 2\nu - \alpha \nu \gamma _2 - \beta \nu \gamma _3 - C\gamma _4 \right) \left( \Vert \varepsilon (u^+) \Vert _{\mathbb {L}^2(\Omega ^+)}^2 + \Vert \varepsilon (u^-) \Vert _{\mathbb {L}^2(\Omega ^-)}^2 \right) \\{} & {} +\gamma _2\left( 1-\frac{C\nu }{\alpha }\right) \left( \Vert p^+\Vert ^2_{\textrm{L}^2(\Omega ^+)} + \Vert p^-\Vert ^2_{\textrm{L}^2(\Omega ^-)} \right) + \gamma _3\left( 1-\frac{C}{\beta } \right) \left( \Vert \lambda ^+ \Vert _{\textbf{W}'}^2 + \Vert \lambda ^- \Vert _{\textbf{W}'}^2 \right) + \gamma _4\Vert \phi \Vert ^2_{\textbf{W}}. \end{aligned}$$

By choosing $\alpha$ and $\beta$ large enough ($\alpha > C\nu$ and $\beta > C$), and next $\gamma _2$, $\gamma _3$ and $\gamma _4$ small enough, we get

$$\begin{aligned} \mathcal {M}(\mathfrak {u},\mathfrak {v}) \ge \delta \Vert \mathfrak {u} \Vert ^2, \end{aligned}$$

(68)

for some constant $\delta >0$, after having used the Korn’s inequality of Lemma 2.0. It remains us to verify that the norm of $\mathfrak {v}$ so chosen is controlled by the norm of $\mathfrak {u}$, namely the estimate $\Vert \mathfrak {v}\Vert \le C \Vert \mathfrak {u}\Vert$, which holds from (61) and (63). Thus we obtain $\displaystyle \frac{\mathcal {M}(\mathfrak {u},\mathfrak {v})}{\Vert \mathfrak {v} \Vert } \ge C\Vert \mathfrak {u} \Vert$, which enables us to complete the proof.

1.2.2 Proof of Corollary 4.1

The result is a direct consequence of the Banach-Nečas-Babuška theorem (see [27, Theorem 2.6, page 85]). The continuity of the linear mapping $\mathcal {G}$ is obvious. Given the inf-sup condition of Proposition 4.1, it remains us to verify the injectivity property for the bilinear form. Let $\mathfrak {u} \in \mathfrak {V}$ be such that $\mathcal {M}(\mathfrak {u},\mathfrak {v}) = 0$ for all $\mathfrak {v} \in \mathfrak {V}$. It is sufficient to choose $\mathfrak {v}$ like in the last step of the proof of Proposition 4.1, so that (68) holds, and implies $\mathfrak {u} = 0$, which concludes the proof.