Abstract
In this work, a new global-in-time solution strategy for incompressible flow problems is presented, which highly exploits the pressure Schur complement (PSC) approach for the construction of a space–time multigrid algorithm. For linear problems like the incompressible Stokes equations discretized in space using an inf-sup-stable finite element pair, the fundamental idea is to block the linear systems of equations associated with individual time steps into a single all-at-once saddle point problem for all velocity and pressure unknowns. Then the pressure Schur complement can be used to eliminate the velocity fields and set up an implicitly defined linear system for all pressure variables only. This algebraic manipulation allows the construction of parallel-in-time preconditioners for the corresponding all-at-once Picard iteration by extending frequently used sequential PSC preconditioners in a straightforward manner. For the construction of efficient solution strategies, the so defined preconditioners are employed in a GMRES method and then embedded as a smoother into a space–time multigrid algorithm, where the computational complexity of the coarse grid problem highly depends on the coarsening strategy in space and/or time. While commonly used finite element intergrid transfer operators are used in space, tailor-made prolongation and restriction matrices in time are required due to a special treatment of the pressure variable in the underlying time discretization. The so defined all-at-once multigrid solver is extended to the solution of the nonlinear Navier–Stokes equations by using Newton’s method for linearization of the global-in-time problem. In summary, the presented multigrid solution strategy only requires the efficient solution of time-dependent linear convection–diffusion–reaction equations and several independent Poisson-like problems. In order to demonstrate the potential of the proposed solution strategy for viscous fluid simulations with large time intervals, the convergence behavior is examined for various linear and nonlinear test cases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent decades, the demand for high resolution fluid simulations has become increasingly important to understand complex physical rheologies or optimize the geometries in production processes. This numerical prediction of the flow behavior is practically relevant only if computations can be performed in a reasonable amount of time. In order to achieve the desired efficiency, parallelization techniques are essential, usually performed in space only. Nowadays high-performance computing (HPC) architectures consist of a numerous number of compute nodes and are designed to perform many computational tasks in parallel. To fully exploit such massively parallel hardware architectures and minimize the total wall-clock time of the overall simulation, parallelization techniques only utilizing the space dimension may fail to provide sufficient loads for parallel tasks. Therefore, one might also want to use the temporal direction to further increase the problem size and the scaling capabilities when spatial parallelization techniques saturate. Unfortunately, the design of corresponding algorithms is not trivial due to the fact that the numerical solution should evolve only forward in time to match the nature of the physical process to be approximated.
To satisfy this design criterion, two main categories can be found in the literature: The first set of methods takes advantage of space–time concurrency by interpreting the temporal direction as another coordinate in space and then applying special discretization techniques to the resulting space-only problem. Other approaches exploit commonly used (sequential) time integrators and converge to the same numerical solution for all time steps. This strategy has the advantage that the underlying discretization (in space and time) is usually already well established and a detailed analysis is not required any more. An overview of parallel-in-time methods and the historical development of those schemes can be found, e.g., in the review articles by Gander [15] or Ong and Schroder [28]. One of the most famous representatives of parallel-in-time methods is Parareal, which was first introduced by Lions et al. [25]. In this scheme, the inherently sequential process of time stepping techniques is relaxed by performing time stepping on temporal subintervals in parallel and then synchronizing the individual auxiliary solutions in a sequential, but inexpensive corrector step. This methodology has proved itself already in various test scenarios. For example, first results for the solution of the incompressible Navier–Stokes equations were presented in [36, 37] using a first order finite volume scheme for discretization in space, while Fischer et al. [14] considered a finite element as well as a spectral approximation in this context. For three-dimensional experiments, the authors of [6] observed speedups up to 2.3 by exploiting the Parareal approach to accelerate a purely space-parallel method. Furthermore, they noticed a decay in the convergence rate for turbulent flows. The affect of the Reynolds number on the convergence behavior of Parareal was investigated more carefully in [32]. Finally, the application of Parareal to non-isothermal flow problems was discussed in [3, 27]. But also other parallel-in-time solution algorithms were extended to the simulation of viscous flow phenomena. While Kooij, Botchev, and Geurts [21] exploited Paraexp in case of fluid flows with rather low viscosity parameters, the MGRIT algorithm was successfully applied to the simulation of the unsteady Reynolds-averaged Navier–Stokes equations [13] and in the context of an adaptively refined space–time mesh [4, 5].
The approach presented in this work for solution of the incompressible Navier–Stokes equations is inspired by the parallel-in-time solution technique proposed in [7]. Therein, the authors employ the Picard iteration to first linearize the continuous problem at hand and apply commonly used sequential discretization techniques in space and time to the resulting Oseen equations. Then several/all time steps are blocked into a single linear system of equations and solved in an all-at-once manner to avoid efficiency bottlenecks caused by the inherently sequential nature of common time integrators. For this purpose, the system is transformed into a global pressure Schur complement (PSC) formulation by algebraically eliminating the unknown velocity field. The resulting linear system of equations is only implicitly defined and each application of the system matrix requires the solution of a vector-valued convection–diffusion(–reaction) equation. In [7], the GMRES method is finally applied to this PSC system using a global-in-time preconditioner, which is mainly based on the solution of several independent Poisson-like problems and, hence, provides a high degree of parallelism. Furthermore, the preconditioner can be interpreted as an all-at-once extension of the well-known pressure convection diffusion (PCD) preconditioner proposed by Kay et al. [20] and proved itself already in various practical applications for solution of the incompressible Navier–Stokes equations in the range of moderate Reynolds numbers.
In this work, we present another type of a global-in-time preconditioner, which is inspired by the least-squares commutator (LSC) preconditioner [10, 11, 30]. By construction, it can be readily applied to more general non-Newtonian fluid rheologies, which may be based on nonlinear diffusivities like the Carreau–Yasuda model [40]. Additionally, it turns out that this preconditioner is more robust with respect to the length of the time interval than the PCD preconditioner. However, in both cases the total number of iterations required to solve the problem at hand is not bounded above independently of the spatial resolution and the number of blocked time steps. This observation calls for acceleration of the solution procedure by embedding the preconditioned GMRES method as a smoother in a space–time multigrid algorithm exploiting either space, time, or space–time coarsening.
Another crucial ingredient of the overall solution strategy is the linearization technique under investigation. The Picard iteration seems to be very robust, but provides only a linear rate of convergence. Therefore, the influence of Newton’s method for solution of the nonlinear problem is also discussed in this work. Although this scheme converges quadratically, it requires sufficiently good initial guesses or a globalization technique. As we will see, this fact becomes important especially when solving the incompressible Navier–Stokes equations for a discretization of second order accuracy in space and time already at small Reynolds numbers.
This work is organized as follows: In Sect. 2, the unsteady incompressible Navier–Stokes equations and some linearized model problems are introduced. Section 3 is concerned with the discretization of the Stokes equations in space and time as well as the construction of the corresponding all-at-once saddle point problem. The pressure Schur complement fixed point iteration for this global linear system of equations and associated all-at-once preconditioners are presented in the next section. The proposed solution strategy is embedded as a smoother in a parallel-in-time multigrid algorithm in Sect. 5, while the behavior of nonlinear solution strategies is discussed in Sect. 6. Section 7 focuses on the numerical analysis of the solution techniques under investigation applied to several linear and nonlinear test cases. Finally, open challenges associated with extensions to convection dominated problems and the outcomes of the presented research are discussed in Sects. 8 and 9, respectively.
2 Continuous Setting
In this work, we focus on efficient solution strategies for the incompressible Navier–Stokes equations





which govern the evolution of a velocity field \({\textbf{v}}: \Omega \times (0,T) \rightarrow {\mathbb {R}}^d\) and a pressure \(p: \Omega \times (0,T) \rightarrow {\mathbb {R}}\). Here, the final time is denoted by \(T > 0\) and \(\Omega \subset {\mathbb {R}}^d\), \(d = 2,3\), is a compact, time-independent domain with a Lipschitz boundary \(\partial \Omega = \Gamma _\text {D}\mathbin {\dot{\cup }} \Gamma _\text {N}\) decomposed into its Dirichlet and Neumann parts. Furthermore, the initial velocity field is given by \({\textbf{v}}_0: \Omega \rightarrow {\mathbb {R}}^d\), \({\textbf{v}}_\text {D}: \Gamma _\text {D}\times (0,T) \rightarrow {\mathbb {R}}^d\) denotes the Dirichlet boundary data, \({\textbf{g}}: \Omega \times (0,T) \rightarrow {\mathbb {R}}^d\) represents the body force density, and \({\textbf{h}}: \Gamma _\text {N}\times (0,T) \rightarrow {\mathbb {R}}^d\) is the force acting on the fluid in the outward normal direction \(\textbf{n}:\partial \Omega \rightarrow {\mathbb {R}}^d\) [23, Chapter 8]. Finally, the density \(\rho \) of the fluid is set to unity for the sake of simplicity, while the dynamic viscosity of the fluid, denoted by \(\mu \), is a positive constant for the time being. In the numerical examples presented below, we will also consider viscosity parameters depending on the shear rate of the fluid and the Laplacian will be replaced by a viscosity model based on the strain rate tensor. These changes require minor algorithmic adjustments, which will be addressed when they come into play.
Due to the nonlinear behavior of the incompressible Navier–Stokes equations, there are hardly any direct solvers for system (1) and iterative solution techniques are commonly used in practice. A prominent representative is the classical Picard iteration
where the initial guess \(({\textbf{v}}, p)\) is assumed to satisfy the boundary conditions (1c)–(1e) and the solution update \(({\bar{{\textbf{v}}}},{\bar{p}})\) solves the Oseen equations





using the residual \({\textbf{r}}\) of the momentum equation

For an improved convergence behavior, Newton’s method can be employed, where the solution update \(({\bar{{\textbf{v}}}}, {\bar{p}})\) of the above fixed point iteration satisfies





corresponding to the Oseen equations involving some additional reactive term \(({\bar{{\textbf{v}}}} \cdot \nabla ) {\textbf{v}}\).
Therefore, in each iteration of the nonlinear solution procedure, the generalized unsteady Oseen equations as defined in (3) or (4) (involving ‘reactive’ terms or not) have to be solved. For this type of (linear) saddle point problems, a wide range of iterative solution techniques can be found in the literature (cf. [16, 18]). However, most methods have in common that they exploit sequential time-stepping by solving the involved linear system of equations for each time step one after the other. One family of such schemes is given by so called projection-like methods, where the pressure Schur complement is used to compute the pressure unknowns iteratively while the velocity field only acts as an auxiliary variable.
In this work, we present a global-in-time counterpart of this technique, where the pressure solution of the generalized Oseen equations is computed at all time instances simultaneously. For this purpose, we first restrict our attention to the simplified case \({\textbf{v}}= 0\) leading to the linear unsteady Stokes equations with nontrivial right hand sides and homogeneous boundary conditions. More precisely, our model problem reads





where the right hand side \(f: \Omega \times (0,T) \rightarrow {\mathbb {R}}\) is introduced due to the occurrence of a nontrivial right hand side in the continuity equations (3b) and (4b). The generalized Oseen equations given by (3) or (4) can be solved similarly. Necessary adjustments of the solution procedure are mentioned at appropriate places.
3 Global-in-Time Discrete Stokes Problem
After introducing the nonlinear solution strategy and motivating our linear model problems, we now discretize the system of partial differential equations in space and time and introduce the resulting global-in-time problem, which is solved by the discrete velocity and pressure solutions at all time instances. In this work, we restrict our attention to spatial discretizations using the stable \(Q_2\)–\(Q_1\) Taylor and Hood [34] finite element pair, where each component of the velocity field is approximated by a continuous and piecewise multi-quadratic function, while the pressure space is given by all continuous functions which are multi-linear in each element. Although many aspects of the solution strategy proposed in this work do not depend on the spatial discretization technique per sé, there are a few ingredients which will highly exploit special properties of the considered finite element spaces. We will emphasize these points whenever they will come into play.
To obtain the global-in-time counterpart of our model problem (5), we first discretize the Stokes equations in space using the above mentioned finite element pair. Then the system of ordinary differential equations reads
where \(\text {u}: (0,T) \rightarrow {\mathbb {R}}^{N_u}\), \(N_u \in {\mathbb {N}}\), and \(\text {p}: (0,T) \rightarrow {\mathbb {R}}^{N_p}\), \(N_p \in {\mathbb {N}}\), are the time-dependent vectors of degrees of freedom corresponding to the velocity and pressure field, respectively. Furthermore, the matrices \(\text {M}_u \in {\mathbb {R}}^{N_u \times N_u}\) and \(\text {D}_u \in {\mathbb {R}}^{N_u \times N_u}\) denote the mass and diffusion matrices of the velocity field, while \(\text {B} \in {\mathbb {R}}^{N_u \times N_p}\) and \(\text {B}^\top \in {\mathbb {R}}^{N_p \times N_u}\) are the discrete counterparts of the gradient and divergence operator, respectively. Finally, the vectors \(\text {g}: (0,T) \rightarrow {\mathbb {R}}^{N_u}\) and \(\text {f}: (0,T) \rightarrow {\mathbb {R}}^{N_p}\) represent the load vectors corresponding to the right hand side functions \({\textbf{g}}\) and f, while the Neumann boundary condition is also incorporated in the former quantity. For the sake of simplicity, we further assume that the boundary conditions prescribed on \(\Gamma _\text {D}\) and \(\Gamma _\text {N}\) are already enforced in system (6). Due to this fact, the matrices \(\text {B}\) and \(\text {B}^\top \) are strictly speaking not adjoint to each other. However, this discrepancy is of minor relevance and will be neglected in what follows. For a detailed description of the finite element approximation, the interested reader is referred, e.g., to [16, 38].
To numerically approximate the solution of the Stokes problem (6), we eventually apply the \(\theta \)-scheme, \(\theta \in [0,1]\), for time integration, where the time increment \({\delta t}> 0\) is assumed to be constant for the sake of simplicity. Then the approximations \(\text {u}^{(n+1)} \approx \text {u}(t^{(n+1)})\) and \(\text {p}^{(n+1)} \approx p(t^{(n+1)})\), \(t^{(n+1)} = (n+1) {\delta t}\), solve the linear system of equations
at each time step \(n = 0, \ldots , K\), where \(K = T {\delta t}^{-1} \in {\mathbb {N}}\) denotes the total number of time steps. Note that the fully implicit treatment of the pressure approximation is common practice and does not affect the accuracy if an appropriate post-processing step is performed (c.f. [38]). We will come back to this aspect in Sect. 5.2 when motivating temporal grid transfer operators for the pressure variable.
By introduction of the right hand side \(\tilde{\text {g}}^{(n+1)} \,{:=}\,{\delta t}\bigl ( \theta \text {g}^{(n+1)} + (1 - \theta ) \text {g}^{(n)} \bigr )\) and the system matrices \(\text {A}_i \,{:=}\,\text {M}_u + \theta {\delta t}\mu \text {D}_u\) as well as \(\text {A}_e \,{:=}\,- \text {M}_u + (1 - \theta ) {\delta t}\mu \text {D}_u\), the velocity field \(\text {u}^{(n+1)}\) and the scaled pressure unknown \(\tilde{\text {p}}^{(n+1)} \,{:=}\,{\delta t}\text {p}^{(n+1)}\) solve the following saddle point problem:
The solution of system (8) is usually advanced in time step-by-step due to the fact that \((\text {u}^{(n+1)}, \tilde{\text {p}}^{(n+1)})\) depends on the previous velocity field \(\text {u}^{(n)}\). However, in this work we intend to circumvent this sequential behavior and speed up the overall solution procedure of (8) by approximating the flow profile at all time instances at once. For this purpose, we treat all K time steps simultaneously and introduce the all-at-once system of equations


Using the Kronecker product notation
the block matrices \({\textbf{A}}_K \in {\mathbb {R}}^{K N_u \times K N_u}\), \({\textbf{B}}_K \in {\mathbb {R}}^{K N_u \times K N_p}\), and \({\textbf{B}}_K^\top \in {\mathbb {R}}^{K N_p \times K N_u}\) can be written as
Note that upright variables equipped with the subscript K correspond to matrices that act only in the temporal direction while global/space–time quantities are denoted by bold-faced letters.
Obviously, the global-in-time system of equations (9) is equivalent to system (8) and, hence, leads to the same velocity and pressure solution for all time instances. Especially, problem (9) collapses to the sequential solution procedure in case of \(K = 1\). Therefore, this reformulation might only yield algebraic benefits for iterative solvers, while, for instance, the discretization error or stability of the solution is not affected.
Due to the fact that time-dependent convective contributions to the momentum equation are omitted in the Stokes equations and the spatial domain is fixed, the mass and diffusion matrices \(\text {M}_u\) and \(\text {D}_u\) do not change in time and the global matrices \({\textbf{A}}_K\), \({\textbf{B}}_K\), and \({\textbf{B}}_K^\top \) can be written in terms of the Kronecker product as mentioned above. In the next section, we will exploit this property to motivate the construction of tailor-made solution strategies for the all-at-once system of equations (9). Although these schemes might be more expensive than algorithms which readily solve (8) in a sequential manner, they provide a high degree of parallelism and, hence, are designed to be efficiently applicable on modern massively parallel systems. Unfortunately, the generalized Oseen equations given by (3) or (4) do not have this special structure of \({\textbf{A}}_K\) for a time-dependent velocity field \({\textbf{u}}\). However, we will see that the solution techniques presented below are still applicable after adequate modifications.
4 Basic Pressure Schur Complement Iteration
In this section, an iterative solution algorithm for the global-in-time Stokes problem is presented, which exploits the Schur complement of the underlying saddle point matrix and is readily extendable to the treatment of the Oseen equations. The main idea behind the derivation of this scheme is to eliminate the degrees of freedom associated with the velocity field and then solve the resulting linear system of equations for the pressure unknowns in an iterative manner. For this purpose, two types of preconditioners are derived which are motivated by their counterparts for the sequential problem at hand. Finally, some remarks are made on how the solution strategy can be performed more efficiently in practice.
4.1 Sequential Version
Before describing the pressure Schur complement (PSC) solution algorithm for the all-at-once problem (9), we recall frequently used global PSC techniques for the sequential system of equations (8), which are very efficient for moderate Reynolds numbers and have in common that they are exact for infinitely small time increments \({\delta t}\). As the name already suggests, these schemes are based on the pressure Schur complement of the saddle point problem (8) given by
which is derived by substituting the velocity field
into the discrete version of the continuity equation \(\text {B}^\top \text {u}^{(n+1)} = \tilde{\text {g}}^{(n+1)}\). Unfortunately, it is hardly possible to explicitly determine the Schur complement matrix \(\text {P}_i \,{:=}\,\text {B}^\top \text {A}_i^{-1} \text {B} \in {\mathbb {R}}^{N_p \times N_p}\) due to the fact that \(\text {A}_i^{-1}\) is generally not sparse. Therefore, iterative solution techniques are commonly used to solve the PSC equation (10). For instance, the pressure update of the preconditioned Richardson iteration is performed using the formula
where the preconditioner \(\text {C}_i\) approximates the system matrix \(\text {P}_i\) while \(\text {r}^{(n+1)} = \text {B}^\top \tilde{\text {u}}^{(n+1)} - \text {f}^{(n+1)}\) is the PSC residual. As the approximation \(\tilde{\text {p}}^{(n+1)}\) converges to the exact solution of (10), the update \(\text {q}^{(n+1)}\) vanishes and the auxiliary velocity field \(\tilde{\text {u}}^{(n+1)} = \text {A}_i^{-1} (\tilde{\text {g}}^{(n+1)} - \text {A}_e \text {u}^{(n)} - \text {B} \tilde{\text {p}}^{(n+1)})\) tends to the velocity solution \(\text {u}^{(n+1)}\) of (8).
For the construction of appropriate preconditioners, we first note that \(\text {A}_i\) is dominated by \(\text {M}_u\) for sufficiently small time increments. In this case, the Schur complement matrix \(\text {P}_i\) can be approximated by the so called pressure Poisson matrix \(\hat{\text {D}}_p \,{:=}\,\text {B}^\top \text {M}_u^{-1} \text {B}\), which is spectrally equivalent to the discrete Laplacian acting on the pressure variable (cf. [12]) and can be determined esplicitely if the velocity mass matrix \(\text {M}_u\) is diagonal, e.g., by using an appropriate quadrature formula to perform mass lumping. This observation calls for the definition of
which corresponds to a SIMPLE-like preconditioner as proposed by Patankar and Spalding [29] and is exact in the limit of a vanishing time step size leading to an improved convergence behavior of the fixed point iteration (11) as \({\delta t}\) decreases. In what follows, we focus on the construction of more advanced preconditioners, which can be classified into two main categories and have in common that they coincide with the above mentioned definition of \(\text {C}_i^{-1}\) for infinitely small time increments.
4.1.1 Pressure Convection–Diffusion (PCD) Preconditioner
The first approach to construct the preconditioner \(\text {C}_i\) is motivated by assuming the commutativity of the underlying differential operators [20]. In a discrete manner, this assumption means that the identity
holds true, where the velocity and pressure mass matrices \(\text {M}_u \in {\mathbb {R}}^{N_u \times N_u}\) and \(\text {M}_p \in {\mathbb {R}}^{N_p \times N_p}\) guarantee correct scalings. Furthermore, the matrix \(\text {A}_{i,p} \in {\mathbb {R}}^{N_p \times N_p}\) approximates \(\text {A}_i\) using the pressure FE space. According to (13), the preconditioner \(\text {C}_i\) can then be introduced as (cf. [20])
Note that the diffusion matrix \(\text {D}_p \in {\mathbb {R}}^{N_p \times N_p}\) involved in the definition of \(\text {A}_{i,p} \,{:=}\,\text {M}_p + \theta {\delta t}\mu \text {D}_p\) can only be computed using the Galerkin discretization if the pressure FE space is \(H^1\)-conforming, which is actually the case for the considered \(Q_2\)-\(Q_1\) FE pair. Otherwise, a mixed formulation of Poisson’s equation can be used to motivate the definition of \(\text {D}_p\) as the discrete pressure Poisson matrix \(\hat{\text {D}}_p = \text {B}^\top \text {M}_u^{-1} \text {B}\). This formulation is also employed in this work and leads to the so called Cahouet-Chabard preconditioner [1]
for the sequential Stokes problem (8), which is obviously exact for infinitely small time increments.
In case of moderate Reynolds numbers, preconditioner (14) also yields good convergence rates of the fixed point iteration (11) for the generalized Oseen equations (3) and (4). However, convective contributions can as well be considered in the definition of \(\text {A}_{i,p}\) by another additive term \(\theta {\delta t}\text {K}_p\). Then the above mentioned preconditioner extends to the so called pressure convection–diffusion (PCD) preconditioner
where the unsplit form of \(\text {C}_i^{-1}\) is more appropriate to apply in practice because only one discrete pressure Poisson problem with system matrix \(\hat{\text {D}}_p\) has to be solved in each application of the preconditioner.
4.1.2 LSC Preconditioner
The definition of the PCD preconditioner as presented in (14) can also be derived by assuming the regularity of \(\text {B}\) and \(\text {B}^\top \). However, this assumption is generally not true so that both inverses have to be replaced by adequate approximations. The use of the Moore-Penrose inverse leads to the so called scaled BFBt preconditioner as proposed by Elman et al. [11]
where we exploited the properties
due to the fact that all columns of \(\text {B}\) and rows of \(\text {B}^\top \) are linearly independent. Originally, this preconditioner was derived using a least-squares formulation and, hence, can also be called least-squares commutator (LSC) preconditioner [30]. As in case of the PCD preconditioner, approximation (15) is exact in the limit of a vanishing time increment, because \(\text {A}_i\) then coincides with \(\text {M}_u\) and, hence,
Furthermore, this approach can be applied to any linear system of equations with a saddle point system matrix and does not require special finite element pairs for discretization purposes. Therefore, the preconditioner can be constructed in a straightforward manner for the generalized Oseen equations (3) and (4) without special treatment of the convective and/or reactive term. On the other hand, application of the LSC preconditioner requires solution of two discrete pressure Poisson problems and, hence, is approximately twice as expensive as the PCD preconditioner.
4.2 Global-in-Time Version
After summarizing a commonly used solution strategy for the Stokes problem (8) in case of moderate Reynolds numbers and reviewing adequate preconditioners, we now extend this approach to the all-at-once system of equations (9), where all time steps are treated simultaneously. For this purpose, the corresponding Schur complement can be constructed as before by expressing the velocity field \({\textbf{u}}\) in terms of the unknown pressure variable \(\tilde{{\textbf{p}}}\), i.e., \({\textbf{u}} = \textbf{A}_K^{-1} (\tilde{{\textbf{g}}} - {\textbf{B}}_K \tilde{{\textbf{p}}})\), and substituting the result into \({\textbf{B}}_K^\top {\textbf{u}} = {\textbf{f}}\). This procedure leads to the system of equations
Then the corresponding preconditioned Richardson iteration is given by
where \({\textbf{C}}_K^{-1}\) is a suitable approximation to the inverse of the Schur complement matrix \({\textbf{P}}_K = {\textbf{B}}_K^\top {\textbf{A}}_K^{-1} {\textbf{B}}_K\), the auxiliary velocity field \(\tilde{{\textbf{u}}}\) satisfies \(\tilde{{\textbf{u}}} = {\textbf{A}}_K^{-1} (\tilde{{\textbf{g}}} - {\textbf{B}}_K \tilde{{\textbf{p}}})\), and the global-in-time PSC residual reads \({\textbf{r}} = {\textbf{B}}_K^\top \tilde{{\textbf{u}}} - {\textbf{f}}\).
The crucial question now is how to extend the preconditioners \(\text {C}_i\) presented in the previous section to the global-in-time Schur complement equations (17) so that an adequate convergence behavior can be achieved in an efficient manner and the all-at-once preconditioner is still exact in the limit of vanishing time increments. For this purpose, it seems to be mandatory to also take into account the off-diagonal block entries \(\text {A}_e\) of the global-in-time matrix \({\textbf{A}}_K\). This requirement seems to imply that the sequential structure of the Stokes problem (8) will directly carry over to the global preconditioner \({\textbf{C}}_K\) and its application might not be efficiently applicable at first glance. However, in what follows we will see that this actually does not have to be true and the preconditioners considered in this work are indeed well suited for accelerating the solution procedure on modern high-performance computing facilities.
4.2.1 PCD Preconditioner
First, we focus on the PCD preconditioner as given by (14) in the sequential case and note that it was motivated by assuming the commutativity of some underlying differential operators. In a discrete manner, this assumption is given by the validity of (13), which is equivalent to

for \(\theta \notin \{0, 1\}\), where \(\text {A}_{e,p}\) approximates \(\text {A}_e\) using the pressure FE space. This property can be exploited to easily show a global-in-time version of assumption (13)
where \({\textbf{A}}_{K,p}\) is given by
Therefore, the global-in-time version of the PCD preconditioner can be defined by (cf. [7])
and, hence,
which is based on the same assumption as the sequential counterpart introduced in Sect. 4.1.1.
For the special case of the Stokes equations with a constant diffusion parameter \(\mu \), the all-at-once matrix \({\textbf{A}}_{K,p}\) can be written as
where the diffusion matrix \(\text {D}_p\) may be set to \(\hat{\text {D}}_p\) as before. Then the global-in-time version of the PCD preconditioner simplifies to
due to the fact that the Kronecker product satisfies
Therefore, the preconditioner \({\textbf{C}}_K\) can be applied to the global-in-time PSC residual \({\textbf{r}} = {\textbf{B}}_K^\top \tilde{{\textbf{u}}} - {\textbf{f}}\) by first computing the modified right hand sides
before linear systems of equations with system matrices \(\text {I}_K \otimes \hat{\text {D}}_p\) and \(\text {I}_K \otimes \text {M}_p\) have to be solved, i.e.,
According to the fact that \(\text {I}_K \otimes \hat{\text {D}}_p\) and \(\text {I}_K \otimes \text {M}_K\) are block diagonal matrices, each block entry of \(\tilde{{\textbf{q}}}_1\) and \(\tilde{{\textbf{q}}}_2\) can be computed independently of each other by solving local subproblems with system matrices \(\hat{\text {D}}_p\) and \(\text {M}_p\), respectively. This solution procedure can be further simplified due to the fact that the system matrix does not change, i.e.,
Therefore, application of \({\textbf{C}}_K^{-1}\) to the residual \({\textbf{r}}\) requires in total the solution of two separate spatial subproblems with K (independent) right hand sides, which provides a much higher degree of parallelism. The corresponding system matrices \(\hat{\text {D}}_p\) and \(\text {M}_p\) are also incorporated in the sequential version of the PCD preconditioner (14). Thus, a single application of the global-in-time preconditioner requires solution of the same and as many linear systems of equations as in the sequential case if the preconditioner (14) is applied once in each time step.
If convective and/or reactive contributions are included in the definition of the preconditioner, too, then formulation (20) should be used. This version requires solution of the same linear systems of equations as occurring in (21) while another all-at-once matrix–vector multiplication has to be performed.
Therefore, the global-in-time preconditioner (20) can be applied very efficiently on modern high-performance computing facilities without the necessity of special solution techniques. On the other hand, the preconditioner \({\textbf{C}}_K\) coincides with the Schur complement matrix \({\textbf{P}}_K\) in the limit of vanishing time increments leading to an improved convergence behavior of the fixed point iteration as the time step size \({\delta t}\) goes to zero. This property stays valid even if only contributions of the mass matrix are considered in the definition of \({\textbf{A}}_{K,p}\) so that \({\textbf{C}}_K\) corresponds to the SIMPLE-like preconditioner
4.2.2 LSC Preconditioner
For the derivation of a global-in-time version of the preconditioner (15), we first note that
by virtue of (16). Then the global-in-time LSC preconditioner can be defined by
and provides an efficient application, because each system matrix of involved linear systems of equations can be decomposed into independent local subproblems. Furthermore, the application of the global-in-time LSC preconditioner is again approximately twice as expensive as applying the PCD preconditioner due to the fact that two discrete pressure Poisson problems have to be solved for each blocked time step.
Both presented preconditioners \({\textbf{C}}_K\) have in common that they exhibit a lower block triangular structure because they can be written as the product of lower block triangular matrices as stated in (20) and (24). According to the fact that the global-in-time Schur complement matrix \(\textbf{P}_K = {\textbf{B}}_K^\top {\textbf{A}}_K^{-1} {\textbf{B}}_K\) is also a lower block diagonal matrix, the iteration matrix of the fixed point iteration (18) given by \({\textbf{J}}_K \,{:=}\,\textbf{I}_K - {\textbf{C}}_K^{-1} {\textbf{P}}_K\) possesses the same structure. Therefore, the asymptotic rate of convergence coincides with the largest spectral radius of the block diagonal entries of \(\textbf{J}_K\), which is given by the asymptotic rate of convergence of the corresponding sequential fixed point iteration (11) and, hence, does not depend on the number of blocked time steps K. However, this property is of minor practical importance as we will see in Sect. 7.
4.3 Inexact Solver for Momentum Equation
Currently, one key ingredient of the solution strategy described above is given by elimination of all velocity unknowns leading to a fixed point iteration for the pressure variable only. Thus, in each application of the implicitly defined system matrix, an auxiliary velocity field has to be calculated, which corresponds to the (exact) solution of a vector-valued unsteady convection–diffusion–reaction equation. Although numerous parallel-in-time solution techniques can be found in the literature for this test problem, the accurate computation might be expensive and, hence, calls for more sophisticated and efficient alternatives.
If a suitable initial guess is also available for the velocity field, one possibility is to improve the accuracy of this quantity iteratively and already accept intermediate solutions in the overall solution procedure. The fixed point iteration given by
converges to the exact auxiliary velocity field \(\tilde{{\textbf{u}}} = {\textbf{A}}_K^{-1} (\tilde{{\textbf{g}}} - {\textbf{B}}_K \tilde{\textbf{p}})\) for a fixed pressure variable \(\tilde{{\textbf{p}}}\) if the preconditioner \(\tilde{{\textbf{A}}}_K \approx {\textbf{A}}_K\), possibly depending on the current solution \(\tilde{{\textbf{u}}}\), is chosen appropriately. If only a single iteration of (25) is performed before calculation of the PSC residual, the update formula for \(\tilde{{\textbf{u}}}\) and \(\tilde{{\textbf{p}}}\) reads
Actually, this more general solution strategy is automatically performed in (18) whenever the old velocity field is used as an initial guess in case of an iterative computation of \(\tilde{{\textbf{u}}}\). However, the stopping criterion of (26) should then take into account the residuals of the continuity and the momentum equation. Eventually, the auxiliary variable \(\tilde{{\textbf{u}}}\) converges as before to the velocity field \({\textbf{u}}\) of the solution \(({\textbf{u}}, {\textbf{p}})\) of the discrete Stokes (or Oseen) equations.
In the numerical examples presented in Sect. 7, we will not exploit the above mentioned approach and will always compute exactly the auxiliary velocity field. In this way, we can evaluate the convergence behavior more carefully without introducing any disturbing side effects, and a sensitive parameter tuning for the velocity solver can be avoided at this point.
5 Multigrid Acceleration
So far, the all-at-once system of equations (9) is solved by a global pressure Schur complement fixed point iteration. It was introduced as a straightforward extension of the sequential counterpart, which has proved its worth in numerous practical applications. Furthermore, both solution strategies yield the same asymptotic rate of convergence due to the lower block triangular structure of the global-in-time iteration matrix. However, the number of iterations for approximately reaching this asymptotic rate highly depends on the number of blocked time steps and, unfortunately, the convergence behavior generally deteriorates during the first iterations as the time horizon is enlarged. Therefore, this theoretical property is only of minor practical interest and calls for the use of more sophisticated solution strategies.
In this section, we introduce a two-grid PSC algorithm using the above mentioned fixed point iteration as a smoother. The key idea is to accelerate the convergence of the iterative solver by means of a so called coarse grid correction. For this purpose, the global-in-time PSC residual is restricted to a coarser space–time grid, where the Stokes problem can be solved more efficiently. Then the coarse grid solution is used to update the pressure variable while the corresponding velocity field could be determined by another solution of the momentum equation. In practice, this solution strategy is performed recursively leading to a real multigrid algorithm.
5.1 Coarse Grid Correction
To introduce the coarse grid problem, we first notice that the global-in-time fixed point iteration (18) is defined as a defect correction for the all-at-once Schur complement (17). This system of equations is derived by algebraically manipulating the Galerkin discretization of the Stokes equations and, hence, is uniquely determined by the triangulation \({\mathcal {T}}_h\) of the spatial domain \(\Omega \) as well as the choice of the time increment \({\delta t}\). Thus, an approximation to the exact solution of (17) can be computed by solving the same system for another discretization in space and time. By using either a coarser spatial triangulation \(\mathcal T_{{\bar{h}}}\) or a larger time increment \({\bar{{\delta t}}}\), the resulting coarse grid problem has less degrees of freedom than the original one so that solution can probably be performed more efficiently.
In the context of the two-grid algorithm, such a coarse grid problem is exploited to improve the quality of an initial guess \(\tilde{{\textbf{p}}}\) by means of a corrector step. For this purpose, the global-in-time PSC residual
is transferred to the coarse space–time grid using a restriction operator \({\textbf{R}}_K^{{\bar{K}}} \in {\mathbb {R}}^{{\bar{N}}_p {\bar{K}} \times N_p K}\), where \({\bar{K}} = T {\bar{{\delta t}}}^{-1} \in {\mathbb {N}}\) is the number of blocked time steps required to reach the final time T using the time increment \({\bar{{\delta t}}}\) while \({\bar{N}}_p\) denotes the number of degrees of freedom associated with the pressure FE space defined on \({\mathcal {T}}_{{\bar{h}}}\). Then the coarse grid Stokes problem reads in its primal form
where all quantities furnished with a bar are defined as before, but now with respect to \({\mathcal {T}}_{{\bar{h}}}\) and \({\bar{{\delta t}}}\). Finally, the pressure approximation \(\bar{\tilde{{\textbf{p}}}}\) is projected to the original mesh using a prolongation operator \({\textbf{P}}_{\bar{K}}^K \in {\mathbb {R}}^{N_p K \times {\bar{N}}_p {\bar{K}}}\) and then added to the initial guess \(\tilde{{\textbf{p}}}\).
In summary, the whole coarse grid correction reads
where \(\hat{{\textbf{C}}}_K^{-1} = {\textbf{P}}_{{\bar{K}}}^K (\bar{\textbf{B}}_{{\bar{K}}}^\top \bar{{\textbf{A}}}_{{\bar{K}}}^{-1} \bar{{\textbf{B}}}_{\bar{K}})^{-1} {\textbf{R}}_K^{{\bar{K}}}\) can be interpreted as a coarse grid preconditioner for the fixed point iteration (18). It is easy to verify that this coarse grid correction produces the exact solution to (17) for \({\textbf{P}}_{{\bar{K}}}^K = {\textbf{R}}_K^{{\bar{K}}} = {\textbf{I}}_K\) if both space–time grids coincide, i.e., \({\mathcal {T}}_{{\bar{h}}} = {\mathcal {T}}_h\) and \({\bar{{\delta t}}} = {\delta t}\). However, this choice obviously does not reduce the computational complexity due to the fact that the original problem still has to be solved, but now for another right hand side. Therefore, the space–time grid should be coarsened in the spatial and/or temporal direction. In the former case, it is common practice to exploit grid hierarchies based on uniform refinements of a coarse grid due the fact that the prolongation and restriction operators \(\text {P} \in {\mathbb {R}}^{N_p \times {\bar{N}}_p}\) and \(\text {R} \in {\mathbb {R}}^{\bar{N}_p \times N_p}\) naturally induced by the pressure FE space can be computed efficiently in this case. On the other hand, it seems to be convenient to enlarge the time increment \({\delta t}\) by a factor of 2 leading to a nested hierarchy of time levels. If corresponding temporal intergrid transfer operators \(\tilde{\text {P}}_{{\bar{K}}}^K \in {\mathbb {R}}^{K \times {\bar{K}}}\) and \(\tilde{\text {R}}_K^{{\bar{K}}} \in {\mathbb {R}}^{{\bar{K}} \times K}\) are given, the global-in-time prolongation and restriction operators can be defined in terms of a Kronecker product as follows:
5.2 Temporal Prolongation and Restriction Operators
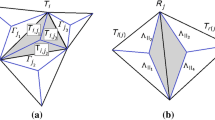
While the involved intergrid transfer operators in space are naturally induced by the pressure FE space, the definition of temporal prolongation and restriction operators requires more sophisticated investigations due to the fully implicit treatment of the pressure variable in (7a). For this purpose, we first note that the finite element function associated with the degrees of freedom \(\text {p}^{(n+1)} = {\delta t}^{-1} \tilde{\text {p}}^{(n+1)}\) can be interpreted as an approximation to the exact pressure field p at the intermediate time level \(t^{(n+\theta )} \,{:=}\,t^{(n)} + \theta {\delta t}\) [22, Appendix D]. Numerical experiments indicate that this approximation is second order accurate in case of the Crank–Nicolson scheme for time integration, i.e., \(\theta = \frac{1}{2}\). According to this observation, we restrict our attention to this special choice of \(\theta \) and introduce the temporal intergrid transfer operators in terms of a tailor-made ‘linear interpolation’ in time. Using the symbols of Fig. 1, the restriction of the residual can be outlined as follows:

The prolongation of a coarse grid pressure approximation exploits ‘interpolation forward in time’:

Therefore, the associated matrices read
if the time increment of the coarse grid problem is given by \({\bar{{\delta t}}} = 2 {\delta t}\). Due to the fact that the pressure solutions \(\tilde{{\textbf{p}}}\) and \(\bar{\tilde{{\textbf{p}}}}\) of the Stokes problems (9) and (27) are scaled by \({\delta t}\) and \({\bar{{\delta t}}} = 2 {\delta t}\), respectively, the actual prolongation matrix has to be multiplied by \(\frac{1}{2}\) leading to the following transfer operators in time:
5.3 Smoothing Operator
After the definition of the coarse grid problem, we now focus on the smoother of the two-grid algorithm. As mentioned before, the preconditioned Richardson iteration as introduced in Sect. 4.2 can be employed for this purpose. However, the convergence of the resulting two-grid algorithm is highly sensitive to the choice of optional damping parameters involved in the smoother. To avoid the necessity of manually tuning this value, the Richardson iteration is embedded into a GMRES solver, which automatically determines ‘optimal’ relaxation parameters in a nonlinear fashion (cf. [22]).
5.4 Sketch of Solution Algorithm
In this section, we briefly summarize the linear solution technique as described so far and highlight important aspects that could be useful in practical implementations. The algorithm at hand is then used in Sect. 7 to solve several numerical test problems and illustrate the potential of a global-in-time pressure Schur complement solution strategy.
The global-in-time multigrid method for the linear Oseen equations, as sketched in Fig. 2, is designed in such a way that an implicitly defined problem for the pressure unknown only is solved iteratively, while the velocity field serves merely as an auxiliary variable. In this approach, high-frequency error modes of the unknown solution are damped by performing a few iterations of a GMRES method using one of the global-in-time preconditioners as introduced in Sect. 4.2. This smoothing procedure is preferred to a (preconditioned) damped Richardson iteration because relaxation parameters are determined automatically to improve and stabilize the convergence behavior. However, the performance of the GMRES method might still deteriorate as the spatial resolution increases or the time interval is enlarged and, hence, calls for a coarse grid acceleration. The underlying coarse grid problem can be constructed in a very general manner and might exploit space and/or time coarsening. While full coarsening in space and time reduces the total number of degrees of freedom most rapidly, we will see that most promising results are observed if coarsening is performed in time only, especially for convection dominated problems.
This solution technique for the Oseen equations just requires an initial guess for the all-at-once pressure variable \(\tilde{\textbf{p}}\), while the right hand side vectors \(\tilde{{\textbf{g}}}\) and \({\textbf{f}}\) are provided by the problem under consideration and correspond to the discrete counterparts of \({\textbf{g}}\) and f, respectively. Furthermore, boundary conditions of Neumann and Dirichlet type are already involved in the definition of \(\textbf{A}_K\), \({\textbf{B}}_K\), and \(\tilde{{\textbf{g}}}\) and do not have to be imposed explicitly in the solution procedure. However, this strategy is not mandatory and just simplifies the notation in this work.
In the coarse grid problem, a homogeneous right hand side vector \(\bar{\tilde{{\textbf{g}}}}\) is used for the momentum equation while the restricted residual \(\bar{{\textbf{r}}}\) occurs in the definition of \(\bar{{\textbf{f}}}\). According to this design criterion, the coarse grid correction just requires the restriction of a single all-at-once quantity, that is, the PSC residual \({\textbf{r}}\), and provides the exact pressure correction if the coarse space–time grid coincides with the original one. In this case, the iterative solution process is terminated after a single iteration and a stopping criterion, e.g., based on the Euclidean norm of the PSC residual, is met. If boundary conditions are not incorporated in the all-at-once system at hand, homogeneous initial and boundary conditions have to be strongly enforced for the coarse grid velocity field to achieve a consistent solution strategy.
6 Solution Techniques for Nonlinear Problems
So far, we solely focused on the design of an efficient solution strategy for the generalized Oseen equations. The proposed solver highly exploits the pressure Schur complement of the linear problem at hand and only uses components that can be performed in a highly parallelizable manner on modern computer architectures. Practically more relevant are the incompressible Navier–Stokes equations, which are characterized by nonlinear convective and/or viscosity terms possibly resulting in very complex flow rheologies. Therefore, robust and fast nonlinear solution strategies are mandatory to achieve reduced run times compared to simulations based on a sequential time stepping scheme. This problem is especially relevant for global-in-time solution strategies, because nonlinear solvers perform much better in the sequential case due to smaller problem sizes and the existence of good initial guesses.
In [7], the authors applied a Picard iteration to the incompressible Navier–Stokes equations as described in Sect. 2. This nonlinear solver provides a linear rate of convergence and the total number of iterations required to solve the nonlinear problem stays approximately constant when considering a fixed time interval for varying time increments and mesh resolutions. However, in the numerical examples presented in Sect. 7, we will observe that the number of nonlinear iterations can be quite large so that the Picard iteration might not be optimal.
Another candidate commonly used for linearization is Newton’s method, which converges at least quadratically if the root has multiplicity 1. Applied to the continuous problem as discussed in Sect. 2, the nonlinear solution procedure requires in each iteration solution of the Oseen equations including a reactive term. This computation can be performed using the multigrid algorithm proposed above without further modifications. However, convergence of Newton’s method can generally only be guaranteed for sufficiently good initial guesses, which can be a major issue in practical applications. Therefore, so called globalization techniques are required to make the scheme more robust and guarantee convergence even for arbitrary initial guesses. Lemoine and Münch [24] construct a minimizing sequence for a least-squares functional so that overall convergence can be guaranteed at the expense of solving two additional unsteady and 2K steady Stokes problems in each nonlinear iteration when K time steps are blocked into an all-at-once system.
This significant increase of complexity can be avoided by providing sufficiently good initial guesses, which might be constructed by using a coarser spatial discretization and/or larger time increments. However, this strategy does not guarantee convergence of Newton’s method without relaxing the solution update and, hence, has to be used with caution.
As mentioned in the road map of the nonlinear solution strategy (cf. Fig. 3), the overall solution time can be further reduced by using an inexact solver for the discrete Oseen problem. In most cases, it seems sufficient to gain only a few digits in accuracy in each iteration to achieve overall convergence without a significant increase in the total number of nonlinear iterations. When the multigrid solver proposed in Sect. 5 is employed to solve the linear problem, a vanishing pressure approximation should be used as an initial guess due to the fact that eventually the norm of the solution update \(({\textbf{w}}, {\textbf{q}})\) tends to zero as Newton’s method converges. In case of this nonlinear fixed point iteration, a stopping criterion based on the Euclidean norm of the PSC residual can again be used.
7 Numerical Examples
The sequential pressure Schur complement iteration as summarized in Sect. 4.1 already proved itself in numerous practical applications to solve the incompressible Navier–Stokes equations for small up to moderate Reynolds numbers. The global-in-time solution strategy proposed in this work is introduced as a straightforward extension of this methodology and, hence, should perform properly for the same range of flow fields. For an in-depth analysis of its solution behavior, we consider several linear and nonlinear test cases in this section. All of them are highly related to practically relevant scenarios and, hence, illustrate the advantages and difficulties of the involved solver components for real-life applications.
To solely focus on the influence of the solver at hand and minimize the impact of other factors, we consider flows around a circular obstacle in all test cases, where the geometry is given by the well-known ‘flow around a cylinder’ domain (cf. Fig. 4). Here, all external forces are set to zero, i.e., \({\textbf{g}} = {\textbf{0}}\) and \({\textbf{h}} = {\textbf{0}}\), and the boundary condition \({\textbf{v}}_\text {D}= {\textbf{0}}\) is strongly enforced on \(\Gamma _\text {wall}\). Furthermore, the flow starts at rest, that is, \({\textbf{v}}_0 = {\textbf{0}}\), and is then smoothly accelerated on the inflow boundary part \(\Gamma _\text {in}\) as prescribed by the parabolic boundary data (cf. [31])
Due to the varying magnitude of the velocity field, different time scalings are involved in the flow behavior and a von Kármán vortex street occurs behind the cylinder if the viscosity parameter \(\mu \) is sufficiently small. In the numerical examples presented below, we especially focus on flow simulations for lower Reynolds numbers, possibly with a nonlinear viscosity model involved (cf. Sect. 7.4). The resulting laminar flow does not exhibit recirculating vortices, but significantly depends on the amount of diffusivity (cf. Fig. 5).
Although the solution strategy under investigation can be applied to various spatial discretizations, all numerical results exploit the isoparametric \(Q_2\)–\(Q_1\) Taylor–Hood finite element pair [34]. The two dimensional Simpson’s rule is used to compute a diagonal velocity mass matrix (cf. Table 1). The underlying triangulation consists of convex quadrilaterals only and is uniformly refined to generate a hierarchy of different mesh levels \({\text {lvl}}\in \{0, 1, \ldots , 5\}\). Furthermore, the Crank–Nicolson scheme, i.e., \(\theta = \frac{1}{2}\), is applied for time integration, while \({\delta t}\) is chosen as commonly used for those benchmark configurations. However, the accuracy of the numerical approximation is only of minor interest due to the fact that it is not affected by the iterative solution strategy at hand.
For solution of the involved linear problems, we distinguish between three main classes of iterative solvers. The most involved solution strategy is given by the proposed multigrid technique as summarized in Sect. 5.4, which is denoted by \({\text {MG}}(c, p)\). In this work, no post-smoothing is performed, while four iterations of the preconditioned GMRES method serve as a pre-smoother. For this purpose, the global-in-time pressure Schur complement equation is preconditioned using the PCD preconditioner (20) or the LSC preconditioner (24), as indicated by the quantity \(p \in \{{\text {PCD}}, {\text {LSC}}\}\). If not mentioned otherwise, the multigrid algorithm is based on a V-cycle using the entire hierarchy of space–time grids, where coarsening is performed in space and/or time as indicated by the parameter \(c \in \{\text {s}, \text {t}, \text {ts}\}\). In case of \(c = \text {ts}\), pure space/time coarsening is also allowed on the coarsest levels if the number of blocked time steps becomes odd or the spatial mesh level is zero already. If the (finest) coarse grid problem is solved exactly, the algorithm corresponds to a two-grid solution strategy denoted by \({\text {TG}}(c, p)\).
By neglecting the coarse grid correction, the multigrid algorithm simplifies to the GMRES method referred to as \({\text {GMRES}}(p)\). It is restarted after four iterations and the total number of restarts is counted to ensure that the numerical complexity per iteration is comparable to the total effort of the multigrid method on the finest mesh level.
Finally, the most simple solution technique considered in the numerical examples is given by the preconditioned Richardson iteration (18), which is labeled by \({\text {RI}}(p)\). As in case of the GMRES method, we only count every fourth iteration so that in each ‘macro iteration’ the involved preconditioner is called as many times as in case of the other solution strategies.
However, note that application of the LSC preconditioner is approximately twice as expensive as in case of the PCD preconditioner, because twice as many discrete pressure Poisson problems have to be solved. Furthermore, only the contributions of the mass, diffusion, and convection matrices are considered in the definition of the PCD preconditioner, while reactive terms are also involved in the definition of the LSC preconditioner. Finally, a vanishing initial guess is used for all linear test cases and the iterative solver terminates if the Euclidean norm of the pressure Schur complement residual is lower than \(10^{-11}\), if not mentioned otherwise.
7.1 Stokes Problem
We start our investigations by considering the Stokes problem for \(\mu = 10^{-2}\). This choice of the viscosity parameter is actually not a restriction due to the fact that the global-in-time system matrix depends just on the product \(\mu {\delta t}\) and only the input boundary data \({\textbf{v}}_\text {D}\) need to be transformed accordingly to achieve the same numerical results for another combination of \(\mu \) and \({\delta t}\). On the other hand, the system matrix of the all-at-once linear system of equations does not depend on the magnitude of the velocity field and, hence, the (asymptotic) rate of convergence should not be sensitive to the choice of U(t) for this problem. Due to the fact that there is no convection or nonlinearity involved, this setup acts as a model problem for our solution strategy and a fast and uniform convergence behavior is desirable.
If the global-in-time linear system of equations is solved by the Richardson iteration using the PCD preconditioner, the total number of iterations highly depends on the length of the time horizon (cf. Fig. 6). Especially for large time increments, the solution strategy becomes more and more expensive as the number of blocked time steps increases and a reduction of the solution time compared to a sequential solver is hardly possible. Although the convergence behavior can be drastically improved by using the GMRES method, the total number of iterations is still proportional to the square root of the number of blocked time steps. For this preconditioner, uniform convergence not depending on the final time T can only be observed, when a coarse grid correction is employed, as in case of the considered two-grid algorithm using time coarsening.
In contrast to this, the use of the LSC preconditioner results in a highly unstable Richardson iteration, but in combination with the GMRES method, the solution strategy becomes very robust and the rate of convergence does not depend on the final time T. As a consequence, the additional coarse grid correction of the two-grid algorithm has only a minor influence on the convergence behavior and seems not to be worth the numerical effort for this configuration.
By construction, both preconditioners have in common that they are exact in the limit of a vanishing time increment. Therefore, they become more and more accurate as \({\delta t}\) tends to zero and, hence, the convergence behavior of all iterative solution strategies improves for a fixed number of blocked time steps (cf. Table 2). Due to the fact that this strategy reduces the length of the time interval under investigation, several global-in-time linear systems of equations would have to be solved one after the other to reach the same final time T. This sequential process can be avoided by choosing the total number of blocked time steps proportional to \({\delta t}^{-1}\). In this case, a reduction of the total number of iterations required to solve the resulting all-at-once problem for smaller time increments can be observed only if a two-grid solution strategy is employed.
The involved coarse grid problem can basically be constructed by performing coarsening either in space, in time, or in both directions. While pure time coarsening leads to very accurate coarse grid problems, the total number of degrees of freedom is only reduced by a factor of 2 and the ratio between temporal and spatial resolution increases accordingly. On the other hand, simultaneous coarsening in space and time can be used to keep this ratio fixed and preserves the structure of the problem at hand. In this case, the resulting coarse grid problem is 8 times smaller in two space dimensions, but might not be accurate enough for the design of a robust two-grid algorithm.
For the Stokes equations under investigation, activation of space coarsening has hardly any effect on the convergence behavior of the multigrid algorithm that performs time coarsening. Therefore, the solution strategy based on space–time coarsening is most efficient for this setup. Compared to the corresponding two-grid solution strategy under investigation, the total number of iterations only slightly increases for the multigrid scheme.
As the spatial resolution of the discretization improves, the LSC preconditioner becomes less accurate and the total number of iterations required to solve the problem at hand increases for the GMRES method employing this preconditioner (cf. Table 3). This adverse effect in performance can not be compensated even if a coarse grid correction is involved in the solution strategy and the time step size is simultaneously reduced by a factor of two to keep the ratio between the spatial and temporal resolution fixed.
The iterative solvers using the PCD preconditioner are much more stable with respect to the spatial resolution and the rate of convergence is uniformly bounded above even if the time increment stays constant and the GMRES method without any coarse grid correction is employed to solve the global-in-time system of equations. Due to the fact that the preconditioner becomes more accurate as \({\delta t}\) goes to zero, the performance of this solution strategy improves for a uniform refinement in space and time if the number of blocked time steps stays constant. In combination with the coarse grid correction, the convergence behavior of the multigrid algorithm does not depend on the number of blocked time steps and, hence, improves on finer space–time meshes even if a fixed time interval is considered. Therefore, this solution technique is the only approach, that provides convergence rates independent of the spatial mesh size and the length of the time horizon and, hence, is the method of choice for the following multigrid investigations on the Oseen equations.
7.2 Oseen Problem
In this section, we focus on the convergence behavior of the linear solution strategies under investigation when an additional convective term contributes to the conservation law of momentum. As a consequence, non-symmetric spatial operators occur in the definition of the system matrix and the characteristics of the flow change noticeably even if the viscosity is dominant. Under these conditions, the preconditioners presented in Sect. 4.2 become less accurate as the viscosity parameter goes to zero and cause an inferior convergence behavior of the iterative solution techniques especially for large time intervals. Therefore, the crucial question is how significant this loss of accuracy is and whether or not the coarse grid correction can rectify the resulting reduction in the convergence rate.
To analyse realistic flow behaviors and avoid convergence issues caused by artificially constructed solutions, we set the velocity field of the convective term to the velocity solution of the associated incompressible Navier–Stokes equations and prescribe the boundary conditions as well as the right hand sides in such a way that the numerical solution also solves the underlying nonlinear problem at hand. The resulting global-in-time linear system of equations then coincides with the one occurring in the Picard iteration for the nonlinear Navier–Stokes equations if the exact solution is used as an initial guess.
Finally, different laminar flow behaviors are considered by varying the viscosity parameter \(\mu \). While the solution profile for \(\mu = 10^{-2}\) only slightly deviates from the one of the Stokes equations, the convective term significantly changes the flow characteristics near the obstacle if the viscosity parameter is set to \(\mu = 10^{-3}\) (cf. Fig. 5). However, even in this case no vortex shedding is to be expected behind the cylinder due to the low value of the Reynolds number [31]
which is defined in terms of the characteristic length L of the geometry and the mean magnitude \({\bar{U}}(t)\) of the velocity field prescribed on the inflow boundary part of the domain, that is, the diameter of the circular obstacle \(L = 0.1\) and \({\bar{U}}(t) = \tfrac{2}{3} U_0 \bigl | \sin (\tfrac{\pi }{8} t) \bigr |\).
For \(\mu = 10^{-2}\), the convergence behavior of the iterative solution procedures is only slightly affected by the non-symmetric contribution to the system matrix and the total number of iterations fits remarkably well with the results for the Stokes equations (cf. Table 4). Especially, all considered solution strategies employing the PCD preconditioner improve as the time increment goes to zero and the two-grid algorithms exhibit a rate of convergence that depends only marginally on the total number of blocked time steps or the spatial mesh level. When considering the impact of the coarsening strategies under investigation, the two-grid algorithm using time-only coarsening minimizes the total number of iterations, while the solver based on space–time coarsening converges as fast as the slowest solution method employing either space or time coarsening. However, the use of full coarsening might still be most efficient due to the fact that the ratio between spatial and temporal resolution stays fixed and the size of the coarse grid problem reduces most rapidly. Both facts are of special interest when it comes to an underresolved solution of the coarse grid problem following the multigrid methodology. Then a coarse grid problem with up to \(4^4 \cdot 2^5 = 8192\) times less degrees of freedom has to be solved while nearly as many iterations are required as in case of the two-grid solution technique. However, the GMRES method might still outperform the multigrid solvers when the time interval under investigation is sufficiently small.
As the viscosity parameter \(\mu \) decreases, the convective contribution becomes more dominant and not only influences the flow behavior around the circular obstacle, but also deteriorates the convergence behavior of most iterative solution techniques (cf. Table 4). Especially for large time intervals, the total number of iterations required to solve the all-at-once linear system of equations grows significantly. Only the convergence rate of the two-grid algorithm employing pure time coarsening does not depend on the length of the time interval and the number of iterations stays bounded above. Unfortunately, the corresponding multigrid scheme using the V-cycle cannot reproduce this behavior and an F-cycle is mandatory in this case (not shown here). For mesh level 2, the coarse grid correction exploiting space(–time) coarsening seems to be very inaccurate and does not reduce the total number of iterations compared to the GMRES method. However, as the spatial resolution increases, the coarse grid problem becomes more accurate and reduces the total number of iterations no matter how many time steps are blocked into a single global-in-time problem.
For both considered values of the viscosity parameter, similar convergence results can also be observed when the LSC preconditioner is exploited (cf. Fig. 7). While the total number of iterations to solve the global system asymptotically does not depend on the length of the time interval for \(\mu = 10^{-2}\) and the GMRES method, the performance of the algorithm significantly deteriorates as more and more time steps are blocked if the viscosity parameter is reduced to \(\mu = 10^{-3}\). Furthermore, only the two-grid algorithm provides a uniform rate of convergence for the problem at hand and, again, the multigrid procedure using the V-cycle and time-only coarsening cannot recover this behavior. However, for small number of blocked time steps, the GMRES method exploiting one of the preconditioners under investigation even improves as the viscosity parameter goes to zero (cf. Fig. 7). Therefore, the loss of accuracy for large time intervals is (mainly) caused by the simultaneous treatment of many time steps so that further improvements might be achievable by using more advanced preconditioners.
7.3 Nonlinear Fluid Model
After the convergence behavior of the (multigrid) PSC solvers was analyzed for linear test cases, we now focus on the performance of the nonlinear solution strategy, which is of high practical interest for the simulation of real life flow fields. In the first problem, we solve the nonlinear Navier–Stokes equations as summarized in (1). The viscosity parameter is fixed to \(\mu = 10^{-2}\). For this configuration, we already observed that the linear multigrid scheme performs well (cf. Sect. 7.2), so similar results are desirable for the nonlinear test case, too. The crucial ingredient responsible for the overall performance is the nonlinear solution strategy, which should guarantee a fast, uniform, and robust convergence to the exact solution of the nonlinear problem under investigation.
In this work, we focus on two different nonlinear solvers, the Picard iteration and Newton’s method. While the former one might be more robust with respect to the initial guess, the latter one requires a sufficiently good starting value, but then converges much faster. However, in the test problem considered in this section, even the vanishing solution seems to be an adequate initial guess because the nonlinearity has only a minor influence on the solution profile (cf. Fig. 5).
Due to the fact that the linearization techniques are applied on a continuous level, the total number of nonlinear iterations required to reach the absolute stopping criterion is not sensitive to the spatial and temporal discretization per sé. Thus, the convergence behavior depends asymptotically only on the final time T and, especially, does not worsen when more accurate results are computed. For the problem under consideration, the iterates of both schemes converge even uniformly with respect to time and the number of nonlinear iterations is bounded above independently of the length of the time horizon (cf. Fig. 8). It takes only four Newton steps to bring the Euclidean norm of the pressure Schur complement residual below \(10^{-10}\), no matter how the final time T is chosen. The Picard iteration requires more than twice as many iterations, which makes the scheme less efficient than Newton’s method, as long as the computational effort for the involved linear iterations is comparable.
Since it is not practical to solve the linear Oseen equations exactly in each nonlinear iteration, we now replace the direct solver by one of the iterative (multigrid) PSC solution strategies using the PCD preconditioner. In this case, the linear solver stops not only when the Euclidean norm of the PSC residual is less than \(10^{-11}\) as before, but also after gaining four digits. The numerical effort required to solve the nonlinear system at hand is then given by the total number of linear iterations. Furthermore, the ratio between spatial and temporal resolution is fixed by the choice of \({\delta t}^{-1} = 25 \cdot 2^{\text {lvl}}\) for the sake of simplicity in all nonlinear test cases. This guarantees second order of convergence in space and time for the error in the pressure variable, while the total number of blocked time steps required to reach the same final time doubles as the space–time mesh is refined.
As observed for the corresponding linear test problem in Sect. 7.2, the convergence behavior of the GMRES method depends only on the length of the time horizon for this nonlinear test problem and deteriorates as the final time T increases (cf. Table 5). Therefore, the solution strategy has to be augmented by a coarse grid correction for achieving a uniform rate of convergence with respect to the space–time resolution as well as the final time. Especially, the total number of iterations is bounded above by a value independent of the length of the time interval for the two-grid solution algorithms. This result can be reproduced by the multigrid methods only if the F-cycle is employed. However, the V-cycle might still be more efficient for these configurations though due to the fact that the solution of the coarse grid problem is approximated in a less expensive way. When comparing different coarsening strategies, pure time coarsening results again in the least number of iterations, whereas the convergence behavior slightly improves as the space–time resolution increases if space coarsening is involved in the construction of the coarse grid problem.
For the different nonlinear solution strategies, the total number of linear iterations is approximately two times larger in case of the Picard iteration. This behavior perfectly reflects the observation made for the nonlinear solution behavior when an exact linear solver is employed. Therefore, Newton’s method indeed outperforms the Picard iteration and is worth to be applied whenever the initial guess is sufficiently good or an appropriate globalization technique is applied to guarantee convergence of the all-at-once iterates.
7.4 Carreau–Yasuda Viscosity Model
In the final example, we focus on the behavior of the global-in-time solution algorithm at hand when a nonlinear viscosity model is involved in the definition of the Navier–Stokes equations. More precisely, the Newtonian fluid rheology exploiting a constant viscosity parameter \(\mu \) is replaced by a non-Newtonian one as described by the Carreau–Yasuda model [40]
where \({\dot{\gamma }} = \sqrt{2} \bigl \Vert \text {D} ({\textbf{v}}) \bigr \Vert _\text {F}\) is the effective shear rate of the strain rate tensor \(\text {D}({\textbf{v}}) = \tfrac{1}{2} (\nabla {\textbf{v}}+ \nabla {\textbf{v}}^\top )\) and \(\mu _\infty \), \(\mu _0\), \(\lambda \), n, and a are nonnegative material coefficients. In the special case of \(a = 2\), formula (29) corresponds to the well-known Carreau-model [2] simulating shear thinning effects for \(n < 1\), which are typically used for predicting the flow behavior of materials like polyetilen. The other parameters for the configuration to be studied are set to \(\mu _\infty = 0\), \(\mu _0 = 10^{-2}\), \(\lambda = 1\), and \(n = 0.31\), which leads to an effective viscosity parameter \(\mu ({\dot{\gamma }}) \in [0.0004, 0.01]\) for the inflow boundary condition (28). Finally, a formulation of the momentum equation based on the deformation tensor is considered

which provides the possibility to describe even more complex flows and introduces an explicit coupling between both velocity components. Obviously, these modifications affect the definition of the system matrix \(\text {A}_i\) for the velocity field, which cannot be readily approximated using the pressure finite element space any more. Therefore, the PCD preconditioner is no longer defined for this problem and only iterative solvers using the LSC preconditioner are employed in this section.
By virtue of the large range of involved viscosity parameters, the flow rheology changes significantly compared to the Newtonian test cases and, for instance, exhibits less pronounced velocity peaks in the vicinity of the circular obstacle (cf. Fig. 5). This observation indicates that the nonlinearity of the momentum equation indeed becomes more dominant and makes solution of the discrete problem under investigation more challenging. When the vanishing approximation is used as an initial guess for the nonlinear solution procedure, about 9 Newton steps are required to reach the stopping criterion, while about 4 times more Picard iterations are mandatory, no matter how the final time is chosen (not shown here). In Table 6, the total number of linear iterations is summarized for different iterative solution strategies, where the Newton’s method is used for linearization. Although this value might to be bounded above independently of the length of the time interval even for the GMRES method, incorporating a coarse grid correction significantly improves the convergence behavior. However, the performance of all solution strategies under investigation deteriorates as the spatial resolution increases and, hence, is unsatisfactory especially in the case when accurate solutions on highly resolved (spatial) meshes have to be computed. These observations are in good agreement with the results for the Stokes equations as considered in Sect. 7.1.
8 Challenge of Simulating Convection-Dominated Problems
In the previous section, the performance of the proposed global-in-time solution strategy was analyzed for different linear and nonlinear test cases. Although good convergence behaviors illustrate the potential of the all-at-once method for many flow problems, difficulties were observed especially for low viscosity parameters (cf. Table 4). In this case, it is well known that the Galerkin discretization should be stabilized to produce reliable and non-oscillatory numerical solutions [19, 35, 39]. These modifications also affect the (global-in-time) iterative solver, which may become more robust and provide a uniform rate of convergence. However, in this work, we focus solely on the unstabilized finite element discretization, where several components of the (nonlinear) solution procedure become less efficient or even fail to converge for higher Reynolds numbers.
One crucial ingredient of the overall solution procedure is the use of Newton’s method to linearize the problem at hand. As the viscosity parameter decreases, the nonlinear convective contribution of the Navier–Stokes equations becomes dominant and more accurate initial guesses are commonly required to guarantee convergence. In some cases, even a hierarchical starting procedure, that is, using the numerical solution on a coarser space(-time) mesh as an initial guess, might not suffice. The Picard iteration seems to be more robust and might even converge for inaccurate starting values, as illustrated in Fig. 10 for the third test case of the well-known flow around a cylinder benchmark [31]. In this case, the viscosity parameter of the problem analyzed in Sect. 7.3 is set to \(\mu = 10^{-3}\), while the velocity magnitude of the inflow boundary data reads \(U_0 = 1.5\). Therefore, the maximum Reynolds number attains the value \(\text {Re}= 100\) at \(t = 4\) and a typical von Kármán vortex street occurs behind the circular obstacle (cf. Fig. 9). While the numerical approximation on level 3 is close to the solution on the next finer mesh, a phase error can be observed in the lift values for mesh level 2. Thus, this approximation is not an appropriate initial guess for Newton’s method and the nonlinear solution procedure must be modified for stabilization purposes. Instead of using an adaptive damping strategy as considered in [24], convergence can also be achieved by reducing the amount of reactivity during the first nonlinear iterations [26]. This is due to the fact that the Picard iteration is nothing but Newton’s method without any reactivity (see Sect. 2) and the former method seems to be sufficiently robust to guarantee convergence, no matter how the initial guess is chosen.
Benchmark 3: lift coefficient on different mesh levels computed in terms of volume integral as proposed in [17]
On the other hand, we already observed in Sect. 7.2 that the convergence behavior of the global-in-time (multigrid) PSC solver deteriorates for the linear Oseen problem as the convective contribution to the momentum equation becomes dominant. One reason for this are the PSC preconditioners under investigation, which are not accurate enough to guarantee a robust overall convergence behavior for large time intervals. This calls for further investigations and the design of more sophisticated approximations \({\textbf{C}}_K^{-1}\) which can handle convection-dominated problems more efficiently.
Finally, we emphasize that computation of the auxiliary velocity field for determining the PSC residual is another crucial ingredient of the solution procedure for high Reynolds numbers. Although these problems were solved exactly throughout this work, it is well known that the construction of corresponding parallel-in-time solvers is still a challenging task and requires further investigations [8, 9, 33]. At this point, it is worth mentioning that those velocity problems should not be solved exactly in practice and underresolved computations following the idea presented in Sect. 4.3 might significantly improve the performance of the overall solution strategy.
9 Conclusions
In this work, we presented a global-in-time pressure Schur complement (PSC) solution strategy for the incompressible Navier–Stokes equations, which exploits Newton’s method for linearization of the all-at-once problem and the multigrid methodology to construct a robust and highly parallelizable linear solver. The numerical scheme can be applied to commonly used (sequential) discretization techniques, but requires the fully implicit treatment of the pressure variable as well as a diagonal velocity mass matrix for the construction of efficient preconditioners. While the former requirement can be satisfied by interpreting the pressure variable as a Lagrange multiplier to enforce a solenoidal velocity field, the latter condition holds true, e.g., for the Galerkin discretization using quadrature-based mass lumping.
For this configuration, various numerical examples illustrate the robustness of the presented parallel-in-time multigrid solver. Especially the use of the PCD preconditioner, as first proposed by Danieli et al. [7], results in convergence rates which seem to be independent of the spatial and temporal resolution. However, in the absence of the coarse grid correction, the performance of the single-grid algorithm deteriorates as the length of the time interval increases. This adverse effect cannot be observed for the GMRES method employing the global-in-time LSC preconditioner as introduced in Sect. 4.2.2, at least for sufficiently large viscosity parameters. This preconditioner is even readily applicable when more complex fluid rheologies are simulated, but the associated solution techniques become less efficient as the spatial mesh is refined. This calls for the construction of more sophisticated preconditioners combining the benefits of both candidates under investigation. Even the design of a solution strategy which does not require a multigrid acceleration might be possible. Otherwise, the development of global-in-time coarse grid solvers, which do not iterate sequentially through all time steps, should also be pursued.
In summary, the most expensive parts of the multigrid scheme are given by the solution of several independent Poisson-like problems in the application of the preconditioner as well as the computation of the auxiliary velocity field to determine the pressure Schur complement residual. While the set of independent Poisson problems provides capabilities for naive parallelism, the latter subproblem corresponds to the solution of a (vector-valued) convection–diffusion–reaction equation and, hence, acts as a model problem for many parallel-in-time solution techniques per sé. Unfortunately, it occurs in each application of the all-at-once PSC system matrix and has to be solved exactly to guarantee convergence of the GMRES method. This makes the solution procedure very expensive in practical applications and calls for a solution technique defined in terms of the primal formulation as considered in Sect. 4.3. In this case, the exact solution of the momentum equation is not required any more due to the fact that only an approximation to the inverse of the velocity system matrix occurs in the definition of the preconditioner. Eventually, it might even be worthwhile to exploit this formulation for transferring the residual and solution update between different mesh hierarchies due to the fact that another calculation of the pressure Schur complement residual then becomes redundant.
From a theoretical point of view, the global-in-time preconditioned Richardson iteration applied to solution of the incompressible Stokes equations should be analyzed in the first place. This linear algorithm behaves similarly to the GMRES method and, hence, is most suitable to investigate the impact of different preconditioners.
Change history
17 August 2023
A Correction to this paper has been published: https://doi.org/10.1007/s00021-023-00819-2
References
Cahouet, J., Chabard, J.-P.: Some fast 3D finite element solvers for the generalized Stokes problem. Int. J. Numer. Methods Fluids 8(8), 869–895 (1988)
Carreau, P.J.: Rheological equations from molecular network theories. Trans. Soc. Rheol. 16(1), 99–127 (1972)
Celledoni, E., Kvamsdal, T.: Parallelization in time for thermo-viscoplastic problems in extrusion of aluminium. Int. J. Numer. Methods Eng. 79(5), 576–598 (2009)
Christopher, J.: Space–time adaptivity with multigrid reduction in time for the compressible Navier–Stokes equations (2019)
Christopher, J., Falgout, R.D., Schroder, J.B., Guzik, S.M., Gao, X.: A space–time parallel algorithm with adaptive mesh refinement for computational fluid dynamics. Comput. Visu. Sci. 23, 1–20 (2020)
Croce, R., Ruprecht, D., Krause, R.: Parallel-in-space-and-time simulation of the three- dimensional, unsteady Navier–Stokes equations for incompressible flow. In: Bock, H.G., Hoang, X.P., Rannacher, R., Schlöder, J.P. (eds.) Modeling, Simulation and Optimization of Complex Processes—HPSC 2012, pp. 13–23. Springer, Cham (2014)
Danieli, F., Southworth, B.S., Wathen, A.J.: Space–time block preconditioning for incompressible flow. SIAM J. Sci. Comput. 44(1), A337–A363 (2022)
De Sterck, H., Friedhoff, S., Howse, A.J.M., MacLachlan, S.P.: Convergence analysis for parallel-in-time solution of hyperbolic systems. Numer. Linear Algebra Appl. 27(1), e2271 (2020)
De Sterck, H., Falgout, R.D., Friedhoff, S., Krzysik, O.A., MacLachlan, S.P.: Optimizing multigrid reduction-in-time and Parareal coarse-grid operators for linear advection. Numer. Linear Algebra Appl. 28(4), e2367 (2021)
Elman, H.C.: Preconditioning for the steady-state Navier–Stokes equations with low viscosity. SIAM J. Sci. Comput. 20(4), 1299–1316 (1999)
Elman, H., Howle, V.E., Shadid, J., Shuttleworth, R., Tuminaro, R.: Block preconditioners based on approximate commutators. SIAM J. Sci. Comput. 27(5), 1651–1668 (2006)
Elman, H., Silvester, D., Wathen, A.: Finite Elements and Fast Iterative Solvers: With Applications in Incompressible Fluid Dynamics. Numerical Mathematics and Scientific Computation, p. 496. Oxford University Press, Oxford (2014)
Falgout, R.D., Katz, A., Kolev, T.V., Schroder, J.B., Wissink, A.M., Yang, U.M.: Parallel Time Integration with Multigrid Reduction for a Compressible Fluid Dynamics Application. Lawrence Livermore National Laboratory, Livermore (2014)
Fischer, P.F., Hecht, F., Maday, Y.: A parareal in time semi-implicit approximation of the Navier–Stokes equations. In: Barth, T.J., Griebel, M., Keyes, D.E., Nieminen, R.M., Roose, D., Schlick, T., Kornhuber, R., Hoppe, R., Périaux, J., Pironneau, O., Widlund, O., Xu, J. (eds.) Domain Decomposition Methods in Science and Engineering, pp. 433–440. Springer, Berlin, Heidelberg (2005)
Gander, M.J.: 50 years of time parallel time integration. In: Carraro, T., Geiger, M., Körkel, S., Rannacher, R. (eds.) Multiple Shooting and Time Domain Decomposition Methods, pp. 69–113. Springer, Cham (2015)
Gresho, P.M., Sani, R.L.: Incompressible flow and the finite element method. Volume 1: Advection–diffusion and isothermal laminar flow (1998)
John, V.: Reference values for drag and lift of a two-dimensional time-dependent flow around a cylinder. Int. J. Numer. Methods Fluids 44(7), 777–788 (2004)
John, V.: Solvers for the Coupled Linear Systems of Equations. Springer, Cham (2016)
John, V., Kaya, S.: A finite element variational multiscale method for the Navier–Stokes equations. SIAM J. Sci. Comput. 26(5), 1485–1503 (2005)
Kay, D., Loghin, D., Wathen, A.: A preconditioner for the steady-state Navier–Stokes equations. SIAM J. Sci. Comput. 24(1), 237–256 (2002)
Kooij, G.L., Botchev, M.A., Geurts, B.J.: An exponential time integrator for the incompressible Navier–Stokes equation. SIAM J. Sci. Comput. 40(3), B684–B705 (2018)
Köster, M.: A hierarchical flow solver for optimisation with PDE constraints. In: Slightly Corrected Version with an Additional Appendix Concerning Prolongation/restriction. PhD Thesis. Lehrstuhl III für Angewandte Mathematik und Numerik: TU Dortmund (2011)
Kuzmin, D., Hämäläinen, J.: Finite Element Methods for Computational Fluid Dynamics: A Practical Guide. Society for Industrial and Applied Mathematics, Philadelphia (2014)
Lemoine, J., Münch, A.: A fully space–time least-squares method for the unsteady Navier–Stokes system. J. Math. Fluid Mech. 23, 1–38 (2021)
Lions, J.-L., Maday, Y., Turinici, G.: Résolution d’EDP par un schéma en temps \(<<\)pararéel \(>>\). C. R. l’Acad. Sci. Ser. I Math. 332(7), 661–668 (2001)
Mandal, S., Ouazzi, A., Turek, S.: Modified Newton solver for yield stress fluids. In: Karasözen, B., Manguoğlu, M., Tezer-Sezgin, M., Göktepe, S., Uğur, Ö. (eds.) Numerical Mathematics and Advanced Applications ENUMATH 2015, pp. 481–490. Springer, Cham (2016)
Miao, Z., Jiang, Y.-L., Yang, Y.-B.: Convergence analysis of a parareal-in-time algorithm for the incompressible non-isothermal flows. Int. J. Comput. Math. 96(7), 1398–1415 (2019)
Ong, B.W., Schroder, J.B.: Applications of time parallelization. Comput. Vis. Sci. 23, 1–15 (2020)
Patankar, S., Spalding, D.: A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 15(10), 1787–1806 (1972)
Quarteroni, A., Valli, A.: Numerical Models for Differential Problems. Springer, Berlin, Heidelberg (2017)
Schäfer, M., Turek, S., Durst, F., Krause, E., Rannacher, R.: Benchmark computations of laminar flow around a cylinder. In: Flow Simulation with High-Performance Computers II, pp. 547–566. Springer (1996)
Steiner, J., Ruprecht, D., Speck, R., Krause, R.: Convergence of parareal for the Navier–Stokes equations depending on the Reynolds number. In: Abdulle, A., Deparis, S., Kressner, D., Nobile, F., Picasso, M. (eds.) Numerical Mathematics and Advanced Applications—ENUMATH 2013, pp. 195–202. Springer, Cham (2015)
Sterck, H.D., Falgout, R.D., Krzysik, O.A.: Fast multigrid reduction-in-time for advection via modified semi-Lagrangian coarse-grid operators (2022)
Taylor, C., Hood, P.: A numerical solution of the Navier–Stokes equations using the finite element technique. Comput. Fluids 1(1), 73–100 (1973)
Tezduyar, T.E., Osawa, Y.: Finite element stabilization parameters computed from element matrices and vectors. Comput. Methods Appl. Mech. Eng. 190(3), 411–430 (2000)
Trindade, J.M.F., Pereira, J.C.F.: Parallel-in-time simulation of the unsteady Navier–Stokes equations for incompressible flow. Int. J. Numer. Methods Fluids 45(10), 1123–1136 (2004)
Trindade, J.M.F., Pereira, J.C.F.: Parallel-in-time simulation of two-dimensional, unsteady, incompressible laminar flows. Numer. Heat Transf. Part B Fundam. 50(1), 25–40 (2006)
Turek, S.: Efficient Solvers for Incompressible Flow Problems: An Algorithmic and Computational Approach. Springer, Berlin, Heidelberg (1999)
Turek, S., Ouazzi, A.: Unified edge-oriented stabilization of nonconforming FEM for incompressible flow problems: numerical investigations. J. Numer. Math. 15(4), 299–322 (2007)
Yasuda, K., Armstrong, R.C., Cohen, R.E.: Shear flow properties of concentrated solutions of linear and star branched polystyrenes. Rheol. Acta 20, 163–178 (1981)
Acknowledgements
The authors gratefully acknowledge the computing time provided on the Linux HPC cluster at TU Dortmund University (LiDO3), partially funded in the course of the Large-Scale Equipment Initiative by the German Research Foundation (DFG) as project 271512359.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original article has been revised as the corrections were missed in Figure captions 9 & 10. The article has been updated.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lohmann, C., Turek, S. On the Design of Global-in-Time Newton-Multigrid-Pressure Schur Complement Solvers for Incompressible Flow Problems. J. Math. Fluid Mech. 25, 64 (2023). https://doi.org/10.1007/s00021-023-00807-6
Accepted:
Published:
DOI: https://doi.org/10.1007/s00021-023-00807-6