1 Introduction

In this paper we consider two-dimensional steady gravity water waves with constant vorticity, subject to the influence of only gravity, but not surface tension. Moreover, we assume that the corresponding flows are unidirectional and that the sign of the vorticity is favorable. For concreteness, we assume that the vorticity \(\omega \) is positive, while the relative horizontal velocity is negative. This means that the waves we consider are “downstream” waves, that is, the underlying currents are sheared in the same direction as the wave propagation (see [4, Section 5]). Such currents can be thought of as being induced by a wind parallel to the direction of the wave propagation. In correspondence with physical intuition and numerical studies (see, for example, [5, 9]), these currents should flatten out the wave. Indeed, we derive an explicit bound for the amplitude of the wave profile, which also shows that the amplitudes have to become very small as the vorticity grows without limit. It is notable that the new bound is independent of the total head and the mass flux constants. This is quite different to the irrotational case, where the maximum amplitude might depend on the mass flux. In particular, for any large relative flux m there exist waves of arbitrarily large amplitudes that depend on m (see Sect. 4 for details).

We emphasize that our result holds for any water wave as described above. In particular, we do not have to assume that the wave is periodic or solitary or symmetric. Also, it does not necessarily have to be on a solution branch bifurcating from a configuration with a flat surface. Quite recently, a bound for the wave amplitude was, among other things, derived in [4], however restricted to the case of periodic and symmetric waves on such a bifurcation branch. Moreover, our proof is much simpler than the one in [4] and the result also in the restricted case is sharper in the sense that it provides an \(\mathcal O(\omega ^{-2})\) (instead of \({\mathcal {O}}(\omega ^{-1})\)) decay of the amplitude as the vorticity \(\omega \) tends to infinity. In the irrotational case, \(\omega = 0\), some new bounds for the wave amplitude were obtained recently in [8]. Similar inequalities for the amplitude, but for a negative constant vorticity, are not known. In this case any bound of the form \({\mathcal {O}}(1)\) as \(\omega \rightarrow -\infty \) would be of great interest.

In general, different a priori bounds such as for the total head or for the surface profile have proved to be useful for the analysis of large-amplitude solutions and extreme waves. Indeed, in typical global bifurcation results (see, for example, [2, 3, 12]) one is often left with several possible alternatives, and such an a priori bound yields that one has to approach a wave of extreme form when following the bifurcation branch. For instance, the result in [12] requires a global bound for the total head. In fact, especially in the rotational case the literature proving this limiting behavior is quite sparse and progress has been made only recently; see [4, 7]. The question of (non)existence for extreme waves with a negative vorticity is more subtle, and no similar bounds for the amplitude are known so far.

Let us also emphasize that the case of constant vorticity is not just a mathematical simplification irrelevant in the real physical world. Indeed, as pointed out in [3], for wavelengths much larger than the average mean depth of the water, the mean of the vorticity is more important than its specific distribution; see [11]. Also, constant vorticity flows are a good model for tidal currents, with positive (negative) vorticity corresponding to the flood (ebb); see also [1].

Furthermore, we remark that, while we derive a bound on the wave amplitude, in our situation bounds on the slope of the water surface have already been established in [10], at least for periodic or solitary waves with symmetry.

2 Statement of the Problem

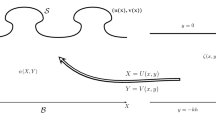
We consider the classical model for two-dimensional steady waves on water of finite depth. We neglect the effects of surface tension and consider an ideal fluid of constant (unit) density. In the corresponding moving reference frame the stationary Euler equations are given by

$$\begin{aligned} (u-c)u_x + vu_y&= -P_x, \end{aligned}$$
(1a)
$$\begin{aligned} (u-c)v_x + vv_y&= -P_y-g, \end{aligned}$$
(1b)
$$\begin{aligned} u_x + v_y&= 0, \end{aligned}$$
(1c)
$$\begin{aligned} u_y - v_x&= \omega , \end{aligned}$$
(1d)

which hold true in a two-dimensional fluid domain \(D_{\eta }\), defined by the inequality

$$\begin{aligned} 0< y < \eta (x). \end{aligned}$$

Here, (u, v) are components of the velocity field, \(y = \eta (x)\) is the surface profile, c is the wave speed, P is the pressure, and g is the gravitational constant. The corresponding boundary conditions are

$$\begin{aligned} v&= 0\qquad \text {on } y=0, \end{aligned}$$
(1e)
$$\begin{aligned} v&= (u-c)\eta _x{} & {} \text {on } y=\eta , \end{aligned}$$
(1f)
$$\begin{aligned} P&= P_{\textrm{atm}}{} & {} \text {on } y=\eta . \end{aligned}$$
(1g)

Note that our definition of the (scalar) vorticity \(\omega \) is the same as in [3, 4], whereas other sources take the vorticity to be \(-\omega \); see e.g. [2, 6, 10, 12].

We reformulate these equations in terms of a stream function \(\psi \), defined implicitly by the relations

$$\begin{aligned} \psi _y = c-u, \ \ \psi _x = v. \end{aligned}$$

This determines \(\psi \) up to an additive constant, while relations (1e), (1f) require \(\psi \) to be constant along the boundaries. Thus, by subtracting a suitable constant we assume that

$$\begin{aligned} \psi = m \text { on } y = \eta , \quad \psi = 0 \text { on } y = 0. \end{aligned}$$

Here m is the mass flux, defined by

$$\begin{aligned} m = \int _0^{\eta } (c-u) dy. \end{aligned}$$

The corresponding problem for the stream function is

$$\begin{aligned} \Delta \psi + \omega&=0 \qquad \text {in } D_{\eta }, \end{aligned}$$
(2a)
$$\begin{aligned} \tfrac{1}{2}|\nabla \psi |^2 + g y&= Q \quad \text {on }y=\eta , \end{aligned}$$
(2b)
$$\begin{aligned} \psi&= m \quad \text {on }y=\eta , \end{aligned}$$
(2c)
$$\begin{aligned} \psi&= 0 \quad \text {on }y=0. \end{aligned}$$
(2d)

In what follows we will consider the case when the flow is unidirectional, that is,

$$\begin{aligned} \psi _y > 0 \end{aligned}$$
(2e)

everywhere in \(\overline{D_\eta }\).

Our main result now can be stated as follows.

Theorem 2.1

Assume that \(\omega > 0\) is a constant. Let \(\psi \in C^{2}(\overline{D_\eta })\) and \(\eta \in C^1(\mathbb {R})\) be an arbitrary solution to (2) for some constants m and Q. Then

$$\begin{aligned} \sup _{x \in \mathbb {R}}{\eta (x)} - \inf _{x \in \mathbb {R}}{\eta (x)} < 2 g \omega ^{-2}, \end{aligned}$$

that is, the maximum possible wave amplitude is controlled by the size of the vorticity.

Our proof is essentially based on fundamental bounds for the surface profile and the Bernoulli constant. We give now all necessary details regarding these bounds.

2.1 Bounds on the Bernoulli Constant and the Surface Profile

Here we state the result that was proved in [6]. We will apply it to various formulations with different gravitational constants and so we need to state it here in a general form. Thus, we consider a problem

$$\begin{aligned} \Delta {\hat{\psi }} + {\hat{\omega }}&=0 \qquad \text {in } D_{{\hat{\eta }}}, \end{aligned}$$
(3a)
$$\begin{aligned} \tfrac{1}{2}|\nabla {\hat{\psi }} |^2 + \hat{g} \hat{y}&= \hat{Q} \quad \text {on }\hat{y}={\hat{\eta }}, \end{aligned}$$
(3b)
$$\begin{aligned} {\hat{\psi }}&= \hat{m} \quad \text {on }\hat{y}={\hat{\eta }}, \end{aligned}$$
(3c)
$$\begin{aligned} {\hat{\psi }}&= 0 \quad \text {on } \hat{y}=0, \end{aligned}$$
(3d)

under the assumption

$$\begin{aligned} {\hat{\psi }}_{\hat{y}} > 0 \end{aligned}$$
(3e)

everywhere in \(\overline{D_{{\hat{\eta }}}}\). In (3a) the vorticity \({\hat{\omega }}\) is a positive constant.

This system admits a class of stream solutions that are independent of \(\hat{x}\). We can compute these solutions \({\hat{\psi }} = {\hat{\Psi }}\), \({\hat{\eta }} = \hat{d}\) explicitly as

$$\begin{aligned} {\hat{\Psi }}(\hat{y};\hat{s}) = - \tfrac{1}{2} {\hat{\omega }} \hat{y}^2 + \hat{s} \hat{y}, \ \ \hat{d}(\hat{s}) = \int _0^{\hat{m}} \frac{1}{\sqrt{\hat{s}^2-2{\hat{\omega }} p}} dp. \end{aligned}$$

The corresponding constant \(\hat{Q}\) in (3b) is then given by

$$\begin{aligned} \hat{Q}(\hat{s}) = \tfrac{1}{2} \hat{s}^2 - {\hat{\omega }} \hat{m} + \hat{g} \hat{d}(\hat{s}). \end{aligned}$$

Note that in order to satisfy (3b), (3e) it is required that

$$\begin{aligned} \hat{s} > \hat{s}_0 = \sqrt{2 \hat{m} {\hat{\omega }}}. \end{aligned}$$

Computing the derivative with respect to \(\hat{s}\), we find

$$\begin{aligned} \frac{\partial \hat{Q}}{\partial \hat{s}} = \hat{s} \left( 1 - \hat{g} \int _0^{\hat{m}} \frac{1}{(\hat{s}^2-2{\hat{\omega }} p)^{3/2}} dp \right) . \end{aligned}$$

Thus, there exists a unique \(\hat{s} = \hat{s}_c\) for which the derivative is zero and this value can be found from the equation

$$\begin{aligned} \hat{g} \int _0^{\hat{m}} \frac{1}{(\hat{s}_c^2-2{\hat{\omega }} p)^{3/2}} dp = 1. \end{aligned}$$

Let us denote by \(\hat{Q}_0=\hat{g}\sqrt{2\hat{m}/{\hat{\omega }}}\) and \(\hat{Q}_c\) the corresponding constants \(\hat{Q}(\hat{s})\) for \(\hat{s} = \hat{s}_0\) and \(\hat{s} = \hat{s}_c\) respectively.

Assume that we are given some \(\hat{q} \in (\hat{Q}_c, \hat{Q}_0)\). Then the equation

$$\begin{aligned} \hat{Q}(\hat{s}) = \hat{q} \end{aligned}$$

has exactly two distinct solutions \(\hat{s} = \hat{s}_-(\hat{q})\) and \(\hat{s} = \hat{s}_+(\hat{q})\) with \(\hat{s}_- < \hat{s}_+\). The corresponding depths are given by

$$\begin{aligned} \hat{d}_+(\hat{q}) = \hat{d}(\hat{s}_-(\hat{q})), \ \ \hat{d}_-(\hat{q}) = \hat{d}(\hat{s}_+(\hat{q})). \end{aligned}$$

They are defined so that \(\hat{d}_- < \hat{d}_+\). Now we are ready to formulate a part of Theorem 1 from [6].

Proposition 2.2

Let \({\hat{\psi }} \in C^2(\overline{D_{{\hat{\eta }}}})\) and \({\hat{\eta }} \in C^1(\mathbb {R})\) be a non-stream solution to (3) for some constant \(\hat{Q}\) in \(\mathbb {R}\). Then \(\hat{Q} \in (\hat{Q}_c, \hat{Q}_0)\) and the following is true:

  1. (i)

    \(\inf {\hat{\eta }} \ge \hat{d}_-(\hat{Q})\) and \(\inf {\hat{\eta }} \le \hat{d}_+(\hat{Q})\);

  2. (ii)

    \(\sup {\hat{\eta }} \ge \hat{d}_+(\hat{Q})\) and \(\sup {\hat{\eta }} \le \hat{d}_0:=\hat{d}(\hat{s}_0)=\sqrt{2\hat{m}/{\hat{\omega }}}\).

Here, \(\hat{d}_-(\hat{Q})\) and \(\hat{d}_+(\hat{Q})\) are well defined because \(\hat{Q} \in (\hat{Q}_c, \hat{Q}_0)\).

A proof of this result is given in [6] even for non-constant vorticity functions.

3 Proof of Theorem 2.1

Without loss of generality we can assume that \((\psi ,\eta )\) is not a stream solution. Then let us consider a scaling of variables, where the relative mass flux and the vorticity are scaled to unity. More precisely, we put

$$\begin{aligned} \tilde{x} = \lambda x, \ \ \tilde{y} = \lambda y,\ \ {\tilde{\eta }}(\tilde{x}) = \lambda \eta (\lambda ^{-1} \tilde{x}), \ \ {\tilde{\psi }}(\tilde{x},\tilde{y}) = m^{-1}\psi (x,y) \end{aligned}$$

where

$$\begin{aligned} \lambda = \left( \frac{\omega }{m}\right) ^{1/2}. \end{aligned}$$

The corresponding non-dimensional problem is

$$\begin{aligned} \Delta {\tilde{\psi }} +1&=0 \qquad \text {in } D_{{\tilde{\eta }}} {:=}\{(\tilde{x},\tilde{y}): 0< \tilde{y} < {\tilde{\eta }}\},\\ \tfrac{1}{2}|\nabla {\tilde{\psi }} |^2 + \epsilon \tilde{y}&= \tilde{Q} \quad \text {on }\tilde{y}={\tilde{\eta }},\\ {\tilde{\psi }}&= 1 \quad \text {on }\tilde{y}={\tilde{\eta }},\\ {\tilde{\psi }}&= 0 \quad \text {on }\tilde{y}=0. \end{aligned}$$

Here

$$\begin{aligned} \epsilon = \frac{g}{m^{1/2}\omega ^{3/2}},\quad \tilde{Q}=\frac{Q}{m\omega }. \end{aligned}$$

We will follow the same notation system as introduced in the previous section. Thus, we define in a similar way all the quantities such as \(\tilde{Q}_0, \tilde{Q}_c, \tilde{d}(\tilde{s})\) and so on. The corresponding values for the original system (2) we will denote with the same letters but without tildes.

By Proposition 2.2 we have

$$\begin{aligned} \tilde{Q} < \tilde{Q}_0 = \epsilon \sqrt{2} \end{aligned}$$

and

$$\begin{aligned} \tilde{d}_1{:=}\tilde{d}_-(\tilde{Q}_0) \le {\tilde{\eta }} \le \tilde{d}_0 = \sqrt{2}. \end{aligned}$$

Our aim is to show that

$$\begin{aligned} \tilde{d}_0 - \tilde{d}_1 < 2 \epsilon . \end{aligned}$$
(4)

If this is true, then

$$\begin{aligned} \sup \eta -\inf \eta = \lambda ^{-1} (\sup {\tilde{\eta }} - \inf {\tilde{\eta }}) \le \lambda ^{-1} (\tilde{d}_0 - \tilde{d}_1) < 2 \lambda ^{-1} \epsilon = 2 g \omega ^{-2} \end{aligned}$$

as desired. Here we used the inequality \(\tilde{d}_-(\tilde{Q}) > \tilde{d}_1\), which is valid since \(\tilde{Q} \in (\tilde{Q}_c,\tilde{Q}_0)\).

In order to verify (4), we consider two cases: First, assume that \(\epsilon \ge \sqrt{2}/2\). Then, clearly,

$$\begin{aligned} {\tilde{d}}_0-{\tilde{d}}_1=\sqrt{2}-{\tilde{d}}_1<\sqrt{2}\le 2\epsilon \end{aligned}$$

and (4) holds.

If on the other hand \(\epsilon <\sqrt{2}/2\), we first note that

$$\begin{aligned} (\sqrt{2},\infty )\ni {\tilde{s}}\mapsto {\tilde{d}}({\tilde{s}})=\int _0^1 \frac{1}{\sqrt{{\tilde{s}}^2-2p} } \, dp={\tilde{s}}-\sqrt{{\tilde{s}}^2-2}\in (0,\sqrt{2}) \end{aligned}$$

is bijective with inverse

$$\begin{aligned} {\tilde{s}}({\tilde{d}})=\frac{{\tilde{d}}}{2}+\frac{1}{{\tilde{d}}}, \quad {\tilde{d}}\in (0,\sqrt{2}). \end{aligned}$$

Let us correspondingly express \({\tilde{Q}}\) as a function of \({\tilde{d}}\):

$$\begin{aligned} {\tilde{Q}}({\tilde{d}})=\frac{1}{2} {\tilde{s}}({\tilde{d}})^2-1+\epsilon {\tilde{d}}=\frac{\tilde{d}^2}{8}+\frac{1}{2{\tilde{d}}^2}-\frac{1}{2}+\epsilon \tilde{d},\quad {\tilde{d}}\in (0,\sqrt{2}). \end{aligned}$$

Therefore,

$$\begin{aligned} {\tilde{Q}}(\sqrt{2}-\delta )-\epsilon \sqrt{2} =-\epsilon \delta +\frac{1}{2} \delta ^2+\frac{\delta ^3(4\sqrt{2}-3\delta )}{8(\sqrt{2}-\delta )^2}>-\epsilon \delta +\frac{1}{2} \delta ^2,\quad \delta \in (0,\sqrt{2}). \end{aligned}$$

Since \((0,2\epsilon )\subset (0,\sqrt{2})\), it follows that \(\tilde{Q}(\sqrt{2}-\delta )-\epsilon \sqrt{2}\) has a root \(\delta \in (0,2\epsilon )\). This root \(\delta \) has to satisfy \(\sqrt{2}-\delta ={\tilde{d}}_1\), that is, \({\tilde{d}}_0-\tilde{d}_1=\delta \). Thus, (4) also holds in this case and the proof of Theorem 2.1 is complete.

4 On the Amplitude for Irrotational Waves

The aim of this section is to show that there exist periodic irrotational waves of large amplitude that depends on the relative mass flux m. A precise statement is given below.

Theorem 4.1

There is an absolute constant \(r_\star \) such that for any positive Q and m with \(Q/(m g)^{2/3} \ge r_\star \) there exist periodic solutions to the problem (2) with \(\omega = 0\) for which the amplitude satisfies the inequality

$$\begin{aligned} \sup _{x \in \mathbb {R}}{\eta (x)} - \inf _{x \in \mathbb {R}}{\eta (x)} \ge \frac{m^2 g}{4Q^2}. \end{aligned}$$

Note that the opposite inequality (with another absolute constant) is always true as was recently shown in [8].

Now we can use this result to show that there exist periodic waves of arbitrary large amplitude. Indeed, we choose \(Q = Q(m) = r_\star (m g)^{2/3}\) so that Q(m) and m satisfy the assumptions of the theorem for any m. Thus, by Theorem 4.1 there exist periodic solutions with amplitudes greater than \(\tfrac{1}{4} m^{2/3} g^{-1/3} r_\star ^{-2}\). Now we clearly see that the amplitude becomes arbitrary large for large m. It is remarkable that for rotational waves this is no longer true as follows from our Theorem 2.1.

Proof of Theorem 4.1

In order to simplify the argument it is convenient to use the non-dimensional variables where m and g are scaled to unity. This leads to an equivalent problem

$$\begin{aligned} \Delta {\bar{\psi }}&=0 \qquad \text {in } D_{{\bar{\eta }}}, \end{aligned}$$
(5a)
$$\begin{aligned} \tfrac{1}{2}|\nabla {\bar{\psi }} |^2 + {\bar{y}}&= r \quad \text {on }{\bar{y}}={\bar{\eta }}, \end{aligned}$$
(5b)
$$\begin{aligned} {\bar{\psi }}&= 1 \quad \text {on }{\bar{y}}={\bar{\eta }}, \end{aligned}$$
(5c)
$$\begin{aligned} {\bar{\psi }}&= 0 \quad \text {on }{\bar{y}}=0. \end{aligned}$$
(5d)

Here

$$\begin{aligned} r = \frac{Q}{(m g)^{2/3}}, \quad {\bar{\eta }} = \frac{\eta }{(m^2/g)^{1/3}}. \end{aligned}$$

It is known that for any sufficiently large r there exists a connected family of periodic solutions approaching an extreme wave with \(\max {\bar{\eta }} = r\). A rigorous proof of this result is given in [7]. On the other hand, we know that for any solution we have

$$\begin{aligned} \inf {\bar{\eta }} \le {\bar{d}}_+(r) \end{aligned}$$

by Proposition 2.2, where \({\bar{d}}_+(r)\) is the greatest root to

$$\begin{aligned} \frac{1}{2 {\bar{d}}^2} + {\bar{d}} = r. \end{aligned}$$

We see that \({\bar{d}}_+(r) \le r - \tfrac{1}{2} r^{-2}\). For an extreme wave \(\sup {\bar{\eta }} = r\) and so there must be periodic solutions with

$$\begin{aligned} \sup {\bar{\eta }} - \inf {\bar{\eta }} \ge \tfrac{1}{4} r^{-2}. \end{aligned}$$

Now scaling back the variables we obtain the desired inequality, provided r is large enough. \(\square \)