Existence of Steady Solutions for a Model for Micropolar Electrorheological Fluid Flows with Not Globally log-Hölder Continuous Shear Exponent

Abstract

In this paper, we study the existence of weak solutions to a steady system that describes the motion of a micropolar electrorheological fluid. The constitutive relations for the stress tensors belong to the class of generalized Newtonian fluids. The analysis of this particular problem leads naturally to weighted variable exponent Sobolev spaces. We establish the existence of solutions for a material function ${\hat{p}}$ that is $\log$-Hölder continuous and an electric field $\textbf{E}$ for that $\vert \textbf{E}\vert ^2$ is bounded and smooth. Note that these conditions do not imply that the variable shear exponent $p={\hat{p}}\circ \vert \textbf{E}\vert ^2$ is globally $\log$-Hölder continuous.

1 Introduction

In this paper we establish the existence of solutions of the system¹

$$\begin{aligned} \begin{aligned} -{{\,\mathrm{{\text {div}}}\,}}{\textbf{S}}+{{\,\mathrm{{\text {div}}}\,}}({\textbf{v}}\otimes {\textbf{v}}) +\nabla \pi&={\textbf{f}}&\text {in} \ \Omega \,, \\ {{\,\mathrm{{\text {div}}}\,}}{\textbf{v}}&=0&\text {in} \ \Omega \,, \\ -{{\,\mathrm{{\text {div}}}\,}}{\textbf{N}}+{{\,\mathrm{{\text {div}}}\,}}(\varvec{\omega }\otimes {\textbf{v}})&=\varvec{\ell }-{\varvec{\varepsilon }}:{\textbf{S}}&\text {in} \ \Omega \,,\\ {\textbf{v}}={\textbf{0}}\,, \quad \varvec{\omega }&={\textbf{0}}&\text {on}\ \partial \Omega \,. \end{aligned} \end{aligned}$$

(1.1)

Here, $\Omega \subseteq \mathbb {R}^d$, $d\ge 2$, is a bounded domain. The three equations in (1.1) represent the balance of momentum, mass and angular momentum for an incompressible, micropolar electrorheological fluid. In it, $\textbf{v}$ denotes the velocity, $\varvec{\omega }$ the micro-rotation, $\pi$ the pressure, $\textbf{S}$ the mechanical extra stress tensor, $\textbf{N}$ the couple stress tensor, $\varvec{\ell }$ the electromagnetic couple force, ${\textbf{f}={\tilde{\textbf{f}}} + \chi ^E{{\,\textrm{div}\,}}(\textbf{E}\otimes \textbf{E})}$ the body force, where ${\tilde{\textbf{f}}}$ is the mechanical body force, $\chi ^E$ the dielectric susceptibility and $\textbf{E}$ the electric field. The electric field $\textbf{E}$ solves the quasi-static Maxwell’s equations

$$\begin{aligned} \begin{aligned}&{{\,\mathrm{{\text {div}}}\,}}{\textbf{E}}=0{} & {} \text {in}\ \Omega \,, \\&{{\,\textrm{curl}\,}}{\textbf{E}}={\textbf{0}}{} & {} \text {in}\ \Omega \,, \\&{\textbf{E}}\cdot {\textbf{n}}={\textbf{E}}_0\cdot {\textbf{n}}{} & {} \text {on}\ \partial \Omega \,, \end{aligned} \end{aligned}$$

(1.2)

where ${\textbf{n}}$ is the outer normal vector field of $\partial \Omega$ and ${\textbf{E}}_0$ is a given electric field. The system (1.1), (1.2) is the steady version of a model derived in [9], which generalizes previous models of electrorheological fluids in [29, 31]. The model in [9] contains a more realistic description of the dependence of the electrorheological effect on the direction of the electric field. Since Maxwell’s equations (1.2) are separated from the balance laws (1.1) and due to the well developed mathematical theory for Maxwell’s equations (cf. Sect. 3), we can view the electric field $\textbf{E}$ with appropriate properties as a given quantity in (1.1). As a consequence, we concentrate in this paper on the investigation of the mechanical properties of the electrorheological fluid governed by (1.1).

A representative example for a constitutive relation for the stress tensors in (1.1) reads, e.g., (cf. [9, 31])

$$\begin{aligned} \begin{aligned} {\textbf{S}}&=(\alpha _{31}+\alpha _{33}\vert {\textbf{E}}\vert ^2) (1+\vert {\textbf{D}}\vert )^{p-2}{\textbf{D}}+ \alpha _{51} (1+\vert {\textbf{D}}\vert )^{p-2}\big ({\textbf{D}} \textbf{E}\otimes \textbf{E}+ \textbf{E}\otimes \textbf{D}\textbf{E}\big ) \\&\quad + \alpha _{71}\vert {\textbf{E}}\vert ^2(1+\vert {\textbf{R}}\vert )^{p-2} {\textbf{R}} + \alpha _{91} (1+\vert {\textbf{R}}\vert )^{p-2}\big ({\textbf{R}} \textbf{E}\otimes \textbf{E}+ \textbf{E}\otimes \textbf{R}\textbf{E}\big )\,, \\ {\textbf{N}}&=(\beta _{31}+\beta _{33}\vert {\textbf{E}}\vert ^2) (1+\vert \nabla \varvec{\omega }\vert )^{p-2}\nabla \varvec{\omega }\\&\quad + \beta _{51}(1+\vert \nabla \varvec{\omega }\vert )^{p-2}\big ((\nabla \varvec{\omega })\textbf{E}\otimes \textbf{E}+ \textbf{E}\otimes (\nabla \varvec{\omega })\textbf{E}\big )\,, \end{aligned} \end{aligned}$$

(1.3)

with material constants $\alpha _{31},\alpha _{33},\alpha _{71},\beta _{33}> 0$ and $\beta _{31}\ge 0$ and a shear exponent $p={\hat{p}} \circ {|{\textbf{E}}|}^2$, where ${\hat{p}}$ is a material function. In (1.3), we employed the common notation²${{\textbf {R}}={\textbf {R}}({\textbf {v}},\varvec{\omega }):= (\nabla {\textbf {v}})^{\text {skew}}+{\varvec{\varepsilon }}:\varvec{\omega }}$ and ${\textbf {D}}= (\nabla {\textbf {v}})^{\text {sym}}$.

Micropolar fluids have been introduced by Eringen in the sixties (cf. [10]). A model for electrorheological fluids was proposed in [29,30,31]. While there exist many investigations of micropolar fluids or electrorheological fluids (cf. [23, 31]), there exist to our knowledge no mathematical investigations of steady motions of micropolar electrorheological fluids except the PhD thesis [11], the diploma thesis [33], the paper [12] and the recent result [21]. Except for the latter contribution these investigations only treat the case of constant shear exponents.

For the existence theory of problems of similar type as (1.1), the Lipschitz truncation technique (cf. [6, 14]) has proven to be very powerful. This method is available in the setting of Sobolev spaces (cf. [6, 8, 13]), variable exponent Sobolev spaces (cf. [6, 8]), solenoidal Sobolev spaces (cf. [1]), Sobolev spaces with Muckenhoupt weights (cf. [12]) and functions of bounded variation (cf. [2]). Since, in general, $\vert \textbf{E}\vert ^2$ does not belong to the correct Muckenhoupt class, the results in [12] are either sub-optimal with respect to the lower bound for the shear exponent p or require additional assumptions on the electric field $\textbf{E}$. These deficiencies are overcome in [21] by an thorough localization of the arguments. Moreover, [21] contains the first treatment of the full model for micropolar electrorheological fluids in weighted variable exponent spaces under the assumption that the shear exponent is globally $\log$–Hölder continuous. The present paper relaxes this condition and shows existence of solutions under the only assumption that the electric field $\textbf{E}$ is bounded and smooth.

This paper is organized as follows: In Sect. 2, we introduce the functional setting for the treatment of the variable exponent weighted case, and collect auxiliary results. Then, Sect. 3 is devoted to the analysis of the electric field, while Sect. 4 is devoted to the weak stability of the stress tensors. Eventually, in Sect. 5, we deploy the Lipschitz truncation technique to prove the existence of weak solutions of (1.1).

2 Preliminaries

2.1 Basic Notation and Standard Function Spaces

We employ the customary Lebesgue spaces $L^p(\Omega )$, $1\le p\le \infty$, and Sobolev spaces $W^{1,p}(\Omega )$, $1\le p\le \infty$, where $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, is a bounded domain. We denote by $\Vert \cdot \Vert _p$ the norm in $L^p(\Omega )$ and by $\Vert \cdot \Vert _{1,p}$ the norm in $W^{1,p}(\Omega )$. The space $W^{1,p}_0(\Omega )$, $1\le p <\infty$, is defined as the completion of $C_0^\infty (\Omega )$ with respect to the gradient norm $\Vert \nabla \cdot \Vert _{p}$, while the space $W^{1,p}_{0,{{\,\textrm{div}\,}}}(\Omega )$, $1\le p <\infty$, is the closure of $C_{0,div }^\infty (\Omega ):=\{\textbf{u}\in C_0^\infty (\Omega ){\,\big |\,}{{\,\mathrm{{\text {div}}}\,}}\textbf{u}=0\}$ with respect to the gradient norm $\Vert \nabla \cdot \Vert _{p}$. For a bounded Lipschitz domain ${G\subseteq \mathbb {R}^d}$, we define $W^{1,\infty }_0(G)$ as the subspace of functions $u \in W^{1,\infty }(G)$ having a vanishing trace, i.e., $u|_{\partial G}=0$. We use small boldface letters, e.g., $\textbf{v}$, to denote vector-valued functions and capital boldface letters, e.g., $\textbf{S}$, to denote tensor-valued functions.³ However, we do not distinguish between scalar, vector-valued and tensor-valued function spaces in the notation. The standard scalar product between vectors is denoted by $\textbf{v}\cdot \textbf{u}$, while the standard scalar product between tensors is denoted by $\textbf{A}:\textbf{B}$. For a normed linear vector space X, we denote its topological dual space by $X^{*}$. Moreover, we employ the notation $\langle u,v\rangle :=\int _{\Omega }uv\,dx$, whenever the right-hand side is well-defined. We denote by $\vert M\vert$ the d–dimensional Lebesgue measure of a measurable set M. The mean value of a locally integrable function $u\in L^1_{{\textrm{loc}}}(\Omega )$ over a measurable set $M\subseteq \Omega$ is denoted by . By $L^p_0(\Omega )$ and $C^\infty _{0,0}(\Omega )$, resp., we denote the subspace of $L^p(\Omega )$ and $C^\infty _{0}(\Omega )$, resp., consisting of all functions u with vanishing mean value, i.e., .

2.2 Weighted Variable Exponent Lebesgue and Sobolev Spaces

In this section, we will give a brief introduction into weighted variable exponent Lebesgue and Sobolev spaces.

Let $\Omega \subseteq {\mathbb {R}}^d$, $d\in {\mathbb {N}}$, be an open set and $p:\Omega \rightarrow [1,\infty )$ a measurable function, called variable exponent in $\Omega$. By ${\mathcal {P}}(\Omega )$, we denote the set of all variable exponents. For $p\in {\mathcal {P}}(\Omega )$, we denote by ${p^+:=ess\,sup _{x\in \Omega }{p(x)}}$ and ${p^-:=ess\,inf _{x\in \Omega }{p(x)}}$ its limit exponents. By ${\mathcal {P}}^{\infty }(\Omega ):=\{p\in {\mathcal {P}}(\Omega ){\,\big |\,}p^+<\infty \}$, we denote the set of all bounded variable exponents.

A weight $\sigma$ on $\mathbb {R}^d$ is a locally integrable function satisfying $0<\sigma <\infty$ a.e.⁴ To each weight $\sigma$, we associate a Radon measure $\nu _{\sigma }$ defined via $\nu _{\sigma } (A):=\int _A \sigma \, dx$ for every measurable set $A\subseteq {\mathbb {R}}^d$.

For an exponent $p\in {\mathcal {P}}^{\infty }(\Omega )$ and a weight $\sigma$, the weighted variable exponent Lebesgue space $L^{p(\cdot )}(\Omega ;\sigma )$ consists of all measurable functions ${u:\Omega \rightarrow {\mathbb {R}}}$, i.e., $u\in {\mathcal {M}}(\Omega )$, for which the modular

$$\begin{aligned} \rho _{p(\cdot ),\sigma }(u):=\int _{\Omega }{\vert u(x)\vert ^{p(x)}\,d\nu _{\sigma }(x)}:=\int _{\Omega }{\vert u(x)\vert ^{p(x)}\sigma (x)\,dx} \end{aligned}$$

is finite, i.e., we have that $L^{p(\cdot )}(\Omega ;\sigma ):=\{u\in {\mathcal {M}}(\Omega ){\,\big |\,}\sigma ^{1/p(\cdot )}u\in L^{p(\cdot )}(\Omega )\}$. We equip $L^{p(\cdot )}(\Omega ;\sigma )$ with the Luxembourg norm

$$\begin{aligned} \Vert u\Vert _{p(\cdot ),\sigma }:=\inf \big \{\lambda > 0{\,\big |\,}\rho _{p(\cdot ),\sigma }(u/\lambda )\le 1\big \}\,, \end{aligned}$$

which turns $L^{p(\cdot )}(\Omega ;\sigma )$ into a separable Banach space (cf. [5, Thm. 3.2.7 & Lem. 3.4.4]). In addition, if ${\sigma =1}$ a.e. in $\Omega$, then we employ the abbreviations $L^{p(\cdot )}(\Omega ):=L^{p(\cdot )}(\Omega ;\sigma )$, $\rho _{p(\cdot )}(u):=\rho _{p(\cdot ),\sigma }(u)$ and ${\Vert u\Vert _{p(\cdot )}:=\Vert u\Vert _{p(\cdot ),\sigma }}$ for every ${u\in L^{p(\cdot )}(\Omega )}$. The identity $\rho _{p(\cdot ),\sigma }(u)\!=\!\rho _{p(\cdot )}(u\sigma ^{1/p(\cdot )})$ implies that

$$\begin{aligned} \Vert u\Vert _{p(\cdot ),\sigma }=\Vert u\sigma ^{1/p(\cdot )}\Vert _{p(\cdot )} \end{aligned}$$

(2.1)

for all $u\in L^{p(\cdot )}(\Omega ;\sigma )$. If $p\in {\mathcal {P}}^{\infty }(\Omega )$, in addition, satisfies $p^->1$, then $L^{p(\cdot )}(\Omega ;\sigma )$ is reflexive (cf. [5, Thm. 3.4.7]). The dual space $(L^{p(\cdot )}(\Omega ;\sigma ))^*\!$ can be identified with respect to ${\langle {\cdot }, {\cdot } \rangle }$ with $L^{p'(\cdot )}(\Omega ;\sigma ')$, where $\sigma ':=\sigma ^{{\frac{-1}{p(\cdot )-1}}}$. The identity (2.1) and Hölder’s inequality in variable exponent Lebesgue spaces (cf. [5, Lem. 3.2.20]) yield for every $u\in L^{p(\cdot )}(\Omega ;\sigma )$ and ${v \in L^{p'(\cdot )}(\Omega ;\sigma ')}$, there holds

$$\begin{aligned} \vert {\langle {u}, {v} \rangle }\vert \le 2\,{\Vert {u}\Vert }_{p(\cdot ),\sigma } {\Vert {v}\Vert }_{p'(\cdot ),\sigma '}. \end{aligned}$$

The relation between the modular and the norm is clarified by the following lemma, which is called norm-modular unit ball property.

Lemma 2.2

Let $\Omega \subseteq \mathbb {R}^d$, ${d\in {\mathbb {N}}}$, be open and let $p\in {\mathcal {P}}^{\infty }(\Omega )$. Then, we have for any $u \in L^{p(\cdot )}(\Omega ;\sigma )$:

• (i) ${\Vert {u}\Vert }_{p(\cdot ),\sigma } \le 1$ if and only if $\rho _{p(\cdot ),\sigma } (u) \le 1$.

• (ii) If ${\Vert {u}\Vert }_{p(\cdot ),\sigma } \le 1$, then $\rho _{p(\cdot ),\sigma } (u) \le {\Vert {u}\Vert }_{p(\cdot ),\sigma }$.

• (iii) If $1< {\Vert {u}\Vert }_{p(\cdot ),\sigma }$, then ${\Vert {u}\Vert }_{p(\cdot ),\sigma } \le \rho _{p(\cdot ),\sigma } (u)$.

• (iv) ${{\Vert {u}\Vert }_{p(\cdot ),\sigma }^{p^-} -1 \le \rho _{p(\cdot ),\sigma } (u) \le {\Vert {u}\Vert }_{p(\cdot ),\sigma }^{p^+} +1}$.

Proof

See [5, Lem. 3.2.4 & Lem. 3.2.5]. $\square$

The following generalization of a classical result (cf. [17]) is very useful in the identification of limits.

Theorem 2.3

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be bounded, $\sigma \in L^\infty (\Omega )$ a weight and $p\in {\mathcal {P}}^{\infty }(\Omega )$. Then, for a sequence $(u_n)_{n\in {\mathbb {N}}}\subseteq L^{p(\cdot )}(\Omega ;\sigma )$ from

• (i) $\lim \limits _{n\rightarrow \infty } u_n=v$ $\nu _{\sigma }$–a.e. in $\Omega$,

• (ii) $u_n\rightharpoonup u$ in $L^{p(\cdot )}(\Omega ;\sigma )$ $(n\rightarrow \infty )$,

it follows that $u=v$ in $L^{p(\cdot )}(\Omega ;\sigma )$.

Proof

For a proof in the case of constant exponents, we refer to [19, Thm. 13.44]. However, because $L^{p(\cdot )}(\Omega ;\sigma )\hookrightarrow L^1(\Omega ;\sigma )$ for both ${p\in {\mathcal {P}}^{\infty }(G)}$ and $\sigma \in L^\infty (G)$, the non-constant case follows from the constant case. $\square$

Let us now introduce variable exponent Sobolev spaces in the weighted and unweighted case. Let us start with the unweighted case. Due to $L^{p(\cdot )}(\Omega )\hookrightarrow L^1_{{\textrm{loc}}}(\Omega )$, we can define the variable exponent Sobolev space $W^{1,p(\cdot )}(\Omega )$ as the subspace of $L^{p(\cdot )}(\Omega )$ consisting of all functions $u\in L^{p(\cdot )}(\Omega )$ whose distributional gradient satisfies $\nabla u\in L^{p(\cdot )}(\Omega )$. The norm ${\Vert \cdot \Vert _{1,p(\cdot )}:=\Vert \cdot \Vert _{p(\cdot )}+\Vert \nabla \cdot \Vert _{p(\cdot )}}$ turns $W^{1,p(\cdot )}(\Omega )$ into a separable Banach space (cf. [5, Thm. 8.1.6]). Then, we define the space ${W^{1,p(\cdot )}_0(\Omega )}$ as the closure of $C_0^\infty (\Omega )$ in ${W^{1,p(\cdot )}(\Omega )}$, while ${W^{1,p(\cdot )}_{0,{{\,\textrm{div}\,}}}(\Omega )}$ is the closure of $C_{0,{{\,\textrm{div}\,}}}^\infty (\Omega )$ in ${W^{1,p(\cdot )}(\Omega )}$. If $p\in {\mathcal {P}}^{\infty }(\Omega )$, in addition, satisfies ${p^->1}$, then the spaces ${W^{1,p(\cdot )}(\Omega )}$, ${W^{1,p(\cdot )}_0(\Omega )}$ and ${W^{1,p(\cdot )}_{0,{{\,\textrm{div}\,}}}(\Omega )}$ are reflexive (cf. [5, Thm. 8.1.6]).

Note that the velocity field $\textbf{v}: \Omega \rightarrow {\mathbb {R}}^d$ solving (1.1), in view of the properties of the extra stress tensor (cf. Assumption 4.1), necessarily satisfies $\textbf{D}\textbf{v}\in L^{p(\cdot )}(\Omega )$. Even though we have that $\textbf{v}=0$ on $\partial \Omega$, we cannot resort to Korn’s inequality in the setting of variable exponent Sobolev spaces (cf. [5, Thm. 14.3.21]), since we do not assume that $p={\hat{p}}\circ \vert \textbf{E}\vert ^2\in {\mathcal {P}}^{\infty }(\Omega )$ is globally $\log$–Hölder continuous. However, if we switch by means of Hölder’s inequality from the variable exponent $p\in {\mathcal {P}}^{\infty }(\Omega )$ to its lower bound $p^-$, for which Korn’s inequality is available, also using Poincaré’s inequality, we can expect that a solution $\textbf{v}$ of (1.1) satisfies ${\textbf{v}\in L^{p^-}(\Omega )}$. Thus, the natural energy space for the velocity possesses a different integrability for the function and its symmetric gradient. This motivates the introduction of the following variable exponent function spaces.

Definition 2.4

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be open and $q,p\in {\mathcal {P}}^{\infty }(\Omega )$. For $\textbf{u}\in C^\infty (\Omega )$, we define

$$\begin{aligned} \Vert \textbf{u}\Vert _{{X^{q(\cdot ),p(\cdot )}_{\textbf{D}}(\Omega )}}:= \Vert \textbf{u}\Vert _{q(\cdot )} +\Vert \textbf{D}\textbf{u}\Vert _{p(\cdot )}. \end{aligned}$$

The space ${X^{q(\cdot ),p(\cdot )}_{\textbf{D}}(\Omega )}$ is defined as the completion of

$$\begin{aligned} {\mathcal {V}}^{q(\cdot ),p(\cdot )}_{{\textbf{D}}}:=\big \{\textbf{u}\in C^\infty (\Omega ){\,\big |\,}\Vert \textbf{u}\Vert _{q(\cdot )}+\Vert \textbf{D}\textbf{u}\Vert _{p(\cdot )}<\infty \big \} \end{aligned}$$

with respect to $\Vert \cdot \Vert _{{X^{q(\cdot ),p(\cdot )}_{\textbf{D}}(\Omega )}}$.

Proposition 2.5

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be open and $q,p\in {\mathcal {P}}^{\infty }(\Omega )$. Then, the space ${X^{q(\cdot ),p(\cdot )}_{\textbf{D}}(\Omega )}$ is a separable Banach space, which is reflexive if $q^-,p^->1$.

Proof

Clearly, $\Vert \cdot \Vert _{{X^{q(\cdot ),p(\cdot )}_{\textbf{D}}(\Omega )}}$ is a norm and, thus, $X^{q(\cdot ),p(\cdot )}_{\textbf{D}}(\Omega )$, by definition, is a Banach space. For the separability and reflexivity, we first observe that $\Pi :{X^{q(\cdot ),p(\cdot )}_{\textbf{D}}(\Omega )}\rightarrow L^{q(\cdot )}(\Omega )^d\times L^{p(\cdot )}(\Omega )^{d\times d}$ is an isometry and, thus, an isometric isomorphism into its range $R(\Pi )$. Hence, $R(\Pi )$ inherits the separability and reflexivity from $L^{q(\cdot )}(\Omega )^d\times L^{p(\cdot )}(\Omega )^{d\times d}$, and by virtue of the isometric isomorphism ${X^{q(\cdot ),p(\cdot )}_{\textbf{D}}(\Omega )}$ as well. $\square$

Definition 2.6

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be open and $q,p\in {\mathcal {P}}^{\infty }(\Omega )$. Then, we define the spaces

$$\begin{aligned} {{X}^{q(\cdot ),p(\cdot )}_{{\textbf {D}}}(\Omega ):=\overline{C_0^\infty (\Omega )}^{{\Vert \cdot \Vert _{{X^{q(\cdot ),p(\cdot )}_{{\textbf {D}}}(\Omega )}}}},\quad {X}^{q(\cdot ),p(\cdot )}_{{\textbf {D}},{{\,\text {div}\,}}}(\Omega ):=\overline{C_{0,\text {div} }^\infty (\Omega )}^{{\Vert \cdot \Vert _{{X^{q(\cdot ),p(\cdot )}_{{\textbf {D}}}(\Omega )}}}}\,.} \end{aligned}$$

For the treatment of the micro-rotation ${\varvec{\omega }}$, we also need weighted variable exponent Sobolev spaces. In analogy with [21, Ass. 2.2], we make the following assumption on the weight $\sigma$.

Assumption 2.7

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be an open set and $q,p\in {\mathcal {P}}^{\infty }(\Omega )$. The weight $\sigma$ is admissible, i.e., if a sequence ${({\varvec{\varphi }}_n)_{n\in {\mathbb {N}}}\subseteq C^\infty (\Omega )}$ and ${\textbf{T}\in L^{p(\cdot )}(\Omega ;\sigma )}$ satisfy ${\int _\Omega \vert {\varvec{\varphi }}_n(x)\vert ^{q(x)}\sigma (x)\,dx\!\rightarrow \! 0}$ $(n\!\rightarrow \!\infty )$ and ${\int _\Omega \vert \nabla {\varvec{\varphi }}_n(x)\!-\!\textbf{T}(x)\vert ^{p(x)}\sigma (x)\,dx\!\rightarrow \! 0}$ $(n\rightarrow \infty )$, then it follows that $\textbf{T}={\textbf{0}}$ in $L^{p(\cdot )}(\Omega ;\sigma )$.

Remark 2.8

If $\sigma \in C^0(\Omega )$, then the same argumentation as in [21, Rem. 2.3 (ii)] shows that Assumption 2.7 is satisfied for every $q,p\in {\mathcal {P}}^{\infty }(\Omega )$.

Definition 2.9

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be open and let $\sigma$ satisfy Assumption 2.7 for $q,p \in {\mathcal {P}}^{\infty }(\Omega )$. For $\textbf{u}\in C^\infty (\Omega )$, we define

$$\begin{aligned} \Vert \textbf{u}\Vert _{q(\cdot ),p(\cdot ),\sigma }:= \Vert \textbf{u}\Vert _{q(\cdot ),\sigma } +\Vert \nabla \textbf{u}\Vert _{p(\cdot ),\sigma }. \end{aligned}$$

The weighted variable exponent Sobolev space ${X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )}$ is defined as the completion of

$$\begin{aligned} {{\mathcal {V}}^{q(\cdot ),p(\cdot )}_{\nabla ,\sigma }:=\big \{\textbf{u}\in C^\infty (\Omega ){\,\big |\,}\Vert \textbf{u}\Vert _{q(\cdot ),p(\cdot ),\sigma }<\infty \big \}} \end{aligned}$$

with respect to $\Vert \cdot \Vert _{q(\cdot ),p(\cdot ),\sigma }$.

In other words, $\textbf{w}\in X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )$ if and only if $\textbf{w}\in L^{q(\cdot )}(\Omega ;\sigma )$ and there is a tensor field $\textbf{T}\in L^{p(\cdot )}(\Omega ;\sigma )$ such that for some sequence $(\varvec{\varphi }_n)_{n\in {\mathbb {N}}}\subseteq C^\infty (\Omega )$ holds $\int _{\Omega }\vert \varvec{\varphi }_n-\textbf{w}\vert ^{q(\cdot )}\sigma \,dx\rightarrow 0$ $(n\rightarrow \infty )$ and ${\int _{\Omega }\vert \nabla \varvec{\varphi }_n-\textbf{T}\vert ^{p(\cdot )}\sigma \,dx\rightarrow 0}$ ${(n\rightarrow \infty )}$. Assumption 2.7 implies that $\textbf{T}$ is a uniquely defined function in $L^{p(\cdot )}(\Omega ;\sigma )$ and we, thus, set ${\hat{\nabla }}\textbf{w}:=\textbf{T}$ in $L^{p(\cdot )}(\Omega ;\sigma )$. Note that ${W^{1,p(\cdot )}(\Omega )=X^{p(\cdot ),p(\cdot )}_{\nabla }(\Omega ;\sigma )}$ if ${\sigma = 1}$ a.e. in $\Omega$ with ${\nabla \textbf{w}={\hat{\nabla }} \textbf{w}}$ for all ${\textbf{w}\in W^{1,p(\cdot )}(\Omega )}$. However, in general, ${\hat{\nabla }\textbf{w}}$ and the usual distributional gradient $\nabla \textbf{w}$ do not coincide.

Theorem 2.10

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be open and let $\sigma$ satisfy Assumption 2.7. Then, ${X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )}$ is a separable Banach space, which is reflexive if ${q^-,p^->1}$.

Proof

The space $X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )$ is a Banach space by definition. So, it is left to prove that it is separable, and if, in addition, $q^-,p^->1$ it is reflexive. To this end, we first note that

$$\begin{aligned} \Vert \textbf{w}\Vert _{q(\cdot ),p(\cdot ),\sigma }=\Vert \textbf{w}\Vert _{q(\cdot ),\sigma }+\Vert {\hat{\nabla }} \textbf{w}\Vert _{p(\cdot ),\sigma } \end{aligned}$$

(2.11)

for all $\textbf{w}\in {X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )}$. In fact, for any $\textbf{w}\in {X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )}$, by definition, there is a sequence $(\varvec{\varphi }_n)_{n\in {\mathbb {N}}}\subseteq {{{\mathcal {V}}^{q(\cdot ),p(\cdot )}_{\sigma }}}$ such that $\varvec{\varphi }_n\rightarrow \textbf{w}$ in $L^{q(\cdot )}(\Omega ;\sigma )$ ${(n\rightarrow \infty )}$ and $\nabla \varvec{\varphi }_n\rightarrow {\hat{\nabla }} \textbf{w}$ in $L^{p(\cdot )}(\Omega ;\sigma )$ $(n\rightarrow \infty )$ and ${\Vert \varvec{\varphi }_n\Vert _{q(\cdot ),p(\cdot ),\sigma }= \Vert \varvec{\varphi }_n\Vert _{q(\cdot ),\sigma } +\Vert \nabla \varvec{\varphi }_n\Vert _{p(\cdot ),\sigma }}$ for all $n\in {\mathbb {N}}$. The limit $n\rightarrow \infty$ yields (2.11) for every ${\textbf{w}\in X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )}$. Then, (2.11) implies that ${\Pi :X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )\rightarrow L^{q(\cdot )}(\Omega ;\sigma )^d\times L^{p(\cdot )}(\Omega ;\sigma )^{d\times d}}$, defined via $\Pi \textbf{w}:=(\textbf{w},\!{\hat{\nabla }} \textbf{w})^\top$ in $L^{q(\cdot )}(\Omega ;\sigma )^d\times L^{p(\cdot )}(\Omega ;\sigma )^{d\times d}$ for all $\textbf{w}\in X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )$, is an isometry, and, thus, an isometric isomorphism into its range $R(\Pi )$. Hence, $R(\Pi )$ inherits the separability and reflexivity, if, in addition, $q^-,p^->1$, of ${L^{q(\cdot )}(\Omega ;\sigma )^d\times L^{p(\cdot )}(\Omega ;\sigma )^{d\times d}}$ and ${X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )}$ as well. $\square$

If, in addition, ${\sigma \in L^\infty (\Omega )}$, then we have that ${W^{1,p(\cdot )}(\Omega )\hookrightarrow {X}^{p(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma )}$ and ${\nabla \textbf{w}={\hat{\nabla }} \textbf{w}}$ for all ${\textbf{w}\in W^{1,p(\cdot )}(\Omega )}$, which follows from the estimate

$$\begin{aligned} {\Vert \textbf{u}\Vert _{p(\cdot ),\sigma }=\Vert \textbf{u}\sigma ^{1/p(\cdot )}\Vert _{{p(\cdot )}}\le 2\, \Vert \sigma \Vert _{\infty }^{1/p^-}\Vert \textbf{u}\Vert _{{p(\cdot )}}} \end{aligned}$$

valid for every $\textbf{u}\in L^{p(\cdot )}(\Omega )$, in the same way as in [18, Sec. 1.9, Sec. 1.10].

Definition 2.12

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be open and let Assumption 2.7 be satisfied for $q,p\in {\mathcal {P}}^{\infty }(\Omega )$. Then, we define the space

$$\begin{aligned} {{X}^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;\sigma ):=\overline{C_0^\infty (\Omega )}^{\Vert \cdot \Vert _{q(\cdot ),p(\cdot ),\sigma }}\,.} \end{aligned}$$

In the particular case ${\sigma =1}$ a.e. in $\Omega$, we employ the abbreviations

$$\begin{aligned} X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ):=X^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;1),\quad {X}^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ):={X}^{q(\cdot ),p(\cdot )}_{{\nabla }}(\Omega ;1). \end{aligned}$$

The following local embedding result will play a key role for the applicability of the Lipschitz truncation technique in the proof of the existence result in Theorem 5.1.

Theorem 2.13

Let $\Omega \subseteq {\mathbb {R}}^d$, $d\ge 2$, be a bounded domain and let $p\in C^0(\Omega )$ satisfy $p^-\ge \frac{2d}{d+2}$. Then, for each $\Omega '\subset \subset \Omega$, there exists a constant ${c(p,\Omega ')>0}$ such that for every ${\textbf{u}\in X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}$, it holds ${\textbf{u}\in L^{p(\cdot )}(\Omega ')}$ with

$$\begin{aligned} \Vert \textbf{u}\Vert _{L^{p(\cdot )}(\Omega ')}\le c(p,\Omega ')\Vert \textbf{u}\Vert _{X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}\,. \end{aligned}$$

(2.14)

i.e., we have that $X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )\hookrightarrow L^{p(\cdot )}_{{\textrm{loc}}}(\Omega )$.

Proof

The proof is postponed to the “Appendix A”. $\square$

2.3 $\log$–Hölder Continuity and Related Results

We say that a bounded exponent $p\in {\mathcal {P}}^\infty (G)$ is locally $\log$–Hölder continuous, if there is a constant $c_1>0$ such that for all $x,y\in G$

$$\begin{aligned} \vert p(x)-p(y)\vert \le \frac{c_1}{\log (e+1/\vert x-y\vert )}\,. \end{aligned}$$

We say that $p \in {\mathcal {P}}^\infty (G)$ satisfies the $\log$–Hölder decay condition, if there exist constants $c_2>0$ and $p_\infty \in \mathbb {R}$ such that for all $x\in G$

$$\begin{aligned} \vert p(x)-p_\infty \vert \le \frac{c_2}{\log (e+1/\vert x\vert )}\,. \end{aligned}$$

We say that p is globally $\log$–Hölder continuous on G, if it is locally $\log$–Hölder continuous and satisfies the $\log$–Hölder decay condition. Then, the maximum ${c_{\log }(p):=\max \{c_1,c_2\}}$ is just called the $\log$–Hölder constant of p. Moreover, we denote by ${\mathcal {P}}^{\log }(G)$ the set of globally $\log$–Hölder continuous functions on G.

$\log$–Hölder continuity is a special modulus of continuity for variable exponents that is sufficient for the validity of the following results.

Theorem 2.15

Let $G\subseteq {\mathbb {R}}^d\!$, $d\ge 2$, be a bounded Lipschitz domain. Then, there exists a linear operator ${\mathcal {B}}_G:C^{\infty }_{0,0}(G)\rightarrow C^\infty _0(G)$ which for all exponents ${p\in {\mathcal {P}}^{\log }(G)}$ satisfying $p^->1$ extends uniquely to a linear, bounded operator ${{\mathcal {B}}_G:L^{p(\cdot )}_0(G)\rightarrow W^{1,p(\cdot )}_0(G)}$ such that $\Vert {\mathcal {B}}_Gu\Vert _{1,p(\cdot )}\le c\,\Vert u\Vert _{p(\cdot )}$ and $div \,{\mathcal {B}}_Gu = u$ for every ${u\in L^{p(\cdot )}_0(G)}$.

Proof

See [7, Thm. 2.2], [4, Thm. 6.4], [5, Thm. 14.3.15]. $\square$

Theorem 2.16

Let $G\subseteq {\mathbb {R}}^d$, $d\ge 2$, be a bounded Lipschitz domain and let $p \in {\mathcal {P}}^{\log }(G)$. Then, there holds the embedding $W^{1,p(\cdot )}(G)\hookrightarrow \hookrightarrow L^{p(\cdot )}(G)$.

Proof

See [22, Thm. 3.8 (iv)], [5, Thm. 8.4.5]. $\square$

Theorem 2.17

Let $G\subseteq {\mathbb {R}}^d\!$, $d\in {\mathbb {N}}$, be a bounded Lipschitz domain and let ${p\in {\mathcal {P}}^{\log }(G)}$ with $p^- > 1$. Then, there exists a constant $c>0$ such that ${ \Vert \nabla \textbf{u}\Vert _{p(\cdot )}\le c\,( \Vert \textbf{D}\textbf{u}\Vert _{p(\cdot )}+\Vert \textbf{u}\Vert _{p(\cdot )})}$ for every ${\textbf{u}\in W^{1,p(\cdot )}(G)}$.

Proof

See [5, Thm. 14.3.23]. $\square$

Theorem 2.18

Let $G\subseteq {\mathbb {R}}^d$, $d\in {\mathbb {N}}$, be a bounded Lipschitz domain, ${p\in {\mathcal {P}}^{\log }(G)}$ with $p^->1$ and $(\textbf{u}^n)_{n\in {\mathbb {N}}} \subseteq {W^{1,p(\cdot )}_0(G)}$ such that $\textbf{u}^n \rightharpoonup {\textbf{0}}$ in ${W^{1,p(\cdot )}_0(G)}$ $(n\rightarrow \infty )$. Then, for any ${j, n\in \mathbb {N}}$, there exist $\textbf{u}^{n,j} \in W^{1,\infty }_0(G)$ and ${\lambda _{n,j} \in \big [2^{2^j}, 2^{2^{j+1}}\big ]}$ such that

$$\begin{aligned} \begin{aligned} { \lim _{n\rightarrow \infty }} \big ( {\sup }_{j \in \mathbb {N}} {\Vert {{\textbf {u}}^{n,j}}\Vert }_{\infty }\big )&=0\,,\\{\Vert {\nabla {\textbf {u}}^{n,j}}\Vert }_{\infty }&\le c\, \lambda _{n,j}\,, \\{\big \Vert {\nabla {\textbf {u}}^{n,j}\, \chi _{ {\{{{\textbf {u}}^{n,j} \not = {\textbf {u}}^n}\}}}}\big \Vert }_{p(\cdot )}&\le c\, \big \Vert \lambda _{n,j} \chi _{{\{{{\textbf {u}}^{n,j} \not = {\textbf {u}}^n}\}}}\big \Vert _{p(\cdot )} \,, \\{\limsup _{n \rightarrow \infty } }\,\big \Vert \lambda _{n,j} \chi _{{\{{{\textbf {u}}^{n,j} \not = {\textbf {u}}^n}\}}}\big \Vert _{p(\cdot )}&\le c\, 2^{-j/p^+}\,,\end{aligned} \end{aligned}$$

(2.19)

where $c=c(d,p,G)>0$. Moreover, for any $j \in \mathbb {N}$, $\nabla \textbf{u}^{n,j} \rightharpoonup {\textbf{0}}$ in $L^s(G)$ ${(n \rightarrow \infty )}$, $s \in [1,\infty )$, and $\nabla \textbf{u}^{n,j} {\mathop {\rightharpoonup }\limits ^{*}} {\textbf{0}}$ in $L^\infty (G)$ $(n \rightarrow \infty )$.

Proof

See [6, Thm. 4.4], [5, Cor. 9.5.2]. $\square$

3 The Electric Field $\textbf{E}$

We first note that the system (1.2) is separated from (1.1), in the sense that one can first solve the quasi-static Maxwell’s equations yielding an electric field $\textbf{E}$, which then, in turn, enters into (1.1) as a parameter through the stress tensors.

It is proved in [27, 28, 31], that for bounded Lipschitz domains, there exists a solution⁵$\textbf{E}\in H({{\,\textrm{curl}\,}}) \cap H({{\,\textrm{div}\,}})$ of the system (1.2) with ${{\Vert {\textbf{E}}\Vert }_2 \le c\, {\Vert {\textbf{E}_0}\Vert }_{H^{-1/2}(\partial \Omega )}}$. A more detailed analysis of the properties of the electric field $\textbf{E}$ can be found in [11]. Let us summarize these results here. Combining (1.2)$_1$ and (1.2)$_2$, we obtain that

$$\begin{aligned} {-\Delta {\textbf{E}}={{\,\textrm{curl}\,}}{{\,\textrm{curl}\,}}{\textbf{E}}-\nabla {{\,\mathrm{{\text {div}}}\,}}{\textbf{E}}=0\,,} \end{aligned}$$

(3.1)

i.e., the electric field is a harmonic function and, thus, real analytic. In particular, for a harmonic function, we can characterize its zero set as follows:

Lemma 3.2

Let $\Omega \subseteq \mathbb {R}^d$, $d\in {\mathbb {N}}$, be a bounded domain and $u:\Omega \rightarrow \mathbb {R}$ a non-trivial analytic function. Then, $u^{-1}(0)$ is a union of $C^1$–manifolds $(M_i)_{i=1,\ldots ,m}$, $m\in {\mathbb {N}}$, with $\dim M_i\le d-1$ for every $i=1,\ldots ,m$, and ${|{u^{-1}(0)}|}=0$.

Proof

See [11, 12, Lem. 3.1]. $\square$

Finally, we observe that using the regularity theory for Maxwell’s equations (cf. [31, 32]), one can give conditions on the boundary data $\textbf{E}_0$ ensuring that the electric field $\textbf{E}$ is globally bounded, i.e., $\Vert \textbf{E}\Vert _\infty \le c(\textbf{E}_0)$. Based on these two observations, we will make the following assumption on the electric field $\textbf{E}$:

Assumption 3.3

The electric field ${\textbf{E}}$ satisfies ${\textbf{E}}\in C^\infty (\Omega ) \cap L^\infty (\Omega )$, and the closed set ${|{\textbf{E}}|}^{-1}(0)$ is a null set, i.e., ${\Omega _0:= \{ x\in \Omega {\,\big |\,}\vert {\textbf{E}}(x)\vert >0\}}$ has full measure.

Note that there, indeed, exist solutions of the quasi-static Maxwell’s equations that satisfy Assumption 3.3, but do not belong to any Hölder space. In particular, there exist a solution of the quasi-static Maxwell’s equations such that for a standard choice of ${\hat{p}}\in {\mathcal {P}}^{\log }({\mathbb {R}})$, we have that $p:={\hat{p}}\circ \vert \textbf{E}\vert ^2\notin {\mathcal {P}}^{\log }(\Omega )$.

Remark 3.4

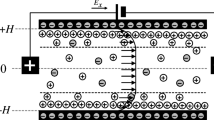
Let $\Omega :=[-2,0]\times [-1,1]\subseteq {\mathbb {R}}^2$ and let $\textbf{E}_0\in H(div ;\Omega )$ be a vector field defined via $\textbf{E}_0(x_1,x_2):=(1/\log (\vert \log (\frac{1}{4}\vert x_2\vert )\vert ),0)^\top$ for every $(x_1,x_2)^\top \in \Omega$. Then, in analogy with [31, Thm. 3.21], a solution $\textbf{E}\in H(curl ;\Omega )\cap H(div ;\Omega )$ of the quasi-static Maxwell’s equation with prescribed data ${\textbf{E}_0\in H(div ;\Omega )}$ is given via the gradient of a solution $u\in W^{1,2}(\Omega )/{\mathbb {R}}$ of the Neumann problem

$$\begin{aligned} \begin{aligned} -\Delta u&= 0{} & {} \quad \text { in }\Omega \,,\\ \nabla u\cdot \textbf{n}&=\textbf{E}_0\cdot \textbf{n}{} & {} \quad \text { on }\partial \Omega \,, \end{aligned} \end{aligned}$$

(3.5)

i.e., $\textbf{E}=\nabla u$. With the help of an approximation of (3.5) using finite elements, the following pictures for the electric field are obtained (Fig. 1):

Fig. 1

Plots of the first (blue/left) and the second (red/right) component of the numerically determined electric field

These pictures indicate that $\textbf{E}\in C^0({\overline{\Omega }})$, or at least that $\textbf{E}\in L^\infty (\Omega )$. In addition, (3.1) in conjunction with Weyl’s lemma implies that $\textbf{E}\in C^\infty (\Omega )$. Note that since $E_1:=\textbf{E}\cdot \textbf{e}_1=\textbf{E}_0\cdot \textbf{e}_1$ on $\{0\}\times [-1,1]$, we find that ${\textbf{E}\notin C^{0,\alpha }({\overline{\Omega }})}$ for any ${\alpha \in \left( 0,1\right] }$. Apart from that, if ${\hat{p}}\in {\mathcal {P}}^{\log }({\mathbb {R}})$ is given via ${\hat{p}}(x):=1/\log (e+1/\vert x\vert )$ for all ${x\in {\mathbb {R}}}$, then it is easily checked that $p:={\hat{p}}\circ \vert \textbf{E}\vert ^2$ satisfies ${p(0,x_2)\log (e+1/\vert x_2\vert )\rightarrow \infty }$ as $x_2\rightarrow 0$ and, thus, $p\notin {\mathcal {P}}^{\log }(\Omega )$.

In the sequel, we do not use that $\textbf{E}$ is the solution of the quasi-static Maxwell’s equations (1.2), but we will only use Assumption 3.3.

Theorem 3.6

Let $\Omega \subseteq \mathbb {R}^d$, ${d\in {\mathbb {N}}}$, be open, $p\in \left[ 1,\infty \right)$ and let Assumption 3.3 be satisfied. Set ${p^*:=\frac{dp}{d-p}}$ if $p<d$ and $p^*:=\infty$ if $p\ge d$. Then, for any open set $\Omega '\subset \subset \Omega$ with ${\partial \Omega '\in C^{0,1}}$ and any ${\alpha \ge 1+\frac{2}{p}}$, it holds

$$\begin{aligned} {X^{p,p}_{\nabla }(\Omega ;\vert {\textbf{E}}\vert ^2) \hookrightarrow L^{r}(\Omega ';\vert \textbf{E}\vert ^{\alpha r})} \end{aligned}$$

with $r \in [1,p^*]$ if $p\ne d$ and $r \in [1,p^*)$ if $p=d$.

Proof

See [21, Thm. 3.3]. $\square$

4 A Weak Stability Lemma

The weak stability of problems of p–Laplace type is well-known (cf. [6]). It also holds for our problem (1.1) if we make appropriate natural assumptions on the extra stress tensor ${\textbf{S}}$ and on the couple stress tensor ${\textbf{N}}$, which are motivated by the canonical example in (1.3). We denote the symmetric and the skew-symmetric part, resp., of a tensor ${\textbf{A}}\in {\mathbb {R}}^{d\times d}$ by ${{\textbf{A}}^{{\textrm{sym}}}:=\frac{1}{2}({\textbf{A}}+{\textbf{A}}^\top )}$ and ${{\textbf{A}}^{{\textrm{skew}}}:=\frac{1}{2}({\textbf{A}} -{\textbf{A}}^\top )}$. Moreover, ${\mathbb {R}^{d\times d}_{{\textrm{sym}}}:=\{{\textbf{A}}\in \mathbb {R}^{d\times d} \mid {\textbf{A}}={\textbf{A}}^{\textrm{sym}}\}}$ and $\mathbb {R}^{d\times d}_{{\textrm{skew}}}:=\{{\textbf{A}}\in \mathbb {R}^{d\times d}\mid {{\textbf{A}}={\textbf{A}}^{\textrm{skew}}}\}$.

Assumption 4.1

For the extra stress tensor ${\textbf{S}}:\mathbb {R}_{{\textrm{sym}}}^{d\times d}\times \mathbb {R}_{{\textrm{skew}}}^{d\times d}\times \mathbb {R}^d\rightarrow \mathbb {R}^{d\times d}$ and some ${\hat{p}} \in {\mathcal {P}}^{\log }(\mathbb {R})$ with ${\hat{p}}^- >1$, there exist constants $c,C >0$ such that:

• (S.1) ${\textbf{S}}\in C^0(\mathbb {R}_{{\textrm{sym}}}^{d\times d}\times \mathbb {R}_{{\textrm{skew}}}^{d\times d}\times \mathbb {R}^d;\mathbb {R}^{d \times d})$.

• (S.2) For every $\textbf{D}\in \mathbb {R}_{{\textrm{sym}}}^{d\times d}$, $\textbf{R}\in \mathbb {R}_{{\textrm{skew}}}^{d\times d}$ and $\textbf{E}\in \mathbb {R}^d$, it holds

  $$\begin{aligned} \vert {\textbf{S}}^{{\textrm{sym}}}({\textbf{D}},{\textbf{R}},{\textbf{E}})\vert&\le c\,\big (1+\vert \textbf{E}\vert ^2 \big ) \big (1+\vert {\textbf{D}}\vert ^{{\hat{p}}({|{\textbf{E}}|}^2)-1}\big )\,, \\ \vert {\textbf{S}}^{{\textrm{skew}}}({\textbf{D}},{\textbf{R}},{\textbf{E}})\vert&\le c\,\vert {\textbf{E}}\vert ^2 \big (1+\vert {\textbf{R}}\vert ^{{\hat{p}}({|{\textbf{E}}|}^2)-1}\big )\,. \end{aligned}$$

• (S.3) For every $\textbf{D}\in \mathbb {R}_{{\textrm{sym}}}^{d\times d}$, $\textbf{R}\in \mathbb {R}_{{\textrm{skew}}}^{d\times d}$ and $\textbf{E}\in \mathbb {R}^d$, it holds

  $$\begin{aligned} {\textbf{S}}({\textbf{D}},{\textbf{R}},{\textbf{E}}):{\textbf{D}}&\ge c\,\big (1+\vert \textbf{E}\vert ^2\big )\, \big ( \vert {\textbf{D}}\vert ^{{\hat{p}}({|{\textbf{E}}|}^2)}-C\big )\,, \\ {\textbf{S}}({\textbf{D}},{\textbf{R}},{\textbf{E}}):{\textbf{R}}&\ge c\,\vert {\textbf{E}}\vert ^2 \big ( \vert {\textbf{R}}\vert ^{{\hat{p}}({|{\textbf{E}}|}^2)}-C\big )\,. \end{aligned}$$

• (S.4) For every $\textbf{D}_1, \textbf{D}_2 \in \mathbb {R}_{{\textrm{sym}}}^{d\times d}$, $\textbf{R}_1, \textbf{R}_2 \in \mathbb {R}_{{\textrm{skew}}}^{d\times d}$ and $\textbf{E}\in \mathbb {R}^d$ with $({\textbf{D}}_1,\vert {\textbf{E}}\vert {\textbf{R}}_1)\ne ({\textbf{D}}_2,\vert {\textbf{E}}\vert {\textbf{R}}_2)$, it holds [-6 mm]

  $$\begin{aligned} \big ({\textbf{S}}(&{\textbf{D}}_1,{\textbf{R}}_1,{\textbf{E}})- {\textbf{S}}({\textbf{D}}_2,{\textbf{R}}_2,{\textbf{E}})\big ): \big ({\textbf{D}}_1-{\textbf{D}}_2+{\textbf{R}}_1-{\textbf{R}}_2\big )>0\,. \end{aligned}$$

Assumption 4.2

For the couple stress tensor ${\textbf{N}}:\mathbb {R}^{d\times d}\times \mathbb {R}^d\rightarrow \mathbb {R}^{d\times d}$ and some ${\hat{p}} \in \mathcal P^{\log }(\mathbb {R})$ with ${\hat{p}}^- >1$, there exist constants $c, C >0$ such that:

• (N.1) ${\textbf{N}}\in C^0(\mathbb {R}^{d\times d}\times \mathbb {R}^d;\mathbb {R}^{d\times d})$.

• (N.2) For every $\textbf{L}\in \mathbb {R}^{d\times d}$ and $\textbf{E}\in \mathbb {R}^d$, it holds

  $$\begin{aligned} \vert {\textbf{N}}({\textbf{L}},{\textbf{E}})\vert \le c\,\big \vert {\textbf{E}}\vert ^2 \big (1+\vert {\textbf{L}}\vert ^{{\hat{p}}({|{\textbf{E}}|}^2)-1}\big )\,. \end{aligned}$$

• (N.3) For every $\textbf{L}\in \mathbb {R}^{d\times d}$ and $\textbf{E}\in \mathbb {R}^d$, it holds

  $$\begin{aligned} {\textbf{N}}({\textbf{L}},{\textbf{E}}):{\textbf{L}}\ge c\,\big \vert {\textbf{E}}\vert ^2 \big (\vert {\textbf{L}}\vert ^{{\hat{p}}({|{\textbf{E}}|}^2)} -C\big )\,. \end{aligned}$$

• (N.4) For every $\textbf{L}_1,\textbf{L}_2 \in \mathbb {R}^{d\times d}$ and $\textbf{E}\in \mathbb {R}^d$ with $\vert {\textbf{E}}\vert >0$ and ${\textbf{L}}_1\ne {\textbf{L}}_2$, it holds [-6 mm]

  $$\begin{aligned} ({\textbf{N}}({\textbf{L}}_1,{\textbf{E}})-{\textbf{N}} ({\textbf{L}}_2,{\textbf{E}})):({\textbf{L}}_1-{\textbf{L}}_2)>0\,. \end{aligned}$$

Remark 4.3

Let Assumptions 3.3, 4.1 and 4.2 be satisfied. Since $\vert \textbf{E}\vert ^2\in W^{1,\infty }(\Omega ')$ for each $\Omega '\subset \subset \Omega$, which follows from ${\textbf{E}\in C^\infty (\Omega )}$, we have that the variable exponent

$$\begin{aligned} p:={\hat{p}}\circ \vert \textbf{E}\vert ^2 \end{aligned}$$

satisfies $p \in {\mathcal {P}}^{\infty }(\Omega )\cap C^0(\Omega )$ and $p|_{\Omega '}\in {\mathcal {P}}^{\log }(\Omega ')$ for each $\Omega '\subset \subset \Omega$.

Lemma 4.4

Let Assumption 3.3, 4.1 and 4.2 be satisfied with ${p^-\ge \frac{2d}{d+2}}$. Then, we have that ${{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )\hookrightarrow W^{1,p(\cdot )}_{{\textrm{loc}}}(\Omega )}$.

Proof

Let $\Omega '\subset \subset \Omega$ be arbitrary. Without loss of generality, we may assume that $\partial \Omega '\in C^{0,1}$. Otherwise, we switch to some $\Omega ''$ such that ${\Omega '\subset \subset \Omega ''\subset \subset \Omega }$ with ${\partial \Omega ''\in C^{0,1}}$. Since ${p\in C^0(\Omega )}$ (cf. Remark 4.3), Theorem 2.13 implies that any ${\textbf{u}\in {{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}}$ satisfies $\textbf{u}\in L^{p(\cdot )}(\Omega ')$ with

$$\begin{aligned} \Vert \textbf{u}\Vert _{L^{p(\cdot )}(\Omega ')}\le c(p,\Omega ')\Vert \textbf{u}\Vert _{{{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}} \end{aligned}$$

(4.5)

for some constant $c(p,\Omega ')\!>\!0$. Next, let $(\textbf{u}_n)_{n\in {\mathbb {N}}}\!\subseteq \! {{\mathcal {V}}^{p^-,p(\cdot )}_{\textbf{D}}}$ be a sequence such that $\textbf{u}_n\rightarrow \textbf{u}$ in ${{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}$ $(n\rightarrow \infty )$. Then, (4.5) gives us that $\textbf{u}_n\rightarrow \textbf{u}$ in $L^{p(\cdot )}(\Omega ')$ $(n\rightarrow \infty )$. In addition, since ${p|_{\Omega '}\in {\mathcal {P}}^{\log }(\Omega ')}$ (cf. Remark 4.3), Korn’s inequality (cf. Theorem 2.17 and ${{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}\hookrightarrow W^{1,p(\cdot )}(\Omega ')$) and (4.5) yield

$$\begin{aligned} \Vert \nabla \textbf{u}_n\Vert _{L^{p(\cdot )}(\Omega ')}+\Vert \textbf{u}_n\Vert _{L^{p(\cdot )}(\Omega ')}&\le c(p,\Omega ')\big (\Vert \textbf{D}\textbf{u}_n\Vert _{L^{p(\cdot )}(\Omega ')} +\Vert \textbf{u}_n\Vert _{L^{p(\cdot )}(\Omega ')}\big )\nonumber \\&\le c(p,\Omega ')\Vert \textbf{u}_n\Vert _{{{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}}\,. \end{aligned}$$

(4.6)

Thus,we observe that $(\textbf{u}_n)_{n\in {\mathbb {N}}}\subseteq {{\mathcal {V}}^{p^-,p(\cdot )}_{\textbf{D}}}$ is bounded in $W^{1,p(\cdot )}(\Omega ')$. This implies the existence of a vector field ${\tilde{\textbf{u}}}\in W^{1,p(\cdot )}(\Omega ')$ and of a not relabeled subsequence such that $\textbf{u}_n\rightharpoonup {\tilde{\textbf{u}}}$ in $W^{1,p(\cdot )}(\Omega ')$ $(n\rightarrow \infty )$. Due to the uniqueness of weak limits, we conclude that $\textbf{u}={\tilde{\textbf{u}}}$ in $W^{1,p(\cdot )}(\Omega ')$ and by taking the limit inferior in (4.6) that $\Vert \textbf{u}\Vert _{W^{1,p(\cdot )}(\Omega ')}\le c(p,\Omega ')\Vert \textbf{u}\Vert _{{{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}}$. $\square$

Lemma 4.7

Let Assumptions 3.3, 4.1 and 4.2 be satisfied with ${p^-\ge \frac{2d}{d+2}}$. Then, we have that ${{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)\hookrightarrow W^{1,p(\cdot )}_{{\textrm{loc}}}(\Omega _0)}$⁶ and ${\nabla (\textbf{w}|_{\Omega '})=({\hat{\nabla }} \textbf{w})|_{\Omega '}}$ for all ${\textbf{w}\in {{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}}$ and $\Omega '\subset \subset \Omega _0$.

Proof

Let $\Omega '\subset \subset \Omega _0$ be arbitrary and fix some $\Omega ''\subset \subset \Omega _0$ such that $\Omega '\subset \subset \Omega ''$. Due to ${\vert \textbf{E}\vert >0 }$ in $\overline{\Omega ''}$ and ${\vert \textbf{E}\vert \in C^0(\overline{\Omega ''})}$, there is a constant $c(\Omega '')>0$ such that $c(\Omega '')\le \vert \textbf{E}\vert ^2$ in $\overline{\Omega ''}$. Thus, for every $\textbf{w}\in C_0^\infty (\Omega )$, Hölder’s inequality in variable Lebesgue spaces and (2.1) imply

$$\begin{aligned} \Vert \textbf{w}\Vert _{{X^{p^-,p(\cdot )}_{{\nabla }}(\Omega '')}}\le 2\,{c(\Omega '')^{\frac{-1}{p^-}} \Vert \textbf{w}\Vert _{{{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}}\,.} \end{aligned}$$

(4.8)

Furthermore, since $p|_{\Omega ''}\in C^0(\Omega '')$ (cf. Remark 4.3) and $p^-\ge \frac{2d}{d+2}$, Theorem 2.13 implies that every $\textbf{w}\in C_0^\infty (\Omega )$ satisfies

$$\begin{aligned} \Vert \textbf{w}\Vert _{L^{p(\cdot )}(\Omega ')}\le c(p,\Omega ',\Omega '')\Vert \textbf{w}\Vert _{{X^{p^-,p(\cdot )}_{{\textbf{D}}}(\Omega '')}}\le c(p,\Omega ',\Omega '')\Vert \textbf{w}\Vert _{{X^{p^-,p(\cdot )}_{{\nabla }}(\Omega '')}} \end{aligned}$$

(4.9)

for some constant $c(p,\Omega ',\Omega '')>0$. Combining (4.8) and (4.9), we find that for every $\textbf{w}\in C_0^\infty (\Omega )$, it holds

$$\begin{aligned} \Vert \textbf{w}\Vert _{W^{1,p(\cdot )}(\Omega ')}\le c(p,\Omega ',\Omega '')\Vert \textbf{w}\Vert _{{{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}} \end{aligned}$$

(4.10)

for some constant $c(p,\Omega ',\Omega '')\!>\!0$. Since ${{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}$ is the closure of ${ C_0^\infty (\Omega )}$, and $C^{\infty }(\overline{\Omega '})$ is dense in $W^{1,p(\cdot )}(\Omega ')$ (cf. [5, Thm. 9.1.7]) since $p|_{\Omega ''}\in {\mathcal {P}}^{\log }(\Omega '')$ (cf. Remark 4.3), (4.10) implies ${{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)\hookrightarrow W^{1,p(\cdot )}(\Omega ')}$ and ${\nabla }(\textbf{w}|_{\Omega '})=(\hat{\nabla } \textbf{w})|_{\Omega '}$ for every ${\textbf{w}\in {{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}}$. $\square$

Now we can formulate the following weak stability property for problem (1.1).

Lemma 4.11

Let $\Omega \subseteq \mathbb {R}^d$, $d\ge 2$, be a bounded domain and let Assumptions 3.3, 4.1 and 4.2 be satisfied with ${p^->\frac{2d}{d+2}}$. Moreover, let ${(\textbf{v}^n)_{n\in {\mathbb {N}}}\subseteq {X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega )}$ and ${(\varvec{\omega }^n)_{n\in {\mathbb {N}}}\subseteq {X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}$ be such that $(\textbf{R}(\textbf{v}^n,\varvec{\omega }^n))_{n\in {\mathbb {N}}}\subseteq L^{p(\cdot )}(\Omega ;\vert \textbf{E}\vert ^2)$ is bounded and

$$\begin{aligned} \begin{aligned} \textbf{v}^n&\rightharpoonup \textbf{v}\quad{} & {} \text {in}\ {X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega ){} & {} \quad (n\rightarrow \infty )\,, \\ \varvec{\omega }^n&\rightharpoonup \varvec{\omega }\quad{} & {} \text {in}\ {X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2){} & {} \quad (n\rightarrow \infty ) \,. \end{aligned} \end{aligned}$$

(4.12)

For every ball ${B\subset \subset \Omega _0}$ such that ${B':=2B\subset \subset \Omega _0}$ and $\tau \in C_0^\infty (B')$ satisfying ${\chi _B\le \tau \le \chi _{B'}}$, we set ${ {\textbf{u}}^n:=({\textbf{v}}^n-{\textbf{v}})\tau }$, ${{\varvec{\psi }}^n:=(\varvec{\omega }^n-\varvec{\omega })\tau } \in W^{1,p(\cdot )}_0(B')$, $n\in {\mathbb {N}}$. Let ${\textbf{u}}^{n,j}\in W^{1,\infty }_0(B')$, $n,j\in {\mathbb {N}}$, and ${\varvec{\psi }}^{n,j}\in W^{1,\infty }_0(B')$, $n,j\in {\mathbb {N}}$, resp., denote the Lipschitz truncations constructed according to Theorem 2.18. Furthermore, assume that for every ${j\in {\mathbb {N}}}$, we have that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\big \vert \big \langle&\textbf{S}\big (\textbf{D}\textbf{v}^n,\textbf{R}(\textbf{v}^n,\varvec{\omega }^n),\textbf{E}\big )-\textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big ), \textbf{D}\textbf{u}^{n,j}+\textbf{R}(\textbf{u}^{n,j},{\varvec{\psi }}^{n,j})\big \rangle \nonumber \\&\quad + \big \langle \textbf{N}(\nabla \varvec{\omega }^n,\textbf{E})-\textbf{N}(\nabla \varvec{\omega },\textbf{E}),\nabla {\varvec{\psi }}^{n,j}\big \rangle \big \vert \le \delta _j\,, \end{aligned}$$

(4.13)

where $\delta _j\rightarrow 0$ $(j\rightarrow 0)$. Then, one has $\nabla \textbf{v}^n\rightarrow \nabla \textbf{v}$ a.e. in B ${(n\rightarrow \infty )}$, ${\nabla \varvec{\omega }^n\rightarrow \nabla \varvec{\omega }}$ a.e. in B $(n\rightarrow \infty )$ and $\varvec{\omega }^n\rightarrow \varvec{\omega }$ a.e. in B $(n\rightarrow \infty )$ for a suitable subsequence.

Remark 4.14

(i) For each ball $B'\subset \subset \Omega _0$, Lemmas 4.4 and 4.7 yield the embeddings ${{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )},{{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}\hookrightarrow {W^{1,p(\cdot )}(B')}$ and, therefore, that ${\textbf{v}^n-\textbf{v},\varvec{\omega }^n-\varvec{\omega }\!\in \! W^{1,p(\cdot )}(B')}$ for all $n\!\in \! {\mathbb {N}}$, which is crucial for the applicability of the Lipschitz truncation technique (cf. Theorem 2.18). In particular, Lemma 4.7 yields that ${\nabla (\varvec{\omega }|_{B'})=(\hat{\nabla }\varvec{\omega })|_{B'}}$ in $L^{p(\cdot )}(B')$ for all $\varvec{\omega }\in {{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}$, which is precisely the sense in which the gradients of both $\varvec{\omega }\in {{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}$ and ${(\varvec{\omega }^n)_{n\in {\mathbb {N}}}\in {{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}}$ are to be understood in (4.13).

(ii) The boundedness of $(\textbf{R}(\textbf{v}^n,\varvec{\omega }^n))_{n\in {\mathbb {N}}}\subseteq L^{p(\cdot )}(\Omega ;\vert \textbf{E}\vert ^2)$ yields a tensor field ${\widehat{\textbf{R}}}\in L^{p(\cdot )}(\Omega ;\vert \textbf{E}\vert ^2)$ such that up to a not relabeled subsequence

$$\begin{aligned} \textbf{R}(\textbf{v}^n,\varvec{\omega }^n)\rightharpoonup {\widehat{\textbf{R}}}\quad \text {in}\ L^{p(\cdot )}(\Omega ;\vert \textbf{E}\vert ^2)\quad (n\rightarrow \infty ) \,. \end{aligned}$$

(4.15)

Using the embedding $L^{p(\cdot )}(\Omega )\hookrightarrow L^{p^-}(\Omega )$, Korn’s inequality for the constant exponent $p^-\ge \frac{2d}{d+2}$ and $L^{p^-}(\Omega )\hookrightarrow L^{p^-}(\Omega ;{|{\textbf{E}}|}^2)$, since ${\textbf{E}\in L^\infty (\Omega )}$, we deduce from (4.12) that

$$\begin{aligned} \begin{aligned} \nabla \textbf{v}^n&\rightharpoonup \nabla \textbf{v}\quad{} & {} \text {in}\ L^{p^-}(\Omega ;\vert \textbf{E}\vert ^2){} & {} \quad (n\rightarrow \infty )\,,\\ \varvec{\omega }^n\cdot \varvec{\epsilon }&\rightharpoonup \varvec{\omega }\cdot \varvec{\epsilon }\quad{} & {} \text {in}\ L^{p^-}(\Omega ;\vert \textbf{E}\vert ^2){} & {} \quad (n\rightarrow \infty )\,. \end{aligned} \end{aligned}$$

(4.16)

Combining (4.15), (4.16), the embedding $L^{p(\cdot )}(\Omega ;{|{\textbf{E}}|}^2)\hookrightarrow L^{p^-}(\Omega ;{|{\textbf{E}}|}^2)$ and the definition of $\textbf{R}(\textbf{v},\varvec{\omega })$, we conclude that $\textbf{R}(\textbf{v},\varvec{\omega })={\widehat{\textbf{R}}}\in L^{p(\cdot )}(\Omega ;\vert \textbf{E}\vert ^2)$ in (4.15). Thus, the expression with $\textbf{R}(\textbf{v},\varvec{\omega })$ in (4.13) is well-defined.

Proof of Lemma 4.11

In view of the embeddings ${{X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega )\hookrightarrow W^{1,p(\cdot )}(B')}$, ${X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert {\textbf {E}}\vert ^2)\hookrightarrow W^{1,p(\cdot )}(B')$ (cf. Lemmas 4.4, 4.7) as well as $W^{1,p(\cdot )}(B')\hookrightarrow W^{1,p^-}(B')$, we deduce from (4.12), also using Rellich’s compact-ness theorem for constant exponents and Theorem 2.16, that

$$\begin{aligned} \begin{aligned} \textbf{v}^n&\rightharpoonup \textbf{v}\quad{} & {} \text {in}\ W^{1,p(\cdot )}(B'){} & {} \quad (n\rightarrow \infty )\,, \\ \textbf{v}^n&\rightarrow \textbf{v}\quad{} & {} \text {in}\ L^q(B')\cap L^{p(\cdot )}(B')\text { and a.e. in } B'{} & {} \quad (n\rightarrow \infty )\,,\\ \varvec{\omega }^n&\rightharpoonup \varvec{\omega }\quad{} & {} \text {in}\ W^{1,p(\cdot )}(B'){} & {} \quad (n\rightarrow \infty )\,, \\ \varvec{\omega }^n&\rightarrow \varvec{\omega }\quad{} & {} \text {in}\ L^q(B')\cap L^{p(\cdot )}(B') \text { and a.e. in } B'{} & {} \quad (n\rightarrow \infty )\,, \end{aligned} \end{aligned}$$

(4.17)

where $q\in \left[ 1,(p^-)^*\right)$. Throughout the proof, we will employ the particular notation

$$\begin{aligned} \begin{aligned} {\widetilde{\textbf{S}}}&:=\textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big )\,, \quad{} & {} {\textbf{S}}^n\,:=\textbf{S}\big (\textbf{D}\textbf{v}^n,\textbf{R}(\textbf{v}^n,\varvec{\omega }^n),\textbf{E}\big )\,, \\ {\widetilde{\textbf{N}}}&:=\textbf{N}(\nabla \varvec{\omega },\textbf{E})\,, \quad{} & {} {\textbf{N}}^n:=\textbf{N}(\nabla \varvec{\omega }^n,\textbf{E})\,. \end{aligned} \end{aligned}$$

(4.18)

Using (S.2), (N.2) Assumption 3.3, (4.12) and Remark 4.14, we obtain a constant ${K:=K(\textbf{E})>0}$ (not depending on $n\in {\mathbb {N}}$) such that

$$\begin{aligned} \begin{aligned} \Vert {\textbf {v}}^n\Vert _{ {{X}^{p^-,p(\cdot )}_{{\textbf {D}},{{\,\text {div}\,}}}(\Omega )}}\! +\Vert {\textbf {v}}\Vert _{{{X}^{p^-,p(\cdot )}_{{\textbf {D}},{{\,\text {div}\,}}}(\Omega )}}\!+ \Vert \varvec{\omega }^n\Vert _{p^-, p(\cdot ),{|{{\textbf {E}}}|}^2}\!+\Vert \varvec{\omega }\Vert _{p^-, p(\cdot ),{|{{\textbf {E}}}|}^2}&\le K, \\\Vert {\textbf {R}}({\textbf {v}}^n,\varvec{\omega }^n)\Vert _{ p(\cdot ),{|{{\textbf {E}}}|}^2}+\Vert {\textbf {R}}({\textbf {v}},\varvec{\omega })\Vert _{ p(\cdot ),{|{{\textbf {E}}}|}^2}&\le K, \\\Vert {{\textbf {S}}}^n\Vert _{p'(\cdot )} \! + \Vert \widetilde{{{\textbf {S}}}}\Vert _{p'(\cdot )}\!+ \Vert ({{\textbf {S}}}^n)^{\text {skew}}\Vert _{{p'(\cdot ),\vert {\textbf {E}}\vert ^{{\frac{-2}{p(\cdot )-1}}}}}\!+\Vert \widetilde{{{\textbf {S}}}}^{\text {skew}}\Vert _{{p'(\cdot ),\vert {\textbf {E}}\vert ^{{\frac{-2}{p(\cdot )-1}}}}}&\le K, \\\Vert {{\textbf {N}}}^n\Vert _{{p'(\cdot ),\vert {\textbf {E}}\vert ^{{\frac{-2}{p(\cdot )-1}}}}}+\Vert {\widetilde{{{\textbf {N}}}}} \Vert _{{p'(\cdot ),\vert {\textbf {E}}\vert ^{{\frac{-2}{p(\cdot )-1}}}}}&\le K. \end{aligned} \end{aligned}$$

(4.19)

Recall that $\tau \in C_0^\infty (B')$ with $\chi _B \le \tau \le \chi _{B'}$. Hence, using (S.4) and (N.4), we get

$$\begin{aligned} I^n\!:&=\!\int _B\! \big [\!\big (\textbf{S}^n\!-\!{\widetilde{\textbf{S}}}\big )\!:\! \big (\textbf{D}(\textbf{v}^n\!-\!\textbf{v})\!+\!\textbf{R}(\textbf{v}^n\!-\!\textbf{v},\varvec{\omega }^n\!-\!\varvec{\omega }) \big ) \!+\!\big (\textbf{N}^n\!-\!{\widetilde{\textbf{N}}}\big )\!:\!\nabla (\varvec{\omega }^n\!-\! \varvec{\omega })\big )^\theta \, dx\nonumber \\&\le \!\int _{B'}\!\big [\big (\textbf{S}^n\!-\!{\widetilde{\textbf{S}}}\big )\!:\! \big (\textbf{D}(\textbf{v}^n\!-\!\textbf{v})\!+\!\textbf{R}(\textbf{v}^n\!-\!\textbf{v},\varvec{\omega }^n\!-\!\varvec{\omega }) \big ) \!+\!\big (\textbf{N}^n\!-\!{\widetilde{\textbf{N}}}\big )\!:\!\nabla (\varvec{\omega }^n\!-\! \varvec{\omega }) \big )^\theta \!\tau ^\theta \,dx\nonumber \\&\le \int _{B'}\big [\big (\textbf{S}^n-{\widetilde{\textbf{S}}}\big ): \big (\textbf{D}(\textbf{v}^n-\textbf{v})+\textbf{R}(\textbf{v}^n-\textbf{v},\varvec{\omega }^n-\varvec{\omega }) \big ) \tau \big )^\theta \, dx \nonumber \\&\quad +\int _{B'}\big [\big (\textbf{N}^n-{\widetilde{\textbf{N}}}\big ):\nabla (\varvec{\omega }^n- \varvec{\omega }) \tau \big )^\theta dx =:\int _{B'} \alpha _n^\theta \,dx +\int _{B'} \beta _n^\theta \, dx \,, \end{aligned}$$

(4.20)

where we also used that

$$\begin{aligned} {\frac{1}{2} }(a^\theta + b^\theta ) \le (a+ b )^\theta \le a^\theta + b^\theta \end{aligned}$$

(4.21)

valid for all $a,b\ge 0$ and ${\theta \in (0,1)}$. Then, splitting the integral of $\alpha _n^\theta$ over $B'$ into an integral over $\{{\textbf{u}}^n\ne {\textbf{u}}^{n,j}\}$ and one over $\{{\textbf{u}}^n={\textbf{u}}^{n,j}\}$, also using Hölder’s inequality with exponents $\frac{1}{\theta },\frac{1}{1-\theta }$, we find that

$$\begin{aligned} \int _{B'} \alpha _n^\theta \, dx&\le \Vert \alpha _n \Vert _{L^1( B')}^\theta \vert \{{\textbf{u}}^n\ne {\textbf{u}}^{n,j}\}\vert ^{1-\theta } + \Vert \alpha _n \chi _{\{{\textbf{u}}^n={\textbf{u}}^{n,j}\} } \Vert _{L^1(B')}^\theta \vert B'\vert ^{1-\theta }\nonumber \\&=:(I_{1}^n)^{\theta } \vert \{{\textbf{u}}^n\ne {\textbf{u}}^{n,j}\}\vert ^{1-\theta } + \Vert \alpha _n \chi _{\{{\textbf{u}}^n={\textbf{u}}^{n,j}\} } \Vert _{L^1(B')}^\theta \vert B'\vert ^{1-\theta } \,. \end{aligned}$$

(4.22)

For the first term, we will use (2.19)$_4$ and, thus, have to show that $(I_1^n)_{n\in {\mathbb {R}}}\subseteq {\mathbb {R}}$ is bounded. In fact, by combining (4.12), (4.19), $\tau \le 1$, as well as

$$\begin{aligned} \textbf{A}:(\textbf{D}\textbf{u}+ \textbf{R}(\textbf{u},\textbf{w})) = \textbf{A}: \nabla \textbf{u}+ \textbf{A}^{\textrm{skew}}:({\varvec{\epsilon }}\cdot \textbf{w})\,, \end{aligned}$$

(4.23)

valid for vector fields $\textbf{u}$, $\textbf{w}$ and tensor fields $\textbf{A}$, we observe that

$$\begin{aligned} \begin{aligned} I_{1}^n&\le \big (\Vert (\textbf{S}^n)^{\textrm{sym}}\Vert _{p'(\cdot )} + \Vert {\widetilde{\textbf{S}}}^{\textrm{sym}}\Vert _{p'(\cdot )} \big ) \Vert \textbf{D}\textbf{v}^n-\textbf{D}\textbf{v}\Vert _{p(\cdot )}\\&\quad + \big (\Vert (\textbf{S}^n)^{\textrm{skew}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} + \Vert \widetilde{\textbf{S}}^{\textrm{skew}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} \big ) \\&\quad \times \Vert \textbf{R}(\textbf{v}^n,\varvec{\omega }^n)-\textbf{R}(\textbf{v},\varvec{\omega })\Vert _{ p(\cdot ),{|{\textbf{E}}|}^2} \\&\le 2\,K^2\,. \end{aligned} \end{aligned}$$

(4.24)

Similarly, we deduce that

$$\begin{aligned} \begin{aligned} \int _{B'} \beta _n^\theta \, dx&\le \Vert \beta _n \Vert _{L^1( B')}^\theta \vert \{{\varvec{\psi }}^n\ne {\varvec{\psi }}^{n,j}\}\vert ^{1-\theta }+ \Vert \beta _n \chi _{\{{\varvec{\psi }}^n={\varvec{\psi }}^{n,j}\} } \Vert _{L^1(B')}^\theta \vert B'\vert ^{1-\theta } \\&=:(I_{2}^n)^{\theta } \vert \{{\varvec{\psi }}^n\ne {\varvec{\psi }}^{n,j}\}\vert ^{1-\theta } + \Vert \beta _n \chi _{\{{\varvec{\psi }}^n={\varvec{\psi }}^{n,j}\} } \Vert _{L^1(B')}^\theta \vert B'\vert ^{1-\theta } \,, \end{aligned} \end{aligned}$$

(4.25)

and that

$$\begin{aligned} \begin{aligned} I_{2}^n&\le \big (\Vert \textbf{N}^n\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} + \Vert \widetilde{\textbf{N}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} \big )\Vert \nabla \varvec{\omega }^n-\nabla \varvec{\omega }\Vert _{p(\cdot ),{|{\textbf{E}}|}^2} \\&\le K^2\,. \end{aligned} \end{aligned}$$

(4.26)

Using (4.22), (4.24)–(4.26) and (4.21) we, thus, conclude that

$$\begin{aligned} \begin{aligned}&\int _{B'} \alpha _n^\theta \, dx +\int _{B'} \beta _n^\theta \, dx \\&\le 2^\theta K^{2\theta } \big (\vert \{\textbf{u}^n\ne \textbf{u}^{n,j}\}\vert ^{1-\theta } +\vert \{{\varvec{\psi }}^n\ne {\varvec{\psi }}^{n,j}\}\vert ^{1-\theta } \big ) \\&\quad + 2\,\vert B'\vert ^{1-\theta } \, \bigg (\int _{B'}{\alpha _n \chi _{\{\textbf{u}^n=\textbf{u}^{n,j}\}}\,dx} +\int _{B'}{\beta _n\,\chi _{\{{\varvec{\psi }}^n={\varvec{\psi }}^{n,j}\}}\,dx} \bigg )^{{\theta }}\,. \end{aligned} \end{aligned}$$

(4.27)

Let us now treat the last two integrals, which we denote by $I_3^{n,j}$ and $I_4^{n,j}$. We have that $\nabla (\textbf{v}^n -\textbf{v}) \tau = \nabla \textbf{u}^{n,j}- (\textbf{v}^n-\textbf{v}) \otimes \nabla \tau$ on $\{{\textbf{u}}^n={\textbf{u}}^{n,j}\}$, which, using (4.23), implies that

$$\begin{aligned} \begin{aligned} I_3^{n,j}&= {\big \langle { \textbf{S}^n- {\widetilde{\textbf{S}}}}, {\big (\nabla \textbf{u}^{n,j}- (\textbf{v}^n-\textbf{v}) \otimes \nabla \tau \big ) \chi _{\{{\textbf{u}}^n={\textbf{u}}^{n,j}\}}} \big \rangle } \\&\quad +{\big \langle { \big (\textbf{S}^n- {\widetilde{\textbf{S}}}\big )^{\textrm{skew}}}, {{\varvec{\epsilon }}\cdot {\varvec{\psi }}^{n,j} \chi _{\{{\varvec{\psi }}^n={\varvec{\psi }}^{n,j}\} }} \big \rangle } \\&\quad +{\big \langle { \big (\textbf{S}^n- {\widetilde{\textbf{S}}}\big )^{\textrm{skew}}}, {{\varvec{\epsilon }}\cdot (\varvec{\omega }^n -\varvec{\omega })\tau \chi _{\{{\textbf{u}}^n={\textbf{u}}^{n,j}\}\cap \{{\varvec{\psi }}^n\ne {\varvec{\psi }}^{n,j}\} }} \big \rangle } \\&\quad -{\big \langle { \big (\textbf{S}^n- {\widetilde{\textbf{S}}}\big )^{\textrm{skew}}}, {{\varvec{\epsilon }}\cdot (\varvec{\omega }^n-\varvec{\omega })\tau \chi _{\{{\textbf{u}}^n\ne {\textbf{u}}^{n,j}\}\cap \{{\varvec{\psi }}^n={\varvec{\psi }}^{n,j}\}}} \big \rangle }\,. \end{aligned} \end{aligned}$$

(4.28)

We have $\nabla (\varvec{\omega }^n -\varvec{\omega }) \tau = \nabla {\varvec{\psi }}^{n,j}- (\varvec{\omega }^n-\varvec{\omega }) \otimes \nabla \tau$ on $\{{\varvec{\psi }}^n={\varvec{\psi }}^{n,j}\}$, which implies that

$$\begin{aligned} \begin{aligned} I_4^{n,j}= {\big \langle { \textbf{N}^n- {\widetilde{\textbf{N}}}}, {\big (\nabla {\varvec{\psi }}^{n,j}-( \varvec{\omega }^{n}-\varvec{\omega })\otimes \nabla \tau \big ) \chi _{\{{\varvec{\psi }}^n={\varvec{\psi }}^{n,j}\} }} \big \rangle }\,. \end{aligned} \end{aligned}$$

(4.29)

Using (4.23) and adding suitable terms, we deduce from (4.28) and (4.29) that

$$\begin{aligned} \begin{aligned} I^{n,j}_{3} + I^{n,j}_{4}&\le {\big |{{\big \langle { \textbf{S}^n- \widetilde{\textbf{S}}}, { \textbf{D}\textbf{u}^{n,j} + \textbf{R}(\textbf{u}^{n,j},{\varvec{\psi }}^{n,j}) } \big \rangle }+{\big \langle { \textbf{N}^n- {\widetilde{\textbf{N}}}}, {\nabla {\varvec{\psi }}^{n,j} } \big \rangle } }\big |} \\&\quad +{\big |{{\big \langle { \textbf{S}^n- {\widetilde{\textbf{S}}}}, {\!\nabla \textbf{u}^{n,j}\chi _{\{{\textbf{u}}^n\ne {\textbf{u}}^{n,j}\}}} \big \rangle }}\big |} \\&\quad + {\big |{{\big \langle { \textbf{N}^n- {\widetilde{\textbf{N}}}}, {\nabla {\varvec{\psi }}^{n,j} \chi _{\{{\varvec{\psi }}^n\ne {\varvec{\psi }}^{n,j}\} }} \big \rangle } }\big |} \\&\quad + {\big |{{\big \langle { \big (\textbf{S}^n- {\widetilde{\textbf{S}}}\big )^{\textrm{skew}}}, {{\varvec{\epsilon }}\cdot {\varvec{\psi }}^{n,j} \chi _{\{{\varvec{\psi }}^n\ne {\varvec{\psi }}^{n,j}\} }} \big \rangle }}\big |} \\&\quad + {\big \langle {{\big |{ \big (\textbf{S}^n- {\widetilde{\textbf{S}}}\big )^{\textrm{skew}}}\big |}}, {{\big |{ \varvec{\omega }^n-\varvec{\omega }}\big |}\tau } \big \rangle } \\&\quad +{\big \langle {{\big |{ (\textbf{S}^n- {\widetilde{\textbf{S}}})^{\textrm{sym}}}\big |}}, {{\big |{( (\textbf{v}^{n}-\textbf{v})\otimes \nabla \tau )^{\textrm{sym}}}\big |}} \big \rangle }\\&\quad +{\big \langle {{\big |{ \textbf{N}^n-{\widetilde{\textbf{N}}}}\big |}}, {{\big |{( \varvec{\omega }^{n}-\varvec{\omega })\otimes \nabla \tau }\big |}} \big \rangle } \\&=: I_{5}^{n,j}+I_{6}^{n,j} +I_7^{n,j}+I_8^{n,j}+I_9^{n,j}+I_{10}^{n,j}+I_{11}^{n,j}\,. \end{aligned} \end{aligned}$$

(4.30)

The term $I_5^{n,j}\!$, i.e., the first line on the right-hand side in (4.30), is handled by (4.13). For the other terms we obtain, using Hölder’s inequality, (2.1) and (4.19),

$$\begin{aligned} I_6^{n,j}&\le 2\,\big (\Vert \textbf{S}^n\Vert _{p'(\cdot )} + \Vert \widetilde{\textbf{S}}\Vert _{p'(\cdot )} \big ) \Vert \nabla \textbf{u}^{n,j}\chi _{\{{\textbf{u}}^n\ne {\textbf{u}}^{n,j}\}} \Vert _{ L^{p(\cdot )}(B')}\nonumber \\&\le 2\,K\Vert \nabla \textbf{u}^{n,j}\chi _{\{{\textbf{u}}^n\ne {\textbf{u}}^{n,j}\}} \Vert _{ L^{p(\cdot )}(B')} \,, \end{aligned}$$

(4.31)

$$\begin{aligned} I_7^{n,j}&\le 2\,\big (\Vert \textbf{N}^n\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} + \Vert \widetilde{\textbf{N}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} \big ) \Vert \nabla {\varvec{\psi }}^{n,j}\chi _{\{{\varvec{\psi }}^n\ne {\varvec{\psi }}^{n,j}\}} \Vert _{ L^{p(\cdot )}(B';{|{\textbf{E}}|}^2)}\nonumber \\&\le 4\,K\,\Vert \textbf{E}\Vert _{\infty }^{\frac{2}{p^-}}\Vert \nabla {\varvec{\psi }}^{n,j}\chi _{\{{\varvec{\psi }}^n\ne {\varvec{\psi }}^{n,j}\}} \Vert _{ L^{p(\cdot )}(B')} \,,\end{aligned}$$

(4.32)

$$\begin{aligned} I_{8}^{n,j}&\le 2\,\big (\Vert (\textbf{S}^n)^{\textrm{skew}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}}\! + \!\Vert \widetilde{\textbf{S}}\,^{\textrm{skew}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} \big ) \Vert {\varvec{\psi }}^{n,j}\Vert _{L^\infty (B')}{|{\Omega }|}^{\frac{1}{p^-}}{\Vert {\textbf{E}}\Vert }_{\infty }^{\frac{2}{p^-}} \nonumber \\&\le 2\, K \, {|{\Omega }|}^{\frac{1}{p^-}}{\Vert {\textbf{E}}\Vert }_{\infty }^{\frac{2}{p^-}} \Vert {\varvec{\psi }}^{n,j} \Vert _{ L^\infty (B')} \,,\end{aligned}$$

(4.33)

$$\begin{aligned} I_{9}^{n,j}&\le 2\,\big (\Vert (\textbf{S}^n)^{\textrm{skew}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} + \Vert \widetilde{\textbf{S}}\,^{\textrm{skew}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} \big ) \Vert \varvec{\omega }^n-\varvec{\omega }\Vert _{L^{p(\cdot )}(B';{|{\textbf{E}}|}^2)}\nonumber \\&\le 4\,K\,\Vert \textbf{E}\Vert _{\infty }^{\frac{2}{p^-}}\Vert \varvec{\omega }^n-\varvec{\omega }\Vert _{ L^{p(\cdot )}(B')} \,,\end{aligned}$$

(4.34)

$$\begin{aligned} I_{10}^{n,j}&\le 2\, \big (\Vert \textbf{S}^n\Vert _{p'(\cdot )} + \Vert \widetilde{\textbf{S}}\Vert _{p'(\cdot )} \big ){\Vert {\nabla \tau }\Vert }_\infty \,\Vert \textbf{v}^n- \textbf{v}\Vert _{L^{p(\cdot )}(B')}\nonumber \\&\le 2\,K\,{\Vert {\nabla \tau }\Vert }_\infty \Vert \textbf{v}^n-\textbf{v}\Vert _{L^{p(\cdot )}(B')} \,,\end{aligned}$$

(4.35)

$$\begin{aligned} I_{11}^{n,j}&\le 2\,\big (\Vert \textbf{N}^n\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} + \Vert \widetilde{\textbf{N}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}} \big ) {\Vert {\nabla \tau }\Vert }_\infty \,\Vert \varvec{\omega }^n- \varvec{\omega }\Vert _{ L^{p(\cdot )}(B';{|{\textbf{E}}|}^2)}\nonumber \\&\le 4\, K\,{\Vert {\nabla \tau }\Vert }_\infty \,\Vert \textbf{E}\Vert _{\infty }^{\frac{2}{p^-}}\Vert \varvec{\omega }^n- \varvec{\omega }\Vert _{ L^{p(\cdot )}(B')} \,. \end{aligned}$$

(4.36)

Using (2.19), (4.12)–(4.17) and $1\le \lambda _{n,j}^p$, we deduce from (4.20), (4.27)–(4.36) for any ${j\in \mathbb {N}}$

$$\begin{aligned} \limsup _{n\rightarrow \infty } I^n\le \delta _j^\theta + c\, K^{2\theta } 2^{-j(1-\theta )}+ c\,(1+ {\Vert {\textbf{E}}\Vert }_{\infty }^{\frac{2}{p^-}}) ^{\theta } K^\theta 2^{\frac{-j\theta }{p^+}}. \end{aligned}$$

Since $\lim _{j\rightarrow \infty } \delta _j =0$, we observe that $I^n\!\rightarrow \! 0$ $(n\!\rightarrow \! \infty )$, which, owing to ${\theta \!\in \! (0,1)}$, (S.4) and (N.4), implies for a suitable subsequence that

$$\begin{aligned} \big (\textbf{S}^n-{\widetilde{\textbf{S}}}\big ): \big (\textbf{D}(\textbf{v}^n-\textbf{v})+\textbf{R}(\textbf{v}^n-\textbf{v},\varvec{\omega }^n-\varvec{\omega }) \big )&\rightarrow 0 \qquad \text { a.e.~in }B{} & {} \quad (n\rightarrow \infty )\,, \\ \big (\textbf{N}^n-{\widetilde{\textbf{N}}}\big )\!:\!\big (\nabla \varvec{\omega }^n-\nabla \varvec{\omega }\big )&\rightarrow 0 \qquad \text { a.e.~in }B{} & {} \quad (n\rightarrow \infty )\,. \end{aligned}$$

In view of (4.17), we also know that $\varvec{\omega }^n \rightarrow \varvec{\omega }$ a.e. in B and, hence, we can conclude the assertion of Lemma 4.11 as in the proof of [3, Lem. 6]. $\square$

Corollary 4.37

Let the assumptions of Lemma 4.11 be satisfied for all balls ${B\subset \subset \Omega _0}$ with ${B':=2B \subset \subset \Omega _0}$. Then, we have for suitable subsequences that $\nabla \textbf{v}^n \rightarrow \nabla \textbf{v}$ a.e. in $\Omega$ $(n\rightarrow \infty )$, ${\hat{\nabla }} \varvec{\omega }^n \rightarrow {\hat{\nabla }} \varvec{\omega }$ a.e. in $\Omega$ $(n\rightarrow \infty )$ and $\varvec{\omega }^n \rightarrow \,\varvec{\omega }$ a.e. in $\Omega$ $(n\rightarrow \infty )$.

Proof

Using all rational tuples contained in $\Omega _0$ as centers, we find a countable family $(B_k)_{k \in \mathbb {N}}$ of balls covering $\Omega _0$ such that $B'_k:=2B_k \subset \subset \Omega _0$ for every ${k \in \mathbb {N}}$. Using the usual diagonalization procedure, we construct suitable subsequences such that $\varvec{\omega }^n \rightarrow \varvec{\omega }$ a.e. in $\Omega _0$ $(n\rightarrow \infty )$, ${\hat{\nabla \varvec{\omega }^n\rightarrow {\hat{\nabla }}\varvec{\omega }}}$⁷ a.e. in $\Omega _0$ $(n\rightarrow \infty )$ and $\nabla \textbf{v}^n\rightarrow \nabla \textbf{v}$ a.e. in $\Omega _0$ $(n\rightarrow \infty )$. Since $\vert \Omega {\setminus } \Omega _0\vert =0$, we proved the assertion. $\square$

5 Main Theorem

Now we have everything at our disposal to prove our main result, namely the existence of solutions to the problem (1.1) for $p^->\frac{2d}{d+2}$ even if the shear exponent p is not globally log–Hölder continuous.

Theorem 5.1

Let $\Omega \subseteq \mathbb {R}^d$, $d\ge 2$, be a bounded domain and let Assumptions 3.3, 4.1 and  4.2 be satisfied. If the shear exponent $p ={\hat{p}} \,\circ \, {|{\textbf{E}}|}^2$ satisfies ${p^-\!>\!\frac{2d}{d+2}}$, then, for any ${\textbf{f}\in ({X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega ))^*}$ and ${\varvec{\ell }\in ({X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2))^*}$, there exist functions ${{\textbf{v}}\in {X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega )}$ and $\varvec{\omega }\in {{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}$ such that for every $\varvec{\varphi }\in C^1_0(\Omega )$ with ${{{\,\textrm{div}\,}}{\varvec{\phi }}= 0}$ and $\varvec{\psi }\in C_0^1(\Omega )$ with ${\nabla \varvec{\psi }\in L^{{\frac{q}{q-2}}}(\Omega ;\vert \textbf{E}\vert ^{{-\frac{\alpha q}{q-2}}})}$ for some ${q\in \left[ 1,(p^-)^*\right) }$, it holds

$$\begin{aligned}&\big \langle \textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big )-\textbf{v}\otimes \textbf{v},\textbf{D}\varvec{\varphi }+\textbf{R}({\varvec{\phi }},\varvec{\psi })\big \rangle \\&\,+\big \langle \textbf{N}({\hat{\nabla }} \varvec{\omega },\textbf{E})-\varvec{\omega }\otimes \textbf{v},\nabla \varvec{\psi }\big \rangle =\big \langle \textbf{f},\varvec{\varphi }\big \rangle +\big \langle \varvec{\ell }, \varvec{\psi }\big \rangle \,. \end{aligned}$$

Moreover, there exists a constant $c>0$ such that

$$\begin{aligned}&\Vert \textbf{v}\Vert _{{{X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega )}}+\Vert \varvec{\omega }\Vert _{{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)} \\&\le c \big (1+{\Vert {\textbf{E}}\Vert }_2+\Vert \textbf{f}\Vert _{({X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega ))^*}+\Vert \varvec{\ell }\Vert _{({X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2))^*}\big )\,. \end{aligned}$$

Proof

1. Non-degenerate approximation and a-priori estimates: Resorting to standard pseudo-monotone operator theory, we deduce that for every $n\in {\mathbb {N}}$, there exist functions $({\textbf{v}}^n,\varvec{\omega }^n) \in ({W^{1,p(\cdot )}_{0,{{\,\textrm{div}\,}}}(\Omega )}\cap L^r(\Omega )) \times (W^{1,p(\cdot )}(\Omega )\cap L^r(\Omega ))$ satisfying for every ${\varvec{\varphi }\in {W^{1,p(\cdot )}_{0,{{\,\textrm{div}\,}}}(\Omega )}\cap L^r(\Omega )}$ and $\varvec{\psi }\in W^{1,p(\cdot )}(\Omega )\cap L^r(\Omega )$

$$\begin{aligned} \begin{aligned}&\big \langle \textbf{S}\big (\textbf{D}\textbf{v}^n,\textbf{R}(\textbf{v}^n,\varvec{\omega }^n),\textbf{E}\big )-\textbf{v}^n\otimes \textbf{v}^n,\textbf{D}\varvec{\varphi }+\textbf{R}({\varvec{\phi }},\varvec{\psi })\big \rangle \\ {}&\quad +\tfrac{1}{n} \big \langle \vert \nabla {\textbf{v}}^n\vert ^{p(\cdot )-2}\nabla {\textbf{v}}^n,\nabla {\varvec{\phi }}\big \rangle +\tfrac{1}{n} \big \langle \big (\vert {\textbf{v}}^n\vert ^{p(\cdot )-2}+\vert {\textbf{v}}^n\vert ^{r-2}\big ){\textbf{v}}^n,{\varvec{\phi }}\big \rangle \\&\quad +\big \langle \textbf{N}(\nabla {\varvec{\omega }}^n,\textbf{E})-\varvec{\omega }^n\otimes \textbf{v}^n,\nabla \varvec{\psi }\big \rangle \\ {}&\quad +\tfrac{1}{n}\big \langle \vert \nabla \varvec{\omega }^n\vert ^{{p(\cdot )-2}{}}\nabla \varvec{\omega }^n,\nabla \varvec{\psi }\big \rangle +\tfrac{1}{n} \big \langle \big (\vert {\varvec{\omega }}^n\vert ^{p(\cdot )-2}+ \vert {\varvec{\omega }}^n\vert ^{r-2}\big ){\varvec{\omega }}^n,{\varvec{\psi }}\big \rangle \\ {}&=\big \langle \textbf{f},\varvec{\varphi }\big \rangle +\big \langle \varvec{\ell },\varvec{\psi }\big \rangle \,, \end{aligned} \end{aligned}$$

(5.2)

where⁸$r>2(p^-)'$. Moreover, there exists a constant $c>0$ (independent of ${n\in {\mathbb {N}}}$) such that

$$\begin{aligned}&\tfrac{1}{n} \big (\, \rho _{p(\cdot )}(\nabla \textbf{v}^n) +\rho _{p(\cdot )}(\textbf{v}^n) + \Vert \textbf{v}^n\Vert _r^{r}+\rho _{p(\cdot )}(\nabla \varvec{\omega }^n) +\rho _{p(\cdot )}(\varvec{\omega }^n) + \Vert \varvec{\omega }^n\Vert _r^{r}\,\big ) \nonumber \\ {}&\quad +\rho _{p(\cdot )}(\textbf{D}\textbf{v}^n) +\rho _{p(\cdot ), {|{\textbf{E}}|}^2}(\textbf{R}(\textbf{v}^n,\varvec{\omega }^n)) + \rho _{p(\cdot ), {|{\textbf{E}}|}^2}(\nabla \varvec{\omega }^n)\le K(\textbf{E},\textbf{f},\varvec{\ell })=:K\,. \end{aligned}$$

(5.3)

Using Lemma 2.2, as well as Korn’s and Poincaré’s inequality for the constant exponent $p^->\frac{2d}{d+2}$, we deduce from (5.3) that

$$\begin{aligned} \begin{aligned}&\tfrac{1}{n}\big (\Vert {\textbf{v}}^n\Vert _r+\Vert {\textbf{v}}^n\Vert _{1,p(\cdot )}+\Vert \varvec{\omega }^n\Vert _r+ \Vert \varvec{\omega }^n\Vert _{1,p}\big )\\ {}&\quad +\Vert \textbf{v}^n\Vert _{{{X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega )}}+\Vert \textbf{R}(\textbf{v}^n,\varvec{\omega }^n)\Vert _{p(\cdot ),\vert \textbf{E}\vert ^2}+\Vert \varvec{\omega }^n\Vert _{{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)} \le K\,.\end{aligned} \end{aligned}$$

(5.4)

Using (S.2),(N.2), (5.4), Assumption 3.3 and the notation introduced in (4.18), we obtain

$$\begin{aligned} \begin{aligned}\Vert {\textbf{S}}^n\Vert _{p'(\cdot )}+ \Vert ({\textbf{S}}^n)^{\textrm{skew}}\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}}+ \Vert {\textbf{N}}^n\Vert _{{p'(\cdot ),\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}}}}\le K. \end{aligned} \end{aligned}$$

(5.5)

2. Extraction of (weakly) convergent subsequences: The estimates (5.4), (5.5) and Remark 4.14 (ii) yield not relabeled subsequences as well as functions ${\textbf{v}\in {X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega )}$, ${\varvec{\omega }\in {X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}$, ${{{\widehat{\textbf{S}}}} \in L^{p'(\cdot )}(\Omega )}$ and ${{{\widehat{\textbf{N}}}}} \in L^{p'(\cdot )}(\Omega ;\vert \textbf{E}\vert ^{{-\frac{2}{p(\cdot )-1}}})$ such that

$$\begin{aligned} {\textbf {v}}^n&\rightharpoonup {\textbf {v}}{} & {} \text {in}\ {X}^{p^-,p(\cdot )}_{{\textbf {D}},{{\,\text {div}\,}}}(\Omega ){} & {} (n\rightarrow \infty )\,,{\,} \nonumber \\ \varvec{\omega }^n&\rightharpoonup \varvec{\omega }{} & {} \text{ in }\ {X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert {\textbf {E}}\vert ^2){} & {} (n\rightarrow \infty )\,, \nonumber \\ {\textbf {R}}({\textbf {v}}^n,\varvec{\omega }^n)&\rightharpoonup {\textbf {R}}({\textbf {v}},\varvec{\omega }){} & {} \text{ in }\ L^{p(\cdot )}(\Omega ;\vert {\textbf {E}}\vert ^2){} & {} (n\rightarrow \infty )\,, \end{aligned}$$

(5.6)

$$\begin{aligned} {{\textbf {S}}}^n&\rightharpoonup {{\widehat{{\textbf {S}}}}}{} & {} \text{ in }\ L^{p'(\cdot )}(\Omega ){} & {} (n\rightarrow \infty )\,, \nonumber \\ ({{\textbf {S}}}^n)^{{\text {skew}}}&\rightharpoonup \widehat{{\textbf {S}}}^{\text {skew}}{} & {} \text{ in }\ L^{p'(\cdot )}(\Omega ;\vert {\textbf {E}}\vert ^{\frac{-2}{p(\cdot )-1}}){} & {} (n\rightarrow \infty )\,, \nonumber \\ {{\textbf {N}}}^n&\rightharpoonup {{\widehat{{\textbf {N}}}}}{} & {} \text{ in }\ L^{p'(\cdot )}(\Omega ;\vert {\textbf {E}}\vert ^{\frac{-2}{p(\cdot )-1}}){} & {} (n\rightarrow \infty )\,. \end{aligned}$$

(5.7)

3. Identification of ${{\widehat{\textbf{S}}}}$ with $\textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big )$ and ${{\widehat{\textbf{N}}}}$ with ${\textbf{N}({\hat{\nabla \varvec{\omega }}},\textbf{E})}$: Recall that $\Omega _0= \{ x\in \Omega \mid \vert {{{\textbf {E}}}(x)\vert > 0}\}$ (cf. Assumption 3.3) and let ${B\!\subset \!\subset \! \Omega _0}$ be a ball such that $B'\!:=\!2B \!\subset \subset \!\Omega _0$. Then, due to Remark 4.3, Lemmas 4.4 and 4.14, we have that ${{X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega ),{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)} \hookrightarrow \! W^{1,p(\cdot )}(B')$. Therefore, from (5.6)$_{1,2}$, Rellich’s compactness theorem and Theorem 2.16, we deduce that

$$\begin{aligned} \begin{aligned} \textbf{v}^n&\rightharpoonup \textbf{v}\quad{} & {} \text {in}\ W^{1,p(\cdot )}(B'){} & {} \quad (n\rightarrow \infty )\,, \\ \textbf{v}^n&\rightarrow \textbf{v}\quad{} & {} \text {in}\ L^{p(\cdot )}(B') \cap L^{q}(\Omega ) \text { and a.e. in } B'{} & {} \quad (n\rightarrow \infty )\,,\\ \varvec{\omega }^n&\rightharpoonup \varvec{\omega }\quad{} & {} \text {in}\ W^{1,p(\cdot )}(B'){} & {} \quad (n\rightarrow \infty )\,, \\ \varvec{\omega }^n&\rightarrow \varvec{\omega }\quad{} & {} \text {in}\ L^{p(\cdot )}(B') \cap L^{q}(\Omega ) \text { and a.e. in } B'{} & {} \quad (n\rightarrow \infty )\,, \end{aligned} \end{aligned}$$

(5.8)

where $q\in \left[ 1,(p^-)^*\right)$. Next, let $\tau \in C_0^\infty (B')$ be such that $\chi _B \le \tau \le \chi _{B'}$. Due to (5.8)$_{1,3}$, it follows that

$$\begin{aligned} \begin{aligned} {\textbf{u}}^n&:=({\textbf{v}}^n-{\textbf{v}})\tau \rightharpoonup {\textbf{0}}{} & {} \text {in}\ W^{1,p(\cdot )}_0(B'){} & {} \quad (n\rightarrow \infty )\,, \\ {\varvec{\psi }}^n&:=(\varvec{\omega }^n-\varvec{\omega })\tau \rightharpoonup {\textbf{0}}{} & {} \text {in}\ W^{1,p(\cdot )}_0(B'){} & {} \quad (n\rightarrow \infty )\,. \end{aligned} \end{aligned}$$

(5.9)

Denote for $n\in {\mathbb {N}}$, the Lipschitz truncations of ${\textbf{u}^n,{\varvec{\psi }}^n\in W^{1,p(\cdot )}_0(B')}$ according to Theorem 2.18 with respect to $B'$ by $({\textbf{u}}^{n,j})_{j\in {\mathbb {N}}}, {({\varvec{\psi }}^{n,j})_{j\in {\mathbb {N}}}\!\subseteq \! W^{1,\infty }_0(B')}$. In particular, based on (5.9), Theorem 2.18 implies that these Lipschitz truncations satisfy for every $j \in \mathbb {N}$ and ${s \in [1,\infty )}$

$$\begin{aligned} \begin{aligned} {\textbf{u}}^{n,j}&\rightharpoonup {\textbf{0}}{} & {} \text {in}\ W^{1,s}_0(B'){} & {} \quad (n\rightarrow \infty )\,, \\ {\textbf{u}}^{n,j}&\rightarrow {\textbf{0}}{} & {} \text {in}\ L^{s}(B'){} & {} \quad (n\rightarrow \infty )\,, \\ {\varvec{\psi }}^{n,j}&\rightharpoonup {\textbf{0}}{} & {} \text {in}\ W^{1,s}_0(B'){} & {} \quad (n\rightarrow \infty )\,, \\ {\varvec{\psi }}^{n,j}&\rightarrow {\textbf{0}}{} & {} \text {in}\ L^{s}(B'){} & {} \quad (n\rightarrow \infty )\,. \end{aligned} \end{aligned}$$

(5.10)

Note that ${\varvec{\psi }}^{n,j}\in W^{1,\infty }_0(B')$, $n,j\in {\mathbb {N}}$, are suitable test-functions in (5.2). However, ${\textbf{u}}^{n,j}\in W^{1,\infty }_0(B')$, ${n,j\in {\mathbb {N}}}$, are not admissible in (5.2) as they are not divergence-free. To correct this, we define ${ \textbf{w}^{n,j}:={\mathcal {B}}_{B'}({{\,\textrm{div}\,}}{\textbf{u}}^{n,j})\in W^{1,s}_{0,{{\,\textrm{div}\,}}}(B')}$, for ${n,j\in {\mathbb {N}}}$, where ${{\mathcal {B}}_{B'}:L^s_0(B')\rightarrow W^{1,s}_0(B')}$ is the Bogovskii operator with respect to $B'$. Since ${\mathcal {B}}_{B'}$ is weakly continuous, (5.10)$_{1,2}$ and Rellich’s compactness theorem imply for every ${j\in \mathbb {N}}$ and ${s \in (1, \infty )}$ that

$$\begin{aligned} \begin{aligned} \textbf{w}^{n,j}&\rightharpoonup {\textbf{0}}{} & {} \text {in}\ W^{1,s}_0(B'){} & {} \quad (n\rightarrow \infty )\,, \\ \textbf{w}^{n,j}&\rightarrow {\textbf{0}}{} & {} \text {in}\ L^s(B'){} & {} \quad (n\rightarrow \infty )\,. \end{aligned} \end{aligned}$$

(5.11)

Apart from that, owing to the boundedness of ${\mathcal {B}}_{B'}$, since $p|_{B'}\in {\mathcal {P}}^{\log }(B')$ holds, (cf. Proposition 2.15), one has for any ${n,j\in \mathbb {N}}$ that

$$\begin{aligned} \begin{aligned} \Vert \textbf{w}^{n,j}\Vert _{W^{1,p(\cdot )}_0(B')}&\le c\,\Vert {{\,\mathrm{{\text {div}}}\,}}{\textbf{u}}^{n,j}\Vert _{L^{p(\cdot )}(B')}. \end{aligned} \end{aligned}$$

(5.12)

On the basis of $\nabla \textbf{u}^n = \nabla \textbf{u}^{n,j}$ on the set ${\{{\textbf{u}^n = \textbf{u}^{n,j} }\}}$ (cf. [25, Cor. 1.43]) and ${{\,\textrm{div}\,}}\textbf{u}^n =\nabla \tau \cdot (\textbf{v}^n -\textbf{v})$ for every ${n,j\in \mathbb {N}}$, we further get for every ${n,j\in \mathbb {N}}$ that

$$\begin{aligned} {{\,\textrm{div}\,}}\textbf{u}^{n,j} = \chi _ { {\{{\textbf{u}^n \not = \textbf{u}^{n,j} }\}}} {{\,\textrm{div}\,}}\textbf{u}^{n,j} + \chi _ { {\{{\textbf{u}^n = \textbf{u}^{n,j} }\}}}\nabla \tau \cdot (\textbf{v}^n -\textbf{v})\quad \text { a.e. in }B'. \end{aligned}$$

(5.13)

Then, (5.12) and (5.13) together imply for every ${n,j\in \mathbb {N}}$

$$\begin{aligned} {\Vert {\textbf{w}^{n,j}}\Vert }_{W^{1,p(\cdot )}_0(B')}\le c\, {\Vert {\nabla \textbf{u}^{n,j}\, \chi _ { {\{{\textbf{u}^n \not = \textbf{u}^{n,j} }\}} } }\Vert }_{L^{p(\cdot )}(B')} + c\,({\Vert {\nabla \tau }\Vert }_\infty ) {\Vert {\textbf{v}^n -\textbf{v}}\Vert }_{L^{p(\cdot )}(B')} \,, \end{aligned}$$

which in conjunction with (2.19) and (5.8)$_2$ yields for every $j \in \mathbb {N}$ that

$$\begin{aligned} \begin{aligned} {\limsup _{n\rightarrow \infty } \Vert \textbf{w}^{n,j}\Vert _{W^{1,p(\cdot )}_0(B')} \le c\,2^{\frac{-j}{p^+}}}\,. \end{aligned} \end{aligned}$$

(5.14)

Setting $\varvec{\varphi }^{n,j}:={\textbf{u}}^{n,j}-\textbf{w}^{n,j}$ for all ${n,j\in \mathbb {N}}$, we observe that $(\varvec{\varphi }^{n,j})_{n,j\in \mathbb {N}}$ belong to $V_s(B') \cap V_{p(\cdot )}(B')$, $s \in (1,\infty )$, i.e., they are suitable test-functions in (5.2). To use Corollary 4.37, we have to verify that condition (4.13) is satisfied. To this end, we test equation (5.2) with the admissible test-functions ${\varvec{\phi }}=\varvec{\varphi }^{n,j}$ and ${\varvec{\psi }}={\varvec{\psi }}^{n,j}$ for every ${n,j\in \mathbb {N}}$ and subtract on both sides

$$\begin{aligned} \big \langle \textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big ), \textbf{D}\textbf{u}^{n,j}+\textbf{R}(\textbf{u}^{n,j},{\varvec{\psi }}^{n,j})\big \rangle + \big \langle \textbf{N}({\hat{\nabla \varvec{\omega }}},\textbf{E}),\nabla {\varvec{\psi }}^{n,j}\big \rangle \,, \quad n,j\in \mathbb {N}\,. \end{aligned}$$

Owing to ${\varvec{\phi }}^{n,j}=\textbf{u}^{n,j}-\textbf{w}^{n,j}$ for every ${n,j\in \mathbb {N}}$, this yields for every ${n,j\in \mathbb {N}}$ that

$$\begin{aligned} \begin{aligned}&\big \langle \textbf{S}^n-\textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big ),\, \textbf{D}\textbf{u}^{n,j}+\textbf{R}(\textbf{u}^{n,j},{\varvec{\psi }}^{n,j})\big \rangle + \big \langle \textbf{N}^n-\textbf{N}({\hat{\nabla \varvec{\omega }}},\textbf{E}),\nabla {\varvec{\psi }}^{n,j}\big \rangle \\&= \big \langle \textbf{f},\varvec{\varphi }^{n,j}\big \rangle + \big \langle \varvec{\ell },{\varvec{\psi }}^{n,j}\big \rangle \\ {}&\quad -\tfrac{1}{n} \big \langle \vert \nabla {\textbf{v}}^n\vert ^{p(\cdot )-2}\nabla {\textbf{v}}^n,\nabla {\varvec{\phi }}^{n,j}\big \rangle -\tfrac{1}{n} \big \langle \big (\vert {\textbf{v}}^n\vert ^{p(\cdot )-2}+ \vert {\textbf{v}}^n\vert ^{r-2}\big ){\textbf{v}}^n,{\varvec{\phi }}^{n,j}\big \rangle \\ {}&\quad -\tfrac{1}{n}\big \langle \vert \nabla \varvec{\omega }^n\vert ^{{p(\cdot )-2}{}}\nabla \varvec{\omega }^n,\nabla {\varvec{\psi }}^{n,j}\big \rangle -\tfrac{1}{n} \big \langle \big (\vert {\varvec{\omega }}^n\vert ^{p(\cdot )-2}+ \vert {\varvec{\omega }}^n\vert ^{r-2}\big ){\varvec{\omega }}^n,{\varvec{\psi }}^{n,j}\big \rangle \\&\quad + \big \langle \textbf{v}^n\otimes \textbf{v}^n,\nabla {\varvec{\phi }}^{n,j}\big \rangle +\big \langle \varvec{\omega }^n\otimes \textbf{v}^n,\nabla {\varvec{\psi }}^{n,j}\big \rangle \\ {}&\quad +\big \langle \textbf{S}\big (\textbf{D}\textbf{v}^n,\textbf{R}(\textbf{v}^n,\varvec{\omega }^n),\textbf{E}\big ),\nabla \textbf{w}^{n,j}\big \rangle \\&\quad -\big \langle \textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big ), \textbf{D}\textbf{u}^{n,j}+\textbf{R}(\textbf{u}^{n,j},{\varvec{\psi }}^{n,j})\big \rangle -\big \langle \textbf{N}({\hat{\nabla \varvec{\omega }}},\textbf{E}),\nabla {\varvec{\psi }}^{n,j}\big \rangle \\&=: {\sum }_{k=1}^{11} J_k^{n,j}\,. \end{aligned} \end{aligned}$$

(5.15)

Because of $\textbf{v}\in {{X}^{p^-,p(\cdot )}_{\textbf{D},{{\,\textrm{div}\,}}}(\Omega )}$, $\varvec{\omega }\in {{X}^{p^-,p(\cdot )}_{{\nabla }}(\Omega ;\vert \textbf{E}\vert ^2)}$ and $\textbf{R}(\textbf{v}, \varvec{\omega }) \in L^{p(\cdot )}(\Omega ;{|{\textbf{E}}|}^2)$, we obtain using (S.2) and (N.2) that $\textbf{N}({\hat{\nabla \varvec{\omega }}},\textbf{E}) \in {L^{p'(\cdot )}(\Omega ;\vert \textbf{E}\vert ^{{\frac{-2}{p(\cdot )-1}}})}$ and $\textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big )\in L^{p'(\cdot )}(\Omega )$ (cf. (5.5)). Using this, (5.10) and (5.11), we conclude for every $j \in \mathbb {N}$ that

$$\begin{aligned} \lim _{n\rightarrow \infty } J_1^{n,j} +J_2^{n,j} +J_{10}^{n,j} +J_{11}^{n,j} =0\,. \end{aligned}$$

(5.16)

From (5.4), (5.10) and (5.11), we obtain for every $j \in \mathbb {N}$ that

$$\begin{aligned} \lim _{n\rightarrow \infty } J_3^{n,j}+J_4^{n,j} +J_5^{n,j} +J_6^{n,j} =0\,. \end{aligned}$$

(5.17)

Recalling (4.18) we get, in view of (5.5) and (5.14), that for every $j\in \mathbb {N}$, it holds

$$\begin{aligned} \limsup _{n\rightarrow \infty } J_9^{n,j} \le \limsup _{n\rightarrow \infty }\Vert \textbf{S}^n\Vert _{p'(\cdot )} \Vert \nabla \textbf{w}^{n,j}\Vert _{L^{p(\cdot )}(B')} \le K\, 2^{\frac{-j}{p^+}}=:\delta _j\,. \end{aligned}$$

(5.18)

From (5.8)$_{2,4}$, it further follows that

$$\begin{aligned} \begin{aligned} {\textbf{v}}^n\otimes {\textbf{v}}^n&\rightarrow {\textbf{v}}\otimes {\textbf{v}}{} & {} \text {in}\ L^{s'}(B'){} & {} \quad (n\rightarrow \infty ), \\ \varvec{\omega }^n\otimes {\textbf{v}}^n&\rightarrow \varvec{\omega }\otimes {\textbf{v}}{} & {} \text {in}\ L^{s'}(B'){} & {} \quad (n\rightarrow \infty ), \end{aligned} \begin{aligned} s'\in \Big [1, \frac{(p^-)^*}{2}\Big ). \end{aligned} \end{aligned}$$

(5.19)

Thus, combining (5.10), (5.11) and (5.19), we find that for every $j \in \mathbb {N}$

$$\begin{aligned} \lim _{n\rightarrow \infty } J_7^{n,j} +J_8^{n,j} =0\,. \end{aligned}$$

(5.20)

From (5.15)–(5.20) follows (4.13). Thus, Corollary 4.37 yields subsequences with

$$\begin{aligned} \begin{aligned} \nabla \textbf{v}^n&\rightarrow \nabla \textbf{v}{} & {} \quad \text { a.e. in }\Omega \,,\\ [-0.5mm] {\hat{\nabla \varvec{\omega }^n}}&\rightarrow {\hat{\nabla \varvec{\omega }}}{} & {} \quad \text { a.e. in }\Omega \,,\\ \varvec{\omega }^n&\rightarrow \,\varvec{\omega }{} & {} \quad \text { a.e. in }\Omega \,.\end{aligned} \end{aligned}$$

(5.21)

Since ${\textbf{S}}\in C^0( {\mathbb {R}}^{d\times d}_{sym }\times {\mathbb {R}}^{d\times d}_{skew }\times {\mathbb {R}}^d;{\mathbb {R}}^{d\times d})$ (cf. (S.1)) and ${\textbf{N}}\in C^0({\mathbb {R}}^{d\times d}\times {\mathbb {R}}^d;{\mathbb {R}}^{d\times d})$ (cf. (N.1)), we deduce from (5.21) that

$$\begin{aligned} \begin{aligned} \textbf{S}^n&\rightarrow \textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big ){} & {} \text {a.e. in}\ \Omega{} & {} \quad (n\rightarrow \infty )\,, \\ \textbf{N}^n&\rightarrow \textbf{N}({\hat{\nabla \varvec{\omega }}},\textbf{E}){} & {} \text {a.e. in}\ \Omega{} & {} \quad (n\rightarrow \infty )\,. \end{aligned} \end{aligned}$$

(5.22)

To identify ${{\widehat{\textbf{S}}}}$, we now argue as in the proof of [12, Thm. 4.6 (cf. (4.21)$_1$–(4.23)$_1$)], while Theorem 2.3 (with $G=\Omega$ and $\sigma ={|{\textbf{E}}|}^2$), (5.7), (5.22) and the absolute continuity of Lebesgue measure with respect to the measure $\nu _{{|{\textbf{E}}|}^2}$ is used to identify ${{\widehat{\textbf{N}}}}$. Thus, we just proved

$$\begin{aligned} \begin{aligned} {{\widehat{\textbf{S}}}}=\textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big )\quad \text{ and } \quad \widehat{\textbf{N}}=\textbf{N}({\hat{\nabla \varvec{\omega }}},\textbf{E})\,. \end{aligned} \end{aligned}$$

(5.23)

Now we have at our disposal everything to identify the limits of all but one term in (5.2). Using (5.4), (5.6), (5.7), (5.19)$_1$, (5.23) as well as $p^-> \frac{2d}{d+2}$, we obtain from (5.2) that for every $\varvec{\varphi }\in C^1_0(\Omega )$ with ${{\,\textrm{div}\,}}{\varvec{\phi }}=0$ and for every $\varvec{\psi }\in C_0^1(\Omega )$, it holds

$$\begin{aligned} \begin{aligned}&\big \langle \textbf{S}\big (\textbf{D}\textbf{v},\textbf{R}(\textbf{v},\varvec{\omega }),\textbf{E}\big )-\textbf{v}\otimes \textbf{v},\textbf{D}{\varvec{\phi }}+\textbf{R}({\varvec{\phi }},\varvec{\psi })\big \rangle \\&\,+\big \langle \textbf{N}({\hat{\nabla \varvec{\omega }}},\textbf{E}),\nabla \varvec{\psi }\big \rangle -\lim _{n\rightarrow \infty }\big \langle \varvec{\omega }^n\otimes \textbf{v}^n,\nabla \varvec{\psi }\big \rangle =\big \langle \textbf{f},\varvec{\varphi }\big \rangle +\big \langle \varvec{\ell },\varvec{\psi }\big \rangle \,. \end{aligned} \end{aligned}$$

(5.24)

Finally, we have to check whether the remaining limit in (5.24) exists and identify it. To this end, we fix an arbitrary $\varvec{\psi }\in C_0^1(\Omega )$ with $\nabla \varvec{\psi }\in L^{{\frac{q}{q-2}}}(\Omega ;\vert \textbf{E}\vert ^{{-\frac{\alpha q}{q-2}}})$ for some $q \in \left[ 1,(p^-)^*\right)$ and choose $\Omega '$ such that $int (supp (\varvec{\psi })) \subset \subset \Omega ' \subset \subset \Omega$. Due to Theorem 3.6 and (5.6)$_3$, it holds

$$\begin{aligned} \varvec{\omega }^n\rightharpoonup \varvec{\omega }\quad \text { in }L^q(\Omega ';\vert \textbf{E}\vert ^{\alpha q})\quad (n\rightarrow \infty ) \end{aligned}$$

for every $\alpha \ge 1+\frac{2}{p^-}$. On the other hand, due to $\nabla \varvec{\psi }\in L^{{\frac{q}{q-2}}}(\Omega ;\vert \textbf{E}\vert ^{{-\frac{\alpha q}{q-2}}})$ and (5.6)$_2$, using Hölder’s inequality, we also see that

$$\begin{aligned} \nabla \varvec{\psi }\textbf{v}^n\rightarrow \nabla \varvec{\psi }\textbf{v}\quad \text { in }L^{q'}(\Omega ';\vert \textbf{E}\vert ^{\frac{-\alpha q}{q-1}})\quad (n\rightarrow \infty )\,. \end{aligned}$$

Since $(L^q(\Omega ',\vert \textbf{E}\vert ^{\alpha q}))^*\simeq L^{q'}(\Omega ',\vert \textbf{E}\vert ^{\frac{-\alpha q}{q-1}})$, we infer that

$$\begin{aligned} \lim _{n\rightarrow \infty }\big \langle \varvec{\omega }^n\otimes \textbf{v}^n,\nabla \varvec{\psi }\big \rangle = \big \langle \varvec{\omega }\otimes \textbf{v},\nabla \varvec{\psi }\big \rangle , \end{aligned}$$

which looking back to (5.24) concludes the proof of Theorem 5.1. $\square$

Appendix A: Proof of Theorem 2.13

An essential ingredient in the proof of Theorem 2.13 is the following Gagliardo–Nirenberg interpolation inequality.

Lemma A.1

Let $\Omega \subseteq {\mathbb {R}}^d$, $d\ge 2$, be a bounded $C^1$–domain and $s,r \in \left[ 1,\infty \right)$. Then, for every ${\textbf{u}\in W^{1,r}(\Omega )\cap L^s(\Omega )}$, it holds ${\textbf{u}\in L^q(\Omega )}$ with

$$\begin{aligned} {\Vert \textbf{u}\Vert _q\le c\,\Vert \textbf{u}\Vert _{1,r}^\theta \Vert \textbf{u}\Vert _s^{1-\theta }\,,} \end{aligned}$$

(A.2)

where $c=c(q,r,s,\Omega )>0$, provided that $\frac{1}{q}=\theta (\frac{1}{r}-\frac{1}{d})+(1-\theta )\frac{1}{s}$ for some ${\theta \in \left[ 0,1\right] }$, unless $r=d$, in which (A.2) only holds for $\theta \in \left[ 0,1\right)$.

Proof

For the case $r\ne d$, we can refer to [15, Thm. 10.1]. For the case ${r=d}$, we can refer to [16] or [26], where (A.2) is proved with an additional $\Vert \textbf{u}\Vert _s$ on the right-hand side. To get rid of this additional term we can use that $\Vert \textbf{u}\Vert _s= \Vert \textbf{u}\Vert _s^\theta \Vert \textbf{u}\Vert _s^{1-\theta }$ $\le c\,\Vert \textbf{u}\Vert _{1,r}^\theta \Vert \textbf{u}\Vert _s^{1-\theta }$. $\square$

Since the Gagliardo–Nirenberg interpolation inequality only takes into account the full gradient, but we only have control over the symmetric part of the gradient, we need to switch locally from the full gradient to the symmetric gradient via Korn’s second inequality.

Lemma A.3

Let $\Omega \subseteq {\mathbb {R}}^d$, $d\ge 2$, be a bounded Lipschitz domain and $p\in \left( 1,\infty \right)$. Then, there exists a constant $c=c(p,\Omega )>0$ such that for every $\textbf{u}\in X^{p,p}_{\textbf{D}}(\Omega )$, it holds ${\textbf{u}\in W^{1,p}(\Omega )}$ with

$$\begin{aligned} \Vert \textbf{u}\Vert _{1,p}\le c\,\Vert \textbf{u}\Vert _{X^{p,p}_{\textbf{D}}(\Omega )}\,. \end{aligned}$$

Proof

See [24, Thm. 5.1.10, (5.1.17)]. $\square$

Aided by Lemmas A.1 and A.3, we can next prove Theorem 2.13.

Proof of Theorem 2.13

The proof is relies on techniques from [20, Lem. 3.20]. We split the proof into two steps:

Step 1: First, let $\textbf{u}\in {\mathcal {V}}^{p^-,p(\cdot )}_{{\textbf {D}}}$ be arbitrary. Since $p\in C^0(\Omega )$ and $\Omega '\subset \subset \Omega$, there exists a finite covering of $\overline{\Omega '}$ by open balls ${(B_i)_{i=1,\dots ,m}}$, ${m\in {\mathbb {N}}}$, with ${B_i\subset \subset \Omega }$, $i=1,\dots ,m$, such that the local exponents $p^+_i=\sup _{x\in B_i}{p(x)}$ and ${p^-_i=\inf _{x\in B_i}{p(x)}}$ satisfy for every ${i=1,\dots ,m}$

$$\begin{aligned} p^+_i<p^-_i\Big (1+\frac{2}{d}\Big )\,. \end{aligned}$$

(A.4)

In addition, there exists some $\Omega ''\subset \subset \Omega$ with $\partial \Omega ''\in C^1$ and $\bigcup _{i=1}^mB_i\subset \subset \Omega ''$. Let us fix an arbitrary ball $B_i$ for some $i=1,\dots ,m$. There are two possibilities. First, we consider the case ${p_i^+\le 2}$. Using $a^{p(x)}\le (1+a)^2\le 2+2a^2$, valid for all $a\ge 0$ and $x\in B_i$, and ${\Vert \textbf{u}\Vert _{L^2(B_i)}\le \Vert \textbf{u}\Vert _{L^2(\Omega '')}}$, where we also used that $\textbf{u}\in L^2(\Omega '')$ since $\textbf{u}\in C^\infty (\overline{\Omega ''})$, we observe that

$$\begin{aligned} \rho _{p(\cdot )}(\textbf{u}\chi _{B_i})\le 2\,\vert B_i\vert +2\Vert \textbf{u}\Vert _{L^2(B_i)}^2\le 2\,\vert \Omega \vert +2\,\Vert \textbf{u}\Vert _{L^2(\Omega '')}^2\,. \end{aligned}$$

(A.5)

Next, assume that ${p_i^+> 2}$. Then, exploiting that ${p_i^-> p_i^+\frac{d}{d+2}> \frac{2d}{d+2}}$ (cf. (A.4)), i.e., $\frac{d-{p_i^-}}{dp_i^-}<\frac{1}{2}$, we deduce that

$$\begin{aligned} 0<\theta _i&:=\frac{\frac{1}{2}-\frac{1}{p_i^+}}{\frac{1}{2}-\frac{d-p_i^-}{dp_i^-}}= \frac{p_i^-}{p_i^+}\frac{d(p_i^+-2)}{d(p_i^--2)+2p_i^-} \overset{((A.4))}{<}\frac{p_i^-}{p_i^+}\frac{d(p_i^-+\frac{2p_i^-}{d}-2)}{d(p_i^--2)+2p_i^-} =\frac{p_i^-}{p_i^+} \le 1\,. \end{aligned}$$

(A.6)

Owing to ${\partial B_i\in C^\infty }$, Korn’s second inequality (cf. Lemma A.3) yields a constant $c_i=c_i(p^-_i,B_i)>0$ such that

$$\begin{aligned} {\Vert \textbf{u}\Vert _{{L^{p^-_i}(B_i)}}+\Vert \nabla \textbf{u}\Vert _{{L^{p^-_i}(B_i)}}\le c_i\big (\Vert \textbf{u}\Vert _{{L^{p^-_i}(B_i)}}+\Vert \textbf{D}\textbf{u}\Vert _{{L^{p^-_i}(B_i)}}\big )\,.} \end{aligned}$$

(A.7)

Thanks to the Gagliardo–Nirenberg interpolation inequality (cf. Lemma A.1), since ${\theta _i\in \left( 0,1\right) }$ satisfies $\frac{1}{p_i^{{+}}}=\theta _i(\frac{1}{p_i^{{-}}}-\frac{1}{d})+(1-\theta _i)\frac{1}{2}$, there exists a constant ${c_i=c_i(p^-_i,p_i^+,\Omega ')}$ such that

$$\begin{aligned} {\rho _{p_i^+}(\textbf{u}\chi _{B_i})\le c_i\big (\Vert \textbf{u}\Vert _{{L^{p^-_i}(B_i)}}+\Vert \nabla \textbf{u}\Vert _{{L^{p^-_i}(B_i)}}\big )^{p_i^+\theta _i}\Vert \textbf{u}\Vert ^{p_i^+(1-\theta _i)}_{L^2(B_i)}\,.} \end{aligned}$$

(A.8)

By inserting (A.7) in (A.8), we get that

$$\begin{aligned} \begin{aligned} \rho _{p_i^+}(\textbf{u}\chi _{B_i})\le c_i\big (\Vert \textbf{u}\Vert _{{L^{p_i^-}(B_i)}}+\Vert \textbf{D}\textbf{u}\Vert _{{L^{p_i^-}(B_i)}}\big )^{p_i^+\theta _i}\Vert \textbf{u}\Vert _{L^2(B_i)}^{p_i^+(1-\theta _i)}\,. \end{aligned} \end{aligned}$$

(A.9)

Since $p_i^+\theta _i<p_i^-$ (cf. (A.6)), we can apply the $\varepsilon$–Young inequality with respect to $\rho _i:=p_i^-(p_i^+\theta _i)^{-1}>1$ with $c_i(\varepsilon ):=(\rho _i\varepsilon )^{{1-\rho _i'}}(\rho _i')^{-1}>0$ for all ${\varepsilon \in (0,\rho _i^{-1})}$ in (A.9). In this way, using $(a+b)^{{p^-_i}}\le 2^{p^+}(a^{{p^-_i}}+b^{{p^-_i}})$ and $a^{{p^-_i}}\le 2^{p^+}(1+a^{{p^+_i}})$ for all ${a,b\ge 0}$, we find that

$$\begin{aligned} \begin{aligned} \rho _{p_i^+}(\textbf{u}\chi _{B_i})&\le c_i\varepsilon \big (\Vert \textbf{u}\Vert _{{L^{p_i^-}(B_i)}}+\Vert \textbf{D}\textbf{u}\Vert _{{L^{p_i^-}(B_i)}}\big )^{p_i^-}+c_i(\varepsilon )\Vert \textbf{u}\Vert _{L^2(B_i)}^{p_i^+(1-\theta _i)\rho _i'}\\&\le c_i\varepsilon 2^{p_i^+}\big (\rho _{p_i^-}(\textbf{u}\chi _{B_i})+\rho _{p_i^-}(\textbf{D}\textbf{u}\chi _{B_i})\big )+c_i(\varepsilon )\Vert \textbf{u}\Vert _{L^2(B_i)}^{p_i^+(1-\theta _i)\rho _i'} \\ {}&\le c_i\varepsilon 2^{2p_i^+}\big (\vert B_i\vert +\rho _{p_i^+}(\textbf{u}\chi _{B_i})+\rho _{p_i^-}(\textbf{D}\textbf{u}\chi _{B_i})\big )+ c_i(\varepsilon )\Vert \textbf{u}\Vert _{L^2(B_i)}^{p_i^+(1-\theta _i)\rho _i'}\,. \end{aligned} \end{aligned}$$

(A.10)

We set $c_0:=\max _{i=1,\dots ,m}{c_i}$ and $c_0(\varepsilon ):=\max _{i=1,\dots ,m}{c_i(\varepsilon )}$. Then, if we choose $\varepsilon :={2^{-2p^+-1}}c_0^{-1}$ and absorb $c_i\varepsilon 2^{2p_i^+}\rho _{{p_i^+}}(\textbf{u}\chi _{B_i})\le \frac{1}{2}\rho _{{p_i^+}}(\textbf{u}\chi _{B_i})$ in the left-hand side in (A.10), we further infer from (A.10) that

$$\begin{aligned} \rho _{p_i^+}(\textbf{u}\chi _{B_i})\le \vert \Omega \vert +\rho _{p_i^-}(\textbf{D}\textbf{u}\chi _{B_i})+2c_0(\varepsilon )\Vert \textbf{u}\Vert _{L^2(B_i)}^{p_i^+(1-\theta _i)\rho _i'}\,. \end{aligned}$$

(A.11)

We set $\gamma :=\max _{i=1,\dots ,m}{p_i^+(1-\theta _i)\rho _i'}$ and use $\alpha ^{p_i^+(1-\theta _i)\rho _i'}\le 2^{\gamma }(1+\alpha ^\gamma )$ for all ${\alpha \ge 0}$, $\rho _{p(\cdot )}(\textbf{u}\chi _{B_i})\le 2^{p^+}(\vert \Omega \vert +\rho _{{p_i^+}}(\textbf{u}\chi _{B_i}))$, ${\rho _{{p_i^-}}(\textbf{D}\textbf{u}\chi _{B_i}) \le 2^{p^+}(\vert \Omega \vert +\rho _{p(\cdot )}(\textbf{D}\textbf{u}\chi _{B_i}))}$ and $\rho _{p(\cdot )}(\textbf{D}\textbf{u}\chi _{B_i})\le \rho _{p(\cdot )}(\textbf{D}\textbf{u})$ in (A.11), to arrive at

$$\begin{aligned} \begin{aligned} \rho _{p(\cdot )}(\textbf{u}\chi _{B_i})&\le 2^{p^+}\big (\vert \Omega \vert +\rho _{p_i^+}(\textbf{u}\chi _{B_i})\big )\\ {}&\le 2^{p^+}\big (2\vert \Omega \vert +\rho _{p_i^-}(\textbf{D}\textbf{u}\chi _{B_i})+2c_0(\varepsilon )\Vert \textbf{u}\Vert _{L^2(B_i)}^{p_i^+(1-\theta _i)\rho _i'}\big )\\&\le 2^{p^+}\Big (2\vert \Omega \vert +2^{p^+}\big (\vert \Omega \vert +\rho _{p(\cdot )}(\textbf{D}\textbf{u})\big )+c_0(\varepsilon )2^{\gamma +1}\big (1+\Vert \textbf{u}\Vert _{L^2(\Omega '')}^{\gamma }\big )\Big )\,. \end{aligned} \end{aligned}$$

(A.12)

If we sum up the inequalities (A.5) and (A.12) with respect to ${j=1,\dots ,m}$, we conclude that

$$\begin{aligned} \begin{aligned} \rho _{p(\cdot )}(\textbf{u}\chi _{\Omega '})&\le m\, 2^{p^+}\Big (2\vert \Omega \vert + 2^{p^+}\big (\vert \Omega \vert + \rho _{p(\cdot )}(\textbf{D}\textbf{u})\big ) \Big ) \\&\quad + m\, 2^{p^+}\,c_0(\varepsilon )2^{\gamma +1}\big (1+\Vert \textbf{u}\Vert _{L^2(\Omega '')}^{\gamma }\big )\,. \end{aligned} \end{aligned}$$

(A.13)

Moreover, since $X^{p^-\!,p^-}_{\textbf{D}}\!(\Omega '')\!=\!W^{1,p^-}\!(\Omega '')$ with norm equivalence by Korn’s second inequality (cf. Lemma A.3), where we, in particular, exploited that ${\partial \Omega ''\in C^{0,1}}$, the Sobolev embedding theorem yields ${X^{p^-,p^-}_{\textbf{D}}(\Omega '')\hookrightarrow L^2(\Omega '')}$ since $p^-\ge \frac{2d}{d+2}$. Therefore, since ${X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )\hookrightarrow X^{p^-,p^-}_{\textbf{D}}(\Omega '')}$, we conclude from (A.13) that there exists a constant $c(p,\Omega ')>0$ such that for every $\textbf{u}\in {{\mathcal {V}}^{p^-,p(\cdot )}_{\textbf{D}}}$, it holds

$$\begin{aligned} \Vert \textbf{u}\Vert _{L^{p(\cdot )}(\Omega ')}\le c(p,\Omega ')\Vert \textbf{u}\Vert _{X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}\,. \end{aligned}$$

Step 2: Let ${\textbf{u}\!\in \! X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}$ be arbitrary. Since ${{\mathcal {V}}^{p^-,p(\cdot )}_{\textbf{D}}}$ is dense in ${X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}$, there is a sequence $(\textbf{u}_n)_{n\in {\mathbb {N}}}\subseteq {{\mathcal {V}}^{p^-,p(\cdot )}_{\textbf{D}}}$ such that $\textbf{u}_n \rightarrow \textbf{u}$ in ${X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}$ $(n\rightarrow \infty )$. According to Step 1, there exists a constant ${c(p,\Omega ')>0}$ such that for every ${n\in {\mathbb {N}}}$

$$\begin{aligned} {\Vert \textbf{u}_n\Vert _{L^{p(\cdot )}(\Omega ')}\le c(p,\Omega ')\Vert \textbf{u}_n\Vert _{X^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}\,.} \end{aligned}$$

(A.14)

As a result, $(\textbf{u}_n)_{n\in {\mathbb {N}}}$ is bounded in $L^{p(\cdot )}(\Omega ')$. Owing to the reflexivity of $L^{p(\cdot )}(\Omega ')$, there exists a cofinal subset $\Lambda \subseteq {\mathbb {N}}$ as well as a function $\tilde{\textbf{u}}\in L^{p(\cdot )}(\Omega ')$ such that $\textbf{u}_n\rightharpoonup \tilde{\textbf{u}}$ in $L^{p(\cdot )}(\Omega ')$ $(\Lambda \ni n\rightarrow \infty )$. Thus, owing to the uniqueness of weak limits, we observe that $\textbf{u}=\tilde{\textbf{u}}\in L^{p(\cdot )}(\Omega ')$. Finally, taking the limit inferior with respect to $n\rightarrow \infty$ in (A.14) proves that (2.14) holds for every $\textbf{u}\in {{X}^{p^-,p(\cdot )}_{\textbf{D}}(\Omega )}$. $\square$