On Loops in Water Wave Branches and Monotonicity of Water Waves

Abstract

We give a quite simple approach how to prove the absence of loops in bifurcation branches of water waves in rotational case with arbitrary vorticity distribution. The supporting flow may contain stagnation points and critical layers and water surface is allowed to be overhanging. Monotonicity properties of the free surface are presented. Especially simple criterium of absence of loops is given for bifurcation branches when the bifurcation parameter is the water wave period. We show that there are no loops if you start from a water wave with a positive/negative vertical component of velocity on the positive half period.

1 Introduction

We consider steady water waves on vortical flows. We admit existence of stagnation points and critical layers inside the flow and the water surface is allowed to be overhanging.

A standard way to prove the existence of large amplitude water waves is a construction of bifurcating branches of solutions which start from a trivial-horizontal wave and then approach a certain limit configuration. We will use here analytic bifurcation theory developed in [1]. According to the analytic theory there are several limit options:

• (a) a stagnation point on the free surface;

• (b) self-intersection of the free surface, when the overhanging is allowed;

• (c) the free surface can touch the bottom.

• (d) constants of the problem, which depend on the bifurcation parameter can go to infinity or zero.

There is another option: existence of a closed curve. Usually this option can be analysed and excluded by using a nodal analysis, see [2] for the case of unidirectional flows and [4] for the case of constant vorticity. The aim of this paper is to study this option in different cases, when the water waves and supporting flow may contain stagnation points and critical layers and when the free surface is allowed to be overhanging, see [13] and [12] for discussions of problems arising in the nodal analysis.

We prove that there are no loops if the closed branch may contain only one uniform stream solution. In the case when the bifurcation parameter is the water wave period, we show that there are no closed branches at all. This is an interesting difference betweed branches with fixed period and when the bifurcation parameter is chosen as the period. The first advantage of the choice of the period as a bifurcation parameter is the fact that the transversality condition, required for existence of small amplitude water waves, is satisfied automatically. The second one there are no loops on the analytic branches of water waves. This means that analytic branches of water waves are unbounded and we can reach realy large water waves along such branches.

The nodal analysis in the case of a presence of stagnation points and critical layers in the supporting flow was performed in papers [4] and [12] under the assumption that the vorticity is constant or an decreasing function respectively. Our main assumption is expressed in terms of the dispersion equation. It is required that it has at least one positive root and if it has several positive roots one must chose the largest one for construction of the branch of Stokes waves. One can show that in the case when the vorticity is decreasing our assumption on the dispersion equation is satisfied.

Let us explain the main idea of our approach. The problem is formulated in the natural Cartesian coordinates (x, y) and the nodal analysis is based on the analysis of the sign of the vertical component of the velocity. The geometry of water domain is not fixed in these variables, it is unknown. To construct branches of water waves another variables are used in which the water domain is fixed. This allows to apply general theorems on existence of global branches of water waves which analytically depend on a bifurcation parameter. We use the variables (x, y) for application of maximum principle to the vertical component of the velocity and the second set of variables for analysis of continuous and analytical properties of the vertical component along the branch of solutions.

1.1 Formulation of the Problem

We consider steady surface waves in a two-dimensional channel bounded below by a flat, rigid bottom and above by a free surface that does not touch the bottom. The surface tension is neglected and the water motion can be rotational. In appropriate Cartesian coordinates (x, y), the bottom ${{\mathcal {B}}}$ coincides with the line $y=0$ and gravity acts in the negative y -direction. We choose the frame of reference so that the velocity field is time-independent as well as the free-surface ${{\mathcal {S}}}$, which is located in the half-plane $y>0$ and given in a parametric form $x=g(s)$, $y=f(s)$, $s\in \mathbb R$. It is assumed that $|f'|+|g'|\ne 0$, $f(s)>0$ and $g(s)\rightarrow \pm \infty$ when $s\rightarrow \pm \infty$. We assume also that the curve ${{\mathcal {S}}}$ does not intersect itself. We denote the strip-like domain between ${{\mathcal {B}}}$ and ${\mathcal S}$ by ${{\mathcal {D}}}$. The domain ${{\mathcal {D}}}$ is assumed to be symmetric with respect to the vertical line $x=0$ and $\Lambda$-periodic with respect to x, where $\Lambda$ is a positive number. If we introduce the set

$$\begin{aligned} \Omega =\{(x,y)\in {{\mathcal {D}}}\,:\,-\Lambda /2<x\le \Lambda /2\}, \end{aligned}$$

then

$$\begin{aligned} {{\mathcal {D}}}=\bigcup _{j=-\infty }^\infty \Omega _j,\;\;\Omega _j=\{(x+j\Lambda ,y)\,:\,(x,y)\in \Omega \}. \end{aligned}$$

The dependence of g and f is also periodic in s but the period can be different from $\Lambda$. If, for example, s is the arc length along ${{\mathcal {S}}}$, measured from the point (0, f(0)) (it is supposed here that $g(0)=0$ and the length comes with the sign $+$ for $s>0$ and with sign − for $s<0$), the period of the functions g and f is equal to the length of the free surface from (0, f(0)) to $(\Lambda ,f(0))$. We assume that ${{\mathcal {D}}}$ is simply connected, i.e. there are no wholes inside ${{\mathcal {D}}}$.

To describe the flow inside ${{\mathcal {D}}}$, we will use the stream function $\psi$. Then the velocity vector is given by $(-\psi _y,\psi _x)$. Since the surface tension is neglected, the function $\psi$ after a certain scaling, satisfies the following free-boundary problem (see for example [7]):

$$\begin{aligned}{} & {} \Delta \psi +\omega (\psi )=0\, \text{ in } {{\mathcal {D}}},\nonumber \\{} & {} \frac{1}{2}|\nabla \psi |^2+y-h=Q\, \text{ on } {{\mathcal {S}}},\nonumber \\{} & {} \psi =0\, \text{ on } {{\mathcal {S}}},\nonumber \\{} & {} \psi =-m\, \text{ for } y=0, \end{aligned}$$

(1.1)

where $\omega$ is a vorticity function, Q is the Bernoulli constant and ${{\mathcal {D}}}$ is an unknown domain. We always assume that the function $\psi$ is even and $\Lambda$ periodic with respect to x and

$$\begin{aligned} \nabla \psi \ne 0\;\; \text{ on } {{\mathcal {S}}}, \end{aligned}$$

(1.2)

which means that there are no stagnation point on the surface ${{\mathcal {S}}}$.

2 Main Lemmas

Let

$$\begin{aligned} D=\{(x,y)\in {{\mathcal {D}}}\,:\, 0<x<\Lambda /2,\}\;\;S=\{(x,y)\in {{\mathcal {S}}}\,:\, 0<x<\Lambda /2\}. \end{aligned}$$

Then the part of the boundary $\partial {{\mathcal {D}}}\cap \{x=0\}$ is an interval $[0,y_0]$ and the part of the boundary $\partial {{\mathcal {D}}}\cap \{x=\Lambda /2\}$ is an interval $[0,y_1]$. The solution $\psi$ solves the problem

$$\begin{aligned}{} & {} \Delta \psi +\omega (\psi )=0\, \text{ in } D,\nonumber \\{} & {} \frac{1}{2}|\nabla \psi |^2+y-h=Q\, \text{ on } S,\nonumber \\{} & {} \psi =0\, \text{ on } S,\nonumber \\{} & {} \psi =-m\, \text{ for } y=0 \end{aligned}$$

(2.1)

and

$$\begin{aligned} \psi _x(0,y)=0\;\; \text{ on } (0,y_0) \,\,\textrm{and}\,\, \psi _x(\Lambda /2,y)=0\, \text{ on } (0,y_1). \end{aligned}$$

(2.2)

We always assume that at least $\omega \in C^{1,\alpha }$ with certain $\alpha \in (0,1)$. This implies, in particular that $\psi \in C^{3,\alpha }(\overline{{\mathcal {D}}})$.

Lemma 2.1

Let $\psi \in C^{3}(\overline{{\mathcal {D}}})$ and let $\psi$ solves the problem (2.1), (2.2). If $\psi _x\ge 0$ in D and $\psi _x$ is not identically zero, then the following assertions are valid for the function $u=\psi _x$:

$$\begin{aligned}{} & {} (i)\;\;\;\;u>0\, \text{ for } (x,y)\in D\cup S\nonumber \\{} & {} (ii)\;\;\;u_x(0,y)>0\;\; \text{ for } 0<y\le y_0,\;\; u_x(\Lambda /2,y)<0 \, \text{ for } 0<y\le y_1 \nonumber \\{} & {} \;\;\;\;\;\;\;\; \text{ and } \;\;u_y(x,0)>0\; \, \text{ for } 0<x<\Lambda /2 \nonumber \\{} & {} (iii)\;\;u_{xy}(0,0)>0,\;\; u_{xy}(\Lambda /2,0)<0. \end{aligned}$$

(2.3)

Proof

Since

$$\begin{aligned} \Delta \psi _x+\omega '(\psi )\psi _x=0\;\; \text{ in } D, \end{aligned}$$

(2.4)

the assertion (i) for the domain D and the inequalities

$$\begin{aligned}{} & {} \psi _{xx}(0,y)>0\;\; \text{ for } 0<y< y_0,\;\; \psi _{xx}(\Lambda /2,y)<0\;\; \text{ for } 0<y< y_1 \\{} & {} \text{ and } \;\;\psi _{xy}(x,0)>0\;\; \text{ for } \;\;0<x<\Lambda /2 \end{aligned}$$

follows from the maximum principle and Hopf lemma (see [2]). Let us prove that

$$\begin{aligned} \psi _{xx}(0,y_0)>0\;\;\; \text{ and } \;\; \psi _{xx}(\Lambda /2,y_1)<0. \end{aligned}$$

(2.5)

Consider the first inequality. The tangent to the boundary curve at the point $(0,y_0)$ is parallel to the x-axis and so the curve near this point can be described by the equation $y=f(x)$ with smooth f and with $f'(0)=0$. The Bernoulli equation on this piece of the curve has the form

$$\begin{aligned} \frac{1}{2}|\nabla \psi |^2+f(x)-h=Q\;\; \text{ for } y=f(x). \end{aligned}$$

Differentiating this relation with respect to x and using that $\psi (x,f(x))=0$, which implies $f'=-\psi _x/\psi _y$, we get

$$\begin{aligned} \partial _\nu (\psi _x)-\rho \psi _x=0\;\; \text{ for } y=f(x). \end{aligned}$$

(2.6)

Here $\nu$ is the outward unit normal and

$$\begin{aligned} \rho = \rho (x)=\frac{(1+\psi _x\psi _{xy}+\psi _y\psi _{yy})}{\psi _y(\psi _x^2+\psi _y^2)^{1/2}}\Big |_{y=f(x)}. \end{aligned}$$

(2.7)

Near the point $(0,y_0)$ the function u satisfies (2.4), (2.6) and $u=0$ for $x=0$. Therefore the asymptotics of u near $(0,y_0)$ has the form (see [5])

$$\begin{aligned} u(x,y)=\psi _x(x,y)=Cp_{n}(x,y-y_0)+O(r^{n+1}), \end{aligned}$$

(2.8)

where $p_n(X,Y)$ satisfies $\Delta p_n=0$, $p_n(0,Y)=0$ and $\partial _Yp_n(X,0)=0$ (only the leading terms of the operators of the boundary value problem are used for determining the leading term of asymptotics of u). Due to the homogeneous Neumann boundary condition we can extend the function $p_n$ for $Y>0$ as an even function and then for $X<0$ as an odd function. The extended so function $p_n$ will be still harmonic. So $p_n$ is harmonic polynomial odd with respect to X and even with respect to Y. Due to the positivity of u inside D established in (i) the first option in (2.8) is $n=1$, i.e. $u(x,y)=cx+O(r^2)$, where $c\ge 0$ and $r^2=x^2+(y-y_0)^2$. Let us show that $c>0$. If $c=0$ then (2.8) is valid with ceratain interger $n\ge 3$. Such harmonic polynomials has 2n nodal domains which are angles of opening $\pi /n$ and therefore they change sign inside D near the point $(0,y_0)$. The same is true for the perturbation (2.8) near the vertex $(0,y_0)$. This contradicts to the fact that $u>0$ in D established in (i). Therefore $C=0$ in (2.8). This implies that $\psi _x$ has zero of infinite order at $(0,y_0)$. By unique continuation property we conclude that $\psi _x$ is identically zero, which contradicts to one of assumptions in formulation of our lemma. This contradiction proves that $\psi _x(x,y)=cx+O(r^2)$ with $c>0$. Similarly, we can prove the second inequality in (2.5). Thus (ii) is proved.

Let us prove (i) for points on S. Denote by K the set of points $(x,y)\in {\overline{S}}$ for which $\psi _y(x,y)=0$. Clearly K is compact and

$$\begin{aligned} \psi _x(x,y)^2\ge c_*:=\min _{(x,y)\in {\overline{S}}}|\nabla \psi |^2. \end{aligned}$$

The right-hand side here is positive by (1.2). If $\psi _y(x_*,y_*)\ne 0$ then there is an interval $(x_*-\varepsilon ,x_*+\varepsilon )$, $\varepsilon >0$, where the curve can be parameterized by $y=f(x)$ near the point $(x_*,y_*)$. Differentiating equation $\psi (x,f(x))=0$ with respect to x we get the relation (2.6). Then if $u(x,y)=0$ on this curve at a certain point (x, y), then $u_\nu (x,y)=0$ by (2.6). On the other hand by the Hopf lemma $u_\nu$ must be different from zero. This contradiction proves (i) for S. So the assertions (i) and (ii) are proved.

Let us prove (iii). From (2.4) and (2.2) it follows that

$$\begin{aligned} \psi _x(x,y)=C_0xy+o(r_0^2),\;\;\;\psi _x(x,y)=C_1(\Lambda /2-x)y+o(r_1^2), \end{aligned}$$

(2.9)

where $r_0$ and $r_1$ are the distances to (0, 0) and $(\Lambda /2,0)$, and $C_0\ge 0$, $C_1 \ge 0$ respectively. Let $C_0=0$. Then the asymptotics has the form

$$\begin{aligned} \psi _x(x,y)=Cp_n(x,y)+o(r_0^{n+1}), \end{aligned}$$

where $p_n$ is a harmonic polynomial of degree $n>2$ vanishing for $x=0$ and for $y=0$. Such polynomials change sign in D, which contradicts to (i), and therefore $C=0$, which leads to $\psi _x(x,y)=O(r_0^n)$ for any n. This implies $\psi _x=0$ by unique continuation property. This contradiction proves that $C_0>0$. Similarly one can prove that $C_1>0$. $\square$

Remark 2.2

We note that the assertion (iii) in the above lemma is equivalent to the asymptotics (2.9) for $\psi _x$ near the points (0, 0) and $(\Lambda /2,0)$, where $C_0>0$, $C_1>0$ respectively.

Corollary 2.3

Let $\psi$ be the same as in the previous lemma. Let also on a piece of the curve S, $\psi _y\ne 0$. Then this piece can be parameterized as $y=f(x)$. Moreover $f'(x)\ne 0$ on this part of the curve and it has the same sign as $-\psi _x/\psi _y$.

Proof

Since the tangent to the curve is $(-\psi _y,\psi _x)$ it can be parameterized as $y=f(x)$ on any interval where $\psi _y\ne 0$. Differentiating the relation $\psi (x,f(x))= \text{ const }$, we get $f'(x)=-\psi _x/\psi _y$. Therefore $f'\ne 0$ and it has the same sign as $-\psi _x/\psi _y$. $\square$

The boundary of D consists of four open segments

$$\begin{aligned}{} & {} L_1=\{0\}\times (0,y_0),\;\;L_2=(0,\Lambda /2)\times \{0\},\;\;L_3=\{\Lambda /2\}\times (0,y_1),\\{} & {} L_4\;\; \text{ is } \text{ the } \text{ boundary } \text{ curve } \text{ between } \text{ the } \text{ points } (0,y_0) \,\,and\,\, (\Lambda /2,y_1), \end{aligned}$$

and four points

$$\begin{aligned} A_1=(0,0),\;\;A_2=(\Lambda /2,0),\;\;A_3=(\Lambda /2,y_1),\;\;A_4=(0,y_0). \end{aligned}$$

So

$$\begin{aligned} \partial D=\bigcup _{j=1}^4L_j\cup \bigcup _{k=1}^4A_k. \end{aligned}$$

Introduce the domain

$$\begin{aligned} R=\{(X,Y)\,:\, 0<X<\Lambda /2,\;a<Y<b\}, \end{aligned}$$

where a and b are arbitrary constants. Similarly, we split the boundary of R. Let

$$\begin{aligned} M_1=\{0\}\times (a,b),\;\;M_2=(0,\Lambda /2)\times \{a\},\;\;M_3=\{\Lambda /2\}\times (a,b)\;\;M_4=(0,\Lambda /2)\times \{b\} \end{aligned}$$

and four points

$$\begin{aligned} B_1=(0,a),\;\;B_2=(\Lambda /2,a),\;\;A_3=(\Lambda /2,b),\;\;B_4=(0,b). \end{aligned}$$

Then

$$\begin{aligned} \partial R=\bigcup _{j=1}^4M_j\cup \bigcup _{k=1}^4B_k. \end{aligned}$$

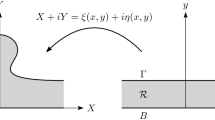
Consider a map

$$\begin{aligned} F=(F_1,F_2)\,:\,{\overline{R}}\rightarrow {\overline{D}}. \end{aligned}$$

We assume that this map is of class $C^2$ and

$$\begin{aligned} F(M_j)=L_j\;\; \text{ and } \;\;F(B_j)=A_j,\;\;j=1,2,3,4. \end{aligned}$$

(2.10)

Moreover we assume that this map is isomorphism, i.e. its Jacobian does not vanish. Having in mind the requirement (2.10) this assumption is

$$\begin{aligned} {{\mathcal {J}}}:=\frac{\partial x}{\partial X}\frac{\partial y}{\partial Y}-\frac{\partial x}{\partial Y}\frac{\partial y}{\partial X}> 0\;\; \text{ in } {\overline{R}}. \end{aligned}$$

(2.11)

Lemma 2.4

Let $u\in C^2({\overline{D}})$ satisfy

$$\begin{aligned} u=0\;\; \text{ on } \bigcup _{j=1}^3L_j, \end{aligned}$$

(2.12)

and properties (i)–(iii) from Lemma 2.1. Then the function $v(X,Y)=u(F(X,Y))$ also belongs to $C^2(\overline{{\mathcal {R}}})$ and satisfies

$$\begin{aligned} v=0\;\; \text{ on } \bigcup _{j=1}^3M_j \end{aligned}$$

(2.13)

together with properties (i)–(iii) from the same Lemma.

Proof

The relation (2.13) follows from (2.10) and the property (i) can be verified directly.

Let us turn to (ii). By (2.10), $y(X,a)=0$, $x(0,Y)=0$ and $x(\Lambda /2,Y)=0$ and hence

$$\begin{aligned} \frac{\partial x}{\partial Y}=0\;\; \text{ on } M_1 \,\,and\,\, M_3,\;\;\frac{\partial y}{\partial X}=0\;\; \text{ on } M_2. \end{aligned}$$

(2.14)

Therefore

$$\begin{aligned} {{\mathcal {J}}}=\frac{\partial x}{\partial X}\frac{\partial y}{\partial Y}> 0\;\; \text{ on } \overline{M_1}\cup \overline{M_2}\cup \overline{M_3}. \end{aligned}$$

(2.15)

From the second relation in (2.10) it follows that

$$\begin{aligned} \frac{\partial x}{\partial X}>0,\;\;\frac{\partial y}{\partial Y}> 0\;\; \text{ on } \overline{M_1}\cup \overline{M_2}\cup \overline{M_3} \end{aligned}$$

(2.16)

Differentiating v and using (2.14), we get

$$\begin{aligned} \partial _Xv=u_x\frac{\partial x}{\partial X}+u_y\frac{\partial y}{\partial X}=u_x\frac{\partial x}{\partial X},\;\;\partial _Yv=u_x\frac{\partial x}{\partial Y}+u_y\frac{\partial y}{\partial Y}=u_y\frac{\partial y}{\partial Y} \end{aligned}$$

on $\overline{M_1}\cup \overline{M_2}\cup \overline{M_3}$. These relations together with (2.16) imply (ii) and that $u_X=u_Y=0$ at the points (0, a) and $(\lambda /2,b)$ since the last is true for similar derivatives with respect to x and y.

To prove (iii) we use Remark 2.2 and hence the asymptotics (2.9) with positive constants $C_0$ and $C_1$ and note that similar asymptotics is true in X and Y variables with additional factor $\frac{\partial x}{\partial X}\frac{\partial y}{\partial Y}$, since

$$\begin{aligned} \partial _X\partial _Yv=\partial _x\partial _yu\frac{\partial x}{\partial X}\frac{\partial y}{\partial Y}\;\; \text{ at } (0,0)\,\, and\,\, (\Lambda /2,0). \end{aligned}$$

This completes the proof of (iii) and proposition. $\square$

Remark 2.5

We can assume that $v\in C^2({\overline{R}})$ satisfies (2.13) and (2.3) (i)–(iii). Then the same proof gives that $u(x,y)=v(X(x,y),Y(x,y))$ satisfies (2.12) together with (2.3) (i)–(iii).

In the next proposition a stability property of the properties (i)–(iii), (2.3) is verified.

Proposition 2.6

Let $u\in C^2({\overline{D}})$ satisfy

$$\begin{aligned} u=0\;\; \text{ on } \bigcup _{j=1}^3L_j \end{aligned}$$

(2.17)

and (i)–(iii) in (2.3), be valid. Then there exist $\varepsilon >0$ such that if $v\in C^2({\overline{D}})$ satisfies (2.17) and $||u-v||_{C^2({\overline{D}})}\le \varepsilon$ then v also satisfies (i)–(iii) in (2.3).

Proof

Let the properties (i)–(iii), (2.3), are true for a certain $u\in C^2({\overline{D}})$ together with (2.17). Then for small $\varepsilon$ and for the function v satisfying (2.17) and $||u-v||_{C^2({\overline{D}})}\le \varepsilon$ all properties in (ii) and (iii) in (2.3) are satisfied. But then the function v is positive in a neighborhood of $L_1\cup L_2\cup L_3$ inside D. Then due to (i) the function v is also positive near $L_4$ provided $\varepsilon$ is small. This together with (i) for D implies positivety of v in D for small $\varepsilon$. $\square$

2.1 Uniform Stream Solution, Dispersion Equation

The uniform stream solution $\psi =\Psi (y)$ with the bottom $y=0$ and the free surface $y=h$, satisfies the problem

$$\begin{aligned}{} & {} \Psi ^{''}+\omega (\Psi )=0\;\; \text{ on } (0,h),\nonumber \\{} & {} \Psi (h)=0,\;\;\Psi (0)=-m \end{aligned}$$

(2.18)

and the Bernoulli relation

$$\begin{aligned} \frac{1}{2}\Psi '(h)^2=Q. \end{aligned}$$

(2.19)

To solve the problem (2.18), (2.19) we start from the following Cauchy problem

$$\begin{aligned}{} & {} \Psi ^{''}+\omega (\Psi )=0\;\; \text{ on } (0,h),\nonumber \\{} & {} \Psi (h)=0,\;\;\Psi '(h)=\lambda . \end{aligned}$$

(2.20)

This problem is uniquely solvable and the solution is non trivial if $\lambda \ne 0$. Using this solution we can construct solution to (2.18), (2.19) with $m=-\Psi (0)$ and $Q=\lambda ^2/2$.

We assume that

$$\begin{aligned} \kappa :=\Psi '(h)\ne 0. \end{aligned}$$

(2.21)

Before introducing the dispersion equation we consider the eigenvalue problem

$$\begin{aligned} -w^{''}-\omega '(\Psi )w=\mu w\;\; \text{ on } (0,h),\;\;w(0)=w(h)=0. \end{aligned}$$

(2.22)

Denote by

$$\begin{aligned} \mu _1<\mu _2<\cdots ,\;\;\mu _j\rightarrow \infty ,\;\; \text{ as } j\rightarrow \infty \end{aligned}$$

the eigenvalues of the problem (2.22), which are simple since we are dealing with one-dimensional problem. Introduce the function $\gamma (y;\tau )$ as solution of the equation

$$\begin{aligned} -\gamma ^{''}-\omega '(\Psi (y))\gamma +\tau ^2\gamma =0,\;\; \text{ on } (0,h), \,\;\gamma (0;\tau )=0,\;\;\gamma (h;\tau )=1. \end{aligned}$$

(2.23)

This function is defined for all $\tau$ if $\mu _1>0$ and for $\tau \ne \sqrt{-\mu _j}$ for all $\mu _j\le 0$. The frequency of small amplitude Stokes waves is determined by the dispersion equation (see, for example, [7] and [6]). We put

$$\begin{aligned} \sigma (\tau )=\kappa (\gamma '(h;\tau )-\rho _0), \end{aligned}$$

(2.24)

where

$$\begin{aligned} \rho _0=\frac{1+\Psi '(h)\Psi ^{''}(h)}{\Psi '(h)^2}. \end{aligned}$$

(2.25)

The dispersion equation is the following

$$\begin{aligned} \sigma (\tau )=0. \end{aligned}$$

(2.26)

We note that

$$\begin{aligned} \frac{1+\Psi '(h)\Psi ^{''}(h)}{\Psi '(h)^2}=\kappa ^{-2}-\frac{\omega (1)}{\kappa } \end{aligned}$$

and hence another form for (2.24) is

$$\begin{aligned} \sigma (\tau )=\kappa \gamma '(d,\tau )-\kappa ^{-1}+\omega (1). \end{aligned}$$

(2.27)

Certainly the function $\sigma$ is defined for the same values of $\tau$ as the function $\gamma$. The main properties of the function $\gamma$ are presented in the following

Proposition 2.7

(i)

$$\begin{aligned} \partial _\tau \gamma '(h;\tau )>0\;\; \text{ for } \text{ all } \tau >0 \text{ for } \text{ which } \gamma \text{ is } \text{ defined } . \end{aligned}$$

(2.28)

(ii) If $\mu _1<0$ and $\tau ^2 <-\mu _1$ then the function $\gamma (y;\tau )$ changes sign on the interval $y\in (0,h)$.

Proof

• (i) This assertion is proved in [7], Lemma 1.1.

• (ii) Let $\tau _1^2=-\mu _1$ and let $\phi _1$ be a positive eigenfunction on (0, h) corresponding to $\mu _1$. Multiplying the equation in (2.23) by $\phi _1$ and integrating over the interval (0, h), we get

$$\begin{aligned} (\tau _1^2-\tau ^2)\int _{0}^h\gamma \phi _1dy=\phi _1'(h). \end{aligned}$$

Since $\phi _1'(h)<0$ and $\tau <\tau _1$ we get

$$\begin{aligned} \int _{0}^h\gamma \phi _1dy<0. \end{aligned}$$

Since $\gamma (h;\tau )=1$ the function $\gamma$ must change sign on (0, h). $\square$

Corollary 2.8

If $\kappa >0$ then the function $\sigma '(\tau )>0$ for $\tau >0$. If $\kappa <0$ then $\sigma '(\tau )<0$ for $\tau >0$.

Proof

The proof follows directly from (2.28) and the definition of $\sigma$. $\square$

The following properties of the function $\sigma$ are proved in [7]

Proposition 2.9

(i)

$$\begin{aligned} \sigma (\tau )=\kappa \tau +O(1)\;\; \text{ as } \tau \rightarrow \infty . \end{aligned}$$

(ii) Let $\tau _*^2$ be an eigenvalue of the problem (2.22) and let $\phi _*(y)$ be the corresponding eigenfunction normalized by $||\phi _*||_{L^2(-h,0)}=1$. Then

$$\begin{aligned} \sigma (\tau )=-\frac{\kappa \phi '_*(h)^2}{\tau ^2-\tau _*^2}+O(1)\;\; \text{ for } \tau \text{ close } \text{ to } \tau _*. \end{aligned}$$

We note that due to the homogeneous Dirichlet boundary condition $\phi '_*(h)\ne 0$.

From Propositions 2.7, 2.9 and Corollary 2.8 we get

Theorem 2.10

The following assertions are valid

(i) Let $\mu _1>0$ then the dispersion equation (2.26) has a positive root if and only if $\sigma (0)<0$ in the case $\kappa >0$ and $\sigma (0)>0$ in the case $\kappa <0$. This root is unique. In both cases ($\kappa \gtrless 0$) the function $\gamma (y;\tau )>0$ for $y\in (0,h]$.

(ii) If $\mu _1\le 0$ then the dispersion equation (2.26) is uniquely solvable on the half-line $\tau >\sqrt{-\mu _1}$. If $\tau _*$ is a root of this equation then the function $\gamma (y;\tau _*)$ is positive for $y\in (0,h]$. The number $\tau _*$ is the only root of the dispertion eqiuation for which the function $\gamma$ is positive on (0, h].

Proof

• (i) this follows from the monotonicity of the function $\sigma$ proved in Proposition 2.8.

• (ii) This assertion also follows from Proposition 2.8.

$\square$

Assumption and the choice of the frequency $\tau _*$. If $\mu _1>0$ we assume that $\sigma (0)<0$, when $\kappa >0$ ($\sigma (0)>0$, when $\kappa <0$) and denote by $\tau _*>0$ the unique root of the equation (2.26). If $\mu _1\le 0$ then $\tau _*>-\mu _1$ is the unique root of the equation (2.26). Under this choice of $\tau _*$ the function $\gamma (y;\tau _*)$ is positive on (0, h].

The choice of the root $\tau _*$ depends on the function $\Psi$, which in turn depends on m and $\lambda$. Since $\tau _*$ will be fixed in what follows, we denote by $\lambda _*$ and $m_*$ the values of these parameters corresponding to $\tau _*$.

2.2 Transevsality Condition. Small Amplitude Water Waves

As a result of bifurcation from the trivial (horizontal) free surface, the small amplitude bifurcation surface and corresponding water domain is described by

$$\begin{aligned} {{\mathcal {D}}}={{\mathcal {D}}}_\eta =\{(x,y)\,:\,x\in \mathbb R,\;0<y<h+\eta (x)\},\;\;{{\mathcal {S}}}={{\mathcal {S}}}_\eta =\{(x,y)\;:\,x\in \mathbb R,\;y=h+\eta (x)\}, \end{aligned}$$

(2.29)

where $\eta$ is even, $\Lambda$-periodic function, which is small together with the first derivative. Furthermore we will assume that the function $\omega$ is analytic.

We use the spaces

$$\begin{aligned} C^{k,\alpha }_{e,\Lambda }(\mathbb R)=\{\xi \in C^{k,\alpha }(\mathbb R)\,:\,\xi \text{ is } \text{ even } \text{ and } \Lambda - \text{ periodic }\},\\ C^{k,\alpha }_{e,\Lambda }({{\mathcal {D}}})=\{w\in C^{k,\alpha }({{\mathcal {D}}})\,:\,w \text{ is } \text{ even } \text{ and } \Lambda - \text{ periodic }\} \end{aligned}$$

and

$$\begin{aligned} {\widehat{C}}^{k,\alpha }_{e,\Lambda }({{\mathcal {D}}})=\{w\in C^{k,\alpha }_{e,\Lambda }({{\mathcal {D}}})\,:\,w \text{ vanishing } \text{ on } \text{ the } \text{ bottom } \text{ of } {{\mathcal {D}}}\}, \end{aligned}$$

where $k=0,1,\ldots$, $\alpha \in (0,1)$. We will use also another strip-like domains ${{\mathcal {R}}}$ and the space $C^{k,\alpha }_{e,\Lambda }({{\mathcal {R}}})$ and ${\widehat{C}}^{k,\alpha }_{e,\Lambda }({{\mathcal {R}}})$ with similar definitions as above.

The case of fixed period. The constructions in Sect. 2.1 can be done for other values of $\lambda$ also. We will use the notation $\Psi ^\lambda$, $m(\lambda )$, $Q(\lambda )$ and $\sigma (\tau ;\lambda )$ to indicate the dependence of all this quantities on $\lambda$, which is considered as the bifurcation parameter. The transversality condition required for existence of small amplitude Stokes waves is equivalent to

$$\begin{aligned} \sigma _\lambda (\tau _*;\lambda )\ne 0\;\; \text{ for } \lambda =\lambda _*, \end{aligned}$$

(2.30)

see [7] and [13]. Let

$$\begin{aligned} X=x,\;\;\;\;Y=\frac{hy}{\eta +h} \end{aligned}$$

(2.31)

and let

$$\begin{aligned} {{\mathcal {R}}}=\{(X,Y)\,:\,X\in \mathbb R,\;\;0<Y<h\}. \end{aligned}$$

(2.32)

According to [13] (see also Theorem 1.3, [7], for the case non-analytic $\omega$), there exists a continuous branch

$$\begin{aligned} (\eta (X;t),\phi (X,Y;t),\lambda (t))\in C^{2,\alpha }_{e,\Lambda _*}(\mathbb R)\times {\widehat{C}}^{2,\alpha }_{e,\Lambda _*}({{\mathcal {R}}})\times \mathbb R, \end{aligned}$$

(2.33)

of solutions to (2.1), which can be reparametrized analytically in a neighborhood of any point on the curve for small t. In (x, y) variables $\psi (x,y;t)=\phi (x,\frac{hy}{\eta +h};t)$. All small amplitude water waves are exhausted by

$$\begin{aligned} \psi (x,y;t)= \Psi ^\lambda (y),\;\;\eta =0,\;\;Q(\lambda )=\lambda ^2/2,m(\lambda )=-\Psi ^\lambda (0), \end{aligned}$$

and by (2.33). The first terms in (2.33) have the following form in (x, y) coordinates:

$$\begin{aligned} \eta (x)=t\cos (\tau _*x)+0(t^2),\;\;\; \lambda (t)=\lambda _*+O(t) \end{aligned}$$

and

$$\begin{aligned} \psi (x,y;t)=\Psi ^\lambda (y)-\kappa t\gamma (y;\tau _*)\cos (\tau _*x)+O(t^2), \end{aligned}$$

(2.34)

where

$$\begin{aligned} \kappa =\Psi ^{\lambda _*}_Y(0) \end{aligned}$$

(2.35)

and $\Psi ^\lambda$ and $\gamma$ are smoothly extended outside [0, h] in order to define then for $y<h$.

Differentiating (2.34) with respect to x, we get

$$\begin{aligned} \psi _x(x,y;t)=\tau _*\kappa t\gamma (y;\tau _*)\sin (\tau _*x)+O(t^2). \end{aligned}$$

(2.36)

This implies the following

Proposition 2.11

Let $\tau _*$ is chosen according to Theorem 2.10 and let (2.30) be valid. Then all small solution of (1.1), such that $\psi _x$ is not identically zero, satisfies (2.36).

Variable period. Here we assume that the Bernoulli constant is fixed and the period of the wave is chosen as a bifurcation parameter. We take

$$\begin{aligned} \Psi (y)=\Psi ^{\lambda _*}(y),\;\;Q=\lambda _*^2/2\;\; \text{ and } \;\; m=-\Psi ^{\lambda _*}(-h) \end{aligned}$$

in (1.1). The bifurcation frequency is defined by “Assumption and the choice of the frequency $\tau _*$” after Theorem 2.10, where $\Psi '(0)=\lambda _*$. So in the case $\mu _1>0$ we have additional restriction on the choice of $\lambda _*$ which must guarantee the right sign of $\sigma (0)$¹. Since the solution $\Psi$ does not depend on x it has an arbitrary period $\Lambda >0$. Using that the frequency

$$\begin{aligned} \tau =2\pi /\Lambda \end{aligned}$$

and that the dispersion equation $\sigma (\tau )=0$ has unique solution $\tau =\tau _*$, we conclude that the only bifurcation point is $\Lambda =\Lambda _*=2\pi /\tau _*$.

As it is shown in [7] the transversality condition (2.30) is always satisfied.

We shall use the following change of variables

$$\begin{aligned} X=\frac{\Lambda _*x}{\Lambda },\;\;Y=\frac{h(y-\eta )}{\eta +h}. \end{aligned}$$

(2.37)

According to Theorem 1.2, [7], there exists a continuous branch

$$\begin{aligned} (\eta (X;t),\phi (X,Y;t),\Lambda (t))\in C^{2,\alpha }_{e,\Lambda _*}(\mathbb R)\times {\widehat{C}}^{2,\alpha }_{e,\Lambda _*}({{\mathcal {R}}})\times \mathbb R, \end{aligned}$$

(2.38)

such that this curve can be reparametrized analytically in a neighborhood of any point on the curve for small t. The analytic vorticity is not considered in [7] but now the extension to the analytic case is quite standard. Here

$$\begin{aligned} \psi (x,y;t)=\phi (\frac{\Lambda _*x}{\Lambda },\frac{h(y-\eta )}{\eta +h};t) \end{aligned}$$

All small water waves are exhausted by

$$\begin{aligned} \psi = \Psi ^{\lambda _*}(Y),\;\;\eta =0, \end{aligned}$$

where the period $\Lambda$ is included implicitly, and by (2.38).

The first terms in the asymptotics is given by

$$\begin{aligned} \eta (x)=t\cos (\tau _*X)+O(t^2), \;\;\Lambda (t)=\Lambda _*+O(t^2) \end{aligned}$$

together with

$$\begin{aligned} \psi (x,y;t)=\Psi ^{\lambda _*}(Y)-\kappa t\gamma (Y;\tau _*)\cos (\tau _*X)+O(t^2),\;\ \end{aligned}$$

(2.39)

where $\kappa$ is given by (2.35).

Differentiating (2.39) with respect to x, we get

$$\begin{aligned} \psi _x(x,y;t)=\tau _*\kappa t\gamma (y;\tau _*)\sin (\tau _*X)+O(t^2). \end{aligned}$$

(2.40)

This implies the following

Proposition 2.12

Let $\tau _*$ is chosen according to Theorem 2.10. Then all small solution of (1.1), such that $\psi _x$ is not identically zero, satisfies

$$\begin{aligned} \psi _x(x,y;t)=\tau _*\kappa t\gamma (y;\tau _*)\sin \Big (\frac{2\pi }{\Lambda }x\Big )+O(t^2). \end{aligned}$$

Thus the function $\psi _x$ satisfies (i)–(iii) in (2.1) for small $t>0$ provided $\kappa >0$ and $-\psi _x$ if $\kappa <0$.

3 Applications

In all forthcoming examples the vorticity function $\omega$ is assumed as before to be analytic.

We assume that the uniform stream solution $\Psi ^{\lambda }$ is fixed and the frequency $\tau _*$ is chosen according to the rule “Assumption and the choice of the frequency $\tau _*$” at the end of Sect. 2.1. We denote $\Lambda _*=2\pi /\tau _*$.

3.1 Waves with Multiple Critical Layers

In paper [13] the problem (1.1) was considered in the case when the free surface is given by $y=\eta (x)$, i.e. $\eta$ is $\Lambda$-periodic and ${{\mathcal {D}}}$ and ${{\mathcal {S}}}$ are defined by (2.29).

$$\begin{aligned} {{\mathcal {D}}}=\{(x,y)\,:\,x\in \mathbb R,\;0<y<h+\eta (x)\},\;\;{{\mathcal {S}}}=\{(x,y)\;:\,x\in \mathbb R,\;y=h+\eta (x)\}. \end{aligned}$$

We assume that the transversality condition (2.30) is satisfied. Then a global analytic branch of solutions was constructed in [13].

We make the change of variables (2.31) and let ${{\mathcal {R}}}$ is given by (2.32). The following result on existence of the analytic branch of water waves is proved in [13].

The local curve obtained in Sect. 2.2 in “The case of fixed period” can be uniquely extended (up to reparametrization) to a continuous curve defined for $t\in \mathbb R$

$$\begin{aligned} (\eta (X;t), \phi (X,Y;t),\lambda (t))\;\in \;C^{2,\alpha }_{e,\Lambda _*}(\mathbb R)\times {\widehat{C}}^{2,\alpha }_{e,\Lambda _*}({{\mathcal {R}}})\times \mathbb R \end{aligned}$$

(3.1)

of solutions to (1.1), such that the following properties hold:

• (i) The curve can be reparametrized analytically in a neighborhood of any point on the curve.

• (ii) The solutions are even and have the frequency $\tau _*$ for all $t\in \mathbb R$.

• (iii) One of the following alternatives occur

  • (A) There exists subsequences $\{t_n\}_{n\in N}$, with $t_n\rightarrow \infty$, along which at least one of (i) the solutions are unbounded, (ii) the surface approaches the bed, or (iii) surface stagnation is approached, hold true.

  • (B) or the curve is closed.

We will discuss the last alternative (B). For this goal we introduce the mapping

$$\begin{aligned} (x,y)\rightarrow (X(x),Y(x,y)). \end{aligned}$$

(3.2)

One can verify that it is an diffeomorphism from ${\overline{D}}$ to ${\overline{R}}$, where

$$\begin{aligned} R=(0,\Lambda _*/2)\times (0,h) \end{aligned}$$

This isomorphism satisfies all conditions from Sect. 2.

Theorem 3.1

If $\Psi _y(0)>0$ ($\Psi _y(0)<0$) then the function $\psi _x=\psi _x(x,y;t)$ ($-\psi _x$) satisfies properties (i)–(iii) (2.3) for any interval containing small positive t and which has no points t where $\psi _x(x,y;t)=0$ identically.

Proof

We consider the case $\Psi _y(0)>0$. the case $\Psi _y(0)<0$ is considered similarly. Denote by $V=V(X,Y;t)$ the image of the function $\psi _x$ under the mapping (3.2). By Sect. 2.2 the function $\psi _x$ satisfies all conditions (i)–(iii), (2.3), for small t. By Lemma 2.4 the same is true for the function V in the domain R.

Let the assertion of theorem is proved for a certain $t_*> 0$. Then by Proposition 2.6 the assertion is true for v close to $V(X,Y;t_*)$ in $C^2({\overline{R}})$. In particular there exist an interval $(t_*-\epsilon ,t_*+\epsilon )$ such that V(X, Y; t) also satisfies (i)–(iii) in (2.3). By Lemma 2.4 the same is true for $\psi (x,y;t)$ for $|t-t_*|<\epsilon$.

Assume that the assertion is true for the function $\psi _x$ in a certain interval $(0,t_*)$. Then the function V satisfies (i)–(iii) on the same interval by Lemma 2.4. Therefore the function $V\ge 0$ for $t=t_*$. This implies that the same is true for the function $\psi _x$. Applying Lemma 2.1, we conclude that the assertion is valid for the function $\psi _x$ at $t_*$. $\square$

Corollary 3.2

The following assertions hold.

• (i) If (3.1) is a closed curve then there are at least two points $\lambda _*$ and $\lambda _1\ne \lambda _*$ such that $(\lambda _*,\Psi ^{\lambda _*}(y),0)$ and $(\lambda _1,\Psi ^{\lambda _1}(y),0)$ belong to the curve.

• (ii) If the only uniform stream solution on the curve (3.1) is $(\lambda _*,\Psi ^{\lambda _*}(y),0)$ then the curve (3.1) is not closed and

If $\Psi _y^{\lambda _*}(0)>0$ then $\eta$ is decreasing on $(0,\Lambda _*/2)$ for $t>0$;

If $\Psi _y^{\lambda _*}(0)<0$ then $\eta$ is increasing on $(0,\Lambda _*/2)$ for $t>0$.

Proof

If there is only one uniform stream solution on the bifurcation curve then $\psi _x$ has the same sign on the curve outside this point but due to analyticity it has different sign for $t>0$ and $t<0$.

The second assertion follows from Theorem 3.1.

$\square$

3.2 Overhanging Free Surface

Here we consider a more general class of domains. We assume that the free surface boundary ${{\mathcal {S}}}$ is given in a parametric form : $(x,y)=(u(s),v(s))$, $s\in \mathbb R$, where both functions are $\Lambda$-periodic, $v(s)>0$ and $u(s)\rightarrow \pm \infty$ when $s\rightarrow \pm \infty$. We assume also that the curve does not intersect itself. Here we use the same change of variables as in [12] and [4].

Let

$$\begin{aligned} {{\mathcal {R}}}_{-h} :=\{(X,Y)\,:\,X\in {\mathbb R},\;-h<Y< 0\} \end{aligned}$$

be a strip with depth h.

Introduce $C_h^{\Lambda _*}$ as the $\Lambda _*$-periodic Hilbert transform given by

$$\begin{aligned} C_h^{\Lambda _*} u(X)=-i\sum _{k\ne 0}\coth (k\tau _* h){\widehat{u}}_k e^{ik\tau _* X}, \end{aligned}$$

for an $\Lambda _*$-periodic function

$$\begin{aligned} u(X) = \sum _{k\ne 0}{\widehat{u}}_ke^{ik\tau _* X} \end{aligned}$$

with zero average, appears. The following assertion on a conformal change of variables can be found in [3] (see also [12])

Lemma 3.3

• (i) There exists a unique positive number h such that there exists a conformal mapping $H = U + iV$ from the strip ${{\mathcal {R}}}$ to ${{\mathcal {D}}}$ which admits an extension as a homeomorphism between the closures of these domains, with $\mathbb R\times \{0\}$ being mapped onto ${{\mathcal {S}}}$ and ${\mathbb R} \times \{-h\}$ being mapped onto $\mathbb R \times \{0\}$, and such that $U(X + \Lambda _*, Y) = U(X, Y) + \Lambda _*$, $V (X + \Lambda _*, Y) = V (X, Y)$, $(X, Y)\in {{\mathcal {R}}}$.

• (ii) The conformal mapping H is unique up to translations in the variable X (in the preimage and the image)

• (iii) U and V are (up to translations in the variable X) uniquely determined by $w=V(\cdot ,0)-h$ as follows: V is the unique ($\Lambda _*$-periodic) solution of

  $$\begin{aligned}{} & {} \Delta V = 0\;\; \text{ in } {{\mathcal {R}}}, \\{} & {} V = w + h\;\; \text{ on } Y = 0,\\{} & {} V = 0\;\; \text{ on } Y =-h, \end{aligned}$$

  and U is the (up to a real constant unique) harmonic conjugate of $-V$. Furthermore, after a suitable horizontal translation, ${{\mathcal {S}}}$ can be parametrised by

  $$\begin{aligned} {{\mathcal {S}}} = \{(X + (C^{\Lambda _*}_hw)(X), w(X) + h)\, :\, X\in {\mathbb R}\} \end{aligned}$$

  (3.3)

  and it holds that

  $$\begin{aligned} S\nabla V = (1 + C^{\Lambda _*}_hw', w') \end{aligned}$$

• (iv) If ${{\mathcal {S}}}$ is of class $C^{1,\beta }$ for some $\beta > 0$, then $U, V \in C^{1,\beta }({{\mathcal {R}}})$ and

$$\begin{aligned} |dH/dz|^2 = |\nabla V |^2\ne 0\;\; \text{ in } \; \overline{{\mathcal {R}}} \end{aligned}$$

Thus the vector function H delivers diffeomorphism

$$\begin{aligned} x=U(X,Y),\;\;\;y=V(X,Y)\;\; \text{ mapping } {{\mathcal {R}}}_{-h}\;\rightarrow \;{{\mathcal {D}}}. \end{aligned}$$

We use the same bifurcation parameter $\lambda \in \mathbb R$ as in Sect. 3.1. The trivial solution corresponding to $\lambda$ is then $\Psi =\Psi ^\lambda (y)$.

In the paper [12] it is proved the existence of a branch

$$\begin{aligned} \phi (X,Y;s),\;w(X;s),\;\lambda (s)\in C^{2,\alpha }_{e,\Lambda _*}\times C^{1,\alpha }_{e,\Lambda _*}\times \mathbb R, \end{aligned}$$

which has a real-analytic reparametrisation locally around each of its points, such that the function

$$\begin{aligned} \psi (x,y;s)=\phi (X(x,y;s),Y(x,y;s);s)\;\; \text{ solves } ((1.1))\,\, in\,\, {{\mathcal {D}}}_s. \end{aligned}$$

Here ${{\mathcal {D}}}_s$ is the domain between $y=0$ and ${{\mathcal {S}}}_s$, where ${{\mathcal {S}}}_s$ is given by (3.3).

Moreover this analytic branch is the extension of the branch of small amplitude water waves constructed in Sect. 3.1.

It is shown in [12] (see also [4] for the case of the constant vorticity) that one of the following alternatives occur:

• (i) this alternative describes typical behavior of the branch for large values of s, see Introduction (a)–(c);

• (ii) the second alternative says that there exists a closed curve.

Let us discuss the second alternative.

The same arguments can show that Theorem 3.1 is true in this more general case. This means that the alternative (ii) can be replace

(ii)’ There are at least two points $\lambda _*$ and $\lambda _1\ne \lambda _*$ such that $(\Psi ^{\lambda _*}(y),0,\lambda _*)$ and $(\Psi ^{\lambda _1}(y),0,\lambda _1)$ belong to the curve (3.1).

Corollary 3.2 can be modified to the following

Corollary 3.4

The following assertions hold.

• (i) If (3.1) is a closed curve then there are at least two points $\lambda _*$ and $\lambda _1\ne \lambda _*$ such that $(\lambda _*,\Psi ^{\lambda _*}(y),0)$ and $(\lambda _1,\Psi ^{\lambda _1}(y),0)$ belong to the curve.

• (ii) If the only uniform stream solution on the curve (3.1) is $(\lambda _*,\Psi ^{\lambda _*}(y),0)$ then the curve (3.1) is not closed and

If $\Psi _y^{\lambda _*}(0)>0$ ($\Psi _y^{\lambda _*}(0)<0$) then $\psi _x>0$ ($\psi _x<0$) on S for $t>0$.

Since the inclination of the bondary curve is defined by $-\psi _x/\psi _y$, the positivity property in Corollary 3.4(ii) can be used to exclude certain configurations of the limit self-intersections of the boundary curves (see [4]).

3.3 Water Waves with Variable Period

Let the variables X and Y are given by (2.37).

The local curve obtained in Sect. 2.2 can be uniquely extended (up to reparametrization) to a continuous curve defined for $t\in \mathbb R$

$$\begin{aligned} (\phi (X,Y;t),\eta (X;t),\Lambda (t))\;\in \;C^{2,\alpha }({{\mathcal {R}}})\times C^{2,\alpha }(\mathbb R)\times \mathbb R \end{aligned}$$

(3.4)

of solutions to (1.1), such that the following properties hold:

• (i) The curve can be reparametrized analytically in a neighborhood of any point on the curve.

• (ii) The solutions are even and have wavenumber $\tau _*$, for all $t\in \mathbb R$. The following asymptotics for small f hold

  $$\begin{aligned} \eta (X;t)=t \cos (\tau _* X)+O(t^2),\;\;\Lambda (t)=\Lambda _*+O(t^2),\;\;\phi (X,Y;t)=\Psi ^{\lambda _*}(Y)-t\kappa \gamma (Y;\tau _*)\cos (\tau _*X)+O(t^2), \end{aligned}$$

  where $\kappa$ is the same as in (2.35).

• (iii) One of the following alternatives occur

  • (A) There exists a subsequence $\{t_n\}_{n\in N}$, with $t_n\rightarrow \infty$, along which at least one of (i) the solutions are unbounded, (ii) the surface approaches the bed, (iii) the period tends to 0 or to $\infty$, or (iv) surface stagnation is approached, hold true.

  • (B) or the curve is closed.

The above assertion can be proved in same way as similar assertion in [13], see Sect. 3.1 for its formulation. The only difference here is that the bifurcation parameter is the period and in verification of compactness and Fredholm properties in the global bifurcation theorem must be changed a little bit. We refer also to [9] and [10] where the assertion is proved for the unidirectional flows.

Let us discuss the option (B).

First we note that Theorem 3.1 is valid with the same proof. Corollary 3.2 can be improved in the part (i) as follows

Corollary 3.5

The following assertions hold.

• (i) The curve is not closed. The only uniform stream solution on this curve is met when $t=0$. So the alternative (B) can be excluded.

• (ii) If $\Psi _y^{\lambda _*}(0)>0$ ($\Psi _y^{\lambda _*}(0)<0$) then $\eta$ is decreasing (increasing) on $(0,\Lambda /2)$ for $t>0$

Proof

Since the option (i) in Corollary 3.2 is excluded, see Sect. 2.2 (variable period), we see that Corollary 3.2(i) can be replaced by assetion (i) from this corollary.

The proof of (ii) is the same as in Corollary 3.2. $\square$