Abstract
The two-dimensional Stokes IBVP on \((0,T)\times \Omega \) is investigated under the assumptions that \(\Omega \subset {\mathbb {R}}^2\) is a smooth exterior domain, the initial datum \(v_0\) belongs to \(L^\infty (\Omega )\) and \((v_0,\nabla \phi )=0\) for all \(\phi \in L^1_{\ell oc}(\Omega )\) with \(\nabla \phi \in L^1(\Omega )\). The well-posedeness in \(L^\infty ((0,T)\times \Omega )\) and the maximum modulus theorem are achieved, in particular one deduces that the Stokes semigroup on \(L^\infty (\Omega )\) is a bounded analytic semigroup.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the following initial boundary value problem for the Stokes system:
where \(\Omega \subset {\mathbb {R}}^2\) is a smooth exterior domain. Following [3, 4], we consider \(v_0\in L^\infty (\Omega )\) with
We are interested to prove
Theorem 1
(Maximum Modulus Theorem) For all \(v_0\in L^\infty (\Omega )\) enjoying (2), there exists a unique solution \((v,\pi )\) to problem (1) such that
for all \(q>2\),
where c is a constant independent of \((v,\pi )\).
We conclude the introduction of the result of the theorem with further possible statements.
If the initial datum belongs to \(L^\infty (\Omega )\cap C(\Omega )\), then, for all \(x\in \Omega \), \(\lim _{t\rightarrow 0}v(t,x)=v_0(x)\) holds.
If we assume that \(v_0(x)\rightarrow 0\) for large |x|, then, for all \(t>0\), the solution has the same property and \(\lim _{t\rightarrow \infty }||v(t)||_\infty =0\) holds too.
The pointwise estimate that one could deduce from (3)-(4)\(_1\) for \(|\nabla v(t,x)|\) is sharp in the following sense: if \(v_0\in L^\infty (\Omega )\) no asymptotic decay holds, and just an o(1) for large t provided that \(v_0(x)\rightarrow 0\) for large |x|. Of course, this relates to the nature of the exterior domain \(\Omega \). In the case of the Cauchy problem or IBVP in \(\Omega \) bounded, one obtains suitable decay properties.
One can proves that the solution \((v,\pi )\) is smooth for all \(t>0\).
Via the same approach proposed in this note, the uniqueness can be deduced in a wider set of solutions. Roughly speaking, on the “boundary of the uniqueness set” we find the solutions whose associated pressure field grows as \(|x_i|\), \(i=1,2\), that are not unique.
With the exception of the uniqueness remark, all the statements are considered and proved in [16] for \(\Omega \subset {\mathbb {R}}^n\), \(n\ge 3\), exterior domain. The argument lines work with no change also in the two-dimensional case. For the sake of brevity we omit any detail. Concerning the non-uniqueness, there is today a wide literature, we refer the interested reader to the one contained in the recent paper [18].
Last, but not least, Theorem 1 is interesting in order to modify the approach used in the papers [20, 21] for the 2D-Navier-Stokes IBVP in exterior domains in \(L^\infty \)-setting and as a consequence to improve some related results.
Theorem 1 follows a series of papers concerning with the well posedeness in \(L^\infty \)-setting and developed by some authors in the last decades.
The first results of the kind stated in Theorem 1, as far as we know, are due to Solonnikov in the articles [25, 27, 28]. Succesively, the Stokes initial boundary value problem with an initial datum in \(L^\infty \), jointly with \(L^\infty \)-estimates of the solutions, has been considered by several authors, both with homogeneous boundary data, see e.g. [3,4,5,6, 13, 16], and with non-homogeneous, see e.g. [7].
In the literature devoted to the question, a distinction is made in connection with the nature of domain \(\Omega \). The IBVP in \(\Omega \) bounded can be considered achieved, whether by means of the methods of the potential theory (essentially [25,26,27,28]) or by means of the methods of functional analysis ([3, 4]). Instead, in the case of the IBVP in exterior domains, the n-dimensional case, \(n>2\), can be considered achieved (cf. [6, 16] too), while in the two-dimensional exterior domain the following results hold.
The contributions given in [27, 28] related to the non-homogeneous and homogeneous boundary data respectively, based on the theory of the hydrodynamic potentials, while the quoted literature, based on methods of functional analysis, achieves some results in a sequence of different papers [3, 4] and [1, 2].
The result in [3, 4] is partial, in the sense that the \(L^\infty \)-estimate a priori holds locally in time:
where the constant c and the size \(T_0\), a priori \(<+\infty \), are independent of u.
Subsequently in [1] estimate (5) is obtained for all \(t>0\), but the result holds losing in terms of generality. Indeed, in [1] the author considers the set of solutions for which the net force satisfies \(\int \limits _{\partial \Omega }\nu \cdot T(u,\pi _u)d{\mathcal {H}}^1=0\), where the symbol \(T(u,\pi _u)\) denotes the stress tensor and \(\nu \) is the normal to \(\partial \Omega \) .
Finally, in [2] the author proves that the Stokes operator is a bounded analytic semigroup of angle \(\frac{\pi }{2}\) on the subset \(L^\infty _\sigma (\Omega )\) of \(L^\infty (\Omega )\), in particular estimate (5) holds for all \(t>0\). The symbol \(L^\infty _\sigma (\Omega )\) denotes the following set:
where \(\nu \) is the normal to the boundary. However, as remarked in [1], \(L^\infty _\sigma (\Omega )\) coincide with the set of initial data considered in Theorem 1. As far as we know, the result in [2] is the most complete in the scope of the 2D-Stokes semigroup results.
We do not know an estimate of the pressure field \(\pi _v\) like the one given in (4). In our approach to the uniqueness, this kind of estimate is crucial. In this regard, we deem it appropriate to make a digression in relation to the problem of the uniqueness of the solutions to the problem (54).
In the \(L^\infty \)-setting the difficulties to obtain a sharp result are connected essentially with the lack of the Helmholtz decomposition of \(L^\infty \), decomposition that in \(L^q\)-setting, for all \(q\in (1,\infty )\), holds. The lack of the Helmholtz decomposition does not allow to state a posteriori the existence of the pressure field as in the case of the \(L^q\)-theory or to define the Stokes operator like in the \(L^q\)-theory.
In the recent paper [18], the present author proves the existence of solutions \((u,\pi )\) enjoying (3)-(4)\(_{1,2}\) with a pressure field \(\pi :=u^\infty (t)\cdot x+{{\overline{\pi }}}\), \(\nabla {{\overline{\pi }}}\in L^q(\Omega )\), that is different from (4)\(_{3}\) of Theorem 1. Moreover, the field v enjoys the property: \(\lim _{|x|\rightarrow \infty }|u(t,x)-u^\infty (t)|=0\). But the limit \(u^\infty (t)\ne 0\) is not a datum of the problem. Actually, following [18], one can construct infinite ones. As a consequence a lack of uniqueness arises.
This critical result is produced considering the two dimensional boundary value problem for steady Stokes system in exterior domains, which admits the same pathologic solutions. That is, a solution admits a value at infinity that is not a datum of the problem.
The result given in [18] is not in contradiction with the ones contained in [3, 4] (or with the statement of Theorem 1 of the present paper). Actually, the pressure field \(\pi \) does not verify the condition \(d(x,\partial \Omega )|\nabla \pi (t,x)|\le c\) with c independent of x, property exhibits in [3, 4] for the solutions (or estimates (4) of the present paper). Since the solution with limit \(u^\infty (t)\) obtained in [18] is unique,Footnote 1 as consequence we get that no solution established in [3, 4] admits \(u^\infty (t)\) as limit at infinity (as well as the one of Theorem 1).
The present paper is devoted to the memory of Professor Carlo Miranda, he was an Eminent Mathematician in Napoli, this year is the 40th anniversary of his death.
1.1 Outline of The Proof
Before outlining the proof of Theorem 1, we consider useful to recall what approaches the present author employed in previous papers studying the question in nD, \(n\ge 3\), exterior domains and the result of non-uniqueness in 2D.
In n-dimensional case, \(n\ge 3\), the results are proved by means of a suitable coupling of the results proved in [3] and in [16], subsequently the same approach is reconsidered in [6]. As already recalled, the first paper is concerned with local in time estimates and the second paper is concerned with the extension of the estimates to large time.
In the two-dimensional case the result of the first paper still works, while the result of the second paper does not work. The result in [16] is based on a technique of duality which does not work in two-dimension, roughly speaking, because the solution \(\varphi (t,x)\) of the (local) adjoint problem has the behavior \(||\varphi (t)||_\infty \le c||\varphi ||_1t^{-1}\) where the exponent \(-1\) is sharp. Actually, in [16] one translates the original question into the study of the problem
where \(F_t^{(1)}\) and G are suitable functions. In this way the difficulty becomes the fact that G, with compact support in \(x\in \Omega \) and belonging to \(L^\infty ((0,T)\times \Omega )\), has no behavior for large t. By a duality approach, in order to obtain an estimate for \(||\omega (t)||_\infty \), one has to tackle the estimate related to
for which, due to the sharpness behavior of \(||\varphi (s)||_\infty \le c||\varphi _0||_1s^{-1} \), one at most is able to deduce \(O(||\varphi _0||_1\log (t+e))\). Hence, via this approach, no uniform bound in t holds for the \(L^\infty \)-norm of the solution \(\omega (t,x)\).
In the paper [18], roughly speaking, the previous problem of \(\omega \) becomes
\(F^{(2)}\) plays the same role of \(F^{(1)}\) but with different properties. The function \(F^{(2)}\) in [18], for all \(t>0\), is the extension of \(-U(t,x)_{|\partial \Omega }+{{\widehat{U}}}(t)\) from \(\partial \Omega \) into \(\Omega \), where U is the solution of heat equation corresponding to \(v_0^R\) and \({{\widehat{U}}}=|\partial \Omega |^{-1}\int \limits _{\partial \Omega }U(t,\xi )d\mathcal H^1\), and the \(L^q\)-norm of \(F^{(2)}(t,x)\) has a “good” space-time decay in (t, x). For all \(t>0\), the extension \(F^{(2)}\) is just the solution to the boundary value problem in \(\Omega \) of the steady Stokes system. Thanks to this construction, for all \(v_0\in L^\infty \) which enjoys (2), we are able to prove the existence of a solution to problem (1) and estimates (3)-(4)\(_{1,2}\) of Theorem 1 for v. But we are not able to furnish estimate (4)\(_{3}\) for the pressure field, which is substituted by \(\pi :={{\widehat{U}}}(t)\cdot x+{{\overline{\pi }}}\), with \(\nabla {{\overline{\pi }}}\in L^q(\Omega )\). Here, we have \(v^R_0:=v_0-v_{0R}\), with \(v_{0R}\) equal to \(v_0\) in a neighbourhood of \(\partial \Omega \) and with compact support in \({{\overline{\Omega }}}\). The disadvantage is that for all \(R>0\) we can construct a different solution (\({{\widehat{U}}}\) depends on R).
In this note, the chief aim is to avoid the difficulties arises by the sharpness of the estimates for the solutions of the two-dimensional adjoint problem.
As it will be clear by the arguments that we develop in the sequel, we realize the task blending the ideas contained in papers [16] and [18]. It is appropriate to say: in medio stat virtus.
We consider an initial datum \(v_0\in L^\infty (\Omega )\) that enjoys (2). We make the decomposition
where g is a smooth cutoff function with \(g=1\) in neighborhood of \(\partial \Omega \) and \(g=0\) for large x, and \(b_0\) is a Bogovskiĭ solution to the problem \(\nabla \cdot b_0=\nabla g\cdot v_0\). The peculiarity of the decomposition is in \({v_0}_c\) with compact support in \({{\overline{\Omega }}}\) and \(v^c_0\) with support in \(\Omega \) but far from the boundary \(\partial \Omega \). Of course, this last property plays an important role in the construction of the solution (see the comments after the the following items). We consider \(v=v^c+v_c\) and \(\pi :=\pi _{v^c}+\pi _{v_c}\). The pairs \((v^c,\pi _{v^c})\) and \((v_c,\pi _{v_c})\) are solutions to problem (1) with initial datum \(v^c_0\) and \({v_0}_c\), respectively.
The solution \((v_c,\pi _{v_c})\) is already known from [3, 4]. In fact, the compact nature of the support of the initial datum \({v_0}_c\) allows us to employ the result of the \(L^q\)-setting (cf. [8, 9]), thus the estimate \(||v_c(t)||_\infty \le ct^{-\frac{1}{q}}||{v_0}_c||_q\le ct^{-\frac{1}{q}}||v_0||_\infty \), achieving an extension, for all \(t>T_0\), of the one established in [3, 4] on \((0,T_0)\) enjoying (5) together other properties in \(L^\infty \) (cf. Corollary 4).
The solution \((v^c,\pi _{v^c})\) is instead constructed as it follows. We look for

In the previous formula:
-
U is the solution to the Cauchy problem with initial datum \(v_0^c\) extended to zero on \({\mathbb {R}}^2\),
-
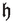 is a cutoff function with support depending on t, and, for all \(t>0\),
is a cutoff function with support depending on t, and, for all \(t>0\), 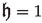 in a ball including \(\partial \Omega \),
in a ball including \(\partial \Omega \), -
\(\widehat{U}(t):=|\partial \Omega |^{-1}\int \limits _{\partial \Omega }U(t,\xi )d{\mathcal {H}}^1\),
-
the trace on \(\partial \Omega \) of \(-U+{{\widehat{U}}}\) has a suitable extension F from \(\partial \Omega \) into \(\Omega \) with compact support,
-
W is a solution to the Bogovskiĭ problem
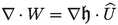 with compact support in \(\Omega \),
with compact support in \(\Omega \), -
finally, \(\omega \) is the solution to the Stokes problem with homogeneous boundary and initial datum, but with a right-hand side given by

The chief properties of U are the behaviors in t for the derivatives of U in \(L^\infty (\Omega _L)\), where \(\Omega _L\supset \partial \Omega \) is bounded, which are not singular in \(t=0\), and U with its derivatives evaluated in \(L^\infty (\Omega _L)\)-norm go to 0, letting \(t\rightarrow 0\). All this is a consequence of the special initial datum \(v_0^c\), cf. sect. 2.1.
The extension F is obtained by the same technique employed in [16] for \(F^{(1)}\). But the new fact is that the boundary value of F is \(-U+{{\widehat{U}}}\), for which \(||\widehat{U}-U||_{L^\infty (\partial \Omega )}=||v_0||_\infty O(t^{-\frac{1}{2}})\) holds, that let us to obtain a decay for \(\Delta F=||v_0||_\infty O(t^{-\frac{1}{2}})\) (\(\Delta F\) has the same meaning of G in (5)) (for the construction of F see sect. 2.2). This property from one side allows us to find the right estimate to discuss (6), from another side leads to discuss the additional term  . The role of this term is to realize the homogeneous boundary value of the solution on \((0,T)\times \partial \Omega \). We recall that at \(t=0\) we have \({{\widehat{U}}}=0\) pointwise on \(\{0\}\times \Omega \), so no correction is due in order to obtain the initial value on \(\{0\}\times \Omega \).
. The role of this term is to realize the homogeneous boundary value of the solution on \((0,T)\times \partial \Omega \). We recall that at \(t=0\) we have \({{\widehat{U}}}=0\) pointwise on \(\{0\}\times \Omega \), so no correction is due in order to obtain the initial value on \(\{0\}\times \Omega \).
The function  is defined by means of the function \(\overline{h}\) with support in the ball \({\mathbb {B}}_\frac{7}{4}\) and \(\nabla {{\overline{h}}}\) has compact support in the shell \(\{\frac{5}{4}<|y|<\frac{7}{4}\}\) (cf. sect. 2.3). The definition of
is defined by means of the function \(\overline{h}\) with support in the ball \({\mathbb {B}}_\frac{7}{4}\) and \(\nabla {{\overline{h}}}\) has compact support in the shell \(\{\frac{5}{4}<|y|<\frac{7}{4}\}\) (cf. sect. 2.3). The definition of  is given by the scale factor \(({{\overline{R}}})^{-1}:=(R+\sqrt{t})^{-1}\), that is
is given by the scale factor \(({{\overline{R}}})^{-1}:=(R+\sqrt{t})^{-1}\), that is  . Hence,
. Hence,  has compact support in the ball \({\mathbb {B}}_{\frac{7}{4}{{\overline{R}}}}\), and
has compact support in the ball \({\mathbb {B}}_{\frac{7}{4}{{\overline{R}}}}\), and  has compact support in the shell \(\{x\in \Omega : \frac{5}{4}(R+\sqrt{t})< |x|<\frac{7}{4}(R+\sqrt{t})\}\). This property ensures that
has compact support in the shell \(\{x\in \Omega : \frac{5}{4}(R+\sqrt{t})< |x|<\frac{7}{4}(R+\sqrt{t})\}\). This property ensures that  and
and  , that are decaying in t for \(q>2\) and \(q>1\), respectively. We take advantage this behavior in t in order to discuss the term
, that are decaying in t for \(q>2\) and \(q>1\), respectively. We take advantage this behavior in t in order to discuss the term  . This is a new fact with respect to the behavior of the term G of the n-dimensional case, that arose the difficulty of the estimate (6) in the two-dimensional case. Instead, in the estimates the time derivative of
. This is a new fact with respect to the behavior of the term G of the n-dimensional case, that arose the difficulty of the estimate (6) in the two-dimensional case. Instead, in the estimates the time derivative of  , as a matter of course, go on without difficulties.
, as a matter of course, go on without difficulties.
However, the term  is not divergence free. Hence, in order to preserve the divergence free of the solution \(v^c\), we introduce the function W. The function W is a solution of the problem
is not divergence free. Hence, in order to preserve the divergence free of the solution \(v^c\), we introduce the function W. The function W is a solution of the problem  in the shell \(\Omega ({{{\overline{R}}}}):=\{(R+\sqrt{t})<|x|<2(R+\sqrt{t})\}\supset \{\frac{5}{4}(R+\sqrt{t})<|x|<\frac{7}{4}(R+\sqrt{t})\}\equiv \)supp
in the shell \(\Omega ({{{\overline{R}}}}):=\{(R+\sqrt{t})<|x|<2(R+\sqrt{t})\}\supset \{\frac{5}{4}(R+\sqrt{t})<|x|<\frac{7}{4}(R+\sqrt{t})\}\equiv \)supp , with homogenous boundary value. The shell \(\Omega ({{{\overline{R}}}})\) is variable in t, but, for all \(t>0\), there is the homothety with the shell \(S:=\{1<|x|<2\} \). Considering a solution to
, with homogenous boundary value. The shell \(\Omega ({{{\overline{R}}}})\) is variable in t, but, for all \(t>0\), there is the homothety with the shell \(S:=\{1<|x|<2\} \). Considering a solution to  in the shell S, with homogeneous boundary value on \(\partial S\), then a solution W in \(\Omega ({{{\overline{R}}}})\) is calculated in the following way: \(W(t,x):=W^S(t,\frac{x}{R+\sqrt{t}})\). We find the suitable estimates for W and its derivatives considering the ones related to \(W^S\) and employing the homothety property of the domain \(\Omega ({\overline{R}})\). It is important to stress that \(W_t\) exists, but \(W_t\) does not solve the time derivative of the Bogowskiĭ problem. Since no interest there is for this last fact, and since \(W_t\) is a “linear” combination of the spatial derivatives of W and of the time derivative of the solution on the fixed shell S, using the homothety property of the domain, we can deduce all the estimates related to \(W_t\) (cf. sect. 2.4).
in the shell S, with homogeneous boundary value on \(\partial S\), then a solution W in \(\Omega ({{{\overline{R}}}})\) is calculated in the following way: \(W(t,x):=W^S(t,\frac{x}{R+\sqrt{t}})\). We find the suitable estimates for W and its derivatives considering the ones related to \(W^S\) and employing the homothety property of the domain \(\Omega ({\overline{R}})\). It is important to stress that \(W_t\) exists, but \(W_t\) does not solve the time derivative of the Bogowskiĭ problem. Since no interest there is for this last fact, and since \(W_t\) is a “linear” combination of the spatial derivatives of W and of the time derivative of the solution on the fixed shell S, using the homothety property of the domain, we can deduce all the estimates related to \(W_t\) (cf. sect. 2.4).
The plan of the paper follows the items detected for the construction of the auxiliary function  . They are discussed and proved in Sect. 2. In Sect. 3 we give the statement of the results due to K. Abe and Y. Giga, that furnish Theorem 1 for initial data with compact support. In sect. 4 we solve the Stokes problem related to \(\omega \). Finally, in Sect. 5 we give the proof of Theorem 1.
. They are discussed and proved in Sect. 2. In Sect. 3 we give the statement of the results due to K. Abe and Y. Giga, that furnish Theorem 1 for initial data with compact support. In sect. 4 we solve the Stokes problem related to \(\omega \). Finally, in Sect. 5 we give the proof of Theorem 1.
Notations.
We assume that the origin \(0\in {\mathbb {R}}^2-\Omega \).
We set \({\mathscr {C}}_0(\Omega ):=\{\varphi \in C_0^\infty (\Omega ) \text{ with } \nabla \cdot \varphi =0\}\). By the symbol \(J^p(\Omega )\) we mean the completion of \({\mathscr {C}}_0(\Omega )\) in \(L^p(\Omega )\), \(p\in (1,\infty )\), instead, \(J^{1,p}(\Omega )\) denotes the completion in \(W^{1,p}(\Omega )\), \(p\in (1,\infty )\).
The symbol \({\mathbb {B}}_\rho (x_0)\) denotes a ball in \({\mathbb {R}}^2\) with center \(x_0\) and radius \(\rho \), in the case of \(x_0=0\), we simply write \({\mathbb {B}}_\rho \).
In the following we consider \(R>3diam({\mathbb {R}}^2-\Omega )\).
We set \(\Omega _R:=\Omega \cap {\mathbb {B}}_{R}\) .
For a Lebesgue’s measurable set D, the symbol |D| denotes the measure.
By the symbol \(L(q,\sigma )(\Omega )\) we mean the G.G. Lorentz spaces and with \(||\cdot ||_{(q,\sigma )}\) its norm. In particular, we consider \(L(q,\infty )(\Omega )\equiv L^q_w(\Omega )\), \(q\in (1,\infty )\), endowed with the Lorentz norm
For a function g(t, x) and \(t\ge 0\), we denote by \({\underset{x}{\text{ supp }}} \, g(t,x)\) the support in the variable x.
In the following the symbol c denotes a numerical constant whose value is inessential for our aims.
2 Preliminry Results
2.1 Heat Solution
We denote by H(t, x) the heat fundamental solution and we indicate by \(H[v_0](t,x)\) the heat solution (transformation) as convolution of H(t, x) and \(v_0\in L^\infty ({\mathbb {R}}^2)\). It is well known that, for \(k,h\in {\mathbb {N}}\cup \{0\}\),
where c is a constant independent of \(v_0\).
For \(\mu \ge 0\), \(q\in [1,\infty ]\) and \(\delta >0\), we set
\((t,x,L,v_0)\in {\mathbb {R}}^+\times {\mathbb {B}}_R\times (R+\delta ,\infty )\times \big \{v_0\in L^\infty ({\mathbb {R}}^2) \text{ with } \text{ supp }v_0\subset \mathbb B_{R+\delta }^c\big \}\).
Lemma 1
Let \(v_0\in L^\infty ({\mathbb {R}}^2)\) with \(\text{ supp }v_0\subset {{\mathbb {B}}}_{R+\delta }^{c}\) and \(M_q^c\) as given in (9). Then, for all \(k,h\in {\mathbb {N}}\cup \{0\}\), there exists a constant \(c(\delta , L)\) such that
Proof
By the definition of \(M^c_q\), we recall that the left hand side of (10)\(_1\) has to be considered for \((t,x)\in {\mathbb {R}}^+\times {\mathbb {B}}_R(O)\). For \(k,h\in {\mathbb {N}}\cup \{0\}\) and \(\mu >0\), we have the well known estimate
If \(L\ge R+\delta \) and \(x\in {\mathbb {B}}_R(0)\), we get that \(|x-z|\in [R+\delta ,2L]\) implies \(|z|\in [\delta ,3L]\), as well as \(|x-z|>2L\) implies \(|z|>L\). Hence, applying Hölder’s inequality, by virtue of the definition of the support of \(v_0\), we deduce
Estimate (10)\(_2\) is a consequence of the previous estimate and of definition of \(M^c_q(t,x,L,v_0)\). \(\square \)
Lemma 2
Let \(u_0\!\in \!L^\infty ({\mathbb {R}}^2)\) and let \(u\!:=\!H[u_0](t,x)\). Then, for all \(q\!\in \![1,\infty )\) and \(R_0\!>\!0\), we get
Proof
We set
where \(\chi _{2R_0}\) denotes the characteristic function of the ball \({\mathbb {B}}_{2R_0}\). Of course, we have \(u=u_{2R_0}+u^{2R_0}\) too. Hence we get
From the \(L^q\)-theory we deduce that \(\lim _{t\rightarrow 0}||u_{2R_0}(t)-u_0||_{L^q({\mathbb {B}}_{2R_0})}=0\). Since for all \((x,y)\in {\mathbb {B}}_{R_0}\times ({\mathbb {R}}^2-{\mathbb {B}}_{2R_0})\) one has \(|x-y|\ge |y|-|x|\ge \frac{|y|}{2}\ge R_0\), by virtue of (11), for \(\mu >0\), we deduce
Hence, letting \(t\rightarrow 0\), we achieve (12). \(\square \)
2.2 The Extension F
We recall some results concerning the boundary value problem in a smooth bounded domain D of the steady Stokes system:
Lemma 3
Let \(a\in W^{2-\frac{1}{q},q}(\partial D)\), \(q>2\). Then, problem (13) has a unique solution \((V,\pi _V)\in W^{2,q}(D) \cap C^\infty (D)\times W^{1,q}({{\overline{D}}}) \cap C^\infty (D)\), such that
with M independent of a. In particular, we deduce \((V,\pi _V)\in C^1({{\overline{D}}})\times C({{\overline{D}}})\).
Proof
The proof of lemma can be found in [10] Ch.IV Lemma 6.1. \(\square \)
The following is an a priori estimate
Lemma 4
Let \(u\in W^{m+2,q}(\Omega )\cap J^{1,q}(\Omega )\,,\) for some \(m\in {\mathbb {N}}_0\). Then there exists a field \(\pi _u\) such that
where c is a constant independent of u.
Proof
This result is contained in [10, 22]. Actually, in our hypotheses, for u we can consider the Helmholtz decomposition of \(\Delta u\), hence, formally u is a solution to the boundary value problem
Then the estimates and regularity follow from the result in [10, 22] for solution to the Stokes problem in exterior domains. \(\square \)
We recall some results concerning the Bogovskiĭ problem. Let E be a smooth bounded domain and
with the compatibility condition \(\displaystyle \int \limits _{E}gdx=0\).
Lemma 5
If \(g\in C_0^\infty (E)\), then there exists at least a solution \(v\in C_0^\infty (E)\) to problem (16) such that, for \(m\in {\mathbb {N}}\) and \(r\in (1,\infty )\),
For the proof of the Lemma we refer to [10].
\(\square \)
It is known that one solves problem (16) by considering the domain E as a union of domains \(C_k,\,k=1,\dots ,N\), star-shaped with respect to the balls \({\mathbb {B}}{(k)}\) of a fixed radius; moreover, using a smooth partition of unity, say \({\underset{k=1}{\overset{N}{\sum }}}\psi _k(x)=1\), with supp\(\psi _k\subset C_k\). Then, a vector field satisfying (16) can be written in the form
where
We also recall that, for each \(k=1,\dots , N\), \(\mathbf{B}^k\) is an operator with weakly singular kernel. Actually, \({\mathbf{B}}^k_j[\,\cdot \,]\) is the integral operator with the kernel
and \(\frac{\partial }{\partial x_j}{\mathbf{B}}^k\) is an operator with singular kernel of Calderon-Zigmund kind. \(\square \)
Lemma 6
Let \(A(x)\in W^{2-\frac{1}{q},q}(\partial \Omega )\), \(q>2\), with \(\displaystyle \int \limits _{\partial \Omega }\)\(A(x)\cdot nd\sigma =0\). Then, the function A admits an extension F into \(\Omega \), such that \( F\in W^{2,q}(\Omega )\cap C^\infty (\Omega )\), F(x) has compact support in \({{\overline{\Omega }}}_R\) and is divergence free in \(\Omega \), with
with c(R) independent of A. In particular, we get \(F(x)\in C^1({{\overline{\Omega }}})\).
Proof
Let us consider the boundary value problem (13) for \(D\equiv \Omega _R\), with boundary data \(a=A\) on \(\partial \Omega \) and \(a=0\) on \(|x|=R\). By virtue of Lemma 3 there exists a unique solution \((V,\pi _{V})\in W^{2,q}(\Omega _R)\), such that
Moreover, we consider a Bogovskiĭ’s solution \({{\overline{V}}}\) to the equation (16) assuming \(E\equiv \{x:\frac{R}{3}<|x|<\frac{2}{3}R\}\), \(g=-\nabla h_R\cdot V\) in E and \({{\overline{V}}}=0\) on \(\partial E\), where \(h_R\) is a smooth cut-off function with \(h_R=1\) on \(\Omega _{R/3}\) and \(h_R=0\) on \(\Omega _R-\Omega _{2R/3}\). By virtue of the estimate of Lemma 5, we get
Setting \(F=Vh_R+{{\overline{V}}}\) we have proved estimate (20). The regularity in \(\Omega \) is a consequence of the ones doable for V and \({{\overline{V}}}\) (see [10]). \(\square \)
Corollary 1
Let A(t, x) be a one parameter family of functions with \(D^k_t A(t,x)\in W^{2-\frac{1}{q},q}(\partial \Omega )\) and \(\displaystyle \int \limits _{\partial \Omega }\)\(A(t,x)\cdot nd\sigma =0\), for all \(t\ge 0\). Then, for \(t>0\), denoted by F(t, x) the extension obtained in Lemma 6, there exist \(D^k_tF\) with
with c independent of t.
Proof
For all \(t\ge 0\), we consider the extension \(F=Vh_R+{{\overline{V}}}\) given in Lemma 6. Hence, recalling the definition of V and \({{\overline{V}}}\), there exists \(D^k_t F=D^k_t Vh_R+D^k_t\overline{V}\). Hence, via estimate (21) for \(D^k_tV\) and via representation formula (18) for \({{\overline{V}}}_t\), in our hypotheses estimate (23) follows by the same arguments developed for the estimates (20). \(\square \)
We set
where U is the solution to the heat equation furnished in Sect. 2.1 and corresponding to \(v_0\) with supp\(v_0\subset \Omega -{\mathbb {B}}_{R+\delta }\) and enjoying (2).
Lemma 7
Let \(A=-U+{{\widehat{U}}}\) in Corollary 1 with U given in (24). For \(k\in {\mathbb {N}}\cup \{0\}\), we get
with c independent of \(v_0\).
Proof
By virtue of Corollary 1, estimate (25) easily follows achieving the estimate \(||D^k_tA(t)||_{2-\frac{1}{q},q}\le c(L^2+t)^{-\frac{1}{2}-k}||v_0||_\infty \,, \text { for } \text { all } t>0\). Then, estimating \(||D^k_tA(t)||_{2-\frac{1}{q},q}\) , the task is to justify the exponent \(-\frac{1}{2}\) on the right hand side of estimate (25). The assumption \(\Omega \) smooth exterior domain leads to assert \(\partial \Omega \equiv {\underset{m=1}{\overset{p}{\cup }}}\partial \Omega _m\). For any continuous function g, the mean valueFootnote 2 is
In order to estimate \(||D^k_tA_i(t)||_{L^q(\partial \Omega )}=||D^k_t(-U_i(t,\xi )+{{\widehat{U}}}_i(t))||_{L^q(\partial \Omega )}\), \(i=1,2\), we initially remark that, by virtue of (26), for \(i=1,2\) and for all \(k\in {\mathbb {N}}\cup \{0\}\) there exist \({{\overline{\xi }}}_h\), \(h=1,\dots ,p\), such that
where \(D^k_tU_i(t,{{\overline{\xi }}}_h)\) is mean value of the integral on \(\partial \Omega _h\). Hence, by virtue of Lagrange’s theorem and assumptions on U, from (27) we get
where in the last step we take (10) into account. This justify the estimate for the \(L^q(\partial \Omega )\) norm of \(D^k_tA\). Instead, for the seminorm we have \(<\nabla D^k_t A>_{1-\frac{1}{q},q}=<\nabla (D^k_tU-D^k_t{{\hat{U}}})>_{1-\frac{1}{q},q}=<\nabla D^k_tU>_{1-\frac{1}{q},q}\). Hence, considering again estimate (10), a fortiori there is for the exponent the increment \(-\frac{1}{2}\) . \(\square \)
2.3 The Function 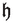
Let \({{\overline{h}}}(\sigma )\) be a smooth cut off function such that \({{\overline{h}}}(\sigma )=1\) for \(\sigma \in [0,\frac{5}{4}]\), \(\overline{h}(\sigma )=0\) for \(\sigma \in [\frac{7}{4},2]\) and \(\overline{h}(\sigma )\in [0,1]\) for \(\sigma \in [\frac{5}{4},\frac{7}{4}]\). For all \(\tau >0\) and \(\rho >0\), we define \(h(\tau ,\rho ):=\overline{h}(\frac{\rho }{R+\sqrt{\tau }})\). One easily verifies the following properties:
We set \( h_\tau :=\frac{\partial }{\partial \tau } h(\tau ,\rho )\) and \({ h_\rho }(\tau ,\rho ):=\frac{\partial }{\partial \rho }h(\tau ,\rho )\,.\) A computation gives
For \(\rho :=|x|\), we set

Recalling that \(R>3diam\Omega ^c\), by our position we have  in \({\mathbb {B}}_{\frac{R}{2}}\cap \Omega \) for all \(t>0\). We have
in \({\mathbb {B}}_{\frac{R}{2}}\cap \Omega \) for all \(t>0\). We have

and via (28)\(_1\)

Finally, via (28) we get

2.4 A Special Bogovskiĭ Problem
For all \(t>0\), we consider the Bogovskiĭ problem

where we set \({{\overline{R}}}:=R+\sqrt{t}\) and \(\Omega ({\overline{R}}):=\Omega \cap \{{{{R}}}+\sqrt{t}<|x|<2({{{R}}}+\sqrt{t})\}\). Of course, for all \({{\overline{R}}}>0\) the domain \(\Omega ({{{\overline{R}}}})\) is homothetic to the shell \(S:=1<|z|<2\). For problem (33), since the compatibility condition holds, Lemma 5 holds too. However, here we are interested to state the result employing the following approach, that is more suitable for the special domain \(\Omega ({{{\overline{R}}}})\).
Lemma 8
There exist a constant c and a smooth solution W(t, x) to problem (33) with compact support in \(\Omega ({{{\overline{R}}}})\) and such that, for all \(t>0\),

and with

Proof
For all \(z\in S\), we set  . We consider the following problem
. We consider the following problem

Taking into account that  on \(|z|=1\) and
on \(|z|=1\) and  on \(|z|=2\), since \({{\widehat{U}}}\) is independent of z, for the Bogovskiĭ problem (36) the compatibility condition holds, and so, by virtue of Lemma 5, we establish the existence of a solution \( W^S(t,z)\) with compact support in the shell S. Easily one verifies that \(W(t,x):= W^S(t,\frac{x}{R+\sqrt{t}})\) is a solution to problem (33) with compact support in \(\Omega ({\overline{R}})\). Being \(\Omega ({{{\overline{R}}}})\) homothetic with the shell S, via estimate (17) for \(m=1\) and via the following trivial chain, we deduce (34)\(_1\):
on \(|z|=2\), since \({{\widehat{U}}}\) is independent of z, for the Bogovskiĭ problem (36) the compatibility condition holds, and so, by virtue of Lemma 5, we establish the existence of a solution \( W^S(t,z)\) with compact support in the shell S. Easily one verifies that \(W(t,x):= W^S(t,\frac{x}{R+\sqrt{t}})\) is a solution to problem (33) with compact support in \(\Omega ({\overline{R}})\). Being \(\Omega ({{{\overline{R}}}})\) homothetic with the shell S, via estimate (17) for \(m=1\) and via the following trivial chain, we deduce (34)\(_1\):

Analogously, via (17) for \(m=2\), we get

Deriving W with respect to t, we get
we point out that the last term has to be considered as the “Eulerian derivative” which arises via formula (18) written for solution \( W^S(t,z)\) where, thanks to the static position, we transport the time derivative on \({{\widehat{U}}}(t)\). Now, let us consider \(\nabla W_t\). From (38) it follows that
Since W and \(\nabla W\) have compact support in \(\Omega ({{\overline{R}}})\) and \(\big |\frac{x}{R+\sqrt{t}}\big |=|\xi |\le 2\), via (17), we get

where, taking the homothety between the sets \(\Omega ({{{\overline{R}}}})\) and S into account, we argued as made in estimate (37). Hence, we arrive at (35)\(_1\) for \(\nabla W\), and thanks to the Poincaré inequality we complete the proof of (35)\(_2\). Finally, from (38) it follows that
where again we stress that the last term is meant as the “Eulerian derivative”. We set
and
Hence, recalling that \(|\xi |=|\frac{x}{R+\sqrt{t}}|\le 2\), employing the homothetic transformation for the coordinates, via (17), we get
then, first via (17), and subsequently applying the homothetic change of variables, we arrive at

Since \(W_{tt}\) has compact support and the sets \(\Omega ({\overline{R}})\) and S are homothetic, we get

where again we consider the “Eulerian derivative”, that is, via formula (18) written for solution \( W^S(t,z)\), we transported the time derivative on \({{\widehat{U}}}(t)\), and then, for the estimate of the Bogovskiĭ solution, we toke into account that the kernel in (18) is weakly singular with exponent \(\alpha =1\). This completes the proof of (35). \(\square \)
Lemma 9
Let W be a solution to the Bogovskiĭ problem (33) stated in Lemma 8 and \(U\equiv H[v_0]\) as in Lemma 1. Then we get
and
for all \(t>0\), where we set
and where c is a constant independent of \(v_0\) and t.
Proof
We have
where all the estimates are consequence of (10). Moreover, as a consequence of (10)\(_2\), for all \(\mu >0\), we have
For \(q\ge 1\), we get

Hence, as a matter of course, the right hand side of (34)\(_1\) is bounded by \(c(R+\sqrt{t})^{\frac{2}{q}-1}||v_0||_\infty \) and the one of (34)\(_2\) is bounded by \(c(R+\sqrt{t})^{\frac{2}{q}-2}||v_0||_\infty \). Hence we get (39) for \(\nabla W\) and \(\nabla \nabla W\).
Employing Gagliardo-Nirenberg inequality, for \(q>2\), we get \(||W(t)||_\infty \le c||\nabla W(t)||_q^b||W(t)||_q^{1-b}\), with exponent \(b:=\frac{2}{q}\). Since estimate (39) is achieved for \(||\nabla W(t)||_q\), via the Poincaré inequality, we obtain \(||W(t)||_\infty \le (R+\sqrt{t})^{1-b}||\nabla W(t)||_q\le c||v_0||_\infty \).
Moreover, by means of the estimates (43) for \(\nabla h\) and \(\nabla \nabla h\), via (41), the right hand side of (35)\(_1\) is bounded by \(c\Big [t^{-\frac{1}{2}}(R+\sqrt{t})^{\frac{2}{q}-2}+{(L^2+t)^{-1}(R+\sqrt{t})^{\frac{2}{q}-1}}\Big ]||v_0||_\infty \), which furnishes (40)\(_2\), and then, again via (35)\(_1\) we arrive at (40)\(_1\).
Estimate given in (43) of  in \(L^2\)-norm is a constant c, instead the one for
in \(L^2\)-norm is a constant c, instead the one for  in \(L^2\)-norm is \(c(R+\sqrt{t})^{-1}\). Hence, for the terms involving the \(L^2\)-norm on the right hand side of (35)\(_2\) we get \(ct^{-1}(t^{-\frac{1}{2}}+(R+\sqrt{t})^{-1}+\sqrt{t}(L^2+ t)^{-1})||v_0||_\infty \). For the estimate of the term involving the \(L^2_w\)-norm on the right hand side of (35)\(_2\), being
in \(L^2\)-norm is \(c(R+\sqrt{t})^{-1}\). Hence, for the terms involving the \(L^2\)-norm on the right hand side of (35)\(_2\) we get \(ct^{-1}(t^{-\frac{1}{2}}+(R+\sqrt{t})^{-1}+\sqrt{t}(L^2+ t)^{-1})||v_0||_\infty \). For the estimate of the term involving the \(L^2_w\)-norm on the right hand side of (35)\(_2\), being  , we get the estimate \(c(L^2+ t)^{-2}(R+\sqrt{t})||v_0||_\infty \). The sum furnishes (40)\(_3\). \(\square \)
, we get the estimate \(c(L^2+ t)^{-2}(R+\sqrt{t})||v_0||_\infty \). The sum furnishes (40)\(_3\). \(\square \)
Lemma 10
Let U be the solution of Lemma 1. Then, for \(\mu >0\), for all \(q\in (1,\infty )\) and \(k=0,1,2\), the following holds

and

both the estimates evaluated for all \(\,t\in (0,1)\) .
Proof
Since U verifies (10)\(_2\) and \({{\widehat{U}}}\) is defined by (24), then, for all \(\mu >0\), we have
Function F is the extension furnished by Corollary 1 with \(A:=-U+{{\widehat{U}}}\). As a consequence of (23) and (46) we have (44) and (45) for F.
Function  is the cutoff function defined in (29), hence estimates (31) and (32)\(_{2,3}\) hold. Then, by virtue of (46) and \(R>0\), we deduce (44) for
is the cutoff function defined in (29), hence estimates (31) and (32)\(_{2,3}\) hold. Then, by virtue of (46) and \(R>0\), we deduce (44) for  and (45) for
and (45) for  .
.
Being W a solution to problem (33), for W we consider (34) and for \(D^k_tW\) we consider estimates (35)\(_{1,2}\). Since we estimate in neighborhood of \(t=0\), the right hand sides of (34) and (35)\(_{1,2}\) admit a bound of the kind \(t^{-\frac{3}{2}}||{{\widehat{U}}}(t)||_\infty \), for \(t\in (0,1)\). So that, applying (46) to the right hand side, we arrive at (44). Analogously, estimates (34)\(_2\) and (46) lead (45) for \(\Delta W\). The lemma is proved. \(\square \)
Of course, since (44)-(45) are stated in a neighborhood of \(t=0\) and since \(\mu >0\) can be chosen as we want, estimates (44) and (45) are not given in sharpness way, but they are given functional to our aims.
2.5 Some Integral Estimates
The symbols  and W have the same meaning given in previous section. We recall that we assumed \(R>3diam({\mathbb {R}}^2-\Omega )\) and \(L>R\), as well in Lemma 1 we assumed supp\(v_0\subset {\mathbb {B}}^c_{R+\delta },\,\delta >0\,.\)
and W have the same meaning given in previous section. We recall that we assumed \(R>3diam({\mathbb {R}}^2-\Omega )\) and \(L>R\), as well in Lemma 1 we assumed supp\(v_0\subset {\mathbb {B}}^c_{R+\delta },\,\delta >0\,.\)
In this section, for all \(\eta >0\), the function \(\varphi \in C(\eta ,T;J^{1,q}(\Omega )\), \(q\in (1,2]\), is such that
for all \(t>0\), for \(r=\infty \) we just consider \(L^\infty \), and c is a constant independent of \(\varphi \).
We set

Lemma 11
For all \(q\in [1,2)\), there exists a constant \(C:=C(R)\) such that
Proof
We separately look for the estimate of each integral term, called \(I_i(t),i=1,2,3,\) of the sum. Applying Hölder’s inequality, we get
where increasing we employed (25) for F, \(R<L\) and (47)\(_2\) for \(\varphi \). Applying Hölder’s inequality and employing (31), we get

Since  , via (47)\(_2\), we get
, via (47)\(_2\), we get
Applying Holder’s inequality, we get
By virtue of estimate (40)\(_2\) for \(W_t\) and estimate (47)\(_2\) for \(\varphi \), we obtain
The above estimates furnish (48). \(\square \)
Lemma 12
For all \(q\in [1,2)\) there exists a constant c such that
where constant c is independent of \(v_0\) and \(\varphi _0\).
Proof
We look for separately the estimate of each integral, called \(I_i(t),\,i=1,2,3,\) of the sum. Via Hölder’s inequality, we get
where increasing we employed (25) for F and (47)\(_1\) for \(\varphi \). Via Hölder’s inequality, and employing (43) for  and (47)\(_1\) for \(\varphi \), we obtain
and (47)\(_1\) for \(\varphi \), we obtain

After applying Hölder’s inequality, we get
where in the last step of the estimate we taken into account (47)\(_2\) for \(\varphi \) and (39) for \(\Delta W\). Collecting the estimates for \(I_i(t)\), we arrive at the wanted one for \({\mathscr {I}}_2(t)\). \(\square \)
Lemma 13
The following estimate holds:
Proof
Applying Hölder’s inequality, for all \(t\in (0,1)\), we get

where increasing we applied (44) for the terms in \(||\cdot ||_{2}\)-norm and (47) for \(\varphi \). Analogously, for all \(\mu >0\), we obtain the estimate

where increasing we employed (45) for the terms in \(||\cdot ||_{2}\)-norm and (47)\(_2\) for \(\varphi \). \(\square \)
We set

Lemma 14
For all \(q\in [1,2]\), there exists a constant \(C:=C(R)\) such that
Proof
We initially point out that \(\mu >0\) can be chosen in Lemma 10 in such a way that the integral is well posed. Moreover, we recall that \(L>R\). In order to deduce (51) we look for separately the estimate of each integral, called \(J_i(t),\,i=1,2,3,\) of the sum. Integrating by parts we get
where in \(t=0\) we used the bound (44) for \(\mu >3\). Applying Hölder’s inequality, we get
where for F we toke estimate (25) into account, as well estimates (47)\(_{2}\) for \(\varphi \). Since \(R<L\) we arrive at (51) for \(J_1\).
After integrating by parts, applying Hölder’s inequality, we obtain

where in \(t=0\), we toke the bound (44)\(_2\) for \(\mu >3\) into account. Recalling that \(\le 1\), employing (31) for  , (10)\(_1\) for U and \(U_t\), and (47)\(_2\) for \(\varphi \), since
, (10)\(_1\) for U and \(U_t\), and (47)\(_2\) for \(\varphi \), since  , being \(R<L\), we have
, being \(R<L\), we have
Recalling that  , since, \(\le 1\) the estimate (31) for
, since, \(\le 1\) the estimate (31) for  and (47)\(_3\) for \(\varphi _\tau \) furnish
and (47)\(_3\) for \(\varphi _\tau \) furnish
Now, applying (10)\(_1\) for the term \(||\widehat{U}_t(t)||_\infty \) and for the term \( ||{{\widehat{U}}}||_\infty \), being \(R<L\), we realize
For the last term we have  . Recalling that
. Recalling that  , via estimates (10) for \({{\widehat{U}}}\) and developing (32)\(_2\) for
, via estimates (10) for \({{\widehat{U}}}\) and developing (32)\(_2\) for  , we get
, we get
where increasing we used the semigroup property of U. Collecting the estimates related to \(J_2^i\), we arrive at
Integrating by parts, applying Hölder’s inequality, we get
where in \(t=0\) we toke the bound (44). Employing (40)\(_{1,3}\) for W, we get
where we considered (47)\(_{2}\) for \(\varphi \). \(\square \)
Lemma 15
For \(q\in [1,2]\), there exists a constant \(C:=C(R)\) such that
Proof
Integrating by parts, we get

We separately look for the estimate of each integral, called \(J_i(t),\,i=1,2,3,4,\) of the sum. Applying Hölder’s inequality, we get
where we toke estimate (25) for F, and (47)\(_1\) for \(\varphi \) into account. Being \(R<L\), we arrive at (53) for \(J_1\). An integration by parts on \((0,\frac{t}{2})\times \Omega \) and Hölder’s inequality furnish

where we employed (10)\(_2\) in \(t=0\). From (10)\(_1\) \(|{{\widehat{U}}}(t)|+(L^2+t)|{{\widehat{U}}}_t(t)|\le c||v_0||_\infty \), via (43) for  and (32)\(_1\) for
and (32)\(_1\) for  , employing (47) for \(\varphi \), we get
, employing (47) for \(\varphi \), we get
Inequality (34) for \(\nabla W\) and (10)\(_2\) for U ensure that \(\lim _{t\rightarrow 0}||\nabla W(t)||_2=0\). Integrating by parts on \((0,\frac{t}{2})\) and applying Hölder’s inequality, we obtain
Recalling estimate (39) for \(\nabla W\) and (40)\(_2\) for \(\nabla W_t\), employing estimate (47)\(_1\) for \(\varphi \), we get
Collecting the above estimates \(J_i,\,i=1,2,3,4,\) we arrive at (51). \(\square \)
2.6 Some Results of The \(L^p\)-Theory for The IBVP
Now, we recall some results concerning the Stokes initial boundary value problem:
In problem (54) the initial condition is given in the weak form \((\vartheta (0),\varphi )=(w_0,\varphi )\), \(\varphi \in \mathscr {C}_0(\Omega )\), in order to state the initial boundary value problem with an initial data \(w_0\) belonging to the weaker Lebesgue space \(L^p(\Omega )\), \(p\ge 1\). With the weak formulation in \(L^p\), \(p\in (1,\infty )\), the continuity of the equation of divergence (also in weak form) at \(t=0\) is lost, as well as the zero value of the normal component of the solution at the initial instant \(t=0\). Of course, if the datum is an element of \(J^p(\Omega )\subset L^p(\Omega )\), \(p>1\), then, the problem is just the classical one.
For our aims the case \(w_0\in C_0^1(\Omega )\subset L^1(\Omega )\) has a special interest. Actually, we look for an estimate in \(L^\infty (\Omega )\) by means of the variational formulation \(||a||_\infty =\displaystyle \sup _{\theta \in C_0^1(\Omega )}\frac{(a,\theta )}{||\theta ||_1}\) . In Lemma 22, by means of a duality argument, the quoted weak formulation of the \(\theta \) solution allows us to give the estimate \(||\omega (t)||_\infty =\displaystyle \sup _{\theta \in C_0^1(\Omega )}\frac{(\omega (t),\theta )}{||\theta ||_1}\) of the auxiliary solution \(\omega (t,x)\) to problem (67).
In Theorem 2 the initial boundary value problem (54) can be considered for \(\Omega \) bounded or exterior, indifferently.
Theorem 2
Let be \(f=0\) in (54). Let \(w_0\in C_0^1(\Omega )\). Then, to the data \(w_0\) it corresponds a unique solution \((\psi ,\pi _\psi )\) of problem (54) such that \(\psi \in {\underset{q>1}{\cap }}C([0,T); J^q(\Omega )),\) for \(\eta >0\), \(\psi \in {\underset{q>1}{\cap }} L^q(\eta ,T;W^{2,q}(\Omega )\cap J^{1,q}(\Omega )) \) and \(\nabla \pi _\psi , \psi _t\in {\underset{q>1}{\cap }}L^q(\eta ,T;L^q(\Omega ))\). Moreover, for \(q\in (1,\infty ]\) and \(r\in [1,q]\),
where the constant c is independent of \(w_0\). Finally, \({\underset{t\rightarrow 0}{\lim }} (\psi (t),\varphi )=(w_0,\varphi )\) for any \(\varphi \in {\mathscr {C}}_0(\Omega ).\)
Proof
For the proof of the above theorem see [17] Theorem 2.1. Actually, the quoted reference is the two-dimensional version of Theorem 3.2 given in [14] . \(\square \)
Remark 1
We stress that the property \(\psi \in C([0,T);J^q(\Omega ))\) is meant in the sense that \(\lim _{t\rightarrow 0}||\psi (t)-P_q(w_0)||_q=0\). In the case of \(w_0\in C_0^1(\Omega )\) in \(t=0\) at most the weak limit property holds, the one stated in the theorem. Of course, if we assume \(w_0\in J^q(\Omega )\), \(q\in (1,\infty )\), the result becomes the classical one, in particular the continuity in norm holds.
Corollary 2
In the same hypothesis of Theorem 2, for \(q\in (r,\infty ),\, \sigma \in [1,\infty ]\) we also get
Proof
We recall that problem (1) can be considered in \(L(q,\sigma )\)-setting (e.g. cf. [29] or [15]). In particular for all \(q>p>1\) one obtains the estimate
Thus, setting \(s=\frac{t}{2}\) and employing (55)\(_{1,3}\), for \(r\le p\), one arrives at (56). \(\square \)
Lemma 16
In problem (54), assume \(f\in L^q(0,T;L^q(\Omega ))\), and \(w_0=0\). Then, there exists a unique solution \((\vartheta ,\pi _\vartheta )\) to problem (54) with \(\vartheta \in C([0,T);J^q(\Omega ))\),
Proof
For a proof of the above theorem see [12, 22, 23]. \(\square \)
Let us consider the equation for the pressure:
We set
For \(\lambda =1-\frac{1}{q}\) we get the seminorm of trace space \(W^{1-\frac{1}{q},q}(\partial \Omega )\) .
We set \( a:=\nabla \times N\). The following result holds:
Lemma 17
Assume that \(\Omega ' \subset \Omega \) bounded with \(\partial (\Omega -\Omega ' )\cap \partial \Omega =\emptyset \) . Assume that \(a\in W^{1-\frac{1}{q},q}(\partial \Omega )\). Then a solution of problem (58) is such that
where c is constant independent of a.
Proof
Estimate (59) is due to Solonnikov in [25], recently, it is also reproduced in [19]. \(\square \)
In the following Lemma 18 and Lemma 19 we assume that \(\Omega ' \subset \Omega \) is a bounded domain with \(\partial (\Omega -\Omega ' )\cap \partial \Omega =\emptyset \) .
By virtue of trace theorems, for any element of \(a\in W^{1-\frac{1}{q},q}(\partial \Omega )\) admits an extension from \(\partial \Omega \) into \(\Omega '\) which is an element of \(W^{1,q}(\Omega ')\). We denote by the same symbol a the element of space trace \(W^{1-\frac{1}{q},q}(\partial \Omega )\) and its extension as element of \(W^{1,q}(\Omega ')\).
Lemma 18
Assume that \(a\in W^{1-\frac{1}{q},q}(\partial \Omega )\). For a solution of problem (58) the following estimate holds:
where \(q>2\), \(\alpha :=\frac{2}{q}\) , \(d:=\frac{q}{1+\lambda q}\) , \(\lambda \in (0,1-\frac{1}{q})\), and c is a constant independent of a .
Proof
For \(q>2\), by virtue of Lemma 17, we obtain
We have
Hence, we get
\(\square \)
Lemma 19
Assume that \(a(t, \xi )\) in Lemma 17 is a smooth one-parameter family of function in \(W^{1-\frac{1}{q},q}(\partial \Omega )\) , the time \(t>0\) is the parameter. Assume that \(t^{\frac{\gamma }{2}}||a(t)||_q+ t^\gamma ||\nabla a(t)||_q\le A\,,\) for some \(\gamma >0\) and for \(t\in (0,1)\), and \(||a(t)||_q+ ||\nabla a(t)||_q\le A\) for \(t\ge 1\). Then, we get
where c is constant independent of a , exponent \({{\overline{\mu }}}\in (0,\frac{1}{2})\), and \(\Omega ' \subset \Omega \) bounded with \(\partial (\Omega -\Omega ' )\cap \partial \Omega =\emptyset \) .
Proof
We have to estimate the right hand side of (60). Estimate (61)\(_1\) is the behavior of \(||\Pi (t)||_{C({{\overline{\Omega }}}')}\) in a right neighborhood of \(t=0\). Hence, we limit ourselves to consider the terms with the major singularity in \(t=0\). This is conditioned by the greater exponent for \(t^{-1}\). Recalling that in estimate (60) we have \(a=\nabla \times N(t,x)\) and the domain \(\Omega '\) is bounded, employing the assumptions \(||a(t)||_q\le c At^{-\frac{\gamma }{2}}\) and \(||\nabla a(t)||_q\le cA t^{-\gamma }\), then we get
with exponent \(\beta := -\frac{1}{2}(1-\frac{1}{q})(1-\frac{1}{d})(1-\alpha )-\big (\frac{1}{q}(1-\frac{1}{d})+\frac{1}{d}\big )(1-\alpha )-\alpha \). By a computation we obtain
where we recall that \(\alpha =\frac{2}{q}\), \(q>2\), \(d=\frac{q}{1+\lambda q}\) and \(\lambda \in (0,1-\frac{1}{q})\). For large q and small \(\lambda \), we arrive at \({{\overline{\mu }}}\in (0,\frac{1}{2})\). Estimate (61)\(_2\) is immediate from (60) and assumptions. \(\square \)
2.7 A Nonlinear Generalization of The Gronwall Inequality
Lemma 20
Let y(t) be a nonnegative function that satisfies the integral inequality
where a(t) and b(t) are continuous nonnegative functions for \(t\ge t_0\). Then, the following inequality holds
Proof
This result is a particular case of a more general result due to A.I. Perov. A proof of the result can be found in [24], Theorem 1, p. 360. \(\square \)
Corollary 3
Assume that y(s) and a(s) are continuous functions on [0, T), \(b(s)=As^{-\frac{1}{2}-{{\overline{\mu }}}},\) A a nonnegative constant and \({{\overline{\mu }}}\in (0,\frac{1}{2})\). Also, assume that the inequality (62) holds for \(t>t_0\ge 0\), \(A_0=A(t_0)\), with \(A(t_0)\) continuous function. Then, inequality (63), initially achieved for \(t>t_0>0\), holds for \(t\in (0,T)\) and \(t_0=0\).
Proof
By assumptions, the right hand-side of (63) is convergent for \(t_0\rightarrow 0\). Hence, letting \(t_0\rightarrow 0\) we achieve the result. \(\square \)
3 A Result by K.Abe and Y.Giga
In this section we recall the following fundamental result due to Abe and Giga in [3] and related to the Stokes IBVP in exterior domains.
Theorem 3
Let us consider the initial boundary value problem (1). Then there exists a \(T_0>0\) such that, for all \(v_0\in L^{\infty }(\Omega )\) enjoying (2), there exists a solution \((u,\pi _u)\in C^2((0,T_0\times {{\overline{\Omega }}})\times C^1((0,T_0\times {{\overline{\Omega }}})\) to the Stokes problem (1), with u(t, x) \(*\)-weakly continuous in \(t = 0\). Also the following estimates hold
where c is independent of \(v_0\) and \(|x||\nabla \pi _u(t,x)|\le c\) for all \(x\in \Omega \).
Lemma 21
Let \(v_0\in L^\infty (\Omega )\cap J^p(\Omega )\), \(p\in (1,\infty )\). Denoted by \((u,\pi _u)\) and \((v,\pi _v)\) the solutions corresponding to \(v_0\) by virtue of Theorem 3 and Theorem 2, respectively. Then the solutions coincide up to function of t for the pressure fields.
Proof
This result is an immediate consequence of the approach employed in [3, 4]. \(\square \)
Corollary 4
Let \(v_0\in L^\infty (\Omega )\) enjoying (2) and with compact support. Then, for all \(T>0\), \(u\in C([0,T);J^p(\Omega ))\),
where \(p\in (1,\infty )\) and the constant c depends on the support of \(v_0\). Moreover, for \({{\overline{\mu }}}\in (0,\frac{1}{2})\), we get
Proof
The result related to estimate (65)\(_1\) is an immediate consequence of Lemma 21. Actually, due to the compact support of the initial datum of the solution, in order to estimate \(||u(t)||_\infty \) we take advantage of estimate (64) in \((0,T_0)\) and, for \(t\ge T_0\), of the ones related to the \(L^p\)-setting, see [8, 9]. Instead, estimate (65)\(_2\) is deduced from the results in \(L^p\)-setting.
In order to prove estimates (66), we start remarking that the pressure field \(\pi _u\) is a solution to equation (58) with \(N=-u\). Moreover, for the nature of compact support of the initial datum, such a solution is such that \((u,\nabla \pi _u)\) belongs to \(L^q(\Omega )\), \(q\in (1,2)\), in the sense specified by Theorem 2. This fact ensures that \(\int \limits _{\partial \Omega }\nu \cdot \nabla \times \nabla \times ud{\mathcal {H}}^1=0\). Hence, for all \(t>0\), letting \(|x|\rightarrow \infty \), we get that \(\pi _u\rightarrow 0\). Thus, by virtue of maximum principium for harmonic solutions, we get
On the other hand, via (65), we satisfy the assumptions of Lemma 19 with \(A:=||v_0||_\infty \) and \(\gamma =1\). Hence, in a neighborhood \(\Omega '\) of \(\partial \Omega \) the max value of \(\pi _u\) satisfies estimate (61). In this way we arrive at (66)\(_1\) in a neighborhood of \(t=0\), and (66)\(_2\) for large t. \(\square \)
4 An Auxiliary Stokes Problem
In this section we consider the following problem

where the functions  are defined in the previous Sects. 2.2, 2.3 and 2.4. In particular, we recall that, for all \(t>0\), they have compact support.
are defined in the previous Sects. 2.2, 2.3 and 2.4. In particular, we recall that, for all \(t>0\), they have compact support.
We are interested to the following
Lemma 22
There exists a unique solution \((\omega ,\pi _\omega )\) to problem (67) such that, for \(p\in (1,\infty )\), \(\omega \in C([0,T;J^p(\Omega ))\cap L^p(0,T;W^{2,p}(\Omega )\cap J^{1,p}(\Omega ))\) and \(\omega _t,\nabla \pi _\omega \in L^p(0,T;L^p(\Omega ))\). Moreover, for \(p>2\), we get
Proof
By virtue of Lemma 7 and Lemmas 9-10, and definition of  , for all \(T>0\) and \(p\in (1,\infty )\), we get that the right hand side of (67) belongs to \( C([0,T;L^p(\Omega ))\). Hence, the existence and the uniqueness are a consequence of Lemma 16. We prove that estimates (68) hold. We denote by \(\varphi (s,x)\) the solution to the Stokes problem ensured by Theorem 2 with initial datum \(w_0\in C_0^1(\Omega )\), and, for all \(t>0\), \(\varphi (t-\tau ,x)\) is the solution \(\varphi (s,x)\) written backward in time on interval (0, t). Multiplying equation (67) by \(\varphi (t-\tau ,x)\), and integrating by parts on \((0,t)\times \Omega \), we getFootnote 3
, for all \(T>0\) and \(p\in (1,\infty )\), we get that the right hand side of (67) belongs to \( C([0,T;L^p(\Omega ))\). Hence, the existence and the uniqueness are a consequence of Lemma 16. We prove that estimates (68) hold. We denote by \(\varphi (s,x)\) the solution to the Stokes problem ensured by Theorem 2 with initial datum \(w_0\in C_0^1(\Omega )\), and, for all \(t>0\), \(\varphi (t-\tau ,x)\) is the solution \(\varphi (s,x)\) written backward in time on interval (0, t). Multiplying equation (67) by \(\varphi (t-\tau ,x)\), and integrating by parts on \((0,t)\times \Omega \), we getFootnote 3
Taking into account that we consider \(p\in (2,\infty ]\), employing Lemmas 11, 12 and 13 with \(q=p'\), we arrive at
This last, for \(p\in (2,\infty ]\), furnishes
Analogously, deriving with respect to t equation (67) and then multiplying by \(\varphi (t-\tau ,x)\), after integrating by parts on \((0,t)\times \Omega \), we get
where for the limit in t we argue as in the case of (69) (actually, for all \(\eta >0,\) \(\omega _t\in C((\eta ,T);J^p(\Omega ))\) holds, hence we can argue as made in footnote 3). We justify the last formula in \(s=0\). Actually, via the equation of \(\omega \), we obtain
with

Applying Hölder’s inequality, the first limit is zero thanks (70). For the second limit, applying Hölder’s inequality, by virtue of (44), we get

Analogously to the limit of the term \(I_1(s)\), integrating by parts, we obtain

that, by virtue of (44), leads to zero limit. Now, from (71), taking into account that for \({\mathscr {I}}_3(t)\) and \({\mathscr {I}}_4(t)\) estimates (51) and (53) hold, for \(q=p'\), for all \(p>2\), we obtain
which furnishes (68)\(_2\). In order to complete the proof of (68), we set  . By virtue of Lemma 4 we deduce
. By virtue of Lemma 4 we deduce
We estimate \(||G(t)||_p\) by means of the results of Sect. 2. We get \(||G(t)||_p\le c||v_0||_\infty \), for all \(t>0\). Thus, via the above estimate of \(\omega \) in \(L^\infty (\Omega )\) and of \(\omega _t\) in \(L^p\)-norm, we arrive at (68)\(_3\). We conclude considering the limit property. The one in \(L^p\)-norm follows from (68)\(_1\). In order to deduce the limit in \(L^\infty \)-norm is enough to consider for \({\mathscr {I}}_1(t)\) and \({\mathscr {I}}_2(t)\) estimates given in Lemma 13. Actually, from (69) we get
Hence, it follows that \(||\omega (t)||_\infty \le ct^{\frac{\mu }{2}-1}\), which achieves the zero limit for \(t\rightarrow 0\), provided that \(\mu >2\).
\(\square \)
Corollary 5
Let \((\omega ,\pi _\omega )\) be the solution of Lemma 22. For \({{\overline{\mu }}}\in (0,\frac{1}{2})\), we get
Proof
The pressure field solves the equation (58) with boundary condition
We justify (74). The normal component deduced from (67) is the following:

Since, on \((0,T)\times \partial \Omega \), we have \(F=-U+{{\widehat{U}}}\) and  , we deduce
, we deduce

where we toke the equation of U into account. For all \(t>0\), the field \(W=0\) on \(\partial \Omega \), hence \(W_t=0\) holds. Since  and \(W=0\) hold in a neighborhood of \(\partial \Omega \), we get
and \(W=0\) hold in a neighborhood of \(\partial \Omega \), we get  . Hence, being the fields \(\omega ,\,F\) and U divergence free, we arrive at (74).
. Hence, being the fields \(\omega ,\,F\) and U divergence free, we arrive at (74).
Since, for \(p\in (1,2)\) and \(t>0\), \(\nabla \pi _\omega \in L^p(\Omega )\), letting \(|x|\rightarrow \infty \), we get \(\pi _\omega (t,x)\rightarrow {{\overline{\pi }}}(t)\) (cf. [10] § II.5) . On the other hand, the right hand side of (74) has integral zero on \(\partial \Omega \). Hence we determine a solution \({{\widetilde{\pi }}}_{\omega }\) on \(\Omega \) that, letting \(|x|\rightarrow \infty \), tends to zero. Since the difference between \(\pi _\omega \) and \({{\widetilde{\pi }}}_{\omega }\) on \(\Omega \) is at most \({{\overline{\pi }}}(t)\), we consider as solution to equation (1) and, as matter of fact to the Neumann problem (74), the one which tends to zero. Since in the sequel there is no confusion, we denote \({{\widetilde{\pi }}}_\omega \) by the symbol \(\pi _\omega \). Hence, by virtue of maximum principium for harmonic solutions, we get
By virtue estimate of Lemma 17, Lemma 18 and then (61), assuming \(\Omega '\supset \Omega \cap {\mathbb {B}}_R\), for some \({{\overline{\mu }}}\in (0,\frac{1}{2})\), we get
In the last estimate, we consider \(\gamma _1:=-1+\frac{1}{p}\) for \(\Delta \omega \), thanks to (68)\(_3\); \(\gamma _2=\frac{\mu }{2}\) for U, deduced from (10)\(_2\); \(\gamma _3=-\frac{1}{2}\) for F, deduced from (25) setting \(k=0\) and \(L=0\). Since the estimate with \(\gamma _1\) holds for \(p>2\), we arrive at (73)\(_1\). Estimate (73)\(_2\) is a consequence of the same previous estimates evaluated for \(t>1\), so that, for the sake of brevity, we omit the details. \(\square \)
5 Proof of Theorem 1
5.1 A First Result
We premise a result. We consider the initial boundary value problem (1) with initial datum \(v_0\in L^\infty (\Omega )\) enjoying (2) and with supp\(v_0\subset \Omega -{\mathbb {B}}_{R+\delta }(0)\). We are going to prove Theorem 1 for this kind of initial data.
Theorem 4
For all \(v_0\in L^\infty (\Omega )\) enjoying (2) and with supp\(v_0\subset \Omega -{\mathbb {B}}_{R+\delta }(0)\), we get the existence of a solution \((v,\pi )\) to problem (1) such that, for all \(q\in (2,\infty )\),
Finally, for the pressure field we have, for all \(q\in (2,\infty )\),
Proof
We consider the initial datum \(v_0\) extended to 0 in \({\mathbb {R}}^2\). We define the pair \((v,\pi )\) as

where we set
-
the field \(U:=H[v_0]\) is the solution to the Cauchy problem enjoying the properties stated in (8) and (10),
-
the field \({{\widehat{U}}}\), defined in (24), is the mean integral on \(\partial \Omega \) of U,
-
for all \(t>0\), the field F is the extension from \(\partial \Omega \) into \(\Omega \) with compact support in \({{\overline{\Omega }}}\) and with value \(-U+{{\widehat{U}}}\) on \(\partial \Omega \), whose existence is ensured by Lemma 7,
-
the field
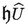 is the product of
is the product of 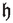 defined by (29) and \({{\widehat{U}}}\),
defined by (29) and \({{\widehat{U}}}\), -
the field W is a solution to the Bogovskiĭ problem (33) given by Lemma 8 and, for \(t>0\), it enjoys the estimates of Lemma 9,
-
the pair \((\omega ,\pi _\omega )\) is the solution to problem (67) furnished by Lemma 22.
By construction the pair \((v,\pi )\) solves equation (1)\(_1\). Moreover, the following estimate holds:
which proves (75)\(_1\) for v. For estimate (78) we check the \(L^\infty \)-norm of each term which appears in (77) for the definition of v. From estimate of Lemma 1 we get  . From estimate (25), recalling that in our hypothesis we have \(R<L\), via the embedding Sobolev theorem, we get \(||F(t)||_\infty \le c||v_0||_\infty ,\,t>0\). For the last terms W and \(\omega \) we recall estimate (39) and estimate (68)\(_1\), respectively. Analogously, for \(||v_t(t)||_\infty \) we employ the estimates related to the time derivative of each term. Hence, we consider (8) to estimate \(U_t\), (31) and (8) to estimate
. From estimate (25), recalling that in our hypothesis we have \(R<L\), via the embedding Sobolev theorem, we get \(||F(t)||_\infty \le c||v_0||_\infty ,\,t>0\). For the last terms W and \(\omega \) we recall estimate (39) and estimate (68)\(_1\), respectively. Analogously, for \(||v_t(t)||_\infty \) we employ the estimates related to the time derivative of each term. Hence, we consider (8) to estimate \(U_t\), (31) and (8) to estimate  , (25) to estimate \(F_t\) and, via the Gagliardo-Nirenberg inequality \(||W_t||_\infty \le c||\nabla W_t||_q^a||W_t||_q^{1-a}\), \(a=\frac{2}{q}\) , employing (39)\(_{2,3}\) we achieve completely the estimate (75)\(_1\).
, (25) to estimate \(F_t\) and, via the Gagliardo-Nirenberg inequality \(||W_t||_\infty \le c||\nabla W_t||_q^a||W_t||_q^{1-a}\), \(a=\frac{2}{q}\) , employing (39)\(_{2,3}\) we achieve completely the estimate (75)\(_1\).
The initial value is assumed in the following sense:
Actually, by virtue of the bounds in \(L^\infty \)-norm stated in (44), choosing \(\mu >3\), we have zero value limit of  and W, and then of \(\omega \) as in (68)\(_4\). Instead, the limit property of U to \(v_0\) is ensured by (12).
and W, and then of \(\omega \) as in (68)\(_4\). Instead, the limit property of U to \(v_0\) is ensured by (12).
Finally, we point out that, for all \(q\in (1,\infty )\) and \(t>0\),
The property (79) is a consequence of the special construction.
To prove the behavior in t claimed in (75)\(_2\), we employ the estimates given in Sect. 2, and we take into account that at \(t=0\) the behavior of U is predominant over that of the other terms of (77). In contrast, for large t the behavior of \(\omega \) becomes predominant over that of the remaining terms in (77).
The integrability on \(\Omega \) of \(\nabla \pi \) is a consequence of the fact that \(\pi \equiv \pi _\omega \) and of Lemma 22. Instead, the estimate of \(\pi \) in \(L^\infty \)-norm is a consequence of (73).
The theorem is completely proved. \(\square \)
5.2 Proof of Theorem 1.
For the initial datum \(v_0\in L^\infty (\Omega )\) that enjoys (2), consider the following decomposition:
where, for \(R>3diam({\mathbb {R}}^2-\Omega )\), g is a non-negative smooth cutoff function such that \(g=1\) for \(|x|\le R+\delta \) and \(g=0\) for \(|x|\ge 2(R+\delta )\), \(\delta >0\), also \(b_0\) is a solution to the Bogovskiĭ problem
We tacitly consider \(v^c_0\) extended to zero on \({\mathbb {R}}^2-\)supp\(v^c_0\), as well as \(v_{0c}\) extended to zero on \({\mathbb {R}}^2-\)supp\(v_{0c}\). Being in particular \(v_{0c}\in L^\infty (\Omega )\cap J^q(\Omega )\), by virtue of Corollary 4, there exists a solution \((v_c,\pi _{v_c})\) to problem (1) with initial datum \(v_{0c}\) enjoying estimates (65).
Since \(v^c_0\in L^\infty (\Omega )\) verifies the hypotheses of Theorem 4, there exists a solution \((v^c,\pi _{v^c})\) to problem (1) with initial datum \(v^c_0\) enjoying estimates (75).
Thanks to the linearity of the Stokes system, considering \(v:=v^c+v_c\) and \(\pi :=\pi _{v^c}+\pi _{v_c}\), by \((v,\pi )\) we solve the value boundary (1), and \((v,\pi )\) enjoys estimates (3)-(4)\(_1\) as a consequence of (65) and (75). The initial datum is achieved by means of (4)\(_2\), which is a consequence of the fact that solution \(v_c\) enjoys the limit property from the \(L^q\)-theory, and solution \(v^c\) enjoys the limit property (75).
The limit property at \(t=0\) allows us to claim that the equation of the divergence is satisfied in weak form up \(t=0\).
We conclude the existence result claming that the pointwise estimate (4)\(_3\) for the pressure field \(\pi \) is a consequence of the estimates (73)-(76), for \(\pi _{v_c}\) and \(\pi _{v^c}\), respectively.
For the uniqueness of the solution we consider a pair \((u,\pi _u)\) solution to the homogeneous initial boundary value problem (1), and enjoying properties (3)-(4)\(_{1,3}\) and (4)\(_2\) substituted by, for all \(R_0>0\), \(\lim _{t\rightarrow 0}||u(t)||_{L^q(\Omega \cap B_{R_0})}=0\). The goal is to prove that \(u=0\). Firstly, we prove that \(u\in L^2(\Omega )\) for all \(t>0\). Subsequently, we realize the uniqueness. For the first goal we are employing the so called weighted energy method (in this regard cf. [11]), that goes back to the first results of stability and uniqueness of solutions in \(L^\infty \)-setting for the IBVP in unbounded domains. We multiply the Stokes equation of \((u,\pi _u)\) by \(\exp [-\alpha |x|]u(t,x)\), where \(\alpha >0\), integrating on \((s,t)\times \Omega \), we get a weighted energy inequality:
Since for all \(R_0>0\) we have \(\lim _{s\rightarrow 0}||u(s)||_{L^2(\Omega \cap {\mathbb {B}}_{R_0})}=0\), with no difficulty one deduces that the limit for \(s\rightarrow 0\) of the first term on the right hand side is null. Instead, thanks to estimate (3) for u and (4) for the pressure field, which furnishes \(||\pi _u\exp [-{\frac{\alpha }{2}}|x|]||_2 \le c\alpha ^{-1}||v_0||_\infty t^{-\frac{1}{2}-{{\overline{\mu }}}}\) , both the integral terms admit limit in \(s=0\). Hence, we arrive at
The validity of (80)-(81) allows us to apply Corollary 3 related to the Gronwall inequality that furnishes
Recalling the above estimate for the pressure field, applying the Beppo-Levi theorem, we deduce
This last easily leads to discuss the uniqueness in \(L^2\)-setting. The theorem is completely proved. \(\square \)
Notes
This sentence could seem in contradiction with the previous result of non-uniqueness. For this reason we explain the meaning of all. The non-uniqueness is with respect the initial datum \(u_0\), in fact we find two solutions corresponding to the same \(u_0\) but one tends to a limit \(u_\infty (t)\) and another tends to a limit \(\overline{u}_\infty (t)\ne u^\infty (t)\) by letting \(|x|\rightarrow \infty \), not only this, the pressure fields are different too. Nevertheless, in corresponding to the same \(u_0\) and \(u_\infty (t)\) the field u and the related pressure \(\pi \) are unique, but, since \(u_\infty (t)\) is not a datum, we arrive at an unsatisfactory result.
We recall that in our notations we denoted by |D| the measure of any Lebesgue’s measurable set.
Just for the completeness, we justify the limit in end point t for the subsequent formula (69). First of all, in order to achieve (69), we can restrict our considerations to \(p\in (2,\infty )\). By Lemma 16 function \(\varphi \in J^{p'}(\Omega )\) for all \(t>0\) and reaches the initial datum in weak form with test function in \({\mathscr {C}}_0(\Omega )\). Hence, we argue in the following way:
$$\begin{aligned}&\displaystyle \lim _{s\rightarrow 0}(\omega (t-s),\varphi (s))\displaystyle \\&\quad = \lim _{s\rightarrow 0}\Big [(\omega (t-s)-\omega (t),\varphi (s))+(\omega (t)-\omega ^m,\varphi (s))+(\omega ^m,\varphi (s))\Big ]\!\\&\quad =:\!\lim _{s\rightarrow 0}\big [I_1(s)+I_2(s)+I_3(s)\big ]\,, \end{aligned}$$where \(\{\omega ^m\}\subset {\mathscr {C}}_0(\Omega )\) is convergent to \(\omega (t,x)\) in \(J^p(\Omega )\). Applying Hölder’s inequality, we get
$$\begin{aligned}\begin{aligned}&\displaystyle \lim _{s\rightarrow 0}|I_1(s)|\le \lim _{s\rightarrow 0}||\omega (t-s)-\omega (t)||_p||\varphi (s)||_{p'}\le \lim _{s\rightarrow 0}||\omega (t-s)-\omega (t)||_p||w_0||_{p'},\\&\displaystyle \lim _{s\rightarrow 0}|I_2(s)|\le \lim _{s\rightarrow 0} ||\omega (t)-\omega ^m||_p||\varphi (s)||_{p'}\le ||\omega (t)-\omega ^m||_p||w_0||_{p'}\\&\displaystyle \lim _{s\rightarrow 0}\,(\omega ^m,\varphi (s))=(\omega ^m,w_0)\,, \end{aligned} \end{aligned}$$where we employed the properties of \(\varphi \) stated in Theorem 2. Hence, letting before \(s\rightarrow 0\) and then \(m\rightarrow \infty \), we arrive at (69).
References
Abe, K.: Liouville theorems for the Stokes equations with applications to large time estimates, Journal of Functional Analysis 278 (2020) Art.108321, https://doi.org/10.1016/j.jfa.2019.108321
Abe, K.: On the large time \(L^\infty \)-estimates of the Stokes semigroup in two dimensional exterior domains. J. Differential Equations 300, 337–355 (2021). https://doi.org/10.1016/j.jde.2021.08.007
Abe, K., Giga, Y.: The \(L^\infty \)-Stokes semigroup in exterior domains. J. Evol. Equ. 14(1), 1–28 (2014)
Abe, K., Giga, Y.: Analyticity of the Stokes semigroup in spaces of bounded functions. Acta Math. 211(1), 1–46 (2013)
Abe, K., Giga, Y., Hieber, M.: Stokes resolvent estimates in spaces of bounded functions. Ann. Sci. Éc. Norm. Supér. 48, 537–559 (2015)
Bolkart, B., Hieber, M.: Pointwise upper bounds for the solution of the Stokes equation on \(L^\infty _ (\Omega )\) and applications. J. of Functional Analysis 268, 1678–1710 (2015)
Chang, T., Choe, H.J.: Maximum modulus estimate for the solution of the Stokes equations. J. Diff. Equations 254, 2682–2704 (2013). https://doi.org/10.1016/j.jde.2013.01.009
Dan, W., Shibata, Y.: Remark on the \(L^q\)-\(L^\infty \)-estimate of the Stokes semigroup in a 2-dimensional exterior domain. Pacific J. Math. 189(2), 223–239 (1999)
Dan, W., Shibata, Y.: On the \(L^q\)-\(L^r\) estimates of the Stokes semigroup in a two-dimensional exterior domain. J. Math. Soc. Japan 51(1), 181–207 (1999)
Galdi, G.P.: An Introduction to the Mathematical Theory of the Navier-Stokes Equations, Steady-state Problems, 2nd edn. Springer Monographs in Mathematics. Springer, New-York (2011)
Galdi, G.P., Rionero, S.: Weighted Energy Methods in Fluid Dynamics and Elasticity. Lecture Notes in Mathematics, vol. 1134. Springer, Berlin (1985)
Giga, Y., Sohr, E.: Abstract \(L^p\) estimates for the Cauchy problem with applications to the Navier-Stokes in Exterior Domains. J. Funct. Analysis 102, 72–94 (1991)
Hieber, M., Maremonti, P.: Bounded analyticity of the Stokes semigroup on spaces of bounded functions, Recent developments of mathematical fluid mechanics, 275–289. Adv. Math. Fluid Mech, Birkhäuser/Springer, Basel (2016)
Maremonti, P.: A remark on the Stokes problem with initial data in \(L^1\). J. Math. Fluid Mech. 13(4), 469–480 (2011)
Maremonti, P.: A remark on the Stokes problem in Lorentz spaces. Discrete and Continuous Dynamical Systems S 6(5), 1323–1342 (2013). https://doi.org/10.3934/dcdss.2013.6.1323
Maremonti, P.: On the Stokes problem in exterior domains: the maximum modulus theorem. Discrete Contin. Dyn. Syst. 34, 2135–2171 (2014). https://doi.org/10.3934/dcds.2014.34.2135
Maremonti, P.: On an interpolation inequality involving the Stokes operator, 710 Contemporary Mathematics 203-209 (2018), https://doi.org/10.1090/conm/710/14371
Maremonti, P.: A remark on the non-uniqueness in \(L^\infty \) of the solutions to the two-dimensional Stokes problem in exterior domains. J. Evol. Equ. 21, 3055–3077 (2021). https://doi.org/10.1007/s00028-020-00662-2
Maremonti, P.: On the \(L^p\) Helmholtz decomposition: A review of a result due to Solonnikov. Lithuanian Math. J. 58(3), 268–283 (2018). https://doi.org/10.1007/s10986-018-9403-6
Maremonti, P., Shimizu, S.: Global existence of solutions to 2-D Navier?Stokes flow with non-decaying initial data in half-plane. J. Differential Equations 265, 5352–5383 (2018). https://doi.org/10.1016/j.jde.2018.07.004
Maremonti, P., Shimizu, S.: Global existence of solutions to 2-D Navier-Stokes flow with non-decaying initial data in exterior domains. J. Math. Fluid Mech. 20, 899–927 (2018). https://doi.org/10.1007/s00021-017-0348-z
Maremonti, P., Solonnikov, V.A.: An estimate for the solutions of a Stokes system in exterior domains, (Russian) Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 180, 105-120 (1990), transl. in J. Math. Sci. 68(2), 229-239 (1994)
Maremonti, P., Solonnikov, V.A.: On nonstationary Stokes problem in exterior domains. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 24(3), 395–449 (1997)
Mitrinović, D.S., Pečarić, J.E., Fink, A.M.: Inequalities Involving Functions and Their Integrals and Derivatives, Springer-Science+Business Media Dordrecht, (1991)
Solonnikov, V.A.: Estimates of the solutions of the nonstationary Navier-Stokes system. (Russian) Boundary value problems of mathematical physics and related questions in the theory of functions, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 38, 153-231 (1973), (e.t.) J. Soviet Math., 8, 467-529 (1977)
Solonnikov, V.A.: On nonstationary Stokes problem and Navier-Stokes problem in a half-space with initial data nondecreasing at infinity, Function theory and applications, J. Math. Sci. (N. Y.) 114(5), 1726-1740 (2003)
Solonnikov, V.A.: On the theory of nonstationary hydrodynamic potentials, in “The Navier-Stokes equations: theory and numerical methids”, edited by R. Salvi, 223 L.N. in Pure and applied mathematics, Marcel-Dekker (2002)
Solonnikov, V.A.: On the estimates of the solution of the evolution Stokes problem in weighted Hölder norms, Annali dell’Univ. di Ferrara, (Sez. VII, Sci. Mat.), 52, 137-172 (2006)
Yamazaki, M.: The Navier-Stokes equations in the weak-Ln space with time-dependent external force. Math. Ann. 317, 635–675 (2000)
Acknowledgements
The author is grateful to two referees whose comments improved the final version of the paper.
Funding
Open access funding provided by Università degli Studi della Campania Luigi Vanvitelli within the CRUI-CARE Agreement. Open access funding provided by UniversitA degli Studi della Campania Luigi Vanvitelli within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest.
The author declares that no conflict of interest occurs.
Additional information
Communicated by Y. Giga
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research activity is performed under the auspices of GNFM-INdAM.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maremonti, P. On The Two-Dimensional Stokes Problem in Exterior Domains: The Maximum Modulus Theorem. J. Math. Fluid Mech. 24, 83 (2022). https://doi.org/10.1007/s00021-022-00716-0
Accepted:
Published:
DOI: https://doi.org/10.1007/s00021-022-00716-0




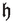 is a cutoff function with support depending on t, and, for all
is a cutoff function with support depending on t, and, for all 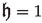 in a ball including
in a ball including 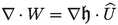 with compact support in
with compact support in 
 is the product of
is the product of  defined by (
defined by (