Abstract
Consider the resolvent problem associated with the linearized viscous flow around a rotating body. Within a setting of classical Sobolev spaces, this problem is not well posed on the whole imaginary axis. Therefore, a framework of homogeneous Sobolev spaces is introduced where existence of a unique solution can be guaranteed for every purely imaginary resolvent parameter. For this purpose, the problem is reduced to an auxiliary problem, which is studied by means of Fourier analytic tools in a group setting. In the end, uniform resolvent estimates can be derived, which lead to the existence of solutions to the associated time-periodic linear problem.
Similar content being viewed by others
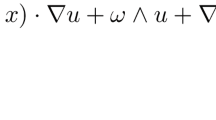
Avoid common mistakes on your manuscript.
1 Introduction
The present article is mainly concerned with the study of the problem
in a three-dimensional exterior domain \(\Omega \subset \mathbb {R}^3\). Here \(s\in \mathbb {R}\) and \(\omega >0\) are given parameters, \(g:\Omega \rightarrow \mathbb {R}^3\) is a given vector field, and \(v:\Omega \rightarrow \mathbb {R}^3\) and \(p:\Omega \rightarrow \mathbb {R}\) are the unknown functions. Then (1.1) can be regarded as a resolvent problem with a purely imaginary resolvent parameter is, \(s\in \mathbb {R}\). Problem (1.1) naturally arises when studying the associated time-periodic problem
System (1.2) may be regarded as the linearization of the nonlinear problem
which describes the time-periodic flow of a viscous incompressible fluid around a rotating rigid body \({{\mathcal {B}}}:=\mathbb {R}^3\setminus \Omega \) in the three-dimensional space. More precisely, here we assume that the fluid adheres to the boundary of \({{\mathcal {B}}}\) and is at rest at infinity, and that the body rotates about the \(x_1\)-axis with (scalar) rotational velocity \(\omega >0\). Then the motion of the fluid flow, described in a frame attached to the body, is governed by (1.3). The functions \(u:{{\mathbb {T}}}\times \Omega \rightarrow \mathbb {R}^3\) and \({\mathfrak {p}}:{{\mathbb {T}}}\times \Omega \rightarrow \mathbb {R}\) are velocity and pressure fields, and \(f:{{\mathbb {T}}}\times \Omega \rightarrow \mathbb {R}^3\) is an external body force. In (1.2) and (1.3) we choose \({{\mathbb {T}}}:=\mathbb {R}/{{\mathcal {T}}}\mathbb {Z}\) for \({{\mathcal {T}}}>0\) as the time axis, so that all occurring functions are intrinsically time periodic. Observe that in the formulation of (1.1) and (1.2) we omitted the condition (1.3)\(_{4}\) at infinity, which is later incorporated in the definition of the function spaces in a generalized sense.
Concerning the analysis of the nonlinear time-periodic problem (1.3), the first result was given by Galdi and Silvestre [1], who showed the existence of weak solution in the more general configuration where the rigid body performs a time-periodic motion. However, in their functional framework the spatial asymptotic properties of the flow were not captured. This problem was recently solved by Galdi [2], who showed existence of regular solutions satisfying certain pointwise decay estimates. A different approach to characterize the spatial behavior of solutions is inspired by the fundamental work of Yamazaki [3], who showed existence of time-periodic solutions to (1.3) in the case \(\omega =0\) in a framework of \(\mathrm {L}^{3,\infty }\) spaces, also known as weak-\(\mathrm {L}^{3}\) spaces. His analysis was based on well-known \(\mathrm {L}^{p}\)–\(\mathrm {L}^{q}\) estimates for the Stokes semigroup. For \(\omega >0\) analogous \(\mathrm {L}^{p}\)–\(\mathrm {L}^{q}\) estimates for the semigroup associated with the initial-value problem corresponding to (1.2) were shown by Hishida and Shibata [4], so that Yamazaki’s method also leads to solutions to (1.3) in the \(\mathrm {L}^{3,\infty }\) framework, as was demonstrated by Hishida [5]. Later, Geissert, Hieber and Nguyen [6] developed a semigroup-based approach in a general framework, where this analysis was also carried out as a special case.
With regard to the linearized time-periodic problem (1.2), observe that for \(\omega =0\), it reduces to the well-known Stokes problem. In this case the unique existence of time-periodic solutions, which satisfy suitable a priori estimates, was successfully derived in [7]. The aim of the present article is to establish a similar result in the case \(\omega >0\). Observe that the additional rotation term \(\omega ( \mathrm {e}_1\wedge u - \mathrm {e}_1\wedge x\cdot \nabla u)\) for \(\omega >0\) cannot be treated as a lower-order perturbation of the Laplace operator because the term \(\mathrm {e}_1\wedge x\cdot \nabla \) is a differential operator with unbounded coefficient. Therefore, for the derivation of a priori estimates, this term has to be handled in a different way. One suitable method was recently developed in [8, 9] and is roughly described as follows: The rotation term \(\omega ( \mathrm {e}_1\wedge u - \mathrm {e}_1\wedge x\cdot \nabla u)\) in (1.2) and (1.3) stems from the change of coordinates from an inertial frame to a rotating frame. Undoing this transformation, one can simply absorb this term again. However, in general this leads to a problem on a time-dependent spatial domain. Therefore, the idea is to first employ this procedure in the setting of the whole space \(\Omega =\mathbb {R}^3\), where the domain is invariant, and to use cut-off techniques to return to the case of an exterior domain afterwards. While in [8, 9] steady motions were investigated, in the recent article [10] the described method was successfully applied to the time-periodic problem
for \(\lambda \ne 0\). System (1.4) differs from (1.2) by the term \(\lambda \partial _1u\), which arises when the body \({{\mathcal {B}}}\) performs, besides a rotation, an additional translation with velocity \(\lambda \mathrm {e}_1\). However, in [10] well-posedness of (1.4) with \(\lambda \ne 0\) was merely shown under the restriction that the time period \({{\mathcal {T}}}\) and the angular velocity \(\omega \) are related by \(\frac{2\pi }{{{\mathcal {T}}}}=\omega \). The results in the forthcoming paper [11] show that this restriction is not necessary but can be weakened and replaced with \(\frac{2\pi }{{{\mathcal {T}}}}/\omega \in \mathbb {Q}\). One main observation of this article is that in the present situation, that is, in the case \(\lambda =0\), where (1.4) reduces to (1.2), such an assumption is not necessary at all, and we provide a framework of well-posedness for any \(\omega ,{{\mathcal {T}}}>0\) without further restrictions.
To this end, the major part of the subsequent analysis is focused on the resolvent problem (1.1). Observe that if \((u,{\mathfrak {p}})\) is a \({{\mathcal {T}}}\)-periodic solution to (1.2), then the Fourier coefficient of order k is a solution to (1.1) with \(s=\frac{2\pi }{{{\mathcal {T}}}}k\). This explains why we restrict our analysis to purely imaginary resolvent parameters is, \(s\in \mathbb {R}\). Moreover, since we want to choose arbitrary time periods \({{\mathcal {T}}}>0\), we need well-posedness of the resolvent problem (1.1) for all \(s\in \mathbb {R}\).
At first glance, it may seem reasonable to analyze (1.1) as the resolvent problem \(isv+A_\omega v=g\) of the closed operator \(A_\omega :D(A_\omega )\subset \mathrm {L}^{q}_{\sigma }(\Omega )\rightarrow \mathrm {L}^{q}_{\sigma }(\Omega )\) given by
where \(\mathrm {L}^{q}_{\sigma }(\Omega )\), \(q\in (1,\infty )\) is the space of all solenoidal functions in \(\mathrm {L}^{q}(\Omega )^3\), and \({{\mathcal {P}}}_\Omega \) is the associated Helmholtz projection. Farwig, Nečasová and Neustupa [12] could show that the essential spectrum of \(A_\omega \) is given by
In particular, we see that is, \(s\in \mathbb {R}\), does not belong to the resolvent set of \(A_\omega \) in general, and this setting does not provide a framework for well-posedness of (1.1) if \(s\in \omega \mathbb {Z}\). Since, as explained above, we need such a framework in order to solve the time-periodic problem (1.2), we introduce a different functional setting instead, namely a setting of homogeneous Sobolev spaces that renders (1.1) well posed for arbitrary \(s\in \mathbb {R}\). One peculiarity of the derived a priori estimate is that instead of the classical form
we deduce the non-classical resolvent estimate
see (3.1) below. In particular, we do not obtain separate estimates of the terms \(isv\) and \(\omega ( \mathrm {e}_1\wedge v - \mathrm {e}_1\wedge x\cdot \nabla v)\) or even of \(isv\), \(\omega \mathrm {e}_1\wedge v\) and \(\omega \mathrm {e}_1\wedge x\cdot \nabla v\). This is not a surprise since a separate estimate of \(isv\) would lead to (1.8) for all \(s\in \mathbb {R}\), which would contradict (1.7). Moreover, it is well known that separate estimates of \(\omega \mathrm {e}_1\wedge v\) and \(\omega \mathrm {e}_1\wedge x\cdot \nabla v\) are not even feasible for the steady-state problem, that is, for (1.1) with \(s=0\); see [13, Theorem VIII.7.2] for example.
The analysis of the resolvent problem (1.1) for an exterior domain \(\Omega \subset \mathbb {R}^3\) goes back to Hishida [14], who derived suitable resolvent estimates in an \(\mathrm {L}^{2}\) framework that showed that the operator \(A_\omega \) generates a contractive \(\mathrm {C}^{0}\)-semigroup if \(q=2\). For general \(q\in (1,\infty )\) a similar statement in the \(\mathrm {L}^{q}\) setting was later proved by Geissert, Heck and Hieber [15]. However, since the resolvent estimate (1.8) is invalid on for all is with \(s\in \omega \mathbb {Z}\), the operator \(A_\omega \) does not generate an analytic semigroup. Nevertheless, one can derive additional smoothing properties of the semigroup that allow to establish solutions to the nonlinear initial-value problem [15, 16] and to carry out a stability analysis of steady-state solutions, as was done by Hishida and Shibata [4, 17]. Moreover, the investigation of the spectrum of the operator \(A_\omega \) was further deepened by Farwig, Nečasová and Neustupa [12, 18, 19].
As explained above, in our investigation of the resolvent problem (1.1) we follow a different approach and investigate (1.1) in a different functional framework. Our analysis is based on the study of the auxiliary problem
which may be regarded as a mixture of the Stokes resolvent problem with the time-periodic Stokes problem. In contrast to (1.1) and (1.2), we can directly derive a formula for the solution to (1.9) by means of a Fourier multiplier on \({{\mathbb {T}}}\times \mathbb {R}^3\). Using tools from harmonic analysis in this group setting, we can further deduce suitable \(\mathrm {L}^{q}\) estimates. By means of the aforementioned transformation, we can then introduce the rotational terms and relate the resolvent problem (1.2) to problem (1.9).
This article is structured as follows: After introducing some notation in Sect. 2, we state our main results on the well-posedness of the resolvent problem (1.1) and the time-periodic problem (1.2) in Sect. 3. In Sect. 4 we study the resolvent problem (1.1) in the case of the whole space \(\Omega =\mathbb {R}^3\), which is based on the examination of the auxiliary time-periodic problem (1.9). In the subsequent Sect. 5 these findings are transferred to the case of an exterior domain. Finally, in Sect. 6 we show the existence of a unique solution to the time-periodic problem (1.2) in a framework of functions with absolutely convergent Fourier series.
2 Notation
In order to state and prove our main results, we first introduce the basic notation.
The symbols C and \(C_j\) with \(j\in \mathbb {N}\) always denote generic positive constants. We occasionally emphasize that C depends on a specific set of quantities \(\{a,b\dots \}\) by writing \(C=C(a,b,\dots )\).
When we fix a time period \({{\mathcal {T}}}>0\), the associated torus group is denoted by \({{\mathbb {T}}}:=\mathbb {R}/{{\mathcal {T}}}\mathbb {Z}\). Then every element of \({{\mathbb {T}}}\) can be identified with a unique representative in \([0,{{\mathcal {T}}})\), which we tacitly do from time to time. Moreover, \({{\mathbb {T}}}\) is always equipped with the normalized Haar measure such that
where \(\mathrm {C}^{}({{\mathbb {T}}})\) is the class of continuous functions on \({{\mathbb {T}}}\). A point \((t,x)\in {{\mathbb {T}}}\times \mathbb {R}^3\) is composed of a time variable \(t\in {{\mathbb {T}}}\) and a space variable \(x=(x_1,x_2,x_3)\in \mathbb {R}^3\). We denote the Euclidean norm of x by \({|x |}\), and \(x\cdot y\), \(x\wedge y\) and \(x\otimes y\) represent the scalar, vector and tensor products of \(x,y\in \mathbb {R}^3\). We further use the shorthand \(x\wedge y\cdot z:=(x\wedge y)\cdot z\) for \(x,y,z\in \mathbb {R}^3\).
Time and spatial derivatives are denoted by \(\partial _t\) and \(\partial _j:=\partial _{x_j}\), \(j=1,2,3\), respectively, and the symbols for (spatial) gradient, divergence and Laplace operator are \(\nabla \), \({{\,\mathrm{div}\,}}\) and \(\Delta \). The symbol \(\nabla ^2u\) denotes the collection of all second-order spatial derivatives of a sufficiently regular function \(u\).
In the whole article we either have \(\Omega =\mathbb {R}^3\) or we let \(\Omega \subset \mathbb {R}^3\) be an exterior domain, that is, \(\Omega \) is a domain and its complement is a compact nonempty set in \(\mathbb {R}^3\). Moreover, \(B_R\subset \mathbb {R}^3\) denotes the ball of radius \(R>0\) centered at 0, and \(\Omega _R:=\Omega \cap B_R\).
For classical Lebesgue and Sobolev spaces we write \(\mathrm {L}^{q}(\Omega )\) and \(\mathrm {W}^{k,q}(\Omega )\), where \(q\in [1,\infty ]\) and \(k\in \mathbb {N}\), and \(\Vert \cdot \Vert _{q;\Omega }\) and \(\Vert \cdot \Vert _{k,q;\Omega }\) denote the associated norms. When the domain is clear from the context, we simply write \(\Vert \cdot \Vert _{q}\) and \(\Vert \cdot \Vert _{k,q}\) instead. This convention is adapted for the norm \(\Vert \cdot \Vert _{q,{{\mathbb {T}}}\times \Omega }\) of the Lebesgue space \(\mathrm {L}^{q}({{\mathbb {T}}}\times \Omega )\) in space and time. We further let \(\mathrm {C}^{\infty }_0(\Omega )\) be the class of all smooth functions with compact support in \(\Omega \), and \(\mathrm {W}^{1,q}_0(\Omega )\) denotes its closure in \(\mathrm {W}^{1,q}(\Omega )\). For the dual space of \(\mathrm {W}^{1,q}_0(\Omega )\) we write \(\mathrm {W}^{-1,q'}(\Omega )\), where \(1/q+1/q'=1\), which we equip with the norm \(\Vert \cdot \Vert _{-1,q';\Omega }\). Moreover, \(\mathrm {L}^{q}_{\mathrm {loc}}(\Omega )\) and \(\mathrm {W}^{k,q}_{\mathrm {loc}}(\Omega )\) denote the classes of all functions that locally belong to \(\mathrm {L}^{q}(\Omega )\) and \(\mathrm {W}^{k,q}(\Omega )\), respectively.
We usually do not distinguish between a space X and its vector-valued version \(X^n\), \(n\in \mathbb {N}\), when the dimension is clear from the context. By \(\Vert \cdot \Vert _X\) we denote the norm of a general normed space X. We write \(\mathrm {L}^{q}({{\mathbb {T}}};X)\) for the corresponding Bochner–Lebesgue space when \(q\in [1,\infty )\), and we define \(\mathrm {W}^{1,q}({{\mathbb {T}}};X):=\bigl \{u\in \mathrm {L}^{q}({{\mathbb {T}}};X) : \partial _tu\in \mathrm {L}^{q}({{\mathbb {T}}};X)\bigr \}\).
In our subsequent analysis, the configuration for \(\Omega =\mathbb {R}^3\) plays an important role. In this case, the space-time domain is given by \(G:={{\mathbb {T}}}\times \mathbb {R}^3\), which is a locally compact abelian group with dual group isomorphic to \({\widehat{G}}:=\mathbb {Z}\times \mathbb {R}^3\). As natural generalizations of the classes of Schwartz functions and tempered distributions in the Euclidean setting, one can define the Schwartz–Bruhat space \({\mathscr {S}}(G)\) and its dual space \(\mathscr {S^\prime }(G)\) on \(G\), which were first introduced by Bruhat [20], see also [21] for more details and a precise definition of these spaces. In this framework, the Fourier transform \({\mathscr {F}}_G\) and its inverse \({\mathscr {F}}^{-1}_G\), defined by
are mutually inverse isomorphisms provided that the Lebesgue measure \({\mathrm d}\xi \) is normalized in a suitable way. By duality, the Fourier transform can be extended to an isomorphism \(\mathscr {S^\prime }(G)\rightarrow \mathscr {S^\prime }({\widehat{G}})\). By analogy, the Fourier transforms on the groups \({{\mathbb {T}}}\) and \(\mathbb {R}^3\) are given by
and
Our investigation of the time-periodic problem (1.2) will mainly be performed in a framework of spaces of absolutely convergent Fourier series. For a normed space X, these are defined by
If X is a Banach space, then \(\mathrm {A}({{\mathbb {T}}};X)\) coincides with the Banach space \({\mathscr {F}}^{-1}_{{\mathbb {T}}}\big [\ell ^{1}(\mathbb {Z};X)\big ]\), and \(\mathrm {A}({{\mathbb {T}}};X)\hookrightarrow \mathrm {C}^{}({{\mathbb {T}}};X)\). Observe that many inequalities in spaces X have natural extensions to the corresponding spaces \(\mathrm {A}({{\mathbb {T}}};X)\), for example, Hölder’s inequality or interpolation inequalities; see [10, Prop. 3.1 and 3.2]. We also use the shorthand \(u\in \mathrm {A}({{\mathbb {T}}};\mathrm {W}^{k,q}_{\mathrm {loc}}(\Omega ))\) when \(u\in \mathrm {A}({{\mathbb {T}}};\mathrm {W}^{k,q}(K))\) for all compact sets \(K\subset \Omega \).
The existence of solutions to the time-periodic problem (1.2) will be established in the following functional framework. We fix \(\omega >0\) and \(q\in (1,3/2)\). Then the space for the velocity field is given by
and the function class for the pressure term is given by
Similarly, we introduce the following function classes for solutions to the resolvent problem (1.1). For \(\omega >0\), \(q\in (1,3/2)\) and \(s\in \mathbb {R}\), we define the class of velocity fields by
and the corresponding pressure belongs to
Observe that the function class \({\mathrm X_{\omega ,s}^q}(\Omega )\) for the velocity field also depends on the resolvent parameter \(s\in \mathbb {R}\). Moreover, if \(u\) belongs to \({{\mathcal {X}}_{\omega }^q}({{\mathbb {T}}}\times \Omega )\), then its k-th Fourier coefficient \(u_k:={\mathscr {F}}_{{\mathbb {T}}}[u](k)\) belongs to \({\mathrm X_{\omega ,s}^q}(\Omega )\) with \(s=\frac{2\pi }{{{\mathcal {T}}}}k\).
3 Main Results
The main results of this article concern the question of well-posedness of the time-periodic linear problem (1.2) and the associated resolvent problem (1.1). At first, we address the resolvent problem.
Theorem 3.1
Let \(\Omega =\mathbb {R}^3\) or \(\Omega \subset \mathbb {R}^3\) be an exterior domain with \(\mathrm {C}^{3}\)-boundary. Let \(s\in \mathbb {R}\) and \(0<\omega \le \omega _0\), and let \(q\in (1,3/2)\) and \(g\in \mathrm {L}^{q}(\Omega )^3\). Then there exists a unique solution \((v,p)\in {\mathrm X_{\omega ,s}^q}(\Omega )\times \mathrm Y^q(\Omega )\) to (1.1) that obeys the estimates
for a constant \(C=C(\Omega ,q,\omega _0)>0\). In particular, C can be chosen independently of \(s\in \mathbb {R}\) and \(\omega \in (0,\omega _0]\).
Note that if \(s\not \in \omega \mathbb {Z}\), then estimate (3.1) implies \(v\in \mathrm {L}^{q}(\Omega )\), which yields \(v\in D(A_\omega )\), where \(D(A_\omega )\) is defined in (1.5). But a similar inclusion cannot be obtained if \(s\in \omega \mathbb {Z}\). This observation is in complete accordance with (1.7).
Working within a framework of absolutely convergent Fourier series, we can then employ Theorem 3.1 on the level of the Fourier coefficients to derive well-posedness of the time-periodic problem (1.2). As will become clear from the proof, to conclude existence of \({{\mathcal {T}}}\)-periodic solutions, it is important that the constant C in (3.1) can be chosen uniformly for \(s\in \frac{2\pi }{{{\mathcal {T}}}}\mathbb {Z}\).
Theorem 3.2
Let \(\Omega =\mathbb {R}^3\) or \(\Omega \subset \mathbb {R}^3\) be an exterior domain with \(\mathrm {C}^{3}\)-boundary. Let \({{\mathcal {T}}}>0\) and \(0<\omega \le \omega _0\), and let \(q\in (1,3/2)\) and \(f\in \mathrm {L}^{q}({{\mathbb {T}}}\times \Omega )^3\). Then there exists a unique \({{\mathcal {T}}}\)-periodic solution \((u,{\mathfrak {p}})\in {{\mathcal {X}}_{\omega }^q}({{\mathbb {T}}}\times \Omega )\times {\mathcal {Y}}^q({{\mathbb {T}}}\times \Omega )\) to (1.2) that obeys the estimates
for a constant \(C=C(\Omega ,q,\omega _0)>0\). In particular, C can be chosen independently of \(\omega \in (0,\omega _0]\) and \({{\mathcal {T}}}>0\).
Remark 3.3
In contrast to the other terms in estimate (3.1), the term \(\Vert {{\,\mathrm{dist}\,}}(s,\omega \mathbb {Z}) \,v\Vert _q\) does not directly correspond to any of the terms in (3.2). However, going through the proof of Theorem 3.2, one may derive an additional estimate. Decompose the set of Fourier indices into \(A_1:=\{k\in \mathbb {Z} : \frac{2\pi }{{{\mathcal {T}}}}k\in \omega \mathbb {Z}\}\) and \(A_2:=\{k\in \mathbb {Z} : \frac{2\pi }{{{\mathcal {T}}}}k\not \in \omega \mathbb {Z}\}\) and split the velocity field \(u\) accordingly as
Then the estimate
follows, where
Of course, this estimate only provides new information when \(d_{\omega ,{{\mathcal {T}}}}>0\). A classical argument shows that this is the case if and only if \(\frac{2\pi }{{{\mathcal {T}}}}/\omega \in \mathbb {Q}\).
4 The Resolvent Problem in the Whole Space
We begin with the study of the resolvent problem (1.1) in the case \(\Omega =\mathbb {R}^3\), where it simplifies to
In this section we show the following result on well-posedness of (4.1).
Theorem 4.1
Let \(\omega >0\) and \(s\in \mathbb {R}\). For each \(g\in \mathrm {L}^{q}(\mathbb {R}^3)^3\) there exists a solution \((v,p)\in \mathrm {W}^{2,q}_{\mathrm {loc}}(\mathbb {R}^3)^3 \times \mathrm {W}^{1,q}_{\mathrm {loc}}(\mathbb {R}^3)\) to (4.1) that satisfies
as well as
for a constant \(C=C(q)>0\). Moreover, if \((w,{\mathfrak {q}})\in \mathrm {L}^{1}_{\mathrm {loc}}(\mathbb {R}^3)^{3+1}\) is another distributional solution to (4.1), then the following holds:
-
(i)
If \(\nabla ^2w,\, isw+\omega ( \mathrm {e}_1\wedge w - \mathrm {e}_1\wedge x\cdot \nabla w)\in \mathrm {L}^{q}(\mathbb {R}^3)\), then
$$\begin{aligned} \begin{aligned} isw+\omega ( \mathrm {e}_1\wedge w - \mathrm {e}_1\wedge x\cdot \nabla w)&=isv+\omega ( \mathrm {e}_1\wedge v - \mathrm {e}_1\wedge x\cdot \nabla v), \\ \nabla ^2w=\nabla ^2v, \qquad \nabla {\mathfrak {q}}&=\nabla p. \end{aligned} \end{aligned}$$ -
(ii)
If \(q<3/2\) or \(s\not \in \omega \mathbb {Z}\), and if \(w\in \mathrm {L}^{r}(\mathbb {R}^3)^3\) for some \(r\in (1,\infty )\), then \(v=w\) and \(p={\mathfrak {q}}+c\) for a constant \(c\in \mathbb {R}\).
For \(s=0\), problem (4.1) reduces to the steady-state problem associated with (1.2) for \(\Omega =\mathbb {R}^3\). In this case, estimate (4.2) was first derived in [22], where an explicit solution formula was derived and examined by means of Littlewood–Paley theory. A different method was later introduced in [8], where the steady-state problem with rotation terms was transformed to a time-periodic Stokes problem without rotation terms by a suitable coordinate transform.
In order to prove Theorem 4.1, we use a similar approach and first consider the auxiliary problem
which can be regarded as a mixture of the Stokes resolvent problem and the time-periodic Stokes problem. In contrast to the original time-periodic problem (1.2), the differential operator associated with (4.5) has constant coefficients, which enables us to express its solution via Fourier multipliers. Since (4.5) is a problem in the locally compact abelian group \(G:={{\mathbb {T}}}\times \mathbb {R}^3\), we work with multiplier arguments in this group framework. This is more involved compared to the usual Euclidean setting, and for a detailed introduction to this theory, with a focus on the analysis of the Navier–Stokes equations, we refer to the book chapter [21] as well as to the monographs [23, 24]. The main tool for the derivation of \(\mathrm {L}^{q}\) multiplier estimates is the so-called transference principle for multipliers, which goes back to de Leuuw [25] and was generalized by Edwards and Gaudry [26, Theorem B.2.1]. In our investigation we employ the following special case.
Theorem 4.2
Let \(G:={{\mathbb {T}}}\times \mathbb {R}^3\) and \(H:=\mathbb {R}\times \mathbb {R}^3\). For each \(q\in (1,\infty )\) there exists a constant \(C_q>0\) with the following property: If a continuous, bounded function \(M:H\rightarrow \mathbb {C}\) is an \(\mathrm {L}^{q}(H)\) multiplier, that is,
for some \(C_M>0\), then the restriction \(m:={M |}_{ \mathbb {Z}\times \mathbb {R}^3}\) is an \(\mathrm {L}^{q}(G)\) multiplier with
This result enables us to reduce Fourier multipliers in \(G={{\mathbb {T}}}\times \mathbb {R}^3\) to Fourier multipliers in the Euclidean space \(H=\mathbb {R}\times \mathbb {R}^3\), where more classical tools for the identification of \(\mathrm {L}^{q}\) multipliers are available. This strategy is used several times in the proof of the following theorem that establishes existence of solutions to (4.5) in an \(\mathrm {L}^{q}\) framework.
Theorem 4.3
Let \(\omega >0\) and \(s\in \mathbb {R}\), and set \({{\mathcal {T}}}_\omega :=\frac{2\pi }{\omega }\) and \({{\mathbb {T}}}:=\mathbb {R}/{{\mathcal {T}}}_\omega \mathbb {Z}\). For each \(f\in \mathrm {L}^{q}({{\mathbb {T}}}\times \mathbb {R}^3)^3\) there exists a solution \((u,{\mathfrak {p}})\) to (4.5) with
that satisfies
as well as
for a constant \(C=C(q)>0\). Moreover, if \((w,{\mathfrak {q}})\in \mathrm {L}^{1}_{\mathrm {loc}}({{\mathbb {T}}}\times \mathbb {R}^3)^{3+1}\) is another distributional solution to (4.5), then the following holds:
-
(i)
If \(\nabla ^2w,\ isw+\partial _tw\in \mathrm {L}^{q}({{\mathbb {T}}}\times \mathbb {R}^3)\), then
$$\begin{aligned} isw+\partial _tw=isu+\partial _tu, \qquad \nabla ^2w=\nabla ^2u, \qquad \nabla {\mathfrak {q}}=\nabla {\mathfrak {p}}. \end{aligned}$$ -
(ii)
If \(q<3/2\) or \(s\not \in \omega \mathbb {Z}\), and if \(w\in \mathrm {L}^{1}({{\mathbb {T}}};\mathrm {L}^{r}(\mathbb {R}^3)^3)\) for some \(r\in (1,\infty )\), then \(u=w\) and \({\mathfrak {p}}={\mathfrak {q}}+d\) for a (space-independent) function \(d:{{\mathbb {T}}}\rightarrow \mathbb {R}\).
Proof
At first, we show that it suffices to consider \(s\in \mathbb {R}\) with \({|s |}\le \omega /2\). Indeed, for \(s\in \mathbb {R}\) there exists \(\ell \in \mathbb {Z}\) such that \({|s-\omega \ell |}\le \omega /2\). We set \({\widetilde{s}}=s-\omega \ell \) and \({\widetilde{f}}(t,x)=f(t,x)\mathrm {e}^{i\omega \ell t}\), and assume that \((w,{\mathfrak {q}})\) is a solution to (4.5) satisfying (4.6)–(4.8) with s and f replaced with \({\widetilde{s}}\) and \({\widetilde{f}}\), respectively. We now define the \({{\mathcal {T}}}_\omega \)-periodic functions \(u(t,x):=w(t,x)\mathrm {e}^{-i\omega \ell t}\) and \({\mathfrak {p}}(t,x):={\mathfrak {q}}(t,x)\mathrm {e}^{-i\omega \ell t}\). Then \((u,{\mathfrak {p}})\) satisfies the original problem (4.5) and the corresponding estimates (4.6)–(4.8). Therefore, it is sufficient to treat the case \({|s |}\le \omega /2\) in the following.
In the case \(s=0\), the system (4.5) reduces to the classical time-periodic Stokes system, for which existence of a solution \((u,{\mathfrak {p}})\) was shown in [27]. More precisely, in [27] the right-hand side was decomposed as \(f=f_0+f_\bot \) with
and existence of a solution \((u,{\mathfrak {p}})=(u_0+u_\bot ,{\mathfrak {p}}_0+{\mathfrak {p}}_\bot )\), decomposed in the same fashion as f, was shown, which satisfies
for constants \(C_1=C_1(q)\) and \(C_2=C_2(q,{{\mathcal {T}}}_\omega )\). In particular, combining these inequalities, we end up with (4.6) with the constant \(C=C_1+C_2\). Moreover, by a classical scaling argument we see that the constant C in (4.6) is independent of \({{\mathcal {T}}}_\omega \). Finally, (4.7) and (4.8) follow from Sobolev’s inequality in space.
Now let us consider the case \(0\ne {|s |}\le \omega /2\). At first, let \(f\in {\mathscr {S}}({{\mathbb {T}}}\times \mathbb {R}^3)^3\). Computing the divergence of (4.5)\(_{1}\), we obtain \(\Delta {\mathfrak {p}}={{\,\mathrm{div}\,}}f\). By means of the Fourier transform \({\mathscr {F}}_G\) on the locally compact abelian group \(G:={{\mathbb {T}}}\times \mathbb {R}^3\), we conclude \(-{|\xi |}^2{\mathscr {F}}_G[{\mathfrak {p}}]=i\xi \cdot {\mathscr {F}}_G[f]\), so that
In particular, \({\mathfrak {p}}\) is well defined as a distribution in \(\mathscr {S^\prime }(G)\), and by continuity of the Riesz transforms \(\mathrm {L}^{q}(\mathbb {R}^3)\rightarrow \mathrm {L}^{q}(\mathbb {R}^3)\), which can be extended to continuous operators \(\mathrm {L}^{q}(G)\rightarrow \mathrm {L}^{q}(G)\), we conclude
Next we apply the Fourier transform to (4.5)\(_{1}\). In view of (4.10), this leads to the representation formula
where \(I\in \mathbb {R}^{3\times 3}\) is the identity matrix and
Since \(0\ne {|s |}\le \omega /2\), the denominator
in the definition of m has no zeros \((k,\xi )\in \mathbb {Z}\times \mathbb {R}^3\), so that m is a well-defined bounded function. Hence \(u\in \mathscr {S^\prime }(G)\) is well defined by means of a Fourier multiplier in \(G\). To deduce estimate (4.6), it remains to derive \(\mathrm {L}^{q}\) estimates for \({{\,\mathrm{dist}\,}}(s,\omega \mathbb {Z})\,u\), \(isu+\partial _tu\) and \(\nabla ^2u\), that is, estimates of \(isu\), \(\partial _tu\) and \(\nabla ^2u\). In virtue of the representation formula (4.12) we have
with \(m_0,\,m_1,\,m_{j\ell }:\mathbb {Z}\times \mathbb {R}^3\rightarrow \mathbb {R}\) defined by
for \(j,\ell =1,2,3\). We set \({\mathfrak {m}} :=\bigl \{m_0,m_1,m_{j\ell } : j,\ell \in \{1,2,3\}\bigr \}\). Then the \(\mathrm {L}^{q}\) estimate (4.6) follows if all \({\widetilde{m}}\in {\mathfrak {m}}\) can be identified as \(\mathrm {L}^{q}(G)\) multipliers. For this purpose, we employ the transference principle from Theorem 4.2. Let \(\chi \in \mathrm {C}^{\infty }(\mathbb {R})\) with \(0\le \chi \le 1\) and such that \(\chi (x)=0\) for \({|x |}\le 1/2\) and \(\chi (x)=1\) for \({|x |}\ge 1\). We define the functions \(M_0,\,M_1,\,M_{j\ell }:\mathbb {R}\times \mathbb {R}^3\rightarrow \mathbb {C}\),
and we set \({\mathfrak {M}}:=\bigl \{M_0,M_1,M_{j\ell } : j,\ell \in \{1,2,3\}\bigr \}\). Observe that
so that the numerator of each term vanishes in a neighborhood of the only zero \((\eta ,\xi )=(-s/\omega ,0)\) of the common denominator \(D_s(\eta ,\xi )\). We thus conclude that every multiplier \({{\widetilde{M}}}\in {\mathfrak {M}}\) is a well-defined continuous function. Moreover, we have \(m_0={M_0 |}_{ \mathbb {Z}\times \mathbb {R}^3}\), \(m_1={M_1 |}_{ \mathbb {Z}\times \mathbb {R}^3}\) and \(m_{j\ell }={M_{j\ell } |}_{ \mathbb {Z}\times \mathbb {R}^3}\). Hence, by the transference principle from Theorem 4.2, all elements of \({\mathfrak {m}}\) are \(\mathrm {L}^{q}(G)\) multipliers if all elements of \({\mathfrak {M}}\) are \(\mathrm {L}^{q}(\mathbb {R}\times \mathbb {R}^3)\) multipliers. By employing the technical inequalities
a lengthy but elementary calculation shows
for all \({{\widetilde{M}}}\in {\mathfrak {M}}\) and for an absolute constant \(C>0\) that is independent of s. By the Marcinkiewicz multiplier theorem (see [28, Corollary 5.2.5] for example), we conclude that \({\widetilde{M}}\) is an \(\mathrm {L}^{q}(\mathbb {R}\times \mathbb {R}^3)\) multiplier such that
where \(C=C(q)\) is independent of s. Since all \({{\widetilde{M}}}\in {\mathfrak {M}}\) are continuous, the transference principle (Theorem 4.2) now implies that all \({\widetilde{m}}\in {\mathfrak {m}}\) are \(\mathrm {L}^{q}(G)\) multipliers with
where \(C=C(q)\). By combining these estimates with the continuity of the Riesz transforms, the representation formulas in (4.13) yield (4.6). Estimates (4.7) and (4.8) now follow from Sobolev’s inequality. In summary, for \(f\in {\mathscr {S}}(G)\) we have now constructed a solution to (4.5) with the desired properties. A classical approximation argument based on the estimates (4.6)–(4.8) finally yields the existence of a solution for any \(f\in \mathrm {L}^{q}(G)\).
It remains to prove the uniqueness assertion for arbitrary \(s\in \mathbb {R}\). We consider the difference \(({\widetilde{u}},\widetilde{{\mathfrak {p}}})=(u-w,{\mathfrak {p}}-{\mathfrak {q}})\in \mathrm {L}^{1}_{\mathrm {loc}}(G)^{3+1}\), which is a solution to (4.5) with \(f=0\). As above, computing the divergence of both sides of (4.5)\(_{1}\), we conclude \(\Delta \widetilde{{\mathfrak {p}}}=0\), which implies \({{\,\mathrm{supp}\,}}{\mathscr {F}}_G[\widetilde{{\mathfrak {p}}}]\subset \mathbb {Z}\times \{0\}\). Since an application of \({\mathscr {F}}_G\) to (4.5)\(_{1}\) leads to \(D_s(k,\xi ){\mathscr {F}}_G[{\widetilde{u}}]=-i\xi {\mathscr {F}}_G[\widetilde{{\mathfrak {p}}}]\) with \(D_s(k,\xi )= is+i\omega k +{|\xi |}^2\), we deduce
Since \(D_s(k,\xi )\) can only vanish for \(\xi =0\), we deduce \({{\,\mathrm{supp}\,}}{\mathscr {F}}_G[{\widetilde{u}}] \subset \mathbb {Z}\times \{0\}\). Hence, \({\widetilde{u}}\in \mathrm {L}^{1}_{\mathrm {loc}}(G)\) implies \({{\,\mathrm{supp}\,}}{\mathscr {F}}_{\mathbb {R}^3}[{\widetilde{u}}](t,\cdot )\subset \{0\}\) for a.a. \(t\in {{\mathbb {T}}}\), so that \({\widetilde{u}}(t,\cdot )\) is a polynomial for a.a. \(t\in {{\mathbb {T}}}\). In the same way we show that \({\mathfrak {p}}(t,\cdot )\) is a polynomial for a.a. \(t\in {{\mathbb {T}}}\). This has the following consequences in the two distinguished cases. In case i we have \(\nabla ^2{\widetilde{u}},\,\nabla \widetilde{{\mathfrak {p}}}\in \mathrm {L}^{q}(G)\). Since both are polynomials in space a.e. in \({{\mathbb {T}}}\), this is only possible if \(\nabla ^2{\widetilde{u}}=0\) and \(\nabla \widetilde{{\mathfrak {p}}}=0\). In virtue of (4.5)\(_{1}\), this also implies \(is{\widetilde{u}}+\partial _t{\widetilde{u}}=0\), which shows the assertion in this case. In case ii we have \({\widetilde{u}}\in \mathrm {L}^{1}({{\mathbb {T}}};\mathrm {L}^{r_0}(\mathbb {R}^3)^3+\mathrm {L}^{r}(\mathbb {R}^3)^3)\) with \(r_0=3q/(3-2q)\) if \(q<3/2\), and \(r_0=q\) if \(s\not \in \omega \mathbb {Z}\). Since \({\widetilde{u}}(t,\cdot )\) is a polynomial for a.a. \(t\in {{\mathbb {T}}}\), this is only possible if \({\widetilde{u}}=0\), and returning to (4.5)\(_{1}\), we also conclude \(\nabla {\mathfrak {p}}=0\). In total, this completes the proof. \(\square \)
Now let us consider the modified time-periodic Stokes problem with rotating effect
which differs from (4.5) by the rotational term \(\omega ( \mathrm {e}_1\wedge u - \mathrm {e}_1\wedge x\cdot \nabla u)\). In the particular case that the angular velocity of the rotation \(\omega \) coincides with the angular frequency \(\frac{2\pi }{{{\mathcal {T}}}}\) associated to the time period \({{\mathcal {T}}}\), this rotational term can be absorbed in the time derivative by a suitable transformation. In this way, we reduce (4.14) to (4.5), and we transfer existence and uniqueness as well as a priori estimates from Theorem 4.3. Observe that the restriction \(\omega =\frac{2\pi }{{{\mathcal {T}}}}\) is crucial for this procedure.
Theorem 4.4
Let \(\omega >0\) and \(s\in \mathbb {R}\), and set \({{\mathcal {T}}}_\omega :=\frac{2\pi }{\omega }\) and \({{\mathbb {T}}}:=\mathbb {R}/{{\mathcal {T}}}_\omega \mathbb {Z}\). For each \(f\in \mathrm {L}^{q}({{\mathbb {T}}}\times \mathbb {R}^3)^3\) there exists a solution \((u,{\mathfrak {p}})\) with
to (4.14) that satisfies
as well as (4.7) and (4.8) for a constant \(C=C(q)>0\).
Moreover, if \((w,{\mathfrak {q}})\in \mathrm {L}^{1}_{\mathrm {loc}}({{\mathbb {T}}}\times \mathbb {R}^3)^{3+1}\) is another distributional solution to (4.14), then the following holds:
-
(i)
If \(\nabla ^2w,\ isw+\partial _tw+\omega ( \mathrm {e}_1\wedge w - \mathrm {e}_1\wedge x\cdot \nabla w)\in \mathrm {L}^{q}({{\mathbb {T}}}\times \mathbb {R}^3)\), then
$$\begin{aligned} \begin{aligned} isw{+}\partial _tw{+}\omega ( \mathrm {e}_1\wedge w - \mathrm {e}_1\wedge x\cdot \nabla w)&=isu{+}\partial _tu{+}\omega ( \mathrm {e}_1\wedge u - \mathrm {e}_1\wedge x\cdot \nabla u), \\ \nabla ^2w=\nabla ^2u, \qquad&\qquad \nabla {\mathfrak {q}}=\nabla {\mathfrak {p}}. \end{aligned} \end{aligned}$$ -
(ii)
If \(q<3/2\) or \(s\not \in \omega \mathbb {Z}\), and if \(w\in \mathrm {L}^{1}({{\mathbb {T}}};\mathrm {L}^{r}(\mathbb {R}^3)^3)\) for some \(r\in (1,\infty )\), then \(u=w\) and \({\mathfrak {p}}={\mathfrak {q}}+d\) for a (space-independent) function \(d:{{\mathbb {T}}}\rightarrow \mathbb {R}\).
Proof
The proof is based on the idea to absorb the rotational term \(\omega ( \mathrm {e}_1\wedge u - \mathrm {e}_1\wedge x\cdot \nabla u)\) into the time derivative by the coordinate transform arising from the rotation matrix
Let \(f\in \mathrm {L}^{q}({{\mathbb {T}}}\times \mathbb {R}^3)^3\) and define the vector field \({{\widetilde{f}}}\) by
Then \({\widetilde{f}}\in \mathrm {L}^{q}({{\mathbb {T}}}\times \mathbb {R}^3)^3\) since \({{\mathbb {T}}}=\mathbb {R}/{{\mathcal {T}}}_\omega \mathbb {Z}\) with \({{\mathcal {T}}}_\omega =\frac{2\pi }{\omega }\). By Theorem 4.3 there exists a solution \(({\widetilde{u}},\widetilde{{\mathfrak {p}}})\) to (4.5) (with f replaced by \({{\widetilde{f}}}\)), which satisfies the estimates (4.6)–(4.8). We now define the \({{\mathcal {T}}}_\omega \)-time-periodic functions
Since \({\dot{Q}}_\omega (t)x = \omega \mathrm {e}_1\wedge [Q_\omega (t)x] = Q_\omega (t)[\omega \mathrm {e}_1\wedge x]\) for any \(x\in \mathbb {R}^3\), a direct computation shows
Moreover, we have
Consequently, \((u,{\mathfrak {p}})\) is a solution to (4.14) and satisfies the estimates (4.15), (4.7), (4.8).
For the uniqueness statement, we set
Mimicking the above calculations, we see that \(({\widetilde{u}},\widetilde{{\mathfrak {p}}})\) and \(({\widetilde{w}},\widetilde{\pi })\) are solutions to (4.5) with the same right-hand side \({{\widetilde{f}}}\). The uniqueness statement now follows from the corresponding statement in Theorem 4.3. \(\square \)
Observe that, by simply considering \(s=0\) in (4.14), we would obtain the original time-periodic problem (1.2), and Theorem 4.4 yields existence of a unique solution to this problem. However, since we required \(\omega =\frac{2\pi }{{{\mathcal {T}}}}\) in Theorem 4.4, we only obtain well-posedness in this special case, and \(\omega \) and \({{\mathcal {T}}}\) cannot be chosen independently.
In contrast, if we consider time-independent solutions \((u,{\mathfrak {p}})(t,x)=(v,p)(x)\) to (4.14) for \(s\in \mathbb {R}\), we obtain the resolvent problem (4.1), where the \({{\mathcal {T}}}\)-dependence does not appear anymore. From Theorem 4.4 we can thus extract Theorem 4.1 as the final result of this section.
Proof of Theorem 4.1
For the proof we set \({{\mathbb {T}}}:=\mathbb {R}/{{\mathcal {T}}}\mathbb {Z}\) with \({{\mathcal {T}}}=\frac{2\pi }{\omega }\). At first, let \(g\in \mathrm {L}^{q}(\mathbb {R}^3)^3\) and define \(f(t,x):=g(x)\). Then \(f\in \mathrm {L}^{q}({{\mathbb {T}}}\times \mathbb {R}^3)^3\), and by Theorem 4.4 there exists a solution \((u,{\mathfrak {p}})\) to (4.14). Then
defines a solution \((v,p)\) to (4.1), and estimates (4.2)–(4.4) follow directly. With regard to uniqueness, observe that every solution to (4.1) is a (time-independent) solution to (4.14), so that the uniqueness statement follows immediately from Theorem 4.4. \(\square \)
5 The Resolvent Problem in an Exterior Domain
After having established well-posedness of the resolvent problem (4.1) in \(\mathbb {R}^3\), we next consider the corresponding problem in an exterior domain \(\Omega \subset \mathbb {R}^3\), given in (1.1). The aim of this section is a proof of Theorem 3.1. At first, we address the question of uniqueness by considering (1.1) for \(g=0\).
Lemma 5.1
Let \(\Omega \subset \mathbb {R}^3\) be an exterior domain of class \(\mathrm {C}^{1,1}\). Let \(\omega >0\), \(s\in \mathbb {R}\), and let \((v,p)\) be a distributional solution to (1.1) with \(g=0\) and \(\nabla ^2v,\,\nabla p\in \mathrm {L}^{q}(\Omega )\) for some \(q\in (1,\infty )\) and \(v\in \mathrm {L}^{r}(\Omega )\) for some \(r\in (1,\infty )\). Then \(v=0\) and \(p\) is constant.
Proof
The proof follows exactly as in [10, Lemma 5.6], where the statement was shown for the case \(s\in \omega \mathbb {Z}\). Therefore, we only give a brief sketch here. The idea is to employ a cut-off argument that leads to a Stokes problem on a bounded domain and to the resolvent problem (1.1) in the whole space, both with error terms on the right-hand side. Using classical elliptic regularity of the Stokes problem and regularity properties for (1.1) established in Theorem 4.1, one can then show that
Next we multiply (1.1)\(_{1}\) by \(v^*\), the complex conjugate of \(v\). The above regularities enable us to integrate the resulting identity over \(\Omega _R\) and to pass to the limit \(R\rightarrow \infty \). Arguing as in [10, Lemma 5.6], one obtains
This yields \(\nabla v=0\) and, in view of the imposed boundary conditions, \(v=0\). From (1.1)\(_{1}\) we finally conclude \(\nabla p=0\), which completes the proof. \(\square \)
In the next step we derive suitable a priori estimates by a cut-off procedure. We begin with the following intermediate result. For simplicity, we only consider the case \(q<\frac{3}{2}\).
Lemma 5.2
Let \(\Omega \subset \mathbb {R}^3\) be an exterior domain of class \(\mathrm {C}^{1,1}\), and \(\omega >0\) and \(s\in \mathbb {R}\). Let \(q\in (1,\infty )\) and \(g\in \mathrm {L}^{q}(\Omega )^3\). Consider a solution \((v,p)\) to (1.1) that satisfies
and \(v\in \mathrm {L}^{r_1}(\Omega )^3\), \(p\in \mathrm {L}^{{{\overline{r}}}_1}(\Omega )\) for some \(r_1,{{\overline{r}}}_1\in (1,\infty )\). Fix \(R>0\) such that \(\partial \Omega \subset B_{R}\). If \(q\in (1,3/2)\), then \((v,p)\) satisfies the estimate
for a constant \(C=C(q,\Omega ,R)>0\).
Proof
Estimate (5.1) can be shown by a classical cut-off procedure. We skip the details here and refer to [10, Lemma 5.7], where the related resolvent problem
in the case \(\lambda >0\) and \(s\in \omega \mathbb {Z}\) was considered. In the present situation one may proceed in the very same way by invoking estimates (4.2)–(4.4) from Theorem 4.1 as well as the uniqueness result from Lemma 5.1. \(\square \)
Based on a compactness argument, we now show how to omit the error terms on the right-hand side of (5.1) and to infer the estimate (3.1).
Lemma 5.3
In the situation of Lemma 5.2 let \(q\in (1,3/2)\) and \(\omega \in (0,\omega _0]\) for some \(\omega _0>0\). Then \((v,p)\) satisfies estimate (3.1) for a constant \(C=C(q,\Omega ,\omega _0)>0\).
Proof
We employ a contradiction argument and assume that there exists no constant \(C>0\) with the claimed properties such that (3.1) holds. Then there exist sequences \((s_j)\subset \mathbb {R}\), \((\omega _j)\subset (0,\omega _0]\), \((v_j)\subset \mathrm {W}^{2,q}_{\mathrm {loc}}(\Omega )^3\), \((p_j)\subset \mathrm {W}^{1,q}_{\mathrm {loc}}(\Omega )\), \((g_j)\subset \mathrm {L}^{q}(\Omega )^3\) with
such that
and
Moreover, there exist sequences \((r_j)\subset (1,\infty )\), \(({{\overline{r}}}_j)\subset (1,\infty )\) such that \(v_j\in \mathrm {L}^{r_j}(\Omega )^3\), \(p_j\in \mathrm {L}^{{{\overline{r}}}_j}(\Omega )\) for all \(j\in \mathbb {N}\). Observe that the left-hand side of (5.3) is finite by Lemma 5.2 and can thus be normalized as in (5.3). By the choice of a suitable subsequence, we may assume that \(\omega _j\rightarrow \omega \in [0,\omega _0]\), \(s_j\rightarrow s\in [-\infty ,\infty ]\) and \({{\,\mathrm{dist}\,}}(s_j,\omega _j\mathbb {Z})\rightarrow \delta \in [-\omega _0/2,\omega _0/2]\) as \(j\rightarrow \infty \). For the moment fix \(R>0\) with \(\partial \Omega \subset B_R\). In virtue of (5.3) and the estimate
the sequences \(({is_jv_j |}_{ \Omega _R})\), \(({v_j |}_{ \Omega _R})\) and \(({p_j |}_{ \Omega _R})\) are bounded in \(\mathrm {L}^{q}(\Omega _R)\), \(\mathrm {W}^{2,q}(\Omega _R)\) and \(\mathrm {W}^{1,q}(\Omega _R)\), respectively. Upon selecting suitable subsequences, we thus obtain the existence of \(w\in \mathrm {L}^{q}_{\mathrm {loc}}(\Omega )^3\), \(v\in \mathrm {W}^{2,q}_{\mathrm {loc}}(\Omega )^3\) and \(p\in \mathrm {W}^{1,q}_{\mathrm {loc}}(\Omega )\) such that
By a Cantor diagonalization argument, we obtain a subsequence such that the limit functions \(w\), \(v\), \(p\) are independent of the choice of R. Moreover, the uniform bounds from (5.3) imply weak convergence of a subsequence in the corresponding spaces, which implies
Firstly, we can now perform the limit \(j\rightarrow \infty \) in (1.1) (\(v\), \(p\), g is replaced with \(v_j\), \(p_j\), \(g_j\)) and deduce
Secondly, the compactness of the embeddings \(\mathrm {W}^{2,q}(\Omega _R)\hookrightarrow \mathrm {W}^{1,q}(\Omega _R) \hookrightarrow \mathrm {L}^{q}(\Omega _R)\hookrightarrow \mathrm {W}^{-1,q}_0(\Omega _R)\) implies the strong convergence
By Lemma 5.2 we have (5.1) with \(v\), \(p\), g replaced with \(v_j\), \(p_j\), \(g_j\). Employing (5.3) and passing to the limit \(j\rightarrow \infty \) in this inequality leads to
We now distinguish the following cases:
-
(i)
If \({|s |}<\infty \) and \(\omega =0\), then \(w=isv\) and (5.5) simplifies to the classical Stokes resolvent problem with resolvent parameter is. If \(s\ne 0\), this yields \(isv=\Delta v-\nabla p\in \mathrm {L}^{q}(\Omega )\), so that \(v\in \mathrm {W}^{2,q}(\Omega )\). Uniqueness in this functional framework is well known, so that \(v=\nabla p=0\); see [29] for example. If \(s=0\), then (5.5) is the steady-state Stokes problem and \(v\in \mathrm {L}^{3q/(3-2q)}(\Omega )\) implies \(v=\nabla p=0\) as follows from [13, Theorem V.4.6] for example.
-
(ii)
If \({|s |}<\infty \) and \(\omega >0\), then \(w=isv\) and (5.5) coincides with (1.1) with \(g=0\). Employing Lemma 5.1 and \(v\in \mathrm {L}^{3q/(3-q)}(\Omega )\), we conclude \(v=\nabla p=0\).
-
(iii)
If \({|s |}=\infty \), we note that for every \(R>0\) such that \(\partial \Omega \subset B_R\), estimate (5.4) implies \(\Vert v_j\Vert _{q;\Omega _R}\le C_R /{|s_j |}\) for some R-dependent constant C. Passing to the limit \(j\rightarrow \infty \) and employing that R was arbitrary, we deduce \(v=0\) in \(\Omega \), and (5.5) reduces to \(w+\nabla p=0\), which, in particular, yields \(w\in \mathrm {L}^{q}(\Omega )\). Since we also have \({{\,\mathrm{div}\,}}w=0\) and \({w |}_{ \partial \Omega }=0\), this equality corresponds to the Helmholtz decomposition in \(\mathrm {L}^{q}(\Omega )\) of the zero function. By uniqueness of this decomposition, we conclude \(w=\nabla p=0\).
Finally, in all three cases we obtain \(w=v=\nabla p=0\), which also yields \(p=0\) due to \(p\in \mathrm {L}^{3q/(3-2q)}(\Omega )\). In total, this is a contradiction to inequality (5.6) and finishes the proof. \(\square \)
After the derivation of suitable a priori estimates in Lemma 5.3, we next show the existence of a solution to the resolvent problem (1.1) for a sufficiently smooth right-hand side g.
Lemma 5.4
Let \(\Omega \subset \mathbb {R}^3\) be an exterior domain of class \(\mathrm {C}^{3}\). Let \(\omega >0\), \(s\in \mathbb {R}\) and \(g\in \mathrm {C}^{\infty }_0(\Omega )^3\). Then there exists a solution \((v,p)\) to (1.1) with
Proof
Existence for the related resolvent problem (5.2) in the case \(s\in \omega \mathbb {Z}\) and \(\lambda >0\) was shown in [10, Lemma 5.11] in full detail based on energy estimates and an “invading domains” technique together with \(\mathrm {L}^{q}\) estimates similar to (3.1). The proof for (1.1) for general \(s\in \mathbb {R}\), which means (5.2) for \(\lambda =0\), follows along the same lines, which is why we only give a rough sketch here.
First of all, we choose \(R>0\) such that \(\partial \Omega \subset B_R\). For \(m\in \mathbb {N}\) with \(m>R\) we first consider the resolvent problem (1.1) on the bounded domain \(\Omega _m=\Omega \cap B_m\), that is,
By formally testing with the complex conjugates of \(v_m\) and \({{\mathcal {P}}}_{\Omega _m}\Delta v_m\), where \({{\mathcal {P}}}_{\Omega _m}\) denotes the Helmholtz projection in \(\mathrm {L}^{2}(\Omega _m)\), one can then derive the a priori estimates
where the constant \(C>0\) is independent of m; see the proof of [10, Lemma 5.11] for further details. In order to derive a uniform estimate on the full second-order norm, we employ the inequality
for all \(w\in \mathrm {W}^{1,2}_0(\Omega _m)^3\cap \mathrm {W}^{2,2}(\Omega _m)^3\) with \({{\,\mathrm{div}\,}}w=0\). Since we assumed \(\partial \Omega \in \mathrm {C}^{3}\), the constant C can be chosen independent of m; see [30, Lemma 1]. Based on these formal a priori estimates and a basis of eigenfunctions of the Stokes operator on the bounded domain \(\Omega _m\), we can then apply a Galerkin method to conclude the existence of a solution \((v_m,p_m)\), which satisfies the a priori estimate
where C is independent of m. After multiplication with suitable cut-off functions, one can then pass to the limit \(m\rightarrow \infty \), which leads to a solution \((v,p)\) to the original resolvent problem (1.1). Finally, another cut-off argument that uses the uniqueness properties from Lemma 5.1 reveals that \((v,p)\in {\mathrm X_{\omega ,s}^q}(\Omega )\times \mathrm Y^q(\Omega )\) for all \(q\in (1,3/2)\). \(\square \)
After having shown existence of a solution for smooth data g, we can now combine the previous lemmas to conclude the proof of Theorem 3.1 by an approximation argument.
Proof of Theorem 3.1
In the case \(\Omega =\mathbb {R}^3\) the statement follows from Theorem 4.1 above. In the case of an exterior domain \(\Omega \subset \mathbb {R}^3\), the uniqueness statement is a consequence of Lemma 5.1, and estimate (3.1) was shown in Lemma 5.3. It thus remains to show existence of a solution for general \(g\in \mathrm {L}^{q}(\Omega )^3\). To this end, consider a sequence \((g_j)\subset \mathrm {C}^{\infty }_0(\Omega )^3\) converging to g in \(\mathrm {L}^{q}(\Omega )^3\). By Lemma 5.4 there exists a solution \((v_j,p_j)\in {\mathrm X_{\omega ,s}^q}(\Omega )\times \mathrm Y^q(\Omega )\) to (1.1) with \(g=g_j\) for each \(j\in \mathbb {N}\). From Lemma 5.3 we infer that \((v_j,p_j)\) is a Cauchy sequence in the Banach space \({\mathrm X_{\omega ,s}^q}(\Omega )\times \mathrm Y^q(\Omega )\). Therefore, there exists a unique limit \((v,p)\in {\mathrm X_{\omega ,s}^q}(\Omega )\times \mathrm Y^q(\Omega )\), which is a solution to (1.1). This completes the proof. \(\square \)
6 The Time-Periodic Problem
Now we consider the time-periodic problem (1.2) and prove the well-posedness results from Theorem 3.2. For the proof, we reduce (1.2) to the resolvent problems for each Fourier mode, which can be solved by means of Theorem 3.1. Due to the a priori estimate (3.1), these solutions constitute a summable sequence in a suitable space, so that the associated Fourier series forms a solution to the time-periodic problem (1.2).
Proof of Theorem 3.2
Let \(f\in \mathrm {A}({{\mathbb {T}}};\mathrm {L}^{q}(\Omega )^3)\). Then there exist \(f_k\in \mathrm {L}^{q}(\Omega )^3\), \(k\in \mathbb {Z}\), such that
By Theorem 3.1 there exists a solution \((u_k,{\mathfrak {p}}_k)\in {\mathrm X_{\omega ,\frac{2\pi }{{{\mathcal {T}}}}k}^q}(\Omega )\times \mathrm Y^q(\Omega )\) to
which satisfies
for C as in Theorem 3.1. Since C is independent of k, the series
define a pair \((u,{\mathfrak {p}})\in {{\mathcal {X}}_{\omega }^q}({{\mathbb {T}}}\times \Omega )\times {\mathcal {Y}}^q({{\mathbb {T}}}\times \Omega )\), which satisfies estimate (3.2) with the same constant C and is a time-periodic solution to problem (1.2).
It remains to prove the uniqueness statement. For this purpose, consider a solution \((u,{\mathfrak {p}})\in {{\mathcal {X}}_{\omega }^q}({{\mathbb {T}}}\times \Omega )\times {\mathcal {Y}}^q({{\mathbb {T}}}\times \Omega )\) to (1.2) with right-hand side \(f=0\). Then the Fourier coefficients \((u_k,{\mathfrak {p}}_k)\in {\mathrm X_{\omega ,\frac{2\pi }{{{\mathcal {T}}}}k}^q}(\Omega )\times \mathrm Y^q(\Omega )\), \(k\in \mathbb {Z}\), defined by (6.2), are solutions to problem (6.1) with \(f_k=0\). From Theorem 3.1 we thus conclude \((u_k,{\mathfrak {p}}_k)=(0,0)\) for all \(k\in \mathbb {Z}\), so that \((u,{\mathfrak {p}})=(0,0)\). This shows uniqueness of the solution and completes the proof. \(\square \)
References
Galdi, G.P., Silvestre, A.L.: Existence of time-periodic solutions to the Navier–Stokes equations around a moving body. Pac. J. Math. 223(2), 251–267 (2006)
Galdi, G.P.: Existence, Uniqueness and Asymptotic Behavior of Regular Time-Periodic Viscous Flow around a Moving Body: Rotational Case (2020). arXiv:2006.03469
Yamazaki, M.: The Navier–Stokes equations in the weak-\(L^n\) space with time-dependent external force. Math. Ann. 317(4), 635–675 (2000)
Hishida, T., Shibata, Y.: \(L_{p}-L_{q}\) Estimate of the Stokes operator and Navier–Stokes flows in the exterior of a rotating obstacle. Arch. Ration. Mech. Anal. 193(2), 339–421 (2009)
Hishida, T.: The Navier–Stokes flow around a rotating obstacle with time-dependent body force. In: Nonlocal and Abstract Parabolic Equations and Their Applications. Banach Center Publ., vol. 86, pp. 149– 162. Polish Acad. Sci. Inst. Math., Warsaw (2009)
Geissert, M., Hieber, M., Nguyen, T.H.: A general approach to time periodic incompressible viscous fluid flow problems. Arch. Ration. Mech. Anal. 220(3), 1095–1118 (2016)
Galdi, G.P., Kyed, M.: Time-periodic flow of a viscous liquid past a body. In: Partial Differential Equations in Fluid Mechanics. London Mathematical Society Lecture Note Series, vol. 452, pp. 20– 49. Cambridge Univ. Press, Cambridge (2018)
Galdi, G.P., Kyed, M.: A simple proof of \(L^q\)-estimates for the steady-state Oseen and Stokes equations in a rotating frame. Part I: strong solutions. Proc. Am. Math. Soc. 141(2), 573–583 (2013)
Galdi, G.P., Kyed, M.: A simple proof of \(L^q\)-estimates for the steady-state Oseen and Stokes equations in a rotating frame. Part II: weak solutions. Proc. Am. Math. Soc. 141(4), 1313–1322 (2013)
Eiter, T., Kyed, M.: Viscous flow around a rigid body performing a time-periodic motion. J. Math. Fluid Mech. 23(1), 28 (2021)
Eiter, T.: On the Oseen–type resolvent problem associated with time-periodic flow past a rotating body (2021). arXiv:2111.00984
Farwig, R., Nečasová, Š., Neustupa, J.: On the essential spectrum of a Stokes-type operator arising from flow around a rotating body in the \(L^q\)-framework. In: Kyoto Conference on the Navier–Stokes Equations and Their Applications. RIMS Kôkyûroku Bessatsu, B1, pp. 93– 105. Res. Inst. Math. Sci. (RIMS), Kyoto (2007)
Galdi, G.P.: An Introduction to the Mathematical Theory of the Navier–Stokes Equations. Steady-State Problems, 2nd edn. Springer, New York (2011)
Hishida, T.: The Stokes operator with rotation effect in exterior domains. Analysis (Munich) 19(1), 51–67 (1999)
Geissert, M., Heck, H., Hieber, M.: \(L^p\)-Theory of the Navier–Stokes flow in the exterior of a moving or rotating obstacle. J. Reine Angew. Math. 596, 45–62 (2006)
Hishida, T.: An existence theorem for the Navier–Stokes flow in the exterior of a rotating obstacle. Arch. Ration. Mech. Anal. 150(4), 307–348 (1999)
Hishida, T., Shibata, Y.: Decay estimates of the Stokes flow around a rotating obstacle. In: Kyoto Conference on the Navier–Stokes Equations and Their Applications. RIMS Kôkyûroku Bessatsu, B1, pp. 167– 186. Res. Inst. Math. Sci. (RIMS), Kyoto (2007)
Farwig, R., Neustupa, J.: On the spectrum of a Stokes-type operator arising from flow around a rotating body. Manuscr. Math. 122(4), 419–437 (2007)
Farwig, R., Nečasová, S., Neustupa, J.: Spectral analysis of a Stokes-type operator arising from flow around a rotating body. J. Math. Soc. Jpn. 63(1), 163–194 (2011)
Bruhat, F.: Distributions sur un groupe localement compact et applications à l’étude des représentations des groupes \(p\)-adiques. Bull. Soc. Math. Fr. 89, 43–75 (1961)
Eiter, T., Kyed, M.: Time-periodic linearized Navier–Stokes equations: an approach based on Fourier multipliers. In: Particles in Flows. Advances in Mathematical Fluid Mechanics, pp. 77– 137. Birkhäuser/Springer, Cham (2017)
Farwig, R., Hishida, T., Müller, D.: \(L^q\)-theory of a singular winding integral operator arising from fluid dynamics. Pac. J. Math. 215(2), 297–312 (2004)
Kyed, M.: Time-Periodic Solutions to the Navier–Stokes Equations. Technische Universität Darmstadt, Habilitationsschrift (2012)
Eiter, T.: Existence and Spatial Decay of Periodic Navier–Stokes Flows in Exterior Domains. PhD thesis, Logos Verlag Berlin, Berlin (2020)
de Leeuw, K.: On \(L_p\) multipliers. Ann. Math. 2(81), 364–379 (1965)
Edwards, R.E., Gaudry, G.I.: Littlewood–Paley and Multiplier Theory. Springer, Berlin-Heidelberg-New York (1977)
Kyed, M.: Maximal regularity of the time-periodic linearized Navier–Stokes system. J. Math. Fluid Mech. 16(3), 523–538 (2014)
Grafakos, L.: Classical Fourier Analysis, 2nd edn. Springer, New York (2008)
Farwig, R., Sohr, H.: Weighted estimates for the Oseen equations and the Navier–Stokes equations in exterior domains. In: Theory of the Navier–Stokes Equations. Ser. Adv. Math. Appl. Sci., vol. 47, pp. 11– 30. World Sci. Publ., River Edge, NJ (1998)
Heywood, J.G.: The Navier–Stokes equations: on the existence, regularity and decay of solutions. Indiana Univ. Math. J. 29, 639–681 (1980)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author states that there is no conflict of interest.
Additional information
Communicated by T. Ozawa.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection “Yoshihiro Shibata” edited by Tohru Ozawa.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eiter, T. On the Stokes-Type Resolvent Problem Associated with Time-Periodic Flow Around a Rotating Obstacle. J. Math. Fluid Mech. 24, 52 (2022). https://doi.org/10.1007/s00021-021-00654-3
Accepted:
Published:
DOI: https://doi.org/10.1007/s00021-021-00654-3


