Study of an Elliptic Partial Differential Equation Modeling the Ocean Flow in Arctic Gyres

Abstract

We study the ocean flow in Arctic gyres using a recent model for gyres derived in spherical coordinates on the rotating sphere. By projecting this model onto the plane using the Mercator projection, we obtain a semi-linear elliptic partial differential equation in an unbounded domain, difficulty which is then overcome by projecting the PDE onto the unit disk via a conformal map. We then study existence, regularity and uniqueness of solutions for constant and linear vorticity functions.

Introduction

The shape of our coasts and the mixing and transportation of temperature, chemicals, and nutrients are largely due to oceanic currents: these currents sometimes link up to form large-scale spiraling circulations called gyres. The movements of gyres drive the “ocean conveyor belt”, which in turn circulates ocean water around the entire planet. This thermohaline circulation also carries around heat from the sun, making gyres essential in understanding the role of the ocean in climate.

The motion of gyres is due mostly to two major forces, the first one being the wind patterns. The waters move in the direction of the winds on small scales but on large-scales they are deflected by the second major force, due to the rotation of the Earth. This force, commonly referred to as the Coriolis force, produces clockwise circular motions in the Northern hemisphere and counterclockwise ones in the Southern hemisphere. Finally, the currents are interrupted and diverted by the landmasses. Note that, whereas winds mostly only act on the surface of the water, landmasses and the Coriolis force also act beneath the surface. Each deeper layer in the water column is deflected by slightly less than the one above it, thus creating in non-equatorial regions a spirally pattern of approximately 100 meters deep, known as the Ekman spiral. We refer to [7, 21] for a discussion of the Ekman spiral.

Gyres can be found in every major ocean, with the Atlantic and the Pacific ocean containing four each. There are five major large-scale gyres and numerous smaller, moderate-scale ones. There are three types of gyres. The first ones are the subpolar gyres. They are the smallest ones on the planet and are situated in the polar regions. There are several in the Northern hemisphere, such as the Beaufort gyre, and two large gyres in the Southern ocean. There are also tropical gyres, formed near the Equator but confined strictly to the Northern or Southern hemispheres (as there is no Coriolis force at the Equator, there are no gyres on or crossing it). Lastly, we have the subtropical gyres, situated between the Equator and the polar regions. Since they lie beneath areas of high atmospheric pressure, they are gigantic placid ocean areas with thousands of kilometers of diameter.

In this paper we will only be focusing on the Arctic gyres. In this respect, we would like to point out that the Arctic is very different from the Antarctic. Whereas the Arctic is made up of sea and ice, surrounded by land, the Antarctic is a landmass surrounded by a very powerful current known as the antarctic circumpolar current (ACC). This geographical difference makes the study of Arctic gyres significantly more difficult than that of the ACC. Indeed, as we will see in the next section, projecting the Arctic region onto the plane using the Mercator projection gives us an unbounded domain whereas the projection of the ACC is a nice bounded strip. See discussions in [6, 15, 17, 19] and the references therein for studies of the ACC.

The plan of the paper is the following: we reduce the model for gyres on the rotating sphere derived by Constantin and Johnson to a semi-linear elliptic partial differential equation by projecting it onto the plane using a cylindrical projection. We then study the existence, uniqueness and regularity of solutions to this PDE for constant and linear vorticity functions.

The Arctic Gyres

Before we recall the Mercator projection, we briefly present the Constantin and Johnson model for gyres derived in [5]. We begin by denoting by $\theta \in [0,\pi )$ the polar angle such that $\theta =0$ corresponds to the South Pole. Consequently, our latitude angle will be $\theta -\frac{\pi }{2}$. We denote by $\varphi$ the azimuthal, or longitude, angle. Following this model for gyres in spherical coordinates, the polar and azimuthal velocity components of the flow on the Earth are given by

$$\begin{aligned} \frac{1}{\sin (\theta )}\psi _{\varphi },\qquad -\psi _{\theta }\,, \end{aligned}$$

respectively, where $\psi (\theta ,\varphi )$ represents the stream function in spherical coordinates.

Furthermore, the governing equation for gyres is given by

$$\begin{aligned} \frac{1}{\sin ^2(\theta )}\Psi _{\varphi \varphi }+\Psi _{\theta }\cot (\theta ) +\Psi _{\theta \theta }=F(\Psi -\omega \cos (\theta )), \end{aligned}$$

(1)

where $\Psi (\theta ,\varphi )=\psi (\theta ,\varphi )+\omega \cos (\theta )$ is associated with the vorticity of motion of the ocean relative to the Earth’s surface, $2\omega \cos (\theta )$ is the spin vorticity due to the rotation of the Earth and $F(\Psi -\omega \cos (\theta ))$ is the oceanic vorticity, due to the motion of the ocean and specific to a particular gyre. Other than linear (and piecewise linear) functions F, the case of exponential functions is of interest because of the link to Stuart vortices (see [8, 9, 20] for more details on Stuart vortices).

We would now like to project this model from the sphere onto the plane. For this, we turn to the Mercator projection, a conformal cylindrical projection (see [10]). Using the change of variable

$$\begin{aligned} {\tilde{X}}=-\ln \left[ \tan \left( \frac{\theta }{2}\right) \right] ,\qquad {\tilde{Y}}=\varphi \end{aligned}$$

(2)

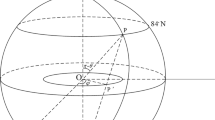
our new plane has the Equator as ${\tilde{Y}}$-axis and the Central Meridian as ${\tilde{X}}$-axis, with the North Pole situated at ${\tilde{X}}=-\infty$ (see Fig. 1).

Fig. 1

The Mercator Projection We project the polar angle onto the ${\tilde{X}}$-axis and the azimuthal angle onto the ${\tilde{Y}}$-axis. The North Pole is situated at ${\tilde{X}}=-\infty$

Using the change of variable (2), we get that ${\tilde{X}}$ is negative in the Northern Hemisphere with

$$\begin{aligned} \cos (\theta )=\tanh ({\tilde{X}}),\qquad \sin (\theta )=\cosh ^{-1}({\tilde{X}}). \end{aligned}$$

Let us set

$$\begin{aligned} U({\tilde{X}},{\tilde{Y}})=\psi (\theta ,\varphi ). \end{aligned}$$

We can then rewrite the governing equation as the following semi-linear elliptic PDE

$$\begin{aligned} \Delta U({\tilde{X}},{\tilde{Y}})=\frac{F(U({\tilde{X}},{\tilde{Y}}))}{\cosh ^2({\tilde{X}})}+2\omega \frac{\sinh ({\tilde{X}})}{\cosh ^3({\tilde{X}})}, \end{aligned}$$

(3)

with boundary condition

$$\begin{aligned} U({\tilde{X}}_0,{\tilde{Y}})=U_0({\tilde{Y}}), \qquad {\tilde{X}}={\tilde{X}}_0<0, \end{aligned}$$

if the boundary of our spherical region corresponds to the parallel $\theta _0=2\arctan (e^{-{\tilde{X}}_0})\in \left( \frac{\pi }{2},\pi \right)$, situated in the Northern Hemisphere.

The North Pole is a stagnation point if and only if

$$\begin{aligned} \lim _{{\tilde{X}}\rightarrow -\infty }\{\left( U_{{\tilde{X}}}({\tilde{X}},{\tilde{Y}}),U_{{\tilde{Y}}}({\tilde{X}},{\tilde{Y}})\right) \cosh ({\tilde{X}})\}=(0,0) \end{aligned}$$

(4)

uniformly in ${\tilde{Y}}\in {\mathbb {R}}$ since the horizontal velocity is

$$\begin{aligned} \left( \frac{1}{\sin (\theta )}\psi _\varphi ,-\psi _\theta \right) =(U_{{\tilde{Y}}},U_{{\tilde{X}}})\cosh ({\tilde{X}}). \end{aligned}$$

We will see that the solutions we construct have this property, which makes them physically admissible.

We are now interested in investigating the partial differential equation (3). However, our domain $\Omega =(-\infty ,{\tilde{X}}_0]\times [0,2\pi )$ is unbounded in the ${\tilde{X}}$ direction, making the analysis difficult. We therefore use a conformal map to project (3) into the unit circle.

The Conformal Mapping

In order to map (3) from the unbounded strip on the plane into the unit circle, we begin by setting ${\tilde{Z}}={\tilde{X}}+i{\tilde{Y}}$. We then translate ${\tilde{Z}}$ to get

$$\begin{aligned} \xi ={\tilde{X}}-{\tilde{X}}_0-i\pi \end{aligned}$$

and finally use an exponential map to get into the unit circle:

$$\begin{aligned} \Lambda =\exp ({\xi }). \end{aligned}$$

We now denote by x and y the new variables in the unit disk, defined by:

$$\begin{aligned} x&=-e^{{\tilde{X}}-{\tilde{X}}_0}\cos ({\tilde{Y}}), \\ y&=-e^{{\tilde{X}}-{\tilde{X}}_0}\sin ({\tilde{Y}}), \end{aligned}$$

and the function u(x, y) in the disk, such that $u(x,y)=U({\tilde{X}},{\tilde{Y}})$.

Notice that in terms of the original spherical variables $(\theta ,\varphi )$, we have

$$\begin{aligned} x=\frac{\tan \tfrac{\theta }{2}}{\tan \tfrac{\theta _0}{2}}\cos (\varphi ),\qquad y=\frac{\tan \tfrac{\theta }{2}}{\tan \tfrac{\theta _0}{2}}\sin (\varphi ). \end{aligned}$$

Therefore, (3) becomes

$$\begin{aligned} \Delta u(x,y)-\frac{4F(u)(x^2+y^2)}{[e^{{\tilde{X}}_0}(x^2+y^2)+e^{-{\tilde{X}}_0}]^2}-8\omega \frac{[e^{{\tilde{X}}_0}(x^2+y^2)-e^{-{\tilde{X}}_0}](x^2+y^2)}{[e^{{\tilde{X}}_0}(x^2+y^2)+e^{-{\tilde{X}}_0}]^3}=0, \end{aligned}$$

(5)

with boundary condition

$$\begin{aligned} u_0(x,y)=U_0\left( \arctan \left( \frac{y}{x}\right) \right) . \end{aligned}$$

We will consider here the case where

$$\begin{aligned} u_0(x,y)=0. \end{aligned}$$

Similarly as in (4), a necessary and sufficient condition for the North Pole to be a stagnation point is the condition

$$\begin{aligned} \lim _{x^2+y^2\rightarrow 0}\{u_x,u_y\}=0. \end{aligned}$$

(6)

Notice that (6) is equivalent to

$$\begin{aligned} \lim _{r\rightarrow 0}u_r=\lim _{r\rightarrow 0}\frac{ u_\theta }{r}=0. \end{aligned}$$

(7)

Constant Vorticity

We begin by looking at the case when our oceanic vorticity is constant: $F(u)=F_0$, where $F_0$ is an arbitrary constant. We therefore obtain the Poisson equation:

$$\begin{aligned} -\Delta u=f(x,y), \end{aligned}$$

(8)

where

$$\begin{aligned} f(x,y)=-\frac{4F_0(x^2+y^2)}{[e^{{\tilde{X}}_0}(x^2+y^2) +e^{-{\tilde{X}}_0}]^2}-8\omega \frac{[e^{{\tilde{X}}_0}(x^2+y^2) -e^{-{\tilde{X}}_0}](x^2+y^2)}{[e^{{\tilde{X}}_0}(x^2+y^2)+e^{-{\tilde{X}}_0}]^3}, \end{aligned}$$

with boundary condition

$$\begin{aligned} u_0=0~\hbox { on }~\partial {\mathbb {D}}. \end{aligned}$$

From the theory of partial differential equations (see [4]), we know that the Poisson equation with homogeneous Dirichlet boundary condition admits a unique weak solution in ${\mathbb {D}}$ and since f(x, y) is smooth in our domain, we have that this unique solution $u(x,y)\in C^{\infty }(\overline{{\mathbb {D}}})$ (uniqueness being recovered using the maximum principle for elliptic partial differential equations). Moreover, since the solution to the Poisson equation on the unit disk is radial, the asymptotic conditions are also satisfied. We can therefore state the following proposition.

Proposition 1

On our domain ${\mathbb {D}}$, the Poisson equation (8) with boundary condition (9) admits a unique solution $u\in C^{\infty }(\overline{{\mathbb {D}}})$ satisfying the asymptotic conditions (7).

Linear Vorticity

We now turn to the case of linear vorticity. We set $F(u)=au+b$ where $a,b\in {\mathbb {R}}$. Our partial differential equation (5) becomes

$$\begin{aligned} -\Delta u+ag(x,y)u=f(x,y). \end{aligned}$$

(9)

Here

$$\begin{aligned} \begin{aligned} g(x,y)&=\frac{4(x^2+y^2)}{[e^{{\tilde{X}}_0}(x^2+y^2)+e^{-{\tilde{X}}_0}]^2}\,, \\ f(x,y)&=-\frac{4b(x^2+y^2)}{[e^{{\tilde{X}}_0}(x^2+y^2)+e^{-{\tilde{X}}_0}]^2}-8\omega \frac{[e^{{\tilde{X}}_0}(x^2+y^2)-e^{-{\tilde{X}}_0}](x^2+y^2)}{[e^{{\tilde{X}}_0}(x^2+y^2)+e^{-{\tilde{X}}_0}]^3}. \end{aligned} \end{aligned}$$

(10)

Theorem 5.1

On the domain ${\mathbb {D}}$, for $b\in {\mathbb {R}}$ and $a\ge 0$, the elliptic equation (9) admits a unique solution $u\in C^{\infty }(\overline{{\mathbb {D}}})$ satisfying the boundary condition $u\big |_{\partial {\mathbb {D}}}=0$. Moreover, for the case $a<0$, such a unique solution u exists if ${\tilde{X}}_0\le -C_a$, where $C_a>0$ is a constant depending on a.

Remark 1

Notice that existence of solutions for $a<0$ depends on the location of ${\tilde{X}}_0$. In fact, we shall see in the proof that the further we move away from the Equator, the more vorticity we can allow.

Proof

We begin by rewriting (9) in its variational formulation. For any $v\in H_0^1({\mathbb {D}})$, we have

$$\begin{aligned} \int _{{\mathbb {D}}}\nabla u\cdot \nabla v +a\int _{{\mathbb {D}}}g u v=\int _{{\mathbb {D}}}f v. \end{aligned}$$

(11)

We set

$$\begin{aligned} \beta (u,v)=\int _{{\mathbb {D}}}\nabla u\cdot \nabla v +a\int _{{\mathbb {D}}}g u v, \end{aligned}$$

(12)

as our bilinear form on $H_0^1({\mathbb {D}})\times H_0^1({\mathbb {D}})$ and

$$\begin{aligned} j(v)=\int _{{\mathbb {D}}}f v, \end{aligned}$$

as our linear form on $H_0^1({\mathbb {D}})$. Clearly, $\beta (u,v)$ and j(v) are continuous (for the bilinear form, this can be shown using the Cauchy-Schwarz inequality).

Using the Poincare inequality, the bilinear form $\beta (u,v)$ is coercive for all $a\ge 0$. Therefore, from the Lax-Milgram theorem, we get that there exists a unique weak solution $u\in H_0^1({\mathbb {D}})$ to (9) for all positive $a\in {\mathbb {R}}$.

It can be shown that the operator $L_a:=-\Delta u+ag(x,y)u=f(x,y)$ is “semi”-Fredholm (has closed range and finite-dimensional kernel). The proof follows exactly as in [14]. Moreover, by self-adjointness of the operator, the index of $L_a$ is equal to zero for all $a\in {\mathbb {R}}$. Consequently, we have existence of solutions for all a for which the operator is injective.

Note that since ${\mathbb {D}}$ is of class $C^{\infty }$ and $f\in C^{\infty }(\overline{{\mathbb {D}}})$ and $g\in C^{\infty }(\overline{{\mathbb {D}}})$, by the theory on regularity for elliptic problems with smooth and periodic coefficients, if the solution u to (9) exists we have a unique solution $u\in C^{\infty }(\overline{{\mathbb {D}}})$. (Uniqueness follows from Lax-Milgram, or alternatively from the maximum principle for elliptic partial differential equations on bounded domains).

We now look at the case when a is negative. Since $g\in L^{\infty }(\overline{{\mathbb {D}}})$, by the generalized maximum principle for elliptic problems (see [18]), if we can find a function $\sigma >0$ on $\overline{{\mathbb {D}}}$ such that $(\Delta -ag)[\sigma ]\le 0$ in ${\mathbb {D}}$, then (9) has at most one solution.

For simplicity of notation, consistency with results in [13, 14], and to make the physical implications easier to see, we will express this $\sigma$ in terms of the variables $({\tilde{X}},{\tilde{Y}})$ in the strip: this can all easily be mapped into the unit disk setting using the change of variables presented at the beginning of this paper.

From [13] we know that a solution to (3) satisfying the asymptotic conditions is the Legendre polynomial (see [1, 2, 16] for more details on such special functions):

$$\begin{aligned} P_l^k(z)=\frac{(-1)^k}{2^l l!}(1-z^2)^{\frac{k}{2}}\frac{d^{k+l}}{dx^{k+l}}(z^2-1)^l, \end{aligned}$$

(13)

where $z=\tanh ({\tilde{X}})$ and $a=-l(l+1)$, $l\in {\mathbb {Z}}$, with l an integer.

For $l=1$, we set $\sigma _1({\tilde{X}})=-\tanh ({\tilde{X}})$ which is strictly positive on $-\infty \le {\tilde{X}}\le {\tilde{X}}_0<0$ and therefore

$$\begin{aligned} \left( \Delta -\frac{a}{\cosh ^2({\tilde{X}})}\right) [\sigma _1]=\Delta \sigma _1+\frac{2}{\cosh ^2({\tilde{X}})}\sigma _1+\frac{(-a-2)}{\cosh ^2({\tilde{X}})}\sigma _1 \end{aligned}$$

(14)

is negative if and only if $a\ge -2$.

For $l=2$, we set $\sigma _2({\tilde{X}})=3\tanh ^2({\tilde{X}})-1$ which is strictly positive for $-\infty \le {\tilde{X}}\le {\tilde{X}}_0\le -0.66$. Similarily as in (14) we get uniqueness for $a\ge -6$.

For $\sigma _3({\tilde{X}})=-\frac{1}{2}(5\tanh ^3({\tilde{X}})-3\tanh ({\tilde{X}}))$ we will require ${\tilde{X}}_0\le -1$ to obtain uniqueness for all $a\ge -12$. For $\sigma _4({\tilde{X}})=\frac{1}{8}(35\tanh ^4({\tilde{X}})-30\tanh ^2({\tilde{X}})+3)$ we will require ${\tilde{X}}_0\le -1.3$ for uniqueness for all $a\ge -20$.

In general, assume that $a\in [-l(l+1),-l(l-1))$ for some integer l. We now seek the associated $\sigma _l$. Notice that for $k=0$, the Legendre polynomial (13) can be expressed as

$$\begin{aligned} \tilde{\sigma _l}=\sum _{j=0}^{l}\begin{pmatrix} n\\ j \end{pmatrix} \begin{pmatrix} n+j\\ j \end{pmatrix} \left( \frac{\tanh ({\tilde{X}}-1)}{2}\right) ^j. \end{aligned}$$

(15)

We denote by ${\tilde{X}}_0^{(l)}$ the largest value of ${\tilde{X}}$ such that $\tilde{\sigma _l}$ has a fixed sign on $(-\infty ,{\tilde{X}}_0^{(l)}]$. If that sign is positive, we define $\sigma _l$ by $\sigma _l=\tilde{\sigma _l}$ and if it is negative, we choose $\sigma _l=-\tilde{\sigma _l}$. We denote by $C_a$ the positive constant such that ${\tilde{X}}_0^{(l)}\le -C_a.$

We therefore notice that the further away from 0 we are, the easier it gets to prove uniqueness. In other words, the further away we are from the Equator, the larger vorticity we can allow. The uniqueness and therefore also the existence of solutions to (9) will depend ${\tilde{X}}_0$.

We now go back to the unit disk setting.

We still need to check the asymptotic condition (7). Notice that the solution u to (9) is radial. Indeed, this can easily be shown using a moving plane argument such as in Sect. 9.5.2 in [11]. As a result, since $u_x(0,0)$ is an odd function of x, which is smooth close to the origin, we get

$$\begin{aligned} u_x(0,0)=u_y(0,0)=0. \end{aligned}$$

This concludes the proof. $\square$

Physical Relevance of the Results

As shown in the previous section, the negative linear vorticities for which we have existence, uniqueness and regularity of solutions depend on ${\tilde{X}}_0$, and in other words, on how far away we are from the Equator. Arctic gyres are located between the North Pole and $84^\circ$N, which is approximately equal to $\frac{14\pi }{15}$.

From our Mercator projection, we therefore have

$$\begin{aligned} {\tilde{X}}_0=-\ln \left[ \tan \left( \frac{14\pi }{30}\right) \right] \approx -2.253. \end{aligned}$$

(16)

Following the process we used in the proof of Theorem 5.1, we notice that

$$\begin{aligned} \sigma _{10}&=\frac{1}{256}(46189\tanh ^{10}({\tilde{X}})-109395\tanh ^8({\tilde{X}})+90090\tanh ^6({\tilde{X}}) \\&\quad -30030\tanh ^4({\tilde{X}})+3465\tanh ^2({\tilde{X}})-63) \end{aligned}$$

which is strictly positive for $-\infty \le {\tilde{X}}\le {\tilde{X}}_0\le -2.17$, and the value of a associated with $\sigma _{10}$ is $a=-110$. (Note that $\sigma _{11}$ already requires that ${\tilde{X}}_0\le -2.255$.)

We now show that we can find an $L^\infty$ bound on u from estimates on $\omega$. Moreover, by estimating F, we then provide some conditions on $a>0$ and b such that the above mentioned $L^\infty$ bound holds. We refer to these values as physically relevant. From the non-dimensionalization described in [5] and recalled [14] the parameter $\omega$, which accounts for the spin vorticity due to the rotation of the Earth, is defined by

$$\begin{aligned} \omega =\frac{\Omega ' R'}{c'}. \end{aligned}$$

Here $\Omega '\simeq 7.29\times 10^{-5}rad.s^{-1}$ is the constant rate of rotation of the Earth (see the discussion in [5]), $R'\simeq 6378$km is the radius of the Earth and $c'\simeq 0.1m.s^{-1}$, the speed scale, is the typical horizontal velocity of large-scale ocean flows [21]. In particular, the typical value of $\omega$ can be calculated to be approximately 4650.

Similarly, as the typical vorticity values for a gyre are of the order of $10^{-5}\mathrm{{rad\,s}}^{-1}$ [3], we get that $F(u)=au+b$ is of order $10^{-4}$ and we can therefore set $|F(u)|\le C_v$, where $C_v>0$ is a constant of order $10^{-4}$.

We use the following weak maximum principle of Aleksandrov (see [12]). Notice that this theorem only holds for $c(x,y):=-ag(x,y)$ negative, which implies that we must choose $a>0$. We will therefore only obtain results for part of the solutions obtained in Theorem 5.1.

Theorem 6.1

Let $\Delta u+c(x,y)u\ge f(x,y)$ with $c<0$, in a bounded domain $\Omega$ and $u\in C^0({\overline{\Omega }})\cap C^2(\Omega )$. Then

$$\begin{aligned} \sup _{\Omega }u\le \sup _{\partial \Omega }u^+ +C\Vert f\Vert _{L^{2}(\Omega )}\le \sup _{\partial \Omega }u^++C(m(\Omega ))^\frac{1}{2} \Vert f\Vert _{L^{\infty }(\Omega )}, \end{aligned}$$

where the constant C only depends on the diameter of $\Omega$ and the dimension of the domain.

In our notation, the domain $\Omega$ is the unit disk ${\mathbb {D}}$ in $\mathbb {R^2}$, where we have $\sup _{\partial {\mathbb {D}}}u=0$ and $c(x,y):=-ag(x,y)$ with $a>0$ and f and g defined as in (10).

The constant C (see [12]) in our case is given by

$$\begin{aligned} C=\text {diam}({\mathbb {D}})\left( e^{\frac{1}{4}}-1\right) ^{\frac{1}{2}}\approx 1.1, \end{aligned}$$

and so we find that

$$\begin{aligned} m({\mathbb {D}})^\frac{1}{2} \Vert f\Vert _{L^{\infty }({\mathbb {D}})}\approx (0,04|b|+0.08\omega )\pi ^ \frac{1}{2} \approx 0.7|b|+7\times 10^2, \end{aligned}$$

since we know from the considerations above that $\omega \simeq 4.7\times 10^{3}$.

As a result, we obtain that

$$\begin{aligned} \Vert u\Vert _{L^{\infty }({\mathbb {D}})}\le 7.8(10^{-2}|b|+10^2). \end{aligned}$$

(17)

We would now like to find conditions on a and b such that the corresponding solution u satisfies (17). Since we know that $|F(u)|\le C_v$, we have $|au+b|\le C_v$ which implies that

$$\begin{aligned} \frac{-C_v-b}{a}\le u \le \frac{C_v-b}{a}. \end{aligned}$$

As a result, we conclude that acceptable values of $a>0$ and $b\in {\mathbb {R}}$ must satisfy

$$\begin{aligned} \frac{-C_v-b}{a}\ge -7.8(10^{-2}|b|+10^2)\qquad \text {and}\qquad \frac{C_v-b}{a}\le 7.8(10^{-2}|b|+10^2). \end{aligned}$$