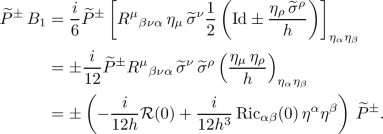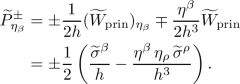Global Propagator for the Massless Dirac Operator and Spectral Asymptotics

Abstract

We construct the propagator of the massless Dirac operator W on a closed Riemannian 3-manifold as the sum of two invariantly defined oscillatory integrals, global in space and in time, with distinguished complex-valued phase functions. The two oscillatory integrals—the positive and the negative propagators—correspond to positive and negative eigenvalues of W, respectively. This enables us to provide a global invariant definition of the full symbols of the propagators (scalar matrix-functions on the cotangent bundle), a closed formula for the principal symbols and an algorithm for the explicit calculation of all their homogeneous components. Furthermore, we obtain small time expansions for principal and subprincipal symbols of the propagators in terms of geometric invariants. Lastly, we use our results to compute the third local Weyl coefficients in the asymptotic expansion of the eigenvalue counting functions of W.

1 Statement of the Problem

Let (M, g) be a connected oriented closed Riemannian 3-manifold. Throughout this paper we denote by $\nabla$ the Levi-Civita connection, by $\Gamma ^\alpha {}_{\beta \gamma }$ the Christoffel symbols and by

$$\begin{aligned} \textstyle \rho (x):=\sqrt{{\det } g_{\alpha \beta }(x)} \end{aligned}$$

(1.1)

the Riemannian density.

Let us clarify straight away why, when dealing with the massless Dirac operator, we restrict our analysis to the 3-dimensional case. The reason is twofold: on the one hand, dimension three is physically meaningful in that it represents the first step towards a potential future analysis of the relativistic 3+1-dimensional setting, and on the other hand, our method requires the eigenvalues of the principal symbol of our operator to be simple, cf. Sect. 3, which is not the case for the massless Dirac operator in higher dimensions.

Let $e_j$, $j=1,2,3$, be a positively oriented global framing, i.e. a set of three orthonormal smooth vector fields¹ whose orientation agrees with the orientation of the manifold. In chosen local coordinates $x^\alpha$, $\alpha =1,2,3$, we will denote by $e_j{}^\alpha$ the $\alpha$-th component of the j-th vector field. Throughout this paper we use Greek letters for holonomic (tensor) indices and Latin for anholonomic (frame) indices. We adopt Einstein’s convention of summation over repeated indices.

Let

$$\begin{aligned} s^1:= \begin{pmatrix} 0&{}1\\ 1&{}0 \end{pmatrix} =s_1 \,, \quad s^2:= \begin{pmatrix} 0&{}-i\\ i&{}0 \end{pmatrix} =s_2 \,, \quad s^3:= \begin{pmatrix} 1&{}0\\ 0&{}-1 \end{pmatrix} =s_3 \end{aligned}$$

(1.2)

be the standard Pauli matrices and let

$$\begin{aligned} \sigma ^\alpha := s^j\,e_j{}^\alpha \end{aligned}$$

(1.3)

be their projection along the framing. The quantity $\sigma ^\alpha$ is a vector-function with values in the space of trace-free Hermitian $2\times 2$ matrices.

Definition 1.1

We call massless Dirac operator the operator

$$\begin{aligned} W:=-i\sigma ^\alpha \left( \! \frac{\partial }{\partial x^\alpha } +\frac{1}{4}\sigma _\beta \left( \! \frac{\partial \sigma ^\beta }{\partial x^\alpha } +\Gamma ^\beta {}_{\alpha \gamma }\,\sigma ^\gamma \! \right) \! \right) :H^1(M;\mathbb {C}^2)\rightarrow L^2(M;\mathbb {C}^2). \end{aligned}$$

(1.4)

Here $H^1$ is the usual Sobolev space of functions which are square integrable together with their first partial derivatives.

In relativistic particle physics the massless Dirac equation is often referred to as the Weyl equation, which explains our notation. Our operator W appears as the result of separating out the time variable in the relativistic Weyl equation, see [19] for details. Henceforth, we refer to the massless Dirac operator simply as the Dirac operator, which conforms with the terminology adopted in differential geometry.

Remark 1.2

The Dirac operator admits several equivalent definitions. The most common is the geometric definition written in terms spinor bundles. Our analytic Definition 1.1 is equivalent to the standard geometric one, see [28, Appendix B].

Definition 1.1 depends on the choice of framing and this issue requires clarification.

Let

$$\begin{aligned} G:M\rightarrow \mathrm {SU}(2) \end{aligned}$$

(1.5)

be an arbitrary smooth special unitary matrix-function and let $\widetilde{W}$ be the Dirac operator corresponding to a given framing. Consider the transformation

$$\begin{aligned} \widetilde{W}\mapsto G^*\widetilde{W}G=:W, \end{aligned}$$

(1.6)

where the star indicates Hermitian conjugation. It turns out that W is also a Dirac operator, only corresponding to a different framing.

Let us now look at the matter the other way round. Suppose that $\widetilde{W}$ and W are two Dirac operators. Does there exist a smooth matrix-function (1.5) such that $W=G^*\widetilde{W}G\,$? If the operators $\widetilde{W}$ and W are in a certain sense ‘close’ then the answer is yes, but in general there are topological obstructions and the answer is no. This motivates the introduction of the concept of spin structure, see [6, 19].

The gauge transformation (1.5), (1.6) is the manifestation, at operator level, of the freedom of pointwise rotating the framing in a smooth way,

$$\begin{aligned} \widetilde{e}_j \mapsto O_j{}^k\, \widetilde{e}_k=:e_j, \qquad O\in C^\infty (M;\mathrm {SO}(3)), \end{aligned}$$

(1.7)

via the double cover

$$\begin{aligned} \mathrm {SU}(2) \overset{2:1}{\rightarrow } \mathrm {SO}(3). \end{aligned}$$

The Dirac operator (1.4) is uniquely determined by the metric and spin structure modulo an $\mathrm {SU}(2)$ gauge transformation.

The Dirac operator is symmetric with respect to the $L^2$ inner product

$$\begin{aligned} \langle u,v\rangle := \int _M u^*v\,\rho \,dx\,, \qquad u,v\in L^2(M;\mathbb {C}^2), \end{aligned}$$

(1.8)

where $dx=dx^1dx^2dx^3$. Furthermore, a simple calculation shows that it is elliptic.²

It is well known that the Dirac operator is self-adjoint and its spectrum is discrete, accumulating to $+\infty$ and to $-\infty$. Let $\lambda _k$ be the eigenvalues of W and $v_k$ the corresponding orthonormal eigenfunctions, $k\in \mathbb {Z}$. The choice of particular enumeration is irrelevant for our purposes, but what is important is that eigenvalues are enumerated with account of their multiplicity. Note that the Dirac operator has the special property that it commutes with the antilinear operator of charge conjugation

$$\begin{aligned} v= \begin{pmatrix} v_1\\ v_2 \end{pmatrix} \mapsto \begin{pmatrix} -\overline{v_2}\\ \overline{v_1} \end{pmatrix} =:\mathrm {C}(v), \end{aligned}$$

see [24, Appendix A] for details, and this implies that eigenvalues have even multiplicity.

Definition 1.3

We define the Dirac propagator as

$$\begin{aligned} U(t) := e^{-itW}. \end{aligned}$$

(1.9)

The Dirac propagator is the (distributional) solution of the hyperbolic Cauchy problem

$$\begin{aligned}&\left( -i\,\frac{\partial }{\partial t} + W \right) U=0\,, \end{aligned}$$

(1.10a)

$$\begin{aligned}&U(0)={\text {Id}}\,. \end{aligned}$$

(1.10b)

It is a time-dependent unitary operator which can written via functional calculus as

$$\begin{aligned} U(t)= \sum _{\lambda _k} e^{-it\lambda _k}\, v_k\, \langle v_k\,,\,\cdot \ \rangle . \end{aligned}$$

(1.11)

The Dirac propagator can be written as a sum of three operators

$$\begin{aligned} U(t)=U^+(t)+U^0+U^-(t) \end{aligned}$$

defined as

$$\begin{aligned}&U^+(t):= \sum _{\lambda _k>0} e^{-it\lambda _k}\, v_k\, \langle v_k\,,\,\cdot \ \rangle , \end{aligned}$$

(1.12a)

$$\begin{aligned}&U^0:= \sum _{\lambda _k=0} v_k\, \langle v_k\,,\,\cdot \ \rangle , \end{aligned}$$

(1.12b)

$$\begin{aligned}&U^-(t):= \sum _{\lambda _k<0} e^{-it\lambda _k}\, v_k\, \langle v_k\,,\,\cdot \ \rangle . \end{aligned}$$

(1.12c)

We call the operators (1.12a), (1.12b) and (1.12c) positive, zero mode and negative propagators, respectively. These are time-dependent partial isometries. Note that the operator $U^0$ is nontrivial only if the Dirac operator has zero modes (i.e. if zero is an eigenvalue).

We define the positive ($+$) and negative (−) local counting functions as

$$\begin{aligned} N_\pm (y,\lambda ):= {\left\{ \begin{array}{ll} 0 &{}{} \text{ for } \lambda \le 0,\\ \sum _{0<\pm \lambda _k<\lambda } [v_k(y)]^* \,v_k(y)&{}{} \text{ for } \lambda >0. \end{array}\right. } \end{aligned}$$

(1.13)

Of course, integration over M gives

$$\begin{aligned} N_\pm (\lambda ) := \int _M N_\pm (y,\lambda )\,\rho (y)\,dy = {\left\{ \begin{array}{ll} 0 &{}{} \text{ for } \lambda \le 0,\\ \sum _{0<\pm \lambda _k<\lambda } 1&{}{} \text{ for } \lambda >0. \end{array}\right. } \end{aligned}$$

(1.14)

The functions (1.14) are the ‘global’ counting functions, the only difference with the usual definition [45] being that we count the positive and negative eigenvalues separately.

Let $\hat{\mu }:\mathbb {R}\rightarrow \mathbb {C}$ be a smooth function such that $\hat{\mu }= 1$ in some neighbourhood of the origin and ${\text {supp}} \hat{\mu }$ is sufficiently small. Here ‘sufficiently small’ means that ${\text {supp}} \hat{\mu }\subset (-T_0,T_0)$, where $T_0$ is the infimum of lengths of all the geodesic loops originating from all the points of the manifold.

Following the notation of [17], we write the Fourier transform as

$$\begin{aligned} \mathcal {F}_{\lambda \rightarrow t}[f](t)=\hat{f}(t)=\int _{-\infty }^{+\infty } e^{-it\lambda } f(\lambda ) \,d\lambda \end{aligned}$$

(1.15)

and the inverse Fourier transform as

$$\begin{aligned} \mathcal {F}_{t\rightarrow \lambda }^{-1}[\hat{f}](\lambda )=f(\lambda )=\dfrac{1}{2\pi }\int _{-\infty }^{+\infty } e^{it\lambda }\hat{f}(t) \,dt. \end{aligned}$$

(1.16)

Accordingly, we put $\mu :=\mathcal {F}^{-1}[\hat{\mu }]$.

It is known [26, 34,35,36, 45] that the mollified derivative of the positive (resp. negative) counting function admits a complete asymptotic expansion in integer powers of $\lambda$:

$$\begin{aligned} (N_\pm '*\mu )(y,\lambda )= c^\pm _{2}(y)\,\lambda ^{2} + c^\pm _{1}(y)\,\lambda + c^\pm _{0}(y) +\dots \quad \text {as} \quad \lambda \rightarrow +\infty . \end{aligned}$$

(1.17)

Here $*$ stands for the convolution in the variable $\lambda$.

Definition 1.4

We call local Weyl coefficients the smooth functions $c^\pm _{k}(y)$ appearing in the asymptotic expansions (1.17).

Remark 1.5

• (i) Our definition of Weyl coefficients does not depend on the choice of mollifier $\mu$. If $\widetilde{\mu }$ is another mollifier with the same support properties, then

  $$\begin{aligned} (N_\pm '*\mu )(y,\lambda )-(N_\pm '*\widetilde{\mu })(y,\lambda )=O(\lambda ^{-\infty })\quad \text {as} \quad \lambda \rightarrow +\infty . \end{aligned}$$

• (ii) Our definition of Weyl coefficients is, in a sense, unusual. The standard convention in the literature is to call local Weyl coefficients the functions appearing in the asymptotic expansion of the mollified counting function $N*\mu \,$, as opposed to its derivative. The two definitions are, effectively, the same up to integrating factors,

  $$\begin{aligned}&{\begin{matrix} (N_\pm *\mu )(y,\lambda )&{}= \int _{-\infty }^\lambda (N_\pm '*\mu )(y,\kappa )\,d\kappa \\ &{}= \frac{1}{3}\, c^\pm _{2}(y)\,\lambda ^{3} + \frac{1}{2}\, c^\pm _{1}(y)\,\lambda ^2 + c^\pm _{0}(y)\,\lambda +\dots \quad \text {as} \quad \lambda \rightarrow +\infty , \end{matrix}} \end{aligned}$$

  (1.18)

  compare (1.17) with (1.18). As a matter of convenience, we will stick with Definition 1.4 throughout this paper.

• (iii) It was shown in [24] that

  $$\begin{aligned} c^\pm _{2}(y)=\frac{1}{2\pi ^2}\,, \qquad c^\pm _{1}(y)=0. \end{aligned}$$

  (1.19)

• (iv) The unmollified counting functions $N_\pm (y,\lambda )$ also admit asymptotic expansions as $\lambda \rightarrow +\infty$, but here the situation is more delicate because these functions are discontinuous and one encounters number-theoretic issues. It is known [23, 24] that

  $$\begin{aligned} N_\pm (y,\lambda ) = \frac{1}{6\pi ^2}\, \lambda ^{3} + O(\lambda ^2) \quad \text {as} \quad \lambda \rightarrow +\infty \end{aligned}$$

  uniformly over $y\in M$ and, furthermore, under appropriate assumptions on geodesic loops,

  $$\begin{aligned} N_\pm (y,\lambda ) = \frac{1}{6\pi ^2}\, \lambda ^{3} + o(\lambda ^2) \quad \text {as} \quad \lambda \rightarrow +\infty . \end{aligned}$$

• (v) An important topic in the spectral theory of first order elliptic systems is the issue of spectral asymmetry [1,2,3,4]. Let us mention that to observe spectral asymmetry for our Dirac operator one as to go as far as the sixth Weyl coefficients. This follows from the fact [12, 31] that the eta function

  $$\begin{aligned} \eta (s):=\sum _{\lambda _k\ne 0}\dfrac{{\text {sgn}} \lambda _k}{|\lambda _k|^s}=\int _0^{+\infty } \lambda ^{-s} (N'_+(\lambda )-N'_-(\lambda ))\,d \lambda \end{aligned}$$

  is holomorphic in the complex half-plane ${\text {Re}}s>-2$ and has its first pole at $s=-2$. The value of the residue of the eta function at $s=-2$, which was computed explicitly by Branson and Gilkey [14], describes the difference

  $$\begin{aligned} \int _M (c^+_{-3}(y)-c^-_{-3}(y))\,\rho (y)\,d y \end{aligned}$$

  between the sixth (global) Weyl coefficients.

Our paper has two main objectives.

Objective 1 Construct the propagators $U^\pm (t)$ explicitly, modulo integral operators with infinitely smooth kernels, and do so as a single invariantly defined oscillatory integral global in space and in time.

Objective 2 Compute the third Weyl coefficient $c^\pm _{0}(y)$.

Remark 1.6

One cannot, in general, identify the third Weyl coefficient by looking at the asymptotic behaviour of the unmollified counting function. In order to illustrate this point, let us consider the 3-torus equipped with standard flat metric. Already in this simple case the mathematical statement

$$\begin{aligned} N_\pm (y,\lambda ) = \frac{1}{6\pi ^2}\, \lambda ^{3} + c^\pm _{0}(y)\,\lambda + o(\lambda ) \quad \text {as} \quad \lambda \rightarrow +\infty \end{aligned}$$

is false. This fact can be established by writing down the eigenvalues explicitly as in [24, Appendix B] and using standard results [32] from analytic number theory.

2 Main Results

The study of Dirac operators in curved space, arguably the most important operators from the point of view of physical applications alongside the Laplacian, has a long and noble history in the mathematical literature. Excellent introductions to the subject can be found in [39] and [30].

Due to the physical significance of the topic, numerous researchers have contributed to our current understanding of the spectrum of Dirac operators on Riemannian manifolds. One can ask, for example, how the eigenvalues behave under perturbations of the metric [13, 25, 28], how the spectrum depends on the spin structure [10], whether zero modes exist [8], et cetera.

Later in this paper we will be concerned with the study of the asymptotic behaviour of large (in modulus) eigenvalues of the Dirac operator on a closed 3-manifold. In the case of scalar elliptic operators, such as for example the Laplace–Beltrami operator, a wide range of classical techniques are available in the literature to compute spectral asymptotics. However, if one is interested in a first order system, whose spectrum is, in general, not semi-bounded, the heat kernel method can no longer be applied, at least in its original form, and even resolvent techniques require major modification [7]. A very natural approach in this case is the so-called wave method, going back to Levitan [40] and Avakumovic [5], which involves recovering information about the eigenvalue counting function from the behaviour of the wave propagator, see (1.11). How this can be done will be explained in greater detail later on. This partly motivates our interest in the Dirac propagator (1.9), which is also of interest on its own. Of course, the hyperbolic Cauchy problem (1.10) for W lies at the heart of relevant applications in theoretical physics (e.g., the mathematical description of neutrinos/antineutrinos in curved space).

In order to construct the propagator (1.9) precisely, one needs to know all eigenvalues and eigenfunctions of W, which is unrealistic for a generic Riemannian manifold. However, microlocal techniques allow one to construct the propagator (1.9) approximately, modulo an integral operator with smooth integral kernel. This fact is well-known and an extensive discussion can be found, for instance, in [33].

There are, however, several issues with this classical construction: (i) it is not invariant under changes of local coordinates, (ii) it is local in space and (iii) it is local in time. The last issue, locality in time, is especially serious: it is to do with obstructions associated with caustics. In practice, constructing a propagator locally in time means that for large times one has to use compositions

$$\begin{aligned} U(t)=U(t-t_j)\circ U(t_j -t_{j-1})\circ \cdots \circ U(t_2 -t_1)\circ U(t_1). \end{aligned}$$

The propagator U(t) is a special case of a Fourier integral operator and it is known that handling compositions of such operators is a daunting task.

Our goal is to construct the Dirac propagator explicitly, in a global—i.e., as a single oscillatory integral—and invariant (under change of coordinates and gauge transformations) fashion. The key idea, originally proposed by Laptev, Safarov and Vassiliev in [38] and further developed in [45], is to use Fourier integral operators with complex-valued, as opposed to real valued, phase function. Crucially, this allows one to circumvent the topological obstructions due to caustics.

Our work partly builds upon [23] and [24]. In [23], using the wave method, Chervova, Downes and Vassiliev obtained an explicit formula for the second Weyl coefficient of an elliptic self-adjoint first order pseudodifferential matrix operator, fixing thirty years of incorrect or incomplete publications in the subject, see [23, Sect. 11]. In [24] the same authors applied the results from [23] to the Dirac operator. Unlike the current paper, the approach from [23] is not geometric in nature and the complexity of phase functions is not actually put to use. Note that some results from [24] were improved by Strohmaier and Li in [41], where the authors studied the second term of the mollified spectral counting function of Dirac type operators and characterised operators in this class with vanishing second Weyl coefficient.

A fully geometric global construction of the (scalar) wave propagator $e^{-it \sqrt{-\Delta }}$ on closed Riemannian manifolds, as a single oscillatory integral with complex-valued phase function, was recently proposed by the authors and Levitin in [17], and subsequently extended to the Lorentzian setting in [16]. The publication [17] is the starting point of the current paper. The extension of the results of the current paper to globally hyperbolic Lorentzian manifolds is carried out in [18].

Our main results are as follows.

• 1. We present a global construction of each of the two propagators, the positive propagator $U^+(t)$ and the negative propagator $U^-(t)$, as a single invariantly defined oscillatory integral, global in space and in time, with distinguished complex-valued phase function (Theorem 3.3, Definition 5.1, Definition 5.3). We provide a closed formula for the principal symbols of the propagators (Theorem 6.1) and an algorithm for the calculation of the subprincipal symbols and all asymptotic components of lower degree of homogeneity in momentum (Sect. 3.3).

• 2. We give an explicit small time expansion of principal and subprincipal symbols of positive and negative propagators in terms of geometric invariants (Theorem 7.13).

• 3. We compute the third local Weyl coefficients in the asymptotic expansion of the two eigenvalue counting functions (1.13) (Theorem 8.1).

Along the way we prove a number of results about general first order elliptic systems and invariant representations of pseudodifferential operators on manifolds. Note that the third Weyl coefficients can, in principle and with some work, be also obtained by a different method using results available in the literature, see Remark 8.3.

Our paper is structured as follows.

In Sect. 3 we explain how to construct explicitly positive and negative propagators for a general first order elliptic self-adjoint (pseudo)differential matrix operator, with a rigorous mathematical justification.

In Sect. 4 we deal with the delicate issue of invariant descriptions of pseudodifferential operators acting on scalar functions. In particular, we examine the relation between our g-subprincipal symbol and the standard notion of subprincipal symbol for operators acting on half-densities.

In Sect. 5 we apply the results from Sect. 3 to the Dirac operator. A formula for the principal symbol of positive and negative Dirac propagators is provided in Sect. 6, whereas small time expansions for principal and subprincipal symbols of positive and negative propagators are obtained in Sect. 7. Our final results are expressed in terms of geometric invariants: curvature of the Levi-Civita connection associated with the metric g and torsion of the Weitzenböck connection generated by the framing defining the Dirac operator.

In Sect. 8 we use the results from Sect. 7 to compute the third local Weyl coefficients for the Dirac operator.

Finally, in Sect. 9 we apply our techniques to two explicit examples: $M=\mathbb {S}^3$, where formulae are isotropic in momentum, and $M=\mathbb {S}^2 \times \mathbb {S}^1$, where they are not.

The paper is complemented by two appendices, containing background material and technical proofs.

3 Preliminary Results for General First Order Systems

In this section we will consider a broader class of first order systems and we will prove fairly general results, which will be later applied to the special case of the Dirac operator. In doing so, we will need some of the technology developed in [23]. The setting of our analysis is somewhat different from that in [23], in that our operators are differential, as opposed to pseudodifferential (see also Remark 3.11), and act on scalar functions on a Riemannian manifold, as opposed to half-densities on a manifold with no metric structure. In particular, the change of the space in which the operator acts raises delicate issues concerning the invariance of the mathematical objects involved. For these reasons we provide here a modified version of some of the results from [23], adapted to the setting of our paper.

Throughout this section, M will be a smooth connected closed Riemannian manifold of dimension $d\ge 2$.

Let A be an elliptic symmetric (with respect to (1.8)) first order $m\times m$ matrix differential operator acting on m-columns of smooth complex-valued scalar functions $v\in C^\infty (M;\mathbb {C}^m)$ and let $A_\mathrm {prin}: T'M \rightarrow \mathrm {Herm}(m,\mathbb {C})$ be the principal symbol of A, where $T'M:=T^*M\setminus \{0\}$ and $\mathrm {Herm}(m,\mathbb {C})$ is the real vector space of $m\times m$ Hermitian matrices.

We denote by $h^{(j)}(x,\xi )$ the eigenvalues of $A_\mathrm {prin}(x,\xi )$ enumerated in increasing order, with positive index $j=1,2,\ldots , m^+$ for positive $h^{(j)}(x,\xi )$ and negative index $j=-1,-2,\ldots , -m^-$ for negative $h^{(j)}(x,\xi )$. We assume that the eigenvalues of the principal symbol $A_\mathrm {prin}$ are simple. Clearly, $m=m^++m^-$, because the ellipticity condition $\det A_\mathrm {prin}(x,\xi )\ne 0$ ensures that all eigenvalues are nonzero. In fact, as our operator is differential, one can show [29, Remark 2.1] that m can only be even and that we have

$$\begin{aligned} m^+=m^-=\frac{m}{2}\,. \end{aligned}$$

(3.1)

Furthermore, the eigenvalues $h^{(j)}$ of the principal symbol and the corresponding normalised eigenvectors $v^{(j)}$ possess the symmetry

$$\begin{aligned} h^{(-j)}(x,\xi )=-h^{(j)}(x,-\xi ), \quad v^{(-j)}(x,\xi )=v^{(j)}(x,-\xi ), \qquad j=1,\ldots ,\frac{m}{2}\,.\nonumber \\ \end{aligned}$$

(3.2)

Under the above assumptions the spectrum of A is discrete and accumulates to $+\infty$ and to $-\infty$. We denote eigenvalues and orthonormalised (smooth) eigenfunctions of A by $\lambda _k$ and $v_k$, respectively, enumerated with account of their multiplicity.

By replacing W with A, one can define the ‘full’ propagator $U_A(t)$ for A via (1.11), as well as the positive, zero mode and negative propagators via (1.12a)–(1.12c), which we denote by $U^+_A(t)$, $U^0_A$ and $U^-_A(t)$, respectively.

Each eigenvalue $h^{(j)}(x,\xi )$ of the principal symbol can be interpreted as a Hamiltonian on the cotangent bundle. The corresponding Hamiltonian flow $(x^{(j)}(t;y,\eta ), \xi ^{(j)}(t;y,\eta ))$, i.e. the (global) solution to Hamilton’s equations

$$\begin{aligned} \dot{x}^{(j)}=h_\xi ^{(j)}(x^{(j)},\xi ^{(j)}), \qquad \dot{\xi }^{(j)}=-h_x^{(j)}(x^{(j)},\xi ^{(j)}) \end{aligned}$$

with initial condition $(x^{(j)}(0;y,\eta ),\xi ^{(j)}(0;y,\eta ))=(y,\eta )$, generates a Lagrangian manifold to which one can, in turn, associate a global Lagrangian distribution. See [17, Sect. 2] and references therein for details. In particular, the singularities of the solution to the initial value problem

$$\begin{aligned} (-i \partial _t+A)v=0, \qquad \left. v\right| _{t=0}=v_0 \end{aligned}$$

(3.3)

propagate along Hamiltonian trajectories generated by the eigenvalues of $A_\mathrm {prin}$.

3.1 Positive and Negative Propagators: An Abstract Approach

Our aim is to show that $U^+_A(t)$ and $U^-_A(t)$ can be separately approximated by a finite sum of global oscillatory integrals. Before doing so, let us state and prove an abstract preparatory theorem.

Notation 3.1

Let

$$\begin{aligned} v\in C^\infty (\mathbb {R}\times M_x\times M_y), \qquad (\lambda ,x,y)\mapsto v(\lambda ,x,y). \end{aligned}$$

We write

$$\begin{aligned} v=O(|\lambda |^{-\infty }) \quad \text {as }\lambda \rightarrow \pm \infty \end{aligned}$$

if for every $\alpha >0$, every $k\in \mathbb {N}$ and every linear partial differential operator P with infinitely smooth coefficients of order k on $M_x\times M_y$ there exists a positive constant $C_{\alpha ,P}$ such that

$$\begin{aligned} |P v|\le C_{\alpha ,P}\, |\lambda |^{-\alpha } \quad \text {for} \ \, \pm \lambda >1\,, \end{aligned}$$

uniformly over $M_x\times M_y\,$.

Theorem 3.2

Let $(T_-,T_+)\subseteq \mathbb {R}$ be an open interval (possibly, the whole real line) and let $u^+(t,x,y)$, $u^-(t,x,y)$, $\widetilde{u}^+(t,x,y)$ and $\widetilde{u}^-(t,x,y)$ be elements of $C^\infty (M_x\times M_y; \mathcal {D}'(T_-,T_+))$, satisfying

• (a) $u^+(t,x,y)+u^-(t,x,y)=\widetilde{u}^+(t,x,y)+\widetilde{u}^-(t,x,y) \mod C^\infty ((T_-,T_+)\times M_x\times M_y)\,$.

Furthermore, assume that for every $\zeta \in C^\infty _0(T_-,T_+)$ we have

• (b) $\mathcal {F}^{-1}_{t\rightarrow \lambda }[\zeta \,u^\pm ]=O(|\lambda |^{-\infty }) \quad \text {as }\lambda \rightarrow \mp \infty$,

• (c) $\mathcal {F}^{-1}_{t\rightarrow \lambda }[\zeta \,\widetilde{u}^\pm ]=O(|\lambda |^{-\infty }) \quad \text {as }\lambda \rightarrow \mp \infty$.

Then

$$\begin{aligned} u^\pm (t,x,y)=\widetilde{u}^\pm (t,x,y) \mod C^\infty ((T_-,T_+)\times M_x\times M_y). \end{aligned}$$

(3.4)

Proof

Let $\zeta \in C_0^\infty (T_-,T_+)$. Multiplying (a) by $\zeta (t)$ we get

$$\begin{aligned}&\zeta (t)\,u^+(t,x,y)+\zeta (t)\,u^-(t,x,y)=\zeta (t)\,\widetilde{u}^+(t,x,y)+\zeta (t)\,\widetilde{u}^-(t,x,y) \nonumber \\&\quad \mod C_0^\infty (\mathbb {R}\times M_x\times M_y). \end{aligned}$$

(3.5)

Applying the inverse Fourier transform $\mathcal {F}^{-1}_{t\rightarrow \lambda }$ to (3.5), letting $\lambda \rightarrow +\infty$ and using assumptions (b) and (c) we obtain

$$\begin{aligned} \mathcal {F}^{-1}_{t\rightarrow \lambda }[\zeta \,u^+]=\mathcal {F}^{-1}_{t\rightarrow \lambda }[\zeta \,\widetilde{u}^+]+O(|\lambda |^{-\infty })\quad \text {as }\lambda \rightarrow +\infty . \end{aligned}$$

(3.6)

Here, when dealing with the remainder from (3.5), we used the fact that the Fourier transform of a compactly supported smooth function is rapidly decreasing. The compactness of M ensures a uniform estimate in the spatial variables.

Furthermore, (b) and (c) immediately imply

$$\begin{aligned} \mathcal {F}^{-1}_{t\rightarrow \lambda }[\zeta \,u^+]=\mathcal {F}^{-1}_{t\rightarrow \lambda }[\zeta \,\widetilde{u}^+]+O(|\lambda |^{-\infty })\quad \text {as }\lambda \rightarrow -\infty . \end{aligned}$$

(3.7)

Combining (3.6) and (3.7) we arrive at

$$\begin{aligned} \mathcal {F}^{-1}_{t\rightarrow \lambda }[\zeta \,(u^+-\widetilde{u}^+)] = O(|\lambda |^{-\infty })\quad \text {as }|\lambda |\rightarrow +\infty , \end{aligned}$$

which implies

$$\begin{aligned} \zeta \,(u^+-\widetilde{u}^+)\in C^\infty (\mathbb {R}\times M_x\times M_y). \end{aligned}$$

As $\zeta \in C^\infty _0(T_-,T_+)$ in the above formula is arbitrary, we conclude that

$$\begin{aligned} u^+-\widetilde{u}^+\in C^\infty ((T_-,T_+)\times M_x\times M_y). \end{aligned}$$

A similar argument gives

$$\begin{aligned} u^--\widetilde{u}^- \in C^\infty ((T_-,T_+)\times M_x\times M_y). \nonumber \\ \end{aligned}$$

$\square$

3.2 Construction of Positive and Negative Propagators

Theorem 3.3

Let A be an elliptic self-adjoint first order pseudodifferential operator acting on m-columns of scalar functions over M, whose principal symbol has simple eigenvalues. The positive and negative propagators $U^+_A(t)$ and $U^-_A(t)$ can be written, modulo an infinitely smoothing operator, as a finite sum of oscillatory integrals, global in space and in time. More precisely, we have

$$\begin{aligned}&U^+_A(t)\overset{\mod \Psi ^{-\infty }}{=}\sum _{j=1}^{m^+} U^{(j)}_A(t), \end{aligned}$$

(3.8)

$$\begin{aligned}&U^-_A(t)\overset{\mod \Psi ^{-\infty }}{=}\sum _{j=1}^{m^-} U^{(-j)}_A(t), \end{aligned}$$

(3.9)

where

$$\begin{aligned}&U^{(j)}_A(t):=\frac{1}{(2\pi )^d}\int _{T'M} e^{i\varphi ^{(j)}(t,x;y,\eta )}\,\mathfrak {a}^{(j)}(t;y,\eta ) \nonumber \\&\quad \chi ^{(j)}(t,x;y,\eta )\,w^{(j)}(t,x;y,\eta )\,\left( \,\cdot \,\right) \rho (y)\,dy\,d\eta \end{aligned}$$

(3.10)

and

• by $\overset{\mod \Psi ^{-\infty }}{=}$ we mean that the operator on the LHS is equal to the operator on the RHS up to an integral operator with infinitely smooth integral kernel;

• $\left( \,\cdot \,\right)$ is meant for insertion of $f_0(y)$ when computing $(U^{(j)}_Af_0)(x)$;

• the phase function $\varphi ^{(j)}\in C^\infty (\mathbb {R}\times M\times T'M; \mathbb {C})$ satisfies

  • (i) $\left. \varphi ^{(j)}\right| _{x=x^{(j)}}=0$,

  • (ii) $\left. \varphi ^{(j)}_{x^\alpha }\right| _{x=x^{(j)}}=\xi ^{(j)}_\alpha$,

  • (iii) $\left. \det \varphi ^{(j)}_{x^\alpha \eta _\beta }\right| _{x=x^{(j)}}\ne 0$,

  • (iv) ${\text {Im}} \varphi ^{(j)}\ge 0$;

• the symbol $\mathfrak {a}^{(j)}\in \mathrm {S}_{\mathrm {ph}}^0(\mathbb {R}\times T'M;\mathrm {Mat}(m;\mathbb {C}))$ is an element in the class of polyhomogeneous symbols of order zero with values in $m\times m$ complex matrices, which means that $\mathfrak {a}^{(j)}$ admits an asymptotic expansion in components positively homogeneous in momentum,

  $$\begin{aligned} \mathfrak {a}^{(j)}(t;y,\eta )\sim \sum _{k=0}^{+\infty } \mathfrak {a}^{(j)}_{-k}(t;y,\eta ), \qquad \mathfrak {a}^{(j)}_{-k}(t;y,\alpha \,\eta )=\alpha ^{{-k}}\, \mathfrak {a}^{(j)}_{-k}(t;y,\eta ), \quad \forall \alpha >0;\nonumber \\ \end{aligned}$$

  (3.11)

• the function $\chi ^{(j)}\in C^\infty (\mathbb {R}\times M \times T'M)$ is a cut-off satisfying

  • (I) $\chi ^{(j)}(t,x;y,\eta )=0$ on $\{(t,x;y,\eta ) \,|\, |h^{(j)}(y,\eta )|\le 1/2\}$,

  • (II) $\chi ^{(j)}(t,x;y,\eta )=1$ on the intersection of $\{(t,x;y,\eta ) \,|\, |h^{(j)}(y,\eta )| \ge 1\}$ with some conical neighbourhood of $\{(t,x^{(j)}(t;y,\eta );y,\eta ) \}$,

  • (III) $\chi ^{(j)}(t,x;y,\alpha \, \eta )=\chi ^{(j)}(t,x;y,\eta )$ for $\alpha \ge 1$ on

    $$\begin{aligned}\{ (t,x;y,\eta ) \, | \, |h^{(j)}(y,\eta )|\ge 1 \};\end{aligned}$$

• the weight $w^{(j)}$ is defined by

  $$\begin{aligned} w^{(j)}(t,x;y,\eta ):= [\rho (x)\,\rho (y)]^{-\frac{1}{2}} \left[ {\det }^2( \varphi ^{(j)}_{x^\alpha \eta _\beta }) \right] ^\frac{1}{4}, \end{aligned}$$

  (3.12)

  where the smooth branch of the complex root is chosen in such a way that

  $$\begin{aligned} w^{(j)}(0,y;y,\eta )=[\rho (y)]^{-1}. \end{aligned}$$

Remark 3.4

Note that the weight $w^{(j)}$ is the inverse of a smooth density in the variable y and a smooth scalar function in all other variables. The powers of the Riemannian density $\rho$ in (3.12) are chosen in such a way that the symbol $\mathfrak {a}^{(j)}$ and the integral kernel

$$\begin{aligned}&u^{(j)}(t,x,y):=\frac{1}{(2\pi )^d}\int _{T'_yM} e^{i \varphi ^{(j)}(t,x;y,\eta )}\,\mathfrak {a}^{(j)}(t;y,\eta )\,\nonumber \\&\quad \chi ^{(j)}(t,x;y,\eta )\,w^{(j)}(t,x;y,\eta )\,d\eta \end{aligned}$$

(3.13)

of the operator (3.10) are scalar functions in all variables. The fact that the symbol is a genuine scalar function on $\mathbb {R}\times T'M$ is a crucial feature of our construction.

Taking the square and then extracting the fourth root in (3.12) serves the purpose of making the weight invariant under inversion of a single coordinate $x^\alpha$ or a single coordinate $y^\alpha$. Note, however, that if one works on an orientable and oriented manifold, then one can simplify (3.12) to read

$$\begin{aligned} w^{(j)}(t,x;y,\eta )= [\rho (x)\,\rho (y)]^{-\frac{1}{2}} \left[ {\det }\varphi ^{(j)}_{x^\alpha \eta _\beta }\right] ^\frac{1}{2}. \end{aligned}$$

Remark 3.5

The existence of a phase function satisfying conditions (i)–(iv) is a nontrivial matter. In fact, the space of phase function satisfying these conditions is nonempty and path-connected, see [38, Lemmata 1.4 and 1.7].

Remark 3.6

Let us emphasise that a phase function $\varphi ^{(j)}$ satisfying conditions (i)–(iv) from Theorem 3.2 automatically satisfies

$$\begin{aligned} \varphi ^{(j)}_t(t,x^{(j)};y,\eta )+h^{(j)}(x^{(j)},\xi ^{(j)})=0, \end{aligned}$$

(3.14)

see, e.g., [45, Sect. 2.4.1]. The equation

$$\begin{aligned} \varphi ^{(j)}_t(t,x;y,\eta )+h^{(j)}(x,\nabla \varphi ^{(j)}(t,x;y,\eta ))=0 \end{aligned}$$

(3.15)

is known in the literature as eikonal equation. Note that when $x=x^{(j)}(t;y,\eta )$ formula (3.15) turns into (3.14). In the classical approach to the construction of hyperbolic propagators, (3.15) is required to be satisfied in some open neighbourhood of

$$\begin{aligned} \{(t,x;y,\eta )\in \mathbb {R}\times M \times T'M \ |\ x=x^{(j)}(t;y,\eta )\}. \end{aligned}$$

(3.16)

This is a fundamental difference with the approach adopted in the current paper, where (3.15) is only required to be satisfied ‘along the Hamiltonian flow’, i.e., one only needs (3.14). Indeed, there is no open neighbourhood of (3.16) where the special phase functions that will be introduced and used in Sect. 5—the Levi-Civita phase functions—satisfy (3.15). Relaxing the requirements on our phase functions is needed in order to accommodate an imaginary part and, consequently, circumvent obstructions arising from caustics.

Proof of Theorem 3.3

Suppose that we have constructed the symbols $\mathfrak {a}^{(j)}$ appearing in the oscillatory integrals (3.10) so that

$$\begin{aligned} \widetilde{U}_A(t):= \sum _jU^{(j)}_A(t) = \sum _{j=1}^{m^+} U^{(j)}_A(t) + \sum _{j=1}^{m^-} U^{(-j)}_A(t) \end{aligned}$$

(3.17)

satisfies

$$\begin{aligned}&\left( -i\,\frac{\partial }{\partial t} + A \right) \widetilde{U}_A(t)\overset{\mod \Psi ^{-\infty }}{=}0\,, \end{aligned}$$

(3.18a)

$$\begin{aligned}&\widetilde{U}_A(0)\overset{\mod \Psi ^{-\infty }}{=} \mathrm {Id}\,. \end{aligned}$$

(3.18b)

How to achieve this will be explained in Sect. 3.3.

Put

$$\begin{aligned}&\widetilde{u}^+(t,x,y):= \sum _{j=1}^{m^+}u^{(j)}(t,x,y),\\&\widetilde{u}^-(t,x,y):= \sum _{j=1}^{m^-}u^{(-j)}(t,x,y), \end{aligned}$$

so that the Schwartz kernel of the operator $\widetilde{U}_A(t)$ reads

$$\begin{aligned} \widetilde{u}(t,x,y) = \widetilde{u}^+(t,x,y) + \widetilde{u}^-(t,x,y). \end{aligned}$$

Let u(t, x, y), $u^+(t,x,y)$ and $u^-(t,x,y)$ be the Schwartz kernels of the operators $U_A(t)$, $U^+_A(t)$, and $U^-_A(t)$, respectively.

Formulae (3.18a) and (3.18b) imply

$$\begin{aligned} u(t,x,y)=\widetilde{u}(t,x,y) \mod C^\infty (\mathbb {R}\times M_x\times M_y;\mathrm {Mat}(m,\mathbb {C})). \end{aligned}$$

(3.19)

This fact can be established as follows.

Let

$$\begin{aligned} u_\infty (t,x,y):=u(t,x,y)-\widetilde{u}(t,x,y). \end{aligned}$$

From the construction algorithm, we know that

$$\begin{aligned}&\left[ \left( -i\,\frac{\partial }{\partial t} + A^{(x)} \right) u_\infty \right] (t,x,y) = f(t,x,y), \end{aligned}$$

(3.20)

$$\begin{aligned}&u_\infty (0,x,y) = \zeta (x,y), \end{aligned}$$

(3.21)

where $f\in C^\infty (\mathbb {R}\times M_x\times M_y;\mathrm {Mat}(m,\mathbb {C}))$ and $\zeta \in C^\infty (M_x\times M_y;\mathrm {Mat}(m,\mathbb {C}))$. Here the superscript in $A^{(x)}$ indicates that the differential operator A acts in the variable x. Using functional calculus, we can write the functions $u_\infty$, f and $\zeta$ in terms of the eigenfunctions of A as

$$\begin{aligned} u_\infty (t,x,y)= & {} \sum _{j,k}a_{jk}(t)\,v_j(x)\,[v_k(y)]^*, \end{aligned}$$

(3.22)

$$\begin{aligned} f(t,x,y)= & {} \sum _{j,k}b_{jk}(t)\,v_j(x)\,[v_k(y)]^*, \end{aligned}$$

(3.23)

$$\begin{aligned} \zeta (x,y)= & {} \sum _{j,k}c_{jk}\,v_j(x)\,[v_k(y)]^*. \end{aligned}$$

(3.24)

Here the smooth functions $b_{jk}$ and the constants $c_{jk}$ are given, whereas the functions $a_{jk}$ are our unknowns. Substituting (3.22)–(3.24) into (3.20), (3.21) we obtain the family of first order ODEs

$$\begin{aligned}&\left[ \left( -i\,\frac{d}{d t} + \lambda _j \right) a_{jk} \right] (t) = b_{jk}(t),\\&\quad a_{jk}(0) = c_{jk}, \end{aligned}$$

whose solutions are

$$\begin{aligned} a_{jk}(t) = e^{-i\lambda _jt} \left( c_{jk} +i \int _0^t e^{i\lambda _js} \,b_{jk}(s)\,ds \right) . \end{aligned}$$

(3.25)

Let $\widehat{\zeta }$ be the operator with integral kernel $\zeta (x,y)$,

$$\begin{aligned} \widehat{\zeta }: \ v(x)\mapsto \int _M\zeta (x,y)\,v(y)\,\rho (y)\,dy\,. \end{aligned}$$

Then

$$\begin{aligned} c_{jk} = \langle v_j,\widehat{\zeta }v_k\rangle = \frac{1}{\lambda _j^l\lambda _k^n} \langle A^l v_j,\widehat{\zeta }A^n v_k\rangle = \frac{1}{\lambda _j^l\lambda _k^n} \langle v_j,(A^l\widehat{\zeta }A^n)v_k\rangle . \quad \end{aligned}$$

(3.26)

The operator $A^l\widehat{\zeta }A^n$ is a pseudodifferential operator of order $-\infty$, so formula (3.26) and the fact that $\lambda _k \sim k^{1/d}$ when $k\rightarrow \infty$ allow one to conclude that the $c_{jk}$ decay faster than any power of j and k as $j,k\rightarrow \infty$. A similar argument shows that the $b_{jk}(t)$ and their time derivatives decay faster than any power of j and k as $j,k\rightarrow \infty$ uniformly over any bounded open interval in $\mathbb {R}$. Formula (3.25) now tells us that the same is true for the $a_{jk}(t)$. This, in turn, implies that the series on the RHS of (3.22) defines a function $u_\infty (t,x,y)$ which is smooth in all variables. So we arrive at (3.19), which gives us assumption (a) in Theorem 3.2 with $(T_-,T_+)=\mathbb {R}$.

Resorting to standard stationary phase arguments—see, e.g., [45, Appendix C]—and using the properties (i)–(iv) of our phase functions, it is easy to see that ${u}^\pm$ and $\widetilde{u}^\pm$ satisfy assumptions (b) and (c) of Theorem 3.2. Hence, Theorem 3.2 gives us (3.8) and (3.9).

The fact that the construction is global in time is guaranteed by [38, Lemma 1.2].$\square$

Remark 3.7

If one is prepared to give up globality in time, Theorem 3.3 and the corresponding proof can be adapted in a straightforward manner to the more customary case of real-valued—as opposed to complex-valued—phase functions. This is achieved by prescribing the phase functions to take values in $\mathbb {R}$, dropping condition (iv) and replacing everywhere in the statement and in the proof the time domain $\mathbb {R}$ with the interval $(T_-,T_+)$, where

$$\begin{aligned} T_+:= & {} \min _j\,\inf \{t>0\,|\,\left. \det \varphi ^{(j)}_{x^\alpha \eta _\beta }\right| _{x=x^{(j)}}=0,\ (y,\eta )\in T'M\}\,, \end{aligned}$$

(3.27)

$$\begin{aligned} T_-:= & {} \max _j\,\sup \{t<0\,|\,\left. \det \varphi ^{(j)}_{x^\alpha \eta _\beta }\right| _{x=x^{(j)}}=0,\ (y,\eta )\in T'M\}\,. \end{aligned}$$

(3.28)

The values of $T_\pm$ depend on the choice of particular real-valued phase functions, but we always have $T_-<0<T_+\,$. Observe that Theorem 3.2 was formulated in such a way that it covers both the case of real-valued and complex-valued phase functions.

The reader will have noticed that the zero mode propagator $U^0_A$ does not appear in our construction. This is due to the fact that, clearly,

$$\begin{aligned} U^0_A\overset{\mod \Psi ^{-\infty }}{=}0. \end{aligned}$$

We end this subsection with the observation that, thanks to the presence of the weight $w^{(j)}$ in formula (3.10), the scalar matrix-function $\mathfrak {a}^{(j)}_0$ does not depend on the choice of the phase functions $\varphi ^{(j)}$. This motivates the following definition.

Definition 3.8

We call $\mathfrak {a}^{(j)}_0$ the principal symbol of the Fourier integral operator (3.10).

The above definition agrees with the standard definition of principal symbol of a Fourier integral operator expressed as a section of the Keller–Maslov bundle, see [38, Sect. 2.4].

3.3 The Algorithm

The integral kernel (3.13) of $U^{(j)}_A(t)$ can be constructed explicitly as follows.

Step 1. Choose a phase function $\varphi ^{(j)}$ compatible with Theorem 3.3. We will see later on that for the special case of the Dirac operator we can identify a distinguished phase function, the Levi-Civita phase function. Furthermore, set $\chi ^{(j)}\equiv 1$. In fact, the purpose of the cut-off is to localise integration in a neighbourhood of the $h^{(j)}$-flow and away from the zero section: different choices of $\chi ^{(j)}$ result in oscillatory integrals differing by an infinitely smooth function.

Step 2. Act with the operator $-i \partial _t+A^{(x)}$ on the oscillatory integral (3.13). This produces a new oscillatory integral

$$\begin{aligned} \frac{1}{(2\pi )^d}\int _{T'_yM} e^{i \varphi ^{(j)}(t,x;y,\eta )}\,a^{(j)}(t,x;y,\eta ) \,w^{(j)}(t,x;y,\eta )\,d\eta \end{aligned}$$

(3.29)

whose amplitude $a^{(j)}\in C^\infty (\mathbb {R}\times M \times T'M;\mathrm {Mat}(m,\mathbb {C}))$ is given by

$$\begin{aligned} a^{(j)}:=e^{-i \varphi ^{(j)}} [w^{(j)}]^{-1} \left( -i\partial _t+A^{(x)}\right) \left( e^{i \varphi ^{(j)}}\,\mathfrak {a}^{(j)} \,w^{(j)} \right) . \end{aligned}$$

By making use of the fact that $\varphi ^{(j)}$ and $w^{(j)}$ are positively homogeneous in momentum $\eta$ of degree 1 and 0, respectively, one can write down an asymptotic expansion for the amplitude $a^{(j)}$ in components positively homogeneous in momentum:

$$\begin{aligned}&a^{(j)}(t,x;y,\eta )\sim \sum _{k=-1}^{+\infty } a^{(j)}_{-k}(t,x;y,\eta ),\\&a^{(j)}_{-k}(t,x;y,\alpha \,\eta )=\alpha ^{-k}\, a^{(j)}_{-k}(t,x;y,\eta ), \quad \forall \alpha >0. \end{aligned}$$

Step 3. As $u^{(j)}(t,x,y)$ is to be the (distributional) solution of the hyperbolic equation

$$\begin{aligned} (-i \partial _t +A^{(x)})u^{(j)}(t,x,y)\overset{\mod C^\infty }{=}0, \end{aligned}$$

one would like to impose the condition $a^{(j)}(t,x,y,\eta )=0$. However, the amplitude $a^{(j)}$, unlike the symbol $\mathfrak {a}^{(j)}$, depends on x, and doing so would result in an unsolvable system of partial differential equations (PDEs). The current step consists in excluding the dependence of $a^{(j)}$ on x by means of a procedure known as reduction of the amplitude, to the end of reducing the system of PDEs to a system of ordinary differential equations instead.

Put³

$$\begin{aligned} L^{(j)}_\alpha :=\left[ (\varphi ^{(j)}_{x\eta })^{-1}\right] _\alpha {}^\beta \,\dfrac{\partial }{\partial x^\beta } \end{aligned}$$

and define

$$\begin{aligned}&\mathfrak {S}_0^{(j)}:=\left. \left( \,\cdot \, \right) \right| _{x=x^{(j)}}\,, \end{aligned}$$

(3.30a)

$$\begin{aligned}&\mathfrak {S}_{-k}^{(j)}:=\mathfrak {S}_0^{(j)} \left[ i \, [w^{(j)}]^{-1} \frac{\partial }{\partial \eta _\beta }\, w^{(j)} \left( 1+ \sum _{1\le |\varvec{\alpha }|\le 2k-1} \dfrac{(-\varphi ^{(j)}_\eta )^{\varvec{\alpha }}}{\varvec{\alpha }!\,(|\varvec{\alpha }|+1)}\,L^{(j)}_{\varvec{\alpha }} \right) L^{(j)}_\beta \right] ^k\,,\nonumber \\ \end{aligned}$$

(3.30b)

where $\varvec{\alpha }\in \mathbb {N}^d$, $|\varvec{\alpha }|=\sum _{j=1}^d \alpha _j$ and $(-\varphi ^{(j)}_\eta )^{\varvec{\alpha }}:=(-1)^{|\varvec{\alpha }|}\, (\varphi ^{(j)}_{\eta _1})^{\alpha _1}\dots ( \varphi ^{(j)}_{\eta _d})^{\alpha _d}$. The operator (3.30b) is well defined, because the differential operators $L^{(j)}_\alpha$ commute [17, Lemma A.2]. Furthermore, the operators $\mathfrak {S}^{(j)}_{-k}$ are invariant under change of local coordinates x and y.

Remark 3.9

Let $f:\mathbb {R}^d\rightarrow \mathbb {R}^d$, $x\mapsto \widetilde{x}$, be a (locally) invertible map. Then the operators

$$\begin{aligned} \widetilde{L}_\alpha :=[(\nabla _x f)^{-1}]_\alpha {}^\beta \dfrac{\partial }{\partial x^\beta } \end{aligned}$$

are the pushforward of partial derivatives $\partial /\partial \widetilde{x}^\alpha$ along $f^{-1}$. Hence, the operators $\widetilde{L}_\alpha$ commute because the partial derivatives $\partial /\partial \widetilde{x}^\alpha$ commute. An adjustment of the above argument to our setting with $f=\varphi ^{(j)}_\eta$ (and with account of the fact that $\varphi ^{(j)}$ is complex-valued) provides an alternative explanation for the commutation of the operators $L^{(j)}_\alpha$.

The amplitude-to-symbol operator is defined as

$$\begin{aligned}&\mathfrak {S}^{(j)}:C^\infty (\mathbb {R}\times M \times T'M)\rightarrow C^\infty (\mathbb {R} \times T'M)\,, \nonumber \\&\mathfrak {S}^{(j)}:=\sum _{j=0}^\infty \mathfrak {S}^{(j)}_{-k}\,. \end{aligned}$$

(3.31)

When acting on a function positively homogeneous in momentum, the operator $\mathfrak {S}^{(j)}_{-k}$ excludes the dependence on x and decreases the degree of homogeneity by k.

The reduction of the amplitude is achieved by replacing the amplitude $a^{(j)}$ in (3.29) by

$$\begin{aligned} \mathfrak {S}^{(j)}a^{(j)}=:\mathfrak {b}^{(j)}, \end{aligned}$$

with

$$\begin{aligned} \mathfrak {b}^{(j)}(t;y,\eta )\sim \sum _{k=-1}^{+\infty } \mathfrak {b}^{(j)}_{-k}(t;y,\eta )\,, \qquad \mathfrak {b}^{(j)}_{-k}=\sum _{l+s=k} \mathfrak {S}^{(j)}_{-l} \,a^{(j)}_{-s}\,. \end{aligned}$$

The oscillatory integral

$$\begin{aligned} \frac{1}{(2\pi )^d}\int _{T'_yM} e^{i \varphi ^{(j)}(t,x;y,\eta )}\,\mathfrak {b}^{(j)}(t;y,\eta ) \,w^{(j)}(t,x;y,\eta )\,d\eta \end{aligned}$$

differs from (3.29) only by an infinitely smooth function.

We refer the reader to [17, Appendix A] for further particulars and detailed proofs concerning the amplitude-to-symbol operator.

Step 4. Set

$$\begin{aligned} \mathfrak {b}^{(j)}_{-k}=0, \qquad k=-1,0,1,\ldots . \end{aligned}$$

(3.32)

Equations (3.32), combined with the initial conditions stemming from the constraint

$$\begin{aligned} \sum _{j} U^{(j)}(0)\overset{\mod \Psi ^{-\infty }}{=}\mathrm {Id}, \end{aligned}$$

(3.33)

yield a hierarchy of (matrix) transport equations for the homogeneous components $\mathfrak {a}^{(j)}_{-k}$.

Remark 3.10

For the special case of the massless Dirac operator, the first few equations in the hierarchy (3.32) are given by (5.9)–(5.13).

Let us make a few remarks warranted by formula (3.33).

The m oscillatory integrals appearing on the RHS of (3.8) and (3.9) are not independent of one another, but they ‘mix’ at $t=0$ via the initial condition (3.33). Now, satisfying (3.33) involves representing the identity operator on $C^\infty (M;\mathbb {C}^m)$ in a somewhat nonstandard fashion, as

$$\begin{aligned}&\mathrm {Id}\overset{\mod \Psi ^{-\infty }}{=}\sum _j \frac{1}{(2\pi )^d}\int _{T'M} e^{i\varphi ^{(j)}(0,x;y,\eta )} \,\mathfrak {s}^{(j)}(y,\eta )\nonumber \\&\chi ^{(j)}(0,x;y,\eta )\,w^{(j)}(0,x;y,\eta )\,(\,\cdot \,)\,\rho (y)\,dy\,d\eta , \end{aligned}$$

(3.34)

with $\mathfrak {s}^{(j)}\in S^0_{\mathrm {ph}}(T'M;\mathrm {Mat}(m;\mathbb {C}))$.

In terms of the symbols $\mathfrak {a}^{(j)}$, the initial condition (3.33) reads

$$\begin{aligned} \mathfrak {a}^{(j)}(0;y,\eta )=\mathfrak {s}^{(j)}(y,\eta ). \end{aligned}$$

From the fact that the principal symbol of the identity operator is the identity matrix it follows that

$$\begin{aligned} \sum _j \mathfrak {a}^{(j)}_0(0;y,\eta )=\sum _j \mathfrak {s}^{(j)}_0(y,\eta )=\mathbf {1}_{m\times m}. \end{aligned}$$

(3.35)

Furthermore, one can show that

$$\begin{aligned} \mathfrak {s}^{(j)}_0(y,\eta )=v^{(j)}(y,\eta )\,[v^{(j)}(y,\eta )]^*. \end{aligned}$$

However, obtaining formulae for subleading components $\mathfrak {s}^{(j)}_{-1}$ is already a challenging task, see [23, Sect. 4.2]. In general, lower order components of $\mathfrak {s}^{(j)}$ depend in a nontrivial manner on the eigenvalues and eigenprojections of the matrix-function $A_\mathrm {prin}(x,\xi )$ and on the choice of phase functions $\varphi ^{(j)}$.

The invariant representation of the identity operator—and, more generally, of pseudodifferential operators—on manifolds is not a well-studied subject. An initial analysis of the scalar case was carried out in [17, Sect. 6]. For the case of the Dirac operator a more detailed examination of (3.34) will be provided in Sect. 5.2. A more extensive analysis of (3.34) for a general operator A is carried out in [15, 20, 21].

Remark 3.11

All statements and results presented in this section carry over verbatim to the case where A is an elliptic symmetric first order $m\times m$ matrix pseudodifferential—as opposed to differential—operator, with the following exceptions:

• formulae (3.1) and (3.2) have to be dropped as they are no longer true;

• ‘Step 2.’ in Sect. 3.3 has to be modified to take into account the action of a pseudodifferential operator on an oscillatory integral in an invariant manner, along the lines of [11, Sect. 4.3].

Remark 3.12

Let us point out that in this section we did not use anywhere the fact that M carries a Riemannian structure. If one replaces the Riemannian density (1.1) with an arbitrary positive density, all statements and results stay the same.

4 Invariant Description of Pseudodifferential Operators Acting on Scalar Functions

In order to prepare ourselves to address the issue of initial conditions for our transport equations in the case of the Dirac operator, we need to discuss first the more general question of invariant representation of a pseudodifferential operator. We devote a separate section to this, as we believe this matter to be of independent interest. Note that we treat the case of a scalar operator merely for the sake of presentational convenience: all the formulae and arguments in this subsection remain unchanged for matrix pseudodifferential operators acting on m-columns of scalar functions.

Definition 4.1

We call time-independent Levi-Civita phase function the function $\phi \in C^\infty (M\times T'M; \mathbb {C})$ defined by

$$\begin{aligned} \phi (x;y,\eta ):=\int _{\gamma } \zeta \, dz +\frac{i\epsilon }{2} h(y,\eta )\,\left[ \mathrm {dist}(x,y)\right] ^2 \end{aligned}$$

(4.1)

when x lies in a geodesic neighbourhood of y and continued smoothly elsewhere in such a way that $\mathrm {Im}\,\phi \ge 0$. Here $\gamma$ is the (unique) shortest geodesic connecting y to x, $\zeta$ is the parallel transport of $\eta$ along $\gamma$,

$$\begin{aligned} h(y,\eta ):=\sqrt{g^{\alpha \beta }(y)\,\eta _\alpha \eta _\beta }\,, \end{aligned}$$

(4.2)

$\mathrm {dist}$ is the geodesic distance and $\epsilon$ is a positive parameter.

Let P be a pseudodifferential operator of order p acting on scalar functions over a Riemannian d-manifold. The operator P can be written, modulo an integral operator with smooth kernel, in the form

$$\begin{aligned} P=\int _{T'M} e^{i\phi (x;y,\eta )} \,\mathfrak {p}(y,\eta )\,\chi _0(x;y,\eta )\,w_0(x;y,\eta )\,(\,\cdot \,)\,\rho (y)\,dy\,d\eta , \end{aligned}$$

(4.3)

where $\phi$ is the time-independent Levi-Civita phase function, $\mathfrak {p}\in S^m_{\mathrm {ph}}(T'M)$, $\chi _0$ is a cut-off localising integration to a neighbourhood of the diagonal and away from the zero section (see also (I)–(III) in Theorem 3.2) and

$$\begin{aligned} w_0(x;y,\eta ):= \left[ \rho (x)\,\rho (y)\right] ^{-\frac{1}{2}}\left[ {\det }^2 \phi _{x^\alpha \eta _\beta }(x;y,\eta ) \right] ^\frac{1}{4}. \end{aligned}$$

(4.4)

Here the smooth branch of the complex root is chosen in such a way that $w_0(y;y,\eta )=[\rho (y)]^{-1}$.

Remark 4.2

Note that (4.3) is, effectively, a special case of (3.10) with $t=0$.

Formula (4.3) provides an invariant representation of the pseudodifferential operator P.

Definition 4.3

We call full symbol of the operator P the scalar function

$$\begin{aligned} \mathfrak {p}(y,\eta )\sim \sum _{k=-p}^{+\infty } \mathfrak {p}_{-k}(y,\eta ). \end{aligned}$$

Furthermore, we call the homogeneous functions $\mathfrak {p}_p$ and $\mathfrak {p}_{p-1}$ the g-principal and g-subprincipal symbol, respectively.⁴

The notions of principal and subprincipal symbols of a pseudodifferential operator are nowadays standard concepts in microlocal analysis. The former makes sense for operators acting either on scalar functions or on half-densities, whereas the latter is only defined for operators acting on half-densities. We refer the reader to [33] for further details. Note that the concept of subprincipal symbol was introduced by Duistermaat and Hörmander in [27, Eqn. (5.2.8)].

It is easy to see that the concept of principal symbol $P_\mathrm {prin}$ and that of g-principal symbol $\mathfrak {p}_p$ coincide. As far as the subprincipal symbol is concerned, the situation is more complicated, in that before drawing a comparison we need to turn our operator into an operator acting on half-densities.

Put

$$\begin{aligned} P_{1/2}:= \rho ^{1/2}\,P\,\rho ^{-1/2} \end{aligned}$$

(4.5)

and let $P_\mathrm {sub}$ be the subprincipal symbol of the operator (4.5) defined in accordance with [27, Eqn. (5.2.8)].

A natural question to ask is: what is the relation between $P_\mathrm {sub}$ and $\mathfrak {p}_{p-1}$?

Theorem 4.4

The invariant quantities $P_\mathrm {sub}$ and $\,\mathfrak {p}_{p-1}$ are related as

$$\begin{aligned} \mathfrak {p}_{p-1}= & {} P_\mathrm {sub}+\frac{i}{2}(P_\mathrm {prin})_{y^\alpha \eta _\alpha }+\frac{i}{2}\,\Gamma ^\alpha {}_{\beta \gamma }\left[ \eta _\alpha (P_\mathrm {prin})_{\eta _\beta }\right] _{\eta _\gamma }\nonumber \\&- \frac{\epsilon }{2}\,g_{\beta \gamma } \left[ h \,(P_\mathrm {prin})_{\eta _\beta } \right] _{\eta _\gamma }. \end{aligned}$$

(4.6)

Theorem 4.4 implies that, in particular, the two notions of subprincipal symbol coincide when the principal symbol does not depend on $\eta$, i.e. when P is a pseudodifferential operator of the type “multiplication by a scalar function plus an operator of order $-1$”. Note that the identity operator, whose invariant representation was investigated in [17, Sect. 6], falls into this class.

Remark 4.5

A tedious, yet straightforward, calculation shows that the RHS of (4.6) is a scalar function on the cotangent bundle. In fact, the second and third summands on the RHS of (4.6) admit an invariant representation in terms of the Laplace–Beltrami operator associated with the neutral metric n on the cotangent bundle $T^*M$, which, in local coordinates $(x^1, \ldots ,x^d, \xi _1, \ldots , \xi _d)$, reads

$$\begin{aligned} n_{jk}(x,\xi )= \begin{pmatrix} -2\, \xi _\gamma \, \Gamma ^\gamma {}_{\alpha \beta }(x) &{} \delta _\alpha {}^\mu \\ \delta ^\nu {}_\beta &{} 0 \end{pmatrix}, \qquad j,k \in \{1,\ldots , 2d\}. \end{aligned}$$

(4.7)

The adjective ‘neutral’ refers to the fact that the metric n has signature (d, d). It turns out that the neutral metric is an effective tool in the development of an invariant theory of pseudodifferential operators on Riemannian manifolds. As the analysis of this matter requires a lengthy discussion and would take us away from the core subject of our paper, we plan to address it in detail elsewhere. See also [46].

Proof of Theorem 4.4

Consider the pseudodifferential operator P and turn it into an operator on half-densities $P_{1/2}$ via (4.5). In what follows we work in an arbitrary coordinate system, the same for x and y.

Dropping the cut-off, the integral kernel of $P_{1/2}$ now reads

$$\begin{aligned} \frac{1}{(2\pi )^d} \int _{T'_yM} e^{i\phi (x;y,\eta )} \,\mathfrak {p}(y,\eta )\, \sqrt{\det \phi _{x\eta }}\,d\eta \,. \end{aligned}$$

(4.8)

Our phase function (4.1) admits the expansion

$$\begin{aligned}&\phi (x;y,\eta )=(x-y)^\alpha \eta _\alpha +\frac{1}{2}\Gamma ^\alpha {}_{\beta \gamma }\,\eta _\alpha (x-y)^\beta (x-y)^\gamma \nonumber \\&\quad +\frac{i\epsilon h}{2}g_{\alpha \beta }(x-y)^\alpha (x-y)^\beta + O(\Vert x-y\Vert ^3), \end{aligned}$$

(4.9)

which implies that

$$\begin{aligned} \sqrt{\det \phi _{x\eta }}=1+ \frac{1}{2}[ \Gamma ^\alpha {}_{\alpha \beta }+i\epsilon h^{-1}\eta _\beta ](x-y)^\beta +O(\Vert x-y\Vert ^2). \end{aligned}$$

(4.10)

Substituting (4.9) and (4.10) into (4.8), we get

$$\begin{aligned}&\frac{1}{(2\pi )^d}\int e^{i(x-y)^\alpha \eta _\alpha } \Bigl \{ \mathfrak {p}_p+\left( \frac{1}{2} \left[ i\Gamma ^\alpha {}_{\beta \gamma }\,\eta _\alpha -\epsilon hg_{\beta \gamma } \right] (x-y)^\beta (x-y)^\gamma \right. \nonumber \\&\quad \left. +\frac{1}{2} \left[ \Gamma ^\alpha {}_{\alpha \beta }+i\epsilon h^{-1}\eta _\beta \right] (x-y)^\beta \right) \mathfrak {p}_p +\mathfrak {p}_{p-1} +O(\Vert \eta \Vert ^{p-2}) \Bigr \}\, d\eta \,. \end{aligned}$$

(4.11)

Excluding the x-dependence from the amplitude in (4.11) by acting with the operator

$$\begin{aligned} \mathcal {S}_\mathrm {right}(\,\cdot \,):=\left. \left[ \exp \left( i\frac{\partial ^2}{\partial x^\mu \,\partial \eta _\mu }\right) (\,\cdot \,)\right] \right| _{x=y}, \end{aligned}$$

(4.12)

we arrive at

$$\begin{aligned}&\frac{1}{(2\pi )^d}\int e^{i(x-y)^\alpha \eta _\alpha } \Bigl \{ \mathfrak {p}_p-\frac{i}{2}\left[ \eta _\alpha \,\Gamma ^\alpha {}_{\beta \gamma }\,(\mathfrak {p}_p)_{\eta _\beta }\right] _{\eta _\gamma }+\frac{\epsilon }{2} \left[ h \,g_{\gamma \beta }\,(\mathfrak {p}_p)_{\eta _\beta } \right] _{\eta _\gamma } \nonumber \\&\quad +\mathfrak {p}_{p-1} +O(\Vert \eta \Vert ^{p-2}) \Bigr \}\, d\eta \,. \end{aligned}$$

(4.13)

Computing the subprincipal symbol of (4.13) and using the fact that $\mathfrak {p}_p=P_\mathrm {prin}=(P_{1/2})_\mathrm {prin}\,$, we obtain (4.6). Note that the sign in front of the correction term

$$\begin{aligned} \frac{i}{2}(P_\mathrm {prin})_{y^\alpha \eta _\alpha } \end{aligned}$$

is opposite to the usual one, see, for example, [19, Eqn. (A.3)]. This is due to the fact that in this paper we use the right—as opposed to left—quantization.$\square$

5 Global Propagator for the Dirac Operator

In this section we will start the analysis of the global propagator for the Dirac operator, specialising Theorem 3.3 to the case $A=W$.

We denote by

$$\begin{aligned} W_\mathrm {prin}(y,\eta ):=\sigma ^\alpha (y)\,\eta _\alpha \end{aligned}$$

(5.1)

the principal symbol of W and by

$$\begin{aligned} W_0(x):=-\frac{i}{4}\sigma ^\alpha (x)\sigma _\beta (x) \left( \frac{\partial \sigma ^\beta }{\partial x^\alpha }(x) +\Gamma ^\beta {}_{\alpha \gamma }(x)\,\sigma ^\gamma (x) \right) \end{aligned}$$

(5.2)

its zero order part, see Definition 1.1.

The principal symbol $W_\mathrm {prin}(y,\eta )$ has eigenvalues $h^\pm =\pm h$, where h is given by (4.2), compare with (3.2). This fact, which can be easily established by writing down (5.1) in local coordinates, shows that the Dirac operator is indeed elliptic.

It is well-known that the Hamiltonian flow $(x^+(t;y,\eta ),\xi ^+(t;y,\eta ))$ generated by h is (co-)geodesic. The two flows $(x^\pm (t;y,\eta ),\xi ^\pm (t;y,\eta ))$ are related as

$$\begin{aligned} (x^-(t;y,\eta ),\xi ^-(t;y,\eta )) = (x^+(t;y,-\eta ),-\xi ^+(t;y,-\eta )). \end{aligned}$$

(5.3)

Our goal is to write down explicitly the positive and negative propagators (1.12a) and (1.12c) in the form (3.10) for a distinguished choice of phase functions.

To this end, we give the following definition (see also [17, Sect. 4]).

Definition 5.1

We call positive ($+$), resp. negative (−), Levi-Civita phase function the infinitely smooth function $\varphi ^{\pm }\in C^\infty (\mathbb {R}\times M \times T'M; \mathbb {C})$ defined by

$$\begin{aligned} \varphi ^\pm (t,x;y,\eta )=\int _{\gamma ^\pm } \zeta ^\pm \,dz+\frac{i\,\epsilon }{2}h(y,\eta ) {\text {dist}}^2(x,x^\pm (t;y,\eta )) \end{aligned}$$

(5.4)

for x in a geodesic neighbourhood of $x^\pm (t;y,\eta )$ and continued smoothly elsewhere in such a way that ${\text {Im}} \varphi ^\pm \ge 0$. Here ${\text {dist}}$ is the Riemannian geodesic distance, the path of integration $\gamma ^\pm$ is the shortest geodesic connecting $x^\pm$ to x, $\zeta ^\pm$ is the result of parallel transport of $\xi ^\pm (t;y,\eta )$ along $\gamma ^\pm$ and $\epsilon$ is a positive parameter.

The positive and negative Levi-Civita phase functions are related as

$$\begin{aligned} \varphi ^-(t,x;y,\eta ) = - \overline{ \varphi ^+(t,x;y,-\eta ) }. \end{aligned}$$

(5.5)

Let us point out that the way one continues $\varphi ^\pm$ outside a neighbourhood of the flow does not affect the singular part of the propagators. The choice of a different smooth continuation results in an error $\overset{\mod \Psi ^{-\infty }}{=}0$, as one can show by a straightforward (non)stationary phase argument.

Remark 5.2

The time-independent phase function $\phi$ introduced in the previous section is the restriction to $t=0$ of the phase functions $\varphi ^\pm$,

$$\begin{aligned} \phi (x;y,\eta )=\varphi ^+(0,x;y,\eta )=\varphi ^-(0,x;y,\eta ). \end{aligned}$$

(5.6)

It is easy to see that the positive and negative Levi-Civita phase functions satisfy conditions (i), (ii) and (iv) from Theorem 3.3. Furthermore, [45, Corollary 2.4.5] implies that condition (iii) is also satisfied. Hence, Theorem 3.3 ensures that the integral kernel of $U^{\pm }$ can be written as a single oscillatory integral

$$\begin{aligned}&u^\pm (t,x,y):=\frac{1}{(2\pi )^3}\int _{T'_yM} e^{i \varphi ^\pm (t,x;y,\eta )}\,\mathfrak {a}^\pm (t;y,\eta )\,\nonumber \\&\quad \chi ^\pm (t,x;y,\eta )\,w^\pm (t,x;y,\eta )\,d\eta , \end{aligned}$$

(5.7)

where $\varphi ^\pm$ is the positive/negative Levi-Civita phase function.

Definition 5.3

We define the full symbol of the positive (resp. negative) propagator to be the scalar matrix-function $\mathfrak {a}^+$ (resp. $\mathfrak {a}^-$), obtained through the algorithm described in Sect. 3.3 with Levi-Civita phase functions.

We define the subprincipal symbol of the positive (resp. negative) propagator to be the scalar matrix-function $\mathfrak {a}^+_{-1}$ (resp. $\mathfrak {a}^-_{-1}$) obtained the same way.

As to the principal symbol, this object was defined earlier, see Definition 3.8.

We stress that the mathematical objects contained in the above definition are uniquely and invariantly defined. They only depend on the phase functions which, in turn, originate from the geometry of M in a coordinate-free covariant manner, cf. Definition 5.1.

To the best of our knowledge, there is no accepted definition of full symbol or subprincipal symbol for a Fourier integral operator available in the literature to date. The geometric nature of our construction allows us to provide invariant definitions of full and subprincipal symbol of the Dirac propagator, analyse them, and give explicit formulae. This paper, alongside [17], aims to build towards an invariant theory for pseudodifferential and Fourier integral operators on manifolds.

Before moving on to computing the principal and subprincipal symbols of the positive (resp. negative) Dirac propagator, an important remark is in order. In addition to what was discussed in Sect. 3 for the general case, the construction of the Dirac propagator has to be consistent with the gauge transformation (1.5), (1.6). In particular, the action of the gauge transformation needs to be carefully accounted for by the construction process.

The transformation (1.6) leads to the transformation

$$\begin{aligned} \mathfrak {a}^\pm (t;y,\eta )\mapsto G^*(x)\, \mathfrak {a}^\pm (t;y,\eta )\, G(y). \end{aligned}$$

in the oscillatory integral (5.7). Note that this introduces an x-dependence which has to be handled by means of amplitude-to-symbol reduction (3.31).

5.1 Transport Equations

By acting with the Dirac operator W on (5.7) in the variable x and dropping the cut-off, we obtain

$$\begin{aligned} W u^\pm (t,x,y)=\frac{1}{(2\pi )^3}\int _{T'_yM} e^{i \varphi ^\pm (t,x;y,\eta )}\,a^\pm (t;y,\eta )\,w^\pm (t,x;y,\eta )\,d\eta , \end{aligned}$$

where

$$\begin{aligned} a= & {} -i e^{-i\varphi ^\pm } (w^\pm )^{-1} \partial _t \left( e^{i\varphi ^\pm }\,\mathfrak {a}^\pm \,w^\pm \right) \\&\quad + \left[ -i e^{-i\varphi ^\pm } (w^\pm )^{-1}\sigma ^\alpha \partial _{x^\alpha } \left( e^{i\varphi ^\pm } \,w^\pm \right) + W_0\right] \mathfrak {a}^\pm \\= & {} \left( \varphi ^\pm _t+\sigma ^\alpha \varphi ^\pm _{x^\alpha }\right) \mathfrak {a}^\pm -i \mathfrak {a}^\pm _t+ \left[ -i (w^\pm )^{-1}\left( w^\pm _t+\sigma ^\alpha w^\pm _{x^\alpha } \right) +W_0 \right] \mathfrak {a}^\pm . \end{aligned}$$

Put

$$\begin{aligned} a\sim \sum _{k=-1}^{+\infty } a_{-k}, \end{aligned}$$

(5.8)

where

$$\begin{aligned} a^\pm _1:=\left( \varphi ^\pm _t+W_\mathrm {prin}(x,\varphi _x^\pm )\right) \mathfrak {a}^\pm _0 \end{aligned}$$

(5.9)

and

$$\begin{aligned} a^\pm _{-k}:= & {} \left( \varphi ^\pm _t+W_\mathrm {prin}(x,\varphi _x^\pm )\right) \mathfrak {a}^\pm _{-k-1} -i (\mathfrak {a}^\pm _{-k})_t\nonumber \\&+ \left[ -i (w^\pm )^{-1}\left( w^\pm _t+\sigma ^\alpha w^\pm _{x^\alpha } \right) +W_0 \right] \mathfrak {a}^\pm _{-k} \end{aligned}$$

(5.10)

for $k\ge 0$. Note that the $a^\pm _{-k}$, $k\ge -1$, are positively homogeneous in momentum of degree $-k$.

Our transport equations read

$$\begin{aligned}&\mathfrak {S}^\pm _0 a^\pm _1=0, \end{aligned}$$

(5.11)

$$\begin{aligned}&\mathfrak {S}^\pm _{-1} a^\pm _1+ \mathfrak {S}^\pm _{0}a^\pm _0=0, \end{aligned}$$

(5.12)

$$\begin{aligned}&\mathfrak {S}^\pm _{-2} a^\pm _1+ \mathfrak {S}^\pm _{-1}a^\pm _0+\mathfrak {S}^\pm _0 a^\pm _{-1}=0, \\&\dots \nonumber \end{aligned}$$

(5.13)

Recalling that $v^\pm$ are the normalised eigenvectors of $W_\mathrm {prin}$ corresponding to the eigenvalues $\pm h$, denote by

$$\begin{aligned} P^\pm (y,\eta ):= v^\pm (y,\eta )\,[v^\pm (y,\eta )]^* \end{aligned}$$

(5.14)

the spectral projections along the eigenspaces spanned by $v^\pm$. Of course,

$$\begin{aligned}&W_\mathrm {prin}=h\, (P^+-P^-), \end{aligned}$$

(5.15)

$$\begin{aligned}&\mathrm {Id}=P^++P^-, \end{aligned}$$

(5.16)

and

$$\begin{aligned} P^\pm =\frac{1}{2}\left( \mathrm {Id}\pm \frac{W_\mathrm {prin}}{h} \right) . \end{aligned}$$

(5.17)

Let us label the transport equations with nonnegative integer numbers in increasing order, so that (5.11) is the zeroth transport equation, (5.12) is the first transport equation and so on. Direct inspection of (5.9) and (5.10) reveals that

• multiplication of the n-th transport equation by $P^\mp (x^\pm , \xi ^\pm )$ on the left allows one to determine

  $$\begin{aligned} P^{\mp }(x^\pm ,\xi ^\pm )\mathfrak {a}^\pm _{-n}(t;y,\eta ), \qquad n\ge 0, \end{aligned}$$

  (5.18)

  algebraically;

• multiplication of the $(n+1)$-th transport equation by $P^\pm (x^\pm , \xi ^\pm )$ on the left and the use of (5.18) allows one to determine

  $$\begin{aligned} P^{\pm }(x^\pm ,\xi ^\pm )\mathfrak {a}^\pm _{-n}(t;y,\eta ), \qquad n\ge 0, \end{aligned}$$

  (5.19)

  upon solving a matrix ordinary differential equation in the variable t.

Summing up (5.18) and (5.19) one obtains $\mathfrak {a}^\pm _{-k}(t;y,\eta )$, in view of (5.16).

5.2 Pseudodifferential Operators $U^\pm (0)$

This subsection is devoted to the examination of operators $U^\pm (0)$. We need to examine these operators because, as explained in Sect. 3.3, their full symbols determine the initial conditions $\mathfrak {a}^\pm _{-k}(0;y,\eta )$ for our transport equations.

We have

$$\begin{aligned} U^\pm (0)=\theta (\pm W), \end{aligned}$$

(5.20)

where

$$\begin{aligned} \theta (\lambda ) := {\left\{ \begin{array}{ll} 1\quad \text {for}\quad \lambda >0, \\ 0\quad \text {for}\quad \lambda \le 0. \end{array}\right. } \end{aligned}$$

We see that the operators $U^\pm (0)$ are self-adjoint pseudodifferential operators of order zero, orthogonal projections onto the positive/negative eigenspaces of the operator W. The operator $\mathrm {Id}-U^+(0)-U^-(0)$ is the orthogonal projection onto the nullspace of the operator W, hence

$$\begin{aligned} U^+(0)+U^-(0)\overset{\mod \Psi ^{-\infty }}{=} \mathrm {Id}. \end{aligned}$$

The principal symbols of the operators $U^\pm (0)$ read

$$\begin{aligned}{}[U^\pm (0)]_\mathrm {prin}=P^\pm (y,\eta ), \end{aligned}$$

(5.21)

where $P^\pm$ are the orthogonal projections onto the positive/negative eigenspaces of the principal symbol of the operator W, see (5.14).

The analysis of the full symbol of $U^\pm (0)$ is a delicate task which was investigated, to a certain extent and in a somewhat different setting, in [23]. In order to develop the ideas from [23] we have to address a number of issues.

• We are now dealing with scalar fields as opposed to half-densities.

• We are now making full use of Riemannian structure.

• We are now working in the special setting of a system of two equations in dimension three with trace-free principal symbol.

• Unlike [23, 24], we are aiming to evaluate the actual matrix-functions $[U^\pm (0)]_\mathrm {sub}$ and not only their traces.

In order to calculate the subprincipal symbols of the pseudodifferential operators $U^\pm (0)$ we will need the following auxiliary result.

Theorem 5.4

Fix a point $y\in M$ and let $\{\widetilde{e}\}_{j=1}^3$ be a framing on M. Let $G\in C^\infty (M;SU(2))$ be a gauge transformation such that $G(y)=\mathrm {Id}$ and let

$$\begin{aligned} {e}_j{}^\alpha :=\frac{1}{2} {\text {tr}}(s_j\,G^*\,s^k\,G)\,\widetilde{e}_k{}^\alpha . \end{aligned}$$

(5.22)

Then

$$\begin{aligned} \nabla _\alpha G(y)=-\frac{i}{2} \left[ \overset{*}{K}{}_{\alpha \beta }(y)-\overset{*}{\widetilde{K}}{}_{\alpha \beta }(y)\right] \,\sigma ^\beta (y), \end{aligned}$$

(5.23)

where K (resp. $\widetilde{K}$) is the contorsion tensor of the Weitzenböck connection (see Appendix A) associated with the framing $\{ e_j\}_{j=1}^3$ (resp. $\{\widetilde{e}_j\}_{j=1}^3$), the star stands for the Hodge dual applied in the first and third indices, see formula (A.7), and $\sigma ^\alpha (y)$ is defined by (1.3).

Proof

The proof is provided in Appendix B.1.$\square$

Remark 5.5

Let $\{\widetilde{e}\}_{j=1}^3$ and $\{e\}_{j=1}^3$ be a pair of framings related in accordance with (5.22), and let $\widetilde{W}$ and W be the corresponding Dirac operators, see Definition 1.1. Then

$$\begin{aligned} W=G^*\widetilde{W}G. \end{aligned}$$

(5.24)

The following theorem is the main result of this subsection.

Theorem 5.6

We have

$$\begin{aligned}{}[U^\pm (0)]_\mathrm {sub}(y,\eta ) = \pm \frac{1}{4(h(y,\eta ))^3}\, \overset{*}{T}{}^{\alpha \beta }(y)\, \eta _\alpha \eta _\beta \,\mathrm {Id}\,, \end{aligned}$$

(5.25)

where T is the torsion tensor of the Weitzenböck connection (see Appendix A) associated with the framing $\{ e_j\}_{j=1}^3$ encoded within the Dirac operator W (see Definition 1.1) and the star stands for the Hodge dual applied in the second and third indices, see formula (A.6).

Proof

Let us fix a point $y\in M$ and choose normal geodesic coordinates x centred at y such that $e_j{}^\alpha (y)=\delta _j{}^\alpha \,$. Consider the (local) operator with constant coefficients

$$\begin{aligned} \widetilde{W}:=-is^\alpha \,\frac{\partial }{\partial x^\alpha }\,, \end{aligned}$$

(5.26)

where the $s^\alpha$ are the standard Pauli matrices (1.2). Let us choose a smooth special unitary $2\times 2$ matrix-function G such that

$$\begin{aligned}&G(0)=\mathrm {Id},\\&[W]_\mathrm {prin}=[G^*\widetilde{W}G]_\mathrm {prin}+O(\,\Vert \eta \Vert \,\Vert x\Vert ^2\,)\,, \end{aligned}$$

compare with (5.24). It is easy to see that such a matrix-function G(x) exists and is defined uniquely modulo $O(\Vert x\Vert ^2)$.

Let us now compare the subprincipal symbols of the pseudodifferential operators $\theta (\pm W)$ and $\theta (\pm G^*\widetilde{W}G)$, with $G^*\widetilde{W}G$ understood as an operator acting in Euclidean space (constant metric tensor $g_{\alpha \beta }(x)=\delta _{\alpha \beta }$). It can be shown that at the origin we have

$$\begin{aligned}{}[W]_\mathrm {sub}(0,\eta )=[G^*\widetilde{W}G]_\mathrm {sub}(0,\eta ). \end{aligned}$$

Thus, the proof of the Theorem 5.6 has been reduced to the case when we are in Euclidean space and the operator W is given by formulae (5.24) and (5.26).

We have

$$\begin{aligned} \theta (\pm \widetilde{W}) = \frac{1}{(2\pi )^3} \int _{T'\mathbb {R}^3} e^{i(x-z)^\alpha \eta _\alpha }\,P^\pm (\eta )\,(\,\cdot \,)\,dz\,d\eta \,, \end{aligned}$$

(5.27)

where

$$\begin{aligned} P^\pm (\eta ) = \frac{1}{2} \left( \mathrm {Id} \pm \frac{1}{\Vert \eta \Vert }s^\beta \eta _\beta \right) . \end{aligned}$$

(5.28)

Formulae (5.27) and (5.28) imply that

$$\begin{aligned} \theta (\pm G^*\widetilde{W}G) = \frac{1}{(2\pi )^3} \int _{T'\mathbb {R}^3} e^{i(x-z)^\alpha \eta _\alpha }\,Q^\pm (x,z,\eta )\,(\,\cdot \,)\,dz\,d\eta \,, \end{aligned}$$

where

$$\begin{aligned} Q^\pm (x,z,\eta ) = G^*(x)\,P^\pm (\eta )\,G(z) = \frac{1}{2}\, G^*(x) \left( \mathrm {Id} \pm \frac{1}{\Vert \eta \Vert }s^\beta \eta _\beta \right) G(z)\,. \end{aligned}$$

Excluding the z-dependence from the amplitude $Q^\pm$ by acting with the operator

$$\begin{aligned} \mathcal {S}_\mathrm {left}(\,\cdot \,):=\left. \left[ \exp \left( -i\frac{\partial ^2}{\partial z^\mu \,\partial \eta _\mu }\right) (\,\cdot \,)\right] \right| _{z=x}, \end{aligned}$$

compare with (4.12), we arrive at

$$\begin{aligned} \theta (\pm G^*\widetilde{W}G) = \frac{1}{(2\pi )^3} \int _{T'\mathbb {R}^3} e^{i(x-z)^\alpha \eta _\alpha }\,\mathcal {Q}^\pm (x,\eta )\,(\,\cdot \,)\,dz\,d\eta \,, \end{aligned}$$

where

$$\begin{aligned}&\mathcal {Q}^\pm (x,\eta ) = \mathcal {Q}_0^\pm (x,\eta ) + \mathcal {Q}_{-1}^\pm (x,\eta ) +O(\Vert \eta \Vert ^{-2})\,, \end{aligned}$$

(5.29)

$$\begin{aligned}&\mathcal {Q}_0^\pm (x,\eta ) = \frac{1}{2}\, G^*(x) \left( \mathrm {Id} \pm \frac{1}{\Vert \eta \Vert }s^\beta \eta _\beta \right) G(x)\,, \end{aligned}$$

(5.30)

$$\begin{aligned}&\mathcal {Q}_{-1}^\pm (x,\eta ) = -\, \frac{i}{2}\, G^*(x) \left( \mathrm {Id} \pm \frac{1}{\Vert \eta \Vert }s^\beta \eta _\beta \right) _{\eta _\mu } G_{x^\mu }(x)\,. \end{aligned}$$

(5.31)

In the Euclidean setting the standard formula [27, Eqn. (5.2.8)] for the subprincipal symbol reads

$$\begin{aligned}{}[\theta (\pm G^*\widetilde{W}G)]_\mathrm {sub} = \mathcal {Q}_{-1}^\pm + \frac{i}{2}(\mathcal {Q}_0^\pm )_{x^\mu \eta _\mu }\,. \end{aligned}$$

(5.32)

Substituting (5.30) and (5.31) into (5.32) and setting $x=0$, we get

$$\begin{aligned}&[\theta (\pm G^*\widetilde{W}G)]_\mathrm {sub} = \pm \frac{i}{4} \left[ G^*_{x^\mu } \left( \frac{1}{\Vert \eta \Vert }s^\beta \eta _\beta \right) _{\eta _\mu } - \left( \frac{1}{\Vert \eta \Vert }s^\beta \eta _\beta \right) _{\eta _\mu } G_{x^\mu } \right] \nonumber \\&\quad = \pm \frac{i( \delta _\beta {}^\mu \Vert \eta \Vert ^2-\eta _\beta \,\eta ^\mu ) }{4\Vert \eta \Vert ^3} \left[ G^*_{x^\mu } s^\beta - s^\beta G_{x^\mu } \right] . \end{aligned}$$

(5.33)

Theorem 5.4 tells us that $G_{x^\mu }=\frac{i}{2}\overset{*}{K}{}_{\mu \nu }\,s^\nu$. Substituting this into (5.33), and using standard properties of Pauli matrices and (A.10), we get

$$\begin{aligned} {\begin{matrix} [\theta (\pm G^*\widetilde{W}G)]_\mathrm {sub} &{} = \pm \frac{ \delta _\beta {}^\mu \Vert \eta \Vert ^2-\eta _\beta \,\eta ^\mu }{8\Vert \eta \Vert ^3} \left[ s^\nu s^\beta + s^\beta s^\nu \right] \overset{*}{K}{}_{\mu \nu } \\ &{} = \pm \frac{ 1 }{4\Vert \eta \Vert ^3} \left( \overset{*}{K}{}^\gamma {}_\gamma \delta _{\mu \nu } -\overset{*}{K}{}_{\mu \nu } \right) \eta ^\mu \eta ^\nu {\text {Id}} \\ &{} = \pm \frac{1}{4\Vert \eta \Vert ^3} \overset{*}{T}{}_{\mu \nu } \,\eta ^\mu \,\eta ^\nu {\text {Id}}. \end{matrix}} \end{aligned}$$

The above argument combined with (5.20) yields (5.25).$\square$

Observe that formula (5.25) implies

$$\begin{aligned} {\text {tr}}\, [U^\pm (0)]_\mathrm {sub}(y,\eta ) = \pm \frac{1}{2(h(y,\eta ))^3}\, \overset{*}{T}{}^{\alpha \beta }(y)\, \eta _\alpha \eta _\beta \,, \end{aligned}$$

which agrees with [23, formula (1.20)] and [24, formula (4.1) with $\mathbf {c}=+1$].

6 Principal Symbol of the Global Dirac Propagator

In this section we provide an explicit geometric characterisation of the principal symbols of the positive and negative Dirac propagators.

Theorem 6.1

The principal symbols of the positive and negative Dirac propagators are

$$\begin{aligned} \mathfrak {a}^\pm _0(t;y,\eta )=\zeta ^\pm (t;y,\eta )\,[v^\pm (y,\eta )]^*, \end{aligned}$$

(6.1)

where $\zeta ^\pm (t;y,\eta )$ is the parallel transport of $v^\pm (y,\eta )$ along $x^\pm$ with respect to the spin connection, i.e.

$$\begin{aligned} \left( \frac{d}{dt} +[\dot{x}^\pm ]^\alpha \,\frac{1}{4} \sigma _\beta \left( \frac{\partial \sigma ^\beta }{\partial x^\alpha }+ \Gamma ^\beta {}_{\alpha \gamma }\sigma ^\gamma \right) \right) \zeta ^\pm =0, \qquad \zeta ^\pm |_{t=0}=v^\pm . \end{aligned}$$

(6.2)

Proof

It is known [43, Sect. 3.4], [44] that the principal symbols $\mathfrak {a}_0^\pm$ are independent of the choice of the phase function and read

$$\begin{aligned} \mathfrak {a}_0^\pm (t;y,\eta )=v^\pm (x^\pm ,\xi ^\pm )\,[v^\pm (y,\eta )]^* \,e^{-i\,\int _0^t q^\pm (x^\pm (\tau ;y,\eta ),\xi ^\pm (\tau ;y,\eta ))\,d \tau }, \end{aligned}$$

(6.3)

where

$$\begin{aligned} q^\pm =[v^\pm ]^* \,W_{\mathrm {sub}} \,v^\pm -\frac{i}{2}\{[v^\pm ]^*,W_\mathrm {prin}-h^\pm ,v^\pm \}-i\, [v^\pm ]^*\{v^\pm ,h^\pm \}\,, \end{aligned}$$

(6.4)

and

$$\begin{aligned} W_{\mathrm {sub}}(y):=W_0(y)+\frac{i}{2} \sigma ^\alpha (y) \,\Gamma ^\beta {}_{\alpha \beta }(y)+ \frac{i}{2}[W_\mathrm {prin}(y,\eta )]_{y^\alpha \eta _\alpha }. \end{aligned}$$

(6.5)

In formula (6.4) curly brackets denote the Poisson bracket

$$\begin{aligned} \{B,C\}:=B_{y^\alpha } C_{\eta _\alpha }- B_{\eta _\alpha } C_{y^\alpha } \end{aligned}$$

and the generalised Poisson bracket

$$\begin{aligned} \{ B,C,D\}:=B_{y^\alpha } C D_{\eta _\alpha }- B_{\eta _\alpha } C D_{y^\alpha } \end{aligned}$$

on matrix-functions on the cotangent bundle. In formula (6.5) the second term on the RHS is the result of switching to half-densities, see (4.5).

Introducing the shorthand $q^\pm (t):=q^\pm (x^\pm (t;y,\eta ), \xi ^\pm (t;y,\eta ))$, the task at hand is to show that

$$\begin{aligned} \zeta ^\pm (t;y,\eta )=e^{-i\,\int _0^t q^\pm (\tau )\,d \tau }\,v^\pm (x^\pm ,\xi ^\pm ). \end{aligned}$$

More explicitly, we need to show that

$$\begin{aligned}&e^{i\,\int _0^t q^\pm (\tau )\,d \tau }\left( \frac{d}{dt} +[\dot{x}^\pm ]^\alpha \,\frac{1}{4} \sigma _\beta \left( \frac{\partial \sigma ^\beta }{\partial x^\alpha }+ \Gamma ^\beta {}_{\alpha \gamma }\sigma ^\gamma \right) \right) \nonumber \\&\quad \times \left[ e^{-i\,\int _0^t q^\pm (\tau )\,d \tau }\,v^\pm (x^\pm ,\xi ^\pm )\right] =0, \end{aligned}$$

(6.6)

where we premultiplied our expression by $e^{i\,\int _0^t q^\pm (\tau )\,d \tau }$ for the sake of convenience.

We shall prove (6.1) for $\mathfrak {a}_0^+$, which corresponds to the upper choice of signs in (6.6). The proof for $\mathfrak {a}_{0}^-$ is analogous.

Let us begin by computing

$$\begin{aligned} e^{i\,\int _0^t q^+(\tau )} \dfrac{d}{dt}\left( e^{-i\,\int _0^t q^+(\tau )\,d \tau }\,v^+(x^+,\xi ^+)\right)= & {} -i q^+(t) \,v^++ v^+_{x^\alpha }[\dot{x}^+]^\alpha +v^+_{\xi _\alpha } [\dot{\xi }^+]_\alpha \nonumber \\= & {} -i q^+(t) \,v^+ + \{v^+,h\}. \end{aligned}$$

(6.7)

To this end, let us choose geodesic normal coordinates centred at $x^+(t;y,\eta )=0$ and such that $[\xi ^+(t;y,\eta )]_\alpha =\delta _{3\alpha }$. Furthermore, up to a global rigid rotation of the framing, we can assume that

$$\begin{aligned} e_j{}^\alpha (0)=\delta _j{}^\alpha . \end{aligned}$$

In our special coordinate system we have

$$\begin{aligned} v^+(0,\xi ^+)= \begin{pmatrix} 1\\ 0 \end{pmatrix}, \qquad v^-(0,\xi ^+)= \begin{pmatrix} 0\\ 1 \end{pmatrix}, \end{aligned}$$

(6.8)

and we can expand our framing about $x^+=0$ as

$$\begin{aligned}&\begin{pmatrix} e_1{}^1(x)&{}e_1{}^2(x)&{}e_1{}^3(x)\\ e_2{}^1(x)&{}e_2{}^2(x)&{}e_2{}^3(x)\\ e_3{}^1(x)&{}e_3{}^2(x)&{}e_3{}^3(x) \end{pmatrix} = \begin{pmatrix} 1&{}l^3(x)&{}-l^2(x)\\ -l^3(x)&{}1&{}l^1(x)\\ l^2(x)&{}-l^1(x)&{}1 \end{pmatrix}\nonumber \\&\quad +O(\Vert x\Vert ^2) \quad \text {as }x\rightarrow 0, \end{aligned}$$

(6.9)

where $l^k(x)=O(\Vert x\Vert )$, $k=1,2,3$.

The fact that $([v^+]^*v^+)(x,\xi )=1$ implies

$$\begin{aligned} \{[v^+]^*,P^+,v^+\}(0,\xi ^+)= [v^+_{x^\alpha }]^*\,v^+\,[v^+]^*\,v^+_{\xi ^\alpha } - [v^+_{\xi _\alpha }]^*\,v^+\,[v^+]^*\,v^+_{x^\alpha }=0, \end{aligned}$$

which, in turn, yields

$$\begin{aligned} \{[v^+]^*,W_\mathrm {prin},v^+\}=h\,\{[v^+]^*,2P^+-\mathrm {Id},v^+\}=-h\,\{[v^+]^*,v^+\}. \end{aligned}$$

(6.10)

A standard perturbation argument gives us

$$\begin{aligned} h\,\{[v^+]^*,v^+\}(0,\xi ^+)=\left. -\frac{i}{2} \left( \dfrac{\partial l^1}{\partial x^1}+\dfrac{\partial l^2}{\partial x^2}\right) \right| _{x=0} \end{aligned}$$

(6.11)

and

$$\begin{aligned} \{v^+,h\}(0,\xi ^+)=\left. \frac{i}{2} \begin{pmatrix} 0\\ \dfrac{\partial l^1}{\partial x^3}+i\dfrac{\partial l^2}{\partial x^3} \end{pmatrix}\right| _{x=0}. \end{aligned}$$

(6.12)

Furthermore, combining (6.9) with (1.3) and (6.5), we get

$$\begin{aligned} W_\mathrm {sub}(0)=-\left. \frac{1}{2}\left( \dfrac{\partial l^1}{\partial x^1}+\dfrac{\partial l^2}{\partial x^2}+\dfrac{\partial l^3}{\partial x^3} \right) \right| _{x=0}\,\mathrm {Id}. \end{aligned}$$

(6.13)

Substituting (6.8), (6.10) and (6.11)–(6.13) into (6.4), and then (6.4) and (6.12) into (6.7), we conclude that

$$\begin{aligned}&e^{i\,\int _0^t q^+(\tau )} \dfrac{d}{dt}\left( e^{-i\,\int _0^t q^+(\tau )\,d \tau }\,v^+(x^+,\xi ^+)\right) \nonumber \\&\quad =\left. \dfrac{i}{2}\begin{pmatrix} \dfrac{\partial l^3}{\partial x^3} \\ 0 \end{pmatrix}\right| _{x=0} +\left. \dfrac{i}{2}\begin{pmatrix} 0\\ \dfrac{\partial l^1}{\partial x^3}+i\dfrac{\partial l^2}{\partial x^3} \end{pmatrix}\right| _{x=0}. \end{aligned}$$

(6.14)

Similarly, in our special coordinate system we have

$$\begin{aligned}&\left. [\dot{x}^+]^\alpha \,\frac{1}{4} \sigma _\beta \left( \frac{\partial \sigma ^\beta }{\partial x^\alpha }+ \Gamma ^\beta {}_{\alpha \gamma }\sigma ^\gamma \right) v^+\right| _{x=0,\ \xi =\xi ^+} = \left. \frac{1}{4} \sigma _\beta \left( \frac{\partial \sigma ^\beta }{\partial x^3}\right) \begin{pmatrix} 1\\ 0 \end{pmatrix} \right| _{x=0}\nonumber \\&\quad = \left. -\frac{i}{2} \begin{pmatrix} \dfrac{\partial l^3}{\partial x^3} \\ \dfrac{\partial l^1}{\partial x^3}+i\dfrac{\partial l^2}{\partial x^3} \end{pmatrix} \right| _{x=0}. \end{aligned}$$

(6.15)

Summing up (6.14) and (6.15) we arrive at (6.6).$\square$

7 Explicit Small Time Expansion of the Symbol

Even though the presence of gauge degrees of freedom represents an additional challenge in the analysis of the propagator, one can put this freedom to use and exploit it to obtain a small time expansion for the propagator.

Our strategy goes as follows.

• 1. Compute the principal and subprincipal symbols of the positive (resp. negative) propagator for a conveniently chosen framing;

• 2. Using the gauge transformation (1.7), (1.6), switch to an arbitrary framing with the same orientation;⁵

• 3. Express the final result in terms of geometric invariants.

7.1 Special Framing

Let us fix an arbitrary point $y\in M$ and let $V_j\in T_yM$, $j=1,2,3$ be defined by

$$\begin{aligned} V_j:=e_j(y). \end{aligned}$$

Definition 7.1

(Levi-Civita framing) Let $\mathcal {U}$ be a geodesic neighbourhood of y. For $x\in \mathcal {U}$, let $\widetilde{e}_j^{\mathrm {loc}}(x)$, $j=1,2,3$, be the parallel transport of $V_j$ along the shortest geodesic connecting y to x. We define the Levi-Civita framing generated by $\{e_j\}_{j=1}^3$ at y to be the equivalence class of framings coinciding with $\{\widetilde{e}_j^{\mathrm {loc}}\}_{j=1}^3$ in a neighbourhood of y.

With slight abuse of notation, in the following we will identify the Levi-Civita framing with one of its representatives, denoted by $\{\widetilde{e}_j\}_{j=1}^3$. The choice of a particular representative does not affect our results.

Using the Levi-Civita framing is especially convenient due to the following property.

Lemma 7.2

In normal coordinates centred at y, the Levi-Civita framing admits the following expansion:

$$\begin{aligned} \widetilde{e}_j{}^\alpha (x)=e_j{}^\alpha (y)+\frac{1}{6} e_j{}^\beta (y)\,R^\alpha {}_{\mu \beta \nu }(y)\,x^\mu x^\nu +O(\Vert x\Vert ^3), \qquad j=1,2,3, \nonumber \\ \end{aligned}$$

(7.1)

where R is the Riemann curvature tensor⁶.

Proof

In normal geodesic coordinates centred at y, the unique geodesic connecting y to x can be written as

$$\begin{aligned} \gamma ^\alpha (t)=\frac{x^\alpha }{\Vert x\Vert _E}\,t, \end{aligned}$$

(7.2)

where $\Vert \,\cdot \,\Vert _E$ is the Euclidean norm, so that $\gamma (\Vert x\Vert _E)=x$. Assuming t and $\Vert x\Vert _E$ to be small and of the same order, let us perform an expansion in powers of t of $\widetilde{e}_j$.

The parallel transport equation defining the framing $\{\widetilde{e}_j\}_{j=1}^3$ reads

$$\begin{aligned} \dot{\widetilde{e}}_j{}^\alpha (\gamma (t))=-\dot{\gamma }^\beta (t)\, \Gamma ^\alpha {}_{\beta \mu }(\gamma (t))\,\, \widetilde{e}_j{}^\mu (\gamma (t)), \qquad j=1,2,3. \end{aligned}$$

(7.3)

Since $\widetilde{e}_j(0)=V_j$ and $\Gamma (0)=0$, at linear order in t we have $\dot{\widetilde{e}}_j(\gamma (t))=O(t),$ which implies

$$\begin{aligned} \widetilde{e}_j(\gamma (t))=V_j+O(t^2). \end{aligned}$$

(7.4)

Substituting (7.4) into (7.3), we get

$$\begin{aligned} \dot{\widetilde{e}}_j{}^\alpha (\gamma (t))=-\frac{x^\beta \,x^\nu }{\Vert x\Vert _E^2} \partial _\nu \Gamma ^\alpha {}_{\beta \mu }(0)\,V_j{}^\mu \,t+O(t^2), \end{aligned}$$

so that

$$\begin{aligned} \widetilde{e}_j{}^\alpha (\gamma (t))=V_j-\frac{1}{2}\frac{x^\beta x^\nu }{\Vert x\Vert _E^2} \partial _\nu \Gamma ^\alpha {}_{\beta \mu }(0) \, V_j{}^\mu \,t^2+O(t^3) \quad \end{aligned}$$

and

$$\begin{aligned} \widetilde{e}_j{}^\alpha (x)=\widetilde{e}_j{}^\alpha (\gamma (\Vert x\Vert _E))=V_j{}^\alpha -\frac{1}{2}\partial _\nu \Gamma ^\alpha {}_{\beta \mu }(0)\,V_j{}^\mu \, x^\beta x^\nu +O(\Vert x\Vert ^3), \end{aligned}$$

(7.5)

$j=1,2,3$. Formula (7.1) follows at once from (7.5) and the elementary identity

$$\begin{aligned} \partial _\nu \Gamma ^\alpha {}_{\beta \mu }(0)=-\frac{1}{3} (R^\alpha {}_{\beta \mu \nu }+R^\alpha {}_{\mu \beta \nu })(0). \end{aligned}$$

(7.6)

$\square$

Corollary 7.3

In normal coordinates x centred at y, the Pauli matrices $\widetilde{\sigma }^\alpha (x)$ projected along the Levi-Civita framing (see (1.3)) satisfy

$$\begin{aligned} \begin{aligned} \widetilde{\sigma }^\alpha (y)=\sigma ^\alpha (y), \qquad [\widetilde{\sigma }^\alpha ]_{x^\beta }(y)=0,\\ [\widetilde{\sigma }^\alpha ]_{x^\mu x^\nu }(y)=\frac{1}{6} \left[ R^\alpha {}_{\nu \beta \mu }(y)+R^\alpha {}_{\mu \beta \nu }(y) \right] \sigma ^\beta (y). \end{aligned} \end{aligned}$$

(7.7)

Proof of Corollary 7.3

Formula (7.7) follows immediately from (7.1).$\square$

Corollary 7.4

Let $\widetilde{W}$ be the Dirac operator (1.4) corresponding to the choice of the Levi-Civita framing. Then, in normal coordinates centred at y, its zero order part $\widetilde{W}_0$ (see formula (5.2)) admits the following expansion:

$$\begin{aligned} \widetilde{W}_0(x)=\frac{i}{4} {\text {Ric}}_{\alpha \beta }(y)\,\widetilde{\sigma }^\beta (y)\, x^\alpha +O(\Vert x\Vert ^2). \end{aligned}$$

(7.8)

Here ${\text {Ric}}$ is the Ricci tensor, ${\text {Ric}}_{\alpha \beta }:=R^\gamma {}_{\alpha \gamma \beta }$.

Proof

Formula (7.8) is obtained by expanding the RHS of (5.2) in powers of x in normal coordinates centred at y, substituting (7.6) and (7.7) in and performing a lengthy but straightforward calculation. It is a somewhat nontrivial fact that the coefficient of the linear term in (7.8) turns out to be trace-free.$\square$

7.2 Small Time Expansion of the Principal Symbols

The first step towards computing small time expansions for principal and subprincipal symbols of W is to obtain an expression for these objects in a neighbourhood of a given point $y\in M$ for the choice of the Levi-Civita framing generated by our framing $\{e_j\}_{j=1}^3$ at y. Observe that, as we are after a small time expansion of the symbols, it is enough to restrict our attention to a small open neighbourhood of y.

In the following, we will denote with a tilde objects associated with the Dirac operator $\widetilde{W}$ corresponding to the choice of the Levi-Civita framing.

Theorem 7.5

For the choice of the Levi-Civita framing, the positive and negative principal symbols are independent of t and read

$$\begin{aligned} \widetilde{\mathfrak {a}}^{\pm }_0(t;y,\eta )=\widetilde{P}^{\pm }(y,\eta ). \end{aligned}$$

(7.9)

Proof

In accordance with Theorem 6.1, the principal symbols are determined by the eigenvectors of $\widetilde{W}_\mathrm {prin}$ and their parallel transport with respect with the spin connection along the Hamiltonian trajectories. Hence, it suffices to show that

$$\begin{aligned} \widetilde{\zeta }^\pm (t;y,\eta )=\widetilde{v}^\pm (y,\eta ). \end{aligned}$$

(7.10)

Once this is achieved, (7.9) follows from the fact that

$$\begin{aligned} \widetilde{W}_\mathrm {prin}(y,\eta )=W_\mathrm {prin}(y,\eta ). \end{aligned}$$

In normal coordinates centred at y the parallel transport equation (6.2) reads

$$\begin{aligned}&\left[ \frac{d}{dt} +[\dot{x}^\pm ]^\alpha \,\frac{1}{4} \widetilde{\sigma }_\beta (x^\pm )\left( \frac{\partial \widetilde{\sigma }^\beta }{\partial x^\alpha }(x^\pm )+\Gamma ^\beta {}_{\alpha \gamma }(x^\pm )\widetilde{\sigma }^\gamma (x^\pm )\right) \right] \widetilde{\zeta }^\pm =0,\nonumber \\&\widetilde{\zeta }^\pm |_{t=0}=\widetilde{v}^\pm . \end{aligned}$$

(7.11)

We claim that

$$\begin{aligned}{}[\dot{x}^\pm ]^\alpha \left( \frac{\partial \widetilde{\sigma }^\beta }{\partial x^\alpha }(x^\pm )+\Gamma ^\beta {}_{\alpha \gamma }(x^\pm )\widetilde{\sigma }^\gamma (x^\pm )\right) =0. \end{aligned}$$

(7.12)

In fact, we have

$$\begin{aligned}{}[\dot{x}^\pm ]^\alpha \left( \frac{\partial \widetilde{\sigma }^\beta }{\partial x^\alpha }(x^\pm )+\Gamma ^\beta {}_{\alpha \gamma }(x^\pm )\widetilde{\sigma }^\gamma (x^\pm )\right) = [\dot{x}^\pm ]^\alpha (\partial _{x^\alpha } \widetilde{e}_j{}^\beta +\Gamma ^\beta {}_{\alpha \gamma }\, \widetilde{e}_j{}^\gamma )(x^\pm ) \,s^j \end{aligned}$$

and

$$\begin{aligned}{}[\dot{x}^\pm ]^\alpha (\partial _{x^\alpha } \widetilde{e}_j{}^\beta +\Gamma ^\beta {}_{\alpha \gamma }\, \widetilde{e}_j{}^\gamma )(x^\pm )=0 \quad \text {for}\quad j=1,2,3 \end{aligned}$$

in view of Definition 7.1 and the properties of the Hamiltonian flows $x^\pm$, i.e. that $x^+(\,\cdot \,;y,\eta )$ is geodesic and relation (5.3). By substituting (7.12) into (7.11) we arrive at (7.10).$\square$

7.3 Small Time Expansion of the Subprincipal Symbols

Let us now turn our attention to the subprincipal symbols $\widetilde{\mathfrak {a}}_{-1}^\pm$.

Unlike the principal symbols, the subprincipal symbols depend on the choice of phase functions. As here we are only interested in small time expansions and the injectivity radius ${\text {Inj}}(M,g)$ is strictly positive, we can work, without loss of generality, in a neighbourhood of y with no conjugate points to y. The absence of conjugate points allows us to construct positive and negative propagators for small times by means of the algorithm described in Sect. 3.3 for the choice of real-valued Levi-Civita phase functions

$$\begin{aligned} \varphi ^\pm (t,x;y,\eta )=\int _{\gamma ^\pm } \zeta ^\pm \,dz, \end{aligned}$$

cf. Definition 5.1 for $\epsilon =0$.

In the remainder of this subsection we adopt the same coordinates for x and y and we choose normal geodesic coordinates centred at y. We remind the reader that, in such coordinates,

$$\begin{aligned}{}[x^\pm ]^\alpha (t;0,\eta )=\pm \frac{\eta ^\alpha }{h}\,t. \end{aligned}$$

(7.13)

According to [17, Eqns. (8.7) and (8.12)] and (5.5), we have

$$\begin{aligned} \varphi ^\pm (t,x;0,\eta )=x^\alpha \eta _\alpha \mp h\,t\pm \frac{{t}}{3h} R^\alpha {}_\mu {}^\beta {}_\nu (0) \eta _\alpha \eta _\beta \,x^\mu x^\nu +O(\Vert x\Vert ^4+t^4)\nonumber \\ \end{aligned}$$

(7.14)

and

$$\begin{aligned} w^\pm (t,x;0,\eta )=1+\frac{1}{12}{\text {Ric}}_{\mu \nu }(0)\,x^\mu \,x^\nu \mp \frac{t}{3h}{\text {Ric}}^\mu {}_\nu (0)\,\eta _\mu \,x^\nu +O(\Vert x\Vert ^3+|t|^3).\nonumber \\ \end{aligned}$$

(7.15)

Recall that the weight w is defined by (3.12).

As explained in Sect. 5.1, the subprincipal symbols are determined by the first and the second transport equations, (5.12) and (5.13). More precisely, if we are interested in expansions with remainder $O(t^2)$, we need to determine (5.13) up to zeroth order in t and (5.12) up to first order in t.

To this end, we begin by observing that formulae (7.14) and (7.15), see also (3.30), imply that the differential evaluation operators $\mathfrak {S}^\pm _{-2}$ and $\mathfrak {S}^\pm _{-1}$ admit the following expansions in normal coordinates centred at y.

Lemma 7.6

We have

• (a)
  $$\begin{aligned} \mathfrak {S}^\pm _{-2}=\left. \frac{1}{2} \left[ i \dfrac{\partial ^2}{\partial x^\alpha \partial \eta _\alpha } \right] ^2 \left( \,\cdot \,\right) \right| _{t=0, \,x=0}+O(t), \end{aligned}$$

  (7.16)
• (b)
  $$\begin{aligned} \mathfrak {S}^\pm _{-1}=i\,\mathfrak {S}_0^\pm \left( \dfrac{\partial ^2}{\partial x^\alpha \partial \eta _\alpha }\pm \frac{t}{2}\, h_{\eta _\alpha \eta _\beta } \dfrac{\partial ^2}{\partial x^\alpha \partial x^\beta } \right) +O(t^2). \end{aligned}$$

  (7.17)

Proof

(a) It is an immediate consequence of (7.13), (7.15) and

$$\begin{aligned} L^\pm _\alpha =\dfrac{\partial }{\partial x^\alpha }+O(\Vert x\Vert +|t|). \end{aligned}$$

(7.18)

(b) Substituting (7.15) into (3.30) with $k=1$ and recalling that

$$\begin{aligned} \left. \varphi ^\pm _{\eta }\right| _{x=x^\pm }=0, \end{aligned}$$

we get

$$\begin{aligned} \mathfrak {S}^{\pm }_{-1}=\mathfrak {S}_0^{\pm }\left[ i \dfrac{\partial ^2}{\partial x^\alpha \partial \eta _\alpha }-\frac{i}{2} \varphi ^{\pm }_{\eta _\alpha \eta _\beta }L^{\pm }_\alpha L^{\pm }_\beta \right] +O(t^2). \end{aligned}$$

(7.19)

Formula (7.18) and the fact that

$$\begin{aligned} \left. \varphi ^\pm _{\eta _\alpha \eta _\beta }\right| _{x=x^\pm }=\mp t\, h_{\eta _\alpha \eta _\beta }+O(t^3) \end{aligned}$$

(7.20)

yield (7.17).$\square$

In order to be able to compute the subprincipal symbols, we need to determine the initial condition $\widetilde{\mathfrak {a}}^\pm _{-1}|_{t=0}$ first.

Lemma 7.7

For the choice of real-valued Levi-Civita phase functions, the positive and negative subprincipal symbols $\widetilde{\mathfrak {a}}^\pm _{-1}$ vanish at $t=0$:

$$\begin{aligned} \widetilde{\mathfrak {a}}^\pm _{-1}(0;y,\eta )=0. \end{aligned}$$

(7.21)

Proof

The subprincipal symbols are scalar functions, so it enough to establish (7.21) in one specific coordinate system. Let us choose normal coordinates centred at $y=0$ such that $\widetilde{e}_j{}^\alpha (0)=\delta _j{}^\alpha$. We observe that the torsion of the Weitzenböck connection generated by the Levi-Civita framing at y vanishes at y, as a consequence of the fact that the first derivatives of the framing are zero, cf. (7.1) and (A.2)–(A.3). Therefore, Theorem 5.6 tells us that

$$\begin{aligned}{}[U^\pm (0)]_\mathrm {sub}(0,\eta )=0. \end{aligned}$$

(7.22)

A straightforward perturbation argument shows that

$$\begin{aligned} (v^\pm )_{x^\alpha }(0,\eta )=0. \end{aligned}$$

(7.23)

Substituting (7.22) and (7.23) into (4.6) with $P=U^\pm (0)$ and $\epsilon =0$ and using the fact that Christoffel symbols vanish at y, we arrive at (7.21).$\square$

We are now in a position to examine the first transport equation.

Lemma 7.8

The projection onto the negative (resp. positive) eigenspace of $\widetilde{W}_\mathrm {prim}$ of the subprincipal symbol of the positive (resp. negative) propagator is given by

$$\begin{aligned}&\widetilde{P}^\mp (x^\pm ,\xi ^\pm )\widetilde{\mathfrak {a}}_{-1}^\pm (t;y,\eta ) =\nonumber \\&\pm it\,\widetilde{P}^\mp (y,\eta ) \left[ \frac{1}{8h^3}\,{\text{ Ric }}_{\alpha \beta }(y)\,\eta ^\alpha \eta ^\beta -\frac{1}{4h}{\text{ Ric }}_{\alpha \beta }(y)\,\eta ^\alpha \widetilde{P}^\pm _{\eta _\beta }(y,\eta ) \right] +O(t^2). \end{aligned}$$

(7.24)

Proof

We will establish formula (7.24) by expanding the first transport equation (5.12) up to first order in t and then acting with $\widetilde{P}^\mp$ on the left. Recall that $a^\pm _{-k}$ is defined by (5.10).

Working in normal coordinates centred at y and using (7.14)–(7.15), we obtain

(7.25)

Furthermore, in view of Theorem 6.1 and Lemma 7.6(b), we have

$$\begin{aligned}&\mathfrak {S}^\pm _{-1}\widetilde{a}^\pm _{1}(t;0,\eta ) \nonumber \\&\quad = \left[ \dfrac{\partial ^2}{\partial x^\alpha \partial \eta _\alpha }\pm \frac{t}{2}\, h_{\eta _\alpha \eta _\beta } \dfrac{\partial ^2}{\partial x^\alpha \partial x^\beta } \right] \times \left. \left( \varphi ^\pm _t+\widetilde{W}_{\mathrm {prin}}(x,\varphi ^\pm _x)\right) \widetilde{\mathfrak {a}}_0^\pm \right| _{x=x^*} \nonumber \\&\qquad +O(t^2)\nonumber \\&\quad = -\frac{2\mathrm {i}t}{3h^2}{\text {Ric}}_{\alpha \nu }(0) \,\eta ^\alpha \eta ^\nu \widetilde{P}^\pm \pm \mathrm {i}t \left[ \frac{2}{3h}R^{\mu }{}_\alpha {}^\nu {}_\beta (0)\,\eta _\mu \eta _\nu \,\widetilde{\sigma }^\beta (0)\widetilde{P}^\pm \right] _{\eta _\alpha }\nonumber \\&\qquad \pm it \frac{\eta ^\beta }{h}\left[ (\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta )\widetilde{P}^\pm \right] _{\eta _\alpha } \nonumber \\&\qquad +\mathrm {i}\,t \left[ \frac{h_{\eta _\alpha \eta _\beta }}{3h}\,R^{\mu }{}_\alpha {}^\nu {}_\beta (0)\,\eta _\mu \eta _\nu \pm \frac{1}{2}h_{\eta _\alpha \eta _\beta }(\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta ) \right] \widetilde{P}^\pm \nonumber \\&\qquad +O(t^2). \end{aligned}$$

(7.26)

Adding up (7.25) and (7.26) and projecting along $\widetilde{P}^{\mp }$, we arrive at

$$\begin{aligned}&\widetilde{P}^{\mp }\widetilde{\mathfrak {a}}_{-1}^\pm (t;0,\eta )\nonumber \\&\quad = \frac{i t}{h}\widetilde{P}^\mp \left\{ \frac{1}{12h}{\text {Ric}}_{\alpha \nu }(0)\,\eta ^\alpha \widetilde{\sigma }^\nu (0) \widetilde{P}^\pm -\frac{i\eta ^\alpha }{2h}(\widetilde{W}_0)_{x^\alpha }(0)\,\widetilde{P}^\pm \right. \nonumber \\&\qquad +\left[ \frac{1}{3h}R^\mu {}_\alpha {}^\nu {}_\beta (0) \,\eta _\mu \eta _\nu \,\widetilde{\sigma }^\beta (0) \,\widetilde{P}^\pm \right] _{\eta _\alpha }+\frac{\eta ^\beta }{2h} \left[ (\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta )\widetilde{P}^\pm \right] _{\eta _\alpha }\nonumber \\&\qquad +\frac{1}{4} h_{\eta _\alpha \eta _\beta }\,(\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta )\,\widetilde{P}^\pm \left. \right\} +O(t^2). \end{aligned}$$

(7.27)

Let us compute the summands in (7.27) separately. To this end, let us put

$$\begin{aligned} \begin{aligned}&A_1:=\frac{1}{12h}{\text {Ric}}_{\alpha \nu }(0)\,\eta ^\alpha \widetilde{\sigma }^\nu (0) \widetilde{P}^\pm ,\\&A_2:=-\frac{i\eta ^\alpha }{2h}(\widetilde{W}_0)_{x^\alpha }(0)\,\widetilde{P}^\pm ,\\&A_3:=\left[ \frac{1}{3h}R^\mu {}_\alpha {}^\nu {}_\beta (0) \,\eta _\mu \eta _\nu \,\widetilde{\sigma }^\beta (0) \,\widetilde{P}^\pm \right] _{\eta _\alpha },\\&A_4:=\frac{\eta ^\beta }{2h} \left[ (\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta )\widetilde{P}^\pm \right] _{\eta _\alpha },\\&A_5:=\frac{1}{4} h_{\eta _\alpha \eta _\beta }\,(\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta )\,\widetilde{P}^\pm . \end{aligned} \end{aligned}$$

• $A_1$: It ensues from elementary properties of $\widetilde{P}^\pm$ that

  

  (7.28)

  Hence

  $$\begin{aligned} \widetilde{P}^\mp A_1=\widetilde{P}^\mp \left( \pm \frac{1}{6}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \widetilde{P}^\pm _{\eta _\beta } \right) . \end{aligned}$$

  (7.29)

• $A_2$: Combining Corollary 7.4 with the identity

  $$\begin{aligned} h_{\eta _\alpha \eta _\beta }=\dfrac{h^2\,\delta ^{\alpha \beta }-\eta ^\alpha \eta ^\beta }{h^3} \end{aligned}$$

  (7.30)

  and using (7.28), we get

  $$\begin{aligned} \widetilde{P}^\mp A_2=\widetilde{P}^\mp \left( \pm \frac{1}{4}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \widetilde{P}^\pm _{\eta _\beta } \right) . \end{aligned}$$

  (7.31)

• $A_3$: We have

  $$\begin{aligned} \begin{aligned} A_3&=\left[ \frac{1}{3h}R^\mu {}_\alpha {}^\nu {}_\beta (0) \,\eta _\mu \eta _\nu \,\widetilde{\sigma }^\beta (0) \,\widetilde{P}^\pm \right] _{\eta _\alpha }\\&=\frac{1}{3h}R^\mu {}_\alpha {}^\nu {}_\beta (0)\,\widetilde{\sigma }^\beta (0)\left[ \eta _\mu \eta _\nu \,\widetilde{P}^\pm \right] _{\eta _\alpha }\\&=-\frac{1}{3 h}{\text {Ric}}_{\mu \nu }(0)\,\eta ^\mu \,\widetilde{\sigma }^\nu (0)\,\widetilde{P}^\pm \pm \frac{1}{6\,h^2} {\text {Ric}}_{\mu \beta }(0)\,\eta ^\mu \eta ^\beta \, \mathrm {Id}, \end{aligned} \end{aligned}$$

  so that, by (7.28),

  $$\begin{aligned} \widetilde{P}^\mp A_3=\widetilde{P}^\mp \left( \mp \frac{2}{3}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \widetilde{P}^\pm _{\eta _\beta }\pm \frac{1}{6\,h^2}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \eta ^\beta \right) . \end{aligned}$$

  (7.32)

• $A_4$: Recalling (7.7), we have

  $$\begin{aligned} \begin{aligned} A_4&= \frac{\eta ^\beta }{2h}(\widetilde{\sigma }^\mu )_{x^\alpha x^\beta }(0) \left[ \eta _\mu \,\widetilde{P}^\pm \right] _{\eta _\alpha }\\&=-\frac{1}{12h}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \widetilde{\sigma }^\beta (0)\,\widetilde{P}^\pm \mp \frac{1}{24 \,h^2} {\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \eta ^\beta \, \mathrm {Id}, \end{aligned} \end{aligned}$$

  so that, by (7.28),

  $$\begin{aligned} \widetilde{P}^\mp A_4=\widetilde{P}^\mp \left( \mp \frac{1}{6}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \widetilde{P}^\pm _{\eta _\beta }\mp \frac{1}{24\,h^2}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \eta ^\beta \right) . \end{aligned}$$

  (7.33)

• $A_5$: In view of (7.30) and (7.7), we have

  $$\begin{aligned} \begin{aligned} A_5&=\frac{1}{4} \left( \frac{\delta ^{\alpha \beta }}{h}-\frac{\eta ^\alpha \eta ^\beta }{h^3} \right) \frac{1}{6} \left[ R^\mu {}_{\beta \nu \alpha }+R^\mu {}_{\alpha \nu \beta }\right] (0)\,\widetilde{\sigma }^\nu (0)\,\eta _\mu \,\widetilde{P}^\pm \\&=\frac{1}{12\,h}\,{\text {Ric}}_{\mu \nu }(0)\,\eta ^\mu \widetilde{\sigma }^\nu (0)\, \widetilde{P}^\pm , \end{aligned} \end{aligned}$$

  so that, by (7.28),

  $$\begin{aligned} \widetilde{P}^\mp A_5=\widetilde{P}^\mp \left( \pm \frac{1}{6}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \widetilde{P}^\pm _{\eta _\beta }\right) . \end{aligned}$$

  (7.34)

Substituting (7.29), (7.31), (7.32), (7.33) and (7.34) into (7.27) we arrive at (7.24).$\square$

Let us now move to the second transport equation.

Lemma 7.9

The projection onto the positive (resp. negative) eigenspace of $\widetilde{W}_\mathrm {prin}$ of the subprincipal symbol of the positive (resp. negative) propagator is given by

$$\begin{aligned}&\widetilde{P}^\pm (x^\pm ,\xi ^\pm )\widetilde{\mathfrak {a}}_{-1}^\pm (t;y,\eta ) \nonumber \\&\quad =\mp it\,\widetilde{P}^\pm \left[ \frac{1}{24 h}\mathcal {R}(0) + \frac{1}{8h^3}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \,\eta ^\beta + \frac{1}{4h}{\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \,\widetilde{P}^\pm _{\eta _\beta } \right] \nonumber \\&\quad +O(t^2). \end{aligned}$$

(7.35)

Proof

We will establish formula (7.35) by computing the second transport equation (5.13) up to zeroth order in t and then acting with $\widetilde{P}^\pm$ on the left.

With account of Lemma 7.6, we have

$$\begin{aligned}&\left. \mathfrak {S}^\pm _{-2}\widetilde{a}^\pm _{1}\right| _{t=0} \nonumber \\&\quad =\left. -\frac{1}{2} \dfrac{\partial ^4}{\partial x^\alpha \partial \eta _\alpha \partial x^\beta \partial \eta _\beta } \left( \varphi _t^\pm +\widetilde{W}_\mathrm {prin}(x,\varphi _x^\pm ) \right) \mathfrak {a}_0^\pm \right| _{x=0,t=0}\nonumber \\&\quad = -\frac{1}{2} \dfrac{\partial ^4}{\partial x^\alpha \partial \eta _\alpha \partial x^\beta \partial \eta _\beta }\left( \mp h\pm \frac{1}{3\,h} \,R^\gamma {}_\mu {}^\rho {}_\nu (0)\,\eta _\gamma \,\eta _\rho \,x^\mu \, x^\nu +O(\Vert x\Vert ^3) \right. \nonumber \\&\qquad \left. +\widetilde{\sigma }^\alpha (0)(\eta _\alpha +O(\Vert x \Vert ^3)) \widetilde{P}^\pm \Bigr ) \right| _{x=0,t=0}\nonumber \\&\quad =-\dfrac{\partial ^2}{\partial \eta _\alpha \partial \eta _\beta } \left( \pm \frac{1}{3\,h} \,R^\gamma {}_\alpha {}^\rho {}_\beta (0)\,\eta _\gamma \,\eta _\rho +\frac{1}{2} (\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta ) \right) \widetilde{P}^\pm , \end{aligned}$$

(7.36)

$$\begin{aligned}&\left. \mathfrak {S}^\pm _{-1}\widetilde{a}^\pm _{0}\right| _{t=0}=i\,\dfrac{\partial ^2}{\partial x^\alpha \partial \eta _\alpha }\left[ \left( \mp h+\widetilde{W}_\mathrm {prin}(x,\eta ) \right) \widetilde{\mathfrak {a}}^\pm _{-1}(0;y,\eta )-i (\widetilde{\mathfrak {a}}^\pm _{0})_t\right. \nonumber \\&\qquad \left. \left. +\left( \pm \frac{i \eta _\mu }{3h}{\text {Ric}}^\mu {}_\nu (0)\,x^\nu +-\frac{i}{6}{\text {Ric}}_{\mu \nu }(0)\,\widetilde{\sigma }^\mu (0)\,x^\nu +O(\Vert x\Vert ^2)\right) \widetilde{P}^\pm \right. \right. \nonumber \\&\qquad \left. \left. +\widetilde{W}_0(x)\widetilde{P}^\pm \right] \right| _{t=0,x=0}\nonumber \\&\quad =\mp \dfrac{\partial }{\partial \eta _\alpha }\left( \frac{\eta _\mu }{3h^{(j)}}{\text {Ric}}^\mu {}_\alpha (0)\widetilde{P}^\pm \right) +\frac{1}{6} {\text {Ric}}_{\alpha \mu }(0)\,\widetilde{\sigma }^\mu (0) \,\widetilde{P}^\pm _{\eta _\alpha }\nonumber \\&\qquad +i\, (\widetilde{W}_0)_{x^\alpha }(0)\widetilde{P}^\pm _{\eta _\alpha } \end{aligned}$$

(7.37)

and

$$\begin{aligned} \begin{aligned} \left. \mathfrak {S}^\pm _{0}\widetilde{a}^\pm _{-1}\right| _{t=0}&=(\mp h+\widetilde{W}_\mathrm {prin}(0,\eta ))\widetilde{\mathfrak {a}}^\pm _{-2}(0)-i\,(\widetilde{\mathfrak {a}}^\pm _{-1})_t|_{t=0}. \end{aligned} \end{aligned}$$

(7.38)

In carrying out the above calculations we used Theorem 7.5 and Lemma 7.7. Note that, when multiplying on the left by $\widetilde{P}^\pm$, the terms containing $\widetilde{\mathfrak {a}}^\pm _{-2}$ disappear. Summing up (7.36), (7.37) and (7.38), and projecting along $\widetilde{P}^\pm$, we obtain

$$\begin{aligned}&(\widetilde{P}^\pm \widetilde{\mathfrak {a}}^\pm _{-1})_t\,(0;y,\eta ) \nonumber \\&\quad =i \widetilde{P}^\pm \dfrac{\partial ^2}{\partial \eta _\alpha \partial \eta _\beta } \left[ \left( \pm \frac{1}{3h} \,R^\gamma {}_\alpha {}^\rho {}_\beta (0)\,\eta _\gamma \,\eta _\rho + \frac{1}{2}(\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta ) \right) \widetilde{P}^\pm \right] \nonumber \\&\qquad \pm i \widetilde{P}^\pm \frac{\partial }{\partial \eta _\alpha }\left[ \frac{\eta _\mu }{3h}{\text {Ric}}^\mu {}_\alpha (0)\widetilde{P}^\pm \right] -\frac{i}{6} {\text {Ric}}_{\alpha \mu }(0)\,\widetilde{\sigma }^\mu (0) \,\widetilde{P}^\pm _{\eta _\alpha }\nonumber \\&\qquad +\widetilde{P}^\pm (\widetilde{W}_0)_{x^\alpha }(0)\widetilde{P}^\pm _{\eta _\alpha }+O(t). \end{aligned}$$

(7.39)

Using the identity

$$\begin{aligned} \pm \dfrac{\partial }{\partial \eta _\beta }\left[ \frac{1}{3h} \,R^\gamma {}_\alpha {}^\rho {}_\beta (0)\,\eta _\gamma \,\eta _\rho \widetilde{P}^\pm \right] =\mp \frac{\eta _\mu }{3h}{\text {Ric}}^\mu {}_\alpha (0)\widetilde{P}^\pm \pm \frac{1}{3h} \,R^\gamma {}_\alpha {}^\rho {}_\beta (0)\,\eta _\gamma \,\eta _\rho \widetilde{P}^\pm _{\eta _\beta }, \end{aligned}$$

formula (7.39) becomes

$$\begin{aligned}&(\widetilde{P}^\pm \widetilde{\mathfrak {a}}^\pm _{-1})_t\,(0;y,\eta )= \frac{i}{2} \widetilde{P}^\pm \dfrac{\partial ^2}{\partial \eta _\alpha \partial \eta _\beta } \left[ (\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta ) \widetilde{P}^\pm \right] \nonumber \\&\quad \pm i \widetilde{P}^\pm \frac{\partial }{\partial \eta _\alpha }\left[ \frac{1}{3h} \,R^\gamma {}_\alpha {}^\rho {}_\beta (0)\,\eta _\gamma \,\eta _\rho \,\widetilde{P}^\pm _{\eta _\beta } \right] \nonumber \\&\quad -\frac{i}{6} {\text {Ric}}_{\alpha \mu }(0)\,\widetilde{\sigma }^\mu (0) \,\widetilde{P}^\pm _{\eta _\alpha }+\widetilde{P}^\pm (\widetilde{W}_0)_{x^\alpha }(0)\widetilde{P}^\pm _{\eta _\alpha }+O(t). \end{aligned}$$

(7.40)

Let us put

$$\begin{aligned} \begin{aligned}&B_1:=\frac{i}{2}\left[ (\widetilde{W}_\mathrm {prin})_{x^\alpha x^\beta }(0,\eta ) \widetilde{P}^\pm \right] _{\eta _\alpha \eta _\beta },\\&B_2:=\frac{i}{3h} \,R^\gamma {}_\alpha {}^\rho {}_\beta (0)\,\eta _\gamma \,\eta _\rho \,\widetilde{P}^\pm _{\eta _\beta },\\&B_3:=-\frac{i}{6} {\text {Ric}}_{\alpha \mu }(0)\,\widetilde{\sigma }^\mu (0) \,\widetilde{P}^\pm _{\eta _\alpha }+(\widetilde{W}_0)_{x^\alpha }(0)\widetilde{P}^\pm _{\eta _\alpha }. \end{aligned} \end{aligned}$$

(7.41)

• $B_1$: It follows from (5.17), Corollary 7.3 and (7.30) that

  

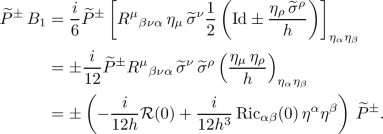  (7.42)

• $B_2$: Differentiating (5.17) with respect to $\eta _\beta$ yields

  

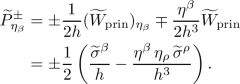  (7.43)

  Substituting (7.43) into $B_2$ in (7.41) we obtain

  $$\begin{aligned} {\begin{matrix} \pm \widetilde{P}^\pm \,B_2&{}=\frac{i}{6} \widetilde{P}^\pm \,R^{\mu }{}_\alpha {}^\nu {}_\beta \left[ \widetilde{\sigma }^\beta \left( \frac{\eta _\mu \eta _\nu }{h^2} \right) _{\eta _\alpha } + \widetilde{\sigma }^\rho \left( \frac{\eta _\mu \eta _\nu \eta ^\beta \eta _\rho }{h^4} \right) _{\eta _\alpha } \right] \\ &{}=-\frac{i}{6\,h^2} \widetilde{P}^\pm \,{\text {Ric}}^{\mu }{}_\beta (0)\,\eta _\mu \,\widetilde{\sigma }^\beta (0). \end{matrix}} \end{aligned}$$

  (7.44)

• $B_3$: By means of Corollary 7.4 and formula (7.43) we get

  $$\begin{aligned} {\begin{matrix} B_3&{}=\left( \pm \frac{i}{4} {\text {Ric}}_{\alpha \beta }(0)\,\sigma ^\alpha \mp \frac{i}{6} {\text {Ric}}_{\alpha \beta }(0)\,\sigma ^\alpha \right) \frac{1}{2}\left( \frac{\sigma ^\beta }{h}-\frac{\eta ^\beta \,\sigma ^\rho \eta _\rho }{h^3} \right) \\ &{}=\pm \frac{i}{24} {\text {Ric}}_{\alpha \beta }(0)\,\sigma ^\alpha \left( \frac{\sigma ^\beta }{h}-\frac{\eta ^\beta \,\sigma ^\rho \eta _\rho }{h^3} \right) \\ &{}=\pm \left( \frac{i}{24h} \mathcal {R}(0)\,\mathrm {Id}-\frac{i}{24h^3}{\text {Ric}}_{\alpha \beta }(0)\, \eta ^\beta \eta _\rho \sigma ^\alpha (0)\,\sigma ^\rho (0)\right) . \end{matrix}} \end{aligned}$$

  (7.45)

  Now, since $\widetilde{P}^\pm \,\widetilde{\sigma }^\rho (0)\eta _\rho =\widetilde{P}^\pm \,\widetilde{W}_\mathrm {prin}(0,\eta )=\pm h\, \widetilde{P}^\pm$ and $\widetilde{\sigma }^\alpha \widetilde{\sigma }^\rho =-\widetilde{\sigma }^\rho \widetilde{\sigma }^\alpha +2\,\delta ^{\alpha \rho }\,\mathrm {Id}$, formula (7.45) implies

  

  (7.46)

Summing up (7.42), (7.44) and (7.46) we arrive at

$$\begin{aligned} (\widetilde{P}^\pm \widetilde{\mathfrak {a}}^\pm _{-1})_t\,(0;y,\eta )=i \widetilde{P}^\pm \left( \mp \frac{1}{24h}\mathcal {R}(0)-\frac{1}{8h^2} {\text {Ric}}_{\alpha \beta }(0)\,\eta ^\alpha \,\widetilde{\sigma }^\beta (0) \right) +O(t). \end{aligned}$$

(7.47)

A straightforward calculation shows that

$$\begin{aligned} \widetilde{P}^\pm \widetilde{\sigma }^\alpha =\pm \widetilde{P}^\pm \left( \frac{\eta ^\alpha }{h}+2h \widetilde{P}^\pm _{\eta _\alpha }\right) . \end{aligned}$$

Substituting the above expression into (7.47) and integrating in time with initial condition (7.21), we obtain (7.35).$\square$

The pieces of information from Lemma 7.8 and Lemma 7.9 can be combined to give the following result.

Theorem 7.10

For the choice of the Levi-Civita framing, the subprincipal symbols of the positive and negative propagators admit the following small time expansion:

$$\begin{aligned}&\widetilde{\mathfrak {a}}_{-1}^\pm (t;y,\eta )\nonumber \\&\quad =\mp it \left( \frac{1}{24\,h}\mathcal {R(}y)\,\widetilde{P}^\pm (y,\eta ) - \frac{1}{8 h^2}{\text {Ric}}_{\alpha \beta }(y)\,\eta ^\alpha \,(\widetilde{W}_\mathrm {prin})_{\eta _\beta }(y,\eta ) \right) + O(t^2)\,.\nonumber \\ \end{aligned}$$

(7.48)

Proof

Summing up formulae (7.24) and (7.35), we obtain

The substitution of (7.43) into the RHS of the above equation gives (7.48).$\square$

Note that if the manifold is Ricci-flat then $\widetilde{\mathfrak {a}}_{-1}^\pm (t;y,\eta )=O(t^2)$.

7.4 Invariant Reformulation

In the previous subsections we derived the quite elegant and compact formulae (7.9) and (7.48), which were obtained under the assumption that the chosen framing is the Levi-Civita framing at y. Now the task at hand is to obtain similar formulae for the Dirac operator W corresponding to an arbitrary framing $\{e_j\}_{j=1}^3$.

Given a framing $\{e_j\}_{j=1}^3$ and a point $y\in M$, there exits a special unitary matrix-function G, defined in a neighbourhood of y, such that $\{e_j\}_{j=1}^3$ and the Levi-Civita framing $\{\widetilde{e}_j\}_{j=1}^3$ generated by $\{e_j\}_{j=1}^3$ at y are related in accordance with

$$\begin{aligned} {e}_j{}^\alpha (x)=\frac{1}{2} {\text {tr}}(s_j\,G^*(x)\,s^k\,G(x))\,\widetilde{e}_k{}^\alpha (x), \qquad G(y)=\mathrm {Id}, \end{aligned}$$

(7.49)

cf. (5.22) and (1.7). The symbols $\widetilde{\mathfrak {a}}^\pm$ and $\mathfrak {a}^\pm$ are related as

$$\begin{aligned} \mathfrak {a}^\pm =\mathfrak {S}^\pm [G^*(x) \, \widetilde{\mathfrak {a}}^\pm \,G(y)], \end{aligned}$$

(7.50)

cf. Sect. 5. Note that on the RHS of (7.50) the transformed symbol is acted upon by amplitude-to-symbol operators (3.31). The latter are needed because the gauge transformation G introduces an x-dependence in the amplitude, which has to be excluded.

Working in normal coordinates centred at y, formula (7.50), combined with (7.13) and (7.9), implies

(7.51)

Similarly, by means of (7.13) and Lemma 7.6, from (7.50) we get

(7.52)

The last step towards expressing (7.51) and (7.52) invariantly is writing $\nabla G$ and $\nabla \nabla G$ in terms of geometric invariants. Theorem 5.4 tells us that

$$\begin{aligned} \nabla _\alpha G(y)=-\frac{i}{2} \overset{*}{K}{}_{\alpha \beta }(y)\,\sigma ^\beta (y). \end{aligned}$$

(7.53)

The following theorem provides an expression for the second covariant derivatives of the gauge transformation.

Theorem 7.11

Let us fix a point y and let the special unitary matrix-function G be such that our framing $\{e_j\}_{j=1}^3$ and the Levi-Civita framing $\{\widetilde{e}_j\}_{j=1}^3$ generated by $\{e_j\}_{j=1}^3$ at y are related in accordance with (7.49) in a neighbourhood of y. Then we have

$$\begin{aligned} \nabla _\alpha \nabla _\beta \,G(y)=-\frac{i}{4} \left( \nabla _\alpha \overset{*}{K}{}_{\beta \mu }(y) + \nabla _\beta \overset{*}{K}{}_{\alpha \mu }(y) \right) \sigma ^\mu (y) -\frac{1}{4} \overset{*}{K}{}_{\alpha \mu }(y)\overset{*}{K}{}_\beta {}^\mu (y){\text {Id}}, \nonumber \\ \end{aligned}$$

(7.54)

where K is the contorsion tensor of the Weitzenböck connection (see Appendix A) associated with the framing $\{ e_j\}_{j=1}^3$ and the star stands for the Hodge dual applied in the first and third indices (see formula (A.7)).

Proof

The proof is given in Appendix B.2.$\square$

Remark 7.12

Note that, remarkably, the curvature of the Levi-Civita connection does not appear in the RHS of (7.54).

Substituting (7.53) and (7.54) into (7.51) and (7.52) we arrive at the following result.

Theorem 7.13

Let W be the Dirac operator (1.4). Then the the principal and subprincipal symbols of the positive and negative propagators admit the following small time expansions:

$$\begin{aligned} \mathfrak {a}_0^\pm= & {} \left[ {\text {Id}} \pm \frac{it}{2}h_{\eta _\alpha }\,\overset{*}{K}{}_{\alpha \beta }\,(W_\mathrm {prin})_{\eta _\beta }\right] P^\pm \nonumber \\&+\frac{t^2}{8}\frac{\eta ^\alpha \eta ^\beta }{h^2} \left[ i\bigl ( \nabla _\alpha \overset{*}{K}{}_{\beta \mu }(y) + \nabla _\beta \overset{*}{K}{}_{\alpha \mu }(y) \bigr ) (W_\mathrm {prin})_{\eta _\mu }-\overset{*}{K}{}_{\alpha \mu }(y)\overset{*}{K}{}_\beta {}^\mu (y)\right] P^\pm \nonumber \\&+O(t^3), \end{aligned}$$

(7.55)

$$\begin{aligned} \mathfrak {a}_{-1}^\pm= & {} -\frac{1}{2} \overset{*}{K}{}_{\alpha \beta }\,(W_\mathrm {prin})_{\eta _\beta }\,P^\pm _{\eta _\alpha }\nonumber \\&\quad \mp it \left( \frac{1}{24\,h}\mathcal {R}\,P^\pm - \frac{1}{8 h^2}{\text {Ric}}_{\alpha \beta }\,\eta ^\alpha \,({W}_\mathrm {prin})_{\eta _\beta } \right) \nonumber \\&\quad \mp \frac{t}{4}\,\left( \nabla _\alpha \overset{*}{K}{}_{\beta \mu } + \nabla _\beta \overset{*}{K}{}_{\alpha \mu } \right) (W_\mathrm {prin})_{\eta _\mu } \left( h_{\eta _\beta }\, P^\pm _{\eta _\alpha }+\frac{1}{2} h_{\eta _\alpha \eta _\beta }\,P^\pm \right) \nonumber \\&\quad \mp \frac{it}{4} \overset{*}{K}{}_{\alpha \mu }\overset{*}{K}{}_\beta {}^\mu \left( h_{\eta _\beta }\, P^\pm _{\eta _\alpha }+\frac{1}{2} h_{\eta _\alpha \eta _\beta }\,P^\pm \right) +O(t^2), \end{aligned}$$

(7.56)

where $\overset{*}{K}$ denotes the Hodge dual in the first and third indices of the contorsion tensor of the Weitzenböck connection associated with the framing $\{e_j\}_{j=1}^3$.

8 An Application: Spectral Asymptotics

In this section we will compute the third Weyl coefficient for the Dirac operator. In doing so we will use the same notation as in Sect. 1—recall in particular formulae (1.17), (1.13) and the definition of the function $\mu$.

Theorem 8.1

The third local Weyl coefficients for the Dirac operator are

$$\begin{aligned} c_0^\pm (y)=-\frac{1}{48\pi ^2}\mathcal {R}(y), \end{aligned}$$

(8.1)

where $\mathcal {R}$ is scalar curvature.

Proof

Let us fix a point $y\in M$ and choose normal geodesic coordinates x centred at y. Let us also choose a Levi-Civita framing $\{\widetilde{e}_j\}_{j=1}^3$, see Definition 7.1; here we make use of the fact that Weyl coefficients do not depend on the choice of framing.

We have

$$\begin{aligned}&(N_+'*\mu )(y,\lambda ) \,=\, \mathcal {F}^{-1} \left[ \mathcal {F} \left[ (N_+'*\mu ) \right] \right] (y,\lambda ) \,=\, \mathcal {F}^{-1} \left[ {\text {tr}}u_+(t,y,y)\,\hat{\mu }(t) \right] , \qquad \end{aligned}$$

(8.2)

$$\begin{aligned}&(N_-'*\mu )(y,\lambda ) \,=\, \mathcal {F}^{-1} \left[ \mathcal {F} \left[ (N_-'*\mu ) \right] \right] (y,\lambda ) \,=\, \mathcal {F}^{-1} \left[ {\text {tr}}\overline{u_-(t,y,y)}\,\hat{\mu }(t) \right] ,\qquad \end{aligned}$$

(8.3)

where $u_\pm$ is the Schwartz kernel of the propagator $U^{\pm }$ and $\,{\text {tr}}\,$ stands for the matrix trace. Note that at each point of the manifold the quantity $\,{\text {tr}}u_\pm (t,y,y)\,$ is a distribution in the variable t and the construction presented in preceding sections allows us to write down this distribution explicitly, modulo a smooth function.

Our task is to substitute (5.7) into the right-hand sides of (8.2) and (8.3) and expand the resulting quantities in powers of $\lambda$ as $\lambda \rightarrow +\infty$. Thus, the problem reduces to the analysis of explicit integrals in four variables, $\eta _1,\eta _2,\eta _3$ and t, depending on the parameter $\lambda \,$. In what follows we drop the y in our intermediate calculations.

The construction presented in preceding sections tells us that the only singularity of the distribution $\,{\text {tr}}u_\pm (t,y,y)\,\hat{\mu }(t)\,$ is at $t=0$. Hence, in what follows, we can assume that the support of $\hat{\mu }$ is arbitrarily small. In particular, this allows us to use the real-valued ($\epsilon =0$) Levi-Civita phase functions $\varphi ^\pm$.

Theorems 7.5 and 7.10 imply that

$$\begin{aligned}&{\text {tr}}\widetilde{\mathfrak {a}}^{\pm }_0(t;\eta )= 1\,, \end{aligned}$$

(8.4)

$$\begin{aligned}&{\text {tr}}\widetilde{\mathfrak {a}}^{\pm }_{-1}(t;\eta )= \mp \, \frac{i}{24\,\Vert \eta \Vert }\,\mathcal {R}\,t+O(t^2)\,. \end{aligned}$$

(8.5)

Formula [17, (B.11)] reads $\,\varphi ^+(t,\eta )=-\Vert \eta \Vert \,t+O(t^4)\,$, which, in view of (5.5), implies

$$\begin{aligned} \varphi ^\pm (t,\eta )=\mp \Vert \eta \Vert \,t+O(t^4)\,. \end{aligned}$$

(8.6)

Using formulae (8.2)–(8.6) and arguing as in [17, Appendix B], we conclude that

$$\begin{aligned} (N_\pm '*\mu )(y,\lambda )= & {} \frac{S_{2}}{(2\pi )^{4}}\int _{\mathbb {R}^{2}} \left( r^{2}-\dfrac{1}{24}\,\mathcal {R} \right) e^{i(\lambda -r)t}\,\hat{\mu }(t)\,dr\,dt \nonumber \\&+\,O(\lambda ^{-1}) \quad \text {as} \quad \lambda \rightarrow +\infty , \end{aligned}$$

(8.7)

where $S_2=4\pi$ is the surface area of the 2-sphere. But

$$\begin{aligned} \frac{1}{2\pi } \int _{\mathbb {R}^{2}} r^m\, e^{i(\lambda -r)t}\,\hat{\mu }(t)\,dr\,dt =\lambda ^m,\qquad m=0,1,2,\ldots , \end{aligned}$$

so (8.7) can be rewritten as

$$\begin{aligned} (N_\pm '*\mu )(y,\lambda ) = \frac{1}{2\pi ^2}\,\lambda ^2 -\frac{1}{48\pi ^2}\,\mathcal {R}(y) +\,O(\lambda ^{-1}) \quad \text {as} \quad \lambda \rightarrow +\infty . \end{aligned}$$

$\square$

Remark 8.2

Let us compare the spectrum of the Dirac operator with the spectrum of the Laplacian. Working on the same 3-manifold, let $\Delta$ be the Laplace–Beltrami operator and let $N(y,\lambda )$ be the local counting function for the operator $\sqrt{-\Delta }\,$. Then

$$\begin{aligned} (N'*\mu )(y,\lambda )= c_{2}(y)\,\lambda ^{2} + c_{1}(y)\,\lambda + c_{0}(y) +\dots \quad \text {as} \quad \lambda \rightarrow +\infty , \end{aligned}$$

where the values of the first three Weyl coefficients are provided by [17, Theorem B.2]. Comparing these with (1.19) and (8.1), we conclude that

$$\begin{aligned} c^\pm _{2}(y)=c_{2}(y)\,, \qquad c^\pm _{1}(y)=c_{1}(y)=0\,, \qquad c^\pm _{0}(y)=-\frac{1}{2}\,c_{0}(y)\,. \end{aligned}$$

We see that the large (in modulus) eigenvalues of the Dirac operator are distributed approximately the same way as the eigenvalues of the operator $\sqrt{-\Delta }\,$, differing only in the third Weyl coefficient.

Remark 8.3

There are, of course, alternative ways of computing the third Weyl coefficients. One can, for example, calculate $c_0^\pm$ by examining the quantities

$$\begin{aligned} {\text {Tr}} e^{-W^2 \,t} \quad \text {and}\quad {\text {Tr}} W\,e^{-W^2 \,t}, \end{aligned}$$

which are related to the counting functions via the Mellin transform, as in [14, 26]. See also [22].

9 Examples

In this section we present two explicit examples, which show how our constructions work in practice and which give us an opportunity to double-check our formulae.

The specific choice of examples is motivated by the fact that the first, $M=\mathbb {S}^3$, is isotropic in momentum whereas the second, $M=\mathbb {S}^2\times \mathbb {S}^1$, is anisotropic in momentum.

9.1 The Case $M=\mathbb {S}^3$

Let $\mathbb {R}^4$ be Euclidean space equipped with Cartesian coordinates ${\textbf {x}}^\alpha$, $\alpha =1,2,3,4$, and put

$$\begin{aligned} \widehat{{\textbf {e}}}_4=\begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix}. \end{aligned}$$

Consider the 3-sphere⁷

with orientation prescribed in accordance with [28, Appendix A], equipped with the standard round metric g and with the global framings $\{V_{\pm ,k}\}_{k=1}^3$ defined as the restriction to $\mathbb {S}^3$ of the vector fields in $\mathbb {R}^4$

$$\begin{aligned} \begin{aligned}&\mathbf {V}_{\pm ,1}:=(1-{\textbf {x}}^4)\dfrac{\partial }{\partial {\textbf {x}}^1}\mp {\textbf {x}}^3\frac{\partial }{\partial {\textbf {x}}^2} \pm {\textbf {x}}^2\dfrac{\partial }{\partial {\textbf {x}}^3}+{\textbf {x}}^1\dfrac{\partial }{\partial {\textbf {x}}^4},\\&\mathbf {V}_{\pm ,2}:= \pm {\textbf {x}}^3\dfrac{\partial }{\partial {\textbf {x}}^1}+(1-{\textbf {x}}^4)\frac{\partial }{\partial {\textbf {x}}^2}\mp {\textbf {x}}^1 \dfrac{\partial }{\partial {\textbf {x}}^3}+{\textbf {x}}^2\dfrac{\partial }{\partial {\textbf {x}}^4},\\&\mathbf {V}_{\pm ,3}:= \mp {\textbf {x}}^2\dfrac{\partial }{\partial {\textbf {x}}^1}\pm {\textbf {x}}^1\frac{\partial }{\partial {\textbf {x}}^2} +(1-{\textbf {x}}^4)\dfrac{\partial }{\partial {\textbf {x}}^3}+{\textbf {x}}^3\dfrac{\partial }{\partial {\textbf {x}}^4}.\\ \end{aligned} \end{aligned}$$

(9.1)

It is easy to check that the vector fields (9.1) are tangent to $\mathbb {S}^3$, so that they restrict to smooth vector fields on the 3-sphere. Note that (9.1) is an adaptation of [28, Eqn. (C.1)] to the case at hand.

Let us introduce coordinates on $\mathbb {S}^3$ with the north pole excised by stereographically projecting it onto the hyperplane tangent to the 3-sphere at the south pole. The stereographic map is given by

$$\begin{aligned} \sigma : \mathbb {R}^3 \rightarrow \mathbb {S}^3 \setminus \begin{pmatrix} 0\\ 0 \\ 0\\ 2 \end{pmatrix} , \qquad \begin{pmatrix} u\\ v\\ w \end{pmatrix} \mapsto \begin{pmatrix} {\textbf {x}}^1\\ {\textbf {x}}^2\\ {\textbf {x}}^3\\ {\textbf {x}}^4 \end{pmatrix} = \dfrac{1}{1+f^2} \begin{pmatrix} u\\ v\\ w\\ 2f^2 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} f^2:=\frac{1}{4} \,(u^2+v^2+w^2). \end{aligned}$$

It is easy to see that the coordinate system (u, v, w) has positive orientation.

In stereographic coordinates the metric reads

$$\begin{aligned} g=\dfrac{1}{(1+f^2)^2}\left[ \mathrm {d}u^2+\mathrm {d}v^2+\mathrm {d}w^2 \right] \end{aligned}$$

(9.2)

and our framings are given by

$$\begin{aligned} \begin{aligned}&2V_{\pm ,1}= (2 - 2f^2+u^2)\frac{\partial }{\partial u} + (u v \mp 2 w)\frac{\partial }{\partial v} + (u w\pm 2v)\frac{\partial }{\partial w}, \\&2V_{\pm ,2}= (u v \pm 2 w)\frac{\partial }{\partial u} + (2 - 2f^2+v^2)\frac{\partial }{\partial v} + (v w\mp 2u)\frac{\partial }{\partial w}, \\&2V_{\pm ,3}= (u w\mp 2v)\frac{\partial }{\partial u} + (v w\pm 2u)\frac{\partial }{\partial v} + (2 - 2f^2+w^2)\frac{\partial }{\partial w}. \end{aligned} \end{aligned}$$

(9.3)

A straightforward calculation shows that $\{V_{\pm ,k}\}_{k=1}^3$ are positively oriented framings formed by (orthonormal) smooth Killing vector fields with respect to the metric g.

The framings $\{V_{\pm ,k}\}_{k=1}^3$ define, via (1.4), two Dirac operators $W_\pm$ related in accordance with

$$\begin{aligned} W_-=G^*W_+G, \end{aligned}$$

where

$$\begin{aligned} G:= \dfrac{1}{4(1+f^2)} \begin{pmatrix} u^2+v^2+(w-2\mathrm {i})^2 &{} 4(v-\mathrm {i}u)\\ -4(v+\mathrm {i}u)&{} u^2+v^2+(w+2\mathrm {i})^2 \end{pmatrix} . \end{aligned}$$

(9.4)

is the SU(2) gauge transformation relating the two framings via (7.49) with $\widetilde{e}_k=V_{+,k}$ and $e_k=V_{-,k}$.

Let us deal with $W_+$ first. On account of the symmetries of the 3-sphere, we will write formulae for principal and subprincipal symbols of the propagator of $W_+$ at the south pole ($y=(0,0,0)$) for the choice of momentum $\overline{\eta }=(0,0,1)$.

The principal symbol $(W_+)_\mathrm {prin}$ has eigenvalues $h^\pm (y,\eta )=\pm \Vert \eta \Vert$, whose Hamiltonian flows in stereographic coordinates read

$$\begin{aligned} z^\pm (t;0,\eta )=\pm 2\tan (t/2) \frac{\eta }{\Vert \eta \Vert }, \qquad \xi ^\pm (t;0,\eta )=\cos ^2(t/2) \,\eta , \end{aligned}$$

(9.5)

see also formula (5.3). Direct inspection of the parallel transport equation (6.2) reveals that the parallel transport of

$$\begin{aligned} v^+(0,\overline{\eta })=\begin{pmatrix} 1\\ 0 \end{pmatrix},\qquad v^-(0,\overline{\eta })=\begin{pmatrix} 0\\ 1 \end{pmatrix} \end{aligned}$$

along $z^+$ and $z^-$, respectively, is given by

$$\begin{aligned} \zeta ^+(t;0,\overline{\eta })=e^{-\frac{it}{2}}\begin{pmatrix} 1\\ 0 \end{pmatrix}, \qquad \zeta ^-(t;0,\overline{\eta })=e^{\frac{it}{2}}\begin{pmatrix} 0\\ 1 \end{pmatrix}, \end{aligned}$$

so that Theorem 6.1 gives us

$$\begin{aligned} \mathfrak {a}^+_0(t;0,\overline{\eta })=e^{-\frac{it}{2}}\begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix}, \qquad \mathfrak {a}^-_0(t;0,\overline{\eta })=e^{\frac{it}{2}}\begin{pmatrix} 0&{} 0 \\ 0 &{} 1 \end{pmatrix}. \end{aligned}$$

(9.6)

Let us now move to the subprincipal symbol. Careful examination of formula (9.3) shows that

$$\begin{aligned} \overset{*}{K}=-g\,, \end{aligned}$$

(9.7)

which means that this particular framing has the ‘Einstein property’, namely, that the Hodge dual of contorsion is proportional to the metric. Formula (9.7) implies that

$$\begin{aligned} \nabla \overset{*}{K}=0. \end{aligned}$$

(9.8)

In view of (9.7) and (9.8), Theorem 7.13 gives us

$$\begin{aligned} \mathfrak {a}_{-1}^+(t;0,\eta )= & {} \frac{1-it}{4\Vert \eta \Vert } {\text {Id}}+O(t^2), \end{aligned}$$

(9.9)

$$\begin{aligned} \mathfrak {a}_{-1}^-(t;0,\eta )= & {} -\frac{1-it}{4\Vert \eta \Vert } {\text {Id}}-\frac{it}{2\Vert \eta \Vert } \begin{pmatrix} \eta _3 &{} \eta _1 -i\eta _2\\ \eta _2+i\eta _2 &{} -\eta _3 \end{pmatrix} +O(t^2). \end{aligned}$$

(9.10)

In particular, formulae (9.9) and (9.10) imply

$$\begin{aligned} \begin{aligned}&\mathfrak {a}_{-1}^+(t;0,\overline{\eta }) = \frac{1}{4} \begin{pmatrix} 1-it &{} 0 \\ 0 &{} 1-it \end{pmatrix} +O(t^2), \\&\mathfrak {a}_{-1}^-(t;0,\overline{\eta }) = -\frac{1}{4} \begin{pmatrix} 1+it &{} 0\\ 0 &{} 1-3it \end{pmatrix} +O(t^2). \end{aligned} \end{aligned}$$

(9.11)

Let us now deal with $W_-\,$. Arguing as above, one obtains the following expressions for the principal symbols

$$\begin{aligned} \mathfrak {a}^+_0(t;0,\overline{\eta })=e^{\frac{it}{2}}\begin{pmatrix} 1 &{} 0 \\ 0 &{} 0 \end{pmatrix}, \qquad \mathfrak {a}^-_0(t;0,\overline{\eta })=e^{-\frac{it}{2}}\begin{pmatrix} 0&{} 0 \\ 0 &{} 1 \end{pmatrix}. \end{aligned}$$

(9.12)

The subprincipal symbols are calculated in a similar fashion, only now we have

$$\begin{aligned} \overset{*}{K}=+g\,, \end{aligned}$$

(9.13)

compare with (9.7). Combining (9.13) with Theorem 7.13 we get

$$\begin{aligned}&\mathfrak {a}_{-1}^+(t;0,\eta ) = -\frac{1+it}{4\Vert \eta \Vert } {\text {Id}}+O(t^2), \end{aligned}$$

(9.14)

$$\begin{aligned}&\mathfrak {a}_{-1}^-(t;0,\eta ) = \frac{1+it}{4\Vert \eta \Vert } {\text {Id}}-\frac{it}{2\Vert \eta \Vert } \begin{pmatrix} \eta _3 &{} \eta _1 -i\eta _2\\ \eta _2+i\eta _2 &{} -\eta _3 \end{pmatrix} +O(t^2). \end{aligned}$$

(9.15)

In particular, formulae (9.14) and (9.15) imply

$$\begin{aligned} \begin{aligned}&\mathfrak {a}_{-1}^+(t;0,\overline{\eta }) = -\frac{1}{4} \begin{pmatrix} 1+it &{} 0 \\ 0 &{} 1+it \end{pmatrix} +O(t^2), \\&\mathfrak {a}_{-1}^-(t;0,\overline{\eta }) = \frac{1}{4} \begin{pmatrix} 1-it &{} 0\\ 0 &{} 1+3it \end{pmatrix} +O(t^2). \end{aligned} \end{aligned}$$

(9.16)

Of course, the principal symbols of positive and negative propagators of $W_-$ at $(t;0,\overline{\eta })$ can also be obtained from (9.6) by means of the gauge transformation (9.4) evaluated at $z^\pm (t;0,\overline{\eta })$,

$$\begin{aligned} \left. G\right| _{(u,v,w)=z^\pm (t;0,\overline{\eta })}=\begin{pmatrix} e^{\mp it} &{} 0\\ 0 &{} e^{\pm it} \end{pmatrix}. \end{aligned}$$

(9.17)

Namely, multiplying (9.6) from the left by the Hermitian conjugate of (9.17), we arrive at (9.12).

Finally, let us run a test for Theorem 8.1. It is well known [9, 10, 49, 50] that the eigenvalues of the Dirac operator on the round 3-sphere are

$$\begin{aligned} \pm \left( k+\frac{1}{2} \right) , \qquad k=1,2,\ldots , \end{aligned}$$

with multiplicity $k(k+1)$. Therefore, in view of (8.2), we have

$$\begin{aligned} \mathcal {F}_{\lambda \rightarrow t}[N_+'*\mu ](y,t) =\frac{1}{2\pi ^2} e^{-\frac{it}{2}} \sum _{k=1}^{+\infty } k(k+1)e^{-ikt}. \end{aligned}$$

(9.18)

Note that the quantity $2\pi ^2$ appearing in the RHS of (9.18) is the volume of the 3-sphere. Taking the Fourier transform of the RHS of (9.18) we get

$$\begin{aligned}&\mathcal {F}^{-1}_{t\rightarrow \lambda }\left[ \frac{1}{2\pi ^2} e^{-\frac{it}{2}} \sum _{k=1}^\infty (k^2+k)e^{-ikt}\hat{\mu }(t) \right] \nonumber \\&\quad =\frac{1}{4\pi ^3}\sum _{k=1}^{+\infty }\int _{-\infty }^{+\infty } e^{it(\lambda -\frac{1}{2}-k)}\,(k^2+k)\,\hat{\mu }(t)\,\mathrm {d}t\nonumber \\&\quad =\frac{1}{4\pi ^3}\sum _{k=-\infty }^{+\infty }\int _{-\infty }^{+\infty } e^{-itk}\,(k^2+k)\,\bigl ( e^{it(\lambda -\frac{1}{2})}\hat{\mu }(t)\bigr )\,\mathrm {d}t +O(\lambda ^{-\infty })\nonumber \\&\quad =\frac{1}{2\pi ^2}\left( (\lambda -\frac{1}{2})^2+(\lambda -\frac{1}{2})+O(\lambda ^{-\infty }) \right) \nonumber \\&\quad =\frac{1}{2\pi ^2}\left( \lambda ^2-\frac{1}{4}+O(\lambda ^{-\infty })\right) . \end{aligned}$$

(9.19)

Combining (9.19) and (9.18) we arrive at

$$\begin{aligned}{}[N_+'*{\mu }](y,\lambda )=\frac{1}{2\pi ^2}\left( \lambda ^2-\frac{1}{4}+O(\lambda ^{-\infty })\right) \qquad \text {as }\lambda \rightarrow +\infty . \end{aligned}$$

(9.20)

Since $\mathcal {R}(y)=6$, formula (9.20) is in agreement with (8.1).

9.2 The Case $M=\mathbb {S}^2\times \mathbb {S}^1$

Let $M=\mathbb {S}^2\times \mathbb {S}^1$ be endowed with the metric $g=g_{\mathbb {S}^2}+d\varphi ^2$, where $g_{\mathbb {S}^2}$ is the round metric on the 2-sphere. Let $y\in M$ be given. In this subsection we shall compute the small time expansion for the subprincipal symbols of the Dirac propagator $\widetilde{W}$ associated with a Levi-Civita framing at y. In this case, the result will not be isotropic in momentum $\eta$, because, unlike the previous example, $(\mathbb {S}^2\times \mathbb {S}^1,g)$ is not an Einstein manifold.

Without loss of generality, we assume that y coincides with the north pole when projected onto $\mathbb {S}^2$. The exponential map $\exp _y:T_yM \rightarrow M$ is realised explicitly by

$$\begin{aligned} (u,v,w) \mapsto (\theta =\sqrt{u^2+v^2}, \phi =\arctan (v/u), \varphi =w), \end{aligned}$$

(9.21)

where $(\theta ,\phi )$ are standard spherical coordinates on $\mathbb {S}^2$. Formula (9.21) defines geodesic normal coordinates (u, v, w) in a neighbourhood of y. In such coordinates, the metric g reads

$$\begin{aligned}&g(u,v,{w})\nonumber \\&\quad =\frac{1}{u^2+v^2} \begin{pmatrix} u^2+\frac{v^2 \,\sin ^2( \sqrt{u^2+v^2})}{u^2+v^2} &{} uv \left( 1-\frac{\sin ^2( \sqrt{u^2+v^2})}{u^2+v^2} \right) &{} 0 \\ uv \left( 1-\frac{\sin ^2( \sqrt{u^2+v^2})}{u^2+v^2} \right) &{} v^2+\frac{u^2 \,\sin ^2( \sqrt{u^2+v^2})}{u^2+v^2} &{} 0 \\ 0 &{} 0 &{} u^2+v^2 \end{pmatrix}.\qquad \end{aligned}$$

(9.22)

We will assume that normal coordinates are chosen so that the Levi-Civita framing satisfies $\widetilde{e}_j{}^\alpha (y)=\delta _j{}^\alpha$. In this case, the Hamiltonian flows generated by the eigenvalues of $\widetilde{W}_\mathrm {prin}$ read, simply,

$$\begin{aligned} z^\pm (t;0,\eta )=\pm t\frac{\eta }{\Vert \eta \Vert }, \qquad \xi ^\pm (t;0,\eta )=\eta . \qquad \end{aligned}$$

The Ricci curvature of g in normal coordinates (u, v, w) is given by

$$\begin{aligned}&{\text {Ric}}(u,v,w)\nonumber \\&\quad = \frac{1}{u^2+v^2} \begin{pmatrix} u^2+\frac{v^2 \,\sin ^2( \sqrt{u^2+v^2})}{u^2+v^2} &{} uv \left( 1-\frac{\sin ^2( \sqrt{u^2+v^2})}{u^2+v^2} \right) &{} 0 \\ uv \left( 1-\frac{\sin ^2( \sqrt{u^2+v^2})}{u^2+v^2} \right) &{} v^2+\frac{u^2 \,\sin ^2( \sqrt{u^2+v^2})}{u^2+v^2} &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix}.\qquad \end{aligned}$$

(9.23)

Hence, Theorem 7.10 tells us that

$$\begin{aligned}&\widetilde{\mathfrak {a}}_{-1}^\pm (t;y,\eta ) \nonumber \\&\quad = \mp it \left( \frac{1}{12\Vert \eta \Vert }\,\widetilde{P}^\pm (y,\eta ) - \frac{1}{8\Vert \eta \Vert ^2}(\eta _1 \,\sigma ^1(y)+\eta _2\,\sigma ^2(y)) \right) + O(t^2)\, \nonumber \\&\quad = \mp \frac{it}{24 \Vert \eta \Vert ^2} \left[ \Vert \eta \Vert {\text {Id}} +(-3\pm 1)\,\eta _\alpha \,\sigma ^\alpha (y) +3\,s^3\,\eta _\beta \,\widetilde{e}_3{}^\beta (y) \right] +O(t^2),\qquad \end{aligned}$$

(9.24)

where the $s^j$ and the $\sigma ^\alpha$ are defined by formulae (1.2) and (1.3) respectively, and $\widetilde{e}_3$ is the vector field $\partial /\partial \varphi$ (unit vector field along the positive direction of the circle $\mathbb {S}^1$).

Let us stress once again that, even though the intermediate steps depend on the choice of coordinates, the final result (9.24) is a scalar matrix-function, thus independent of the choice of coordinates. The only assumption involved in the derivation of formula (9.24) is that we used a particular Levi-Civita framing at the point y, one which respects the product structure of the manifold. The presence of the vector field $\widetilde{e}_3$ in formula (9.24) is a manifestation of anisotropy.

Appendices

Appendix A: The Weitzenböck Connection

In this appendix we recall the main properties of the Weitzenböck connection and fix our sign conventions, which are chosen in agreement with [42].

Let M be an oriented Riemannian 3-manifold and let $\{e_j\}_{j=1}^3$ be a global orthonormal framing.

Definition A.1

The Weitzenböck connection is the affine connection $\nabla ^W$ on M defined by the condition

$$\begin{aligned} \nabla ^W_v (f^i\, e_i)=v(f^i)\, e_i\,, \end{aligned}$$

(A.1)

for every vector field v and $f^i\in C^\infty (M;\mathbb {R})$, $i=1,2,3$.

The Weitzenböck connection is a curvature-free metric-compatible connection. Formula (A.1) implies

$$\begin{aligned} 0=\nabla ^W_{e_k} e_j{}^\alpha =e_k{}^\beta \, \dfrac{\partial e_j{}^\alpha }{\partial x^\beta }+ e_k{}^\beta \,\Upsilon ^\alpha {}_{\beta \gamma }\, e_j{}^\gamma , \end{aligned}$$

which, in turn, yields a formula for the Weitzenböck connection coefficients $\Upsilon ^\alpha {}_{\beta \gamma }$ in terms of the framing:

$$\begin{aligned} \Upsilon ^\alpha {}_{\beta \gamma }=- \,e^j{}_\gamma \dfrac{\partial e_j{}^\alpha }{\partial x^\beta }= e_j{}^\alpha \dfrac{\partial e^j{}_\gamma }{\partial x^\beta }\,. \end{aligned}$$

(A.2)

Here $e^j{}_\alpha :=\delta ^{jk}\,g_{\alpha \beta }\,e_k{}^\beta$. The torsion tensor associated with $\nabla ^W$ is

$$\begin{aligned} T^\alpha {}_{\beta \gamma }= \Upsilon ^\alpha {}_{\beta \gamma }-\Upsilon ^\alpha {}_{\gamma \beta } \end{aligned}$$

(A.3)

and the curvature tensor vanishes identically. The Weitzenböck connection coefficients and the Christoffel symbols are related via the identity

$$\begin{aligned} \Upsilon ^\alpha {}_{\beta \gamma }=\Gamma ^\alpha {}_{\beta \gamma }+\frac{1}{2}\left( T^\alpha {}_{\beta \gamma }+T_\beta {}^\alpha {}_\gamma +T_\gamma {}^\alpha {}_\beta \right) , \end{aligned}$$

(A.4)

see [42, Eqn. (7.34)]. The second summand on the RHS of (A.4)

$$\begin{aligned} K^\alpha {}_{\beta \gamma }:=\frac{1}{2}\left( T^\alpha {}_{\beta \gamma }+T_\beta {}^\alpha {}_\gamma +T_\gamma {}^\alpha {}_\beta \right) \end{aligned}$$

(A.5)

is called contorsion of $\nabla ^W$. Note that the torsion tensor is antisymmetric in the second and third indices, $T^\alpha {}_{\beta \gamma }=-T^{\alpha }{}_{\gamma \beta }$, whereas the contorsion tensor is antisymmetric in the first and third ones, $K_{\alpha \beta \gamma }=-K_{\gamma \beta \alpha }$ (the first index was lowered using the metric). Torsion and contorsion can be expressed one in terms of the other and capture the geometric information encoded within the framing.

In dimension three antisymmetric tensors of order two are equivalent to vectors. Therefore, we define

$$\begin{aligned} \overset{*}{T}{}_{\alpha \beta }:=\frac{1}{2}T_\alpha {}^{\mu \nu }\,E_{\mu \nu \beta }\,, \end{aligned}$$

(A.6)

$$\begin{aligned} \overset{*}{K}{}_{\alpha \beta }:=\frac{1}{2}K^\mu {}_\alpha {}^\nu \,E_{\mu \nu }{}_\beta \,, \end{aligned}$$

(A.7)

where

$$\begin{aligned} E_{\alpha \beta \gamma }(x):=\rho (x)\,\varepsilon _{\alpha \beta \gamma }\,, \end{aligned}$$

(A.8)

$\rho$ is the Riemannian density and $\varepsilon$ is the totally antisymmetric symbol, $\varepsilon _{123}:=+1$. It is often convenient to use (A.6) and (A.7) instead of T and K because the former have lower order—two instead of three.

As a final remark, we observe that formulae (A.6), (A.7) and (A.5) imply

$$\begin{aligned}&\overset{*}{K}_{\alpha \beta }=\overset{*}{T}_{\alpha \beta }-\frac{1}{2} \overset{*}{T}{}^\gamma {}_\gamma \, g_{\alpha \beta }, \end{aligned}$$

(A.9)

$$\begin{aligned}&\overset{*}{T}_{\alpha \beta }=\overset{*}{K}_{\alpha \beta }-\overset{*}{K}{}^\gamma {}_\gamma \, g_{\alpha \beta }. \end{aligned}$$

(A.10)

Appendix B: Some techincal proofs

1.1 B.1. Proof of Theorem 5.4

In the following we work in normal coordinates centred at $y=0$ such that

$$\begin{aligned} e_j{}^\alpha (0)=\widetilde{e}_j{}^\alpha (0)=\delta _j{}^\alpha . \end{aligned}$$

Since $G\in C^\infty (M;SU(2))$ and $G(0)=\mathrm {Id}$, there exist smooth real-valued functions $A_k$, $k=1,2,3$, such that $A_k(0)=0$ and

$$\begin{aligned} G(x)=e^{is^k\,A_k(x)} \end{aligned}$$

(B.1)

in a neighbourhood of $y=0$. Differentiating (B.1) with respect to x and evaluating the result at 0, we obtain

$$\begin{aligned} G_{x^\alpha }(0)=i s^k\,F_{k\alpha }, \end{aligned}$$

(B.2)

where $F_{k\alpha }:=[A_k]_{x^\alpha }(0)$.

Now, differentiating (5.22) with respect to x and evaluating the result at 0, we obtain

(B.3)

Contracting (B.3) with $e^j{}_\gamma (0)=\widetilde{e}^j{}_\gamma (0)=\delta ^j{}_\gamma$, using (A.2) and rearranging, we obtain

(B.4)

In view of (A.3), formula (B.4) implies

$$\begin{aligned} {\begin{matrix} T^\alpha {}_{\beta \gamma }(0)-\widetilde{T}^\alpha {}_{\beta \gamma }(0)=2\,\varepsilon _{\gamma }{}^{\alpha l}\,F_{l\beta }-2\,\varepsilon _{\beta }{}^{\alpha l}\,F_{l\gamma }. \end{matrix}} \end{aligned}$$

(B.5)

Contracting (B.5) with $\frac{1}{2}E_\sigma {}^{\beta \gamma }(y)=\frac{1}{2}\varepsilon _\sigma {}^{\beta \gamma }$, cf. (A.8), we get

(B.6)

Inverting (B.6) so as to express F in terms of $[\overset{*}{T}-\overset{*}{\widetilde{T}}](0)$, we arrive at

$$\begin{aligned} -2F_{k\beta }= & {} \delta _k{}^\alpha \,[\overset{*}{T}-\overset{*}{\widetilde{T}}]_{\alpha \beta }(y)-\frac{1}{2}\,\delta _{k\beta }\,[\overset{*}{T}-\overset{*}{\widetilde{T}}]^\gamma {}_\gamma (0)\nonumber \\= & {} \delta _k{}^\alpha \bigl [\overset{*}{K}-\overset{*}{\widetilde{K}}\bigr ]_{\alpha \beta }(0). \end{aligned}$$

(B.7)

Substitution of (B.7) into (B.2) gives (5.23).

1.2 B. 2. Proof of Theorem 7.11

Recall that according to formula (7.49) we have $G(y)=\mathrm {Id}$. In the following we work in a sufficiently small neighbourhood $\mathcal {U}$ of y and we choose normal coordinates centred at $y=0$ such that $\widetilde{e}_j{}^\alpha (0)=e_j{}^\alpha (0)=\delta _j{}^\alpha$.

Since $G\in C^\infty (M;SU(2))$ and $G(0)=\mathrm {Id}$, there exist smooth real-valued functions $A_k$, $k=1,2,3$, such that $v_k(0)=0$ and

$$\begin{aligned} G(x)=e^{is^k\,A_k(x)} \end{aligned}$$

(B.8)

in a neighbourhood of $y=0$. Differentiating (B.8) twice with respect to x and evaluating the result at zero we obtain

$$\begin{aligned} {\begin{matrix} G_{x^\alpha x^\beta }(0) &{} = i s^k \,[A_k]_{x^\alpha x^\beta }(0)-\frac{1}{2} s^k\,s^j\,(F_{k\alpha }F_{j\beta }+F_{j\alpha }F_{k\beta })\\ = &{} i s^k\, H_{k\alpha \beta }-\delta ^{jk}\,\mathrm {Id}\,F_{j\alpha }F_{k\beta }. \end{matrix}} \end{aligned}$$

(B.9)

Here $H_{k\alpha \beta }:=[A_k]_{x^\alpha x^\beta }(0)$ and $F_{k\alpha }:=[A_k]_{x^\alpha }(0)$. The task at hand is to express H in terms of the contorsion tensor K and its derivatives.

Differentiating the identity

$$\begin{aligned} {\begin{matrix} \Upsilon ^\alpha {}_{\beta \gamma }(x)&{}=e_k{}^\alpha (x) \dfrac{\partial e^k{}_\gamma }{\partial x^\beta }(x)\\ \end{matrix}} \end{aligned}$$

with respect to $x^\mu$, evaluating the outcome at $y=0$ and resorting to Lemma 7.2, we obtain

$$\begin{aligned} {\begin{matrix} \left[ \Upsilon ^\alpha {}_{\beta \gamma }\right] _{x^\mu }(0) &{} = \dfrac{\partial e_k{}^\alpha }{\partial x^\mu }(0) \dfrac{\partial e^k{}_\gamma }{\partial x^\beta }(0)+e_k{}^\alpha (0) \dfrac{\partial ^2 e^k{}_\gamma }{\partial x^\beta \partial x^\mu }(0) \\ &{} = -\Upsilon ^\alpha {}_\mu {}_\rho (0) \, \Upsilon ^\rho {}_{\beta \gamma }(0) \\ &{}\quad +\delta _k{}^\alpha {\text {Re}} {\text {tr}}[s^k \,G^*_{x^\beta x^\mu }(0)\,s_l+s^k\,G^*_{x^\beta }(0)\,s_l\,G_{x^\mu }(0)]\,\delta ^l{}_\gamma \\ &{}\quad +\delta _k{}^\alpha \,[\widetilde{e}^k{}_\gamma ]_{x^\beta x^\mu }(0)\qquad \\ &{} = -\Upsilon ^\alpha {}_\mu {}_\rho (0) \, \Upsilon ^\rho {}_{\beta \gamma }(0)+ \delta _k{}^\alpha \delta ^l{}_\gamma {\text {Re}} {\text {tr}}[s_l\,s^k \,G^*_{x^\beta x^\mu }(0)] \\ &{}\quad +\delta _k{}^\alpha \delta ^l{}_\gamma {\text {Re}} {\text {tr}}[s^k\,G^*_{x^\beta }(0)\,s_l \,G_{x^\mu }(0)]+\delta _k{}^\alpha \,[\widetilde{e}^k{}_\gamma ]_{x^\beta x^\mu }(0). \end{matrix}} \end{aligned}$$

(B.10)

Straightforward calculations show that

$$\begin{aligned}&{\begin{matrix} -\Upsilon ^\alpha {}_\mu {}_\rho (0) \, \Upsilon ^\rho {}_{\beta \gamma }(0) &{} =-{\text {Re}}\,{\text {tr}}\left[ s^\alpha \,G^*_{x^\mu }(0)s_\rho \right] {\text {Re}}\,{\text {tr}}\left[ s^\rho \,G^*_{x^\beta }(0)s_\gamma \right] \qquad \\ &{} = 4\delta ^\alpha {}_\gamma F^r{}_\beta F_{r\mu }-4\delta ^{\alpha j}\,\delta _\gamma {}^k\,F_{j\beta } F_{k\mu },\qquad \end{matrix}} \end{aligned}$$

(B.11)

$$\begin{aligned}&\delta _k{}^\alpha \delta ^l{}_\gamma {\text {Re}} {\text {tr}}[s_l\,s^k\,G^*_{x^\beta x^\mu }(0)]=-2 \varepsilon ^\alpha {}_{\gamma }{}^r\,H_{r\beta \mu }-2\delta ^\alpha {}_\gamma \,F^r{}_\beta \,F_{r\mu } \end{aligned}$$

(B.12)

and

$$\begin{aligned}&\delta _k{}^\alpha \delta ^l{}_\gamma {\text {Re}} {\text {tr}}[s_l\,G^*_{x^\beta }(0)\,s^k \,G_{x^\mu }(0)]\nonumber \\&\quad = 2(\delta ^{\alpha k}\delta ^j{}_\gamma +\delta ^{\alpha j}\delta ^k{}_\gamma )\,F_{j\mu }F_{k\beta }-2\delta ^\alpha {}_\gamma \,F^r{}_\beta \,F_{r\mu }. \end{aligned}$$

(B.13)

Substituting (B.11)–(B.13) into (B.10) we obtain

$$\begin{aligned}&\left[ \Upsilon ^\alpha {}_{\beta \gamma }\right] _{x^\mu }(0)\nonumber \\&\quad = -2 \varepsilon ^\alpha {}_{\gamma }{}^r\,H_{r\beta \mu }+2(\delta ^{\alpha j}\delta ^k{}_\gamma -\delta ^{\alpha k}\delta ^j{}_\gamma )\,F_{j\mu }F_{k\beta }+\delta _k{}^\alpha \,[\widetilde{e}^k{}_\gamma ]_{x^\beta x^\mu }(0). \qquad \quad \end{aligned}$$

(B.14)

Summing up (B.14) and (B.14) with indices $\beta$ and $\mu$ swapped, we arrive at

$$\begin{aligned} \left[ \Upsilon ^\alpha {}_{\beta \gamma }\right] _{x^\mu }(0)+\left[ \Upsilon ^\alpha {}_{\mu \gamma }\right] _{x^\beta }(0)= -4\varepsilon ^\alpha {}_{\gamma }{}^r\,H_{r\beta \mu }+2\delta _k{}^\alpha \,[\widetilde{e}^k{}_\gamma ]_{x^\beta x^\mu }(0).\qquad \end{aligned}$$

(B.15)

Now, formula (A.4) and the fact that the Christoffel symbols vanish at $y=0$ imply

$$\begin{aligned} \varepsilon _\alpha {}^{\gamma }{}_\rho \,\Upsilon ^\alpha {}_{\mu \gamma }(0)=\varepsilon _\alpha {}^{\gamma }{}_\rho \,K^\alpha {}_{\mu \gamma }(0)=2 \overset{*}{K}_{\mu \rho }(0).\qquad \end{aligned}$$

(B.16)

Hence, by contracting (B.15) with $\varepsilon _\alpha {}^{\gamma }{}_\rho$, substituting (B.16) in, and resorting to the identity

$$\begin{aligned} \varepsilon _\alpha {}^{\gamma }{}_\rho \,\varepsilon ^\alpha {}_{\gamma }{}^r=2\delta _\rho {}^r, \end{aligned}$$

we obtain

$$\begin{aligned}{}[\overset{*}{K}_{\beta \rho }]_{x^\mu }(0)+ [\overset{*}{K}_{\mu \rho }]_{x^\beta }(0) =-4\,\delta _\rho {}^r\,H_{r\beta \mu }+\varepsilon _\alpha {}^{\gamma }{}_\rho \,\delta _k{}^\alpha \,[\widetilde{e}^k{}_\gamma ]_{x^\beta x^\mu }(0). \end{aligned}$$

(B.17)

We claim that

$$\begin{aligned} \varepsilon _\alpha {}^{\gamma }{}_\rho \,\delta _k{}^\alpha \,[\widetilde{e}^k{}_\gamma ]_{x^\beta x^\mu }(0)=0. \end{aligned}$$

(B.18)

To see this, let us observe that formula (7.1) implies

$$\begin{aligned} \widetilde{e}^k{}_\gamma (x)=e^k{}_\gamma (0)-\frac{1}{6} e^k{}_\rho (0)\,R_{\gamma \tau }{}^\rho {}_\nu (0)\,x^\tau x^\nu +O(\Vert x\Vert ^3), \qquad j=1,2,3, \end{aligned}$$

so that

$$\begin{aligned} \delta _k{}^\alpha \,[\widetilde{e}^k{}_\gamma ]_{x^\beta x^\mu }(0)=-\frac{1}{6} \left( R_{\gamma \beta }{}^\alpha {}_\mu +R_{\gamma \mu }{}^\alpha {}_\beta \right) (0). \end{aligned}$$

(B.19)

The RHS of (B.19) is symmetric in $\alpha$ and $\gamma$, whereas $\varepsilon _\alpha {}^{\gamma }{}_\rho$ is antisymmetric in the same indices, so (B.18) follows.

All in all, (B.9), (B.17) and (B.18) give us

$$\begin{aligned} \nabla _\alpha \nabla _\beta \, G(0)=-\frac{i}{4} [ \nabla _\alpha \overset{*}{K}_{\beta \rho }(0)+ \nabla _\beta \overset{*}{K}_{\alpha \rho }(0) ]\sigma ^\rho (0)-\delta ^{jk}\,\mathrm {Id}\,F_{j\alpha }F_{k\beta }.\qquad \end{aligned}$$

(B.20)

Finally, substitution of (B.7) with $\widetilde{K}(0)=0$ (which is the case for the Levi-Civita framing) into (B.20) yields (7.54).