Abstract
The weighted shifts are long known and form an important class of operators. One of generalisations of this class are weighted shifts on directed trees, where the linear order of coordinates in \(\ell ^2\) is replaced by a more involved graph structure. In this paper we focus on the question of joint backward extending of a given family of weighted shifts on directed trees to a weighted shift on an enveloping directed tree that preserves subnormality or power hyponormality of considered operators. One of the main results shows that the existence of such a “joint backward extension” for a family of weighted shifts on directed trees depends only on the possibility of backward extending of single weighted shifts that are members of the family. We introduce a generalised framework of weighted shifts on directed forests (disjoint families of directed trees) which seems to be more convenient to work with. A characterisation of leafless directed forests on which all hyponormal weighted shifts are power hyponormal is given.






Similar content being viewed by others
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
Except for the weights attached to the roots, which equal 0 by definition.
Note that if a root has no children (it is not considered as a child of itself) it still cannot be called a ‘leaf’.
Note that “\(\mathtt {h}_{k}(\omega )\)” is computed for \(S_ {\varvec{{\tilde{\lambda }}}} \) on the directed tree
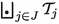 , while “\(\mathtt {h}_{k}\bigl (\omega _{({\mathcal {T}}_j)_{\langle 1\rangle }} \bigr )\)” refers to the weighted shift \(S_{{\varvec{\lambda }}_j}\) on \({{\mathcal {T}}_j}_{\langle 1\rangle }\).
, while “\(\mathtt {h}_{k}\bigl (\omega _{({\mathcal {T}}_j)_{\langle 1\rangle }} \bigr )\)” refers to the weighted shift \(S_{{\varvec{\lambda }}_j}\) on \({{\mathcal {T}}_j}_{\langle 1\rangle }\).We follow the convention that \(\frac{1}{0}=\infty \). In particular \(\int _0^\infty \frac{1}{x^k} \mathrm {\,d}\mu (x) <\infty \) implies \(\mu (\{0\})=0\).
References
Conway, J.B.: The theory of subnormal operators, Mathematical Surveys and Monographs, 36. Amer. Math. Soc, Providence, RI (1991)
Curto, R.E.: Quadratically hyponormal weighted shifts. Integr. Equ. Oper. Theory 13, 49–66 (1990)
Curto, R.E., Lee, S.H., Yoon, J.: \(k\)-hyponormality of multivariable weighted shifts. J. Funct. Anal. 229, 462–480 (2005)
Curto, R., Putinar, M.: Nearly subnormal operators and moment problems. J. Funct. Anal. 115(2), 480–497 (1993)
Curto, R., Putinar, M.: Polynomially hyponormal operators. In: A Glimpse at Hilbert Space Operators. Operator Theory Advances and Applications, vol 207. Springer, Basel (2010)
Dibrell, P., Campbell, J. T.: Hyponormal powers of composition operators. Proc. Amer. Math. Soc. 102(4), 914–918 (1988)
Fuglede, B.: The multidimensional moment problem. Expo. Math. 1, 47–65 (1983)
Halmos, P.R.: Normal dilations and extensions of operators. Summa Brasil. Math. 2, 125–134 (1950)
Halmos, P.R.: A Hilbert Space Problem Book. Springer-Verlag, New York Inc. (1982)
Hazarika, M., Kalita, B.: Back-step extension of weighted shifts. Bull. Calcutta Math. Soc 106(3), 169–188 (2014)
Hoover, T., Jung, I.B., Lambert, A.: Moment sequences and backward extensions of subnormal weighted shifts. J. Austral. Math. Soc. 73, 27–36 (2002)
Ito, T., Wong, T.K.: Subnormality and quasinormality of Toeplitz operators. Proc. Amer. Math. Soc. 34, 157–164 (1972)
Jabński, Z., Jung, I. B., Stochel, J.: Weighted shifts on directed trees. Mem. Amer. Math. Soc. 216(1017), viii+106 (2012)
Jabłoński, Z.J., Jung, I.B., Stochel, J.: Normal extensions escape from the class of weighted shifts on directed trees. Complex Anal. Oper. Theory 7, 409–419 (2013)
Jung, I.B., Li, C.: Backward extensions of hyponormal weighted shifts. Math. Japon. 52(2), 267–278 (2000)
Jung, I.B., Li, C.: A formula for \(k\)-hyponormality of backstep extensions of subnormal weighted shifts. Proc. Amer. Math. Soc. 129, 2343–2351 (2001)
Lambert, A.: Subnormality and weighted shifts. J. London Math. Soc. 14, 476–480 (1976)
McCullough, S., Paulsen, V.: A note on joint hyponormality. Proc. Amer. Math. Soc. 107, 187–195 (1989)
Shields, A. L.: Weighted shift operators and analytic function theory, Topics in operator theory, Math. Surveys, No. 13, Amer. Math. Soc., Providence, R.I., pp. 49–128 (1974)
Shohat, J. A., Tamarkin, J. D.: The problem of moments, Math. Surveys 1, Amer. Math. Soc., Providence, R.I., (1943)
Simon, B.: The classical moment problem as a self-adjoint finite difference operator. Adv. Math. 137, 82–203 (1998)
Stampfli, J.G.: Which weighted shifts are subnormal? Pacific J. Math. 17(2), 367–379 (1966)
Szafraniec, F.H.: Boundedness of the shift operator related to positive definite forms: an application to moment problems. Ark. Mat. 19, 251–259 (1981)
Acknowledgements
I would like to thank my supervisor, prof. Jan Stochel, for all his guidance while working on this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Pikul, P. Backward Extensions of Weighted Shifts on Directed Trees. Integr. Equ. Oper. Theory 94, 26 (2022). https://doi.org/10.1007/s00020-022-02704-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00020-022-02704-5
Keywords
- Directed forest
- Directed tree
- Weighted shift
- Backward extension
- Subnormal operator
- Power hyponormal operator



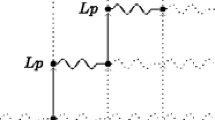

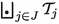 , while “
, while “