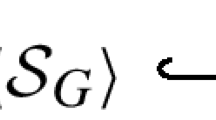Pontryagin duality for metrizable groups

Abstract.

This paper deals with the validity of the Pontryagin duality theorem in the class of metrizable topological groups. We prove that completeness is a necessary condition for the Pontryagin reflexivity of those groups. We also prove that in order for a metrizable separable topological group to be Pontryagin reflexive it is sufficient that the canonical embedding into its bidual group be an algebraic isomorphism.¶ On the other hand, we consider the notion of reflexivity introduced by E. Binz and H. Butzmann. In [5] it was proved that, for topological abelian groups, the Pontryagin reflexivity and the Binz-Butzmann reflexivity, in general, are independent notions. Here we prove that these notions coincide in the class of metrizable topological abelian groups.